Linear Model Predictive Control and Back-Propagation Controller for Single-Point Magnetic Levitation with Different Gap Levitation and Back-Propagation Offline Iteration
Abstract
1. Introduction
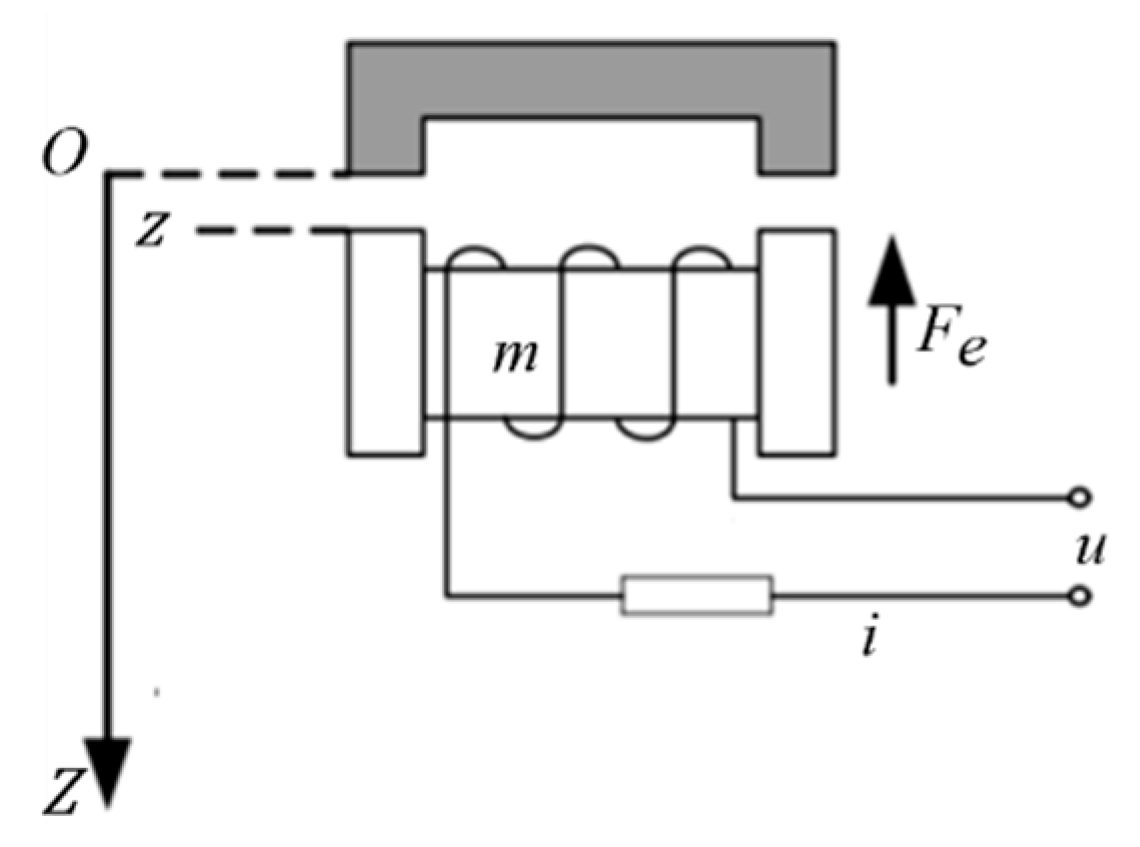
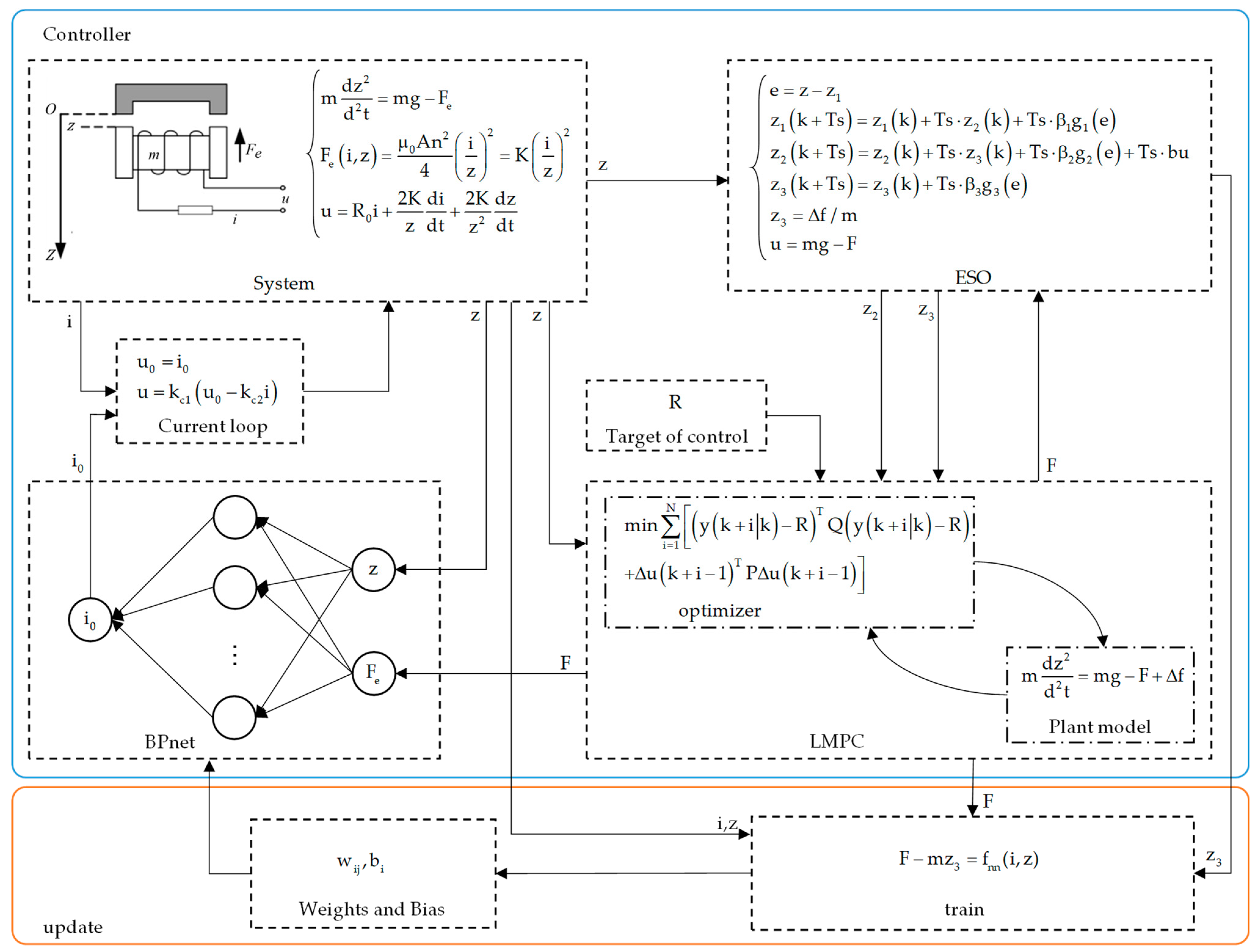
2. Modeling and Controller Design
2.1. System Modeling
2.2. Controller Design
2.2.1. LMPC
- The measurable interference is invariant after moment k, i.e.,
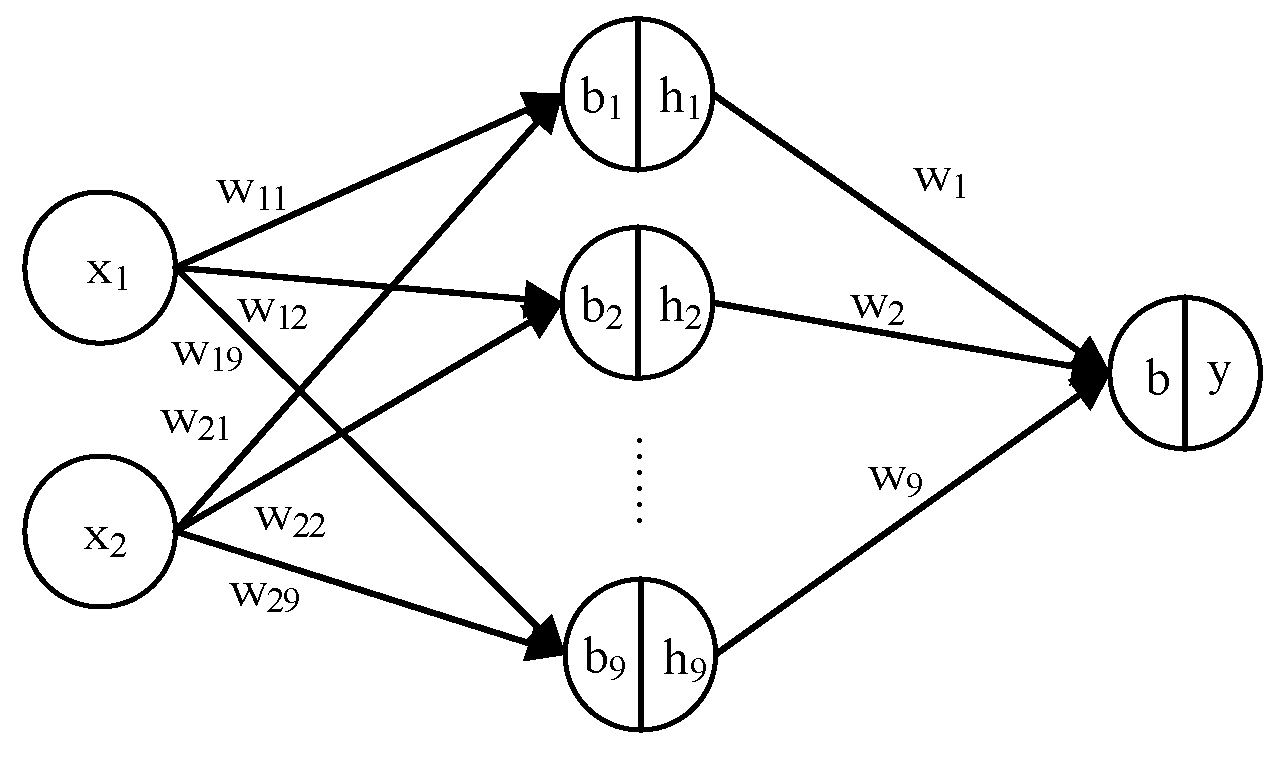
2.2.2. BP Neural Network Prediction Model
2.2.3. ESO
2.3. Network Offline Update
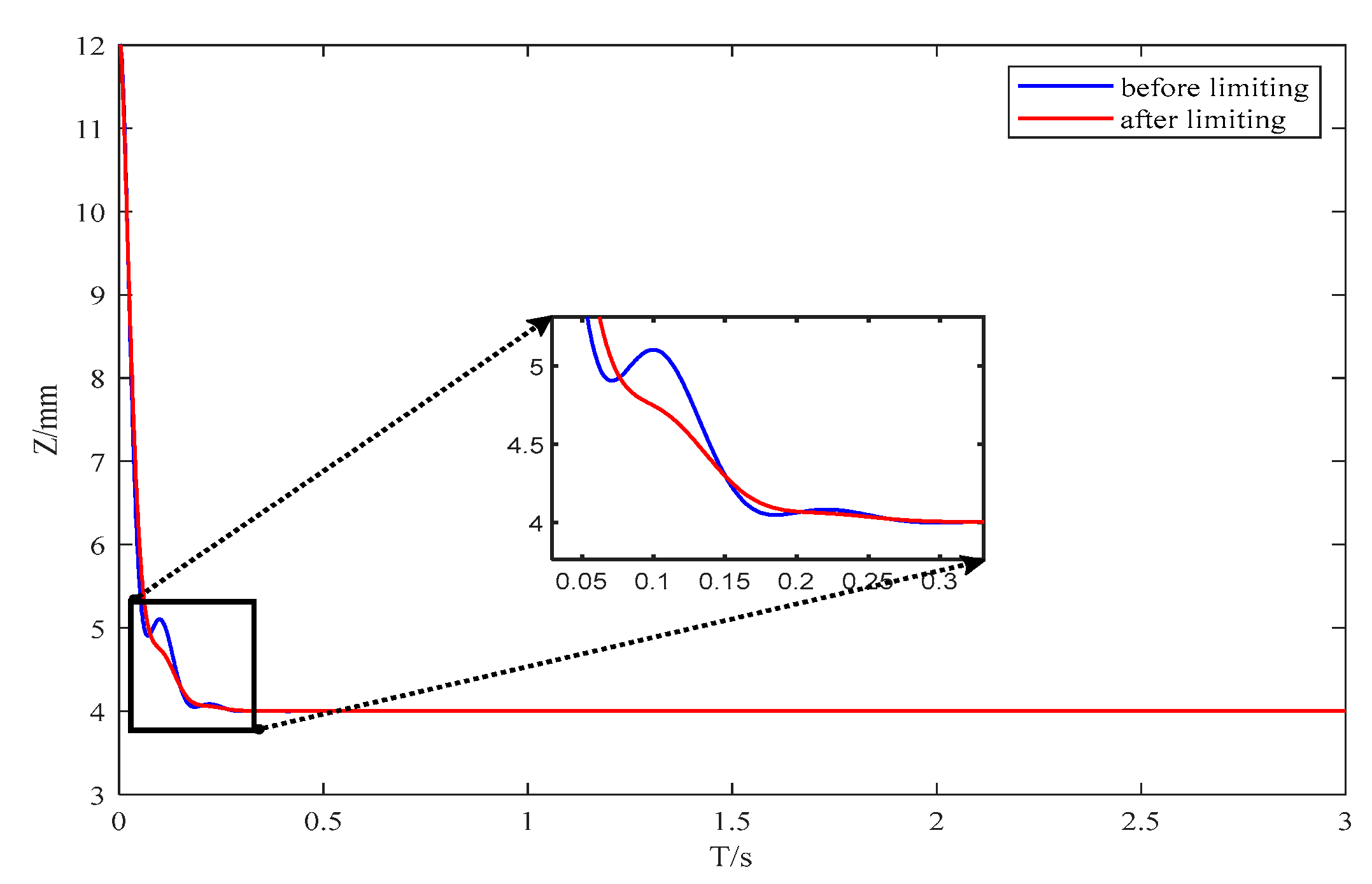
3. Simulation Results and Analysis
3.1. Step Response
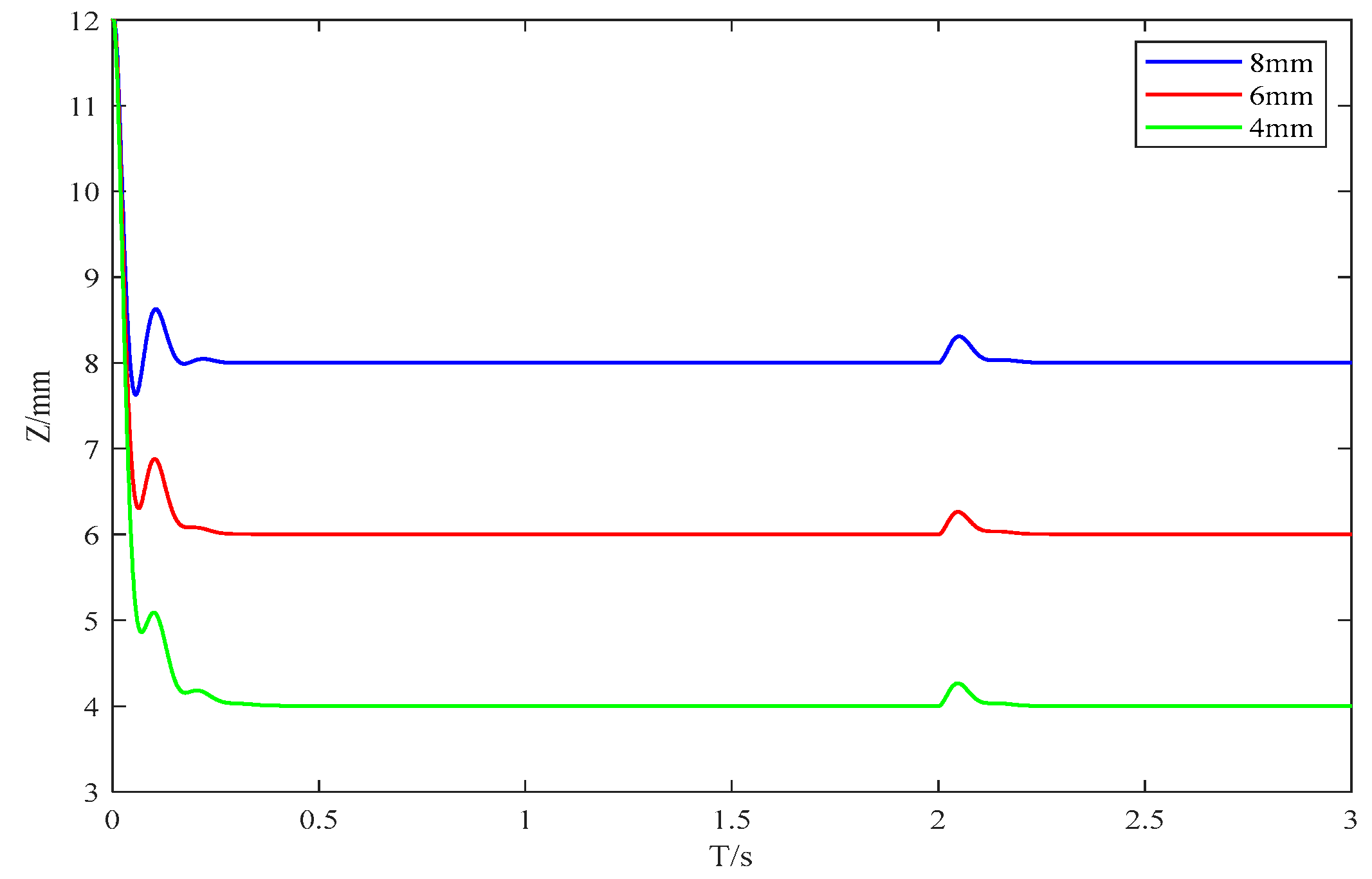
3.2. Suspension at Different Gaps
3.3. Comparison of Controller Performance after Updating the Network
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, F.; Zhao, C.; Bai, Z. A modified electromagnetic force calculation method has high accuracy and applicability for EMS maglev vehicle dynamics simulation. ISA Trans. 2023, 137, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xu, J.; Wu, H. Deep Learning Based Semi-Supervised Control for Vertical Security of Maglev Vehicle With Guaranteed Bounded Airgap. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4431–4442. [Google Scholar] [CrossRef]
- Zhou, T.; Yang, Z.; Zhu, C. Internal model control-PID control of an active magnetic bearing high-speed motor rotor system. Trans. China Electrotech. Soc. 2020, 35, 3414–3425. [Google Scholar]
- Takarli, R.; Amini, A.; Khajueezadeh, M.A. Comprehensive Review on Flywheel Energy Storage Systems: Survey on Electrical Machines, Power Electronics Converters, and Control Systems. IEEE Access 2024, 11, 81224–88125. [Google Scholar] [CrossRef]
- Daiki, K.; Hiroki, S.; Asei, T. Magnetic Suspension and Balance System for High-Subsonic Wind Tunnel. AIAA J. 2019, 57, 2489–2495. [Google Scholar]
- Daiki, K.; Hiroki, S.; Asei, T. Dynamic Wind-Tunnel Testing of a Sixty-Degree Delta-Wing Model Without Support Interference. AIAA J. 2021, 59, 1099–1108. [Google Scholar]
- Liu, L.; Zuo, J. Parameter self-adjusting control method of fuzzy PID for magnetic levitation ball system. J. Control Eng. 2021, 28, 354–359. [Google Scholar]
- Marcin, M.; Arkadiusz, L. Speed observer structure of induction machine based on sliding super-twisting and backstepping techniques. IEEE Trans. Ind. Inform. 2021, 17, 1122–1131. [Google Scholar]
- Zhang, T.; Xu, Z.; Li, J. A third-order super-twisting extended state observer for dynamic performance enhancement of sensorless IPMSM drives. IEEE Trans. Ind. Electron. 2021, 67, 5948–5958. [Google Scholar] [CrossRef]
- He, L. Auto-Disturbance-Rejection Control of Maglev System; National University of Defense Technology: Changsha, China, 2006. [Google Scholar]
- Wei, Q.; Wu, Z.; Zhou, Y. Active Disturbance-Rejection Controller (ADRC)-Based Torque Control for a Pneumatic Rotary Actuator with Positional Interference. Actuators 2024, 13, 66. [Google Scholar] [CrossRef]
- Chen, C.; Sun, Y. Research on dynamics modeling and control of the nonlinear maglev system. Mach. Des. Manuf. 2019, 11, 16–19. [Google Scholar]
- Sun, Y.; Qiang, H.; Wan, L. A Fuzzy-Logic-System-Based Cooperative Control for the Multielectromagnets Suspension System of Maglev Trains With Experimental Verification. IEEE Trans. Fuzzy Syst. 2023, 31, 3411–3422. [Google Scholar] [CrossRef]
- Tao, L.; Wang, P.; Ma, X. Variable Form LADRC-Based Robustness Improvement for Electrical Load Interface in Microgrid: A Disturbance Response Perspective. IEEE Trans. Ind. Inform. 2024, 20, 432–441. [Google Scholar] [CrossRef]
- Ren, Y.M.; Alhajeri, M.S.; Luo, J.; Chen, S.; Abdullah, F.; Wu, Z.; Christofides, P.D. A tutorial review of neural network modeling approaches for model predictive control. Comput. Chem. Eng. 2022, 165, 107956. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, M.; Chen, Y. Hybrid Grey Wolf Optimization Nonlinear Model Predictive Control for Aircraft Engines Based on an Elastic BP Neural Network. Appl. Sci. 2019, 9, 1254. [Google Scholar] [CrossRef]
- Grady, W.; Nolan, W.; Brian, G. Information theoretic MPC for model-based reinforcement learning. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 1714–1721. [Google Scholar]
- Nagabandi, A.; Kahn, G.; Fearing, R.S. Neural Network Dynamics for Model-Based Deep Reinforcement Learning with Model-Free Fine-Tuning. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 7559–7566. [Google Scholar]
- Iman, A.; Babak, B.; Thomas, W. Sampling-Based Nonlinear MPC of Neural Network Dynamics with Application to Autonomous Vehicle Motion Planning. In Proceedings of the 2022 American Control Conference, Atlanta, GA, USA, 8–10 June 2022; pp. 2084–2090. [Google Scholar]
- Sun, Y.; Xu, J.; Chen, C. Reinforcement learning-based optimal tracking control for levitation system of maglev vehicle with input time delay. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Giulio, B.; Marcello, F.; Riccardo, S. A robust MPC algorithm for offset-Free tracking of constant reference signals. IEEE Trans. Autom. Control 2013, 58, 2394–2400. [Google Scholar]




| Parameters | Value |
|---|---|
| n | 910 |
| R | 3.1 Ω |
| × 10−7 H/m | |
| m | 14 kg |
| A | 3 × 10−3 m2 |
| Controllers | Tr/s | Ts/s | σ |
|---|---|---|---|
| PID | 0.20 | 0.29 | 1.63% |
| LMPC-BP | 0.14 | 0.16 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Dou, F. Linear Model Predictive Control and Back-Propagation Controller for Single-Point Magnetic Levitation with Different Gap Levitation and Back-Propagation Offline Iteration. Actuators 2024, 13, 331. https://doi.org/10.3390/act13090331
Liu Z, Dou F. Linear Model Predictive Control and Back-Propagation Controller for Single-Point Magnetic Levitation with Different Gap Levitation and Back-Propagation Offline Iteration. Actuators. 2024; 13(9):331. https://doi.org/10.3390/act13090331
Chicago/Turabian StyleLiu, Ziyu, and Fengshan Dou. 2024. "Linear Model Predictive Control and Back-Propagation Controller for Single-Point Magnetic Levitation with Different Gap Levitation and Back-Propagation Offline Iteration" Actuators 13, no. 9: 331. https://doi.org/10.3390/act13090331
APA StyleLiu, Z., & Dou, F. (2024). Linear Model Predictive Control and Back-Propagation Controller for Single-Point Magnetic Levitation with Different Gap Levitation and Back-Propagation Offline Iteration. Actuators, 13(9), 331. https://doi.org/10.3390/act13090331






