Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances
Abstract
1. Introduction
- In contrast to existing control strategies [17,18,19,20,23] that overlook transient performance, this paper introduces a non-singular fast terminal sliding mode controller (NFTSMC) for robotic systems that incorporates the prescribed performance principle. An enhanced TSM-type reaching law is proposed to confine the trajectory tracking error within a predefined boundary in a finite-time convergence rate.
- To mitigate the demands on prior knowledge of system uncertainties and disturbances in traditional HSMC controllers, an adaptive sliding mode disturbance observer (ASMDO) is introduced. It is complemented by an adaptive update law designed to estimate the upper bound of the derivative of lumped uncertainties. The ASMDO’s estimation error is proven to achieve practical finite-time stability.
- To the best of our knowledge, this paper presents the preliminary validation of a finite-time PPC sliding-mode controller integrated with a dual-motor anti-backlash strategy on a real serial-type dual-motor joints-driven robotic manipulator. This validation underscores the practical applicability and robustness of the proposed control scheme.
2. System Description and Preliminaries
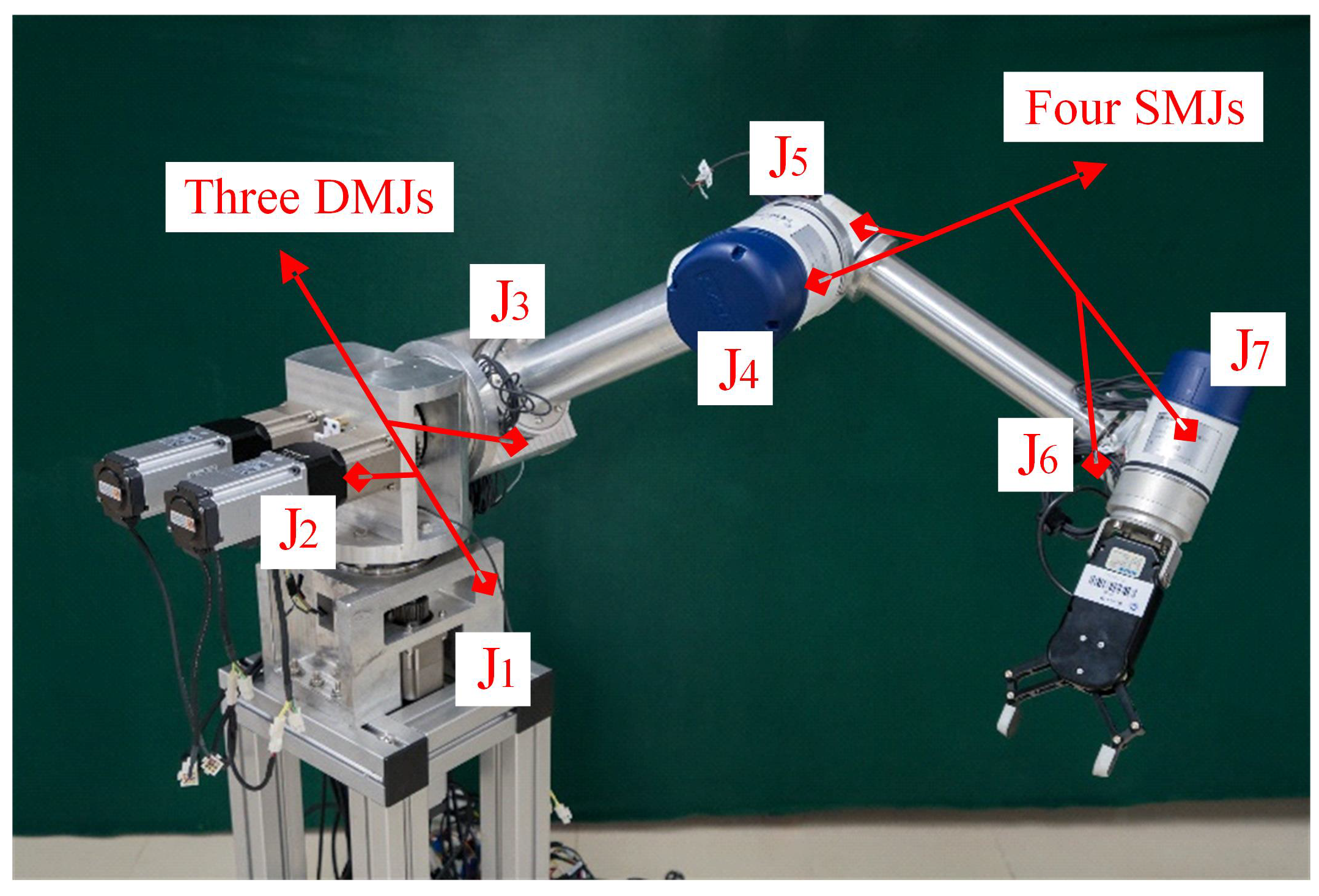
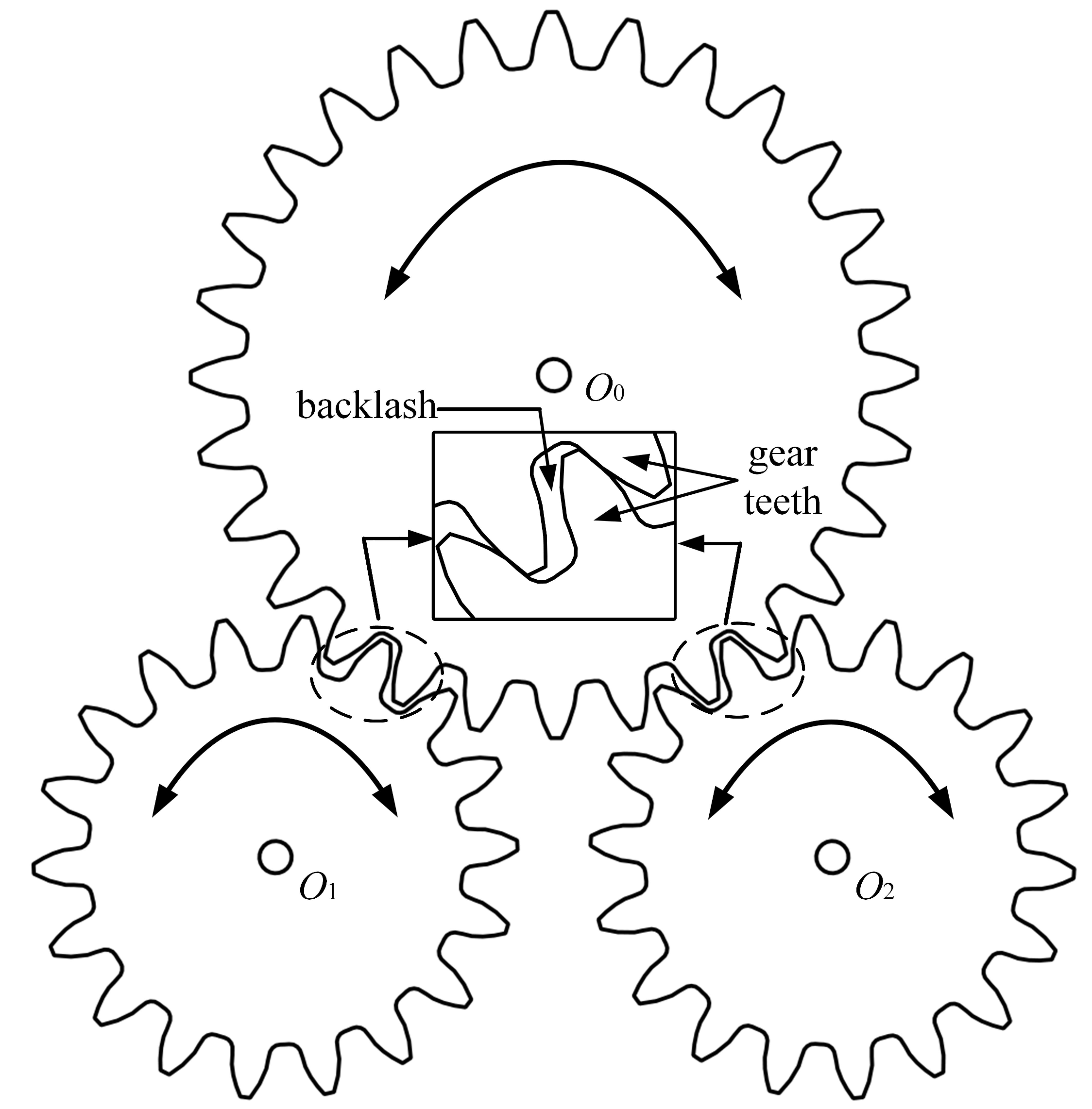
2.1. Dual-Motor Joints-Driven Robotic Manipulator and Anti-Backlash Strategy
2.2. System Model and Preliminaries
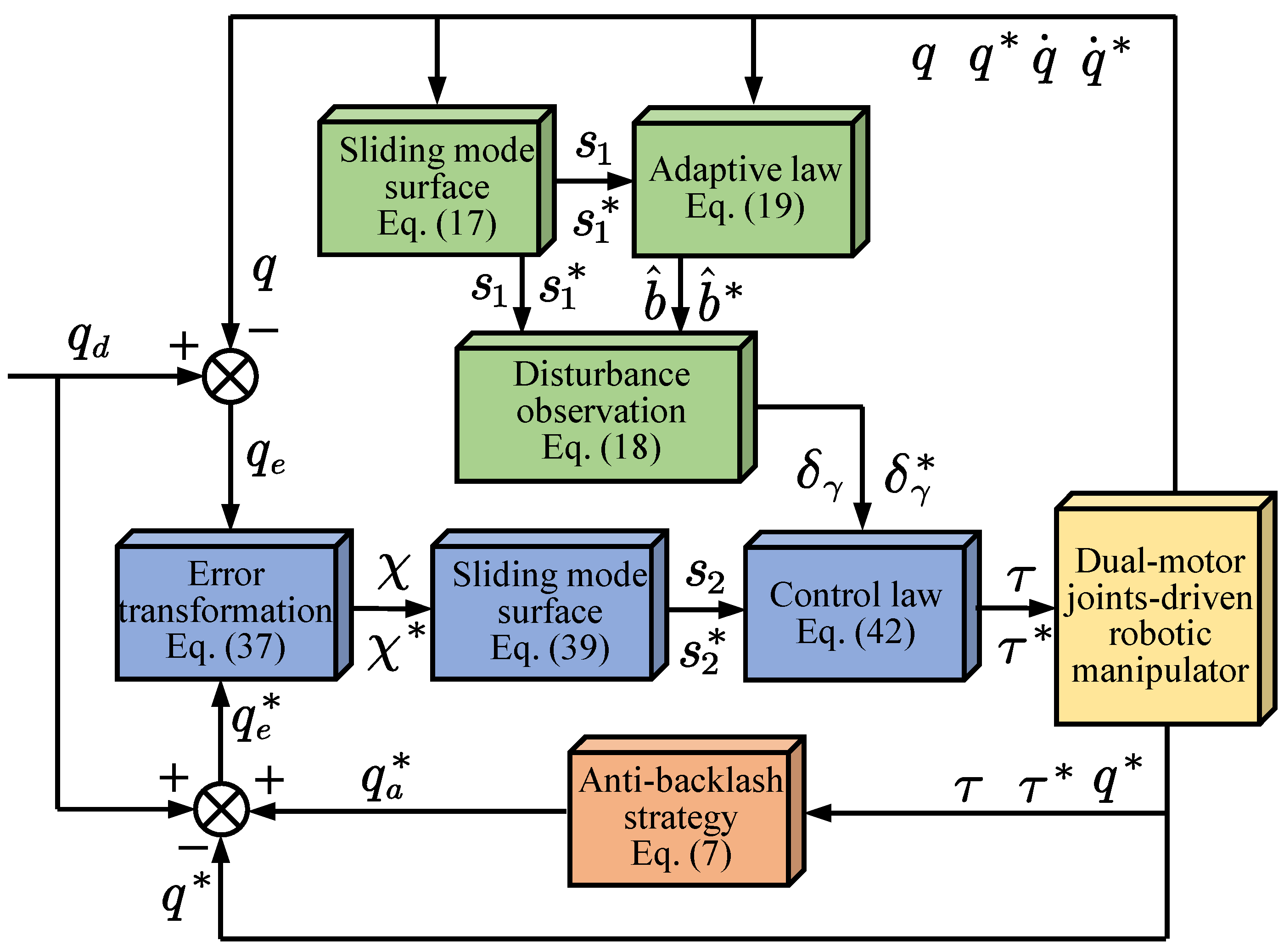
3. Observer-Based Finite-Time Tracking Control for Backlash-Free Robotic Systems
3.1. Design of Adaptive Sliding Mode Observer
3.2. Design of Prescribed Performance Sliding Mode Controller
| Algorithm 1 The algorithm of the proposed controller |
1: Initialization: Set dual-motor anti-backlash control parameters , and adaptive sliding mode observer parameters , and prescribed performance function parameters , and sliding mode control parameters ; 2: Run procedure: 2.1: Compute the desired position of auxiliary motor from Equation (8); 2.2: Compute the sliding mode surface from Equation (17); 2.3: Update the adaptive law given in Equation (19); 2.4: Compute the lumped uncertainties via Equation (18); 2.5: Calculate the transformed error from Equation (37); 2.6: Calculate the sliding mode surface via Equation (39); 2.7: Calculate the control law by Equation (42) at , ; 2.8: Continuation: ; 3: End procedure |
4. Simulation and Experimental Results
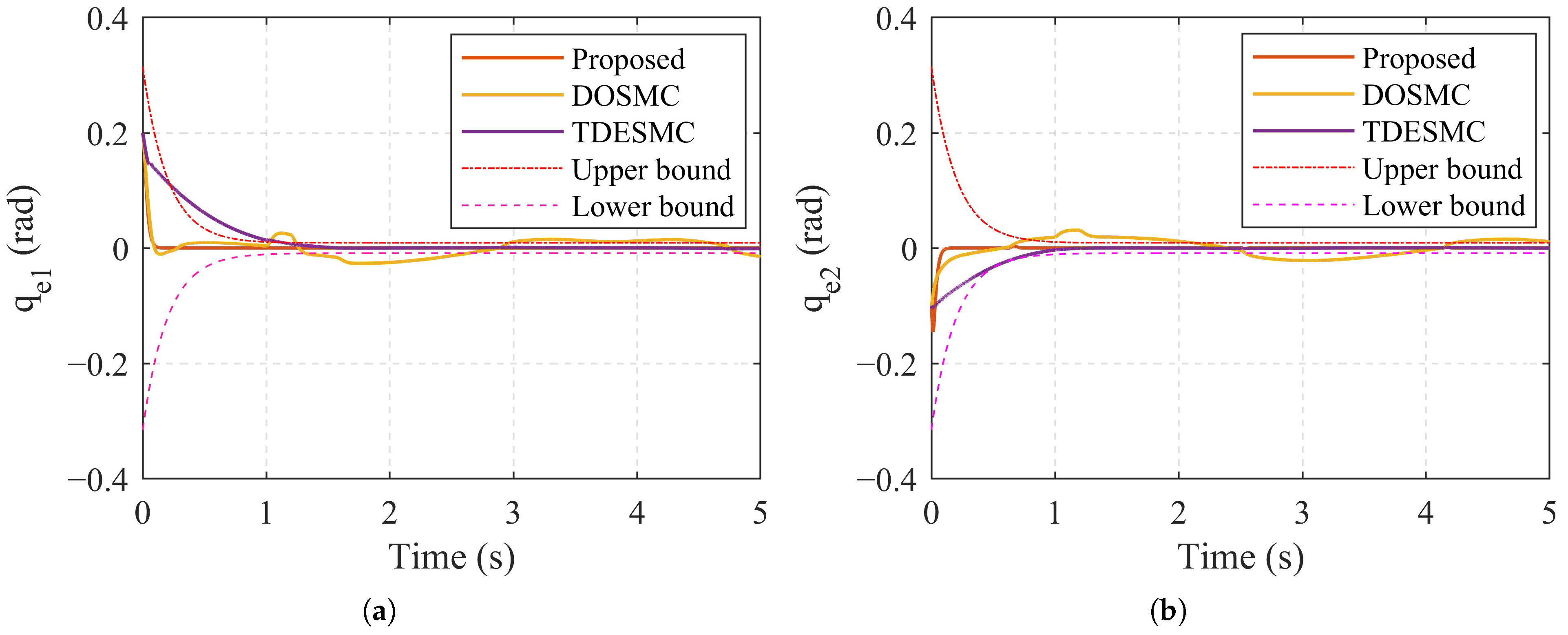
4.1. Numerical Simulation
- For the sliding mode surface defined by Equation (39), the gain and are selected to facilitate the convergence of the sliding mode. In practical applications, an appropriately chosen can enhance the convergence rate, especially when the sliding mode variable is significantly displaced from the equilibrium point. Subsequently, the designer should primarily focus on adjusting the value of to optimize the system performance.
- Based on the prescribed performance function Equation (36), the initial tracking error condition should be fulfilled by suitable and a.
- The larger gain could improve the convergence rate of ASMDO. However, larger gain will cause large overshoot in the transient stage.
- The parameter play an important roles in convergence time and accuracy for ASMDO.
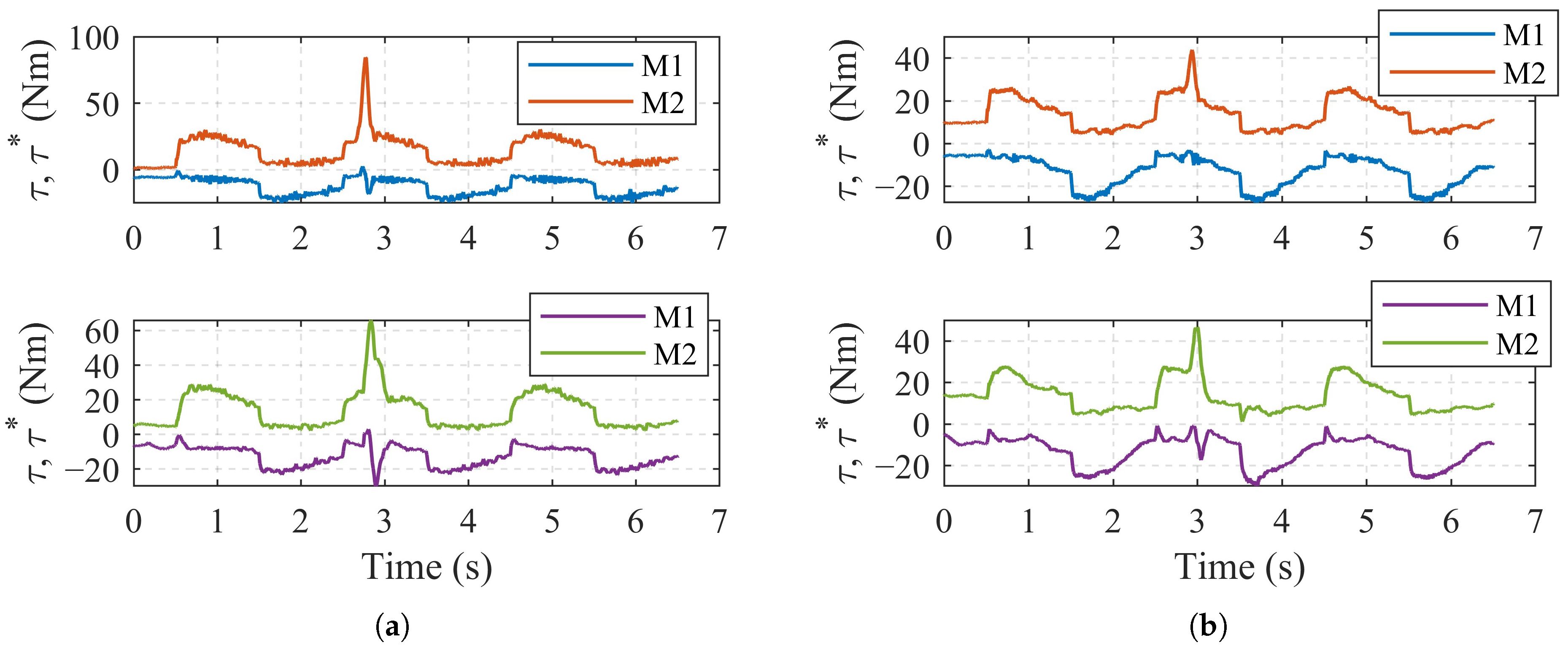
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, B.; Zhao, X.; Ding, H. Mobile-Robotic Machining for Large Complex Components: A Review Study. Sci. China Technol. Sci. 2019, 62, 1388–1400. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.; Yang, Z.; Jiang, Y.; Xu, J. A State-of-the-Art Review on Robotic Milling of Complex Parts with High Efficiency and Precision. Robot. Comput.-Integr. Manuf. 2023, 79, 102436. [Google Scholar] [CrossRef]
- Li, D.; Zhao, H.; Ge, D.; Li, X.; Ding, H. A Novel Robotic Multiple Peg-in-Hole Assembly Pipeline: Modeling, Strategy, and Control. IEEE/ASME Trans. Mechatron. 2023, 29, 2602–2613. [Google Scholar] [CrossRef]
- Pham, A.D.; Ahn, H.J. Rigid Precision Reducers for Machining Industrial Robots. Int. J. Precis. Eng. Manuf. 2021, 22, 1469–1486. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Hu, K.; Xu, D. Analysis and Suppression of Limit Cycle Oscillation for Transmission System with Backlash Nonlinearity. IEEE Trans. Ind. Electron. 2017, 64, 9261–9270. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Hou, Y.; Li, H. Fixed-Time Sliding Mode Control for Uncertain Robot Manipulators. IEEE Access 2019, 7, 149750–149763. [Google Scholar] [CrossRef]
- Weigand, J.; Gafur, N.; Ruskowski, M. Flatness Based Control of an Industrial Robot Joint Using Secondary Encoders. Robot. Comput.-Integr. Manuf. 2021, 68, 102039. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, D.; Wu, Z.G.; Li, H. Neural Network-Based Adaptive Second-Order Sliding Mode Control for Uncertain Manipulator Systems with Input Saturation. ISA Trans. 2023, 136, 126–138. [Google Scholar] [CrossRef]
- Wang, H.; Fang, L.; Hu, M.; Song, T.; Xu, J. Adaptive Funnel Fast Nonsingular Terminal Sliding Mode Control for Robotic Manipulators with Dynamic Uncertainties. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 3678–3693. [Google Scholar] [CrossRef]
- Xu, J.; Wang, H.; Zhao, Q.; Gao, Y.; Wan, Y.; Fang, L. A Robotic Manipulator Using Dual-Motor Joints: Prototype Design and Anti-Backlash Control. IEEE Robot. Autom. Lett. 2023, 8, 8327–8334. [Google Scholar] [CrossRef]
- Formentini, A.; Oliveri, A.; Marchesoni, M.; Storace, M. A Switched Predictive Controller for an Electrical Powertrain System with Backlash. IEEE Trans. Power Electron. 2017, 32, 4036–4047. [Google Scholar] [CrossRef]
- Yu, Z.; Tang, T. Limited Amplitude-Disturbance Observer Control for Backlash-Containing Electromechanical System. IEEE Trans. Ind. Electron. 2024, 71, 5960–5971. [Google Scholar] [CrossRef]
- Verl, A.; Engelberth, T. Adaptive Preloading for Rack-and-Pinion Drive Systems. CIRP Ann. 2018, 67, 369–372. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Yang, S.; Chen, W. Dual-Motor Drive Image Stabilization System for Elevation-Azimuth Photoelectric Survey Telescope under Long Exposure. IEEE/ASME Trans. Mechatron. 2024, 29, 3065–3073. [Google Scholar] [CrossRef]
- Robertz, S.G.; Halt, L.; Kelkar, S.; Nilsson, K.; Robertsson, A.; Schär, D.; Schiffer, J. Precise Robot Motions Using Dual Motor Control. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 5613–5620. [Google Scholar] [CrossRef]
- Meng, D.; Xu, H.; Xu, H.; Sun, H.; Liang, B. Trajectory Tracking Control for a Cable-Driven Space Manipulator Using Time-Delay Estimation and Nonsingular Terminal Sliding Mode. Control. Eng. Pract. 2023, 139, 105649. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Y.; Zhu, M.; Wu, Q. Adaptive Fuzzy Integral Sliding Mode Cooperative Control Based on Time-Delay Estimation for Free-Floating Close-Chain Manipulators. Sensors 2024, 24, 3718. [Google Scholar] [CrossRef]
- Zeng, H.; Lyu, Y.; Qi, J.; Zou, S.; Qin, T.; Qin, W. Adaptive Finite-Time Model Estimation and Control for Manipulator Visual Servoing Using Sliding Mode Control and Neural Networks. Adv. Robot. 2023, 37, 576–590. [Google Scholar] [CrossRef]
- Xi, R.D.; Ma, T.N.; Xiao, X.; Yang, Z.X. Design and Implementation of an Adaptive Neural Network Observer–Based Backstepping Sliding Mode Controller for Robot Manipulators. Trans. Inst. Meas. Control 2024, 46, 1093–1104. [Google Scholar] [CrossRef]
- Hong, M.; Gu, X.; Liu, L.; Guo, Y. Finite Time Extended State Observer Based Nonsingular Fast Terminal Sliding Mode Control of Flexible-Joint Manipulators with Unknown Disturbance. J. Frankl. Inst. 2023, 360, 18–37. [Google Scholar] [CrossRef]
- Algrnaodi, M.; Saad, M.; Saad, M.; Fareh, R.; Kali, Y. Extended State Observer–Based Improved Non-Singular Fast Terminal Sliding Mode for Mobile Manipulators. Trans. Inst. Meas. Control 2024, 46, 785–798. [Google Scholar] [CrossRef]
- Yan, Z.; Lai, X.; Meng, Q.; She, J.; Wu, M. Time-Varying Disturbance-Observer-Based Tracking Control of Uncertain Flexible-Joint Manipulator. Control. Eng. Pract. 2023, 139, 105624. [Google Scholar] [CrossRef]
- Abbasi, S.J.; Lee, S. Enhanced Trajectory Tracking via Disturbance-Observer-Based Modified Sliding Mode Control. Appl. Sci. 2023, 13, 8027. [Google Scholar] [CrossRef]
- Guo, K.; Shi, P.; Wang, P.; He, C.; Zhang, H. Non-Singular Terminal Sliding Mode Controller with Nonlinear Disturbance Observer for Robotic Manipulator. Electronics 2023, 12, 849. [Google Scholar] [CrossRef]
- Naderian, S.; Farrokhi, M. Adaptive Back-Stepping Data-Driven Terminal Sliding-Mode Controller for Nonlinear MIMO Systems with Disturbance Observer. IEEE Access 2023, 11, 78059–78073. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Hu, X.; Liu, Q.; Yao, J. Barrier Lyapunov Function-Based Adaptive Output Feedback Prescribed Performance Controller for Hydraulic Systems with Uncertainties Compensation. IEEE Trans. Ind. Electron. 2023, 70, 12500–12510. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Ahn, C.K.; Yang, Y. Prescribed-Time Extended State Observer and Prescribed Performance Control of Quadrotor UAVs against Actuator Faults. Aerosp. Sci. Technol. 2023, 138, 108322. [Google Scholar] [CrossRef]
- Kong, L.; Reis, J.; He, W.; Silvestre, C. Experimental Validation of a Robust Prescribed Performance Nonlinear Controller for an Unmanned Aerial Vehicle with Unknown Mass. IEEE/ASME Trans. Mechatron. 2024, 29, 301–312. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Liu, Q. Output-Feedback Prescribed Performance Control for the Full-State Constrained Nonlinear Systems and Its Application to DC Motor System. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3898–3907. [Google Scholar] [CrossRef]
- Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed Performance Tracking Control of Time-Delay Nonlinear Systems with Output Constraints. IEEE/CAA J. Autom. Sin. 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
- Jia, X.; Yang, J.; Shi, T.; Wang, W.; Pan, Y.; Yu, H. Robust Precision Motion Control Based on Enhanced Unknown System Dynamics Estimator for High-DoF Robot Manipulators. IEEE/ASME Trans. Mechatron. 2024, 1–12. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Tian, Y. Adaptive High-Order Terminal Sliding Mode Control Based on Time Delay Estimation for the Robotic Manipulators with Backlash Hysteresis. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1128–1137. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control with Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude Stabilization of Rigid Spacecraft with Finite-Time Convergence. Int. J. Robust Nonlinear Control 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Li, G.; Wu, Y.; Xu, P. An Observer-Based Fixed-Time Position Tracking Strategy for DC Torque Motor Systems. Mech. Syst. Signal Process. 2020, 142, 106774. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M.; Ran, D. Faster Fixed-Time Control of Flexible Spacecraft Attitude Stabilization. IEEE Trans. Ind. Inform. 2020, 16, 1281–1290. [Google Scholar] [CrossRef]
- Wang, H.; Fang, L.; Song, T.; Xu, J.; Shen, H. Model-Free Adaptive Sliding Mode Control with Adjustable Funnel Boundary for Robot Manipulators with Uncertainties. Rev. Sci. Instrum. 2021, 92, 065101. [Google Scholar] [CrossRef]
- Huang, Y.; Ke, J.; Zhang, X.; Ota, J. Dynamic Parameter Identification of Serial Robots Using a Hybrid Approach. IEEE Trans. Robot. 2023, 39, 1607–1621. [Google Scholar] [CrossRef]

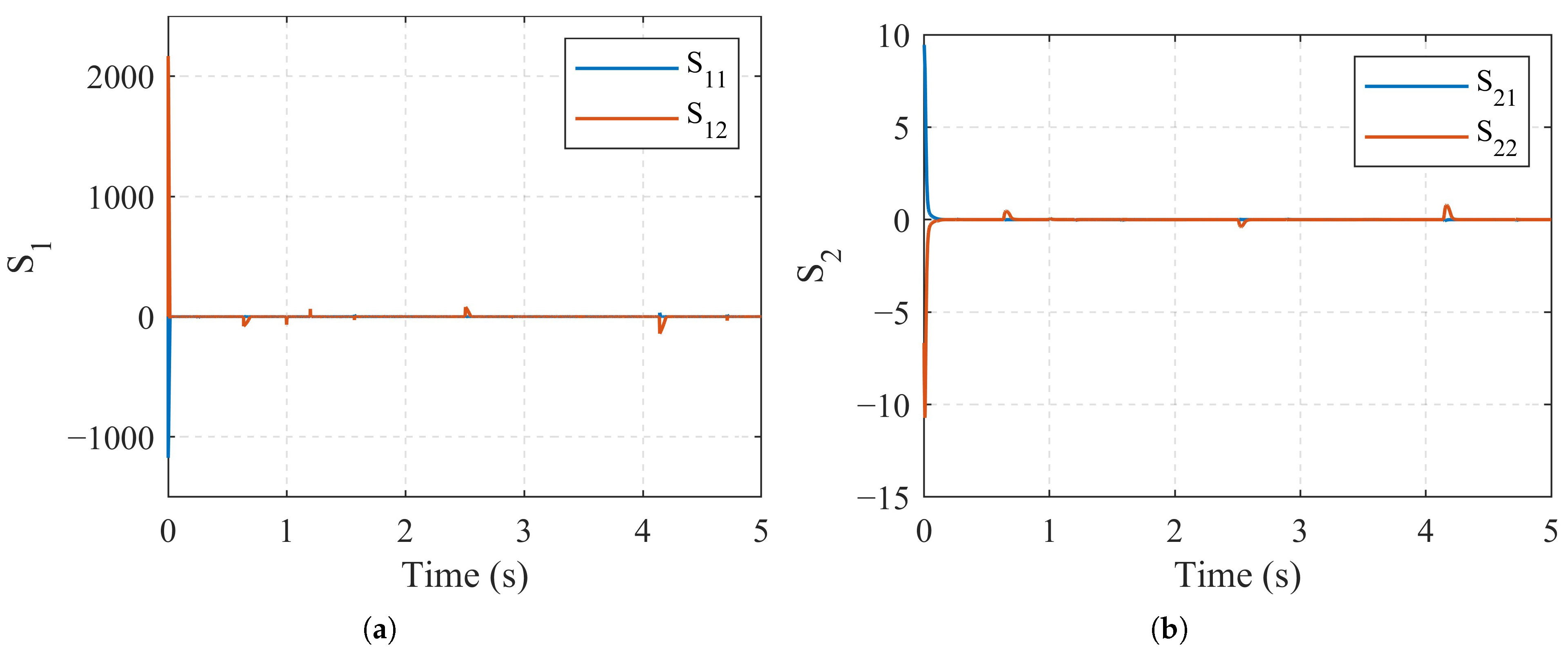
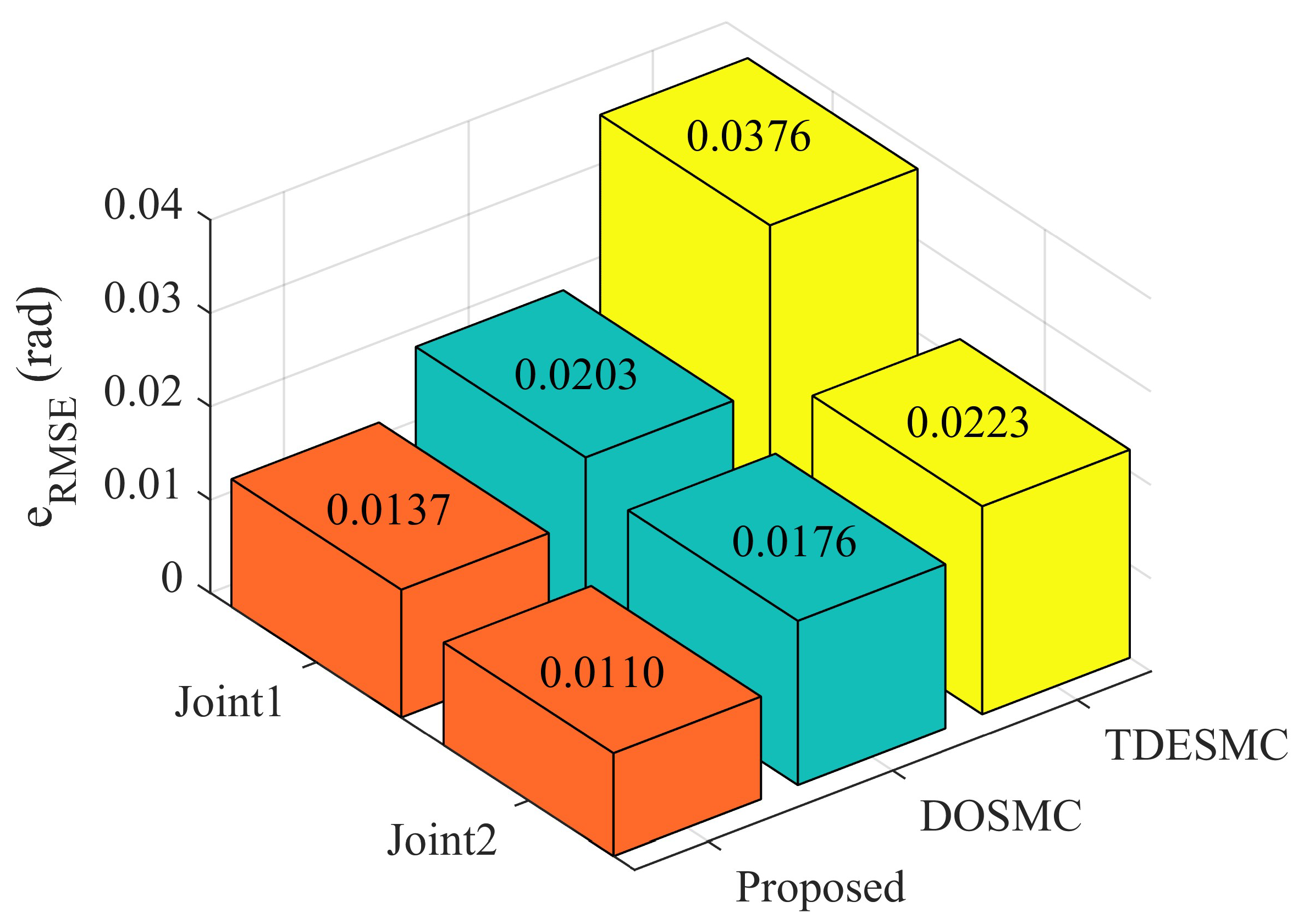
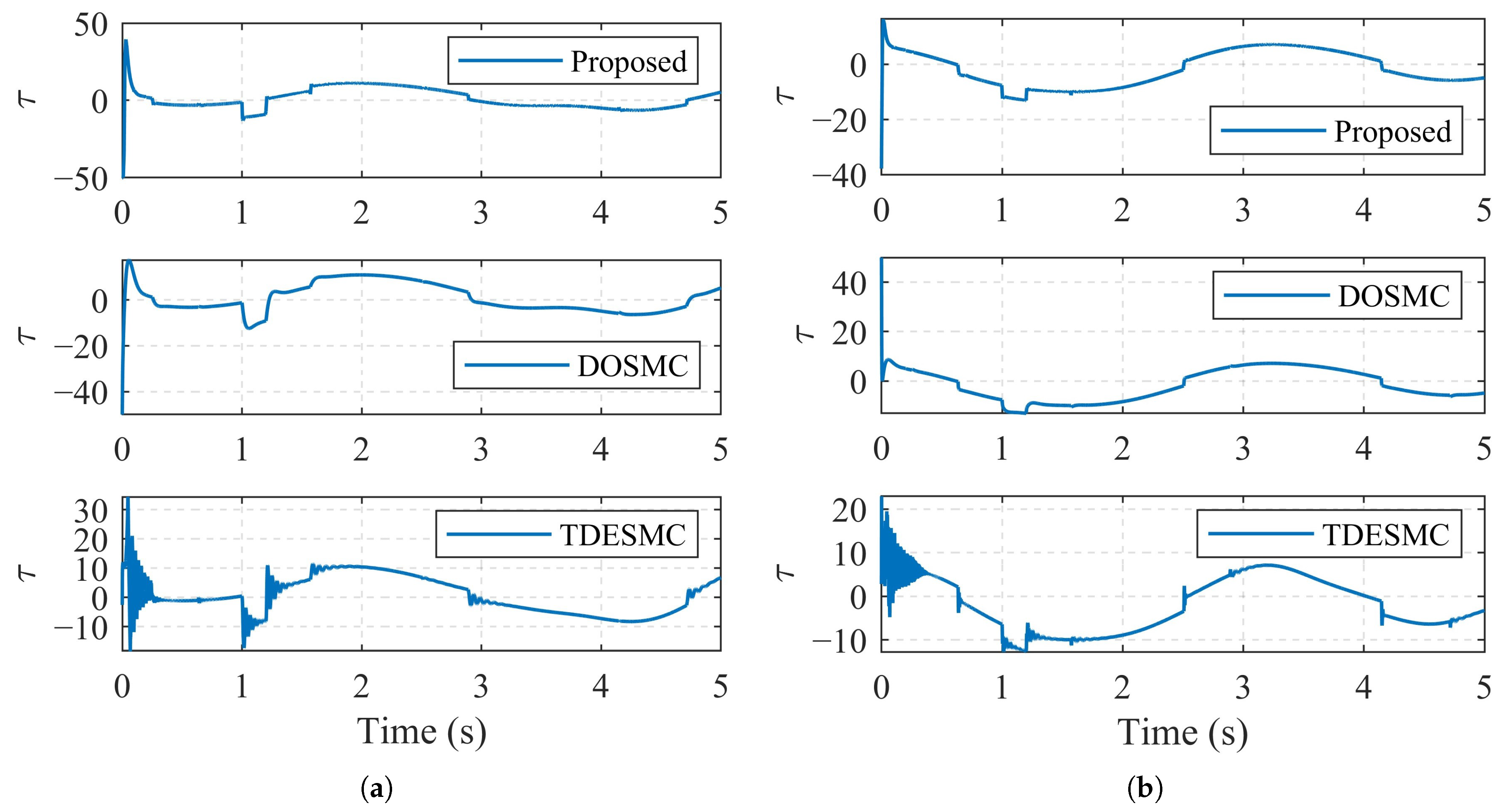



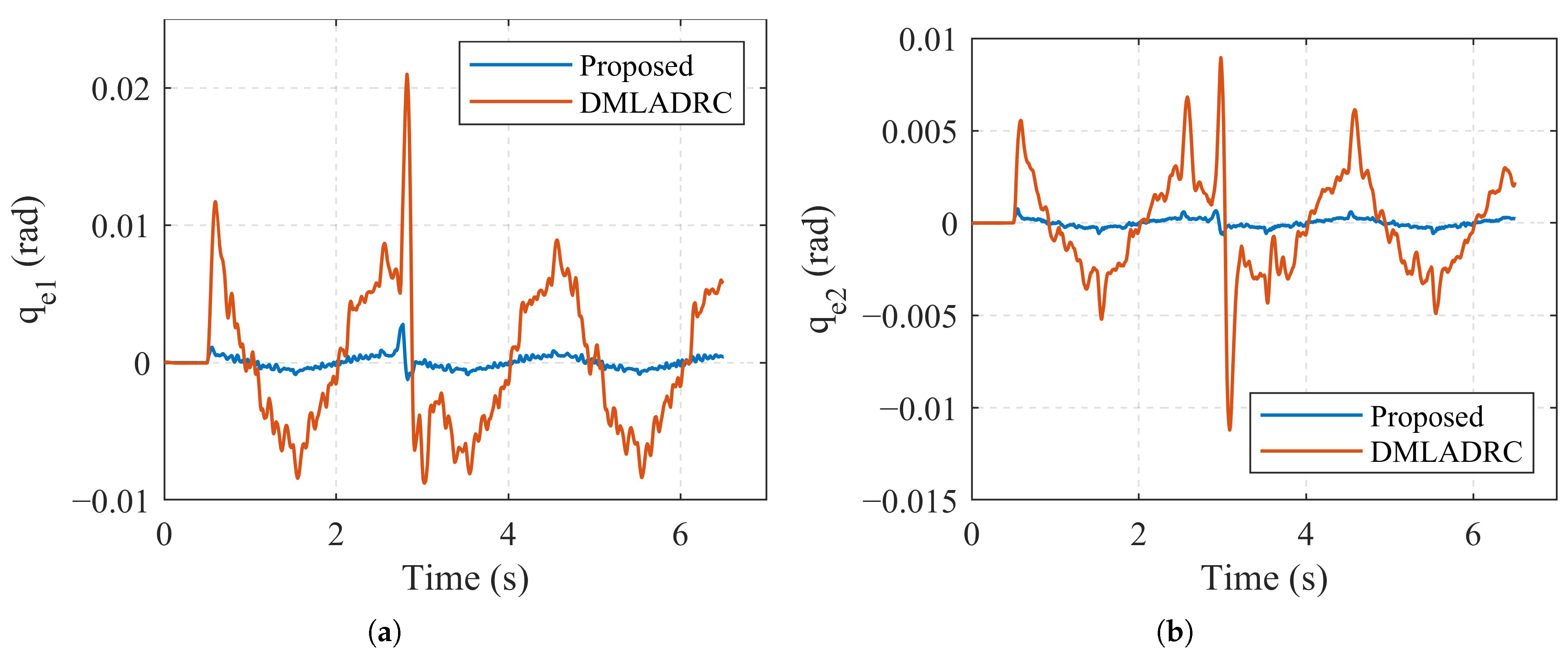
| Parameter | Description | Value |
|---|---|---|
| Length of first link | ||
| Length of second link | ||
| Mass of first link | ||
| Mass of second link | ||
| Inertia of first link | ||
| Inertia of second link | ||
| g | Gravitational constant | |
| Coulomb friction coefficient | ||
| viscous friction coefficient | ||
| Stribeck friction coefficient | ||
| Stribeck friction velocity |
| Section | Parameters |
|---|---|
| APDMAB | |
| PPF | |
| NFTSMC | |
| ASMDO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Fang, L.; Wang, H.; Zhao, Q.; Wan, Y.; Gao, Y. Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances. Actuators 2024, 13, 325. https://doi.org/10.3390/act13090325
Xu J, Fang L, Wang H, Zhao Q, Wan Y, Gao Y. Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances. Actuators. 2024; 13(9):325. https://doi.org/10.3390/act13090325
Chicago/Turabian StyleXu, Jiqian, Lijin Fang, Huaizhen Wang, Qiankun Zhao, Yingcai Wan, and Yue Gao. 2024. "Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances" Actuators 13, no. 9: 325. https://doi.org/10.3390/act13090325
APA StyleXu, J., Fang, L., Wang, H., Zhao, Q., Wan, Y., & Gao, Y. (2024). Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances. Actuators, 13(9), 325. https://doi.org/10.3390/act13090325






