Abstract
In robotic manipulation, achieving efficient and reliable grasping in cluttered environments remains a significant challenge. This study presents a novel approach that integrates pushing and grasping actions using deep reinforcement learning. The proposed model employs two fully convolutional neural networks—Push-Net and Grasp-Net—that predict pixel-wise Q-values for potential pushing and grasping actions from heightmap images of the scene. The training process utilizes deep Q-learning with a reward structure that incentivizes both successful pushes and grasps, encouraging the robot to create favorable conditions for grasping through strategic pushing actions. Simulation results demonstrate that the proposed model significantly outperforms traditional grasp-only policies, achieving an 87% grasp success rate in cluttered environments, compared to 60% for grasp-only approaches. The model shows robust performance in various challenging scenarios, including well-ordered configurations and novel objects, with completion rates of up to 100% and grasp success rates as high as 95.8%. These findings highlight the model’s ability to generalize to unseen objects and configurations, making it a practical solution for real-world robotic manipulation tasks.
1. Introduction
These Robots are designed to assist or replace humans in performing tedious and hazardous tasks, especially those beyond human capabilities due to physical constraints or harsh conditions [1]. Robotic arms, as automated electromechanical devices, execute specific tasks with applications ranging from household chores to large-scale industrial operations.
The UR5 robot from Universal Robots, featuring six degrees of freedom, is widely used in research for its lightweight design, speed, programmability, flexibility, and safety. Each of its six revolute joints contributes to the transformational and rotational movements of its end effector [1].
Artificial intelligence (AI) plays a crucial role in robotics. AI involves creating intelligent agents that interact with their environment and take actions to maximize their success. Artificial neural networks (ANNs), inspired by biological neural networks, consist of numerous interconnected artificial neurons (units) that process inputs and produce outputs [2]. Deep learning, a subset of machine learning, excels in various domains, including computer vision, data processing, decision-making, and data manipulation [3].
Reinforcement learning (RL) is a type of machine learning where agents learn optimal behaviors through trial-and-error interactions with their environment, aiming to maximize cumulative rewards [4]. Deep reinforcement learning (DRL) combines deep learning and RL, enabling intelligent agents to learn complex features and optimize performance over time through experiential learning [5].
This paper is organized as follows. Section 1 briefly introduces the work with respect to AI. Section 2 presents a review of recently published related works regarding deep reinforcement learning-based grasping in cluttered scenes, whereas Section 3 presents the methods and materials which includes mathematical modeling of the UR5 robot and the design of a deep reinforcement learning algorithm. The results and discussion of the findings are presented in Section 4. Lastly, the conclusion, recommendations, and potential future works are stated in Section 5.
2. Related Works
The field of robotic manipulation has seen significant advancements, with various techniques being proposed to enhance the efficiency and effectiveness of robotic grasping and object handling in cluttered environments. This review summarizes the key contributions of several notable works in the domain, highlighting the approaches and performance metrics that have driven progress.
In “Learn to grasp unknown objects in robotic manipulation”, ref. [6] presents a method for grasping unknown objects using a deep reinforcement learning framework. Their approach focuses on learning from interactions within a cluttered environment, achieving a grasp success rate of 62%. The study emphasizes the importance of adaptability in handling novel objects, although it reports relatively lower success rates compared to more recent techniques. The methodology is based on only grasping policy, and as a result, it fails to perform well in a cluttered environment. Without a non-prehensile action (pushing), it is difficult to grasp an object in a dense scene.
Paper [7], titled “Robotic Grasping using Deep Reinforcement Learning”, explores the use of deep reinforcement learning to improve robotic grasping capabilities. The model, tested in sparse environments, achieves a grasp success rate of 87% and a completion rate of 100%. It tested the model in both a Baxter Gazebo simulated environment and with a real robot. Even though adopting a multi-view model increases grasping accuracy in comparison to a single-view model, the training experiment was performed only with three regularly shaped colored objects: a sphere, cylinder, and cube. This study highlights the efficacy of reinforcement learning in sparse settings, though it lacks detailed exploration in highly cluttered scenarios.
The study in [8], “‘Good Robot!’: Efficient Reinforcement Learning for Multi-Step Visual Tasks with Sim to Real Transfer”, proposes an efficient reinforcement learning model for multi-step visual tasks. The method, focusing on both pushing and grasping without specific push rewards, achieves a grasp success rate of 76% and a completion rate of 93.7%. This approach underlines the importance of sim-to-real transfer in enhancing the model’s applicability to real-world tasks. The proposed system failed to give a reward for pushing actions that lead to a lower grasp success. Without a push reward, the robot will not learn push policies.
In “Pick and Place Objects in a Cluttered Scene Using Deep Reinforcement Learning”, [9] addresses the challenge of object manipulation in cluttered environments. Their model, implemented on a GeForce GTX-1660Ti GPU [NVIDIA, Santa Clara, CA, USA], demonstrates a grasp success rate of 74.3% and a completion rate of 100%. This study’s contribution lies in efficiently handling pick-and-place tasks within cluttered settings. Even though the paper proposes a pick and place robot in a cluttered environment, it failed to provide a solution for better grasping of an object in the cluttered environment. The grasping process is not enhanced by the non-prehensile actions, which resulted in low grasping efficiency and grasping success rate of an object.
In [10], an earlier work on “Pushing and Grasping”, a method integrating both actions to improve grasp success in cluttered environments is presented. Using a NVIDIA Titan X GPU [NVIDIA, Santa Clara, CA, USA], the model achieves a grasp success rate of 65.4% and a completion rate of 100%. This foundational study emphasizes the synergy between pushing and grasping, laying the groundwork for subsequent research. The paper’s key weakness is that since the heightmap’s rotation is limited to only 16 directions, the agent repeatedly pushes an object out of the workspace. Here, the push reward is not based on the heightmap difference. A second limitation is that the system has trained and tested with only blocks; it would be interesting to train and test on a greater variety of shapes and objects and further examine the learned policies’ generalization capabilities.
The collaborative method proposed in [11], “A pushing-grasping collaborative method based on deep Q-network algorithm in dual viewpoints”, utilizes a deep Q-network to enhance the pushing and grasping strategy. This model, tested with a Nvidia GTX 1080Ti, achieves an 83.5% grasp success rate and a 100% completion rate. The dual viewpoint approach provides a comprehensive understanding of the environment, leading to improved manipulation performance.
The authors of [12] explore “Efficient push-grasping for multiple target objects in clutter environments” and achieve a grasp success rate of 75.3% with an action efficiency of 54.1%. Their approach focuses on optimizing push-grasping actions for multiple objects, demonstrating significant improvements in cluttered environments.
In “Efficient Stacking and Grasping in Unstructured Environments”, the study [13] proposes a model that excels in stacking and grasping tasks within unstructured environments. Utilizing an NVIDIA GTX 2080TI, the model achieves an 86% grasp success rate and a 100% completion rate. This study highlights the model’s robustness in diverse and unpredictable settings. The grasping of an unseen target object in a clutter trained by self-supervision in simulation was presented in [14]. The method employed three fully connected convolutional neural networks, DenseNet-121, for feature extraction of color, depth, and the target object, which has a high computational cost. It has a low grasping success rate and performs more motions. This is because it seeks to grasp the object directly without separating the objects. It tends to push the cluttered environment after multiple continuous grasp failures. Grasping is also limited to a target, goal-oriented single object.
Related works reveal a trend towards integrating pushing and grasping actions to enhance robotic manipulation in cluttered environments. Each study contributes unique methodologies and performance improvements, with a general progression towards higher grasp success and completion rates. However, this paper’s proposed model tries to address key gaps identified in related works through enhanced integration of pushing and grasping actions and advanced reward structures in order to obtain better performance.
There have been notable developments in the field of robotic manipulation, particularly with regard to increasing the effectiveness and efficiency of robotic grasping in cluttered environments. But there are still a few significant gaps:
Limited ability to handle cluttered environments: Several studies [6,7,8,9] have demonstrated success in sparse environments but have not been able to handle extremely cluttered scenarios.
Combining non-prehensile actions: Techniques that do not use pushing actions [9,10] frequently have poorer success rates because they cannot move objects into different positions before grabbing hold of them. Transferring learned behaviors from simulations to real-world environments can be difficult for approaches [8,11,12,13] because of conditions that differ.
The majority of the research [7,9,13] assesses performance using small object sets or particular scenarios, which make them difficult to extrapolate to a variety of unique object configurations.
By combining pushing and grasping actions, using sophisticated reward structures, and guaranteeing robustness in both simulated and real-world environments, the suggested model fills in these gaps. This work effectively bridges the identified gaps by demonstrating higher completion and grasp success rates in scenarios involving cluttered and novel objects.
Major Contributions
This work makes several significant contributions to the field of robotic manipulation and deep reinforcement learning, particularly in the context of handling in cluttered environments.
- Synergizing of pushing and grasping actions to enhance the overall grasping performance in cluttered environments.
- Usage of a dual-network approach for pushing actions (Push-Net) and for grasping actions (Grasp-Net)
- Self-supervised learning with grasp and push rewards
- Robust performance in diverse scenarios (randomly arranged clutter, well-ordered difficult configurations, and novel objects).
- Adopting of a unique technique called pixel-wise depth heightmap image differencing (PDD) for reward strategy.
By addressing the challenges of robotic manipulation in cluttered environments through innovative use of deep reinforcement learning and pushing actions, this work lays the groundwork for more intelligent and capable robotic systems in industrial and domestic applications.
3. Materials and Methods
- 1.
- Simulation Setup
The simulation was conducted using a UR5 robotic arm from Universal Robots, equipped with a two-finger parallel gripper. An RGB-D camera was fixed in the environment to capture the scene and generate heightmap images. These images were used as inputs for the neural networks.
- Overview
The simulation setup involves using a UR5 robotic arm to test and validate the proposed robotic manipulation model. The UR5 robot is a versatile and widely used industrial robot known for its precision and flexibility, making it ideal for tasks involving grasping and manipulation in cluttered environments. The setup is designed to evaluate the model’s performance in various scenarios, including randomly arranged clutter, well-ordered configurations, and interactions with novel objects.
- Hardware components
- 1.
- UR5 Robotic Arm:Model: Universal Robots UR5.Degrees of Freedom: 6.Payload: 5 kg.Reach: 850 mm.Repeatability: ±0.1 mm.
- 2.
- End Effector:Type: RG2 parallel jaw gripper.Grip Force: 20–235 N.Grip Stroke: 0–85 mm.
- 3.
- Vision System:Camera: Intel RealSense Depth Camera D435.Resolution: 640 × 480 at 30 fps.Depth Range: 0.2–10 m.
- 4.
- Computing System:Processor: Intel Core i7.GPU: NVIDIA Quadro P2000 Intel(R) Xeon(R)RAM: 32 GB.
- Software Components
- 1.
- Operating System: Ubuntu 18.04 LTS.
- 2.
- Robotics Middleware: Virtual Robot Experimentation Platform (V-REP).
- 3.
- Control Interface: CoppeliaSim VR interface with the UR5 robot.
- 4.
- Simulation Environment: CoppeliaSim simulation.
- 5.
- Machine Learning Framework: PyTorch for model training and deployment.
- Simulation Procedure
- 1.
- Environment Setup:
- The robot is placed in a controlled test area with a flat, non-reflective surface to minimize visual noise.
- Objects for manipulation are randomly placed within the robot’s workspace to simulate cluttered environments.
- A mix of known and novel objects is used to evaluate the model’s adaptability.
- 2.
- Calibration:
- The vision system is calibrated using standard calibration techniques to ensure accurate depth perception.
- The end effector is calibrated to ensure precise gripping force and stroke control.
- 3.
- Task Execution:
- The robot is programmed to perform a series of grasping tasks, starting with randomly arranged clutter.
- The tasks are repeated with well-ordered object configurations and novel objects to test the model’s adaptability and performance consistency.
- Each task involves identifying the object, planning a grasp, and executing the grasp.
3.1. UR5 Mathematical Modeling and Deep Reinforcement Algorithm
3.1.1. UR5 Mathematical Modeling
Six revolute joints make up the UR5 robotic arm. Base, Shoulder, Elbow, Wrist1, Wrist2, and Wrist3 are the names of these joints as shown in Figure 1. The shoulder and elbow joints rotate perpendicular to the base joint. Long linkages connect the shoulders, elbows, and base joints [1].

Figure 1.
UR5 robotic arm.
3.1.2. D-H Representation of Forward Kinematic Equations of UR5
The UR5 robot’s kinematics can be studied using the D-H modified representation as shown in Figure 2. To efficiently control the end effector with regard to the base, the relationship between the coordinate frames attached to the end effector and the base of the UR5 robot must be discovered. This is accomplished by recursively describing transformations of the coordinates between the coordinate frames connected to each link and yielding an overall description.
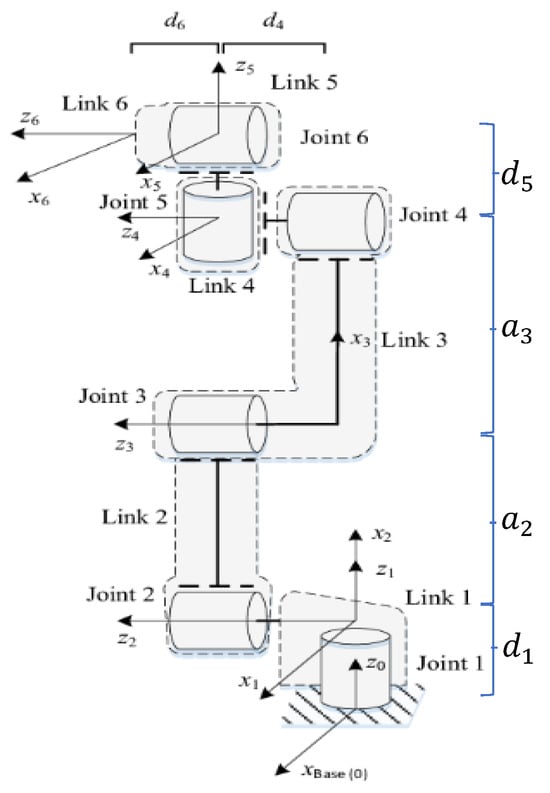
Figure 2.
Schematic and frames assignment of UR5.
The parameters in each row of Table 1 correspond to the sequence of movements made to the coordinate system to pass the joint i, where the sequence of the movements is first about the X axis and later along the Z axis.

Table 1.
D-H modified parameters of the UR5.
The D-H modified for the UR5 robot that shows a transformation from the base to the end effector of the UR5 robot can be rewritten as:
where denotes a rotation along the X-axis with angle , , represents a translation along the X-axis with distance , , represents a rotation along the Z-axis with angle and , is a translation about the Z-axis with distance d.
Using the above D-H modified general formula, the transformation matrix for the UR5 robot can be given by:
3.2. Data Collection
The dataset consisted of various objects including toy blocks of different shapes and colors, as well as novel objects like bottles, bananas, screwdrivers, cups, forks, and adjustable wrenches. The objects were arranged in three different configurations for testing:
- ♦
- Randomly arranged clutter.
- ♦
- Challenging well-ordered configurations.
- ♦
- Novel object configurations.
The state of the proposed system is represented as an RGB-D heightmap image of the scene at time t. The RGB-D images from a fixed-mount RGB-D camera are taken, the data are projected into a 3D point cloud, and then are back-projected orthographically upwards in the gravity direction using a known extrinsic camera parameter to calculate both color (RGB) and height-from-bottom (D) channels’ heightmap images as shown in Figure 3. The RGB-D camera’s additional depth information is critical for robots that interact with a three-dimensional environment. The working environment area covered a 448 by 448 mm tabletop surface.
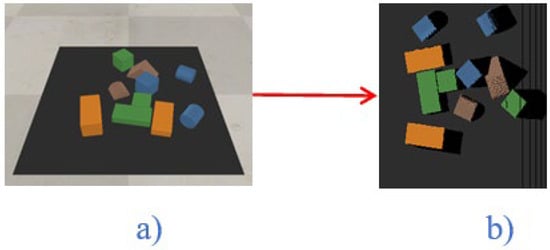
Figure 3.
RGB color image (a) and RGB heightmap (b).
Working with raw heightmap pictures, which are 224 by 224 pixel RGB-D images, can be time-consuming and memory-intensive [2]. Normalization of input data is a critical step that assures that each input heightmap has a consistent data distribution. Convergence of the deep neural network is accelerated as a result of this. heightmap normalization in a heightmap image is accomplished by subtracting the mean from each pixel and dividing the result by the standard deviation.
The input heightmap is rotated by 36 orientations θ, each of which corresponds to a push or grasp action with distinct products of 10° angle from the original state, before being sent to the DenseNet-121 to generate a set of 36 pixelwise Q-value maps to make learning-oriented pushing and grasping actions easier.
3.3. Deep Reinforcement Learning
In deep reinforcement learning, the agent uses a deep neural network to learn complex features and decides on its own what action to take by interacting with its environment. The agent strives to discover the best decision-making method that will allow it to maximize the rewards acquired over time through its experience.
As it allows the interaction process of reinforcement learning to be defined in probabilistic terms, the Markov Decision Process serves as the theoretical foundation for reinforcement learning. Representing all possible states that the agent could find itself in by the set and the set of actions that the agent can execute to the system to translate from one state to the next state by is a common practice. At a given time , the UR5 chooses and performs an action based on the optimal policy , and will cause the state to change from to. In response to this transition of state, the environment gives a reward to the UR5. After receiving the reward, the UR5 is in state and performs the next action. This action will cause the environment to change to state. And that will be followed by the environment granting the robot a reward; this process is repeated for each time step, as illustrated in Figure 4.
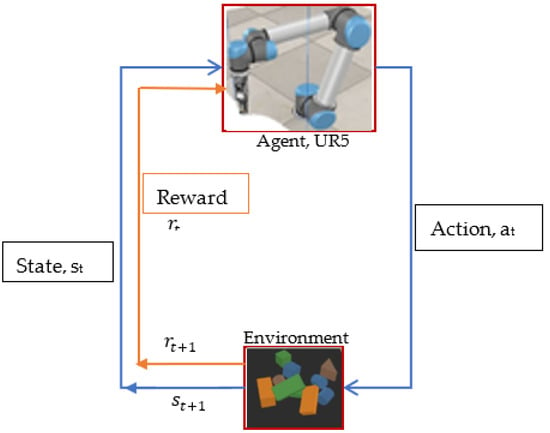
Figure 4.
Deep Reinforcement Learning (DRL) agent (UR5)–environment interaction.
The deep reinforcement learning problem is used to find the best policy , that maximizes the expected sum of future reward for performing an action over time horizon T and the discount factor , which accounts for degree of the importance of the future rewards at the present state. Deep Q-learning was used to train an optimal policy that chooses an action from that maximizes a state–action value function , a measure of the reward for performing action in state at time t.
The equation to determine the new update Q-value for the state–action pair at time t is given by the Bellman equation:
where is a set of all future available actions, is the learning rate , is the current Q-value that has to be updated, is an immediate reward, and is an estimation of the optimal future reward value.
The two important aspects of the DQN algorithm, as proposed by [2], are the use of a target network and experience replay. In this work, the target network , which is parameterized by and is the same with the normal DQN except that the parameters are updated every time steps from the DQN, was used. So that at every C step, , and this was kept fixed on all other steps. The target used by DQN at the ith layer, is then:
Minimizing the temporal difference error of to a fixed target value between individual updates, is the objective of the learning. Therefore, the temporal difference can be given by:
The main idea of the experience replay mechanism is that during the DQN training process, the UR5 robot saves every experience tuple at each time point,. The experience would be used as training data to update the DQN weights and the biases. The experience tuple is stored in the replay memory M of length N, where . A stochastic rank-based prioritization for prioritizing experience was employed in this study so that significant transitions might be replayed more frequently and so learned more effectively. In particular, the probability of sampling transition from the replay buffer of size N is defined as:
where denotes the priority of transition , and the exponent denotes the amount of prioritizing employed. As a result, this value determines how much prioritization is employed. In particular, the transition in the replay buffer is ranked by the absolute value of temporal difference (TD) error.
where is the rank of the transition in the replay buffer sorted according to the temporal difference error .
3.3.1. Densely Connected Convolutional Neural Networks
The deep Q-function was modelled as two feed-forward fully connected convolutional networks (FCNs) for each motion primitive behavior; one for the pushing network, , and another for the grasping networks, , by extending the vanilla deep Q-networks (DQN) [2]. It has recently been demonstrated that to train deeper, more accurate and more efficient features, the connection between layers next to the input and close to the output of the convolutional network should be shorter [15]. The normalized and rotated heightmap is fed to the DenseNet-121 network.
Figure 5 illustrates the DenseNet-121, used in both the push and grasp neural networks. The depth and color heightmaps are concatenated in channel-wise order after the DenseNet-121 network, followed by two additional similar blocks with batch normalization, nonlinear activation function (ReLU), and convolutional layers for feature embedding. The pixel-wise state-action prediction value is then bilinearly up sampled. The Q-value guess at pixel p depicts the expected reward for performing a primitive action at the position , where q maps from pixel , and bilinear upsampling creates the same heightmap size and resolution as of each dense 36 pixel-wise map of Q-values. Table 2 summarizes the DenseNet-121 layers.
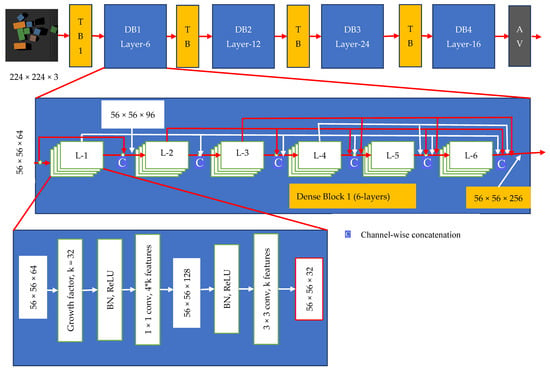
Figure 5.
A deep DenseNet-121 with four dense blocks.

Table 2.
DenseNet-121 Layers.
3.3.2. Pushing Primitive Actions
The beginning points of a 10 cm push and the push direction in one of k = 36 orientations are denoted by the push primitive action , . The goal of the pushing primitive action is to learn pushes so that subsequent grasps can be made with as few steps as feasible. Among all possible Q-values of the push Net , an action with maximum Q-value is selected as a push action as shown in Figure 6. The tip of a closed two-finger gripper is used to physically execute the push action in this thesis.

Figure 6.
Push Net Q-values.
3.3.3. Grasping Primitive Actions
Similarly, among all possible Q-values of the grasp Net , the grasp action with the maximum Q-value is selected as the best grasp action, as shown in Figure 7.
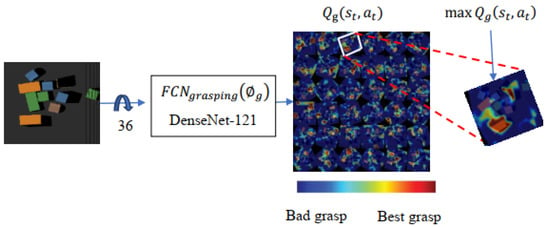
Figure 7.
Grasp Net Q-values.
The predicted Q-values are represented as a heatmap, with hotter locations indicating higher Q-values. The white cycle in the heightmap image highlights the highest Q-value map, which correlates to the best grip action. signifies the median position of a top-down parallel-jaw grab in one of k = 36 orientations in grasping primitive action. Both fingers attempt to move 3 cm below during a grip attempt before closing the fingers at the object’s point of grasp.
The action selection strategy is based on the maximum of the primitive motions (FCNs) and . The primitive action in the proposed model is the maximum Q-value prediction of the best push action and best grasp action Q-value predictions as illustrated in Figure 8.
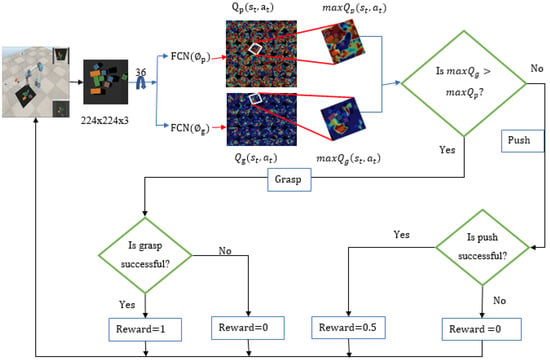
Figure 8.
Framework for pushing and grasping objects.
At each iteration of the training session, the Huber loss function to train Q-learning on FCNs is employed. For the ith iteration, the Huber loss function can be written as follows below:
where , denotes the parameters (weights and biases) of the neural network at the ith iteration, and signifies the target network parameters between individual updates.
A learning rate () of , a momentum coefficient of 0.9, and a weight decay factor of are used to train fully connected convolutional neural networks. During the training session, the agent learned exploration using the epsilon greedy (ϵ-greedy) policy, which started at 0.5 and was decreased to 0.1 via exponential decay. The agent begins by exploring more, and as it gains more experience via trial and error, it begins to exploit more of what it has learned. Future reward discount factor was set to a fixed amount of 0.5. Over the training iterations, the gripping action’s learning performance improved incrementally.
3.3.4. Reward Modeling
A successful grasp is assigned a reward value as shown below:
Grasp success is confirmed when the antipodal distance between gripper fingers after a grasp attempt is greater than the threshold value of the antipodal distance. While for a successful push, the reward value is modeled as:
If there is a detectable change in the environment, the push is successful. The pixel-wise depth heightmap image differencing approach subtracts data from the previous depth heightmap image from those of the current depth heightmap image, to calculate the change sensed therein. Pixel-wise depth heightmap image differencing (PDD) is calculated by subtracting the current state’s depth heightmap image from the previous state’s depth heightmap image. That is:
The robot’s workspace was examined with various threshold values, and it was discovered that this may be determined by trying different simulations. Increasing the threshold value implies that the robot can detect if there is only a considerable change. When the threshold value is reduced, the robot can detect even minor changes that the human eye might miss. If the pixel-wise depth heightmap image differencing (PDD) exceeds the threshold value, a change observation is evaluated with the acquired threshold value ;
In general, if the PDD value is greater than the threshold value and the grasping attempt is successful, a change has occurred. Aside from that, there has been no change in the workspace.
3.3.5. Training Procedures
The proposed model simulation was performed using a DELL E2417H desktop with NVIDIA Quadro P2000 Intel(R) Xeon(R) E-2124 CPU @3.30 GHz, with Ubuntu 18.04 LTS operating system, Python v3.80, PyTorch v1.0, OpenCV v4.5.5 and V-REP v4.2.0.
V-REP is a general-purpose robot simulation framework that is versatile, scalable, and powerful. Kinematics, dynamics, collision detection, motion planning, and mesh–mesh distance calculation modules are among the various calculation modules in V-REP [16]. V-REP was utilized in conjunction with Bullet 2.83 Physics, an open-source collision detection, soft body, and rigid body dynamics package [17]. It is used to identify collisions, resolve collisions, and resolve other limitations.
In this investigation, a UR5 robot with an RG2 parallel jaw gripper was used. The robot uses a stationary RGB-D camera to observe its surroundings. With a pixel resolution of 640 × 480, the camera gathers picture and depth maps.
During training, ten objects with various sizes and colors are dropped at random into a 448 × 448 mm robot’s workspace/environment. By trial and error, the robot learned to perform either a grip or a push action based on the highest Q-value. Following the removal of all objects from the workspace, a new batch of 10 objects was dropped at random for additional training. Data was collected constantly until the robot had completed 3000 training iterations.
3.3.6. Testing Procedures
Randomly arranged, challenging arrangements of ordered objects and novel objects are provided throughout test scenarios. Bottles, variously sized and shaped cups, a screwdriver, a banana, and a scissor are among the novel objects.
To assess the performance and generality of the proposed model, the following metrices measurements were used, with the greater the value, the better.
- Average percent clearance: Over the n test runs, the average percentage clearance rate assesses the policy’s ability to complete the task by picking up all objects in the workspace without failing more than 10 times.
- The ratio of successful grasps in all grasp attempts per completion, which assesses the grasping policy’s accuracy, is called the average percent grasp success per clearance.
- The average grasp-to-push ratio is the number of successful grasps divided by the number of successful pushes in each test case’s complete run tests.where is number of successful grasps, is the number of successful pushes.
4. Results
In this section, the findings of this work, including the training and the testing sessions, are presented. After training the proposed model using self-supervised deep reinforcement learning, a different set of test scenarios with different clutter and novel objects are provided. Here, the performance of the proposed model in a cluttered environment, tested over challenging well-ordered objects and novel objects are presented.
4.1. Performance in Cluttered Environments
The results demonstrate the effectiveness of the proposed model in handling cluttered environments. Compared to traditional grasping-only policies, which achieved a grasping success rate of just 60%, the proposed model attained a significantly higher success rate of 87%. This improvement is primarily due to the synergy between pushing and grasping actions. Pushing helps to create space around the target object, allowing the robotic gripper to secure a better grasp. The use of rewards for successful pushes further encourages this behavior, leading to a more efficient and effective grasping strategy.
The above graph illustrates the grasping success rate of the grasping-only policy, no-reward for push model, SGD-without momentum, and the proposed model. A lot of researchers used the grasping-only policy in clutter to grasp an object. In a cluttered environment, the grasping success rate of the grasping-only policy is unsatisfactory. There should be room for the robotic gripper to successfully grasp an object in the clutter. Also, there is research that trained both pushing policy and grasping policy but without rewards for successful pushing. The grasping success rate of the proposed model has shown an interesting performance.
The proposed model reached 80% grasping success rate at 1500 iterations, and the overall grasping success rate is 87%. This shows that in a clutter, synergizing pushing policies with grasping improves the grasping performance. The pushing action is used to separate the clutter and to find room for the gripper. The purpose of the pushing action is to improve future grasping. Providing a reward for successful pushes also improves a grasp success. The momentum in stochastic gradient descent is used to create an inertia to accelerate the training in the direction of minimum gradient. Momentum is used to increase the convergence rate of the training session. As shown in Figure 9 the grasping-only policy’s grasping success rate is low. In clutter, it is recommended to use both pushing and grasping policies.
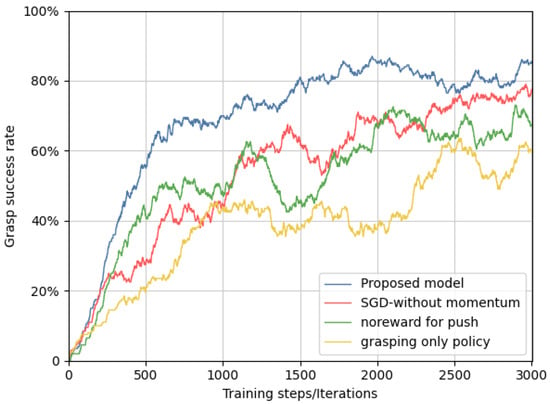
Figure 9.
Grasping performance comparison of grasping-only policy, no-reward for push model, SGD-without momentum, and the proposed model.
Here, the grasping performance and push-then-grasp success (dotted line) of the proposed model, SGD-without momentum, and models offering no reward for the pushing action are presented. Over 3000 iterations of training, as it can be inferred from the above graph, the proposed model performed best in both grasping success rate and push-then-grasp success over the SGD-without momentum and models offering no reward for pushing actions. In the graph, the dotted lines infer the grasping successes after successful pushing actions. The grasping success rate of the proposed model has shown fast convergence. As can be inferred from Figure 10 over 3000 iterations, the grasping success rate of the proposed model, SGD-without momentum, and models with no reward for pushing actions is 87%, 79%, and 71%, respectively.
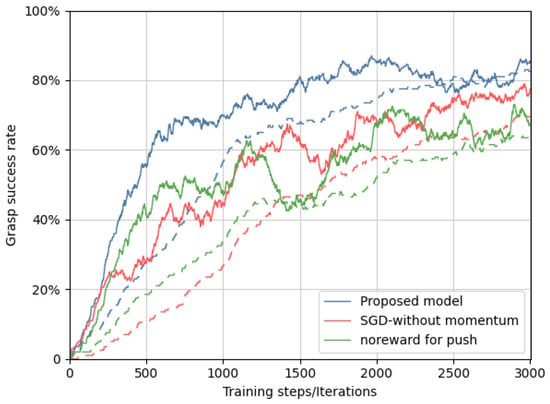
Figure 10.
Grasping success rate and push-then-grasp success comparison between the proposed model and SGD-without momentum.
4.2. Randomly Arranged Objects
Increasing the number of objects from 10 objects to 26 objects during training is done with the purpose of creating more dense clutter. The model’s performance was evaluated through various test scenarios, including random arrangements of objects, well-ordered challenging configurations, and novel objects. In randomly arranged environments, the model showed a robust grasp success rate, indicating its ability to generalize well to unseen configurations. Specifically, the model completed 80 test cases with a grasp success rate of 50.5% and a grasp-to-push ratio of 77.1%. This indicates that even in highly cluttered scenes, the model can effectively manage the environment to achieve successful grasps.
The randomly arranged, more cluttered objects used during the testing of the generalized performance of the trained model are presented in Appendix A: Figure A2.
As can be inferred from Table 3, the generalization ability of the proposed trained model in more cluttered environment is interesting. The proposed model can grasp objects in clutter by synergizing push policy with grasp policy.

Table 3.
Simulation results for random arrangements of 26 objects.
4.3. Challenging Well-Ordered Configurations
The model’s performance was further tested with three difficult test cases featuring well-ordered configurations of objects. These test cases, designed to simulate challenging gripping conditions, included objects stacked closely together and placed in orientations that complicate grasping. Despite these difficulties, the proposed model performed admirably. Test case 00 showed a completion rate of 96.8%, with a grasp success rate of 84.7% and a grasp-to-push ratio of 99.5%. Test cases 01 and 02 also exhibited strong performance, with grasp success rates of 61.4% and 75.1%, respectively.
Three difficult test cases with difficult clutter are provided. These configurations are created by hand to simulate difficult gripping conditions and are not used in the training process. Objects are stacked close together in several of these test cases, in near locations and orientations. A single isolated object is placed in the workspace separately from the arrangement as a sanity check. Appendix A contains the challenging well-ordered configuration test cases from Figure A3, Figure A4 and Figure A5.
As shown in Table 4, the proposed model performs well for challenging configurations of objects in the robot workspace where the arrangements are not seen during the training session.

Table 4.
Evaluation metrices of well-ordered arrangements test cases.
4.4. Generalization to Novel Objects
One of the most compelling aspects of the proposed model is its ability to be generalized to novel objects. In tests with novel objects, which included items such as bottles, bananas, screwdrivers, and variously sized cups, the model maintained high performance. The grasp success rates for the three novel test cases were 73.9%, 65.4%, and 95.8%, respectively. The completion rates and grasp-to-push ratios in these tests also remained high, indicating that the model can effectively handle objects with different shapes and sizes that were not part of the training set.
Simulation tests with novel objects that are more complex in shape than those employed during training are undertaken (Table 5). As shown in Appendix A Figure A6, Figure A7 and Figure A8, three separate test cases with different novel objects are provided.

Table 5.
Simulation results for novel object arrangements.
Novel objects in the test were provided to understand the generalization of the proposed trained model. These are different objects that were never seen during the training session. The objects include bottles, bananas, screwdrivers, different-sized cups, forks, and an adjustable wrench.
This generalization capability is crucial for real-world applications, where robots must handle a wide variety of objects. The ability to successfully grasp novel objects without additional training underscores the robustness and versatility of the proposed model.
4.5. Discussion
The proposed method demonstrates significant improvements in robotic manipulation within cluttered environments when compared to existing techniques, as in Table 6. Here is a detailed discussion of the performance metrics:
- 1.
- Grasp Success Rate:
Our proposed method achieves an 87% grasp success rate, which is on par with the best-performing existing technique from 2020 (87%), but significantly outperforms most other methods, particularly those from earlier years, such as the 62% success rate achieved in by [6,10].
- 2.
- Action Efficiency:
The proposed approach shows an action efficiency of 91%, which is slightly lower than the highest efficiency of 95.2% reported in [7]. However, it surpasses many other methods, indicating a more balanced and efficient action strategy within cluttered environments. This is a notable improvement over methods such as [12] approach, which reported an efficiency of 54.1%.
- 3.
- Completion Rate:
The proposed model consistently achieves a 100% task completion rate, indicating robust performance in complex, cluttered scenarios. This matches the performance of several other top methods from 2020 to 2024, showing that the proposed method is reliable for practical applications in industrial settings.
- 4.
- Hardware and Computational Efficiency:
The proposed method utilizes a DELL E2417H desktop, which is more accessible and cost-effective compared to high-end GPUs like the Nvidia RTX 2080 Ti or Titan X used in other studies. Despite this, it maintains competitive performance, highlighting its efficiency and potential for broader application.
- 5.
- Training time and Epoch:
Our proposed model’s training time is about 5 h for 3000 epochs. This shows that with less training time and epoch, our proposed model shows an interesting performance increase over other works.
Table 6 shows a comparison among different state of the art researches and our proposed model.

Table 6.
Performance comparison with related works.
Table 6.
Performance comparison with related works.
| Year | Action | GPU | Epochs | Time | Work Area | Ref | Completion | Grasp Success | Action Efficiency |
|---|---|---|---|---|---|---|---|---|---|
| 2021 | Grasping | Nvidia RTX 2080 | 2500 | N/A | Clutter | [6] | 53.1% | 62% | 51.4% |
| 2020 | Grasping | N/A | 7000 | N/A | Sparse | [7] | 100% | 87% | 95.2% |
| 2020 | Pushing and grasping | Titan X (12 GB) | 10,000 | 34 h | Clutter | [8] | 93.7% | 76% | 84% |
| 2020 | Pick and place | GeForce GTX-1660Ti | 3000 | 10 h | Clutter | [9] | 100% | 74.3% | 92% |
| 2018 | Pushing and grasping | NVIDIA Titan X | 2500 | 5.5 h | Clutter | [10] | 100% | 65.4% | 59.7% |
| 2022 | Pushing and grasping | Nvidia GTX 1080Ti | 250 | N/A | Clutter | [11] | 100% | 83.5% | 69% |
| 2023 | Pushing and grasping | N/A | 1000 | N/A | Clutter | [12] | 93.8% | 75.3% | 54.1% |
| 2024 | Stacking and grasping | NVIDIA GTX 2080TI | 10,000 | N/A | Clutter | [13] | 100% | 86% | 69% |
| 2024 | Proposed | DELL E2417H desktop | 3000 | 5 h | Clutter | N/A | 100% | 87% | 91% |
5. Conclusions and Future Work
Grasping an object in a cluttered scene has been a subject of researchers, yet a challenging and less explored one. It is tough to grasp an object in a cluttered environment without using non-prehensile motions. In this work, to improve grasping in a cluttered environment, a non-prehensile action, namely pushing, was adopted. Using available resources, the proposed model has improved on the ability to grasp an object in clutter by synergizing pushing and grasping actions. The proposed model has achieved a grasping success rate of 87%. The proposed model has also shown grasping success rate improvement of 27%, 16%, and 8% over a grasping-only policy, no-reward-for-pushing policy, and SGD-without momentum strategies, respectively. So, it can be concluded that synergizing pushing and grasping policies improves the grasping performance of objects in a cluttered scene. Giving a reward for successful pushing actions encourages synergizing the pushing and grasping actions for improved grasping success rate. Also, SGD with momentum optimization improves the convergence rate of training. The proposed framework has also shown a great generalization skill for randomly arranged dense clutter, and challenging, well-ordered, and novel objects.
Light Changes: The RGB-D camera’s depth information compensates for lighting variations. Color saturation, hue, brightness, and contrast were generated with data augmentation features available in PyTorch, ensuring the model’s robustness, which ensures accurate object detection regardless of color or light intensity. Noise Interference: We strongly feel that the reward structure and deep learning algorithm is resilient towards noise impacts.
Domain Randomization: Varying simulation parameters to expose the model to diverse scenarios. Transfer Learning: Fine-tuning the model with real-world data to enhance performance (But we will incorporate in this in future work).
Moreover, Robust Reward Structures: Ensuring consistency between simulated and real-world environments. These techniques collectively bridge the gap, ensuring the model’s effectiveness in real-world applications.
The proposed model never considered the properties of the objects to be grasped. Fragile and deformable properties of objects have to be considered for more inclusiveness. In the future, it is recommended to consider these properties.
Author Contributions
Conceptualization, B.A.S. and R.S.; Data curation, B.A.S.; Formal analysis, T.F.A. and A.S.A.; Funding acquisition, R.S.; Methodology, B.A.S., T.F.A. and R.S.; Project administration, A.S.A.; Resources, T.F.A. and R.S.; Software, B.A.S. and R.S.; Supervision, T.F.A.; Validation, B.A.S.; Writing—original draft, B.A.S.; Writing—review and editing, T.F.A., A.S.A. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by “The Deanship of Scientific Research, Vice-Presidency for Graduate Studies and Scientific Research, King Faisal University, Ministry of Education, Saudi Arabia under Grant A393”.
Data Availability Statement
The data that support the findings of this study can be generated by the reader by creating the set-up as mentioned in the Section 2.
Acknowledgments
The authors express their gratitude to the Deanship of Scientific Research at King Faisal University in Al-Ahsa, Saudi Arabia, for providing financial assistance for this study under (Grant No. A393).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The Proposed Model Training and Test Cases

Figure A1.
Training objects.

Figure A2.
Random configuration.

Figure A3.
Test-case-00.

Figure A4.
Test-case-01.

Figure A5.
Test-case-02.

Figure A6.
Novel-test-case-00.

Figure A7.
Novel-test-case-01.

Figure A8.
Novel-test-case-02.
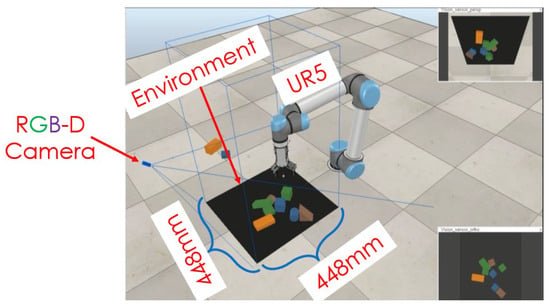
Figure A9.
Agent–environment interaction of the proposed model.
References
- Liu, R.; Nageotte, F.; Zanne, P.; de Mathelin, M.; Dresp-Langley, B. Deep reinforcement learning for the control of robotic manipulation: A focussed mini-review. Robotics 2021, 10, 22. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Rai, S.; Dev, A. A Comprehensive Study of Artificial Neural Networks. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2012, 2, 278–284. [Google Scholar]
- Sutton, R.S.; Barto, A.G.; Learning, R. No play, bad work, and poor health. Lancet 1998, 258, 675–676. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends® Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Al-Shanoon, A.; Lang, H.; Wang, Y.; Zhang, Y.; Hong, W. Learn to grasp unknown objects in robotic manipulation. Intell. Serv. Robot. 2021, 14, 571–582. [Google Scholar] [CrossRef]
- Joshi, S.; Kumra, S.; Sahin, F. Robotic Grasping using Deep Reinforcement Learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1461–1466. [Google Scholar] [CrossRef]
- Hundt, A.; Killeen, B.; Greene, N.; Wu, H.; Kwon, H.; Paxton, C.; Hager, G.D. ‘Good Robot!’: Efficient Reinforcement Learning for Multi-Step Visual Tasks with Sim to Real Transfer. IEEE Robot. Autom. Lett. 2020, 5, 6724–6731. [Google Scholar] [CrossRef]
- Mohammed, M.Q.; Chung, K.L. Pick and Place Objects in a Cluttered Scene Using Deep Reinforcement Learning. Int. J. Mech. Mechatron. Eng. 2020, 20, 50–57. [Google Scholar]
- Zeng, A.; Song, S.; Welker, S.; Lee, J.; Rodriguez, A.; Funkhouser, T. Learning Synergies between Pushing and Grasping with Self-Supervised Deep Reinforcement Learning. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4238–4245. [Google Scholar] [CrossRef]
- Peng, G.; Liao, J.; Guan, S.; Yang, J.; Li, X. A pushing-grasping collaborative method based on deep Q-network algorithm in dual viewpoints. Sci. Rep. 2022, 12, 3927. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Chen, Y.; Li, Z.; Liu, Z. Efficient push-grasping for multiple target objects in clutter environments. Front. Neurorobot. 2023, 17, 1188468. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, Y.; Shi, M.; Chen, C.; Liu, S.; Zhu, J. Efficient Stacking and Grasping in Unstructured Environments. J. Intell. Robot. Syst. Theory Appl. 2024, 110, 57. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, H.; Choi, C. A Deep Learning Approach to Grasping the Invisible. IEEE Robot. Autom. Lett. 2020, 5, 2232–2239. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Rohmer, E.; Singh, S.P.N.; Freese, M. V-REP: A versatile and scalable robot simulation framework. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1321–1326. [Google Scholar] [CrossRef]
- Coumans, E. Bullet 2.82 Physics SDK Manual Table of Contents. 2013. Available online: https://wiki.blender.jp/images/9/95/Dev-Physics-bullet-documentation.pdf (accessed on 23 June 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).