Abstract
Body weight support (BWS) systems are crucial in gait rehabilitation for individuals incapacitated due to injuries or medical conditions. Traditional BWS systems typically employ either static mass–rope or dynamic mass–spring–damper configurations, which can result in inadequate support stiffness, thereby leading to compromised gait training. Additionally, these systems often lack the flexibility for easy customization of stiffness, which is vital for personalized rehabilitation treatments. A novel BWS system with online variable stiffness is introduced in this study. This system incorporates a drive mechanism governed by admittance control that dynamically adjusts the stiffness by modulating the tension of a rope wrapped around a drum. An automated control algorithm is integrated to manage a smart anti-gravity dynamic suspension system, which ensures consistent and precise weight unloading adjustments throughout rehabilitation sessions. Walking experiments were performed to evaluate the displacement and load variations within the suspension ropes, thereby validating the variable-stiffness capability of the system. The findings suggest that the online variable-stiffness BWS system can reliably alter the stiffness levels and that it exhibits robust performance, significantly enhancing the effectiveness of gait rehabilitation. The newly developed BWS system represents a significant advancement in personalized gait rehabilitation, offering real-time stiffness adjustments and ongoing weight support customization. It ensures dependable control and robust operation, marking a significant step forward in tailored therapeutic interventions for gait rehabilitation.
1. Introduction
In the modern world, permanent disability is predominantly caused by neurological and cardiovascular diseases, including stroke, spinal cord injuries [1], cerebral palsy [2], and Parkinson’s disease. These conditions affect a significant number of individuals, with an estimated 83 million disabled persons worldwide experiencing long-term challenges in their daily lives. Prolonged bedridden patients often endure substantial changes in muscle and bone mass, especially in the lower limbs. These changes can result in complications such as osteoporosis, spasticity, and bedsores. Facilitating movement and maintaining balance in an upright position is crucial for restoring function in these patients. Treadmill walking with body weight support (BWS) has proven to be an effective approach for initiating early gait rehabilitation in individuals who are unable to bear their full body weight due to impairment. This method allows patients to begin their rehabilitation process while providing necessary support.
With numerous randomized controlled trials supporting its efficacy, BWS treadmill training has emerged as the “gold standard” in gait rehabilitation [3]. During this training, patients are suspended in a specialized harness above a treadmill, which provides support for a portion of their body weight during gait retraining. This innovative approach has been demonstrated to yield superior functional outcomes by reducing the impact of gravitational forces on the body and enhancing stability through external assistance. Notably, Hesse et al. [4] demonstrated the positive effects of BWS training on gait ability and walking velocity in stroke patients.
The study highlighted that treadmill training with partial body weight support can significantly improve these key parameters. Furthermore, Barbeau et al. [5] conducted a comprehensive investigation involving 100 stroke survivors to assess the impact of BWS treadmill training on walking speed, endurance, balance, and motor recovery. The findings concluded that gait training with BWS is an effective method for improving gait and postural abilities. Meanwhile, Miyai et al. [6] employed the near-infrared spectroscopic topography technique and discovered increased brain activity during BWS treadmill training. Their findings suggest that this rehabilitation method stimulates neural activity, potentially contributing to functional improvements in stroke patients. Similarly, Enzinger et al. [7] utilized functional MRI scans on 18 subcortical ischemic stroke patients and observed changes in cortical activation associated with rehabilitation-related improvements in walking abilities.
While BWS systems have become commonplace in clinical settings for locomotor retraining, recent research has identified some issues with their use. Firstly, overhead harness BWS systems mounted on the ceiling can restrict pelvic motion in the horizontal plane, leading to significant deviations in gait kinematics and temporospatial parameters from normative patterns due to variations in sensorimotor feedback and proprioceptive input [8]. Additionally, BWS systems not only provide vertical support against gravity but also offer support in other directions, potentially reducing the challenge and effort required for balance and postural control during walking. Furthermore, walking on a treadmill can result in different gait dynamics compared to over-ground walking, influenced by factors such as additional inertia, friction, weight, greater cadence, forward-tilted trunk motion, and increased vertical acceleration [9,10].
The biomechanical effects of BWS seem to be divergent in different groups. Lewek conducted an analysis of the kinetics and muscle activity of fifteen patients with neurological impairments during treadmill walking in a study.
Unexpectedly, it was found that BWS not only failed to increase their stance time and step length but also impaired their capacity for relearning walking [11]. Dobkin and colleagues studied the gait of patients with spinal cord injury and found the rehabilitative effect was similar between treadmill walking with BWS and other interventions [12]. Van Hedel et al. [13] reported abnormal muscle profile changes, specifically at the rectus femoris, lateral hamstring, and medial hamstring, due to elevated levels of BWS. Similarly, Hicks et al. [14] discovered that treadmill training resulted in significant improvements in treadmill walking for patients with spinal cord injuries while yielding limited improvements in over-ground walking after long-term treadmill training. Among the fourteen patients participating in their study, only five demonstrated an improvement in their over-ground walking post-training, with three of these patients reverting to their initial walking scores at the follow-up assessment. Furthermore, when investigating gait patterns in children with cerebral palsy, Celestino and colleagues reported that BWS combined with over-ground walking led to significant improvements in functional gait outcomes when compared to treadmill walking [15].
The inconsistencies in the biomechanical effects of BWS can be attributed to variations in the devices used in different experiments. Different research groups utilized different harnesses and control systems in their treadmill-based BWS devices, potentially resulting in distinct gait patterns. BWS systems are vital for assisting with weight bearing and propulsion throughout the gait cycle. However, the incorporation of a human–robot system introduces additional factors such as inertia, friction, and weight, which require compensation through control theories and methods. In the past, most BWS systems were either mass–rope static support systems or mass–spring–damping second-order dynamic support systems [16]. The dynamic body weight support over-ground co-walker was designed to provide a variable unloading ratio and motion tracking, allowing for more natural and dynamic movement [17]. The evaluation method of the stability of a cable-driven rehabilitation robot was studied, and the evaluation index of the static stability, the evaluation index of the dynamic stability, and the stability distribution rule of a cable-driven lower-limb rehabilitation robot were given [18]. Consequently, this limitation significantly impacts the rehabilitation process and treatment outcomes for patients. The function of body weight support (BWS) was realized by using a variable-stiffness mechanism (VSM). By controlling the virtual stiffness of the spring system, different levels of BWS were realized. The virtual stiffness of the spring system can be adjusted by using the rigid actuator [3]. A novel BWS system was developed, which is driven by two compact actuators. In addition to the conventional constant-weight force compensation, the proposed trunk motion assistance design also incorporates the impedance-control-type assisted control design, which can assist humans in completing various actions by adjusting the dynamic force [19]. A BWS system based on series elastic actuator principle was designed, and a variable-parameter admittance control strategy based on the BWS system model was proposed to achieve dynamic weight loss and compensation weight loss control effect [20].
Ensuring a precise and consistent unloading force is considered a crucial prerequisite for BWS gait therapy. Each patient, characterized by distinct height, weight, musculature, and body composition, requires a specialized stiffness spring to maintain a constant desired force. In this paper, we present the development of an alterable-stiffness BWS system. The system consists of two active closed-loop controlled electric drives: one is dedicated to generating a steady desired force, while the other facilitates dynamic stiffness adjustment, similar to a virtual elastic spring element. This dual-unit system provides accurate support to patients, making a significant contribution to optimizing gait rehabilitation efficacy for individuals with diverse needs.
2. Methods
2.1. Participants
A total of 5 young adults [1 female, 4 males, mean age: 26.80 (±3.71) years, mean height: 1.71 (±0.10) m, mean weight: 72.04 (±17.08) kg], without any documented musculoskeletal or neurological disorders, voluntarily participated in the study. This research received approval from the Ethics Committee of Hubei University of Technology.
2.2. Body Weight Support System
The overall conceptual design of the online variable-stiffness BWS system is shown in Figure 1. This device seamlessly integrates both active dynamic and passive static weight-unloading principles. It comprises two actively controlled electric drives in a closed-loop configuration. One drive generates the desired force, while the other dynamically adjusts the stiffness, functioning like a virtual elastic spring element. Both force-generating units exert their influence on the patient through a polyester rope connected to a harness worn by the patient. The length of the rope can be adjusted with an electric winch, allowing the system to be tailored to accommodate patients of different sizes.
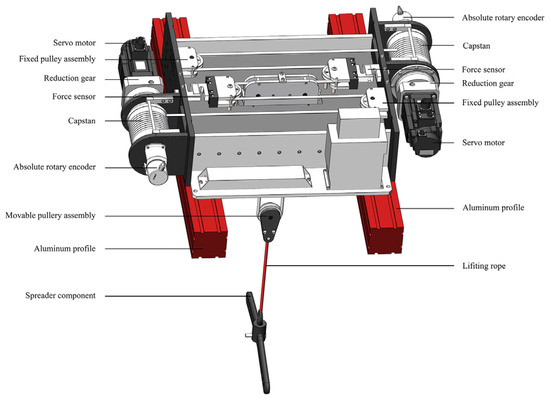
Figure 1.
The online variable-stiffness BWS system.
To ensure a stable force and smooth walking experience for patients, two electric drives are implemented for the real-time adjustment of the suspension rope. The two electric drives are assembled onto the corresponding left and right mounting plates, respectively, using hexagonal screws. Additionally, the pulley components and force sensors are installed on the left and right mounting plates. The lifting rope, wound around the capstan, intricately threads through the pulley components to establish a connection between the two force sensors. The configuration links the lifting rings via the central output pulley assembly, forming the suspension assembly of the device.
The electric drive comprises a servo motor, reduction gear, capstan, and an absolute rotary encoder. The reduction gear is strategically positioned between the capstan and the servo motor. The output of this reduction gear rotates in unison with the flange, securely connected by bolts, thereby driving the capstan to rotate simultaneously. The capstan’s other end is bolted to the bearing support end cover, from which a short shaft extends outward. This shaft connects to the encoder via a coupling, enabling the encoder to record data such as the capstan’s rotation speed. Once this information is transmitted to the host computer, precise instructions are sent to the motor. This orchestrated process allows the host computer to control the drum rotation in real time, enhancing the stability of force for patients during walking.
The entire framework uses an xPC Target real-time kernel to enable real-time data transmission from the BWS system (Figure 2). We selected the YASKAWA-SGM7J-08A servo motor (Yaskawa America, Waukegan, IL, USA), with a rated power of 750 W and a rated torque of 2.39 N·m, for its high efficiency and precision, which are essential for the operation of our BWS system. This choice ensures that the motor can handle the dynamic loads and provide the necessary power for supporting the body weight effectively. The control program for the BWS system is programmed in MATLAB Simulink, with instructions transmitted to the xPC Target computer via a network cable. Simultaneously, data from the motor and force sensor are relayed back to the host PC via National Instruments (NI) acquisition cards. This intricately designed system ensures seamless information flow, fostering effective communication and synchronization between the user interface, control software, and the real-time components of the BWS system.
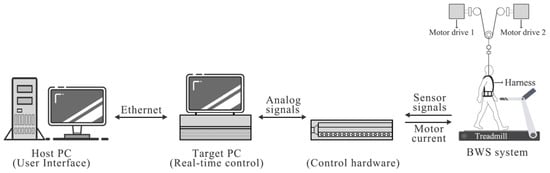
Figure 2.
Overall framework of BWS system.
2.3. Controller
The online variable-stiffness intelligent anti-gravity dynamic suspension system consists of two active drive systems. System 1 employs admittance control to enable the on-line adjustment of the simulated spring stiffness by adjusting relevant parameters in the control system. System 2 provides the stable unloading force of the whole system by determining the relevant parameters in the control system. The realization principles of these systems are introduced below.
For an active dynamic body weight support (BWS) system, the objective is not only to accommodate the static unweighting of the body but also to minimize the inertial forces generated during dynamic processes [19]. Hence, as an effective BWS system, reductions in weight should correspondingly decrease inertial forces, ultimately providing users with a more comfortable experience. The auxiliary force is described as follows:
In the formula, represents the weight compensation; represents the inertial force compensation; and and are proportional coefficients that control the size of the required compensation force. For the weight force compensation, represents the mass of an individual; represents the acceleration of gravity; and represents the vertical acceleration of an individual. Note that when is determined, it remains constant and becomes the primary unloading force of the system. Furthermore, can be adjusted in response to changes in the acceleration observed in human motion dynamics. Given that the magnitude of is limited during walking, the value of falls within a narrow range, primarily ensuring comfort for the subjects. Therefore, is crucial in achieving adjustability through the control algorithm.
In our suspension system, the rope passes through a movable pulley output component, winds around a fixed pulley component connected to an S-type tension sensor, and is anchored to a fixed pulley assembly on the short side support plate before winding into the capstan. This arrangement allows for the vertical movement of the rope. These components generate auxiliary forces to compensate for weight and dynamically adjust to human movements or environmental conditions, thereby reducing muscular effort. Since two driving systems act on a traction rope, if the expected driving force is , the expected driving force of system 1 is , while that of system 2 is . Their relationship with the auxiliary force is as follows:
Specifically, the desired driving force of the system is controlled by the admittance control algorithm. Admittance control is a force–position control strategy that ensures precise control over the force and position of the load by managing the system’s admittance [21]. This method incorporates an inner loop focused on position control and an outer loop centered on force control; specifically, a desired position generated by the second-order admittance model is adjusted to conform to a predefined position trajectory before being forwarded to the position control’s inner loop for final adjustments. The implementation process is shown in Figure 3.
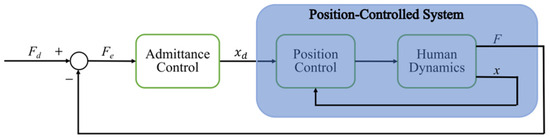
Figure 3.
Working process of admittance control algorithm of system 1 and 2.
The core expression of the admittance control module in the flow chart is as follows:
Among them, represent the inertia, damping, and stiffness characteristics, respectively; the dynamic properties of the robot can be altered by adjusting these parameters. represent the expected acceleration, velocity, and trajectory of the target, respectively. represent the initial expected acceleration, velocity, and trajectory of the target, respectively. is the difference between the actual contact force and the expected force . In the control module, the S-type pressure sensor is connected to the fixed pulley assembly, allowing to be measured in real time. The actual output position, , is converted by the servo motor encoder.
The transfer function of admittance control is as follows:
In order to improve the performance of the admittance control, we added links such as balancing noise, displacement, and speed compensation on the basis of the admittance control, as shown in Figure 4. The purpose of the compensator is to prevent large variations in the displacement and speed of the subject, thereby avoiding discomfort. When the displacement exceeds the prescribed limits, the algorithm will reduce the displacement appropriately, and it maintains the subject within acceptable bounds; when the displacement is within these bounds, the speed will be mildly adjusted to prevent excessive movement of the traction rope. The function of noise balancing is to mitigate minor disturbances in the system.
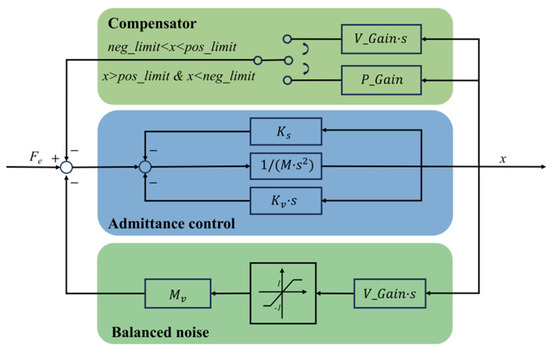
Figure 4.
Admittance control module.
In this admittance control configuration, the system compliance can be easily adjusted by modifying the values . The principle of the position control module in the control chart involves designing a position controller to track . The position controller used in this study is a proportional–differential (PD) controller. The mathematical expression of the PD controller used for position control is as follows:
In the formula, is the proportional gain, which controls the influence of the proportional part. is the differential gain, which controls the influence of the differential part. Since are known, in Formula (4) remains the only unknown. Once the reference contact force is set, the above differential equation can be solved. The solution to this differential equation is a time-varying function. Subsequently, the expected position is continuously adjusted via the position closed loop in Formula (6), drawing the driving load mechanism progressively closer to this target value until it stabilizes at the desired position.
In the steady state, the force balance equation of the controller becomes Equation (7), and the stiffness can be adjusted by modifying .
Since and are adjustable, we can configure two distinct driving systems by setting appropriate parameter values. Therefore, when the relevant parameters in the control system are dynamically adjusted, drive system 1 can be obtained, thus realizing the online adjustment of the simulated spring stiffness. By setting fixed parameters in the control system, drive system 2 can be established, which is designed to deliver a stable unloading force throughout the system. The specific parameters are listed in Table 1.

Table 1.
Parameters setting of the BWS system.
By integrating admittance control principles with two active drive systems and employing an automatic control algorithm to ensure consistent weight loss, the components—sensor, rope, and active drive system—function cohesively as a unified suspension system. This configuration allows the intelligent anti-gravity dynamic suspension system, equipped with adjustable online stiffness, to synchronize the center of gravity precisely with the user’s gait cycle. Consequently, this system achieves stable force control and dynamic weight management effectively.
2.4. Evaluation
A comprehensive evaluation of the body weight support (BWS) system was conducted, focusing on two primary dimensions: 1. to explore the displacement and force variations in ropes across different participants under various stiffness settings and to observe the system’s real-time performance under conditions of online variable stiffness, assessing its adaptability and responsiveness; and 2. to evaluate the consistency of the weight reduction among the same participants under different stiffness settings, aiming to determine the most suitable stiffness parameters tailored to the unique needs of specified participants.
Prior to the experiment, the system was calibrated using standard weights as an initial step. Subsequently, participants were instructed to walk on the treadmill (Figure 5), and force signals were measured to calculate both the average and maximum unloading errors. The results demonstrated that the system is suitable for patients weighing up to 200 kg, with a maximum dynamic unloading capacity of 150 kg. Upon receiving the automatic unloading control command, the motor engaged, lifting the participant to the desired unloading force. Throughout the walking training session, the system maintained a consistent unloading force with minimal fluctuation. Notably, the required unloading can be adjusted in real time during walking training without interrupting the treadmill activity or physically lifting the patient.

Figure 5.
BWS system test by a participant.
In weight unloading rehabilitation training, it is crucial to gradually reduce the unloading weight mass based on the patient’s recovery progress until they can independently support their own weight without relying on the BWS system. Inadequate weight unloading can lead to muscle injury, whereas excessive weight unloading may fail to achieve the desired rehabilitation effect. In this experiment, five healthy subjects with weights ranging approximately from 50 kg to 100 kg were selected. Half of their body weight was unloaded during the training. The treadmill was set to a walking speed of 4 km/h, and the stiffness of the system varied from 0 to 1000 N/m. NI acquisition cards with a sampling frequency of 2 kHz were employed to capture accurate data. During each experiment, the subjects walked on the treadmill for a duration of 1 min. A pre-written MATLAB program (R2024a) was utilized to record the displacement, tension, and other relevant data during the walking process. To ensure reliability and validity, each experiment was repeated three times, allowing for comprehensive data collection and analysis.
2.5. Safety
To ensure the experiment’s safety, this system incorporated three carefully designed safety measures. Firstly, an emergency stop circuit was implemented. When the therapist or subject activated the emergency stop button, this circuit engaged, causing the winch to lock into its final position. Secondly, a limit swing rod support was strategically positioned on the long side plate at the system’s main structure’s bottom. A magnetic switch mounting base was symmetrically installed to the limit the swing rod support using an internal hexagonal screw. One end of the circular limit rod was hinged to the limit swing rod support via an internal hexagonal screw, while the other end was positioned to make contact with the magnetic switch mounting base. This configuration ensured that if the displacement of the flexible rope end exceeded the predetermined safety limit, it would trigger the circular limit rod, activating the magnetic switch and prompting an urgent system brake. Finally, a manual switch was incorporated on the main system structure’s side. This allowed the user to pull down the manual switch pull rope in case of an emergency, enabling an immediate emergency brake for the system.
3. Results
3.1. The System Realizes Adjustable Support Stiffness
In examining the results of this experiment, we focused on the system’s performance in achieving adjustable stiffness. To substantiate stiffness adaptability, it is essential to examine the correlation between the rope elongation and unloading force. Therefore, we conducted experiments on participants with weights approximating 50, 60, 70, 80, and 100 kg. The rope displacement under varying stiffness levels was determined by converting the data collected from the encoder, as shown in Figure 6.
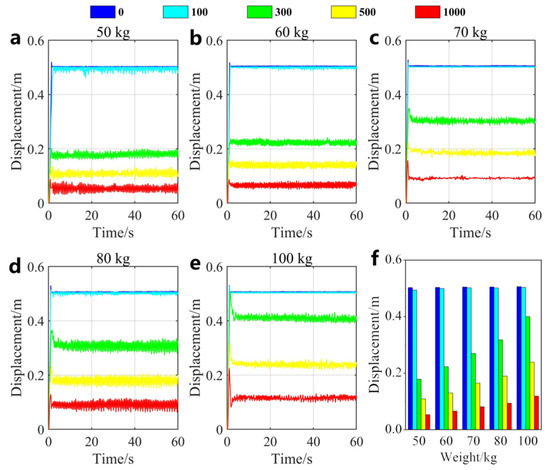
Figure 6.
The rope displacement of different subjects under different stiffness. (a) The rope displacement of 50 kg test object under different stiffness. (b) The rope displacement of 60 kg object under different stiffness. (c) The rope displacement of 70 kg test object under different stiffness. (d) The rope displacement of 80 kg test object under different stiffness. (e) The rope displacement of 100 kg test object under different stiffness. Among them, stiffnesses of 0, 100, 300, 500, and 1000 correspond to the rope displacement of red, green, black, magenta, and yellow lines. (f) Mean value statistics of rope displacement under different stiffness in steady state.
At 0 stiffness, the rope exhibited characteristics akin to infinite extensibility, thus reaching the maximum displacement, as illustrated by the red curve in Figure 6a. At a stiffness of 100, the rope exhibited a noticeable elastic potential energy, resulting in significant elongation, as depicted by the green curve in the diagram. Subsequently, at stiffness levels of 300, 500, and 1000, the elongation sequentially decreased. This observation leads us to conclude that the system can achieve a rope stiffness from 0 to 1000. In Figure 6b–e, the relationship between the rope displacement and stiffness is distinctly evident. At a stiffness of 100, as the load increased, the rope’s displacement also reached the limit range. At stiffness levels of 300, 500, and 1000, under the same load, the elongation gradually decreased with increasing stiffness. Although the actual rope displacement may deviate due to the fluctuation of the experimenter’s center of mass, there seems to be a linear relationship between elongation and mass, as shown in Figure 6f. In order to further explain this “linear relationship” quantitatively, we use Pearson’s correlation coefficient to verify Hooke’s law theoretically. Pearson’s correlation coefficient is a statistic used to measure the strength and direction of a linear relationship between two continuous variables, and its expression is as follows.
where and are data points, respectively, and and are the average values of the data, respectively. is the number of samples. If the correlation coefficient is close to 1 or −1, it shows that there is a strong linear relationship between them; if it is close to 0, it shows that there is no obvious linear relationship between them. Therefore, when the stiffness levels were 300, 500, and 1000, respectively, we calculated the Pearson correlation coefficient of elongation and mass, and the values are shown in the following table. Table 2 shows the change in elongation (unit: m) of different objects (50–100 kg) under different stiffness. When the stiffness is 0 and 100, with the increase of load, the displacement of the rope reaches the limit range. Therefore, Pearson’s correlation coefficient in these two cases is not considered.

Table 2.
Pearson’s correlation coefficient of elongation and mass.
In the table, we can see that the Pearson correlation coefficient between mass and rope elongation was very close to 1 under different stiffness conditions, which indicates that there was a significant linear correlation between them. In other words, with the increase in application quality, the elongation of the rope also increases, and this increase shows a linear growth trend. The establishment of this linear relationship provides strong statistical support for the further study of the mechanical behavior of ropes under different load conditions.
3.2. Motion Stability of the System When Stiffness Changes
This study investigated the stress dynamics of the rope under varying stiffness settings while maintaining dynamic equilibrium, providing insights into the system’s stability. Our examination tested the stress performance at the rope’s end across various stiffness levels with different subjects. The purpose was to determine the stress experienced at the rope’s end in the system’s dynamic equilibrium state. Focusing on the statistical value of the expected and measured forces at the rope’s end, we used the results from the 50 kg subject as a reference, as shown in Figure 7a–e.
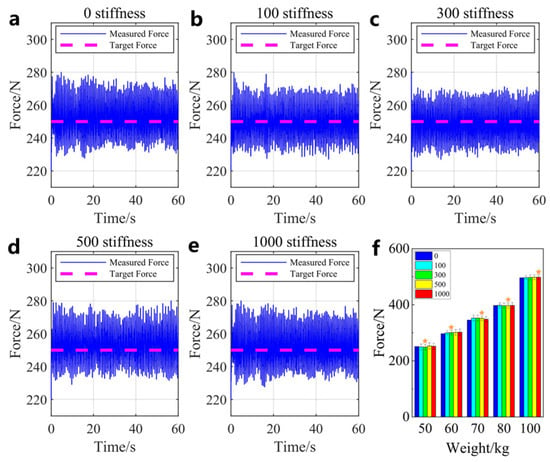
Figure 7.
The experimental results are given at different unloading weights with feedback from the experimenters. (a) Expected force and measured force of the rope end of 50 kg experimental object under 0 support stiffness. (b) Expected force and measured force of the rope end of 50 kg experimental object under 100 support stiffness. (c) Expected force and measured force of the rope end of 50 kg experimental object under 300 support stiffness. (d) Expected force and measured force of the rope end of 50 kg experimental object under 500 support stiffness. (e) Expected force and measured force of the rope end of 50 kg experimental object under 1000 support stiffness. (f) RMS (bar) and RMSE (black line on the bar) of measuring force, and the stars in the figure are suitable stiffness for different objects.
The system’s control goal is to minimize the deviation between the measured and target unloading weights (half of the mass). The observations show that the system’s unloading weight fluctuated around half of the mass across different stiffness settings. To quantitatively assess the system performance, two indicators were selected: root mean square (RMS) and root mean square error (RMSE). Their mathematical expressions are as follows:
where is the observed value, is the target value, and is the number of observed values. In our experiment, is the measured force and is the expected force, as shown in Figure 7a–e. The ratio of these indicators was used to compute a dimensionless metric, the “Relative Root Mean Square Error (R-RMSE)”. This index, commonly used in data analysis, measures the root mean square error relative to the population. It offers additional insights into error analysis by accounting for the variability of the root mean square error in relation to the data. The R-RMSE is typically used to compare different models’ performance, aiding in model selection and accuracy evaluation [22]. The evaluation indicators’ statistical results are detailed in Table 3, Table 4, Table 5, Table 6 and Table 7. To facilitate comparison, these statistical outcomes are visually presented in Figure 7f, illustrating the root mean square results.

Table 3.
Rope stress data of a 50 kg person.

Table 4.
Rope stress data of a 60 kg person.

Table 5.
Rope stress data of a 70 kg person.

Table 6.
Rope stress data of an 80 kg person.

Table 7.
Rope stress data of a 100 kg person.
It is important to note that the support reached the maximum elongation at 0 stiffness. Similarly, in the experiments with 60, 70, 80, and 100 kg unloading weights, the maximum displacement occurred at a support stiffness of 100, as shown in Figure 6. Therefore, we will not discuss the force at 100 support stiffness. The experimental results demonstrate that our system control method accurately managed the unloading force. The Relative Root Mean Square Error (R-RMSE), which is the ratio between the RMSE and the RMS, remained consistently below 5% when unloading half the weight at different stiffness levels. As the stiffness varied, so did the RMSE, allowing us to identify suitable stiffness intervals for different subjects. The very small R-RMSE values indicate satisfactory system performance. Smaller error bars indicate better performance. The error bars reveal that the optimal stiffness was around 300 for the 50 kg and 60 kg subjects, around 500 for the 70 kg and 80 kg subjects, and about 1000 for the 100 kg subjects, as marked by the stars in Figure 7f.
Finally, we focused on the subjects’ actual experiences, conducting interviews and investigations. The five subjects reported comfort, aligning with the experimental results. Therefore, in clinical settings, medical staff can adjust the unloading force based on individual patient needs to enhance gait rehabilitation training outcomes [23].
In summary, our system’s adjustable stiffness helps balance control performance and user experience. By adjusting the support stiffness, each subject can find their optimal setting. This offers a new approach to personalized therapy.
4. Discussion
In traditional body weight support (BWS) systems, mechanical designs frequently utilize rope and spring suspensions [24]. This design provides vertical support using ropes or springs, thereby reducing patient weight and facilitating walking or other rehabilitation exercises. For example, M. Frey et al. [25] introduced a BWS system that enhanced the rope suspension system, incorporated spring suspension, and they explored how the system simulated the anti-gravity effect to aid patients in regaining walking abilities. Similarly, Pennycott A et al. [26] employed a BWS system featuring a spring suspension. These studies show that the spring system is very important for gait rehabilitation. Although spring suspensions provide moderate support, their stiffness, once selected, is cumbersome to adjust frequently according to patient needs. By enhancing the traditional mechanical structure, we developed a variable-stiffness weight support system based on admittance control, effectively addressing the issue of stiffness in conventional BWS systems.
As early as 2000, Colombo et al. [27] explored how support stiffness affects gait patterns and movement freedom. Chen G et al. [28] supplemented this research, noting that rigid support might restrict patient movement and impede natural gait. Flexible support allows for greater freedom and more natural gait patterns. Hidler J and colleagues discovered that adjusting the support stiffness can modify patient support levels, where more rigid settings enhance stability and reduce the risk of swaying and falling [29]. In 2012, Moreno J C et al. [30] analyzed how various stiffness settings influence patient support and rehabilitation outcomes. Pennycott A et al. [31] later demonstrated that personalized rehabilitation could be achieved by adjusting support stiffness. Flexible support, requiring greater balance and core stability, may benefit certain patients. During rehabilitation training, support stiffness can be progressively adjusted, allowing patients to reduce the support gradually, increase their weight load, and enhance their capability to return to normal walking [32]. Medical professionals can select the optimal stiffness tailored to each patient’s specific needs and rehabilitation goals, enhancing the overall rehabilitation outcomes. In summary, support stiffness is a crucial parameter in body weight support systems, significantly impacting their performance and effectiveness. Therefore, developing an online adjustable BWS system is essential, as it impacts the support level, stability, freedom, and personalized treatment, aiding patients in gradually regaining their ability to walk. This advancement will significantly enhance both the efficiency of medical staff during rehabilitation processes and patient outcomes.
In our experiments, it was demonstrated that our variable-stiffness weight support system effectively addresses key issues such as variable support stiffness and facilitates online adjustment of support stiffness. By setting different stiffness gradients, a support stiffness that is suitable for diverse user groups can be consistently achieved. The system’s performance and stability have proven excellent across various demographics, and experimenter feedback has been overwhelmingly positive, promising a novel intelligent approach for personalized patient treatment.
However, our variable-stiffness weight support system is still in the initial stage, and its stability and comfort are contingent upon the ongoing development and refinement of the control system. In the future, we need to design a special control algorithm in an unloading system to adjust the support level and offer personalized support. Additionally, sensor technologies like electromyography and motion capture systems will be employed to obtain real-time biofeedback, with the data being integrated into the control algorithm to adjust the support level and gait [33]. Furthermore, virtual reality and augmented reality can be integrated with the BWS system to create a more engaging and effective rehabilitation environment. Experimental evidence indicates that virtual reality training can significantly enhance the gait abilities of stroke patients [34]. Further research will be conducted to expand on these findings. Going forward, more experimental data and interdisciplinary research are needed to further optimize our system’s performance and enhance its robustness.
5. Conclusions
Given the complexities associated with adjusting support stiffness in traditional BWS systems, which typically employ either a mass–rope static support or a mass–spring–damping dynamic support system and often lead to abnormal gait training, we have developed a BWS system featuring variable online stiffness based on admittance control and confirmed that the support stiffness could be adjusted through design experiments. Moreover, it was demonstrated that the system can simulate the unloading amount under various stiffness settings, which facilitates unloading weight gait rehabilitation training for patients and offers suitable stiffness for different experimenters. The system enables medical staff to select the supporting stiffness suitable for individual rehabilitation training based on the needs of diverse patient groups and to adjust the stiffness in real time based on patient condition, thereby facilitating personalized rehabilitation therapy.
Author Contributions
X.L. carried out the experiments, collected the results, performed the data analysis, and wrote the manuscript; S.A. designed the figures and contributed to the writing of the manuscript; J.Z. performed the data analysis, contributed to the writing of the manuscript, and designed and manufactured the equipment; Y.H. verified and supervised this study. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52005169), and the Doctoral Research Initiation Fund of Hubei University of Technology (XJ2022001101).
Data Availability Statement
The datasets used during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to thank the study participants.
Conflicts of Interest
Author Yizhe Huang was employed by the company Dongfeng Liuzhou Motor Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
BWS: body weight support; RMSE: root mean square error; RMSE: root mean square error.
References
- Wang, Y.L.; Wang, K.Y.; Zhang, Z.X.; Han, Z.; Wang, W.L. Analysis of dynamical stability of rigid-flexible hybrid-driven lower limb rehabilitation robot. J. Mech. Sci. Technol. 2020, 34, 1735–1748. [Google Scholar] [CrossRef]
- Li, X.; He, B.; Deng, Z.; Chen, Y.; Wang, D.; Fan, Y.; Su, H.; Yu, H. A Center of Mass Estimation and Control Strategy for Body-Weight-Support Treadmill Training. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Salazar, J.; Hirata, Y. Development of Walking Assist Robot with Body Weight Support Mechanism. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Iwaki, Fukushima, Japan, 11–14 January 2021; pp. 554–559. [Google Scholar] [CrossRef]
- Hesse, S.; Bertelt, C.; Jahnke, M.T.; Schaffrin, A.; Baake, P.; Malezic, M.; Mauritz, K.H. Treadmill training with partial body weight support compared with physiotherapy in nonambulatory hemiparetic patients. Stroke 1995, 26, 976–981. [Google Scholar] [CrossRef] [PubMed]
- Barbeau, H.; Visintin, M. Optimal outcomes obtained with body-weight support combined with treadmill training in stroke subjects. Arch. Phys. Med. Rehabil. 2003, 84, 1458–1465. [Google Scholar] [CrossRef] [PubMed]
- Miyai, I.; Tanabe, H.C.; Sase, I.; Eda, H.; Oda, I.; Konishi, I.; Tsunazawa, Y.; Suzuki, T.; Yanagida, T.; Kubota, K. Cortical mapping of gait in humans: A near-infrared spectroscopic topography study. NeuroImage 2001, 14, 1186–1192. [Google Scholar] [CrossRef] [PubMed]
- Enzinger, C.; Dawes, H.; Johansen-Berg, H.; Wade, D.; Bogdanovic, M.; Collett, J.; Guy, C.; Kischka, U.; Ropele, S.; Fazekas, F.; et al. Brain activity changes associated with treadmill training after stroke. Stroke 2009, 40, 2460–2467. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.Y.; Wang, Y.L.; Yin, P.C. Design and remote collaboration control of asymmetric rigid-flexible hybrid-driven lower limb rehabilitation robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 236, 1796–1814. [Google Scholar] [CrossRef]
- Sethi, D.; Bharti, S.; Prakash, C. A comprehensive survey on gait analysis: History, parameters, approaches, pose estimation, and future work. Artif. Intell. Med. 2022, 129, 102314. [Google Scholar] [CrossRef] [PubMed]
- Villa-Parra, A.C.; Lima, J.; Delisle-Rodriguez, D.; Vargas-Valencia, L.; Frizera-Neto, A.; Bastos, T. Assessment of an assistive control approach applied in an active knee orthosis plus walker for post-stroke gait rehabilitation. Sensors 2020, 20, 2452. [Google Scholar] [CrossRef]
- Apte, S.; Plooij, M.; Vallery, H. Influence of body weight unloading on human gait characteristics: A systematic review. J. Neuroeng. Rehabil. 2018, 15, 1–18. [Google Scholar]
- Dobkin, B.; Apple, D.; Barbeau, H.; Basso, M.; Behrman, A.; Deforge, D.; Ditunno, J.; Dudley, G.; Elashoff, R.; Fugate, L.; et al. Weight-supported treadmill vs over-ground training for walking after acute incomplete SCI. Neurology 2006, 66, 484–493. [Google Scholar] [CrossRef] [PubMed]
- van Hedel HJ, A.; Rosselli, I.; Baumgartner-Ricklin, S. Clinical utility of the over-ground bodyweight-supporting walking system Andago in children and youths with gait impairments. J. Neuroeng. Rehabil. 2021, 18, 29. [Google Scholar] [CrossRef] [PubMed]
- Hicks, A.; Adams, M.; Ginis, K.M.; Giangregorio, L.; Latimer, A.; Phillips, S.; McCartney, N. Long-term body-weight-supported treadmill training and subsequent follow-up in persons with chronic SCI: Effects on functional walking ability and measures of subjective well-being. Spinal Cord 2005, 43, 291. [Google Scholar] [CrossRef] [PubMed]
- Celestino, M.L.; Gama, G.L.; Barela, A.M. Gait characteristics of children with cerebral palsy as they walk with body weight unloading on a treadmill and over the ground. Res. Dev. Disabil. 2014, 35, 3624–3631. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Salazar, J.; Hirata, Y. Control and Evaluation of Body Weight Support Walker for Overground Gait Training. IEEE Robot. Autom. Lett. 2021, 6, 4632–4639. [Google Scholar] [CrossRef]
- Zhang, X.; Shang, P.; Li, B. A novel Dynamic Body Weight Support overground co-walker enabling variable unloading ratio and Motion Tracking. Front. Neurosci. 2023, 17, 1188776. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.L.; Wang, K.-Y.; Zhang, Z.-X. Design, comprehensive evaluation, and experimental study of a cable-driven parallel robot for lower limb rehabilitation. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 371. [Google Scholar] [CrossRef]
- Kwak, J.; Choi, W.; Lee, C.; Oh, S. Gravity and impedance compensation of body weight support system driven by two series elastic actuators. IEEE/ASME Trans. Mechatron. 2021, 27, 190–201. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Liu, X.; Zhang, P.; Wang, W. Design and Variable Parameter Control Strategy of Weight Support Gait Training Robot. In Proceedings of the International Conference on Intelligent Robotics and Applications’, Hangzhou, China, 5–7 July 2023; Springer Nature: Singapore, 2023; pp. 575–587. [Google Scholar]
- Roveda, L.; Maskani, J.; Franceschi, P.; Abdi, A.; Braghin, F.; Molinari Tosatti, L.; Pedrocchi, N. Model-based reinforcement learning variable impedance control for human-robot collaboration. J. Intell. Robot. Syst. 2020, 100, 417–433. [Google Scholar] [CrossRef]
- Huo, J.; Huang, J.; Tu, X.; Fu, Z. Force sensorless admittance control of body weight support system. Adv. Robot. 2021, 35, 425–436. [Google Scholar] [CrossRef]
- Angeli, C.A.; Boakye, M.; Morton, R.A.; Vogt, J.; Benton, K.; Chen, Y.; Ferreira, C.K.; Harkema, S.J. Recovery of Over-Ground Walking after Chronic Motor Complete Spinal Cord Injury. N. Engl. J. Med. 2018, 379, 1244–1250. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.R.; Lo, W.L.; Lin, Q.; Li, L.; Xiao, X.; Raghavan, P.; Huang, D.F. The Effect of Body Weight Support Treadmill Training on Gait Recovery, Proximal Lower Limb Motor Pattern, and Balance in Patients with Subacute Stroke. BioMed Res. Int. 2015, 2015, 175719. [Google Scholar] [CrossRef] [PubMed]
- Frey, M.; Colombo, G.; Vaglio, M.; Bucher, R.; Jorg, M.; Riener, R. A Novel Mechatronic Body Weight Support System. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Pennycott, A.; Wyss, D.; Vallery, H.; Riener, R. Effects of added inertia and body weight support on lateral balance control during walking. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–5. [Google Scholar]
- Colombo, G.; Joerg, M.; Schreier, R.; Dietz, V. Treadmill training of paraplegic patients using a robotic orthosis. J. Rehabil. Res. Dev. 2000, 37, 693–700. [Google Scholar] [PubMed]
- Chen, G.; Patten, C.; Kothari, D.H.; Zajac, F.E. Gait deviations associated with post-stroke hemiparesis: Improvement during treadmill walking using weight support, speed, support stiffness, and handrail hold. Gait Posture 2005, 22, 57–62. [Google Scholar] [CrossRef]
- Hidler, J.; Nichols, D.; Pelliccio, M.; Brady, K.; Campbell, D.D.; Kahn, J.H.; Hornby, T.G. Multicenter randomized clinical trial evaluating the effectiveness of the Lokomat in subacute stroke. Neurorehabilit. Neural Repair 2009, 23, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Moreno, J.C.; Barroso, F.; Farina, D.; Gizzi, L.; Santos, C.; Molinari, M.; Pons, J.L. Effects of robotic guidance on the coordination of locomotion. J. Neuroeng. Rehabil. 2013, 10, 79. [Google Scholar] [CrossRef]
- Pennycott, A.; Vallery, H. Body Weight Support Devices for Overground Gait and Balance Training. In Neurorehabilitation Technology; Reinkensmeyer, D.J., Marchal-Crespo, L., Dietz, V., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Dong, Z.; Hirata, Y. Control of Body Weight Support Walker Using Variable Stiffness Mechanism. In Proceedings of the JSME Annual Conference on Robotics and Mechatronics (Robomec); The Japan Society of Mechanical Engineers: Tokyo, Japan, 2021. [Google Scholar] [CrossRef]
- Havashinezhadian, S.; Chiasson-Poirier, L.; Sylvestre, J.; Turcot, K. Inertial Sensor Location for Ground Reaction Force and Gait Event Detection Using Reservoir Computing in Gait. Int. J. Environ. Res. Public Health 2023, 20, 3120. [Google Scholar] [CrossRef]
- Kim, M.J. Virtual Reality Community Gait Training Using a 360° Image Improves Gait Ability in Chronic Stroke Patients. J. Korean Phys. Ther. 2020, 32, 186–192. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).