1. Introduction
Pneumatic artificial muscles (PAMs) differ from more conventional actuators due to the inherently compliant behaviour and nonlinear dynamics arising from their construction of flexible materials and actuation method. These properties make them desirable for applications such as medical robotics in rehabilitation scenarios and prosthetics as they more closely mimic biological muscle than conventional actuators. This allows for a more comfortable human–robot interaction, as the compliance allows the user some give in their voluntary movement when under the external influence of a robot, as well as making the systems safer as it is less likely that unexpected forces or motion will injure the user or cause damage to the robot. They are also applicable to robotic platforms where a human-like motion is desired.
Various types of PAMs exist, suitable for different purposes based on differing characteristics, but all operate under the same principle. An elastic bladder is sealed and fixed at two ends, and upon pressurisation by compressed air will expand, applying force to the fixed ends of the actuator. A less elastic material surrounding the bladder, such as a harder rubber shell or braided fibre mesh, directs the force to cause the PAM to contract, expand, or bend about an axis depending on the construction [
1]. The original fluidic artificial muscles used in robotics were developed by Joseph McKibben in the 1950s for orthotics [
2,
3]. A more detailed review of the development of PAMs is presented in [
1].
While the compliant behaviour of PAMs is desirable in many branches of industry and research, this and their nonlinear dynamics makes accurate motion control a challenge. Standard linear control systems such as proportional integral derivative (PID) are less effective than in more conventional applications as the friction present in the contraction/expansion of PAMs causes a hysteresis and changing behaviour with time, as well as the uncertainties caused by the fluid dynamics of pressurised air. Model-based control schemes can alleviate this problem by mapping the behaviour of the actuator to allow for more accurate control, but a similar problem arises with the complexity of these models. Many different approaches have been developed and studied in order to model PAMs that attempt to balance complexity with functionality, to find a solution that is accurate but does not take an exceedingly long time or large amount of computation to produce. The review presented in [
4] describes some of the different approaches to the modelling problem of PAMs. The review suggests that geometric modelling is less suitable for these actuators as their parameters are difficult to accurately measure during use; however, their simplicity still makes the approach suitable for certain applications. The phenomenological modelling approach, which approximates the muscle as a mass–spring–damper system, is more suitable as this is a close approximation to the dynamics of PAMs based on their construction and flexible materials, and the simplicity makes them fairly easy to calculate. However, the hysteresis and nonlinearity over time is often not taken into consideration in these models. A simplified empirical model is also mentioned in which the PAM is simplified to that of a mechanical spring. Polynomial approximations of the parameters are used that allow for easy adjustment of the complexity/accuracy by increasing the degree of the model; however, again, these models suffer from not properly modelling the nonlinear behaviour of the PAMs.
Applications of these physical/mathematical models of PAMs are present throughout the literature. An early study on the phenomenological model for a McKibben muscle is presented in [
5]. Experiments were performed to determine the changing parameters of the PAM with pressure, resulting in a model with 15% root mean squared error (RMSE), with the largest error and the peak and trough of the actuator’s motion. An empirical model based on geometric constants of a McKibben muscle is presented in [
6] including experimental parameter estimation. This model is used in model-based PID control of the actuator, with performance deemed satisfactory and within tolerance levels. A non-linear numerical model for a McKibben muscle is shown in [
7], showing a maximum error in experimental comparisons of 3% of the total displacement. Various models for contractile length, pulling force, and a specific application of four McKibben muscles in an arm configuration are shown in [
8]. A mathematical model for an extensor PAM is presented in [
9], differing from more commonplace contraction PAMs as these increase in length with increased pressure rather than decreasing.
PAMs developed by FESTO are popular in industrial applications as their construction makes them more reliable. These PAMs have longer operating lives than typical nylon-braided McKibben muscles and a greater force output capability; thus, they are also studied in many research applications including modelling. A piecewise three-element model of a FESTO PAM is presented in [
10] for improved model predictive control (MPC). The piecewise model uses multiple three-element systems for different pressure levels in the PAM in order to overcome the nonlinearity of the actuator. The MPC developed with this piecewise model, in comparison with PID control, has much better performance. Mathematical models of FESTO PAMs are presented in [
11,
12], and phenomenological models are shown in [
13,
14].
In recent years, more research has gone into applying machine intelligence in the form of learning and optimisation to the problem of PAM modelling. This gives the advantage of potentially more accurate models with more sophisticated parameters as well as alleviating some of the need to measure the actuator’s complex parameters and dynamics. Neural networks are a popular algorithm used in this application; neural networks can be tailored to the specific needs of the model, and their complexity can be varied easily. A modelling method using an artificial neural network as well as hybrid backpropagation algorithm and genetic algorithm for the learning stage is presented in [
15] for modelling a novel pleated PAM with promisingly accurate results obtained in experiments. Various other neural network-based modelling approaches have been applied to FESTO PAMs, including a recurrent fuzzy-neuro approach in [
16] and neural network approaches for antagonistic pairs of PAMs in [
17,
18]. The architecture of each neural network used in these studies is widely similar, with multiple input nodes, a similar number of hidden nodes, and a single output.
Another common approach in applying intelligence in modelling is optimisation, with particle swarm optimisation (PSO) algorithms being a popular choice. PSO uses a swarm of particles that interact with each other as they move around a search space attempting to minimise some cost function. By using a large number of particles in the swarm, solutions can be found much faster. In the case of actuator modelling, each particle has a number of parameters that describe both its position in the search space as well as the parameters used in the equation describing the dynamics of the actuator. The objective function is typically some combination of errors between the actual behaviour of the actuator and the approximated behaviour based on each particle’s parameters. Using this method, the actual parameters can be approximated rapidly and accurately, with the calculation time being largely invariant to the complexity of the model. An empirical model of a McKibben muscle with parameters generated using PSO is presented in [
19] with the aim of characterising the hysteresis behaviour of the muscle. The model was verified to be accurate; however, the nonlinearities of the PAM are mentioned for causing some inaccuracies, and more intelligent control strategies are suggested as a solution. An inverse model for a PAM is presented in [
20], also based on an PSO algorithm for system identification.
Limitations exist for all modelling practices. As mentioned in [
4], geometric modelling is difficult to apply to PAMs accurately as online measuring of their nonlinear dynamic properties is difficult to achieve accurately. The standard phenomenological model using mass–spring–damper approximation also suffers lower accuracy due nonlinearity, as the linear model approximation does not account for hysteresis and disproportionate motion–input relationships. Intelligent learning algorithms, such as neural networks and genetic algorithm as presented in [
15,
16,
17,
18] and to an extent optimisation algorithms like PSO, can achieve highly accurate models of even complex nonlinear systems, but better approximations rely on sufficiently complex model parameterisation and learning datasets that can greatly increase the computational load and model generation time. This trade-off in model accuracy, complexity, and computation time must be accounted for.
This paper will present a piecewise PSO modelling method for a FESTO DMSP-20-400N PAM based on the phenomenological modelling approach. A three-parameter model based on the dynamics of the mass–spring–damper approximation for the PAM will be used as a template for the model, used for its good approximation of PAMs as well as its simplicity and low parameter count, reducing model complexity and improving generation time. In order to compensate for the nonlinearity of the PAM, a piecewise modelling method will be used with multiple different models for different sections of the actuator’s stroke length. Models generated in this manner will be compared experimentally with the PAM under different loads and inputs to validate their accuracy.
2. Materials and Methods
2.1. Phenomenological Model
The phenomenological model is commonly used in modelling PAMs due to their approximately similar behaviour to mass–spring–damper systems. A three-element model based on this will be used as a template for optimisation in this study. The equation of motion for this model is given as follows:
where M is the mass of the PAM, D is the damping element, C is the spring constant, Fc is the contractile force element applied by the internal pressure of the PAM, Fl is the force applied by external load to the system, and x(t) is the displacement of the actuator from its nominal position at a given time step. This model is shown in
Figure 1.
The contractile force applied by the PAM is proportional to the input pressure, making Fc proportional to the control input of the system, which will be henceforth denoted with U.
Using the displacement and velocity of the system as state variables, the following equations are obtained:
The equation of motion can be re-written in terms of these states:
The output of the system is the displacement of the actuator, so the output of the model
y(
t) is expressed as follows:
The state-space representation of this model in matrix form is given by the following:
The unknown parameters of the system based on Equation (8) are
,
, and
. These three elements will be approximated through optimisation using the PSO algorithm and will be referred to henceforth as
,
, and
respectively. The model equations for each state-space solution are given by Equations (9) and (10).
2.2. Particle Swarm Optimisation Algorithm
The classical PSO algorithm is referenced extensively in the literature [
19,
20,
21,
22]. It uses a group of potential solutions (particles) to an optimisation function that iteratively updates their parameters in response to some fitness function, with these parameters acting as coordinates in a search space. The particles base their movement around the search space on both their own best fitness performance and the overall best fitness found in the swarm. This sharing of data between solutions allows for fast optimisation convergence. The following equations describe the velocity and position updates for the particles at each iteration of the algorithm:
where
i is the current particle;
k is the current iteration of the algorithm;
V is the particle’s velocity in the search space;
X is a particle’s position in the search space quantified by its parameters;
Rand is a random value between 0 and 1;
Xibest is the position of the current particle which achieved the best (lowest) fitness;
Gbest is the global best position of all particles in the swarm; and
W,
C1, and
C2 are algorithm parameters that are tuned manually.
The parameters to be optimised using PSO algorithm in this study are
,
, and
as described in Equation (10). As such the search space is three-dimensional. The optimisation function used to determine the fitness of each particle is the root mean squared error (RMSE) between the expected displacement of the PAM based on the model generated by a particle’s parameters and the actual displacement of the PAM, measured over a period of one repeated sin wave motion, as described in Equation (13).
where
is the fitness value for the current particle;
t is the time step;
N is the number of time steps in the measured motion sequence;
x is the measured displacement of the PAM; and
is the output of the model based on Equations (9) and (10) using the three parameters of particle
as
,
, and
at time step
t.
Using this method, generated model solutions are iteratively improved based on how accurately they match the motion of the PAM. The update parameters of the algorithm are W = 0.9 to prevent divergent swarm motion and C1 = C2 = 2 to increase the efficacy of the algorithm and reach solutions in fewer iterations, while maintaining low enough velocities to keep the swarm coherent. The number of particles in the swarm is set to 50 as a balance between the time taken for each iteration and convergence time to a solution.
2.3. Piecewise Model
The nonlinear nature of PAMs makes them difficult to accurately approximate with linear models such as the three-element model described in
Section 2.1. Nonlinear models of this nature are much more computationally complex and not feasible to generate using optimisation methods such as PSO. As such, a compromise is made in the form of piecewise models. Multiple models will be generated using different reference target motions of the PAM, as well as different input ranges within those motions. These models are then put together, each operating during the specific range of inputs to the system as specified by how they were generated. The resulting piecewise model comprised of multiple linear models should better approximate the nonlinearity of the PAM than a single linear model.
The nature of the PAM’s nonlinearity is twofold. Internal friction caused by the braided fibres in the outer mesh cause a hysteresis to occur, and the method of actuation in inflation by pressurised air makes the displacement not linearly proportional to input pressure, with displacement velocity gradually decreasing along the stroke length of the actuator. To account for the hysteresis, different models can be generated for the actuator’s inflation and deflation. The disproportionate motion across the stroke length can again be accounted for by generating multiple models for different input ranges.
Each piecewise model is therefore comprised of multiple individual three-parameter solutions as described in Equation (10). In order to generate the whole piecewise model solution, the PSO algorithm is run once for each model section, generating three parameters per section.
The model output for each part of a piecewise model solution would therefore be described using Equations (14) and (15).
With the specific model used based on the input
according to the following:
As well as differentiation of the inflating and deflating states according to the following:
where
is the model section,
is the total number of linear model sections of the piecewise model, and
is the input bound determining the upper bound of the model section
and the lower bound of the model section
. Each model section
will have a set of
,
, and
that are independently generated for each
using the PSO algorithm for a total parameter count of
per piecewise model.
In cases where both the input ranges and inflating/deflating state differentiations are used, each model section
will constitute both an inflating and deflating state, resulting in both
and
, such that
would be given by the following equation:
However, there then exists a trade-off between accuracy and computational efficiency in using piecewise modelling. A greater number of models across the stroke length will ultimately cause the model to be more accurate as the nonlinearity is better approximated; however, this also results in the model being far more complicated, taking much longer to generate, and having far more parameters. There is also the issue of reference motions becoming too small to properly approximate the overall motion of the PAM, potentially causing each individual model to be less accurate within its own input range. As such the piecewise models generated in this study will comprise of six input ranges, spaced across the stroke length of the actuator to best model the nonlinearity of motion, as well as different models generated for the inflating and deflating state.
2.4. Experimental Setup
The actuator to be used in this work is a FESTO DMSP-20-400N PAM. As previously discussed, PAMs provide compliant motion, which is desirable in a rehabilitation robot. They are also controlled with a single pressurised air input, meaning the only necessary control value is the air pressure flowing into the PAM. The main output measure of the setup is the actuator’s displacement to be used to generate target references for the optimisation function as well as measure the error and calculate accuracy of the models. The load force applied to the PAM will also be measured to test the effects of external loads on the accuracy of the models. To measure each of these, a linear encoder and a load cell will be connected to the actuator.
The load cell used is a FUTEK LCM300 model and has a 300 Lb load limit and sufficient precision for any force changes required by the system. The displacement encoder connected to the bottom of the linear actuator is a FESTO MLO-POT-300-TLF with a resolution of 0.01 mm and stroke length of 300 mm, both of which are sufficient for the system. The proportional pressure regulator used is a FESTO VPPM-6L-L-1-G18-0L6H. The system is held in place with a frame consisting of slotted aluminium extrusion, and the PAM is positioned vertically to ensure motion and forces are not adversely affected by the actuator’s intrinsic compliance regarding gravity.
To control the system, a RoboRIO is connected to a desktop PC and coded using National Instruments LabVIEW. The outputs of the load cell and the displacement encoder are input to the RoboRIO to be measured on the display. The load cell is connected to a FUTEK IAA100 strain gauge voltage amplifier before the output is taken by the RoboRIO to allow for easier signal processing.
Figure 2 shows a diagram of the experimental setup alongside the circuitry and computer communication systems used for data acquisition and actuator control.
Figure 3 shows the PAM in the experimental setup.
4. Discussion
Performance criteria for real-time operating models of actuators such as the ones presented here are numerous; thus, a consensus on the best performing model is difficult to reach. These criteria include accuracy to the physical system, robustness to external forces including both load and environmental noise and to different operating modes and input sequences, and computational complexity in generation and during runtime.
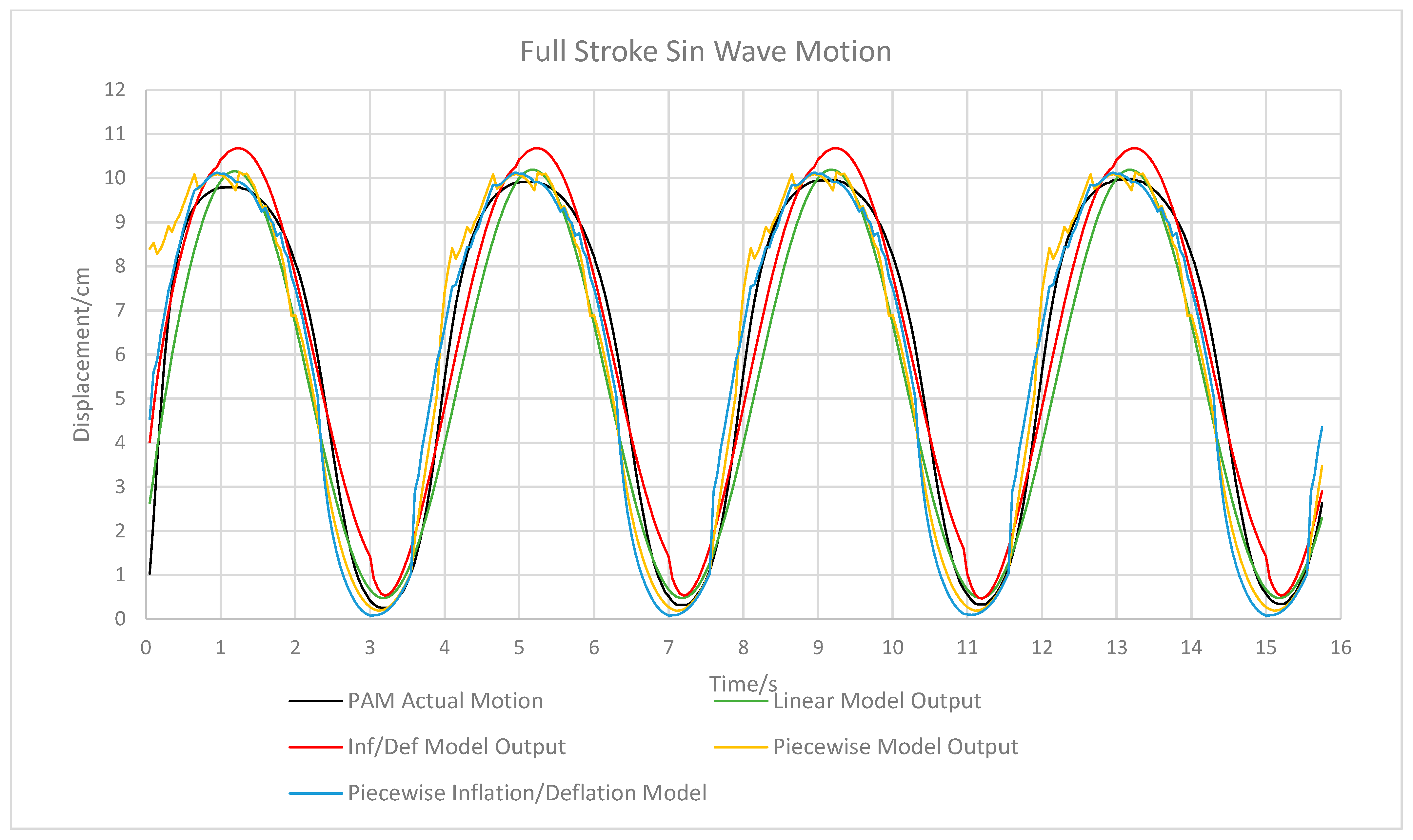
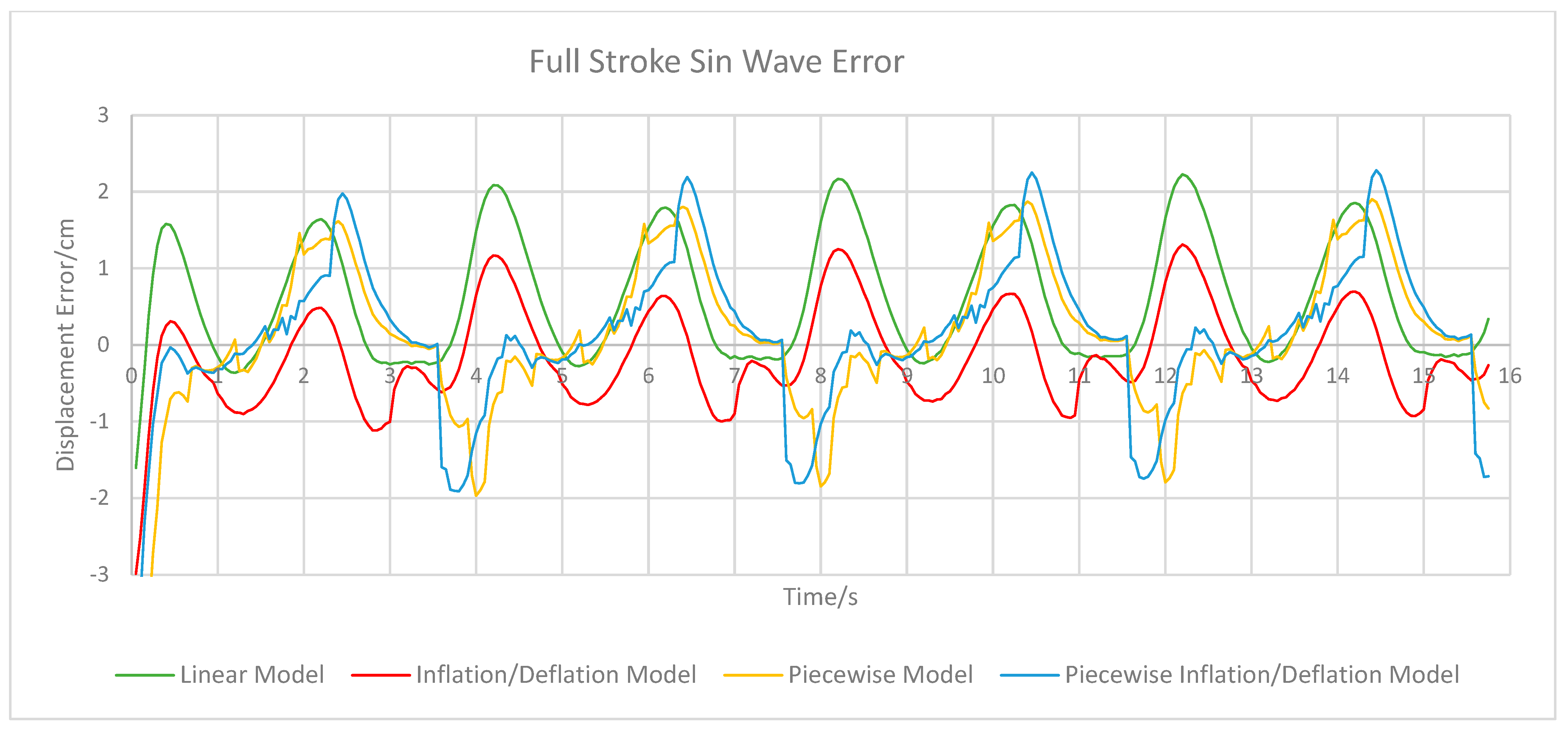
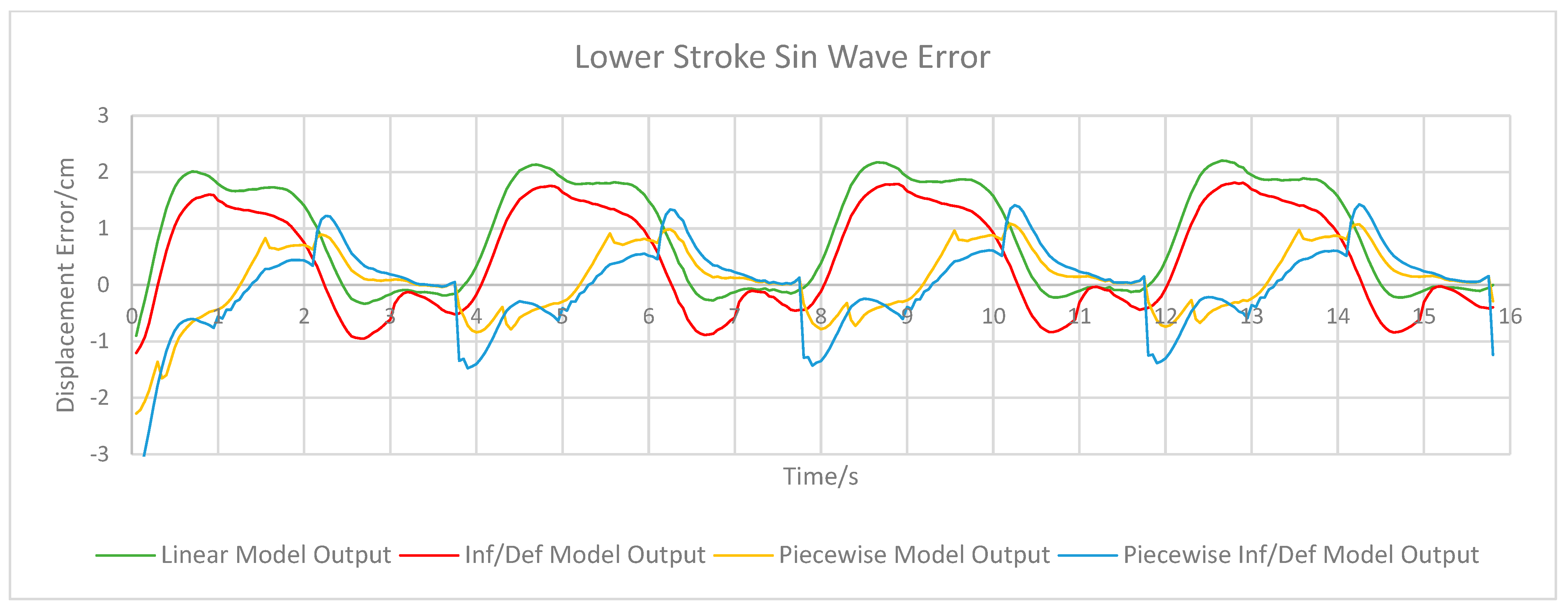
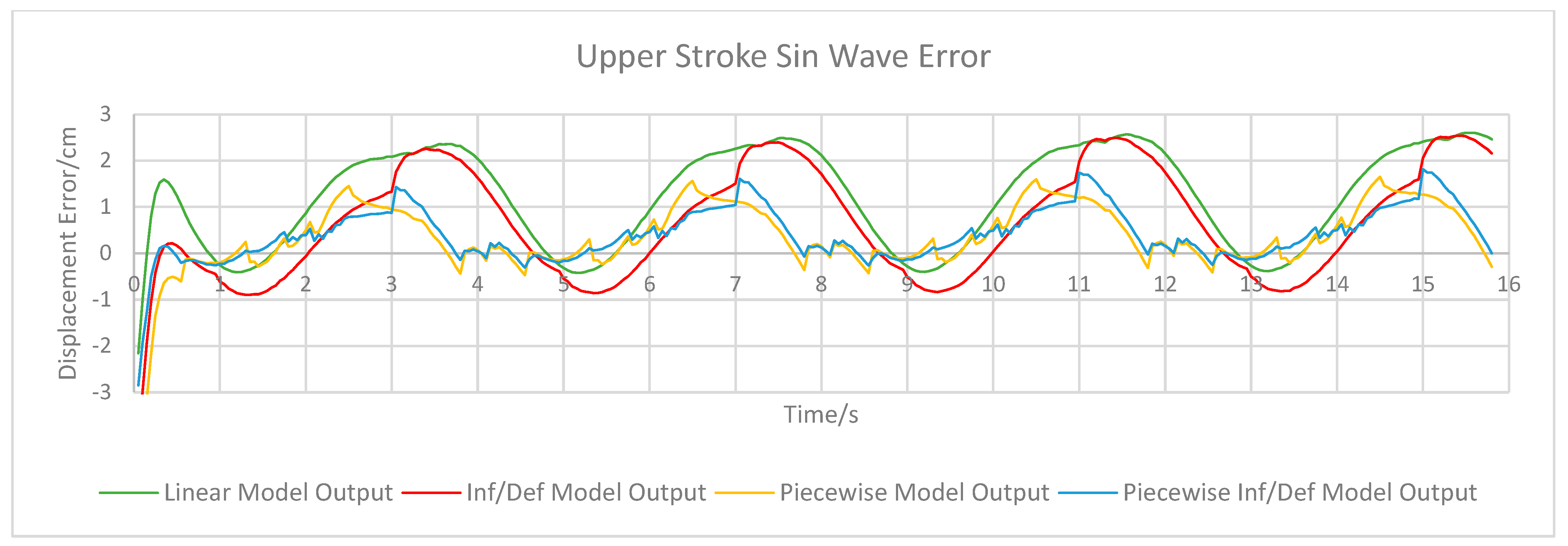
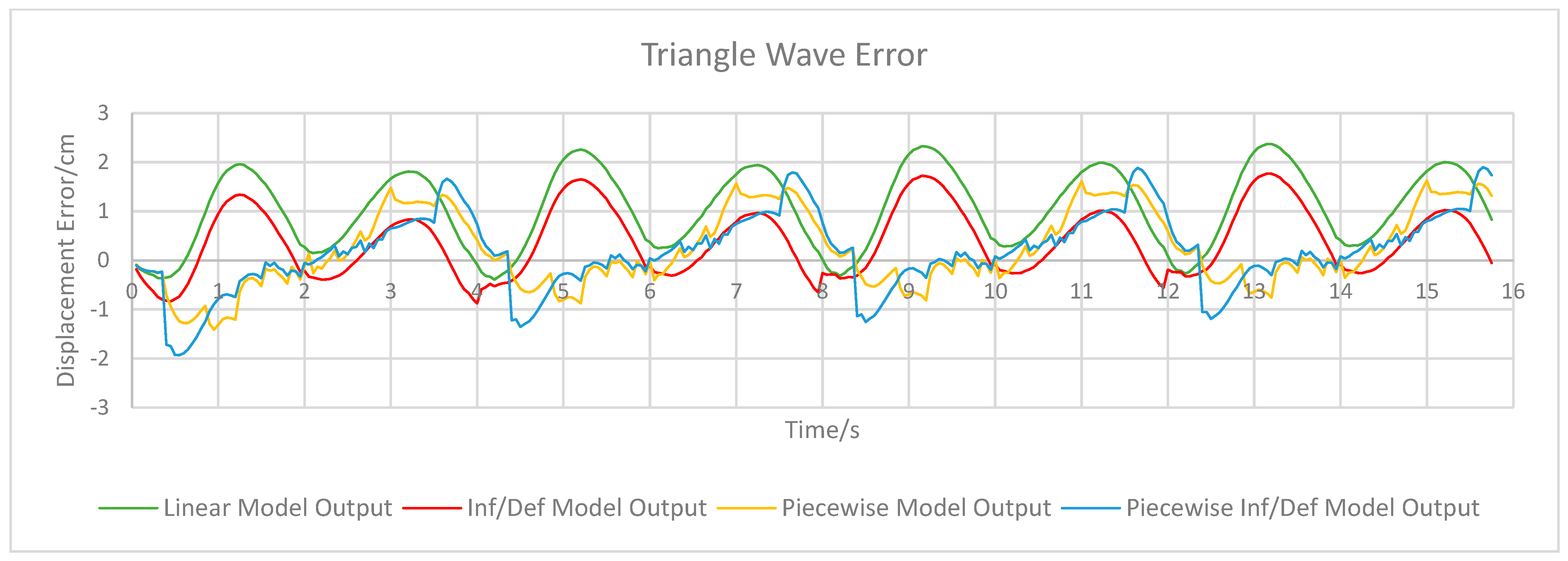
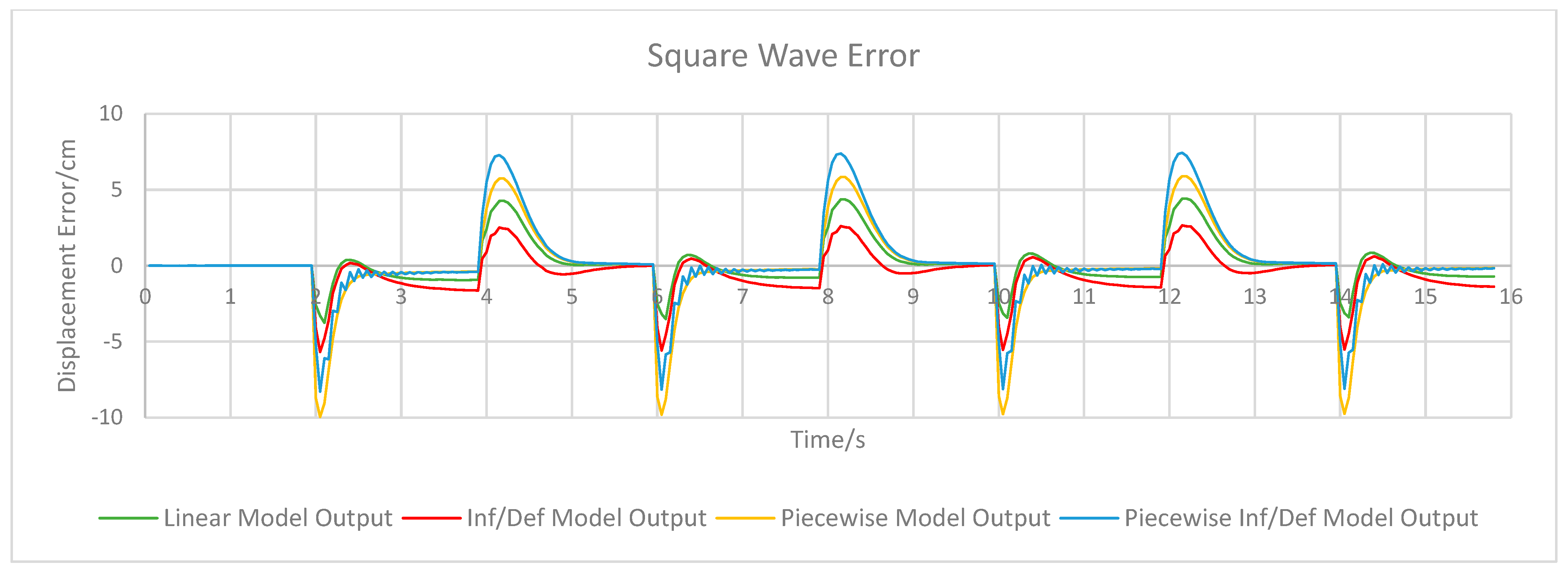
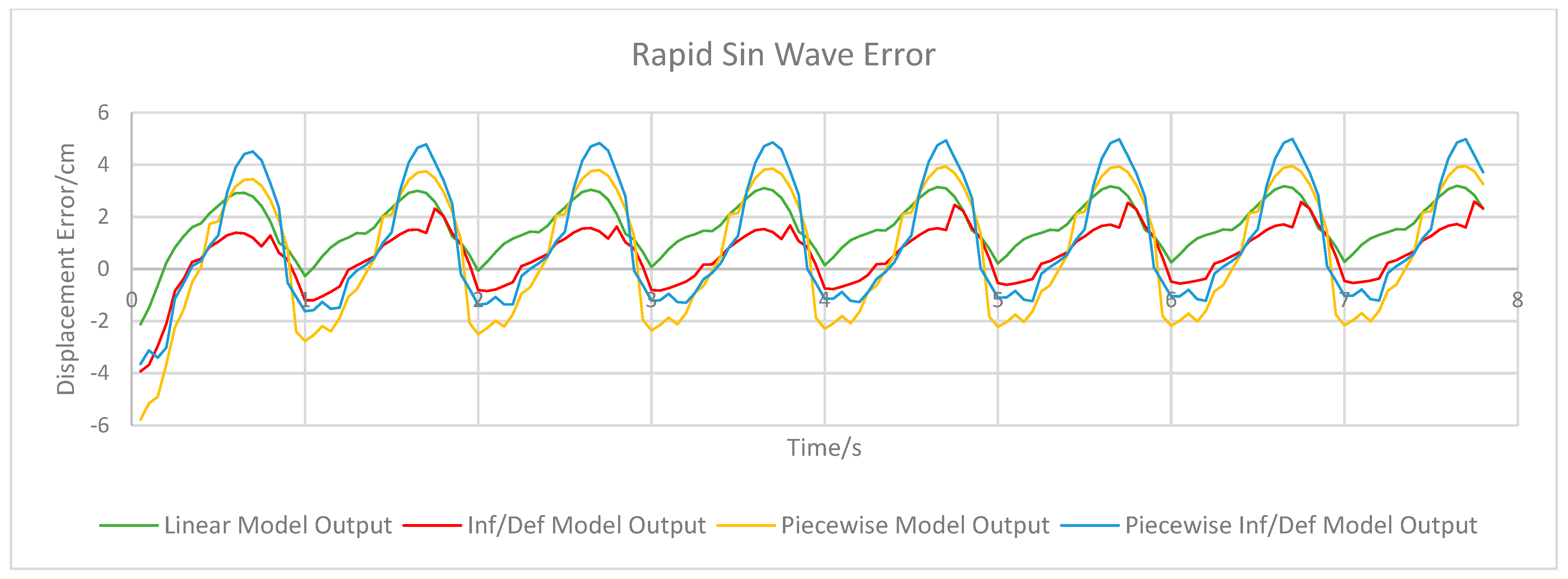
Displacement error of the linear PSO and piecewise PSO models are shown in
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11, while maximum error values for displacement and velocity and RMSE values are shown in
Table 3. In general, the absolute error values in each experiment reach a maximum of around 2 cm for all models, except during the square wave experiment in which the maximum error was much higher due to the very rapid change in displacement of the PAM that exacerbates the model’s slight lag/lead of the real motion. The rapid motion experiment also showed larger error values, see
Figure 10, again due to rapid motion of the PAM but also due to the hysteresis effect in the actuator altering the dynamics during faster motion. The linear and inflate/deflate models have similar error functions with time in most experiments, with the inflate/deflate model having generally lower error values. However, as particularly evident in the upper stroke sin wave, see
Figure 7, and rapid sin wave experiments, see
Figure 10, the changing between inflating and deflating states can cause the inflate/deflate model to have a sharp spike in error as it switches between parameters. Both of these models do not properly follow the nonlinearity of the PAM towards the peak of its displacement. They also suffer much larger error values during the lower- and upper stroke tests than in the full stroke test, as the use of a single reference trajectory in the model generation causes the PSO algorithm to overfit to the specific motion used to calculate fitness. The use of piecewise models reduces this effect as both the piecewise and piecewise inflate/deflate models have generally lower error values during the upper- and lower stroke tests. In terms of displacement RMSE, the piecewise model has the lowest error in each experiment as shown in
Table 3 except during the rapid motion and square wave tests, where both the RMSE and maximum displacement error is greater than that of the linear and inflate/deflate models. This is slightly mitigated by the piecewise inflate/deflate model.
Figure 4 shows the jumps between input ranges in the piecewise model’s output; while this model does exhibit lower error values than the piecewise inflate/deflate model, these sharp jumps are undesirable in online operation. Thus, the piecewise inflate/deflate model may be more suited to real time applications.
In comparison with other PAM models in literature, especially those pertaining to the FESTO PAMs, the piecewise PSO modelling method shows similar motion prediction behaviour to other mathematical models. Results from [
11] show similar model accuracy in online comparative displacement tests, with models overshooting at higher displacement values of the PAM, similar to that of the linear and inflate/deflate models presented here. Hysteresis is also not properly accounted for. The phenomenological model presented in [
14] shows lower RMSE values and closer fitting motion prediction than the piecewise PSO models here; however, the experiments were conducted over much smaller contraction ranges, making accurate comparisons difficult. Models presented in [
12,
13] are also difficult to compare as experiments focus on force output estimation over pressure input range rather than displacement over time. Neural network-based models, such as those presented in [
15,
16,
17,
18], have very low error values in motion estimation experiments; however, the results in [
17,
18] utilise an antagonistic pair of PAMs and measure angle rather than displacement. The algorithm used in [
15] for model generation uses a hybrid genetic algorithm and backpropagation neural network. There are several mentions of both algorithms having slow convergence times, and the model used in experiments required 3000 iterations of the backpropagation learning function. In [
16], the error values converged to a satisfactory value after 250 iterations of the fuzzy neural network training. Exact generation time is not mentioned; however, the large number of iterations required for neural network-based modelling alongside the computational complexity and required training data make the piecewise PSO modelling method presented here a favourable option in terms of the model generation stage. The PSO-based empirical model presented in [
19] shows similar motion tracking results to those presented here, although accuracy is generally better. However, this empirical model is based on a McKibben muscle, and, as mentioned in the paper, the model would not apply to other compliant or soft actuators. Therefore, the simple three-element estimation used here may be more generally useful in modelling various PAMs and other similar soft actuators.
Table 4 shows a brief comparison of important points between the proposed piecewise PSO modelling method and those more commonly used modelling techniques.
The error values in the weighted test are generally similar to those in the unweighted full stroke test. This is mainly due to the FESTO PAM’s high load tolerance causing the weight to have little effect on the motion. In order to properly determine the effects of larger loads on the model’s accuracy, a more sophisticated experimental setup is required. As the piecewise PSO modelling method does not include any real-time measurement in the parameters, the models do not change dynamics based on external factors and do not respond to loads and noise that would impact their robustness in an industrial setting. The inclusion of measures from the attached load cell to the parameter calculation could improve this and have the models respond to loads and environmental factors affecting the PAM’s motion.
The three-element phenomenological model used as the template of the piecewise PSO modelling method makes it computationally simple, and the use of state-space solutions for each individual model mode makes for fast runtime operation and simple implementation when compared to more involved methods such as deep learning modelling. The use of an optimisation function for parameter estimation also removes the need to measure these parameters manually, and as such this modelling method could be applied to other linear actuators for which the mass–spring–damper approximation is a good estimation of their dynamic properties. Under a different dynamic model template, the proposed PSO modelling method could apply to other types of actuators, but this would require further testing to properly validate. The PSO algorithm has fast optimisation time and requires very little training data when compared to deep learning methods, as only a single trajectory is required to calculate model fitness for each set of parameters. The piecewise inflate/deflate model, being the most complicated with 12 separate state-space solutions, takes approximately one hour to generate using the algorithm parameters mentioned previously. With further tuning of the C1 and C2 parameters, as well as swarm size and number of iterations used, this time can be reduced at little cost to the model’s accuracy.
5. Conclusions
A piecewise PSO modelling method for pneumatic artificial muscles is presented in this paper. A phenomenological model was adopted as a model template, based on the approximation of the PAM as a mass–spring–damper system, with three parameters based on the spring constant, damping constant, and mass of the muscle. Models were generated using reference trajectories from a displacement encoder connected to a FESTO PAM with sin waveform inputs to a pressure regulator forming a constant sin motion, and the RMSE calculated between each particle solution was used as the fitness function for the PSO algorithm. Four different models were generated for testing using this method: a linear model using a single three-element solution, an inflate/deflate model with two solutions differentiating between the PAM’s inflating and deflating states, a piecewise model using six pressure ranges for six different solutions, and a piecewise inflate/deflate model using both the inflation/deflation modes as well as input pressure ranges. Experiments show that these models have good accuracy, with the piecewise PSO modelling method effectively accounting for the nonlinearity present in the PAM. Compared to other PAM models in literature, results show similar motion behaviour and similar or slightly worse prediction accuracy to mathematical and physical models. When comparing to neural network and genetic algorithm-based models, the error values from the piecewise PSO modelling method are noticeably higher; however, the use of deep learning algorithms greatly increases the time to generate models as well as the computational requirements and complexity. The use of the phenomenological model approximation of the PAM could also allow for more generalised use cases than other model examples, including other PAM types and some other actuators with similar operating principles for which the phenomenological model used here is applicable.
Improvements can be made to the robustness of these models. Measurements of external forces applied to the PAM during operation can be incorporated into the model parameters to allow for dynamic adjustment of the model in response to load and environmental factors. Improvements to the accuracy, as well as generation time, can be made in fine-tuning the PSO algorithm parameters. Accuracy can also be improved using a greater number of pressure ranges for piecewise model generation, as well as more efficient spacing of these ranges within the PAM stroke length. This does come with a trade-off of modelling time and complexity as each additional model requires further optimisation, but the simple phenomenological model template makes the increase in complexity minimal.