A Semi-Global Finite-Time Decentralized Control Method for High-Order Large-Scale Nonlinear Systems
Abstract
1. Introduction
For high-order large-scale systems with unknown disturbances, is it feasible to design a finite-time decentralized controller to achieve stabilization/tracking?
2. Problem Formulation and Preliminaries
3. Main Results
4. Robust Tracking Control Design
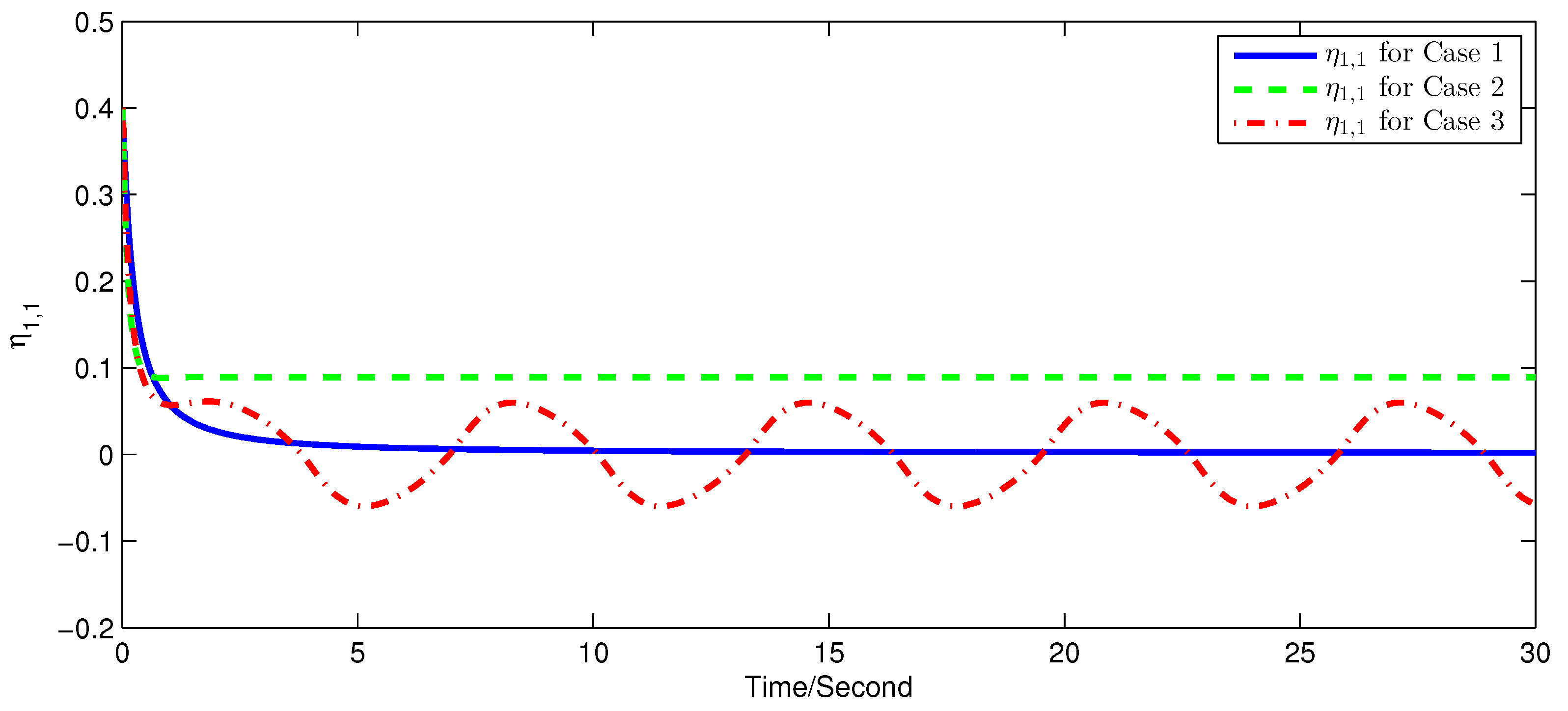
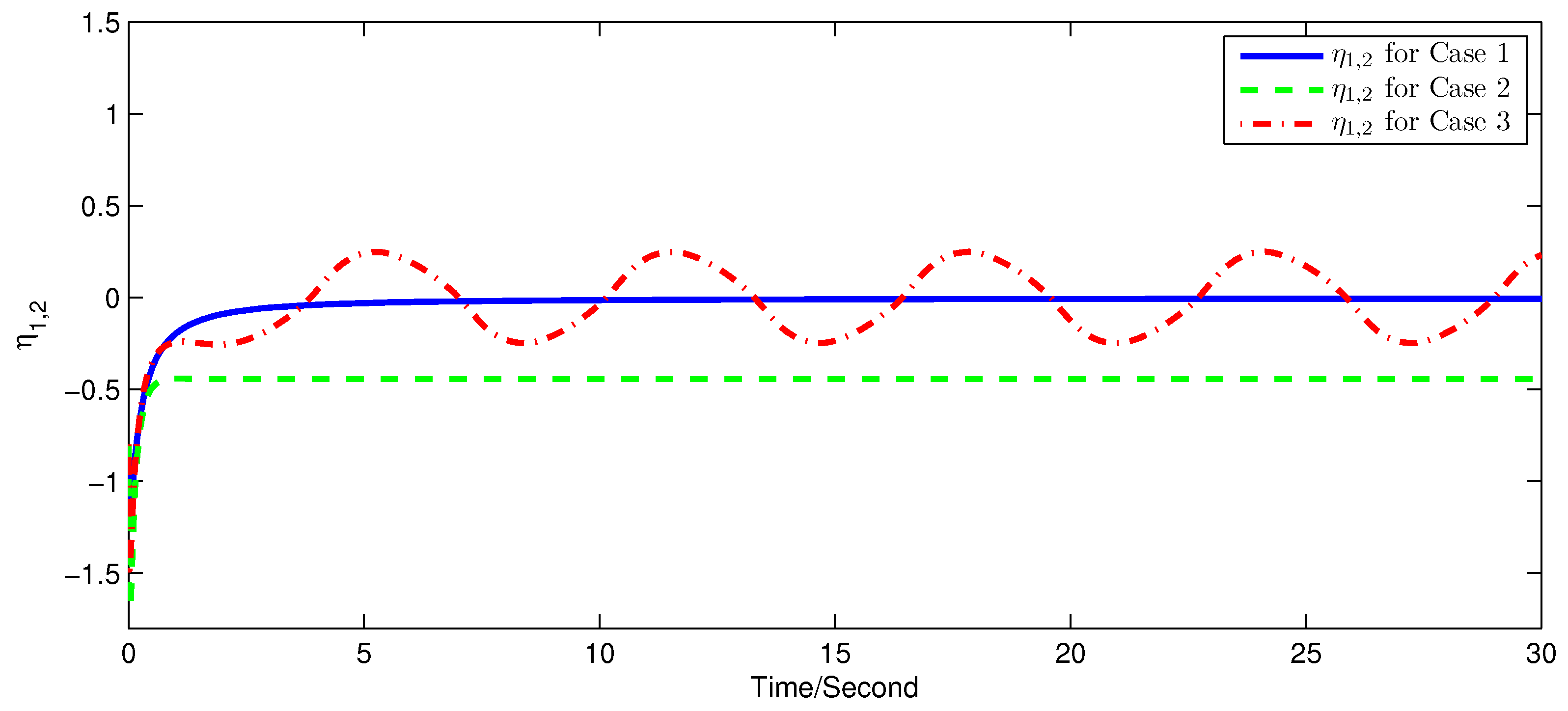
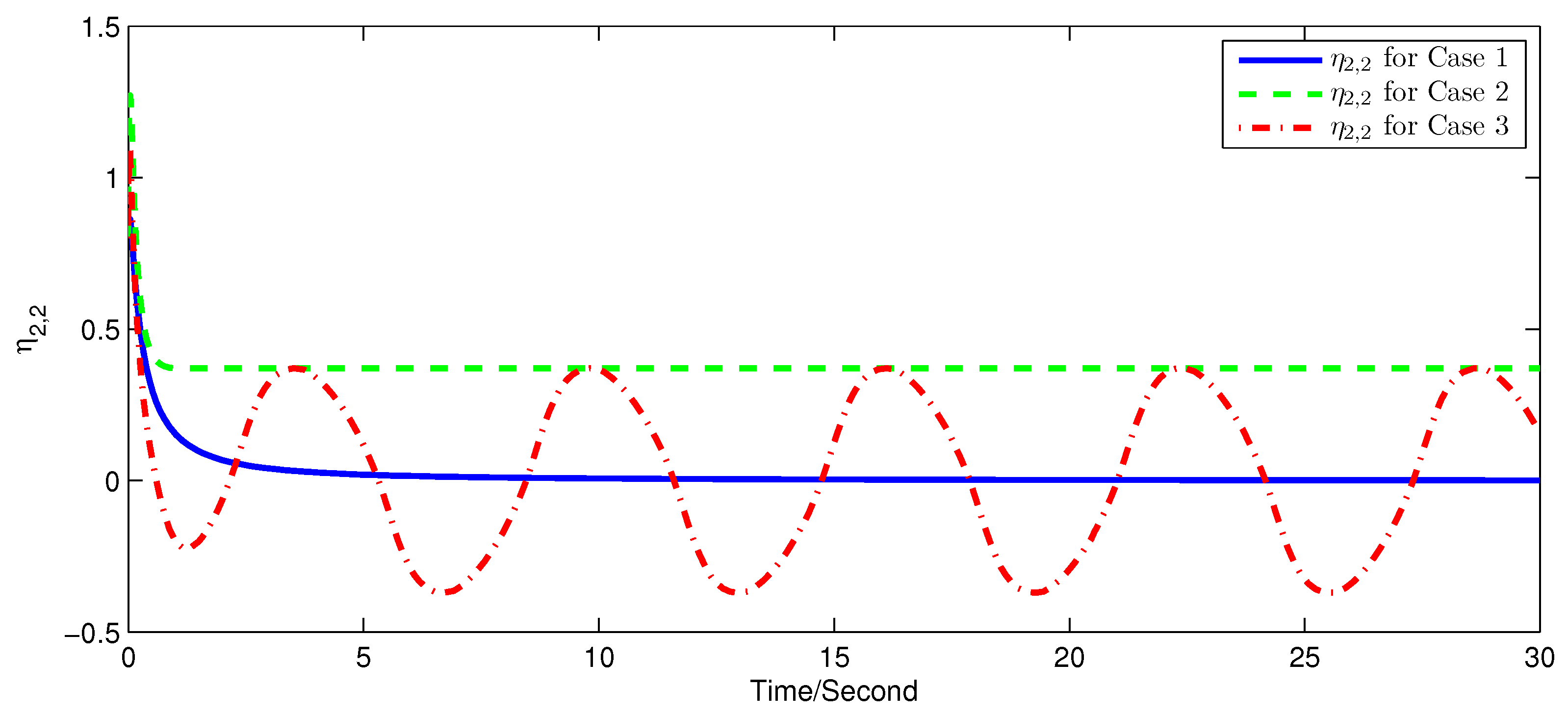
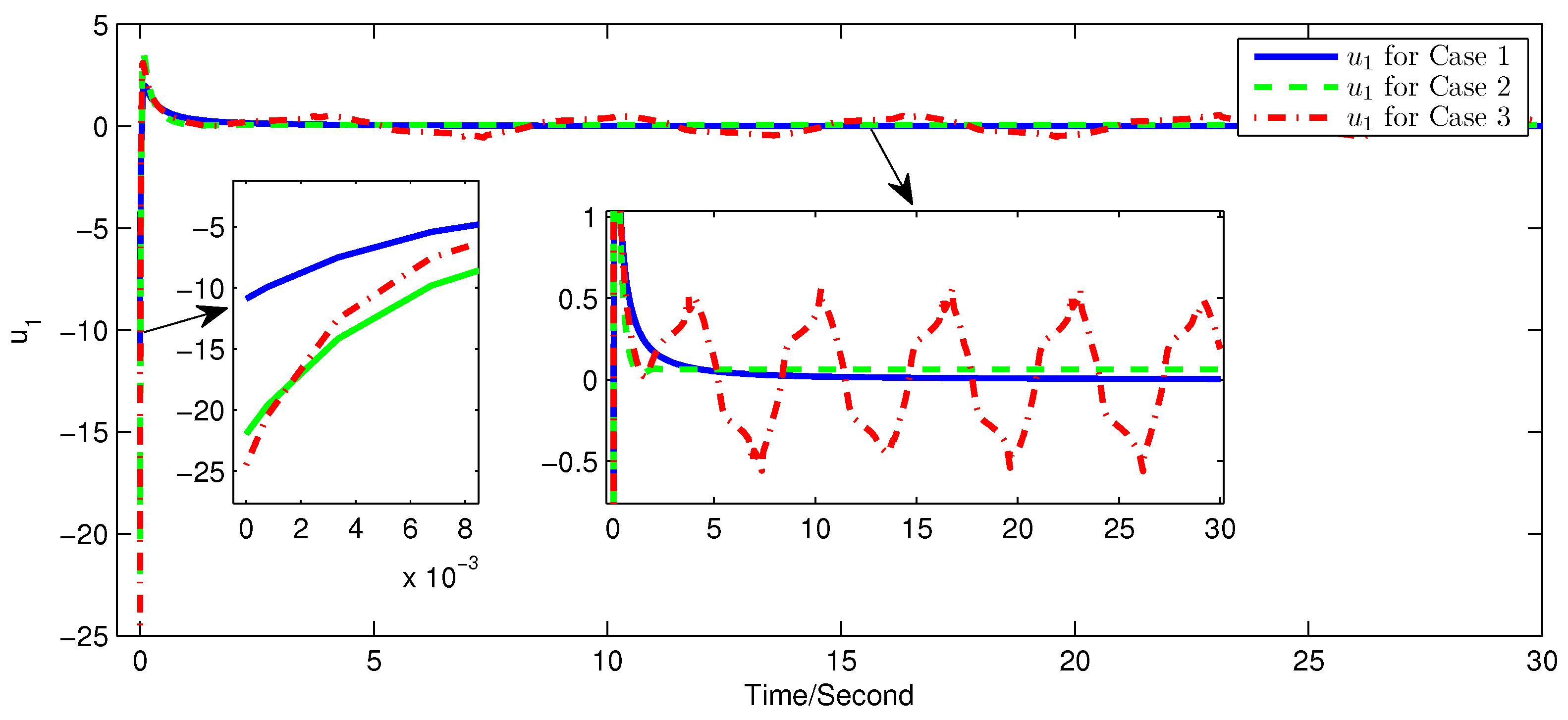
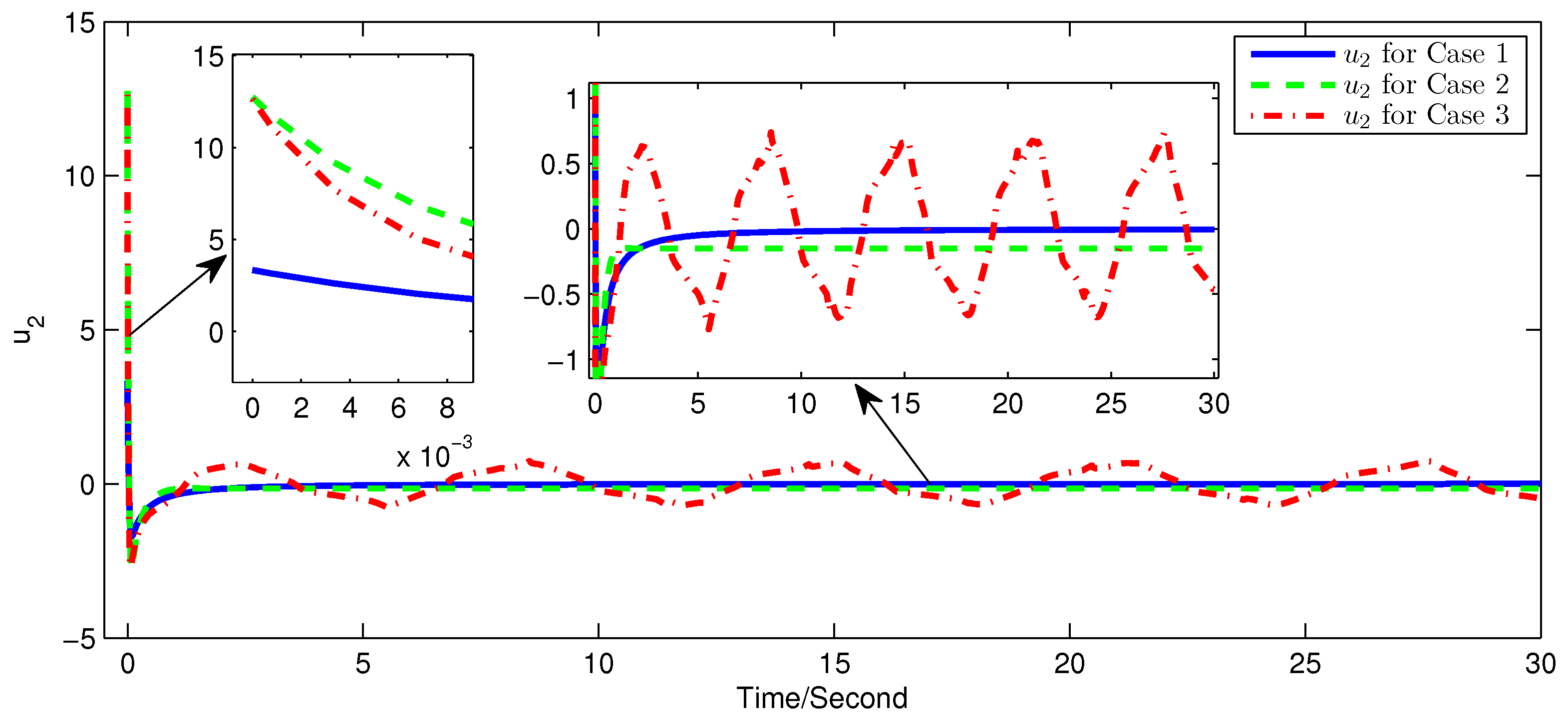
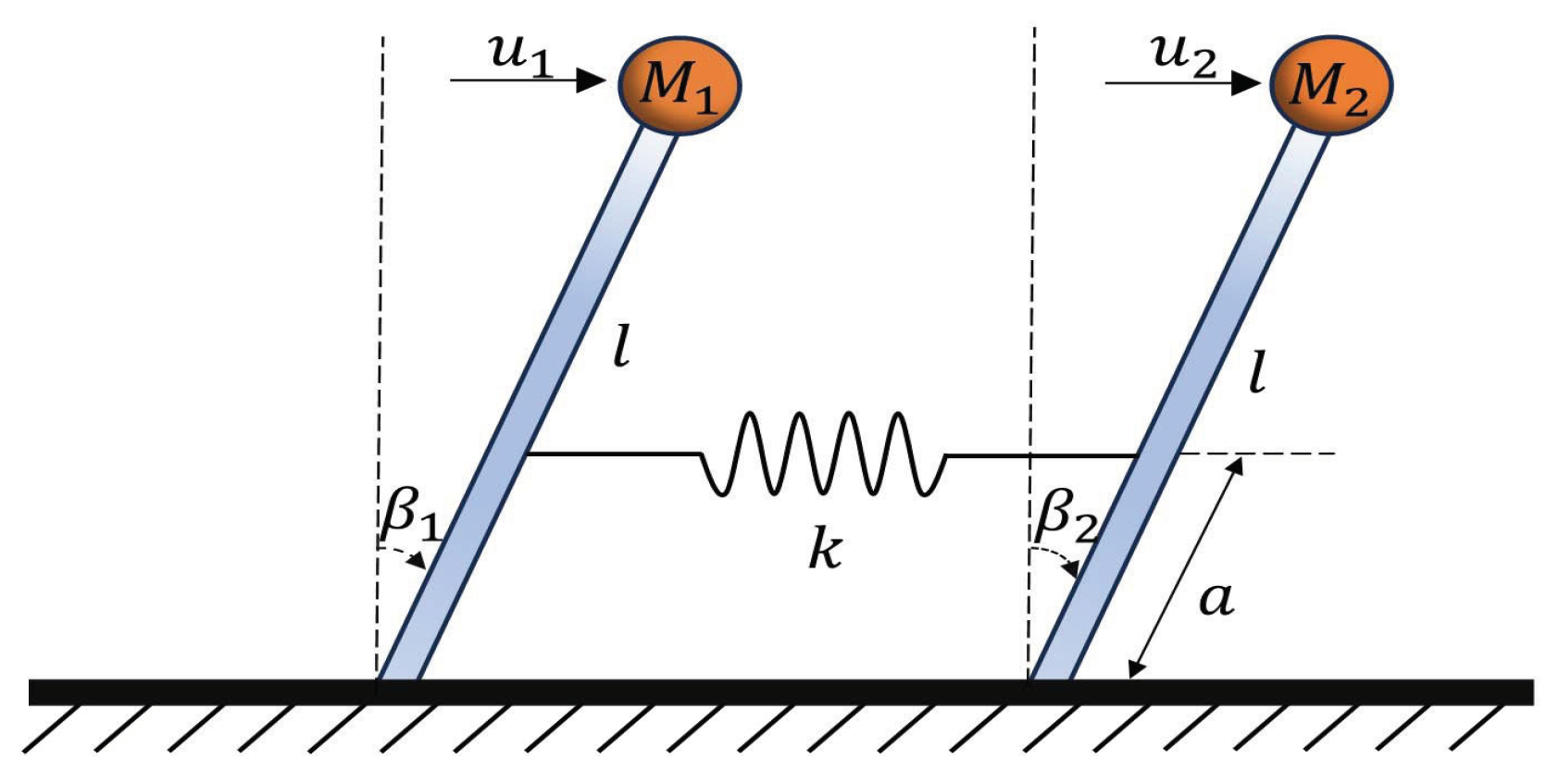
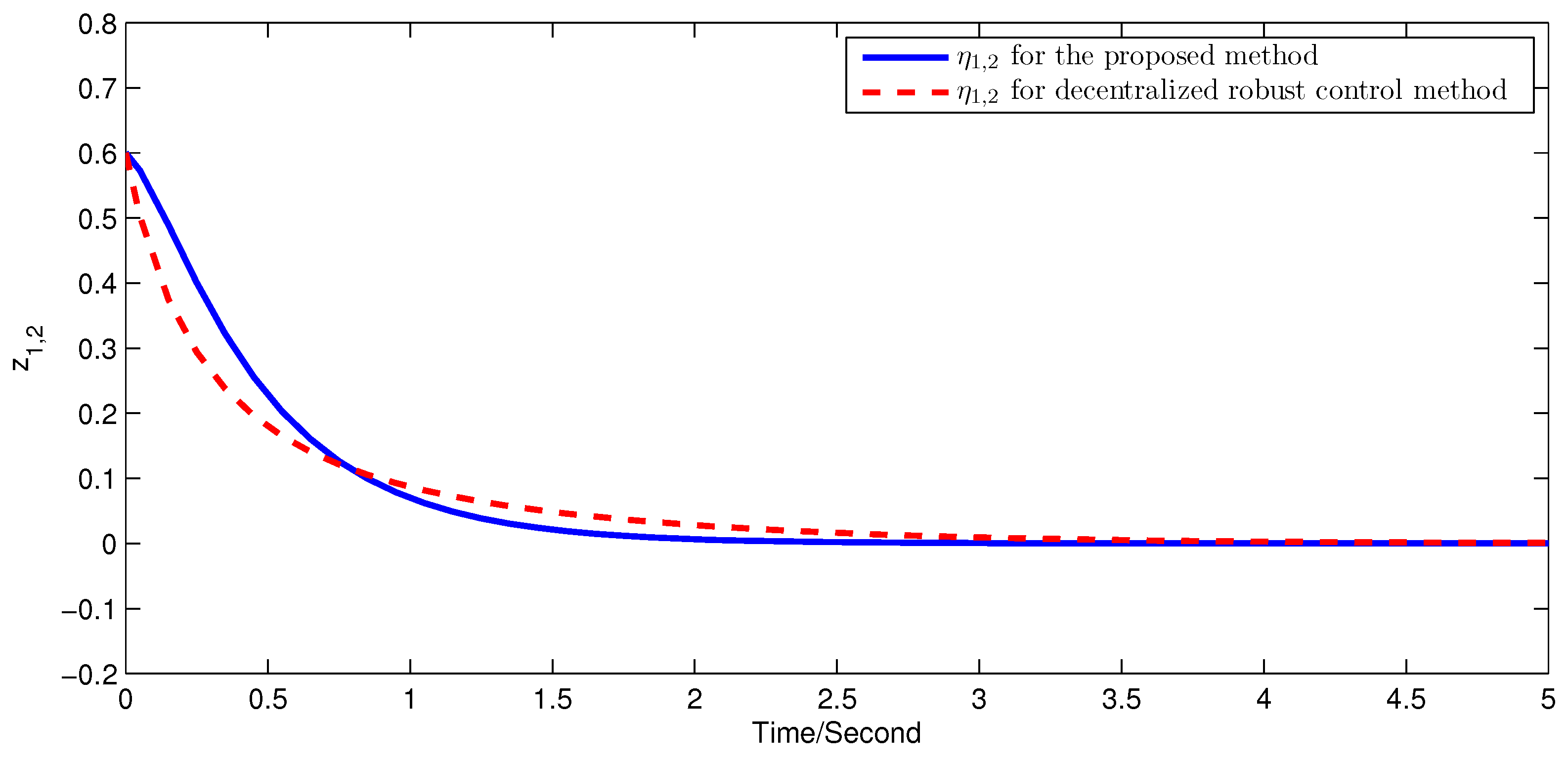
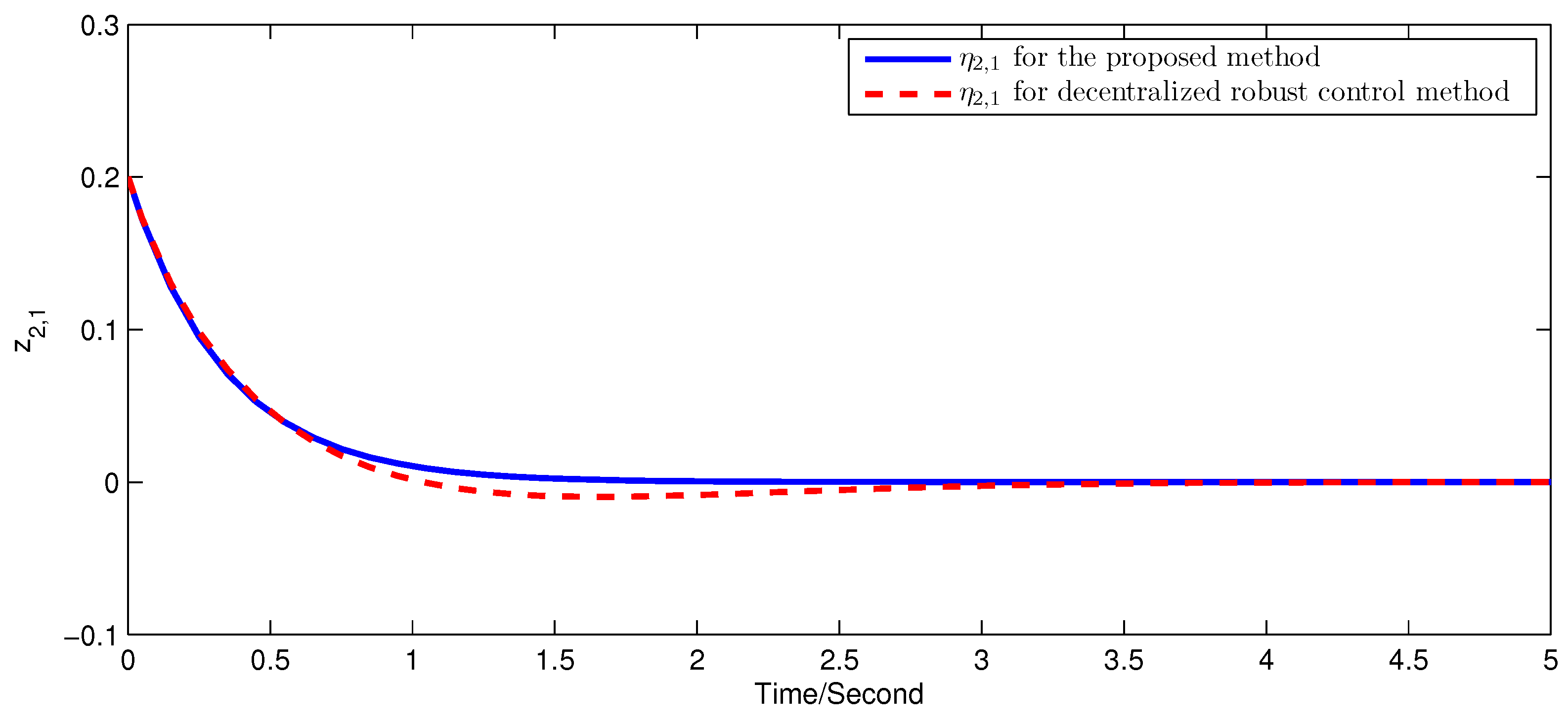
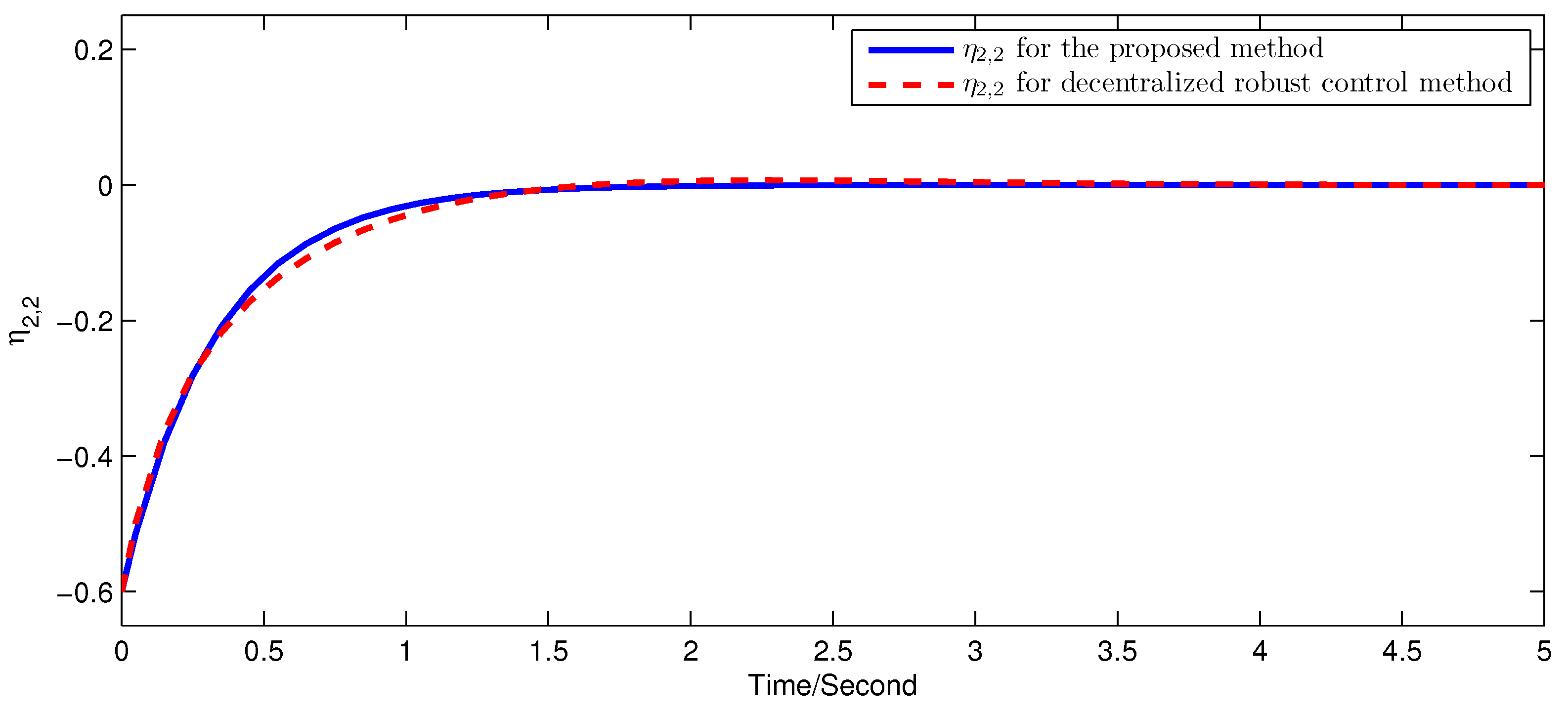
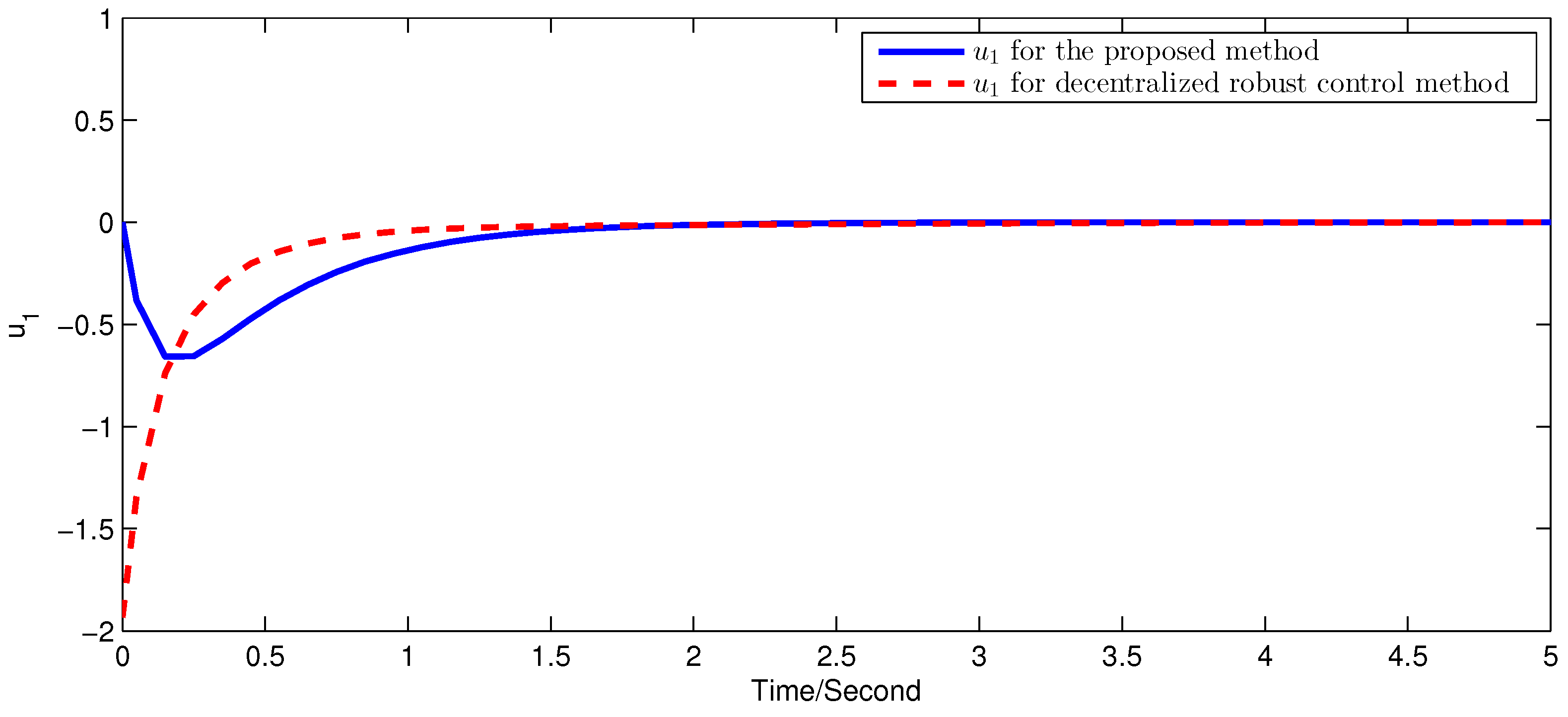
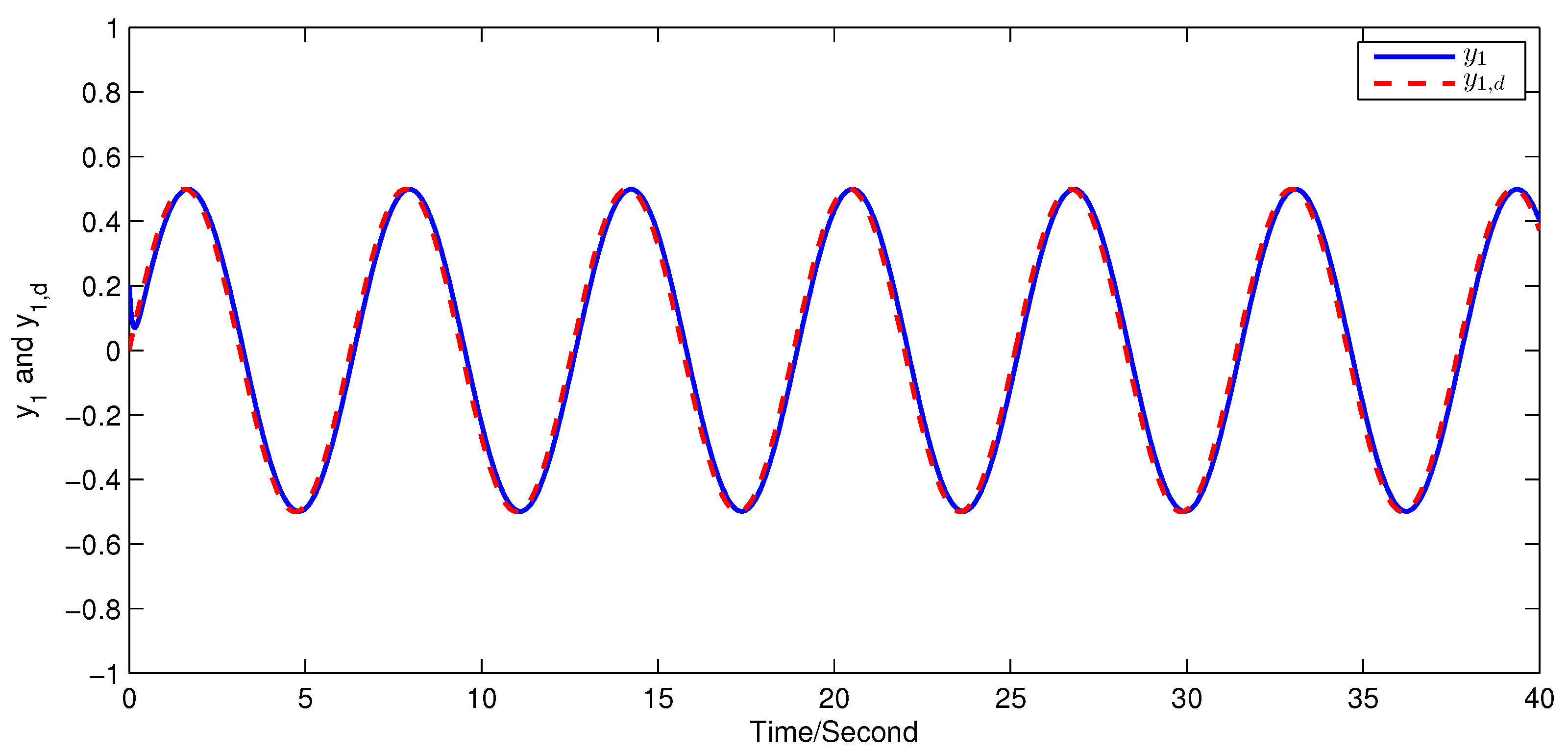
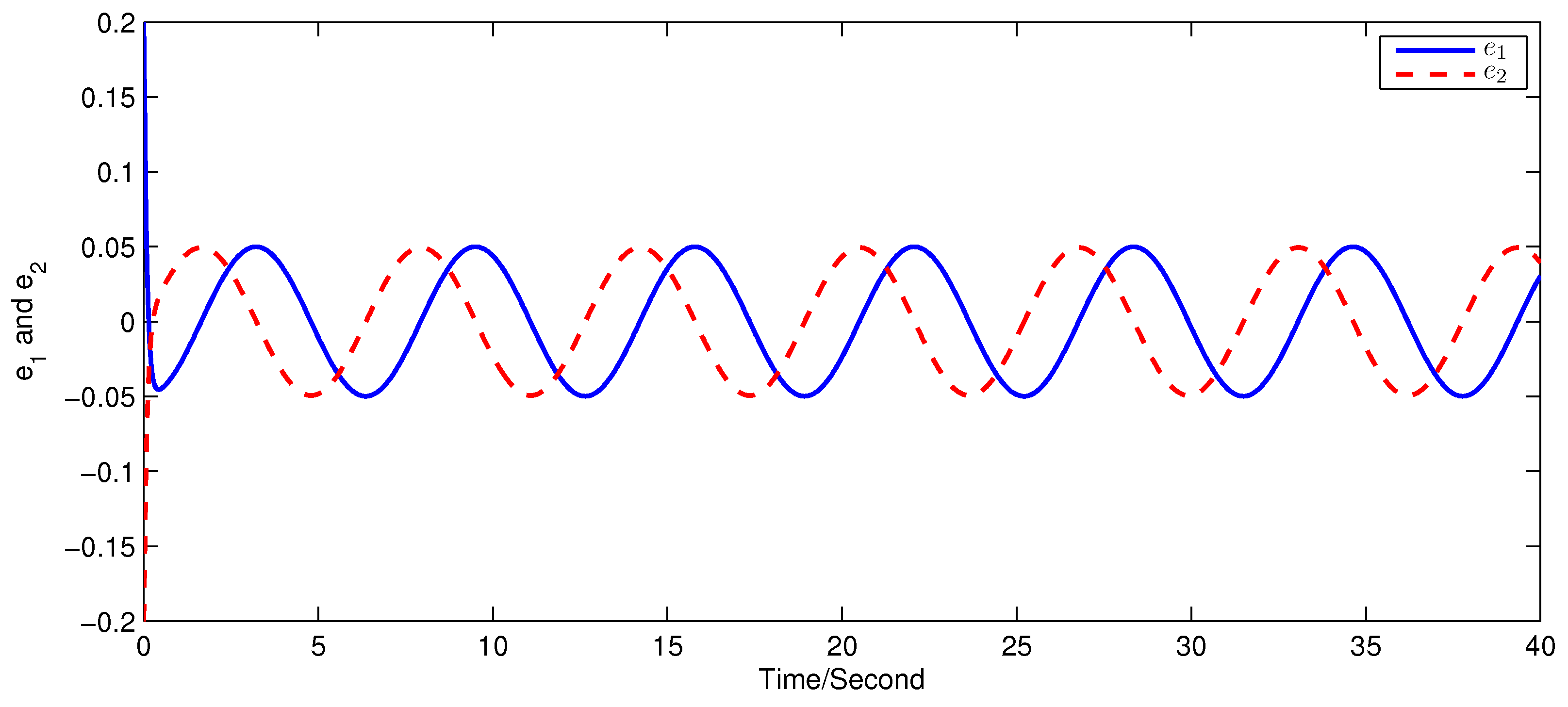
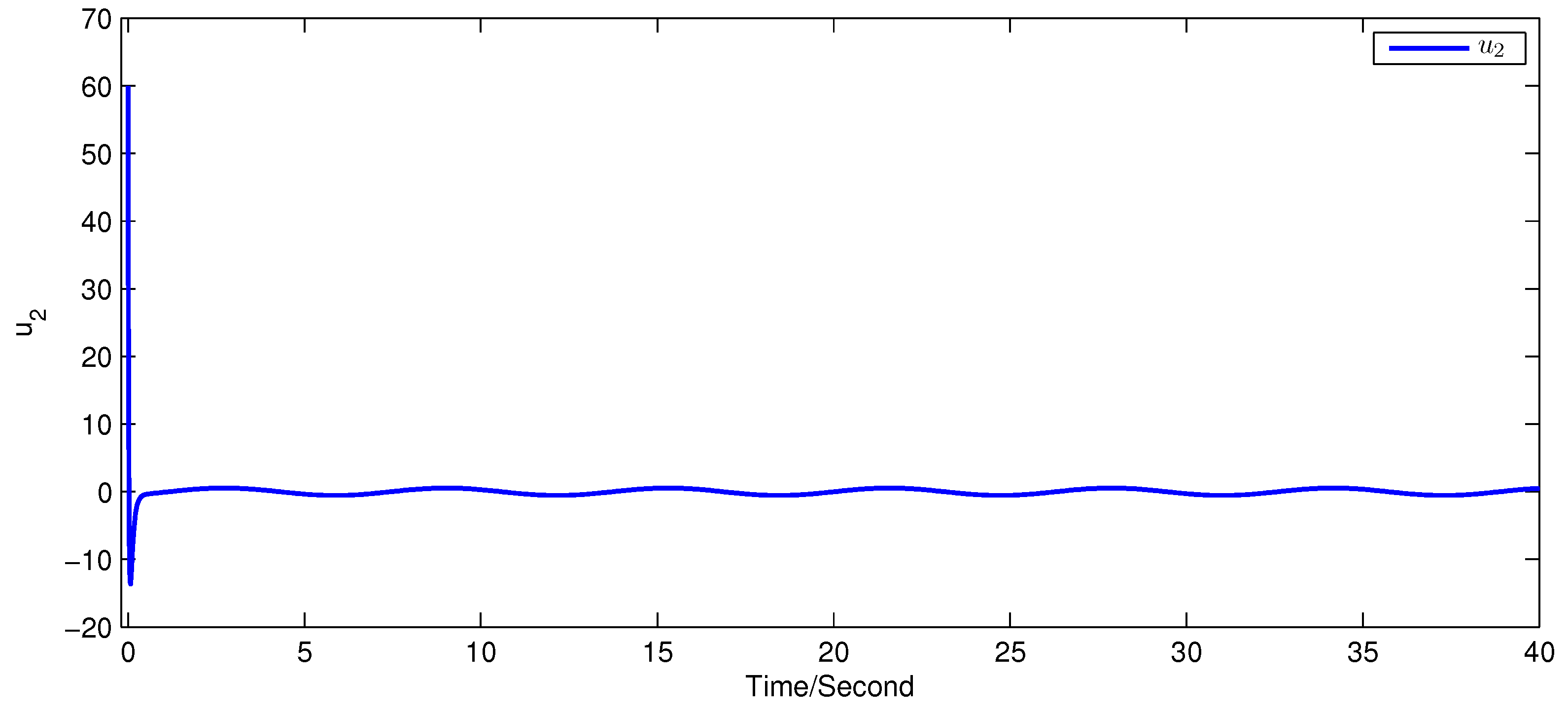
5. Simulation Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siljak, D.D. Decentralized Control of Complex Systems; Courier Corporation: Washington, DC, USA, 2011. [Google Scholar]
- Yousfi, M.; Ben Njima, C.; Garna, T. Decentralized robust control of nonlinear uncertain multivariable systems. Arab. J. Sci. Eng. 2021, 46, 9899–9924. [Google Scholar] [CrossRef]
- Davison, E.J.; Aghdam, A.G.; Miller, D.E. Decentralized Control of Large-Scale Systems; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhang, X.; Zhang, C.; Wang, Y. Decentralized output feedback stabilization for a class of large-scale feedforward nonlinear time-delay systems. Int. J. Robust Nonlinear Control. 2014, 24, 2628–2639. [Google Scholar] [CrossRef]
- Zhai, J.Y. Decentralised output-feedback control for a class of stochastic non-linear systems using homo-geneous domination approach. IET Control. Appl. 2013, 7, 1098–1109. [Google Scholar] [CrossRef]
- Chen, W.; Li, J. Decentralized output-feedback neural control for systems with unknown interconnections. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 38, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z. Decentralized disturbance attenuating output-feedback trackers for large-scale nonlinear systems. Automatica 2002, 38, 1407–1415. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, J.B. Neural-network-based decentralized adaptive control for a class of large-scale non-linear systems with unknown time-varying delays. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 1316–1323. [Google Scholar]
- Li, Y.; Yu, K. Adaptive fuzzy decentralized sampled-data control for large-scale nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 30, 1809–1822. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, D.; Shi, G.; Liu, D.; Li, Y. Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1725–1735. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Y. Nonlinear decentralized control of large-scale systems with strong interconnections. Automatica 2014, 50, 2419–2423. [Google Scholar] [CrossRef]
- Shi, L.; Wang, X.; Huang, L.; Cheng, Y. Dynamic event-triggered decentralized control of interconnected systems. Int. J. Robust Nonlinear Control. 2022, 32, 8628–8645. [Google Scholar] [CrossRef]
- Zhan, Y.; Tong, S. Adaptive fuzzy output-feedback decentralized control for fractional-order nonlinear large-scale systems. IEEE Trans. Cybern. 2021, 52, 12795–12804. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Tong, S. Adaptive prescribed performance decentralized control for stochastic nonlinear large-scale systems. Int. J. Adapt. Signal Process. 2018, 32, 1782–1800. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Sun, Y.; Gao, Y.; Lin, C. Finite-time fuzzy control of stochastic nonlinear systems. IEEE Trans. Cybern. 2019, 50, 2617–2626. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Shao, Y.; Chen, C.C. Fast finite-time stability and its application in adaptive control of high-order nonlinear system. Automatica 2019, 106, 339–348. [Google Scholar] [CrossRef]
- Wang, L.; Liu, P.X.; Wang, H. Fast finite-time control for nonaffine stochastic nonlinear systems against multiple actuator constraints via output feedback. IEEE Trans. Cybern. 2022, 53, 3253–3262. [Google Scholar] [CrossRef] [PubMed]
- Cui, R.H.; Xie, X.J. Finite-time stabilization of output-constrained stochastic high-order nonlinear systems with high-order and low-order nonlinearities. Automatica 2022, 136, 110085. [Google Scholar] [CrossRef]
- Xi, Q.; Liu, X.; Li, X. Practical Finite-Time Stability of Nonlinear Systems With Delayed Impulsive Control. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7317–7325. [Google Scholar] [CrossRef]
- Xue, L.; Liu, Z.G.; Zhang, W. A new finite time control method to nonlinear systems with uncertain dy-namics and time-varying powers. Int. J. Robust Nonlinear Control. 2023, 33, 8087–8102. [Google Scholar] [CrossRef]
- Zhai, J.; Zha, W.; Fei, S. Semi-global finite-time output feedback stabilization for a class of large-scale uncertain nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3181–3189. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y. Finite time control for MIMO nonlinear system based on higher-order sliding mode. ISA Trans. 2014, 53, 1838–1846. [Google Scholar] [CrossRef]
- Du, P.; Liang, H.; Zhao, S.; Ahn, C.K. Neural-based decentralized adaptive finite-time control for nonline-ar large-scale systems with time-varying output constraints. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3136–3147. [Google Scholar] [CrossRef]
- Hua, C.; Li, Y.; Guan, X. Finite/fixed-time stabilization for nonlinear interconnected systems with dead-zone input. IEEE Trans. Autom. Control. 2016, 62, 2554–2560. [Google Scholar] [CrossRef]
- Xue, L.; Liu, Z.; Zhang, W. Decentralized tracking control for a class of stochastic high-order time-delay nonlinear systems under arbitrary switchings. J. Frankl. Inst. 2020, 357, 887–905. [Google Scholar] [CrossRef]
- Sui, S.; Tong, S.; Chen, C.L.P. Finite-time filter decentralized control for nonstrict-feedback nonlinear large-scale systems. IEEE Trans. Fuzzy Syst. 2018, 26, 3289–3300. [Google Scholar] [CrossRef]
- Sui, S.; Xu, H.; Tong, S.; Chen, C.L.P. Prescribed performance fuzzy adaptive output feedback control for nonlinear MIMO systems in a finite time. IEEE Trans. Fuzzy Syst. 2021, 30, 3633–3644. [Google Scholar] [CrossRef]
- Liu, J.D.; Niu, B.; Kao, Y.G.; Zhao, P.; Yang, D. Decentralized adaptive command filtered neural tracking control of large-scale nonlinear systems: An almost fast finite-time framework. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3621–3632. [Google Scholar] [CrossRef]
- Guo, H.Y.; Zhang, X.G. Sampled observer-based adaptive decentralized control for strict-feedback inter-connected nonlinear systems. J. Frankl. Inst. 2021, 358, 5845–5861. [Google Scholar] [CrossRef]
- Shao, Y.; Jia, X.; Zhang, J.; Shi, X. Adaptive output feedback control of large-scale nonlinear time-delay systems with uncertain output equations. J. Frankl. Inst. 2022, 359, 1795–1820. [Google Scholar] [CrossRef]
- Choi, H.L.; Lim, J.T. Stabilization of a class of nonlinear systems by adaptive output feedback. Automatica 2005, 41, 1091–1097. [Google Scholar] [CrossRef]
- Liu, Z.G.; Wu, Y.Q. A decoupled adaptive control algorithm for global state feedback stabilization of a class of nonlinear systems. Int. J. Adapt. Control. Signal Process. 2015, 29, 1165–1188. [Google Scholar] [CrossRef]
- Zha, W.; Zhai, J.; Fei, S. Output feedback control for a class of stochastic high-order nonlinear systems with time-varying delays. Int. J. Robust Nonlinear Control. 2014, 24, 2243–2260. [Google Scholar] [CrossRef]
- Gong, Z.; Wen, C.; Mital, D.P. Decentralized robust controller design for a class of interconnected uncer-tain systems: With unknown bound of uncertainty. IEEE Trans. Autom. Control. 1996, 41, 850–854. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Zhang, H.; Xue, L. A Semi-Global Finite-Time Decentralized Control Method for High-Order Large-Scale Nonlinear Systems. Actuators 2024, 13, 250. https://doi.org/10.3390/act13070250
Jiang Z, Zhang H, Xue L. A Semi-Global Finite-Time Decentralized Control Method for High-Order Large-Scale Nonlinear Systems. Actuators. 2024; 13(7):250. https://doi.org/10.3390/act13070250
Chicago/Turabian StyleJiang, Ziwen, Hanwen Zhang, and Lingrong Xue. 2024. "A Semi-Global Finite-Time Decentralized Control Method for High-Order Large-Scale Nonlinear Systems" Actuators 13, no. 7: 250. https://doi.org/10.3390/act13070250
APA StyleJiang, Z., Zhang, H., & Xue, L. (2024). A Semi-Global Finite-Time Decentralized Control Method for High-Order Large-Scale Nonlinear Systems. Actuators, 13(7), 250. https://doi.org/10.3390/act13070250




