Design and Implementation of a Hardware-in-the-Loop Air Load Simulation System for Testing Aerospace Actuators

Abstract

This paper presents the design and implementation of the hardware and control strategies of an electrohydraulic air load simulation system for testing aerospace actuators. The system is part of an Iron Bird, which is an energy management research platform developed in collaboration between Saab AB and Linköping University. The purpose of the air load system is to provide realistic forces on the test object through the integration of a flight simulator for full mission evaluation. The challenge with electrohydraulic force control is tackled by increasing the hydraulic capacitance from increased load cylinder dead volumes, together with a feed-forward link based on accurate modelling of the test object and load system by adopting an optimisation routine to find model parameters. The system is implemented for both an electromechanical and servohydraulic actuator as test objects with different performance requirements. The control design is based on nonlinear and linear modelling of the system, and experimental test data are used to tune the models. Finally, test results of the air load system prove its force-tracking performance.

1. Introduction

This article describes the process of designing and implementing an electrohydraulic air load simulation system for the testing of aerospace actuators. The work is part of the development of the Iron Bird shown in Figure 1, as a collaboration between Saab AB and Linköping University. An Iron Bird is a vital part of the validation procedure of the flight control system [1,2,3], and enables ground testing, which reduces cost and risk. Increased ground testing is also a response to a growing complexity of aircraft systems [4]. The Iron Bird usually also includes hydraulics, landing gear, and necessary computers. Moreover, the benefit of integrated testing and flight simulations provided by an Iron Bird is stressed by [5] for the purpose of actuator health monitoring. The platform referred to here, however, is strictly a research test rig for energy management studies. Studies on the test rig include hydraulic and electric actuation, hydraulic and electric power generation and distribution, and power management. The actuation system in particular is one of the key technologies in the transition towards more electric aircraft, with traditional servohydraulic actuators, electrohydrostatic actuators, and electromechanical actuators as alternatives for future aircraft [6]. The test rig allows one to perform a hardware-in-the-loop simulation of complete missions or different manoeuvres anywhere in the flight envelope.

The purpose of the air load simulation system is to apply realistic loads on the actuators under test and resemble the hinge moment on the control surface caused by the aerodynamic loads. This is carried out by controlling the applied force in a closed loop considerably faster than the response of the test object. The performance requirements are high so as to not interfere with the test results. The challenge lies in designing a system that can handle a large operating range, with both high forces and high speed, with good performance and accuracy. Actuators are specified to handle extreme scenarios in case of failure or combat manoeuvres where the hinge loads become very high. But, for the majority of the mission, the actuator only operates at partial loads [7]. The inherent property of hydraulic systems where the oil compression gives a rise in the pressure means that there is an interaction between the test object and the air load system. Every time the test object initiates a movement, the oil in the air load system cylinder is compressed, which causes a disturbance to the force controller. This is one of the main challenges with electrohydraulic force control.

The development of Iron Bird test rigs and the challenges with hydraulic force control is documented in the literature, with various approaches to the problem, as well as common denominators. The concept of the modular Iron Bird [8,9,10] allows for the adaptation to different actuators and layouts by the use of independent functions: structure, test or load system, test equipment (aeroplane systems to be tested). Hardware-in-the-loop simulation together with a cockpit simulator enables an even more integrated test environment [11]. The load system is used for the aerodynamic and inertial loads simulation and excitation on the test object, and is typically an electrohydraulic system. This is a versatile solution found in different applications, other than aerospace testing, due to the offered power density and controllability [12].

The force control problem with electrohydraulic actuators is challenging due to the many nonlinear effects, such as servo valve null lap characteristics, hysteresis, threshold, friction, and structural compliance, as well as the high load velocity requirements for several applications [13]. General considerations when designing a force control system are to select proper components and to use linear analysis for the control design and nonlinear simulation for final tuning [13,14]. The model should include the hydraulic capacitance, servo valve characteristics, digital effects, mechanical compliance, and hydraulic supply system [15]. Other considerations are that the servo valve performance has a direct influence on the force control performance, increasing the cylinder compliance by adding additional volumes reduces the force error, and an increased leakage between the force cylinder chambers improves the velocity disturbance rejection and high-frequency damping. PI controllers should be avoided due to limit cycle oscillations caused by static nonlinearities. It is suggested to implement a force set point and speed compensation instead.

Speed compensation through a feed-forward control link is widely proven to be a successful approach for improving the control performance during the dynamic testing of actuators [16,17,18]. In [19], a feed-forward link is developed together with a state-space controller and a Luenberger state observer to further improve the performance. The test rig for the M-346 jet trainer adopts feed-forward compensation since the speed is high, which negatively affects the tracking performance. The speed is measured and used to calculate the servo valve input. Proportional and derivative feedback are used together with an integrator in the control path, where adaptive gains are used to make the controller independent of operating conditions. Acceleration feedback is also used to improve low-frequency tracking and complex filters are required to cancel out noise in the speed signal. A by-pass valve improves the performance by reducing the gain in the servo valve null region and can be used for further tuning. An important aspect is also the structural stiffness; if too low, it can cause a delay in the measured force signal, resulting in an unstable system [20].

Although various forms of the classical PID controller with a feed-forward link are widespread with good performance, there are several other techniques that improve performance. A nonlinear model predictive controller is applied to the force control of a modular Iron Bird and integrated with a flight simulator that generates the reference force [21]. The tracking performance is improved compared to a PID controller but the computational burden does not allow for real-time implementation with low-cost hardware. A synchronisation controller to suppress motion disturbance that matches the dynamics of the actuator system is developed in [22]. An adaptive update law handles parameter uncertainties using model reference adaptive control. Robust control techniques are applied to handle plant parameter uncertainties such as servo valve flow gain, natural frequency, and damping. An example is the quantitative feedback theory (QFT) controller [23,24]. This allows one to have fixed controller gains while still being robust, and has successfully been demonstrated on electrohydraulic force control systems. A nonlinear QFT controller is designed to overcome deficiencies in linearised models [25]. Both a robust feedback controller and a speed compensator are designed using the same QFT framework to improve tracking performance. The controller is implemented in an HIL flight simulator. A pre-filter further shapes reference tracking. QFT control design is used in [26], where also a flexible hose is used to increase the hydraulic compliance, which makes the system less difficult to control.

Friction in the load cylinder can deteriorate the tracking performance. A cylinder with hydrostatic bearings is a good option with very low internal friction [16]. Control performance can also be improved by including a friction compensator in the control loop [27,28]. Hysteresis is another nonlinear phenomenon with negative impact and can cause limit cycle oscillations. The hysteresis can come from the electromagnetic hysteresis in the servo valve, and a multi-term lead controller was proposed to quench the cycles and improve the controller’s performance in [29].

This work takes theory to practice by presenting practical considerations and the experience gained when developing, implementing, and integrating the air load simulation system for two different test objects, one servohydraulic actuator (SHA) and one electromechanical actuator (EMA), with different performance requirements. This work is a continuation from [30]. An extensive model-based analysis is given to support the design process. Several considerations, including ones from the literature, are analysed and implemented to handle practical implications. The main approach is to adopt the method of a feed-forward controller based on the estimation of the cylinder speed while increasing the hydraulic capacitance of the air load system, and a proportional feedback loop. This allows one to increase the gain without affecting control loop stability, while the increased capacitance also reduces the effect from the test objects’ movement. The cylinder speed is estimated from a model where an optimisation routine is used to tune model parameters and different filters are used to handle imperfections in the integration.

This article starts by describing the Iron Bird and how the air load system interacts with the flight simulator and test objects in Section 2. The design process, requirements definition, and installation are described in Section 3. The nonlinear model is explained in Section 4, while the linear modelling and analysis, control design, and simulation results are found in Section 5. The implementation and practical considerations are analysed in Section 6, together with results from testing in the Iron Bird. The conclusions are finally described in Section 7.

2. System Description: Iron Bird

The air load simulation system is part of an integrated test environment with hardware-in-the-loop capabilities provided by the Iron Bird. The original Iron Bird was donated to the university by Saab AB in the late 1990s and has been gradually modified to support new functionality. The overall architecture is seen in Figure 2. The test rig provides in total five control surfaces, where, currently, the inner horizontal surfaces and rudder have servohydraulic actuators and the outer horizontal surfaces have electromechanical actuators. All actuators are dual-channel. The EMA is of permanent magnet type. The rig provides stand-alone testing of the actuators but also in an integrated test environment with a flight simulator and other systems that are emulated through the use of programmable power supply units. It is possible to integrate any type of aircraft but a generic single-engine fighter is currently implemented. The flight simulator is based on the model provided in [31], which includes the flight control laws and aerodynamic data. The commanded control surface position is sent to the actuation system and the corresponding hinge moment due to the aerodynamic load is sent to the air load system. The loop is closed by returning the actual actuator position to the flight simulator.

3. System Design and Installation

This section describes the system’s mechanical design and installation and discusses the system requirements. The design is partly based on existing components from previous projects due to funding and time limitations. This means that the design is not fully optimised from every aspect. The mechanical structure is also kept from the original Iron Bird.

3.1. Design Process

The design process considers that the air load system must fulfill the requirements and work satisfactorily for both the stand-alone testing of the devices under test (DUTs), which are the flight control actuators, as well as integrated testing with a flight simulator. The design and implementation of the air load system is a highly iterative process, with system modelling, control design, and experimental testing used to gradually increase knowledge and improve system performance. The general process is illustrated in Figure 3. Some initial requirements are initially defined. These should include both the static and dynamic performance of the force controller, but also other functions could be included if necessary, like safety functions. An initial sizing follows that determines the size of the force actuator, valve, and pressure level. The system is modelled in a nonlinear fashion using modern library-based tools. This model is used for controller parameter tuning and verification before hardware testing. Measurements of the static and dynamic valve performance are used to initially validate the nonlinear model, in particular, the servo valve, which has a very large impact on force control performance. The nonlinear model is updated if necessary. A linear model and analysis are derived from the nonlinear model parameters. The linear model is a tool used to gain insight into the system and design the force controller. The controller is verified and updated with nonlinear simulation. An initial test with the force controller integrated with the flight simulator is performed. When the force controller performance is verified with simulation, it is implemented in the test rig. Tests are structured to validate the performance of the controller, both with a locked test object and a moving test object. If the performance is satisfactory, the controller is integrated with the flight simulator for real-time testing. An overlook of the requirements is carried out to see if they must be tuned.

3.2. Requirements

To give a full detailed requirement specification is no easy task. The static requirements are given from each test object. Both actuators have a total stall load slightly higher than 40 kN. For the EMA side, the ratio between the EMA and the load actuator is one. The EMA has a top speed close to 0.2 m/s so the ratio between the EMA and load actuator is 1:1 so as to not increase the load actuator speed, stroke, and hinge arm length, which has mechanical limitations. The speed for the SHA is around 0.06 m/s. The hinge arms are already in place from the original Iron Bird and the ratio is 1:2. This is advantageous since the cylinder size can be smaller but the top speed is still not high.

The required response depends on the specific test case. The severest condition is for step response tests of the DUT. Since the load depends on the DUT’s position, the initial assumption is that the air load system’s response needs to be 10 times faster than the DUT’s position control response. For the EMA side, this means a response time of 2 ms, and for the SHA side, a response time of 9 ms. The achieved response is later verified during testing.

A different approach is taken for the required control accuracy. The static accuracy is straightforward and can be achieved with integrating a control loop, or large enough steady-state gain, to handle any steady-state error. However, due to the inherent compliance of the hydraulic oil, the control system will have to cope with the pressure spikes due to the flow change every time the DUT moves. The effect of the pressure spikes on the DUT depends on its characteristics and test purpose. The pressure spike is relatively more severe at lower forces but will be less noticeable by the DUT. The effect on the EMA is on the motor current since it is directly proportional to the load. The effect on the SHA is on the flow. The disturbance directly affects the required system response. This can be seen by analysing the pressure change from a flow disturbance. The oil flow continuity equation states that the pressure rate is proportional to the flow q, volume V, and bulk modulus $\beta$ as shown in Equation (1), with p being the pressure. The flow has a first-order response due to the fact that it is a result of the DUT’s movement.

$$\dot{p}=\frac{V}{\beta }\frac{q}{\tau ·s+1}$$

(1)

By solving the resulting differential equation, the force, as pressure times piston area, can be plotted over time for the two cases, as shown in Figure 4. The time it takes to reach the allowed force change due to the flow disturbance gives an indication of how fast the system needs to respond. It depends on the piston area, the DUT’s response, and cylinder volume.

Since it is difficult to exactly determine the required dynamic accuracy, the taken approach is to implement different strategies that will reduce the effect from the disturbance as much as possible and later verify if the performance is satisfactory.

3.3. System Design and Installation

An illustration of the installation for the EMA side is shown in Figure 5. The same design is used for the SHA side but with different hinge arm lengths. The air load system is hydraulically actuated. The constant pressure supply system is a fixed displacement pump driven from a servomotor. It includes an accumulator to cover pressure variations and instant flow demand. The supply pressure is set to 300 bar, which is what the servo valve can handle, to guarantee maximum performance. The Moog servo valve has electronic feedback, is rated at 38 L/min at 70 bar, and has a response of over 500 Hz at a 5% control signal. These valves are used for both the EMA and SHA sides, and are reused from a previous project and larger than required. Nevertheless, a large capacity means that the valve displacement remains small where the response is higher compared to large displacements. A by-pass valve is installed between the servo valve and the cylinder that connects both cylinder chambers to the return line when deactivated. This is a safety measure to protect the DUT in case of system failure or malfunctioning. The EMA-side load cylinder has an effective piston area of 0.00194 m² with a hinge arm of 0.16 m and, on the SHA side, it is 0.001159 m² with a hinge arm of also 0.16 m. All control and data logging is provided from a Performance Real-time machine from Speedgoat and the IO133 card with a base rate of 0.1 ms.

The photos of the installation in Figure 6 show additional volumes attached to each cylinder chamber through the valve block. The volumes are regular accumulators at 2.5 litres with the bladder removed. This is to reduce the impact from the flow disturbance and is further analysed in Section 5.2. Two different block designs are evaluated: one where the volumes are connected with hoses to the valve block, and one that is a modified valve block that allows the volumes to sit closer to the cylinder without hoses. The volumes are only installed on the EMA side as the requirement analysis showed that this is the challenging side.

4. System Modelling

A nonlinear model is developed for the design and verification of the controller before implementation on the test rig. The model is also linearised in Section 5.1, where the detailed set of equations are defined, to support the design process. The model is implemented in Matlab/Simulink using the Simscape package. The servo valve is characterised by its pressure-to-flow curve and its response. The static characteristic is derived from measuring the flow for different input signals at a constant supply pressure, here, 70 bar. By assuming a turbulent flow and a constant oil density and flow coefficient, the opening area is calculated. The model is found by the curve-fitting technique. The response is derived from measurements of the spool position for a sine input signal with different frequencies at a 5% amplitude and taking the FFT. The magnitude of the frequency response slope is about −60 dB per decade. A response model of third order is found to follow the measured response well according to Equation (2), with Laplace operator s.

$$G_{sv}=\frac{1}{\frac{s^2}{{\omega }^2}+\frac{2\delta s}{\omega }+1}\frac{e^{-{\tau }_{d}s}}{\tau ·s+1}$$

(2)

The resonance $\omega$ is set to 500 Hz, the damping $\delta$ to 1, and the time constant $\tau$ to 0.4 ms. A small time delay ${\tau }_d$ of 0.4 ms is also introduced to better fit the phase margin to experiments. The static and dynamic servo valve characteristics are seen in Figure 7, together with the corresponding models. Additional details on the model are found in [30]. In addition to the valve, the load cylinder is modelled as two volumes accounting for the oil compressibility.

5. Control Design and Analysis

5.1. Linear Analysis

Based on the sketch in Figure 5 and the nonlinear model, a linearised version in the Laplace domain is derived to support the control design and analysis. The basic nomenclature follows what is defined in, e.g., [32]. The analysis requires the expressions for the servo valve response, the flow through the valve, and the oil continuity equation for the pressure rate in the cylinder chambers. All variables when linearised represent a delta change from a steady-state condition and s being the Laplace operator.

The servo valve position $x_{sv}$ from an input voltage u is expressed by Equation (3), with the response give by Equation (2) and with gain $K_{sv}$.

$$x_{sv}=K_{sv}{G}_{sv}\left(s\right)·u$$

(3)

The flow q through the servo valve is assumed to be equal for both the inlet and outlet ports. The flow is expressed by Equation (4), assuming that it is turbulent.

$$q=K_{flow}{x}_{sv}\sqrt{P_s-P_L}$$

(4)

The gain $K_{flow}$ accounts for the conversion from valve position to flow given a pressure drop. Here, $P_s$ is the supply pressure and $P_L$ is defined as the load pressure, that is, the difference between the cylinder chamber pressures. Equation (5) gives the linearised form of the flow, with $K_q$ and $K_c$ being the flow gain and pressure–flow gain and being the derivatives with respect to valve position and pressure, respectively [32].

$$q=K_q{x}_{sv}-K_c{P}_L$$

(5)

The final piece, the continuity equation, is given by Equation (6). Here, $A_p$ is the cylinder piston area, v the piston speed, and V the total cylinder volume. The sign of the speed depends on the direction of the movement.

$$q+A_{p}v=\frac{V}{4\beta }{P}_L·s$$

(6)

The linearised equations are rearranged and combined to give an expression for the cylinder load pressure, or, in this case, the force, by taking the pressure times the piston area, as defined in Equation (7). It consists of two terms: the first term dictates how the force changes due to a change in input signal, and the other term dictates how the force changes due to a change in piston speed.

$$F=\frac{A_p{K}_q{K}_{sv}{G}_{sv}\left(s\right)/K_c}{\frac{V}{4K_c\beta }s+1}u+\frac{A_p^2/K_c}{\frac{V}{4K_c\beta }s+1}v$$

(7)

From here, it is possible to define the static gain $K_v$ and volume break frequency ${\omega }_s$ as

$$\begin{array}{cc}\hfill & K_v=\frac{A_p{K}_q{K}_{sv}}{K_c}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & {\omega }_s=\frac{4K_c\beta }{V}\hfill \end{array}$$

(9)

It is now possible to form the block diagram in Figure 8, which also shows the feedback loop of the measured force. A controller $G_c\left(s\right)$ is introduced.

The block diagram is used for analysing the system and to find a first guess of the control parameters. The controller will be verified with the nonlinear simulation model and later tuned when implemented in the real-time system. From the block diagram, both the open-loop and closed-loop gains are derived, used for analysing the system’s stability margin and closed-loop response, respectively. As the system is in linearised form, the gains depend on the actual operating condition, that is, the load pressure (or force) and the speed. A good practice is to look at the worst condition, meaning where the gain is at its highest, to guarantee stability over the entire operating range. However, it is not certain that the response will be sufficient for every condition, and it has to be verified during nonlinear simulation, and later testing. Techniques like gain scheduling could be applicable if deemed necessary, but it is preferred to avoid introducing noise from sensor data and additional dependencies. The preferred approach is to keep the controller as simple as possible by relying on a proportional controller. A reason for this is mainly due to the possible introduction of limit-cycle oscillations when an integrating controller is combined with the servo valve hysteresis. Another is that the requirement analysis showed that a very fast response is required to compensate for the flow disturbance. This is best performed with a feed-forward link. This also brings the possibility of opening the servo valve just at the right moment by tuning the link. Relying purely on a feedback link implies that an error has to occur before the servo valve reacts.

The severest operating condition selected for the linear analysis is when the load and speed are very low, or, in practice, zero, since the system gain is at its highest here. The controller gain, 0.00005 and 0.0001 for the EMA and SHA sides, respectively, is selected so that the gain and phase margins are around 10 dB and 60°, which gives a closed-loop response of around 110–120 Hz. The responses are shown in Figure 9.

Since the plant on the SHA side has a lower gain, a higher control gain is used. With a higher flow, the plant’s gain reduces, which impacts the steady-state control accuracy. The approach is to let the feed-forward link compensate for the steady-state gain and be added to the servo valve signal. This will be evaluated through nonlinear simulation and testing.

5.2. Nonlinear Simulation and Analysis

The feed-forward link is the inverse of the measured flow curve from Figure 7a, shown in Figure 10. A third-degree polynomial fit is used to describe the curve.

The feed-forward function takes the nominal flow as input, which is the required flow to move the actuator divided by the pressure difference $P_s-P_L$. In this way, the flow variation due to the load is accounted for. The required flow is based on the load actuator speed. Only the actuator position is available. It is commonly known that deriving the speed is difficult since it involves derivation of noisy signals. As described in the literature, a better approach is to estimate the speed from a model of the DUT. This model is tuned from measurements during implementation and testing but, for initial simulations, the simplified model in Figure 11 could be used, but should be gradually tuned when data are available. By constructing the feedback loop around the position, derivation is avoided and the speed is directly extracted before the integrator block. Saturation limits the maximum speed. The gain K and time delay $\tau$ are tuned to approximately fit the EMA and SHA responses.

Initial simulation results verify the controller and the control strategy, shown in Figure 12. The left figure shows when the test object (DUT) is locked in place and a step force command is applied. A similar response time of around 3.5 ms is seen from both systems. The controller gains are 0.00005 and 0.0001 for the EMA and SHA side, respectively, i.e., somewhat smaller on the SHA side compared to the linear analysis. It is somewhat longer than anticipated from the linear analysis but still in the same region, the difference being that the nonlinear effects are now accounted for. In the right figure, a step command is applied to the DUT of 10 mm. The reference load is proportional to the DUT’s position, with gains $1\times {10}^5$ and $2\times {10}^6$, respectively. It is higher on the SHA side since the ratio between the DUT and load actuator is twice the EMA side. As expected from the requirements analysis, the performance on the SHA side is satisfying but is severely hampered on the EMA side.

As was discussed in the introduction, one way to improve the flow disturbance rejection is to increase the system’s capacitance by increasing the cylinder’s volume. Additional volumes are added to the load cylinder on the EMA side as shown in Figure 6. The effect from the volumes is analysed by studying the open-loop response, Figure 13, for different total volume sizes, i.e., the basic size plus an additional volume: the basic volume of $2.9\times {10}^{-4}$ m³, $5\times {10}^{-3}$ m³, $10\times {10}^{-3}$ m³, and $20\times {10}^{-3}$ m³. The controller gain is adjusted so that the stability margins are equal for each case. With a larger volumes, the volume break frequency is reduced and becomes the dominating response since the valve response is much faster. This allows one to increase the gain with a much better steady-state performance as a result. This is actually similar to introducing a lag filter in the feedback loop. This is shown in the same figure for the case with no additional volumes, the difference being that the flow disturbance acts directly on the volume. The lag-filter only acts through the feedback.

The choice of volume size is a compromise regarding what is feasible to install. Larger volumes require a larger servo valve to provide the extra flow required for the oil compressibility. A good compromise was found to be a volume of 2.5 L for each load cylinder chamber. The same simulation, shown in Figure 14, with a step command on the DUT and two different gains on the load, with a low gain at $1\times {10}^5$ to the left and a high gain at $5\times {10}^5$ to the right, was carried out. The results are much improved now. The flow disturbance still affects the dynamic performance, particularly in the lower force region. As the load increases, the effects from the disturbance become negligible. The larger load is still only 10% of the total capacity.

The systems are also verified and validated together with the flight simulator, shown in Figure 15. The flight conditions are 5000 m and M 0.7, where the pilots make roll and pitch manoeuvres. The results indicate a satisfying performance. Further tuning is possible but is performed in the next step, which is implementation and real-time testing.

6. Implementation and Results

This section presents the implementation of the air load simulation system controllers, the tuning process, and how practical implications are handled. The same controller structure as in the simulations is implemented. The basic setup is to use the same control gain, which is slightly tuned during testing, to find a good performance while maintaining a stable system. Mainly step response and sine wave inputs to the actuator are used to generate the force reference signal, which is proportional to the measured actuator position. Different gains on the force reference are used throughout the tuning process. The final step is to integrate the force controller with the flight simulator and evaluate its performance.

Results from the tuning process are excluded since it is straightforward. The subsequent subsections focus on the implementation of key functions to increase performance and the final results with the flight simulator.

6.1. Speed Estimation Optimisation

The air load system force controller’s performance is very dependent on the accuracy and performance of the feed-forward link. The key is to accurately estimate the DUT’s speed together with the inverse flow function of the servo valve. Since the DUT’s position is measured with external sensors, several techniques were investigated that involve filtering of the position signal and simplified representations of the DUT, similar to what is shown in Figure 11. However, the most accurate result has shown to be through representing the DUT by physical modelling. An optimisation routine is applied to find the model parameters by comparing to tests of the actual DUT.

6.1.1. Servohydraulic Actuator

The SHA is based on the nonlinear flow–pressure relation and a second-order transfer function in order to include the dynamic characteristics of the actuator control loop. The model is implemented as shown in Figure 16.

The transfer function $G_{SHA}\left(s\right)$ is defined as Equation (10), with resonance $\omega$ and damping coefficient $\delta$.

$$G_{SHA}\left(s\right)=\frac{1}{\frac{s^2}{{\omega }^2}+\frac{2\delta }{\omega }s+1}$$

(10)

The flow–pressure relation $f\left(F\right)$ is defined according to Equation (11). The coefficients define the flow–pressure relation, where $C_q=0.7$, the oil density is $\rho =856$ kg/m³, A is the piston area, and the supply pressure $P_s$ is set to 210 bar. The measured force F is an input to the model, as well as the commanded position $x_{cmd}$. A saturation block limits the maximum and minimum valve position. A delay is placed at the command signal. This is used for tuning the model when implemented in the real-time system.

$$f\left(F\right)=\frac{C_{q}w}{A}\sqrt{\frac{1}{\rho }(P_s-F/A)}$$

(11)

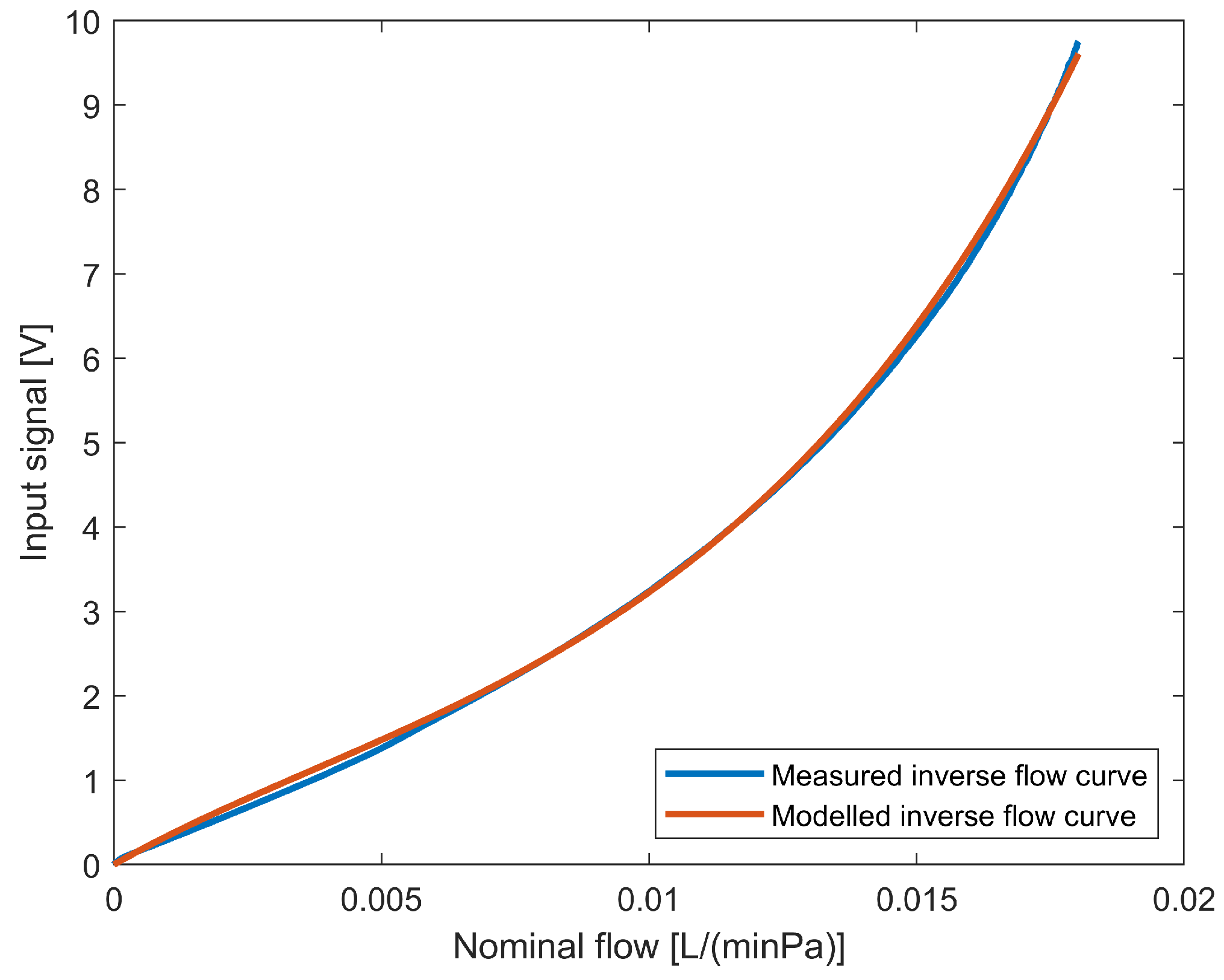
Optimisation is applied to find model parameters. There are several possible algorithms, e.g., using least-square methods or particle swarm optimisation [33,34], which have proven to give good results on DC motor model parameters. The optimisation in this work uses the ComplexRF routine, see [35], to find the parameters $K_p$, w, $\delta$, max valve position, and min valve position. The optimisation is set up to minimise the error between the measured and simulated actuator position. The test data are a series of step responses with different amplitudes in both directions in order to capture the static and dynamic characteristics. A sample of the test is shown in Figure 17.

The speed estimation model is slightly modified when implemented in the real-time system. Instead of using the estimated position as the feedback signal, the actual measured position is used. This prevents any deviation between the estimated position and measured position erroneously estimating the speed.

6.1.2. Electro-Mechanical Actuator

The approach that was found to give satisfying results was to develop a DC-equivalent model of the EMA in combination with a model of the controller implemented in the EMA’s control unit. The model cannot be too computationally heavy as it would require too high a performance of the real-time system. Any high-frequency dynamics are therefore excluded. Equations (12)–(16) describe the model, where $T_m$ is the motor torque, $K_t$ the torque constant, $J_m$ the motor inertia, B the viscous friction coefficient, i the motor current, ${\omega }_m$ the motor speed, ${\theta }_m$ the motor angle, x the actuator position, $F_L$ the external load on the ball screw, and L the ball-screw lead.

$$\begin{array}{cc}\hfill & T_m=K_{t}i\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & J_m{\dot{\omega }}_m=T_m-B{\omega }_m-T_L\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\dot{\theta }}_m={\omega }_m\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & x=\frac{L{\theta }_m}{2\pi }\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & T_L=\frac{L·F_L}{2\pi }\hfill \end{array}$$

(16)

The model of the controller is a cascaded controller including the motor speed control loop and the actuator position control loop, according to Figure 18. In reality, the EMA also has an inner-current controller that is neglected due to the very fast dynamics involved.

The optimisation routine is this set up for tuning the motor inertia, viscous friction coefficient, and torque constant. The measured data are derived from a combination of step commands and running the flight simulator since the force control performance is very sensitive to the accuracy of the speed estimation. The results from the optimisation are shown in Figure 19.

6.1.3. Implementation of the Feed-Forward Link and Speed Estimation Models

When the feed-forward link is finally implemented in the real-time system, a gain scales the actual contribution. If the feed-forward link is perfectly matched, it would not be necessary to have the feedback signal, apart from the dynamic characteristics, which the feed-forward link does not account for. By applying a rather slow sine wave command signal at the DUT to avoid triggering any dynamics and applying a load proportional to the DUT’s position, the feed-forward link’s contribution is slightly tuned by varying the gain so that the feedback control signal is minimised. The feed-forward signal is also slightly biased to compensate for a small asymmetry in the servo valve. An example is seen in Figure 20, where the feedback signal is close to zero. The noise from the signal is discussed below.

To demonstrate the effect of the accuracy of the speed estimation, the model of the EMA has been optimised with two different measurements. Since the model is merely a representation of the actual system, there will always be some discrepancy between the model and the actual test object. This turned out to be the case here. Figure 21 illustrates when the speed estimation is optimised to a step response against when it is optimised to the flight simulator’s command inputs, which do not yield the exact same behaviour. The test case highlights a very low load for an EMA step command but shows that a very good force control performance is achievable when the feed-forward link is very accurate. For higher loads, but still roughly only 6% of the total load actuator’s capacity, the inaccuracy of the speed estimation has a much lower negative impact and can be considered negligible.

Another technique that has been adopted to tune the feed-forward link is by slightly delaying the command signal to the speed estimator model. This was applied for the SHA side by 5 ms, where the estimated speed was slightly ahead of the actual speed, causing the servo valve to open slightly too early. The delay resulted in an improved performance.

6.2. Filter Techniques

The increased cylinder volume size using external containers on the EMA side does not generate a homogeneous volume for each cylinder chamber. Ideally, a longer cylinder would have given the desired effect, but connecting the containers through the valve block and hoses gives a certain disconnection between the cylinder and containers, i.e., dynamically, there are two volumes connected through a resistance. This means that the high-frequency content of the control signal will see a small volume, making the system unstable since the control gain is adapted for a system with large volumes. This is seen from the measurement in Figure 22, where, in figure a), the feedback signal is the measured force, which results in an unstable system. The implementation is shown in Figure 23.

Two pressure sensors are installed in the vicinity of the containers. This signal’s characteristics are much more affected by the larger volume size, even for high-frequency content, than the force signal. By using the measured load pressure as feedback, the system becomes stable. The downside is that the load pressure is not exactly the same as the measured force due to internal friction inside the load cylinder. This is seen in Figure 22b, where there is a discrepancy between the load pressure and force. To overcome this, a filter is used that mixes the high-frequency content from the load pressure signal and the low-frequency content from the force signal. This stabilises the controller since the large volumes affect the high-frequency spectrum by increasing the stability margins, as shown in the previous analysis, while the control accuracy is improved in the low-frequency spectrum since the controller follows the measured force.

To further improve the quality of the signal and remove unwanted noise, an extended Kalman filter (EKF) is implemented, which is the nonlinear version of the Kalman filter, since the hydraulic system is nonlinear in nature. It was realised during testing that the control performance is sensitive to the quality of the feedback signal. Noise was fed back through the controller, with an audible noise as a result. This noise could, e.g., come from the pump pulsation, which is at a relatively low frequency since the pump runs at a low speed when the required flow is low. The EKF effectively removed the noise to such an extent that the performance was improved. Figure 22b shows all the elements in the signal: the force, the load pressure, the high-pass filter content, the mix filter signal, and the extended Kalman filter signal. The implementation of the EKF follows the same principle as in Section 4 but is somewhat reduced. The nonlinear set of system derivatives are defined by Equations (17) and (20). The valve’s dynamic response of the spool position $x_V$ is, here, assumed to be of first order, where U is the input signal and ${\tau }_v$ the response time. A nonlinear valve opening curve is assumed as defined by Equation (19).

$$\begin{array}{cc}\hfill & {\dot{P}}_L=(1+A_{p}v)\frac{4\beta }{V}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & q=C_{q}A\left(x_v\right)\sqrt{\frac{1}{\rho }(P_s-P_L)}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & A\left(x_v\right)=A_1{x}_v^2+A2x_v\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\dot{x}}_v=\frac{-x_v+U}{{\tau }_v}\hfill \end{array}$$

(20)

The set of equations are transformed into discrete form. Defining $x_1=x_v$, $x_2=P_L$, $u_1=U$, and $u_2=v$ yields the following set of Equations (21) and (22), where $T_s$ is the time step (0.1 ms in the real-time system) and k is the index for the current step:

$$\begin{array}{cc}\hfill & x_{1_{k+1}}=f_1({\overline{x}}_k,{\overline{u}}_k)=x_{1_k}(1-\frac{T_s}{{\tau }_v})+\frac{T_s}{{\tau }_v}{u}_{1_k}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & x_{2_{k+1}}=f_2({\overline{x}}_k,{\overline{u}}_k)=x_{2_k}+\frac{T_{s}4\beta }{V}\left(C_q(A_1{x}_{1_k}^3+A_2{x}_{1_k})\sqrt{\frac{1}{\rho }(P_s-x_{2_k})}+A_p{u}_{2_k}\right)\hfill \end{array}$$

(22)

The extendend Kalman filter also requires the Jacobian, J, to compute the next time step. It is defined according to Equations (23)–(27).

$$\begin{array}{cc}\hfill & J=\left[\begin{array}{cc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\end{array}\right]\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & \frac{\partial f_1}{\partial x_1}=1-\frac{T_s}{{\tau }_v}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & \frac{\partial f_1}{\partial x_2}=0\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \frac{\partial f_2}{\partial x_1}=\frac{4\beta T_s{C}_q}{V}(3A_1{x}_1^2+A_2)\sqrt{\frac{1}{\rho }(P_s-x_2)}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & \frac{\partial f_2}{\partial x_2}=1-\frac{2\beta C_q{T}_s(A_1{x}_1^3+A_2{x}_1)}{\rho V\sqrt{\frac{1}{\rho }(P_s-x_2)}}\hfill \end{array}$$

(27)

The load system on the EMA side option B follows a different approach. The idea is to reduce the restriction between the cylinder chambers and the containers as much as possible by avoiding valve blocks with internal passages and hoses. The solution is seen in Figure 6, where a new set of block adapters are manufactured that allows the containers to sit right below the cylinder in direct connection to the cylinder chamber ports. The internal passage is as large as the hydraulic connectors allow for. For this case, it is possible to use the measured force as a feedback signal together with the EKF without any mix filter. However, as it turns out, the mix filter improves the performance even for this case. The results are shown in Figure 24, where the case without the mix filter, and the measured force as feedback, shows a larger overshoot. Interestingly, studying the load pressure shows how the static friction from the valve affects the system’s behaviour. The force felt by the test object and measured by the force sensor is the sum of the load pressure and the cylinder’s friction. However, the force controller acts on the load pressure by controlling the servo valve. Since the friction is part of the equation, the load pressure acts initially in the opposite direction to the reference force to compensate for the friction’s behaviour.

6.3. Model Validation and Performance Evaluation

The complete model is validated here against the step response command of the flight actuators. The validation gives confidence in the results of the air load system’s performance. The force control performance is also evaluated for sine sweep inputs from the flight actuator. The force reference is proportional to the measured flight actuator position. Besides model validation, the results also reveal the force control system’s performance under different conditions.

6.3.1. SHA Side

Figure 25 shows the validation of the force control model on the SHA side with both a light and a heavy load for a step command to the flight actuator. The simulated force and valve positions follow the measured values well, particularly for the heavy load, where friction, servo valve null-position tolerances, and flow disturbance have little effect on the control performance. The DUT controls the reference and reaches 63% of its final value within 90 ms for its maximum performance (for small amplitude inputs where no speed saturation is reached). However, it reaches 63% of its maximum velocity within 13 ms, which causes the flow disturbance. The force controller’s ability to track the reference with good performance indicates that the expected design performance is reached; see Section 5.

The performance for a sine sweep input of the flight actuator is shown in Figure 26 for two different frequency inputs at 0.2 Hz and 1 Hz.

6.3.2. EMA Side

The EMA side is validated in the same way. Figure 27 shows the results of the test case when the feed-forward link is optimised for this specific case. The model represents the implemented system well for both the low- and high-load case. Again, it is the DUT dictating the reference response, which reaches its final value within 30 ms. The force controller’s ability to follow the reference well is an indication that the expected design performance is reached.

The performance for a sine sweep input of the flight actuator is shown in Figure 28 for two different frequency inputs of 0.2 Hz and 1 Hz.

6.4. Integration Results

The final integration with the flight simulator and implementation of the control structure for the EMA are depicted in Figure 29. The only difference for the SHA side is that the load pressure is directly used as feedback without any filters since the load cell signals were too noisy to be used in the control loop. Based on pre-configured flight manoeuvres, the flight simulator calculates the control surface positions, which are converted into commanded positions for the physical flight actuators. The measured flight actuator positions are fed to the hinge moment calculation, where it is converted to a flight actuator load and acts as the reference to the force controller. The hinge moment is scaled to the physical flight actuator’s max load. A maximum hinge moment, $M_{max}$, is assumed for each control surface to scale the load according to Equation (28), where l is the hinge arm length, $F_{max}$ is the maximum allowed actuator load, and R is the ratio between the flight actuator and load actuator.

$$F_{ref}=M_{hinge}\ast l\ast \frac{F_{max}}{M_{max}}R$$

(28)

Testing the air load system together with the flight simulator is carried out by simulating a roll and pitch manoeuvre at an altitude of 5000 m and at Mach 0.7. The performance of the SHA and EMA side is shown in Figure 30. Even if the loads are low, at only 10% of the stall load, the air load system has no problem following the reference signal. The force reference is different for both sides due to the different scaling.

6.5. Possible Improvements

There are a few points to mention where further improvements might be possible. One is the servo valve’s response. Even if a high response valve has been used, there are faster valves on the market. A faster valve would shift the system’s crossover frequency higher on the frequency scale, effectively increasing stability and the possibility of increasing the controller gain.

It was shown how an increased cylinder volume is an effective means to reduce the impact from the flow disturbance. How the increased volume is installed also affects the solution’s effectiveness. The best solution would be to increase the cylinder chambers or increase the cylinder’s port size so that two external containers can be installed without any disruption in the flow.

The cylinder’s friction is an objective for improvement by either using a compensation link or hydrostatic bearings, as mentioned in the literature. A possible solution might be to remove the internal sealing completely, if possible, at the cost of increased pump flow. For testing, this might be an acceptable cost.

By introducing the load pressure in the control loop, any flow pulsations from the supply system have a negative impact. Flow pulsations should be reduced as much as possible, or sould be shifted to a higher-frequency spectrum. Since the supply system in the test rig is driven by an electric motor, the pump speed is typically low since the needed flow is low when running only one actuator. The supply system is sized for running all actuators in the rig simultaneously.

Finally, as mentioned in the literature, a by-pass valve increases the damping and reduces the system gain at the servo valve null region. This could further shape the tracking response, but an integral in the control loop or a compensation link in the feed-forward path would be necessary. The latter could be tuned in the same way as explained in this work.

7. Conclusions

This work has demonstrated how to design and implement an air load simulation system for the testing of aerospace actuators. The performance of the force controller depends on the servo valve’s response and relies to a great deal on a feed-forward link to compensate for the interaction between the air load system and the test object. It is important to accurately estimate the test actuator’s speed. A purely proportional feedback controller was then sufficient to achieve a satisfactory performance, even for very low force set points. Physical-based modelling and optimising model parameters has proven to be a successful method. The force controller’s response requirements depend on the response of the test actuator. For cases where the flow disturbance from the actuator movement becomes severe, increasing the load actuator cylinder volume can effectively reduce its negative impact. Care must be taken when installing the volumes so as to not reduce their effect by restricting the flow to the cylinder chambers. Different filtering techniques, including Kalman filters, further improve the performance by eliminating unwanted noise that would otherwise be introduced in the control loop. A few additional techniques are possible to further improve the performance, like a faster servo valve, which would allow one to increase the controller gain, reducing the load cylinder’s friction, and installing a small by-pass between the load cylinder’s chambers to increase damping.