Gust Load Alleviation Control Strategies for Large Civil Aircraft through Wing Camber Technology
Abstract
1. Introduction
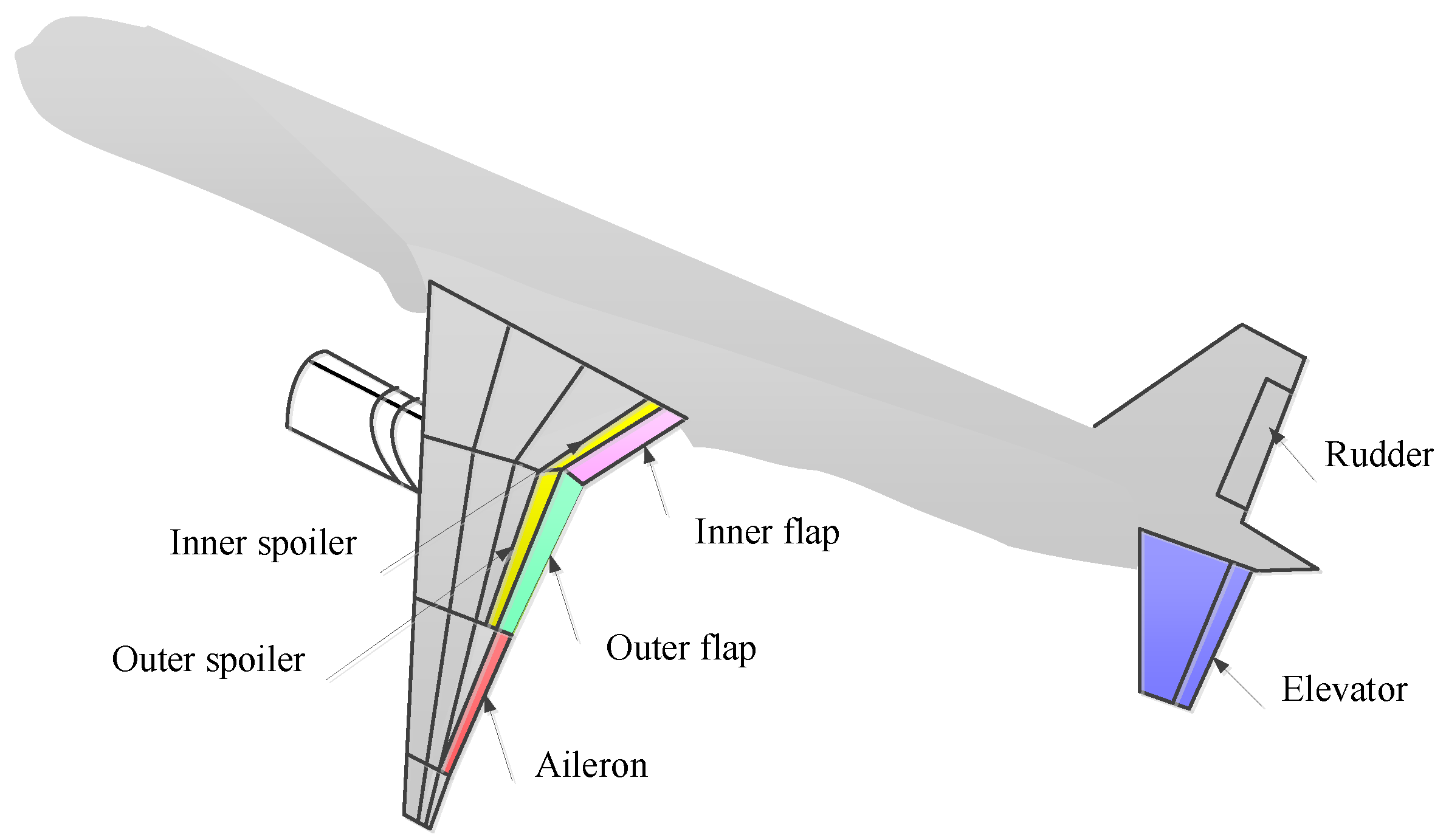
2. Preliminary Materials
Principle of Variable Wing Camber

3. Results
3.1. Existing Load Alleviation Logic Design Methods

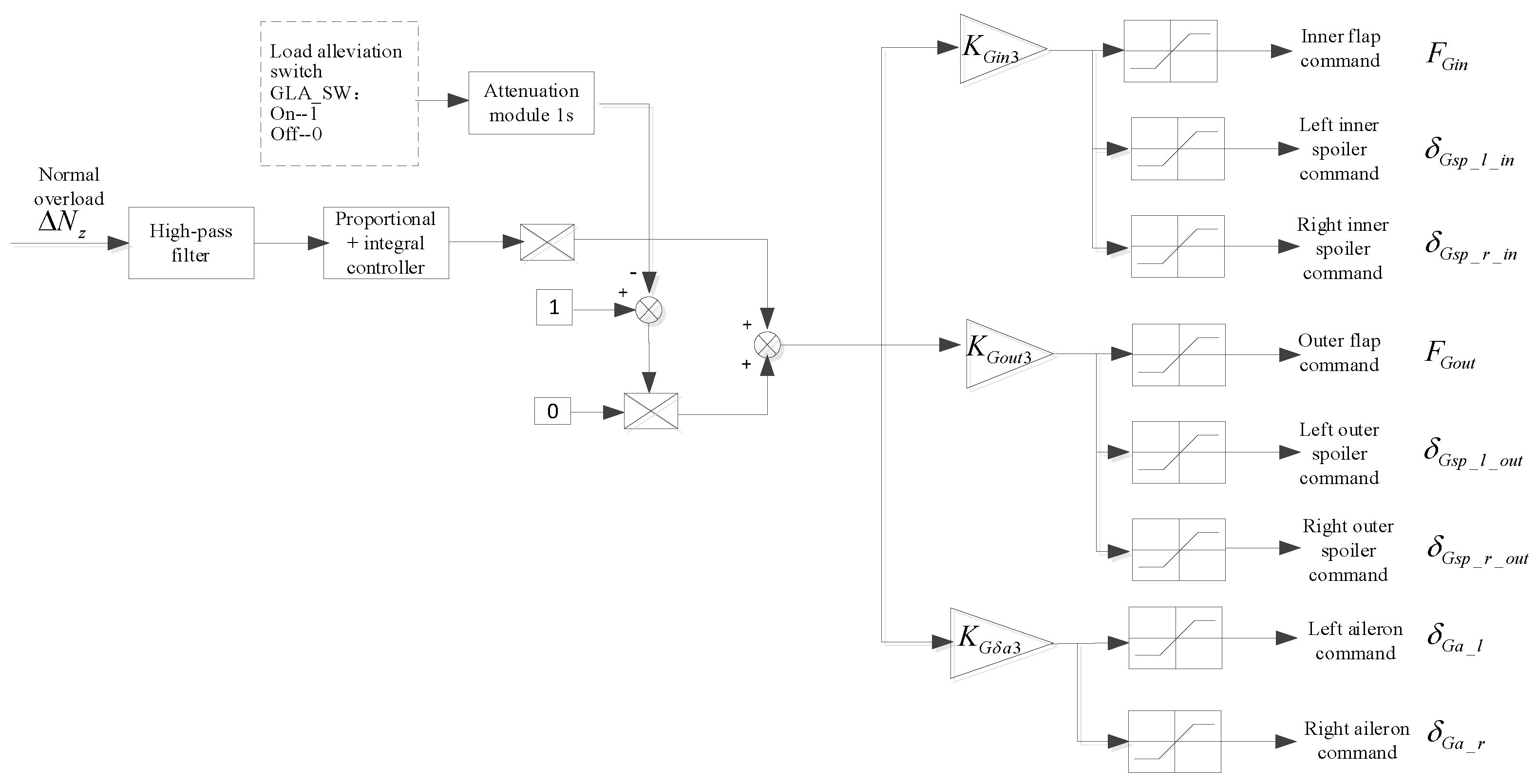
3.2. Load Alleviation Control Schemes


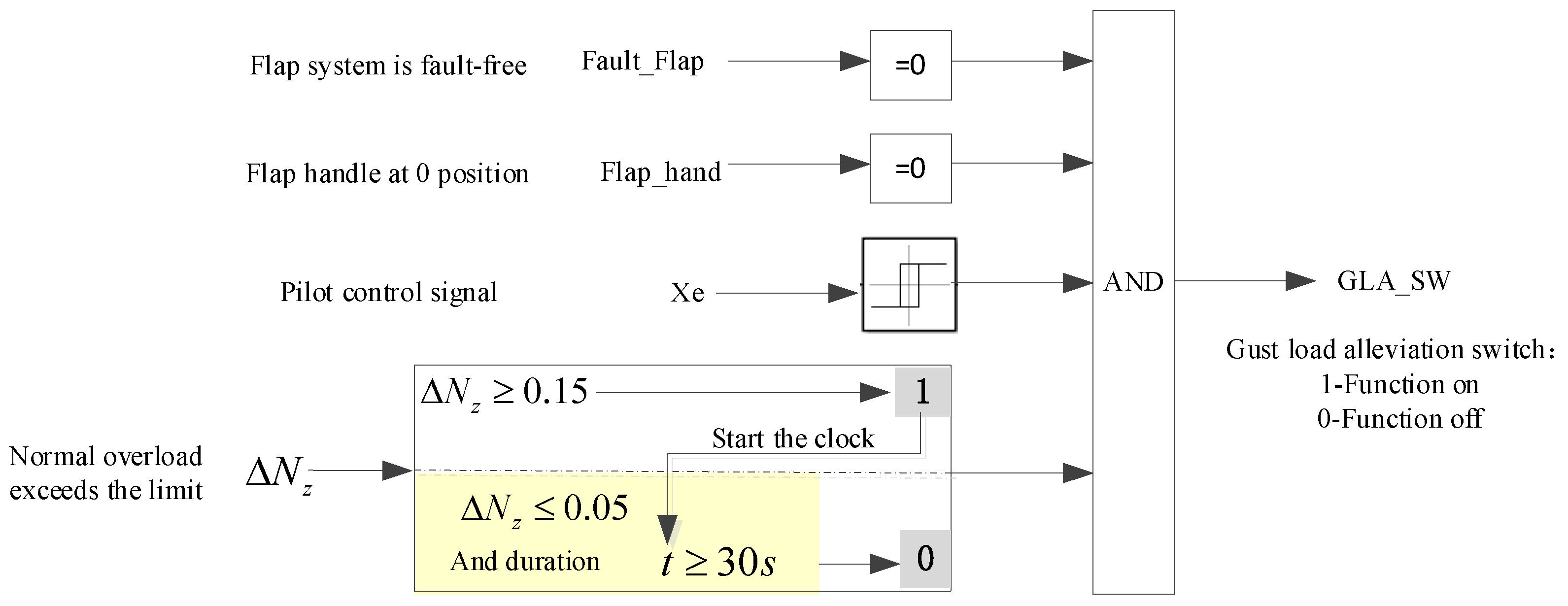
3.3. Functions Switching Logic Design
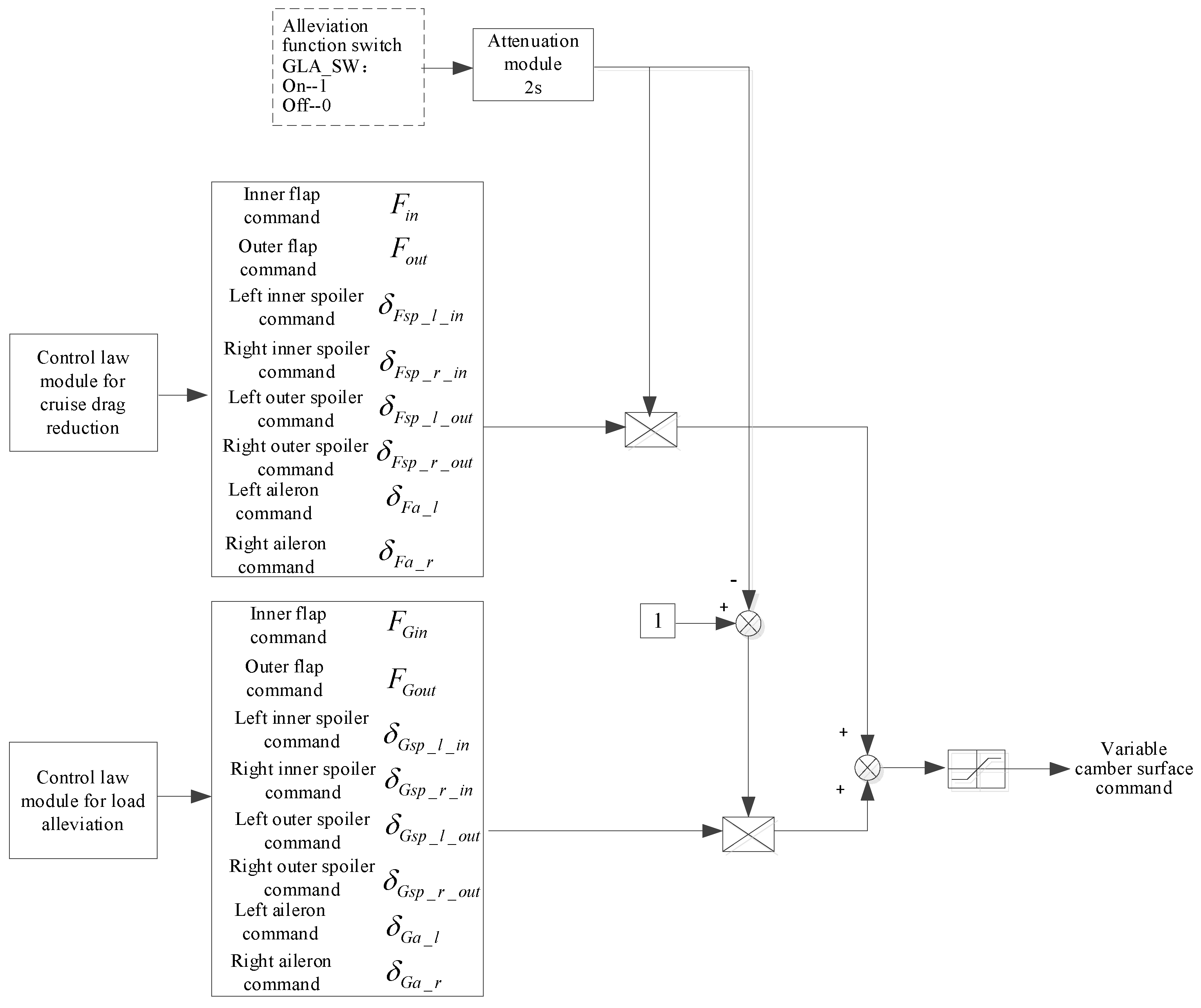
4. Simulation Results
4.1. Wind Model
4.2. Ride Quality
4.3. Atmospheric Turbulence Is Considered in Simulation Case 1
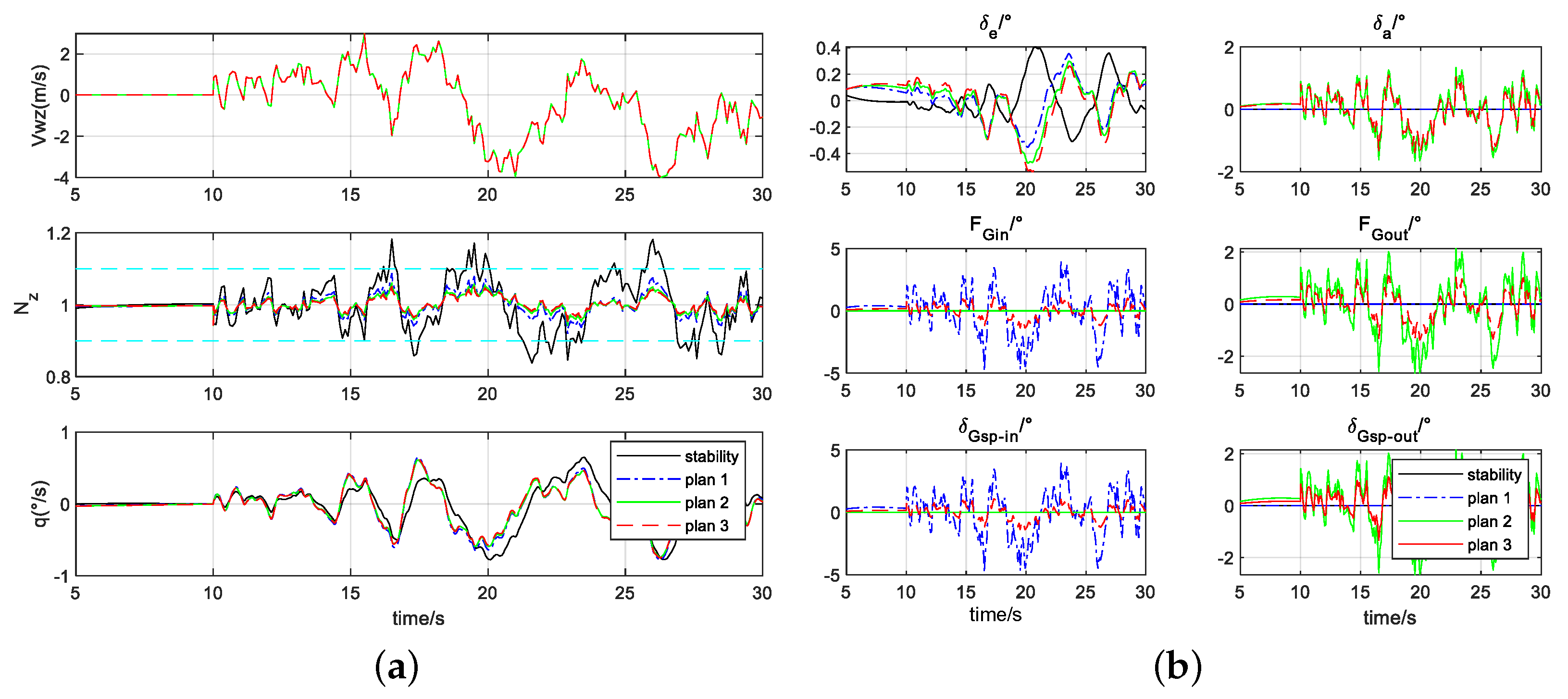
4.4. Discrete Gust Is Considered in Simulation Case 2

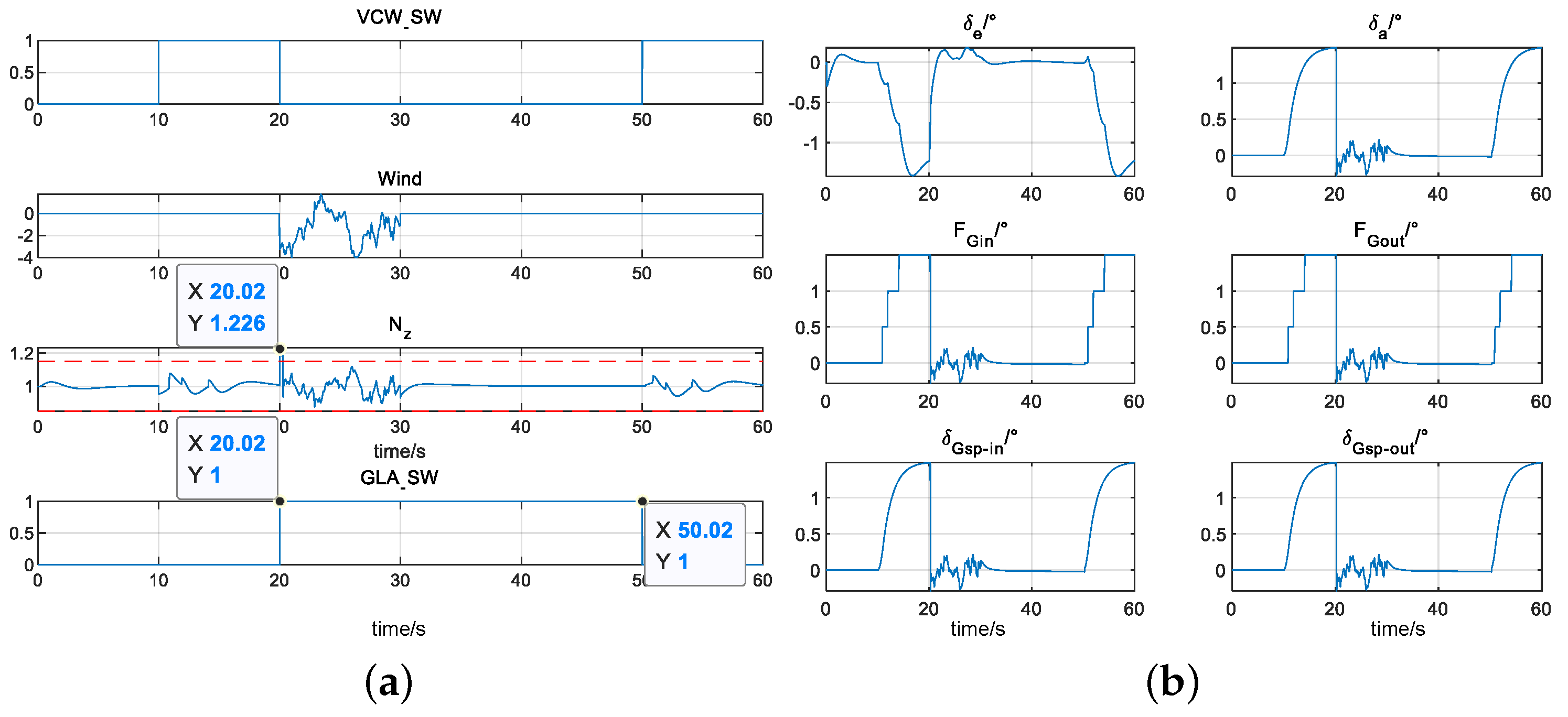
4.5. Functions Logic Switching Simulation Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive trailing edge device (ATED) design process review. Chin. J. Aeronaut. 2021, 34, 187–210. [Google Scholar] [CrossRef]
- Rivero, A.E.; Weaver, P.M.; Cooper, J.E.; Woods, B.K.S. Parametric structural modelling of fish bone active camber morphing aerofoils. J. Intell. Mater. Syst. Struct. 2018, 29, 2008–2026. [Google Scholar] [CrossRef]
- Nguyen, N.; Cramer, N.; Hashemi, K.; Ting, E.; Drew, M.; Wise, R.; Boskovic, J.; Precup, N.; Mundt, T.; Livne, E. Real-time adaptive drag minimization wind tunnel investigation of a flexible wing with variable camber continuous trailing edge flap system. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; pp. 1–47. [Google Scholar]
- Shen, G.; Bai, J.; Liu, N.; Liu, R. Mechanical simulation and aerodynamic analysis on a new type of wing trailing edge variable camber. J. Northwestern Polytech. Univ. 2016, 34, 578–586. [Google Scholar]
- Liu, R.; Bai, J.; Qiu, Y.; Li, Y. Design and analysis of variable camber wing of propeller aircraft using the actuator disc method. Aeronaut. J. 2022, 126, 2134–2155. [Google Scholar] [CrossRef]
- Szodruch, J. The influence of camber variation on the aerodynamics of civil transport aircraft. In Proceedings of the AlAA 23rd Aerospace Sciences Meeting, Reno, NV, USA, 14–17 January 1985; p. 0353. [Google Scholar]
- Kang, N.; Shi, Y. Variable camber differential flap technology applied in aircraft high lift system. In Proceedings of the 2018 CSAA/IET International Conference on Aircraft Utility Systems, Guiyang, China, 19–22 June 2018; pp. 160–164. [Google Scholar]
- Struber, H. The aerodynamic design of the A350 XWB-900 high lift system. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014; pp. 1–6. [Google Scholar]
- Liu, F.; Li, X.; Dou, G.; Nie, R. A design of tandem drive variable camber wing and analysis of aerodynamic performance. J. Air Force Eng. Univ. 2024, 25, 62–68. [Google Scholar]
- Rajagopal, S.; Ganguli, R. Multidisciplinary design optimization of long endurance unmanned aerial vehicle wing. CMES—Comput. Model. Eng. Sci. 2011, 81, 1–34. [Google Scholar]
- Wang, W.; Feng, H.; Liu, C.; Huang, R. Aerodynamic optimization for multi-parameter variable-camber airfoil. Sci. Technol. Eng. 2024, 24, 1259–1267. [Google Scholar]
- Zhang, Y.; Ge, W.; Zhang, Z.; Mo, X.; Zhang, Y. Design of compliant mechanism-based variable camber morphing wing with nonlinear large deformation. Int. J. Adv. Robot. Syst. 2019, 16, 1–19. [Google Scholar] [CrossRef]
- Lei, C.; Yang, C.; Song, C. Optimization design of active aeroelastic wing with variable camber. J. Beijing Univ. Aeronaut. Astronaut. 2024, 1–11. [Google Scholar] [CrossRef]
- Pecora, R.; Concilio, A.; Dimino, I.; Amoroso, F.; Ciminello, M. Structural design of an adaptive wing trailing edge for enhanced cruise performance. In Proceedings of the 24th AIAA/AHS Adaptive Structures Conference, San Diego, CA, USA, 12–16 June 2016; pp. 1–12. [Google Scholar]
- Shi, X.; Yang, Y.; Ge, W.; Wang, Z.; Sun, X. Structure design of variable camber wing trailing edge based on multi-block rotating mechanism. J. Northwestern Polytech. Univ. 2023, 41, 942–949. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Z.; Yang, C. Gust alleviation and wind tunnel test by using combined feedforward control and feedback control. Aerospace 2022, 9, 225. [Google Scholar] [CrossRef]
- Wang, X.; Mkhoyan, T.; Mkhoyan, I.; De Breuker, R. Seamless active morphing wing simultaneous gust and maneuver load alleviation. J. Guid. Control Dyn. 2021, 44, 1649–1662. [Google Scholar] [CrossRef]
- Mengali, G.; Pieracci, A. Ride quality of civil aircraft from a probabilistic viewpoint. J. Guid. Control Dyn. 2000, 23, 319–324. [Google Scholar] [CrossRef]
- Bernhammer, L.O.; Teeuwen, S.P.; De Breuker, R.; Van Der Veen, G.J.; Van Solingen, E. Gust load alleviation of an unmanned aerial vehicle wing using variable camber. J. Intell. Mater. Syst. Struct. 2014, 25, 795–805. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, Z.; Zeng, X.; Yu, J.; Gao, Y.; Huang, G. Wind tunnel test of gust load alleviation for a large-scale full aircraft model. Chin. J. Aeronaut. 2023, 36, 201–216. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q. Improved LQG method for active gust load alleviation. J. Aerosp. Eng. 2017, 30, 04017006. [Google Scholar] [CrossRef]
- Zeng, X.; Zhao, D.; Li, J.; Yan, Z.; Liu, C. Wind tunnel test on gust alleviation control strategies of elastic wing. Acta Aeronaut. Astronaut. Sin. 2023, 44, 220–230. [Google Scholar]
- Wu, Z.; Cao, Y.; Ismail, M. Heavy rain effects on aircraft longitudinal stability and control determined from numerical simulation data. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1824–1842. [Google Scholar] [CrossRef]
- Thorsen, A.T.; Horn, J.F.; Ozdemir, G.T. Use of redundant controls to enhance transient response and handling qualities of a compound rotorcraft. In Proceedings of the 70th American Helicopter Society International Annual Forum, Montreal, QC, Canada, 20–22 May 2014; pp. 3085–3098. [Google Scholar]
- Wang, Y.; Li, F.; Da Ronch, A. Flight testing adaptive feedback/feedforward controller for gust loads alleviation on a flexible aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, San Diego, CA, USA, 13–17 June 2016; pp. 1–7. [Google Scholar]
- Khalil, A.; Fezans, N. Gust load alleviation for flexible aircraft using discrete-time preview control. Aeronaut. J. 2021, 125, 341–364. [Google Scholar] [CrossRef]
- Wang, B.; Yang, Y.; Qian, Z.; Wang, Z.; Lyu, S.; Sun, X. Technical development of variable camber wing: Review. Acta Aeronaut. Astronaut. Sin. 2022, 43, 144–163. [Google Scholar]
- Huang, T. Aircraft Performance Engineering; Science Press: Beijing, China, 2005; pp. 52–63. [Google Scholar]
- Nguyen, N.; Precup, N.; Urnes Sr., J.; Nelson, C.; Lebofsky, S.; Ting, E.; Livne, E. Experimental investigation of a flexiblewing with a variable camber continuous trailing edge flap design. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; pp. 1–13. [Google Scholar]
- Yuan, G.; Li, A.; Wang, C.; Xu, X. Gust alleviation control system design of large civil aircraft based on multiple control surfaces. Flight Dyn. 2011, 29, 65–67. [Google Scholar]
- Qu, X.; Li, T. Design of gust load alleviation control based on UD-PSO for civil aircraft. In Proceedings of the 5th International Conference on Advanced Algorithms and Control Engineering, Sanya, China, 20–22 January 2022; pp. 1–9. [Google Scholar]
- Commission of Science Technology and Industry for National Defense. Flying Qualities Standard for Airplane with Fly-by-Wire Control System: GJB 2874-97; Commission of Science Technology and Industry for National Defense: Beijing, China, 1997.
- Sun, Q. Calculation of passenger quality response of a large aircraft under atmospheric turbulence. Flight Dyn. 1984, 1, 61–82. [Google Scholar]
- Qu, X.; Wang, N. Probabilistic index and calculation of ride quality for civil aircraft. Acta Aeronaut. Astronaut. Sin. 2007, 6, 1323–1326. [Google Scholar]
| State Point | Height (m) | Weight (t) | Lift Coefficient | Lift-Drag Ratio | Outer Flap () | Inner Flap () | Varying Camber Lift-Drag Ratio | Aileron | Spoiler |
|---|---|---|---|---|---|---|---|---|---|
| P1 | 9114 | 160 | 0.531053 | 15.790 | 1.5 | 1.5 | 16.361 | 16.451 | 16.523 |
| P2 | 9114 | 153 | 0.507907 | 15.556 | 0.5 | 1.0 | 15.834 | 15.918 | 16.000 |
| P3 | 9114 | 146 | 0.484754 | 15.307 | 0.5 | 0.5 | 15.361 | 15.369 | 15.448 |
| P4 | 9754 | 146 | 0.530511 | 15.785 | 1.5 | 1.5 | 16.358 | 16.443 | 16.516 |
| P5 | 9754 | 140 | 0.508791 | 15.565 | 0.5 | 1.0 | 15.840 | 15.930 | 16.012 |
| P6 | 9754 | 133 | 0.483444 | 15.292 | 0.5 | 0.5 | 15.343 | 15.350 | 15.429 |
| P7 | 10,363 | 133 | 0.529914 | 15.779 | 1.5 | 1.5 | 16.355 | 16.435 | 16.507 |
| P8 | 10,363 | 127 | 0.506098 | 15.537 | 0.5 | 1.0 | 15.822 | 15.893 | 15.975 |
| P9 | 10,363 | 121 | 0.482275 | 15.279 | 0.5 | 0.5 | 15.327 | 15.334 | 15.411 |
| P10 | 10,973 | 121 | 0.529499 | 15.775 | 1.5 | 1.5 | 16.352 | 16.429 | 16.502 |
| P11 | 10,973 | 115 | 0.503341 | 15.508 | 0.5 | 1.0 | 15.804 | 15.855 | 15.937 |
| P12 | 10,973 | 110 | 0.481536 | 15.271 | 0.5 | 0.5 | 15.317 | 15.323 | 15.401 |
| P13 | 11,582 | 110 | 0.529131 | 15.771 | 1.5 | 1.5 | 16.351 | 16.424 | 16.497 |
| P14 | 11,582 | 105 | 0.505170 | 15.527 | 0.5 | 1.0 | 15.816 | 15.880 | 15.962 |
| P15 | 11,582 | 100 | 0.481201 | 15.267 | 0.5 | 0.5 | 15.312 | 15.319 | 15.396 |
| P16 | 12,192 | 100 | 0.528764 | 15.767 | 1.5 | 1.5 | 16.348 | 16.418 | 16.491 |
| Range | Ride Quality Rank |
|---|---|
| 2 ≤ C < 3 | Comfortable |
| 3 ≤ C < 4 | Moderatly comfortable |
| 4 ≤ C < 5 | Not comfortable |
| C ≤ 5 | Very uncomfortable |
| State Point | Passenger Comfort Index C-Value | Alleviation of Wing Root Bending Moment (Relative Increase in Stability%) | |||||
|---|---|---|---|---|---|---|---|
| Increase Stability | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 1 | Scheme 2 | Scheme 3 | |
| P1 | 2.070 | 2.011 | 2.006 | 2.004 | 15.074 | 13.864 | 13.634 |
| P2 | 2.076 | 2.011 | 2.006 | 2.004 | 15.035 | 13.785 | 13.666 |
| P3 | 2.082 | 2.012 | 2.006 | 2.004 | 14.987 | 13.673 | 13.664 |
| P4 | 2.065 | 2.010 | 2.005 | 2.004 | 15.084 | 13.977 | 13.760 |
| P5 | 2.070 | 2.010 | 2.005 | 2.004 | 15.049 | 13.907 | 13.791 |
| P6 | 2.076 | 2.011 | 2.006 | 2.004 | 15.000 | 13.792 | 13.793 |
| P7 | 2.060 | 2.009 | 2.005 | 2.003 | 15.087 | 14.070 | 13.864 |
| P8 | 2.065 | 2.009 | 2.005 | 2.004 | 15.050 | 13.996 | 13.899 |
| P9 | 2.070 | 2.010 | 2.005 | 2.004 | 15.005 | 13.890 | 13.898 |
| P10 | 2.057 | 2.009 | 2.004 | 2.003 | 15.072 | 14.096 | 13.892 |
| P11 | 2.062 | 2.009 | 2.005 | 2.003 | 15.028 | 14.010 | 13.925 |
| P12 | 2.067 | 2.009 | 2.005 | 2.004 | 14.983 | 13.908 | 13.918 |
| P13 | 2.056 | 2.009 | 2.004 | 2.003 | 15.053 | 14.088 | 13.883 |
| P14 | 2.060 | 2.009 | 2.005 | 2.003 | 15.007 | 14.006 | 13.909 |
| P15 | 2.066 | 2.009 | 2.005 | 2.003 | 14.951 | 13.888 | 13.895 |
| P16 | 2.048 | 2.008 | 2.004 | 2.003 | 15.113 | 14.206 | 13.988 |
| State Point | Passenger Comfort Index C-Value | Alleviation of Wing Root Bending Moment (Relative Increase in Stability%) | |||||
|---|---|---|---|---|---|---|---|
| Increase Stability | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 1 | Scheme 2 | Scheme 3 | |
| P1 | 2.039 | 2.008 | 2.005 | 2.003 | 16.190 | 15.132 | 17.228 |
| P2 | 2.042 | 2.008 | 2.005 | 2.004 | 16.130 | 14.832 | 17.068 |
| P3 | 2.045 | 2.008 | 2.005 | 2.004 | 16.055 | 14.489 | 16.872 |
| P4 | 2.041 | 2.008 | 2.005 | 2.004 | 16.195 | 15.112 | 17.223 |
| P5 | 2.044 | 2.008 | 2.005 | 2.004 | 16.138 | 14.828 | 17.071 |
| P6 | 2.047 | 2.009 | 2.005 | 2.004 | 16.054 | 14.448 | 16.851 |
| P7 | 2.043 | 2.008 | 2.005 | 2.004 | 16.227 | 15.101 | 17.244 |
| P8 | 2.046 | 2.009 | 2.005 | 2.004 | 16.165 | 14.782 | 17.073 |
| P9 | 2.049 | 2.009 | 2.006 | 2.004 | 16.084 | 14.414 | 16.859 |
| P10 | 2.046 | 2.009 | 2.005 | 2.004 | 16.311 | 15.105 | 17.316 |
| P11 | 2.049 | 2.010 | 2.006 | 2.004 | 16.244 | 14.745 | 17.124 |
| P12 | 2.053 | 2.010 | 2.006 | 2.005 | 16.172 | 14.396 | 16.922 |
| P13 | 2.049 | 2.010 | 2.006 | 2.004 | 16.428 | 15.120 | 17.423 |
| P14 | 2.052 | 2.010 | 2.006 | 2.005 | 16.375 | 14.786 | 17.250 |
| P15 | 2.056 | 2.011 | 2.006 | 2.005 | 16.302 | 14.396 | 17.031 |
| P16 | 2.047 | 2.010 | 2.006 | 2.004 | 15.777 | 14.507 | 16.706 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Qiu, Y.; Sun, J.; Wang, B.; Gao, Z. Gust Load Alleviation Control Strategies for Large Civil Aircraft through Wing Camber Technology. Actuators 2024, 13, 229. https://doi.org/10.3390/act13060229
Zhang S, Qiu Y, Sun J, Wang B, Gao Z. Gust Load Alleviation Control Strategies for Large Civil Aircraft through Wing Camber Technology. Actuators. 2024; 13(6):229. https://doi.org/10.3390/act13060229
Chicago/Turabian StyleZhang, Shanshan, Yueheng Qiu, Junshuai Sun, Ban Wang, and Zhenghong Gao. 2024. "Gust Load Alleviation Control Strategies for Large Civil Aircraft through Wing Camber Technology" Actuators 13, no. 6: 229. https://doi.org/10.3390/act13060229
APA StyleZhang, S., Qiu, Y., Sun, J., Wang, B., & Gao, Z. (2024). Gust Load Alleviation Control Strategies for Large Civil Aircraft through Wing Camber Technology. Actuators, 13(6), 229. https://doi.org/10.3390/act13060229








