Abstract
Quadrotors are widely applied in many fields, but they often face various external disturbances in actual operation. This makes it necessary to design a controller that can handle disturbances. Disturbance observer and adaptive control techniques are commonly used disturbance rejection techniques, the core idea of which is to estimate the disturbances in real time and incorporate the estimated values into the controller to suppress the disturbances. In this paper, various disturbance observers and adaptive control techniques, including nonlinear disturbance observers, extended state observers, neural networks, and fuzzy logic systems, are introduced, along with their variants or different structures. These techniques improve the adaptability and robustness of quadrotors to complex environments. Finally, future research directions for the disturbance rejection of quadrotors are also presented.
1. Introduction
In recent years, the rapid development of unmanned aerial vehicles (UAVs) technology has attracted widespread attention. UAVs are reusable aircrafts that do not carry an operator and rely on an onboard flight control system to adjust their flight states in real time according to predetermined procedures. They can fly autonomously along a predetermined route or be controlled by wireless control equipment and ground control stations. The value of UAVs lies in their ability to form aerial platforms that can be used to extend the range of applications by integrating a variety of equipment. UAVs can replace human labor in high-altitude operations in various areas such as logistics delivery [1,2], agricultural plant protection [3,4], forest management [5,6], power patrols [7,8], displacement monitoring [9,10], disaster monitoring [11,12], disaster rescue [13,14], traffic analysis [15,16], railway inspections [17,18], and so on.
Most UAVs can be classified into two categories: fixed-wing UAVs and rotorcraft UAVs. Fixed-wing UAVs rely on the pressure differences generated by their wings to stay in flight and need to maintain a certain speed to do so [19]. On the other hand, rotorcraft UAVs like quadrotors use the lift generated by their propellers to stay in the air, which allows them to operate in tight spaces and make quick changes in their flying position, giving them a significant advantage in agility and maneuverability [20]. Quadrotors are known for their small size, light weight, simple mechanical structure, quick assembly, and easy maintenance, which makes them cost-effective. They are also highly maneuverable, produce low flight noise, and can perform vertical take-off, landing, and hovering. They are adaptable to different environments, including harsh ones, making them ideal for special missions such as disaster rescue. Due to their potential applications, the motion control of quadrotors have gained unprecedented interest from academia and industry in recent years.
However, quadrotors face external disturbances while operating in complex environments, which can harm their control performance and even lead to control instability [21]. Disturbance observers and adaptive control techniques are commonly used disturbance rejection techniques, the core idea of which is to estimate the disturbances in real time and incorporate the estimated values into the controller to suppress the disturbances. Disturbance observers include the nonlinear disturbance observer (NDO) [22], the extended state observer (ESO) [23], etc. They construct the observers through a mathematical model to estimate external disturbances in real time. The adaptive control techniques include adaptive estimation methods [24], neural networks (NN) [25], fuzzy logic systems (FLS) [26], etc., which use tracking errors to estimate and compensate for disturbances independently of the model.
Disturbance estimation methods are widely used in various motion control scenarios such as attitude control [27,28], trajectory tracking [29,30,31], obstacle avoidance [32,33,34], and formation flying [35,36,37]. In [38], three major challenges in quadrotor controller design, including underdrivability, model uncertainty, and actuator failure, were described, and existing control methods were summarized. In [39], the methods of adaptive nonlinear control techniques for quadrotors, including traditional nonlinear control methods and their adaptive/observer-enhanced variants, were summarized. In [40], the methods of controller design for quadrotors when subjected to external uncertainties such as wind were summarized, which focus on describing the wind field model, the dynamic model of the quadrotor under wind, and various control methods used for wind resistance. However, disturbance rejection techniques are not exhaustively described in [40]. In summary, most of the works focus on reviewing the control methods for quadrotors but lack a systematic review and analysis of disturbance estimation methods for quadrotors.
In light of the above discussion, we provide a survey of common disturbance rejection techniques for quadrotors. Section 2 describes the nonlinear dynamic model of quadrotors. Section 3 introduces two disturbance observer techniques and their variants. Section 4 discusses the application of adaptive control techniques in disturbance rejection. Section 5 proposes future work on disturbance rejection techniques. Section 6 is the conclusion of the survey. The structure of the survey is shown in Figure 1.
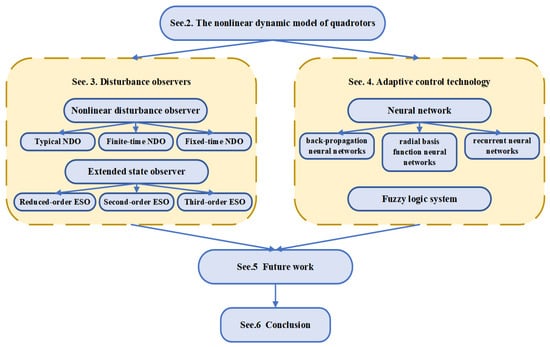
Figure 1.
Structure of the survey.
2. The Nonlinear Dynamic Model of Quadrotors
The quadrotor is a system with four inputs and six outputs. It is a strongly coupled nonlinear system with coupling between its three attitude angles and position. To describe the dynamic model of the quadrotor, two coordinate systems need to be established, which are the inertial coordinate system and the body coordinate system . The schematic diagram of the coordinate system is shown in Figure 2.
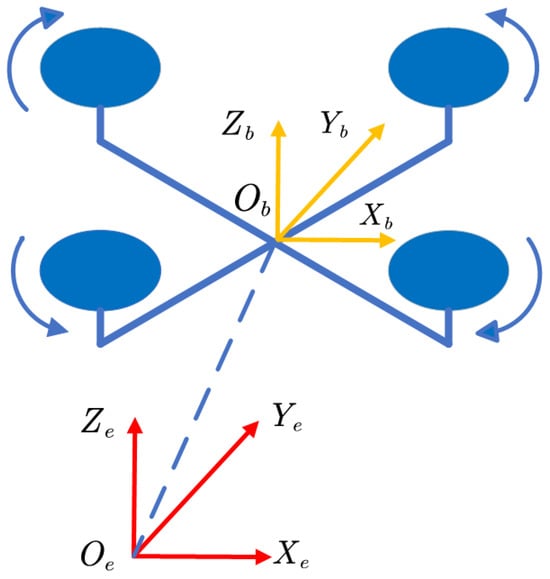
Figure 2.
Schematic of the coordinate system.
The rotation matrix from B to I can be described by
where and represent and , and and denote the roll angle, pitch angle, and yaw angle of the quadrotor, respectively.
To simplify the nonlinear dynamic model of quadrotors, certain physical quantities that have a small effect on the quadrotor are often omitted or simplified. The following assumptions are commonly used:
- Assumption 1: The quadrotor structure is symmetric.
- Assumption 2: The quadrotor is not affected by the Earth’s rotation and revolution.
- Assumption 3: The gravitational acceleration to which the quadrotor is subjected remains constant.
- Assumption 4: The quadrotor performs low-speed, small-angle flight.
- Assumption 5: The disturbances meet , , where and are constants.
According to the Newton–Euler principle, the dynamic model of the quadrotor is established as [41]:
where m is the mass of the quadrotor; g is the acceleration due to gravity; , where x, y, and z are the position of the quadrotor; , where , , and are the the linear velocity of the quadrotor; is the attitude angle vector; , where p, q, and r are the angular velocity; and are external disturbances; , where , , and are the moment inertias of the quadrotor; ; ; and
where , , , and are the control inputs of the quadrotor.
Remark 1.
This paper presents the nonlinear dynamic model of quadrotors based on the Newton–Euler principle. The dynamic model of quadrotors can also be expressed by the Lagrange–Euler formalism [42,43]. In addition, quaternions can be used instead of Euler angles to circumvent the singularity problem that may result from the use of Euler angles [44].
To address the underdrive and coupling issues of the quadrotor, the hierarchical control structure is commonly employed [45], as is the control block diagram in the case of disturbances, as shown in Figure 3. This paper will focus on the disturbance estimation part. The quadrotor is divided into two control loops, which are the position control loop and the attitude control loop. The position control loop is governed by a single control input , whereas the attitude loop is controlled by three control inputs , , and . The ground operator provides the desired position and yaw angle of the quadrotor, i.e., , , , and . According to Equation (3), the desired roll angle and pitch angle can be obtained through and , enabling the decoupling between the position and the attitude.
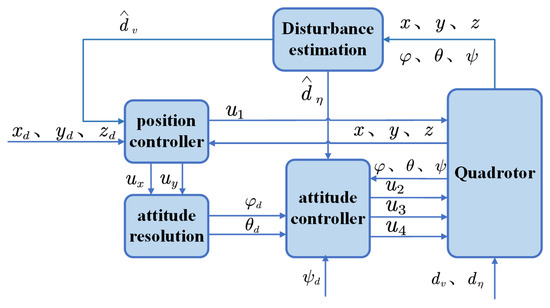
Figure 3.
The structure of controller.
3. Disturbance Observers
3.1. Nonlinear Disturbance Observer
Research on the NDO has been going on for a long time. The NDO was summarized in [46] and the global uniform ultimate boundedness of the tracking errors was demonstrated by applying the Lyapunov stability theory. This approach was subsequently widely applied to deal with uncertainties and external disturbances in various nonlinear systems [47,48,49].
Combining the NDO with other control strategies has become an important way to solve various disturbances in quadrotor systems and improve their performance. In [21], the nonlinear dynamic model of quadrotors considering wind disturbances was developed, and a controller that can compensate for negative wind effects was designed by combining backstepping and an NDO. In [50], a robust backstepping sliding mode control method was proposed for the trajectory tracking of a quadrotor, while an NDO was employed to address the effects of external disturbances and parameter uncertainties. In [51], a quadrotor attitude control technique based on a composite disturbance observer was proposed, which achieves effective control of a quadrotor attitude subjected to an unknown bounded perturbation by introducing an NDO in combination with an adaptive backstepping sliding mode control and auxiliary gain. In [52], an adaptive sliding mode control strategy based on an NDO was presented. This strategy employs an adaptive sliding mode approach to cope with actuator faults, while incorporating an NDO to mitigate the effects of external disturbances. In [53], a control method based on feedback linearization and an NDO was proposed, which effectively addresses model uncertainty, and suppresses high nonlinearities in the model. In [54], an adaptive fuzzy controller was proposed that integrates a modified NDO to estimate uncertainties and disturbances. The experimental results showed that the controller has stronger elastic stability and tracking performance compared to the conventional method. In [55], an adaptive fuzzy tracking control scheme for quadrotors was proposed, which uses an FLS and NDO to approximate the unknown dynamics of the quadrotor system. By combining NDO with various control methods, various disturbance problems in quadrotor control systems can be effectively solved, improving their performance and enabling them to operate stably and reliably in complex environments.
The application of NDO has also been extended to wider areas such as collision avoidance, target tracking, and multi-UAV formation control. In [56], a method combining the fast finite-time convergence guidance law and an NDO was proposed for the collision avoidance problem to ensure the safety of UAVs. In [57], a standoff tracking and guidance method for UAVs under windy conditions was proposed. The method uses an NDO to estimate wind disturbance, and combines it with the Lyapunov guided vector field technique to compensate for wind effects and achieve ground target tracking successfully. In [58], a disturbance rejection formation control method was proposed, which uses an NDO to estimate external disturbances. These works further demonstrate the wide applicability and effectiveness of NDO in modern control systems.
The mathematical expression for NDO is presented next. As described by [46], the NDO derived from models (1) and (2) can be expressed in the following manner:
where and are auxiliary variables, and are gain matrices, , , and , and are the estimation of and , respectively.
Next, the stability of the NDO is proved. This part of the proof focus on the NDO of the position system, and the process of proving the NDO of the attitude system is the same as that of the position system. We take the Lyapunov function as
where .
Due to , it can be obtained that
From (8), we can obtain
From the above equation, it can be seen that, as long as , then the disturbance estimate of the NDO will converge to its true value .
In [59], it is described how to choose the appropriate gain matrix such that the NDO (4) and (5) are exponentially stable. In addition, to apply this approach to assess the effect of uncertainty, the error dynamics of the observer must be faster than the dynamics of the closed-loop system, as can be seen in [48].
With the theoretical development, the finite-time NDO has been proposed in recent years. In [60], the finite-time control problem of a quadrotor under input saturation and external disturbances was investigated, using a finite-time NDO to estimate the external disturbances and a combination of an auxiliary system and a fast-terminal sliding mode controller for stabilization control and trajectory tracking of the quadrotor. In [61], a control scheme based on a perturbation observer and an integral sliding mode technique was proposed for spacecrafts affected by external perturbation moments and actuator failures. The scheme uses a finite-time NDO to reconstruct the composite uncertainties caused by actuator failures and external disturbances. In [62], a composite control scheme combining a finite-time NDO and adaptive non-singular fast terminal sliding mode control was proposed to cope with the problems of parameter uncertainty, external disturbances, and actuator failures. The finite-time NDO ensures that the estimation of the disturbance is completed within a finite time. This can reduce the response time of the system and enhance its dynamic performance and robustness. One of the finite-time NDO are as follows [62]:
where and are the estimations of and , , , and are auxiliary variables, and , , , and are gain matrices.
We take the Lyapunov function as
It can be obtained that
Based on the Lemma 1 in [62], it can be concluded that the disturbance estimate will converge to its true value in finite time.
The fixed-time NDO was proposed as a further development of the finite-time NDO. In [63], a robust fault-tolerant tracking control scheme for uncertain quadrotors was proposed, which uses a fixed-time NDO to cope with model uncertainty, external disturbances, actuator failures, and input delays to ensure that the quadrotor can track the predefined trajectory. In [64], a fixed-time dynamic surface control method based on a fixed-time NDO was proposed to achieve trajectory tracking control tasks under disturbances. In [65], a fixed-time perturbation observer was constructed to accurately estimate the wind perturbation, and a robust fixed-time controller was designed for the position attitude system by combining the sliding mode control theory with the fixed-time technique. Compared with the finite-time NDO, the fixed-time NDO can not only complete the disturbance estimation within a fixed time, but, also, the upper time limit is not affected by initial conditions, which makes it more flexible and predictable in practical applications. One of the fixed-time NDO are as follows:
where and are auxiliary variables; and , where and are the estimations of and , respectively; and ; , , , , , , , and are gain matrices; and , and , .
We take the Lyapunov function as
From (15), we can obtain
It can be obtained that
Based on the Lemma 1 in [63], it can be concluded that the estimate will converge to zero in fixed time.
Because the estimate will converge to zero in fixed time, the disturbance estimate will converge to its true value in fixed time.
Next, the estimation performance of the NDO, finite-time NDO, and fixed-time NDO are simulated and compared, as shown in Figure 4, analyzed only for the roll angle channel. The external disturbance is modeled as a sinusoidal signal. The simulation results show that the fixed-time NDO outperforms the finite-time NDO, which, in turn, outperforms the NDO, and all three observers have smaller errors and are able to estimate the disturbance more accurately. Their advantages and disadvantages are summarized in Table 1.
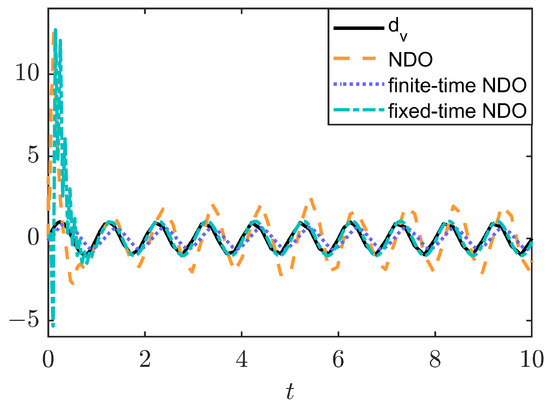
Figure 4.
Estimation performance of NDOs.

Table 1.
NDO: advantages and disadvantages.
This subsection details the classical form of the NDO and its finite-time and fixed-time variants. In addition to the specific forms mentioned, many other variants of the NDO exist that can be adapted for different control methods and application scenarios. However, NDO usually require an accurate system model to estimate disturbances.
3.2. Extended State Observer
In this section, we will introduce the ESO, which is an observation technique that can observe the external disturbances of the system and estimate its internal state simultaneously. This property makes the ESO widely applicable in the disturbance rejection of quadrotors.
The ESO is an important part of active disturbance rejection control (ADRC), but the application of ESO in quadrotor control is not limited to a single control strategy; it can be combined with other control methods. In [66], a fast non-singular terminal sliding mode tracking controller was proposed, and an ESO was integrated into the controller, which can guarantee accurate trajectory tracking in the presence of disturbances. In [67], ADRC and a predictive control strategy were employed for solving the trajectory tracking problem of the quadrotors with gust. The approach also combined an ESO for estimating and compensating gust disturbances to achieve accurate trajectory tracking. In [68], an ESO-based disturbance compensator and a novel sliding mode controller were proposed for quadrotor attitude control under unknown disturbances. The method can effectively estimate the low-frequency and high-frequency components of the superimposed disturbances and reduces the effect of the virtual disturbance estimation error, which improves the performance and robustness of the attitude control. In [69], a cascaded ADRC strategy with a two-stage Kalman filter was proposed and an ESO was designed in the ADRC controller to further compensate the effect of the Kalman filter estimation error. In [70], a novel U-model-enhanced double sliding mode controller based on a multiple-input and multiple-output ESO was presented, where the ESO was designed to estimate unmeasurable velocities and uncertain aerodynamics. In [71], a tracking differentiator was introduced to obtain a smooth tracking signal, and an ESO was proposed to estimate the modeling uncertainty and unknown disturbances of the system. Based on the tracking differentiator and ESO, a novel finite-time convergent smooth tracking controller was developed, which enabled the system to achieve the desired tracking performance in finite time. In [72], a variable gain ESO was developed to accurately estimate unknown external disturbances. It effectively mitigated the peak problem that conventional methods face.
In more complex application scenarios, such as fault diagnosis and localization of UAVs, and target tracking and path tracing, the ESO demonstrates its applicability and flexibility. In [73], ESO successfully completed the fault diagnosis and localization tasks of UAVs by combining residual feature analysis and deep forest techniques. In [74], an ESO-based controller was proposed to ensure precise tracking performance of UAVs in 2D space, demonstrating the great potential of ESO in group intelligence and cooperative control. In [75], a guidance law based on a novel ESO was proposed for the broken path tracking problem of UAVs, which was combined with a folded path switching method, and the ESO parameter tuning method was further proposed for engineering applications.
The mathematical expression for the ESO is presented next. Its basic idea is to expand the disturbance into a new state variable in the original system, and design a state observer for the expanded state system. For systems (1) and (2), the model of the system after adding the expanded state becomes
where and are extended states.
Firstly, the reduced-order ESO is introduced; for systems (21) and (22), the reduced-order ESO can be represented as follows [76]:
where and are auxiliary variables, and and are gain matrices. In [76], it is demonstrated that by appropriately choosing the gain matrices of the ESO, it can make the estimations asymptotically track the state of the system, and that it can efficiently compensate for unknown disturbances suffered in the control system.
We take the Lyapunov function as
It can be obtained that
From (27), we can obtain
From the above equation, it can be seen that, as long as , then the disturbance estimate of the reduced-order ESO will converge to its true value .
The reduced-order ESO, described above, can only estimate the disturbances. In [66], a second-order ESO was used that is capable of estimating the velocity and disturbance of the system:
where , , , and are the estimations of v, , , and , respectively, and , , , and are gain matrices.
It can be obtained that
Based on the Lemma 1 in [77], it can be proved that will converge to its true value v and the disturbance estimate will converge to its true value .
In addition to the above two ESO, a third-order ESO has been proposed in [71] to estimate the full state of the system, which is the most commonly used method, with the following expression:
where , , , , , and are the estimations of , v, , , , and , respectively, and , , , , , and are gain matrices.
It can be obtained that
Based on the Lemma 1 in [77], it can be proved that will converge to its true value , will converge to its true value v, and the disturbance estimate will converge to its true value .
Next, the estimation performance of the reduced-order ESO, second-order ESO, and third-order ESO are simulated and compared, as shown in Figure 5, analyzed only for the roll angle channel. The external disturbance is modeled as a sinusoidal signal. The simulation results show that all three observers have smaller errors and are able to estimate the disturbance more accurately. Their advantages and disadvantages are summarized in Table 2.
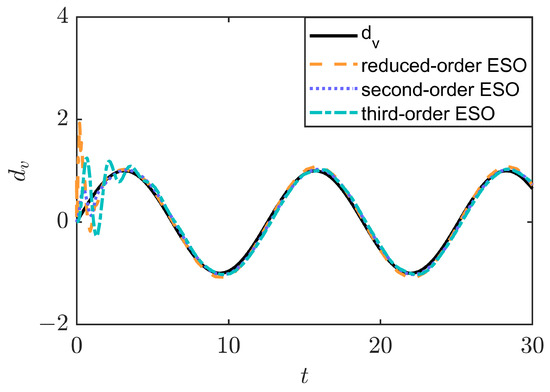
Figure 5.
Estimation performance of ESOs.

Table 2.
ESO: advantages and disadvantages.
Similarly to NDO, the derivatives of disturbances in ESO need to be bounded and ESO require accurate mathematical modeling. It should be noted that the forms of ESO may change depending on different control methods and are not necessarily limited to the forms given above. These ESO can be adapted and improved to suit different control scenarios and applications based on specific control requirements and system characteristics.
4. Adaptive Control Technology
In Section 3, it was established that NDO and ESO can observe disturbances, but need to know the nonlinear dynamics of the quadrotor. Adaptive control methods usually only need the tracking error information without having a detailed model of the system. In this section, some adaptive control methods are described. The simplest adaptive estimation method is as follows [78]:
where and are estimations of and ; , , , and are desired values; and and are the controller parameters.
Some work has added the convergence term to the above adaptive law as follows:
where , , , and are the controller parameters. The error terms and can vary depending on the control method; for example, in sliding mode control they can be sliding mode variables, but the basic form is shown above. The equations for estimating disturbances using NN and FLS all have similar forms.
As the proof of convergence of the adaptive estimation method needs to be combined with a controller, it will not be described in detail here, nor will the subsequent NN and FLS.
4.1. Neural Network
The powerful learning ability and excellent nonlinear function approximation capability of NN make them widely applied in the controller of the quadrotor. Travis et al. [79] used an NN combined with output feedback to construct a nonlinear controller. The controller uses an NN to approximate the uncertain nonlinear terms in the dynamics model and estimates the translational and angular velocities of quadrotors via an NN observer. In [80], an NN-based adaptive compensatory control scheme was proposed. The scheme ensures bounded trajectory tracking for the position subsystem and asymptotic trajectory tracking for the attitude subsystem under external disturbances. Yang et al. [81] used a non-singular fast terminal sliding mode control strategy incorporating an NN to ensure fast convergence and high robustness of the quadrotor. In [82], a robust neural adaptive backstepping control method was proposed. The method utilizes the global estimation property of NN to estimate external disturbances. In [83], an adaptive predetermined time sliding mode controller based on an NN was used to enable the quadrotor formation to track the planned trajectory within a specified time. In [84], a geometrically adaptive controller for quadrotors incorporating three layers of NN was presented. This controller adapts the NN weights to the variations of unstructured forces and moments online by means of an adaptive law. In [85], an adaptive integral sliding mode control strategy was proposed and the equivalent control law of the system was estimated using an NN. Through online learning and real-time updating, the controller achieves adaptive tuning, ensures the finite-time stability of the system, and verifies the effectiveness of the method in experiments.
There are three types of NN discussed below. The first and most commonly used one is the radial basis function neural network (RBFNN). RBFNN has three layers, including an input layer, a hidden layer, and an output layer, as shown in Figure 6. The input layer is responsible for transferring input data to the nodes in the hidden layer. The hidden layer nodes are connected to the output layer through transfer functions, which are usually Gaussian. The output layer produces a linear combination of the input signals, and the final output data is a linear weighted sum of the hidden layer neuron outputs.
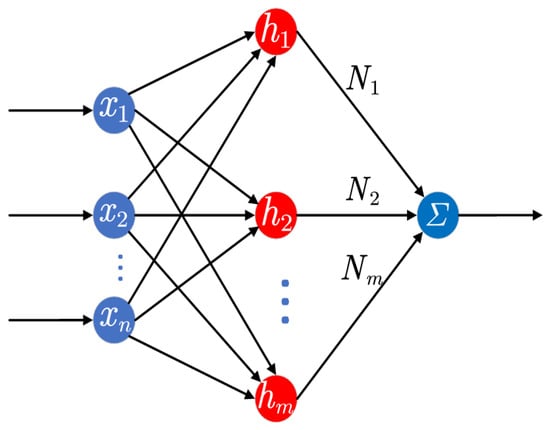
Figure 6.
The structure of RBFNN.
Disturbance estimation can be achieved using back-propagation neural networks (BPNN) in addition to RBFNN. Unlike the single hidden layer structure of RBFNN, BPNN can have multiple hidden layers, as shown in Figure 7. This allows for the construction of deeper models that can capture more complex nonlinear relationships in the data. Each layer nonlinearly transforms the input using an activation function, then passes the information to the next layer through weights and biases. The algorithm core of BPNN lies in the error back-propagation mechanism, which optimizes the model’s performance by calculating the output error and back-propagating it through the network, updating the weights and biases layer by layer.
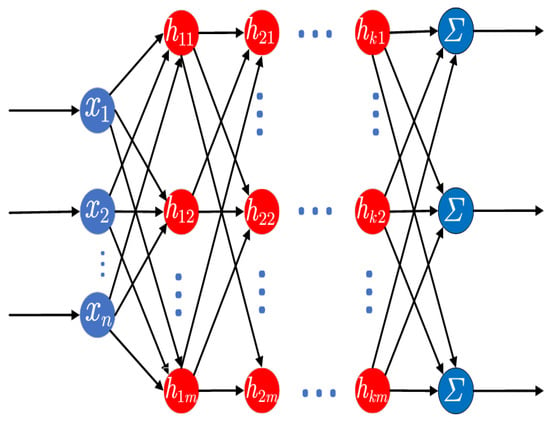
Figure 7.
The structure of BPNN.
The recurrent neural network (RNN) is a popular tool for disturbance estimation. The RNN is particularly useful when working with sequential data, due to their ability to pass states through their layers in a cyclic fashion. This allows them to retain information over time and take into account the effects of historical data, which leads to more accurate predictions and adjustments for interference due to time-dependent changes. In RNN, there is an input layer, one or more hidden layers that are cyclically connected, and an output layer, which is depicted in Figure 8. These cyclic connections enable the network to generate outputs, not just based on current inputs, but on previous activities as well. This provides continuous data flow analysis and prediction capabilities for dynamic systems. The RNN is well-suited for handling disturbances in dynamic and nonlinear systems, due to their ability to remember past information.
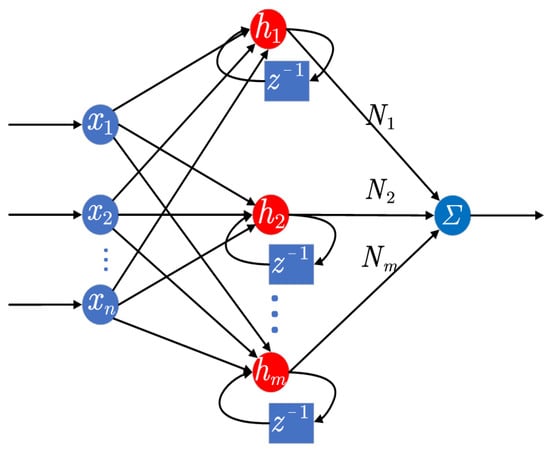
Figure 8.
The structure of RNN.
Although the various NN have different structures, their expressions are usually similar when used to estimate disturbances, and the RBFNN is used here as an example. According to [86], the disturbances can be expressed by the RBFNN as
where x is the input of the RBFNN, and are the optimal output weight matrices, and and are the approximation errors of the RBFNN, which are generally small. and are radial basis functions, and most work is usually done with Gaussian functions of the following form:
where represents the value of the center point of the basis function, and represents the width parameter of the basis function.
To estimate the unknown disturbance, the RBFNN is used as follows:
where and are the estimations of and , and and are the estimations of and . The adaptive law of the output weight matrices are designed as follows:
where , , and are the controller parameters.
It can be observed from the equation mentioned above that NN do not require a system model for disturbance estimation. Only the tracking error is sufficient. However, a suitable basis function and some parameters, such as the width of the basis function, must be chosen and adjusted appropriately to achieve good estimation performance. Furthermore, NN can usually demonstrate their stability without strictly constraining the disturbances, which expands their range of applications. Moreover, different control methods might have different requirements for NN, and, thus, the design of NN must be changed based on specific control schemes and system characteristics.
4.2. Fuzzy Logic System
Fuzzy control is a method of dealing with complex systems based on fuzzy mathematics. In classical control theory, the performance of the control system is assumed to be better when the system model is more accurate. However, real systems often have complex nonlinearities and unknown parameters, making accurate modeling difficult. To overcome these challenges, researchers have turned to intelligent control methods, such as fuzzy control.
FLS are an important part of fuzzy control, which use fuzzy linguistic information to deal with system uncertainty and complexity. In adaptive FLS control methods, controllers can be adjusted in real time by adaptive laws to cope with system changes. Compared to traditional adaptive control methods, FLS are more flexible, using fuzzy instructions to enhance the adaptability and robustness of the control system. A number of quadrotor control works have used this control approach and superior results have been reported. Liu et al. [26] proposed an adaptive FLS based on a nonsingular fast terminal sliding mode controller for compensating block disturbances and adjusting the control gain in real time. In [87], an adaptive fuzzy output feedback control method was proposed for a quadrotor with random perturbations. The method uses an FLS to approximate unknown nonlinear functions in the model. In addition, an observer with an FLS was designed for estimating the unmeasurable states through an adaptive backstepping technique. In [88], a novel fuzzy adaptive nonlinear fault-tolerant control design scheme was proposed for the attitude dynamics of a quadrotor with four sensor failures, in which an FLS was used to approximate the mismatched uncertainty and unknown nonlinear function vectors. In [89], an FLS was combined with adaptive backstepping control, which was used to observe mass variations and external disturbances. In [90], a combination of an FLS and adaptive integral terminal sliding mode controller was used to solve the trajectory tracking problem of quadrotors with actuator failure, external disturbances, and input saturation. In [91], an adaptive fuzzy output feedback control method was proposed for quadrotors with stochastic disturbance, which used an FLS to approximate unknown nonlinear functions and introduce a dynamic surface control technique and an adaptive backstepping observer that ensures that the system error converges in a small neighborhood of the origin.
The FLS consists of four basic parts: the fuzzification operator, fuzzy rule base, fuzzy inference, and defuzzification operator. The basic structure of the FLS is shown in Figure 9. Fuzzy rule bases are formed by “if-then” of the following form:
where N is the number of rules, and y are inputs and outputs, respectively, and and are the fuzzy set. From single point fuzzification, product inference and center average weighted defuzzification, the following FLS can be obtained:
where , and and are the membership functions.
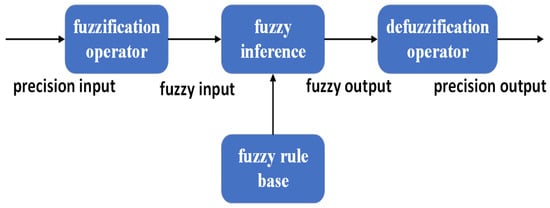
Figure 9.
The basic structure of FLS.
We define the fuzzy basis function as
We define , and , ; it can be obtained that
According to [26], the disturbances can be expressed by FLS as
where and are the inputs of the FLS, and are the optimal output weight matrices, and and are the approximation errors of the FLS, which are generally small. The unknown disturbance is estimated using the FLS as follows:
where and are the estimations of and , and and are the estimations of and . The adaptive law of the output weight matrices is designed as follows:
where , , , and are the controller parameters.
Next, the estimation performance of the adaptive estimation, NN and FLS are simulated and compared, as shown in Figure 10, analyzed only for the roll angle channel. The external disturbance is modeled as a sinusoidal signal. The simulation results show that all three observers have smaller errors and are able to estimate the disturbance more accurately. Their advantages and disadvantages are summarized in Table 3.
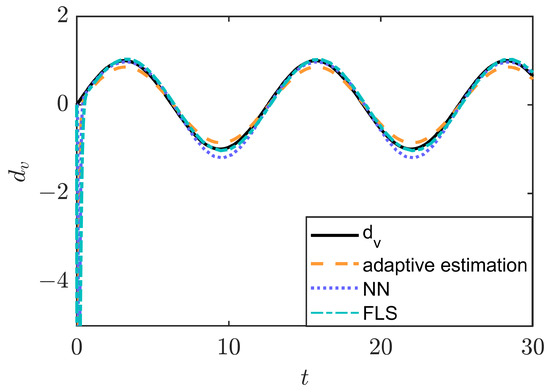
Figure 10.
Estimation performance of adaptive control technology.

Table 3.
Adaptive control technology: advantages and disadvantages.
Both FLS and NN can estimate disturbances without relying on an accurate mathematical model of the system, instead using tracking errors directly. However, while FLS depend heavily on fuzzy sets and subordinate functions for describing and processing data, this approach may not be precise enough to handle highly precise or subtle variations. Moreover, the relatively high computational complexity of FLS may pose a challenge in resource-constrained application environments. Similarly, NN present similar challenges, especially when large amounts of data and complex network structures need to be processed. Therefore, the computational complexity and accuracy of these methods need to be considered in practical applications, as well as their applicability and efficiency in specific environments.
4.3. Simulation Comparison
In this subsection, the NDO, reduced-ESO, and adaptive estimation are selected as representatives of the three types of observers, and their estimation performances are compared through a simulation, as shown in Figure 11. To further validate the effectiveness of these observers, the external disturbances were modeled as irregular disturbances such as white noise. The simulation results show that the NDO and adaptive methods have more obvious overshooting phenomena during the estimation process, but the estimation performance of the NDO is better than that of adaptive methods, while the overall performance of the ESO is optimal. The NDO shows a strong ability in dealing with irregular disturbances, and its fast response characteristic makes the estimation error small despite the presence of certain overshoot. On the other hand, adaptive methods do not rely on mathematical models and are prone to large overshoots, leading to an unstable estimation in a short period of time. However, the ESO is able to better balance the response speed and stability due to its intrinsic structural design. Their respective advantages and disadvantages are shown in Table 4.
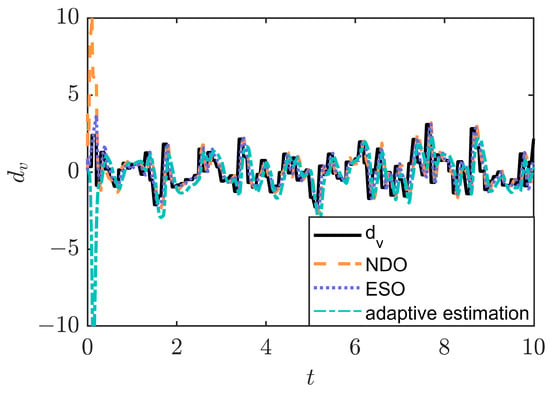
Figure 11.
Estimation performance of the three types of observers.

Table 4.
Disturbance estimation methods: advantages and disadvantages.
5. Future Work
Disturbance observers such as NDO and ESO, and adaptive control techniques such as NN and FLS have shown great potential in observing disturbances and dealing with control problems. Although these techniques are very advanced in many aspects, there are still some aspects that need further improvement and development.
In high-speed dynamic systems, NDO and ESO may face the problem of insufficient response speed. To address this problem, it is possible to develop more efficient algorithms or advanced hardware implementations that can improve the observer response speed. In addition, it is crucial to enhance real-time performance, especially in systems with high safety requirements such as aerospace and self-driving cars.
Although NN and FLS can adapt to changing environmental conditions, they may not perform well when faced with complex and high-frequency disturbances. To improve their adaptability, better learning algorithms or online updating mechanisms are needed. At the same time, both NN and FLS are usually accompanied by high computational complexity, which can be a limiting factor, especially in resource-limited systems. Therefore, optimizing the structure of the algorithms or reducing the computational burden by using techniques such as edge computing and hardware acceleration are important ways to improve their practicality.
To improve the performance of the system, optimization algorithms can be studied and used to estimate and provide initial parameters. Additionally, new composite disturbance estimation methods can be developed. This will make the control system more accurate and able to meet more requirements. Combining different technologies with complementary characteristics can significantly enhance the overall performance of the system.
6. Conclusions
This paper has focused on the application of disturbance observers and adaptive control techniques for disturbance rejection of quadrotors. This paper has provided a survey of the similarities and differences between these techniques, and their application to quadrotor control. Four main control methods were described: NDO, ESO, NN, and FLS, and their associated variants, which are classic NDO, finite-time NDO, and fixed-time NDO, reduced-order ESO, second-order ESO, and third-order ESO, and several forms of neural networks, including BPNN, RBFNN, and RNN. Finally, some guiding recommendations for future research were proposed to promote further development in related fields.
Author Contributions
Writing—original draft preparation, R.W.; writing—review and editing, J.S.; supervision, J.S.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 61973156.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, B.D.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Li, Z.; Liu, H. An air route network planning model of logistics UAV terminal distribution in urban low altitude airspace. Sustainability 2021, 13, 13079. [Google Scholar] [CrossRef]
- Sun, F.; Wang, X.; Zhang, R. Task scheduling system for UAV operations in agricultural plant protection environment. J. Ambient. Intell. Humaniz. Comput. 2020, 1–15. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Fu, H.; Fu, X.; Qi, L. Distribution regularity of downwash airflow under rotors of agricultural UAV for plant protection. Int. J. Agric. Biol. 2021, 14, 46–57. [Google Scholar] [CrossRef]
- Zhu, Y.; Jeon, S.; Sung, H.; Kim, Y.; Park, C.; Cha, S.; Jo, H.; Lee, W. Developing UAV-based forest spatial information and evaluation technology for efficient forest management. Sustainability 2020, 12, 10150. [Google Scholar] [CrossRef]
- Christensen, B. Use of UAV or remotely piloted aircraft and forward-looking infrared in forest, rural and wildland fire management: Evaluation using simple economic analysis. N. Z. J. For. Sci. 2015, 45, 16. [Google Scholar] [CrossRef]
- Obayashi, S.; Kanekiyo, Y.; Uno, H.; Shijo, T.; Sugaki, K.; Kusada, H.; Nakakoji, H.; Hanamaki, Y.; Yokotsu, K. 400-W UAV/drone inductive charging system prototyped for overhead power transmission line patrol. In Proceedings of the 2021 IEEE Wireless Power Transfer Conference, San Diego, CA, USA, 1–4 June 2021; pp. 1–3. [Google Scholar]
- Lin, Y.; LI, B.; Wang, D.; GAO, J. Application of multi-rotor UAV Patrol System in UHV Power Grid Construction. Electr. Power 2017, 50, 141–147. [Google Scholar]
- Bentley, M.J.; Foster, J.M.; Potvin, J.J.; Bevan, G.; Sharp, J.; Woeller, D.J.; Take, W.A. Surface displacement expression of progressive failure in a sensitive clay landslide observed with long-term UAV monitoring. Landslides 2023, 20, 531–546. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Ren, Y.; Zhu, C. UAV photogrammetry and AFSA-Elman neural network in slopes displacement monitoring and forecasting. KSCE J. Civ. Eng. 2020, 24, 19–29. [Google Scholar] [CrossRef]
- Yun, L.; Wei, X.; Wei, W. Application research on aviation remote sensing UAV for disaster monitoring. J. Catastrophology 2011, 26, 138–143. [Google Scholar]
- Joshi, A.; Dhongdi, S.; Dharmadhikari, M.; Mehta, O.; Anupama, K. Enclosing and monitoring of disaster area boundary using multi-UAV network. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 6287–6305. [Google Scholar] [CrossRef]
- Liu, H.; Ge, J.; Wang, Y.; Li, J.; Ding, K.; Zhang, Z.; Guo, Z.; Li, W.; Lan, J. Multi-UAV optimal mission assignment and path planning for disaster rescue using adaptive genetic algorithm and improved artificial bee colony method. Actuators 2021, 11, 4. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Shvetsova, S.V.; Alhartomi, M.A.; Hawbani, A.; Rajput, N.S.; Srivastava, S.; Saif, A.; Nyangaresi, V.O. UAV computing-assisted search and rescue mission framework for disaster and harsh environment mitigation. Drones 2022, 6, 154. [Google Scholar] [CrossRef]
- Zhang, H.; Liptrott, M.; Bessis, N.; Cheng, J. Real-time traffic analysis using deep learning techniques and UAV based video. In Proceedings of the 2019 16th IEEE International Conference on Advanced Video and Signal Based Surveillance, Taipei, Taiwan, 18–21 September 2019; pp. 1–5. [Google Scholar]
- Bisio, I.; Garibotto, C.; Haleem, H.; Lavagetto, F.; Sciarrone, A. Traffic analysis through deep-learning-based image segmentation from UAV streaming. IEEE Internet Things J. 2022, 10, 6059–6073. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Guo, Y.; Jia, L. Discretization—Filtering—Reconstruction: Railway detection in images for navigation of inspection UAV. IEEE Trans. Instrum. Meas. 2022, 71, 3530313. [Google Scholar] [CrossRef]
- Banić, M.; Miltenović, A.; Pavlović, M.; Ćirić, I. Intelligent machine vision based railway infrastructure inspection and monitoring using UAV. Facta Univ. Ser. Mech. Eng. 2019, 17, 357–364. [Google Scholar] [CrossRef]
- Sujit, P.; Saripalli, S.; Sousa, J.B. Unmanned aerial vehicle path following: A survey and analysis of algorithms for fixed-wing unmanned aerial vehicless. IEEE Control. Syst. Mag. 2014, 34, 42–59. [Google Scholar]
- Vargas, A.M.; Gomez, G.R.; Carranza, J.M. Ground effect on rotorcraft unmanned aerial vehicles: A review. Intell. Serv. Robot. 2021, 14, 99–118. [Google Scholar] [CrossRef]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jiang, B. A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer. Nonlinear Dyn. 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Kothari, M.; Ozana, S. Disturbance observer-based backstepping control of tail-sitter UAVs. Actuators 2021, 10, 119. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Anti-disturbance trajectory tracking of quadrotor vehicles via generalized extended state observer. J. Vib. Control. 2020, 26, 1173–1186. [Google Scholar] [CrossRef]
- Antonelli, G.; Cataldi, E.; Arrichiello, F.; Giordano, P.R.; Chiaverini, S.; Franchi, A. Adaptive trajectory tracking for quadrotor MAVs in presence of parameter uncertainties and external disturbances. IEEE Trans. Control. Syst. Technol. 2017, 26, 248–254. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Wang, X.; Wang, X. Anti-saturation adaptive finite-time neural network based fault-tolerant tracking control for a quadrotor UAV with external disturbances. Aerosp. Sci. Technol. 2021, 115, 106790. [Google Scholar] [CrossRef]
- Liu, K.; Yang, P.; Wang, R.; Jiao, L.; Li, T.; Zhang, J. Observer-based adaptive fuzzy finite-time attitude control for quadrotor UAVs. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8637–8654. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, L.; Xia, Y.; Yuan, Y. Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind. IEEE Trans. Control. Syst. Technol. 2017, 26, 1400–1405. [Google Scholar] [CrossRef]
- Zhang, R.; Quan, Q.; Cai, K.Y. Attitude control of a quadrotor aircraft subject to a class of time-varying disturbances. IET Control. Theory Appl. 2011, 5, 1140–1146. [Google Scholar] [CrossRef]
- Zuo, Z. Trajectory tracking control design with command-filtered compensation for a quadrotor. IET Control. Theory Appl. 2010, 4, 2343–2355. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Cao, H.; Shen, C.; Wang, H. Robust dynamic surface trajectory tracking control for a quadrotor UAV via extended state observer. Int. J. Robust Nonlinear Control 2018, 28, 2700–2719. [Google Scholar] [CrossRef]
- Ai, X.; Yu, J. Fixed-time trajectory tracking for a quadrotor with external disturbances: A flatness-based sliding mode control approach. Aerosp. Sci. Technol. 2019, 89, 58–76. [Google Scholar] [CrossRef]
- Chang, K.; Xia, Y.; Huang, K.; Ma, D. Obstacle avoidance and active disturbance rejection control for a quadrotor. Neurocomputing 2016, 190, 60–69. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Q.; Chen, H. A joint guidance and control framework for autonomous obstacle avoidance in quadrotor formations under model uncertainty. Aerosp. Sci. Technol. 2023, 138, 108335. [Google Scholar] [CrossRef]
- Li, B.; Zhang, H.; Niu, Y.; Ran, D.; Xiao, B. Finite-time disturbance observer-based trajectory tracking control for quadrotor unmanned aerial vehicle with obstacle avoidance. Math. Methods Appl. Sci. 2023, 46, 1096–1110. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying. IEEE Trans. Ind. Electron. 2016, 64, 5014–5024. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y. Distributed Robust Formation Tracking Control for Quadrotor UAVs with Unknown Parameters and Uncertain Disturbances. Aerospace 2023, 10, 845. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, J.; Zhang, W.; Zeng, T.; Ye, L. Distributed formation control for multiple quadrotor based on multi-agent theory and disturbance observer. Math. Probl. Eng. 2019, 2019, 7234969. [Google Scholar] [CrossRef]
- Emran, B.J.; Najjaran, H. A review of quadrotor: An underactuated mechanical system. Annu. Rev. Control 2018, 46, 165–180. [Google Scholar] [CrossRef]
- Mo, H.; Farid, G. Nonlinear and adaptive intelligent control techniques for quadrotor UAV: A survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Shen, J.; Wang, B.; Chen, B.M.; Bu, R.; Jin, B. Review on wind resistance for quadrotor UAVs: Modeling and controller design. Unmanned Syst. 2023, 11, 5–15. [Google Scholar] [CrossRef]
- Wang, H.; Cui, G.; Li, H. Fixed-time adaptive tracking control for a quadrotor unmanned aerial vehicle with input saturation. Actuators 2023, 12, 130. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Guo, K.; Jia, J.; Yu, X.; Guo, L.; Xie, L. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances. Control. Eng. Pract. 2020, 102, 104560. [Google Scholar] [CrossRef]
- Tayebi, A.; McGilvray, S. Attitude stabilization of a VTOL quadrotor aircraft. IEEE Trans. Control. Syst. Technol. 2006, 14, 562–571. [Google Scholar] [CrossRef]
- Wang, R.; Liu, J. Trajectory tracking control of a 6-DOF quadrotor UAV with input saturation via backstepping. J. Frankl. Inst. 2018, 355, 3288–3309. [Google Scholar] [CrossRef]
- Mohammadi, A.; Marquez, H.J.; Tavakoli, M. Nonlinear disturbance observers: Design and applications to Euler-Lagrange systems. IEEE Control. Syst. Mag. 2017, 37, 50–72. [Google Scholar] [CrossRef]
- Guo, L.; Chen, W.H. Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach. Int. J. Robust Nonlinear Control 2005, 15, 109–125. [Google Scholar] [CrossRef]
- Chen, W. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles. J. Guid. Control Dyn. 2003, 26, 161–166. [Google Scholar] [CrossRef]
- Kim, K.S.; Rew, K.H.; Kim, S. Disturbance observer for estimating higher order disturbances in time series expansion. IEEE Trans. Autom. Control 2010, 55, 1905–1911. [Google Scholar]
- Fethalla, N.; Saad, M.; Michalska, H.; Ghommam, J. Robust observer-based dynamic sliding mode controller for a quadrotor UAV. IEEE Access 2018, 6, 45846–45859. [Google Scholar] [CrossRef]
- Ahmed, N.; Raza, A.; Shah, S.A.A.; Khan, R. Robust composite-disturbance observer based flight control of quadrotor attitude. J. Intell. Robot. Syst. 2021, 103, 11. [Google Scholar] [CrossRef]
- Wang, B.; Yu, X.; Mu, L.; Zhang, Y. Disturbance observer-based adaptive fault-tolerant control for a quadrotor helicopter subject to parametric uncertainties and external disturbances. Mech. Syst. Signal Process. 2019, 120, 727–743. [Google Scholar] [CrossRef]
- Aboudonia, A.; El Badawy, A.; Rashad, R. Disturbance observer-based feedback linearization control of an unmanned quadrotor helicopter. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 877–891. [Google Scholar] [CrossRef]
- Ghasemi, A.; Azimi, M.M. Adaptive fuzzy PID control based on nonlinear disturbance observer for quadrotor. J. Vib. Control 2023, 29, 2965–2977. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Yang, X. Adaptive fuzzy control of a quadrotor using disturbance observer. Aerosp. Sci. Technol. 2022, 128, 107784. [Google Scholar] [CrossRef]
- Zhang, N.; Gai, W.; Zhong, M.; Zhang, J. A fast finite-time convergent guidance law with nonlinear disturbance observer for unmanned aerial vehicles collision avoidance. Aerosp. Sci. Technol. 2019, 86, 204–214. [Google Scholar] [CrossRef]
- Shin, D.; Song, Y.; Oh, J.; Oh, H. Nonlinear disturbance observer-based standoff target tracking for small fixed-wing UAVs. Int. J. Aeronaut. Space Sci. 2021, 22, 108–119. [Google Scholar] [CrossRef]
- Guo, K.; Liu, C.; Zhang, X.; Yu, X.; Guo, L.; Zhang, Y. Disturbance perception based quadrotor UAV maneuvering formation against unknown external disturbance. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems, Athens, Greece, 1–4 September 2020; pp. 117–122. [Google Scholar]
- Chen, W. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Huang, D.; Huang, T.; Qin, N.; Li, Y.; Yang, Y. Finite-time control for a UAV system based on finite-time disturbance observer. Aerosp. Sci. Technol. 2022, 129, 107825. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.; Yang, Y.; Postolache, O.A. Finite-time disturbance observer based integral sliding mode control for attitude stabilisation under actuator failure. IET Control Theory Appl. 2019, 13, 50–58. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M. Finite-time fault tolerant attitude tracking control of spacecraft using robust nonlinear disturbance observer with anti-unwinding approach. Adv. Space Res. 2020, 66, 1659–1671. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Zheng, S.; Dong, S.; Sun, G. Fixed-time disturbance observer-based robust fault-tolerant tracking control for uncertain quadrotor UAV subject to input delay. Nonlinear Dyn. 2022, 107, 2363–2390. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, F.; Liu, X.; Gu, S.; Geng, H. Fixed-time dynamic surface control for pneumatic manipulator system with unknown disturbances. IEEE Robot. Autom. Lett. 2022, 7, 10890–10897. [Google Scholar] [CrossRef]
- Cai, X.; Zhu, X.; Yao, W. Fixed-time trajectory tracking control of a quadrotor UAV under time-varying wind disturbances: Theory and experimental validation. Meas. Sci. Technol. 2024, 35, 086205. [Google Scholar] [CrossRef]
- Zhao, Z.; Xiao, L.; Jiang, B.; Cao, D. Fast nonsingular terminal sliding mode trajectory tracking control of a quadrotor UAV based on extended state observers. Control Decis. 2022, 37, 2201–2210. [Google Scholar]
- Ma, D.; Xia, Y.; Li, T.; Chang, K. Active disturbance rejection and predictive control strategy for a quadrotor helicopter. IET Control Theory Appl. 2016, 10, 2213–2222. [Google Scholar] [CrossRef]
- Xiong, J.; Pan, J.; Chen, G.; Zhang, X.; Ding, F. Sliding mode dual-channel disturbance rejection attitude control for a quadrotor. IEEE Trans. Ind. Electron. 2021, 69, 10489–10499. [Google Scholar] [CrossRef]
- Du, Y.; Huang, P.; Cheng, Y.; Fan, Y.; Yuan, Y. Fault tolerant control of a quadrotor unmanned aerial vehicle based on active disturbance rejection control and two-stage Kalman filter. IEEE Access 2023, 11, 67556–67566. [Google Scholar] [CrossRef]
- Li, R.; Zhu, Q.; Nemati, H.; Yue, X.; Narayan, P. Trajectory tracking of a quadrotor using extend state observer based U-model enhanced double sliding mode control. J. Frankl. Inst. 2023, 360, 3520–3544. [Google Scholar] [CrossRef]
- Hua, C.; Wang, K.; Chen, J.; You, X. Tracking differentiator and extended state observer-based nonsingular fast terminal sliding mode attitude control for a quadrotor. Nonlinear Dyn. 2018, 94, 343–354. [Google Scholar] [CrossRef]
- Shen, H.; Du, J.; Yan, K.; Liu, Y.; Chen, J. VGESO-Based Finite-Time Fault-Tolerant Tracking Control for Quadrotor Unmanned Aerial Vehicle. Int. J. Aerosp. Eng. 2024, 2024, 2541698. [Google Scholar] [CrossRef]
- Song, J.; Shang, W.; Ai, S.; Zhao, K. Model and data-driven combination: A fault diagnosis and localization method for unknown fault size of quadrotor UAV actuator based on extended state observer and deep forest. Sensors 2022, 22, 7355. [Google Scholar] [CrossRef]
- Huang, Y.; Li, W.; Ning, J.; Li, Z. Formation Control for UAV-USVs Heterogeneous System with Collision Avoidance Performance. J. Mar. Sci. Eng. 2023, 11, 2332. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Su, Z.; Shao, X. UAV broken-line path following under disturbance conditions. J. Aerosp. Eng. 2018, 31, 04018089. [Google Scholar] [CrossRef]
- Han, X.; Tomita, K.; Kamimura, A. Reduced-Order Active Disturbance Rejection Control Scheme for a Quadrotor and Its Autotuning Method. In Proceedings of the 2022 61st Annual Conference of the Society of Instrument and Control Engineers, Kumamoto, Japan, 6–9 September 2022; pp. 1151–1157. [Google Scholar]
- Li, S.; Yang, J.; Chen, W.; Chen, X. Generalized extended state observer based control for systems with mismatched uncertainties. IEEE Trans. Ind. Electron. 2011, 59, 4792–4802. [Google Scholar] [CrossRef]
- Escareño, J.; Salazar, S.; Romero, H.; Lozano, R. Trajectory control of a quadrotor subject to 2D wind disturbances: Robust-adaptive approach. J. Intell. Robot. Syst. 2013, 70, 51–63. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Output feedback control of a quadrotor UAV using neural networks. IEEE Trans. Neural Netw. 2009, 21, 50–66. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; He, T.; Wu, X.; Wang, H.; Chi, J. Robust adaptive neural network-based compensation control of a class of quadrotor aircrafts. J. Frankl. Inst. 2020, 357, 12241–12263. [Google Scholar] [CrossRef]
- Yang, P.; Wang, Z.; Zhang, Z.; Hu, X. Sliding mode fault tolerant control for a quadrotor with varying load and actuator fault. Actuators 2021, 10, 323. [Google Scholar] [CrossRef]
- Mohd Basri, M.A. Trajectory tracking control of autonomous quadrotor helicopter using robust neural adaptive backstepping approach. J. Aerosp. Eng. 2018, 31, 04017091. [Google Scholar] [CrossRef]
- Liu, H.; Tu, H.; Huang, S.; Zheng, X. Adaptive predefined-time sliding mode control for quadrotor formation with obstacle and inter-quadrotor avoidance. Sensors 2023, 23, 2392. [Google Scholar] [CrossRef]
- Bisheban, M.; Lee, T. Geometric adaptive control with neural networks for a quadrotor in wind fields. IEEE Trans. Control Syst. Technol. 2020, 29, 1533–1548. [Google Scholar] [CrossRef]
- Yogi, S.C.; Tripathi, V.K.; Behera, L. Adaptive integral sliding mode control using fully connected recurrent neural network for position and attitude control of quadrotor. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5595–5609. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Shen, J.; Zhang, Z. Practical fixed-time tracking control of quadrotor unmanned aerial vehicles with input saturation. Asian J. Control 2024. [Google Scholar] [CrossRef]
- Yu, D.; Ma, S.; Liu, Y.J.; Wang, Z.; Chen, C.P. Finite-time adaptive fuzzy backstepping control for quadrotor UAV with stochastic disturbance. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1335–1345. [Google Scholar] [CrossRef]
- Hu, C.; Cao, L.; Zhou, X.; Sun, B.; Wang, N. Fuzzy adaptive nonlinear sensor-fault tolerant control for a quadrotor unmanned aerial vehicle. Asian J. Control 2020, 22, 1163–1176. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; Dou, J.; Wen, B. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. J. Adapt. Control Signal Process. 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Mallavalli, S.; Fekih, A. A fault tolerant tracking control for a quadrotor UAV subject to simultaneous actuator faults and exogenous disturbances. Int. J. Control 2020, 93, 655–668. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Y.; Liu, Y. Neural-network-based robust terminal sliding-mode control of quadrotor. Asian J. Control 2022, 24, 427–438. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).