Abstract
Multimodal motion capability is an emerging topic in the robotics field, and this paper presents a hybrid robot system maneuvering in both terrestrial and aerial environments. Firstly, a micro quadruped–quadrotor robot with onboard sensing and computing is developed. This robot incorporates both the high mobility of unmanned aerial vehicles and the long endurance of mobile robots on the ground. A coordinated motion control scheme is then exploited for adaptive terrestrial–aerial motion transition. In this scheme, a bio-inspired terrestrial locomotion controller is proposed to generate various quadruped locomotions, and a model-based aerial locomotion controller is proposed to generate various quadrotor configurations. Then, an unified motion controller for the two subsystems which dynamically adjusts crawling and flying motion in a complicated environment is presented. Consequently, several practical trials are conducted to demonstrate the adaptability and the robustness of the proposed system.
1. Introduction
Robots with multimodal locomotion capabilities, which benefit from combinational advantages to overcome the individual limitations, have drawn increasingly great attention in robotics. In order to maneuver in versatile domains such as terrestrial, aerial, and aquatic, several state-of-the-art hybrid robots have been explored [1,2,3,4,5,6,7,8,9]. Among these multimodal forms, legged systems with dexterous locomotion possess advanced potential in irregular terrain like walls [10], slopes [11], and uneven terrain [12], but the legged defect limits large-scale mobilities and tremendous obstacles. In nature, insects usually have evolved the ability of both crawling and flying over millions of years of natural selection. Much progress has been made in figuring out and replicating animal locomotion. As a result, robotics can benefit from these biological counterparts to develop corresponding hybrid behaviors. In order to enhance the adaptability of insect-like robots, several novel studies on leg-multirotor robots have attempted to adopt the ideas and mechanisms from nature: in [13], the authors investigate a land–air robot that performs structural separation with the four-legged robot and the quadrotor for multipurpose investigation, so the size of the quadrotor is fixed and only the ground motion is discussed; a novel air–ground amphibious quadruped robot called SPIDAR is developed to explore an integrated PID-based control strategy and optimization-based control allocation in [14], but the computing cost and solving complexity are increasing for such a large 16-rotor and 8-joint robot in real-time scenarios; the authors of [15] presented a hexarotor with three-manipulator with the advantages of taking off and landing on unstable surface, but the leg-like manipulators are only used to stand rather than walking; a walking-and-flying robotic system based on the ANYmal quadruped robot is proposed for collaborative exploration in [16], but the system is divided into two subsystems to explore individually; the authors of [17] designed a multimodal locomotion robot called LEONARDO with two legs, but the bipedal motions require strong stability and delicate balance on uneven terrains via complicatedly controlling the rotary propellers of aerial locomotion.
Although many multimodal robot designs with both terrestrial locomotion and aerial locomotion have been widely investigated in recent years, only a few of these robots can deal with uncertainties in practical environments. The robot size, motion agility, and control complexity have a great effect on limited spaces and costs. In this work, a hybrid Quadruped–Quadrotor Robot, namely QQR, is customized, and either increases the mechanical complexity or decreases the controllability of the system. Owing to the long power endurance and great stability of quadrupeds as well as the excellent maneuverability and transformable flight of quadrotors [18], the proposed QQR may be applied for long-term missions and extreme terrains such as search and rescue and active detection, as well as by appropriately switching between available locomotion modes, while a single quadrotor with relatively short endurance can hardly complete the entire mission. Furthermore, the deformation characteristics of the QQR with several controllable degrees of freedom can modify any configuration during flight to undertake specific tasks [19] such as traversing a narrow gap to enter a collapsed building in Figure 1: firstly, the QQR flies fast with standard X configuration; then, the QQR switches to the H configuration for smaller size to pass through the narrow gap; finally, after entering the building, the QQR uses the T configuration for closer inspection, and the lack of flight condition will enforce the crawling modes of the QQR to localize the targets. In order to execute such collaborative missions, a hierarchical coordination control scheme is further proposed to improve the performance in practical environments. Several experiments and comparisons in actual environments are conducted to verify the effectiveness and reliability of the proposed hierarchical coordination control scheme. The results demonstrate that the proposed controllers can generate and transfer the locomotion of the robot with the changing environments. Contributions of this paper are as follows:

Figure 1.
Passing through a narrow gap to enter a collapsed building.
- (1)
- A micro, lightweight, and integrated robot prototype that enables both crawling motion and morphing flight.
- (2)
- A hierarchical coordination control scheme consisting of a low-level locomotion controller and a high-level motion controller that provides hybrid air-ground robots with multimodal locomotion capabilities.
- (3)
- Implementing foundational experiments and comparisons on such a hybrid robotic system to address the challenge of practical applications.
2. System Overview
In this section, the mechanical design of the QQR combining the peculiarity of both a common quadrotor and a bio-inspired quadruped is first presented. The drawbacks as short endurances in quadrotors and low rates in quadrupeds can be compensated by the adaptivity in our designed QQR. Then, the mathematical models are established separately for further control.
2.1. Robot Design
Figure 2 illustrates the mechanical configuration of the QQR prototype consisting of four legs and one body. Each leg with two degrees of freedom (DoF) is equipped with one brushless motor (connected to the propeller) and two servo motors (connected together to act as two actuated joints). The lightweight legs are significantly vital for the flight performance and morphing motion. A microprocessor (CUAV Nora+ autopilot) is located in the body to send control commands to brushless motors (TMOTOR F40) and servo motors (KINGMAX KM0940), as well as receiving decision commands from the upper intelligent computing module (Jetson Xavier NX). A stereo camera (RealSense D435), a GPS (NEO 3) and an integrated optical flow (HereFlow) are employed to sense environmental information. Besides that, a customized printed circuit board (PCB) is designed for the reliability of the electrical connections and a 4S battery is embedded under the body. Hence, the entire robotic system can be divided into legged module, flight module and control module. Moreover, the specifications of the QQR prototype are given in Table 1.
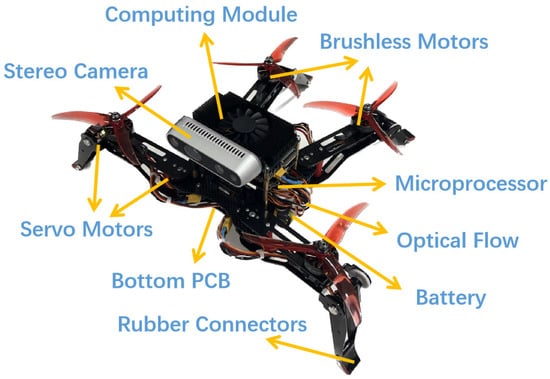
Figure 2.
The mechanical configuration of the QQR prototype.

Table 1.
Technical specifications of the QQR prototype.
2.2. Modeling
In this section, the mathematical model of the QQR is divided into two parts: the multi-joint torque model for quadrupeds and the multi-rotor thrust model for quadrotors, as illustrated in Figure 3.
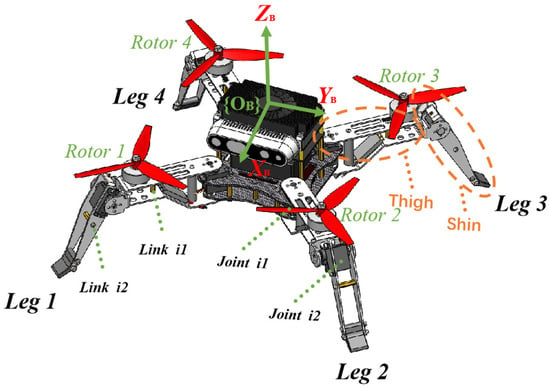
Figure 3.
Illustration of the QQR. is the body coordinate.
2.2.1. Terrestrial Dynamics of Multi-Joint Torque
In order to build the terrestrial dynamics of quadrupeds, the joint coordinates of the robot should be firstly defined, as depicted in Figure 4.
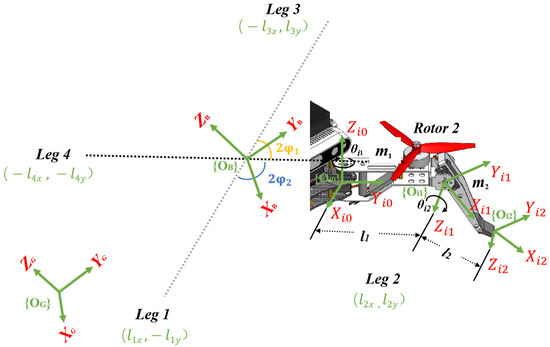
Figure 4.
Coordinates at different joints on each leg (such as leg 2). denotes the global coordinate, and ( and ) represents the floating frame whose origin fixed on the joints or the foot tip. are defined as the position of the thigh motors in the body frame and in the QQR case. are the length of the leg links, respectively. are the rotational joint angles around axis of the leg and . Because the symmetrical design of the QQR’s thigh motors in the diagonal of the square body, in this work.
The kinematic model is represented by Denavit–Hartenberg (DH) parameters for resolving inverse kinematic of each leg. According to these fixed frames, the transformation parameters and DH parameters are demonstrated in Table 2 and Table 3, respectively.

Table 2.
Transformation parameters from the to the . The thigh joint position is defined as . denotes the direction angle in the body frame . Where and in the QQR prototype.

Table 3.
Denavit–Hartenberg parameters, where is the joint number from thigh joint to shin joint of each leg. And is the link twist indicating the angle from to around ; is the joint distance meaning the distance from the intersection of and to the origin of ; is the link length representing the distance from the intersection of and to the origin of ; is the joint angle showing the angle from to around .
The relative translation and rotation between the and the joint coordinates are computed by the transformation matrix (1):
In addition, the transition matrix between the body coordinate and the hip joint coordinate is represented by (2):
Consequently, the foot tip coordinate can be transformed into the body coordinate by multiplying the previous matrixes sequentially:
Thus, the position of the foot tip with respect to the body coordinate can be derived from the below:
where is the position coordinate of the foot tip and is the joint angle of the joint j on the leg i.
The leg of the QQR is designed to connect the body trunk with the ground as a complex joint-link system, so closed kinematics chains exist in the QQR system. Since forces and moments propagate via the kinematics chains among different legs [20], the kinematics and dynamics of the robot are coupled. The dynamic model of such a coupled quadruped robot with eight actuators is derived from the Lagrangian–Euler method:
where is the joint torque vector of the leg consisting of thigh joint torque and shin joint torque . are the joint angle, joint angle velocity, and joint angle acceleration vector of the leg, respectively. is an inertia matrix of the leg. is the Coriolis force matrix of the leg. is the link gravitational force vector of the leg. represents ground reaction forces of the foot tip with the coordinate , which are solved by the minimization of norm of feet forces approach [20]. is the Jacobian matrix of the leg, computed by (6). To clarify the controller design, the position and velocity of the QQR in this work are transformed to the global coordinate .
2.2.2. Aerial Dynamics of Multi-Rotor Thrust
The aerial coordinates of each rotor i are shown in Figure 3 and Figure 4. The six-DoF rigid body kinematic and dynamic equations are adopted to establish a quadrotor model with the state , including the position , the linear velocity , the unit quaternion , the body angular rate , and the rotational speed vector of the four rotors , where represents the rotational speed of the rotor [21].
The translational dynamics can be expressed by
where and are the collective thrust force and the external drag force, respectively. M is the total mass of the QQR, is the Earth’s gravitational vector, and is the Z axis of the body coordinate in the global coordinate .
The rotational dynamics can be written as
where is the skew-symmetric matrix. and are the total torque of the QQR and the body torque of model uncertainties, respectively. J is the diagonal inertial tensor matrix. The rotational speed vector of the four rotors is set as a first-order system:
where is the desired speed and is the time constant.
Hence, the collective thrust and torque produced by the rotors can be calculated as
where is the individual motor thrust on each rotor and . is the time-variant control allocation matrix, expressed by [22]
where and declare the thrust coefficient and the torque coefficient, respectively. is the position of the center of gravity (COG). is the current position of the rotor in the body coordinate which changes in different aerial locomotion patterns and .
It should be noted that all of the motors have limited thrust thresholds :
3. Hierarchical Coordination Control Scheme
The hierarchical coordination control scheme by controlling rotors and articulated joints is depicted in Figure 5, which consists of a separate locomotion control for locomotion generation at low levels and an unified motion control for motion transition at high levels.
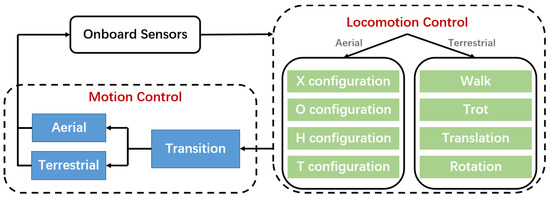
Figure 5.
Diagram of the proposed hierarchical coordination control scheme.
3.1. Low-Level Locomotion Control
In low-level locomotion control, to ensure the controllability and stability of flying and crawling simultaneously on such a hybrid QQR, a terrestrial locomotion controller and an aerial locomotion controller are proposed to produce active terrestrial locomotion (such as walk, trot, translation, and rotation) and aerial locomotion (such as X, O, H, and T configurations), respectively.
3.1.1. Terrestrial Locomotion Control
In nature, biological central pattern generations (CPGs) are mainly involved in the generation of coordinated and rhythmic movements for animals [23]. Considering the similarity between legged animals and quadruped robots, a bio-inspired terrestrial locomotion controller based on central pattern generation (CPG) is adopted in our work. Moreover, the CPG-based model is able to couple dynamics of the QQR to produce various locomotion behaviors, as well as being modulated further via a high-level motion controller [24] in Figure 6.
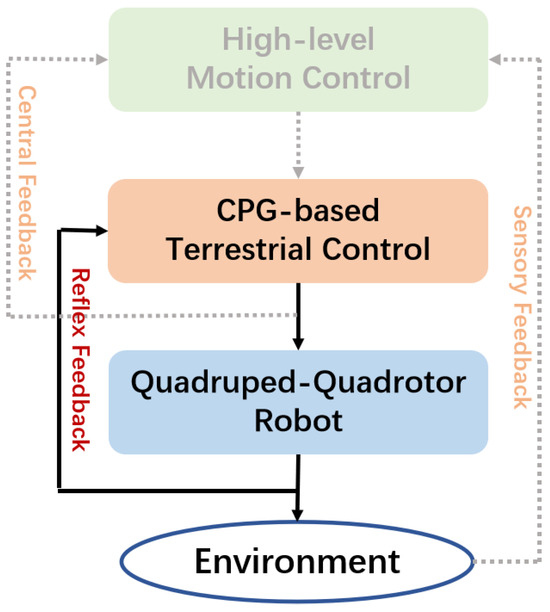
Figure 6.
The CPG-based terrestrial controller architecture.
Similar to their biological counterparts, the QQR performs dexterous terrestrial locomotion capabilities in cluttered terrains, such as walk locomotion for slow movements, trot locomotion for fast running, and translation locomotion and rotation locomotion for agile turning [25]. The aforementioned terrestrial dynamics model helps the QQR to learn various locomotion patterns. The terrestrial locomotions and the phase characteristics are illustrated in Figure 7. In every cycle, four legs in the walk locomotion are separated into four sets of , , , and to move successively, while in the trot locomotion, they are separated into two sets of and , moving alternately. Moreover, the translation locomotion and the rotation locomotion are supposed to accomplish gentle turns and sharp turns, respectively. In this work, the locomotion patterns can be altered in different situations adaptively.
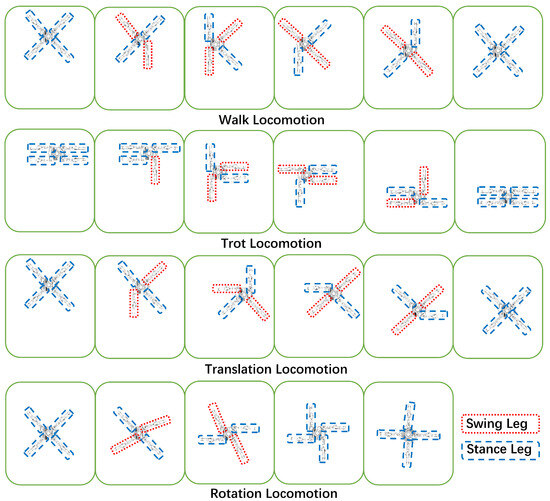
Figure 7.
The typical QQR’s terrestrial locomotion patterns.
Owing to stable limit cycles and explainable parameters, Hopf oscillators are suitable for building CPG networks for robotic locomotion patterns [26]. A traditional Hopf oscillator can be formulated by (16):
where x and y are two state variables. and represent the amplitude and the frequency of the Hopf oscillator. and are constants determining the convergence rate of the limit cycle. In this work, x is defined as the output signal.
As the proposed QQR in this work is equipped with four 2-DoF legs, eight Hopf oscillators are utilized in the QQR’s CPG network and need to be connected together to guarantee the performance of synchronization and coordination. In order to generate desired terrestrial locomotion, we propose a terrestrial CPG network based on the aforementioned multi-joint dynamic model, and the topology of the CPG network is illustrated as shown in Figure 8. Due to complicated couplings and high dimensions on the QQR, the proposed CPG-based locomotion control is decomposed into two layers: (1) The thigh layer includes four oscillators with bidirectional couplings. (2) The shin layer consists of four oscillators with unidirectional connection under the control of the corresponding oscillator in the thigh layer. The thigh layer provides priori knowledge to determine locomotion patterns of the QQR, while the shin layer fine-tunes locomotion performance for quick response to external contact environments.
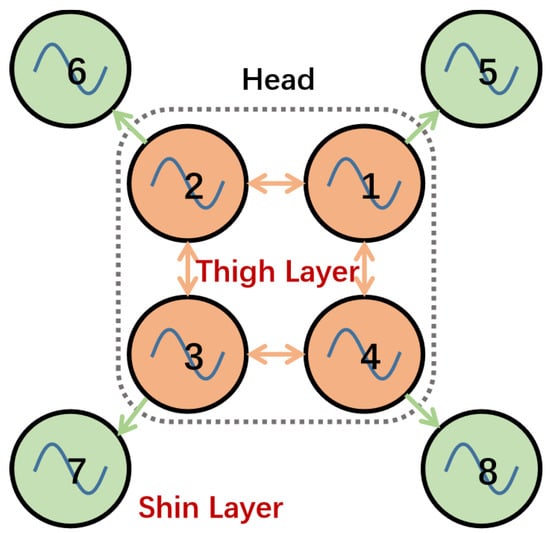
Figure 8.
The topology network of the proposed terrestrial CPG.
Motivated by the work presented by [27], the proposed CPG model with diffusive couplings has the advantage of dealing with kinematic constraints, which can be simplified and described by
where with the leg number and the joint number denote two state variables, and is chosen as the output signal. The constant coupling strength and the convergence coefficients are set for all oscillators, which are determined through trial-and-error simulations on the stability of limit cycle in this work. The oscillator frequencies are unified as for simplifying the further coordinated motion control. Additionally, with and represents the phase difference between the joint and the joint . The associated 2D rotation matrix can be written as
This proposed two-layer terrestrial CPG model not only introduce the coupling relations among various Hopf oscillators to achieve locomotion patterns of the QQR, but also can fine-tune locomotion performance via explicit CPG parameters to improve environmental adaptability. The proposed CPG-based architecture effectively reduces the control difficulty of the eight-joint QQR. Although there are only fewer parameters like amplitudes, frequencies, and phase differences in the proposed terrestrial locomotion controller, the parameter modulation process affects the interacting performance with environments that need to be fine-tuned by a high-level motion controller.
3.1.2. Aerial Locomotion Control
The QQR utilizes four servo motors in the thigh layer for aerial morphing locomotion in midair, including X configuration for efficient flight, H configuration for narrow flight (with the angle change of 45 deg in four thigh joints conversely), T configuration for closer inspection (with the angle change of 45 deg in anterior two thigh joints), and O configuration for omnidirectional shrinking (with the angle change of 45 deg in four thigh joints uniformly), as shown in Figure 9.
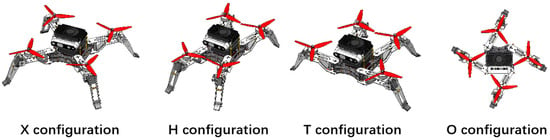
Figure 9.
The specific QQR’s aerial configurations.
While morphing in midair with the overlap between the propellers and the central body of the robot, the QQR will experience a sudden loss of thrust to deviate from the original position. To overcome the effect of fast changes in aerial configurations, a robust geometry-aware compensation controller aiming at modifying the motor speeds of the propeller is deployed as described in Figure 10.
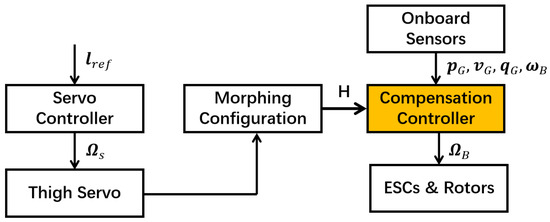
Figure 10.
The aerial locomotion control diagram for the QQR’s morphing.
The individual thrust provided by a single rotor without morphing is given by Equation (13), where the thrust coefficient called is a positive constant. Considering the presence of a morphing case under the actuated thigh servo motors, we reformulate Equation (13) as [28]:
where is the morphing angle of the rotor depicting the overlap between the propellers and the central body of the robot. is a related variable coefficient called the angle-dependent coefficient. Notably, in this case is equal to .
Assuming that the tips of the rotor contribute the major thrust due to the high velocity airflow [29] and each arm with the morphing servo motor is capable of rotating in the limited range of , the angular speeds of the rotors need to be increased for avoiding the QQR’s thrust loss and the modified rotor speeds can be defined as
where is the desired thrust of the rotor, and C is a scaling factor that depends on the angle-dependent coefficient and the thrust coefficient . In this work, the angle-dependent coefficient function is attained via an experimental parameter identification method. If there is no overlap between the propellers and the central body of the QQR, the thrust mapping maintains unchanged.
Moreover, a thigh servo motor controller with regard to transformation flight can be approximated as a first-order system with time constant :
where is related to the QQR’s position under commanded aerial configurations.
3.2. High-Level Motion Control
Owing to the efficient locomotion controller, the high-level control strategy can be defined by if–else switching law for smooth and fast motion transition in this work. Hence, a unified motion control based on a full finite-state machine with various locomotion patterns is demonstrated as Algorithm 1. In order to accomplish collaborative missions, various terrestrial–aerial motions of the QQR must be dynamically and automatically transformed according to the needs of actual situations. The locomotion switching control strategies is exactly assisted by onboard stereo camera and IMU/optical flow sensors to capture the terrains and judge the QQR’s center of gravity, the terrain types allow the QQR to choose aerial or terrestrial modes and the center of gravity variations help the QQR to modify the locomotion patterns.
In the quadruped parameters modulation process, the reward function r is adopted and defined as
where and are the positive weight coefficients. The first term drives the QQR to move forward fast and the second term penalizes the energy consumption of the robot. The average reward of the terrestrial controller is proved to converge to a stable value in different terrain types [30].
In the quadrotor locomotion compensation process, a simplified identification mechanism based on experimental approach is developed for any combination of the rotors morphing. In this work, we used the motion capture system to capture the QQR position and computed the range of the trust loss in different aerial configurations by the drop distance of the QQR, where , , and are the collective trust of X configuration, H configuration, T configuration and O configuration, respectively. Due to the a priori knowledge of the average loss rate of desired configurations, the morphology compensation in Algorithm 1 can be quantified effectively. Compared with the standard X configuration, the loss of collective trust in the H configuration and the T configuration are smaller than the O configuration and the results of Figure 11 in the QQR shows the loss rate are , and (with the error ), respectively. The stability of the aerial controller is quantified by experimental identification data.
| Algorithm 1 The full finite-state machine control algorithm for terrestrial–aerial motion transition. |
|
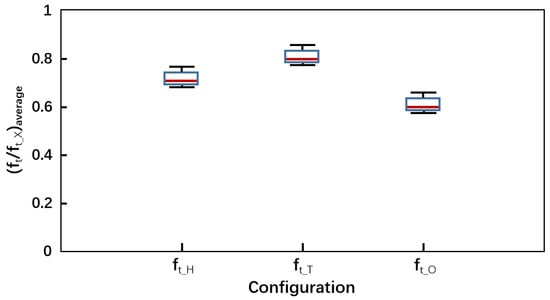
Figure 11.
The collective trust loss in different aerial configurations.
The proposed unified motion control method enables the stable crawling and morphing flight of the QQR. Multimodal motions are desired to extend potential practical applications in long-endurance and specific tasks.
4. Results
The proposed hierarchical coordination control scheme has been evaluated on the QQR platform and numerous trials in diverse challenging environments have been executed.
4.1. Simulations
Firstly, two simulations with the terrestrial locomotion controller and the aerial locomotion controller are conducted in MATLAB R2018 to test the effectiveness of locomotion generations.
4.1.1. Terrestrial CPG-Based Controller Verification
A single oscillator is usually adopted to produce rhythmic control signals for a single joint. The oscillator output model (16) is simulated by x curves and from the results of Figure 12, a single joint signal can be modulated by the typical Hopf oscillator parameters, such as the amplitude , the frequency and the convergence rate .
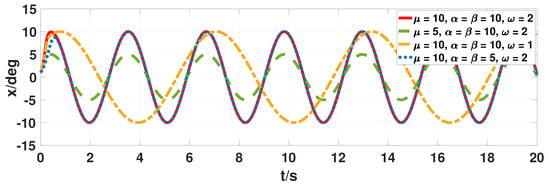
Figure 12.
Effect of oscillator parameters on a single joint output.
Moreover, as can be seen from Figure 13, the stable limit cycle property of the Hopf oscillator for leg 1 with the convergence coefficient was plotted, which alleviates the partial effect of external disturbances and guarantees smooth transition among the QQR’s terrestrial locomotion. These simulation results show that the proposed Hopf-based locomotion controller carries the potential of simple controllability and excellent robustness on complex terrestrial terrains.
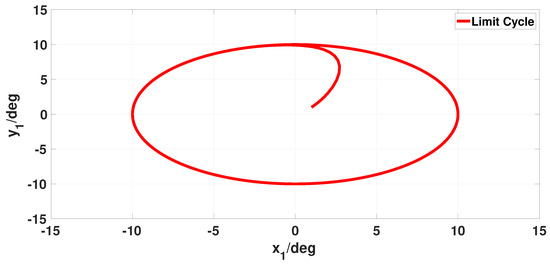
Figure 13.
The limit cycle property of the proposed Hopf oscillator.
The output of a single oscillator should be coupled to fit the locomotion patterns with all joints of the QQR. A good terrestrial locomotion controller is expected to generate various locomotion patterns and allows smooth transition among these locomotion patterns. Taking the walk locomotion pattern as an instance with four Hopf oscillators in thigh layer are set as , we demonstrated the locomotion generation capability of the proposed CPG-based terrestrial locomotion controller. The output signals in the thigh layer of the CPG network model (17) are presented in Figure 14 and the result shows that the thigh layer produce four coupled curves for four joints to constitute a corresponding walk locomotion pattern cycle by cycle. Meanwhile, the shin layer also receives reflex feedback from the external environment to improve the interactive performance of this walk locomotion pattern.
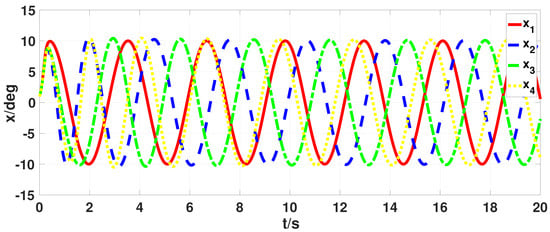
Figure 14.
The walk locomotion pattern generated by the proposed CPG-based terrestrial controller.
4.1.2. Aerial Compensation Controller Verification
The aerial compensation controller enhances position tracking performances in midair when morphing occurs. Taking three romdom curves (circle, sine and helix) as reference paths, we simulated trajectory tracking comparisons to emphasize the effectiveness of the proposed compensation locomotion controller in Matlab Simulink, as shown in Figure 15.
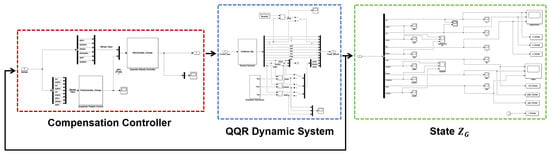
Figure 15.
Simulation blocks of aerial locomotion controller.
As the comparisons show in Figure 16, the QQR follows a circular trajectory at a speed of 0.5 m/s on a circle of radius 1 m, at a constant height of 1 m. The QQR changes its shape during flight switching between the X and O configurations on and off the compensation mechanism with a varying error that ranges from a minimum 0.1 m to a maximum of 0.2 m. Moreover, we also summarize some quantitative results in Figure 17 and Figure 18, in which the QQR transformed from X configuration to H configuration with compensation shows better tracking performance on different trajectories, and the de-stability error was less than 0.1m away from the desired path. The compensation controller improves the position tracking both in hovering and forward flight.
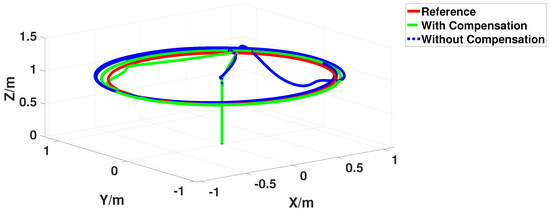
Figure 16.
The tracking performance of the proposed aerial compensation controller on a circle path.
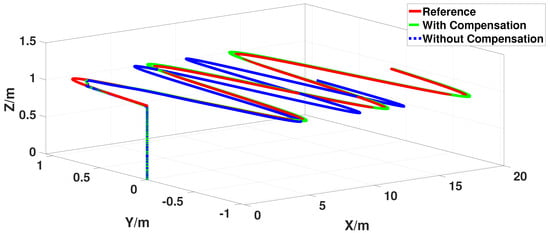
Figure 17.
The tracking performance of the proposed aerial compensation controller on a sine path.
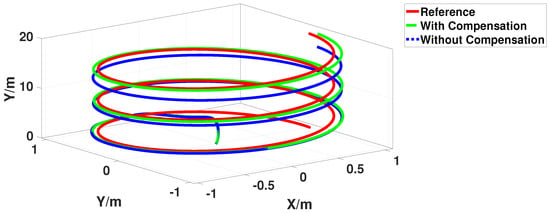
Figure 18.
The tracking performance of the proposed aerial compensation controller on a helix path.
4.2. Experiments
Several experimental setups similar to the scenes in Figure 1 have been established for practical applications, and comparative experiments have been conducted. The QQR is shown running over different surfaces, including smooth ground, rough sand, and midair. Firstly, the aerial endurance test is set as hovering on the constant height of 2.5 m, and the terrestrial endurance test is set as spinning in circles with a second timer, as shown in Figure 19. The endurance time in the aerial case is approximately 10 min and the maximum flight distance is around 2000 m, while a longer terrestrial duration is up to 30 minutes and the maximum crawling distance on the ground is about 150 m. The QQR is able to address the trade-off between flight time and crawling time on different tasks. Then, to validate the effectiveness of the proposed hierarchical coordination control scheme, we decomposed the motion skills of the QQR against dynamic circumstances into three motion primitives: crawling on smooth and rough surfaces, crossing through big and small obstacles, adapting to terrestrial-to-aerial and aerial-to-terrestrial motion transition.

Figure 19.
The practical endurance tests on the QQR.
4.2.1. Crawling on Unknown Terrains
As stated before, various terrestrial locomotion patterns suit different terrains. To demonstrate the environmental adaptability of the proposed bio-inspired terrestrial controller, we evaluated the performance with ground friction comparisons ranging from smooth surfaces to rough surfaces. From the experimental results in Figure 20 and Figure 21 (where the red circle on the ground is regarded as the object of motion reference), the trot locomotion pattern is usually chosen on a smooth case by the QQR automatically, which can bring the fastest motion at the forward speed of 10 cm/s. However, on a rough terrain, the QQR tends to the walk locomotion pattern to enhance crawling reliability and reduce energy consumption. Both trot and the walk locomotion were demonstrated as effective locomotion patterns. Moreover, the QQR actively selected various locomotion patterns adapting to environmental uncertainties via the terrestrial locomotion controller in Figure 22. It is worth highlighting that more terrestrial locomotions can be mimicked and developed via a CPG-based controller to close the gap between the QQR and biological counterparts.

Figure 20.
QQR crawls on smooth ground with trot locomotion.

Figure 21.
QQR crawls on rough ground with walk locomotion.

Figure 22.
QQR crawls on complex terrains with the adaptive locomotion.
4.2.2. Morphing and Trajectory Tracking in Midair
Morphing flight was assessed through a series of laboratory tests, the aerial configurations are described in detail in Section 3.1.2. From the test results in Figure 23, Figure 24 and Figure 25, the aerial compensation controller was shown to be a useful strategy to make the QQR stable under morphing situations without requiring any symmetry of the morphology.
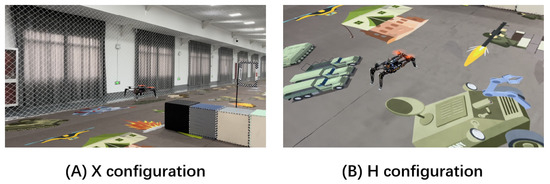
Figure 23.
X configuration to H configuration for narrow spaces.

Figure 24.
X configuration to T configuration for closer inspection.

Figure 25.
X configuration to O configuration for omnidirectional shrinking.
Compared with common quadrotors, the actuated thigh joints along with scalable body sizes enable the QQR to adapt to aerial obstructive environments, especially narrow spaces. A big horizontal semicircle with a diameter of 60 cm and a small rectangle with the width of 20 cm are tailored to test adaptive transformations of the robot in midair. The initial size of the QQR with standard X configuration is aforementioned 26 cm and the robot cannot cross through holes directly where the robot needs to change its configuration.
As presented in Figure 26 and Figure 27, we also offered contrast experiments to explain the superiority of the designed morphing characteristics in the presence of obstacles and holes. It can be found that if the target hole is big enough, the QQR holds on the standard X configuration for less energy cost. Nevertheless, the QQR shrinks actively from X configuration to H configuration while detecting dimensional risks with onboard perceptions. This morphing superiority stems from our aerial locomotion controller, which compensates in advance for this morphing configuration with less performance degradation.

Figure 26.
A big target beyond the size of the QQR (without morphing).

Figure 27.
A small target below the size of the QQR (with morphing).
Then, to show the effectiveness of the proposed aerial compensation controller in a real test, the following comparison between the simulation and the experiment is designed. Consider an arbitrary ellipse as a reference based on the limited experimental field:
The simulation result obtained from the Section 4.1.2 and the real test result carried on Figure 28 are shown as Figure 29 and Figure 30. Figure 29 shows the tracking performance of the proposed controller, and the maximum error is less than 0.1 m, even in real turning situations. Moreover, the tracking error on X axis, Y axis and Z axis are given in Figure 30, respectively. The results imply that even though the aerial configuration of the QQR are changed and the stochastic disturbances are considered, the proposed aerial compensation controller can ensure the stability of the QQR system.

Figure 28.
The trajectory tracking experiment on an ellipse reference.
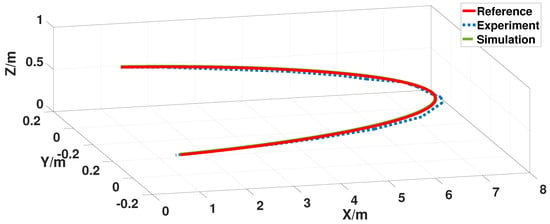
Figure 29.
Trajectory tracking for the proposed aerial compensation controller.

Figure 30.
The tracking error on X axis, Y axis and Z axis.
4.2.3. Adaptive Terrestrial–Aerial Motion Transition
Based on an open-source simulation scenario in Figure 31, we quickly checked the proposed coordinated motion control scheme at an extreme environment of a whole linear obstacle. From motion transition simulations, the QQR tries to utilize terrestrial locomotion patterns for lower energy consumption until the robot cannot search feasible spaces on the ground. Then, the QQR transfers to aerial locomotion patterns for traverse maneuverability.
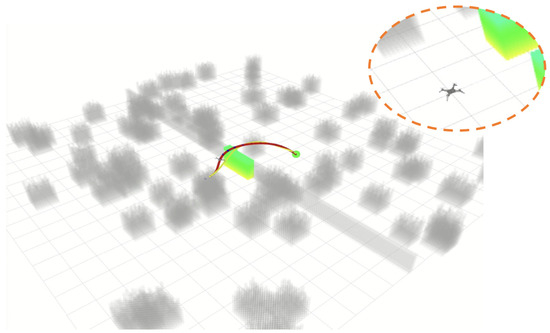
Figure 31.
Simulations in a cluttered case with terrestrial-aerial motion transition.
The feasibility of seamless motion transition has been further validated experimentally. As shown in Figure 32, adaptive motion transition from crawling mode to flight mode permits the QQR to traverse a complex occasion successfully: the QQR firstly passes through a board obstacle via a legged mode with a much better power utilization; then, the QQR automatically starts the propellers to cross a box obstacle at a higher rate. Hence, the QQR is able to overcome any obstacle using the transition between its terrestrial and aerial modes and the terrestrial–aerial adaptivity shows the superiority of optimal motion allocation in intricate missions. The terrestrial–aerial motion transition strategy endows robots with hybrid intelligence and brings tremendous application prospects on collaborative missions.

Figure 32.
Experiments in a complex occasion with terrestrial–aerial motion transition.
Using only the proposed control algorithm, numerous experimental results show that the QQR can adapt to various typical terrains based on the optimized mechanical design. Compared with other hybrid robots shown in Table 4, the QQR exhibits perfect multimodality and maneuverability under the limited mass and dimension in complicated terrains.

Table 4.
Characteristics of the hybrid robots.
5. Conclusions
The proposed terrestrial–aerial QQR enables both a crawling motion and morphing flight with the compact and agile combination of the high maneuverability in quadrotors and the long endurance in quadrupeds. In this paper, based on the design of a micro, lightweight, and integrated quadruped–quadrotor robot, a hierarchical coordination control scheme consisting of a low-level locomotion control and a high-level motion control is explored. Hence, the adaptive robot system achieves both terrestrial locomotion and aerial locomotion as well as smooth terrestrial-to-aerial or aerial-to-terrestrial transition in unknown and uneven environments. Several crucial trials are performed to validate the proposed QQR’s agility and adaptability. In the future, we will focus on enhancing autonomous navigation for intelligent motion planning with onboard sensing and computing in demanding terrains and real-world application scenarios [33,34,35,36,37].
Author Contributions
Conceptualization, Q.R. and W.O.; methodology, W.O.; mechanical design and maintenance, L.L.; software and tests, W.O. and C.W.; simulation and validation, H.C. and W.O.; writing—original draft preparation, W.O.; writing—review and editing, H.C. and Q.R.; project administration, Q.R. and W.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to privacy restrictions.
Conflicts of Interest
Author Wenjuan Ouyang was employed by the company, CETHIK Group Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Deng, L.; Yang, B.; Dong, X.; Cui, Y.; Gao, Y.; Li, D.; Tu, Z. Self-Spin Enabled Docking and Detaching of a UAV-UGV System for Aerial-Terrestrial Amphibious and Independent Locomotion. IEEE Robot. Autom. Lett. 2023, 8, 2454–2461. [Google Scholar] [CrossRef]
- Baines, R.; Patiballa, S.K.; Booth, J.; Ramirez, L.; Sipple, T.; Garcia, A.; Fish, F.; Kramer-Bottiglio, R. Multi-environment robotic transitions through adaptive morphogenesis. Nature 2022, 610, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jiang, Z.; Xu, R.; Ji, X.; Zhang, L.; Qian, H. Design and Optimization of a Magnetic Catcher for UAV Landing on Disturbed Aquatic Surface Platforms. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), IEEE, Philadelphia, PA, USA, 23–27 May 2022; pp. 1162–1168. [Google Scholar]
- Li, L.; Wang, S.; Zhang, Y.; Song, S.; Wang, C.; Tan, S.; Zhao, W.; Wang, G.; Sun, W.; Yang, F.; et al. Aerial-aquatic robots capable of crossing the air-water boundary and hitchhiking on surfaces. Sci. Robot. 2022, 7, eabm6695. [Google Scholar] [CrossRef]
- Pope, M.T.; Kimes, C.W.; Jiang, H.; Hawkes, E.W.; Estrada, M.A.; Kerst, C.F.; Roderick, W.R.; Han, A.K.; Christensen, D.L.; Cutkosky, M.R. A multimodal robot for perching and climbing on vertical outdoor surfaces. IEEE Trans. Robot. 2016, 33, 38–48. [Google Scholar] [CrossRef]
- Pan, N.; Jiang, J.; Zhang, R.; Xu, C.; Gao, F. Skywalker: A Compact and Agile Air-Ground Omnidirectional Vehicle. IEEE Robot. Autom. Lett. 2023, 8, 2534–2541. [Google Scholar] [CrossRef]
- Guetta, O.; Shachaf, D.; Katz, R.; Zarrouk, D. A novel wave-like crawling robot has excellent swimming capabilities. Bioinspiration Biomimetics 2023, 18, 26006. [Google Scholar] [CrossRef]
- Arif, M.A.; Zhu, A.; Mao, H.; Zhou, X.; Song, J.; Tu, Y.; Ma, P. Design of an Amphibious Spherical Robot Driven by Twin Eccentric Pendulums With Flywheel-Based Inertial Stabilization. IEEE/ASME Trans. Mechatron. 2023, 28, 2690–2702. [Google Scholar] [CrossRef]
- Kong, J.; Niu, S.; Lu, P.; Li, A.; Xiang, X.; Zhao, W.; Zhou, Z. Design of a Bio-inspired Water-ground-air Amphibious and Cross Domain Robot Platform. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; pp. 2177–2182. [Google Scholar]
- Tanaka, Y.; Shirai, Y.; Lin, X.; Schperberg, A.; Kato, H.; Swerdlow, A.; Kumagai, N.; Hong, D. Scaler: A tough versatile quadruped free-climber robot. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE, Kyoto, Japan, 23–27 October 2022; pp. 5632–5639. [Google Scholar]
- David, N.B.; Zarrouk, D. Design and analysis of FCSTAR, a hybrid flying and climbing sprawl tuned robot. IEEE Robot. Autom. Lett. 2021, 6, 6188–6195. [Google Scholar] [CrossRef]
- Bellegarda, G.; Ijspeert, A. CPG-RL: Learning Central Pattern Generators for Quadruped Locomotion. IEEE Robot. Autom. Lett. 2022, 7, 12547–12554. [Google Scholar] [CrossRef]
- Li, K.; Han, B.; Zhao, Y.; Zhu, C. Motion Planning and Simulation of Combined Land-Air Amphibious Robot. IOP Conf. Ser. Mater. Sci. Eng. 2018, 428, 12057. [Google Scholar] [CrossRef]
- Zhao, M.; Anzai, T.; Nishio, T. Design, Modeling and Control of a Quadruped Robot SPIDAR: Spherically Vectorable and Distributed Rotors Assisted Air-Ground Amphibious Quadruped Robot. arXiv 2023, arXiv:2301.04050. [Google Scholar] [CrossRef]
- Paul, H.; Miyazaki, R.; Kominami, T.; Ladig, R.; Shimonomura, K. A Versatile Aerial Manipulator Design and Realization of UAV Take-Off from a Rocking Unstable Surface. Appl. Sci. 2021, 11, 9157. [Google Scholar] [CrossRef]
- De Petris, P.; Khattak, S.; Dharmadhikari, M.; Waibel, G.; Nguyen, H.; Montenegro, M.; Khedekar, N.; Alexis, K.; Hutter, M. Marsupial Walking-and-Flying Robotic Deployment for Collaborative Exploration of Unknown Environments. arXiv 2022, arXiv:2205.05477. [Google Scholar]
- Kim, K.; Spieler, P.; Lupu, E.S.; Ramezani, A.; Chung, S.J. A bipedal walking robot that can fly, slackline, and skateboard. Sci. Robot. 2021, 6, eabf8136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Wu, Y.; Zhang, L.; Xu, C.; Gao, F. TIE: An Autonomous and Adaptive Terrestrial-Aerial Quadrotor. arXiv 2021, arXiv:2109.04706. [Google Scholar]
- Sakaguchi, A.; Yamamoto, K. A Novel Quadrotor With a 3-Axis Deformable Frame Using Tilting Motions of Parallel Link Modules Without Thrust Loss. IEEE Robot. Autom. Lett. 2022, 7, 9581–9588. [Google Scholar] [CrossRef]
- Roy, S.S.; Pratihar, D.K. Kinematics, Dynamics and Power Consumption Analyses for Turning Motion of a Six-Legged Robot. J. Intell. Robot. Syst. 2014, 74, 663–688. [Google Scholar] [CrossRef]
- Penicka, R.; Song, Y.; Kaufmann, E.; Scaramuzza, D. Learning minimum-time flight in cluttered environments. IEEE Robot. Autom. Lett. 2022, 7, 7209–7216. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, F.; Wang, Z.; Wang, K.; Cao, Y.; Xu, C.; Gao, F. Ring-Rotor: A Novel Retractable Ring-Shaped Quadrotor With Aerial Grasping and Transportation Capability. IEEE Robot. Autom. Lett. 2023, 8, 2126–2133. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Crespi, A.; Ryczko, D.; Cabelguen, J.M. From Swimming to Walking with a Salamander Robot Driven by a Spinal Cord Model. Science 2007, 315, 1416–1420. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Deng, Z. Enhancing Adaptability with Local Reactive Behaviors for Hexapod Walking Robot via Sensory Feedback Integrated Central Pattern Generator. Robot. Auton. Syst. 2020, 124, 103401. [Google Scholar] [CrossRef]
- Lipeng, Y.; Bing, L. Research on Gait Switching Control of Quadruped Robot Based on Dynamic and Static Combination. IEEE Access 2023, 11, 14073–14088. [Google Scholar] [CrossRef]
- Seo, K.; Chung, S.J.; Slotine, J.J.E. CPG-Based Control of a Turtle-like Underwater Vehicle. Auton. Robot. 2010, 28, 247–269. [Google Scholar] [CrossRef]
- Campos, R.; Matos, V.; Santos, C. Hexapod Locomotion: A Nonlinear Dynamical Systems Approach. In Proceedings of the 2010 36th Annual Conference on IEEE Industrial Electronics Society (IECON), Glendale, AZ, USA, 7–10 November 2010; pp. 1546–1551. [Google Scholar] [CrossRef]
- Fabris, A.; Kleber, K.; Falanga, D.; Scaramuzza, D. Geometry-aware compensation scheme for morphing drones. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), IEEE, Xi’an, China, 30 May–5 June 2021; pp. 592–598. [Google Scholar]
- Yoon, S.; Diaz, P.V.; Boyd, D.D., Jr.; Chan, W.M.; Theodore, C.R. Computational aerodynamic modeling of small quadcopter vehicles. In Proceedings of the American Helicopter Society (AHS) 73rd Annual Forum, Fort Worth, TX, USA, 9–11 May 2017. [Google Scholar]
- Ouyang, W.; Chi, H.; Pang, J.; Liang, W.; Ren, Q. Adaptive locomotion control of a hexapod robot via bio-inspired learning. Front. Neurorobotics 2021, 15, 627157. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zhang, R.; Pan, N.; Xu, C.; Gao, F. Skater: A Novel Bi-modal Bi-copter Robot for Adaptive Locomotion in Air and Diverse Terrain. arXiv 2024, arXiv:2403.01991. [Google Scholar] [CrossRef]
- Falanga, D.; Kleber, K.; Mintchev, S.; Floreano, D.; Scaramuzza, D. The foldable drone: A morphing quadrotor that can squeeze and fly. IEEE Robot. Autom. Lett. 2018, 4, 209–216. [Google Scholar] [CrossRef]
- Luo, Y.; Yu, H.; Zhang, H.; Zhou, Y. A Novel Newton—Euler Method-Based Nonlinear Anti-Swing Control for a Quadrotor UAV Carrying a Slung Load. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 2266–2275. [Google Scholar] [CrossRef]
- Yu, D.; Ma, S.; Liu, Y.J.; Wang, Z.; Chen, C.P. Finite-time adaptive fuzzy backstepping control for quadrotor UAV with stochastic disturbance. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1335–1345. [Google Scholar] [CrossRef]
- Feng, S.; Zeng, L.; Liu, J.; Yang, Y.; Song, W. Multi-UAVs Collaborative Path Planning in the Cramped Environment. IEEE/CAA J. Autom. Sin. 2024, 11, 529–538. [Google Scholar] [CrossRef]
- Madruga, S.P.; Tavares, A.H.; Luiz, S.O.; do Nascimento, T.P.; Lima, A.M.N. Aerodynamic effects compensation on multi-rotor UAVs based on a neural network control allocation approach. IEEE/CAA J. Autom. Sin. 2021, 9, 295–312. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Li, W.; Brand, H.; Jiang, B.; Xiao, J. Concrete defects inspection and 3D mapping using CityFlyer quadrotor robot. IEEE/CAA J. Autom. Sin. 2020, 7, 991–1002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).