1. Introduction
Robotic manipulators are advanced modern equipment supporting intelligent manufacturing and unmanned production. They play an important role in smart manufacturing in Industry 5.0 [
1]. The end effector (EE) is the most flexible component of robotic manipulators, enabling a diverse range of industrial application possibilities which include, but are not limited to, point-to-point (PTP) movements such as stacking [
2,
3,
4], as well as movements along specific paths, such as laser cutting, spraying, etc. [
5,
6,
7].
As industrial environments gradually advance towards intelligence and precision in development, the key technology of robotic manipulators can be cast as the trajectory planning (TP) problem of the EE along specific paths, where an optimal time law of the specific geometric path followed by the EE can be solved with a series of complex constraints including robot dynamics. It is noticed that the trajectory can be viewed as a path subject to a time law [
8].
Due to the high nonlinearity and coupling of robot dynamics, the TP problem is divided into two part. The first part is about the design of a high-level planner generating an optimal path or trajectory, and the other part is about the design of a lower-level controller supporting the implementation of tracking the optimal path or trajectory [
9]. When it comes to TP along specific paths, the related research mainly focuses on the design of the high-level planner. In this situation, the lower-level controller is used as a discrete data receiver and enables actuators in the tracking mission, so that the specific path data from the planner can be executed.
Related research frames the above optimal trajectory planning (OTP) problem as an optimal control (OC) problem, which accounts for kinematic and dynamic constraints to achieve the most optimal performance index [
10].
OC problems can be typically solved by indirect and direct methods. On the one hand, the Pontryagin Minimum Principle serves as the core technology of the indirect methods, providing optimal necessary conditions for OC problems and the derivation of an explicit solution. However, the indirect methods are often challenging to reconcile with complex engineering systems due to difficulties in formulating state–space equations. On the other hand, the direct methods, leveraging the progress in computers and numerical techniques, can discretize the OC problem and convert it into a Nonlinear Programming (NLP) problem. This transformation enables the application of a general NLP solver, effectively addressing the aforementioned challenge. Consequently, the direct collocation (DC) method which belongs to the latter direct methods finds widespread application in the industrial field [
11].
Nonetheless, general DC methods are time-consuming and unstable when applied to solve the TP problem of robotic manipulators along a specified path due to the ‘curse of dimensionality’. Therefore, researchers are actively investigating this issue. The related research began in 1985. J. E. Bobrow et al. solved the minimum-time manipulator control problem along a specified path by constructing the maximum velocity curve (MVC) in the phase plane [
12]. This method utilizes the so-called Frenet–Serret Frames [
13] where the time-independent variable arc length is used to describe the entire path. As a result, the number of states is streamlined from twice the degree of freedom (DOF) to just two variables including arc length and arc velocity, so that the problem can be simplified to find the MVC in the phase plane consisting of arc length and arc velocity. Finally, a type of numerical integration method is proposed to solve the specified path TP problem of three-axis manipulators. For simplicity, we refer to this kind of method as MVC methods.
Meanwhile, O. V. Stryk et al. studied the optimization problem of PTP motion for three-axis manipulators with several performance indices based on OC methods, and provided a numerical solution for the OC problem using a combination of a DC method and an indirect multiple shooting method in 1994 [
14].
The above studies constitute prototypes of two main methods for solving OC problems. They are MVC methods and DC methods. A series of methods based on these two prototypes have evolved to the present day.
For the former, P. Shen et al. provide a summary of three time-optimal methods for TP along a specified path, which include Dynamic Programming (DP), Numerical Integration (NI), and Convex Optimization (CO) [
15]. A classical DP approach presented by K. G. Shin et al. [
9] was developed to solve the TP problem for three-axis robotic manipulators. This method includes discretizing the phase plane of MVC into separate grids and calculating the cost of forward movement between adjacent grids, facilitating the consideration of multiple performance indices. However, its demand for substantial data storage space is incredibly huge due to the ‘curse of dimensionality’. Then, the method proposed by J. E. Bobrow et al. in 1985, as mentioned earlier, is an original NI approach. This method seeks the limit of the motion performance and possesses a bang–bang structure of torque inputs, but it can only focus on the time-optimal problem. Furthermore, Q. C. Pham [
16] provides a general, fast, and robust implementation for time-optimal trajectory planning (TOTP) using the NI method, improving algorithm robustness by addressing dynamic singularities [
17]. In a related context, E. Barnett and C. Gosselin [
18] propose a simpler and faster bisection algorithm to modify constraint violations during the NI process. Finally, the CO methods concentrate more on mathematical derivation. The convexity of the time-optimal path tracking problem should be explicitly studied to find the global optimal solution. D. Verscheure and F. Debrouwere [
19,
20] conducted related research. However, the CO methods may not be suitable for a general solver due to the necessity for unique mathematical derivations for each problem.
For the latter, since O. V. Stryk et al. proposed a numerical solution framework for OC problems, numerous methods have been derived. Z. Xiong et al. integrated the framework with a Functional Mock-up Unit (FMU), accomplishing optimal PTP TP for six-axis robotic manipulators [
21]. However, the above technology is limited to solve the PTP TP problem. In response to this situation, J. T. Betts et al. published a path-constrained trajectory optimization method based on DC methods in 1993 [
22], which may provide a way to solve the specified path TP problem. Furthermore, Betts summarized a general technology framework for solving OC problems in a book in 2010 [
23]. Simultaneously, Victor M. Becerra implemented the program PSOPT based on the book and published it in the open-source community [
24]. Afterwards, M. Kelly published an introduction in 2016 to assist others in solving TP problems using DC methods, including the utilization of multiphase direct collocation (MPDC) methods [
10]. As a result, a brand-new method inspired by Kelly for solving the specified path trajectory planning problem came out; Y. Wen improved this MPDC method and successively accomplished a novel 3D path following a control framework for a robot [
11] and a path-constrained and collision-free OTP scheme [
25]. A simple literature review is shown in
Figure 1.
At the same time, there are some other studies altogether. F. Vesentini adapts a velocity obstacle algorithm for planning collision-free trajectories for anthropomorphic arms [
26]. J. Chen presents a convex TOTP method for industrial robotic manipulators with jerk constraints and achieves smooth and efficient trajectories enabling contour following and pick-and-place tasks to validate the proposed method [
27]. A. Tika works on the online TOTP of cooperative robotic manipulators based on a model predictive control algorithm and realizes synchronous pick-and-place tasks [
28]. JG Batista develops a TP method to avoid collisions for collaborative robotics [
29]. G. Wu gives a jerk–continuous TP method for robotic manipulators by using the fourth-order S-curve to smooth the motion [
30].
In summary, MVC methods and MPDC methods are two ways proven to have the ability to solve the TP problem along a specified path at present. They have different features. On the one hand, MVC methods simplify the problem but demand additional solver design, which can be categorized into NI, DP, and CO. Among them, NI is a simple and effective method but is limited to solving TOTP problems. DP can accommodate more performance indices but faces the curse of dimensionality. CO lacks universality due to the need for unique mathematical skills to transform the original problem into a convex one. On the other hand, MPDC methods support solving the target problem by a general NLP solver, and is more direct and general than MVC methods. When we use MPDC methods, the complex transformation in CO is skipped, the performance indices are not limited, the calculation storage requirement is reduced, and a local optimal solution can be provided. As we can see, the MPDC method has greater compatibility which supports its utilization in a general industrial environment.
What is more, the DC method enables the transition from OC problems to NLP problems, where each continuous variable is segmented into numerous nodes. It is evident that the quantity of these nodes significantly influences both solution accuracy and computation time. In essence, a higher number of nodes leads to increased computation time and a more accurate solution, while fewer nodes result in shorter computation time and a less accurate solution. Hence, we can find it is crucial to identify an appropriate number of nodes to strike a balance between solution accuracy and acceptable computation time. In light of the above issues, several approaches have been proposed. In 1998, John T. Betts studied a mesh refinement (MR) algorithm, which outlines a technique for changing the discretization to enhance the accuracy of the approximation [
31]. This allows the nodes to start with a small quantity and gradually increase until the desired solution accuracy is achieved. However, each MR iteration happens after an entire NLP solving process. When the OC problem involves a complex system dynamics, such as a six-axis robotic manipulator, a single NLP solving process takes too much time, making the MR algorithm unsuitable for application in this scenario. In 2021, Y. Wen proposed a combined method that applies a small quantity of nodes to ensure the efficiency of the solving process and utilizes a self-designed controller to manage experimental accuracy [
11].
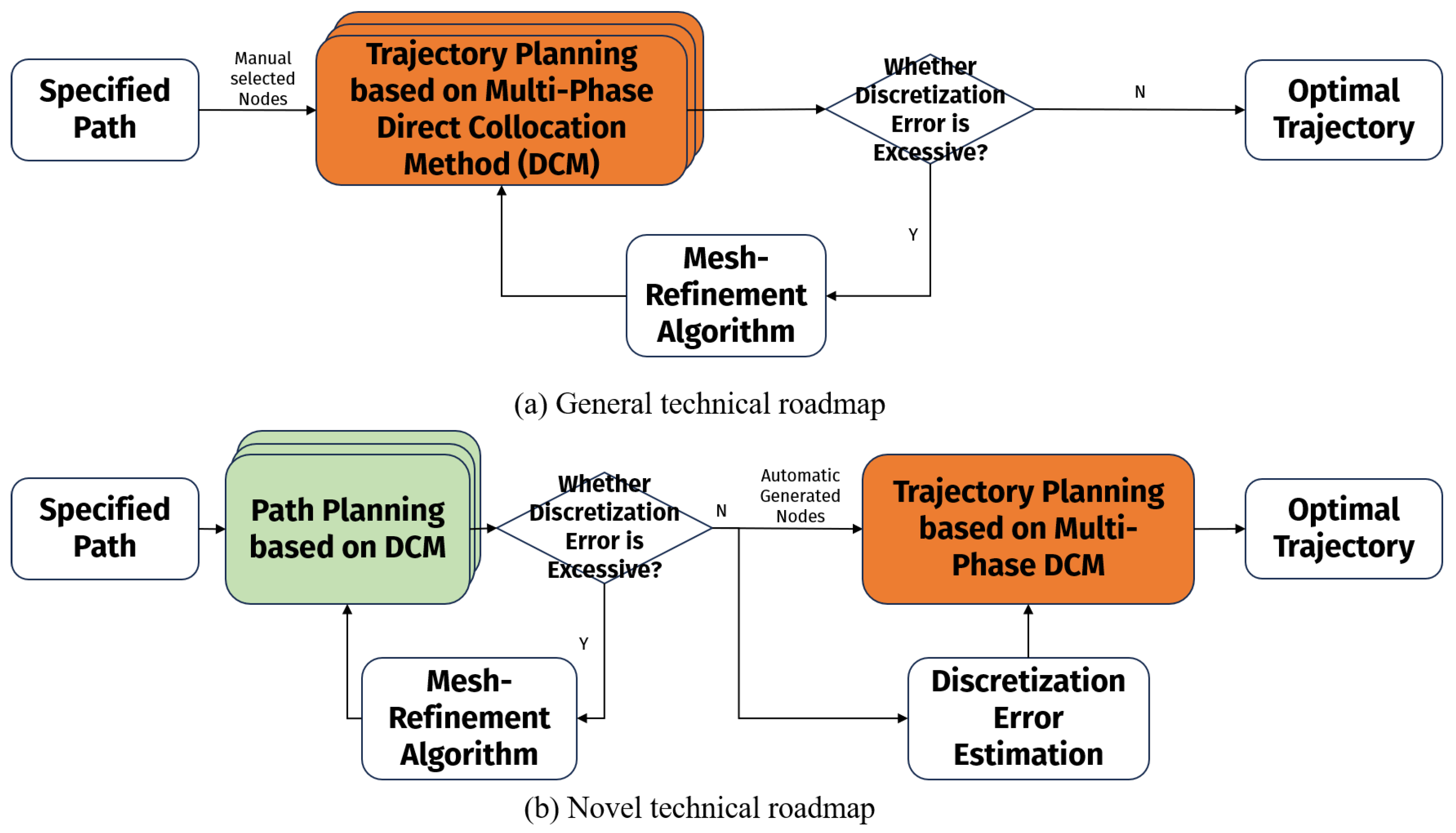
In this paper, we present a novel sequential optimization scheme for TP problems. This scheme divides the complex specified path TP problem into two parts. In the first part, the TP problem is simplified into a path planning (PP) problem. This PP problem is designed to find a series of key nodes in the joint space to represent the specified path in Cartesian space. In this regard, a time-independent geometry optimization method is proposed based on the DC method and the MR algorithm for solving this problem. As a result, the path discretization error between the ideal path and the continuous approximate path that passes through these nodes can be minimized. What is more, the solving time is significantly reduced compared to the traditional use of the MR algorithm, and the minimum number and distribution of nodes along the specified path can be found to minimize the path discretization error. In the second part, a general MPDC method can be enabled by setting the key nodes produced in the first part as the bound conditions. In this way, we can get the time nodes corresponding to the path nodes, and the resulting continuous approximate trajectory not only minimizes the path discretization error, but also maximizes the motion performance. To sum up, a novel sequential specified path OTP scheme considering the complex system dynamics comes out.
The rest of the paper is organized as follows.
Section 2 provides the problem description of the PP process, and gives the presentation of the MR algorithm to control the path discretization error.
Section 3 utilizes the key nodes produced in last section to enable a MPDC method; the uniform arc-velocity condition is presented to estimate the path discretization error without another mesh optimization. Finally
Section 4 and
Section 5 show solutions to verify the validity of the method. The technical roadmap is given in
Figure 2.
2. Path Planning
In the general application of robotic manipulators, the TP problem along the specified path is typically solved by direct methods, and the resulting solution is discrete. At the same time, the general controller of robotic manipulators periodically receives the discrete desired states (referring to joint positions and joint velocities) as input and adjusts the controls (referring to joint torques and actuator currents) to achieve the trajectory tracking mission. In conclusion, we have to reduce the path discretization error in Cartesian space by applying a series of discrete nodes in joint space. It is obvious that both the discretization process and the transformation from Cartesian space to joint space introduce the path discretization error. Therefore, we can propose an optimization method that utilizes the fewest nodes possible to achieve the desired path accuracy. In this section, we regard the above optimization problem as a PP problem, and present the problem based on DC methods and the MR algorithm.
2.1. Problem Presentation
In this part, we want to present the PP problem as an OC problem. The general OC problem presentation is given as follows referring to [
10,
21,
23].
Minimize the performance index:
subject to the following:
the system dynamics:
boundary conditions:
constraints:
where
J is the performance index.
and
L are two constituents, referring to boundary cost and process cost, respectively.
is the system dynamics.
is the boundary condition.
is the general constraint.
and
are the start time and the end time in most situations [
23], but it is noted that we replace them with the arc length
s in the following path planning problem presentation.
u refers to the system control variable.
x refers to the system state variable.
refers to the system differential states.
According to the above problem formulation, the path planning problem can be given as follows.
Minimize the performance index:
subject to the following:
the system dynamics:
path constraints:
boundary conditions:
constant constraints:
This problem description involves finding an approximate path in the joint space, aiming to execute the path in Cartesian space as closely as possible to the ideal path through forward kinematics. Thus, we consider setting joint positions as the states and the differentials of joint positions with respect to the arc length as the controls. In this way, the performance index J refers to the integration of the path discretization error along the ideal path in Cartesian space. and refer to positions of the executed path and the ideal path in Cartesian space, respectively. s refers to the arc length. refers to the joint position. refers to the differential of joint positions with respect to the arc length, and is set as the control variable at the same time. refers to the forward kinematic function, which takes joint positions as inputs and takes positions in Cartesian space as outputs. and refer to the initial and the final joint position, respectively. and refer to the constant constraints of and , respectively.
As a result, DC methods can be applied to discretize the OC problem into an NLP problem. The Hermite–Simpson (H-S) collocation method is used here, and the NLP problem presentation after discretization referring to [
10,
21,
23] is given as below.
Minimize the performance index:
subject to the following:
the system dynamics:
path constraints:
boundary conditions:
constant constraints:
A series of nodes are used to discretize the original problem, with a total number of nodes represented by . Here, k denotes the serial number of the interval between nodes. indicates the arc length at node k, while represents the single step length between and . Additionally, and denote the states and the controls at node k, respectively. and denote the state and the control at the midpoint between nodes k and . It is worth noting that the differential constraint is substituted by a number of algebraic constraints. Consequently, the original OCP transforms into an NLP, allowing for the utilization of general NLP solvers.
2.2. Mesh Refinement Algorithm
After outlining and resolving the PP problem, we consider the discrete solution nodes as a mesh. The MR algorithm can construct a new mesh by introducing a specified number of new nodes to diminish the path discretization error until it reaches an acceptable level. The execution of the MR algorithm involves adding a node to the interval with the largest path discretization error in each iteration, repeating this process until the path discretization error is deemed acceptable.
In the first step, we need to evaluate the discretization error for each interval. Thus, the ideal path and the execution path in the joint space should be given. Because the ideal path in the Cartesian space is given as a prior, a suitable inverse kinematic solution can be derived conveniently. We denote the ideal path in the joint space as
and the inverse kinematic function as
, where inputs and outputs are opposite to those of the forward kinematic function
. Then, we have the following:
According to the H-S collocation method [
10], a continuous execution path based on the NLP solution can be derived as follows.
Then, the local path discretization error in interval
k, denoted as
, is given by the following:
Furthermore, for ordinary differential equations (ODEs), the global error is
and the local error is
, where
p refers to the order of accuracy. The H-S discretization is of order
. As a result, the alternative representation of the local path discretization error is of the form
where the coefficient
can be solved. Then, when we insert new nodes into interval
k evenly, the estimation of the local discretization path discretization error of the new mesh, denoted as
, is given by the following:
where
refers to the total number of new nodes added in interval
k. Consequently, an MR algorithm is designed to reduce the discretization path discretization error until it is acceptable (the tolerance error in the joint space is denoted as
; the tolerance error in the Cartesian space is denoted as
). Here we show the procedure of Algorithm 1.
| Algorithm 1 Mesh Refinement Algorithm |
- 1:
start - 2:
- 3:
Estimate path discretization error from ( 25); - 4:
Set ; - 5:
while - 6:
Add a new node to interval k, ; - 7:
Refresh error from ( 27), ; - 8:
if - 9:
Sort nodes and return to step 2; - 10:
Output the mesh; - 11:
end
|
In conclusion, the PP gives an improved mesh making the discretization path discretization error acceptable.
4. Numerical Simulation
This section contains a complete simulation planning process for executing a specified circular path using a six-axis robotic manipulator ROCR6 manufactured by Si Vally, China. The simulation environment is a personal computer with an AMD Ryzen 7 5800H processor with 8 cores (3.20 GHz). The device information can be found in the official website or in the research [
21].
The specified circular path in the PP process is shown in
Figure 3. The coordinates of the circle center are
, the radius is 100, and the starting coordinates are
. The length unit used in this paper is mm; the joint position unit is rad. The ideal path functions can be written as follows:
so that the path constraints (
7) can be given with the forward kinematics.
The boundary and inequality conditions are set as follows:
The initial total number of intervals is set as
. The initial guesses of decision variables at node
are given as below:
Then, a software for large-scale nonlinear optimization named Interior Point OPTimizer (IPOPT) can be applied to solve (
12)–(
20). In addition,
and
have to be set to enable Algorithm 1. It is known that the location accuracy of ROCR6 is 0.02 mm. Furthermore, we can find a linear relationship between the path discretization error in the PP process and that in the TP process, as indicated by (
64). A rough optimization without constant arc velocity is used to define
m/s. Then, we have the following:
Therefore, let
be
mm and
be
rad according to experiment experience. Finally, the solutions are presented in
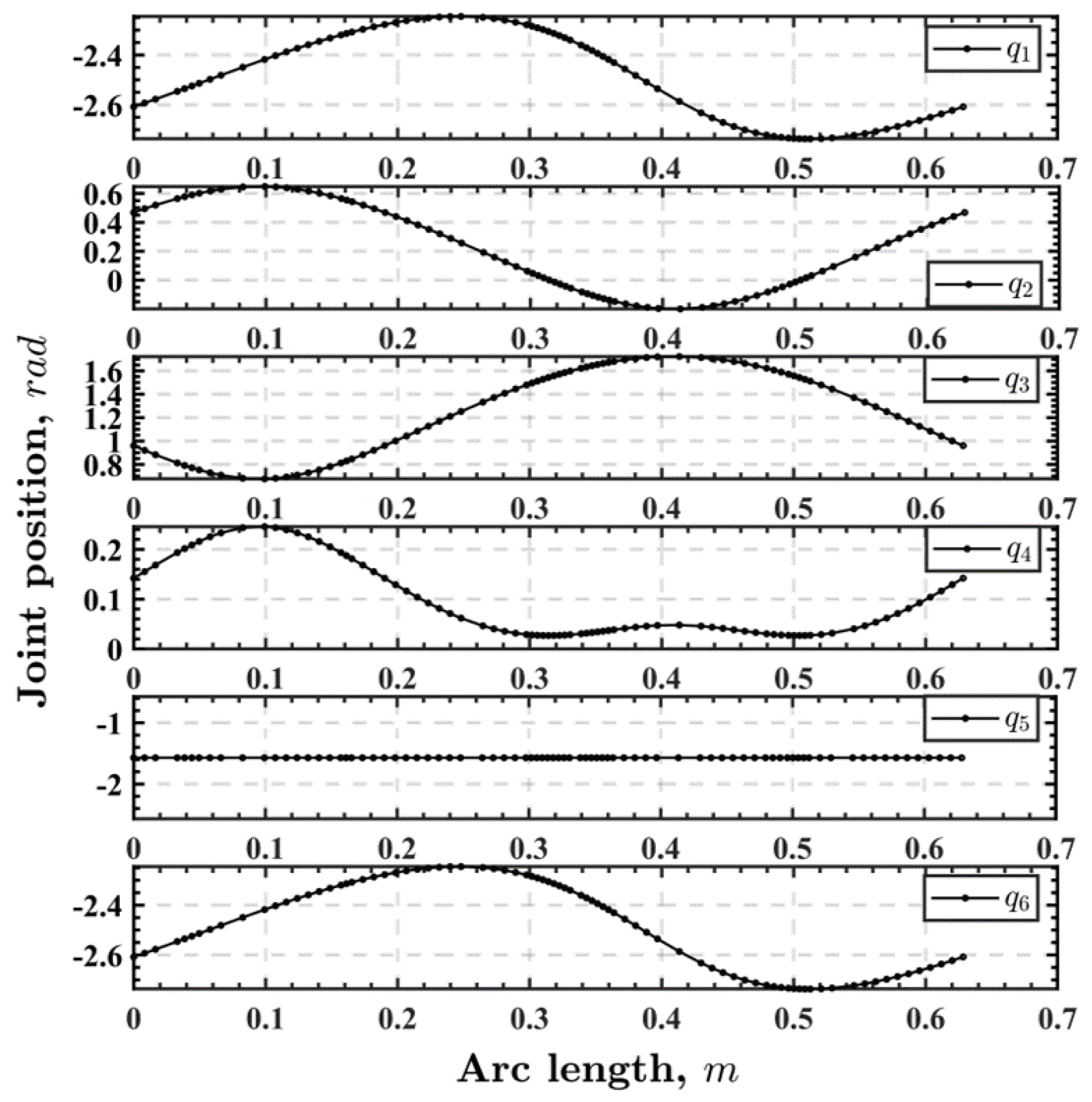
Figure 4, where the position function with respect to the arc length of each joint is given. In addition, the MR algorithm produces a heterogeneous mesh to minimize the path discretization error.
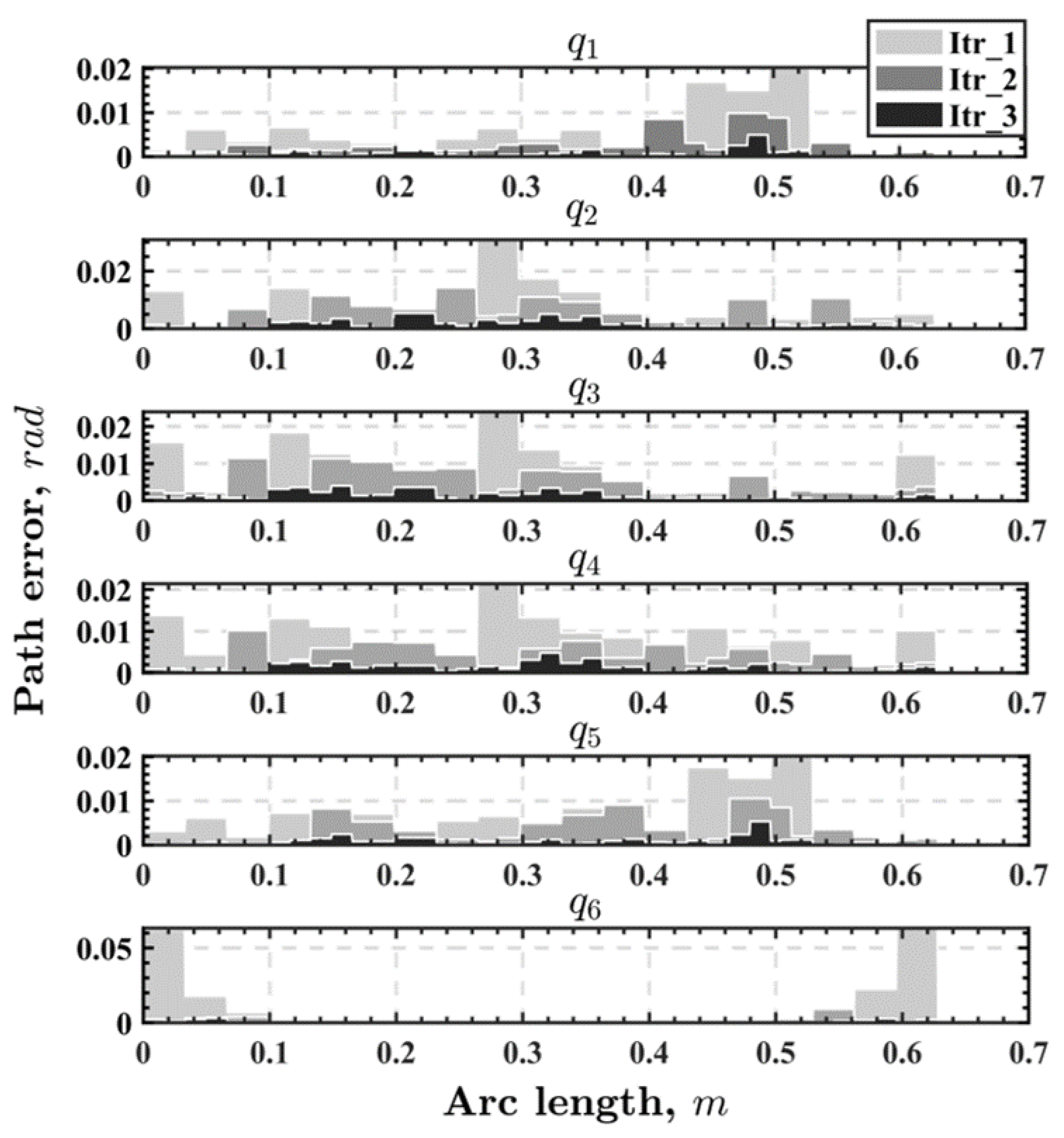
The PP process includes six iterations where the MR algorithm introduces 8, 11, 15, 21, and 7 nodes into the mesh, respectively. The maximum path discretization error in each iteration is presented in
Table 1, where we can find that the path discretization error is gradually reduced with the introduction of nodes in each iteration. In addition, the path discretization error reduction in each iteration is shown in
Figure 5. The different color blocks refer to the path discretization error at different iterations, and we observe a consistent reduction in the path discretization error across iterations. So far, the PP process is finished.
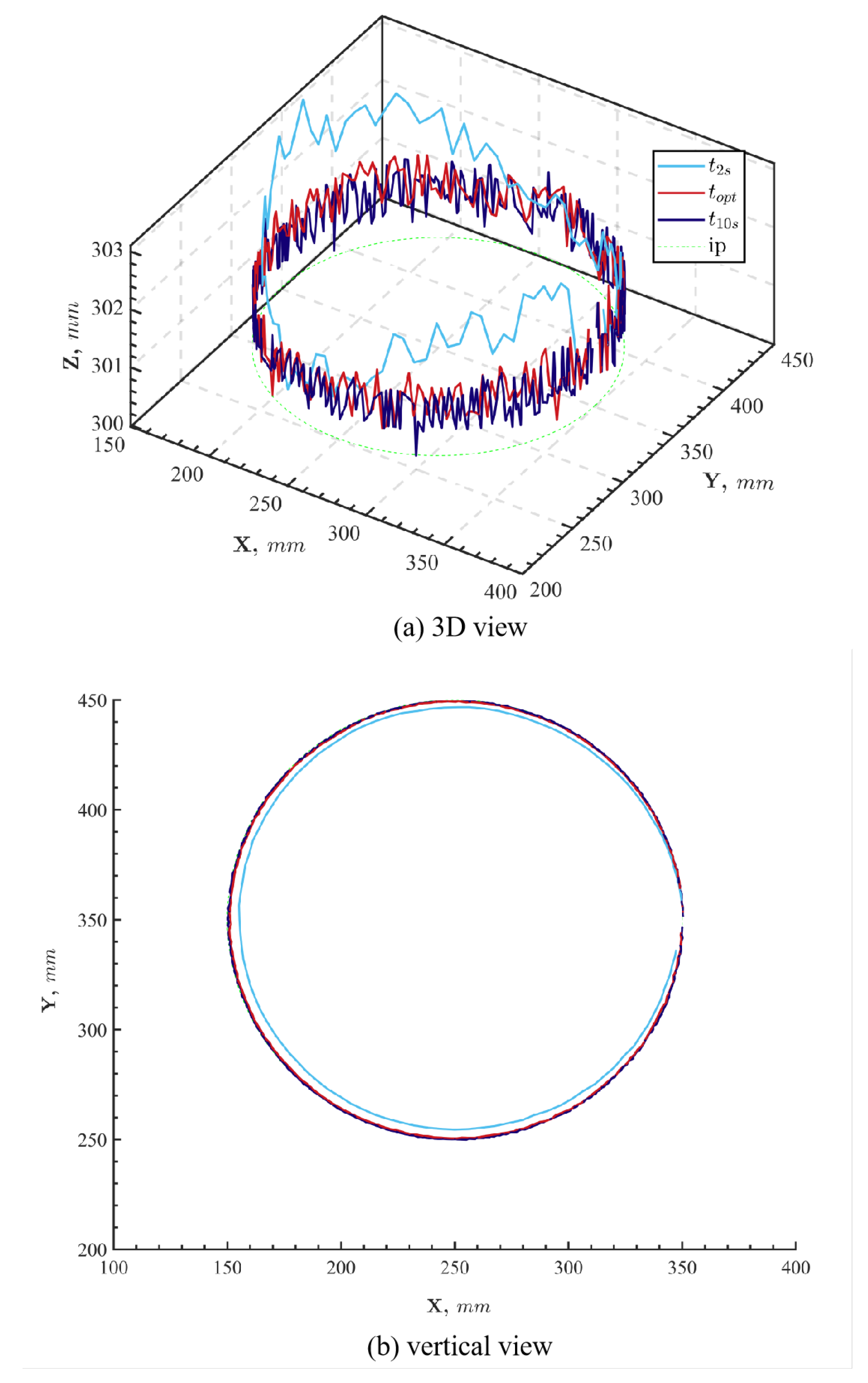
Next, the above solution mesh is used as boundary conditions for the TP process, where the aim is to find the time law tied to the solution mesh from the PP process. And this process solves the average arc velocity along the specified path and gives the optimal time as the result, which can be set as the input of the experimental device ROCR6. The solution is shown in
Figure 6.