1. Introduction
Visual servoing is a crucial technology in intelligent robot systems, as it greatly enhances the ability of robots to perceive the environment. Various applications of visual servoing have been developed, including visual-based formation control [
1,
2], visual grasping [
3,
4], object tracking [
5], and human–robot collaboration [
6]. Visual servoing employs image features extracted from visual sensors, such as RGB cameras, as feedback for the controller. This approach makes the controller more flexible, reliable, and efficient when dealing with complex scenes.
Scientists have performed a great deal of work in visual servoing. These works are generally thought to fall into three categories. The first kind of visual servoing is called image-based visual servoing (IBVS) [
7,
8] and only uses the pixel coordinates of feature points as feedback. IBVS is insensitive to calibration errors. The second kind of visual servoing is called position-based visual servoing (PBVS) [
9,
10] and uses the 3D positions of the corresponding feature points as feedback for the controller. The 3D positions can be obtained through an RGB-D camera (RealSense) or a stereo camera (ZED). This means that PBVS needs the camera model to be accurate. The last kind of visual servoing is called hybrid visual servoing (HVS) [
11,
12], which combines 2D and 3D servoing techniques. HVS aims to improve precision and robustness in robotic tasks by integrating the advantages of different dimensional visual information. Compared to other servoing techniques, IBVS shows better movement in the image plane; however, it is not optimal for 3D motion because of the lack of 3D information. By contrast, PBVS has enhanced access to the movement path of the 3D space but cannot access the optimal route in the image plane. The hybrid method merges the information of the pixel plane and the 3D space. Both camera calibration and hand-eye calibration are indispensable in attaining highly accurate parameters, and these parameters are easily changed through the aging of the equipment or a change in the relative displacement between the camera and the manipulator. Therefore, research has focused on IBVS.
Researchers have extensively studied IBVS and made notable contributions. IBVS has been applied to robot development [
1,
2] and a quadcopter that mimics bird predation [
4]. Keshmiri et al. [
13] transformed pixel error propagation into the expected acceleration of the camera and used the computed torque method (CTM) to obtain the joint angular acceleration. Some researchers have used light field cameras for feature extraction [
14], while others have usedutilized image feature extraction methods such as Bézier curves [
15]. Incremental control laws have been used to avoid the multiple solutions yielded by some algorithms in inverse kinematics [
16]. In addition to the common serial manipulators, there have been algorithmic studies conducted on parallel manipulator IBVS [
17].
However, one common challenge faced by these algorithms is computing the inverse Jacobian matrix. For kinematic control near singularity, the joint movements of the manipulator may no longer satisfy the end-effector motion requirements, resulting in increases in joint movement velocity and acceleration. This can lead to significant force and torque demands, potentially causing the manipulator to be overloaded or generate abnormal accelerations, increasing energy consumption and mechanical component wear.
To solve this problem, Wang et al. [
18] designed a virtual-goal-guided RRT algorithm for trajectory planning to fit the field of view and other physical constraints. Kazemi et al. [
19] built a cyber–physical system that alternates between exploring the state space of the camera and the configuration space of the robot to obtain feasible camera/robot paths, thereby obtaining feasible feature trajectories in the image space. The main idea of these method is to plan a trajectory that is in compliance with constraints and avoids the singularities of the manipulator [
20]. These methods attempt to avoid singular points, but they do not actually solve the problem of abnormal motion near the singular points.
In recent years, visual servoing methods based on the optimization algorithm have been developed for a redundant manipulator. These methods consider the visual servoing as a linear parameter-varying (LPV) model. A convex objective function of joint velocity has been built, and several constraints have been applied to the optimization algorithm. These constraints involve the angle, velocity, and acceleration of a joint, as well as the mapping between the error derivative and angular velocity. The servo task is then transformed into a quadratic programming (QP) problem. Afterward, a neural network is used to solve this QP problem. Hajiloo et al. [
21] designed a robust model of a predictive controller to avoid the inverse of the Jacobian matrix. Jin et al. [
22] built a dynamic recurrent neural network for redundant robots. Zhang et al. [
23] changed the network mentioned in [
22] and created a single-layer neural network for image-based visual servoing. Although these optimization algorithms merge the limitation of joint velocity and angle into one constraint, they approximate the curve portion of the merged constraint function using a line [
24], which substantially wastes the feasible region and is not very intuitive.
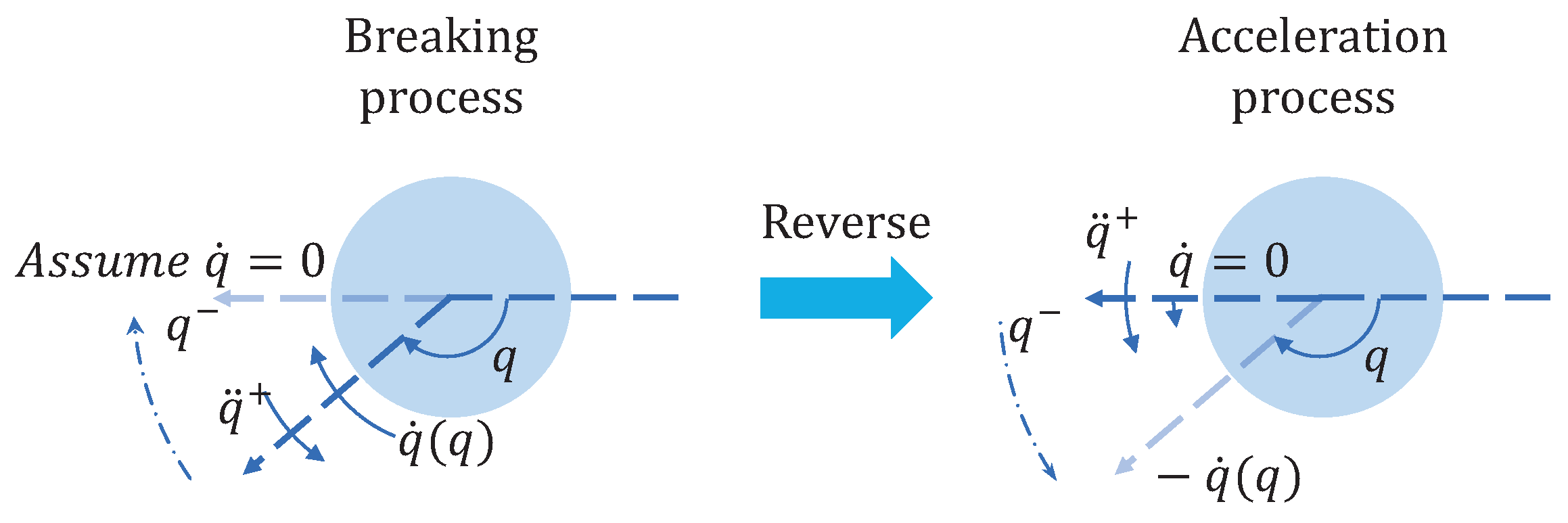
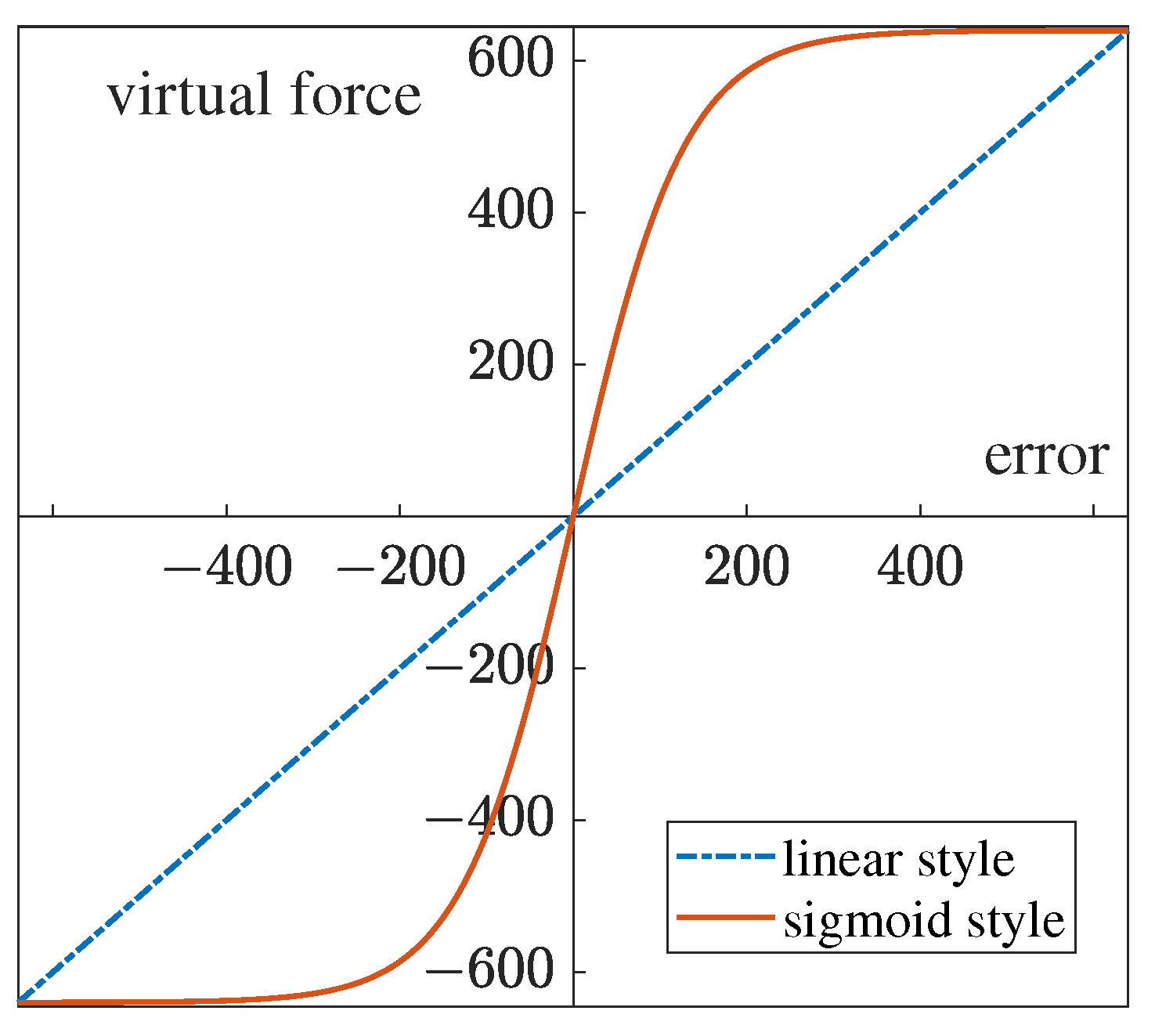
Even though the above-mentioned controllers avoid the inverse of the Jacobian matrix, the optimization-based derivation process is complex, and once derived, the format is fixed. Inspired by the principle of virtual work, this article proposes a new visual servoing framework that converts errors into virtual forces using an impedance model and drives joint displacement using an admittance model through backward force propagation. This framework also avoids calculating the Jacobian matrix inversion and can design different impedance/admittance controllers based on different environments, involving support for linear and nonlinear functions.
The main contributions of this paper can be summarized by the following three aspects:
This study transforms the propagation of errors into the transmission of virtual forces and provides an intuitive understanding at the physical level. This transformation eliminates the inverse of the Jacobian matrix, thus avoiding the risks caused by the abnormal movements of certain joints near the singularities of a manipulator.
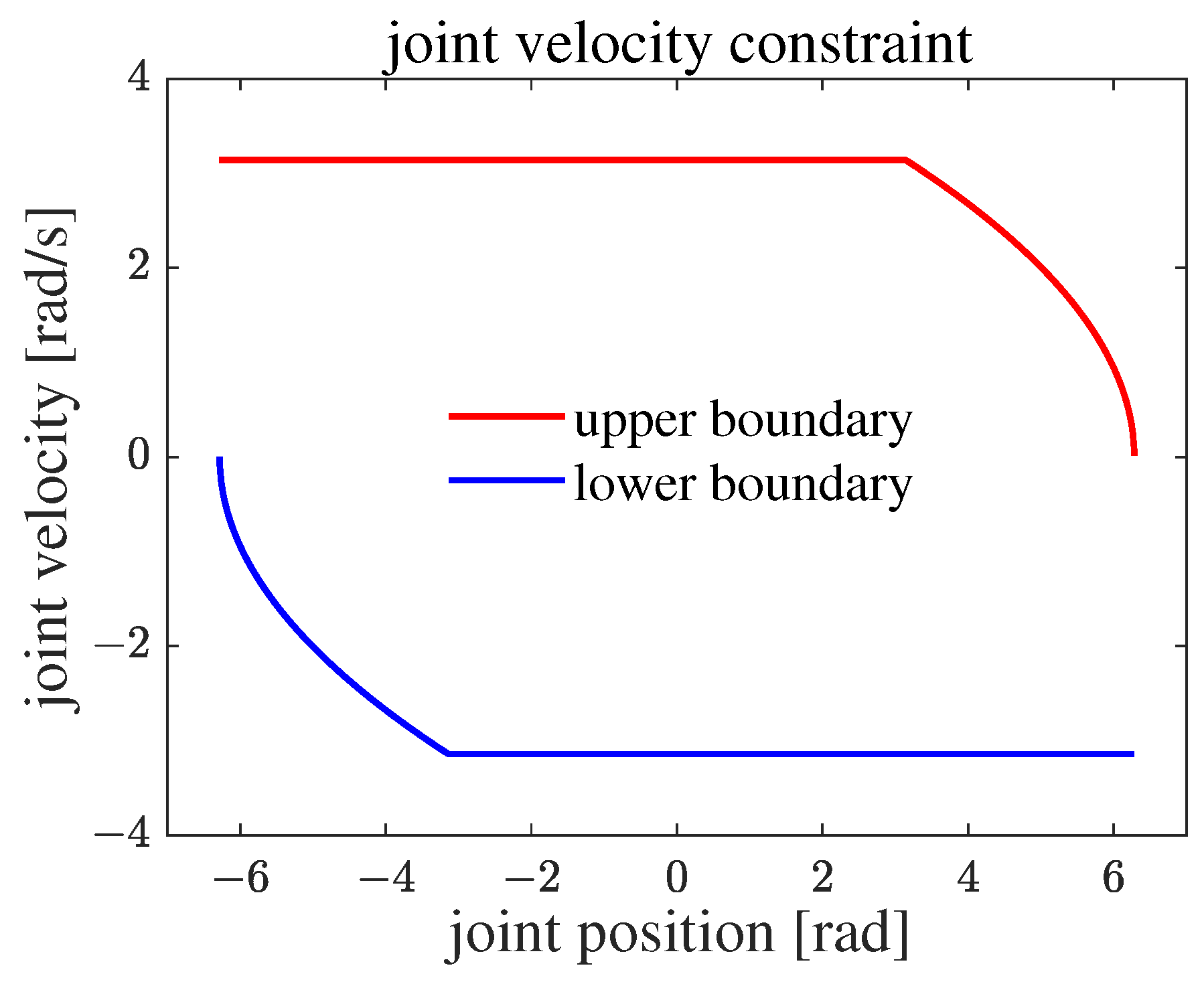
This article provides a function that expresses the limits of the joint angular velocity as a function of the angle. It integrates angle constraints, angular velocity constraints, and angular acceleration constraints. These limits can be obtained by directly setting the maximum and minimum values for the angle, angular velocity, and angular acceleration, without the need to calculate additional parameters.
This article demonstrates the design process of a controller, and its effectiveness was validated through simulation experiments and physical experiments.
The rest of this paper is structured as follows.
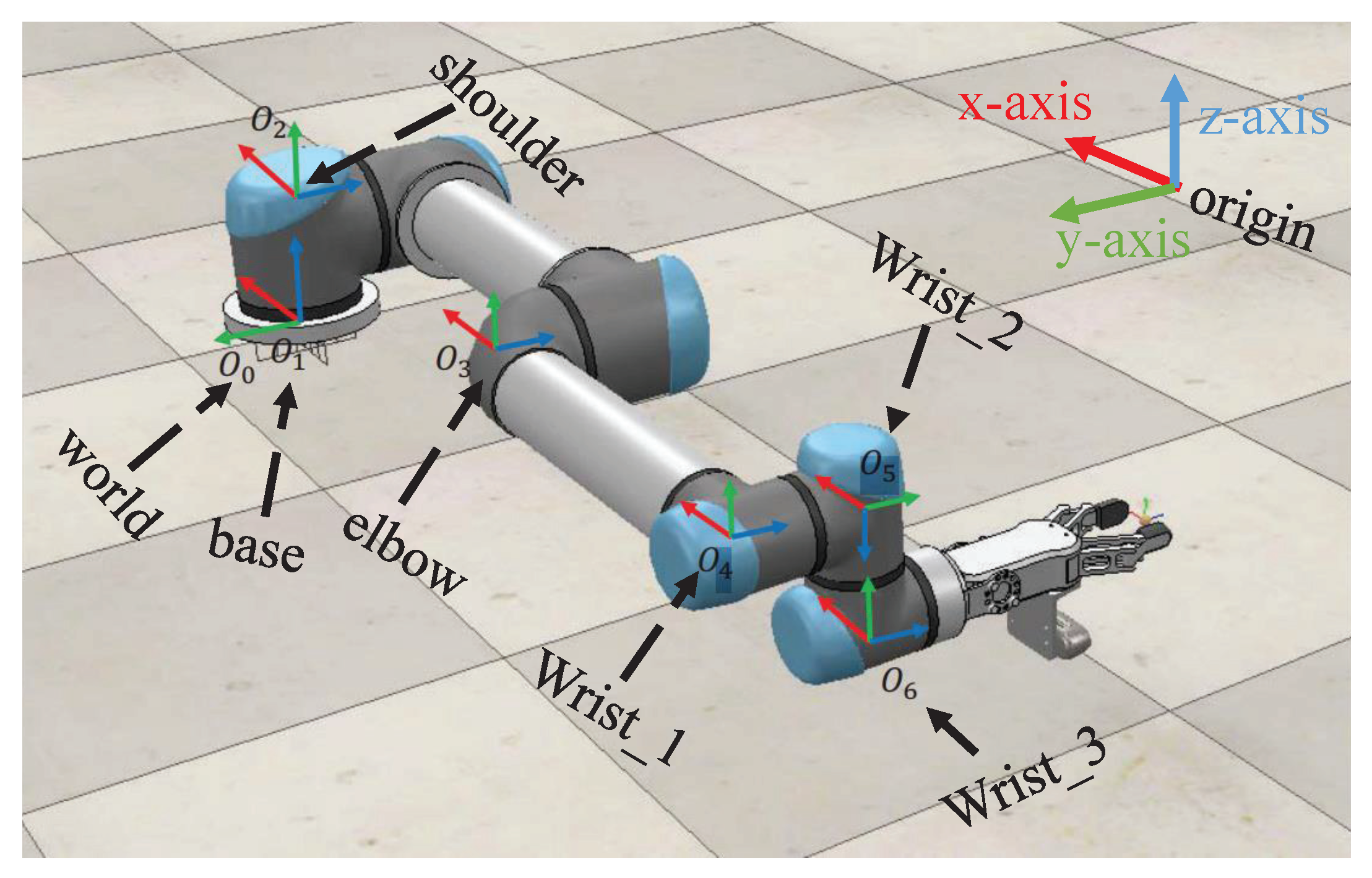
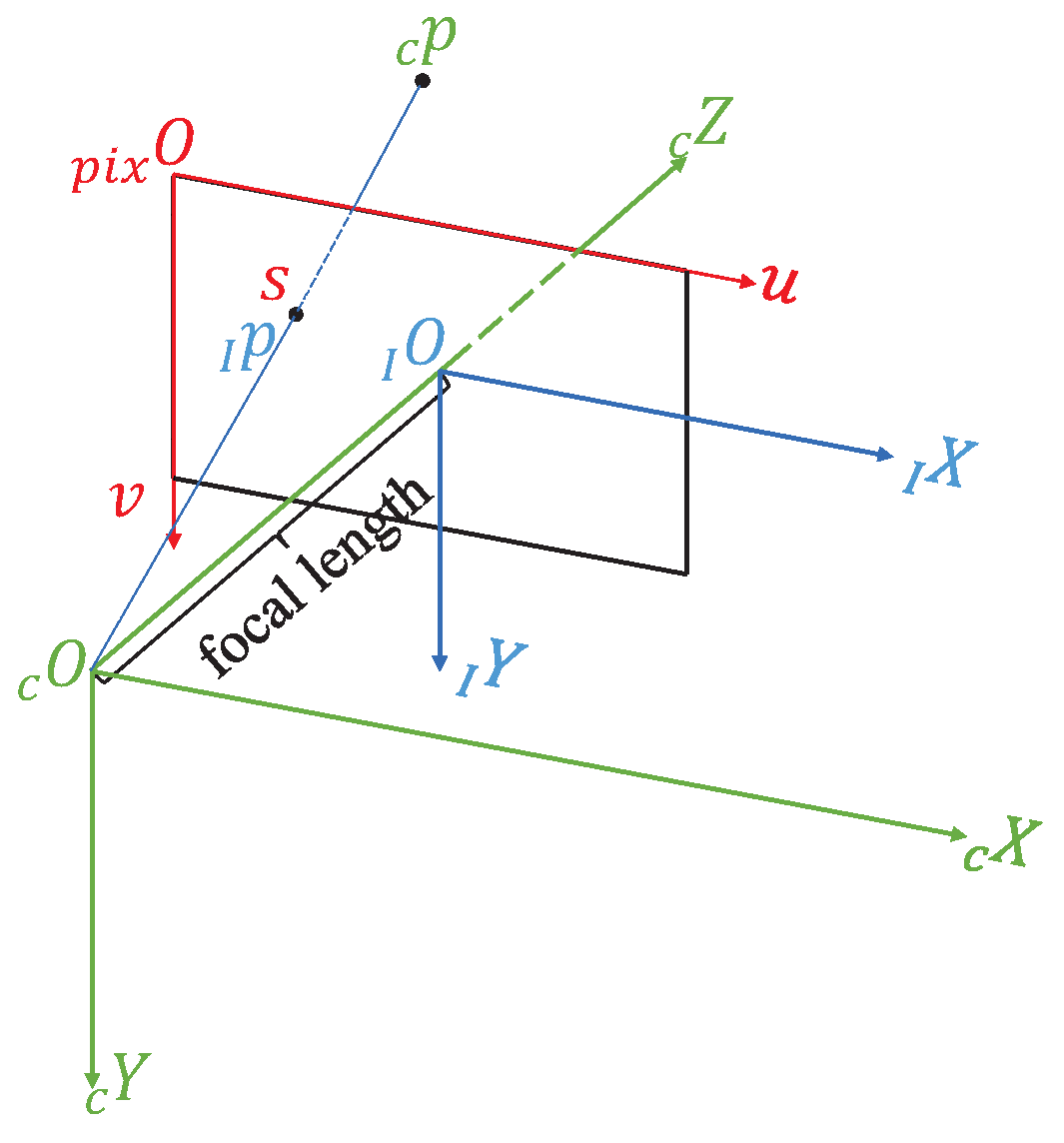
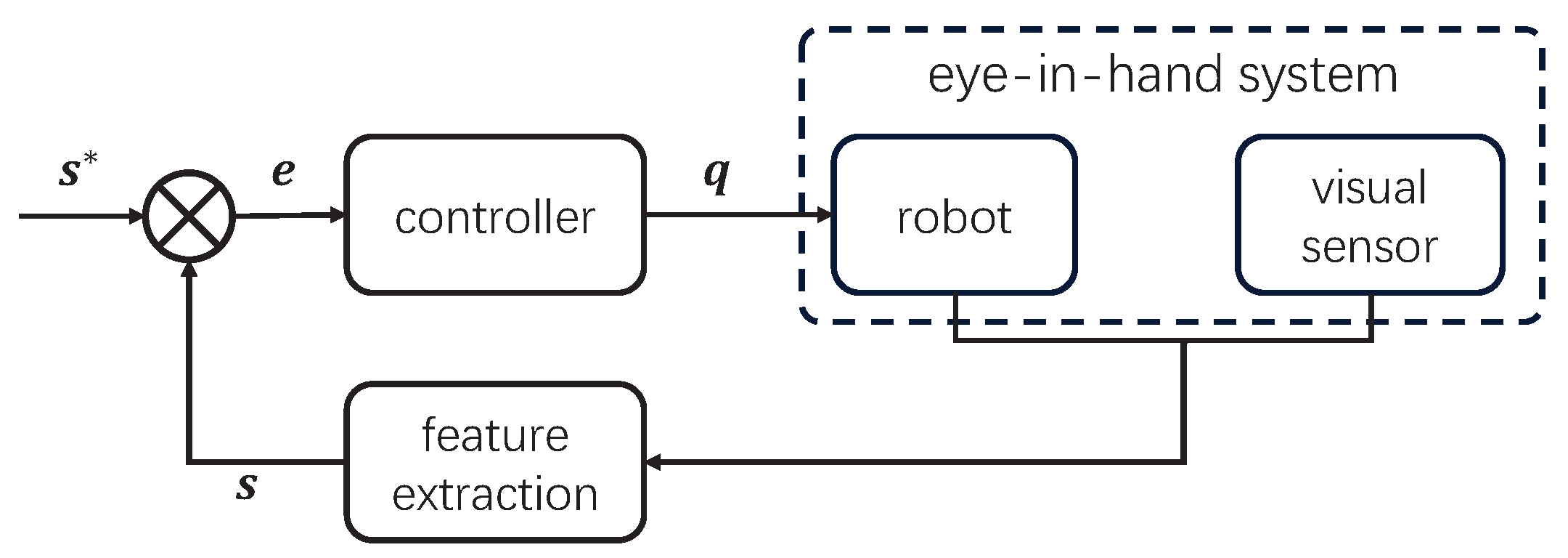
Section 2 provides an overview of the model of the eye-in-hand system and presents fundamental definitions. In
Section 3, the proposed image-based visual servoing framework is described in detail, along with a design example based on this framework. In
Section 4, the experiments conducted using both the VREP simulation platform and real robots are discussed, and the results are analyzed. The main findings of this study are then summarized, and prospects for future research are discussed in
Section 5.
4. Results and Discussion
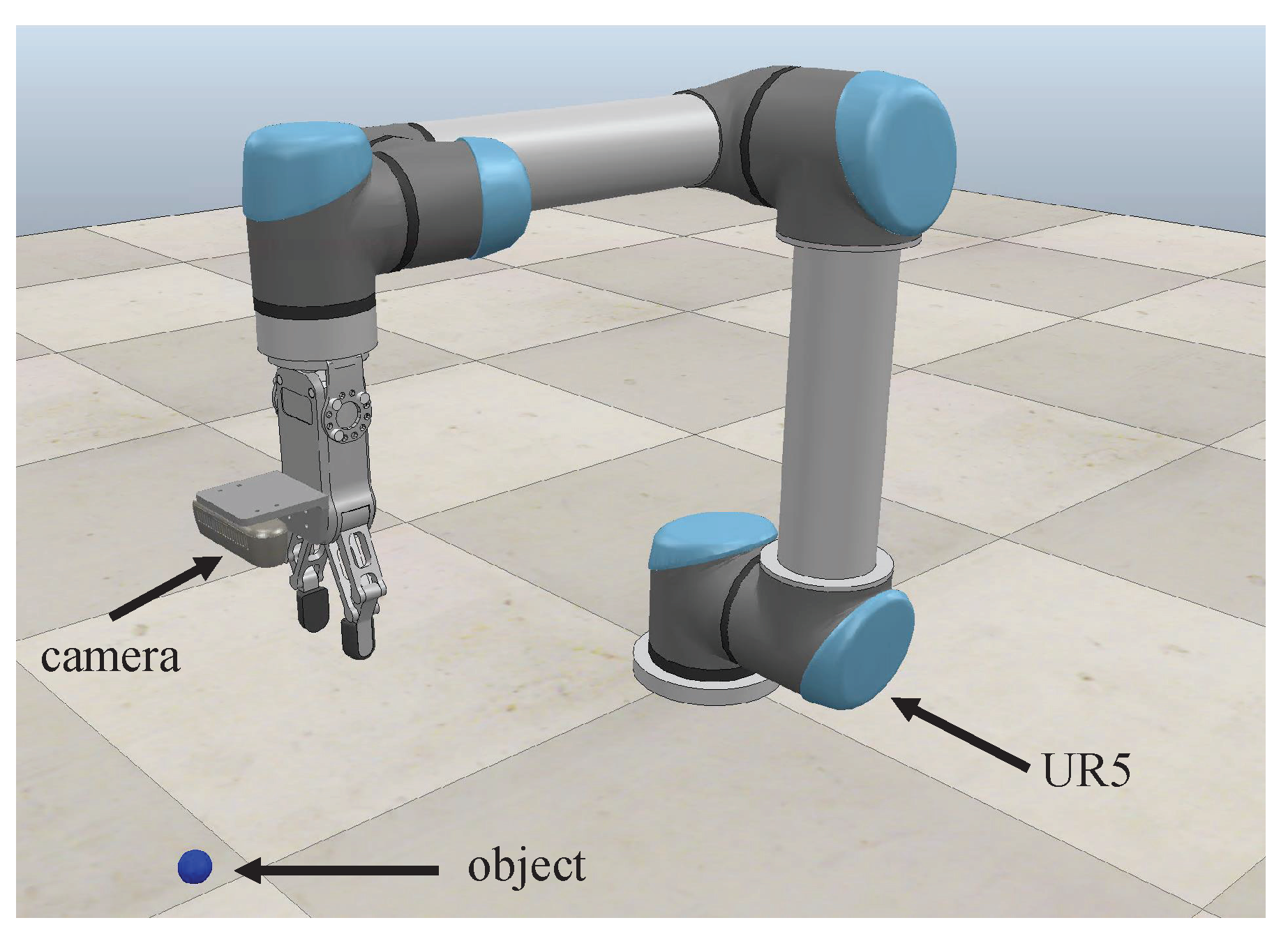
In this study, an experiment was conducted using the VREP simulation environment to validate the proposed method. The UR5 robotic was utilized for this experiment. The D-H parameters for the UR5 are provided in
Table 1.
The physical constraints of the manipulator are shown in
Table 2.
The improved physical constraint boundary function is depicted in
Figure 8. If the joint velocity is beyond the boundary, there must be a physical constraint that is not satisfied at some times.
A visual sensor was mounted at the end-effector of the UR5. The parameters of the camera are shown in
Table 3.
The neural network control algorithm proposed in [
23] was reproduced for a comparison. This method does not include the inverse of the Jacobian matrix and does not have a singularity problem. The controller in [
23] is described as follows:
where
is the velocity vector of the joint, and
projects the output within the physical constraints.
and
are the parameters that need to be adjusted. The physical constraints in [
23] are described in Equation (
24). Therefore, there is another parameter
k in the physical constraints.
Hence, to meet the physical constraints, we drew a line between
and
in
Figure 8 and obtained the parameter
.
Table 4 describes the adjusted parameters in the neural network method.
The final parameters applied to the proposed algorithm are shown in
Table 5.
The control period was dt = 0.05 s in order to fit the real environment, which satisfies most real-time image frame rates. To verify the performance of the algorithm under different tasks, after the parameters were properly adjusted, it was maintained constant across all experiments.
4.1. Convergence Performance Simulation
Convergence performance is one of the most important indexes used to evaluate a visual servoing algorithm. We set a static object and designated the target points as
and
. The former point is near the corner of the image, which easily loses sight of the object. The latter is at the center of the image, which is near the major target point of the visual servoing tasks. The experimental environment is shown in
Figure 3.
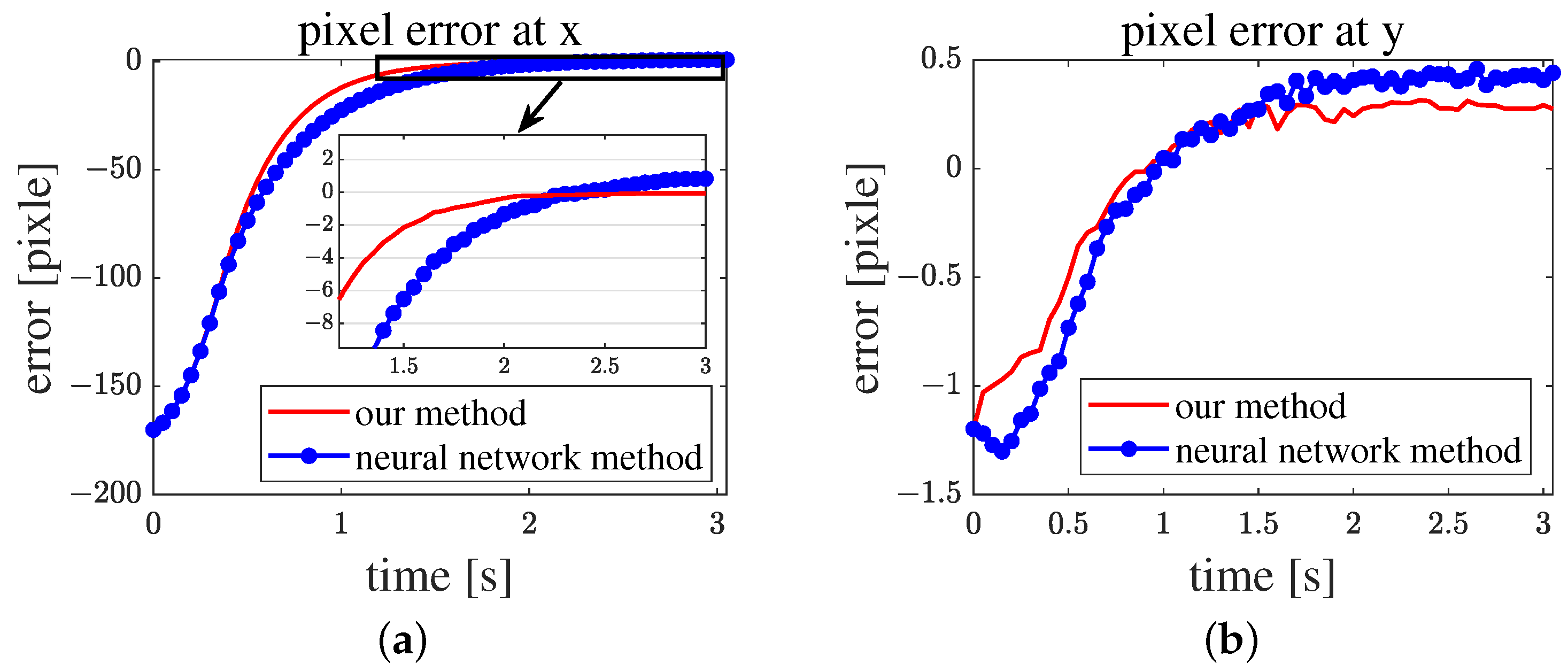
The neural network method needs a long time to converge because it has an integral. When the error becomes too small, the neural network controller needs a long time to overcome the accumulated error. The proposed sigmoid-style impedance module enhances the influence of error on the controller when the error is small. Without the integration of errors, the proposed algorithm converges close to zero. The final error in the pixel of the proposed algorithm is (0.01, 0.2), and that of the neural network method is (2.6, 0.8), as shown in
Figure 9.
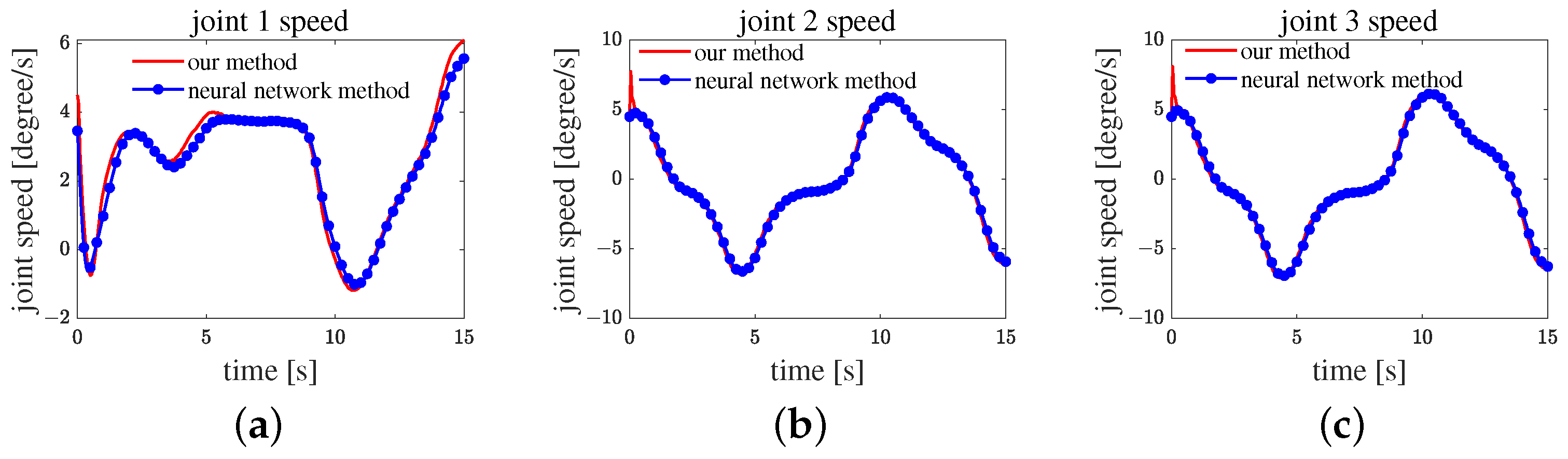
Figure 10 displays the curve of the joint velocity. Both algorithms speed up with the maximum joint acceleration at the beginning and then decelerate to zero. At approximately 0.4 s, the acceleration of the neural network method decreased, as shown in
Figure 10b–d, mainly because the error is very small. Hence, velocity was mainly determined through the integral portion in Equation (
23). The proposed algorithm could keep a rapid response when the error was small.
In many cases, the target point of the visual servoing task is located near the center of the image; thus, the center of the image is representative.
Figure 11 shows that the proposed algorithm has a fast convergence rate, although the convergence rate when the servo is near
is equivalent. As mentioned before, the neural network method can converge to a narrow range. However, it needs a long time to converge to zero.
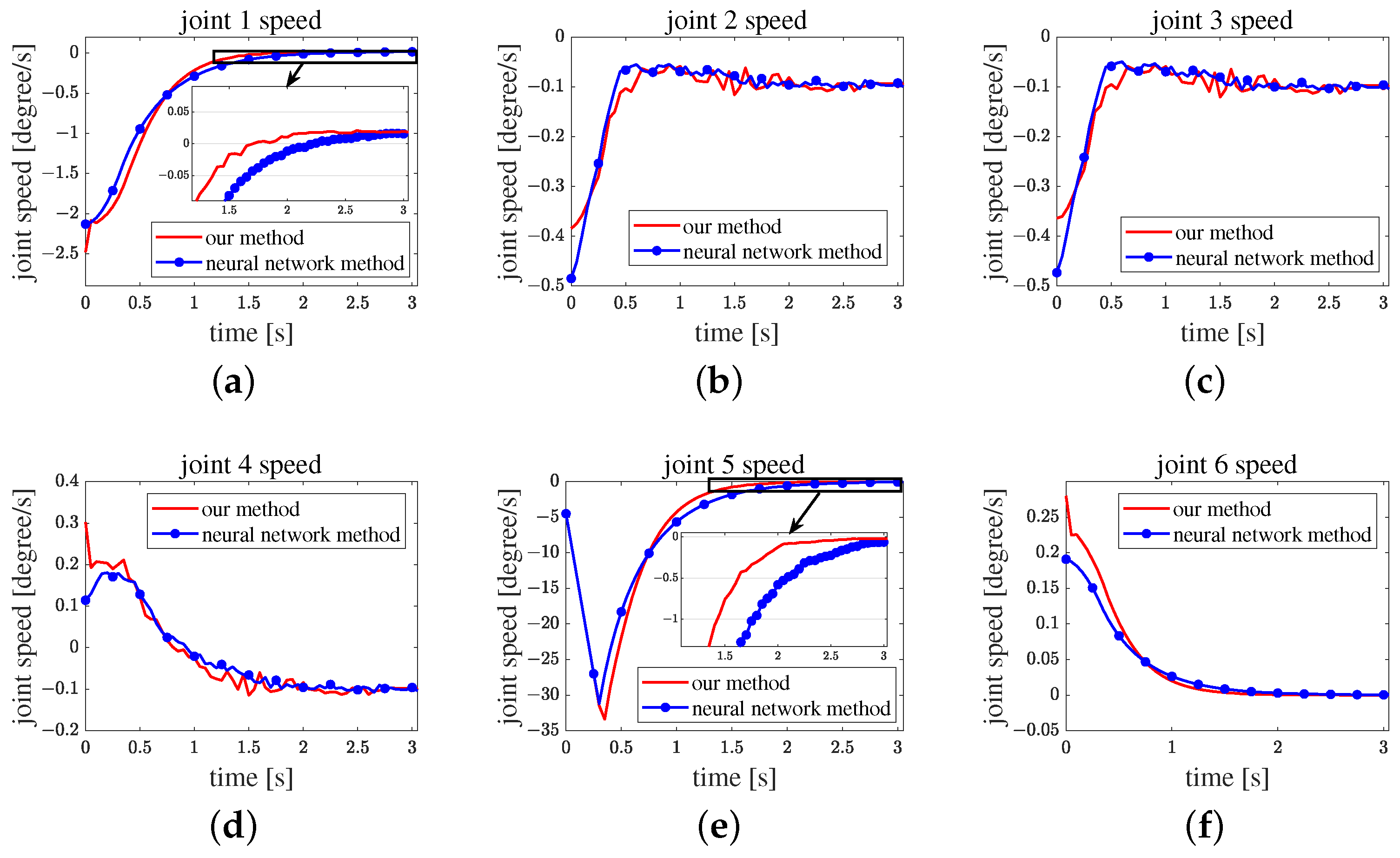
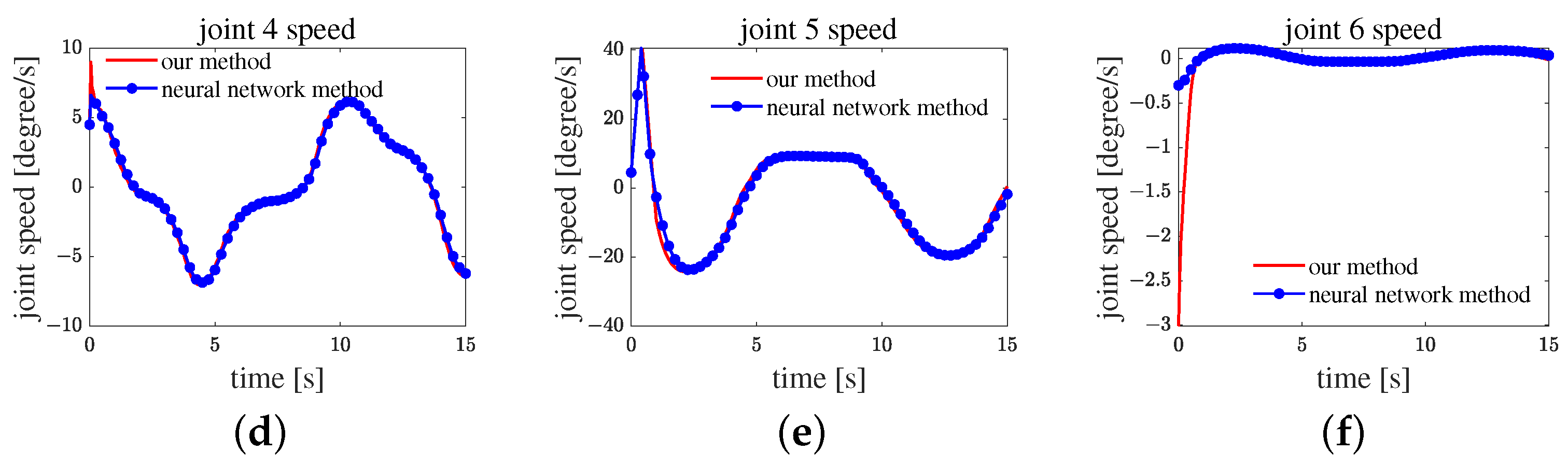
Figure 12 shows the velocity curve of each joint. The velocities in (b), (c), and (d) of this figure are near zero, which means that these joints are near the target joint angles. The curve of velocity in (a), (e), and (f) show that the proposed algorithm always exhibits high acceleration. Thus, the proposed algorithm enhances the performance of the manipulator.
4.2. Object Tracking Task Simulation
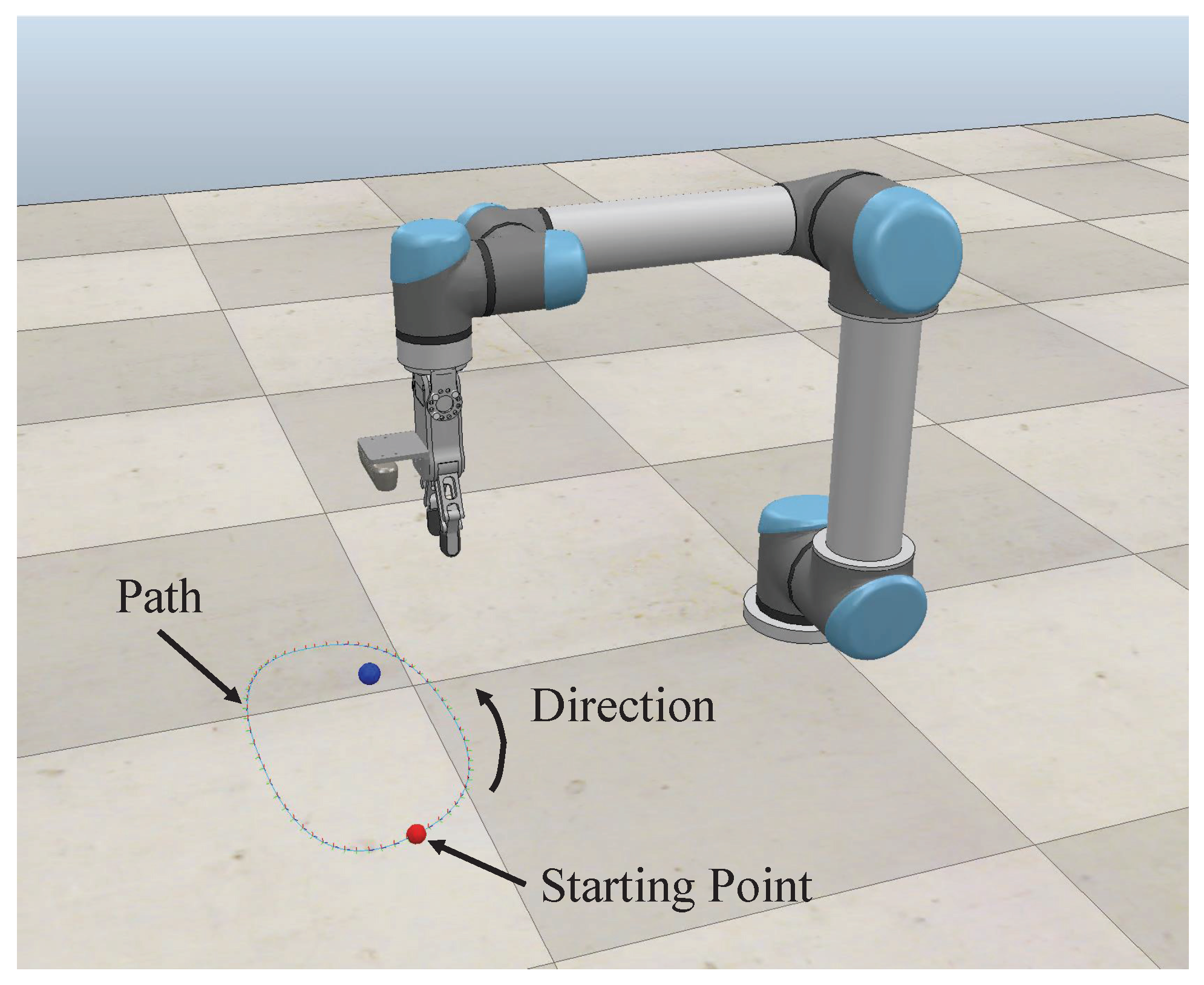
Object tracking is another widely used application in dynamic object grasping and photography. We set up the environment as shown in
Figure 13.
We built a curved path and let the blue ball move along it at a speed of 0.1 m/s. This movement can reflect the response performance when the error changes in different directions.
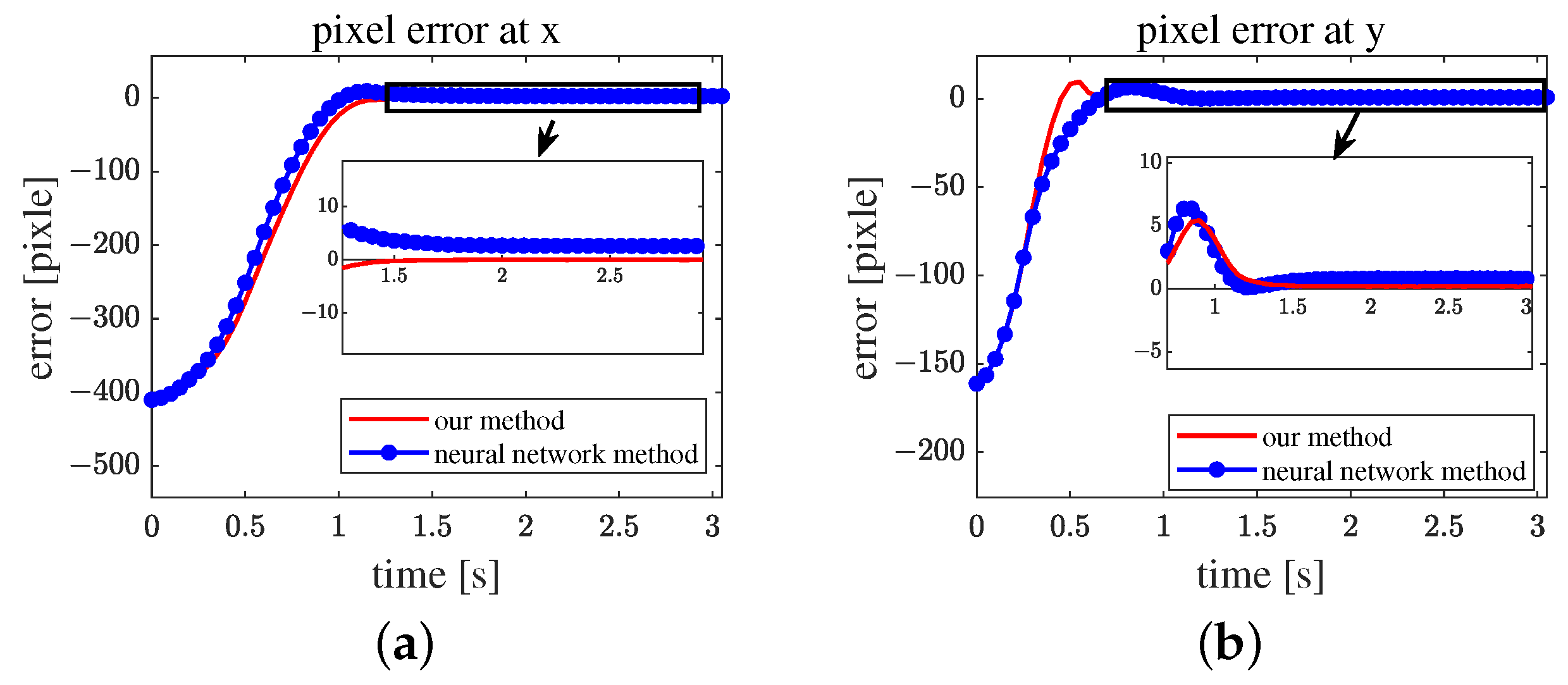
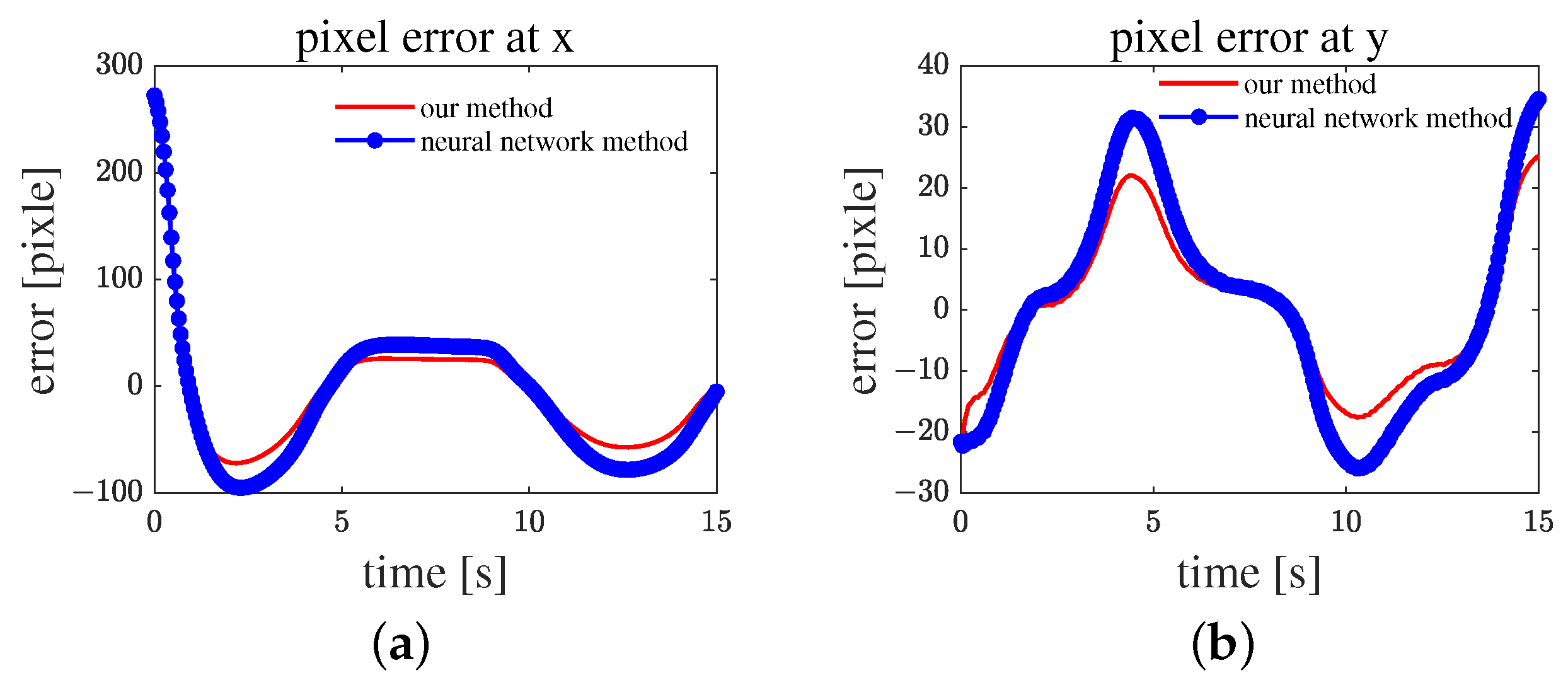
Figure 14a shows the pixel error on the
x-axis, and (b) shows the pixel error on the
y-axis. Both systems can track the target within a margin of error of 0.35 s. Compared with the method in [
23], the proposed algorithm shows a smaller pixel error both on the
x- and
y-axes.
Figure 15 shows that the proposed algorithm can speed up to a higher velocity, which means that it can catch the target faster. The proposed algorithm also has a faster response to velocity, which is especially obvious in
Figure 15a.
4.3. Physical Experiment
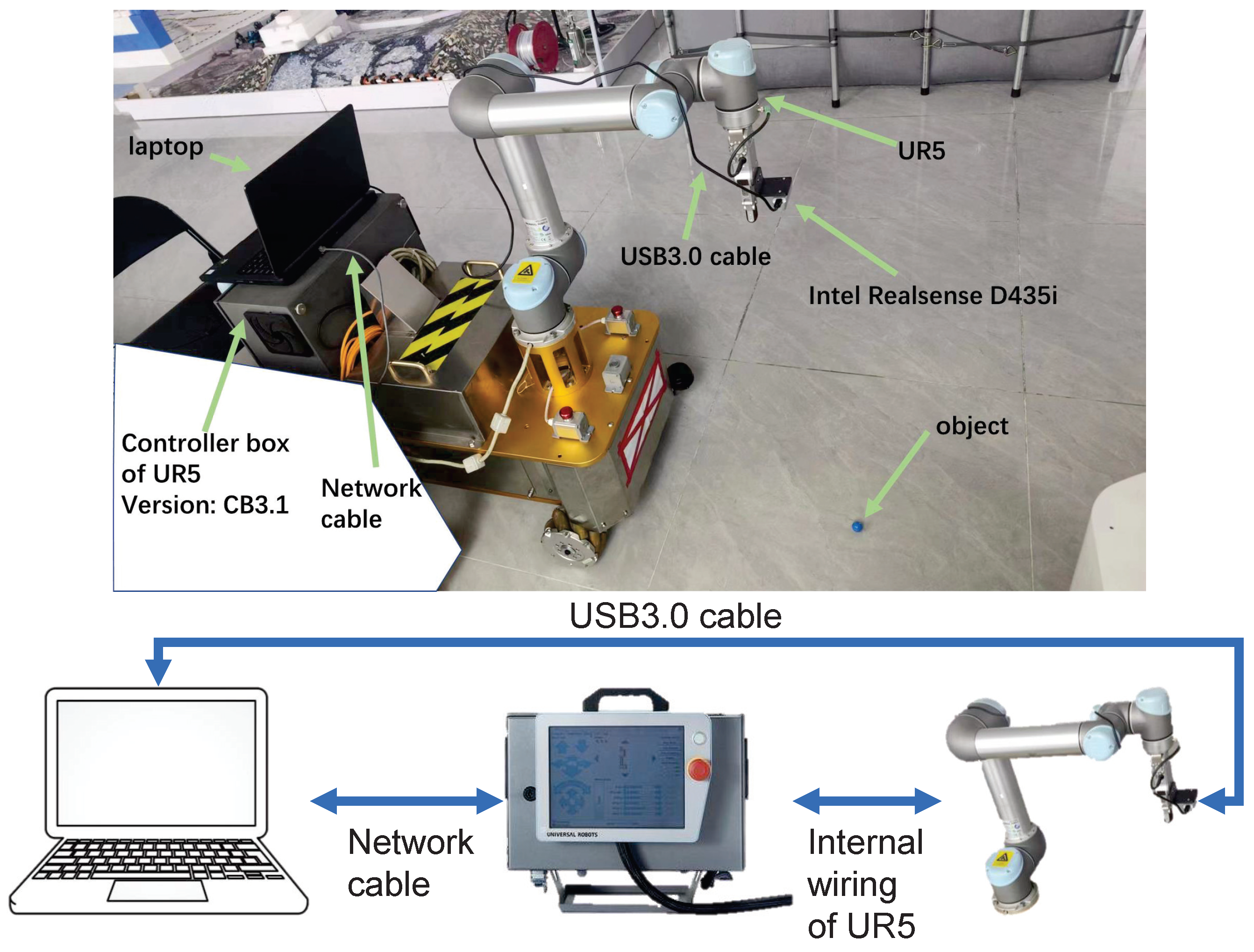
To validate the feasibility of the proposed algorithm in practical applications, we replicated the simulation environment at a 1:1 scale. However, because of the difficulty of maintaining a fixed trajectory for a small ball to follow a constant speed in a real-world environment, we conducted only static servo experiments. Using a UR5 with a body manufactured in 2015 (The manufacturer is Universal Robots USA, Inc 27175 Haggerty Road, Suite 16048377 Novi, MI, USA, We introduced the UR5 in 2017 by purchasing a third party mobile robot equipped with UR5 in Shenzhen, China) and a control system upgraded to version CB3.1 (
Figure 16), we controlled the UR5 by sending velocity commands through TCP/IP protocol communication using a Python (version 3.10.12) script running on a laptop. During actual operation, the maximum control frequency of the UR5 in this control mode was 10 Hz, due to the reporting frequency of the state of UR5 being 10Hz. Therefore, we adjusted the control cycle of the controller to 0.1 s.
The notebook configuration adopted in this study was as follows: an Intel 9th Generation Core i7, 16 GB DDR4, and an NVIDIA GeForce RTX 2060 GPU. With this configuration, the controller’s computation time ranged from 3 ms to 5 ms, which is significantly shorter than the control cycle of 100 ms.
The parameters of the real camera can be obtained from the Intel RealSense API.
Table 6 shows the detailed parameters.
In this study, the traditional PID control was also incorporated into the comparison. The design of the PID controller is depicted in the following figure (
Figure 17).
Here, , , and , respectively, represent the proportional, integral, and derivative coefficients. is the pseudoinverse of the Jacobian matrix.
The parameters of the controller used in the physical experiment are shown in
Table 7.
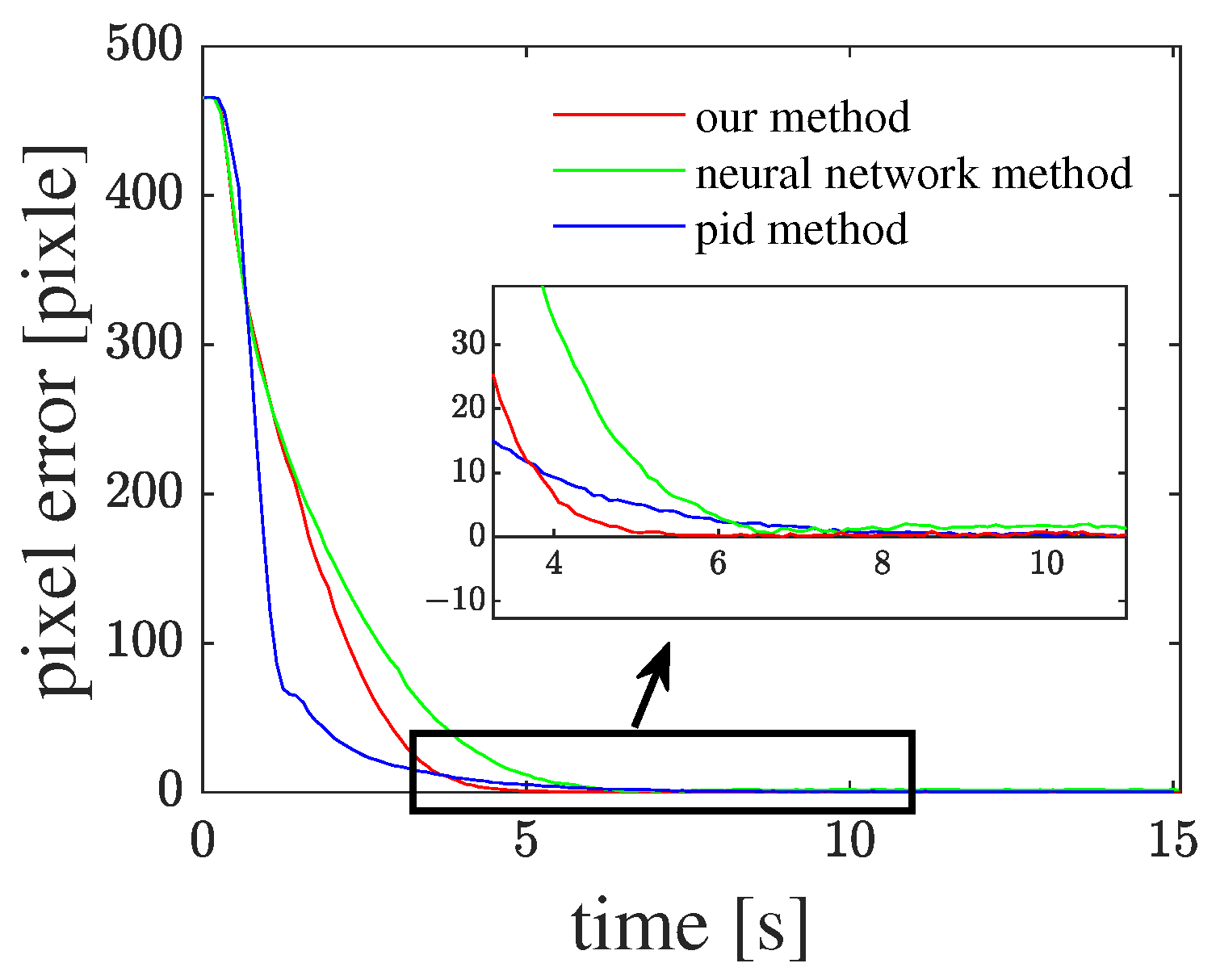
Our proposed algorithm shows superiority over the compared method, as it converged approximately 2 s earlier than others (
Figure 18). From the error curve, it can be observed that, initially, the convergence speed of the proposed algorithm is not the fastest. However, in the final 10 pixels, the convergence speed of the proposed algorithm surpasses those of other comparative algorithms.
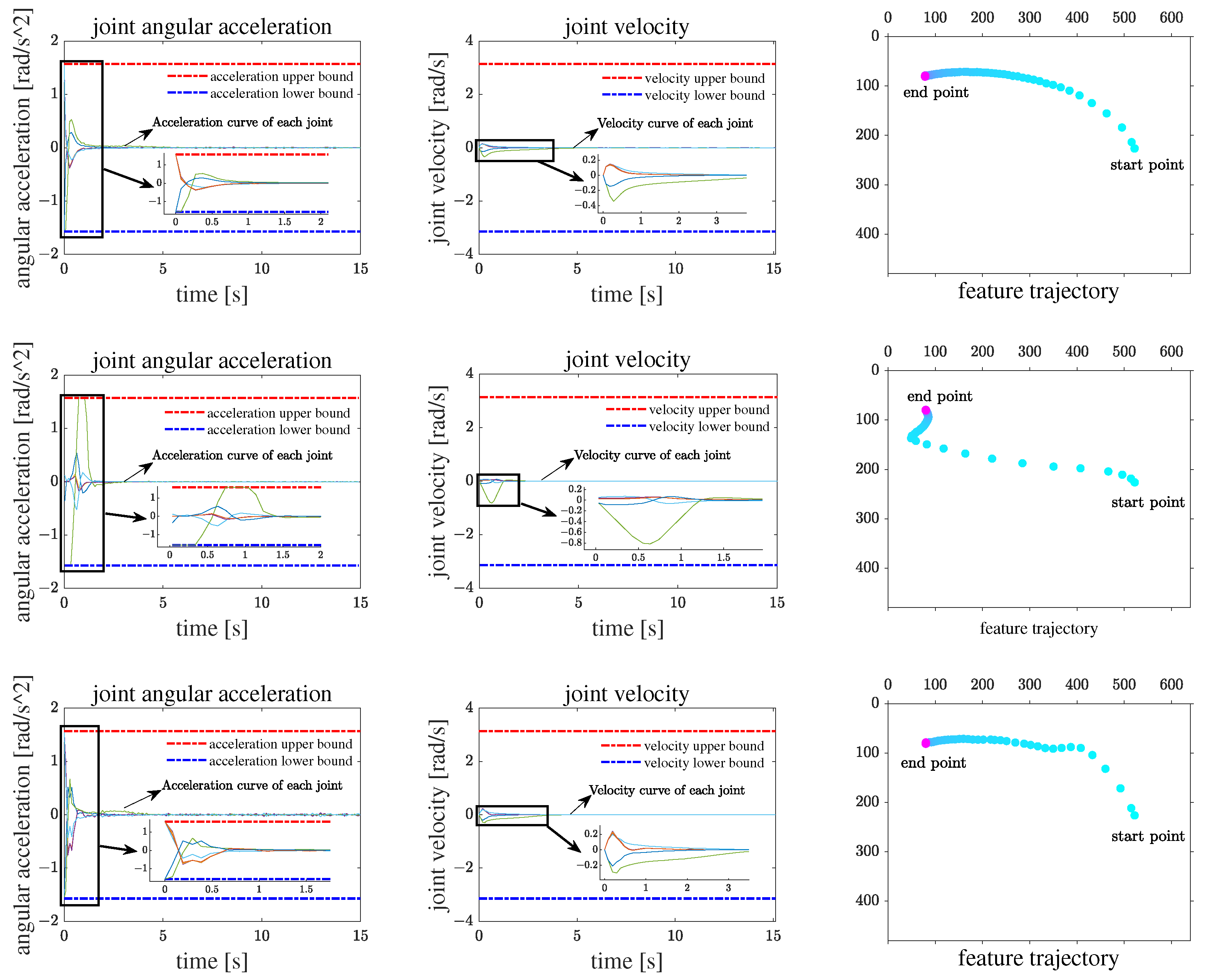
The first column in
Figure 19 shows the curves of the joint velocity in, it can be seen that the PID controller using the pseudoinverse algorithm tends to concentrate the joint motion on a certain joint, causing the acceleration of that joint to quickly reach its upper limit, thereby affecting the convergence speed of the error. However, in using the transposition method, it can be seen that, initially, all joints reach the maximum acceleration, and in the subsequent stage, the acceleration of all joints does not exceed the joint’s acceleration limit, and the speed distribution is relatively uniform. In comparison, this method is more conducive to the performance of the robotic arm.
The third column in
Figure 19 shows the trajectory of featrue point
at each sample time, it can be observed that the transposition method and inverse method exhibit different directions of fastest convergence. According to our understanding of the proposed framework, when the virtual power is transformed into the joint space, the inverse method guides the joint motion by calculating the velocity using kinematics, whereas the transposition method guides the joint motion by generating the target velocity through the admittance control based on virtual torque. In assuming that the propagated virtual power in both algorithms is the same, there is an inverse relationship between the joint velocity obtained by the inverse method and the virtual torque derived from the transposition method. Thus, it can be inferred that in the direction where the inverse method converges rapidly, the transposition method converges slower, whereas in the direction where the inverse method converges slowly, the transposition method exhibits a faster convergence.
Compared with the two transposed methods, it can be seen that the proposed method has a more aggressive speed adjustment and faster convergence rate when the error is small, which indicates the effectiveness of the proposed architecture for a visual servo controller design. Moreover, from the acceleration curve, it can be seen that in the first 0.1 s, the reference method experiences a maximum acceleration due to excessive output caused by a large error, which reaches the physical acceleration limit of the joint. Thanks to the design of the impedance controller, the algorithm based on the proposed framework can limit the output to prevent divergence in discrete systems when there is a large error, while amplifying the impact of errors on joints when there is a small error, thereby achieving a faster convergence speed in small errors. Furthermore, from the speed curve, it can be seen that while the joint with the fastest speed has almost the same speed as the reference method with our proposed method, the other joints rotate faster with our proposed method than with the reference method. As shown in the trajectory image on the right, our solution has a faster convergence speed while maintaining an equivalent overshoot compared to the reference method.