Structural Optimization Study on a Three-Degree-of-Freedom Piezoelectric Ultrasonic Transducer
Abstract
1. Introduction
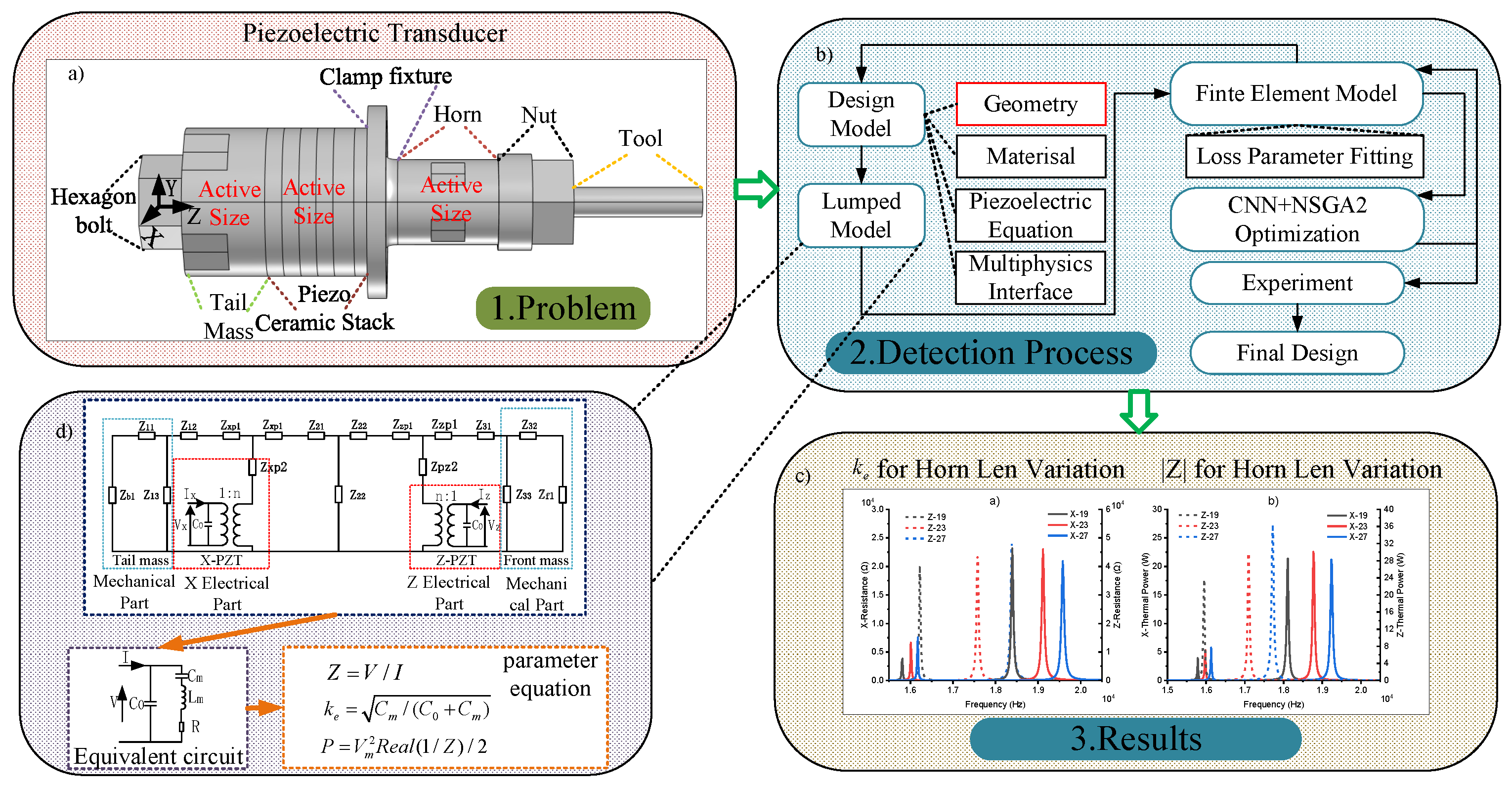
2. Geometry and Working Principle
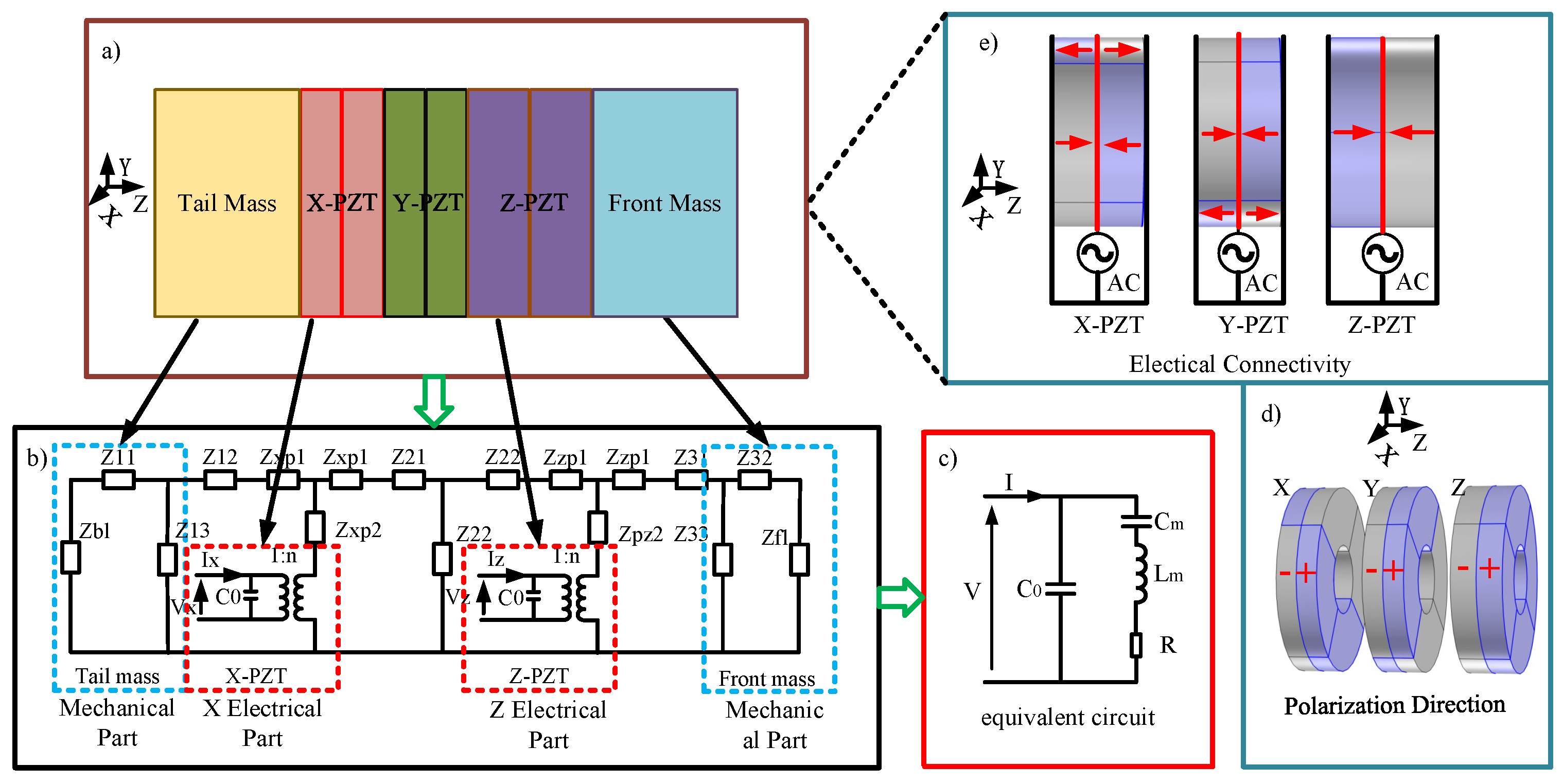
2.1. Working Principle
2.1.1. Piezoelectric Constitutive Equations
2.1.2. Lumped Model
3. Finite Element Model of the Transducer
3.1. Fitting of Mechanical Loss Parameters
3.2. Finite Element Model of Geometric Variations
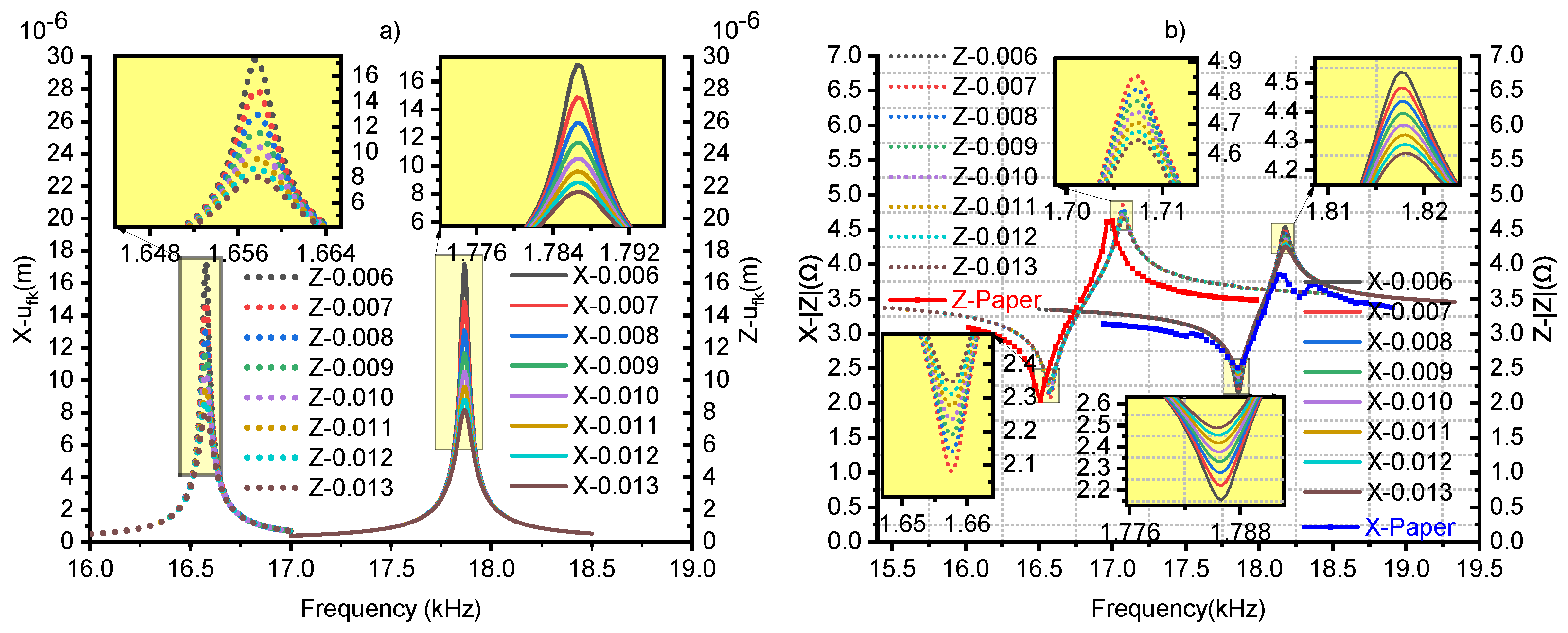
3.3. Simulation Calculation and Results
4. Geometric Structure Optimization Method
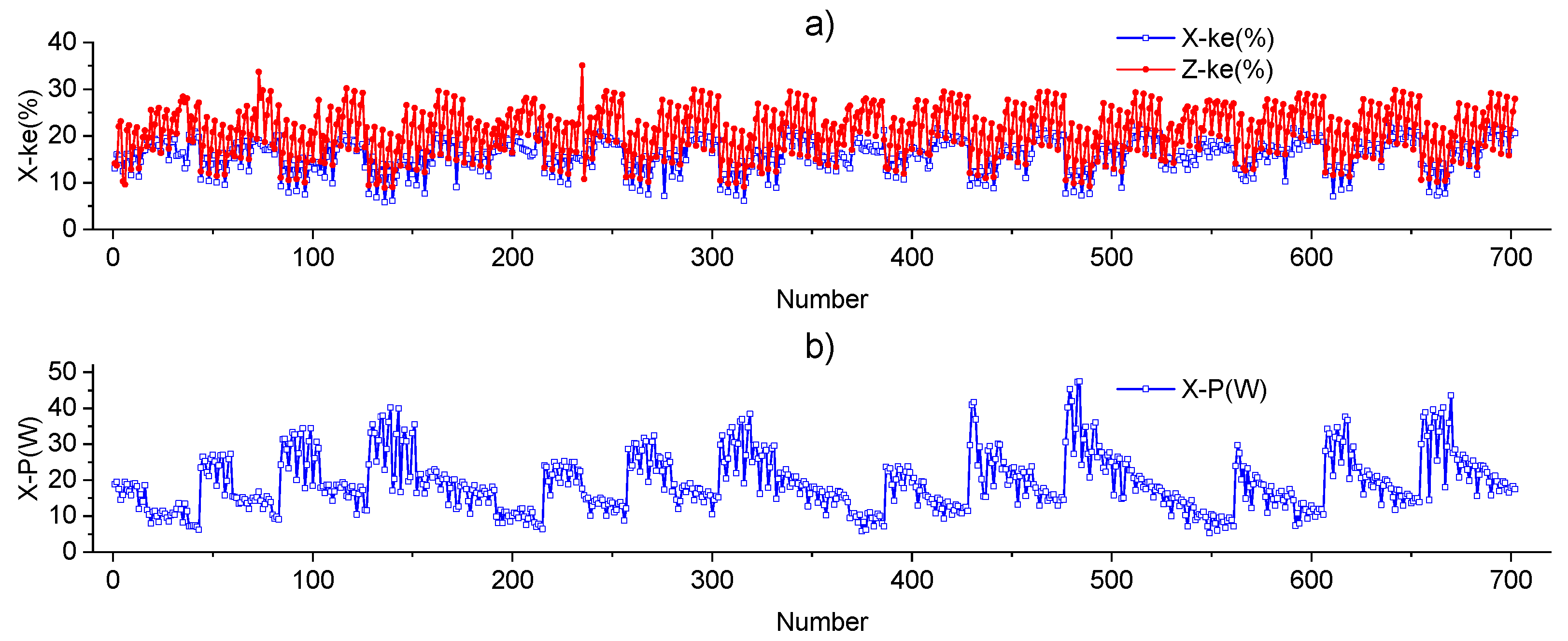
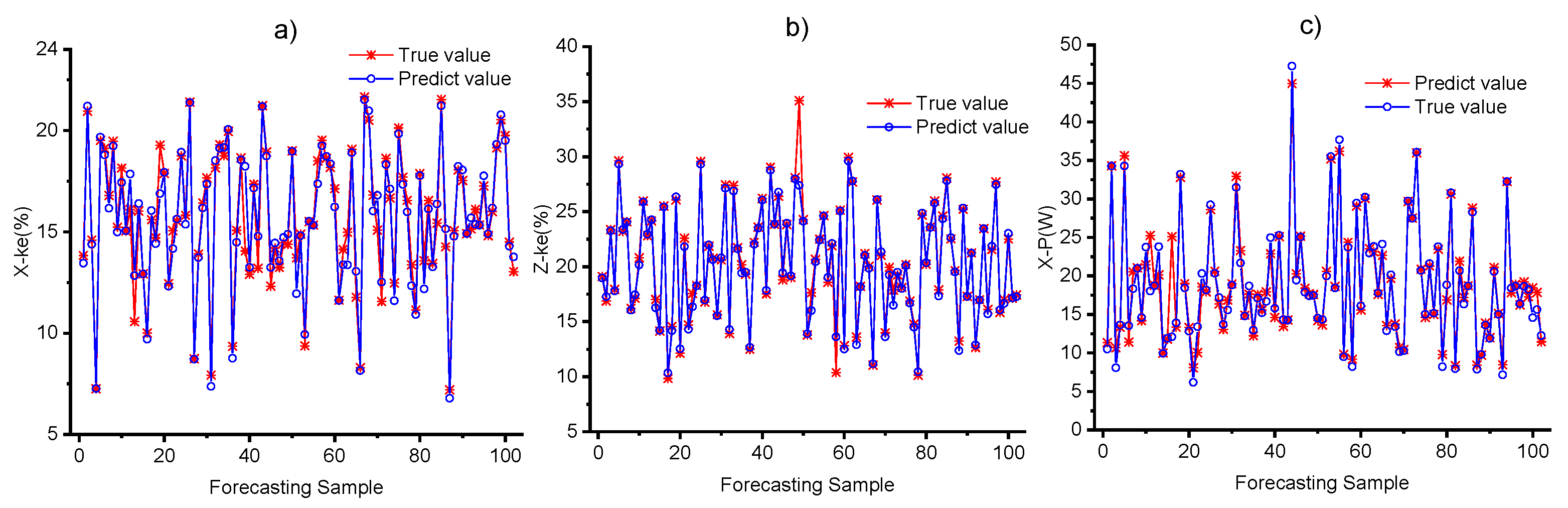
4.1. Indicator Parameter CNN Model
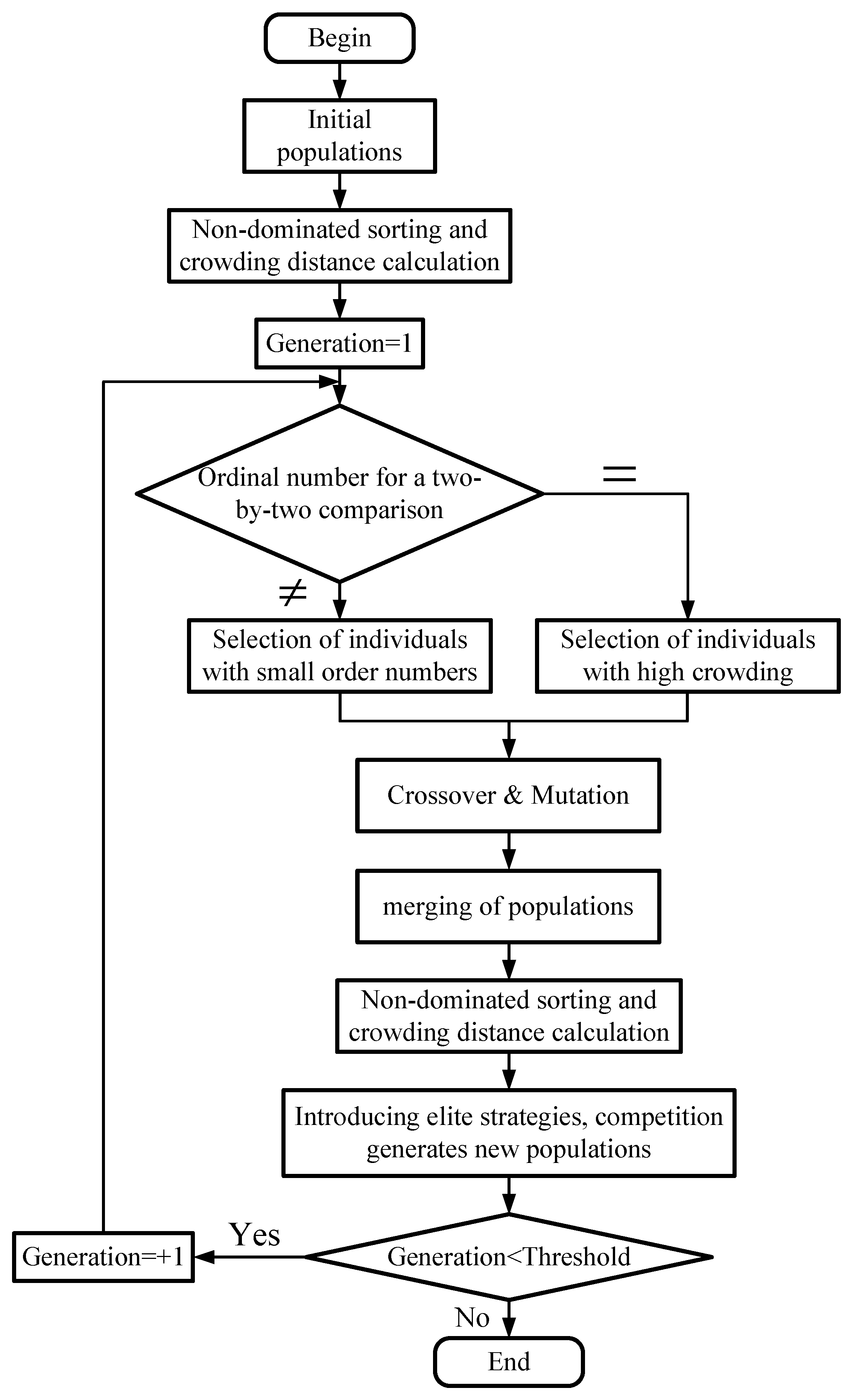
4.2. Based on NSHA2 Geometric Structure Optimization
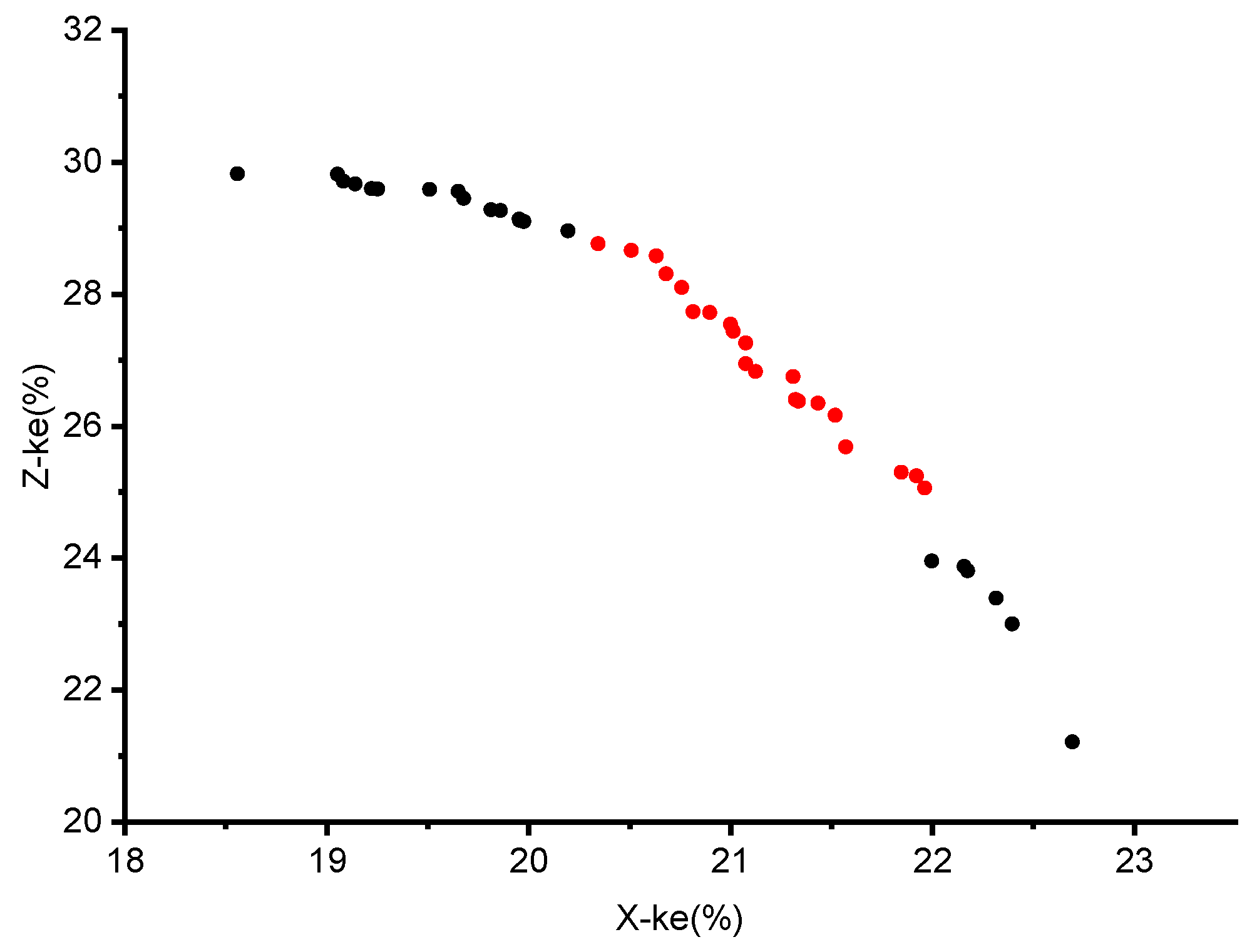
4.2.1. Optimization of Two Targets
4.2.2. Dual-Objective Optimization Decision
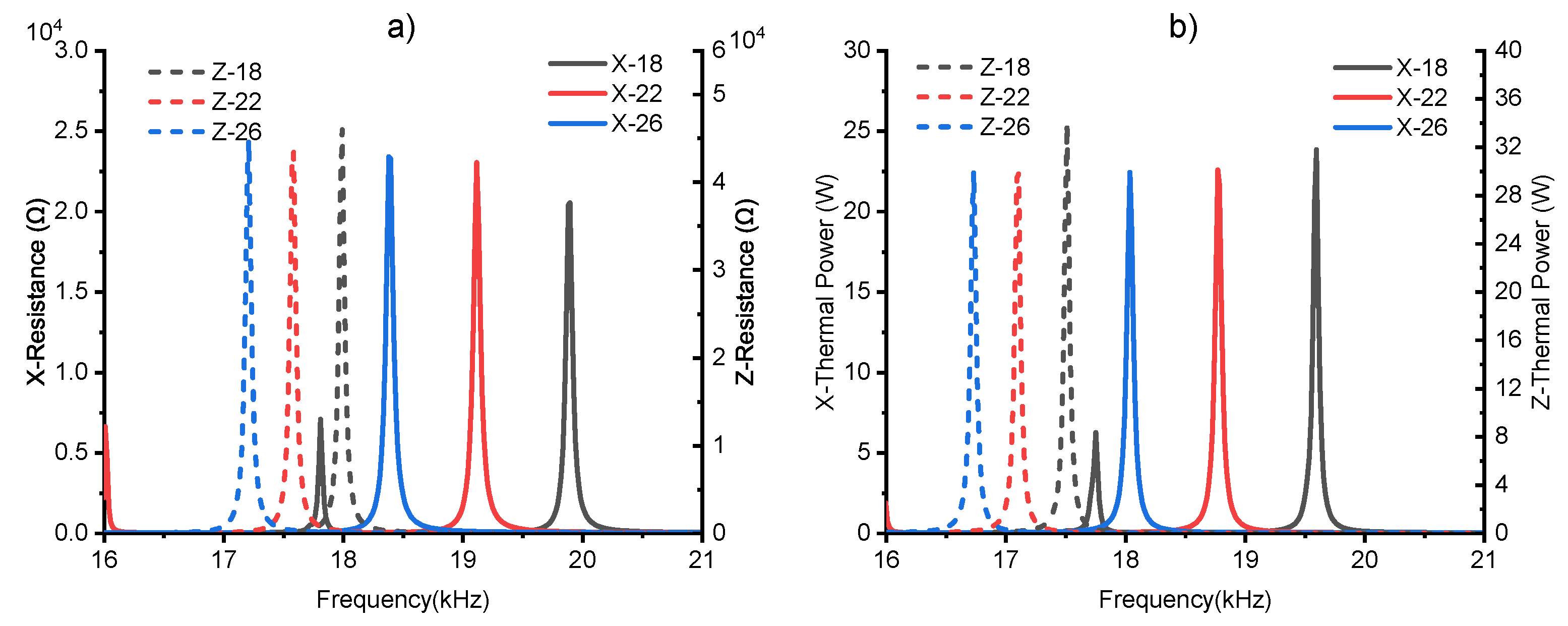
5. Finite Element Verification
5.1. Geometric Variation
5.1.1. Tail Mass Variation
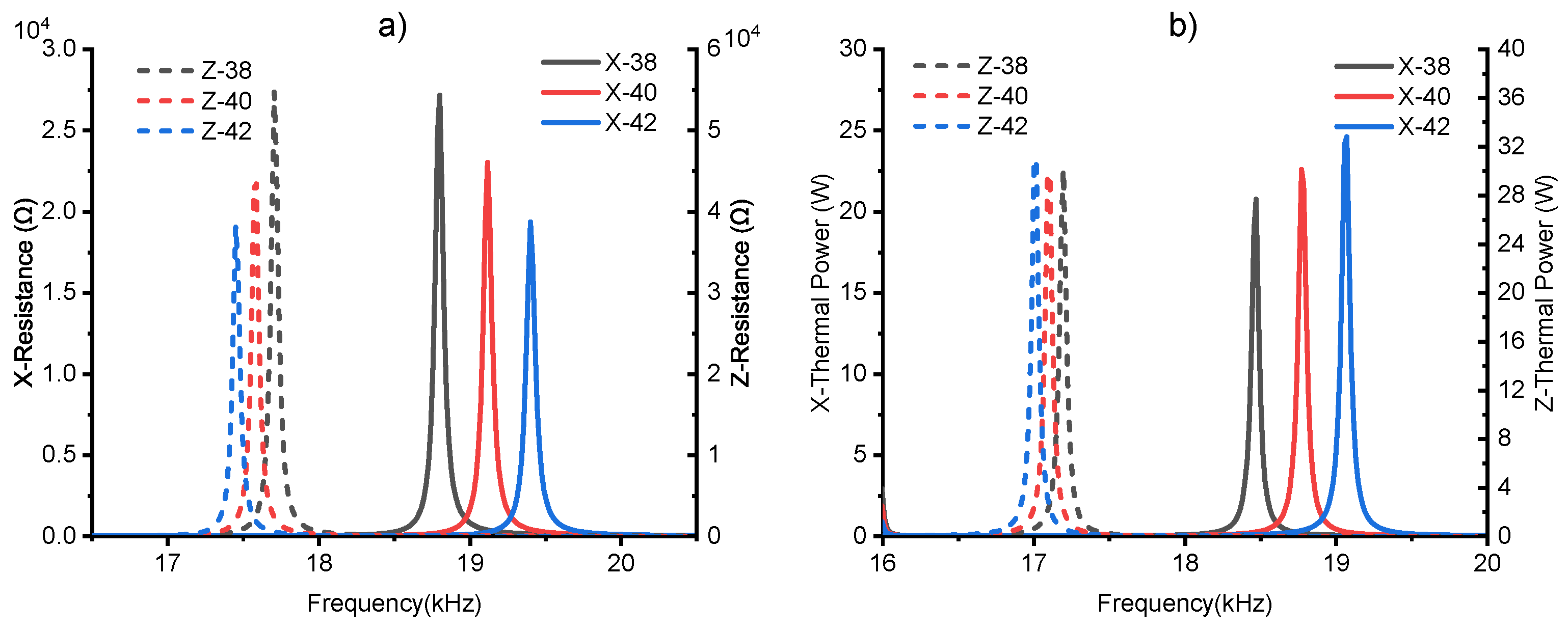
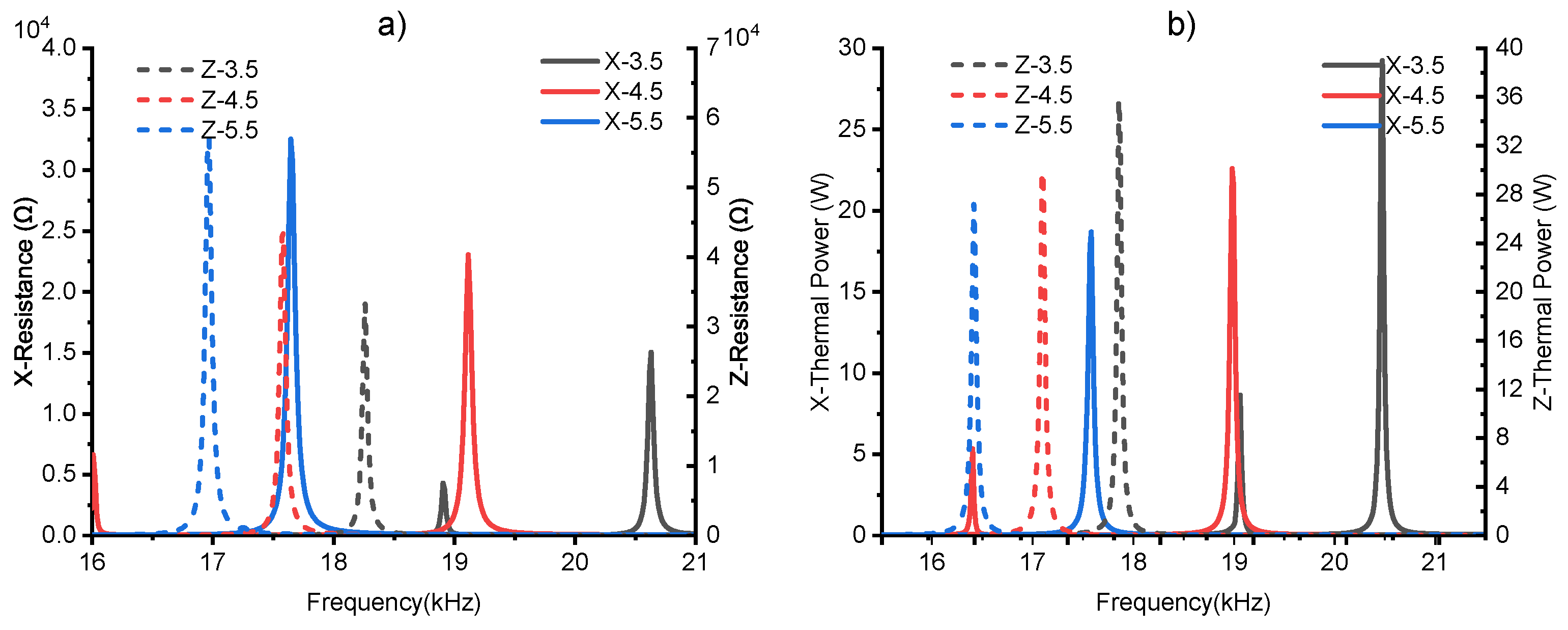
5.1.2. X-PZT Variation
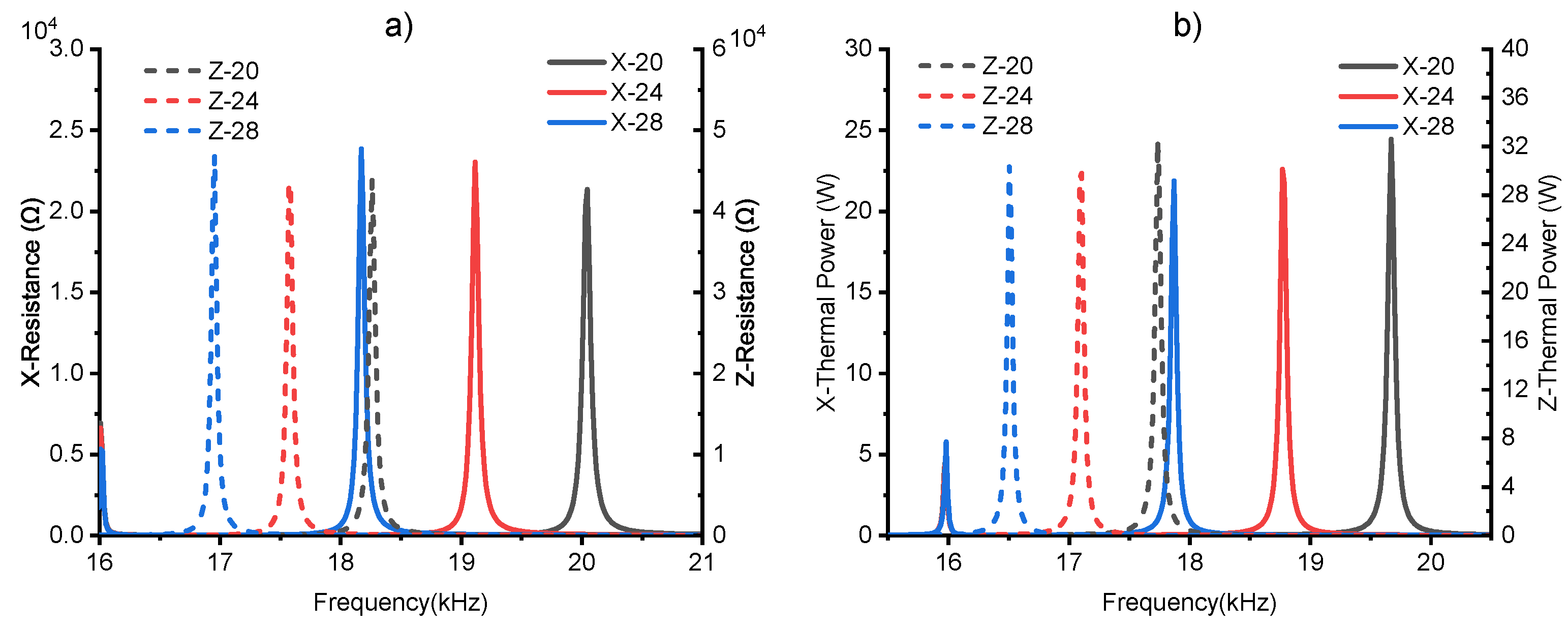
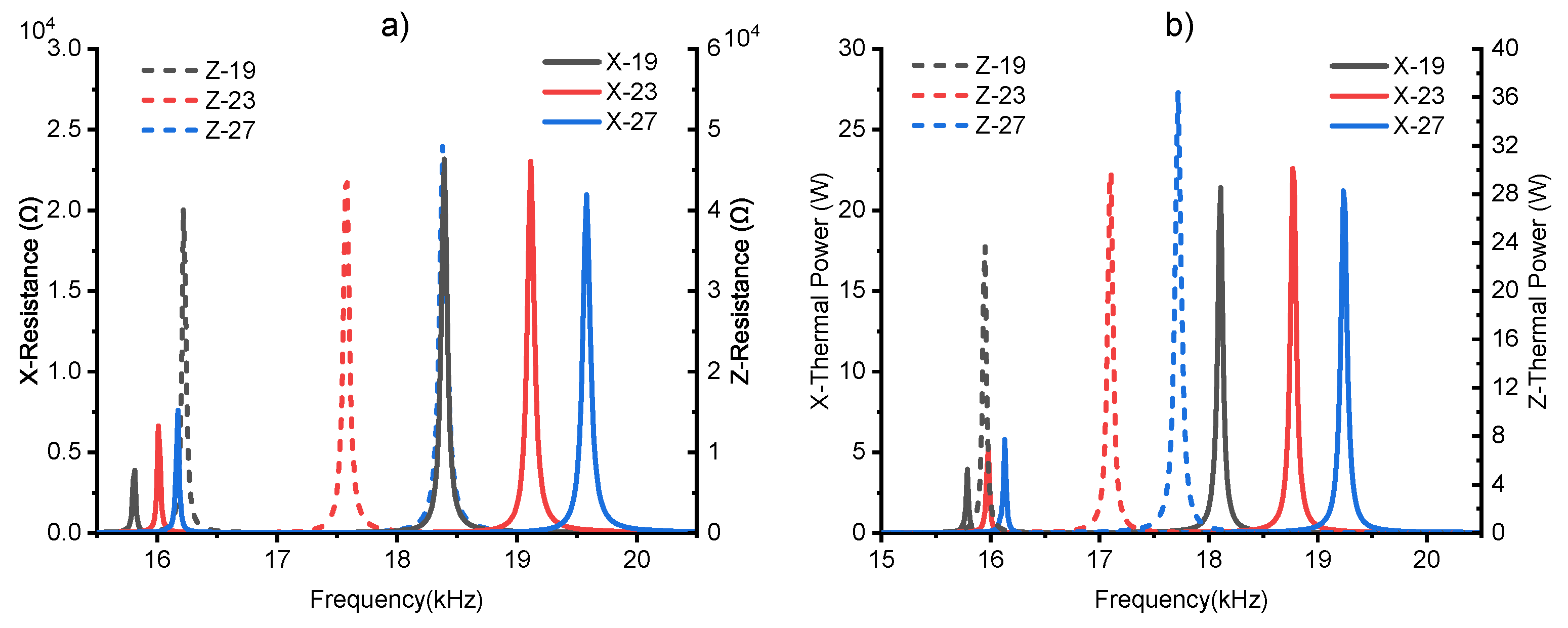
5.1.3. Horn Variation
5.2. Optimized Transducer Structure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Gao, J.; Altintas, Y. Development of a three-degree-of-freedom ultrasonic vibration tool holder for milling and drilling. IEEE ASME Trans. Mechatron. 2019, 24, 1238–1247. [Google Scholar] [CrossRef]
- Han, X.; Zhang, D. Effects of separating characteristics in ultrasonic elliptical vibration-assisted milling on cutting force, chip, and surface morphologies. Int. J. Adv. Manuf. Technol. 2020, 108, 3075–3084. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Geng, D.; Shao, Z.; Liu, Y.; Jiang, X. Effects of tool vibration on surface integrity in rotary ultrasonic elliptical end milling of Ti–6Al–4V. J. Alloys Compd. 2020, 821, 153266. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, X.; Han, X.; Zhang, D. Influence of parameter matching on performance of high-speed rotary ultrasonic elliptical vibration-assisted machining for side milling of titanium alloys. Int. J. Adv. Manuf. Technol. 2019, 101, 1333–1348. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Geng, D.; Liu, J.; Shao, Z.; Jiang, X. Surface and sub-surface analysis of rotary ultrasonic elliptical end milling of Ti-6Al-4V. Mater. Des. 2020, 191, 108658. [Google Scholar] [CrossRef]
- Du, P.; Han, L.; Qiu, X.; Chen, W.; Deng, J.; Liu, Y.; Zhang, J. Development of a high-precision piezoelectric ultrasonic milling tool using longitudinal-bending hybrid transducer. Int. J. Mech. Sci. 2022, 222, 107239. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, J.; Yu, H. Experimental study of tool wear and its effects on cutting process of ultrason-ic-assisted milling of Ti6Al4V. Int. J. Adv. Manuf. Technol. 2020, 108, 2917–2928. [Google Scholar] [CrossRef]
- Jing, L.; Niu, Q.; Yue, W.; Rong, J.; Gao, H.; Tang, S. Groove bottom material removal mechanism and machinability evaluation for longitudinal ultrasonic vibration–assisted milling of Al-50wt% Si alloy. Int. J. Adv. Manuf. Technol. 2023, 127, 365–380. [Google Scholar] [CrossRef]
- Xie, W.; Wang, X.; Liu, E.; Wang, J.; Tang, X.; Li, G.; Zhang, J.; Yang, L.; Chai, Y.; Zhao, B. Research on cutting force and surface integrity of TC18 titanium alloy by longitudinal ultrasonic vibration assisted milling. Int. J. Adv. Manuf. Technol. 2022, 119, 4745–4755. [Google Scholar] [CrossRef]
- Su, Y.; Li, L. Surface integrity of ultrasonic-assisted dry milling of SLM Ti6Al4V using polycrystalline diamond tool. Int. J. Adv. Manuf. Technol. 2022, 119, 5947–5956. [Google Scholar] [CrossRef]
- Zhang, J.-G.; Long, Z.-L.; Ma, W.-J.; Hu, G.-H.; Li, Y.-M. Electromechanical Dynamics Model of Ultrasonic Transducer in Ul-trasonic Machining Based on Equivalent Circuit Approach. Sensors 2019, 19, 1405. [Google Scholar] [CrossRef]
- Satpute, V.; Huo, D.; Hedley, J.; Elgendy, M. Design of a novel 2D ultrasonic transducer for 2D high-frequency vibration–assisted micro-machining. Int. J. Adv. Manuf. Technol. 2023, 126, 1035–1053. [Google Scholar] [CrossRef]
- Abdullah, A.; Malaki, M. On the damping of ultrasonic transducers’ components. Aerosp. Sci. Technol. 2013, 28, 31–39. [Google Scholar] [CrossRef]
- Shekhani, H.N.; Uchino, K. Characterization of mechanical loss in piezoelectric materials using tem-perature and vibration measurements. J. Amer. Ceram. Soc. 2014, 97, 2810–2814. [Google Scholar] [CrossRef]
- Wang, P.; Liu, J.; Chen, W.; Zhang, Q. Study on electromechanical coupling model of piezoelectric ultrasonic transducer. In Proceedings of the IEEE International Conference on Mechatronics & Automation, Takamatsu, Japan, 4–7 August 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Vasiljev, P.; Mazeika, D.; Borodinas, S. Minimizing heat generation in a piezoelectric Langevin transducer. In Proceedings of the 2012 IEEE International Ultrasonics Symposium, Dresden, Germany, 7–10 October 2012; pp. 2714–2717. [Google Scholar] [CrossRef]
- Visvanathan, K. Bulk Micromachined Piezoelectric Transducers for Ultrasonic Heating of Biological Tissues. Dissertations & Theses—Gradworks. 2011. Available online: https://deepblue.lib.umich.edu/handle/2027.42/86544 (accessed on 12 April 2024).
- Miyake, S.; Ozaki, R.; Hosaka, H.; Morita, T. High-power piezoelectric vibration model considering the interaction between nonlinear vibration and temperature increase. Ultrasonics 2019, 93, 93–101. [Google Scholar] [CrossRef]
- Wang, L.; Hofmann, V.; Bai, F.; Jin, J.; Liu, Y.; Twiefel, J. Systematic electromechanical transfer matrix model of a novel sand-wiched type flexural piezoelectric transducer. Int. J. Mech. Sci. 2018, 138, 229–243. [Google Scholar] [CrossRef]
- Lin, S. Study on the Langevin piezoelectric ceramic ultrasonic transducer of longitudinal–flexural compo-site vibrational mode. Ultrasonics 2006, 44, 109–114. [Google Scholar] [CrossRef]
- Zhou, G.P. The performance and design of ultrasonic vibration system for flexural mode. Ultrasonics 2000, 38, 979–984. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.P.; Zhang, Y.H.; Zhang, B.F. The complex-mode vibration of ultrasonic vibration systems. Ultrasonics 2002, 40, 907–911. [Google Scholar] [CrossRef]
- Zhang, Q.; Shi, S.; Chen, W. An electromechanical coupling model of a longitudinal vibration type piezoe-lectric ultrasonic transducer. Ceram. Int. 2015, 41, S638–S644. [Google Scholar] [CrossRef]
- Uchino, K.; Zheng, J.H.; Chen, Y.H.; Du, X.H.; Ryu, J.; Gao, Y.; Ural, S.; Priya, S.; Hirose, S. Loss mechanisms and high power piezoelectrics. In Frontiers of Ferroelectricity; Springer: Boston, MA, USA, 2006. [Google Scholar] [CrossRef]
- Shi, H.; Chen, Z.; Chen, X.; Liu, S.; Cao, W. Self-heating phenomenon of piezoelectric elements excited by a tone-burst electric field. Ultrasonics 2021, 117, 106562. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Uchino, K.; Jiang, C.; Jin, L.; Xu, Z.; Yuan, Y. Electromechanical Equivalent Circuit Model of a Piezoelectric Disk Considering Three Internal Losses. IEEE Access 2020, 8, 181848–181854. [Google Scholar] [CrossRef]
- Stewart, M.; Cain, M.G. Measurement and Modelling of Self-Heating in Piezoelectric Materials and Devices; Springer Series in Measurement Science and Technology; Springer: Dordrecht, The Netherlands, 2014; Volume 2. [Google Scholar] [CrossRef]
- Algueró, M.; Alemany, C.; Pardo, L.; González, A.M. Method for obtaining the full set of linear electric, mechanical, and electromechanical coefficients and all related losses of a piezoelectric ceramic. J. Am. Ceram. Soc. 2004, 87, 209. [Google Scholar] [CrossRef]
- Uchino, K.; Hirose, S. Loss mechanisms in piezoelectrics: How to measure different losses separately. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 307–321. [Google Scholar] [CrossRef] [PubMed]
- Mattiat, O.E.; Mason, W.P. Ultrasonic Transducer Materials. Phys. Today 1972, 25, 57–58. [Google Scholar] [CrossRef]
- Wu, Q.; Xie, D.-J.; Si, Y.; Zhang, Y.-D.; Li, L.; Zhao, Y.-X. Simulation analysis and experimental study of milling surface residual stress of Ti-10V-2Fe-3Al. J. Manuf. Process. 2018, 32, 530–537. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI. PPSN 2000; Schoenauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E., Merelo, J.J., Schwefell, H.-P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1917. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recogni-tion unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]

| Component | Parameter | Unit (mm) | Material | Speed of Sound (m/s) |
|---|---|---|---|---|
| Tail mass | Length | 22 | 304 steel | 5019 |
| Diameter | 40 | |||
| X-PZT | Length | 4.5 | PZT-8 | 3122 |
| Z-PZT | Length | 5.5 | ||
| Horn | Length | 27 | 304 steel | 5019 |
| Diameter | 23 | |||
| Tool | Length | 50 | WC-11 Co carbide | 6709 |
| Diameter | 8 | |||
| Hexagon bolt | Hgrip | 22 | 304 steel | 5019 |
| Hthic | 12 | |||
| Ndia | 15 | |||
| Blen | 57 | |||
| Clamp | Outer diameter | 52 | ||
| Inner diameter | 44 | |||
| Length | 5 |
| Properties | Name | PZT-8 | Unit | Property Group |
|---|---|---|---|---|
| Density | ρ | 7600 | kg/m3 | Basic |
| Flexibility matrix | SE | {1.15, −0.37, 1.15, −0.48, −0.48, 1.35, 0, 0, 0, 3.19, 0, 0, 0, 0, 3.19, 0, 0, 0, 0, 0, 3.04} | (1/Pa) | Strain–charge form |
| Coupling matrix | d | {0, 0, −9.7, 0, 0, −9.7, 0, 0, 22.5, 0, 33, 0, 33, 0, 0, 0, 0, 0} | (C/N) | Strain–charge form |
| Relative permittivity | {1290, 1290, 1000} | Strain–charge form |
| Geometry Parts | Tmaxerial | Poisson’s Ratio | Density (kg/m3) | Young’s Modulus (GPa) |
|---|---|---|---|---|
| Rear Cover, Clamp, Bolt, Horn | 304 steel | 0.29 | 7860 | 198 |
| Tool [31] | WC-11 Co | 0.25 | 14,440 | 650 |
| Variation | X-- Ture | X-- Predict | Error (%) | Z-- Ture | Z-- Predict | Error (%) | X-P- Ture | X-P- Predict | Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| (22, 40, 5.5, 20, 23) | 22.33 | 21.51 | 3.63 | 25.89 | 26.16 | 1.03 | 18.97 | 19.97 | 5.01 |
| (24, 42, 5.5, 20, 23) | 22.60 | 21.92 | 3.01 | 25.21 | 25.24 | 0.13 | 21.45 | 21.65 | 0.92 |
| (22, 42, 5.5, 25, 27) | 21.29 | 20.81 | 2.23 | 27.64 | 27.73 | 0.33 | 19.19 | 19.50 | 1.59 |
| (22, 42, 5.5, 20, 25) | 21.59 | 21.30 | 1.29 | 26.74 | 26.75 | 0.04 | 20.20 | 20.80 | 2.88 |
| (26, 42, 5.5, 25, 25) | 21.93 | 21.33 | 2.70 | 26.14 | 26.37 | 0.89 | 19.54 | 20.16 | 3.07 |
| (22, 42, 5.5, 20, 23) | 22.50 | 21.84 | 2.91 | 25.09 | 25.29 | 0.83 | 21.75 | 22.07 | 1.45 |
| (22, 42, 5.5, 25, 29) | 20.57 | 20.19 | 1.82 | 28.93 | 28.95 | 0.09 | 18.00 | 18.26 | 1.42 |
| Tail Mass Len Variation (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 24, 23) | 19,115 | 18,770 | 18.91 | 17,585 | 17,105 | 23.20 | 23.20 |
| (26, 40, 4.5, 24, 23) | 18,380 | 18,035 | 19.28 | 17,210 | 16,730 | 23.40 | 23.45 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
| Tail Mass Dis Variation (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 24, 23) | 19,115 | 18,770 | 18.91 | 17,585 | 17,105 | 23.20 | 22.59 |
| (22, 42, 4.5, 24, 23) | 19,400 | 19,070 | 18.36 | 17,450 | 17,015 | 22.19 | 20.76 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
| X-PZT Len Variation (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 24, 23) | 19,115 | 18,770 | 18.91 | 17,585 | 17,105 | 23.20 | 22.59 |
| (22, 40, 5.5, 24, 23) | 17,645 | 17,255 | 20.91 | 16,970 | 16,415 | 25.36 | 18.68 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
| Horn Len Variation (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 24, 23) | 19,115 | 18,770 | 18.91 | 17,585 | 17,105 | 23.20 | 22.59 |
| (22, 40, 4.5, 28, 23) | 18,170 | 17,870 | 18.09 | 16,955 | 16,505 | 22.88 | 21.86 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
| Horn Dis Variation (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 24, 23) | 19,115 | 18,770 | 18.91 | 17,585 | 17,105 | 23.20 | 22.59 |
| (22, 40, 4.5, 24, 27) | 19,580 | 19,235 | 18.68 | 16,220 | 15,950 | 18.17 | 21.20 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
| Optimized Structure (mm) | X- (Hz) | X- (Hz) | X- (%) | Z- (Hz) | Z- (Hz) | Z- (%) | X-P (W) |
|---|---|---|---|---|---|---|---|
| (22, 40, 4.5, 27, 23) | 18,169 | 17,804 | 19.94 | 17,038 | 16,539 | 24.02 | 20.38 |
| (22, 40, 5.5, 20, 23) | 17,959 | 17,002 | 22.33 | 18,424 | 17,602 | 25.89 | 18.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, Z.; Wu, D.; Chen, Y.; Hu, F.; Guo, C.; Tang, L. Structural Optimization Study on a Three-Degree-of-Freedom Piezoelectric Ultrasonic Transducer. Actuators 2024, 13, 177. https://doi.org/10.3390/act13050177
Wu Z, Zhang Z, Wu D, Chen Y, Hu F, Guo C, Tang L. Structural Optimization Study on a Three-Degree-of-Freedom Piezoelectric Ultrasonic Transducer. Actuators. 2024; 13(5):177. https://doi.org/10.3390/act13050177
Chicago/Turabian StyleWu, Zhizhong, Zhao Zhang, Deguang Wu, Yuanhang Chen, Fan Hu, Chenxin Guo, and Lijun Tang. 2024. "Structural Optimization Study on a Three-Degree-of-Freedom Piezoelectric Ultrasonic Transducer" Actuators 13, no. 5: 177. https://doi.org/10.3390/act13050177
APA StyleWu, Z., Zhang, Z., Wu, D., Chen, Y., Hu, F., Guo, C., & Tang, L. (2024). Structural Optimization Study on a Three-Degree-of-Freedom Piezoelectric Ultrasonic Transducer. Actuators, 13(5), 177. https://doi.org/10.3390/act13050177






