Synchronization Control with Dynamics Compensation for Three-Axis Parallel Motion Platform
Abstract
1. Introduction
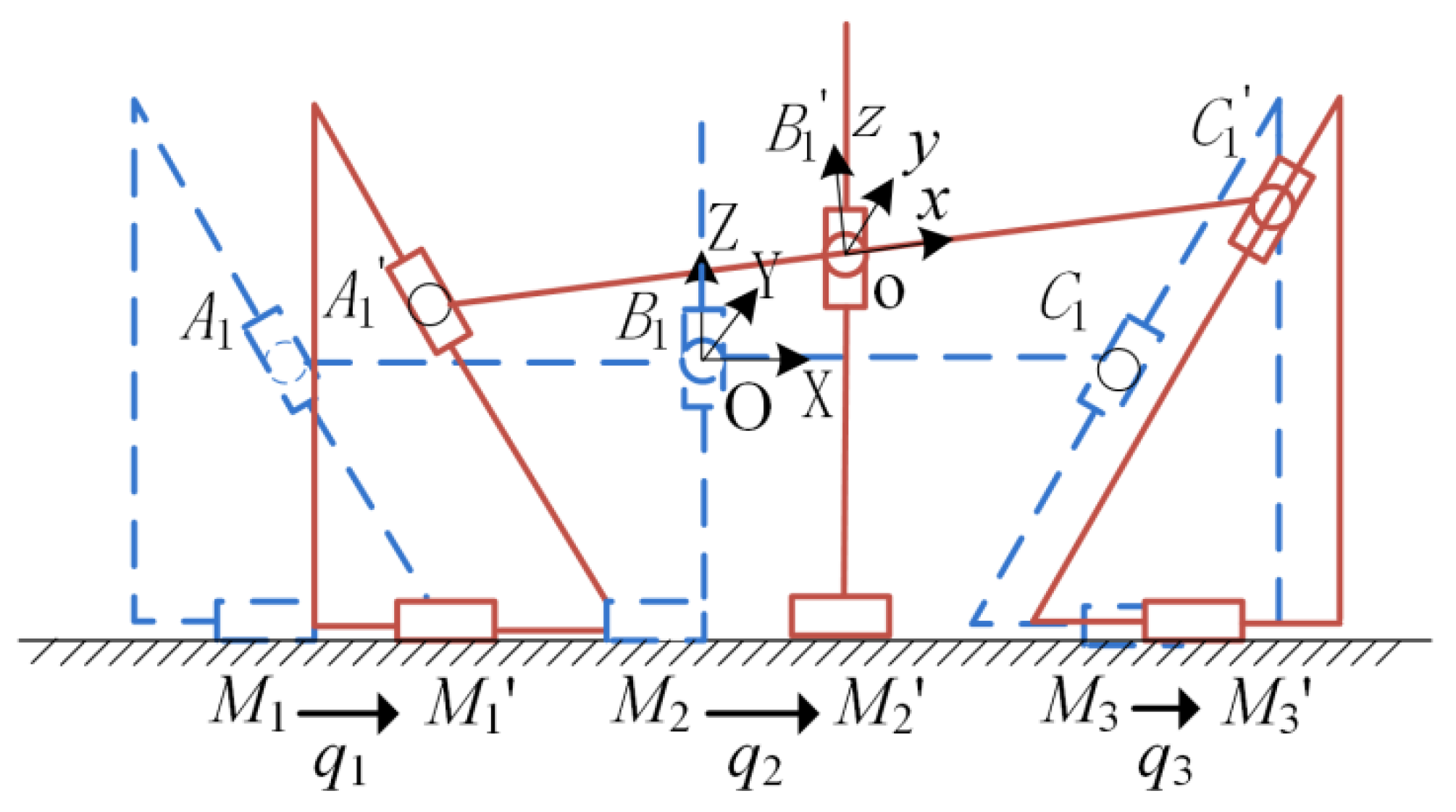
2. Kinematic Modeling of the TAPMP
2.1. Structural Description
2.2. Kinematic Modeling
3. Dynamic Modeling of the TAPMP
3.1. Moving Platform Dynamics
3.2. Auxiliary Block Dynamics
3.3. Overall Dynamics of the TAPMP
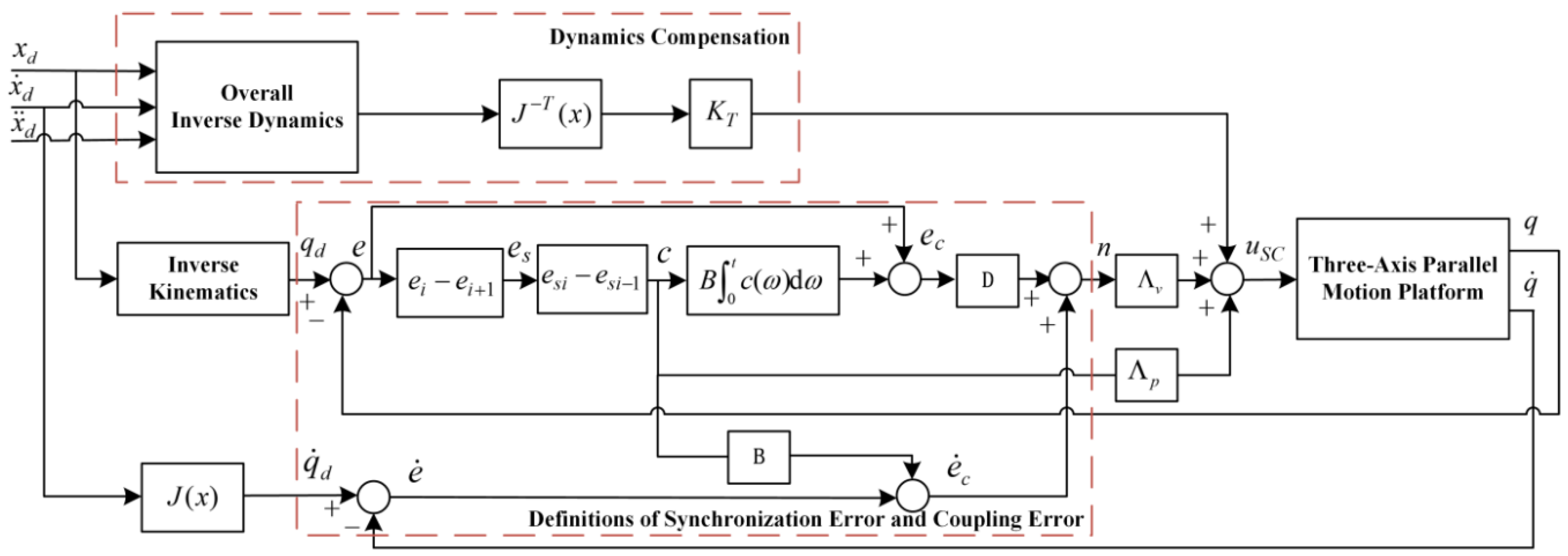
4. Synchronization Controller with Dynamics Compensation
4.1. Definitions of Synchronization Error and Coupling Error
4.2. Formulation of Synchronization Controller with Dynamics Compensation
4.3. Stability Analysis
5. Simulation Analysis of the SC–DC
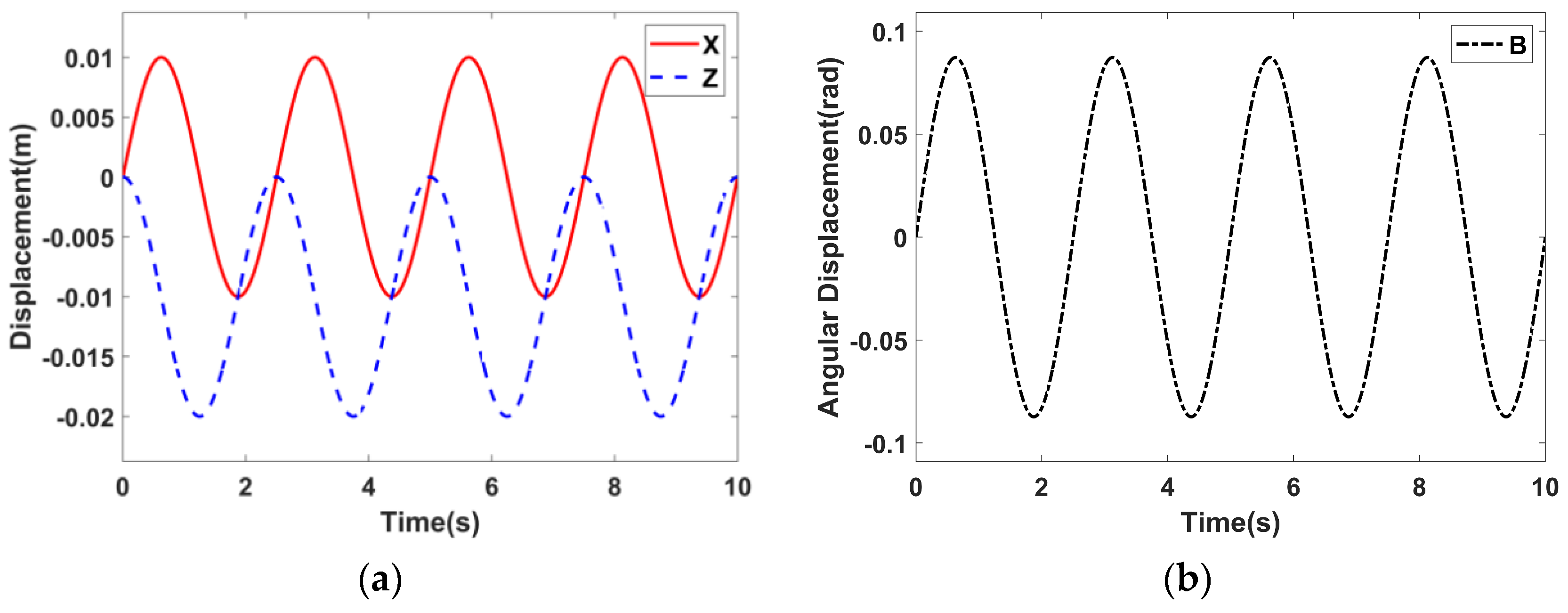
5.1. Simulation Setup
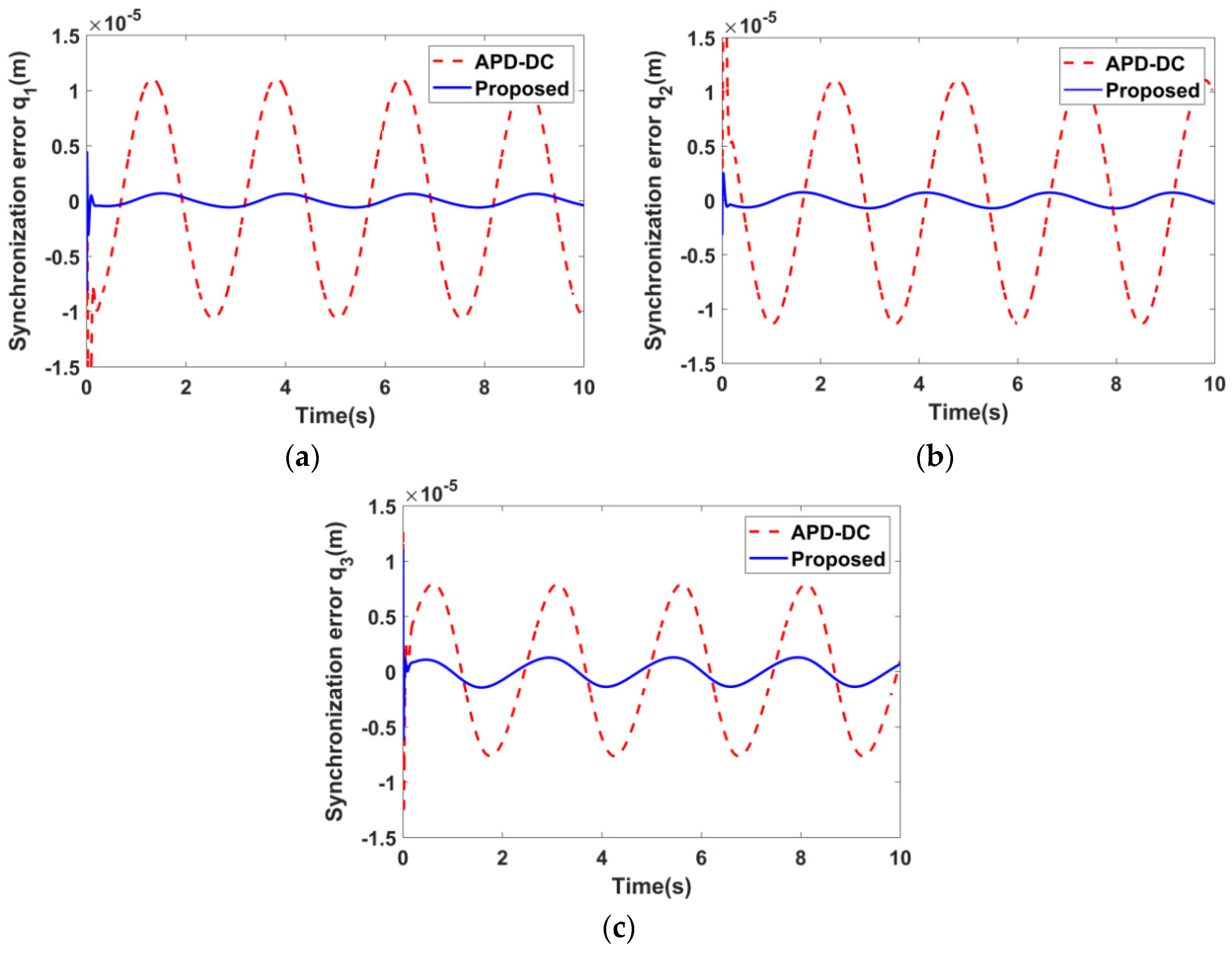
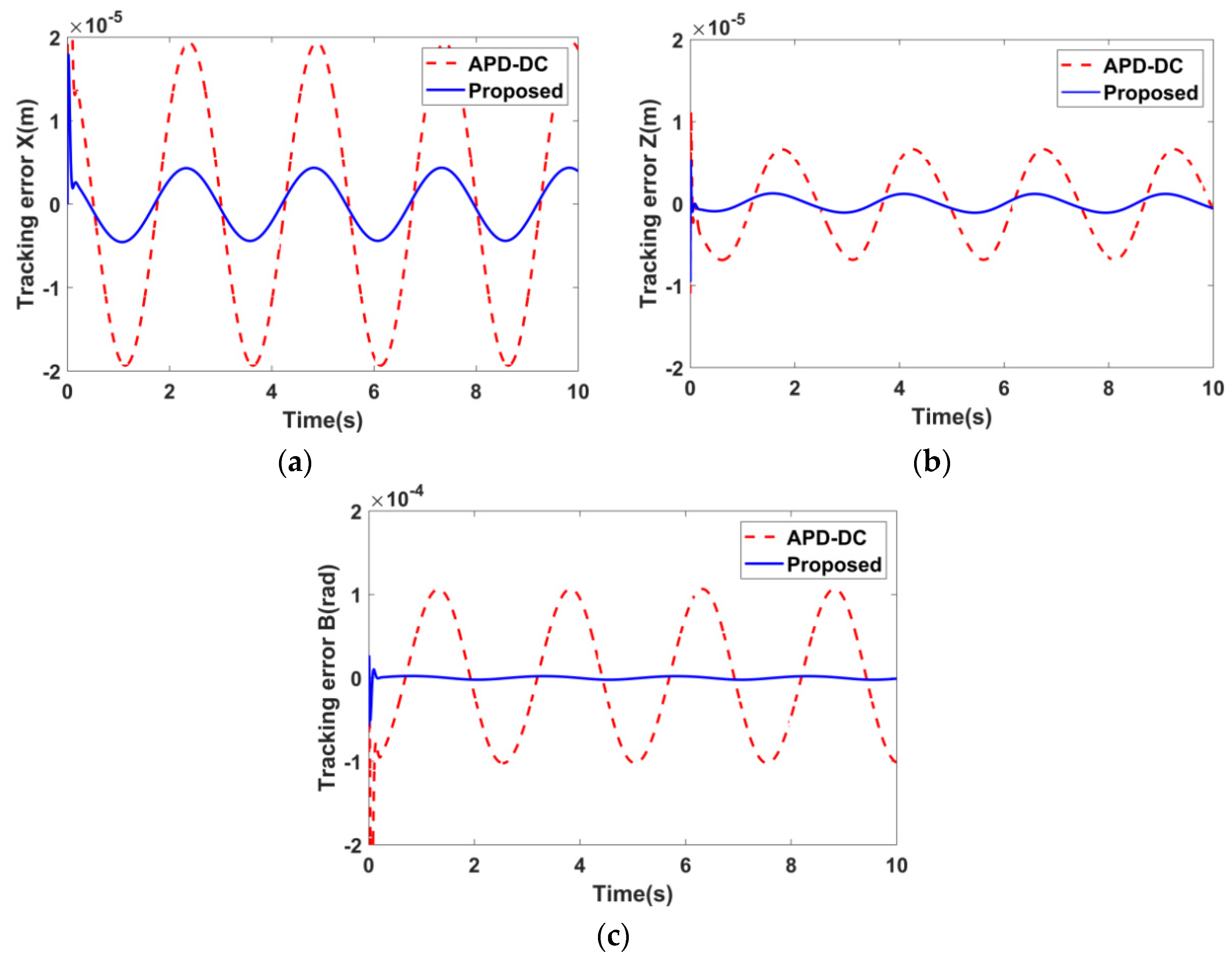
5.2. Simulation Results
6. Experimental Verification of the SC–DC
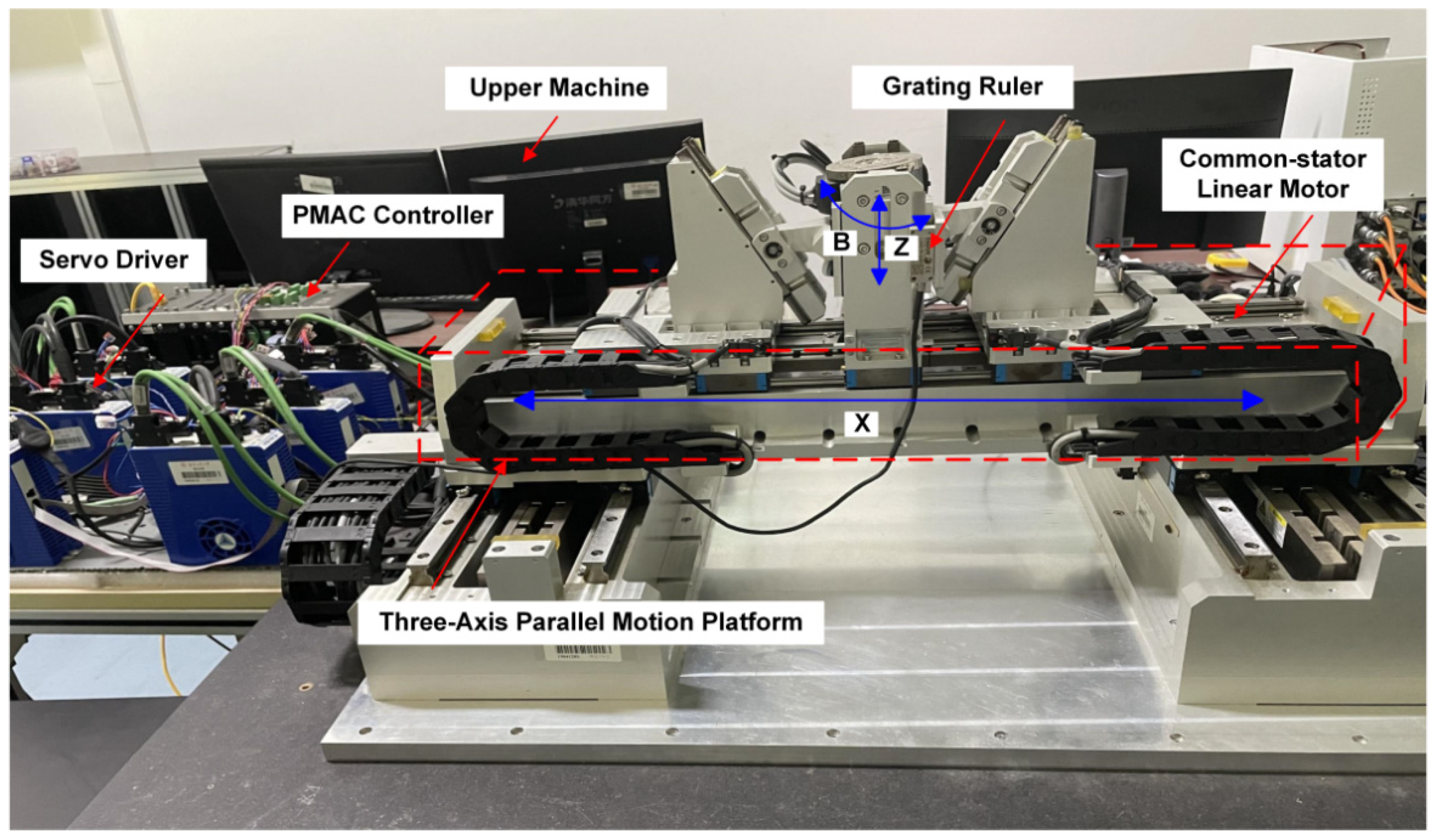
6.1. Experimental Setup
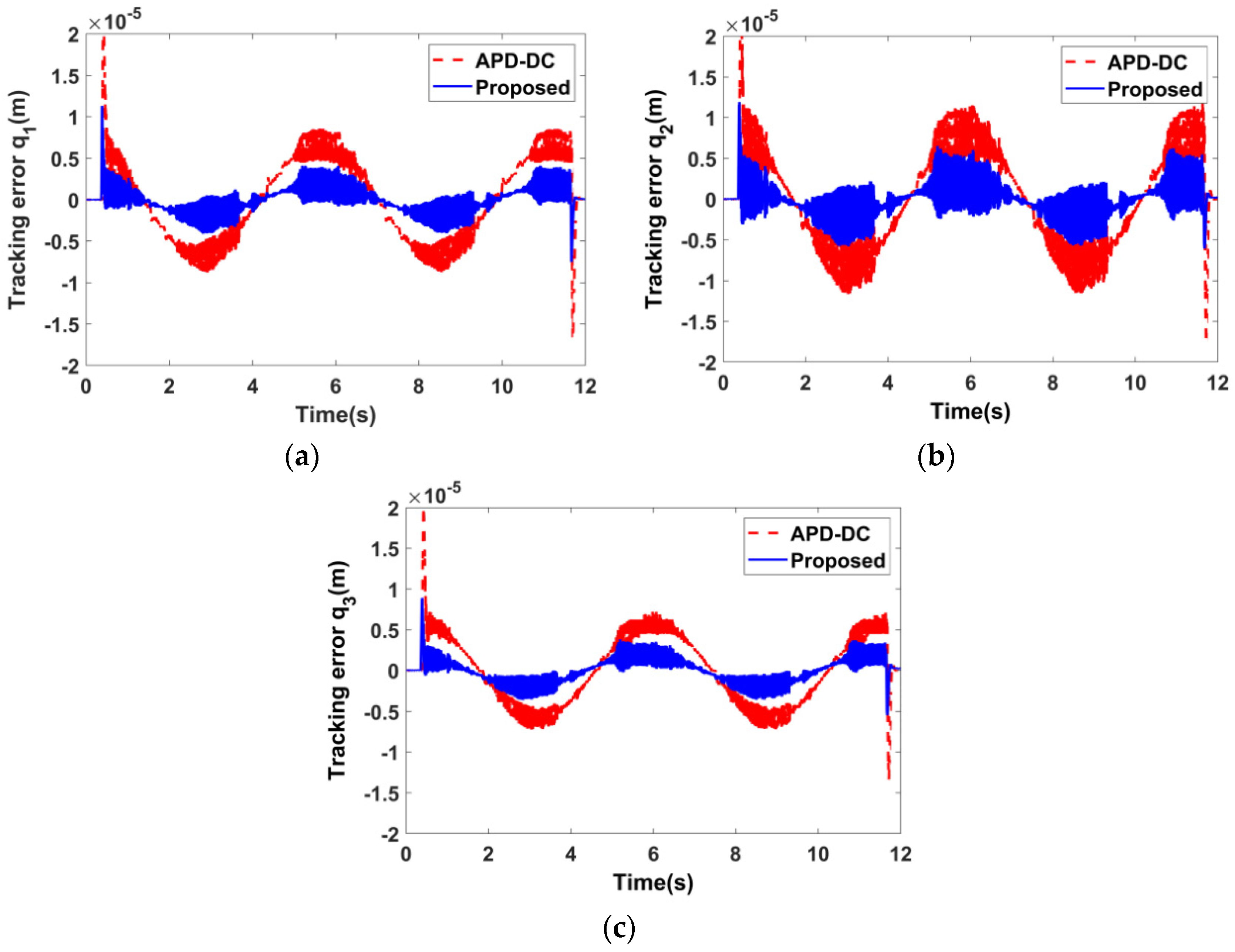
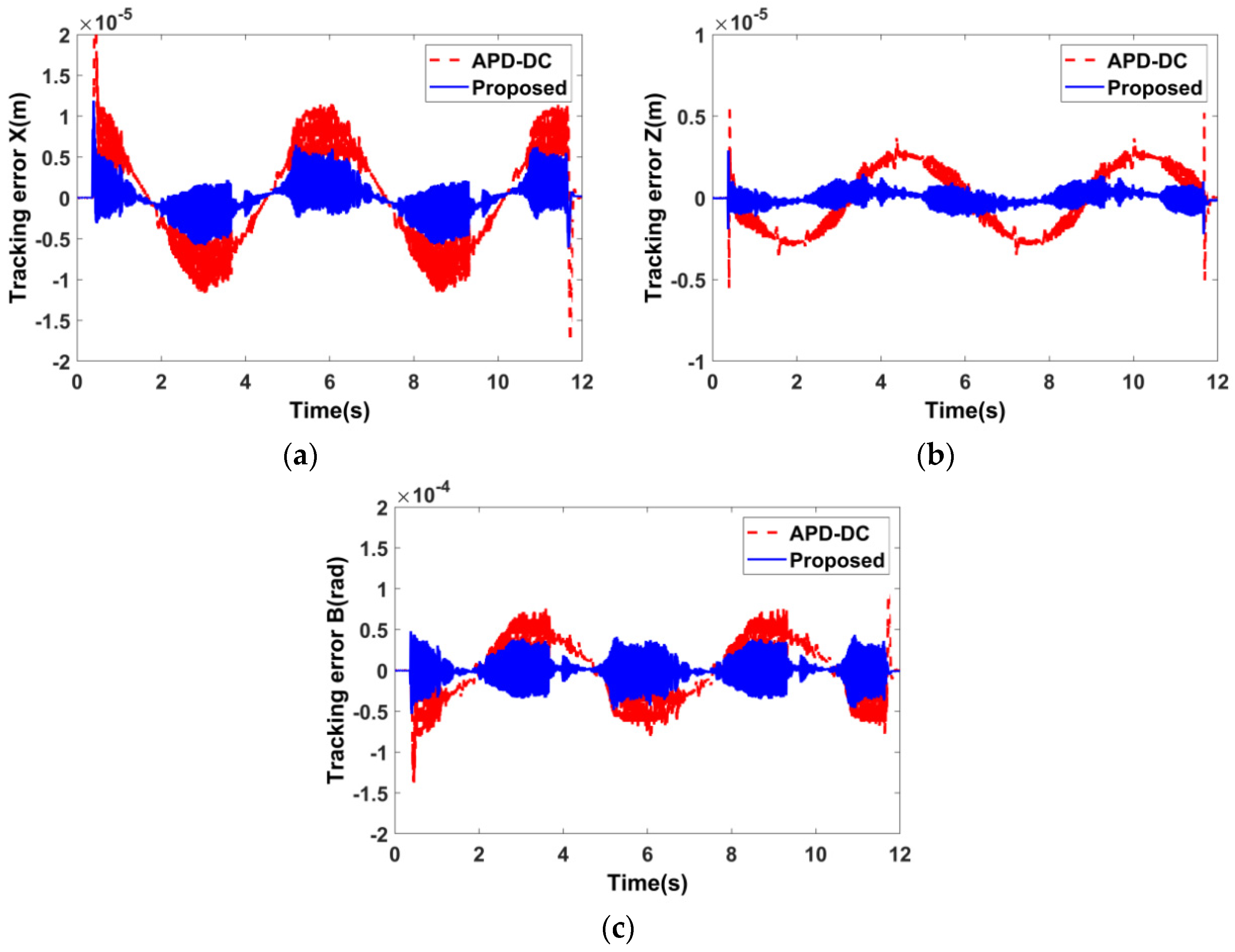
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosyid, A.; Stefanini, C.; El-Khasawneh, B. A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures. Robotics 2022, 11, 110. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Shen, H.P.; You, J.J.; Yang, T.L. Inverse Dynamics of A 3-DOF Parallel Mechanism Based on Analytical Forward Kinematics. Chin. J. Mech. Eng. 2022, 35, 212–221. [Google Scholar] [CrossRef]
- Shen, H.P.; Zhao, Y.N.; Li, J.; Wu, G.L.; Chablat, D. A novel partially-decoupled translational parallel manipulator with symbolic kinematics, singularity identification and workspace determination. Mech. Mach. Theory 2021, 164, 104388. [Google Scholar] [CrossRef]
- Luo, Y.H.; Gao, J.; Zhang, L.Y.; Chen, D.S.; Chen, X. Kinematic calibration of a symmetric parallel kinematic machine using sensitivity-based iterative planning. Precis. Eng. 2022, 77, 164–178. [Google Scholar] [CrossRef]
- Ye, H.; Wang, D.; Wu, J.; Yue, Y.; Zhou, Y.L. Forward and inverse kinematics of a 5-DOF hybrid robot for composite material machining. Robot. Comput. Integr. Manuf. 2020, 65, 101961. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.S.; You, Z. A comparison study on the dynamics of planar 3-DOF 4-RRR, 3-RRR and 2-RRR parallel manipulators. Robot. Comput. Integr. Manuf. 2011, 27, 150–156. [Google Scholar] [CrossRef]
- Wang, G.L.; Wang, Y.; Lv, B.R.; Ma, R.P.; Liu, L. Research on a New Type of Rigid-Flexible Coupling 3-DOF Micro-Positioning Platform. Micromachines 2020, 11, 1015. [Google Scholar] [CrossRef] [PubMed]
- Bettega, J.; Richiedei, D.; Trevisani, A. Using Pose-Dependent Model Predictive Control for Path Tracking with Bounded Tensions in a 3-DOF Spatial Cable Suspended Parallel Robot. Machines 2022, 10, 453. [Google Scholar] [CrossRef]
- Wang, H.; Ren, W.; Cheah, C.C.; Xie, Y.; Lyu, S. Dynamic Modularity Approach to Adaptive Control of Robotic Systems with Closed Architecture. IEEE Trans. Autom. Control 2020, 65, 2760–2767. [Google Scholar] [CrossRef]
- Harandi, M.R.J.; Khalilpour, S.A.; Taghirad, H.D.; Romero, J.G. Adaptive control of parallel robots with uncertain kinematics and dynamics. Mech. Syst. Signal Process. 2021, 157, 107693. [Google Scholar] [CrossRef]
- Azarfar, A.; Azarfar, B.; Vahedi, M. Self-Tuning Fuzzy Task Space Controller for Puma 560 Robot. J. Electr. Eng. Technol. 2020, 16, 579–589. [Google Scholar] [CrossRef]
- Khalilpour, S.A.; Khorrambakht, R.; Taghirad, H.D.; Cardou, P. Robust cascade control of a deployable cable-driven robot. Mech. Syst. Signal Process. 2019, 127, 513–530. [Google Scholar] [CrossRef]
- Zi, B.; Duan, B.Y.; Du, J.L.; Bao, H. Dynamic modeling and active control of a cable-suspended parallel robot. Mechatronics 2008, 18, 1–12. [Google Scholar] [CrossRef]
- Zhu, Y.K.; Qiao, J.Z.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control With Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Fonseca, M.D.P.A.; Adorno, B.V.; Fraisse, P. Coupled Task-Space Admittance Controller Using Dual Quaternion Logarithmic Mapping. IEEE Robot. Autom. Lett. 2020, 5, 6057–6064. [Google Scholar] [CrossRef]
- Altan, A.; Hacioglu, R. Model predictive control of three-axis gimbal system mounted on UAV for real-time target tracking under external disturbances. Mech. Syst. Signal Process. 2020, 138, 106548. [Google Scholar] [CrossRef]
- Zhou, S.L.; Sun, J.; Gao, F. Influence of flexible spherical joints parameters on accuracy of the six-axis force/torque sensor with three-three orthogonal parallel mechanism. Mech. Mach. Theory 2020, 145, 103697. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Caverly, R.J. Cable-Driven Parallel Robot Pose Estimation Using Extended Kalman Filtering with Inertial Payload Measurements. IEEE Robot. Autom. Lett. 2021, 6, 3615–3622. [Google Scholar] [CrossRef]
- Bayani, H.; Masouleh, M.T.; Kalhor, A. An experimental study on the vision-based control and identification of planar cable-driven parallel robots. Robot. Auton. Syst. 2016, 75, 187–202. [Google Scholar] [CrossRef]
- Li, P.C.; Shu, T.T.; Xie, W.F.; Tian, W. Dynamic Visual Servoing of A 6-RSS Parallel Robot Based on Optical CMM. J. Intell. Robot. Syst. 2021, 102, 40. [Google Scholar] [CrossRef]
- Merlet, J.P. Simulation of Discrete-Time Controlled Cable-Driven Parallel Robots on a Trajectory. IEEE Trans. Robot. 2017, 33, 675–688. [Google Scholar] [CrossRef]
- Dong, C.L.; Liu, H.T.; Xiao, J.L.; Huang, T. Dynamic modeling and design of a 5-DOF hybrid robot for machining. Mech. Mach. Theory 2021, 165, 104438. [Google Scholar] [CrossRef]
- Bodie, K.; Tognon, M.; Siegwart, R. Dynamic End Effector Tracking with an Omnidirectional Parallel Aerial Manipulator. IEEE Robot. Autom. Lett. 2021, 6, 8165–8172. [Google Scholar] [CrossRef]
- Ji, H.; Shang, W.W.; Cong, S. Adaptive Synchronization Control of Cable-Driven Parallel Robots with Uncertain Kinematics and Dynamics. IEEE Trans. Ind. Electron. 2021, 68, 8444–8454. [Google Scholar] [CrossRef]
- Fang, S.; Franitza, D.; Torlo, M.; Bekes, F.; Hiller, M. Motion control of a tendon-based parallel manipulator using optimal tension distribution. IEEE/ASME Trans. Mechatron. 2004, 9, 561–568. [Google Scholar] [CrossRef]
- Hosseini, M.I.; Khalilpour, S.A.; Taghirad, H.D. Practical robust nonlinear PD controller for cable-driven parallel manipulators. Nonlinear Dyn. 2021, 106, 405–424. [Google Scholar] [CrossRef]
- Feng, C.L.; Chen, W.D.; Shao, M.Q.; Ni, S.H. Trajectory Tracking and Adaptive Fuzzy Vibration Control of Multilink Space Manipulators with Experimental Validation. Actuators 2023, 12, 138. [Google Scholar] [CrossRef]
- Yang, H.; Wu, S.; Huang, G. Fuzzy neural network control for mechanical arm based on adaptive friction compensation. J. Vibroeng. 2020, 22, 1099–1112. [Google Scholar] [CrossRef]
- Escorcia-Hernandez, J.M.; Aguilar-Sierra, H.; Aguilar-Mejia, O.; Chemori, A.; Arroyo-Nunez, J.H. A New Adaptive RISE Feedforward Approach based on Associative Memory Neural Networks for the Control of PKMs. J. Intell. Robot. Syst. 2020, 100, 827–847. [Google Scholar] [CrossRef]
- Zhang, B.B.; Wu, J.; Wang, L.P.; Yu, Z.Y. Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot. Comput. Integr. Manuf. 2020, 63, 101923. [Google Scholar] [CrossRef]
- Yen, P.L.; Lai, C.C. Dynamic modeling and control of a 3-DOF Cartesian parallel manipulator. Mechatronics 2009, 19, 390–398. [Google Scholar] [CrossRef]
- Xie, Z.H.; Xie, F.G.; Liu, X.J.; Wang, J.S.; Mei, B. Tracking error prediction informed motion control of a parallel machine tool for high-performance machining. Int. J. Mach. Tools Manuf. 2021, 164, 103714. [Google Scholar] [CrossRef]
- Makarem, S.; Delibas, B.; Koc, B. Data-Driven Tuning of PID Controlled Piezoelectric Ultrasonic Motor. Actuators 2021, 10, 148. [Google Scholar] [CrossRef]
- Baek, J.; Cho, S.; Han, S. Practical Time-Delay Control with Adaptive Gains for Trajectory Tracking of Robot Manipulators. IEEE Trans. Ind. Electron. 2018, 65, 5682–5692. [Google Scholar] [CrossRef]
- Sun, Y.G.; Qiang, H.Y.; Wang, L.; Ji, W.; Mardani, A. A Fuzzy-Logic-System-Based Cooperative Control for the Multielectromagnets Suspension System of Maglev Trains with Experimental Verification. IEEE Trans. Fuzzy Syst. 2023, 31, 3411–3422. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, C.J. Dynamics Modeling and Adaptive Sliding Mode Control of a Hybrid Condenser Cleaning Robot. Actuators 2022, 11, 119. [Google Scholar] [CrossRef]
- Ning, B.D.; Han, Q.L.; Sanjayan, J.; Shang, W.W.; Lam, W.Y. Robust trajectory tracking control for cable-driven parallel with model uncertainty. Control. Eng. Pract. 2023, 140, 105662. [Google Scholar] [CrossRef]
- Zhong, Y.B.; Gao, J.; Zhang, L.Y. Fractional-order feedforward control method for permanent magnet linear synchronous motor based on frequency-domain adjustment theory. Mech. Syst. Signal Process. 2023, 190, 110115. [Google Scholar] [CrossRef]
- Luo, Y.H.; Gao, J.; Chen, D.S.; Zhang, L.Y.; Liu, Y.C.; Zhong, Y.B. Accurate error compensation method for multi-axis parallel machine via singularized jacobi geometric parameter correction and coupling error evaluation. Robot. Comput. Integr. Manuf. 2024, 89, 102771. [Google Scholar] [CrossRef]
- Martinez, O.; Soto, I.; Campa, R. Mathematical modeling of a 3-CUP parallel mechanism using the Fermat point. Mech. Mach. Theory 2021, 161, 104326. [Google Scholar] [CrossRef]
- Guo, F.; Cheng, G.; Pang, Y.S. Explicit dynamic modeling with joint friction and coupling analysis of a 5-DOF hybrid polishing robot. Mech. Mach. Theory 2022, 167, 104509. [Google Scholar] [CrossRef]




| Control Strategy | Tracking Error (μm) | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| q1 | q2 | q3 | q1 | q2 | q3 | |
| APD–DC | 7.83 | 14.21 | 6.69 | 6.87 | 12.53 | 5.87 |
| Proposed | 3.16 | 3.28 | 3.29 | 2.74 | 2.85 | 2.89 |
| Reduction (%) (proposed compared with APD–DC) | 59.64 | 76.92 | 50.82 | 60.12 | 77.25 | 50.77 |
| Control Strategy | Synchronization Error (μm) | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| q1 | q2 | q3 | q1 | q2 | q3 | |
| APD–DC | 7.89 | 8.20 | 5.49 | 6.98 | 7.26 | 4.92 |
| Proposed | 0.48 | 0.52 | 0.95 | 0.40 | 0.46 | 0.83 |
| Reduction (%) (proposed compared with APD–DC) | 93.92 | 93.66 | 82.7 | 94.27 | 93.66 | 83.13 |
| Control Strategy | Tracking Error | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| X (μm) | Z (μm) | B (μrad) | X (μm) | Z (μm) | B (μrad) | |
| APD–DC | 14.21 | 4.75 | 75.95 | 12.53 | 4.26 | 67.16 |
| Proposed | 3.28 | 0.82 | 3.18 | 2.85 | 0.72 | 1.62 |
| Reduction (%) (proposed compared with APD–DC) | 76.92 | 82.74 | 95.81 | 77.25 | 83.1 | 97.59 |
| Control Strategy | Tracking Error (μm) | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| q1 | q2 | q3 | q1 | q2 | q3 | |
| APD–DC | 4.93 | 5.98 | 4.27 | 4.16 | 5.00 | 3.62 |
| Proposed | 1.59 | 2.02 | 1.54 | 1.17 | 1.43 | 1.21 |
| Reduction (%) (proposed compared with APD–DC) | 67.75 | 66.22 | 63.93 | 71.88 | 71.4 | 66.57 |
| Control Strategy | Synchronization Error (μm) | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| q1 | q2 | q3 | q1 | q2 | q3 | |
| APD–DC | 2.17 | 1.86 | 2.16 | 1.89 | 1.47 | 1.89 |
| Proposed | 0.65 | 0.88 | 0.46 | 0.51 | 0.62 | 0.37 |
| Reduction (%) (proposed compared with APD–DC) | 70.01 | 52.69 | 78.7 | 73.02 | 57.82 | 80.42 |
| Control Strategy | Tracking Error | |||||
|---|---|---|---|---|---|---|
| STD | MAE | |||||
| X (μm) | Z (μm) | B (μrad) | X (μm) | Z (μm) | B (μrad) | |
| APD–DC | 5.98 | 1.87 | 33.01 | 5.00 | 1.63 | 26.55 |
| Proposed | 2.02 | 0.39 | 14.21 | 1.43 | 0.32 | 10.17 |
| Reduction (%) (proposed compared with APD–DC) | 66.22 | 79.14 | 56.95 | 71.4 | 80.37 | 61.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Gao, J.; Zhang, L. Synchronization Control with Dynamics Compensation for Three-Axis Parallel Motion Platform. Actuators 2024, 13, 166. https://doi.org/10.3390/act13050166
Zhou Z, Gao J, Zhang L. Synchronization Control with Dynamics Compensation for Three-Axis Parallel Motion Platform. Actuators. 2024; 13(5):166. https://doi.org/10.3390/act13050166
Chicago/Turabian StyleZhou, Zhiwei, Jian Gao, and Lanyu Zhang. 2024. "Synchronization Control with Dynamics Compensation for Three-Axis Parallel Motion Platform" Actuators 13, no. 5: 166. https://doi.org/10.3390/act13050166
APA StyleZhou, Z., Gao, J., & Zhang, L. (2024). Synchronization Control with Dynamics Compensation for Three-Axis Parallel Motion Platform. Actuators, 13(5), 166. https://doi.org/10.3390/act13050166





