State Observer-Based Conditioned Reverse-Path Method for Nonlinear System Identification
Abstract
1. Introduction
2. Methodology Outline and Contributions
- (1)
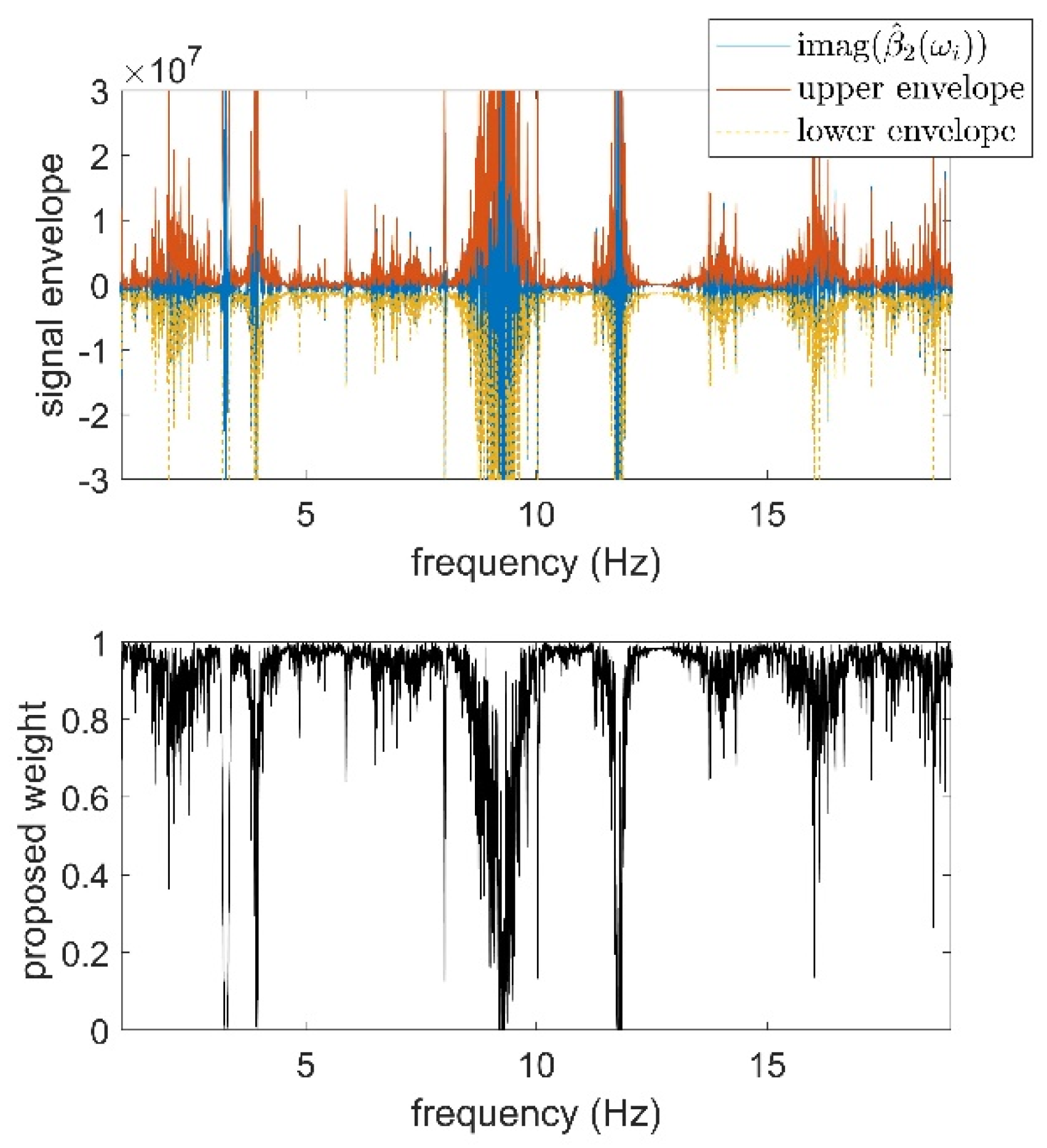
- The introduction of frequency-dependent weighting in the calculation of the nonlinear coefficients in the RP method is motivated by their spectral dependencies. Accordingly, the estimations are polluted by artifacts propagated from the inaccurate estimation of the ULM, which results in a complex (non-real) estimation of the physical variables (the coefficients). The weighting proposed by Muhamad et al. [24] based on the reciprocal of the magnitude of the imaginary part of the estimated spectra is used as a background. Such weighting functions suppress the contribution of highly distorted parts of the estimated data (for the nonlinear coefficients), i.e., parts of the estimated data that have large imaginary parts. We have noticed that not only the contribution of the frequency bandwidth of the data with large imaginary parts should be suppressed in estimating these coefficients, but also a frequency window around that bandwidth should be weighted properly. Additionally, it is observed that the normalization of the frequency-dependent weighting function between zero and one is beneficial in the correct estimation of the coefficients. To this end, it is proposed to employ the normalized envelope of the imaginary part based on the Hilbert finite impulse filter as a new weighting function. It should be noted that we have abandoned the minor revision explained before on the recursive nature of the estimation of the coefficients [24] because it induces negligible improvements at the cost of the enormous computational burden for each unknown coefficient.
- (2)
- As stated previously by Worden [33], the concepts in nonlinear dynamics are often implemented for systems with low modal density, e.g., lumped parameter systems, since in practice, for large-scale continuous structures, the order of involved linear and nonlinear dynamics may be huge. Consequently, identifying appropriate measurement protocols to detect the active dynamics out of several hundred of them is a challenging task [34]. Some real-time implementations of the CRP method are tackled in the literature [23,24,35]. In this paper, based on the grey-box frequency domain linear subspace system identification, the dynamics of a continuous system is first represented in modal coordinates, which can be represented subsequently by a lumped parameter system of limited DoF for a specific operational bandwidth. The linear grey-box modeling process may result in a biased estimation of the ULM by neglecting the contribution of the unmodeled dynamics that may occur outside of the bandwidth of interest [36]. This tradeoff between the model order/model structure and the matching quality between the grey- and black-box models is discussed in detail in [37]. Then, Kalman filter state estimation is employed in order to reconstruct the system states even in nonlinear settings. It is worth mentioning that the state estimation mechanism should possess fast dynamics to accommodate the nonlinearities. Accordingly, in the formulation of the non-steady-state Kalman filtering, the contribution of the nonlinearity is addressed by considering large values for the covariance matrix associated with the process noise signal. This signal in the context of control systems can be classified as the source of matched/mismatched disturbances that invoke nonlinear behavior in the first place. Consequently, the requirement for a large number of sensors to capture a handful of states is relieved in this paper.
- (3)
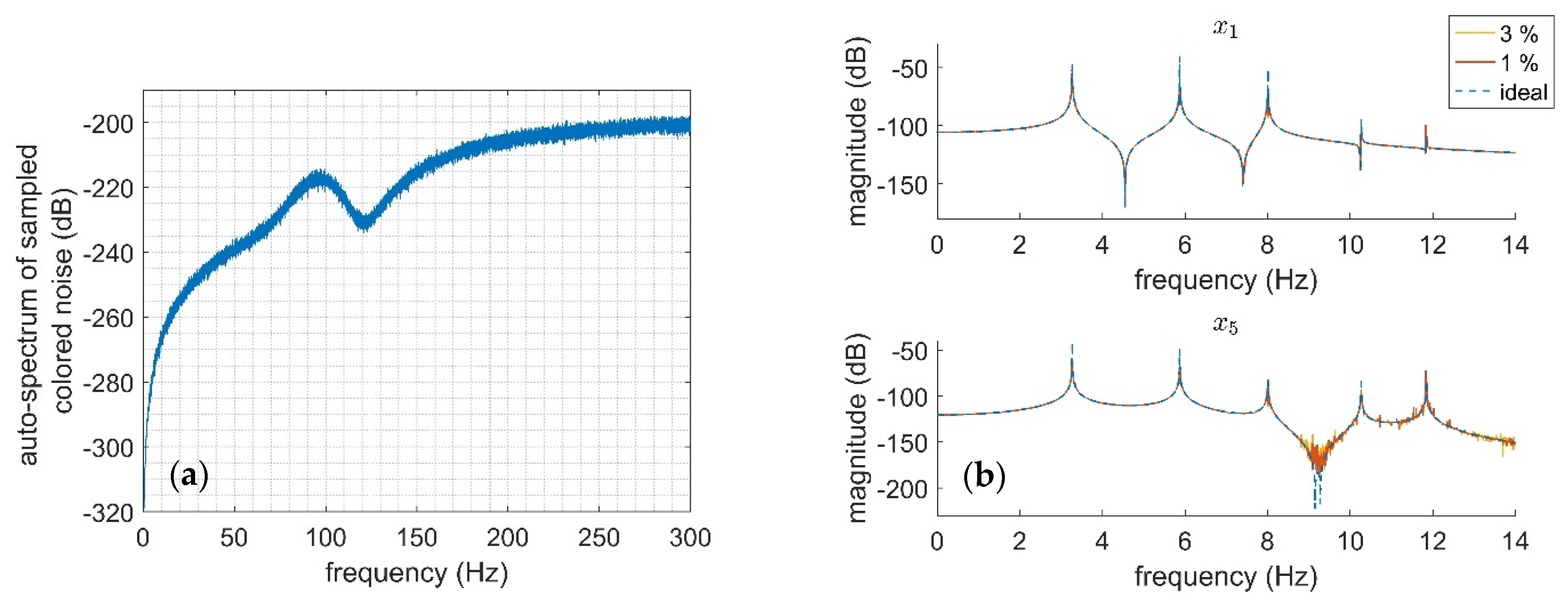
- To address the presence of distortion in FRFs, a detection phase is performed based on the robust LPM, followed by employing the characterization results of closed-form modeling of geometrically nonlinear systems. As shown in the paper, the latter may be replaced in local nonlinearities by the ASM. This combination follows the well-known three-step paradigm for detecting, characterizing, and quantifying linearity in structural dynamics, as discussed in [25]. For this purpose, in contrast to the various forms of RP methods in the literature where the input signal is merely a Gaussian random variable, we have used single-reference random-phase multi-sine excitation. The advantages of this decision are discussed in the course of the paper. In short, it improves the estimates of the dynamic compliance functions and the coefficients of the analytically predicted (characterized) nonlinear functions. Further remarks are discussed regarding the justification of the use of spectral conditioning and the computational effort in the case of the OBCRP method. In order to highlight the sensitivity of the method in terms of measurement noise, a simulation problem is carefully designed.
3. Methodology of the Observer-Based Conditioned Reverse-Path Approach
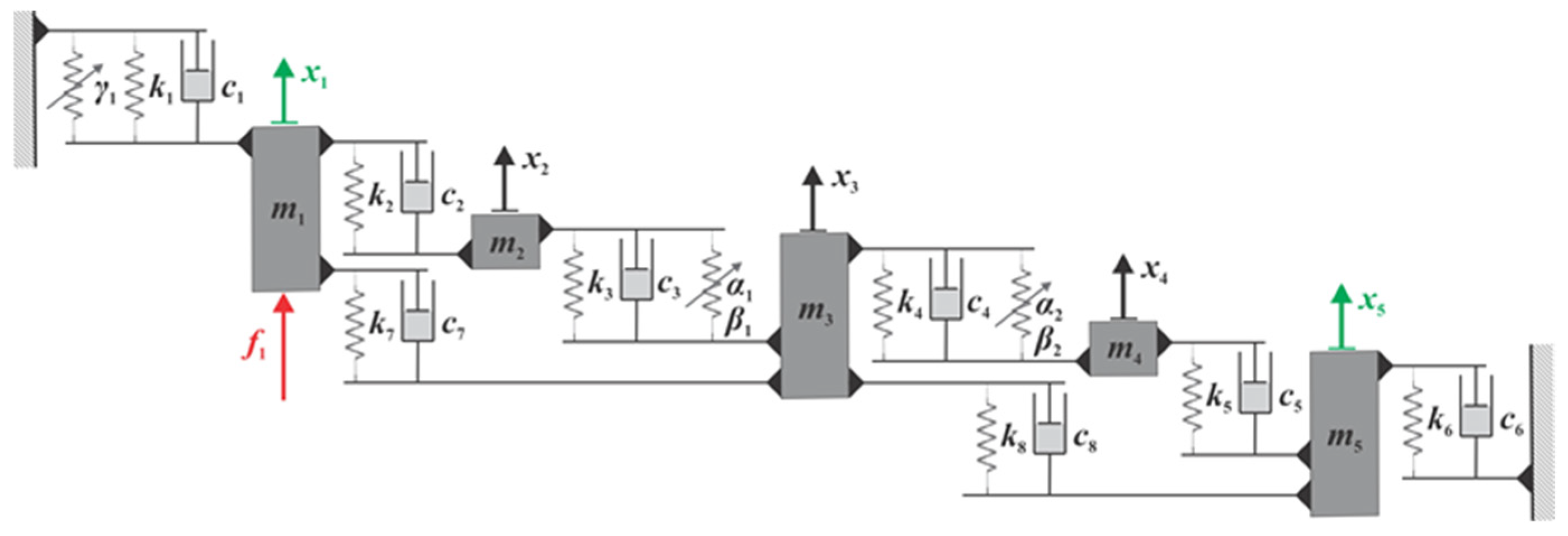
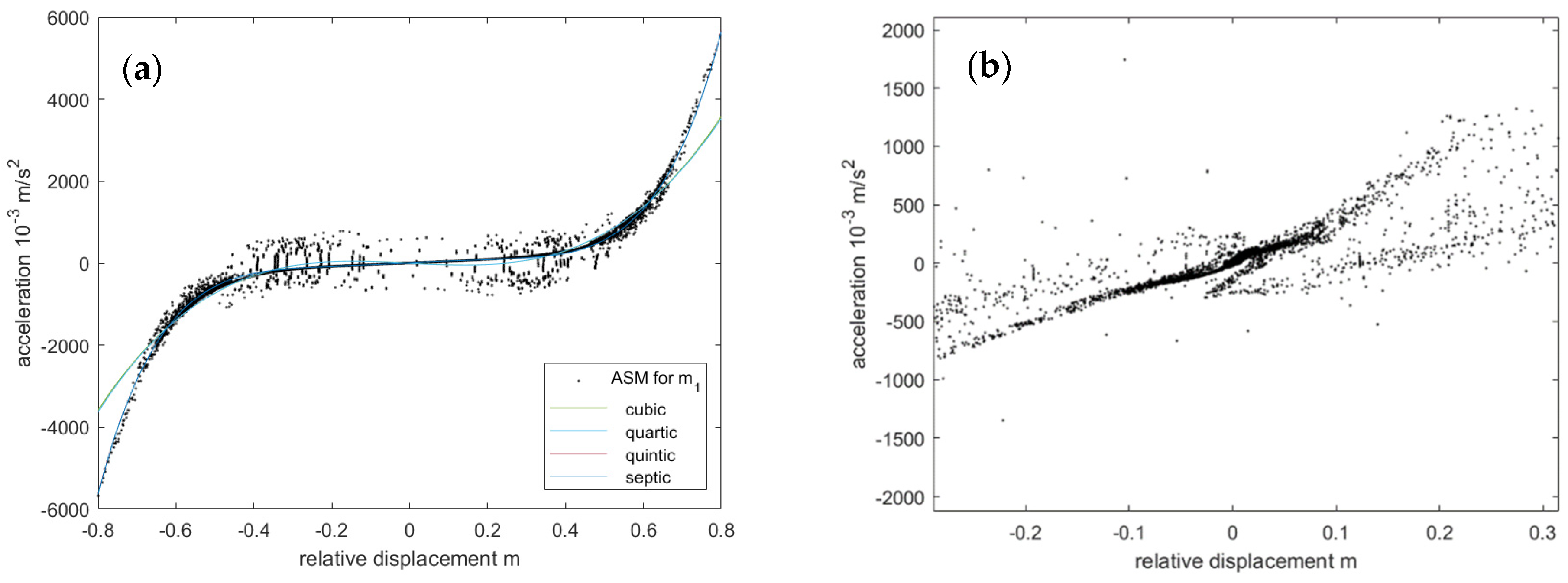
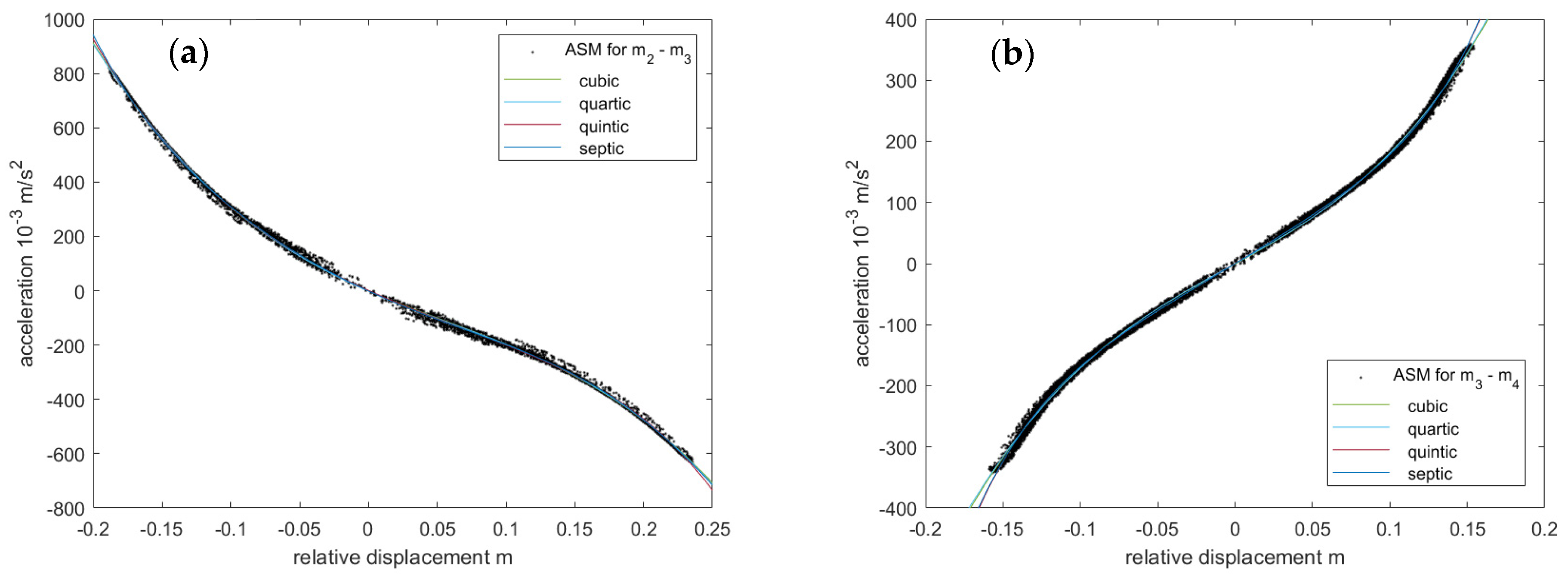
3.1. Localization and Characterization of the Nonlinearity Using the Acceleration Surface Method
3.2. Excitation Signal
3.3. The Fast Method
3.4. The Algorithm of the CRP Method
| Algorithm 1 Summary of the CRP method |
|
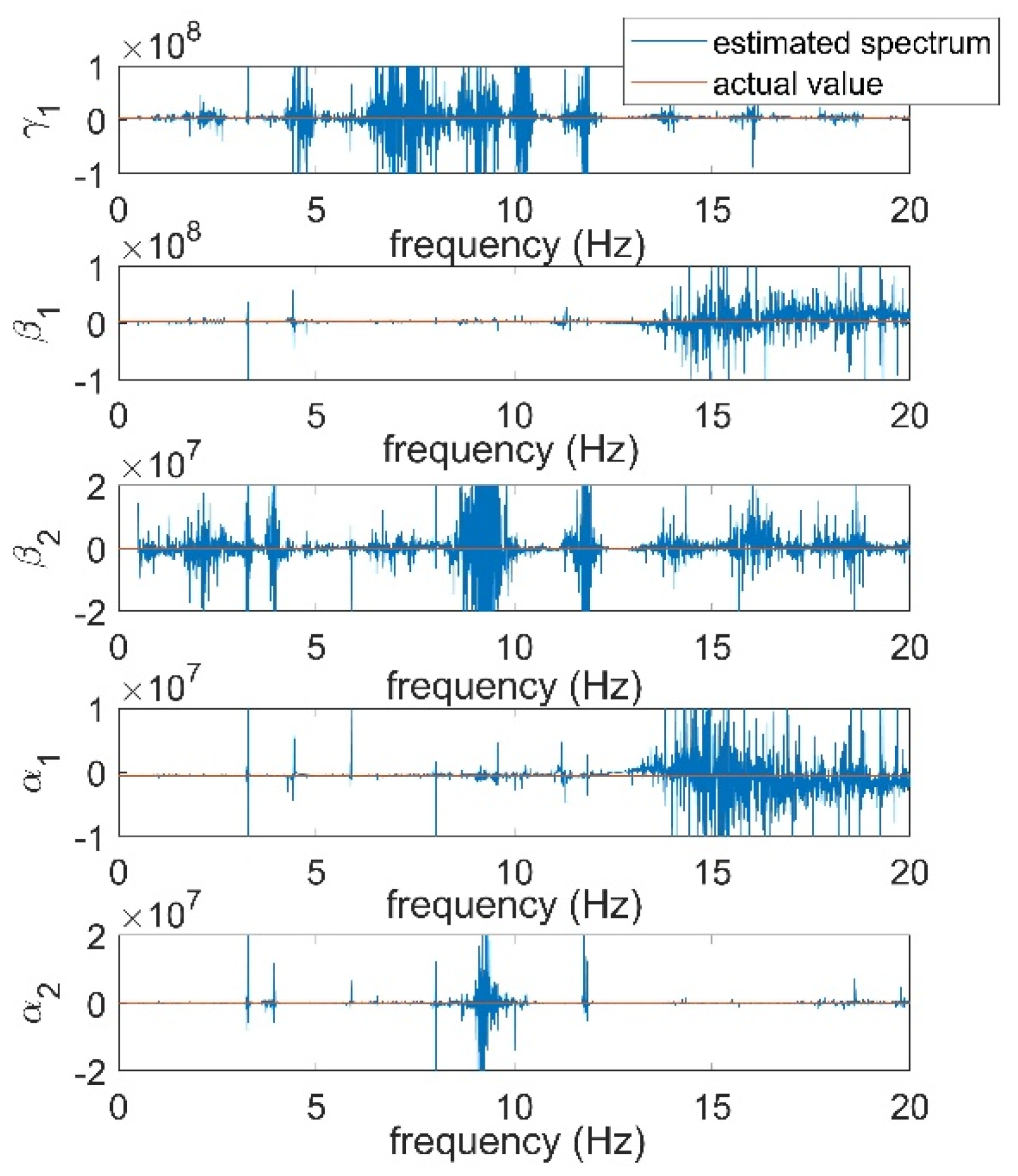
3.5. Spectral Mean Estimation
| Algorithm 2 Enhanced weighting procedure |
|
4. Implementation of the OBCRP Method
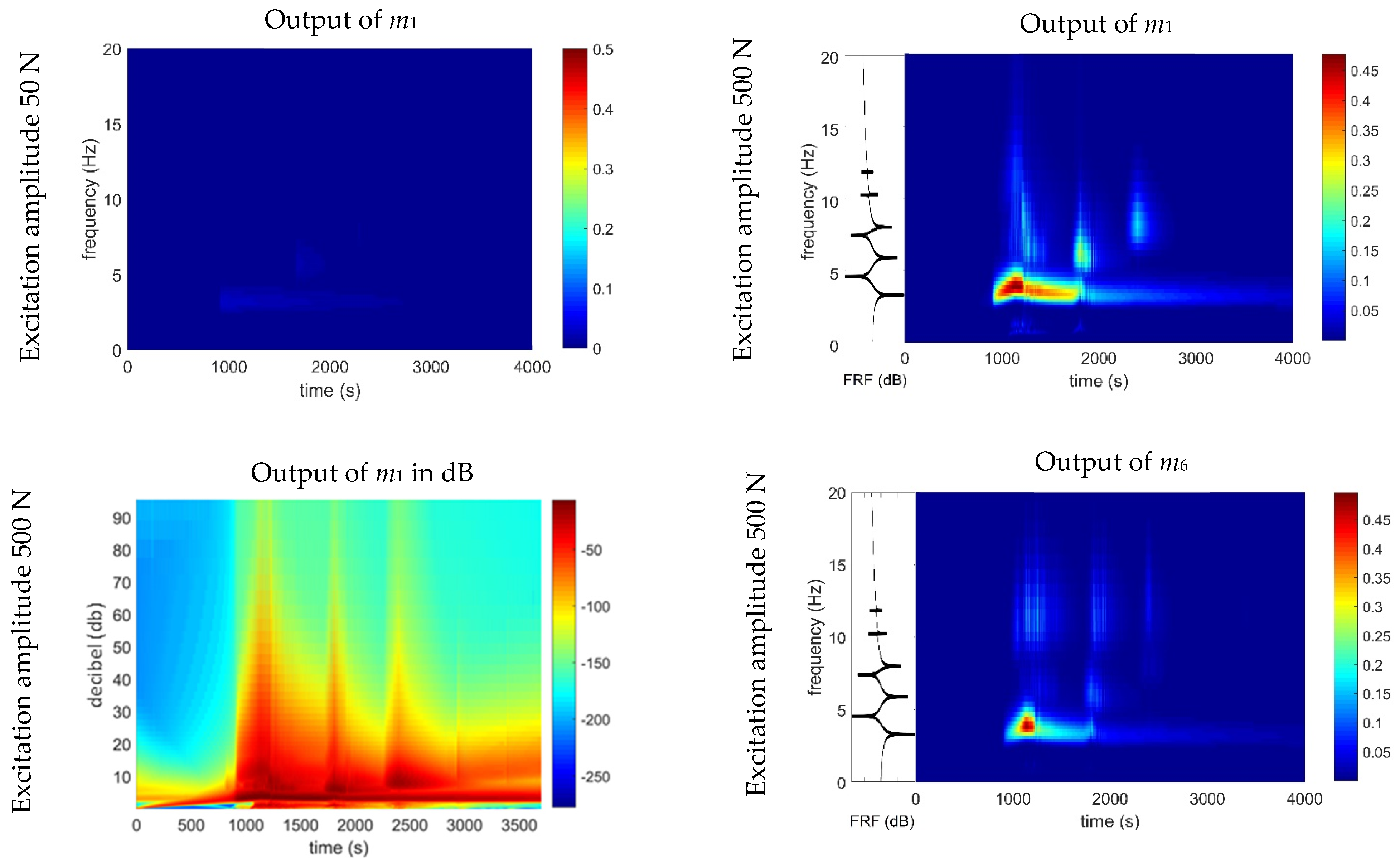
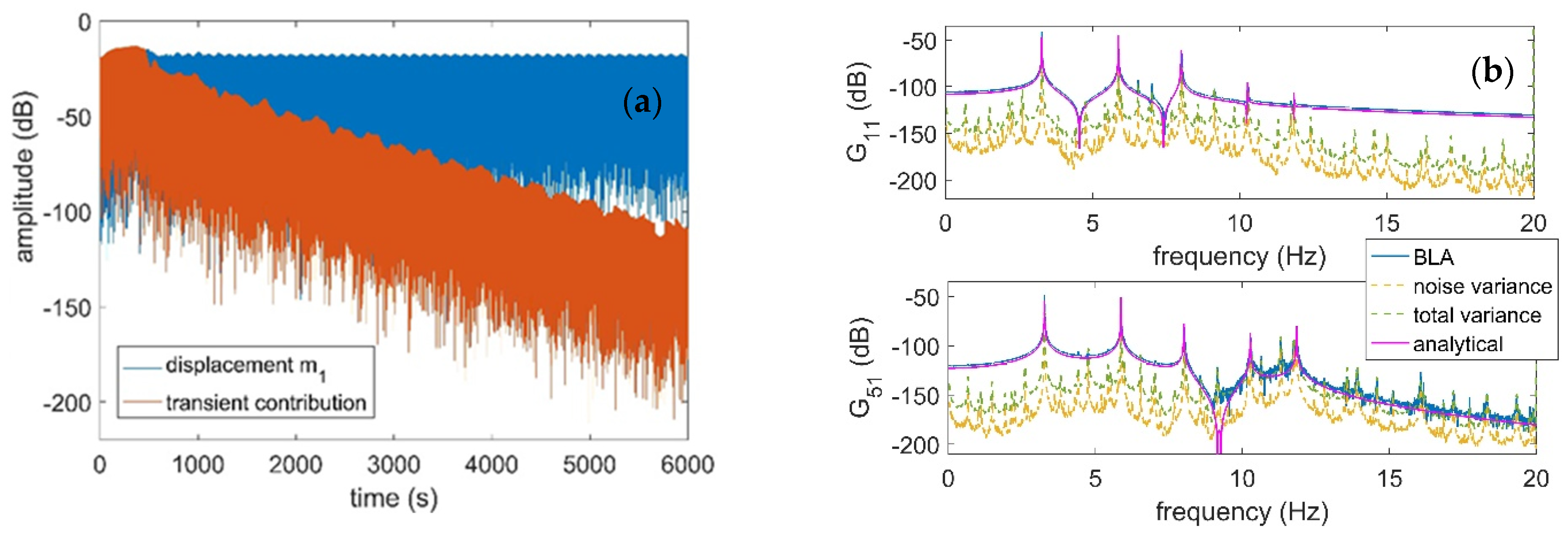
4.1. Time-Frequency Analysis
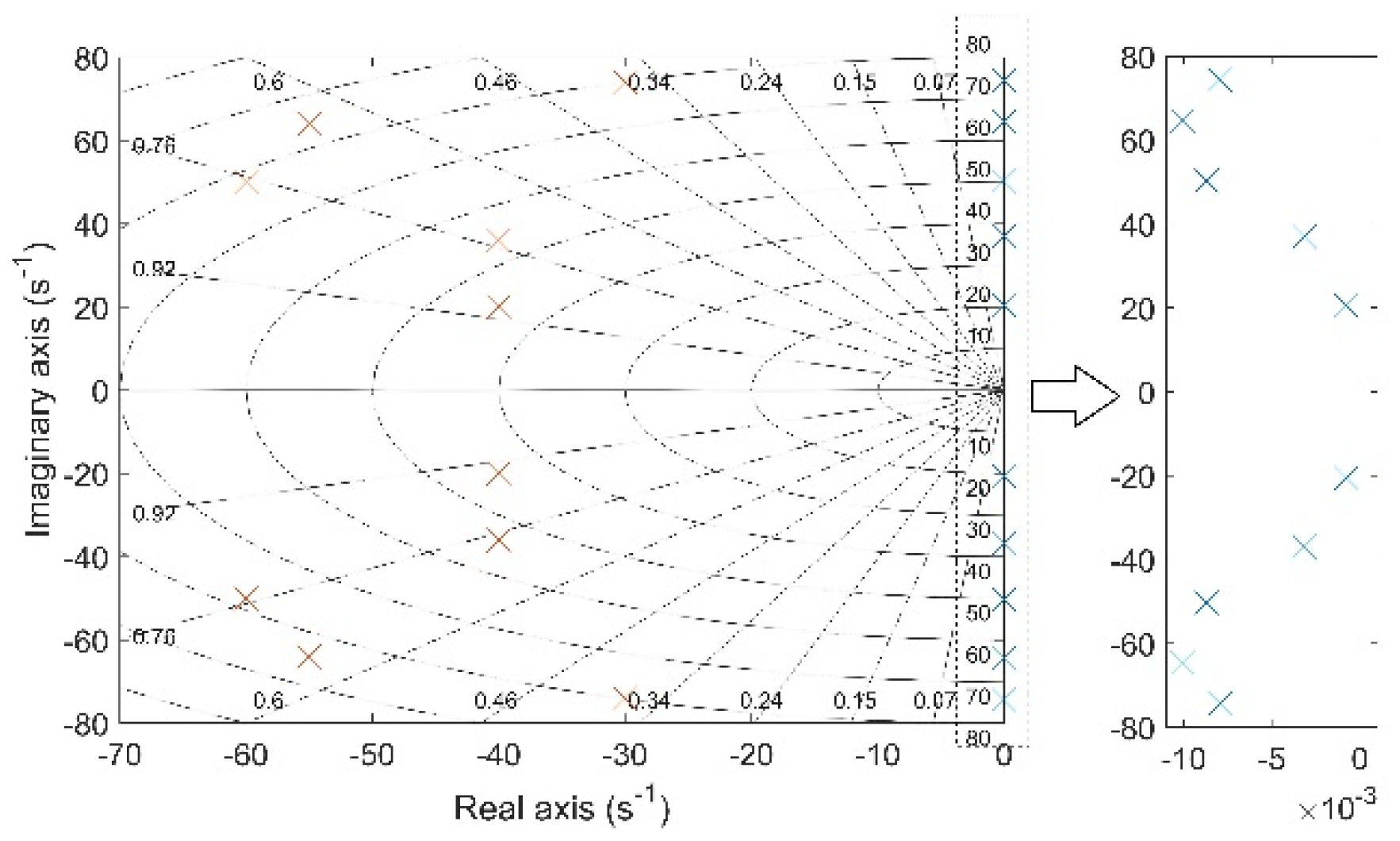
4.2. Implementation of the Acceleration Surface Method
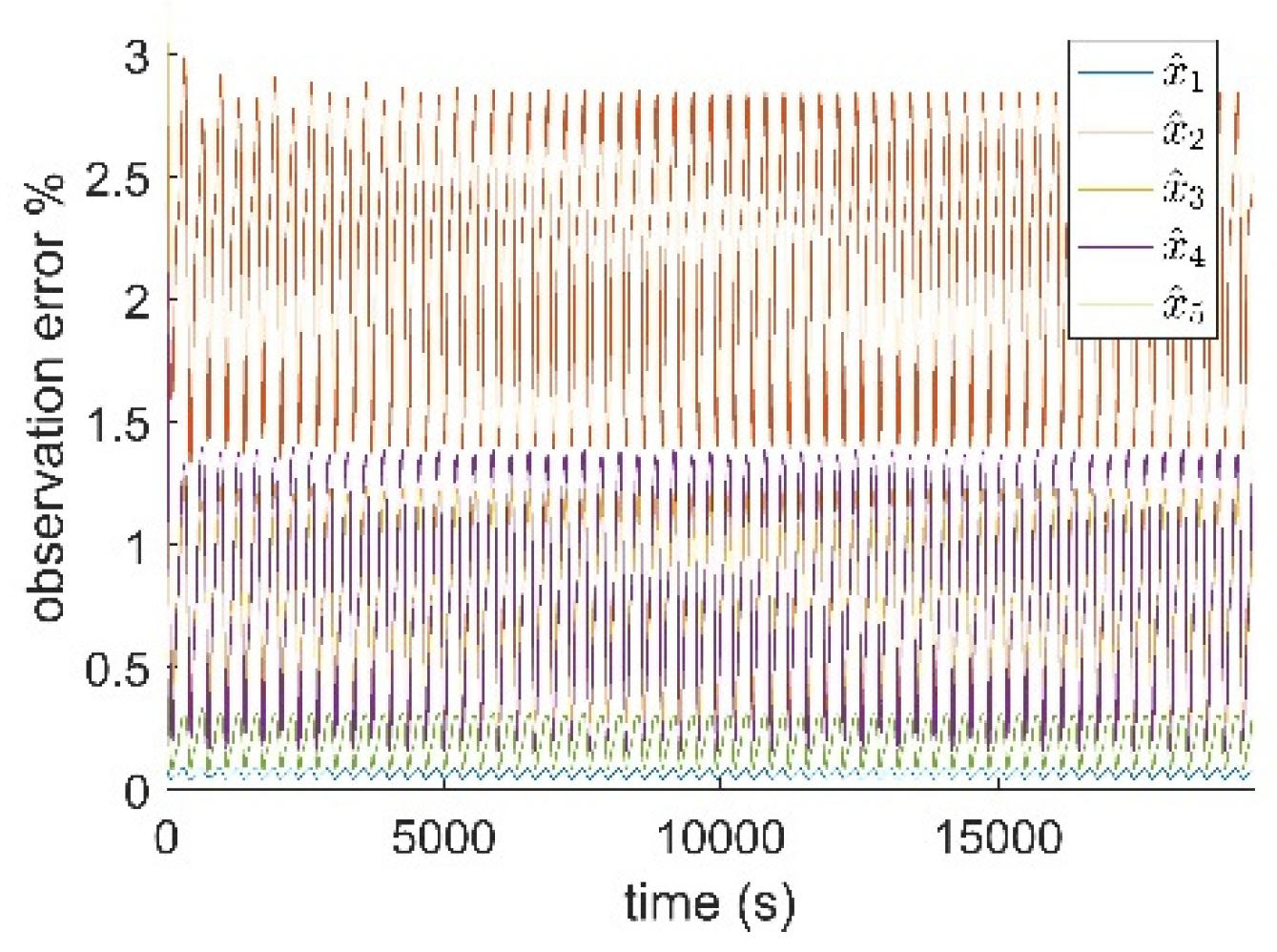
4.3. Implementation Results of the OBCRP Method
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. State Observer in the Context of the OBCRP Method
Appendix A.1. State Estimation Using Kalman Filtering
Appendix A.2. Matrix Fraction Decomposition of the Riccati Differential Equation
Appendix A.3. The Square Root Filter
References
- Orszulik, R.R.; Gabbert, U. An Interface Between Abaqus and Simulink for High-Fidelity Simulations of Smart Structures. IEEE/ASME Trans. Mechatron. 2016, 21, 879–887. [Google Scholar] [CrossRef]
- Oveisi, A.; Nestorović, T. Robust observer-based adaptive fuzzy sliding mode controller. Mech. Syst. Signal Process. 2016, 76–77, 58–71. [Google Scholar] [CrossRef]
- Oveisi, A.; Nestorović, T. Robust nonfragile observer-based H2/H∞ controller. J. Vib. Control 2018, 24, 722–738. [Google Scholar] [CrossRef]
- Paduart, J.; Lauwers, L.; Swevers, J.; Smolders, K.; Schoukens, J.; Pintelon, R. Identification of nonlinear systems using Polynomial Nonlinear State Space models. Automatica 2010, 46, 647–656. [Google Scholar] [CrossRef]
- Esfahani, A.F.; Dreesen, P.; Tiels, K.; Noël, J.-P.; Schoukens, J. Parameter reduction in nonlinear state-space identification of hysteresis. Mech. Syst. Signal Process. 2018, 104, 884–895. [Google Scholar] [CrossRef]
- Noël, J.-P.; Schoukens, J. Grey-box state-space identification of nonlinear mechanical vibrations. Int. J. Control. 2017, 91, 1118–1139. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, D.; Zhai, L.; Hu, L.; Li, L.; Qin, H.; Li, D.; Fan, J. A two-stage model updating method for the linear parts of structures with local nonlinearities. Front. Mater. 2023, 10, 1331081. [Google Scholar] [CrossRef]
- Prawin, J.; Rao, A.R.M. An improved version of conditioned time and frequency domain reverse path methods for nonlinear parameter estimation of MDOF systems. Mech. Based Des. Struct. Mach. 2023, 51, 2713–2756. [Google Scholar] [CrossRef]
- Prawin, J.; Rao, A.R.M.; Sethi, A. Parameter identification of systems with multiple disproportional local nonlinearities. Nonlinear Dyn. 2020, 100, 289–314. [Google Scholar] [CrossRef]
- Oveisi, A.; Anderson, A.; Nestorović, T.; Montazeri, A. Optimal Input Excitation Design for Nonparametric Uncertainty Quantification of Multi-Input Multi-Output Systems. IFAC-PapersOnLine 2018, 51, 114–119. [Google Scholar] [CrossRef]
- Pintelon, R.; Barbé, K.; Vandersteen, G.; Schoukens, J. Improved (non-)parametric identification of dynamic systems excited by periodic signals. Mech. Syst. Signal Process. 2011, 25, 2683–2704. [Google Scholar] [CrossRef]
- Pintelon, R.; Vandersteen, G.; Schoukens, J.; Rolain, Y. Improved (non-)parametric identification of dynamic systems excited by periodic signals—The multivariate case. Mech. Syst. Signal Process. 2011, 25, 2892–2922. [Google Scholar] [CrossRef]
- Mallat, S.G.; Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: San Diego, CA, USA, 2003; p. 637. [Google Scholar]
- Lee, Y.S.; Kerschen, G.; Vakakis, A.F.; Panagopoulos, P.; Bergman, L.; McFarland, D.M. Complicated dynamics of a linear oscillator with a light, essentially nonlinear attachment. Phys. D Nonlinear Phenom. 2005, 204, 41–69. [Google Scholar] [CrossRef]
- Oveisi, A. System Identification and Model-Based Robust Nonlinear Disturbance Rejection Control. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2021. [Google Scholar] [CrossRef]
- Nestorović, T.; Trajkov, M.; Patalong, M. Identification of modal parameters for complex structures by experimental modal analysis approach. Adv. Mech. Eng. 2016, 8, 168781401664911. [Google Scholar] [CrossRef]
- Richards, C.M.; Singh, R. Identification of Multi-Degree-of-Freedom Non-Linear Systems Under Random Excitations by the “Reverse Path” Spectral Method. J. Sound Vib. 1998, 213, 673–708. [Google Scholar] [CrossRef]
- McKelvey, T.; Akcay, H.; Ljung, L. Subspace-based multivariable system identification from frequency response data. IEEE Trans. Autom. Control. 1996, 41, 960–979. [Google Scholar] [CrossRef]
- Shyu, R.J. A Spectral Method for Identifying Nonlinear Structures; IEEE: Piscataway, NJ, USA, 1994. [Google Scholar]
- Yang, Z.-J. Frequency domain subspace model identification with the aid of the w-operator. In Proceedings of the 37th SICE Annual Conference, International Session Papers, SICE’98, Chiba, Japan, 29–31 July 1998; The Society of Instrument and Control Engineers (SICE): Sapporo, Japan, 1998; pp. 1077–1080. [Google Scholar] [CrossRef]
- Bendat, J.S.; Palo, P.A.; Coppolino, R.N. A general identification technique for nonlinear differential equations of motion. Probabilistic Eng. Mech. 1992, 7, 43–61. [Google Scholar] [CrossRef]
- Garibaldi, L. Application of the Conditioned Reverse Path Method. Mech. Syst. Signal Process. 2003, 17, 227–235. [Google Scholar] [CrossRef]
- Kerschen, G.; Lenaerts, V.; Golinval, J.-C. Identification of a continuous structure with a geometrical non-linearity. Part I: Conditioned reverse path method. J. Sound Vib. 2003, 262, 889–906. [Google Scholar] [CrossRef]
- Muhamad, P.; Sims, N.D.; Worden, K. On the orthogonalised reverse path method for nonlinear system identification. J. Sound Vib. 2012, 331, 4488–4503. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.-C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Noël, J.P.; Kerschen, G. Nonlinear system identification in structural dynamics: 10 more years of progress. Mech. Syst. Signal Process. 2017, 83, 2–35. [Google Scholar] [CrossRef]
- Masri, S.F.; Caughey, T.K. A Nonparametric Identification Technique for Nonlinear Dynamic Problems. J. Appl. Mech. 1979, 46, 433–447. [Google Scholar] [CrossRef]
- Worden, K. Data processing and experiment design for the restoring force surface method, part I: Integration and differentiation of measured time data. Mech. Syst. Signal Process. 1990, 4, 295–319. [Google Scholar] [CrossRef]
- Noël, J.P.; Renson, L.; Kerschen, G.; Peeters, B.; Manzato, S.; Debille, J. Nonlinear dynamic analysis of an F-16 aircraft using GVT data. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Bristol, UK, 24–26 June 2013; Volume 2013. [Google Scholar]
- Oveisi, A.; Nestorović, T. Transient response of an active nonlinear sandwich piezolaminated plate. Commun. Nonlinear Sci. Numer. Simul. 2017, 45, 158–175. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Khalil, H.K.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control. 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Worden, K. Nonlinearity in structural dynamics: The last ten years. In Proceedings of the Conference on System Identification and Structural Health Monitoring, Madrid, Spain, 6–9 June 2000. [Google Scholar]
- Bossi, L.; Rottenbacher, C.; Mimmi, G.; Magni, L. Multivariable predictive control for vibrating structures: An application. Control. Eng. Pract. 2011, 19, 1087–1098. [Google Scholar] [CrossRef]
- Lenaerts, V.; Kerschen, G.; Golinval, J.-C. Identification of a continuous structure with a geometrical non-linearity. Part II: Proper orthogonal decomposition. J. Sound Vib. 2003, 262, 907–919. [Google Scholar] [CrossRef]
- Cauberghe, B.; Guillaume, P.; Pintelon, R.; Verboven, P. Frequency-domain subspace identification using FRF data from arbitrary signals. J. Sound Vib. 2006, 290, 555–571. [Google Scholar] [CrossRef]
- Cavallo, A.; de Maria, G.; Natale, C.; Pirozzi, S. Grey-Box Identification of Continuous-Time Models of Flexible Structures. IEEE Trans. Control. Syst. Technol. 2007, 15, 967–981. [Google Scholar] [CrossRef]
- Dossogne, T.; Masset, L.; Peeters, B.; Noël, J.P. Nonlinear dynamic model upgrading and updating using sine-sweep vibration data. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20190166. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification. A Frequency Domain Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Guillaume, P.; Schoukens, J.; Pintelon, R.; Kollar, I. Crest-factor minimization using nonlinear Chebyshev approximation methods. IEEE Trans. Instrum. Meas. 1991, 40, 982–989. [Google Scholar] [CrossRef]
- Pintelon, R.; Vandersteen, G.; de Locht, L.; Rolain, Y.; Schoukens, J. Experimental Characterization of Operational Amplifiers: A Sys-tem Identification Approach—Part I: Theory and Simulations. IEEE Trans. Instrum. Meas. 2004, 53, 854–862. [Google Scholar] [CrossRef]
- Schoukens, J.; Pintelon, R.; Dobrowiecki, T.; Rolain, Y. Identification of linear systems with nonlinear distortions. Automatica 2005, 41, 491–504. [Google Scholar] [CrossRef]
- Noël, J.P.; Esfahani, A.F.; Kerschen, G.; Schoukens, J. A nonlinear state-space approach to hysteresis identification. Mech. Syst. Signal Process. 2017, 84, 171–184. [Google Scholar] [CrossRef]
- Schoukens, J.; Pintelon, R.; Rolain, Y. Mastering System Identification in 100 Exercises; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; p. 264. [Google Scholar]
- Proakis; John, G.; Manolakis, D.G. Digital Signal Processing Principles, Algorithms, and Applications (Chapter 10), 3rd ed.; Prentice-Hall International: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Kerschen, G.; Peeters, M.; Golinval, J.C.; Vakakis, A.F. Nonlinear normal modes, Part I: A useful framework for the structural dynamicist. Mech. Syst. Signal Process. 2009, 23, 170–194. [Google Scholar] [CrossRef]
- Peeters, M.; Viguié, R.; Sérandour, G.; Kerschen, G.; Golinval, J.-C. Nonlinear normal modes, Part II: Toward a practical computation using numerical continuation techniques. Mech. Syst. Signal Process. 2009, 23, 195–216. [Google Scholar] [CrossRef]
- Noël, J.P.; Marchesiello, S.; Kerschen, G. Subspace-based identification of a nonlinear spacecraft in the time and frequency domains. Mech. Syst. Signal Process. 2014, 43, 217–236. [Google Scholar] [CrossRef]
- Luo, H. Plug-and-Play Monitoring and Performance Optimization for Industrial Automation Processes; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017; p. 149. [Google Scholar]
- Goodwin, G.C.; Sin, K.S. Adaptive Filtering Prediction and Control; Courier Corporation: Chelmsford, MA, USA, 2014. [Google Scholar]
- Yu, K.; Watson, N.R.; Arrillaga, J. An Adaptive Kalman Filter for Dynamic Harmonic State Estimation and Harmonic Injection Tracking. IEEE Trans. Power Deliv. 2005, 20, 1577–1584. [Google Scholar] [CrossRef]
- Musavi, N.; Keighobadi, J. Adaptive fuzzy neuro-observer applied to low cost INS/GPS. Appl. Soft Comput. 2015, 29, 82–94. [Google Scholar] [CrossRef]
- Doostdar, P.; Keighobadi, J. Design and implementation of SMO for a nonlinear MIMO AHRS. Mech. Syst. Signal Process. 2012, 32, 94–115. [Google Scholar] [CrossRef]
- Nourmohammadi, H.; Keighobadi, J. Decentralized INS/GNSS System With MEMS-Grade Inertial Sensors Using QR-Factorized CKF. IEEE Sens. J. 2017, 17, 3278–3287. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation. Kalman, H [Infinity] and Nonlinear Approaches; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 526. [Google Scholar]



| Parameter | ||||||||
| value [kg] | ||||||||
| Parameter | ||||||||
| value [N/m] | ||||||||
| Parameter | ||||||||
| value [Ns/m] | ||||||||
| Parameter unit | [MN/m2] | [MN/m2] | [MN/m3] | [MN/m3] | [MN/m5] | |||
| value |
| Coefficients of the Polynomial in the Form of | Norm of Residuals | |||||||
|---|---|---|---|---|---|---|---|---|
| Cubic | N.A. | N.A. | N.A. | |||||
| Quartic | N.A. | N.A. | ||||||
| Quintic | N.A. | |||||||
| Septic | ||||||||
| Coefficients of the Polynomial in the Form of | Norm of Residuals | ||||||
|---|---|---|---|---|---|---|---|
| Quadratic | N.A. | N.A. | N.A. | 16,987 | |||
| Cubic | N.A. | N.A. | 3941 | ||||
| Quartic | N.A. | 3921.4 | |||||
| Quintic | 3775.6 | ||||||
| Coefficients of the Polynomial in the Form of | Norm of Residuals | ||||||
|---|---|---|---|---|---|---|---|
| Quadratic | N.A. | N.A. | N.A. | 7836 | |||
| Cubic | N.A. | N.A. | 2877.8 | ||||
| Quartic | N.A. | 2871.4 | |||||
| Quintic | 2571.6 | ||||||
| Coefficients | True Value | Error (%) | ||
|---|---|---|---|---|
| Unweighted Mean | Weighted: Muhamad et al. [24] | Weighted: Present | ||
| 23.38 | 21.42 | 4.02 | ||
| 48.1 | 2.39 | 13.58 | ||
| 22.32 | 74.74 | 1.09 | ||
| 407.22 | 8.96 | 0.79 | ||
| 18.72 | 12.70 | 27.4 | ||
| Coefficients | Error (%) | |
|---|---|---|
| 1% Noise Power | 3% Noise Power | |
| 11.35 | 11.76 | |
| 9.77 | 5.80 | |
| 36.55 | 31.17 | |
| 32.33 | 7.76 | |
| 15.04 | 19.34 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oveisi, A.; Gogilan, U.; Keighobadi, J.; Nestorović, T. State Observer-Based Conditioned Reverse-Path Method for Nonlinear System Identification. Actuators 2024, 13, 142. https://doi.org/10.3390/act13040142
Oveisi A, Gogilan U, Keighobadi J, Nestorović T. State Observer-Based Conditioned Reverse-Path Method for Nonlinear System Identification. Actuators. 2024; 13(4):142. https://doi.org/10.3390/act13040142
Chicago/Turabian StyleOveisi, Atta, Umaaran Gogilan, Jafar Keighobadi, and Tamara Nestorović. 2024. "State Observer-Based Conditioned Reverse-Path Method for Nonlinear System Identification" Actuators 13, no. 4: 142. https://doi.org/10.3390/act13040142
APA StyleOveisi, A., Gogilan, U., Keighobadi, J., & Nestorović, T. (2024). State Observer-Based Conditioned Reverse-Path Method for Nonlinear System Identification. Actuators, 13(4), 142. https://doi.org/10.3390/act13040142






