A Study on Robust Finite-Time Visual Servoing with a Gyro-Stabilized Surveillance System

Abstract

This article presents the design and validation of a novel visual servoing scheme for a surveillance system. In this system, a two-axis gimbal mechanism operates the rotation of a camera which is able to provide visual information on the tracked target for the control system. The control objective is to bring the target’s projection to the center of the image plane with the smallest steady-state error and a smooth transient response, even with the unpredictable motion of the target and the influence of external disturbances. To fulfill these tasks, the proposed control scheme is designed consisting of two parts: (1) an observer estimates simultaneously the matched and unmatched disturbances; and (2) a motion control law guarantees the finite-time stability and visual servoing performance. Finally, experiments are conducted for validation and evaluation. The proposed control system shows its consistency and ought to perform better than previous approaches.

1. Introduction

A gyro-stabilized system is a system that uses information from a gyroscope to mechanically stabilize a camera assembly. This is carried out by using a gimbal mechanism to operate the camera rotation. The captured images can also be used to generate a reference for the autonomous tracking operation. Similar mechanisms also find applications in gun-turret control, missile guidance, drone gimbal photography, handheld cameras, etc. It is worth noting that while specific applications may use other optical sensors or weapon systems instead of vision cameras, controlling their line of sight (LOS) remains essential [1,2,3]. In particular, controlling the LOS of the vision camera by the gimbal using the measurement from the camera itself is a type of visual servoing problem. Some fundamental studies on this problem have been established [4,5,6], and many others are still open.

Locating the target of interest in optical imagery is the first control action to be performed. Here, an image tracker implemented with image processing techniques and computer vision algorithms tracks the target’s projection in the image plane frame-by-frame [7,8]. The projection reflects the location of the target in the coordinate fixed to the camera, or in other words, the deviation angle between the camera’s LOS and a vector pointing at the target. Then, the control requirements of pointing the camera’s LOS to the target can be expressed as bringing the target’s projection to the center of the image plane with zero steady-state error and a smooth transient response. However, the inevitable constraints of an image tracker significantly affect the efficiency of the system.

The gimbal motion control is the second action taken. Most of the existing works using visual data to control the gimbal are rather simple, despite the complexities in the characteristics of the gimbal and camera. A straightforward control approach is a proportional controller mentioned in [4,9]. Hurak et al. [8] proposed a controller based on the classical image-based pointing and tracking approach. The study considered the couplings and under-actuation of the two-axis gimbal to control the gimbal’s angular rate. Unfortunately, the stability of the designed control system has not been proven and the completed form of the control law requires numerous measurements. The image-based tracking control approach for the gimbal camera was also adopted in [10,11]. In [10], the image-based tracking control of a gimbal mounted on an unmanned aerial vehicle was compared to another classical approach, the position-based tracking. The study showed that the former provided higher tracking accuracy, and the latter was more robust but required sufficient measurements. The image-based control for a gimbal in a flying wing wildfire tracking in [11] gave a similar remark, where a deviation between the position of the tracking target in the image and its center was noticeable in the task of gliding descent trajectory. F. Guo et al. [12] proposed a feedback linearization control scheme with command planning for the problem of LOS tracking. J. Guo et al. [13] introduced a cascade vision-based tracking control, consisting of a proportional lag compensator in the inner loop, and a feedback linearization-based sliding mode controller in the outer loop. However, in the presence of carrier disturbances and target movement, large deviations in tracking errors are created. T. Pham et al. [14] adopted reinforcement learning to optimally train the parameters of an adaptive proportional–integral–derivative image-based tracking control with a two-axis gimbal system. Unfortunately, this approach is preferable for repetitive tasks and was only validated in simulations. It is also worth noting that the above studies deal with regulator problems, that is, the tracking target is stationary and its projection should die out at the desired rate.

Tracking a moving target, i.e., visual servoing, was considered by X. Liu et al. [15]. They combined a model predictive controller with a disturbance observer to reduce the number of required measurements and obtain both disturbance rejection and good tracking performances. Furthermore, the model predictive control technique requires high computational load and high complexity, making it difficult to implement. In addition to the constraints in image streaming, the gimbal’s dynamics, vehicle maneuvers, and other disturbances are also worthy of concern. In their later studies [16,17], different control approaches were proposed for the visual servoing of gyro-stabilized systems. In [16], a time-delay disturbance observer-based sampled-data control was developed to deal with the measurement delay generated by the acquisition and processing of the image information. On the other hand, an active disturbance compensation and variable gain function technique was proposed in [17] for the two-axis system with output constraints and disturbances. In particular, all of these studies [15,16,17] dealt with kinematics control only, i.e., the control inputs are the speed of the gimbal channels without considering their dynamics. Thus, all disturbances and constraints act as matched disturbances. Meanwhile, the completed representation of these kinds of systems contains both matched and unmatched disturbances, which is more challenging.

Considering the dynamic control of the gimbal systems, classical control strategies use an additional rate control loop to stabilize the LOS and isolate it from the above-mentioned influences. Hence, a cascade control arrangement is usually used [3,18]. Recent works rely on robust control techniques such that both target tracking and disturbance rejection are simultaneously achieved. Sliding mode control (SMC) [19,20], H_∞ control [21], and active disturbance rejection control [22] are popular schemes, thanks to their robustness and effectiveness. Nevertheless, the preferable approach for controlling a gimbal system is the combination of a disturbance observer and a robust control law, thanks to its capability of active disturbance rejection. Li et al. [23] incorporated an integral SMC and a reduced-order cascade extended-state observer. The disturbance/uncertainty estimator-based integral SMC was introduced by Kurkcu et al. [24]. The newest studies take advantage of the SMC’s robustness to design both the observer and controller. The higher-order sliding mode observers were incorporated with a terminal SMC [19,25] or a super-twisting SMC [26]. Finite-time stability, that is, the convergence time is bounded by a predefined constant regardless of initial conditions, was desired and met. However, unmatched disturbance cannot be compensated, and the so-called chattering effect caused by high-frequency switching control still appears.

Therefore, this paper introduces a novel method for the finite-time visual servoing problem with the surveillance system. The proposed control system consists of two main components. Firstly, a single observer estimates both unmatched disturbances in the tracking target’s projection dynamics and matched disturbances in the gimbal dynamics. Then, a control law is designed to bring the projection to the center of the image plane and ensure the system’s finite-time stability, regardless of the target motion and the disturbances. Experiments are conducted for validation. The comparison to available approaches shows the superiority of the proposed control system. In short, the contributions of the paper can be summarized as follows:

-

An observer is proposed to be able to estimate the states and disturbances of the gyro-stabilized surveillance system.

-

A new visual servoing scheme ensures the boundedness and finite-time stability of the visual servoing system.

-

Proof for the finite-time stability of the closed-loop system is provided. Experimental results evaluate the effectiveness of the proposed system.

Accordingly, the remainder is organized as follows. The complete model of the system with a vision camera is introduced in Section 2. The observer is presented in Section 3. The control law design and proof of stability are given in Section 4. Experimental studies are conducted and their results are discussed in Section 5, where the proposed system is compared with others. Finally, conclusions are drawn.

2. System Modeling

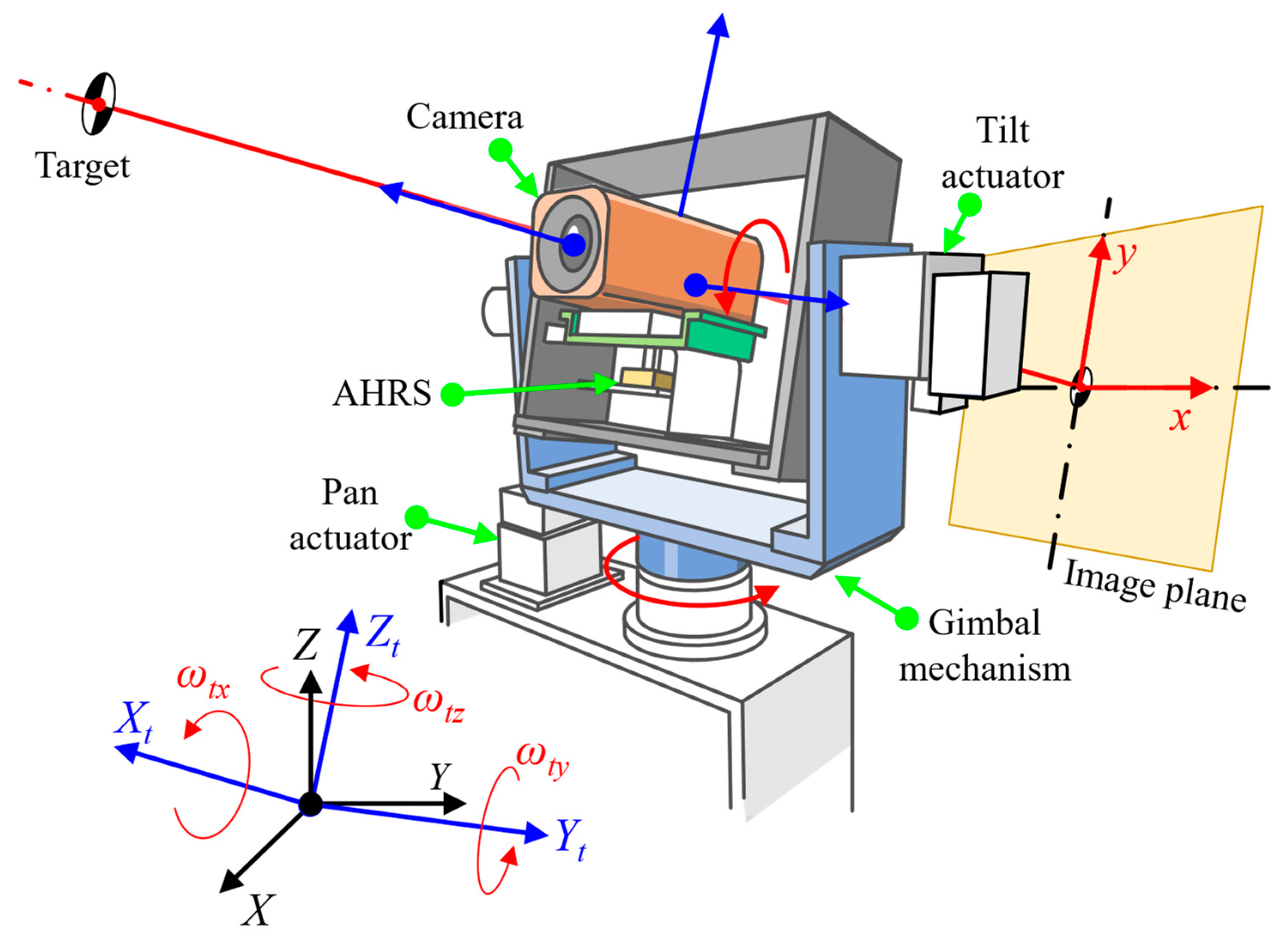
The structure of the gyro-stabilized system to be controlled is shown in Figure 1. A completed representation of the system, with the dynamics of a two-axis gimbal and kinematics of a projection on the image plane, is as follows [27]:

$$\begin{array}{c}\hspace{0.17em}{\dot{e}}_{xy}=L_w\omega +L_x\hspace{0.17em}{e}_{xy}+L_v{\nu }_t+e_d,\\ \dot{\omega }=B_{\omega }u-K\omega +d,\end{array}$$

(1)

Vector $\hspace{0.17em}{e}_{xy}={[\begin{array}{cc}x& y\end{array}]}^T$ indicates the location on the image plane of the projection of a given target in the 3-dimensional camera frame. $\omega ={\left[\begin{array}{cc}{\omega }_{ty}& {\omega }_{tz}\end{array}\right]}^T$ is the vector of the angular rates about the tilt and pan axes of the inner gimbal, respectively. Meanwhile, ${\omega }_{tx}$ is the rate of rotation about the roll axis, which is uncontrollable by the two-axis gimbal mechanism. The instantaneous linear velocity of the camera frame origin is given by $v_t$. $u$ is the command vector for the gimbal’s actuators. Additionally, $e_d$ and $d$ are the vectors of kinematic and dynamic disturbances, respectively. In detail, $e_d$ is the result of the unpredictable movement of the tracking target on its projection’s location. $d$ contains external torques acting on the gimbal mechanism due to the motion of the carrying vehicle, the imbalance mass of the gimbal, the nonlinear friction between channels, etc. The time variable has been neglected in the equation for the sake of simplicity.

Meanwhile, from the so-called pinhole camera model, the interaction matrices between the system motions and the projected point’s velocity, $L_{\omega }$, $L_x$, and $L_v$ are written as follows:

$$L_{\omega }=\frac{1}{f}\left[\begin{array}{cc}-xy& f^2+x^2\\ -f^2-y^2& xy\end{array}\right],L_x=\left[\begin{array}{cc}0& {\omega }_{tx}\\ -{\omega }_{tx}& 0\end{array}\right],L_v=\frac{1}{Z_c}\left[\begin{array}{ccc}x& f& 0\\ y& 0& f\end{array}\right],$$

(2)

with $f$ being the camera’s focal length and Z_c being the distance between the camera center and the tracking target. On the other hand, the system matrices of the gimbal mechanism are given by the following:

$$K=diag\{K_1,K_2\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{B}_{\omega }=diag\{B_1,B_2\cos \theta \}$$

(3)

with $K_1$, $K_2$, $B_1$, and $B_2$ being constant values and $\theta$ being the relative angle between the inner and outer channels. $\left|\theta \right|<\hspace{0.17em}\pi /2\hspace{0.17em}\hspace{0.17em}\left[\mathrm{rad}\right]$ thanks to mechanical locks such that the gimbal lock phenomenon is avoided.

Moreover, let the system model (1) be rewritten as follows:

$$\begin{array}{c}\dot{X}=A(X)X+Bu+Dw,\\ Y=CX\end{array}$$

(4)

with

$$\begin{gathered} X={\left[\begin{array}{cccc}x& y& {\omega }_{ty}& {\omega }_{tz}\end{array}\right]}^T,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}w={\left[{\left(L_v{\nu }_t+e_d\right)}^T\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{d}^T\right]}^T, \\ A(X)=\left[\begin{array}{cc}{L}_x& L_w\\ O_2& -K\end{array}\right],\hspace{0.17em}\hspace{0.17em}B=\left[\begin{array}{c}{O}_2\\ B_{\omega }\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C=I_4,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}D=I_4 \end{gathered}$$

(5)

O_n and I_n are the n-by-n null matrix and identity matrix, respectively. Then, one can see the following properties:

-

The system satisfies the observer matching condition [28]:

$$rank(CD)=rank(D)$$

(6)

-

The nonlinear term satisfies the local Lipchitz condition in a region Ω including the origin with respect to X. That is, for any X₁ and X₂ in Ω, there exists a positive $\kappa$ such that [29]

$$\Vert A(X_1)X_1-A(X_2)X_2\Vert \le \kappa \Vert X_1-X_2\Vert$$

(7)

3. State and Input Observer Design

To estimate the value of $w$, which consists of both unmatched and matched disturbances acting on the system, an observer is proposed such that its states match the system states and subsequently, the disturbances are asymptotically estimated. Assume that the disturbances are bounded and generated by a vector of exogenous signals $\upsilon$ such that

$$\dot{w}=-Hw+\upsilon$$

(8)

where $H\in R^{4\times 4}$ is a diagonal positive definite matrix. Then, the observer is proposed in the form

$$\begin{array}{c}\dot{\widehat{X}}=A(\widehat{X})\widehat{X}+Bu+\widehat{w}+L(Y-C\widehat{X}),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \dot{\widehat{w}}=-H\widehat{w}+\lambda Q(Y-C\widehat{X}),\\ \widehat{Y}=C\widehat{X}\end{array}$$

(9)

where $\widehat{X}$ and $\widehat{w}$ are the estimated states and disturbances, respectively. $\widehat{Y}$ is the observer output. The matrices $L$ and $Q$ and the positive scalar $\lambda$ are the gains of the observer.

Theorem 1. 

The $L_2$ gain of the observer is bounded by a positive $\gamma$ if there exist the matrices $L$, $P$ and $Q\in R^{4\times 4}$ and the positive scalar $\lambda$ such that

$$\begin{array}{c}\left[\begin{array}{ccc}-PLC-C^T{L}^{T}P+(\kappa +1)I& P& \left(1-\lambda \right)P\\ P& -I_4& O_4\\ \left(1-\lambda \right)P& O_4& -2H+\frac{1}{\gamma }{I}_4\end{array}\right]\le 0\\ P>0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}QC=P\end{array}$$

(10)

holds.

Proof of Theorem 1. 

 

A Lyapunov function candidate is considered as follows:

$$V_1={\tilde{X}}^{T}P\tilde{X}+{\tilde{w}}^T\tilde{w}$$

(11)

where $\tilde{X}=X-\widehat{X}$ and $\tilde{w}=w-\widehat{w}$ are the observation errors. Taking the time derivative of $V_1$ results in

$$\begin{array}{l}{\dot{V}}_1=2{\tilde{X}}^{T}P[A(X)X-A(\widehat{X})\widehat{X}]-{\tilde{X}}^T(PLC+C^T{L}^{T}P)\tilde{X}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+2(1-\lambda ){\tilde{w}}^{T}P\tilde{X}-2{\tilde{w}}^{T}H\tilde{w}+2{\tilde{w}}^T\upsilon \end{array}$$

(12)

Applying Young’s inequality and the inequality given in (7) for the not-quadratic terms of ${\dot{V}}_1$ yields the following:

$$\begin{array}{c}2{\tilde{X}}^{T}P[A(X)X-A(\widehat{X})\widehat{X}]\le {\tilde{X}}^T(PP+\kappa I_4)\tilde{X}\\ 2{\tilde{w}}^T\upsilon \le \frac{1}{\gamma }{\tilde{w}}^T\tilde{w}+\gamma {\upsilon }^T\upsilon \end{array}$$

(13)

Therefore, the derivative in (12) deduces to ${\dot{V}}_1\le {\dot{\overline{V}}}_1$, where

$$\begin{array}{l}{\dot{\overline{V}}}_1={\tilde{X}}^T(-PLC-C^T{L}^{T}P+PP+\kappa I_4)\tilde{X}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+2(1-\lambda ){\tilde{w}}^{T}P\tilde{X}-2{\tilde{w}}^{T}H\tilde{w}+\frac{1}{\gamma }{\tilde{w}}^T\tilde{w}+\gamma {\upsilon }^T\upsilon \end{array}$$

(14)

Additionally, consider the following inequality:

$${\dot{\overline{V}}}_1+{\tilde{X}}^T\tilde{X}+{\tilde{w}}^T\tilde{w}-\gamma {\upsilon }^T\upsilon \le 0$$

(15)

By substituting (14) into (15) and performing the Schur complement, inequality (10) is derived. Since ${\dot{V}}_1\le {\dot{\overline{V}}}_1$, (15) still holds if replacing ${\dot{\overline{V}}}_1$ with ${\dot{V}}_1$. The resultant inequality is equivalent to the boundedness of the $L_2$ gain of the observer being as follows [30]:

$$\underset{{\Vert \upsilon \Vert }_2\ne 0}{\sup }\frac{{\Vert {\left[{\tilde{X}}^T\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\tilde{w}}^T\right]}^T\Vert }_2}{{\Vert \upsilon \Vert }_2}\le \gamma$$

(16)

One can also see from (16) that the smallest upper bound of the $L_2$ gain is the result of minimizing $\gamma$ in (10). Hence, the influence of $\upsilon$ is also minimized and the estimated states and disturbances follow closely their actual values. □

4. Finite-Time Visual Servoing Controller Design

Recall that the control objective is to bring the target’s projection to the center of the image frame in a finite time regardless of its initial location. This objective is reflected in two control errors defined by

$$\begin{array}{l}{s}_{xy}=\hspace{0.17em}{e}_{xy}+{\Lambda }_f{f}_{xy},\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}{e}_w=\omega -{\omega }_{df}\end{array}$$

(17)

where ${\dot{f}}_{xy}=\hspace{0.17em}\hspace{0.17em}{e}_{xy}$ and ${\Lambda }_f\in R^{2\times 2}$ is a diagonal positive definite matrix such that $s_{xy}$ is Hurwitz. Hence, the convergence of $s_{xy}$ leads to the convergence of both $\hspace{0.17em}{e}_{xy}$ and $f_{xy}$. ${\omega }_{df}$ is the filtered desired angular rates about the tilt and pan axes of the inner gimbal and is designed as follows:

$$\begin{array}{c}\tau {\dot{\omega }}_{df}=-e_f,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{e}_f={\omega }_{df}-{\omega }_d,\\ {\omega }_d=-L_w^{-1}({\Lambda }_1\hspace{0.17em}{s}_{xy}+{\Lambda }_3\hspace{0.17em}{s}_{xy}^{\beta }+L_x{e}_{xy}+{\Lambda }_{w1}\widehat{w}+{\Lambda }_f{e}_{xy})\end{array}$$

(18)

In which $\tau$ is a positive scalar, and $L_{\omega }^{-1}$ is the inverse of $L_{\omega }$ from (2). The controller gains ${\Lambda }_{w1}=\left[\begin{array}{cc}{I}_2& O_2\end{array}\right]$ so that ${\Lambda }_{w1}\widehat{w}$ is the vector of estimated disturbances that correspond to those in the image plane. ${\Lambda }_1$ and ${\Lambda }_3\in R^{2\times 2}$ are diagonal positive definite matrices. $\beta \in \left(0,1\right)$ and the operation ${(\ast )}^{\beta }$ is defined by

$${(\ast )}^{\beta }={\left[\begin{array}{cccc}{\left|{\ast }_1\right|}^{\beta }\mathrm{sgn}({\ast }_1)& {\left|{\ast }_2\right|}^{\beta }\mathrm{sgn}({\ast }_2)& \dots & {\left|{\ast }_n\right|}^{\beta }\mathrm{sgn}({\ast }_n)\end{array}\right]}^T$$

(19)

with

$$\hspace{0.17em}(\ast )={[\begin{array}{cccc}{\ast }_1& {\ast }_2& \dots & {\ast }_n\end{array}]}^T$$

(20)

and $\mathrm{sgn}({\ast }_i)$ being the signum function of $({\ast }_i)$.

The dynamics of the control errors are then written as follows:

$$\begin{array}{c}{\dot{s}}_{xy}=-{\Lambda }_1\hspace{0.17em}{s}_{xy}-{\Lambda }_3\hspace{0.17em}{s}_{xy}^{\beta }+L_w(e_w+e_f)+L_v{\nu }_t+e_d-{\Lambda }_{w1}\widehat{w},\\ {\dot{e}}_w=B_{\omega }u-K\omega +d+\frac{1}{\tau }{e}_f\end{array}$$

(21)

From (21), the control is designed as in (22) to ensure the convergence of both control errors:

$$u=B_{\omega }^{-1}(Kw-\frac{1}{\tau }{e}_f-\alpha L_w\hspace{0.17em}{s}_{xy}-{\Lambda }_2\hspace{0.17em}{e}_{\omega }-{\Lambda }_4\hspace{0.17em}{e}_{\omega }^{\beta }-{\Lambda }_{w2}\widehat{w})$$

(22)

Here, ${\Lambda }_{w2}=\left[\begin{array}{cc}{O}_2& I_2\end{array}\right]$, $\alpha$ is a positive scalar, ${\Lambda }_2$ and ${\Lambda }_4\in R^{2\times 2}$ are diagonal positive definite matrices.

Theorem 2. 

When the control law (22) is conducted for the gyro-stabilized surveillance system whose dynamics are represented by (1), the finite-time stability of the visual servoing system is preserved with a proper choice of the controller gains.

Proof of Theorem 2. 

 

The finite-time convergence of the proposed system is derived from the following Lyapunov function candidate:

$$V_2=\frac{1}{2}{s}_{xy}^T{s}_{xy}+\frac{1}{2\alpha }{e}_{\mathsf{\omega }}^T{e}_{\mathsf{\omega }}$$

(23)

With the dynamics (21) and the proposed control law (22), the time derivative of $V_2$ is obtained as follows:

$$\begin{array}{ll}{\dot{V}}_2& =s_{xy}^T{\dot{s}}_{xy}+\frac{1}{\alpha }{e}_{\omega }^T{\dot{e}}_{\omega }\\ & =-s_{xy}^T{\Lambda }_1\hspace{0.17em}{s}_{xy}-s_{xy}^T{\Lambda }_3\hspace{0.17em}{s}_{xy}^{\beta }+s_{xy}^T\left(L_{\omega }(e_{\omega }+e_f)+L_v{\nu }_t+e_d-{\Lambda }_{w1}\widehat{w}\right)\\ & +\frac{1}{\alpha }{e}_{\omega }^T\left(K\omega -\frac{1}{\tau }{e}_f-\alpha L_{\omega }\hspace{0.17em}{s}_{xy}-{\Lambda }_2\hspace{0.17em}{e}_{\omega }-{\Lambda }_4\hspace{0.17em}{e}_{\omega }^{\beta }-{\Lambda }_{w2}\widehat{w}-K\omega +d+\frac{1}{\tau }{e}_f\right)\\ & =-s_{xy}^T{\Lambda }_1\hspace{0.17em}{s}_{xy}-s_{xy}^T{\Lambda }_3\hspace{0.17em}{s}_{xy}^{\beta }-\frac{1}{\alpha }{e}_{\omega }^T{\Lambda }_2\hspace{0.17em}{e}_{\omega }-\frac{1}{\alpha }{e}_{\omega }^T{\Lambda }_4\hspace{0.17em}{e}_{\omega }^{\beta }\\ & +s_{xy}^T(L_w{e}_f+{\Lambda }_{w1}\tilde{w})+\frac{1}{\alpha }{e}_{\omega }^T{\Lambda }_{w2}\tilde{w}\end{array}$$

(24)

Based on Young’s inequality for products,

$$\begin{array}{c}2s_{xy}^T\left(L_w{e}_f+{\Lambda }_{w1}\tilde{w}\right)\le s_{xy}^T{s}_{xy}+{\Vert L_w{e}_f+{\Lambda }_{w1}\tilde{w}\Vert }_2^2,\\ 2e_w^T{\Lambda }_{w2}\tilde{w}\le e_w^T\hspace{0.17em}{e}_{\omega }+{\Vert {\Lambda }_{w2}\tilde{w}\Vert }_2^2\end{array}$$

(25)

Thus, the differential Lyapunov function candidate is represented as follows:

$$\begin{array}{l}{\dot{V}}_2\le -s_{xy}^T\left({\Lambda }_1-\frac{1}{2}{I}_2\right)\hspace{0.17em}{s}_{xy}-s_{xy}^T{\Lambda }_3\hspace{0.17em}{s}_{xy}^{\beta }-\frac{1}{\alpha }{e}_w^T\left({\Lambda }_2-\frac{1}{2}{I}_2\right)\hspace{0.17em}{e}_{\omega }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\frac{1}{\alpha }{e}_w^T{\Lambda }_4\hspace{0.17em}{e}_{\omega }^{\beta }+\frac{1}{2}{\Vert L_w{e}_f+{\Lambda }_{w1}\tilde{w}\Vert }_2^2+\frac{1}{2\alpha }{\Vert {\Lambda }_{w2}\tilde{w}\Vert }_2^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le -{\kappa }_1{V}_2-{\kappa }_2{V}_2^{\frac{1+\beta }{2}}+\epsilon \end{array}$$

(26)

where

$$\begin{array}{c}{\kappa }_1=2\min ({\lambda }_{\min }({\Lambda }_1-\frac{1}{2}{I}_2),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\lambda }_{\min }({\Lambda }_2-\frac{1}{2}{I}_2)),\\ {\kappa }_2=2\min ({\lambda }_{\min }({\Lambda }_3),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\lambda }_{\min }({\Lambda }_4)),\\ \epsilon =\max \left(\frac{1}{2}{\Vert L_w{e}_f+{\Lambda }_{w1}\tilde{w}\Vert }_2^2+\frac{1}{2\alpha }{\Vert {\Lambda }_{w2}\tilde{w}\Vert }_2^2\right)\end{array}$$

(27)

One can see that only the errors of the observer and filter remain in the residual term $\epsilon$. Then, a proper choice of the controller’s gains is that ${\kappa }_1$ and ${\kappa }_2$ in (27) are positive. Based on Theorem 2 in [31], there exists a scalar $\delta \in \left(0,\hspace{0.17em}\hspace{0.17em}1\right)$ such that the control errors converge to the following region:

$$\underset{t\to T_f}{\lim }{V}_2\le \min \left(\frac{\epsilon }{(1-\delta ){\kappa }_1},{\left(\frac{\epsilon }{(1-\delta ){\kappa }_2}\right)}^{\frac{2}{1+\beta }}\right)$$

(28)

in a finite time $T_f$ given by

$$T_f\le \frac{2}{(1-\beta )}\max \left(\frac{1}{\delta }\ln \frac{\delta {\kappa }_1{V}_2^{\frac{1+\beta }{2}}(e_0)+{\kappa }_2}{{\kappa }_2},\hspace{0.17em}\hspace{0.17em}\frac{1}{{\kappa }_1}\ln \frac{{\kappa }_1{V}_2^{1-\beta }(e_0)+\delta {\kappa }_2}{\delta {\kappa }_2}\right)$$

(29)

which can be seen as the functions of ${\kappa }_1$ and ${\kappa }_2$. In other words, the finite-time stability of the proposed control system is preserved. □

On another note, the integral in (17) guarantees zero steady states of the projection’s motion; however, its accumulation can lead to a large overshoot and a long settling time. Therefore, an approximate integral ${\widehat{f}}_{xy}$ and the corresponding control error $s_{xy}$ are modified as follows [32,33]:

$${\dot{\widehat{f}}}_{xy}=-{\Lambda }_f{\widehat{f}}_{xy}+\eta \mathrm{sat}\frac{s_{xy}}{\eta },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{s}_{xy}=\hspace{0.17em}{e}_{xy}+{\Lambda }_f{\widehat{f}}_{xy}$$

(30)

where $\eta$ is a positive scalar and $\mathrm{sat}(\cdot )$ denotes for the saturation function. One can see that inside the boundary of the saturation, ${\dot{\widehat{f}}}_{xy}=e_{xy}$, above the positive boundary, ${\dot{\widehat{f}}}_{xy}<e_{xy}$, and otherwise ${\dot{\widehat{f}}}_{xy}>e_{xy}$. In other words, the integral action takes place completely only inside the saturation function’s boundary.

5. Experimental Studies

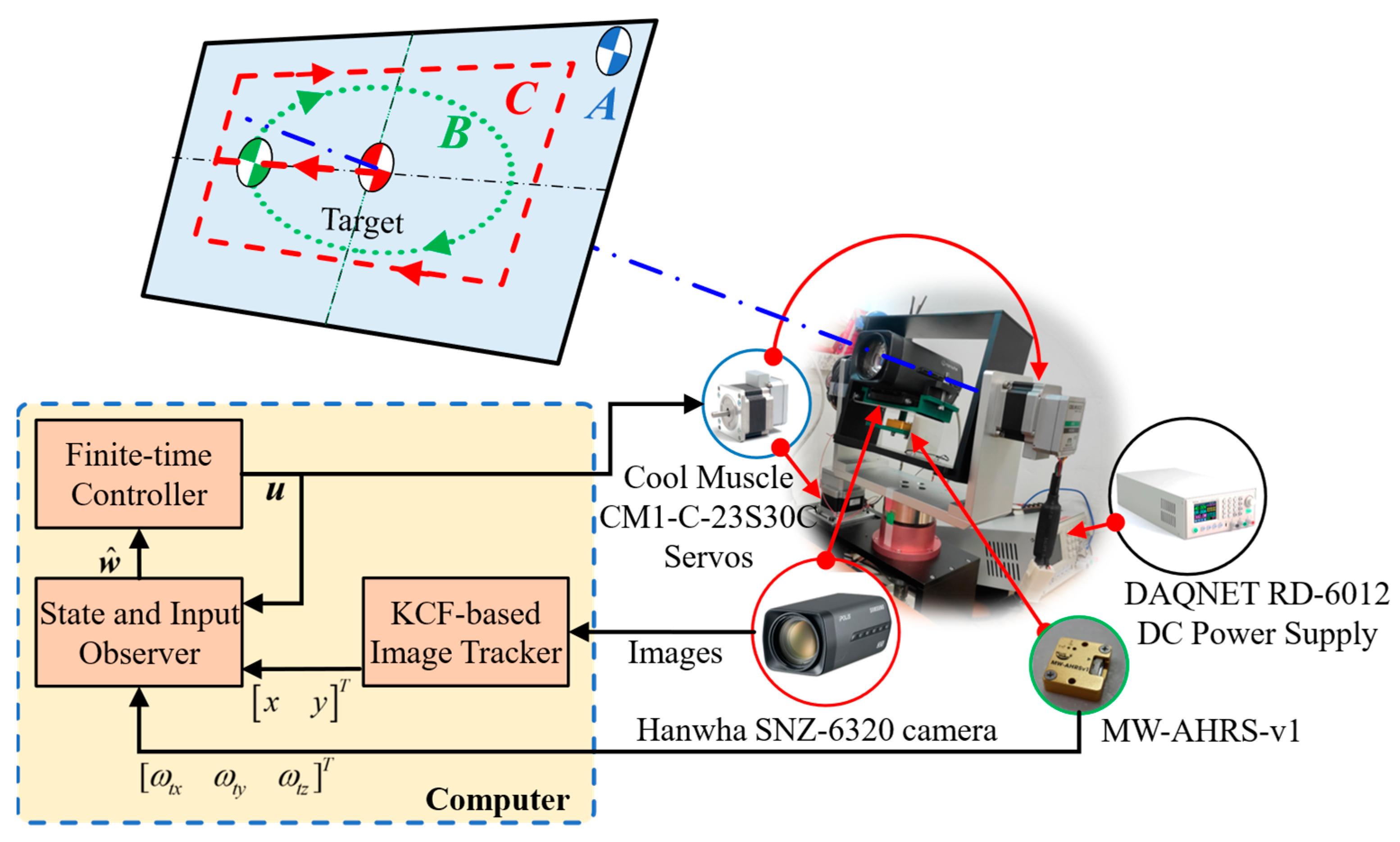
The experiments were conducted in order to validate the proposed control system. For this objective, Figure 2 depicts the experimental apparatus that was used with the proposed control scheme and experiment scenarios. In detail, the experimental system consists of a two-channel gimbal prototype that carries the Hanwha SNZ-6320 camera on its inner channel. Given a captured image from the camera that contains the tracked object, an image tracker uses the KCF algorithm [34] working with the histogram of oriented gradients (HOG) descriptor and the Gaussian kernel and returns the location of the object’s projection on this image. The rotational motions of two channels are operated by two servo systems CM1-C-23S30C from Muscle Corporation. The inner channel is directly driven by the servo, while the outer one adopts a belt drive with a gear ratio of 3:1. The orientation of the camera and the inner gimbal is sensed by an attitude heading reference system, MW-AHRS v1. Additionally, the image tracker, observer, and controller were executed by Matlab/Simulink on a desktop computer and interacted with the experimental apparatus. The gains of those are listed in

Table 1. Control system specifications.

Parameter	Value
System matrices	$\begin{array}{c}K=diag\left\{6.146,\hspace{0.17em}\hspace{0.17em}5.207\right\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}H=10I_4,\\ B_{\omega }=diag\left\{7.232,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1.402\cos \theta \right\}\end{array}$
Observer’s gains	$\begin{array}{c}L=diag\left\{33.143,\hspace{0.17em}\hspace{0.17em}33.143,\hspace{0.17em}\hspace{0.17em}41.429,\hspace{0.17em}\hspace{0.17em}41.429\right\},\\ Q=1.671I_4,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\lambda =100\end{array}$
Finite-time controller’s gains	$\begin{array}{c}{\Lambda }_f=diag\left\{0.058,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0.022\right\},\\ {\Lambda }_1=diag\left\{45.376,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}50.218\right\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\Lambda }_3=diag\left\{10.086,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}15.731\right\},\\ {\Lambda }_2=diag\left\{10.427,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}10.739\right\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\Lambda }_4=diag\left\{2.068,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2.077\right\},\\ \beta =0.667,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha =0.0001\end{array}$
Sampling time	0.05 [s]

.

The experiments involved three scenarios, as illustrated in Figure 2. In scenario A, the surveillance system had to track a stationary target whose projection’s initial location was out of the center of the image plane. In the other two scenarios, the system was required to track a moving target, i.e., a visual servoing problem. Different characteristics of the mentioned scenarios help validate different aspects of the proposed control system. In these experiments, unmatched disturbances arise from the unpredictable movement of the tracking target and constraints of the tracker, such as low-resolution measurement, long processing, and communication time. Match disturbances come from the imbalance mass of the inner gimbal, nonlinear frictions, and the actuator’s dead zone and saturation. For the sake of comparisons, the simple proportional controller from [2], the image-based pointing controller proposed by Hurak et al. [8], and the vision-based back-stepping control from [27] were also taken into the tests. The results from the tests are shown in Figure 3, Figure 4 and Figure 5, respectively. It is noted that the displayed unit of the variables x and y is [pixel], instead of [m], to correspond to displayed images in user interfaces. Additionally, the control action was taken from the 5th [s] of each test.

5.1. Experiment A

The initial location of the target’s projection is at $[\begin{array}{cc}-105& -190{]}^T\end{array}$ [pixel] in the image plane. The tilt angle of the inner channel that carries the camera was initialized at 04 [deg]. The tracking path depicted in Figure 3a shows that the backstepping control system struggled to bring the projection to zero. The proportional control system was able to do so but had difficulty in following a linear path to the image central. The main reason is the kinematic interactions of all three rotations of the gimbal mechanism in each direction of the projection’s movement and they act as additive disturbances. This results in a curve in the tracking path. Meanwhile, in both the proposed system and Hurak’s one, the interaction matrices are taken into the control law. Thus, the projections were able to follow linear paths. This is the shortest path from the initial location to the image center. This also indicated that responses in both coordinates converge smoothly to zeros at the same time without any overshoot, as clearly seen in Figure 3b,d. Additionally, the control signals in Figure 3c hint that the proposed control law requires less effort in the tilt direction in comparison with the others. After settling time, all controllers effectively stabilize the system at a steady state. However, the backstepping controller failed to compensate for the steady-state error, while the others were able to correct it. This is because of the input-to-state stability of the backstepping control system, i.e., the system is bounded by a function of the size of the input disturbances that currently exist in the gimbal camera.

5.2. Experiment B

In this experiment, the target projection was at location ${[180\hspace{0.17em}\hspace{0.17em}80]}^T$ [pixel] in the image plane in the beginning. From the 5th [s], the target moved continuously on an ellipse line in a vertical plane facing the camera from a distance of 600 [mm]. The horizontal and vertical motions of the target were given by sinusoidal trajectories with a 0.01 [Hz] frequency and 410 [mm] and 210 [mm] amplitudes, respectively. The tracking paths in Figure 4a show that all the controllers quickly brought the target’s projection to the center of the image plane and then kept it there, even with the motion of the target. However, a large variation around the image center in Figure 4a demonstrated that the comparison controllers could not track the moving target effectively. In particular, in the x-coordinate, the proportional control system and Hurak’s system result in the largest variation. In the y-coordinate, the proportional control and the backstepping control systems have the largest tracking errors, then the control system designed by Hurak et al. In contrast, the proposed control system guarantees the boundedness of the control errors in finite time, hence resulting in a small variation in the projection’s location in both coordinates during the test, which can easily be seen in Figure 4a,b. The control inputs in Figure 4c show the adjustment that the proposed controller made. Since the target followed an ellipse line, the tilt and pan rotations of the inner gimbal also followed sinusoidal trajectories, as seen in Figure 4d, so that the LOS of the carried camera could track the desired target.

5.3. Experiment C

For this test, the target moved on the same plane in the previous scenario. It departed from the intersection point of the camera’s LOS and this plane, so the initial location of its projection was at the center of the image. The target followed a rectangular trajectory with a total distance of 480 [mm] horizontally and 250 [mm] vertically. This required the inner gimbal to rotate with trapezoidal trajectories, as seen in Figure 5d. The time response in the x-coordinate of the image plane shows that the backstepping control achieved the smallest tracking error in the first half of the test period. However, it then required a lot of adjustment and resulted in a large vibration in the second half of the test. It was also the worst one from the view in the y-coordinate. The proportional approach also led to significant errors in the image plane. In particular, the tracking movement of the camera’s LOS was visibly lagging behind that of the target since this simple control strategy cannot compensate effectively for nonlinearities and disturbances in the system. Hurak’s system and the proposed one were quite comparable in the x-coordinate, but the latter showed its superiority in the other direction.

For quantitative evaluation, the root-mean-square errors (RMSEs) of the projection were computed and are listed in

Table 2. Comparison of performance indices.

Experiment	Coordinate	RMSE
		Proportional	Hurak’s	Backstep	Proposed
A	x [pixel]	5.1228	5.0181	5.0935	5.0979
	y [pixel]	2.9051	2.8063	3.3195	2.8124
B	x [pixel]	0.3269	0.2607	0.2334	0.2893
	y [pixel]	0.5041	0.3590	0.5344	0.2244
C	x [pixel]	0.6422	0.4906	0.4491	0.5515
	y [pixel]	0.5520	0.3884	0.5528	0.3350

. The results of Experiment A imply that the proposed system is only the second best. However, the time responses from Figure 3b indicate that these large values of RMSE are due to the longer rise time, especially in the x-coordinate, though the settling times are almost the same. The reason is found to be due to the lower peak velocities of the gimbal during the transient period in the proposed system, which is better from the perspective of the image-tracking algorithm. Similarly, in Experiments B and C, the proposed system achieves a significantly better RMSE in the y-coordinate, but only the third best in the other coordinate because of the large transient period of this coordination. If the transient period at the beginning of Experiment B is neglected, i.e., the zoom in Figure 4b, the RMSE of the proposed system in the x-coordinate is 0.1107 [pixel], just less than 0.0934 [pixel] of the backstepping control system. In Experiment C, apart from the transient period, the proposed system achieves the smallest steady-state error. Generally, the proposed controller shows its consistency and ought to perform better than the others. On another note, the proposed control law is quite complicated in comparison to the comparative controls, though it does not need more measurements than the others. The results of the three experiments also reveal that the proposed system requires more control adjustments, and so do the control efforts, especially in comparison to the proportional control and the control proposed by Hurak. Finally, although the proposed system achieves the smallest steady-state errors in most cases, finite-time boundedness is preserved but not the asymptotic stability.

6. Conclusions

In this paper, the novel visual servoing controller was designed and implemented for a gyro-stabilized surveillance system. The proposed control scheme consists of a disturbance observer and a continuous control law. The control system design was presented in detail, and the mathematical proofs show that the proposed scheme guarantees finite-time stability for the system. With this approach, effective visual servoing performance was obtained. In experimental studies, the proposed control system was challenged through different tracking scenarios and compared with validated approaches. The results show the stability, consistency, and effectiveness of the proposed system. In future works, a more robust tracking algorithm and control technique will be considered to achieve a fast and continuous tracking performance.