Abstract
Robotic ultrasound scanning has excellent potential to reduce physician workload, obtain higher-quality imaging, and reduce costs. However, the traditional admittance control strategy for robotics cannot meet the high-precision force control requirements for robots, which are critical for improving image quality and ensuring patient safety. In this study, an integral adaptive admittance control strategy is proposed for contact force control between an ultrasound probe and human skin to enhance the accuracy of force tracking. First, a robotic ultrasound scanning system is proposed, and the system’s overall workflow is introduced. Second, an adaptive admittance control strategy is designed to estimate the uncertain environmental information online, and the estimated parameters are used to modify the reference trajectory. On the basis of ensuring the stability of the system, an integral controller is then introduced to improve the steady-state response. Subsequently, the stability of the proposed strategy is analysed. In addition, a gravity compensation process is proposed to obtain the actual contact force. Finally, through a simulation analysis, the effectiveness of the strategy is discussed. Simultaneously, a series of experiments are carried out on the robotic ultrasound scanning system, and the results show that the strategy can successfully maintain a constant contact force under soft uncertain environments, which effectively improves the efficiency of scanning.
1. Introduction
Ultrasound (US) is a unique medical imaging technique that is widely used for lesion diagnosis and intraoperative guidance. Compared to other medical imaging methods, US has the advantages of being non-invasive, radiation-free, low-cost, and portable []. However, the traditional US procedure requires sonographers to scan the entire lesion area by using a hand-held probe. To maintain good contact between the US probe and the skin, sonographers must remain in the same position for long periods, which puts them at risk for muscle damage []. In contrast, the probe’s position, orientation, and contact force with the body surface are entirely determined by the sonographer’s experience. Hence, the probe attitude control and scanning path are random. It is difficult to quickly and accurately reproduce previous lesion images for subsequent repeat diagnosis and intraoperative guidance []. In addition, many patients report discomfort during US examinations owing to the sonographer’s shaky hands and inability to control the contact force accurately. US images have a variety of viewpoints, and even different pressures from the same viewpoint can result in clinical differences in US images, making US scanning highly dependent on the physician’s diagnostic imaging experience []. Furthermore, this technical workload has exacerbated the shortage of sonographers [], making it difficult for patients in remote rural areas to receive high-level US examinations due to the lack of experienced sonographers.
Robotic US systems have been widely studied as effective solutions []. A robotic US system is mainly composed of a manipulator that drives the movement of the probe and the US imaging device. Currently, robotic US systems are grouped into three categories according to the characteristics of the mode of operation: teleoperated, human–robot cooperation, and autonomous. In the teleoperated mode, a physician remotely controls the robotic arm to examine a patient using a joystick [] or a haptic device []. In the human–robot cooperation mode, the basic scanning trajectory is controlled by the operator, whereas the controller provides assistance in terms of contact force or vision []. Our proposed study is based on the autonomous scanning mode, in which the system performs scanning autonomously based on force sensation, vision, and other information without the help of the sonographer. Because the contact posture and contact force between the US probe and human skin greatly influence the US image quality, most studies have been conducted based on these two components. In [], the authors studied the relationship between the probe angle and image quality in depth. They concluded that the image quality was significantly improved when the US probe was oriented closer to the normal direction. Thus, the probe should remain in the normal direction when in contact with the surface of the skin tissue. In [], the authors approximated the local skin plane by randomly selecting three points around each path point to form a triangle and determine the normal vector of the plane. In [], the authors visually optimized the probe orientation using a confidence map, but it was limited to adjusting only the in-plane orientation. In [], the authors identified the normal direction using the contact force value estimated from the joint torque; however, the result was affected by the accuracy of the joint sensor.
To obtain high-quality images and ensure patient safety, maintaining appropriate contact between the probe and the skin is another crucial goal for robotic US scanning []. Therefore, many researchers have attempted to control the contact force during scanning, and the controller design can be divided into three main categories. In the first category, compatible probe holders are integrated into a robotic arm [,,,], which is designed based on unique mechanical structures. Rational control strategies have been developed for probe steering, force control, and localized scanning. However, the end-effector becomes larger, and motion adjustments become more complex, which are detrimental to the control and scanning efficiency of the robotic arm. In the second category, some systems use built-in force/torque sensors in the manipulator to estimate the contact force and maintain a constant contact force in the probe’s direction [,,,,]. In the third category, the force/torque (F/T) sensor is mounted between the end of the robotic arm and the probe to measure the force applied to the probe. Compared to the first two approaches, it not only ensures the precision of the contact force data but also makes the system lightweight; however, its disadvantage is that the F/T sensor has a high cost.
Several force control strategies have been introduced to maintain constant force contact with US probes. An adaptive fuzzy PID force control algorithm was proposed in [] to maintain the desired contact force during liver scanning. In [], the authors proposed an adaptive control strategy based on event triggering and conducted an experiment on a virtual simulation platform for the robotic US system to perform transverse abdominal scanning. In [], the authors proposed a variable-rate adaptive admittance control strategy and discussed the effectiveness of the strategy through V-rep. In [], an admittance force control system was proposed based on an F/T sensor to compensate for the force required by the sonographer during scanning. In addition, in the field of industrial robotics, a series of force tracking control strategies have been proposed, such as adaptive control [,], fuzzy logic [,], and neural networks [].
The studies mentioned above improved the force control performance from different perspectives and significantly increased its interaction experience. However, the ability of robots to perform tasks in the unknown complex environment of soft tissue skin is still limited. During human–robot interaction, not only should the response speed of force tracking and the force tracking error at the steady state be considered, but the force overshoot should also be avoided. Excessive contact force can be uncomfortable or even dangerous for patients. Unfortunately, few researchers have simultaneously considered these metrics. Therefore, we propose integral adaptive admittance control algorithms that simultaneously consider these aspects.
In order to help sonographers improve the quality of US examinations and to provide patients with a better interactive experience, this study aims to solve the force tracking problem in robotic US scanning. The key contributions of this research can be encapsulated as follows:
- (1)
- A robotic US system is constructed, the scan trajectory is visually acquired, and the real contact force is obtained through gravity compensation.
- (2)
- To solve the problems of force tracking accuracy and force overshooting, an integral adaptive admittance control (IAAC) strategy is proposed, which can effectively avoid force overshooting and maintain a stable force during scanning.
- (3)
- The proposed IAAC strategy is compared and investigated using traditional admittance (AC) control methods. The proposed control scheme is validated using an experimental platform. It is shown that the performance achieved by the proposed IAAC strategy can satisfy the requirements of soft uncertain environments, such as US scanning, and its adaptability is significantly better than that of an AC controller.
2. Robotic US Scanning System
2.1. System Setup
The system comprises five components: a 6-DoF robotic arm (EC612, ELITE, Shanghai, China), a US machine (Clover, Wisonic Medical Technology Company, Ltd., Shenzhen, China) with a linear array probe (C5-1) to acquire the B-scans, an F/T sensor (γ82, DST Sensing System Engineering Company, Ltd., Shenzhen, China), an RGB-D camera (D132s, Zhisensor Technologies Company, Ltd., Xi’an, China), and a heart phantom (BPH700, Intel, Woodruff, NC, USA), as shown in Figure 1. The system’s control algorithm is completed using Python on an Intel Corei7-5800H 2.5 GHz PC with 16 GB RAM. The US probe is attached to the end of the robot with a customized clamp, and an F/T sensor is installed between them for contact force measurements. The RGB-D camera is also attached to the end of the robot with a clamp on the side of the probe, which is used to capture the point cloud of the heart phantom.
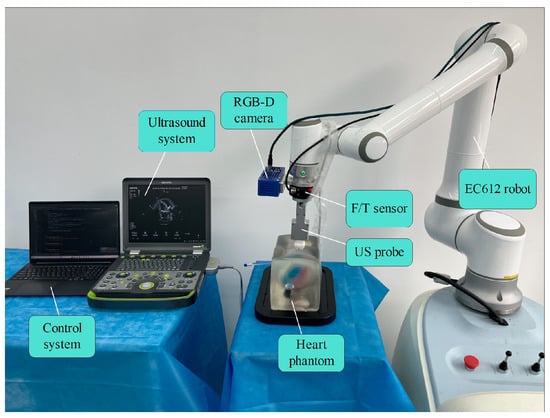
Figure 1.
Composition of robotic US scanning system.
The overall workflow of the system is shown in Figure 2. represents the expected reference position, is the expected position sent to the robotic, represents the actual position, and is the position change value of the probe in the vertical direction. represents the external contact force applied to the probe, represents the desired force, and is the difference between them. represents the joint angle of the robot. When the system operates, the point cloud information of the lesion area is first collected using an RGB-D camera. Then, the probe position is automatically outputted by point cloud processing and path planning. A point cloud normal vector finding framework is established to control the vertical direction of the US probe to ensure that it is perpendicular to the skin surface during the US scanning process. Trajectory planning is then performed for the path points, and the robot’s inner loop controller executes the scanning task. The system can control the probe to fit the skin surface for scanning and adjust the contact force in real time according to the feedback.
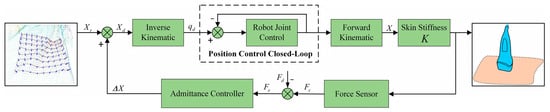
Figure 2.
The overall workflow of the system.
2.2. Gravity Compensation
To obtain the real contact force, a gravity compensation process based on the raw force data of the autonomous robotic US scanning system is performed. The coordinate system used in this study is shown in Figure 3, where the effect of the inertial forces can be disregarded because of the low speed of the robotic US system. The sensor values are mainly composed of the tool gravity , the sensor zero value , and the real contact force , and the relationship between them is given below:
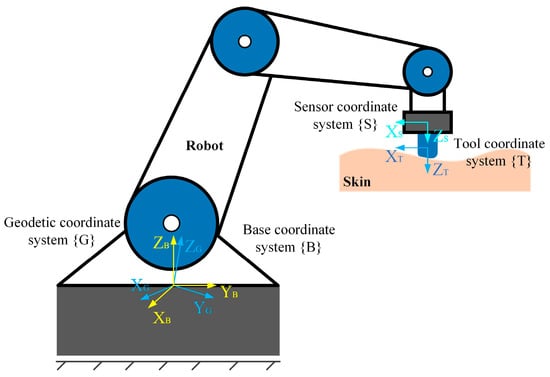
Figure 3.
The diagram of the coordinate frames.
To obtain reliable US images, it is necessary to keep the normal direction of the probe coinciding with the normal direction of the skin contact surface during the robotic US scanning process, while the human skin is irregularly curved. Therefore, the robot must adjust its attitude, resulting in a change in the probe gravity in . In addition, owing to the sensor’s phenomenon of zero drift, it is necessary to determine the actual zero value of the sensor. In this study, we collected 16 sets of sensor data under the general attitude of the robot and used the least squares method to obtain the sensor zero-point, robot mounting inclination, load gravity, and centre of mass simultaneously, thereby eliminating the influences of the sensor zero-point and load gravity on the force perception, and accurately obtained the real contact force and torque data.
The rotation matrix from to is determined using the following equation:
The definition is obtained by first rotating along the axis by an angle and then rotating it along the axis by another angle . , , and represent the zero of the three-dimensional force; , , and represent the zero of the three-dimensional torque; the load centroid position at is ; and is the identity matrix of the third order. Sensor data are obtained using the following equations:
Thus, the sensor zero-point, robot mounting inclination, load gravity, and load centroid position are derived, and the actual contact force can be determined by substituting them into Equation (1).
When the robot is separated from the environment, the external contact force should be 0 N. As shown in Figure 4, , , , , , and are calculated after gravity compensation to eliminate other influences. The RMSE of the contact force is 0.10981. The RMSE of the contact torque is 0.00832.
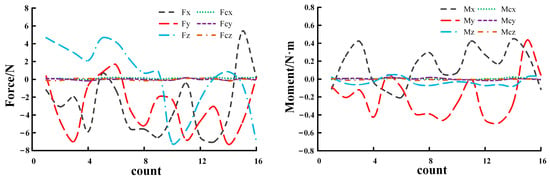
Figure 4.
Comparison of data before and after gravity compensation.
2.3. Admittance Control System Description
As shown in Figure 5a, the probe should be maintained perpendicular to the contact surface of the patient’s skin to obtain high-quality US images. Because the coupling agent with high lubrication is filled between the probe and skin during scanning, the friction in the X and Y-axis directions can be ignored. Therefore, only the contact force in the Z-axis direction must be considered, whereas only the position control is required in the X and Y-axis directions. The probe is equivalent to a second-order mass-damping-spring system to model the contact between the probe and skin. The probe and skin tissue are described as first-order spring models, which assume that the contact force is proportional to the distance of the probe embedded in the environment, as shown in Figure 5b. The contact process is divided into three stages: free space, collision, and stable contact. Accordingly, the contact force varies, as shown in Figure 5c,d, and it can be seen that there is a large force overshoot in the collision phase, which is not allowed for human–robot interactions. Although the occurrence of the collision phase is unavoidable, a compliant transition can be achieved as much as possible by improving the performance of the force control strategy. Similarly, the accuracy of force tracking during the stabilized contact phase is also a key consideration.
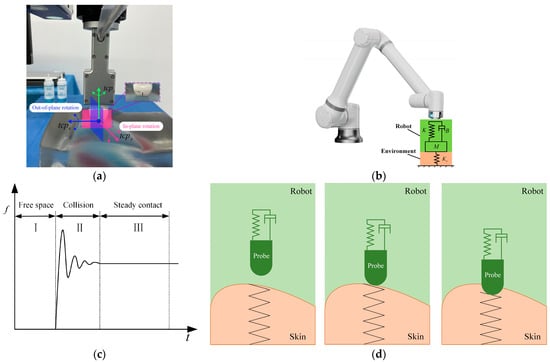
Figure 5.
Interaction model. (a) Diagram of probe motion direction. (b) Interaction model between robot and environment. (c) The process of variation for contact force. (d) Modelling the dynamic relationship between the US probe and the patient’s skin.
The actual contact force between the probe and skin tissue is simplified to a first-order spring model as follows:
where is the actual contact force between the probe and skin; and represent the environmental stiffness and position, respectively; and is the current position of the probe.
Figure 6 depicts the structure of the traditional admittance control, which was first proposed in []. The system consists of an inner position control loop and an outer admittance control loop. Because the current position controllers for cooperative robots that are used in practice have good control accuracy and tracking capability, it is considered that . Based on the force feedback information, the desired position can be calculated by adding the position deviation calculated using the admittance control outer loop to the reference position . Subsequently, the manipulator’s inner-loop position controller ensures that the robot reaches the desired position, thereby achieving compliance.
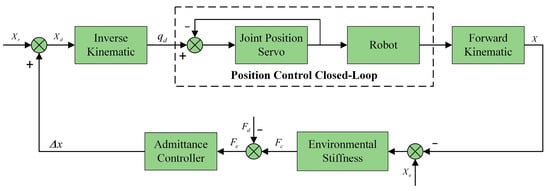
Figure 6.
Structure diagram of AC.
The traditional admittance formula is constructed as follows:
where , , and are the user-specified n-order mass and damping and stiffness diagonal matrix admittance models, respectively. Given the decoupling of the admittance control model across each degree of freedom, our focus can be exclusively directed towards the degrees of freedom along the z-axis. As a result, the matrix and vector in Equation (8) are simplified into scalars. For the sake of simplification, , , , , , , , and are replaced by , , , , , , , and respectively. Then, Equation (8) can be written as follows:
Similarly, , , and are replaced with , , and , respectively, and is replaced with . Then, Equation (7) can be written as follows:
From Equation (10), the correlation between the current probe position and the force can be expressed as follows:
In addition,
The resultant formula, derived from the amalgamation of Equations (11) and (12), is presented as follows:
Assuming that the ambient stiffness is constant, the derivative and second-order derivative of Equation (13) can be calculated as follows:
By substituting Equations (13)–(15) into Equation (9), the new formula can be expressed as follows:
The Laplace transform of Equation (16) can be obtained as follows:
For convenience, assume that the inputs are all step inputs; that is, , , and . The steady-state error of the contact force deviation is obtained as follows:
From Equation (18), there are two methods to fulfil the condition of a zero steady-state error: the first is to ensure that the admittance parameter satisfies , and the other is to ensure that satisfies the following:
Because is the key parameter in the control system, this study will be conducted using the latter approach. As shown in Equation (19), can be computed if the exact position of the environment and the exact value of the environmental stiffness are known. However, in most cases, the environmental stiffness and precise environmental position are unknown. Therefore, it is difficult to realize precise force control during the contraction process by using a traditional admittance controller.
3. Integral Adaptive Admittance Controller
3.1. Adaptive Admittance Control Strategy
In practice, and are unknown due to the uncertainty of the contact environment. It is assumed that and denote the estimates of and , respectively. Therefore, the estimates of the reference trajectory are as follows:
The actual contact force is estimated as follows:
The estimation error of the contact force is
Simplifying Equation (22) yields
where , , , and .
Therefore, the control strategy dynamically adjusts and based on the contact force error. When tends toward infinity, approaches . When , from Equations (20) and (21), we obtain
Combining Equations (9) and (24) yields
According to Equation (25), when , or . Obviously, and ; in other words, Equation (25) is satisfied by , that is, .
Based on the above analysis, the Lyapunov function is designed as follows:
where is a diagonal positive definite matrix. and are the positive constants.
The first-order derivative of is denoted as follows:
is as follows:
where represents the change rate of the estimated parameter.
The further computation of Equation (28) can be obtained:
Applying the second method of Lyapunov and combining Equations (27) and (29) yields
Since the system satisfies the stability condition , the system is stable. Furthermore, the adaptive algorithm can be expressed as follows:
where and , and they are positive scalar constants.
Finally, can be expressed as follows:
In conclusion, the designed adaptive admittance control (AAC) algorithm estimates the environmental information parameters and in real time based on the robot end-effector position and the actual contact force, and then is calculated, improving the robot’s force tracking performance.
The AAC structure is shown in Figure 7. However, steady-state tracking errors still exist because of soft unknown skin tissue. Therefore, in order to further improve the performance of the system, an integral controller is designed on the basis of AAC.
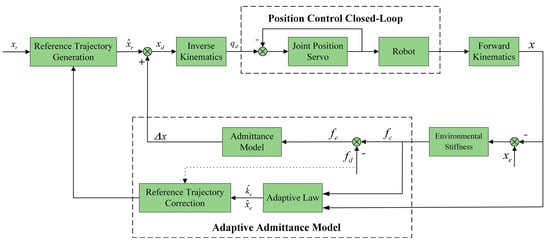
Figure 7.
Structure diagram of AAC.
3.2. Integral Adaptive Admittance Control Strategy
The AAC controller can make the steady-state error almost zero when the environmental position and the desired force are constant. However, adaptive admittance control has a significant force tracking error when the environmental position continuously changes.
To eliminate steady-state errors and improve the accuracy of force tracking, an integral controller with an improved admittance model is proposed and designed as follows:
where is the integral coefficient of force error.
It can be obtained from Equation (34) as follows:
The stability of Equation (35) can be ensured through the following characteristics:
According to the Routh criterion, the Routh array is obtained as follows:
If the stability of the system is to be satisfied, it can be obtained according to the principle of the Routh judging stability:
Simplifying Equation (38) shows that it is bounded by the following:
In the current interactive environment, the environmental stiffness is significantly greater than the admittance stiffness, which can be obtained as follows:
Equations (39) and (40) show that IAAC can maintain stability, provided that the appropriate value is chosen.
The value changes due to the complex environment; suppose , where represents a constant.
Similarly, through the application of the Laplace transform to (34) and using the final value theorem, we obtain the following:
Therefore, when , . In other words, adding an integral controller makes the control system converge to the desired force.
By comparing (18) and (42), it can be seen that with the introduction of an integral controller, the expression of the reference trajectory represented by the numerator in (42) remains unchanged. Due to the introduction of the integral term, the order of the numerator is increased, and the adaptability to the environment is improved. At the same time, the increase in the denominator reduces the steady-state error. Therefore, we conclude that it is reasonable to introduce an integral controller to improve the admittance model. This is because it not only does not weaken the control effect of AAC, but it also further reduces the steady-state error. The block diagram of IAAC is shown in Figure 8.
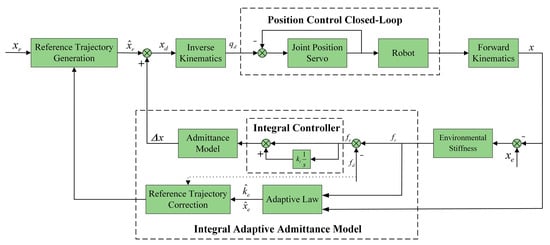
Figure 8.
Structure diagram of IAAC.
3.3. The Algorithm Implementation of IAAC
To facilitate its application in collaborative robots, the control algorithm needs to be discretized according to the sampling time. Figure 9 shows the implementation of the IAAC control algorithm. First, the relevant parameters of the system are initialized. Second, the scan path of the probe is sent to the robot. Third, the external contact force of the probe is collected from the F/T sensor, and the force error values and force error gradient are computed. Fourth, the values of , , and are obtained using the adaptive strategy. Fifth, the reference trajectory is calculated. Sixth, is substituted into the integral admittance controller, and the value of is obtained by double integration. Finally, the command trajectory at the next time is obtained and executed. From Step 3 to Step 6, a closed loop is executed cyclically. The entire control cycle period is 2 ms.
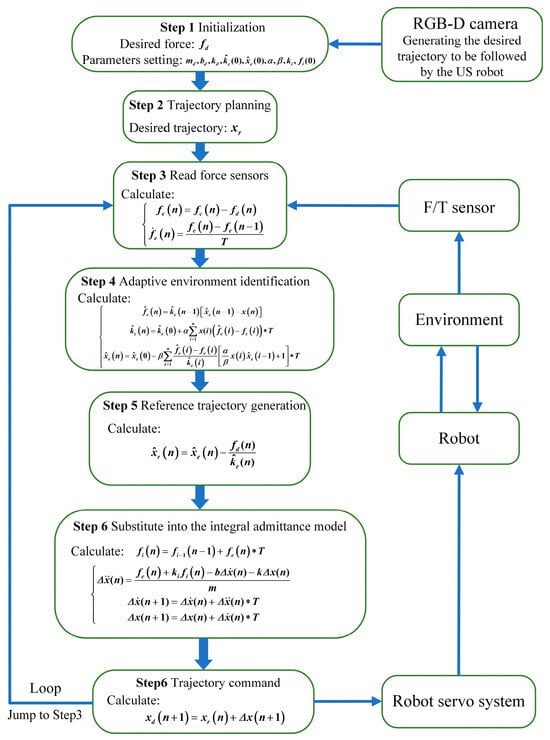
Figure 9.
Flow chart for the IAAC algorithm.
4. Simulation Studies
Simulation experiments were conducted to test and compare three controls, namely AC, IAC, and IAAC, across various environments. Tissues in various parts of the human body exhibit different shapes. For instance, the abdomen and back are relatively flat, while the chest and spine are more complex. Therefore, to test the performance of the proposed control strategy, three representative scenes (flat surface, slope surface, and sine surface) are selected for the experiment. The simulation, executed in MATLAB/Simulink, includes components like the admittance model, adaptive and integral controllers, robot motion servo system, and environmental dynamics model, as shown in Figure 10. The sample time and admittance parameters are selected, as shown in Table 1. The simulation does not consider any interference. The simulation analysis results are as follows.
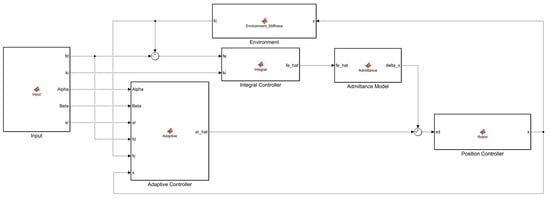
Figure 10.
The block diagram of simulation.

Table 1.
Parameter settings.
4.1. Force Tracking on Flat Surface
If the contact environment is flat, the environment position is set as , and . The desired force is set as , and Figure 11 shows the force variation curves for the three control strategies. As shown in Figure 11a, the overshoot of the AC reaches 5 N during the contact collision phase, representing a significant error compared to the desired force. Conversely, both AAC and IAAC exhibit minimal overshoot. Moreover, AC has the slowest response, whereas the other two controllers both reach the steady state within 0.2 s. In the steady-state contact phase, IAAC has a smaller error than AAC, as shown in Figure 11b. In conclusion, IAAC has a better force tracking performance.
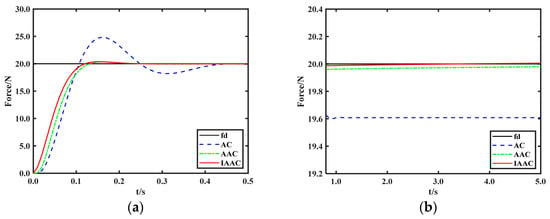
Figure 11.
Force tracking on flat surface. (a) In the contact collision phase. (b) In the steady-state contact phase.
4.2. Force Tracking on Slope Surface
If the contact environment is sloped, then , and . Figure 12 shows the force tracking and position tracking performances of AC, AAC, and IAAC when the contact environment is a sloped surface. It can be observed that the force overshoot of AC is more severe on the slope surface, and the steady-state error is larger. The overshoots of AAC and IAAC are within 2 N, and the steady-state error is small. In addition, the force tracking speed of IAAC is faster than that of AAC. In conclusion, the IAAC achieves accurate steady-state force tracking quickly with a small force overshoot in a sloped environment.
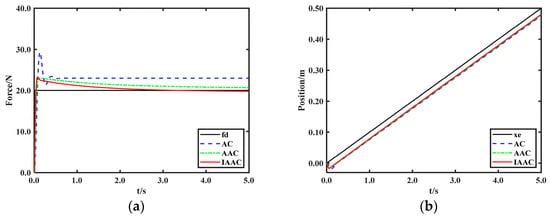
Figure 12.
Simulation results. (a) Force tracking on slope surface. (b) Position tracking on slope surface.
4.3. Force Tracking on Sine Surface
If the contact environment is a sine surface, then , and . Figure 13 shows the position tracking and force tracking performances of the three control strategies on the sine surface. It can be seen that regardless of the mode chosen, the force tracking error always exists. However, the fluctuation in the force profile is minimized for IAAC compared with AC and AAC. Overall, the force tracking performance of IAAC is the best in complex environments.
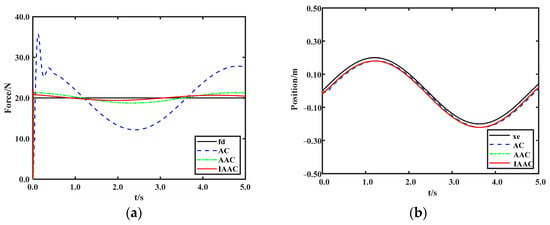
Figure 13.
Simulation results. (a) Force tracking on sine surface. (b) Position tracking on sine surface.
In addition, a comprehensive evaluation of the force tracking control performance of AC, AAC, and IAAC is conducted. The mean square error (MSE) is used for a quantitative comparison, and the comparison results are listed in Table 2. It can be seen that IAAC can achieve a good force tracking effect with an increase in environmental complexity.

Table 2.
MSE analysis of three control algorithms under simulation.
5. Experimental Studies
In order to confirm the above simulation study, we conducted experiments on a test bed, as shown in Figure 14. The composition of this test bed is detailed in Section 2, in which the RGB-D camera, robot motion controller, six-dimensional force sensor, and industrial PC communicate via an Ethernet switch. The US system and the industrial PC transmit US images using HDMI. Meanwhile, the robot and RGB-D camera communicate through the TCP/IP protocol. The F/T sensor relays the collected force information to the industrial PC via the Modbus communication protocol. Subsequently, the industrial PC combines the trajectory plan’s position with the probe position correction, calculated using the proposed force algorithm, and transmits the command to the robot motion controller.
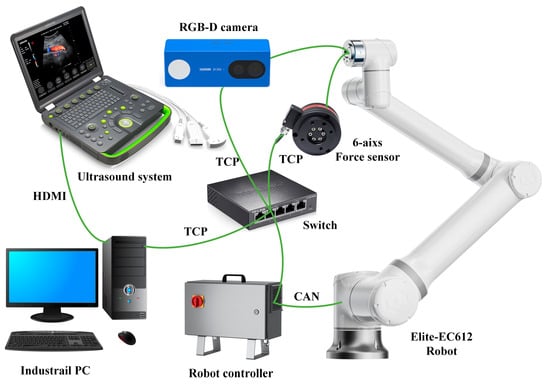
Figure 14.
Hardware architecture of experimental setup.
As shown in Figure 15, Figure 16 and Figure 17, in order to verify the accuracy of our simulation study, we conducted experiments on different tissue models, including a flat skin model, a kidney model, and a heart model. Additionally, we also presented the trajectory point cloud information of the probe on each model. Note that the stiffness values of the three models are unknown and different. To ensure the stability of the system, the relevant parameters of the controller are as follows: , , , , , , and . is obtained using an RGB-D camera. Given the quality of US imaging, we set the desired force in the Z-axis direction during probe scanning. This decision was based on our previous probe pressure experiment and the advice we received from the sonographer.

Figure 15.
Experiment on flat skin. (a) Experimental setup—flat surface skin. (b) Point cloud scan trajectories of flat surface skin.

Figure 16.
Experiment on kidney phantom. (a) Experimental setup—kidney phantom. (b) Point cloud scan trajectories of kidney phantom.
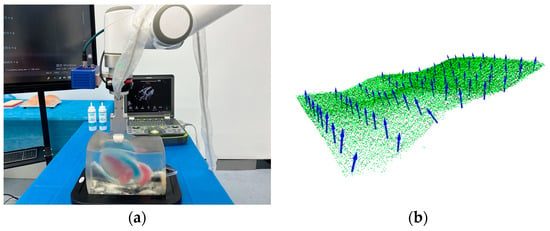
Figure 17.
Experiment on heart phantom. (a) Experimental setup—heart phantom. (b) Point cloud scan trajectories of heart phantom.
The first experiment was conducted to test the performances of AC and IAAC on flat surface skin, and the experimental results are shown in Figure 18 and Figure 19, respectively. The second and third experiments were performed on a kidney model and a heart model, respectively, as shown in Figure 20 and Figure 21, demonstrating the performance of IAAC. In the initial state, the probe moves from free space to a point above the starting point of the scan, and the desired contact force drives the robot into contact with the model. Comparing Figure 18 and Figure 19, when in contact with the flat surface skin model, AC has an initial overshoot of approximately 2 N, whereas IAAC has almost no overshoot. Both schemes stabilize at 6 N in approximately 1 s. In the steady-state phase, the contact force fluctuation range is 5.885 ± 0.315 N (5.57–6.20 N) for AC and 5.96 ± 0.14 N (5.82–6.10 N) for IAAC. Compared to AC, the force fluctuation range of IAAC is reduced by 55.6%. So, IAAC can compensate for the steady-state error of AC. Furthermore, in the kidney and heart models, the force overshoots of IAAC are 8.3% and 2.6% of the desired force, respectively. In other words, IAAC is able to track the changes in the environment position in real time by modifying the reference trajectory, which significantly reduces the fluctuation range of the contact force during the change in the environment position, and quickly realizes the desired force tracking with almost no overshoot, as shown in Figure 20 and Figure 21. In summary, the control algorithm exhibits good force tracking performance in a soft uncertain environment.
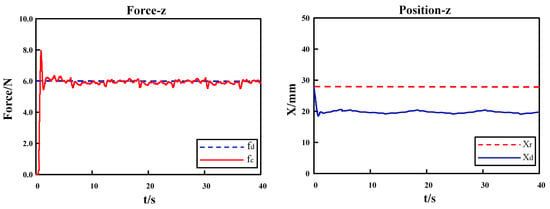
Figure 18.
Experiment I: results of AC on flat surface skin.
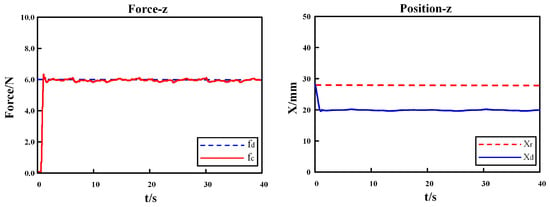
Figure 19.
Experiment I: results of IAAC on flat surface skin.
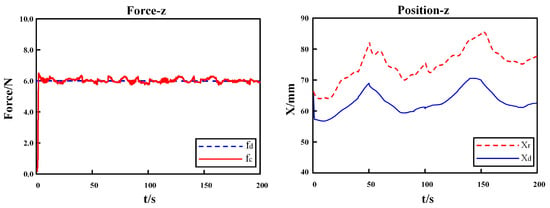
Figure 20.
Experiment II: results of IAAC on kidney phantom.
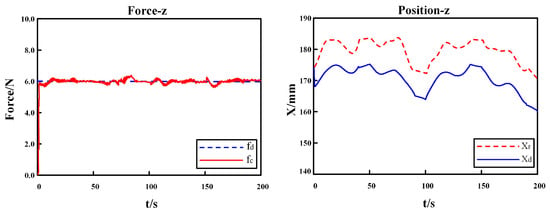
Figure 21.
Experiment III: results of IAAC on heart phantom.
6. Conclusions
A robotic US system plays a vital role in improving the efficiency of US scanning and reducing the work intensity of doctors. An integral adaptive admittance control strategy is designed in this study with the aim of solving the problem of the traditional admittance control being unable to adapt to the complex and changing environment and being unable to realize the high-precision force tracking effect. The proposed control scheme has many significant advantages over other existing methods. Firstly, the proposed strategy can estimate the environmental information in real time, respond quickly, and reduce the force overshoot effectively. Secondly, the introduction of the integral controller further improves the system’s ability to adapt to complex environments. In addition, the proposed control scheme is scalable and equally applicable to scenarios that require force interaction, such as industrial robot grinding.
In order to obtain the external actual contact force of the probe, the raw data of the force sensor are gravity compensated. The final value theorem is used to obtain the conditions under which the contact force reaches the desired force; that is, the suitable reference trajectory is required. In order to solve the problem of force tracking control under the condition of insufficient or unknown environmental information, this paper designs an adaptive control strategy from the perspective of real-time estimation of the environmental position and stiffness so as to predict and generate the subsequent reference trajectory points. Subsequently, the convergence proof of the proposed control strategy is provided in conjunction with the Lyapunov stability theory. In addition, in order to improve the system’s ability to handle complex environments, an integral controller is introduced, and the boundary conditions are obtained by combining the Routh criterion. Finally, through the final value theorem, the validity of the introduced integral controller is proven.
Through simulation experiments of three control strategies in different scenarios, it is proven that IAAC can achieve the fast and compliant adjustment of the contact force. The results show that the force overshoot is significantly reduced, and the force tracking mean square error is the smallest in IAAC compared to AC. Finally, the experiments are carried out on the robotic ultrasonic scanning system. The results show that the force overshot of IAAC is reduced by 69.2%, and the steady-state force fluctuation range is reduced by 55.6% compared with AC on the flat skin surface. On the kidney and heart models, the force overshooting values of IAAC are 8.3% and 2.6% of the desired force, respectively, and high force tracking accuracy is maintained. In conclusion, the proposed strategy can significantly improve the force control performance of a robotic US system in a soft uncertain environment. This is a promising and meaningful study because it shows that the proposed system can partially play the role of a sonographer and act as a medical assistant to reduce the workload. Future work should consider the influence of patient motions, such as breathing and heartbeats, and consider the ultrasound image quality as one of the control objectives to improve the applicability of the control strategy further.
Author Contributions
Conceptualization, H.W.; methodology, J.J.; software, J.L.; validation, X.T., F.N.; formal analysis, J.L. and L.Q.; writing—original draft preparation, J.J. and H.W.; writing—review and editing, J.J. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (grant number 2019YFB1311700) and the National Key Research and Development Program of China (grant numbers 2022YFC361400 and 2022YFC3601401).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chan, V.; Perlas, A. Basics of ultrasound imaging. In Atlas of Ultrasound-Guided Procedures in Interventional Pain Management; Narouze, S.N., Ed.; Springer: New York, NY, USA, 2011; pp. 13–19. ISBN 978-1-4939-7752-9. [Google Scholar]
- Harrison, G.; Harris, A. Work-related musculoskeletal disorders in ultrasound: Can you reduce risk? Ultrasound 2015, 23, 224–230. [Google Scholar] [CrossRef]
- Barr, R.G.; Zhang, Z. Effects of precompression on elasticity imaging of the breast: Development of a clinically useful semiquantitative method of precompression assessment. J. Ultrasound Med. 2012, 31, 895–902. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Li, Y.; Li, B.; Leng, Y.; Peng, J.; Wu, J.; Luo, B.; Chen, X.; Rong, Y.; Fu, C. Automatic Generation of Autonomous Ultrasound Scanning Trajectory Based on 3-D Point Cloud. IEEE Trans. Med. Robot. 2022, 4, 976–990. [Google Scholar] [CrossRef]
- Holzgrefe, R.E.; Wagner, E.R.; Singer, A.D.; Daly, C.A. Imaging of the peripheral nerve: Concepts and future direction of magnetic resonance neurography and ultrasound. J. Hand. Surg. Am. 2019, 44, 1066–1079. [Google Scholar] [CrossRef]
- Priester, A.M.; Natarajan, S.; Culjat, M.O. Robotic ultrasound systems in medicine. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 507–523. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Lan, J. Remote control of a robotic prosthesis arm with six-degree-of-freedom for ultrasonic scanning and three-dimensional imaging. Biomed. Signal Process. Control 2019, 54, 101606. [Google Scholar] [CrossRef]
- Sartori, E.; Tadiello, C.; Secchi, C.; Muradore, R. Tele-echography using a two-layer teleoperation algorithm with energy scaling. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 1569–1575. [Google Scholar]
- Salcudean, S.E.; Moradi, H.; Black, D.G.; Navab, N. Robot-assisted medical imaging: A review. Proc. IEEE Inst. Electr. Electron. Eng. 2022, 110, 951–967. [Google Scholar] [CrossRef]
- Jiang, Z.; Grimm, M.; Zhou, M.; Hu, Y.; Esteban, J.; Navab, N. Automatic force-based probe positioning for precise robotic ultrasound acquisition. IEEE Trans. Ind. Electron. 2021, 68, 11200–11211. [Google Scholar] [CrossRef]
- Huang, Q.; Lan, J.; Li, X. Robotic arm based automatic ultrasound scanning for three-dimensional imaging. IEEE Trans. Ind. Inform. 2019, 15, 1173–1182. [Google Scholar] [CrossRef]
- Chatelain, P.; Krupa, A.; Navab, N. Confidence-driven control of an ultrasound probe. IEEE Trans. Robot. 2017, 33, 1410–1424. [Google Scholar] [CrossRef]
- Jiang, Z.; Grimm, M.; Zhou, M.; Esteban, J.; Simson, W.; Zahnd, G.; Navab, N. Automatic normal positioning of robotic ultrasound probe based only on confidence map optimization and force measurement. IEEE Robot. Autom. Lett. 2020, 5, 1342–1349. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, B.; Zhang, P.; Yao, L.; Wang, Q.; Li, B.; Meng, M.; Hu, Y. Full-Coverage Path Planning and Stable Interaction Control for Automated Robotic Breast Ultrasound Scanning. IEEE Trans. Ind. Electron. 2023, 70, 7051–7061. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Hu, X.; Yang, K.; Zhu, Y.; Jin, H. Compliant Joint Based Robotic Ultrasound Scanning System for Imaging Human Spine. IEEE Trans. Ind. Electron. 2023, 8, 5966–5973. [Google Scholar] [CrossRef]
- Bao, X.; Wang, S.; Zheng, L.; Housden, R.J.; Hajnal, J.V.; Rhode, K. A Novel Ultrasound Robot with Force/Torque Measurement and Control for Safe and Efficient Scanning. IEEE Trans. Instrum Meas. 2023, 72, 4002012. [Google Scholar] [CrossRef]
- Lindenroth, L.; Housden, R.J.; Wang, S.; Back, J.; Rhode, K.; Liu, H. Design and integration of a parallel, soft robotic end-effector for extracorporeal ultrasound. IEEE. Trans. Biomed. Eng. 2020, 67, 2215–2229. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, T.; Wang, Y.; Jiang, W.; Yang, K.; Jin, H.; Zhu, Y. Self-adaptive ultrasound scanning system for imaging human spine. IEEE Trans. Ind. Electron. 2022, 69, 570–581. [Google Scholar] [CrossRef]
- Virga, S.; Zettinig, O.; Esposito, M.; Pfister, K.; Frisch, B.; Neff, T.; Navab, N.; Hennersperger, C. Automatic force-compliant robotic ultrasound screening of abdominal aortic aneurysms. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 508–513. [Google Scholar]
- Hennersperger, C.; Fuerst, B.; Virga, S.; Zettinig, O.; Frisch, B.; Neff, T.; Navab, N. Towards MRI-based autonomous robotic US acquisitions: A first feasibility study. IEEE Trans. Med. Imaging 2017, 36, 538–548. [Google Scholar] [CrossRef] [PubMed]
- Graumann, C.; Fuerst, B.; Hennersperger, C.; Bork, F.; Navab, N. Robotic ultrasound trajectory planning for volume of interest coverage. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 736–741. [Google Scholar]
- Kojcev, R.; Khakzar, A.; Fuerst, B.; Zettinig, O.; Fahkry, C.; DeJong, R.; Navab, N. On the reproducibility of expert-operated and robotic ultrasound acquisitions. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1003–1011. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Xu, Y.; Meng, M.Q.H. An overview of systems and techniques for autonomous robotic ultrasound acquisitions. IEEE Trans. Med. Robot. 2021, 3, 510–524. [Google Scholar] [CrossRef]
- Karar, M.E. A simulation study of adaptive force controller for medical robotic liver ultrasound guidance. Arab. J. Sci. Eng. 2018, 43, 4229–4238. [Google Scholar] [CrossRef]
- Abbas, M.; Al Issa, S.; Dwivedy, S.K. Event-triggered adaptive hybrid position-force control for robot-assisted ultrasonic examination system. J. Intell. Robot. Syst. 2021, 102, 84. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, Z. Varying rate adaptive hybrid position–impedance control for robot-assisted ultrasonic examination system. Mech. Sci. 2022, 13, 559–575. [Google Scholar] [CrossRef]
- Finocchi, R.; Aalamifar, F.; Fang, T.Y.; Taylor, R.H.; Boctor, E.M. Co-robotic ultrasound imaging: A cooperative force control approach. Mech. Imaging 2017, 10135, 270–280. [Google Scholar]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robot. Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Li, K.; He, Y.; Li, K.; Liu, C. Adaptive fractional-order admittance control for force tracking in highly dynamic unknown environments. Ind. Robot. 2023, 50, 530–541. [Google Scholar] [CrossRef]
- Cao, H.; Chen, X.; He, Y.; Zhao, X. Dynamic adaptive hybrid impedance control for dynamic contact force tracking in uncertain environments. IEEE Access 2019, 7, 83162–83174. [Google Scholar] [CrossRef]
- Li, Z.; Huang, H.; Song, X.; Xu, W.; Li, B. A fuzzy adaptive admittance controller for force tracking in an uncertain contact environment. IET Control Theory Appl. 2021, 15, 2158–2170. [Google Scholar] [CrossRef]
- Hamedani, M.H.; Sadeghian, H.; Zekri, M.; Sheikholeslam, F.; Keshmiri, M. Intelligent Impedance Control using Wavelet Neural Network for dynamic contact force tracking in unknown varying environments. Control Eng. Pract. 2021, 113, 104840. [Google Scholar] [CrossRef]
- Hogan, N. Impedance control: An approach to manipulation. In Proceedings of the 1984 American Control Conference, San Diego, CA, USA, 6–8 June 1984; pp. 304–313. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).