Free Vibration Analysis of Hydraulic Quick Couplings Considering Fluid–Structure Interaction Characteristics
Abstract
1. Introduction
2. Dynamic Model of the Hydraulic Quick Coupling System
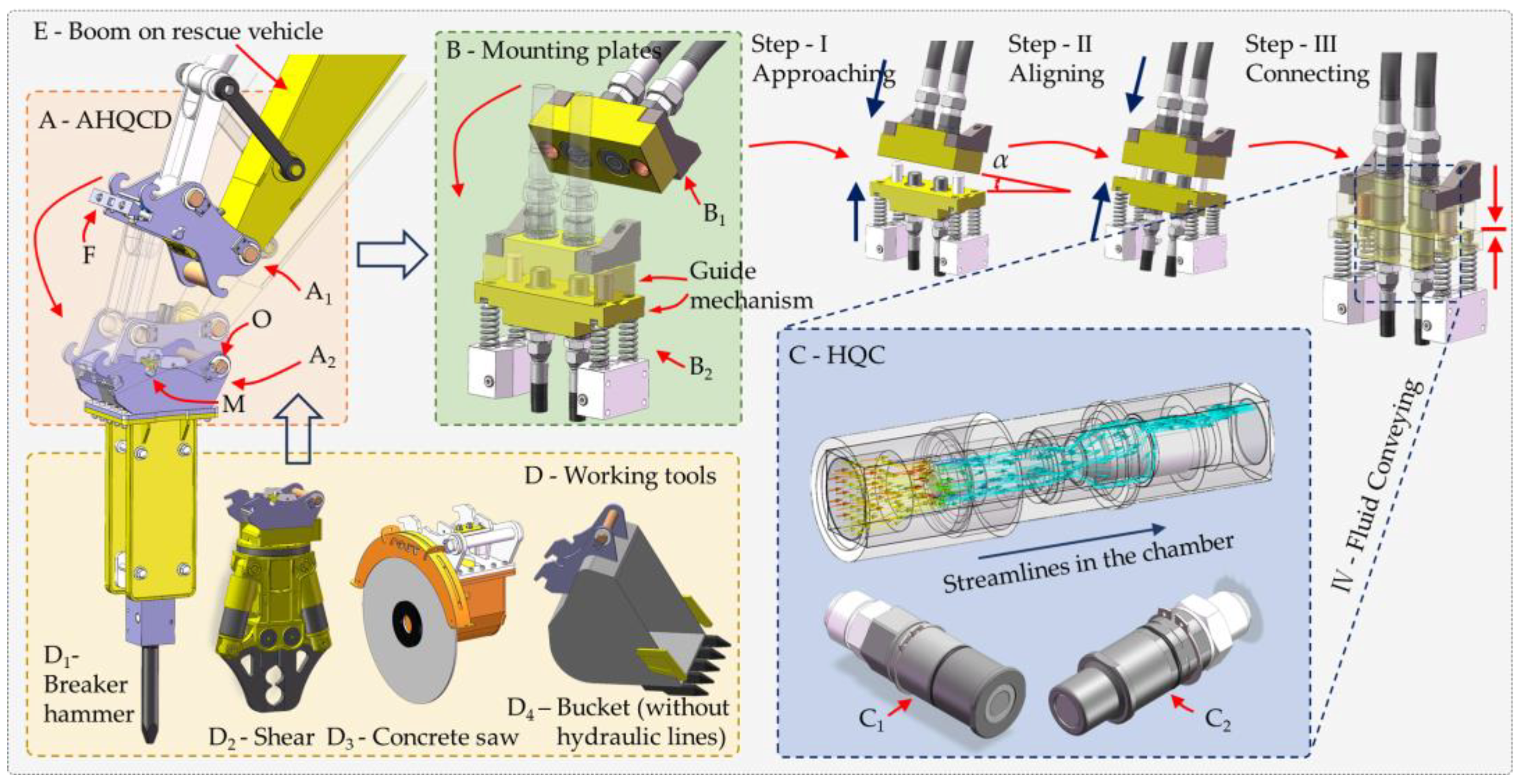
2.1. Introduction to the Automatic Hydraulic Quick Coupling Devices and Hydraulic Quick Coupling System
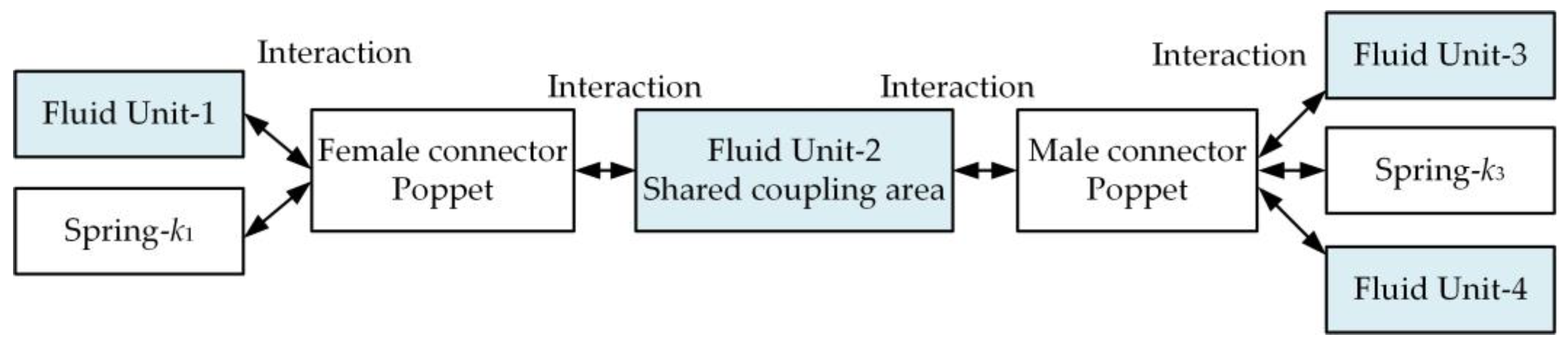
2.2. Dynamic Model of the Hydraulic Quick Couplings Considering Fluid–Structure Interaction
- (1)
- The HQC system is modeled based on the lumped parameter method. It is assumed that the density, stiffness, pressure, and other attribute parameters of each fluid unit in the HQC system are uniformly distributed across the control volume.
- (2)
- Except for the fluid units and springs, it is assumed that components such as the poppets, body enclosure, and hydraulic hoses are rigid, and their deformation under pressure is neglected.
- (3)
- Only the axial motion of the poppets is considered, and the forces exerted by the fluid units on the poppets are represented as linear spring forces in the axial direction.
- (4)
- The damping between the fluids and the poppets is reduced to linear damping in the axial direction.
- (5)
- Mechanical tolerances and installation errors, such as eccentricity, are neglected.
3. Equations of the Hydraulic Quick Coupling System
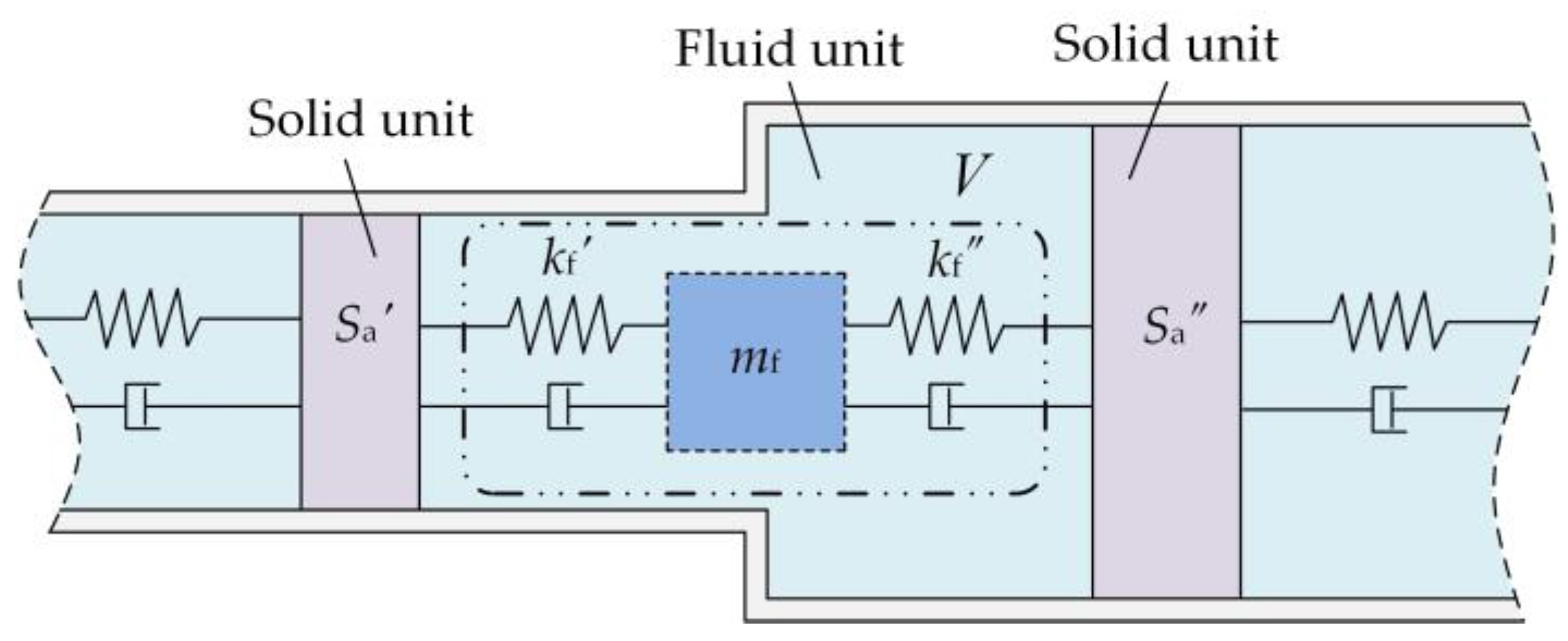
3.1. Equivalent Stiffness Model of the Fluid Unit
3.2. Free Vibration Equation of the Hydraulic Quick Coupling System
4. Modal Analysis of the Hydraulic Quick Coupling System
4.1. Natural Frequencies and Mode Shapes
4.2. Influence of Important Parameters on the Natural Frequency
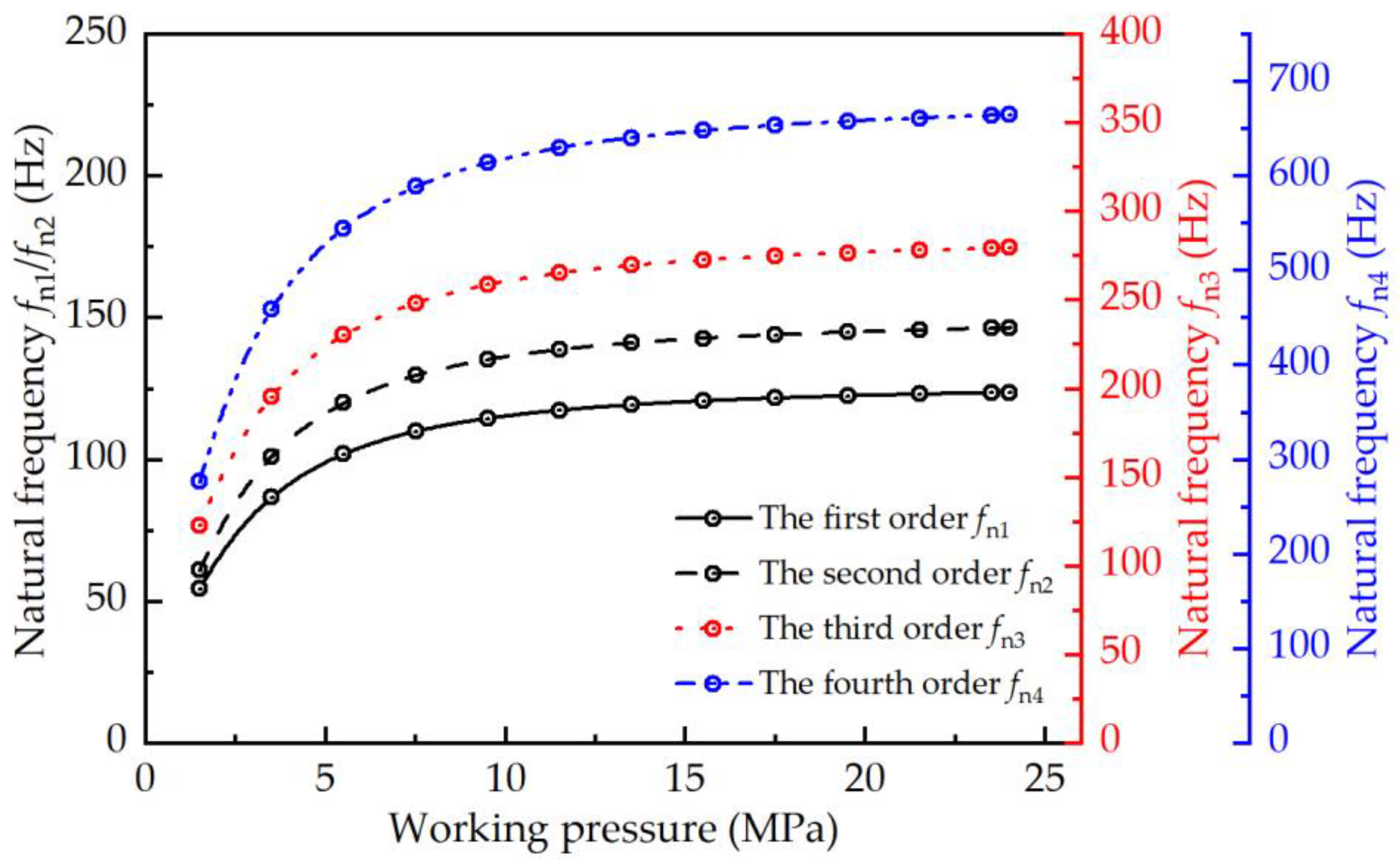
4.2.1. Effect of Working Pressure on the Natural Frequency
4.2.2. Effect of Air Content on the Natural Frequency
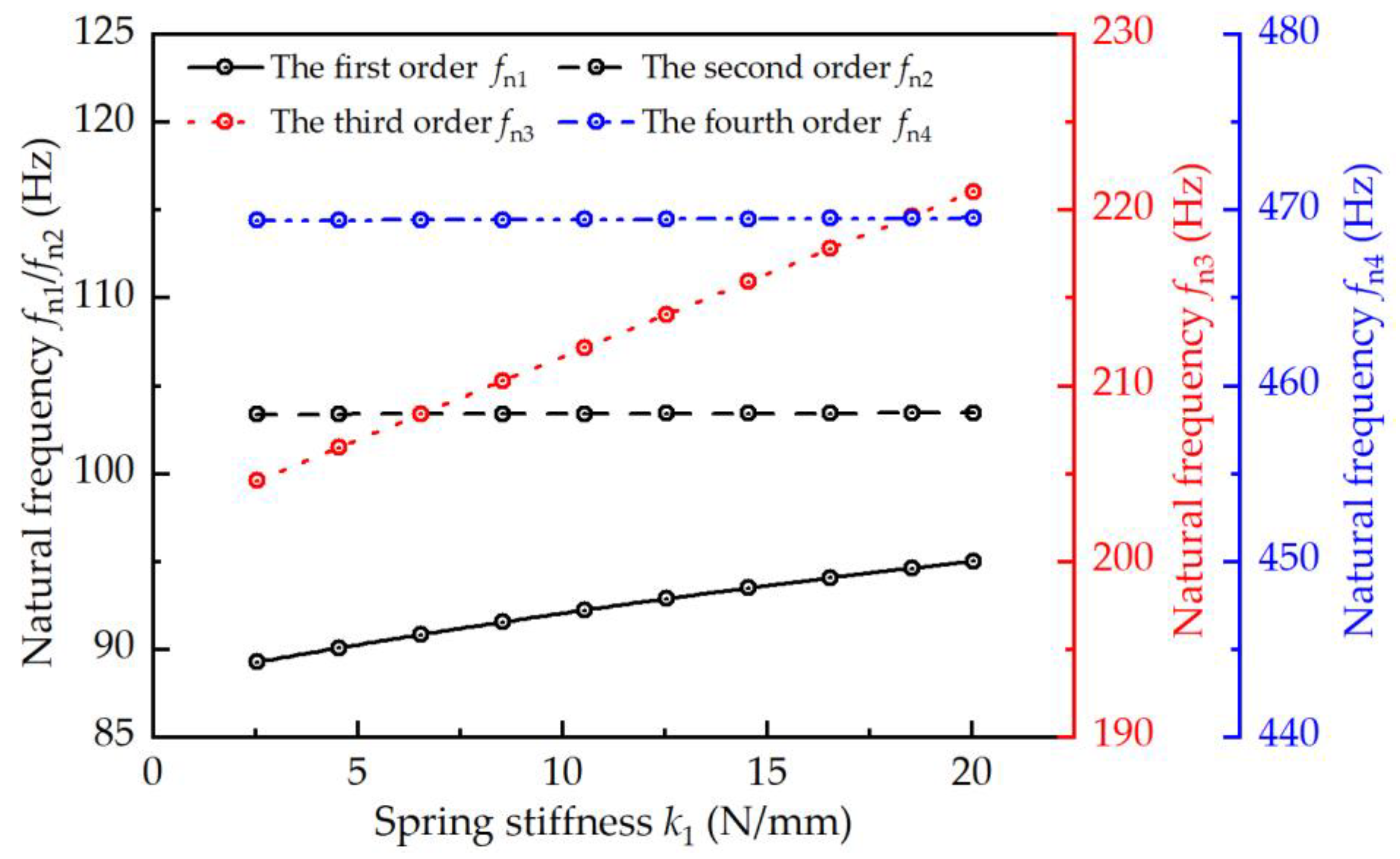
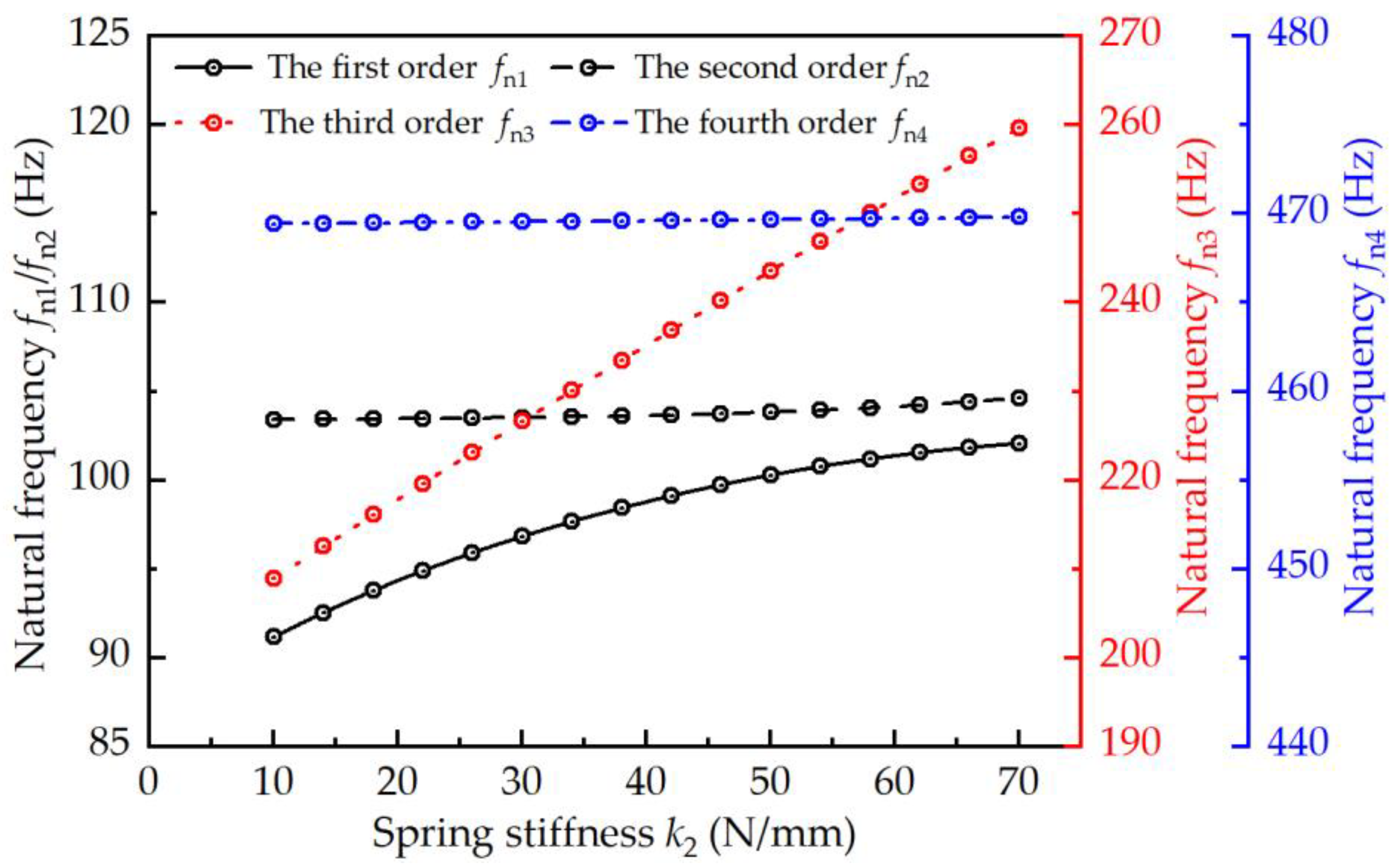
4.2.3. Effect of Spring Stiffness on the Natural Frequency
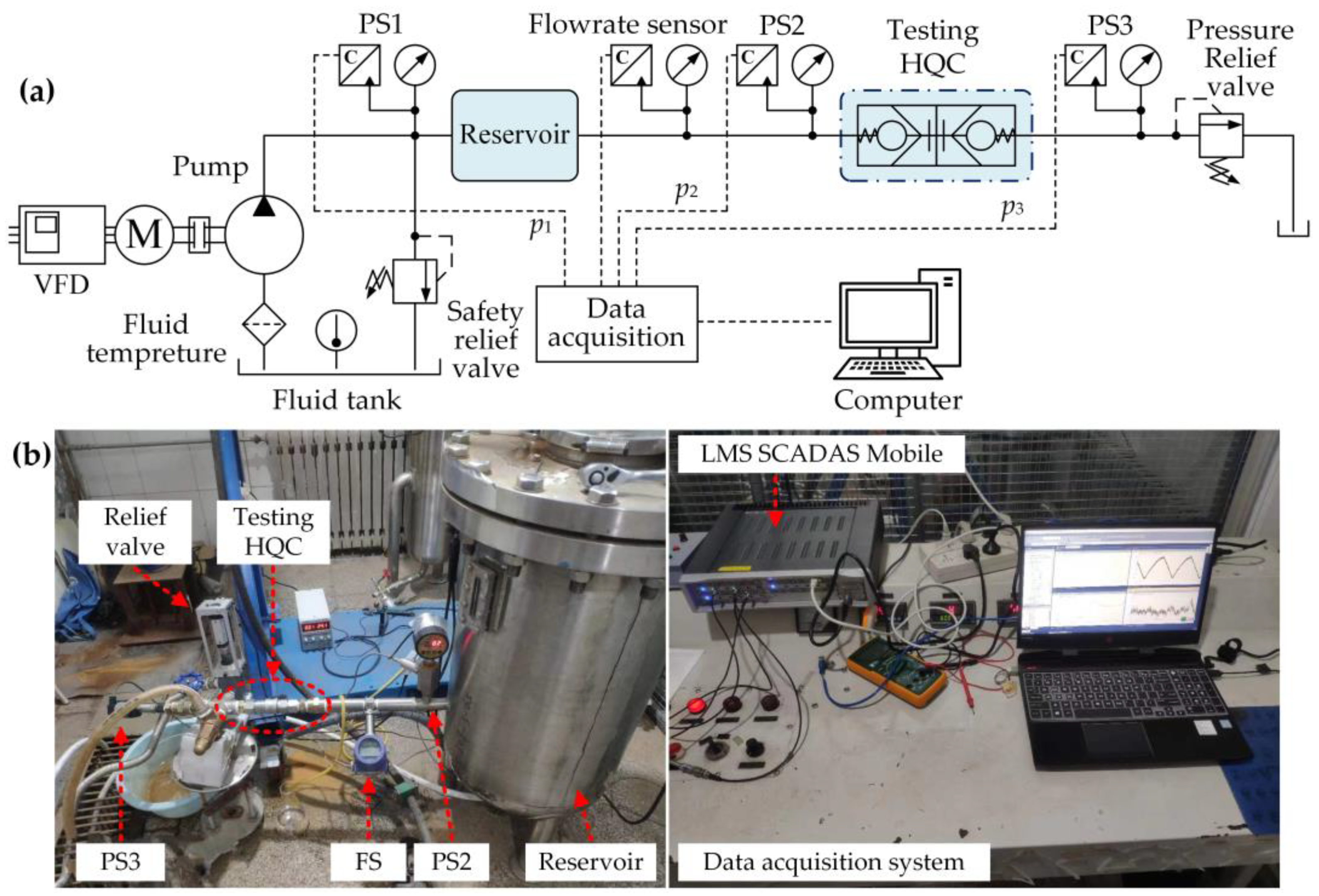
5. Experimental Verification
5.1. Experimental Set-Up
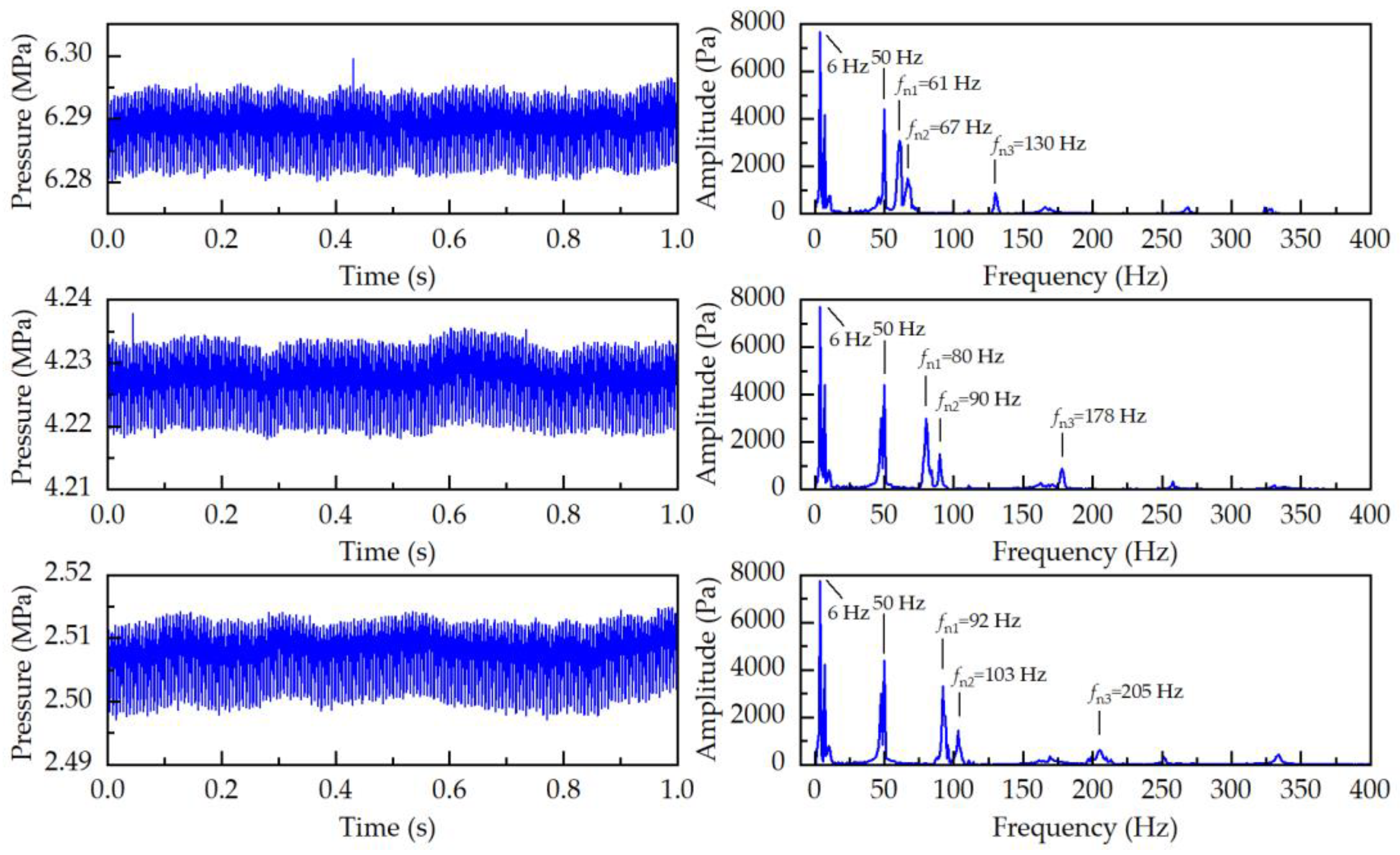
5.2. Experimental Results
6. Conclusions
- Considering the fluid–structure interaction within the HQC system, the dynamic model and 6-DOF equations were developed based on the lumped parameter method. The equivalent stiffness of the fluid units was derived and quantitatively calculated based on the compressibility of the fluid and the configuration of the HQC system.
- A free vibration analysis of the docking system was conducted. The natural frequencies for each mode, along with their corresponding mode shapes under given conditions, were obtained. The first four natural frequencies below 500 Hz were primarily analyzed, and the characteristics of poppet oscillation and pressure pulsation were thoroughly discussed under resonance conditions based on the corresponding mode shapes. Additionally, it was found that the natural frequencies increase with an increase in working pressure and a decrease in air content, while the spring stiffness only affects the first- and third-order natural frequencies.
- An experimental test platform for the dynamic model of the HQC system was constructed, and the theoretical model results were compared with experimental data based on the frequency spectrum of the pressure signal. It was found that the error in first-order natural frequency was only 2.7%, while the errors in the second-order and third-order natural frequencies were 5.8% and 6.7%, respectively. These errors may be attributed to the neglect of elastic deformation in hydraulic lines. However, both results exhibit good agreement in terms of magnitudes and trends, confirming the accuracy of the proposed model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Dong, B.; Zhang, Z.; Xu, L. Research Status and Development Trend of Intelligent Emergency Rescue Equipment. J. Mech. Eng. 2020, 56, 1–25. [Google Scholar] [CrossRef]
- Wang, Z. A preliminary report on the Great Wenchuan Earthquake. Earthq. Eng. Eng. Vib. 2008, 7, 225–234. [Google Scholar] [CrossRef]
- Chen, J.; Guan, P.; Zhang, Y. Key technology analysis of full-automatic quick coupling device of rescue vehicle. Mech. Res. Appl. 2020, 33, 238–242. [Google Scholar] [CrossRef]
- Zhong, J.; Jiang, W.; Zhang, Q.; Zhang, W. Design and Simulation of a Seven-Degree-of-Freedom Hydraulic Robot Arm. Actuators 2023, 12, 362. [Google Scholar] [CrossRef]
- Quick Coupling Systems. Available online: https://www.liebherr.com/en/usa/products/attachments/quick-couplers/quick-couplers.html (accessed on 31 October 2023).
- Automatic Quick Coupler System for Excavators. Available online: https://www.oilquick.com/en/products/oq/ (accessed on 4 May 2024).
- CW-70 Quick Coupler the Fast Connection. Available online: https://www.cat.com/zh_CN/products/new/attachments/couplers-excavator.html (accessed on 10 May 2024).
- ADX Auto-Dock Couplings. Available online: https://www.cejn.com/ (accessed on 12 May 2024).
- PC490HRD-11 High Reach Demolition machine with K100 Quick Boom Change System. Available online: https://www.komatsu.eu/en/campaign/k100-quick-boom-change-system (accessed on 1 June 2021).
- Tang, Z.; Yun, C. Quick action coupling technology in full-automatic quick coupling device: A review. J. Zhejiang Univ. Eng. Sci. 2017, 51, 461–470. [Google Scholar] [CrossRef]
- Tang, Z.; Yun, C. Precise docking technology in full-automatic quick hitch coupling device. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 1859–1872. Available online: https://html.rhhz.net/BJHKHTDXXBZRB/20170918.htm (accessed on 8 December 2024).
- Yang, Q.; Dong, R.; Luo, X.; Lv, Q. Vibration Characteristics of Hydraulic Pipe Network Under Multi-Source Excitation. Chin. Hydraul. Pneumat. 2021, 45, 163–170. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.; Zhou, X.; Li, W.; Ma, J.; Qiu, Y. Analytic expression and series expansion of pulsation pressures of aviation hydraulic pumps. J. Aerospace Power 2023, 38, 197–205. [Google Scholar] [CrossRef]
- Geng, X.; Ma, F.; Ma, W.; Zhou, Z.; Liu, Y. Experimental on Impact Powerless of Heavy Hydraulic Rock Drill with Double Damper System. J. Vib. Meas. Diagn. 2018, 38, 1051–1087. [Google Scholar] [CrossRef]
- Su, J. Characteristics analysis of breaker hydraulic system of hydraulic vibration impact robot. Hydraul. Pneum. Seals 2022, 42, 29–33. [Google Scholar] [CrossRef]
- Misra, A.; Behdinan, K.; Cleghorn, W.L. Self-excited vibration of a control valve due to fluid-structure interaction. J. Fluids Struct. 2002, 16, 649–665. [Google Scholar] [CrossRef]
- Su, Y.; He, J.; Zhang, M.; Gong, W. Vibration characteristics of a rocket engine flow pipeline under external excitation. J. Vib. Shock 2024, 43, 60–70. [Google Scholar] [CrossRef]
- Li, H.; Gu, J.; Li, J.; Sun, Z.; Sun, K.; Liu, X.; Wang, X.; Zhang, B.; Wang, X.; Ma, H. Dynamics modeling and validation of L-shaped pipeline in aero-engine subjected to base random vibration excitation and fluid pressure pulsation excitation loads. Acta Aeronaut. Astronaut. Sin. 2024, 45, 229375. Available online: https://link.cnki.net/urlid/11.1929.V.20240204.0851.004 (accessed on 8 December 2024).
- Persson, B.N.J.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter 2008, 20, 315011. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Wu, W.; Yu, B.; Zhang, P. Effects of Vibration and Shock on the Transient Performance of the Mechanical Seal. Tribology 2024, 44, 1–13. [Google Scholar] [CrossRef]
- Pan, Y.; Cai, T.; Ma, F.; Qiu, L.; Gao, L. Device Configuration and Frequency Characteristics of Self-resonating Water Jet. J. Mech. Eng. 2020, 56, 207–213. [Google Scholar] [CrossRef]
- Cao, Y.; Guo, X.; Ma, H.; Ge, H.; Li, H.; Lin, J.; Jia, D.; Wang, B.; Ma, Y. Dynamic modelling and natural characteristics analysis of fluid conveying pipeline with connecting hose. Mech. Syst. Sig. Process. 2023, 193, 110244. [Google Scholar] [CrossRef]
- Ding, H.; Tan, X.; Dowell, E.H. Natural frequencies of a super-critical transporting Timoshenko beam. Eur. J. Mech. A Solids 2017, 66, 79–93. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, C.; Zhao, S.; Zhang, L. Analysis of Free Vibration of Adaptive Head Jet System of Fire Water Monitor. J. Mech. Eng. 2020, 56, 256–262. [Google Scholar] [CrossRef]
- Yuan, X.; Zhu, X.; Wang, C.; Zhang, L.; Zhu, Y. Natural Frequency Sensitivity Analysis of Fire-Fighting Jet System with Adaptive Gun Head. Processes 2019, 7, 808. [Google Scholar] [CrossRef]
- Liao, M.; Zheng, Y.; Gao, Z.; Song, W. Fluid-structure coupling modelling and parameter optimization of a direct-acting relief valve for underwater application. Nonlinear Dyn. 2021, 105, 2935–2958. [Google Scholar] [CrossRef]
- Kang, J.; Yuan, Z.; Wang, J. Numerical study on hydrodynamic oscillation and forced vibration in front stage of pressure servo valve. J. Vib. Shock 2021, 40, 120–128. [Google Scholar] [CrossRef]
- Chris, B.; Abraham, E. Analysis of flow-induced instability in a redesigned steam control valve. Appl. Therm. Eng. 2015, 83, 40–47. [Google Scholar] [CrossRef]
- Buscarino, A.; Famoso, C.; Fortuna, L.; La Spina, G. Nonlinear Jump Resonance: Recent Trends from Analysis to Electronic Circuits Implementations. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1727–1732. [Google Scholar] [CrossRef]
- Wu, W.; Tian, G.; Hao, Q. Analysis and optimization of abnormal opening of main port of relief valve under alternating pressure. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 46, 78–83. [Google Scholar] [CrossRef]
- Ma, F.; Jin, C.; Liu, Y.; Shen, Y.; Gao, L. Multi-Degree-of-Freedom Automatic Center-Adjusting Device, Hydraulic Quick-Coupling Device, and Rescue Equipment. U.S. Patent No. US 11,035,093 B2, 15 June 2021. [Google Scholar]
- Wei, C.; Zhou, J.; Yuan, S. Comparison of Steady and Dynamic Models for the Bulk Modulus of Hydraulic Oils. Acta Armamentarii 2015, 36, 1153–1159. [Google Scholar] [CrossRef]
- Clayton, T.C.; Donald, F.E.; Barbara, C.W.; John, A.R. Engineering Fluid Mechanics, 9th ed.; John Wily & Sons, Inc.: New York, NY, USA, 2009. [Google Scholar]




| Fluid Unit | Segment | Axial Length of the Fluid Domain Li/(mm) | Average Area of Flow Cross-Section Sai/(mm2) |
|---|---|---|---|
| Fluid Unit 1 | I–II | L1 = 1500 | Sa1 = 401.1 |
| II–III | L2 = 55.5 | Sa2 = 201.1 | |
| III–IV | L3 = 7.5 | Sa3 = 471.4 | |
| IV–V | L4 = 13.5 | Sa4 = 283.5 | |
| V–VI | L5 = 8 | Sa5 = 57.7 | |
| VI–I | L6 = 34.5 | Sa6 = 99.5 | |
| Fluid Unit 2 | II–VII | L8 = 26.1 | Sa8 = 171.1 |
| Fluid Unit 3 | VII–VIII | L10 = 26.5 | Sa10 = 35.3 |
| VIII–IX | L11 = 5.2 | Sa11 = 283.5 | |
| IX–X | L12 = 40 | Sa12 = 153.9 | |
| X–XI | L13 = 1500 | Sa13 = 201.1 | |
| Fluid Unit 4 | III–VIII | L9 = 36.75 | Sa9 = 63.6 |
| Poppet | Location of the End Face 1 | End Face Area Api/mm2 |
|---|---|---|
| Female poppet | VI | Ap11 = 68.33 |
| I | Ap12 = 37.70 | |
| Male poppet | VII | Ap21 = 168.73 |
| III | Ap22 = 63.62 |
| Fluid Unit | Equivalent Stiffness (N/mm) | Value |
|---|---|---|
| Fluid Unit 1 | kf11 | 199.7 |
| kf12 | 7.6 | |
| Fluid Unit 2 | kf21 | 1761.8 |
| kf22 | 8460.1 | |
| Fluid Unit 3 | kf31 | 62.2 |
| kf32 | 88.4 | |
| Fluid Unit 4 | kf41 | 8.8 |
| kf42 | 8.8 |
| Parameter Name | Value |
|---|---|
| Mass of female poppet m1 (kg) | 0.029 |
| Mass of male poppet m3 (kg) | 0.022 |
| Mass of Fluid Unit 1 mf1 (kg) | 0.4934 |
| Mass of Fluid Unit 2 mf2 (kg) | 0.0041 |
| Mass of Fluid Unit 3 mf3 (kg) | 0.2802 |
| Mass of Fluid Unit 4 mf4 (kg) | 0.0020 |
| Stiffness of the spring for female poppet k1 (N/mm) | 1.23 |
| Stiffness of the spring for male poppet k2 (N/mm) | 3.85 |
| Density of hydraulic oil ρ (kg·m−3) | 875 |
| Initial gas content of hydraulic oil α (%) | 5 |
| Bulk elastic modulus of hydraulic oil Ev (MPa) | 700 |
| Temperature T (°C) | 25 |
| Order | First-Order | Second-Order | Third-Order | Fourth-Order | Fifth-Order | Sixth-Order | |
|---|---|---|---|---|---|---|---|
| Natural frequency fni/Hz | fn1 | fn2 | fn3 | fn4 | fn5 | fn6 | |
| 88.7 | 103.4 | 203.4 | 469.4 | 1691 | 8505 | ||
| Modal shapes uni | Fluid Unit 1 | 0.1408 | 1 | −0.0127 | 0 | 0.0001 | 0 |
| Female poppet | 1 | −0.1146 | 1 | −0.0239 | −0.8379 | −0.0217 | |
| Fluid Unit 2 | 0.9993 | −0.1187 | 0.9782 | −0.0206 | 0.7153 | 1 | |
| Male poppet | 0.9990 | −0.1195 | 0.9729 | −0.0198 | 1 | −0.1558 | |
| Fluid Unit 3 | 0.9786 | −0.2296 | −0.1973 | 0.0005 | −0.0020 | 0 | |
| Fluid Unit 4 | 0.5182 | −0.0628 | 0.6002 | 1 | −0.0413 | 0.0002 | |
| Parameter | Value |
|---|---|
| Bulk modulus of elasticity Ev (MPa) | 220 |
| Viscosity μ (N·s/m2) | 1 × 10−3 |
| Mass density ρ (kg·m−3) | 998 |
| Order | Pressure Conditions | Experimental Data (Hz) | Proposed Model (Hz) | Error (%) | |
|---|---|---|---|---|---|
| fn1 | 2.51 | 61 | 62.5 | 2.4 | Avg. 2.7 |
| 4.23 | 80 | 82.2 | 2.8 | ||
| 6.29 | 92 | 94.7 | 2.9 | ||
| fn2 | 2.51 | 67 | 70.0 | 4.5 | Avg. 5.8 |
| 4.23 | 90 | 94.8 | 5.3 | ||
| 6.29 | 103 | 110.9 | 7.6 | ||
| fn3 | 2.51 | 130 | 136.2 | 4.8 | Avg. 6.7 |
| 4.23 | 178 | 190.4 | 6.9 | ||
| 6.29 | 205 | 222.4 | 8.4 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ma, F.; Geng, X.; Wang, S.; Zhou, Z.; Jin, C. Free Vibration Analysis of Hydraulic Quick Couplings Considering Fluid–Structure Interaction Characteristics. Actuators 2024, 13, 515. https://doi.org/10.3390/act13120515
Liu Y, Ma F, Geng X, Wang S, Zhou Z, Jin C. Free Vibration Analysis of Hydraulic Quick Couplings Considering Fluid–Structure Interaction Characteristics. Actuators. 2024; 13(12):515. https://doi.org/10.3390/act13120515
Chicago/Turabian StyleLiu, Yuchao, Fei Ma, Xiaoguang Geng, Songyuan Wang, Zhihong Zhou, and Chun Jin. 2024. "Free Vibration Analysis of Hydraulic Quick Couplings Considering Fluid–Structure Interaction Characteristics" Actuators 13, no. 12: 515. https://doi.org/10.3390/act13120515
APA StyleLiu, Y., Ma, F., Geng, X., Wang, S., Zhou, Z., & Jin, C. (2024). Free Vibration Analysis of Hydraulic Quick Couplings Considering Fluid–Structure Interaction Characteristics. Actuators, 13(12), 515. https://doi.org/10.3390/act13120515







