Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators
Abstract
1. Introduction
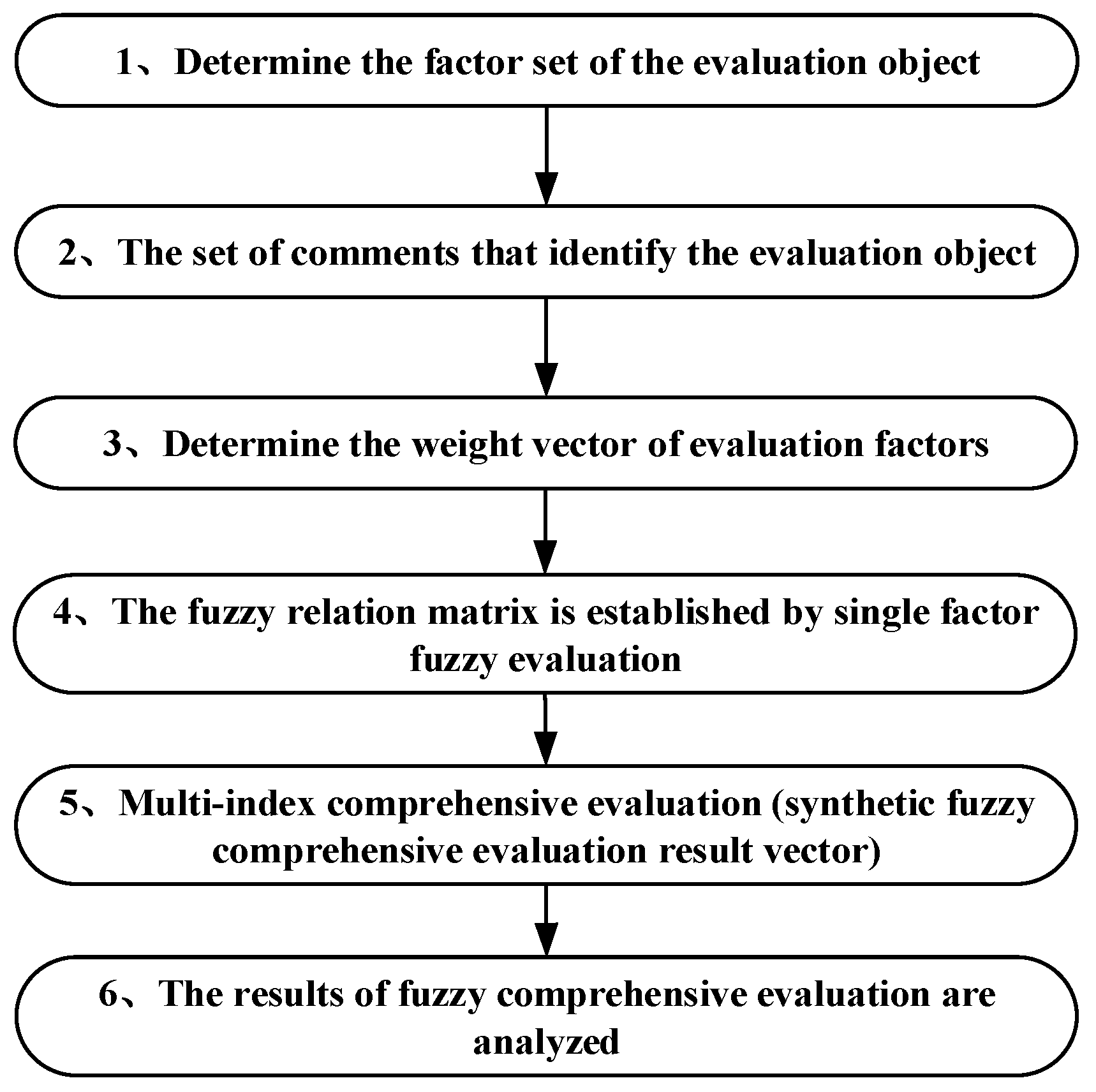
- In view of the shortcomings of traditional FMECA, fuzzy FMECA for EMA was proposed. We analyzed the PMSM of EMA using traditional FMECA and then built a fuzzy FMECA model for EMA based on the comments of industry experts and experimental experience, including the fuzzy comprehensive evaluation matrix and the method of fuzzy comprehensive evaluation.
- PMSM (Permanent Magnet Synchronous Motor) was further analyzed as the key component of EMA to give an example of using fuzzy FMECA on EMA. The result came out that the interturn short circuit fault is the highest risk of failure in PMSM, and the ranking of faults were also presented. Finally, the results of fuzzy FMECA and traditional FMECA were compared to prove the correctness and progressiveness of the method.
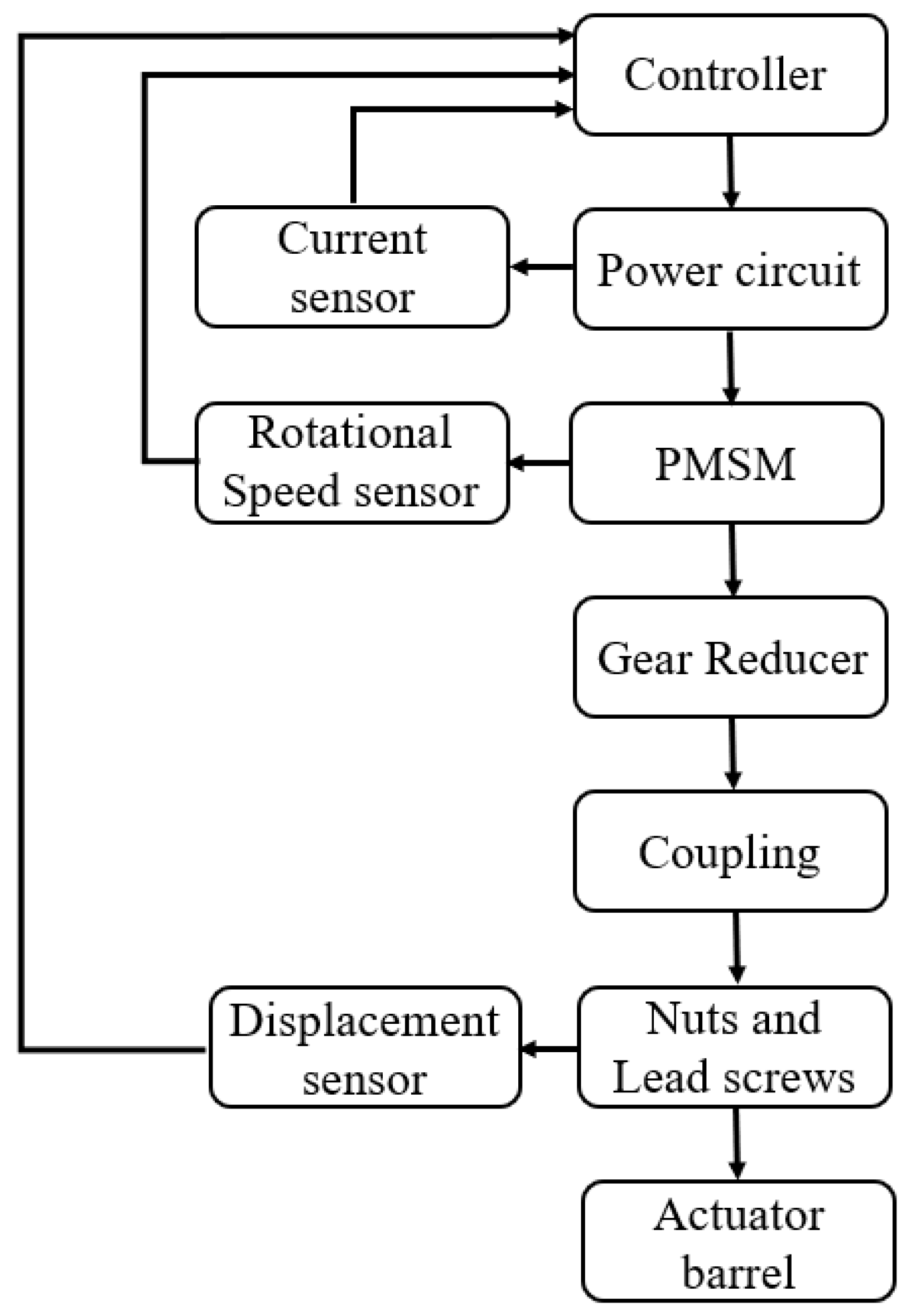
2. Structure and Working Principle of EMA
2.1. Driving Part
2.2. Reduction Part
2.3. Transmission Part
2.4. Feedback Part
3. Fuzzy FMECA of PMSM
3.1. Traditional FMECA of PMSM
3.2. Determine the Factor Set of PMSM
3.3. Determine the Comments Set of PMSM
3.4. Determine the Fuzzy Evaluation Matrix of PMSM
3.5. Determine the Weight by the Analytic Hierarchy Method
3.6. Primary Fuzzy Comprehensive Evaluation of PMSM
3.7. Secondary Fuzzy Comprehensive Evaluation of PMSM
3.8. Sharpening of Evaluation Results of PMSM
3.9. Comprehensive CA Model for Evaluation of PMSM
4. Conclusions
- (1)
- This paper analyzed the structure and working principle of EMA, comprehensively analyzed the four components and working principles of EMA, laid the foundation for the subsequent failure mode analysis, and identified PMSM as the research object.
- (2)
- The traditional FMECA method was used to analyze nine common faults of PMSM, the most important components of EMA. The results showed a general rank of the risk of the failure modes of PMSM, but we cannot get the specific ranking of failure modes.
- (3)
- In view of the limitation of the traditional FMECA method, which is easily affected by subjective factors, fuzzy comprehensive evaluation was applied to quantify the qualitative evaluation index. Then, the fuzzy FMECA model based on fuzzy comprehensive evaluation was constructed. Nine kinds of faults in PMSM were analyzed and ranked by the FMECA method based on fuzzy comprehensive evaluation.
- (4)
- Finally, the results of fuzzy FMECA were compared with traditional FMECA. It came out that fuzzy FMECA can bring out a more precise and quantitative result. Both the results showed that the interturn short-circuit fault was the riskiest fault in PMSM.
- (5)
- In the future, we will conduct further research and experiments on the fault diagnosis and prediction of PMSM in EMA based on the research results of this article, combined with deep learning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Canciello, G.; Cacciapuoti, L.; Perrotta, A.; Guida, B.; Cavallo, A. Multi-Objective Supervisory Control in More-Electric Aircraft Using Model Predictive Control: An ORCHESTRA Application. Energies 2024, 17, 3799. [Google Scholar] [CrossRef]
- Wang, L.; Dai, Z.; Yang, S.; Mao, L.; Yan, Y. Overview of Research on Intelligent Design of Electrified Aircraft Power System. Chin. J. Aeronaut. 2019, 40, 522405. (In Chinese) [Google Scholar]
- Li, M.; Wang, Y.; Peng, P.; Chen, Z. Toward efficient smart management: A review of modeling and optimization approaches in electric vehicle-transportation network-grid integration. Green Energy Intell. Transp. 2024, 3, 100181. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, J. Overview of the Development of High Power, High Performance and Redundancy Aerospace Electric Servo Technology. Navig. Position. Timing 2017, 4, 1–7. (In Chinese) [Google Scholar]
- Qiao, G.; Liu, G.; Shi, Z.; Wang, Y.; Ma, S.; Lim, T.C. A review of electromechanical actuators for more/all electric aircraft systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4128–4151. [Google Scholar] [CrossRef]
- Bertolino, A.C.; De Martin, A.; Jacazio, G.; Sorli, M. Design and Preliminary Performance Assessment of a PHM System for Electromechanical Flight Control Actuators. Aerospace 2023, 10, 335. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Miao, Q. An attention graph stacked autoencoder for anomaly detection of electro-mechanical actuator using spatio-temporal multivariate signals. Chin. J. Aeronaut. 2024, 37, 506–520. [Google Scholar] [CrossRef]
- Sulaiman, S.F.; Ngateni, N.A.; Osman, K.; Samsudin, S.I.; Sulaiman, N.A.; Sunar, N. Modeling and Development of Predictive Controller for Positioning Control of Electro-Hydraulic Actuator (EHA) System. Przegląd Elektrotechniczny 2024, 2024, 177–181. [Google Scholar] [CrossRef]
- Du, S.; Zhou, J.; Hong, J.; Zhao, H.; Ma, S. Application and progress of high-efficiency electro-hydrostatic actuator technology with energy recovery: A comprehensive review. Energy Convers. Manag. 2024, 321, 119041. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, N.; Chen, J.; Yang, Y.; Shen, G. A review of fault diagnosis, prognosis and health management for aircraft electromechanical actuators. IET Electr. Power Appl. 2022, 16, 1249–1272. [Google Scholar] [CrossRef]
- de la Hoz, C.C.; Fioriti, M.; Boggero, L. Performance and Reliability Evaluation of Innovative High-Lift Devices for Aircraft Using Electromechanical Actuators. Aerospace 2024, 11, 468. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, X.; Yang, J.; Mao, Q. Review of fault diagnosis technology for flight electromechanical actuation system. Electr. Drive 2022, 52, 3–11. (In Chinese) [Google Scholar]
- Spreafico, C.; Russo, D.; Rizzi, C. A state-of-the-art review of FMEA/FMECA including patents. Comput. Sci. Rev. 2017, 25, 19–28. [Google Scholar] [CrossRef]
- Luo, X.; He, H.; Zhang, X.; Ma, Y.; Bai, X. Failure Mode Analysis of Intelligent Ship Positioning System Considering Correlations Based on Fixed-Weight FMECA. Processes 2022, 10, 2677. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, C.; Tan, L.; Cui, J.; Xiao, W.; Liu, J.; Wang, H.; Wang, T. Reliability analysis of subsea manifold system using FMECA and FFTA. Sci. Rep. 2024, 14, 22873. [Google Scholar] [CrossRef]
- Elidolu, G.; Teixeira, Â.P.; Arslanoğlu, Y. A risk assessment of inhibited cargo operations in maritime transportation: A case of handling styrene monomer. Ocean Eng. 2024, 312, 119049. [Google Scholar] [CrossRef]
- Tian, J.; Shi, E.; Zhong, J.; Chen, Y.; Deng, X.; Li, G. Reliability Analysis and Structural Optimization of Circuit Board Based on Vibration Mode Analysis and Random Vibration. Processes 2024, 12, 1726. [Google Scholar] [CrossRef]
- Yousaf, A.; Amro, A.; Kwa, P.T.H.; Li, M.; Zhou, J. Cyber risk assessment of cyber-enabled autonomous cargo vessel. International Journal of Critical Infrastructure Protection. Int. J. Crit. Infrastruct. Prot. 2024, 46, 100695. [Google Scholar] [CrossRef]
- Huang, C.; Wu, J.; Shan, Z.; Wang, Q.; Yu, Z. Reliability Prediction for New Prefabricated Track Structures Based on the Fuzzy Failure Modes, Effects, and Criticality Analysis Method. Appl. Sci. 2024, 14, 5338. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, L.; Zhao, J.; Qi, Z.; Deng, H. An improved FMECA method for equipment reliability based on information fusion. Phys. Scr. 2024, 99, 055207. [Google Scholar] [CrossRef]
- Sezer, S.I.; Camlıyurt, G.; Aydin, M.; Akyuz, E.; Boustras, G.; Park, S. A holistic risk assessment under the D–S evidential theory and FMECA approach of ship recycling process hazards in the maritime environment. Hum. Ecol. Risk Assess. Int. J. 2024, 30, 201–216. [Google Scholar] [CrossRef]
- Castro, P.F.; de Lira, G.R.S.; Vilar, P.B.; Vilar, P.B.; Costa, E.G.d.; Carvalho, F.B.S. Fuzzy Inference System Development for Turbogenerator Failure Diagnosis on Floating Production Offloading and Storage Platform. Energies 2024, 17, 392. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, H.; Zeng, X.; Li, L.; Cui, S.; Du, Z. A quantitative safety assessment for offshore equipment evaluation using fuzzy FMECA: A case study of the hydraulic submersible pump system. Ocean Eng. 2024, 293, 116611. [Google Scholar] [CrossRef]
- Zúñiga, A.A.; Fernandes, J.F.P.; Branco, P.J.C. Fuzzy-Based Failure Modes, Effects, and Criticality Analysis Applied to Cyber-Power Grids. Energies 2023, 16, 3346. [Google Scholar] [CrossRef]
- del Olmo, A.; de Lacalle, L.N.L.; Martínez de Pissón, G.; Pérez-Salinas, C.; Ealo, J.A.; Sastoque, L.; Fernandes, M.H. Tool wear monitoring of high-speed broaching process with carbide tools to reduce production errors. Mech. Syst. Signal Process. 2022, 172, 109003. [Google Scholar] [CrossRef]
- Aldekoa, I.; del Olmo, A.; Sastoque-Pinilla, L.; Sendino-Mouliet, S.; Lopez-Novoa, U.; de Lacalle, L.N.L. Early detection of tool wear in electromechanical broaching machines by monitoring main stroke servomotors. Mech. Syst. Signal Process. 2023, 204, 110773. [Google Scholar] [CrossRef]
- Huangfu, H.; Zhou, Y.; Zhang, J.; Ma, S.; Fang, Q.; Wang, Y. Research on Inter-Turn Short Circuit Fault Diagnosis of Electromechanical Actuator Based on Transfer Learning and VGG16. Electronics 2022, 11, 1232. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; He, S.; Zhou, D.; Zhou, Y. Failure Modes, Effect and Criticality Analysis of Electro-Mechanical Actuator; ICIC: Tianjin, China, 2024. [Google Scholar]

| Serial Number | Failure Factors of PMSM |
|---|---|
| Interturn short circuit fault of stator windings | |
| Phase to phase short-circuit fault of stator windings | |
| Ground fault | |
| Open-circuit fault | |
| Demagnetizing fault of permanent magnet | |
| Fatigue fault of bearings | |
| Corrosion fault of bearings | |
| Fracture fault of bearings | |
| Eccentricity fault of rotor |
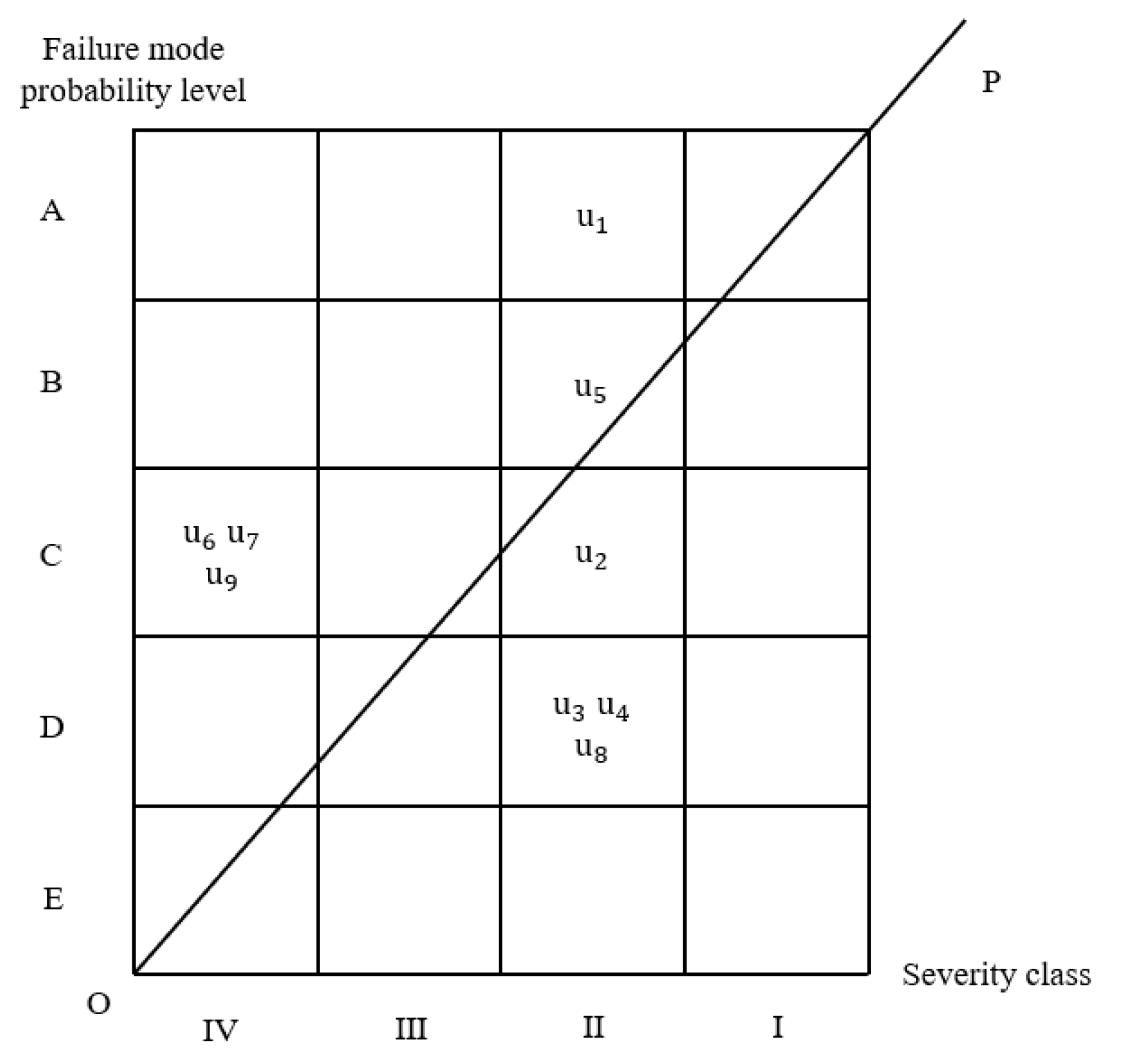
| Serial Number | Failure Mode Probability Level | Severity Class |
|---|---|---|
| II | A | |
| II | C | |
| II | D | |
| II | D | |
| II | B | |
| IV | C | |
| IV | C | |
| II | D | |
| IV | C |
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 17 | ||
| 0 | 1 | 2 | 2 | 0 | 2 | 2 | 2 | 2 | 13 | ||
| 0 | 0 | 1 | 1 | 0 | 2 | 2 | 2 | 2 | 10 | ||
| 0 | 0 | 1 | 1 | 0 | 2 | 2 | 2 | 2 | 10 | ||
| 0 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 15 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 1 | 6 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 1 | 6 | ||
| 1 | 47/15 | 71/15 | 71/15 | 31/15 | 103/15 | 9 | 9 | 103/15 | ||
| 15/47 | 1 | 13/5 | 13/5 | 15/31 | 71/15 | 103/15 | 103/15 | 71/15 | ||
| 15/71 | 5/13 | 1 | 1 | 3/11 | 47/15 | 79/15 | 79/15 | 47/15 | ||
| 15/71 | 5/13 | 1 | 1 | 3/11 | 47/15 | 79/15 | 79/15 | 47/15 | ||
| 15/31 | 31/15 | 11/3 | 11/3 | 1 | 29/5 | 119/15 | 119/15 | 29/5 | ||
| 15/103 | 15/71 | 15/47 | 15/47 | 5/29 | 1 | 47/15 | 47/15 | 1 | ||
| 1/9 | 15/103 | 15/79 | 15/79 | 15/119 | 15/47 | 1 | 1 | 15/47 | ||
| 1/9 | 15/103 | 15/79 | 15/79 | 15/119 | 15/47 | 1 | 1 | 15/47 | ||
| 15/103 | 15/71 | 15/47 | 15/47 | 5/29 | 1 | 47/15 | 47/15 | 1 | ||
| weight () | 0.29939 | 0.14361 | 0.11146 | 0.09847 | 0.22082 | 0.0337 | 0.02809 | 0.02691 | 0.03754 |
| Frequency of Fault | Severity of Impact | The Difficulty of Detection | |
|---|---|---|---|
| Weight () | 0.1488 | 0.7767 | 0.0745 |
| Post-Unification | Comment | Value | |
|---|---|---|---|
| Relatively bad | 4 | ||
| Bad | 3 | ||
| Relatively good | 2 | ||
| Very good | 1 |
| Evaluation Level | Recommended Measures | Safety Level |
|---|---|---|
(Very good) | The system works well, each performance is intact, without special treatment | Very safe |
(Relatively good) | The system has a small possibility of failure, only need to strengthen the regular maintenance and inspection of some weak parts | Relatively safe |
(In general) | The system has some fault possibilities, so it is necessary to maintain the weak parts regularly and make some improvement measures at the same time to prevent the failure | Generally safe |
(Relatively bad) | The system has a relatively large possibility of failure, so it is necessary to maintain the weak parts regularly and make some improvement measures at the same time, to reduce the probability and influence of failure | Relatively unsafe |
(Very bad) | The system has a great possibility of failure, and it needs to improve the weak parts. Finally, the improved system is re-evaluated to improve the reliability of the system to meet the requirements | Very unsafe |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chen, B.; Li, X. Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators. Actuators 2024, 13, 510. https://doi.org/10.3390/act13120510
Zhang C, Chen B, Li X. Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators. Actuators. 2024; 13(12):510. https://doi.org/10.3390/act13120510
Chicago/Turabian StyleZhang, Chao, Boyuan Chen, and Xiangzhi Li. 2024. "Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators" Actuators 13, no. 12: 510. https://doi.org/10.3390/act13120510
APA StyleZhang, C., Chen, B., & Li, X. (2024). Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators. Actuators, 13(12), 510. https://doi.org/10.3390/act13120510






