A Maximum Power Point Tracking (MPPT) Strategy Based on Harris Hawk Optimization (HHO) Algorithm

Abstract

To address the multi-peak characteristics of the P-U output characteristic curve when the photovoltaic array is partially shaded, a Maximum Power Point Tracking (MPPT) method combining Harris Hawk optimization, and a variable step conductance increment method is proposed in this article. Although the Harris Hawk Optimization algorithm has advantages in optimizing multi-modal P-U curves, when the lighting conditions suddenly change, the output characteristic curve will undergo drastic changes, causing the algorithm to oscillate repeatedly at the maximum power point. Moreover, due to its inherent limitations, the Harris Hawk algorithm has a low convergence accuracy, slow tracking speed, and is prone to getting trapped in a local optimum. In order to compensate for the shortcomings of the Harris Hawk Optimization algorithm, the variable step conductance increment method is switched for local exploration to improve the algorithm’s ability to escape from the local optimal solution and reduce power oscillation. Finally, the MPPT control of the proposed strategy was simulated and verified on the MATLAB/Simulink simulation (2021) platform. In the MPPT test experiment, the proposed composite algorithm was applied to simulate and verify uneven irradiance conditions.

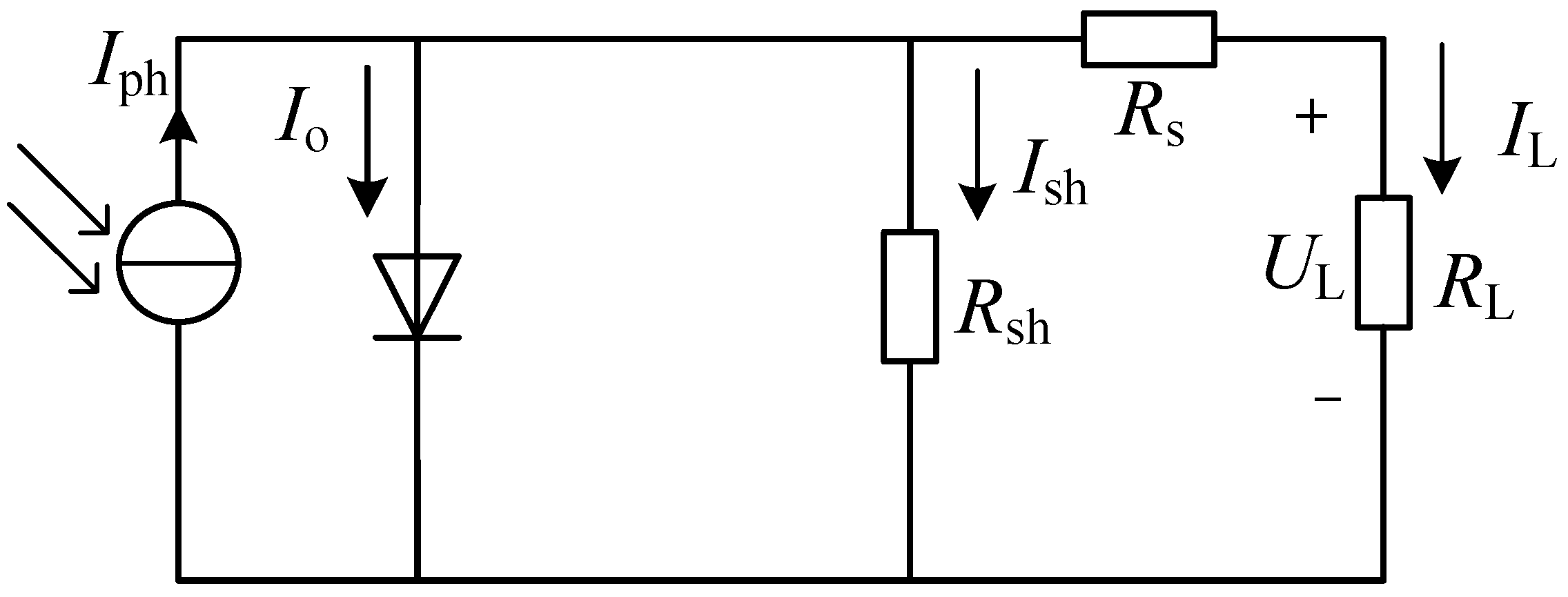
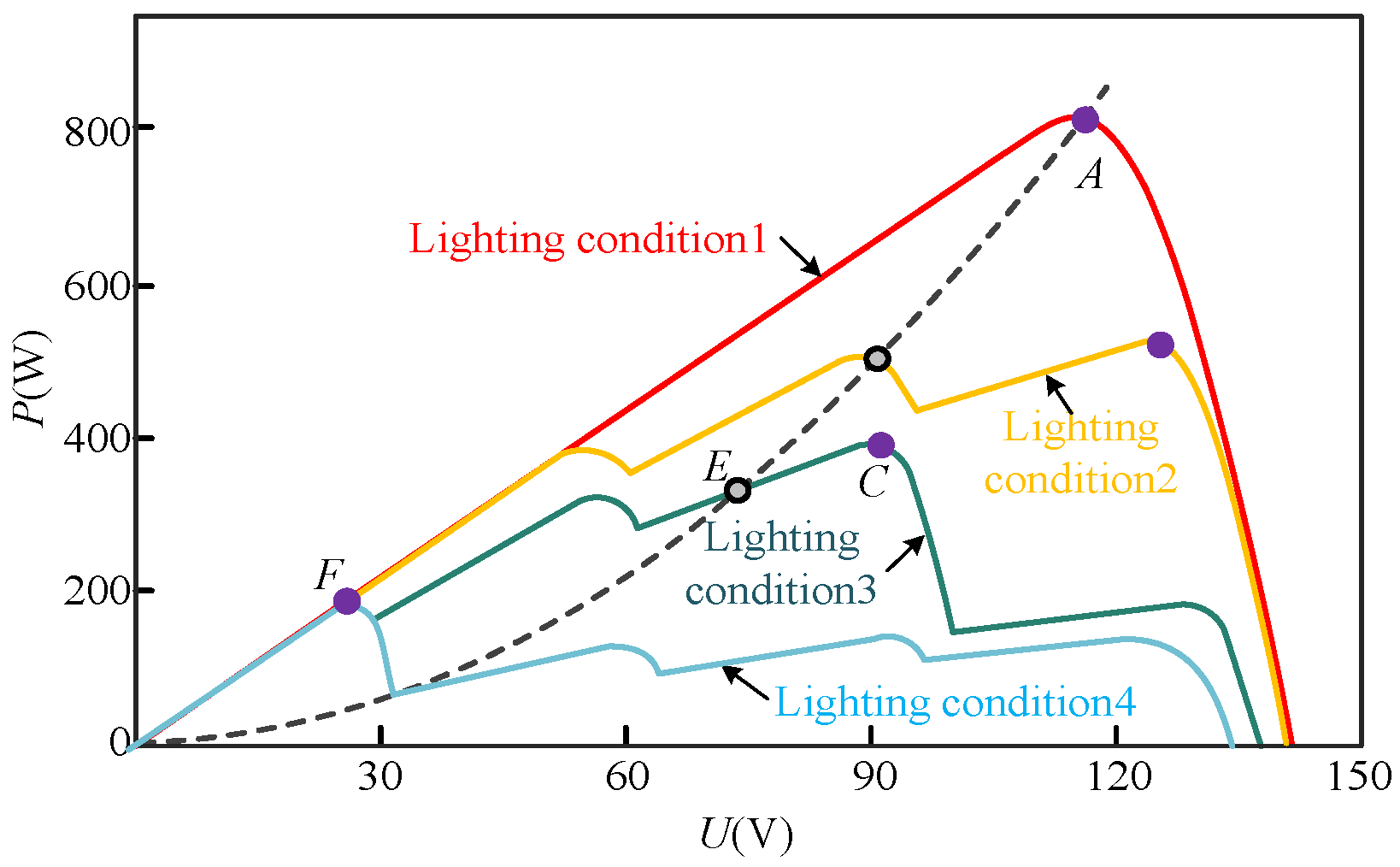
1. Introduction

Solar photovoltaic technology, which has been in use since the early 1970s, has undergone a long process of development. Initially, the application of this technology was relatively limited, but in recent years, the solar photovoltaic industry has experienced rapid growth and has become one of the most critical renewable energy technologies in the world [1]. Solar power generation is susceptible to weather conditions, such as overcast and snowy weather conditions that can partially obstruct the solar panels, preventing them from receiving even lighting. These conditions will lead to a position where the photovoltaic cell operating point may not always be at the maximum power, and there is a power multi-peak phenomenon, which will affect the power generation efficiency of photovoltaic cells [2,3]. In order to use solar energy efficiently, some scholars have focused their research on Maximum Power Point Tracking (MPPT).

Traditional Maximum Power Point Tracking methods, such as the constant voltage method, the increment conductance method (INC), and the perturbation and observation method (P&O), are suitable for single-peak optimization under uniform illumination [4]. The increment conductance method (INC) and the perturbation and observation method (P&O) were improved with a variable step size. According to the relationship between the actual photovoltaic working point position and the maximum power point position, the step size is changed in real time to improve the tracking effect, including improving the response speed and reducing the system oscillation [5,6]. However, when light irradiation becomes uneven due to the external environment, the P-U curve of the photovoltaic array exhibits multi-peak characteristics [7], and traditional control methods face the problem of failure.

In view of the above problems, domestic and foreign scholars have studied and proposed the application of intelligent algorithms. The literature [8] introduces a control strategy that combines a prediction model and a perturbation observation method, which can quickly and accurately track MPPT in a constantly changing environment. However, this method requires an understanding of the mathematical model of the system, which is difficult to implement. In reference [9], an improved particle swarm optimization (IPSO) algorithm was proposed to improve the tracking speed of the system in view of the situation of the traditional particle swarm optimization (PSO) algorithm in the local shadow environment. Although the maximum power tracking speed has been improved, there are still fluctuations in the output power. The literature [10] proposes an immune firefly algorithm that uses a vaccine library to accelerate the search process and improves the accuracy and stability of the algorithm through immune enhancement and elimination of inefficient individuals. However, this algorithm has a slow convergence speed, is easy to fall into local optimum, and has an early convergence, which limits its effectiveness and efficiency. The literature [11,12] introduced a particle swarm optimization algorithm and ANN neural network using adaptive variation strategy to design a MPPT controller, aiming to improve the accuracy of photovoltaic MPPT, but the control effect of the neural network may be limited by weight adjustment, and the PSO algorithm has a slow convergence rate. The literature [13] discusses a composite algorithm combining PSO, a genetic algorithm, and a fuzzy control. By combining the advantages of the first two algorithms and introducing a fuzzy control, the output fluctuation and power loss when the maximum power point (MPP) is reached can be reduced. However, the control model of this composite algorithm is complex, the computation is large, and the optimization speed is not significantly improved. In the literature [14], the improved gray Wolf optimization algorithm was adopted for maximum power point tracking. However, while the tracking speed was effectively improved, there was a power oscillation problem in the algorithm optimization process, resulting in a certain power loss. In [15], Harris Hawk Optimization (HHO) was proposed by imitating Harris Hawk, which has a strong global search ability and does not require complicated parameter tuning. However, the Harris Hawk algorithm has a low convergence accuracy, a slow tracking speed, and is prone to getting trapped in a local optimum. The literature [16,17] comprehensively compares all kinds of algorithms, and the composite algorithm is more balanced in performance and complexity.

Aiming at the shortcomings of the above algorithms, this paper proposes a MPPT strategy based on the Harris Hawk optimization (HHO) algorithm to solve the problem where the traditional maximum power easily falls into a local optimal and is difficult to balance tracking accuracy and speed. The rest of this article is organized as follows. In Section 2, the working principle of photovoltaic cells is introduced, its mathematical modeling is carried out, and the working characteristics of photovoltaic cells are simulated and analyzed in MATLAB/Simulink for different conditions under different lighting conditions. The P-U curves of its output are analyzed for uniform and non-uniform lighting conditions. Then, the Harris Hawk optimization (HHO) algorithm is introduced in Section 3. Aiming at the problem where the traditional MPPT algorithm easily falls into a local optimal in the case of a multi-peak value, which leads to the decrease of system efficiency. Section 4 introduces a matching algorithm based on Harris Hawk optimization (HHO) and the variable step length conductance increment method (INC). The experiment results are presented in Section 5 to prove the accuracy of the analyses and the effectiveness of the proposed MPPT algorithm. Finally, the conclusions are drawn in Section 6.

2. Principle and Characteristic Analysis of Photovoltaic Cell

The photovoltaic power generation system mainly consists of three parts: photovoltaic array, MPPT controller, and DC–DC conversion unit. Because isolation is very important in practical applications, according to reference [18], the authors of this paper adopted an isolation type DC–DC converter. The task of the MPPT controller is to adjust the working state of the photovoltaic array in real time to ensure that the maximum output power can be captured under any given environmental conditions. Photovoltaic cells provide output voltage for the entire system. As the energy source of photovoltaic power generation systems, the higher its conversion rate, the more energy the system can get, and the higher the system power generation efficiency. The position of the photovoltaic cell operating point will change due to changes in the external environment, which may mean the maximum power point changes. Only by making the photovoltaic work at its MPP at all times can the high utilization rate of solar energy be maintained. Therefore, to study the efficiency of a photovoltaic power generation system, we must study the mathematical model and output characteristics of photovoltaic cells.

2.1. Mathematical Model of Photovoltaic Cell

The equivalent circuit of the photovoltaic cell is shown in Figure 1, $R_{sh}$ and $R_s$ are the resistances generated by no ideal effects in photovoltaic cells, and $I_{ph}$ is photocurrent.

According to the equivalent circuit diagram of the photovoltaic cell, the output current expression can be obtained as:

$$I_L=I_{ph}-I_o({{\displaystyle e}}^{{\displaystyle \frac{q(U_L+I_L{R}_S)}{nKT}}-1})-{\displaystyle \frac{{{\displaystyle U}}_L+I_L{R}_S}{R_{sh}}}$$

(1)

where $U_L$ and $I_L$ are the output voltage and current of a single photovoltaic cell, respectively; n is the diode index; K is the Boltzmann constant; q is the unit charge; $T$ is the external temperature.

Due to the small value of $R_S$ and the large value of $R_{sh}$, the last term in expression (1) can be ignored. For ease of application, Equation (1) can be simplified as follows:

$$I_L=I_{sc}[1-C_1{I}_{sc}({{\displaystyle e}}^{{\displaystyle \frac{{{\displaystyle U}}_L}{C_2{{\displaystyle U}}_{oc}}}}-1)]$$

(2)

where $I_{sc}$ represents short-circuit current; $U_{oc}$ represents open circuit voltage.

When the photovoltaic cell outputs its maximum power, $I_L=I_m; U_L=U_m$, the expressions for $C_1$ and $C_2$ are as follows:

$$\left\{\begin{array}{l}{C}_1=\left(1-{\displaystyle \frac{I_m}{I_{sc}}}\right)e^{{\displaystyle \frac{-U_m}{C_2{U}_{oc}}}}\hfill \\ C_2=\left({\displaystyle \frac{U_m}{U_{oc}}}-1\right){\left[In\left(1-{\displaystyle \frac{I_m}{I_{sc}}}\right)\right]}^{-1}\hfill \end{array}\right.$$

(3)

2.2. Multi-Peak Characteristics of Photovoltaic Arrays

The local shadows generated by obstructions in photovoltaic arrays can cause the P-U curve of the photovoltaic array to exhibit multi-peak characteristics. To further research multi-peak optimization control methods to improve photovoltaic power generation efficiency, a $4\times 1$ photovoltaic array model in MATLAB/Simulink was built, considering the occlusion situation of the photovoltaic array the situation is shown in

Table 1. Irradiance of each component of photovoltaic array.

	Case 1	Case 2	Case 3	Case 4
PV1 ($\mathrm{W}/{\mathrm{m}}^2)$	1000	1000	1000	1000
PV2 ($\mathrm{W}/{\mathrm{m}}^2)$	1000	1000	800	300
PV3 ($\mathrm{W}/{\mathrm{m}}^2)$	1000	800	600	150
PV4 ($\mathrm{W}/{\mathrm{m}}^2)$	1000	600	400	200
MPP ($\mathrm{W})$	795	535.2	389.4	181

. The open circuit voltage of the photovoltaic cell is 35 V, the short circuit current is 7.5 A, and the MPP voltage, and currents are 28 V and 7 A, respectively.

The P-U characteristic curves of the photovoltaic array are shown in Figure 2. The gray curve is the equivalent resistance load characteristic curve corresponding to MPP under standard conditions. From Figure 2, the four lines in the graph represent P-U curves under four different lighting conditions, and each point represents an extreme point on the corresponding curve, it can be seen that the photovoltaic array will have multiple extreme points in the case of local occlusion. The classical perturbation based MPPT algorithm may mistakenly identify one of the multiple extreme points as the maximum point, resulting in a loss of success rate. Therefore, using the photovoltaic characteristic curve law to improve the MPPT algorithm with a stronger global search ability can effectively solve the problem.

3. Proposed MPPT Technique Based on IHHO

According to the analysis of the output characteristics of photovoltaic cells in Section 2, it is concluded that the output power of solar cells is greatly affected by light. Therefore, only by ensuring that the output power remains stable at the maximum point under any lighting conditions can the system efficiency be optimized. In response to multiple local power peaks caused by local shading, this chapter proposes an improved Harris Hawk algorithm.

In the Harris Hawk Optimization algorithm, each Harris Hawk represents a potential solution, and the goal pursued in each iteration represents the global optimal solution. The hunting stage of this population is mainly divided into three stages: the research stage, the transition stage between search and development, and the development stage.

In the initial stage, the algorithm performs a global search, with Harris Hawks randomly distributed in the solution space, waiting for opportunities within the search range and searching for prey. During the search process, they will constantly change their positions based on two different strategies to approach the target. The specific mathematical expression is:

$$X(t+1)=\left\{\begin{array}{ll}{X}_h(t)-r_1\left|X_h(t)-2r_{2}X(t)\right|\hfill & q\ge 0.5\hfill \\ (X_r(t)-X_m(t))-r_3(LB+r_4(UB-LB))\hfill & q<0.5\hfill \end{array}\right.$$

(4)

where t is the current iteration count; $X(t+1)$ is the position of individual i after the t-th iteration; $X_h$ represents randomly selecting individual positions after t iterations; $r_1,{ r}_2,{ r}_3,{ r}_4$, and q represents a constant between 0 and 1; $UB$ and $LB$ represent the upper and lower limits of the search space; $x_m\left(t\right)$ represents the average position of the population after t iterations, its expression as follows:

$$X_m(t)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{X}_i}(t)$$

(5)

where N is the population size.

The HHO algorithm can flexibly switch between exploration and development stages and can adjust its development strategy based on the remaining energy of prey. As the prey’s energy gradually depletes, their escape behavior will affect the hunting methods of the eagle flock, causing them to dynamically switch between different search and development behaviors based on the prey’s energy level $E$. When $| E | \ge 1$, enter the global search phase; When $| E |<1$, enter the local development phase. The formula for escape energy is:

$$E=2E_0\left(1-{\displaystyle \frac{t}{T}}\right)$$

(6)

where $E_0$ represents the initial energy state of the prey, which is a random number of $[-1, 1]$. As the number of iterations increases, the escape energy $E$ decreases.

When the escape energy $| E |<1$, HHO enters the development phase and begins to implement local search. Based on the hunting characteristics of Harris eagles, four different strategies were developed to perform local searches and rearrange their positions, taking into account variables such as the size of E and whether the prey escaped or not. R represents the probability of escape. When $r<0.5$, the prey successfully escapes; $r>0.5$, Harris Eagle will conduct a hunt. The escape energy E is used to determine the strategy, and for the judgment of the encirclement strategy: when $| E | \ge 0.5$, a soft encirclement strategy is adopted; When $| E |<0.5$, adopt a hard siege.

Soft Siege: When $r \ge 0.5$ and $| E | \ge 0.5$, the prey has energy to escape but ultimately fails, and the Harris Eagle adopts a soft encirclement strategy. At this point, Harris Eagle will update its position according to Equation (7):

$$\begin{array}{c}X(t+1)=\mathsf{\Delta }X(t)-E\left|J{X}_r(t)-X(t)\right|\\ \mathsf{\Delta }X(t)=X_r(t)-X(t)\end{array}$$

(7)

where $X (t+1)$ represents the next update position of Harris Hawk, $\mathsf{\Delta } X \left(t\right)$ represents the distance between the current prey and Harris Hawk, and $J$ represents the jumping intensity of the prey, which is a random number within $[0, 2]$ that varies with iteration.

Hard Siege: When $r<0.5$ and $| E | \ge 0.5$, the prey has no energy to escape, and the Harris Hawk does not need to wait for a direct attack. At this point, use the following equation to update the current position:

$$X(t+1)=X_r(t)-E\left|\mathsf{\Delta }X(t)\right|$$

(8)

Accumulated speed diving soft siege: When $r<0.5$ and $| E | \ge 0.5$, the escape energy is sufficient, and the prey successfully escapes. Harris hawks still use soft siege before attacking their prey. In the HHO algorithm, the Levy flight module is introduced to simulate the escape and jumping behavior of prey, corresponding to a new position update strategy. By introducing it, the convergence speed and optimization ability of the system are enhanced. During Levy’s flight, the Harris Hawk will follow a specific position update strategy to ensure that the search direction and range meet actual needs:

$$X(t+1)=\left\{\begin{array}{ll}Y\hfill & \mathrm{if} F(Y)<F(X(t))\hfill \\ Z\hfill & \mathrm{if} F(Z)<F(X(t))\hfill \end{array}\right.$$

(9)

$$Y=X_r(t)-E\left|J{X}_r(t)-X(t)\right|$$

(10)

$$Z=Y+S\times LF(D)$$

(11)

where $D$ is the dimension of the current problem, S is a $1\times D$ random row vector, LF is the Levy flight function, which is calculated using Equation (12):

$$LF(x)=0.01\times {\displaystyle \frac{u\times \sigma }{|v{|}^{\frac{1}{\beta }}}},\sigma ={\left({\displaystyle \frac{\mathsf{\Gamma }(1+\beta )\times \sin \left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}}\right)}^{{\displaystyle \frac{1}{\beta }}}$$

(12)

Accumulated speed diving hard siege: When $r<0.5$ and $| E |<0.5$, if the prey cannot escape, the Harris Hawk will adopt a hard siege strategy to capture the prey. Update the location according to the following strategy:

$$X(t+1)=\left\{\begin{array}{ll}Y\hfill & \mathrm{if} F(Y)<F(X(t))\hfill \\ Z\hfill & \mathrm{if} F(Z)<F(X(t))\hfill \end{array}\right.$$

(13)

$$Y=X_r(t)-E\left|J{X}_r(t)-X_m(t)\right|$$

(14)

$$Z=Y+S\times LF(D)$$

(15)

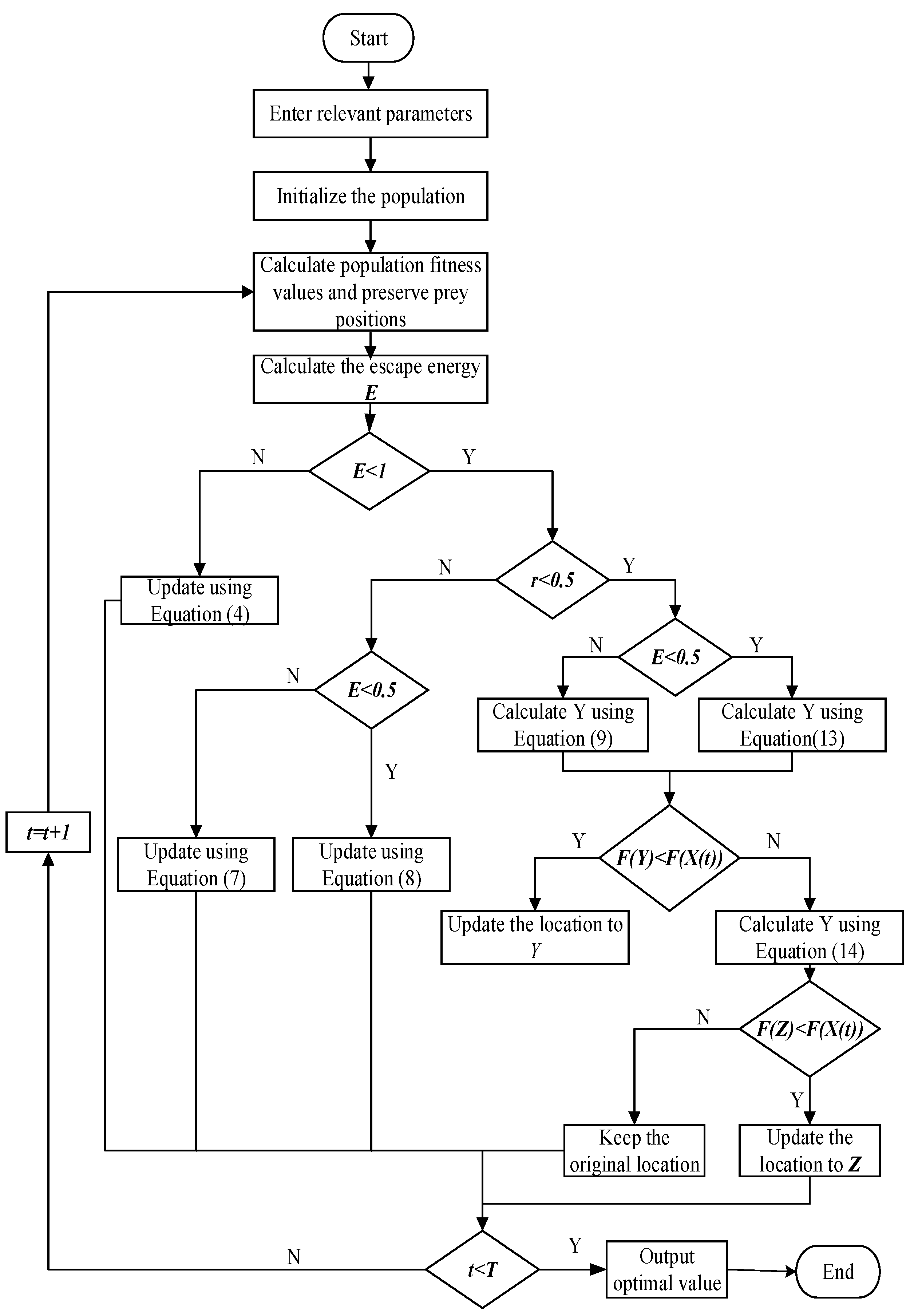
According to the above steps, the flowchart of HHO algorithm is as Figure 3:

4. Proposed Improved MPPT Algorithm Is Based on HHO and INC

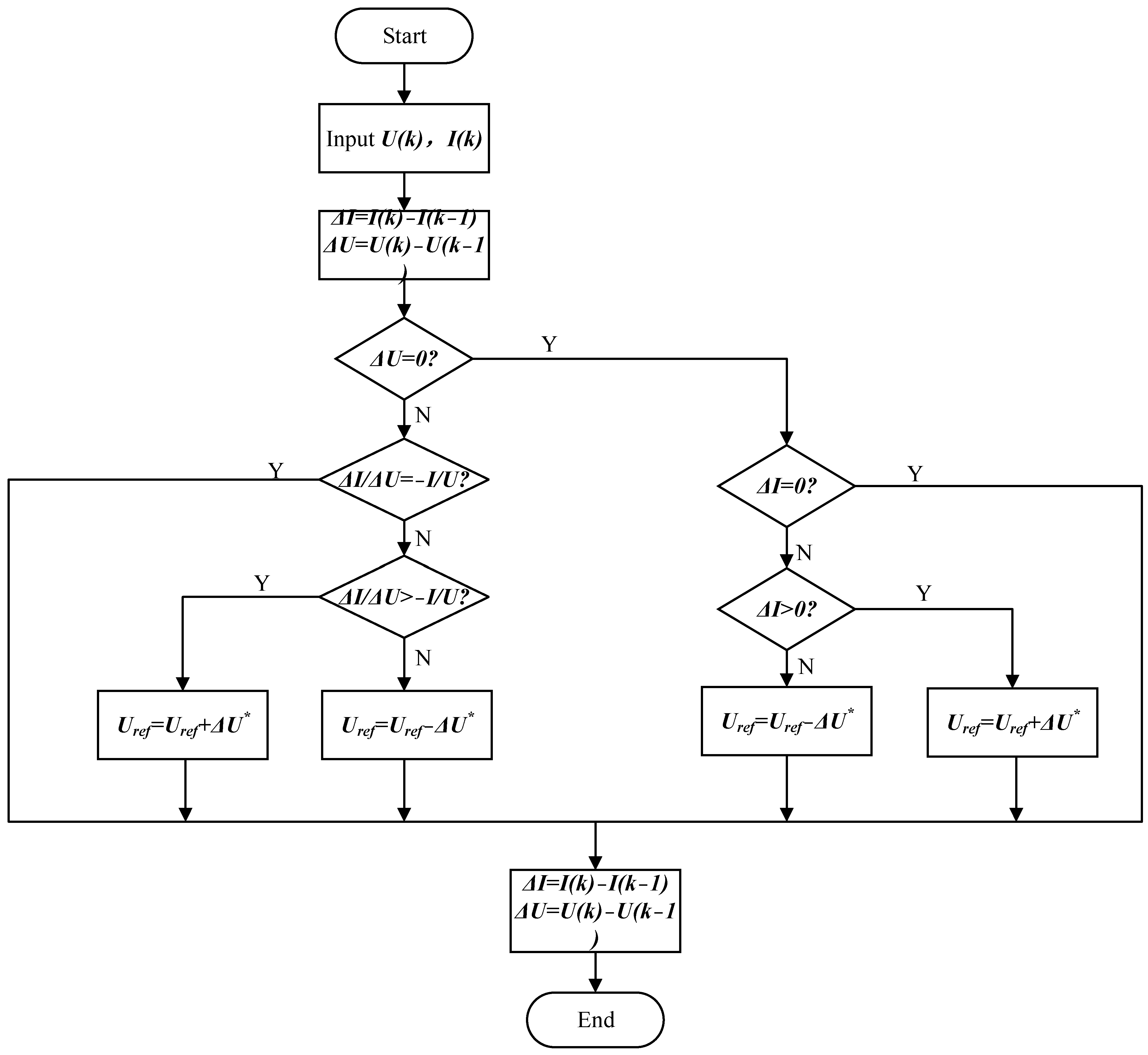
The fixed step conductance increment method can quickly track the maximum power point, and the tracked position is also very accurate. However, due to the fixed step size, this method has contradictions in terms of accuracy and speed. The variable step size conductance increment method adjusts the step size by the difference between the operating point and the maximum power point position, improving the problem of oscillation at the maximum power point and achieving better steady-state performance.

The step size of INC varies from large to small according to the rule of infinitely approaching MPP based on its distance from MPP. Until it decreases to zero, it indicates that the maximum power point has been reached. The problem of oscillation in the fixed step INC algorithm at the maximum power point has been solved by using a variable step tracking method.

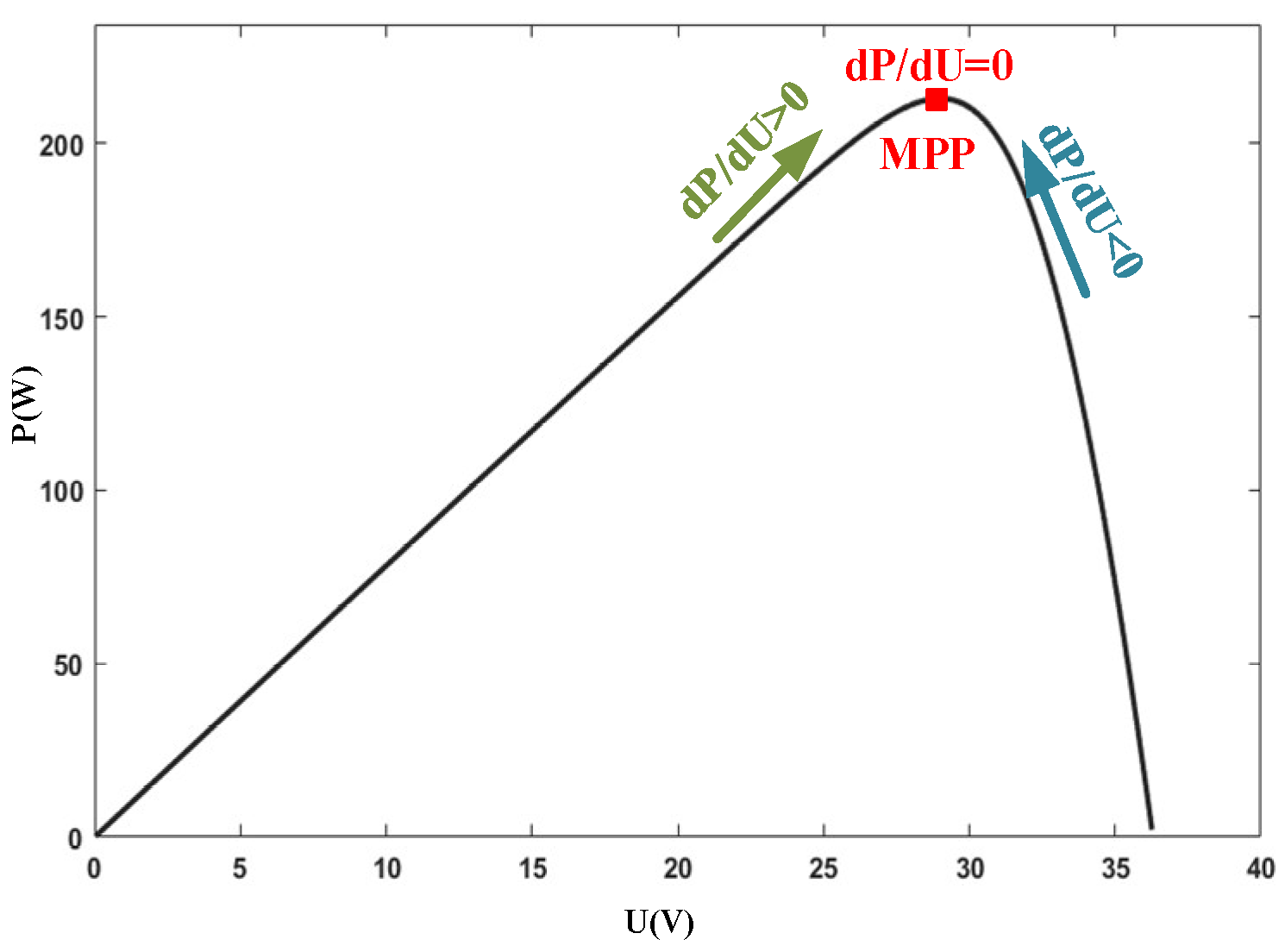
When the external environment is in a steady state, the derivative of the output power of the battery can be expressed as:

$${\displaystyle \frac{dP}{dU}}=I+U{\displaystyle \frac{dI}{dU}}$$

(16)

From the above analysis, the system is at its maximum power point when $dP/dU=0$. In INC, the relationship between the voltage and current of the system and its conductivity needs to satisfy the following conditions:

$${\displaystyle \frac{dI}{dU}}=-{\displaystyle \frac{I}{U}}$$

(17)

When $∆I/∆U>-I/U$, the maximum power point is located to the right of that point; When $∆I/∆U=-I/U$, this point is the maximum power point; When $∆I/∆U<-I/U$, the maximum power point is on the left side of that point. The basic principle of the incremental conductance method is shown in Figure 4.

The incremental conductance method has demonstrated significant stability in the maximum power point tracking control of photovoltaic power generation. This method can accurately adapt to external environmental conditions, such as changes in irradiance, and achieve effective response to environmental changes. Its tracking effect is not affected by the performance characteristics of the photovoltaic module or the specific parameters of the battery, ensuring robust tracking of the optimal power point by the system. The flowchart of the incremental conductance method is shown in Figure 5.

Although the Harris Hawk algorithm has advantages in optimizing multi-modal P-U curves, when the lighting conditions suddenly change, the output characteristic curve will undergo drastic changes, causing the algorithm to oscillate repeatedly at the maximum power point. Moreover, the Harris Hawk algorithm is prone to getting stuck in local optima in the later stages of iteration due to its inherent characteristics. Therefore, combining the HHO algorithm with the variable step size INC algorithm, and then transitioning to the variable step size INC in the later stage of HHO algorithm optimization, can improve the algorithm’s ability to jump out of local optima and reduce power oscillations, thereby increasing its stability. When the HHO algorithm reaches the number of iterations, terminate the algorithm to output the optimal solution, satisfy the following Equation (18), and switch to the variable step INC algorithm.

$$\mathsf{\Delta }P=\left|{\displaystyle \frac{P_2-P_1}{P_2}}\right|<0.05$$

(18)

where $P_1$ and $P_2$ represent the power of the first and second cycles, respectively; $\mathsf{\Delta }P$ is the maximum allowable power variation.

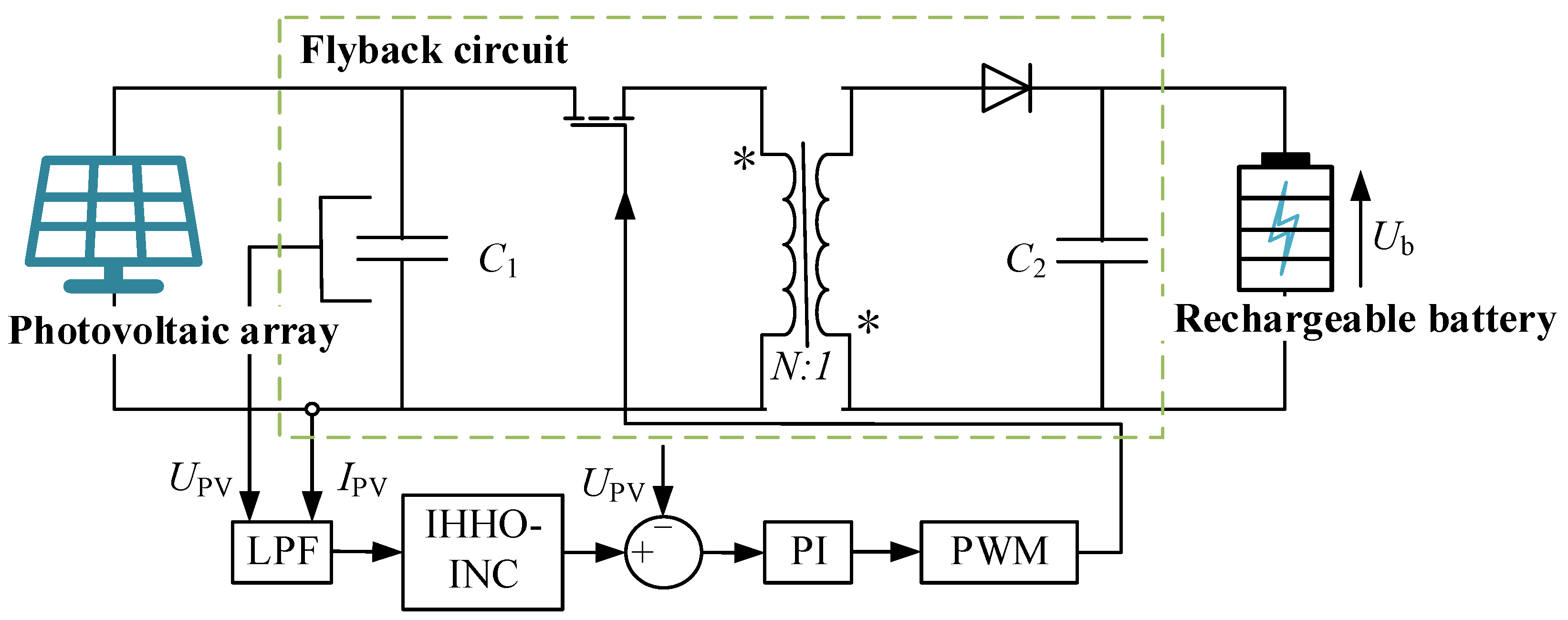
Based on the above analysis, when designing a photovoltaic power generation system, isolation requirements are important. According to reference [18], this design employs an isolation DC–DC converter. The system structure diagram of the isolated photovoltaic maximum power point tracking mode is shown in Figure 6.

5. Simulation Analysis

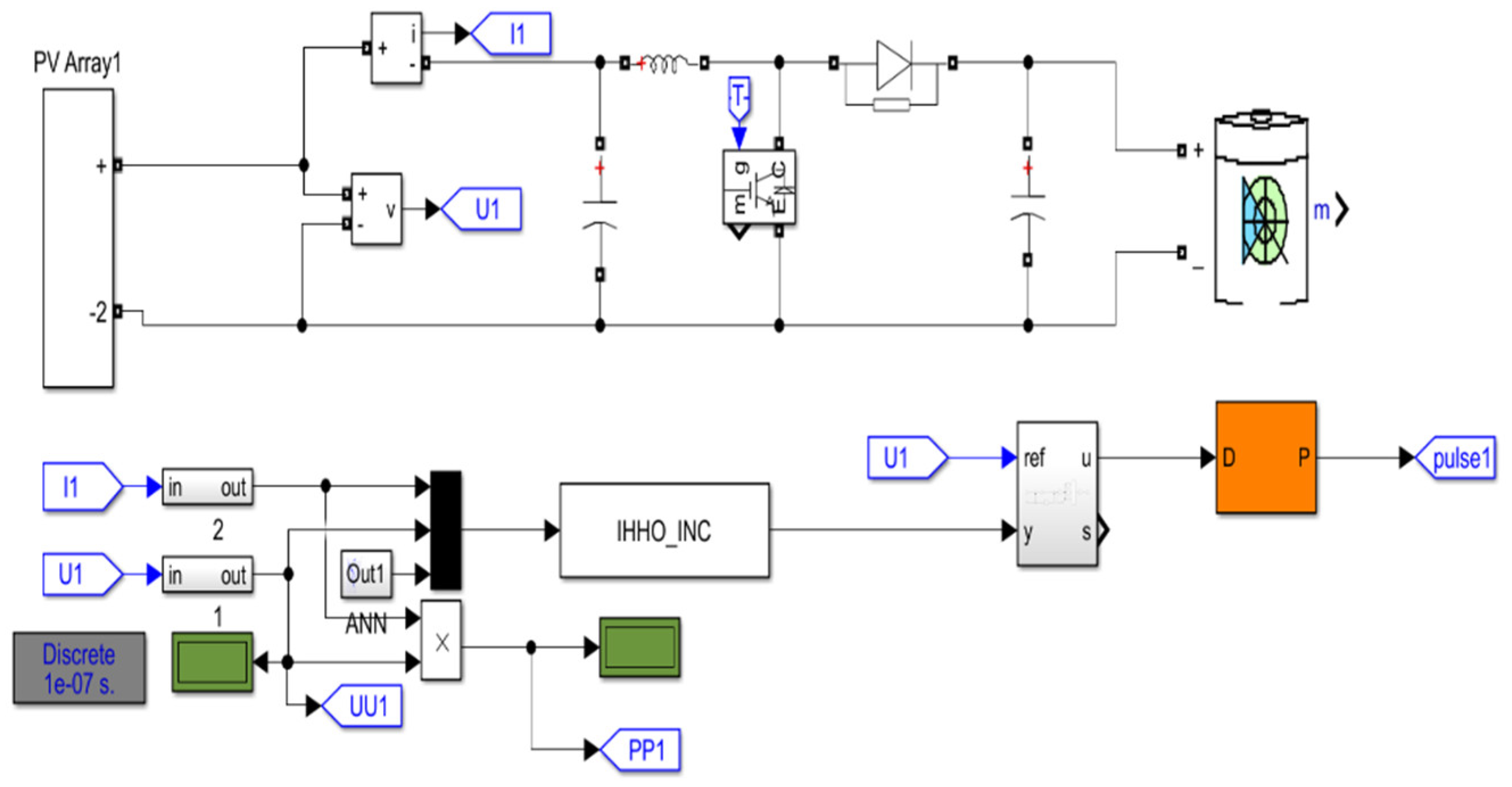
In order to verify whether the proposed algorithm can achieve the task of tracking the maximum power point of photovoltaic power generation while balancing tracking accuracy and speed, this section uses a MATLAB/Simulink (2021) simulation platform to simulate MPPT control based on a IHHO-INC composite algorithm.

The simulation model diagram is shown in Figure 7, mainly composed of four modules: a photovoltaic array model, a DC–DC converter, a PWM pulse signal model, and a MPPT controller model. Among them, the battery is used instead of the load.

This article takes a 12 × 1 photovoltaic array as an example to build an MPPT control model. The parameters of the photovoltaic cells under standard test conditions are shown in

Table 2. Battery parameters under standard testing conditions.

Parameter	Value	Unit
Maximum power Pm	217.5	W
Maximum power point voltage Um	29	V
Maximum power point current Im	7.5	A
Open-circuit voltage Uoc	36.3	V
Short-circuit current Isc	7.84	A
Equivalent series resistance $R_S$	0.39	Ω
Equivalent shunt resistance $R_{sh}$	313.4	Ω

.

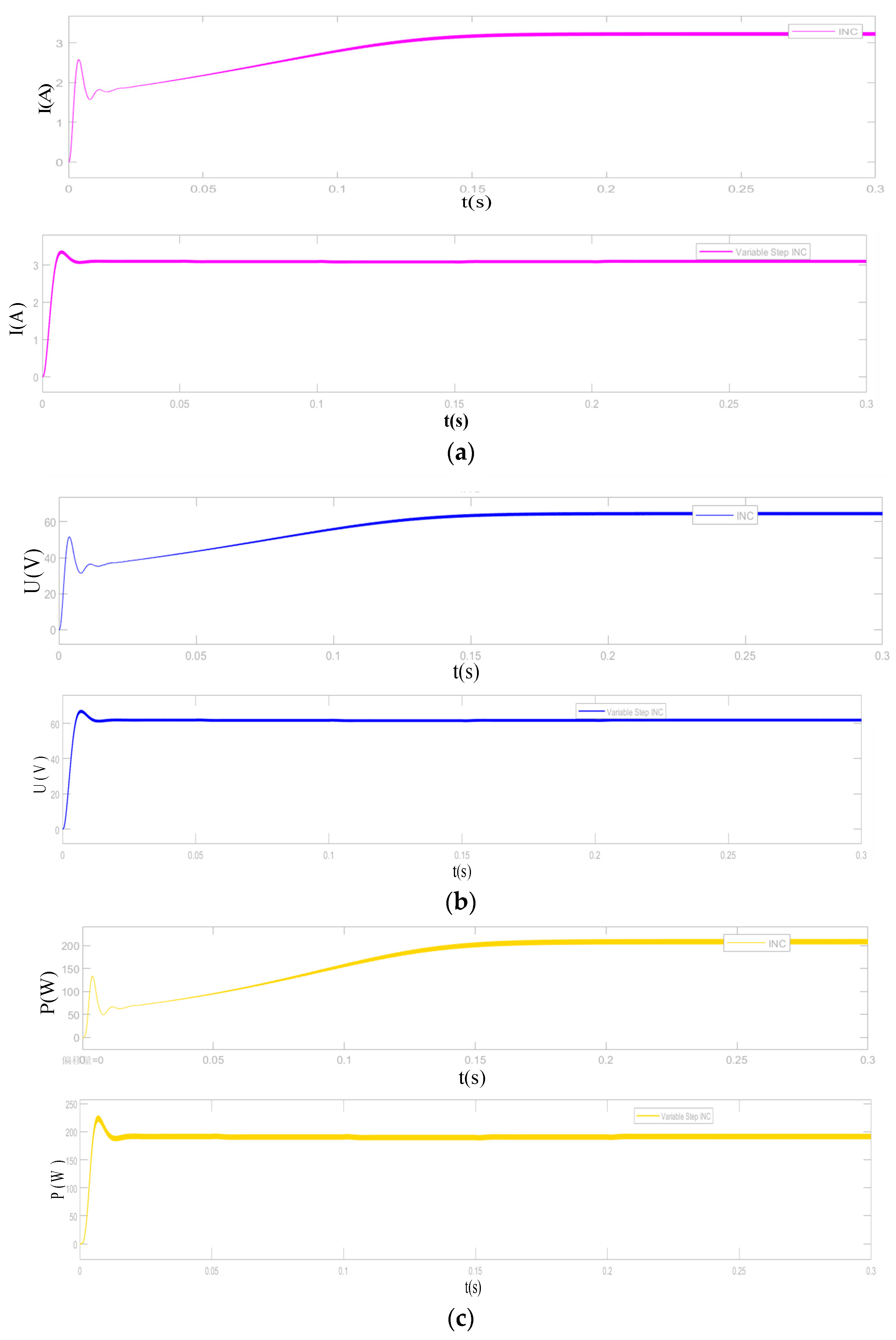
Firstly, the traditional MPPT control algorithm was simulated and analyzed under the standard conditions of S = 1000 W/m² and T = 25 °C. The simulation results obtained for a single photovoltaic array are shown in Figure 8. The I curves under variable step conductance increment method and incremental conductance method (INC) are shown in Figure 8a, Figure 8b shows the U curves under the two methods, and Figure 8c presents the P curves under the two methods.

The INC algorithm finds the maximum power point at 0.15 s, and the variable step conductance increment method finds the maximum power point at 0.017 s. It can be concluded that the variable step conductance method has a better steady-state performance and can find the maximum power point in a shorter time.

In order to verify the superiority of the MPPT control strategy applied in this paper, the experimental results of commonly used and effective particle swarm optimization algorithm, the Harris Hawk algorithm, and the IHHO-INC composite algorithm proposed in this paper were compared and analyzed at an ambient temperature of T = 25 °C. Simulation comparison analysis was conducted under uniform and non-uniform lighting conditions. The parameter settings are shown in the following

Table 3. Photovoltaic array illumination intensity setting.

Photovoltaic Array Irradiance	Uniform Illumination	Non-Uniform Illumination
PV1 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV2 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV3 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV4 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV5 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV6 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	1000
PV7 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	800
PV8 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	800
PV9 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	600
PV10 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	600
PV11 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	400
PV12 $(\mathrm{W}/{\mathrm{m}}^2)$	1000	400

:

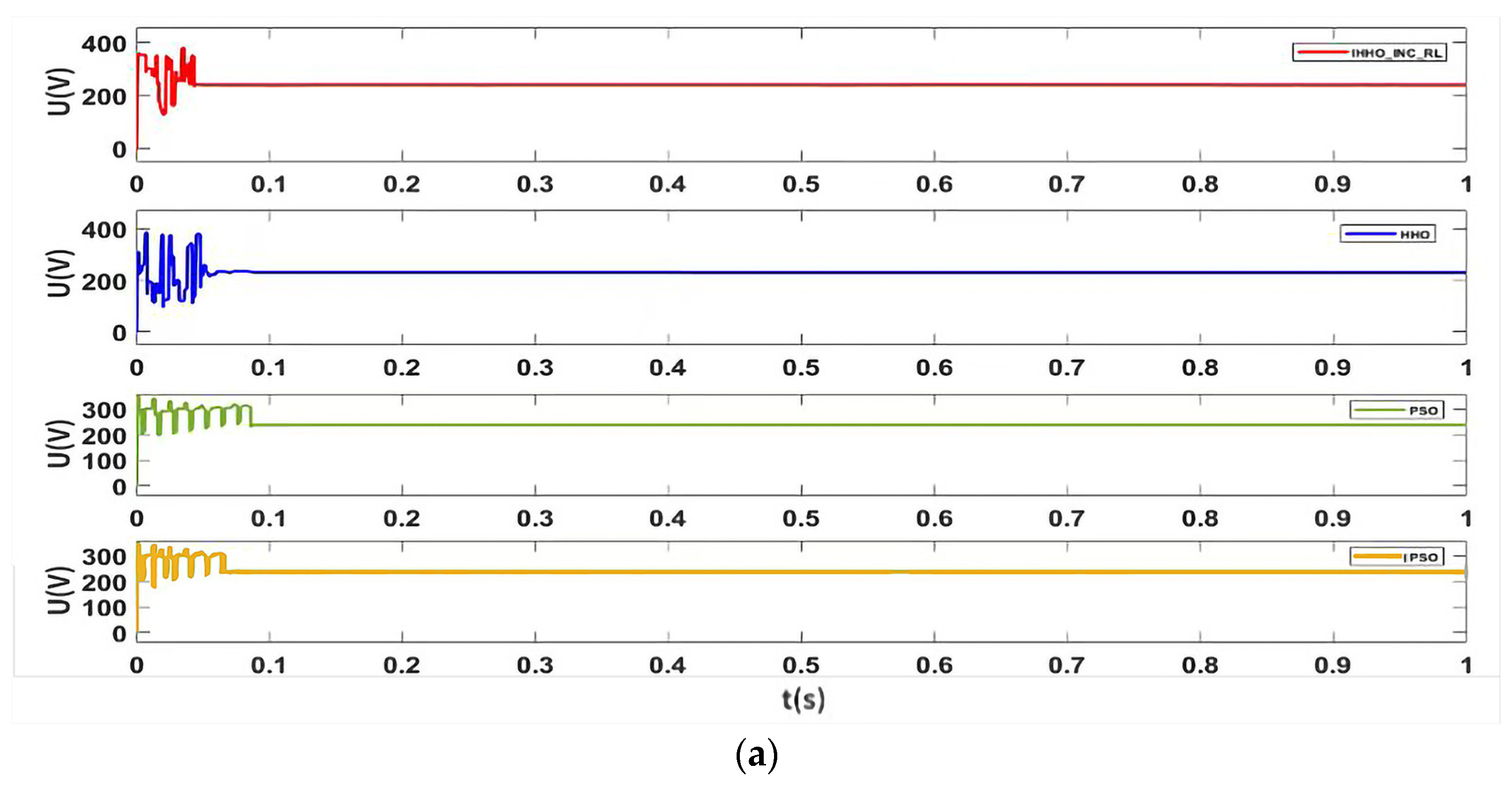
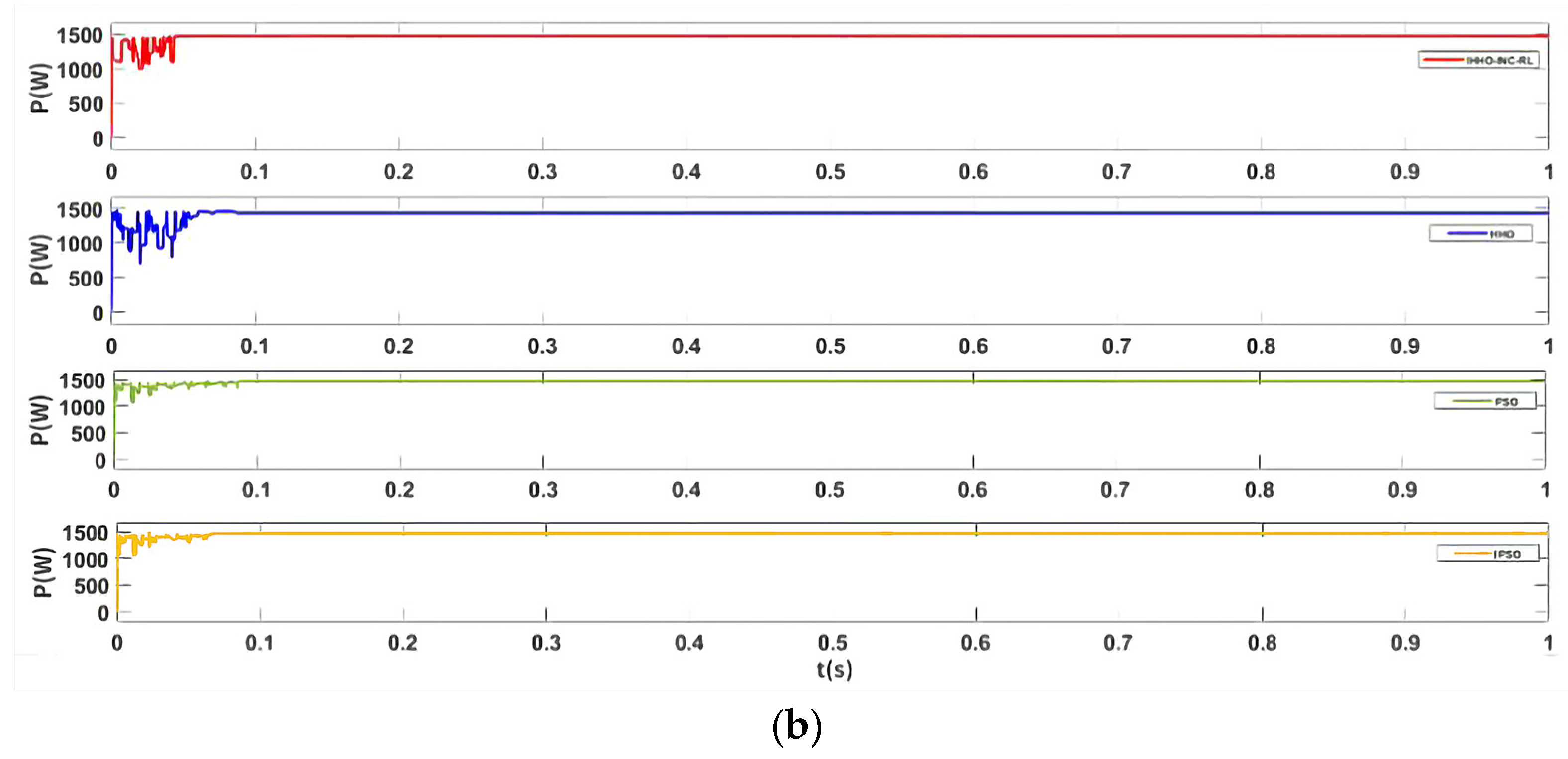
Three algorithms: PSO, IPSO, HHO, IHHO-INC, output voltage, and output power curves under uniform irradiation are shown in Figure 9, and the output voltage and power curves under non-uniform irradiation are shown in Figure 10.

From Figure 9a,b, it can be seen that the PSO, IPSO, HHO, and IHHO-INC algorithms can all track the maximum power point under uniform irradiance, with particle swarm optimization algorithm tracking the maximum power point of 2550 W in 0.09 s; IPSO tracking the maximum power point of 2552 W in 0.05 s; Harris Eagle algorithm tracking the maximum power point of 2555 W in 0.08 s; IHHO-INC composite algorithm tracking the maximum power point of 2557 W in 0.04 s, and the actual maximum power of the system in this environment was 2557.18 W, with a tracking accuracy of up to 99.97%.

From Figure 10, under non-uniform irradiance, the particle swarm algorithm tracked the maximum power point of 1467 W in 0.09 s, the improved particle swarm algorithm tracked the maximum power point of 1467 W in 0.06 s, the Harris Hawk algorithm tracked the maximum power point of 1469 W in 0.08 s, and the IHHO-INC composite algorithm tracked the maximum power point of 1470 W in 0.04 s.

Therefore, the improved Harris Hawk algorithm has a faster optimization speed and can accurately track the maximum power point under both uniform and non-uniform lighting conditions. And from the power waveform, it can be seen that its volatility is significantly reduced, indicating that the composite algorithm applied in this paper can reduce the power oscillation of the system and maintain the stable operation of the photovoltaic array.

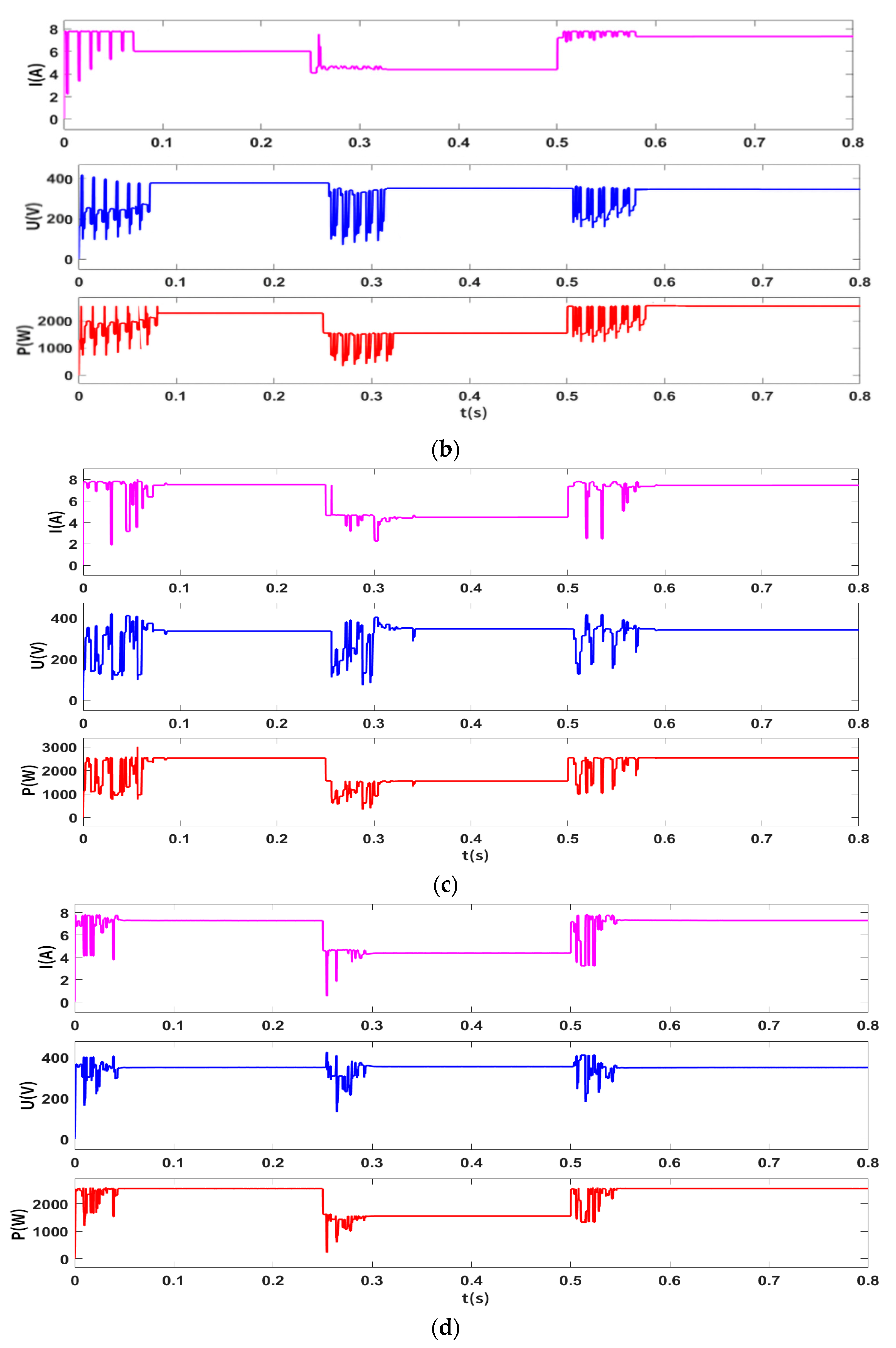
Finally, the PSO, IPSO, HHO, and IHHO-NIC algorithms were simulated and validated in a non-uniform irradiance and irradiance mutation working environment. The irradiance of the photovoltaic array was set to 1000 W/m² within 0–0.25 s, 600 W/m² within 0.25–0.5 s, and 1000 W/m² within 0.5–0.8 s to simulate dynamic shading conditions. The output current, voltage, and power curves are shown in Figure 11.

As shown in Figure 11, under dynamic shading conditions, the particle swarm algorithm reduces power at 0.25 s, drops to 1551 W at 0.34 s, increases power at 0.5 s, and reaches 2550 W at 0.59 s; The improved particle swarm algorithm reduces power at 0.25 s, drops to 1551 W at 0.32 s, increases power at 0.5 s, and reaches 2555 W at 0.56 s; The Harris Hawk algorithm reduces power at 0.25 s, drops to 1548 W at 0.33 s, increases power at 0.5 s, and reaches 2555 W at 0.58 s; The power of the IHHO-INC composite algorithm reached 2557 W at MPP in 0.04 s, decreased due to a sudden change in irradiance at 0.25 s, and dropped to 1549 W at 0.29 s; At 0.5 s, the sudden change in irradiance caused a change in power, reaching 2556 W at 0.54 s; It can be seen that it takes 0.04 s to re-track to the maximum power point after each mutation, indicating that the composite algorithm completes optimization every 0.04 s.

In summary, at 0.25 s, the light intensity suddenly decreased to 600 W, compared with the simulation results, and the IHHO-INC algorithm proposed in this paper achieves the maximum power in the shortest time with higher accuracy. At 0.5 s, the light intensity suddenly increased again, and the IHHO-INC algorithm proposed in this paper still achieved the maximum power in the shortest time with higher accuracy. The experiment verifies that the IHHO-INC algorithm proposed in this paper has good stability when the light intensity suddenly changes.

6. Conclusions

Under partial shading conditions, the output characteristic curve of the photovoltaic array has multiple inflection points. By analyzing the MPP position pattern of the multi-peak curve, this paper proposes an improved MPPT method combining Harris Hawk optimization (HHO) and a variable step conductance increment method (INC), which solves the problem where the traditional maximum power point tracking (MPPT) method easily to falls into a local optimum and it is difficult to balance the tracking precision and speed when faced with local shading. For the local development precision deficiency of the HHO algorithm, when the Harris Hawk optimization (HHO) algorithm reaches the maximum iteration number, the algorithm is terminated and the optimal solution is output, and then switched to the variable step conductance increment method (INC) algorithm. This paper conducts simulation verification of the maximum power tracking IHHO-INC algorithm, concluding that the algorithm has extremely small steady-state error and good steady-state and dynamic performance, with a significant improvement in convergence speed and efficiency compared to the HHO and PSO algorithms.