A Design Method for Road Vehicles with Autonomous Driving Control
Abstract
1. Introduction
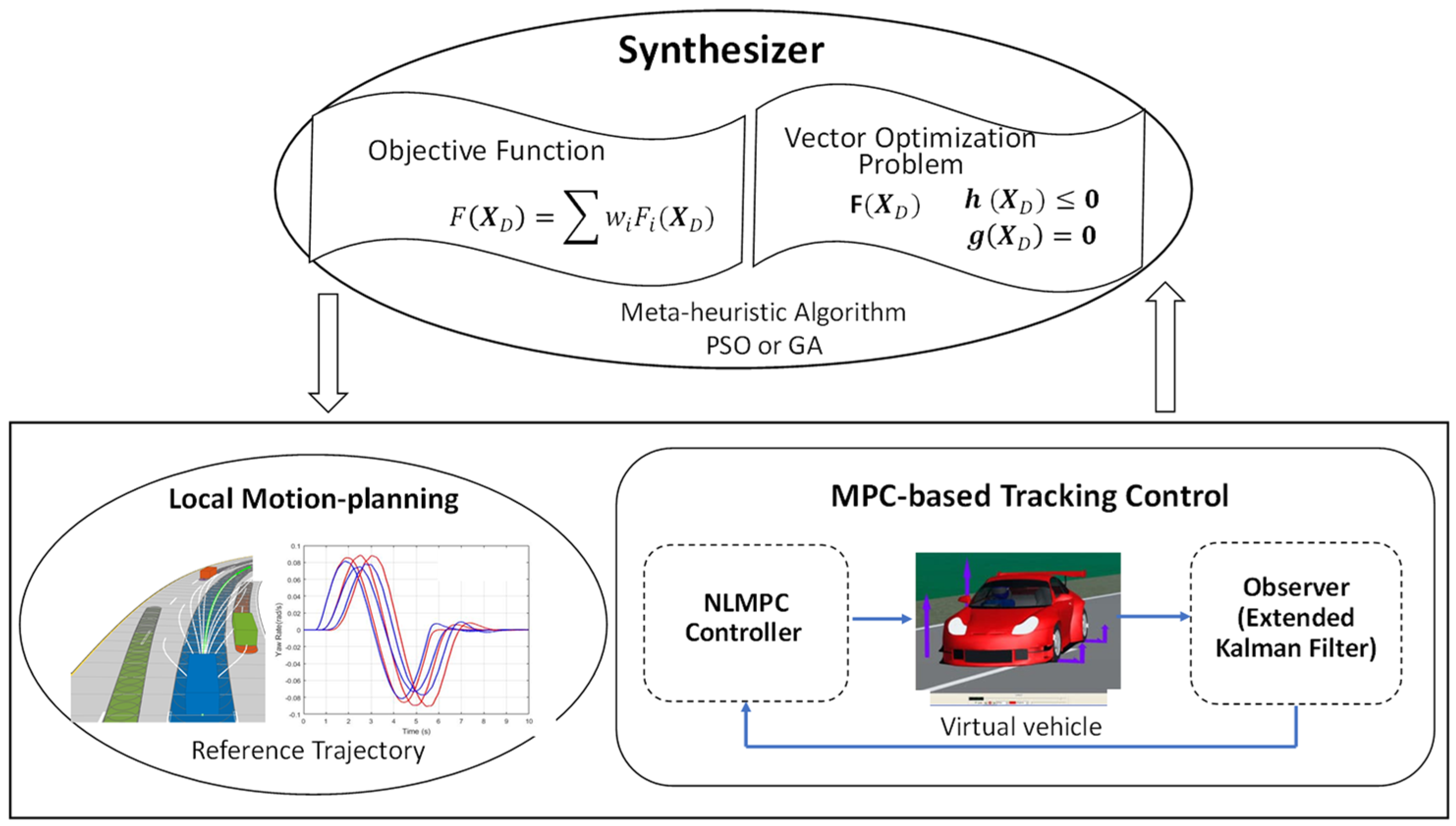
2. Design Methodology
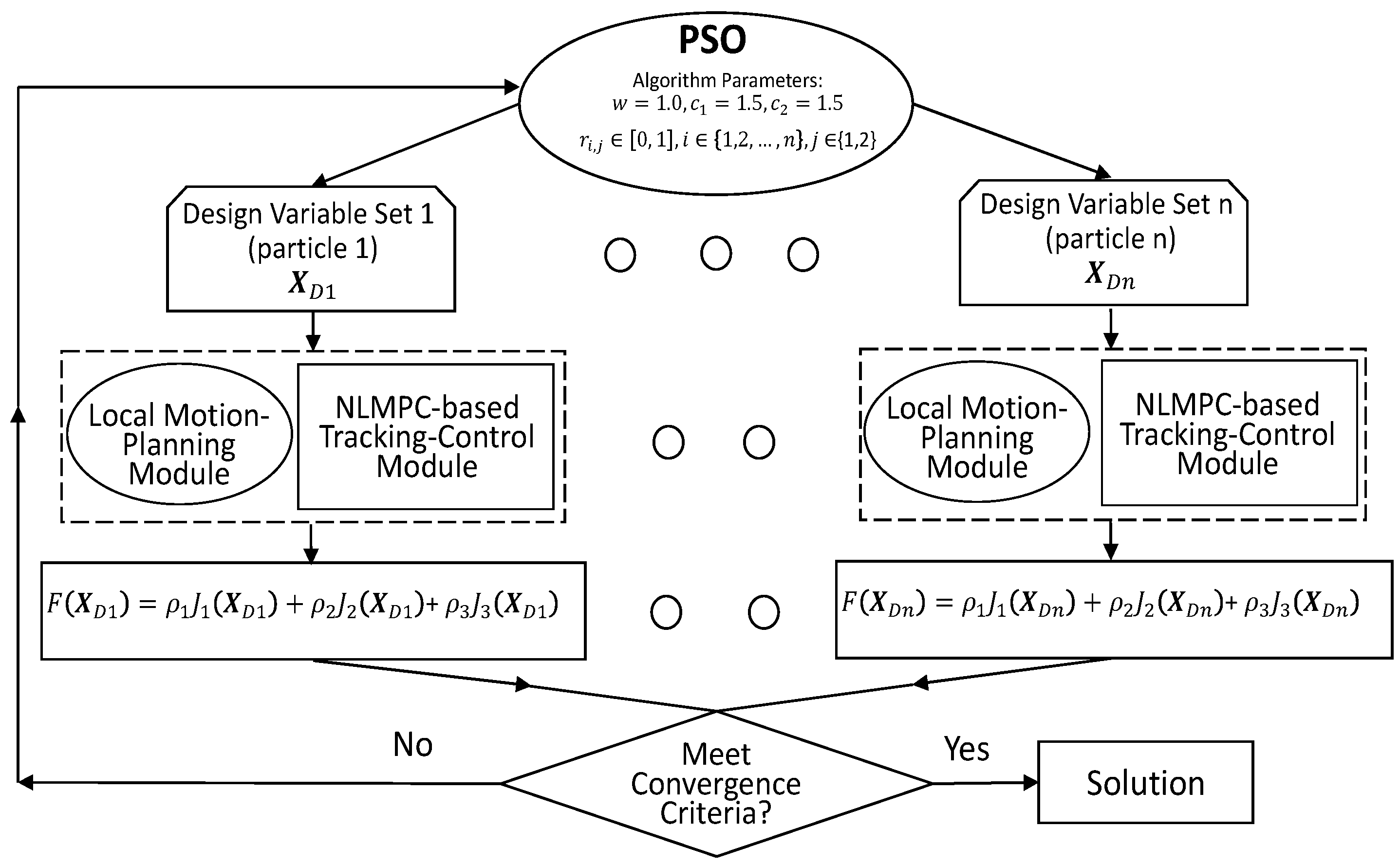
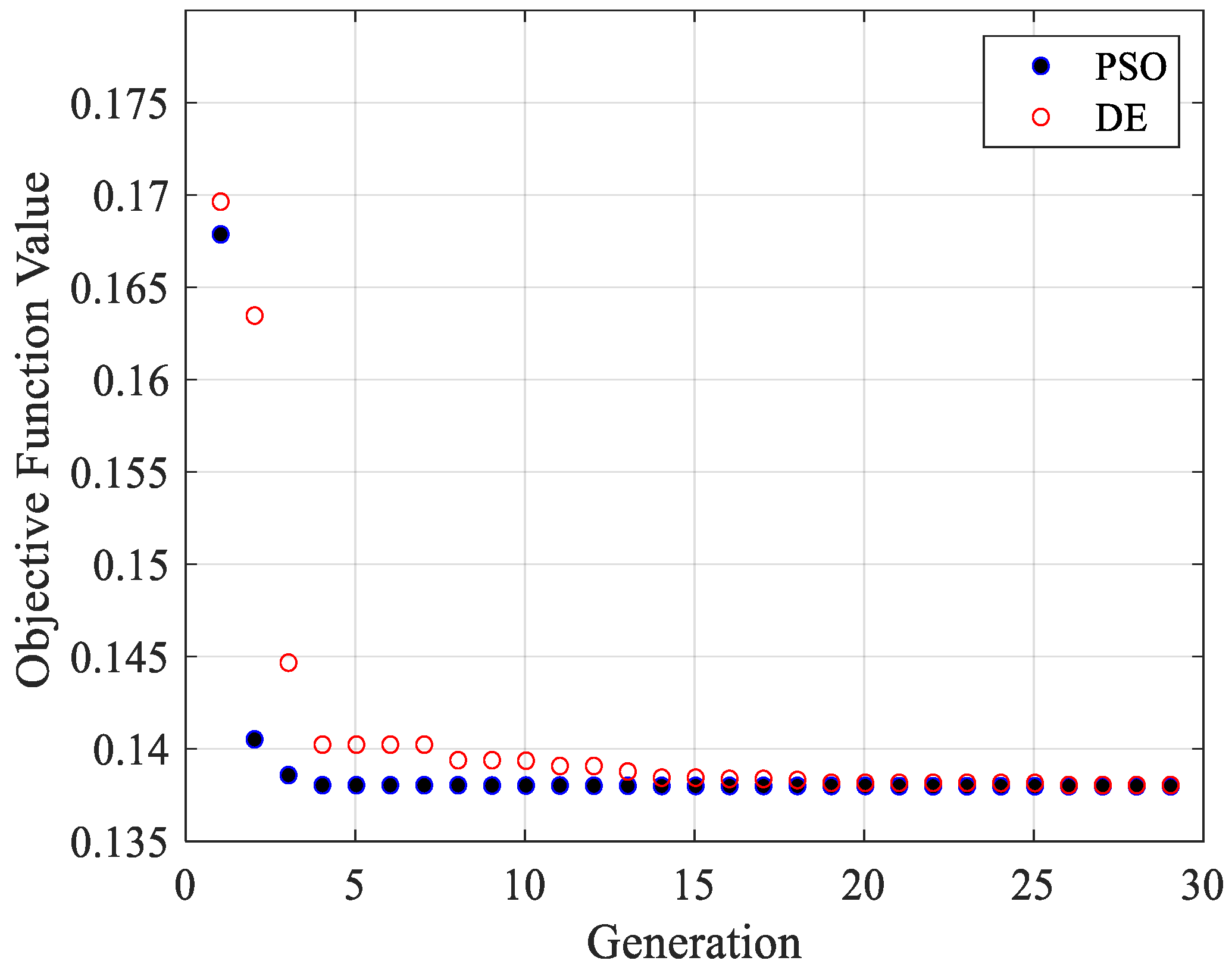
3. Particle Swarm Optimization (PSO) Algorithm
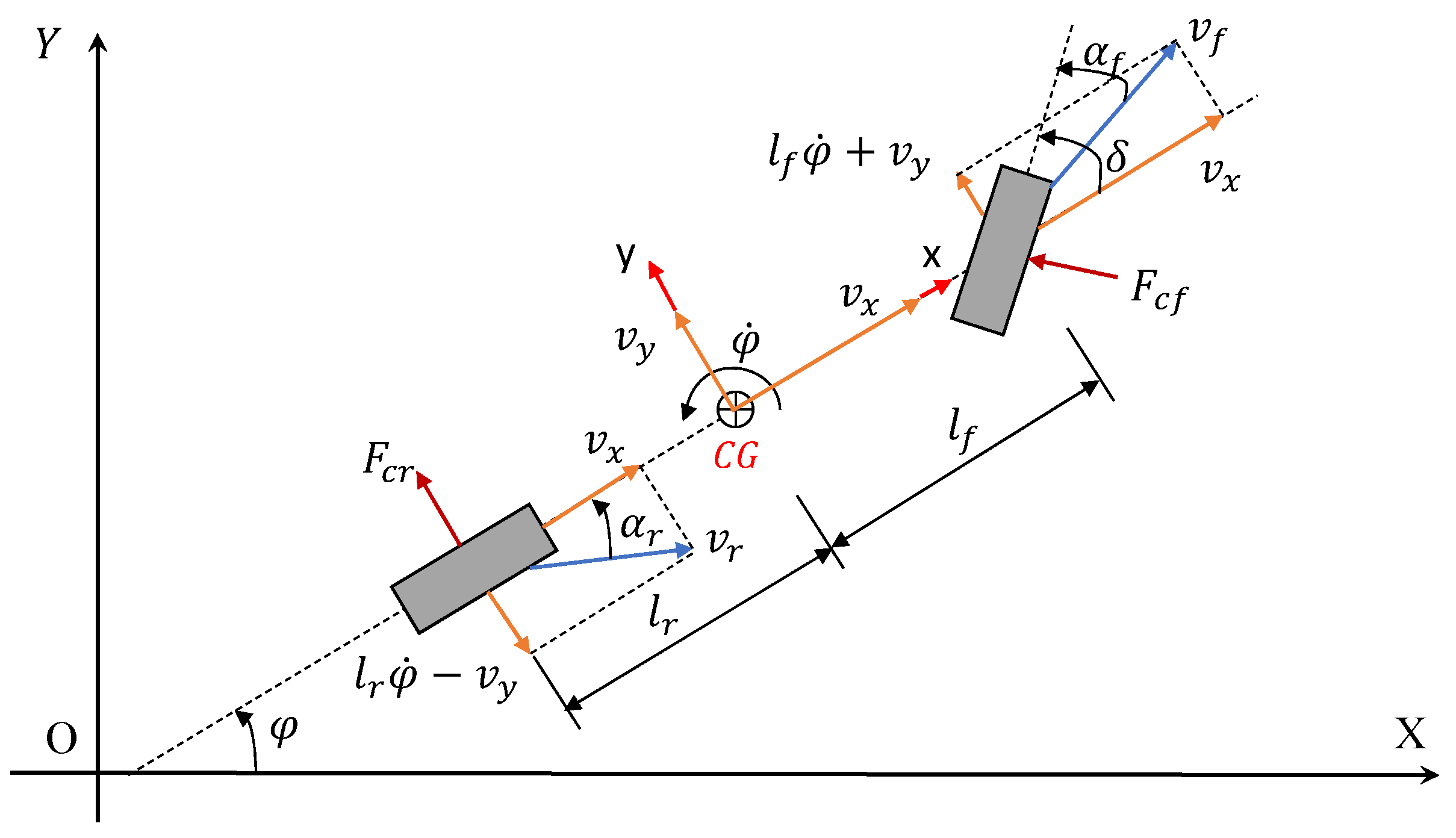
4. Vehicle System Models
4.1. 2-DOF Nonlinear Yaw-Plane Vehicle Model
4.2. CarSim Vehicle Model
5. NLMPC Controller Design
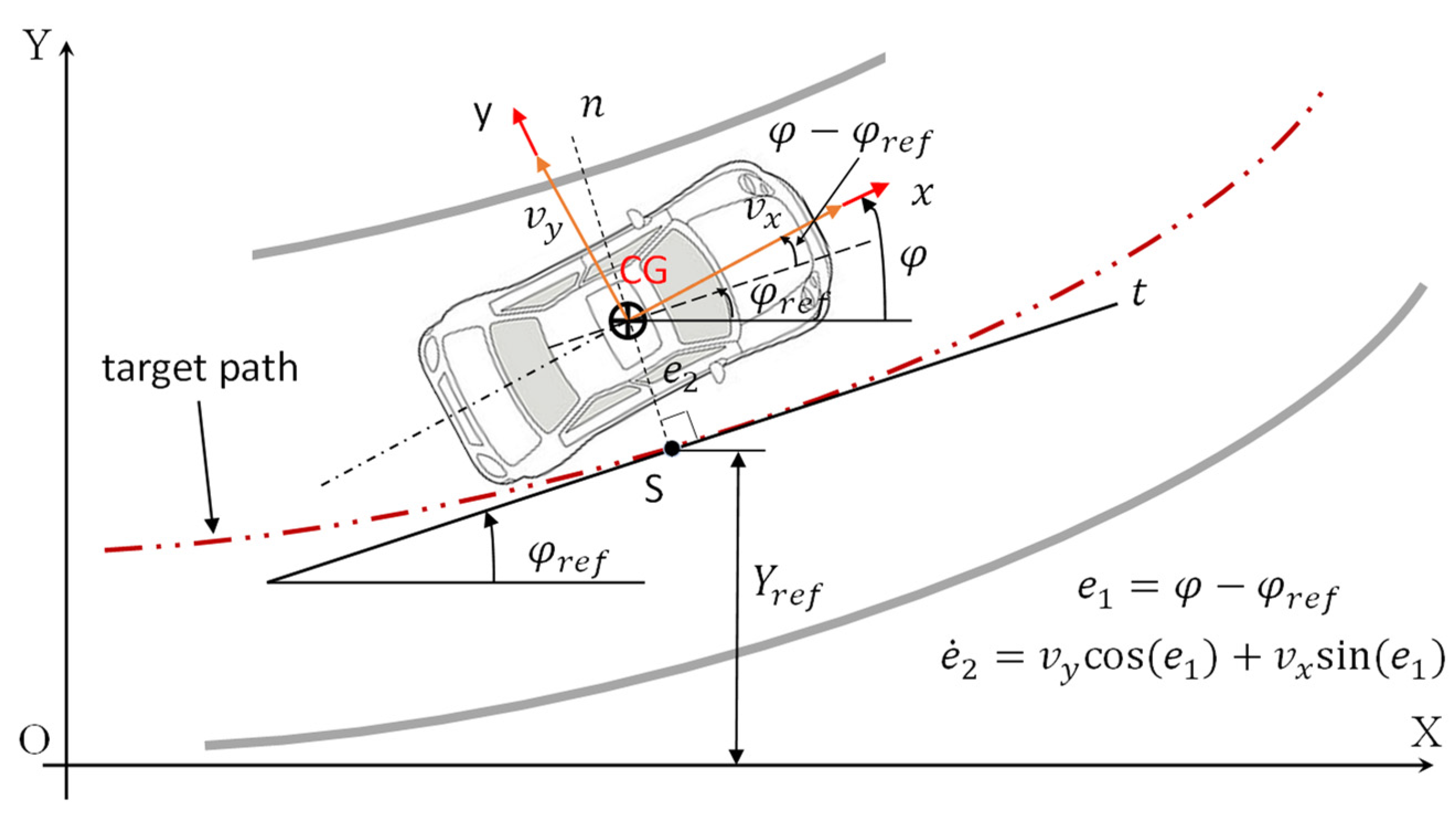
5.1. Tracking Controller Design
5.2. Reference Trajectory
6. Design Synthesis Problem Formulation and Implementation
6.1. Design Objectives, Variables, and Constraints
6.2. Two-Layer Optimization Problem Implementation
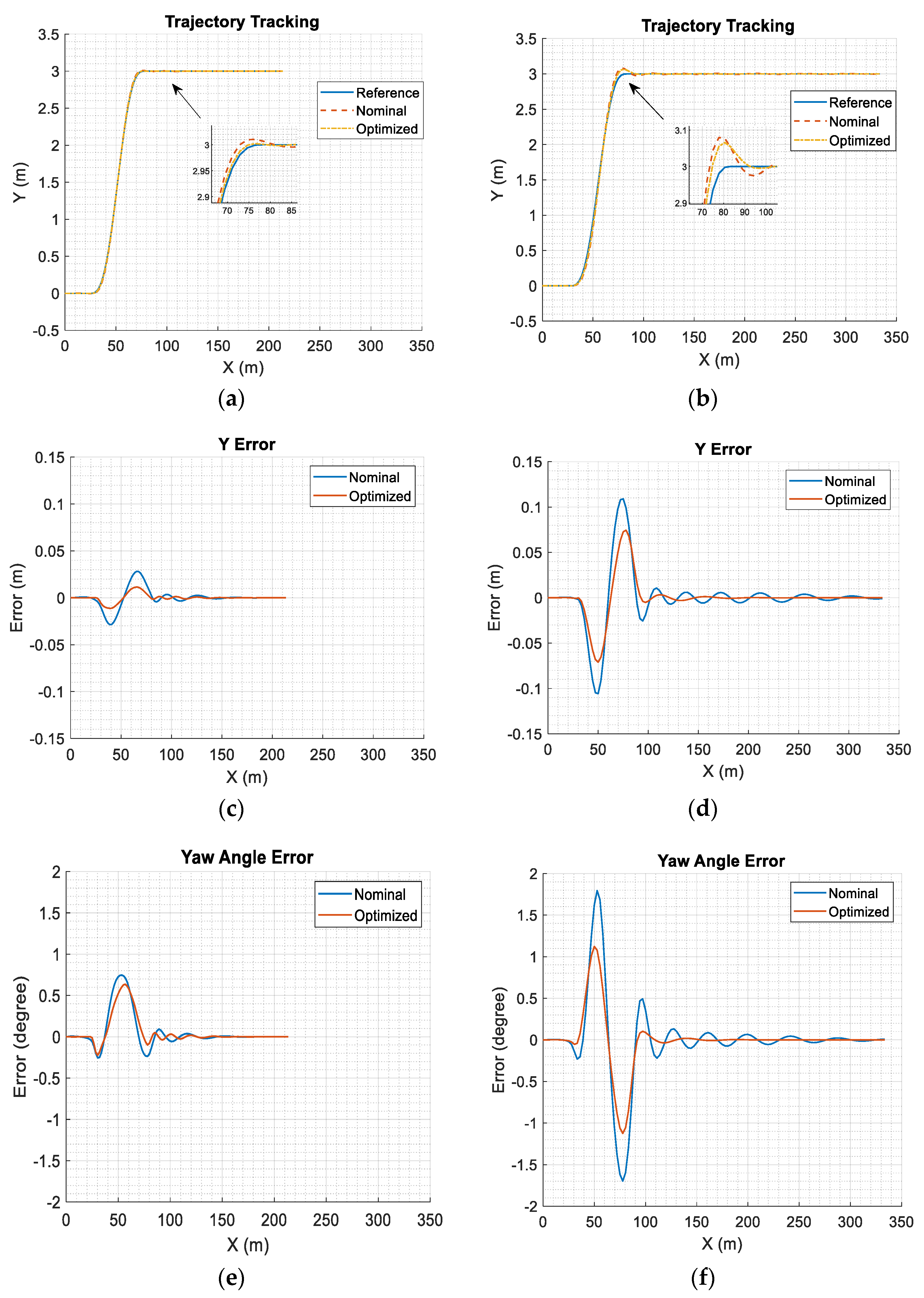
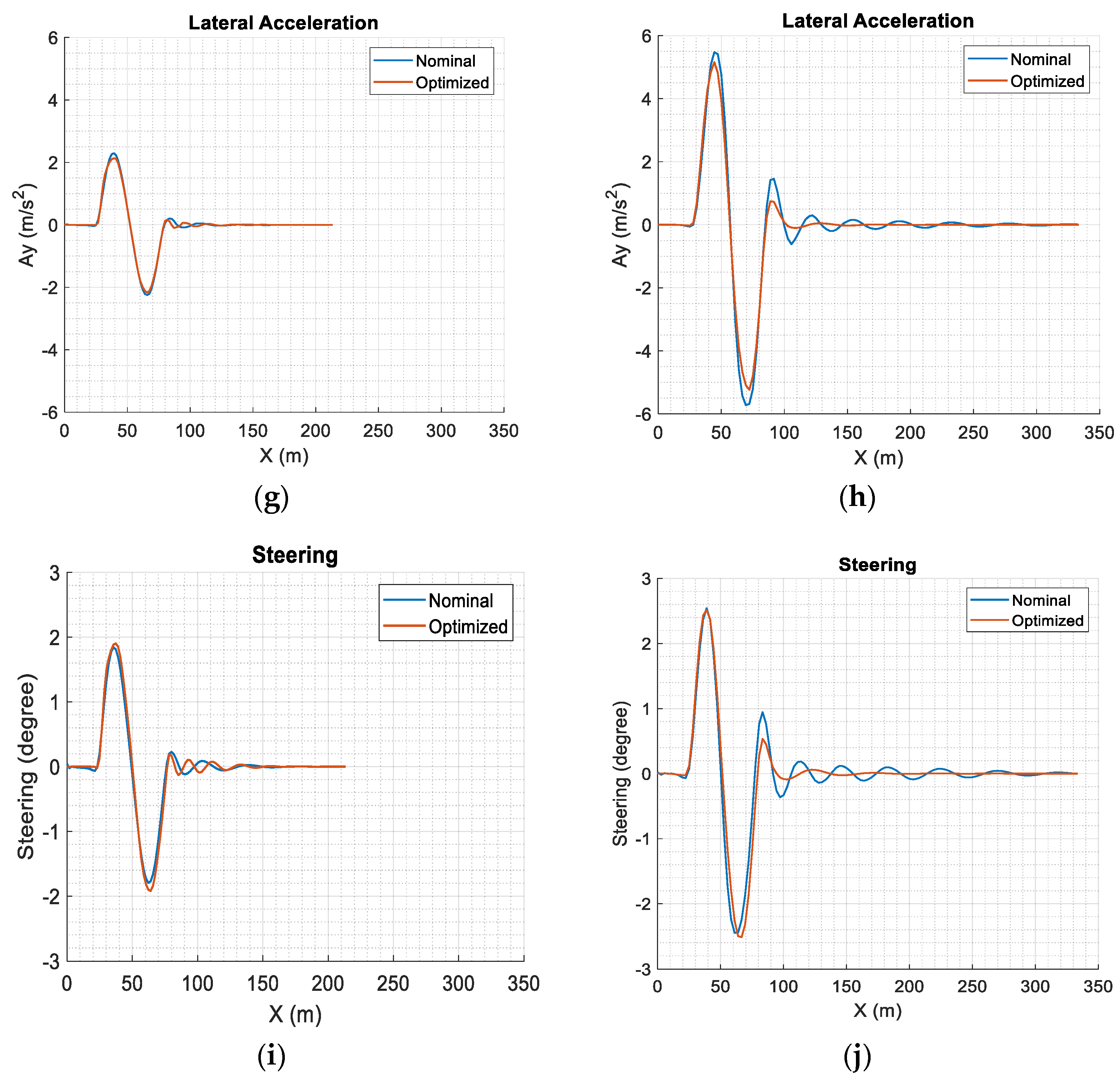
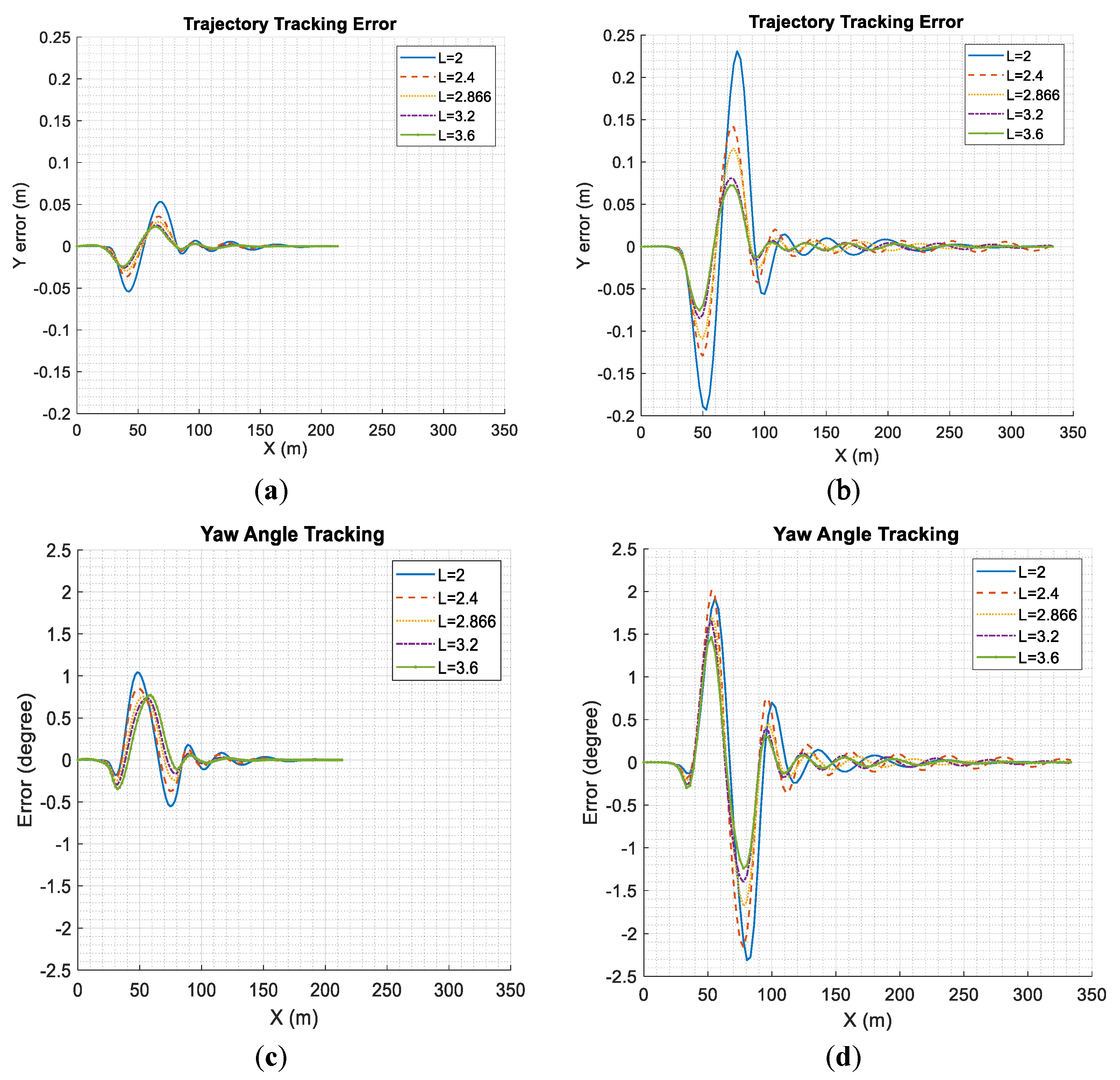
7. Results and Discussion
7.1. Performance Measures
7.2. Effects of Design Variables
8. Conclusions
- (1)
- The proposed method can be applied in the early design states for AVs for identifying desired design variables and predicting performance envelops.
- (2)
- The optimal designs (including optimal tracking-control and vehicle system design variables) for an AV are operating condition-dependent. This implies that in highway and urban operations, distinct optimal design variable sets should be determined, respectively, in order to achieve desired performance envelops.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Rosique, F.; Navarro, P.J.; Fernández, C.; Padilla, A. A systematic review of perception system and simulators for autonomous vehicles research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef] [PubMed]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and sensor fusion technology in autonomous vehicles: A review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Ananda, M.P.; Bernstein, H.; Cunningham, K.E.; Feess, W.A.; Stroud, E.G. Global Positioning System (GPS) autonomous navigation. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20 March 1990; pp. 497–508. [Google Scholar]
- Rahiman, W.; Zainal, Z. An overview of development GPS navigation for autonomous car. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications, ICIEA 2013, Melbourne, VIC, Australia, 19–21 June 2013. [Google Scholar]
- Mohamed, S.A.S.; Haghbayan, M.H.; Westerlund, T.; Heikkonen, J.; Tenhunen, H.; Plosila, J. A survey on odometry for autonomous navigation systems. IEEE Access 2019, 7, 97466–97486. [Google Scholar] [CrossRef]
- Kaminer, I.; Pascoal, A.; Hallberg, E.; Silvestre, C. Trajectory tracking for autonomous vehicles: An integrated approach to guidance and control. J. Guid. Control Dyn. 1998, 21, 29–38. [Google Scholar] [CrossRef]
- Kanayama, Y.; Kimura, Y.; Miyazaki, F.; Noguchi, T. A stable tracking control method for an autonomous mobile robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990. [Google Scholar]
- d’Andr’ea Novel, B.; Campion, G.; Bastin, G. Control of nonholonomic wheeled mobile robots by state feedback linearization. Int. J. Robot. Res. 1995, 14, 543–559. [Google Scholar] [CrossRef]
- Falcone, P.; Eric Tseng, H.; Borrelli, F.; Asgari, J.; Hrovat, D. MPC-based yaw and lateral stabilisation via active front steering and braking. Veh. Syst. Dyn. 2008, 46, 611–628. [Google Scholar] [CrossRef]
- Rawlings, J.B. Tutorial overview of model predictive control. IEEE Control Syst. Mag. 2000, 20, 38–52. [Google Scholar]
- Guo, H.; Zhang, H.; Chen, H.; Jia, R. Simultaneous trajectory planning and tracking using an MPC method for cyber-physical systems: A case study of obstacle avoidance for an intelligent vehicle. IEEE Trans. Ind. Informat. 2018, 14, 4273–4283. [Google Scholar] [CrossRef]
- He, Y.; McPhee, J. Multidisciplinary design optimization of mechatronic vehicles with active suspensions. J. Sound Vib. 2005, 283, 217–241. [Google Scholar] [CrossRef]
- Pil, A.; Asada, H. Integrated structure/control design of mechatronic systems using a recursive experimental optimization method. IEEE/ASME Trans. Mechatron. 1996, 1, 191–203. [Google Scholar] [CrossRef]
- Nebeluk, R.; Ławryńczuk, M. Tuning of multivariable model predictive control for industrial tasks. Algorithms 2021, 14, 10. [Google Scholar] [CrossRef]
- Yamashita, A.S.; Alexandre, P.M.; Zanin, A.C.; Odloak, D. Reference trajectory tuning of model predictive control. Control. Eng. Pract. 2016, 50, 1–11. [Google Scholar] [CrossRef]
- Júnior, G.A.N.; Martins, M.A.F.; Kalid, R. A PSO-based optimal tuning strategy for constrained multivariable predictive controllers with model uncertainty. ISA Trans. 2014, 53, 560–567. [Google Scholar] [CrossRef] [PubMed]
- Gu, T.; Snider, J.; Dolan, J.M.; Lee, J. Focused trajectory planning for autonomous on-road driving. In Proceedings of the 2013 IEEE Intelligent Vehicle Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013. [Google Scholar]
- Islam, M.M.; Ding, X.; He, Y. A closed-loop dynamic simulation based design method for articulated heavy vehicles with active trailer steering systems. Veh. Syst. Dyn. 2012, 50, 675–697. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Mechanical Simulation Corporation. CARSIM: Math Models. 26 September 2021. Available online: https://www.carsim.com/downloads/pdf/CarSim_Math_Models.pdf (accessed on 26 September 2021).
- Bakker, E.; Nyborg, L.; Pacejka, H.B. Tyre modelling for use in vehicle dynamics studies. SAE Trans. 1987, 96, 190–204. [Google Scholar]
- Liu, C.; Zhan, W.; Tomizuka, M. Speed profile planning in dynamic environments via temporal optimization. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Gu, T.; Dolan, J.M.; Lee, J. Runtime-bounded tunable motion planning for autonomous driving. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016. [Google Scholar]
- Koibuchi, K.; Yamamoto, M.; Fukada, Y.; Inagaki, S. Vehicle stability control in limit cornering by active brake. SAE Tech. Pap. 1996, 960487. [Google Scholar] [CrossRef]
- ISO-2631-1:1997/Amd 1:2010; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements—Amendment 1. International Organization for Standardization: Geneva, Switzerland, 2022. Available online: https://www.iso.org/standard/45604.html (accessed on 16 February 2022).
- Zhu, S.; He, Y. A driver-adaptive stability control strategy for sport utility vehicles. Veh. Syst. Dyn. 2017, 55, 1206–1240. [Google Scholar] [CrossRef]
- ISO-14791:2000(E); Road Vehicles—Heavy Commercial Vehicle Combinations and Articulated Buses—Lateral Stability Test Methods. International Organization for Standardization: Geneva, Switzerland, 2000.
- Rahimi, A.; Huang, W.; Sharma, T.; He, Y. An autonomous driving control strategy for multi-trailer articulated heavy vehicles with enhanced active trailer safety. In Proceedings of the 27th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Saint-Petersburg, Russia, 16–20 August 2021. [Google Scholar]
- Duprey, B.; Sayers, M.; Gillespie, T. Using TruckSim to test performance based standards. SAE Tech. Pap. 2012. [Google Scholar] [CrossRef]
- Australian Transport Council. Performance-Based Standards Scheme—The Standards and Vehicle Assessment Rules. National Transport Commission, Australia. 2022. Available online: https://www.nhvr.gov.au/files/media/document/123/202211-0020-pbs-standards-and-vehicle-assessment-rules.pdf (accessed on 7 May 2024).
- Zhu, S.; He, Y. A unified lateral preview driver model for road vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4858–4868. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous space. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]


| Human Reaction | |
|---|---|
| Not uncomfortable | |
| A little uncomfortable | |
| Fairly uncomfortable | |
| Uncomfortable | |
| Very uncomfortable | |
| Extremely uncomfortable |
| Reference Path Parameters | Urban SLC | Highway SLC |
|---|---|---|
| Vehicle forward speed, | 16.67 (60 km/h) | 27.78 (100 km/h) |
| Time period, | 3.00 | 2.00 |
| Maximum lateral displacement, | 3.00 | |
| Nominal Values | Lower Bound Values | Upper Bound Values | Optimal Values (Urban) | Optimal Values (Highway) | |
|---|---|---|---|---|---|
| 15.00 | 0.00 | 20.00 | 4.30 | 16.40 | |
| 5.00 | 0.00 | 20.00 | 11.52 | 4.51 | |
| 10.00 | 0.00 | 40.00 | 2.25 | 4.77 | |
| 1530.0 | 1200.0 | 2000.0 | 1934.0 | 1986.0 | |
| 2.87 | 2.00 | 3.60 | 3.16 | 3.55 | |
| 1.11 | 1.00 | 2.00 | 1.08 | 1.43 |
| Performance Measures | Urban | Highway | ||||
|---|---|---|---|---|---|---|
| Nominal Design | Optimal Design | Variation * (%) | Nominal Design | Optimal Design | Variation * (%) | |
| 0.0287 | 0.0115 | −59.9 | 0.1090 | 0.0744 | −31.7 | |
| (°) | 0.7462 | 0.6357 | −14.8 | 1.7948 | 1.6982 | −5.4 |
| (RMS) | 0.7845 | 0.7599 | −3.1 | 1.6573 | 1.5026 | −9.3 |
| (°) | 1.8425 | 1.9201 | 4.2 | 2.4473 | 2.5177 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, C.; He, Y.; Agelin-Chaab, M. A Design Method for Road Vehicles with Autonomous Driving Control. Actuators 2024, 13, 427. https://doi.org/10.3390/act13110427
Mao C, He Y, Agelin-Chaab M. A Design Method for Road Vehicles with Autonomous Driving Control. Actuators. 2024; 13(11):427. https://doi.org/10.3390/act13110427
Chicago/Turabian StyleMao, Chunyu, Yuping He, and Martin Agelin-Chaab. 2024. "A Design Method for Road Vehicles with Autonomous Driving Control" Actuators 13, no. 11: 427. https://doi.org/10.3390/act13110427
APA StyleMao, C., He, Y., & Agelin-Chaab, M. (2024). A Design Method for Road Vehicles with Autonomous Driving Control. Actuators, 13(11), 427. https://doi.org/10.3390/act13110427







