An Improved Adaptive Finite-Time Super-Twisting Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motors
Abstract
1. Introduction
- (1)
- An improved equivalent sliding mode model is proposed. By analyzing the traditional sliding mode model, the observation accuracy of the sliding mode observer is improved by adding a linear term and defining a perturbation term.
- (2)
- An adaptive gain finite time super-twisting algorithm sliding mode observer (AGFSTA-SMO) is proposed. Compared with the traditional Linear Super-twisting Algorithm Sliding-mode Observer (LSTA-SMO), the observer algorithm proposed in this paper requires only one parameter to be designed, and the parameter is a rotational speed adaptive function with gain self-adjustment capability.
- (3)
- A novel counter electromotive force optimization strategy is employed. Since the presence of high harmonics in the extended back EMF waveforms leads to a reduction in estimation accuracy from the phase-locked loop, a synchronous reference frame filter (SRFF) is designed in this paper to filter out the high harmonics in the extended back EMF. The addition of the back EMF optimization process will reduce the influence of high harmonics on the estimation results, decrease the jitter phenomenon, and improve the estimation accuracy compared to the current position of sensorless control strategy.
- (4)
- A novel Adaptive quadrature phase-locked loop (AQPLL) is used to estimate the rotor information. In order to solve the problems of low estimation accuracy and poor stability of the traditional phase-locked loop during the switching of motor speed, an improved adaptive quadrature phase-locked loop is used in this paper. The inverse potential normalization method is first used to eliminate the effect of speed variables on the phase-locked loop bandwidth, followed by the inclusion of a parameter adaptive tuning module based on the stochastic gradient descent method. Therefore, the new adaptive quadrature phase-locked loop is able to improve the speed tracking performance during speed switching and always maintain the stability of the motor.
2. PMSM Mathematical Model
3. Adaptive Sliding Mode Algorithm
3.1. Traditional Super-Twisting Algorithms
3.2. Gain Adaptive LSTA-SMO
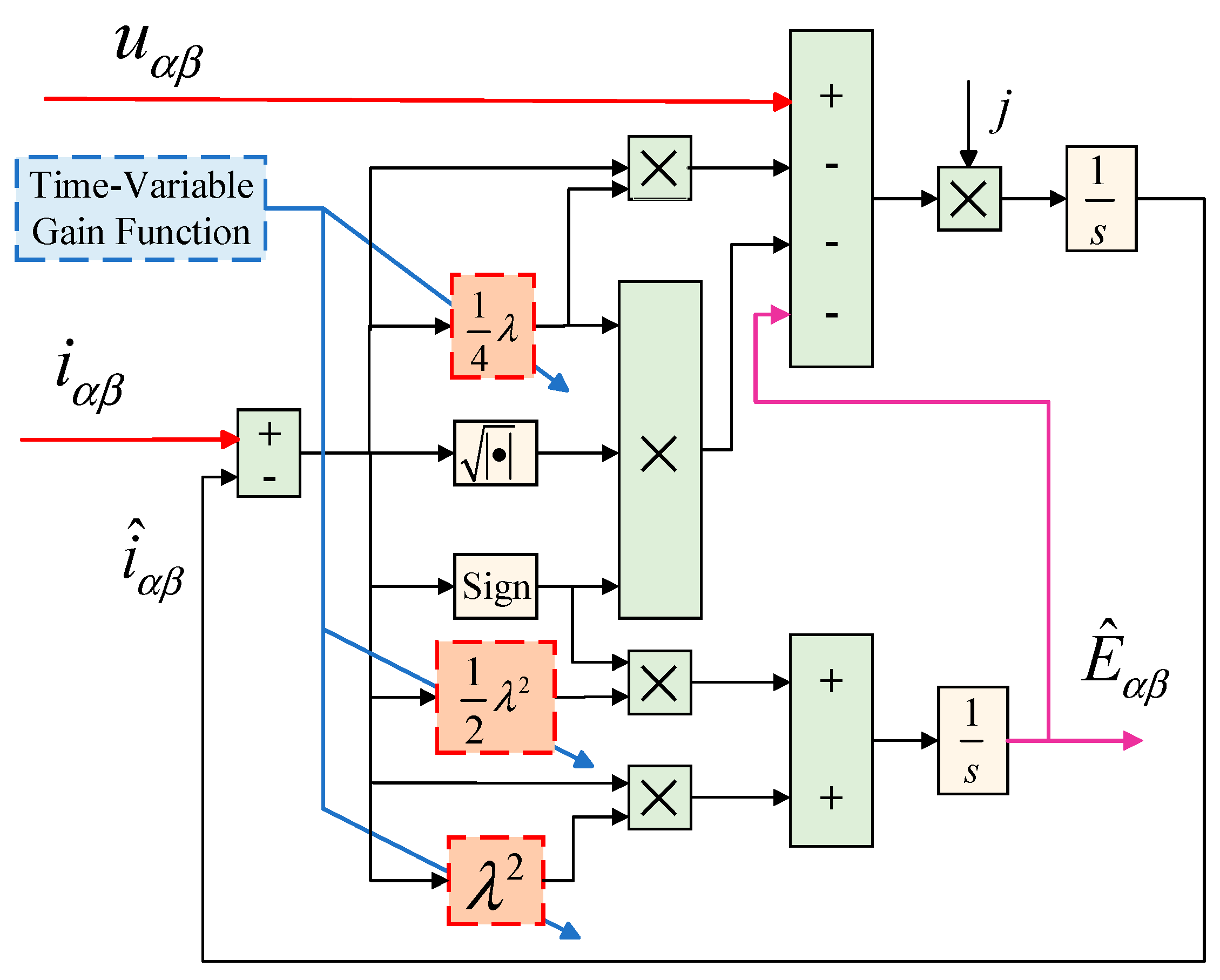
3.3. AGFSTA–SMO
3.4. Stability Proofs
3.4.1. Analyze
3.4.2. Analyze
3.4.3. Consider the Following Factual Circumstances
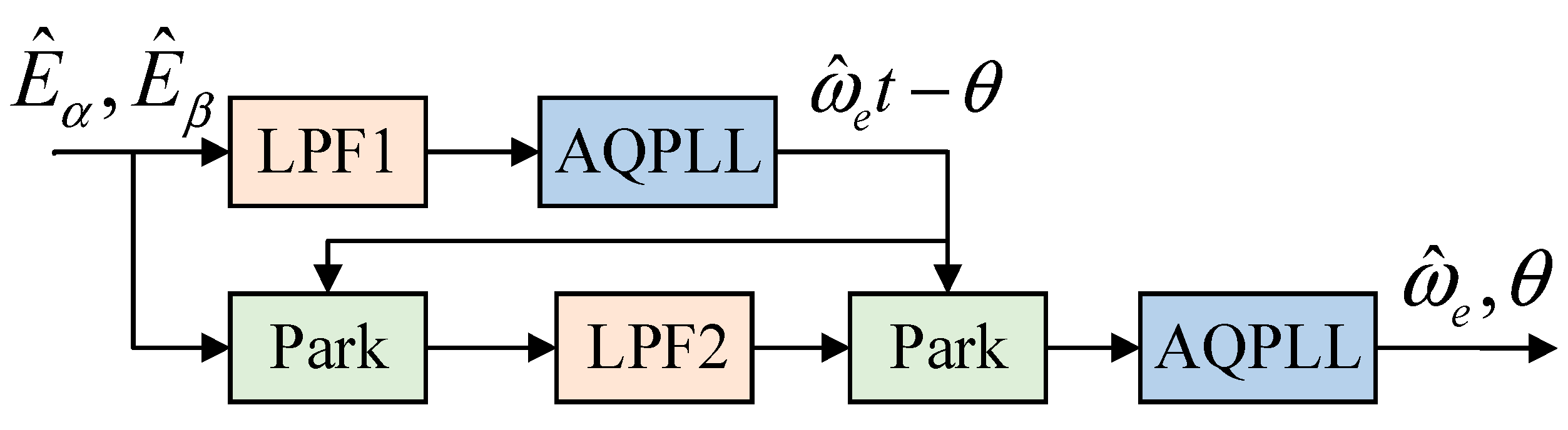
4. Rotor Information Extraction Program
4.1. Synchronized Reference System Filter
4.2. Adaptive Quadrature Phase-Locked Loop
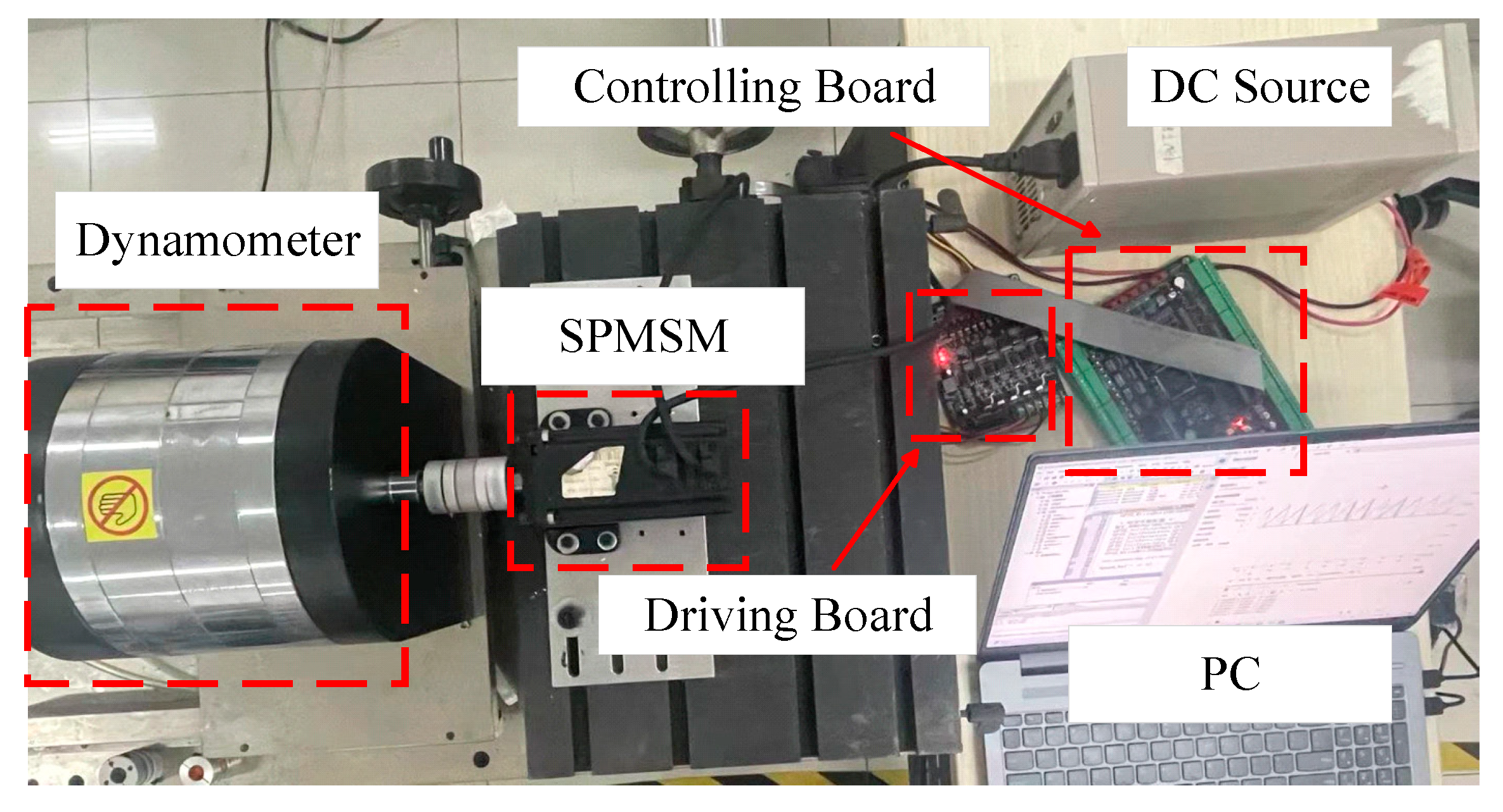
5. Simulation and Experimental Verification
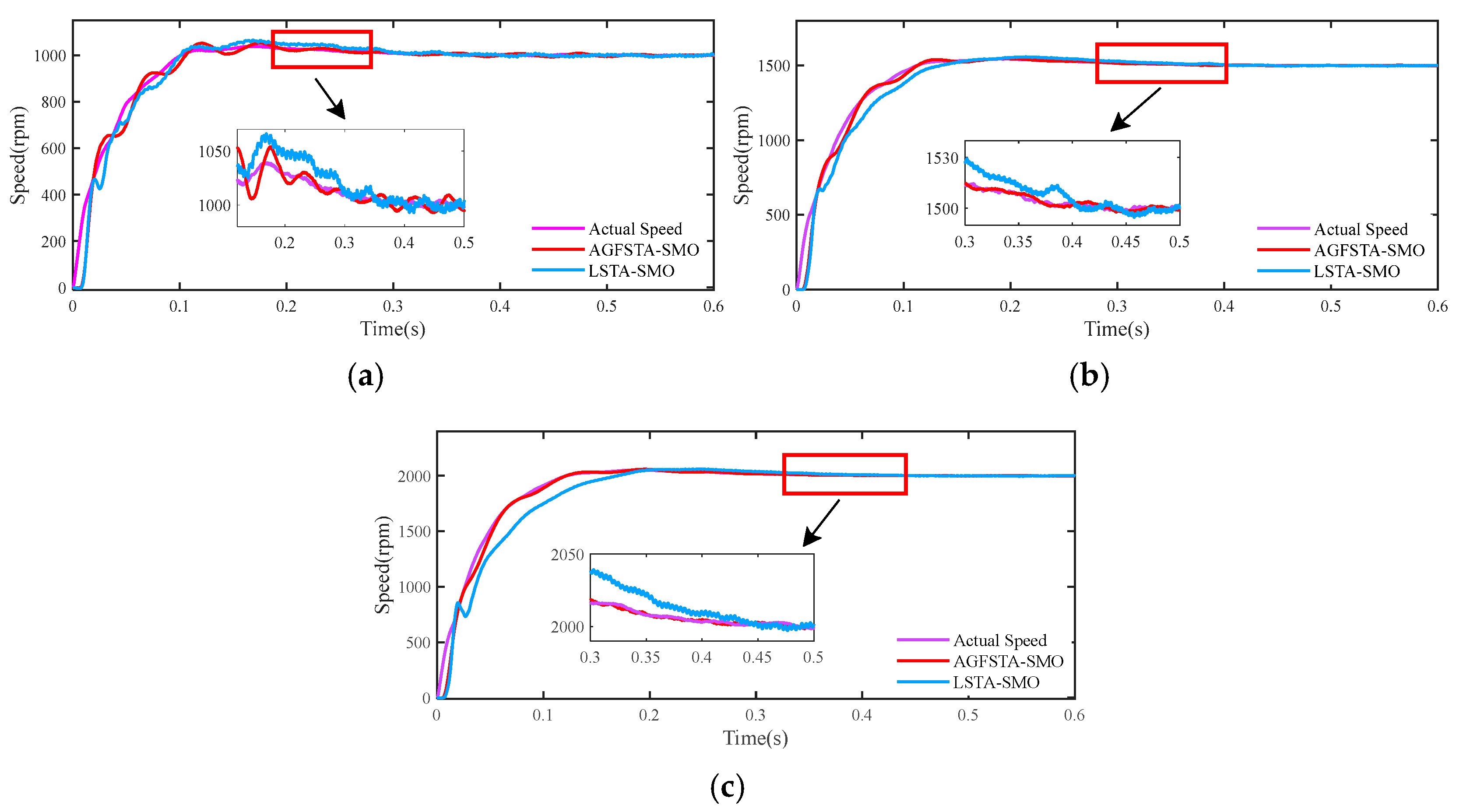
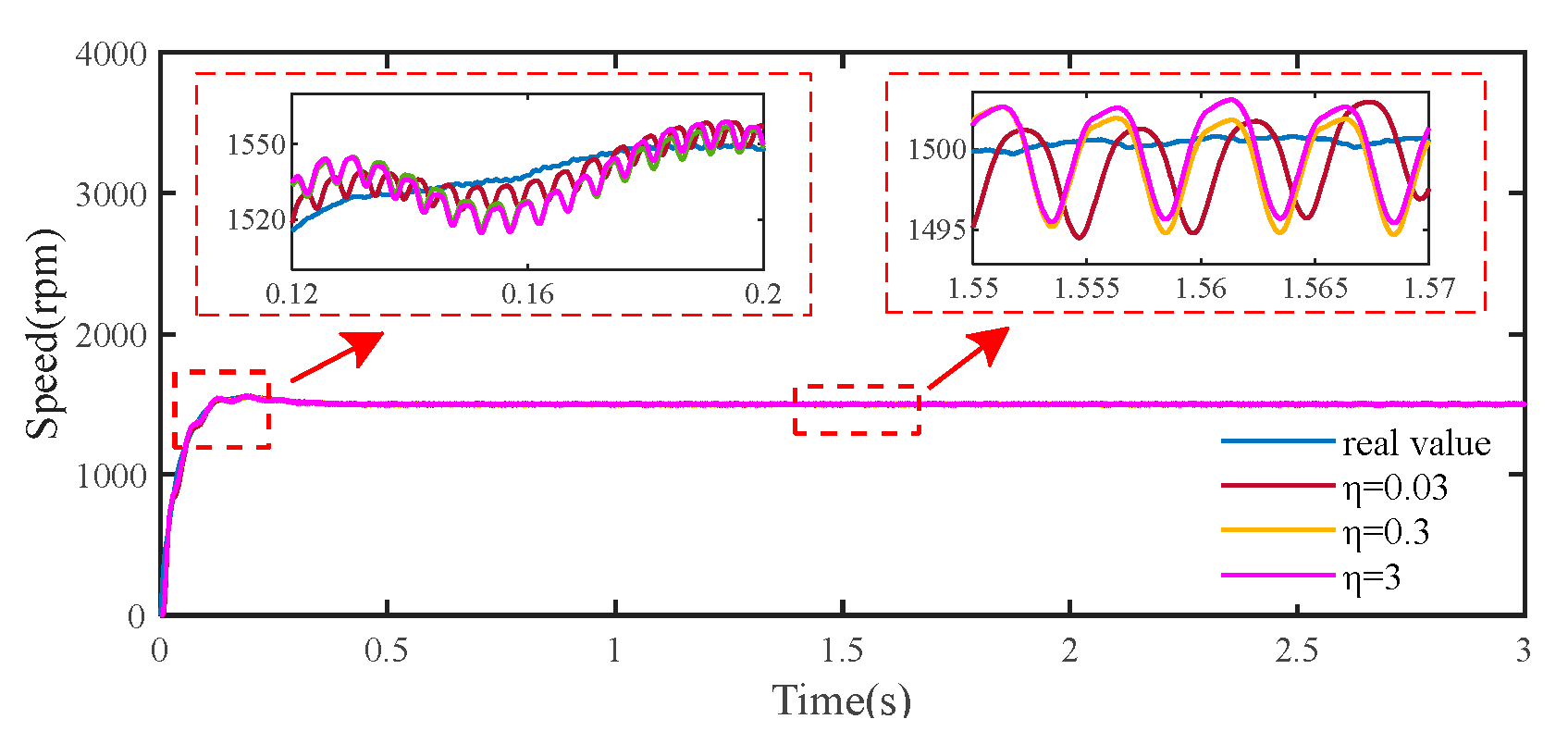
5.1. Simulation Analysis
5.2. Experimental Verification Analysis
5.2.1. No-Load Experiment
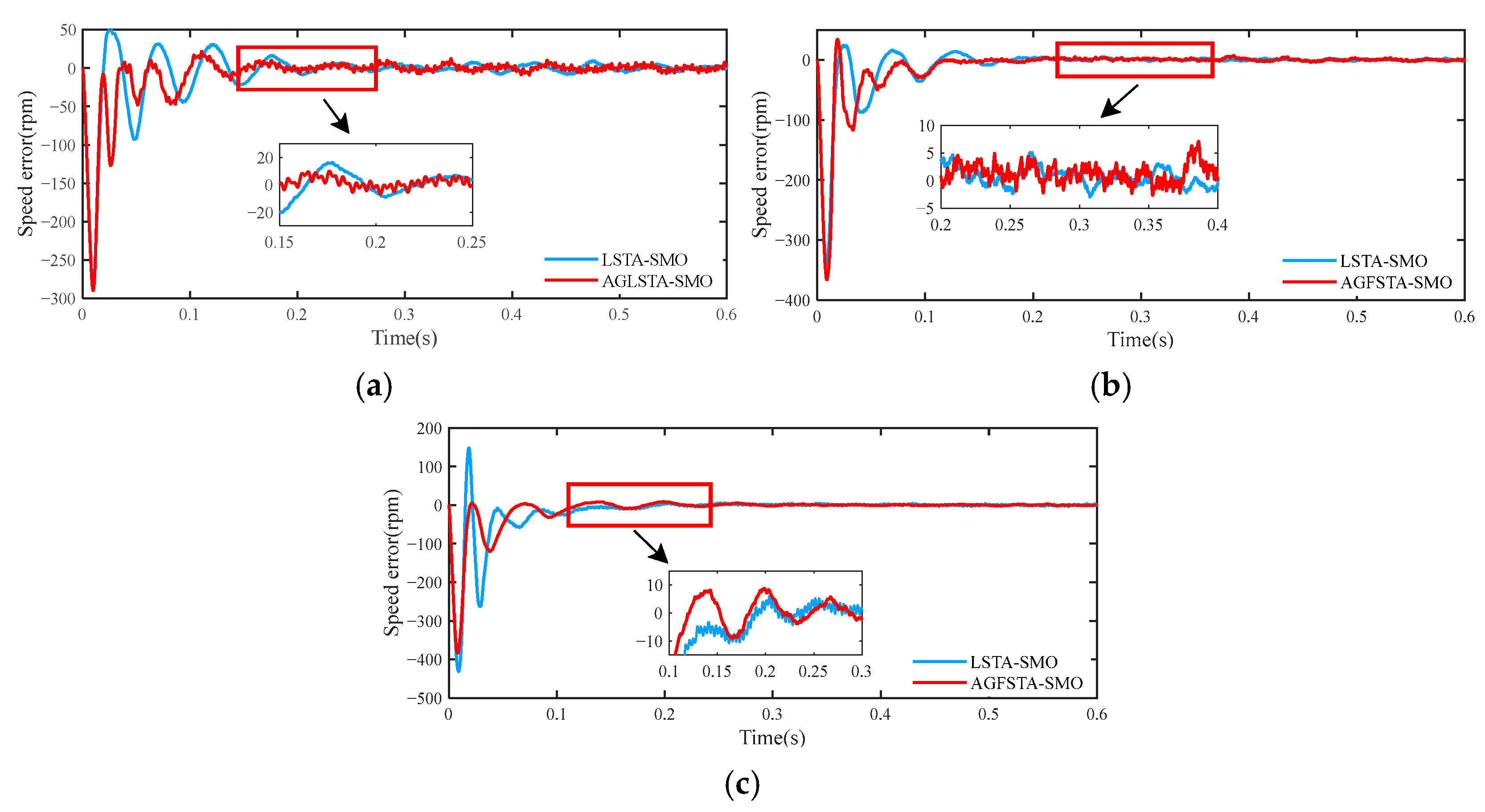
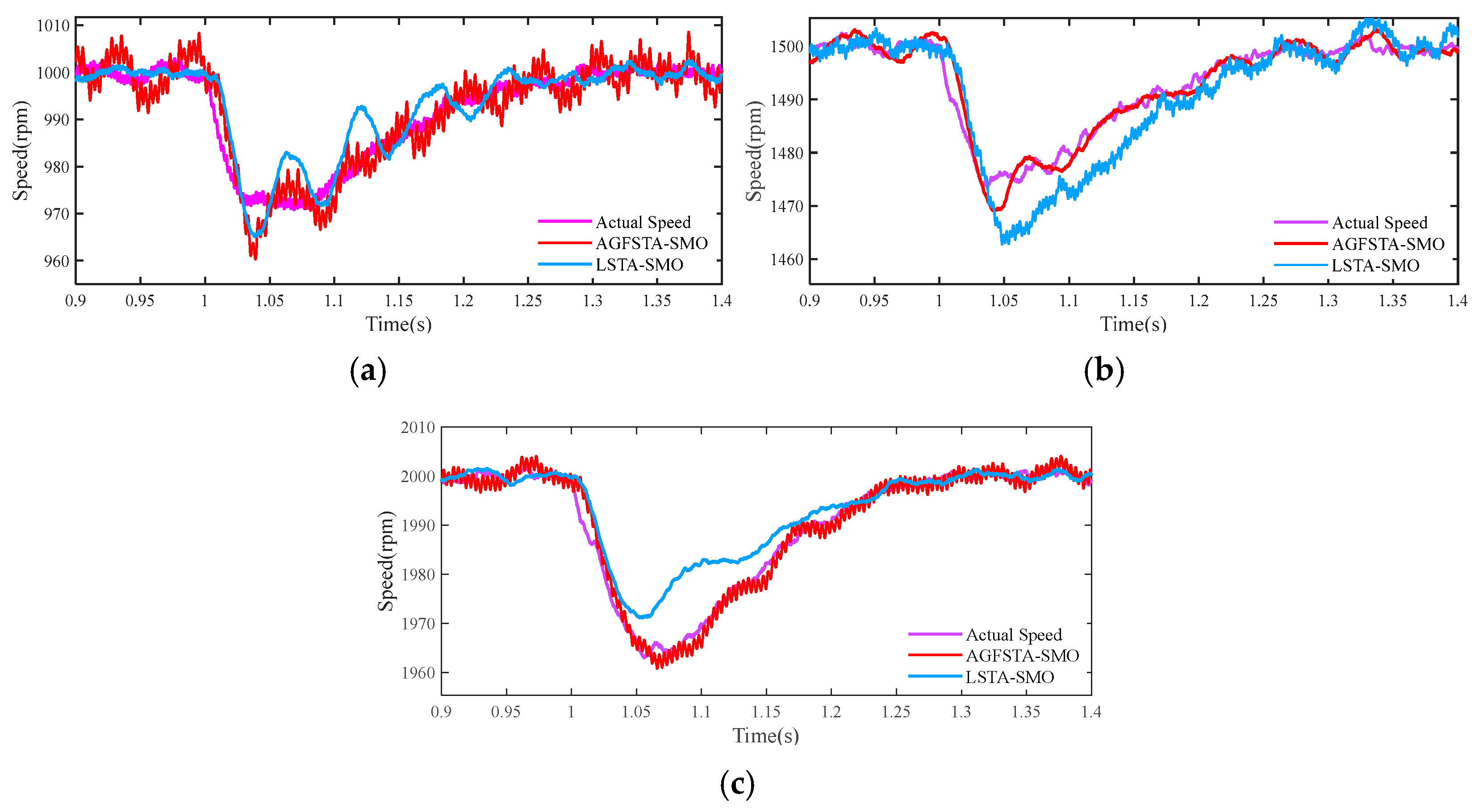
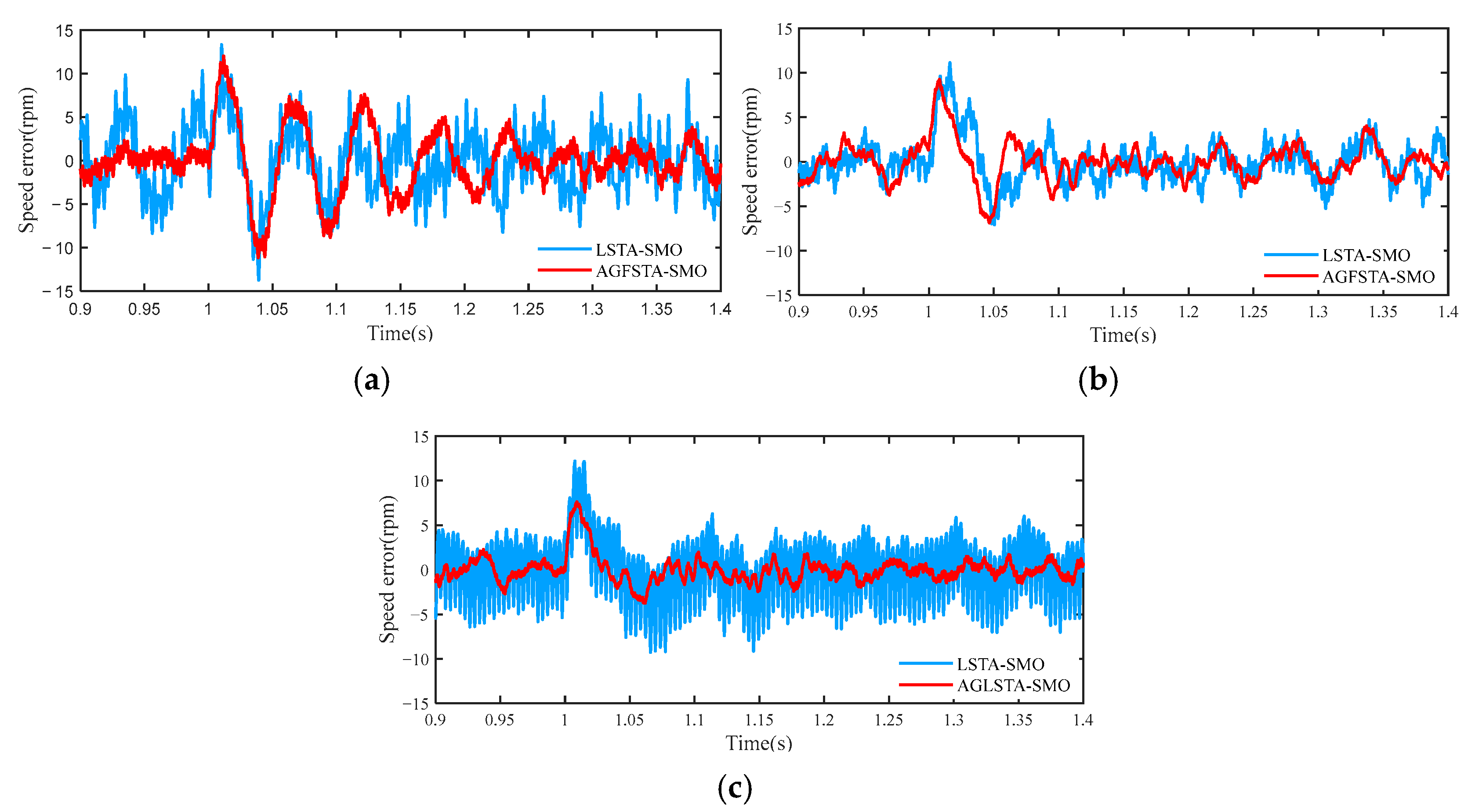
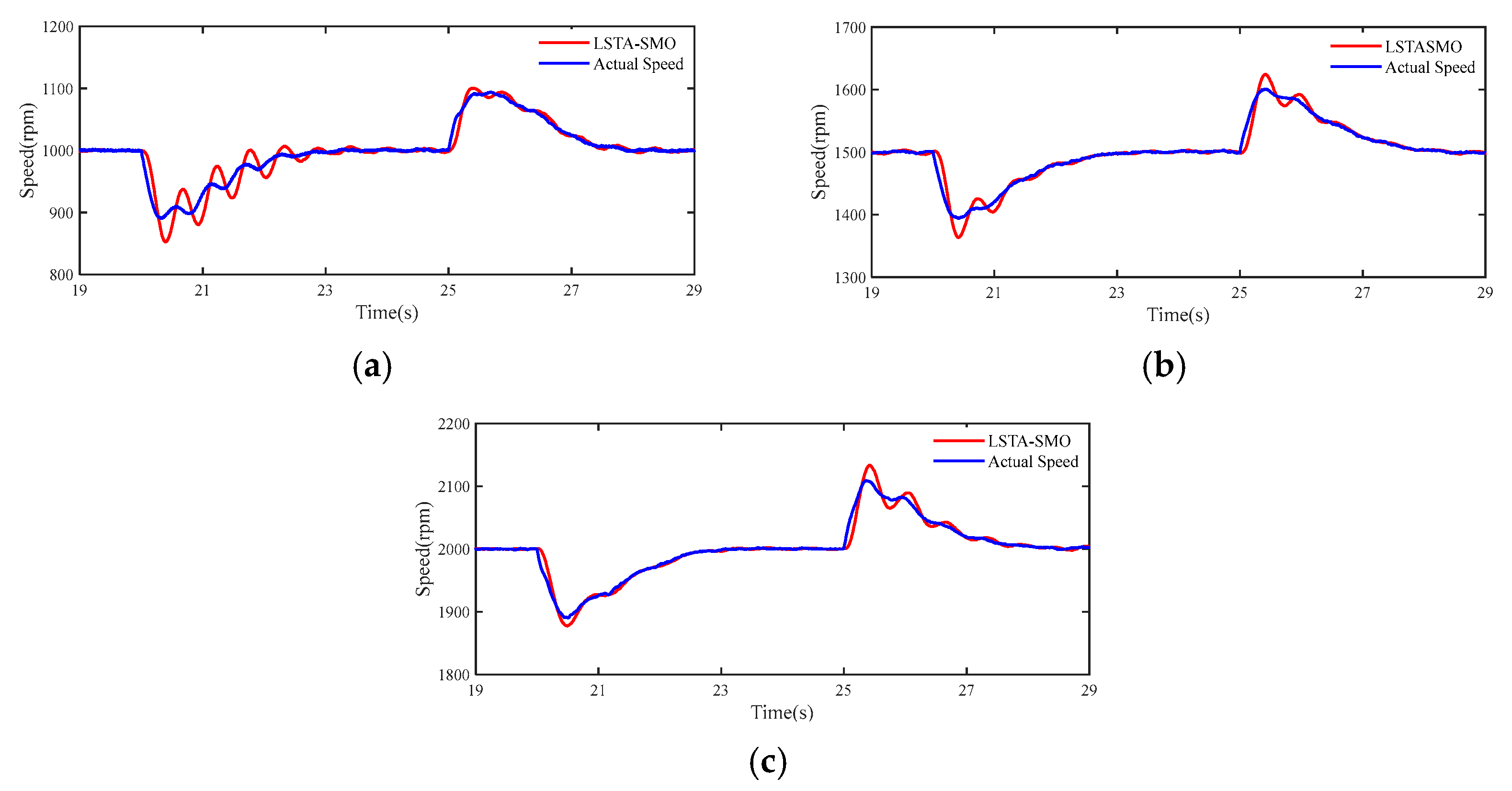
5.2.2. Comparison of Speed Tracking Performance of LSTA–SMO Algorithm and AGFSTA–SMO Algorithm under Sudden Load Change Conditions
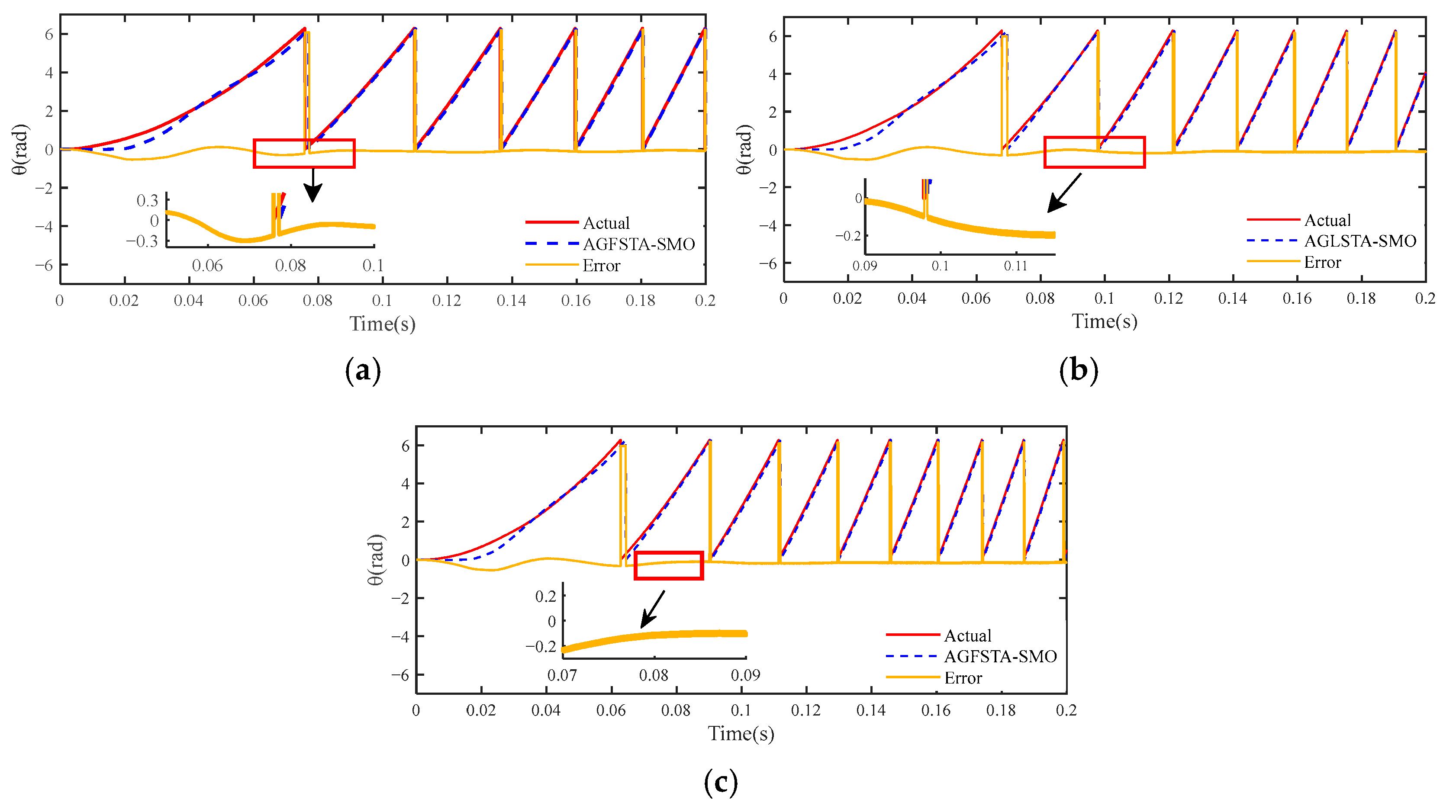
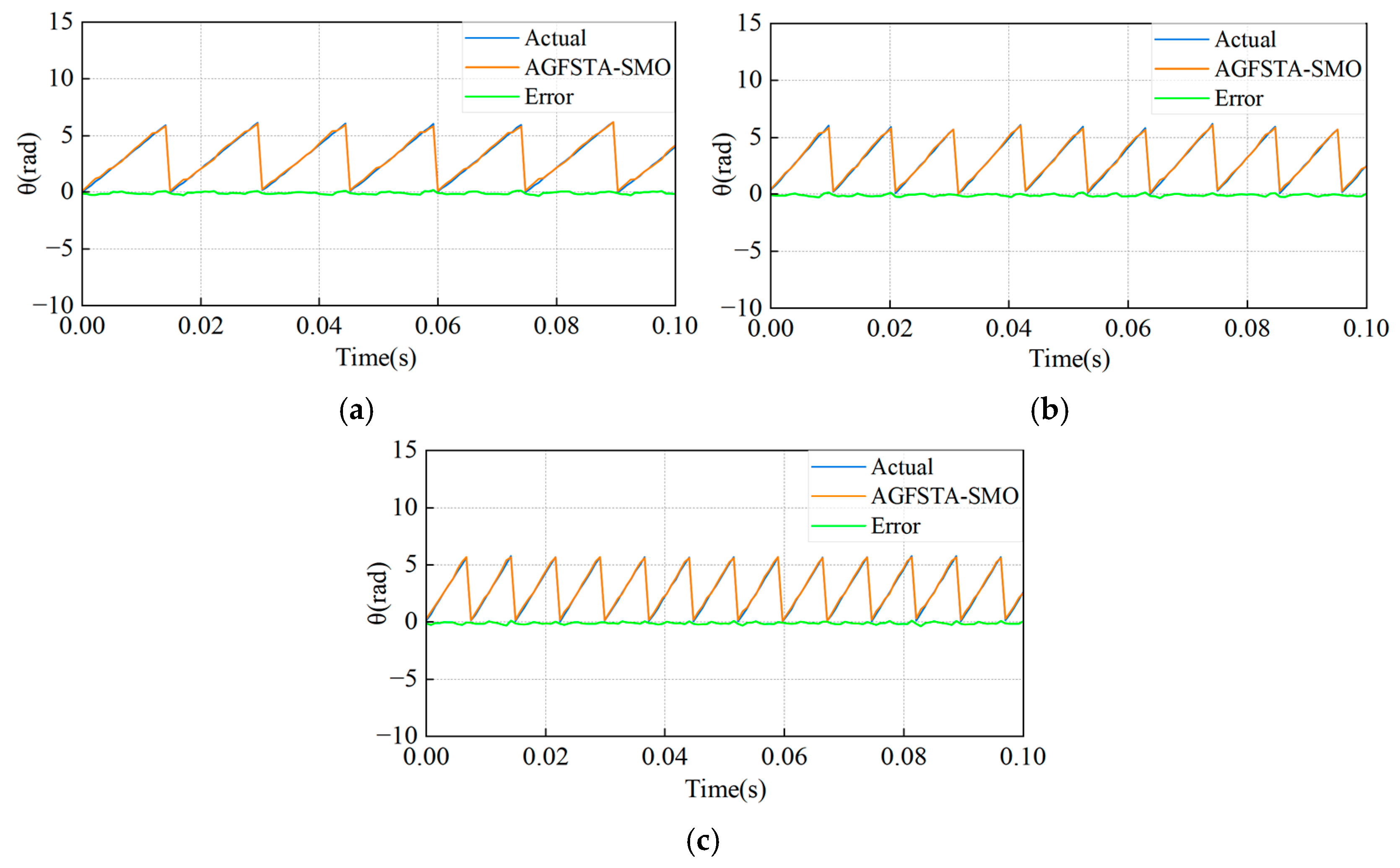
5.2.3. Performance of AGFSTA–SMO Method for Rotor Position Estimation during Sudden Load Changes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Xu, Y.; Zou, J. Sliding-mode sensorless control of PMSM with inverter nonlinearity compensation. IEEE Trans. Power Electron. 2019, 34, 10206–10220. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wang, Y.; Yan, L. An improved delay-suppressed sliding-mode observer for sensorless vector-controlled PMSM. IEEE Trans. Ind. Electron. 2019, 67, 5913–5923. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Dou, M. Full-speed range encoderless control for salient-pole PMSM with a novel full-order SMO. Energies 2018, 11, 2423. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, V.A.; Mehta, H.; Walambe, R. Disturbance-observer-based sensorless control of PMSM using integral state feedback controller. IEEE Trans. Power Electron. 2019, 35, 6082–6090. [Google Scholar] [CrossRef]
- Volpato Filho, C.J.; Xiao, D.; Vieira, R.P.; Emadi, A. Observers for high-speed sensorless pmsm drives: Design methods, tuning challenges and future trends. IEEE Access 2021, 9, 56397–56415. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, Y.; Cao, X.; Yuan, D.; Liu, J. Estimated position error suppression using novel PLL for IPMSM sensorless drives based on full-order SMO. IEEE Trans. Power Electron. 2021, 37, 4463–4474. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; Zhang, H.; Liu, C.; Luo, G. Adaptive sliding mode observer-based sensorless control for SPMSM employing a dual-PLL. IEEE Trans. Transp. Electrif. 2021, 8, 1267–1277. [Google Scholar] [CrossRef]
- Ni, Y.; Shao, D. Research of improved mras based sensorless control of permanent magnet synchronous motor considering parameter sensitivity. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; Volume 4, pp. 633–638. [Google Scholar]
- Zerdali, E.; Barut, M. The comparisons of optimized extended Kalman filters for speed-sensorless control of induction motors. IEEE Trans. Ind. Electron. 2017, 64, 4340–4351. [Google Scholar] [CrossRef]
- Nurettin, A.; İnanç, N. Sensorless vector control for induction motor drive at very low and zero speeds based on an adaptive-gain super-twisting sliding mode observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4332–4339. [Google Scholar] [CrossRef]
- Benevieri, A.; Formentini, A.; Marchesoni, M.; Passalacqua, M.; Vaccaro, L. Sensorless control with switching frequency square wave voltage injection for SPMSM with low rotor magnetic anisotropy. IEEE Trans. Power Electron. 2023, 38, 10060–10072. [Google Scholar] [CrossRef]
- Xu, W.; Qu, S.; Zhao, L.; Zhang, H. An improved adaptive sliding mode observer for middle-and high-speed rotor tracking. IEEE Trans. Power Electron. 2020, 36, 1043–1053. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, K.L.V. A review of sliding mode observer based sensorless control methods for PMSM drive. IEEE Trans. Power Electron. 2023, 38, 11352–11367. [Google Scholar] [CrossRef]
- Ren, N.; Fan, L.; Zhang, Z. Sensorless PMSM control with sliding mode observer based on sigmoid function. J. Electr. Eng. Technol. 2021, 16, 933–939. [Google Scholar] [CrossRef]
- Jin, D.; Liu, L.; Lin, Q.; Liang, D. Sensorless Control Strategy of PMSM with Disturbance Rejection Based on Adaptive Sliding Mode Control Law. IEEE Trans. Transp. Electrif. 2023, 10, 5424–5438. [Google Scholar] [CrossRef]
- Wang, C.; Gou, L.; Dong, S.; Zhou, M.; You, X. Sensorless control of IPMSM based on super-twisting sliding mode observer with CVGI considering flying start. IEEE Trans. Transp. Electrif. 2021, 8, 2106–2117. [Google Scholar] [CrossRef]
- Ge, Y.; Yang, L.; Ma, X. A harmonic compensation method for SPMSM sensorless control based on the orthogonal master-slave adaptive notch filter. IEEE Trans. Power Electron. 2021, 36, 11701–11711. [Google Scholar] [CrossRef]
- Chen, L.; Jin, Z.; Shao, K.; Wang, H.; Wang, G.; Iu, H.H.; Fernando, T. Sensorless Fixed-time Sliding Mode Control of PMSM Based on Barrier Function Adaptive Super-Twisting Observer. IEEE Trans. Power Electron. 2023, 39, 3037–3051. [Google Scholar] [CrossRef]
- Yang, C.; Song, B.; Xie, Y.; Zheng, S.; Tang, X. Adaptive Identification of Nonlinear Friction and Load Torque for PMSM Drives via a Parallel-Observer-Based Network with Model Compensation. IEEE Trans. Power Electron. 2023, 38, 5875–5897. [Google Scholar] [CrossRef]
- Jiang, T.; Ni, R.; Gu, S.; Wang, G. A study on position estimation error in sensorless control of PMSM based on back EMF observation method. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 1999–2003. [Google Scholar]
- Chen, Y.; Li, M.; Gao, Y.W.; Chen, Z.Y. A sliding mode speed and position observer for a surface-mounted PMSM. ISA Trans. 2019, 87, 17–27. [Google Scholar] [CrossRef]
- Wang, B.; Shao, Y.; Yu, Y.; Dong, Q.; Yun, Z.; Xu, D. High-order terminal sliding-mode observer for chattering suppression and finite-time convergence in sensorless SPMSM drives. IEEE Trans. Power Electron. 2021, 36, 11910–11920. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Q.; Sun, X.; Lu, C.; Zhu, H. Speed sensorless control of a bearingless induction motor based on sliding mode observer and phase-locked loop. ISA Trans. 2022, 123, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Qu, S.; Zhang, H. A composite sliding-mode observer with PLL structure for a sensorless SPMSM system. Int. J. Electr. Power Energy Syst. 2022, 143, 108510. [Google Scholar] [CrossRef]
- Naderian, M.; Markadeh, G.A.; Karimi-Ghartemani, M.; Mojiri, M. Improved sensorless control strategy for IPMSM using an ePLL approach with high-frequency injection. IEEE Trans. Ind. Electron. 2023, 71, 2231–2241. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Dou, W.; Jiang, L. Estimated Position Error Suppression Using Quasi-Super-Twisting Observer and Enhanced Quadrature Phase-Locked Loop for PMSM Sensorless Drives. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3865–3869. [Google Scholar] [CrossRef]
- Zhu, W.; Li, S.; Du, H.; Yu, X. Nonsmooth observer-based sensorless speed control for permanent magnet synchronous motor. IEEE Trans. Ind. Electron. 2022, 69, 13514–13523. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE conference on decision and control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Lin, S.; Zhang, W. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives. Int. J. Electr. Power Energy Syst. 2017, 88, 63–74. [Google Scholar] [CrossRef]
- Novak, Z.; Novak, M. Adaptive PLL-based sensorless control for improved dynamics of high-speed PMSM. IEEE Trans. Power Electron. 2022, 37, 10154–10165. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, H.; Song, X. Position-estimation deviation-suppression technology of PMSM combining phase self-compensation SMO and feed-forward PLL. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 335–344. [Google Scholar] [CrossRef]





| Items | Values | Parameters | Values |
|---|---|---|---|
| Stator winding resistance Rs | 0.56 Ω | k1 | 100 |
| Stator winding inductance LS | 0.62 mH | k2 | 400 |
| Flux linkage ψf | 0.0125 Wb | k3 | 100 |
| Rotational inertia J | 1.5 kg·cm2 | k4 | 50 |
| Pole pairs p | 4 | λ | 0.001 |
| Rated power | 250 W | Rated current | 7.5 A |
| Rated toque | 0.796 N·m | Rated speed | 3000 rpm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, M.; Ruan, J.; Zhang, Y.; Yan, H.; Wang, L. An Improved Adaptive Finite-Time Super-Twisting Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motors. Actuators 2024, 13, 395. https://doi.org/10.3390/act13100395
Luan M, Ruan J, Zhang Y, Yan H, Wang L. An Improved Adaptive Finite-Time Super-Twisting Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motors. Actuators. 2024; 13(10):395. https://doi.org/10.3390/act13100395
Chicago/Turabian StyleLuan, Mingchen, Jiuhong Ruan, Yun Zhang, Haitao Yan, and Long Wang. 2024. "An Improved Adaptive Finite-Time Super-Twisting Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motors" Actuators 13, no. 10: 395. https://doi.org/10.3390/act13100395
APA StyleLuan, M., Ruan, J., Zhang, Y., Yan, H., & Wang, L. (2024). An Improved Adaptive Finite-Time Super-Twisting Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motors. Actuators, 13(10), 395. https://doi.org/10.3390/act13100395






