Abstract
Nonskeletal animals such as worms achieve locomotion via crawling. We consider them as an inspiration to design robots that help underline the mechanisms of crawling. In this paper, we aim to identify an approach with the simplest structure and actuators. Our robots consist of cut-and-fold bodies equipped with pneumatically-driven soft actuators. We have developed fabrication techniques for coin-sized robots. Experiments showed that our robots can move up to 4.5 mm/s with straight motion (i.e., 0.1 body lengths per second) and perform cornering and U-turns. We have also studied the friction characteristics of our robots with the ground to develop a multistate model with stick–slip contact conversions. Our theoretical analyses depict comparable results to experiments demonstrating that simple and straightforward techniques can illustrate the crawling mechanism. Considering the minimal robots’ structure, this result is a critical step towards developing miniature crawling robots successfully.
Keywords:
robotics; bio-inspiration; crawling robot; fluid-driven actuation; soft actuator; modeling; friction 1. Introduction
Nature is an excellent inspiration for researchers focusing on robots. Animals use their muscles to move their bodies or pressurized fluids to operate their exoskeletons. They can also exhibit compliant characteristics that largely differentiate them from rigid robots [1]. Soft robots involving multiple forms of actuation have been widely studied to mimic these features. Fluidic actuation leverages both pneumatics [2,3,4] and hydraulics [5,6], while piezoelectric drives are another alternative [7,8,9]. Then, additional types of actuators include magnetically responsive [10,11,12], chemically responsive [13,14], and thermally responsive [15,16] devices. All these solutions provide generic actuation. However, when focusing on the locomotion of robots, Calisti et al. categorized several modes, namely crawling, legged locomotion, leaping gait, flying gait, swimming gaits, and other less common forms [17]. Crawling is popular among soft animals such as worms and larvae [18]. This process involves repetitive transitions of the contact points with the ground between stick and slip conditions [19]; this operation carries some complexities because active control of the contact points is possible in nature, for instance, via gripping spines [20]. Moreover, typical crawling can be seen as quasistatic motion since animals move slowly while passing between continuum equilibria (i.e., inertial effects become negligible).
Using these observations from animals, several attempts to develop crawling robots were conducted in the past [3,4,21,22,23,24,25,26,27,28,29]. Active interaction with the ground can be replicated by using active adhesion [30] or friction manipulation [21,23,27,31], while other devices leverage passive frictional contacts [22,25,28,29]. The structure of these robots is often very complex. Some researchers have developed soft robots that crawl like inchworms by mimicking their joints and gait [3,26,28]. The advantage of these robots is that they have multiple degrees of freedom that potentially allow for complex maneuvers. The corresponding disadvantages are poor control capabilities and heavy bodies. Origami robots can solve weight problems, reduce size, and are simple to manufacture [21,32], but they need higher temperatures for actuation purposes. Another example of simple design and actuation was proposed for a crab-inspired robot to explore adaptive locomotion [33]. Some other robots use multiple layers of materials to function, which increases complexity [23]. Finally, researchers studied crawling using static [28] and dynamic analyses [7,29,34]. The resulting mathematical modeling is, in any case, intricate.
Trying to simplify the abovementioned approaches, we aim to develop crawling robots with minimum complexity in terms of design, modeling, and implementation but still show motion control capabilities. This effort is motivated by the unanswered need to understand the mechanisms of crawling in a straightforward way. Thus, our paper is divided as follows: Section 2 describes the methods used in this study; Section 3 introduces robot modeling; Section 4 proposes our prototype and experimental results; Section 5 discusses the final remarks; and, lastly, the Appendix A addresses friction tests that support our investigation.
2. Methods
The procedures addressed in our study comprise different stages, such as design, prototyping, control, and modeling of the proposed robots.
2.1. Robot Design
We conceived the structure of our robots by observing the crawling motion of inchworms. These animals maintain contact points with the ground at the rear and front ends, as visible in Figure 1. The friction conditions at these interfaces change depending on the action being performed, including both stick and slip. The intermediate portion of the animal (soft) body is lifted and lowered accordingly to achieve locomotion. Starting from a lifted condition, the inchworm lowers its middle body (slip is present at the front end, while stick is present at the rear interface) and then moves its middle body up to the previous configuration (stick is now present at the front-end, while slip is present at the rear interface). Trying to understand this sequence better, it is convenient to visualize the animal as two equivalent (rigid) segments of equal length arranged in an inverse V-shape. One end of each segment is the contact point with the ground, whereas the other ends are connected to a revolute joint capable of delivering torque.
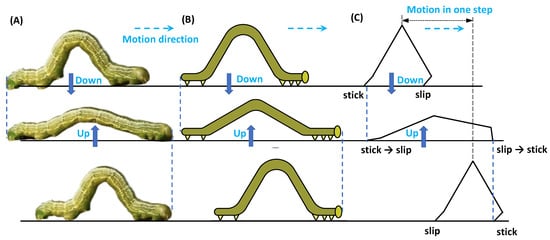
Figure 1.
Bio-inspiration from inchworm crawling: (A) motion of a real inchworm; (B) equivalent visualization; and (C) simplified modeling.
Therefore, we propose a bio-inspired design with the simplest structure consisting of only one cut-and-fold element with a shape that emerged from the previous figure. When choosing this inverse V-shape, achieving locomotion requires that the friction conditions at the two interfaces are different, as explained above. This difference is the case when bending the end sections of the segments in contact with the ground (Figure 2). An anchoring effect is, in fact, exploited to achieve forward or reverse motion (maintaining straight segments only generates an up-and-down motion of the robot without moving it away from that spot). Bending only one extremity is enough to ensure propulsion, choosing either an acute angle or an obtuse one.
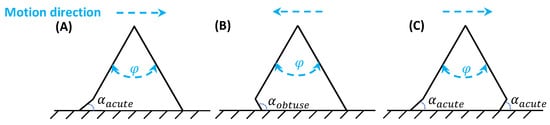
Figure 2.
Motion direction of the robot when bending the extremities with different attack angles ( is the actuated joint’s angle): (A) rear segment with acute angle; (B) front segment with obtuse angle; and (C) both segments with acute angles.
In the first case (A), the robot moves by keeping the straight extremity in the front (the attack angle of the rear extremity creates sufficient friction to preclude reverse motion). Conversely, the robot moves by maintaining the straight extremity in the rear when using an obtuse angle like in case B. Some experiments not reported here for brevity showed that the robot has some slippage if only one end is folded. This issue is almost entirely solved by bending both segments with the same angle type (acute or obtuse) as in case C, which is the approach chosen for our final design.
We included a pneumatically-driven, bubble-like soft actuator at the joint between the two segments to enable crawling; this solution was preferred to an electric motor for weight and size reasons. Thus, our robots achieve straight propulsion in one direction by inflating/deflating the actuator using an electro-pneumatic power supply. The robots can also turn when doubling this inverse V-shape structure and rigidly connecting the two halves with adhesive tape (case B in Figure 3); two soft actuators are, however, needed because their asymmetric control dictates the steering action. We define this design as the dual-actuator version, as opposed to the single-actuator version introduced before.

Figure 3.
Versions of the proposed robots: (A) single-actuator limited to straight motion; and (B) dual-actuator capable of cornering.
2.2. Robot Prototyping
Implementing our robots requires prototyping several parts, such as the body, the soft actuator, and the power supply. Even if our devices are scalable, we initially focus on coin-sized robots because they perform similarly to inchworms.
The robot body is made of a PVC sheet with a 0.1 mm thickness (Figure 4). This material must be rigid enough to return to the unactuated position when the pressurized air is removed from the actuator (the edge where the body is folded acts as an equivalent spring). A template of the desired body shape was created with a laser cutter for repeatability so that the robot body could be drawn on a PVC sheet and then manually cut and folded. The ends of both segments in contact with the ground are bent in the same direction (acute angles) to achieve the desired friction characteristics discussed in the Appendix A. These terminal parts present a serrated profile instead of a straight edge. The reduced contact area favors the anchoring effect of the extremities on the ground (we used a foam pad). It also eliminates vibrations during crawling that cause undesired small jumps resulting in loss of traction, as experimentally observed in prototypes with flat edges. A similar tendency to slip was also noticed when encasing the straight edge with soft material such as latex, therefore supporting the selection of a serrated edge.

Figure 4.
The prototyping process: (A) materials required for the prototype (from the left: glue, flexible tube, latex sheet, PVC board, and paper ring); (B) gluing stage to secure one side of the latex sheet on the PVC board; (C) final shape of the robot with detailed view of an extremity in the red box.
The soft actuator is made of a thin layer of latex that can withstand significant extension. Only the flat annulus area delimited by a paper ring (external diameter of 24 mm) is glued on one side of the robot body. By contrast, only a small portion toward the center of the actuator is glued to the other side of the robot body to secure the actuator. A pneumatic tube with a 0.6 mm external diameter is inserted under the latex layer to drive the bubble-like actuator. Such a small tube with negligible mass was chosen so that the robot motion is not affected and the position of the center of mass is not moved away from the center. The key components, materials, and dimensions of the robot are listed in Table 1.

Table 1.
Main characteristics of the coin-size robot prototypes.
The tailormade robot’s power supply is electro-pneumatic and provides direct actuation of the robot without using any control valves (Figure 5). A step-motor (20k-2M-50.8) with its dedicated driving board (DM422) is supplied by a 24 V electric power supply and drives back and forth a ball-screw mechanism attached to a 10 mL metal syringe that is encapsulated into a 3D-printed mount (the syringe’s piston has a 16 mm diameter and a 50 mm stroke). The syringe port is connected to the soft actuator via a pneumatic tube, controlling the robot’s motion. The dual-actuator version of the robot requires two electro-pneumatic power supplies so that each soft actuator can be driven independently.

Figure 5.
Overview of the set-up required to drive the single-actuator version of the robot.
2.3. Robot Control
Motion control of the robot is achieved by inflating/deflating the bubble-like actuator. The rotation of the step motor generates the pumping effect of the syringe depending on the operation commanded by the microcontroller (a battery-powered Arduino Uno board). The crawling velocity of the robot is defined by the amount of air being transferred between the actuator and the power supply according to an open-loop control algorithm that commands cyclic motions of the syringe. Signal pulses are given to the step motor, where we change their width (PWM technique) to meet the desired robot performance. Due to the extremely low pressure needed to fully inflate the soft actuator (less than 5 kPa) and the slow dynamics of the robots, it is appropriate to assume that the air behaves as an incompressible fluid. This scenario gives a simple relationship connecting the motion of the step motor to that of the robots, as detailed in the next section. Moreover, there are functional limits on the minimum and maximum angle φ of the robot joint. Proper balancing is achieved when φ ≥ 30°, which is a value that ensures the robot’s standing position. Admissible deformations of the soft actuator take place if φ ≤ 70°; this condition avoids contact between the fully inflated actuator and the ground that would lift the robot extremities, therefore losing its control. At any rate, we can adjust the robot velocity as desired by changing the actuation frequency and the stroke of the pneumatic power supply. These degrees of freedom give sufficient flexibility to our robots to deal with multiple operating scenarios.
3. Mathematical Modeling
Modeling the motion of our robots leverages a quasi-static approach in consideration of the bio-inspired inchworm’s slow dynamics. We differentiate between straight motion for the single-actuator version and curved motion for the dual-actuator alternative.
3.1. Modeling Straight Motion
The inverse V-shape structure proposed in Section 2.1 is the reference for our multistate model with stick–slip contact conversions, where one extremity sticks while the other slips. Although the serrated edge extremities of the robot have a certain amount of bending with respect to the main segments going to the robot joint, this micro-motion has minimal effect on the whole geometry, as experimentally observed. Thus, the two-bar simplification shown in Figure 6 holds, where L = 40 mm is the length of each segment and m/2 = 0.7 g represents the mass located at about half length (we also include the actuator mass in this term since it is extremely low, as elucidated in Table 1). The robot actuation is controlled by the time-varying torque applied to the joint, whose angle is:
where the amplitude A and frequency ω depend on the input given to the electro-pneumatic power supply, and the average phase delay γ is related to the dynamics of the fluid-driven subsystem. The horizontal distance separating the two contact points with the ground results as follows:
where is the total variation of the joint angle during strides. This distance predicts the position of the robot extremities ( and ) and of the center-of-mass () measured from a reference point for a given input command.
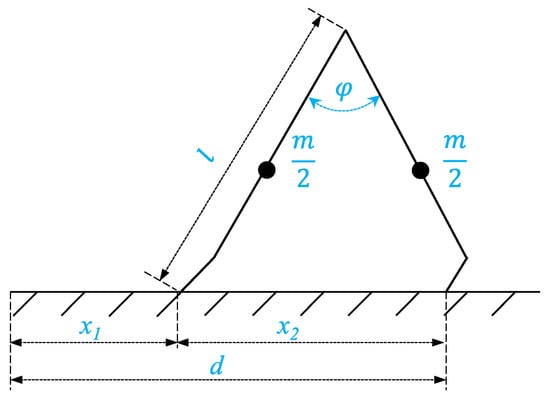
Figure 6.
Schematics for modeling the straight motion of the single-actuator robot.
Figure 7 reports the position of the robot’s contact points and the center-of-mass predicted by the model when inputting a representative (sinusoidal) joint angle variation.
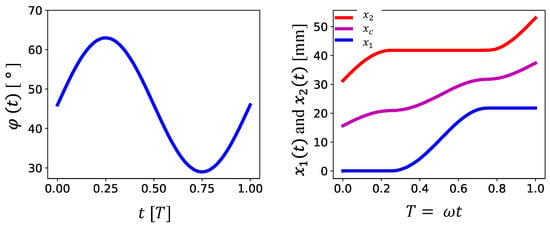
Figure 7.
Joint angle (left-hand side) and resulting positions of the robot’s contact points and center-of-mass when using , , , and .
After elucidating the relationship between the joint angle and the corresponding robot crawling, we focus on understanding the syringe position required to perform a given motion; due to the essentially incompressible fluid, knowing the syringe position corresponds to identifying the input command for the power supply. The empirical relationship results are as:
where , , and . This equation comes from specific measurements reported in Figure 8, where the soft actuator was gradually inflated by manually operating the syringe. This test spans the entire range of the joint angle for completeness, going even beyond the operating limits mentioned above.
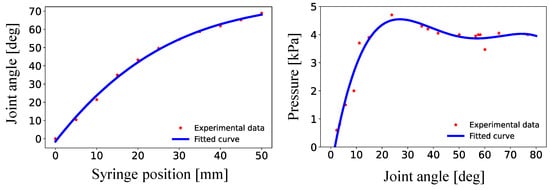
Figure 8.
Experimental relationship between the syringe position and the joint angle of the robot (left-hand side) and between the joint angle and the actuator pressure (right-hand side).
Moreover, Figure 8 shows the relationship between the joint angle and the corresponding pressure in the actuator that always remains below 5 kPa (a pressure sensor XGZP6847A was used for this test). Such a trend is characterized by three stages: (1) a pressure increase before the bubble formation of the soft actuator at about ; (2) bubble formation accompanied by a drop in pressure at about ; and (3) actuator deformation under constant pressure at about . This type of expansion behavior is aligned with observations for an accumulator manufactured from polyurethane that presents similar mechanical characteristics [35].
3.2. Modeling Curved Motion
Our emphasis is now on modeling the robot trajectories when cornering, so the dual-actuator version is shown in Figure 9 with indications of crucial parameters. The key points of this robot are the outermost, middle, and innermost. If the two actuators are inflated/deflated differently, the robot will turn accordingly due to the rigid connections of the two halves.
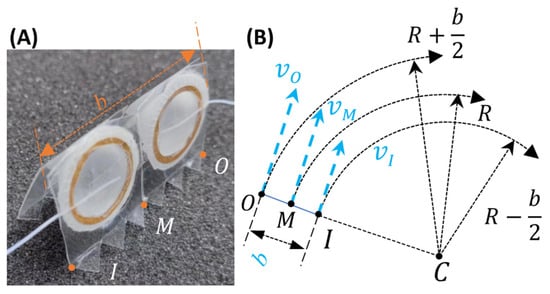
Figure 9.
Modeling curved motion of the robot (dual-actuator version): (A) indication of critical parameters; and (B) top-view schematic of the robot trajectory.
Assuming that the robot is rotating around the center point with angular velocity , the linear velocities of the endpoints depend on the radius of curvature and the robot width ():
Manipulation of the previous equations yields:
So that the radius can be expressed by recalling the velocity ratio :
Using the width of our prototype, Figure 10 shows the theoretical radius of the curvature. Practical reasons indicate that the robot can handle turns with a radius down to about 85 mm.
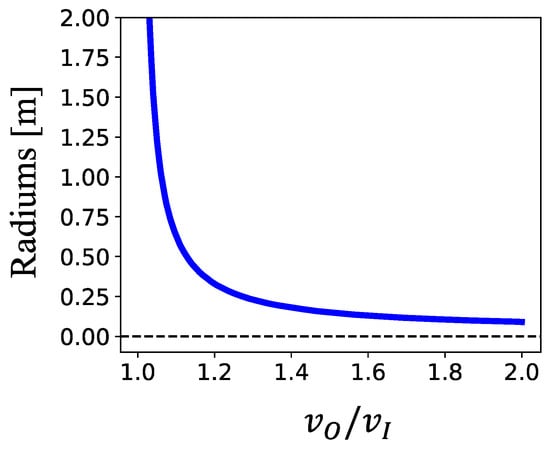
Figure 10.
Predicted curvature radius as a function of the velocities of the robot extremities.
4. Experimental Verifications
Once we had developed the robot design, prototyping, and modeling, we conducted different experimental validations to prove the functions.
4.1. Testing Straight Motion
The single-actuator version performs straight motion, so the results reported in Figure 11 recall this scenario. Two key aspects emerged from this experiment. First, the robot maintained a straight trajectory characterized by reasonably constant velocity even without feedback control (the open-loop command, namely the syringe velocity, is shown). The robot position has been extrapolated from video frames and plotted (a few examples are reported in the upper portion). The resulting linear fitting has an angular coefficient equal to 3.94 mm/s, which is the average robot velocity for the entire test duration. The robot crawled on a foam pad characterized by a slightly uneven surface, so the consistency of the motion and the straight trajectory are relevant achievements. Second, there is a good overlap between the measurements and the model prediction proposed in Section 3.1. The position of the robot extremities is illustrated for one pumping cycle of the power supply that lasts 5.2 s (this scenario refers to inflating and deflating the soft actuator once). The robot’s corresponding stride is about 20 mm.
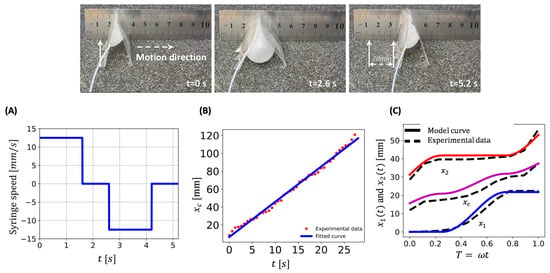
Figure 11.
Testing straight motion: robot configuration in different instants (upper portion); input command (A); measured robot position (B); and model validation (C).
It is worth noticing that the internal diameter of the tube might limit the robot response due to the restriction in the air path when high crawling velocities are sought. This issue is prone to happen during the actuator deflation because its low pressure below 5 kPa drives the flow discharge. The depression inside the syringe is limited so that the pressure drop across the tube stays very low, restraining the achievable mass flow rate. Installing a tube bigger in diameter solves this flow-related issue but affects the stability of the robot during operations (e.g., we tested a tube with a 4 mm inner diameter).
Moreover, the analysis of the straight motion also includes calculating the cost of transport (), namely the energy efficiency for moving the robot. Its definition involves the amount of energy required to overcome friction and the work associated with the vertical shift of the center-of-mass as follows:
We used the parameters listed in Table 2 for this calculation, where the friction forces refer to the different positions illustrated in Figure 12.

Table 2.
Parameters used for calculating the cost of transport.
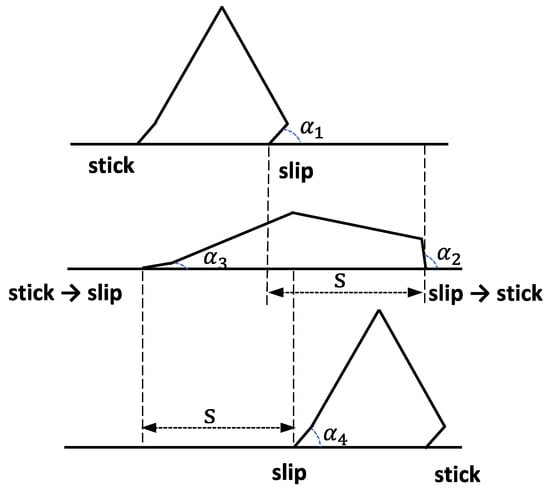
Figure 12.
Illustrative diagram of one robot stride (the attack angles represent the initial and final conditions of each movement of the robot segments).
In this regard, we assumed average friction values for each movement of the two robot extremities due to the almost linear trends of these forces as reported in the Appendix A. The resulting indicates that the robot exhibits suboptimal energy efficiency, even if it is deemed satisfactory due to the small size of the device.
4.2. Testing Curved Motion
Considering the dual-actuator robot, we tested its ability to turn following a U-shaped path. As mentioned, curved motion requires different velocities of the two robot halves. We operated the inner and outer sections with a 1:2 frequency ratio, which refers to the commands given to the electro-pneumatic power supplies reported in Figure 13. The command in the upper plot was also used for both actuators during the straight sections of the path going into and coming out of the U-shape. The robot position was tracked with a motion-capture device (Vicon 3D motion-capture system) that required detection marks on the robot. The resulting motion is also plotted in Figure 13.
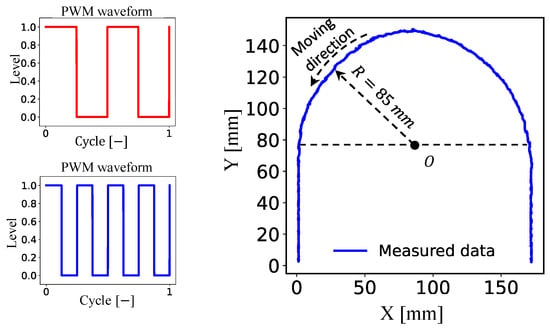
Figure 13.
Testing of the dual-actuator robot along a U-shaped path: PWM input commands given to the electro-pneumatic power supplies and resulting robot motion.
The recorded trajectory indicates that the robot behaved predictably. The robot performed cornering with a turning radius of about 85 mm, which is relatively close to the 90 mm predicted by the theoretical model elucidated in Section 3.2. Despite the resulting 5.5% average error due to unmodeled uncertainties (i.e., the locomotion mechanism has limited robustness and sensitivity to external conditions), the dual-actuator robot can successfully move along a straight line when desired and maintain a constant radius while steering. It should be noted that both versions of the robot cannot operate in unfavorable conditions, such as on surfaces characterized by extremely low friction coefficients and on uneven terrains with obstacles. In any case, our robots can mimic inchworm crawling with minimum complexity and sensorless operations in open-loop control.
5. Conclusions
In this research paper, we have presented novel, bio-inspired crawling robots that mimic the locomotion of inchworms to help underline the mechanisms of crawling. The main contributions of our study are summarized as follows:
- (1)
- We have designed and prototyped two coin-sized robot versions with the simplest structures (cut-and-fold bodies) and actuators (fluid-driven soft actuators), namely single- and dual-actuator robots that perform straight motion alone or both straight and curved motion.
- (2)
- We have studied the friction characteristics of the robot extremities in touch with the ground that deal with stick–slip contact conversions. We have understood how to design these contact points to achieve proper attack angles and anchoring capability that ensure crawling.
- (3)
- We have developed mathematical models for describing the robot motion in open-loop control. These straightforward techniques illustrate the crawling mechanism by giving predictions comparable to experiments.
- (4)
- We have conducted experiments showing that the robots can move up to 4.5 mm/s with straight motion (i.e., 0.1 body lengths per second) and perform cornering and U-turns while maintaining a constant curvature radius.
In summary, such robots can crawl with desired velocities along predetermined paths on flat surfaces despite their minimal complexity in both design and control. This minimal and easily replicable approach represents an important contribution toward the successful development of miniature crawling robots. The low-cost characteristics and straightforward structure also make these robots excellent candidates for research and education purposes. They can be deployed to expand this investigation to other areas since future efforts should focus on making crawling robots suitable for multiple environments. Developments should enhance robustness to perform highly repeatable operations and flexibility to navigate uneven surfaces (e.g., multi-legged design). Exploring new materials for the contact points with the ground could enable climbing capabilities on vertical surfaces to complete advanced maneuvers.
Author Contributions
Conceptualization, M.L. and D.P.; methodology, J.W., M.L. and D.P.; investigation, J.W.; data curation, J.W.; original draft preparation, D.P.; review and editing, J.W., M.L. and D.P.; internal funding acquisition, D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding authors.
Acknowledgments
The authors would like to acknowledge the support of the Guangdong Technion–Israel Institution of Technology’s Key Disciplinary Fund.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This section describes the tests used to characterize the friction at the interfaces with the ground for diverse crawling conditions. We designed a frame for holding in place two robot segments with the desired attack angle, which is manually adjustable (Figure A1).
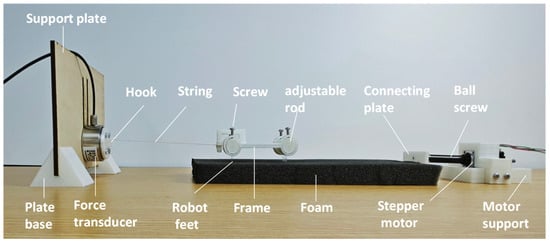
Figure A1.
Experimental set-up for measuring the friction force at the robot extremities.
The foam pad underneath the frame is pulled by a ball-screw drive (the same used for the power supply), while the frame holding the robot segments is attached to a rigid support plate by a string connected to a force sensor (ZNLBM-IIX-1kg). Moving the foam pad allows us to measure the robot friction force. Thus, we varied the sliding velocity and the attack angle to address multiple combinations reported in Figure A2.
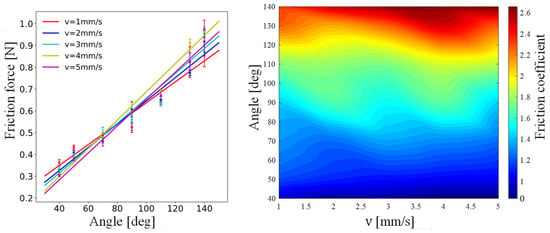
Figure A2.
Measured friction forces at the robot interface with the ground for multiple attack angles and sliding velocities (left-hand side) and resulting friction coefficients.
We observed that the friction force is almost linearly proportional to the attack angle of the robot segment (the left-hand side plot shows linear fitting curves of the experimental points collected during several repetitions of the same test). Specifically, friction is lower when the attack angle is small. By changing the velocity of the sliding motion from 1 up to 5 mm/s, the almost linear trends between friction and attack angle are confirmed. However, there is no clear pattern connecting sliding velocity and friction for a given angle. Thus, we can conclude that friction is predominantly a function of the attack angle. The right-hand side plot presents the same data differently (the friction coefficient is now reported), confirming the reduced impact of the sliding velocity on friction for a given attack angle.
These experimental observations support the understanding of the crawling mechanism for such robots. As the soft actuator undergoes expansion so that the joint angle increases (left-hand side of Figure A3), the angle of attack at the robot’s rear end is larger than at the front end. Thus, the rear friction force is higher than , causing stick at the rear extremity and slip at the front one (i.e., the robot moves forward by “flattening” toward the ground). This friction condition is valid for the entire range of motion when increases (we have estimated the variation of the attach angles assuming a constant angle between the main robot segment and the bent extremity with serrated edge, reasonable results according to our observations). As the soft actuator deflates, reducing, therefore, the joint angle (right-hand side of Figure A3), the friction conditions at the interfaces change. The attack angle at the rear end is smaller than at the front end (it is worth noting that the angles of interest are now different due to the modified motion direction of the robot extremities). Thus, the rear friction force is smaller than , resulting in stick at the front extremity and slip at the rear one (i.e., the robot “gets up” from the ground).
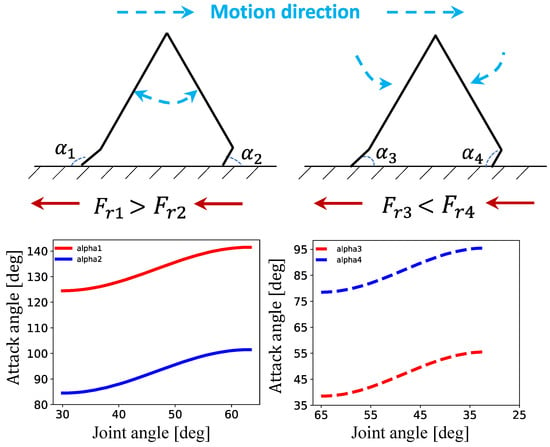
Figure A3.
Simplified diagrams showing the attack angles and the friction forces during crawling with the red arrows pointing out their direction (upper portion); variation of the attack angles during motion (lower plots).
References
- Ren, L.; Li, B.; Wei, G.; Wang, K.; Song, Z.; Wei, Y.; Ren, L.; Liu, Q. Biology and bioinspiration of soft robotics: Actuation, sensing, and system integration. Iscience 2021, 24, 103075. [Google Scholar] [CrossRef] [PubMed]
- Michael, T.T.; Shepherd, R.C.; Galloway, K.J.; Wood, R.; Whitesides, M.G. A resilient, untethered soft robot. Soft Robot. 2014, 1, 213–223. [Google Scholar]
- Duggan, T.; Horowitz, L.; Ulug, A.; Baker, E.; Petersen, K. Inchworm-inspired locomotion in untethered soft robots. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; pp. 200–205. [Google Scholar]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed]
- Mao, S.; Dong, E.; Zhang, S.; Xu, M.; Yang, J. A new soft bionic starfish robot with multi-gaits. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 1312–1317. [Google Scholar]
- Yuk, H.; Lin, S.; Ma, C.; Takaffoli, M.; Fang, N.X.; Zhao, X. Hydraulic hydrogel actuators and robots optically and sonically camouflaged in water. Nat. Commun. 2017, 8, 14230. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, T.; Wang, J.; Li, B.; Hong, J.; Zhang, J.X.; Wang, M.Y. Dynamic modeling and simulation of inchworm movement towards bio-inspired soft robot design. Bioinspiration Biomim. 2019, 14, 066012. [Google Scholar] [CrossRef]
- Mu, W.; Li, M.; Chen, E.; Yang, Y.; Yin, J.; Tao, X.; Liu, G.; Yin, R. Spiral-Shape Fast-Moving Soft Robots. Adv. Funct. Mater. 2023, 2023, 2300516. [Google Scholar] [CrossRef]
- Park, T.; Cha, Y. Soft mobile robot inspired by animal-like running motion. Sci. Rep. 2019, 9, 14700. [Google Scholar] [CrossRef]
- Niu, H.; Feng, R.; Xie, Y.; Jiang, B.; Sheng, Y.; Yu, Y.; Baoyin, H.; Zeng, X. Magworm: A biomimetic magnet embedded worm-like soft robot. Soft Robot. 2021, 8, 507–518. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Chung, H.J.; Parsons, A.M.; Zheng, L. Magnetically controlled soft robotics utilizing elastomers and gels in actuation: A review. Adv. Intell. Syst. 2021, 3, 2000186. [Google Scholar] [CrossRef]
- Bartlett, N.W.; Tolley, M.T.; Overvelde, J.T.; Weaver, J.C.; Mosadegh, B.; Bertoldi, K.; Whitesides, G.M.; Wood, R.J. A 3D-printed, functionally graded soft robot powered by combustion. Science 2015, 349, 161–165. [Google Scholar] [CrossRef] [PubMed]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, K.; Li, X.; Cui, H.; Liu, G.; Xu, H.; Wu, X.; Yao, W.; Zhong, B.; Huang, X.; et al. Electro-thermally driven flexible robot arms based on stacking-controlled graphite nanocomposites. Carbon 2019, 152, 873–881. [Google Scholar] [CrossRef]
- Wu, S.; Baker, G.L.; Yin, J.; Zhu, Y. Fast thermal actuators for soft robotics. Soft Robot. 2022, 9, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
- Calisti, M.; Picardi, G.; Laschi, C. Fundamentals of soft robot locomotion. J. R. Soc. Interface 2017, 14, 20170101. [Google Scholar] [CrossRef]
- Lvan Griethuijsen, I.; Trimmer, B.A. Caterpillar crawling over irregular terrain: Anticipation and local sensing. J. Comp. Physiol. A 2010, 196, 397–406. [Google Scholar] [CrossRef]
- Paoletti, P.; Mahadevan, L. A proprioceptive neuromechanical theory of crawling. Proc. R. Soc. B Biol. Sci. 2014, 281, 20141092. [Google Scholar] [CrossRef]
- Crooks, W.; Rozen-Levy, S.; Trimmer, B.; Rogers, C.; Messner, W. Passive gripper inspired by Manduca sexta and the Fin Ray® Effect. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417721155. [Google Scholar] [CrossRef]
- Koh, J.-S.; Cho, K.-J. Omegabot: Biomimetic inchworm robot using SMA coil actuator and smart composite microstructures (SCM). In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 18–22 December 2009; pp. 1154–1159. [Google Scholar]
- Umedachi, T.; Vikas, V.; Trimmer, B.A. Highly deformable 3-D printed soft robot generating inching and crawling locomotions with variable friction legs. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4590–4595. [Google Scholar]
- Felton, S.M.; Tolley, M.T.; Onal, C.D.; Rus, D.; Wood, R.J. Robot self-assembly by folding: A printed inchworm robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 277–282. [Google Scholar]
- Noorani, M.R.S.; Ghanbari, A.; Aghli, S. Design and fabrication of a worm robot prototype. In Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 073–078. [Google Scholar]
- Guo, H.; Zhang, J.; Wang, T.; Li, Y.; Hong, J.; Li, Y. Design and control of an inchworm-inspired soft robot with omega-arching locomotion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4154–4159. [Google Scholar]
- Ning, J.; Ti, C.; Liu, Y. Inchworm inspired pneumatic soft robot based on friction hysteresis. J. Robot. Autom. 2017, 1, 54–63. [Google Scholar]
- Wang, J.; Min, J.; Fei, Y.; Pang, W. Study on nonlinear crawling locomotion of modular differential drive soft robot. Nonlinear Dyn. 2019, 97, 1107–1123. [Google Scholar] [CrossRef]
- Gamus, B.; Salem, L.; Gat, A.D.; Or, Y. Understanding inchworm crawling for soft-robotics. IEEE Robot. Autom. Lett. 2020, 5, 1397–1404. [Google Scholar] [CrossRef]
- Gamus, B.; Gat, A.D.; Or, Y. Dynamic inchworm crawling: Performance analysis and optimization of a three-link robot. IEEE Robot. Autom. Lett. 2020, 6, 111–118. [Google Scholar] [CrossRef]
- Wu, Q.; Jimenez, T.G.D.; Qu, J.; Zhao, C.; Liu, X. Regulating surface traction of a soft robot through electrostatic adhesion control. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 488–493. [Google Scholar]
- Vikas, V.; Cohen, E.; Grassi, R.; Sözer, C.; Trimmer, B. Design and locomotion control of a soft robot using friction manipulation and motor–tendon actuation. IEEE Trans. Robot. 2016, 32, 949–959. [Google Scholar] [CrossRef]
- Rus, D.; Sung, C. Spotlight on origami robots. Sci. Robot. 2018, 3, eaat0938. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q.; Zhou, J.; Song, A. Crab-inspired compliant leg design method for adaptive locomotion of a multi-legged robot. Bioinspiration Biomim. 2022, 17, 025001. [Google Scholar] [CrossRef]
- Du, L.; Ma, S.; Tokuda, K.; Tian, Y.; Li, L. Bidirectional locomotion of soft inchworm crawler using dynamic gaits. Front. Robot. AI 2022, 9, 899850. [Google Scholar] [CrossRef]
- Pedchenko, A.; Barth, E.J. Design and validation of a high energy density elastic accumulator using polyurethane. In Proceedings of the 2009 Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009; Volume 48920, pp. 283–290. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).