Fixed-Time Stabilization of a Class of Stochastic Nonlinear Systems

Abstract

This paper investigates an improved fixed-time stability theory together with a state feedback controller for a class of nonlinear stochastic systems. First, a delicate transformation is performed, and next, a Gamma function is utilized to directly derive the value of the integral function, which ultimately yields a fixed-time stabilization theorem with a higher precision upper bound for the settling time. Unlike the existing estimation process of amplifying twice, we only performed one amplification, which weakens the effect of amplification. Then, a state feedback controller is constructed for stochastic systems by the method of adding a power integrator. Utilizing the proposed stochastic fixed-time stability theory, simulations show that the intended controller ensures that the trivial solution of the suggested system is fixed-time stable in probability. The results of the simulation demonstrate that the suggested control scheme is meaningful.

1. Introduction

The stabilization of stochastic nonlinear systems has always been a concern of control theorists. For example, in one study, the asymptotic stability of stochastic nonlinear systems was studied via the application of the backstepping technique [1]; in another study [2], the output feedback stability matter of stochastic nonlinear systems was examined, and so on. However, using this approach, in asymptotic stability, the equilibrium point converges to zero as time approaches infinity. An infinite convergence time may not be conducive to practical applications. To tackle this issue, the stochastic finite-time stability theorem was proposed [3,4]. Subsequently, many finite-time stability control schemes have been devised for a variety of stochastic systems [5,6,7,8,9,10,11]. For instance, two studies [7,10] discussed finite-time stabilization for strict-feedback nonlinear stochastic systems, while a third [11] considered switching stochastic nonlinear systems. Following this, one group of researchers [12] addressed the finite-time stability matter of p-norm stochastic constrained systems. While another [13] investigated finite-time stabilization for nonlinear stochastic systems with asymmetric output constraints.

It needs to be emphasized that the upper bound estimation of settling time functions attained in the aforementioned studies are sensitive to the initial states of the system. In other words, the convergence time is also uncertain if the initial value is not available, and it may increase unboundedly with an increasing initial value. Additionally, significant improvement in the convergence time requires placing the initial state at a suitable location within the state space in advance, which is not viable. To alleviate this problem, a theorem of fixed-time stability was proposed [14,15]. Furthermore, a finite settling time estimation was gained from the obtained theorem, guaranteeing that the estimation is independent of the initial conditions. Currently, the research on fixed-time control has made many achievements. For instance, a fixed-time HOSM (high-order sliding mode) controller under asymmetric output constraints was proposed in one study [16]; in a second study [17], through sliding mode theory and adaptive control technology, two controllers were designed to improve system performance; while a third study [18] examined the adaptive fixed-time tracking control of stochastic pure-feedback nonlinear systems.

Nevertheless, estimating the upper bound of the settling time is not a simple task. To date, some interesting conclusions have been obtained on settling time estimation for deterministic fixed-time stability systems. For example, a non-conservative upper bound for special circumstance was provided in one [19]. While, in a second, by using integral transformation technology, a smaller estimation of settling time was achieved [20]. However, for fixed-time stability of stochastic nonlinear systems, there have been only a few studies on how to enhance the estimation accuracy of settling time. In one [21], a relatively accurate estimation was obtained compared to that in one of the studies in which the theorem was proposed [14], but the achieved upper bound for settling time remained conservative. Hence, the primary goal of this paper is to investigate this issue and yield a higher-precision estimation of the settling time for nonlinear stochastic systems. As a secondary goal, we will also consider the design of the state feedback controller.

The major contributions of this essay can be summed up in two parts:

(1)

A new estimation of the settling time is obtained through an ingenious variable transformation and the application of the Gamma function that is more accurate than existing settling time estimations;

(2)

Applying adding a power integration approach, a continuous state feedback controller is created for a stochastic system. Utilizing the theory of fixed-time stability, it is shown that the suggested controller ensures that the investigated system is fixed-time stable in probability.

The rest of the paper is structured as follows. The relevant theories are given in Section 2, the main theorem of the paper and the design of a state feedback controller are given in Section 3, and a numerical simulation is given in Section 4 to illustrate the effectiveness of the proposed methodology. Section 5 concludes the paper.

2. Problem and Preliminaries

Consider the following stochastic system:

$$dx=f(x)dt+g(x)d\omega ,\forall x(0)=x_0\in R^n.$$

(1)

where $x\in R^n$ is the state vector, $\omega$ is an r dimensional standard Wiener process defined on probability space ($\mathrm{\Omega },𝟊,P$ ) with $\mathrm{\Omega }$ being a simple space, $𝟊$ is the domain of the $\sigma$-field, and P is measurable in probability, $f(x):R^n\to R$, and $g(x):R^n\to R^r$ are Borel measurable continuous functions, and $f(0)=0,g(x)=0$.

Definition 1

([7]). $\forall V(x)\in C^2$ relating to system (1), the differential operator of $V(x)$ is described by

$$\mathcal{L}V=\frac{\partial V}{\partial x}f(x)+\frac{1}{2}tr\left\{g^T(x)\frac{{\partial }^{2}V}{\partial x^2}g(x)\right\}.$$

(2)

where $\frac{1}{2}tr\left\{g^T(x)\frac{{\partial }^{2}V}{\partial x^2}g(x)\right\}$ is called the Hessian term.

Definition 2

([7,11]). The origin of system (1) is framed as finite-time stable in probability, if the solution exists for an arbitrary initial vector, labeled as $x(t;x_0)$, and the subsequent definitions establish

(1) 

Finite-time attractiveness in probability: for each initial data $x_0\in R^n\setminus \left\{0\right\}$, the stochastic settling time $t_{x_0}=inf\{t\ge 0;x(t,x_0)=0\}$ is finite almost everywhere, i.e., $P\{t_{x_0}<+\infty \}=1$;

(2) 

Stability in probability: for each pair of ${\epsilon }_1\in (0,1)$ and $r_1>0$, there exists a ${\delta }_1({\epsilon }_1,r_1)>0$ makes $P\{|x(t,x_0)|,\forall t\ge 0\}\ge 1-{\epsilon }_1$,$|x_0|<{\delta }_1$.

Definition 3

([14]). The origin of system (1) is termed as fixed-time stable, if

(1) 

The equilibrium solution is finite-time stable in probability;

(2) 

$E(t_{x_0})\le T_{max},\forall x_0\in R^n\setminus \left\{0\right\}$, where $T_{max}>0$ and independent of the initial data.

Definition 4

([22]). Let $\alpha >0$, then the Gamma function is defined as follows:

$$\mathrm{\Gamma }(\alpha )={\int }_0^{+\infty }{z}_1^{\alpha -1}{e}^{-z_1}d{z}_1.$$

(3)

Definition 5

([23]). Let $\alpha >0,\varrho >0$, and the Beta function be labeled as $B(\alpha ,\varrho )$, which is defined as follows:

$$B(\alpha ,\varrho )={\int }_0^1{z}_1^{\alpha -1}{(1-z_1)}^{\varrho -1}d{z}_1=\frac{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\varrho )}{\mathrm{\Gamma }(\alpha +\varrho )}.$$

(4)

Lemma 1

([8]). Suppose that there exists a non-negative function $V(x)\in C^2$, which is radially unbounded, that is, ${lim}_{x\to +\infty }V(x)=+\infty$. If $\mathcal{L}V\le 0$, then system (1) has a solution for an arbitrary initial date.

Lemma 2

([21]). For system (1), if $\exists V(x):R^n\to R^{+}$, which is positive definite, $C^2$ and radially unbounded, and a continuous differentiable function ${\gamma }_1(·)>0$, for arbitrary $0<\epsilon <+\infty$, ${\int }_0^{\epsilon }\frac{1}{{\gamma }_1(s)}ds\le M_1$ where $M_1>0$ and ${\gamma }_1^{\prime }(s)\ge 0$ for arbitrary $s>0$, such that

$$\mathcal{L}V(x)\le -{\gamma }_1(V(x))$$

(5)

therefore, system (1) possesses a fixed-time stable origin; in addition, its corresponding settling time meets $E(t_{x_0})\le M_1,\forall x_0\in R\setminus \left\{0\right\}.$

Lemma 3

([24]). For every real number $q_1>0$, and arbitrary variables $z_i\in R,i=1,\dots ,n$, we have

$${(|z_1|+|z_2|+\dots +|z_n|)}^{q_1}\le max\{1,n^{q_1-1}\}({|z_1|}^{q_1}+{|z_2|}^{q_1}+\dots +{|z_n|}^{q_1}).$$

(6)

Lemma 4

([24]). Let $q_2,q_3\in (0,+\infty ),q_2\ge 1,\forall z_1,z_2\in R$, then the following inequalities hold

$$\begin{array}{cc}\hfill & (1)|z_1^{q_2}-z_2^{q_2}|\le q_2(2^{q_2-2}+2)(|z_1-z_2|)(|z_1^{q_2-1}-z_2^{q_2-1}|),\hfill \\ \hfill & (2)|z_1^{\frac{q_3}{q_2}}-z_2^{\frac{q_3}{q_2}}|\le 2^{1-\frac{1}{q_2}}{(|z_1^{q_3}-z_2^{q_3}|)}^{\frac{1}{q_2}},\hfill \\ \hfill & (3){(|z_1|+|z_2|)}^{\frac{1}{q_2}}\le {|z_1|}^{\frac{1}{q_2}}+{|z_2|}^{\frac{1}{q_2}}\le 2^{1-\frac{1}{q_2}}{(|z_1|+|z_2|)}^{\frac{1}{q_2}}.\hfill \end{array}$$

(7)

Lemma 5

([25]). Let $z_1,z_2\in R$, $\forall q_4>0,q_5>0$, and any real valued functions $C(·)>0$ and $Q(·)\ge 0$, then it holds that

$$\begin{array}{cc}\hfill C(·){|z_1|}^{q_4}{|z_2|}^{q_5}\le & \frac{q_{4}Q(·)}{q_4+q_5}{|z_1|}^{q_4+q_5}+\frac{q_5{(C(·))}^{\frac{q_4+q_5}{q_5}}}{q_4+q_5}{(Q(·))}^{-\frac{q_4}{q_5}}{|z_2|}^{q_4+q_5}.\hfill \end{array}$$

(8)

3. Main Results

In this section, we will use the above ingenious variable transformation and Gamma function to acquire a more precise upper-bound estimation of the settling time function, and design a fixed-time stabilizing controller for a stochastic strict-feedback system.

3.1. A Fixed-Time Stability Theorem

Theorem 1.

Suppose system (1) has a positive definite $C^2$ and a radially unbounded Lyapunov function $V(x)$ with $\mu \in R^{+}$, $\rho \in R^{+},0<s<1,r>1$, makes $\mathcal{L}V\le -\mu V{(x)}^s-\rho V{(x)}^r,\forall x\in R^n\setminus \left\{0\right\}$. Therefore, system (1) possesses a fixed-time stable equilibrium solution; moreover, the relevant settling time meets

$$E(t_{x_0})\le T_{max}=\frac{{(\mu /\rho )}^{\frac{1-s}{r-s}}\mathrm{\Gamma }(\frac{1-s}{r-s})\mathrm{\Gamma }(\frac{r-1}{r-s})}{\mu (r-s)},\forall x_0\in R^n\setminus \left\{0\right\}.$$

(9)

Proof. 

Let ${\gamma }_1(V(x))=\mu V{(x)}^s+\rho V{(x)}^r\ge 0$. Then, from the definition of $V(x)$, we can attain ${\gamma }_1^{\prime }(V(x))=s\mu V{(x)}^{s-1}+r\rho V{(x)}^{r-1}\ge 0$. Next, let $Z=\frac{1}{(\mu /\rho )V^{s-r}+1}$, thereby one is able to attain that $V={((\rho /\mu )(1/Z-1))}^{\frac{1}{s-r}},dV=\frac{{(\rho /\mu )}^{\frac{1}{s-r}}{(1/Z-1)}^{\frac{1}{s-r}-1}}{Z^2(r-s)}dZ$. Furthermore, for any $0<\epsilon <+\infty$, one can infer that

$$\begin{array}{cc}\hfill {\int }_0^{\epsilon }\frac{1}{{\gamma }_1(V(x))}dV& ={\int }_0^{\epsilon }\frac{1}{\mu V{(x)}^s+\rho V{(x)}^r}dV\hfill \\ \hfill & \le {\int }_0^{+\infty }\frac{1}{\mu V{(x)}^s+\rho V{(x)}^r}dV\hfill \\ \hfill & ={\int }_0^{+\infty }\frac{{\rho }^{-1}{V}^{-r}}{(\mu /\rho )V^{s-r}+1}dV\hfill \\ \hfill & ={\int }_0^1\frac{Z{((\rho /\mu )(1/Z-1))}^{\frac{-r}{s-r}}{(\rho /\mu )}^{\frac{1}{s-r}}}{Z^2(r-s)\rho }{(1/Z-1)}^{\frac{1}{s-r}-1}dZ\hfill \\ \hfill & ={\int }_0^1\frac{{(\mu /\rho )}^{\frac{1-s}{r-s}}}{\mu (r-s)}\frac{{(1-Z)}^{\frac{s-1}{r-s}}}{Z^{\frac{r-1}{r-s}}}dZ\hfill \\ \hfill & =\frac{{(\mu /\rho )}^{\frac{1-s}{r-s}}}{\mu (r-s)}{\int }_0^1{Z}^{-\frac{r-1}{r-s}}{(1-Z)}^{-\frac{1-s}{r-s}}dZ.\hfill \end{array}$$

(10)

By the definitions of the $Beta$ function and $Gamma$ function, one has

$${\int }_0^1{Z}^{-\frac{r-1}{r-s}}{(1-Z)}^{-\frac{1-s}{r-s}}dZ=\mathrm{\Gamma }(\frac{1-s}{r-s})\mathrm{\Gamma }(\frac{r-1}{r-s})$$

(11)

Clearly, $T_{max}=\frac{{(\mu /\rho )}^{\frac{1-s}{r-s}}\mathrm{\Gamma }(\frac{1-s}{r-s})\mathrm{\Gamma }(\frac{r-1}{r-s})}{\mu (r-s)}$ is a positive constant. Then, in accordance with Lemma 2, it can be inferred that system (1) has a fixed-time stable equilibrium point with a holding inequality (9). □

Remark 1.

Although other authors [14,21] have also studied fixed-time stability, the fixed-time stability theorems in these two studies provided conservative upper bounds, something that requires improvement. Specifically, the settling time satisfies $E(t_{x_0})\le {\tilde{T}}_{max}=\frac{1}{\mu (1-s)}+\frac{1}{\rho (r-1)}$ in the first study [14], while in the second [21], it satisfies $E(t_{x_0})\le {\widehat{T}}_{max}=\frac{{(\mu /\rho )}^{\frac{1-s}{r-s}}}{\mu (1-s)}+\frac{{(\mu /\rho )}^{\frac{1-r}{r-s}}}{\rho (r-1)}$. Comparing the above proof with these two studies, we can see that the upper bound estimations of the settling time functions in the previous studies were obtained by amplifying the integral function and the integration region, while we only amplify the integration region to gain the upper bound. Hence, it is easily known that $T_{max}$ is less than ${\tilde{T}}_{max},{\widehat{T}}_{max}$. Thus, this paper proposes a improved method to obtain a more accurate settling time estimation.

3.2. State-Feedback Controller Design

Consider a class of nonlinear stochastic systems as follows:

$$\left\{\begin{array}{c}d{x}_i=(x_{i+1}+f_i({\overline{x}}_i))dt+g_i({\overline{x}}_i)d\omega \hfill \\ 1\le i\le n-1\hfill \\ d{x}_n=(u+f_n({\overline{x}}_n))dt+g_n({\overline{x}}_n)d\omega \hfill \end{array}\right.$$

(12)

where $u\in R$ is denoted as the input state and $x={(x_1,\dots ,x_n)}^T\in R^n$ is denoted as the state variable; ${\overline{x}}_i={(x_1,x_2,\dots ,x_i)}^T$; the definition of $\omega$ is consistent with system (1); in addition, $f_i({\overline{x}}_i):R^i\to R$ and $g_i({\overline{x}}_i):R^i\to R^r$ are known smooth functions, and satisfy $f_i(0,\cdots ,0)=0,g_i(0,\cdots ,0)=0$, and referred to as system drift and the diffusion term, respectively.

Assumption 1.

For $i=1,\dots ,n$, there exist known non-negative smooth functions ${\zeta }_i({\overline{x}}_i),{\eta }_i({\overline{x}}_i)$ such that

$$\begin{array}{cc}\hfill & |f_i({\overline{x}}_i)|\le {\zeta }_i({\overline{x}}_i)\sum _{j=1}^i{|x_j|}^{\frac{{\tau }_i+\theta }{{\tau }_j}},\hfill \\ \hfill & \parallel g_i({\overline{x}}_i)\parallel \le {\eta }_i({\overline{x}}_i)\sum _{j=1}^i{|x_j|}^{\frac{2{\tau }_i+\theta }{2{\tau }_j}}.\hfill \end{array}$$

(13)

where $\theta \in (-\frac{1}{n},0)$, ${\tau }_1=1,{\tau }_i=1+(i-1)\theta ,i=2,\dots ,n+1$.

Remark 2.

Assumption 1 is borrowed from references [26,27], which considered the finite-time stability of deterministic nonlinear systems. In this paper, we take stochastic factors into account and the growth condition is similarly given for the diffusion term. For convenience, we can choose $\theta =-\frac{d_1}{d_2},$ with $d_1,d_2$ of even and odd numbers, respectively, which implies that ${\tau }_i=1+(i-1)\theta$ is always odd.

Firstly, the following coordinate transformation are given

$${\xi }_1=x_1^{\frac{1}{{\tau }_1}},x_1^{\ast }=0,{\xi }_i=x_i^{\frac{1}{{\tau }_i}}-x_i^{\ast \frac{1}{{\tau }_i}},i=2,3,\dots ,n+1.$$

(14)

where $x_2^{\ast },x_3^{\ast },\dots ,x_{n+1}^{\ast }$ are virtual controllers and will be constructed subsequently.

Step 1. Select the Lyapunov function $V_1={\int }_{x_1^{\ast }}^{x_1}{({\nu }^{\frac{1}{{\tau }_1}}-x_1^{\ast \frac{1}{{\tau }_1}})}^{4-{\tau }_1}d\nu$.

By Definition 1, Lemma 4, and Assumption 1, we can gain the following inequality:

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1& ={\xi }_1^{4-{\tau }_1}(x_2+f_1(x_1))+\frac{4-{\tau }_1}{2{\tau }_1}{\xi }_1^{4-2{\tau }_1}{|g_1(x_1)|}^2\hfill \\ \hfill & \le {\xi }_1^{4-{\tau }_1}(x_2-x_2^{\ast })+{\xi }_1^{4-{\tau }_1}{x}_2^{\ast }\hfill \\ \hfill & +{\zeta }_1(x_1){|{\xi }_1|}^{4+\theta }+\frac{4-{\tau }_1}{2{\tau }_1}{\eta }_1^2(x_1){|{\xi }_1|}^{4+\theta }\hfill \\ \hfill & \le {\xi }_1^{4-{\tau }_1}(x_2-x_2^{\ast })+{\xi }_1^{4-{\tau }_1}{x}_2^{\ast }+N_1(x_1){|{\xi }_1|}^{4+\theta }.\hfill \end{array}$$

(15)

where $N_1(x_1)=N_{11}(x_1)+N_{12}(x_1),N_{11}(x_1)\ge {\zeta }_1(x_1)$, and $N_{12}(x_1)\ge \frac{4-{\tau }_1}{2{\tau }_1}{\eta }_1^2(x_1)$ are smooth functions.

So, we construct the first virtual controller as

$$\begin{array}{c}{x}_2^{\ast }=-{\beta }_1(x_1){\xi }_1^{{\tau }_2},\hfill \\ {\beta }_1(x_1)=c_1+(n-1)+N_1(x_1)+c_2{\left|{\xi }_1\right|}^{\sigma },\hfill \end{array}$$

(16)

where $\sigma >-\theta$, and $c_1>0,c_2>0$ are design parameters.

Hence, substituting (16) into (15), we can obtain

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1& \le -c_1{|{\xi }_1|}^{4+\theta }-(n-1){|{\xi }_1|}^{4+\theta }\hfill \\ \hfill & -c_2{|{\xi }_1|}^{4+\sigma +\theta }-{\xi }_1^{4-{\tau }_1}(x_2-x_2^{\ast }).\hfill \end{array}$$

(17)

Step $i(2\le i\le n-1)$. Assuming that at step $i-1$ there is a Lyapunov function $V_{i-1}={\Sigma }_{j=1}^{i-1}{W}_j$, with $W_j={\int }_{x_j^{\ast }}^{x_j}{({\nu }^{\frac{1}{{\tau }_j}}-x_j^{\ast \frac{1}{{\tau }_j}})}^{4-{\tau }_j}d\nu$, and a string of virtual controllers $x_2^{\ast }(x_1)=-{\beta }_2({\overline{x}}_2){\xi }_2^{{\tau }_3},\dots ,x_i^{\ast }({\overline{x}}_{i-1})=-{\beta }_{i-1}({\overline{x}}_{i-1}){\xi }_{i-1}^{{\tau }_i}$, such that

$$\begin{array}{cc}\hfill \mathcal{L}{V}_{i-1}& \le -\sum _{j=1}^{i-1}{c}_1{|{\xi }_j|}^{4+\theta }-(n-i+1)\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }\hfill \\ \hfill & -\sum _{j=1}^{i-1}{c}_2{|{\xi }_j|}^{4+\sigma +\theta }+{\xi }_{i-1}^{4-{\tau }_{i-1}}(x_i-x_i^{\ast })\hfill \end{array}$$

(18)

where ${\beta }_1(x_1),{\beta }_2({\overline{x}}_2),\dots ,{\beta }_{i-1}({\overline{x}}_{i-1})$ are non-negative continuous functions.

Then, we can construct the ith Lyapunov function

$$V_i=V_{i-1}+W_i,W_i={\int }_{x_i^{\ast }}^{x_i}{({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}})}^{4-{\tau }_i}d\nu .$$

(19)

According to the definition of $W_i,x_i^{\ast }$, we can obtain

$$\begin{array}{cc}\hfill & \frac{\partial W_i}{\partial x_i}={\xi }_i^{4-{\tau }_i};\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \frac{\partial W_i}{\partial x_j}=-(4-{\tau }_i)\frac{\partial x_i^{{\ast }^{\frac{1}{{\tau }_i}}}}{\partial x_j}{\int }_{x_i^{\ast }}^{x_i}({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}{)}^{3-{\tau }_i}d\nu ;\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \frac{{\partial }^2{W}_i}{\partial x_i^2}=\frac{4-{\tau }_i}{{\tau }_i}{x}_i^{\frac{1}{{\tau }_i}-1}{\xi }_i^{3-{\tau }_i};\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & \frac{{\partial }^2{W}_i}{\partial x_j\partial x_i}=-(4-{\tau }_i){\xi }_i^{3-{\tau }_i}\frac{\partial x_i^{{\ast }^{\frac{1}{{\tau }_i}}}}{\partial x_j};\hfill \end{array}$$

(23)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{{\partial }^2{W}_i}{\partial x_j\partial x_l}& =-(4-{\tau }_i)\frac{{\partial }^2(x_i^{{\ast }^{\frac{1}{{\tau }_i}}})}{\partial x_j\partial x_l}{\int }_{x_i^{\ast }}^{x_i}({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}{)}^{3-{\tau }_i}d\nu \hfill \\ & +(4-{\tau }_i)(3-{\tau }_i)\frac{\partial x_i^{{\ast }^{\frac{1}{{\tau }_i}}}}{\partial x_j}\frac{\partial x_i^{{\ast }^{\frac{1}{{\tau }_i}}}}{\partial x_l}{\int }_{x_i^{\ast }}^{x_i}({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}{)}^{2-{\tau }_i}d\nu ;\hfill \end{array}\end{array}$$

(24)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{{\partial }^2{W}_i}{\partial x_j^2}& =-(4-{\tau }_i)\frac{{\partial }^2(x_i^{{\ast }^{\frac{1}{{\tau }_i}}})}{\partial x_j^2}{\int }_{x_i^{\ast }}^{x_i}({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}{)}^{3-{\tau }_i}d\nu \hfill \\ & +(4-{\tau }_i)(3-{\tau }_i){\left(\frac{\partial x_i^{{\ast }^{\frac{1}{{\tau }_i}}}}{\partial x_j}\right)}^2{\int }_{x_i^{\ast }}^{x_i}({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}{)}^{2-{\tau }_i}d\nu .\hfill \end{array}\end{array}$$

(25)

Therefore, from Definition 1 and Equations (18) and (19), one attains

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i& =-\sum _{j=1}^{i-1}{c}_1{|{\xi }_j|}^{4+\theta }-(n-i+1)\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }\hfill \\ \hfill & -\sum _{j=1}^{i-1}{c}_2{|{\xi }_j|}^{4+\sigma +\theta }+\frac{\partial W_i}{\partial x_i}{x}_{i+1}+{\xi }_{i-1}^{4-{\tau }_{i-1}}(x_i-x_i^{\ast })\hfill \\ \hfill & +\frac{\partial W_i}{\partial x_i}{f}_i({\overline{x}}_i)+\sum _{j=1}^i\frac{\partial W_i}{\partial x_j}(x_{j+1}+f_j({\overline{x}}_i))+\frac{1}{2}tr\left\{G_i^T({\overline{x}}_i)\frac{{\partial }^2{W}_i}{\partial {\overline{x}}_i^2}{G}_i({\overline{x}}_i)\right\}\hfill \end{array}$$

(26)

where $G_i^T({\overline{x}}_i)=(g_1^T(x_1),g_2^T({\overline{x}}_2),\cdots ,g_i^T({\overline{x}}_i))$,

$$\begin{array}{cc}\hfill \frac{1}{2}tr\left\{G_i^T({\overline{x}}_i)\frac{{\partial }^2{W}_i}{\partial {\overline{x}}_i^2}{G}_i({\overline{x}}_i)\right\}& =\sum _{j,l=1,j\ne l}^{i-1}\frac{{\partial }^2{W}_i}{\partial x_j\partial x_l}{g}_j^T({\overline{x}}_j)g_l({\overline{x}}_l)+\frac{1}{2}\sum _{j=1}^{i-1}\frac{{\partial }^2{W}_i}{\partial x_j^2}{g}_j^T({\overline{x}}_j)g_j({\overline{x}}_j)\hfill \\ \hfill & +\sum _{j=1}^{i-1}\frac{{\partial }^2{W}_i}{\partial x_j\partial x_i}{g}_j^T({\overline{x}}_j)g_i({\overline{x}}_i)+\frac{1}{2}\frac{{\partial }^2{W}_i}{\partial x_i^2}{g}_i^T({\overline{x}}_i)g_i({\overline{x}}_i).\hfill \end{array}$$

To facilitate the subsequent calculations, we render the following propositions and will provide specific proofs in Appendix A.

Proposition 1.

A positive constant called $N_{i1}$ exists that makes

$$|{\xi }_{i-1}^{4-{\tau }_{i-1}}(x_i-x_i^{\ast })|\le \frac{1}{4}{|{\xi }_{i-1}|}^{4+\theta }+N_{i1}{|{\xi }_i|}^{4+\theta }$$

(27)

Proposition 2.

A positive smooth function called $N_{i2}({\overline{x}}_i)$ exists, which thereby makes

$$\left|\frac{\partial W_i}{\partial x_i}{f}_i({\overline{x}}_i)\right|\le \frac{1}{4}\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }+N_{i2}({\overline{x}}_i){|{\xi }_i|}^{4+\theta }.$$

(28)

Proposition 3.

There exists a positive smooth function $N_{i3}({\overline{x}}_i)$ that makes

$$\left|\sum _{j=1}^{i-1}\frac{\partial W_i}{\partial x_j}(x_{j+1}+f_j({\overline{x}}_j))\right|\le \frac{1}{4}\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }+N_{i3}({\overline{x}}_i){|{\xi }_i|}^{4+\theta }.$$

(29)

Proposition 4.

There exists a positive smooth function $N_{i4}({\overline{x}}_i)$ that makes

$$\left|\frac{1}{2}tr\left\{G_i^T({\overline{x}}_i)\frac{{\partial }^2{W}_i}{\partial {\overline{x}}_i^2}{G}_i({\overline{x}}_i)\right\}\right|\le \frac{1}{4}\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }+N_{i4}({\overline{x}}_i){|{\xi }_i|}^{4+\theta }.$$

(30)

Substituting Propositions 1–4 into (26) results in

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i& \le -(n-i+1)\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }-\sum _{j=1}^{i-1}{c}_1{|{\xi }_j|}^{4+\theta }-\sum _{j=1}^{i-1}{c}_2{|{\xi }_j|}^{4+\sigma +\theta }\hfill \\ \hfill & +\sum _{j=1}^{i-1}{|{\xi }_j|}^{4+\theta }+{\xi }_i^{4-{\tau }_i}(x_{i+1}-x_{i+1}^{\ast })+{\xi }_i^{4-{\tau }_i}{x}_{i+1}^{\ast }\hfill \\ \hfill & +(N_{i1}+N_{i2}({\overline{x}}_i)+N_{i3}({\overline{x}}_i)+N_{i4}({\overline{x}}_i)){|{\xi }_i|}^{4+\theta }.\hfill \end{array}$$

(31)

Therefore, a virtual controller can be designed

$$\begin{array}{cc}\hfill & x_{i+1}^{\ast }=-{\beta }_i({\overline{x}}_i){\xi }_i^{{\tau }_{i+1}},\hfill \\ \hfill & {\beta }_i({\overline{x}}_i)=c_1+(n-i)+N_i({\overline{x}}_i)+c_2{\left|{\xi }_i\right|}^{\sigma },\hfill \end{array}$$

(32)

where $N_i({\overline{x}}_i)=N_{i1}+N_{i2}({\overline{x}}_i)+N_{i3}({\overline{x}}_i)+N_{i4}({\overline{x}}_i)$. Then, substituting (32) into (31), we will acquire

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i& \le -(n-i)\sum _{j=1}^i{|{\xi }_j|}^{4+\theta }-\sum _{j=1}^i{c}_1{|{\xi }_j|}^{4+\theta }\hfill \\ \hfill & -\sum _{j=1}^i{c}_2{|{\xi }_j|}^{4+\sigma +\theta }+{\xi }_i^{4-{\tau }_i}(x_{i+1}-x_{i+1}^{\ast }).\hfill \end{array}$$

(33)

Step n. Based on the previous induction step, a series of virtual controllers can be obtained, so the Lyapunov function $V_n$ can be selected as

$$V_n=V_{n-1}+W_n,W_n={\int }_{x_n^{\ast }}^{x_n}{({\nu }^{\frac{1}{{\tau }_n}}-x_n^{{\ast }^{\frac{1}{{\tau }_n}}})}^{4-{\tau }_n}d\nu .$$

(34)

and the actual controller can be constructed as

$$u=x_{n+1}^{\ast }=-{\beta }_n({\overline{x}}_n){\xi }_n^{{\tau }_{n+1}},$$

(35)

where ${\beta }_n({\overline{x}}_n)=c_1+N_n({\overline{x}}_n)+c_2{\left|{\xi }_n\right|}^{\sigma }$ is non-negative. Then, when $i=n$, substituting (35) into Equation (33) will gives the following

$$\mathcal{L}{V}_n\le -\sum _{j=1}^n{c}_1{|{\xi }_j|}^{4+\theta }-\sum _{j=1}^n{c}_2{|{\xi }_j|}^{4+\sigma +\theta }.$$

(36)

Remark 3.

It should be noted that both this paper and previous authors [7] have considered stochastic strict feedback nonlinear systems, but that earlier study mainly considered the finite-time stability issue, while the fixed-time stability is investigated in this paper. As we know, finite-time settling time estimation depends on the initial conditions, while fixed-time settling time estimation is independent of the initial states. The method of adding a power integrator was applied to design the actual controller in this paper as well as in the earlier paper, but the gain functions of the controllers designed in the two papers are very different. Compared to finite-time controllers, the gain function ${\beta }_n({\overline{x}}_n)$ of the controller designed in this paper has one additional term $c_2{\left|{\xi }_n\right|}^{\sigma }$, which renders a quicker convergence rate.

3.3. Stability Analysis

The next criterion will indicate the stability perorations for system (12).

Theorem 2.

If system (12) matches Assumption 1, hence, under the suggested controller (35), the origin of the system (12) is anticipated to be fixed-time stable; meanwhile, the stochastic settling time meets

$$E(t_{x_0})\le \frac{4{(\mu /\rho )}^{\frac{-\theta }{\sigma }}\mathrm{\Gamma }(\frac{-\theta }{\sigma })\mathrm{\Gamma }(\frac{\theta +\sigma }{\sigma })}{\mu \sigma },\forall x_0\in R^n\setminus \left\{0\right\}$$

(37)

where $\mu =2^{-\frac{4+\theta }{4}}{c}_1,\rho =n^{-\frac{\theta +\sigma }{4}}{2}^{-\frac{4+\sigma +\theta }{4}}{c}_2$.

Proof. 

By Lemma 4, we can prove that

$$\begin{array}{cc}\hfill \left|x_i-x_i^{\ast }\right|& =\left|{(x_i^{\frac{1}{{\tau }_i}})}^{{\tau }_i}-{(x_i^{{\ast }^{\frac{1}{{\tau }_i}}})}^{{\tau }_i}\right|\hfill \\ \hfill & \le 2^{1-{\tau }_i}{\left|x_i^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}}\right|}^{{\tau }_i}\hfill \\ \hfill & =2^{1-{\tau }_i}{\left|{\xi }_i\right|}^{{\tau }_i}.\hfill \end{array}$$

(38)

Furthermore, combining Equation (38), it can be verified that

$$\begin{array}{cc}\hfill W_i& ={\int }_{x_i^{\ast }}^{x_i}{({\nu }^{\frac{1}{{\tau }_i}}-x_i^{{\ast }^{\frac{1}{{\tau }_i}}})}^{4-{\tau }_i}d\nu \hfill \\ \hfill & \le {\xi }_i^{4-{\tau }_i}\left|x_i-x_i^{\ast }\right|\hfill \\ \hfill & \le 2^{1-{\tau }_i}{\xi }_i^{4-{\tau }_i}{|{\xi }_i|}^{{\tau }_i}\hfill \\ \hfill & \le 2^{1-{\tau }_i}{\xi }_i^4\hfill \\ \hfill & \le 2{\xi }_i^4.\hfill \end{array}$$

(39)

In light of the definition of $V_n$, it holds that

$$V_n\le 2({\xi }_1^4+{\xi }_2^4+\dots +{\xi }_n^4).$$

(40)

From (36), (40), and Lemma 3, we can gain

$$\begin{array}{cc}\hfill \mathcal{L}{V}_n& \le -c_1\sum _{j=1}^n{\left|{\xi }_j\right|}^{4+\theta }-c_2\sum _{j=1}^n{\left|{\xi }_j\right|}^{4+\theta +\sigma }\hfill \\ \hfill & =-c_1\sum _{j=1}^n{({\xi }_j^4)}^{\frac{4+\theta }{4}}-c_2\sum _{j=1}^n{({\xi }_j^4)}^{\frac{4+\theta +\sigma }{4}}\hfill \\ \hfill & \le -c_1{(\sum _{j=1}^n{\xi }_j^4)}^{\frac{4+\theta }{4}}-c_2{n}^{-\frac{\theta +\sigma }{4}}{(\sum _{j=1}^n{\xi }_j^4)}^{\frac{4+\theta +\sigma }{4}}\hfill \\ \hfill & \le -c_1{(\frac{V_n}{2})}^{\frac{4+\theta }{4}}-c_2{n}^{-\frac{\theta +\sigma }{4}}{(\frac{V_n}{2})}^{\frac{4+\theta +\sigma }{4}}\hfill \\ \hfill & =-\mu V_n^{\frac{4+\theta }{4}}-\rho V_n^{\frac{4+\theta +\sigma }{4}}.\hfill \end{array}$$

(41)

where $\mu =2^{-\frac{4+\theta }{4}}{c}_1,\rho =n^{-\frac{\theta +\sigma }{4}}{2}^{-\frac{4+\sigma +\theta }{4}}{c}_2$ are positive parameters. Because $\sigma +\theta >0,\theta \in (-\frac{1}{n},0)$, we can obtain $0<\frac{4+\theta }{4}<1,\frac{4+\sigma +\theta }{4}>1$. Thus, using Theorem 1, one is able to conclude that the origin of the stochastic nonlinear system is fixed-time stable in probability. Meanwhile, inequality (37) holds. □

4. Simulation Example

This section provides the outcomes of simulations of the following systems to further verify the conclusion of Theorem 1

$$\left\{\begin{array}{c}d{x}_1=x_{2}dt,\hfill \\ d{x}_2=udt+\frac{1}{3}{x}_2^{2}dt+\frac{1}{5}{x}_1^{\frac{4}{11}}{x}_2^{\frac{4}{9}}d\omega .\hfill \end{array}\right.$$

(42)

We choose $\theta =-\frac{2}{11}\in (-\frac{1}{2},0)$; then, ${\tau }_1=1,{\tau }_2=\frac{9}{11},{\tau }_3=\frac{7}{11}.$ Obviously, Assumption 1 holds with

$$\left|\frac{1}{3}{x}_2^2\right|\le \frac{1}{2}{\left|x_2\right|}^{\frac{11}{9}}(|x_1{|}^{\frac{7}{11}}+|x_2{|}^{\frac{7}{9}})$$

(43)

$$\left|\frac{1}{5}{x}_1^{\frac{4}{11}}{x}_2^{\frac{4}{9}}\right|\le \frac{1}{2}|x_1^{\frac{4}{11}}{x}_2^{\frac{4}{9}}|\le \frac{1}{4}(|x_1{|}^{\frac{8}{11}}+|x_2{|}^{\frac{8}{9}}).$$

(44)

Hence, ${\zeta }_2({\overline{x}}_2)=\frac{1}{2}{\left|x_2\right|}^{\frac{11}{9}},{\eta }_2({\overline{x}}_2)=\frac{1}{4}$. The controller can be created as follows

$$\begin{array}{cc}\hfill & {\xi }_1=x_1^{\frac{1}{{\tau }_1}},{\xi }_2=x_2^{\frac{1}{{\tau }_2}}-x_2^{\ast \frac{1}{{\tau }_2}}\hfill \\ \hfill & x_2^{\ast }=-(c_1+1+N_1(x_1)+c_2|{\xi }_1{|}^{\sigma }){\xi }_1^{{\tau }_2}\hfill \\ \hfill & u=-(c_1+N_2({\overline{x}}_2)+c_2|{\xi }_2{|}^{\sigma }){\xi }_2^{{\tau }_3}.\hfill \end{array}$$

(45)

where $\begin{array}{l}{N}_1(x_1)=0,\\ N_2(x_1,x_2)=\frac{3}{14}{2}^{\frac{28}{33}}{(\frac{3}{10})}^{-\frac{14}{3}}+\frac{1}{2}|x_2{|}^{\frac{11}{9}}+\\ \frac{5}{6}{(\frac{3}{2})}^{-\frac{1}{5}}(\frac{1}{2}|x_2{|}^{\frac{11}{9}}(1+(c_1+1+c_2|{\xi }_1{|}^{\sigma }{)}^{\frac{7}{9}}{))}^{\frac{6}{5}}+\\ \frac{65}{864}{(\frac{21}{32})}^{-\frac{8}{13}}(\frac{35}{288}(1+(c_1+1+c_2|{\xi }_1{|}^{\sigma }{)}^{\frac{16}{9}}{))}^{\frac{21}{13}}\\ +2^{\frac{2}{11}}\frac{35}{11}((c_1+1+c_2|{\xi }_1{|}^{\sigma }{)}^{\frac{11}{9}}+\frac{11\sigma }{9}(1+c_1+c_2|{\xi }_1{|}^{\sigma }{)}^{\frac{2}{9}}|{\xi }_1{|}^{\sigma })+\\ (\frac{11}{14}){(\frac{7}{6})}^{-\frac{3}{11}}(2^{\frac{2}{11}}\frac{35}{11}(1+c_1+c_2{|\xi |}^{\sigma })(\frac{11\sigma }{9}(1+c_1+c_2|{\xi }_1{|}^{\sigma }{)}^{\frac{2}{9}}|{\xi }_1{|}^{\sigma }))\end{array}$.

We can choose $c_1=\frac{1}{4},c_2=\frac{1}{2},\sigma =2.$ According to Theorem 1, it can be calculated that $T_{max}$ = 172.8405, which is less than the ${\tilde{T}}_{max}=186.3245$ of a previous paper [21].

Next, we select various initial data $x_0={(-2,-1)}^T$ and $x_0={(4,10)}^T$. Figure 1, Figure 2, Figure 3 and Figure 4 show the numerical results of two different initial vectors. Figure 1 and Figure 3 show the trajectories of $x_1(t)$ and $x_2(t)$ under different initial conditions and which reach a stable state within the same time. In addition, the trajectory of controller u is shown in Figure 2 and Figure 4 and which reaches a stable state within the same time. When $x_0={(-2,-1)}^T$, it can be seen from Figure 1 and Figure 2 that the convergence time of the system states and controller is almost 3.5 s, satisfying $E(t_{x_0})\le 172.8405$. When $x_0={(4,10)}^T$, from Figure 3 and Figure 4, we can see that the convergence time of the system states and controller is almost 3.5 s. These results indicate that the origin of system (42) with different initial values is always fixed-time stable in probability and different the initial states do not affect the convergence time of the system.

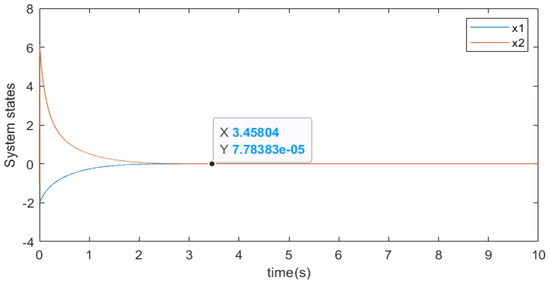
Figure 1. System state response with $x={(-2,-1)}^T$.

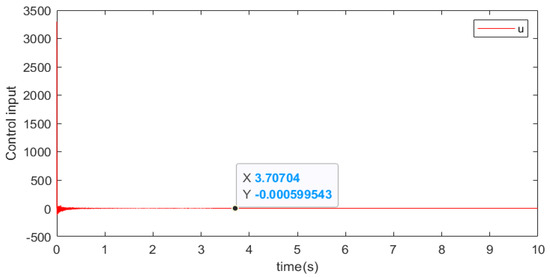
Figure 2. Input control response with $x={(-2,-1)}^T$.

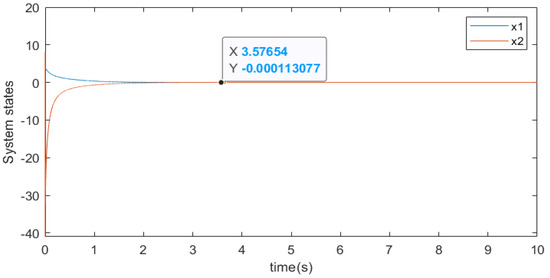
Figure 3. System state response with $x={(4,10)}^T$.

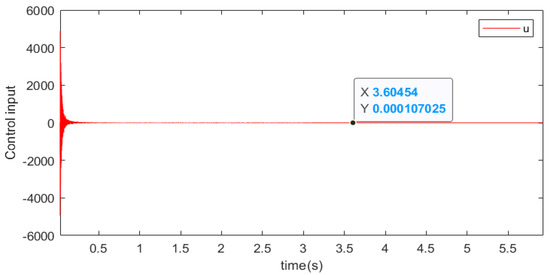
Figure 4. Input control response with $x={(4,10)}^T$.

5. Conclusions

In this paper, a fixed-time theorem with a more accurate estimate of the settling time has been proposed and demonstrated to work. By the proposed ingenious transformation and using a Gamma function to directly calculate the value of the integral function, a more accurate settling time estimation of stochastic nonlinear systems has been obtained than in existing approaches. In addition, a fixed-time stabilizing controller for the investigated system was designed via the method of adding a power integrator, which allowed us to demonstrate that the investigated system is fixed-time stable. In future work, we will consider the fixed-time stabilization of stochastic nonlinear systems with unmeasurable states.