Design Method of the Stroke Ring Based on Deformation Pre-Compensation
Abstract
1. Introduction
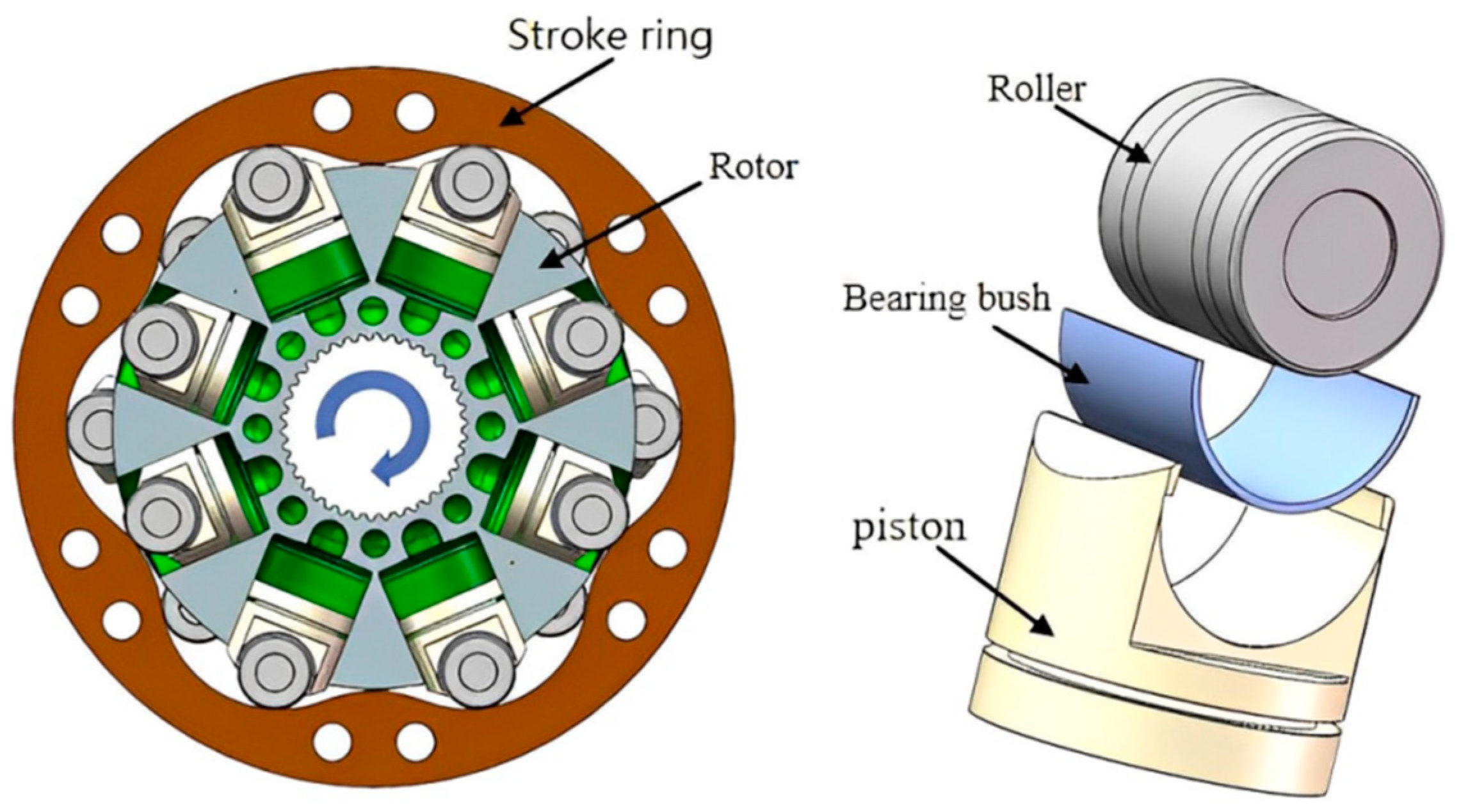
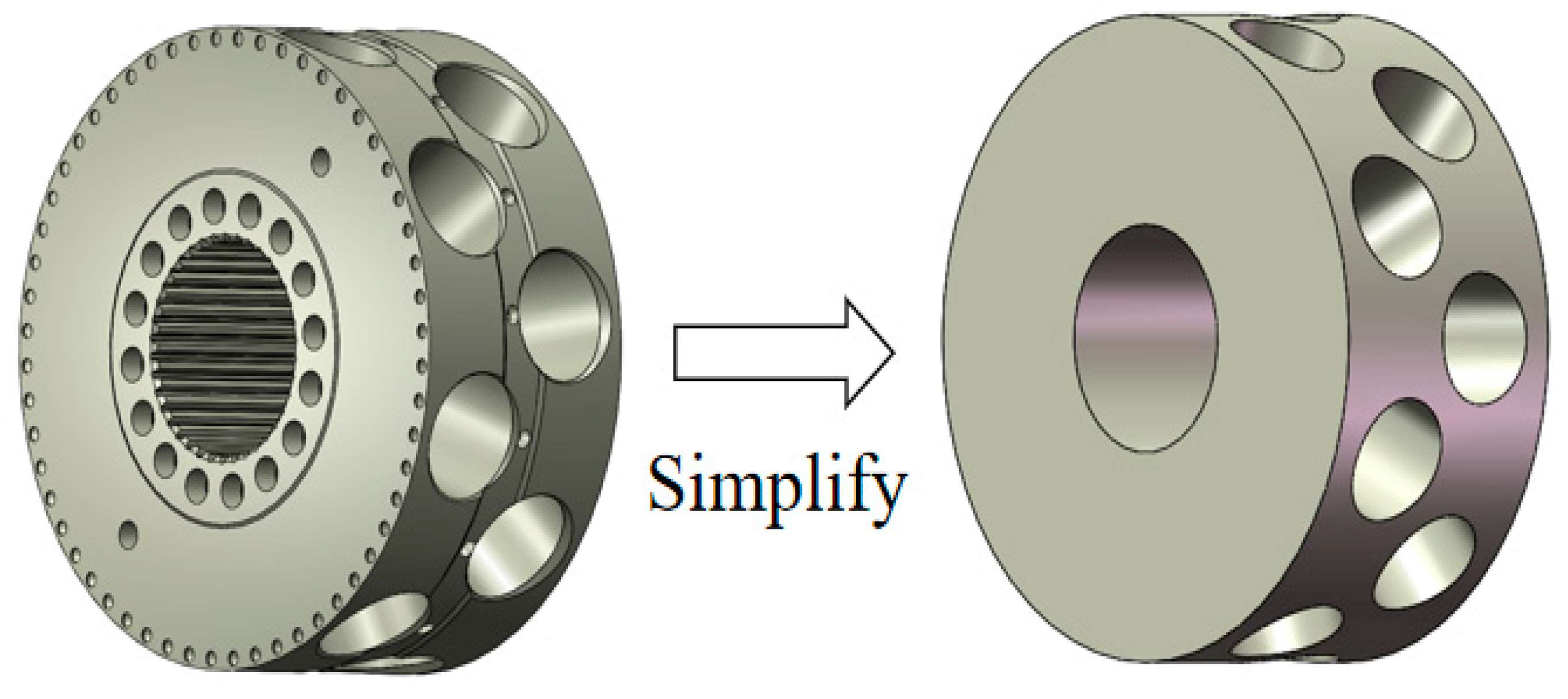
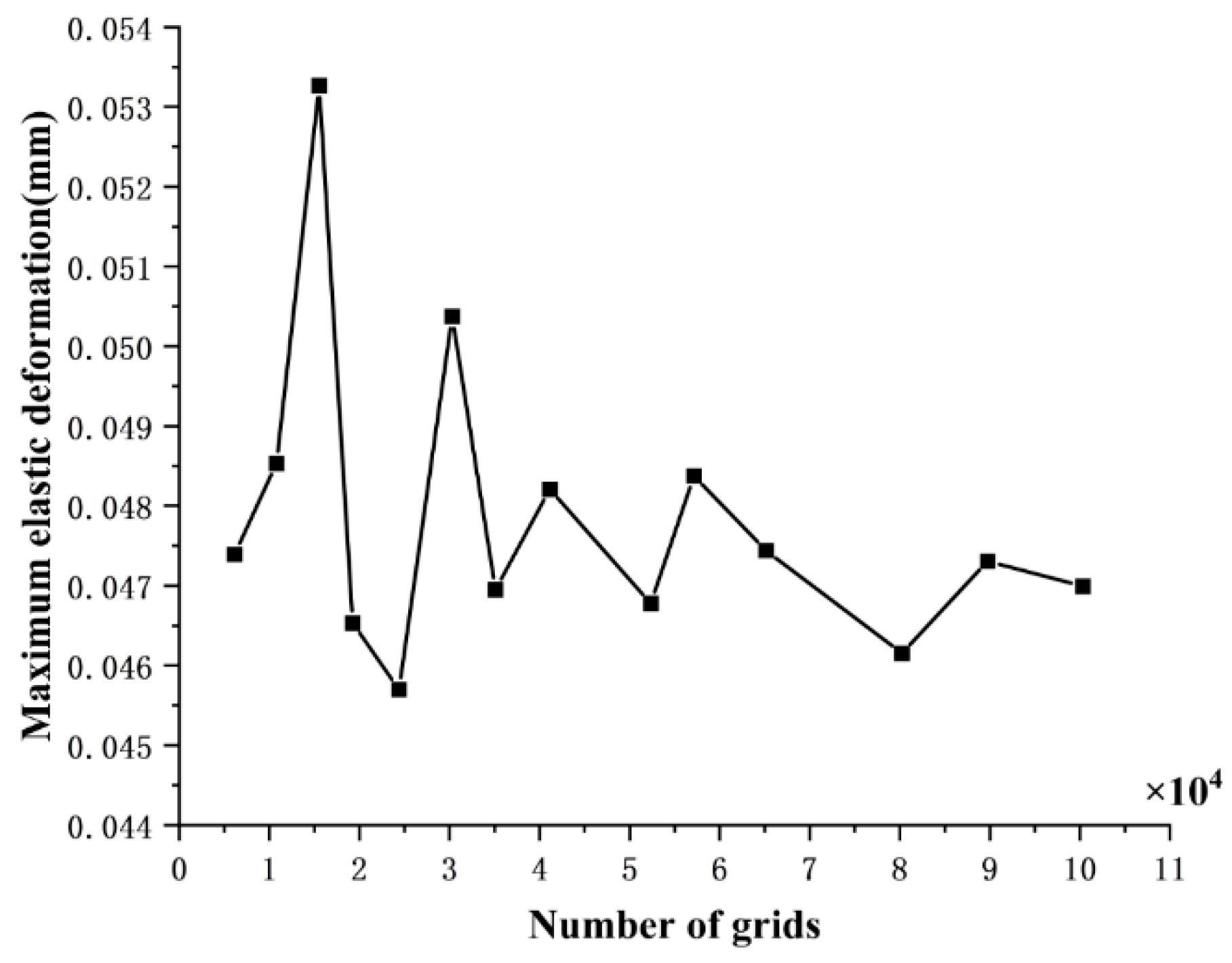
2. Simulation Model
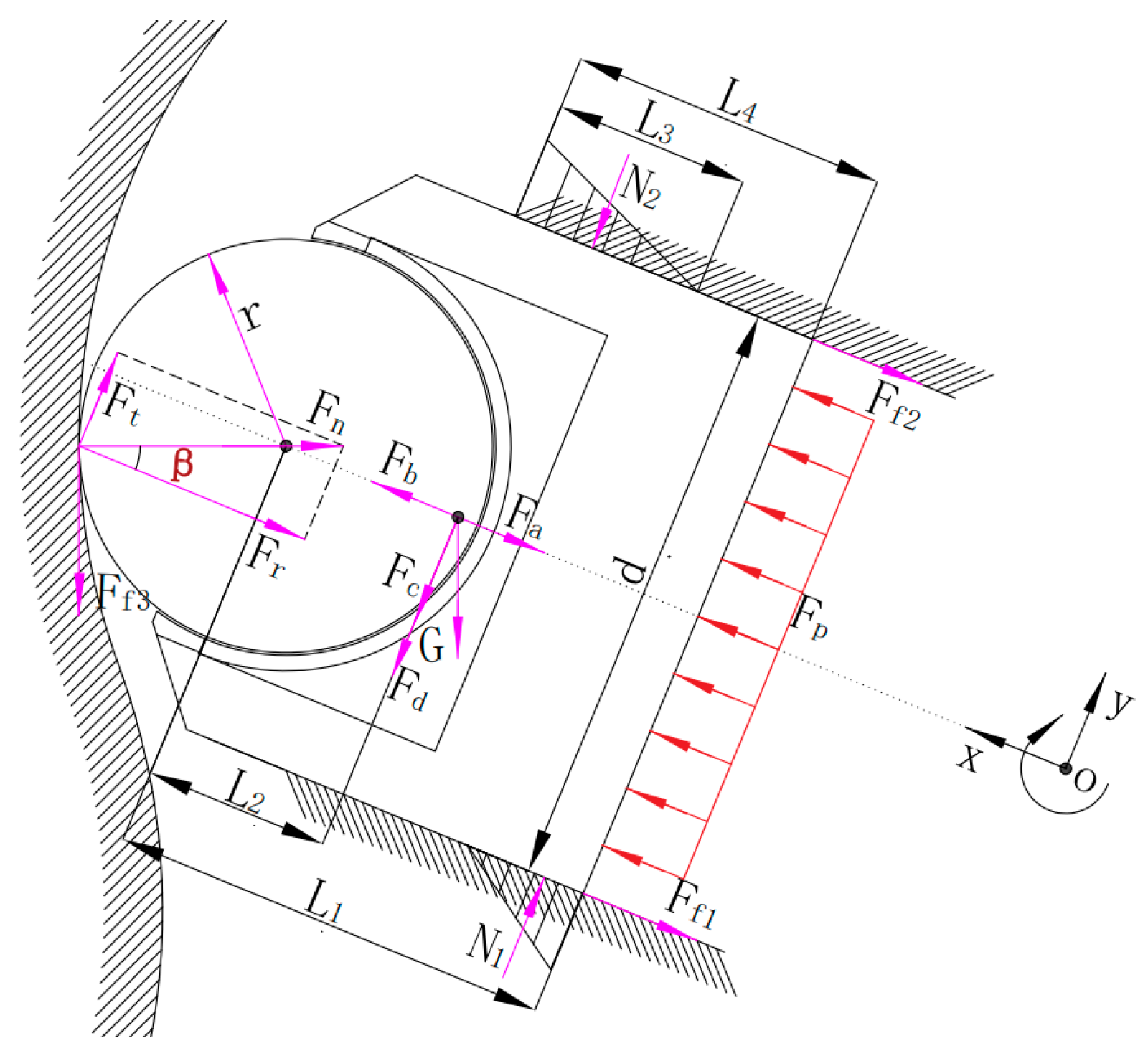
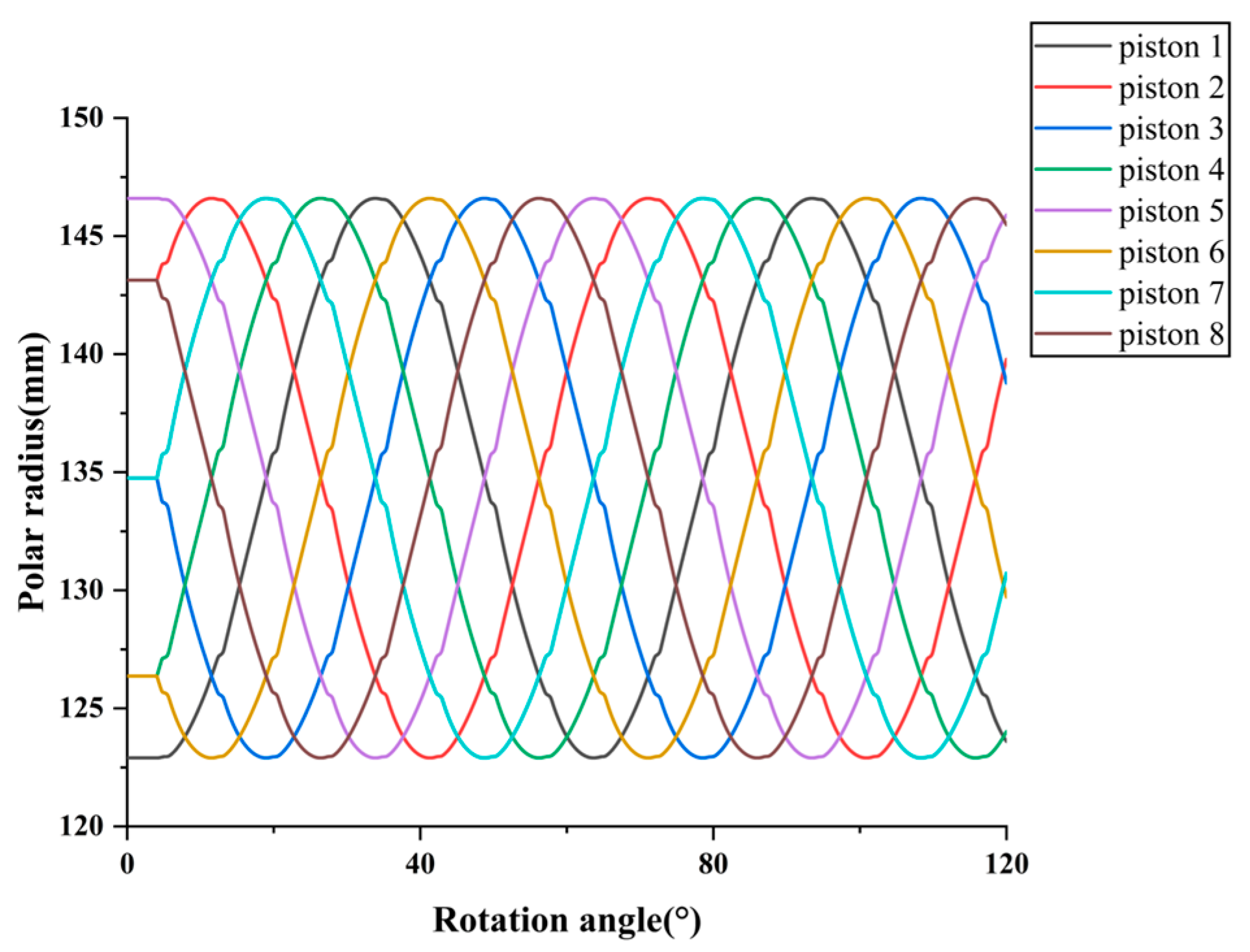
2.1. Force Analysis
2.2. Transient Dynamic Model
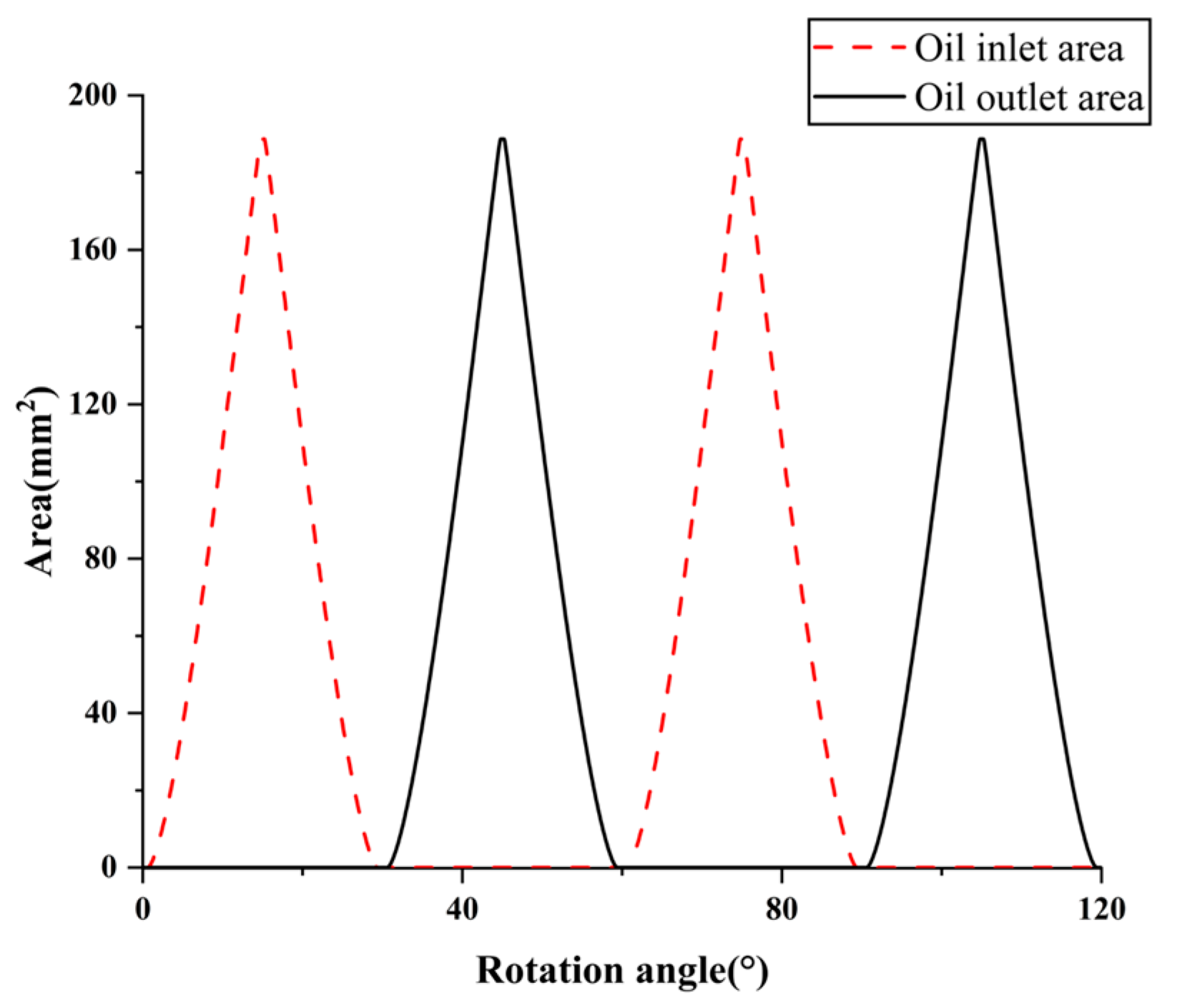
2.3. Hydraulic Model
3. Influence of Elastic Deformation
3.1. Deformation Analysis
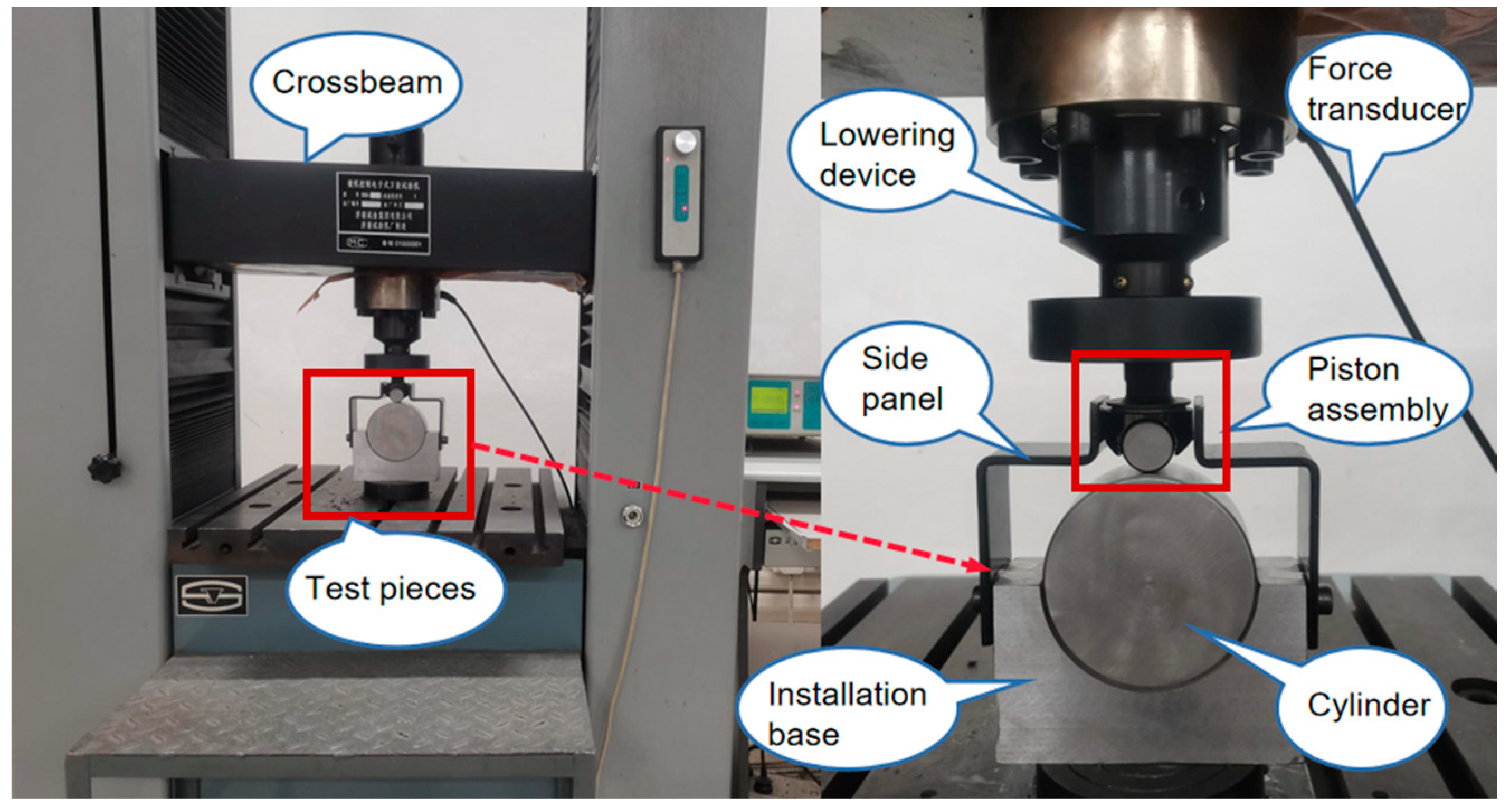
3.2. Deformation Test Verification
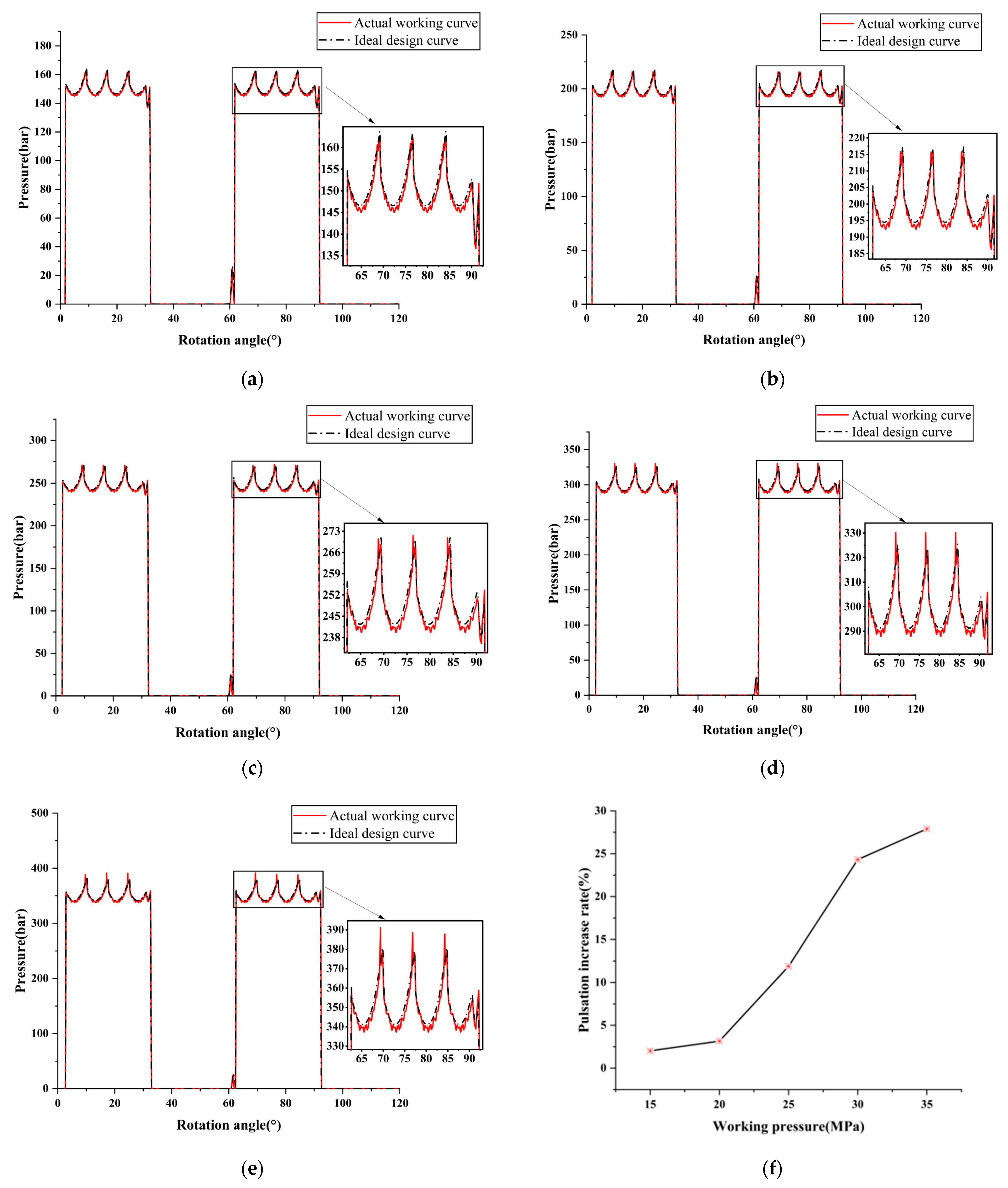
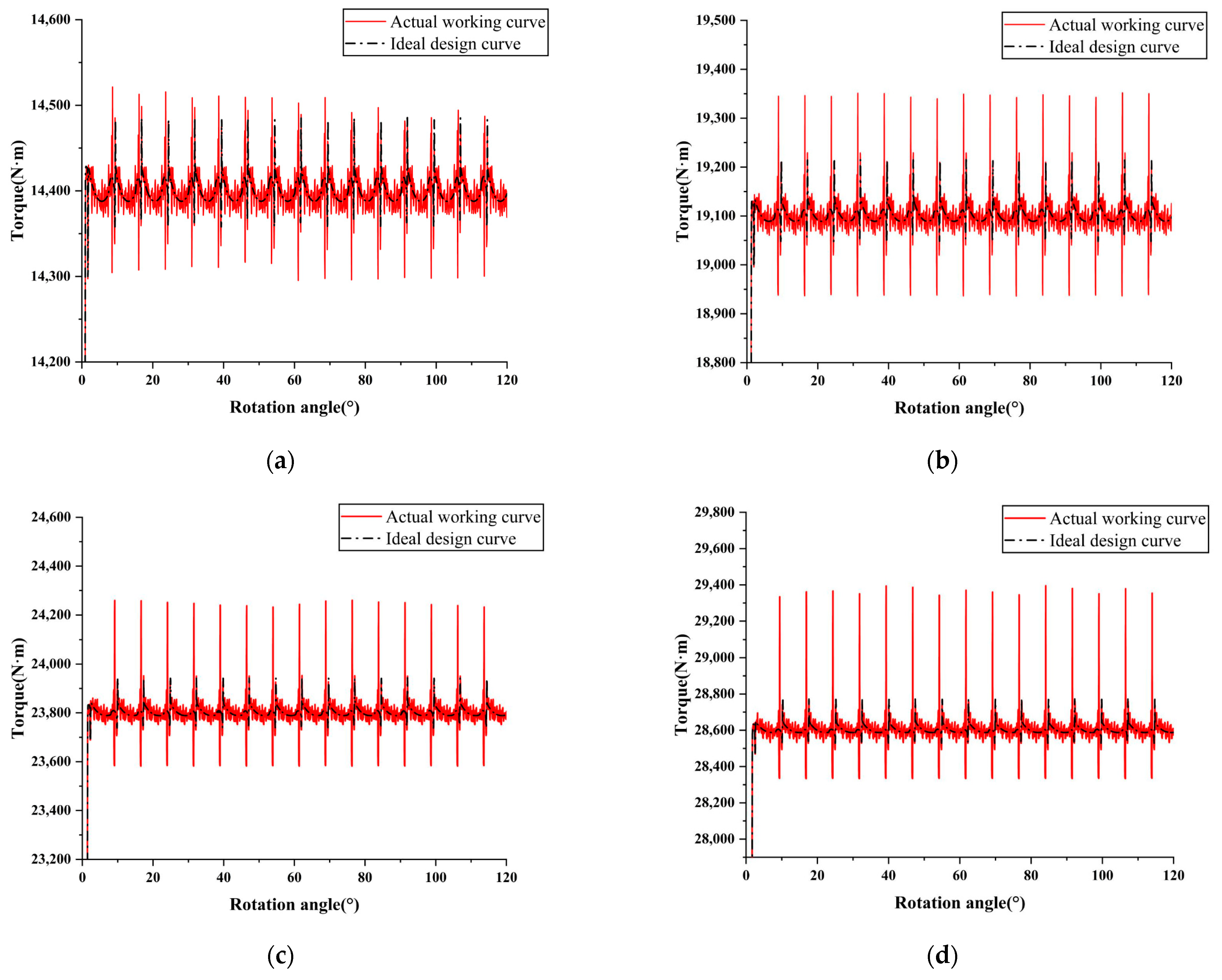
3.3. Influence of Deformation on Motor Output Characteristics
4. Numerical Analyses Based on Deformation Compensation Optimization
4.1. Compensation Method
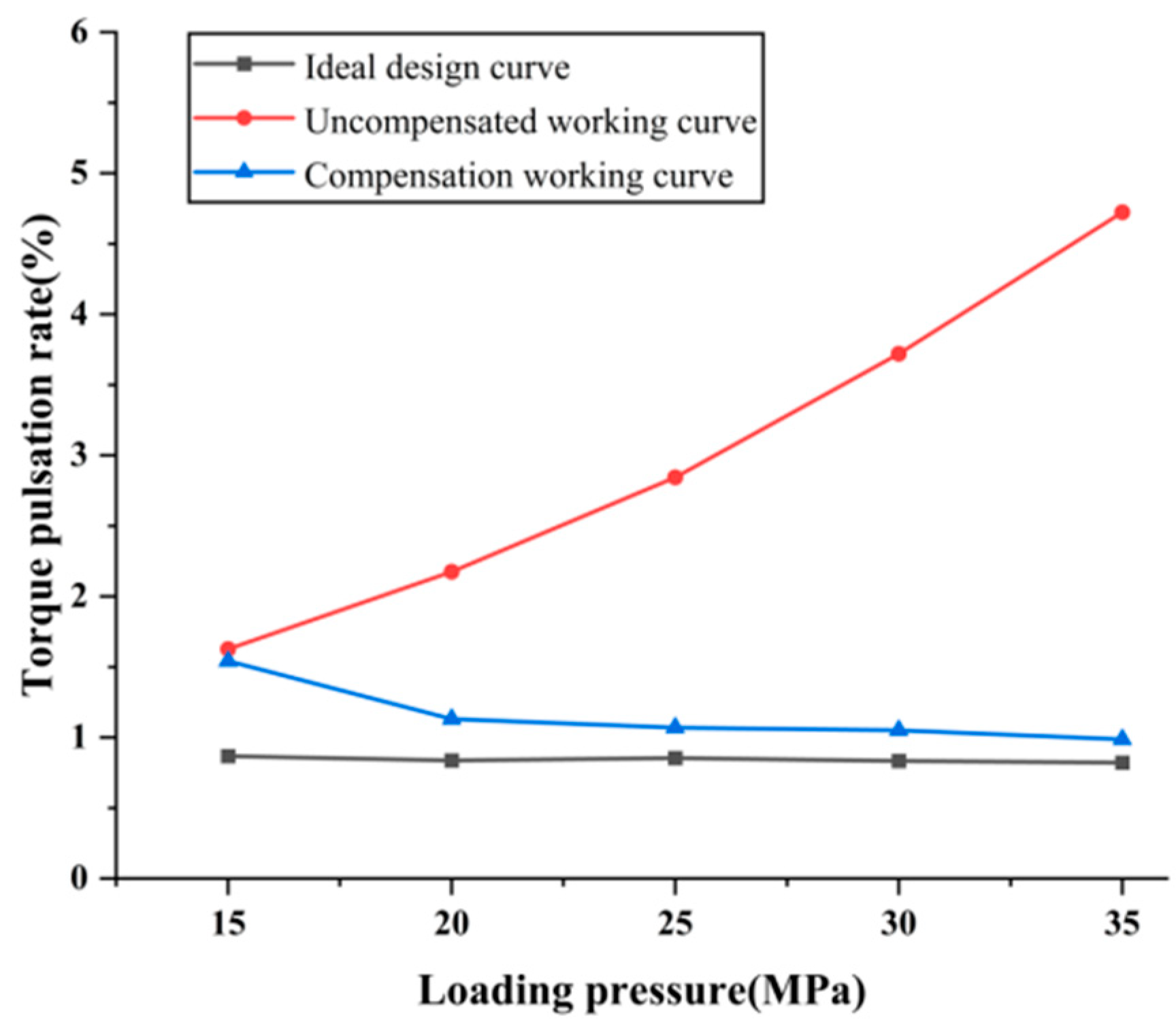
4.2. Result Verification
5. Conclusions
- A finite element simulation model was established to calculate the elastic deformation value of the stroke ring curve, which was verified using tests;
- The elastic deformation of the stroke ring curve has a significant effect on the output torque of the motor. Under the condition of 35 MPa, the pulsation rate of the uncompensated working curve is 3.902% higher than that of the ideal design curve;
- An effective deformation compensation optimization method was proposed. The results show that the pulsation rate of the deformation-compensated working curve was significantly reduced compared with the uncompensated working curve, and the reduction rate of torque pulsation reached 79.12% under 35 MPa working conditions;
- The research contents of this paper can provide reference for structural optimization and performance improvement of multiple-stroke piston motor used in military, marine, and engineering machinery and other occasions with high requirements for impact and noise;
- In the future, based on this research, factors such as oil film thickness and fatigue stress can be considered to better optimize the service life and performance of the multiple-stroke piston motor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kogler, H.; Plöckinger, A.; Foschum, P. Cybernetic Proportional System for a Hydraulic Cylinder Drive Using Proportional Seat-Type Valves. Actuators 2023, 12, 370. [Google Scholar] [CrossRef]
- Tao, J.; Wang, H.; Liao, H.; Yu, S. Mechanical design and numerical simulation of digital-displacement radial piston pump for multi-megawatt wind turbine drivetrain. Renew. Energy 2019, 143, 995–1009. [Google Scholar] [CrossRef]
- Lu, J.; Gu, C.; Zhao, Y.; Tan, C.; Lu, Y.; Fu, C. Refined Modeling Method and Analysis of an Electromagnetic Direct-Drive Hydrostatic Actuation System. Actuators 2022, 11, 281. [Google Scholar] [CrossRef]
- Zhu, Q. Radial piston motor cam ring curve design analysis. Mech. Res. Appl. 2002, 1, 34–35. [Google Scholar]
- Akers, A.; Gassman, M.; Smith, R. Hydraulic Power System Analysis; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Jirawattana, P. Design, Simulation, Fabrication and Testing of a Low-Speed High-Torque (LSHT) Pump/Motor for a Hydrostatic Vehicle. Ph.D. Thesis, The University of Wisconsin-Madison, Madison, WI, USA, 2000. [Google Scholar]
- Chen, Z.R. Theory, Calculation and Design of Low Speed and High Torque Hydraulic Motor; China Machine Press: Beijing, China, 1989. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing; Akademia Books International: New Delhi, India, 2001. [Google Scholar]
- Dasgupta, K.; Mukherjee, A.; Maiti, R. Theoretical and experimental studies of the steady state performance of an orbital rotor low-speed high-torque hydraulic motor. Proc. Inst. Mech. Eng. Part A J. Power Energy 1996, 210, 423–429. [Google Scholar] [CrossRef]
- Yu, H.Y.; Zhong, H.T.; Li, S. The analysis on the flow pulsation of radial piston motor with the modified heart-shaped curve as inner curve. J. Harbin Inst. Technol. 2012, 44, 44–48. [Google Scholar]
- Liu, X.B.; Chen, X.Y.; Zhan, C.C.; Liu, Y. Influence of full flow coefficient on output torque of hydraulic motor with inner curve radial piston. J. Wuhan Univ. Sci. Technol. 2017, 40, 290–294. [Google Scholar]
- Zhang, X.L.; Zhang, J.H.; Zhang, H.J.; Xu, B. Optimized design of cam ring curve of cam lobe radial-piston motor. J. Huazhong Univ. Sci. Technol. 2021, 49, 30–35. [Google Scholar]
- Nguyen, T.N.; Kurtenbach, S.; Hüsing, M.; Corves, B. A general framework for motion design of the follower in cam mechanisms by using non-uniform rational B-spline. Mech. Mach. Theory 2019, 137, 374–385. [Google Scholar] [CrossRef]
- Xin, J.B. Research on Generalized Stator Orbit Curve of Radial Piston Motor. Master’s Thesis, Nanchang University, Nanchang, China, 2019. [Google Scholar]
- Khalifa, M.Z. The effects of multi-layers surfaces on the elastic deformation of journal bearing. J. Eng. Sci. Technol. 2021, 16, 3521–3533. [Google Scholar]
- Zhang, Y.; Chen, G.; Wang, L. Effects of thermal and elastic deformations on lubricating properties of the textured journal bearing. Adv. Mech. Eng. 2019, 11, 10. [Google Scholar] [CrossRef]
- Linjamaa, A.; Lehtovaara, A.; Larsson, R.; Kallio, M.; Söchting, S. Modelling and analysis of elastic and thermal deformations of a hybrid journal bearing. Tribol. Int. 2018, 118, 451–457. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. Force-induced deformation prediction and flexible error compensation strategy in flank milling of thin-walled parts. J. Mater. Process. Technol. 2021, 297, 117–258. [Google Scholar] [CrossRef]
- Huang, H.W.; Tsai, M.S.; Huang, Y.C. Modeling and elastic deformation compensation of flexural feed drive system. Int. J. Mach. Tools Manuf. 2018, 132, 96–112. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Bi, Q.; Zhu, L.; Ding, H. An accelerated convergence approach for real-time deformation compensation in large thin-walled parts machining. Int. J. Mach. Tools Manuf. 2019, 142, 98–106. [Google Scholar] [CrossRef]
- Petrović, R.; Pezdirnik, J.; Banaszek, A.; Đuričić, L. Influence of compressibility of working fluid on hydrodynamic processes in the axial piston pump with combined distribution/flow of working fluid. In Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, Beijing, China, 17–20 August 2011; pp. 335–339. [Google Scholar]
- Nakhatakyan, F.G. Solution of a plane contact problem of the theory of elasticity on the basis of an elastic half-space model. J. Mach. Manuf. Reliab. 2011, 40, 458–462. [Google Scholar] [CrossRef]
- Nor, K.M.; Ibrahim, M.N.; Choiron, M.A. An overview of fracture mechanics with ANSYS. Mech. Eng. 2018, 10, 59–67. [Google Scholar]
- Lei, J.; Su, B.; Zhang, S.; Yang, H.; Cui, Y. Dynamics-Based Thermal Analysis of High-Speed Angular Contact Ball Bearings with Under-Race Lubrication. Machines 2023, 11, 691. [Google Scholar] [CrossRef]
- Banaszek, A.; Petrović, R.; Zylinski, B. Finite element method analysis of pipe material temperature changes influence on line expansion loops in hydraulic installations on modern tankers. Therm. Sci. 2011, 15, 81–90. [Google Scholar] [CrossRef]
- Liang, Q.; Wang, W.; Zhai, Y.; Sun, Y.; Zhang, W. Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim. Actuators 2023, 12, 417. [Google Scholar] [CrossRef]







| Name | Material | Density/kg (m3)−1 | Young’s Modulus/MPa | Poisson’s Ratio | Yield Strength/MPa |
|---|---|---|---|---|---|
| Piston | 38CrMoAl | 7870 | 213,000 | 0.286 | 835 |
| Roller | GCr15 | 7810 | 208,000 | 0.3 | 750 |
| Bearing bush | PEEK | 1320 | 3200 | 0.41 | 97 |
| Stroke ring | 42CrMo | 7850 | 212,000 | 0.28 | 930 |
| Rotor | QT700 | 7300 | 145,000 | 0.3 | 420 |
| Constraint Type | Component 1 | Component 2 |
|---|---|---|
| Fixed support | Stroke ring | Ground |
| Bearing bush | Piston | |
| Revolute support | Rotor | Ground |
| Roller | Bearing bush | |
| Translation support | Piston | Rotor |
| Contact | Stroke ring | Roller |
| Experimental Force (kN) | Displacement (μm) | Deformation (mm) | |
|---|---|---|---|
| Error | ±0.2% | ±0.5% | ±0.5% |
| Resolution ratio | 0.002 | 0.04 | 0.002 |
| Measurement range | 0.4–100 | \ | \ |
| Location/° | Cylinder Diameter/mm | Roller Diameter/mm | Simulation Deformation Value/μm | Test Deformation Value/μm | Error/% |
|---|---|---|---|---|---|
| 0 | 99.47 | 40 | 31.51 | 32.8 | 4.09 |
| 7 | 249.78 | 40 | 31.47 | 32.7 | 3.91 |
| 15 | 250.22 | 40 | 43.25 | 45.2 | 4.51 |
| 20 | 126.22 | 40 | 29.14 | 30.2 | 3.64 |
| 25 | 86.31 | 40 | 24.18 | 25.1 | 3.81 |
| 30 | 74.99 | 40 | 23.25 | 24.7 | 6.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, G.; Gao, K.; Dong, H.; Liu, B.; Li, L.; Hu, Z. Design Method of the Stroke Ring Based on Deformation Pre-Compensation. Actuators 2024, 13, 22. https://doi.org/10.3390/act13010022
An G, Gao K, Dong H, Liu B, Li L, Hu Z. Design Method of the Stroke Ring Based on Deformation Pre-Compensation. Actuators. 2024; 13(1):22. https://doi.org/10.3390/act13010022
Chicago/Turabian StyleAn, Gaocheng, Kai Gao, Hongquan Dong, Baoyu Liu, Lin Li, and Zhenhua Hu. 2024. "Design Method of the Stroke Ring Based on Deformation Pre-Compensation" Actuators 13, no. 1: 22. https://doi.org/10.3390/act13010022
APA StyleAn, G., Gao, K., Dong, H., Liu, B., Li, L., & Hu, Z. (2024). Design Method of the Stroke Ring Based on Deformation Pre-Compensation. Actuators, 13(1), 22. https://doi.org/10.3390/act13010022






