Design and Analysis of a New Dual-Stator Hybrid Magnet Flux Modulation Machine
Abstract
1. Introduction
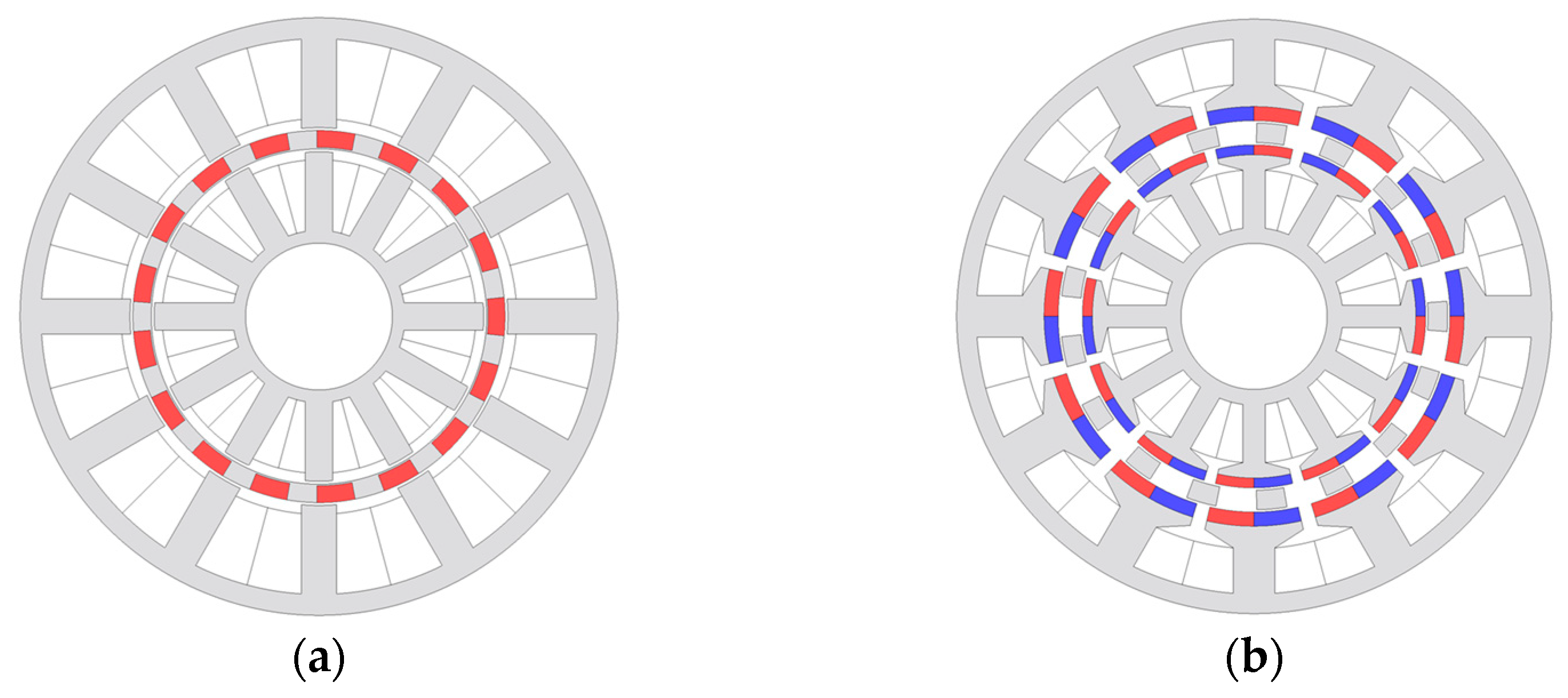
2. Machine Configuration and Operating Principle
2.1. Machine Configuration
2.2. Operating Principle
3. Multi-Objective Optimization and Influence of Magnet Dimensions
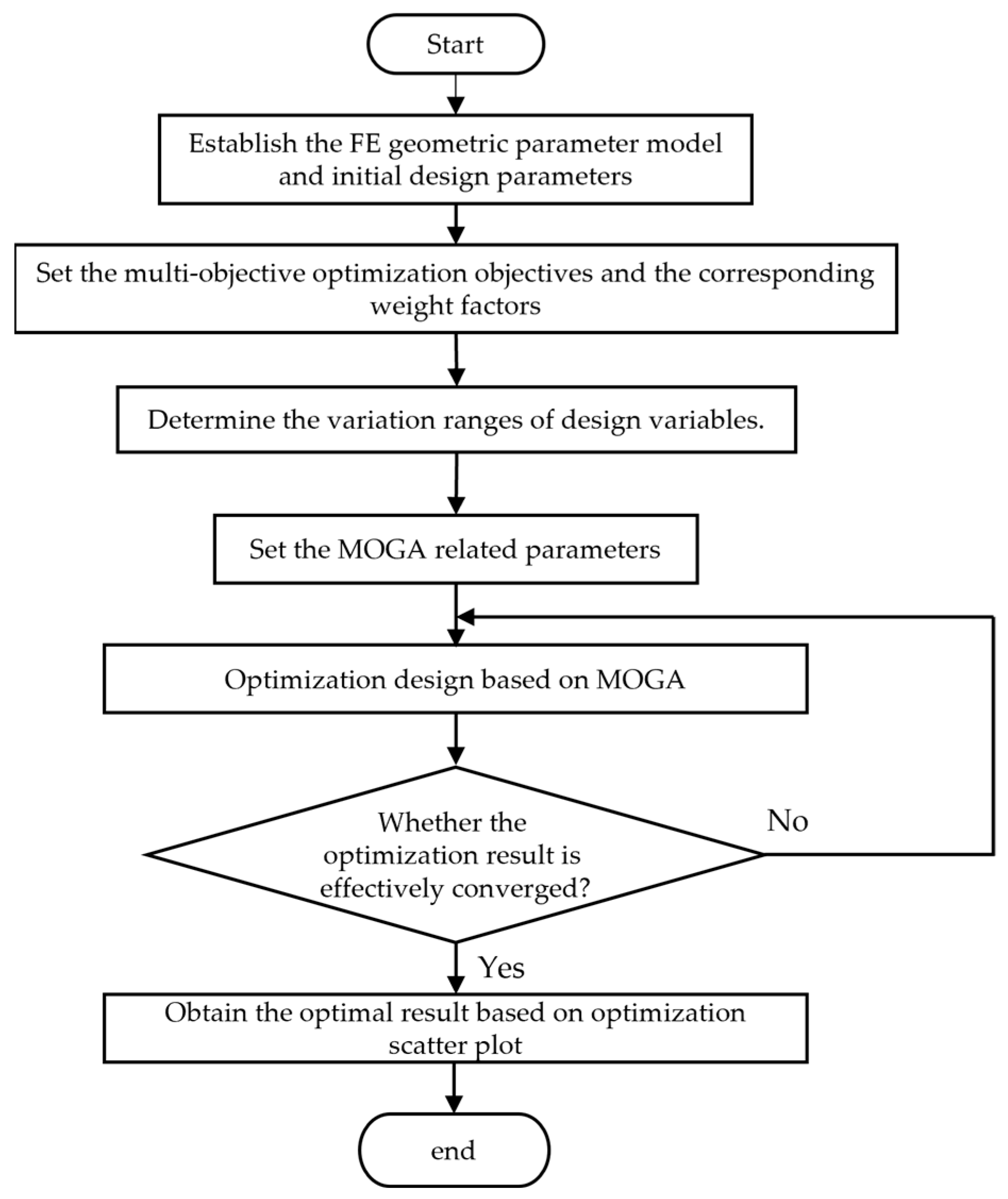
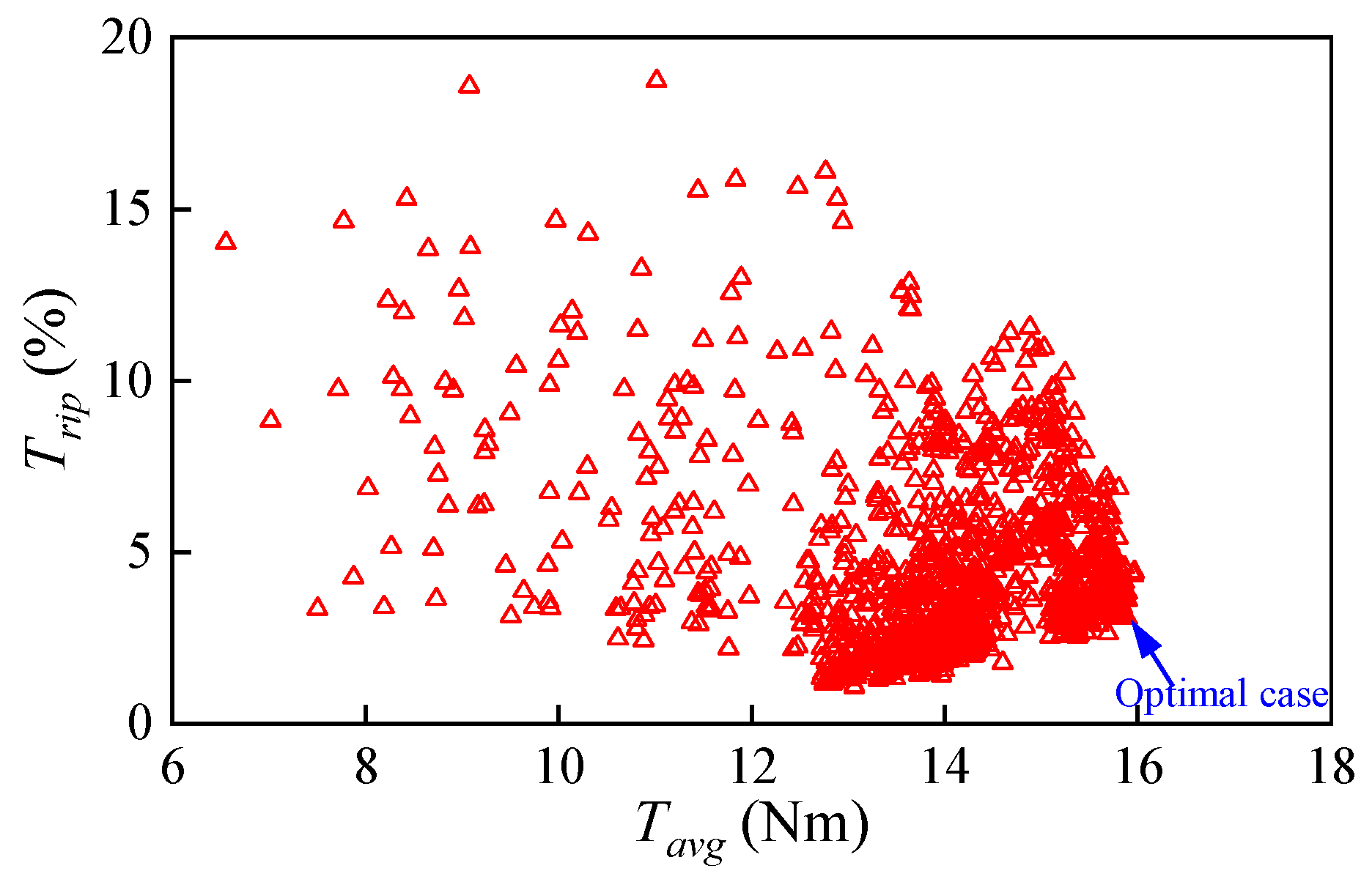
3.1. Multi-Objective Optimization Design
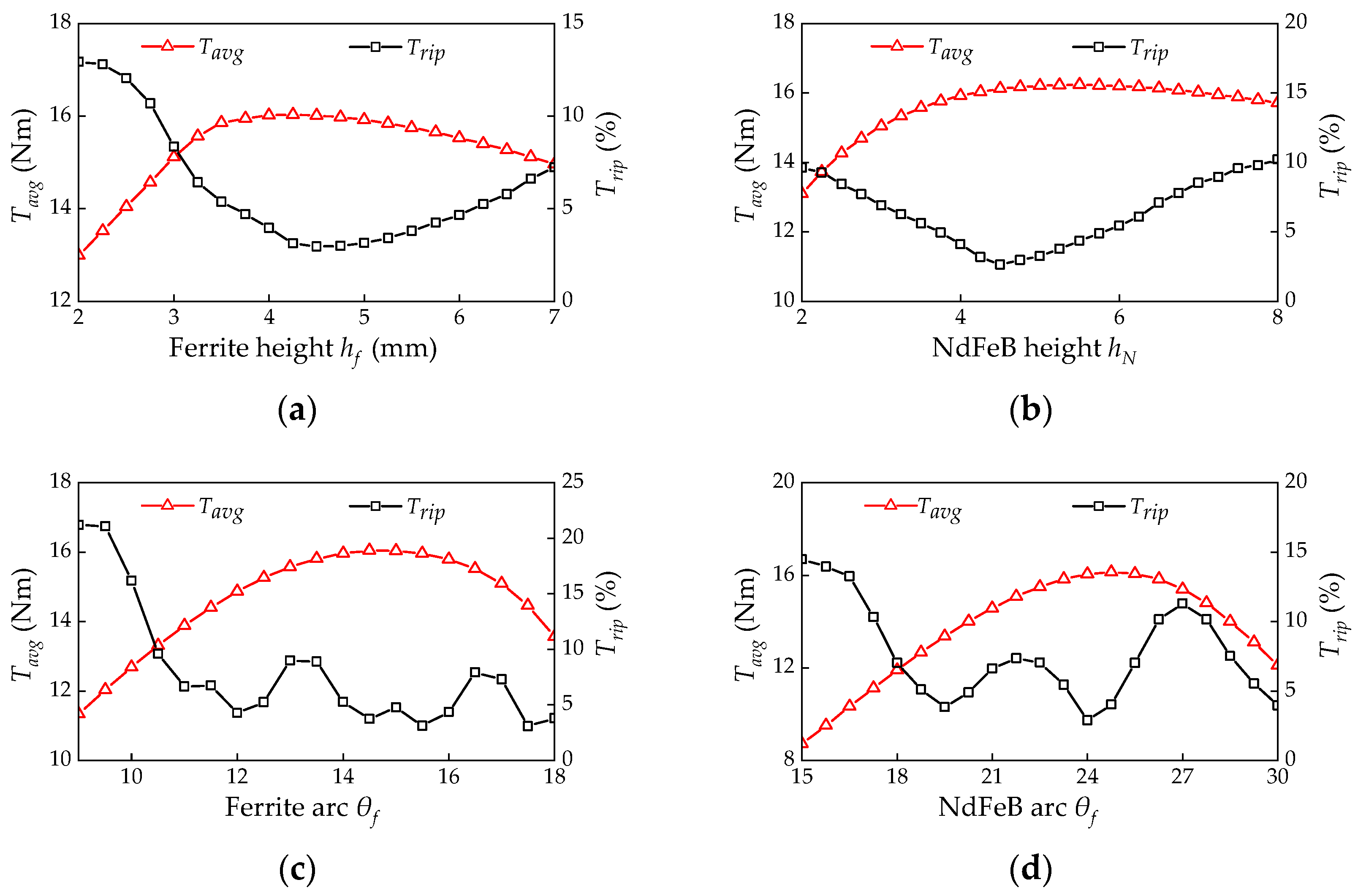
3.2. Influence of Magnet Dimensions on Torque Characteristics
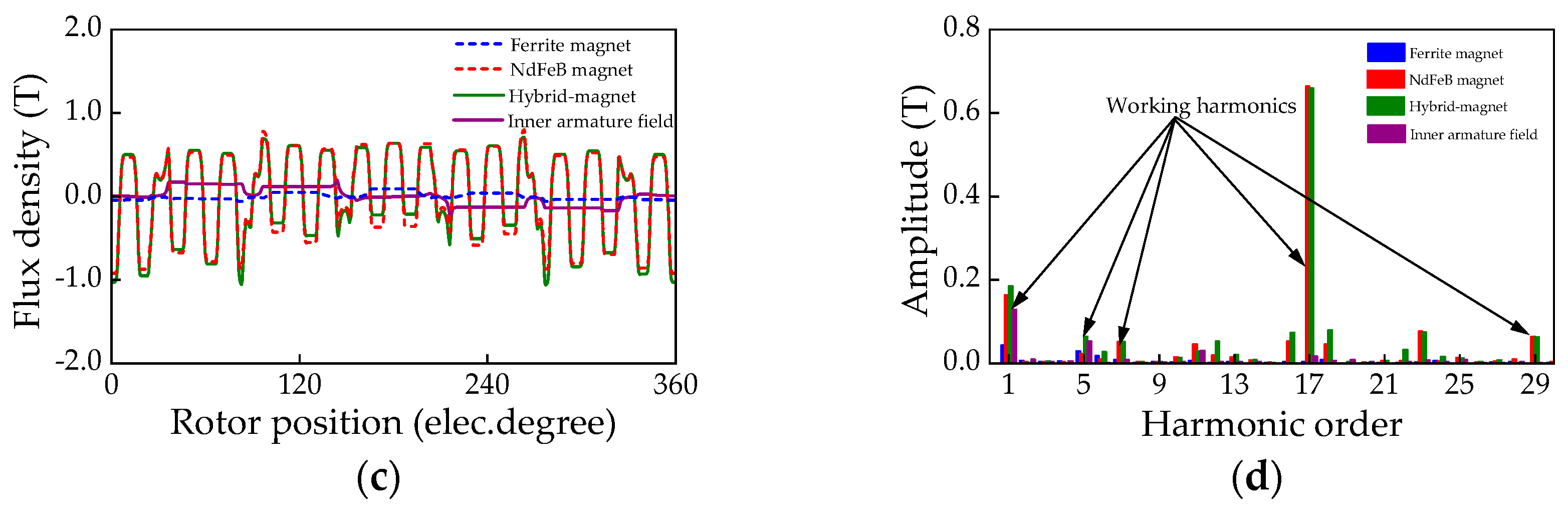
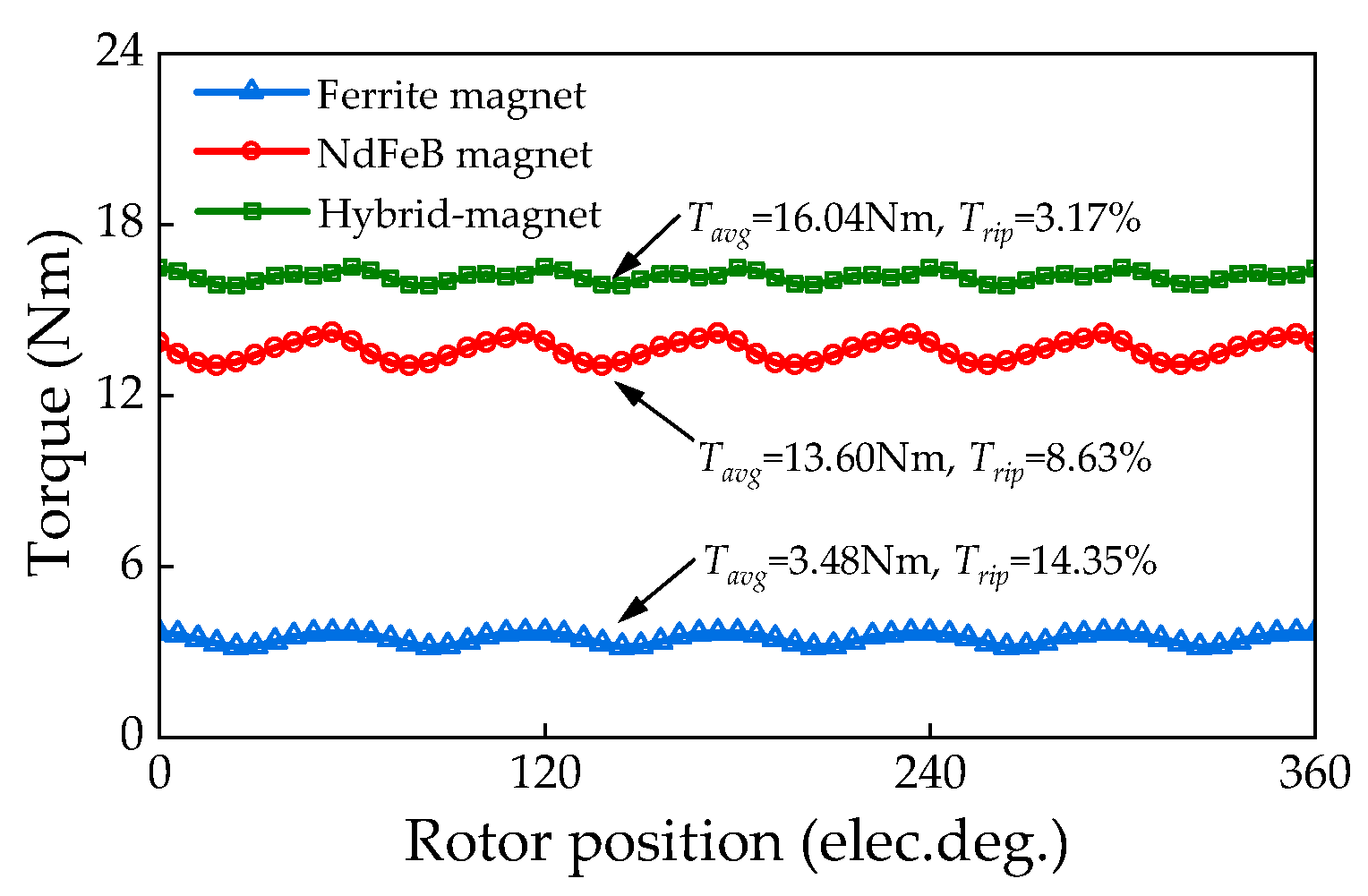
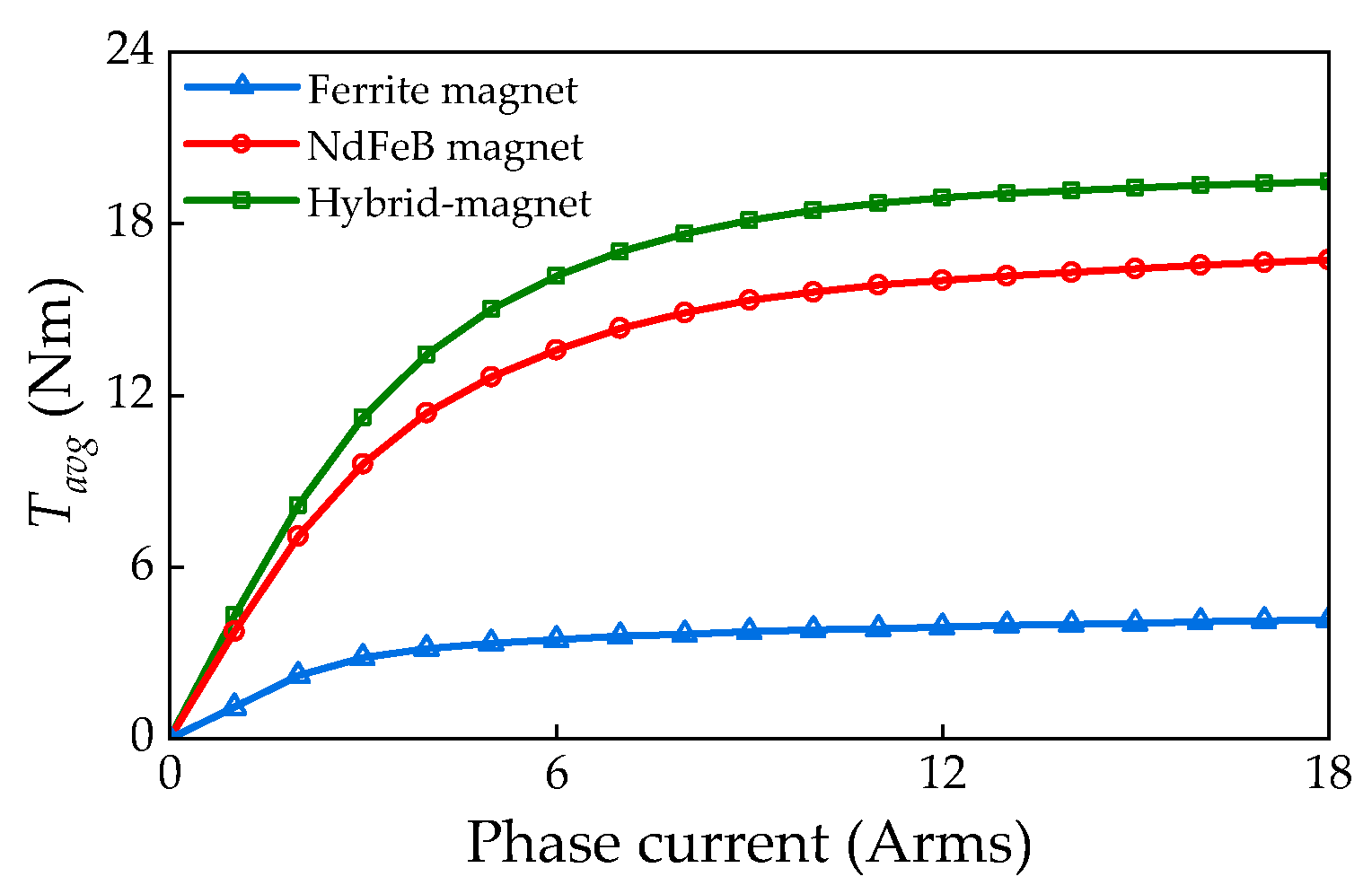
4. Electromagnetic Performance Analysis and Comparison
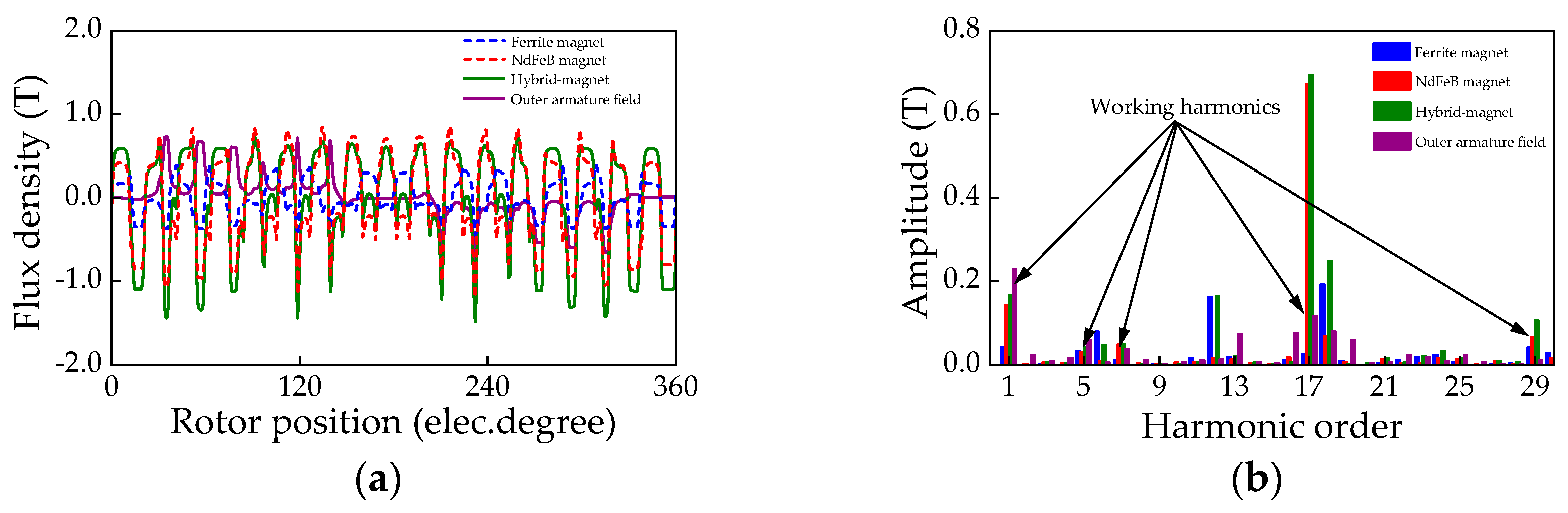
4.1. Electromagnetic Performance Analysis
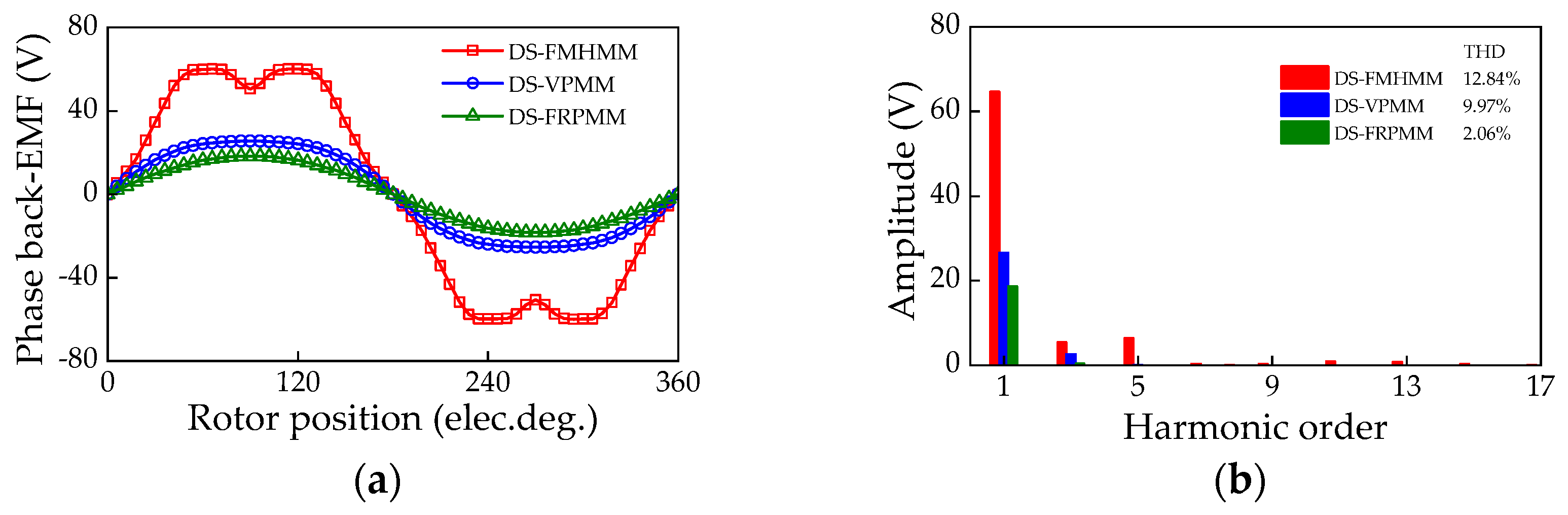
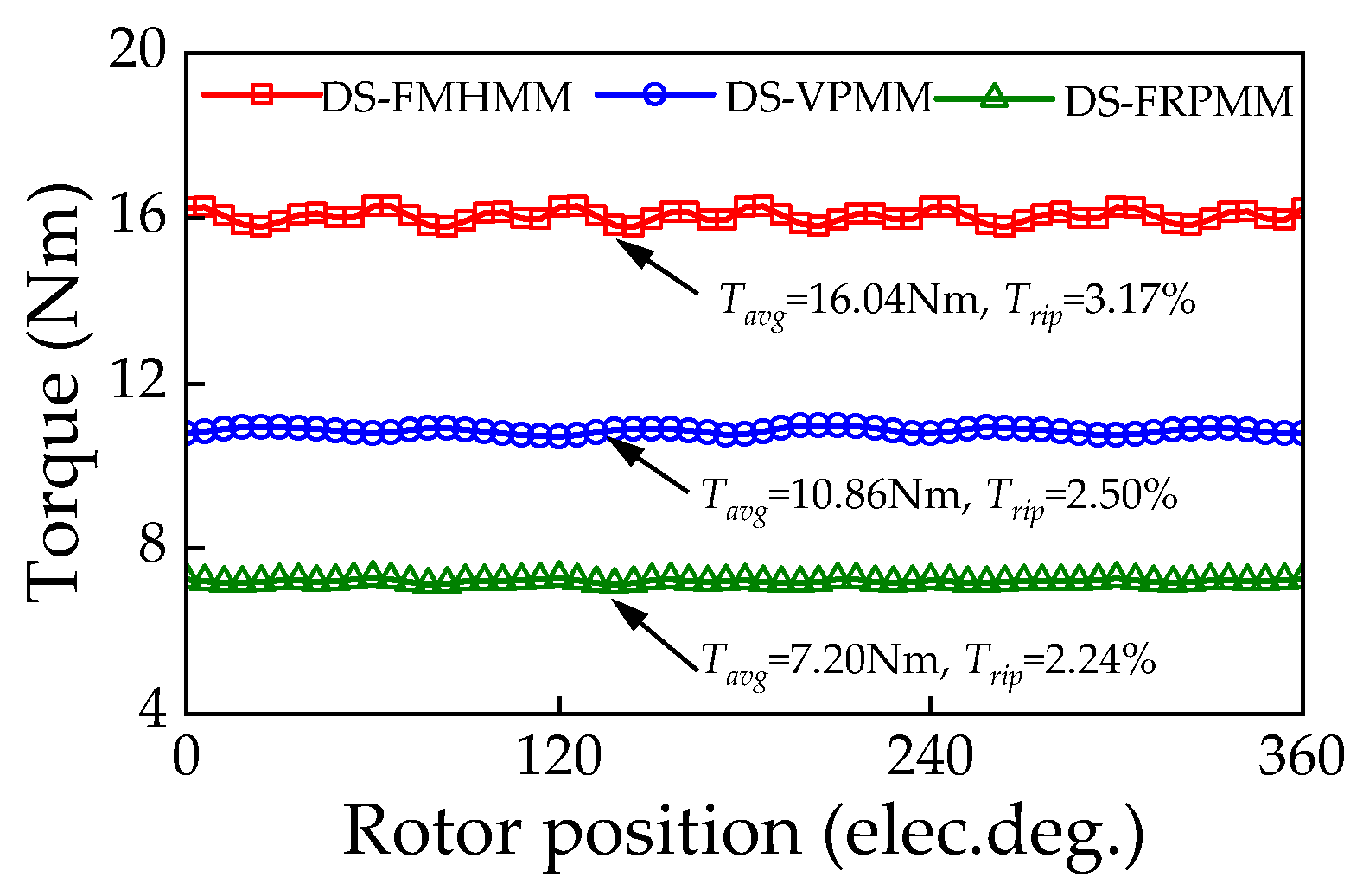
4.2. Electromagnetic Performance Comparison of DS-FMHMM and Two Existing DSFMMs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krings, A.; Cossale, M.; Tenconi, A.; Soulard, J.; Cavagnino, A.; Boglietti, A. Magnetic materials used in electrical machines: A comparison and selection guide for early machine design. IEEE Ind. Appl. Mag. 2017, 23, 21–28. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid and fuel cell vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Nerg, J.; Rilla, M.; Ruuskanen, V.; Pyrhonen, J.; Ruotsalainen, S. Direct-driven interior magnet permanent-magnet synchronous motors for a full electric sports car. IEEE Trans. Ind. Electron. 2013, 61, 4286–4294. [Google Scholar] [CrossRef]
- Wrobel, R.; Mellor, P.H. Design considerations of a direct drive brushless machine with concentrated windings. IEEE Trans. Energy Convers. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Ching, T.W.; Chen, M. A new magnet less flux-reversal HTS machine for direct-drive application. IEEE Trans. Appl. Supercond. 2015, 25, 5203105. [Google Scholar] [CrossRef][Green Version]
- Du, J.; Liang, D.; Liu, X. Performance analysis of a mutually coupled linear switched reluctance machine for direct-drive wave energy conversions. IEEE Trans. Magn. 2017, 53, 8108110. [Google Scholar] [CrossRef]
- Li, D.; Zou, T.; Qu, R.; Jiang, D. Analysis of fractional-slot concentrated winding PM vernier machines with regular open-slot stators. IEEE Trans. Ind. Appl. 2018, 54, 1320–1330. [Google Scholar] [CrossRef]
- Kim, B.; Lipo, T.A. Analysis of a PM vernier motor with spoke structure. IEEE Trans. Ind. Appl. 2015, 52, 217–225. [Google Scholar] [CrossRef]
- Zahid, A.; Khan, F.; Ahmad, N.; Sami, I.; Ullah, W.; Ullah, N.; Ullah, N.; Alkhammash, H.I. Design and analysis of dual mover multi-tooth permanent magnet flux switching machine for ropeless elevator applications. Actuators 2021, 10, 81. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Liu, Y. Analysis of air-gap field modulation and magnetic gearing effect in fractional-slot concentrated-winding permanent magnet synchronous machines. IEEE Trans. Ind. Electron. 2017, 65, 3688–3698. [Google Scholar] [CrossRef]
- Cheng, M.; Han, P.; Hua, W. General airgap field modulation theory for electrical machines. IEEE Trans. Ind. Electron. 2017, 64, 6063–6074. [Google Scholar] [CrossRef]
- Niu, S.; Chau, K.T.; Jiang, J.; Liu, C. Design and control of a new double-stator cup-rotor permanent-magnet machine for wind power generation. IEEE Trans. Magn. 2007, 43, 2501–2503. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, H.; Ding, S.; He, C.; Jin, Z.; Wei, Z. A new hybrid magnet dual stator field modulation machine with different split ratios of stators. IEEE Trans. Magn. 2022, 58, 8105806. [Google Scholar] [CrossRef]
- Li, D.; Qu, R.; Xu, W.; Li, J.; Lipo, T.A. Design procedure of dual-stator spoke-array vernier machine permanent-magnet machines. IEEE Trans. Ind. Appl. 2015, 51, 2972–2983. [Google Scholar] [CrossRef]
- Huang, J.; Fu, W.; Niu, S.; Zhao, X. Analysis of a complementary dual-stator vernier machine with reduced non-working Harmonics for low-speed direct-drive applications. IEEE Trans. Energy Convers. 2023. early access. [Google Scholar] [CrossRef]
- Li, Y.; Bobba, D.; Sarlioglu, B. Design and performance characterization of a novel low-pole dual-stator flux-switching permanent magnet machine for traction application. IEEE Trans. Ind. Appl. 2016, 52, 4304–4314. [Google Scholar] [CrossRef]
- Ning, S.; Seangwong, P.; Siritaratiwat, A.; Khunkitti, P. A novel double stator hybrid-excited flux reversal permanent magnet machine with Halbach PM arrays. In Proceedings of the 2023 IEEE International Magnetic Conference—Short Papers (INTERMAG Short Papers), Sendai, Japan, 15–19 May 2023; pp. 1–2. [Google Scholar]
- Meng, Y.; Fang, S.; Li, Y.; Zhong, Y.; Qin, L. Design and analysis of new dual-stator flux modulated machines with dual-PM excitation. IEEE Trans. Ind. Appl. 2022, 59, 1383–1393. [Google Scholar] [CrossRef]
- Meng, Y.; Fang, S.; Wang, H.; Pan, Z.; Qin, L. Design and analysis of a new dual-stator consequent-pole flux reversal machine with triple-PM excitation. IEEE Trans. Magn. 2021, 57, 8105904. [Google Scholar] [CrossRef]
- Meng, Y.; Fang, S.; Pan, Z.; Liu, W.; Qin, L. Machine learning technique based multi-level optimization design of a dual-stator flux modulated machine with dual-PM excitation. IEEE Trans. Transport. Electrific. 2022, 9, 2606–2617. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S.; Yang, L. Design optimization and comparative study of novel dual-PM excited machines. IEEE Trans. Ind. Electron. 2017, 64, 9924–9933. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, W.; Liu, G.; Ji, J.; Niu, S. A novel dual-permanent-magnet excited machine with non-uniformly distributed permanent-magnets and flux modulation poles on the stator. IEEE Trans. Veh. Technol. 2020, 69, 7104–7115. [Google Scholar] [CrossRef]
- Galioto, S.J.; Reddy, P.B.; EL-Refaie, A.M.; Alexander, J.P. Effect of magnet types on performance of high-speed spoke interior-permanent-magnet machines designed for traction applications. IEEE Trans. Ind. Appl. 2014, 51, 2148–2160. [Google Scholar] [CrossRef]
- Qiao, Z.; Zhang, Y.; Luo, J.; Fu, W.; Shao, D.; Cao, H. A Non-Permanent Magnet DC-Biased Vernier Reluctance Linear Machine with Non-Uniform Air Gap Structure for Ripple Reduction. Actuators 2023, 12, 7. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S.; Yang, L. Design optimization of a novel scaledown hybrid-excited dual permanent magnet generator for direct-drive wind power application. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar]
- Yu, J.; Liu, C. Multi-objective optimization of a double-stator hybrid-excited flux-switching permanent-magnet machine. IEEE Trans. Energy Convers. 2019, 35, 312–323. [Google Scholar] [CrossRef]
- Sun, M.; Xu, Y.; Han, K. Structure and optimization design of cup winding permanent magnet synchronous machine in flywheel energy storage system. IEEE Trans. Magn. 2023, 59, 8100805. [Google Scholar] [CrossRef]

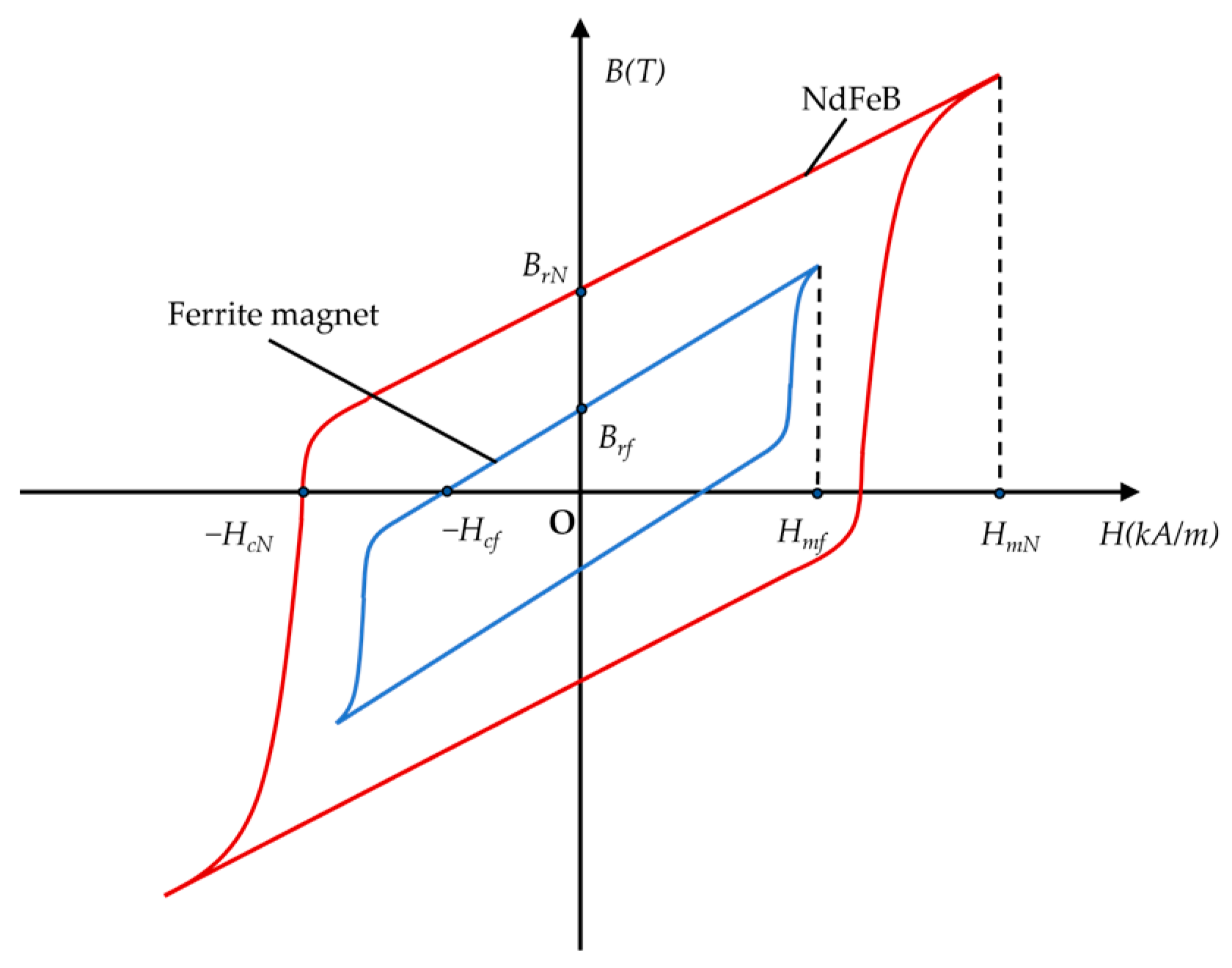
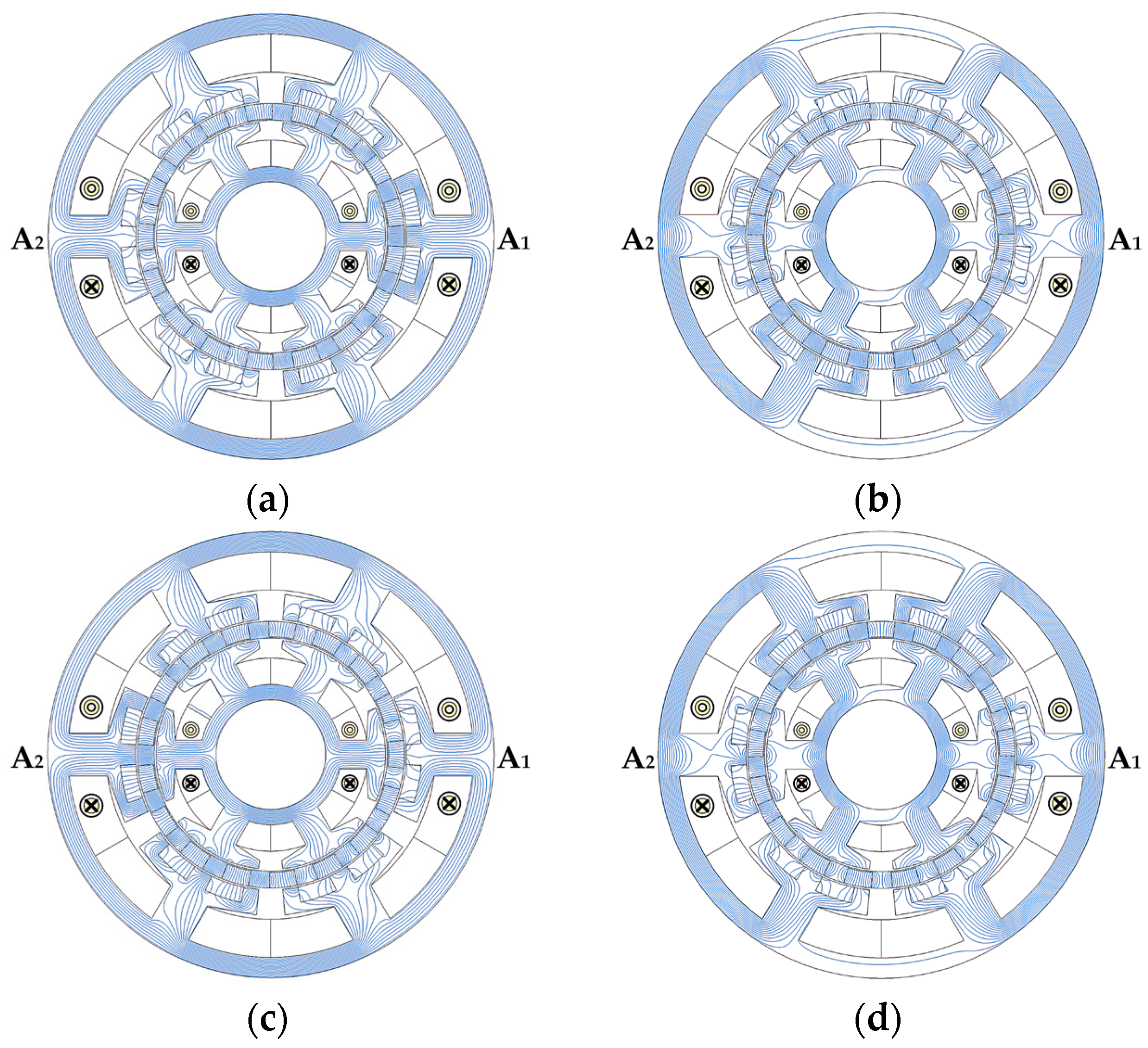
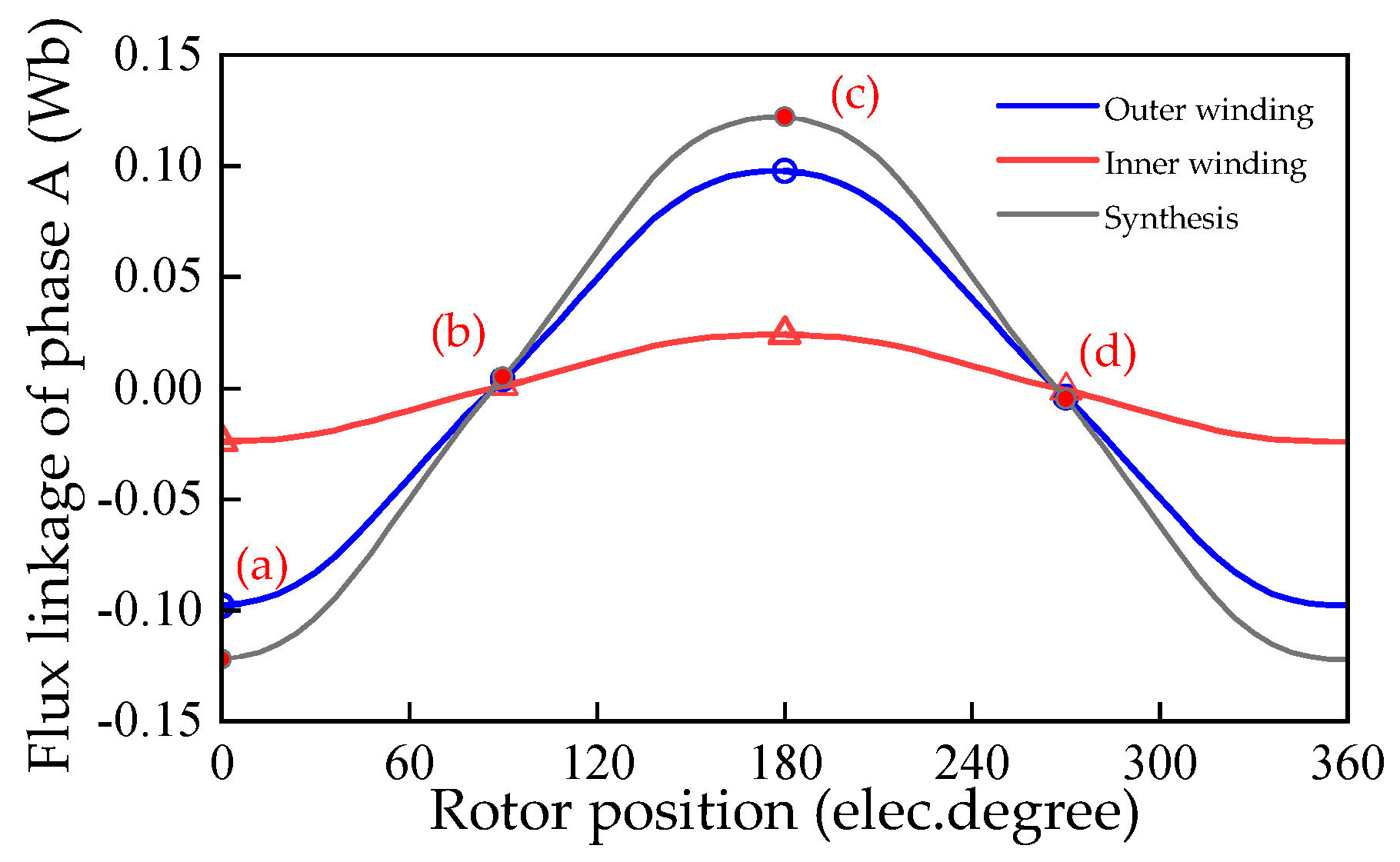
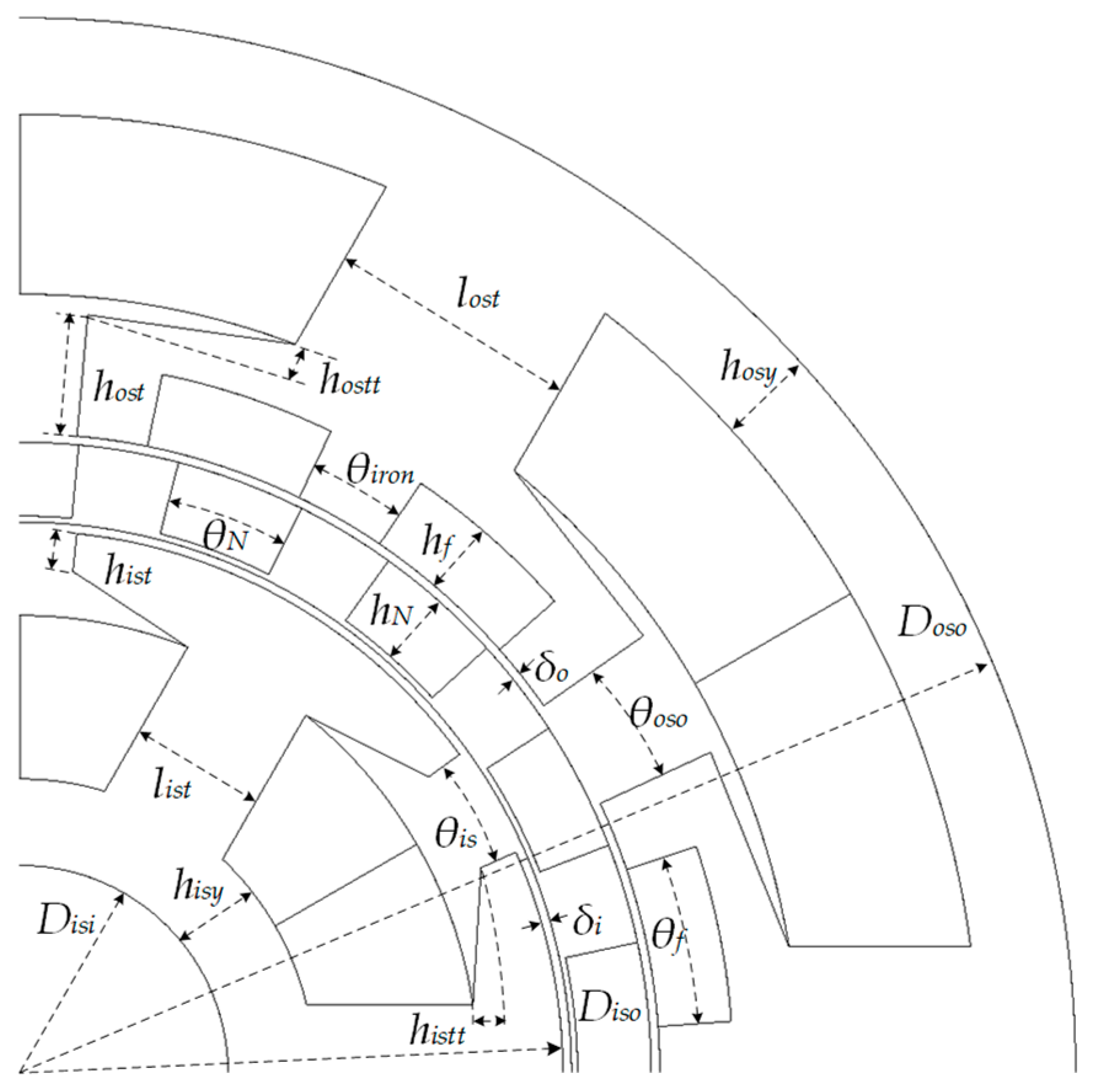


| Parameter | Value | |
|---|---|---|
| NdFeB | Material | N35SH |
| Remanence | 1.23T | |
| Ferrite | Material | AC-12 |
| Remanence | 0.4T |
| Working Harmonics H [m,n,i,j,ia,ja] | PPN |
|---|---|
| H [1,0,−2,0,2,0] | |4Ns − Nr| |
| H [1,0,−1,0,0,0] | |2Ns − Nr| |
| H [1,0,0,0,−2,0] | Nr |
| H [1,1,1,1,0,2] | 2Ns + Nr |
| Parameters | Limits | |
|---|---|---|
| Upper Value | Lower Value | |
| Width of outer stator tooth, lost (mm) | 18 | 10 |
| Width of inner stator tooth, list (mm) | 10 | 6 |
| Outer stator slot opening, θoso (deg.) | 12 | 4 |
| Inner stator slot opening, θiso (deg.) | 12 | 4 |
| Height of NdFeB, hN (mm) | 5 | 3 |
| Height of Ferrite magnet, hf (mm) | 5 | 3 |
| Width of NdFeB, θN (deg.) | 25 | 17 |
| Width of Ferrite magnet, θf (deg.) | 18 | 15 |
| Outer stator yoke thickness, hosy (mm) | 6 | 4 |
| Inner stator yoke thickness, hisy (mm) | 5 | 3 |
| Outer stator tooth tip thickness hostt (mm) | 1 | 3 |
| Inner stator tooth tip thickness histt (mm) | 1 | 3 |
| Split ratio (Diso/Doso) | 0.65 | 0.55 |
| Parameter | Value |
|---|---|
| Outer diameter of outer/inner stator, Doso/Diso (mm) | 122/62.7 |
| Inner diameter of outer/inner stator, Dosi/Disi (mm) | 73.92/30 |
| Outer stator yoke thickness, hosy (mm) | 5.59 |
| Inner stator yoke thickness, hisy (mm) | 4.19 |
| Width of outer stator tooth, lost (mm) | 11.61 |
| Width of inner stator tooth, list (mm) | 7.87 |
| Outer stator slot opening, θoso (deg.) | 10.13 |
| Inner stator slot opening, θiso (deg.) | 11.93 |
| Height of Ferrite magnet, hf (mm) | 4.24 |
| Width of Ferrite magnet, θf (deg.) | 14.37 |
| Outer/inner air-gap length, δo/δi | 0.5/0.5 |
| Height of NdFeB, hN (mm) | 4.26 |
| Width of NdFeB, θN (deg.) | 11.95 |
| Stack length (mm) | 70 |
| Turns per coil of outer/inner stator | 89/24 |
| Number of outer/inner stator teeth | 6/6 |
| PPN of ferrite magnet in the outer stator | 12 |
| PPN of Rotor | 17 |
| Rotor iron pole number | 17 |
| Rated speed (r/min) | 300 |
| Item | DS-FMHMM | DS-VPMM | DS-FRPMM |
|---|---|---|---|
| Tavg (Nm) | 16.04 | 10.86 | 7.20 |
| Trip (%) | 3.17 | 2.50 | 2.24 |
| Machine volume (cm3) | 818.28 | 818.28 | 818.28 |
| Torque density (Nm/cm3) | 0.020 | 0.0133 | 0.0087 |
| Total PM volume (cm3) | 71.23 | 31.41 | 64.47 |
| PM utilization (Nm/cm3) | 0.23 | 0.346 | 0.113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Yang, X.; Wang, H.; Bai, X. Design and Analysis of a New Dual-Stator Hybrid Magnet Flux Modulation Machine. Actuators 2024, 13, 17. https://doi.org/10.3390/act13010017
Meng Y, Yang X, Wang H, Bai X. Design and Analysis of a New Dual-Stator Hybrid Magnet Flux Modulation Machine. Actuators. 2024; 13(1):17. https://doi.org/10.3390/act13010017
Chicago/Turabian StyleMeng, Yao, Xinyu Yang, Haitao Wang, and Xingzhen Bai. 2024. "Design and Analysis of a New Dual-Stator Hybrid Magnet Flux Modulation Machine" Actuators 13, no. 1: 17. https://doi.org/10.3390/act13010017
APA StyleMeng, Y., Yang, X., Wang, H., & Bai, X. (2024). Design and Analysis of a New Dual-Stator Hybrid Magnet Flux Modulation Machine. Actuators, 13(1), 17. https://doi.org/10.3390/act13010017





