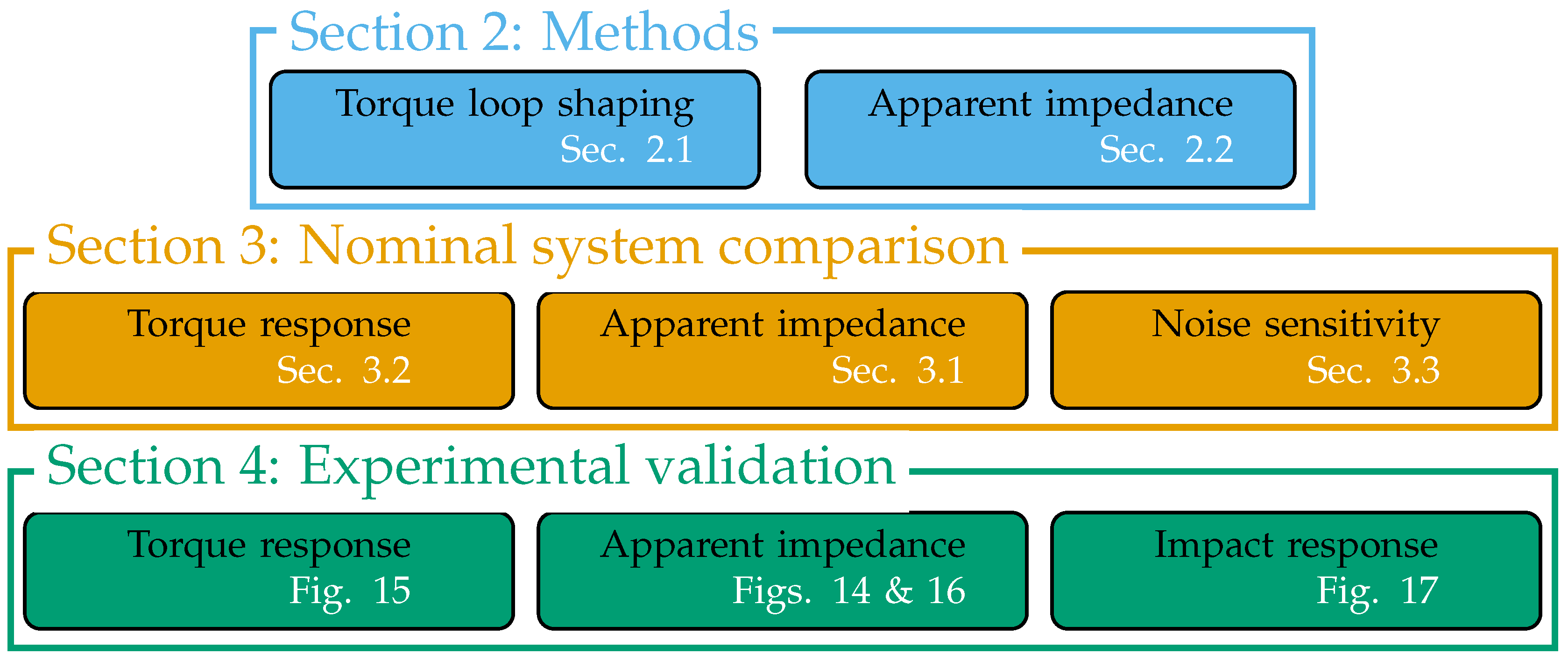
Evaluation and Comparison of SEA Torque Controllers in a Unified Framework
Abstract
1. Introduction
1.1. State of the Art
1.2. Our Approach
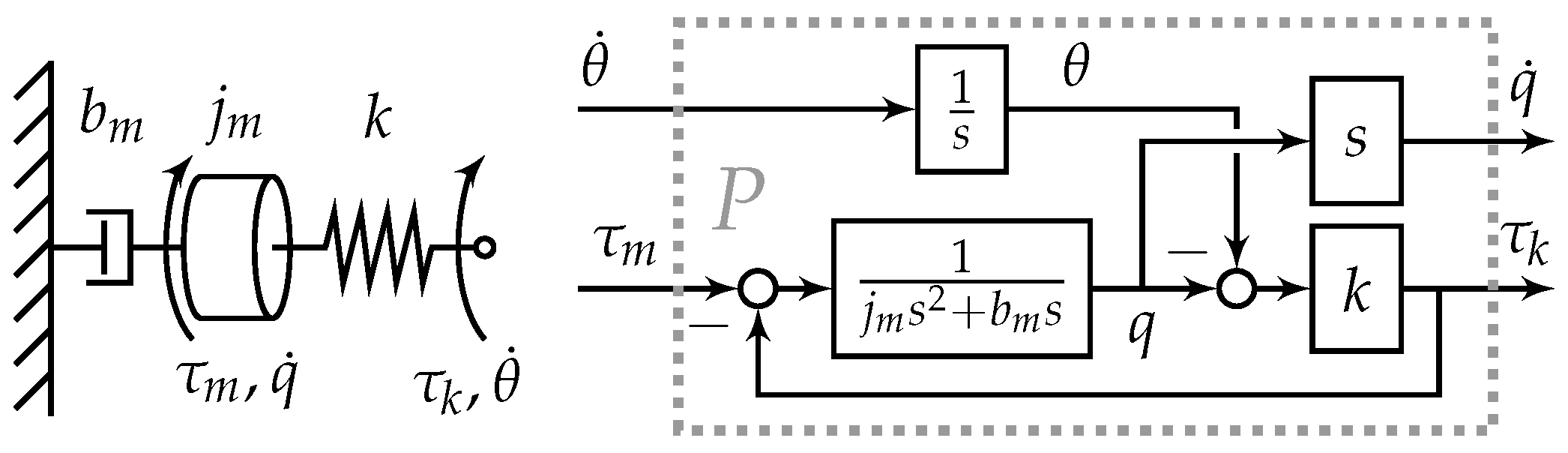
2. Methods
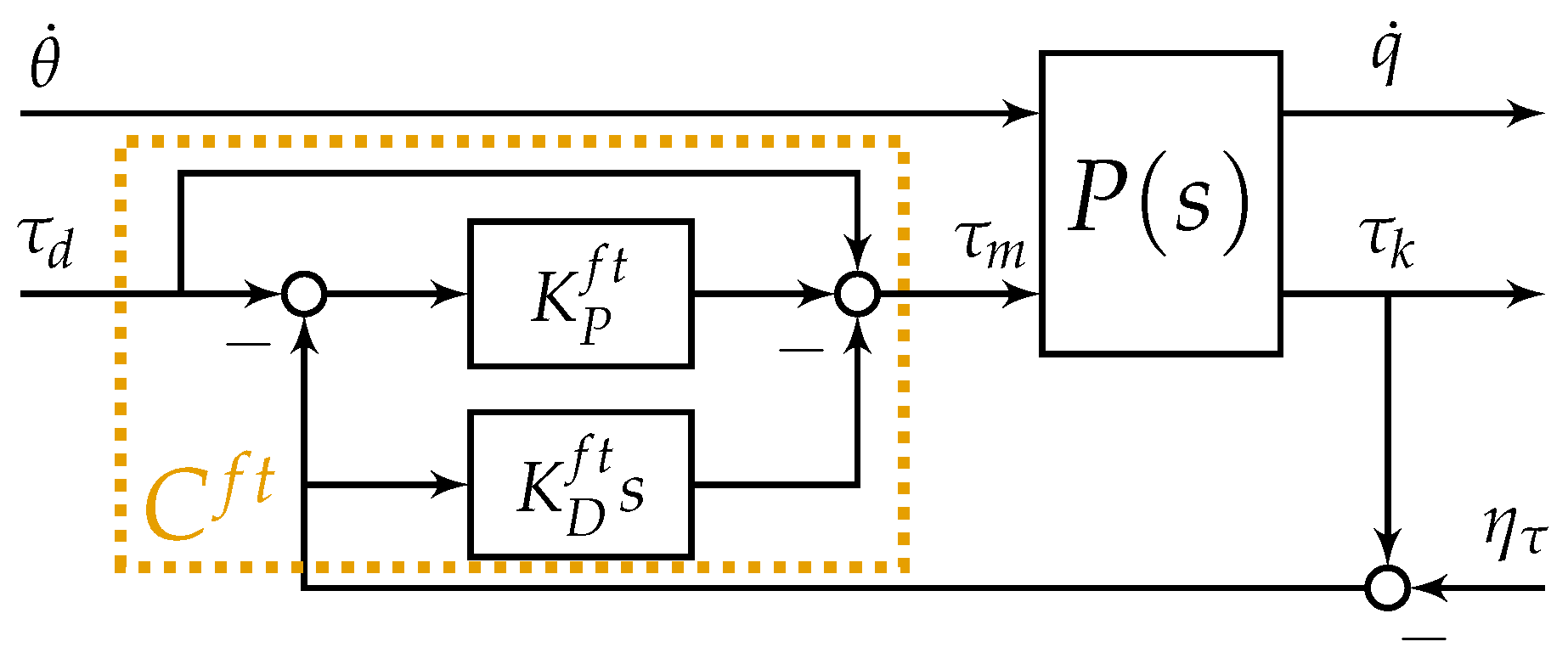
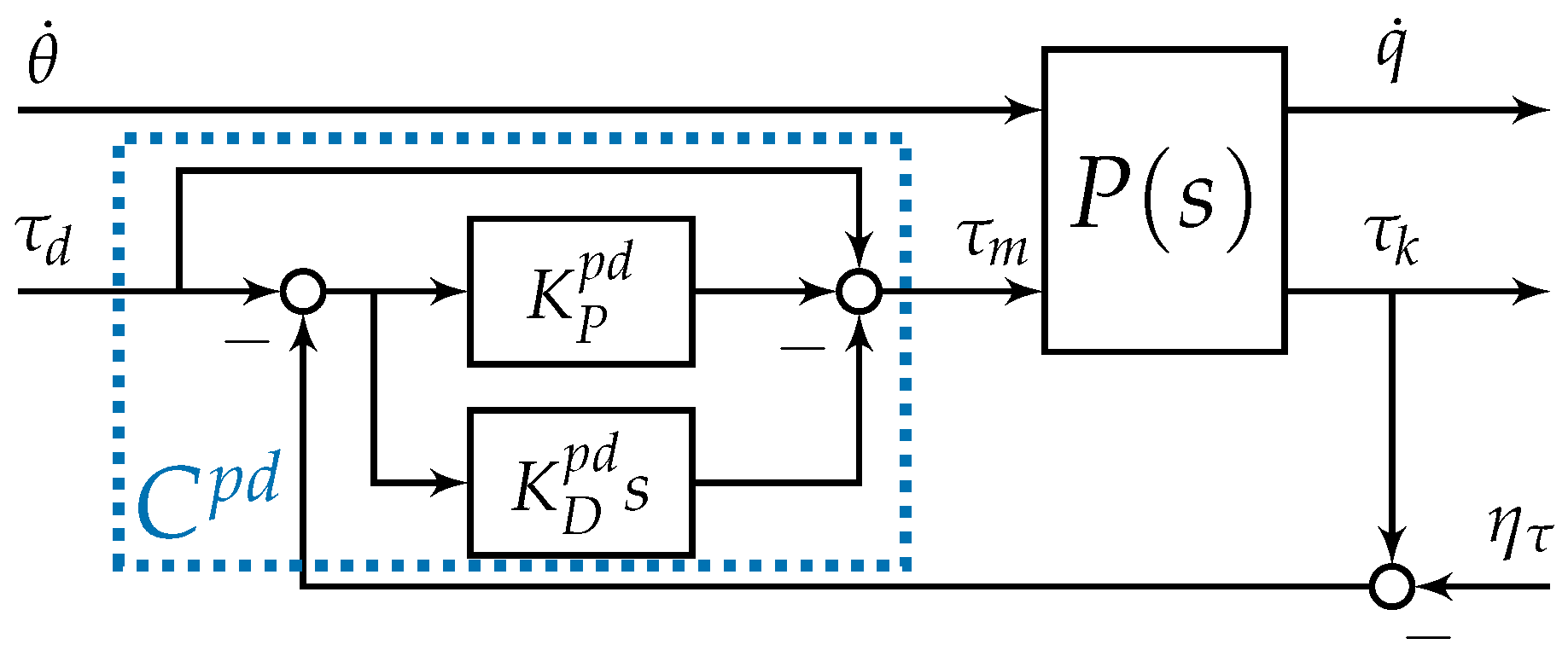
2.1. Shaping the Torque Transfer
2.1.1. Full State Feedback
2.1.2. Cascaded PID
2.1.3. PD Controller
2.1.4. MRAC
2.2. Shaping the Apparent Impedance
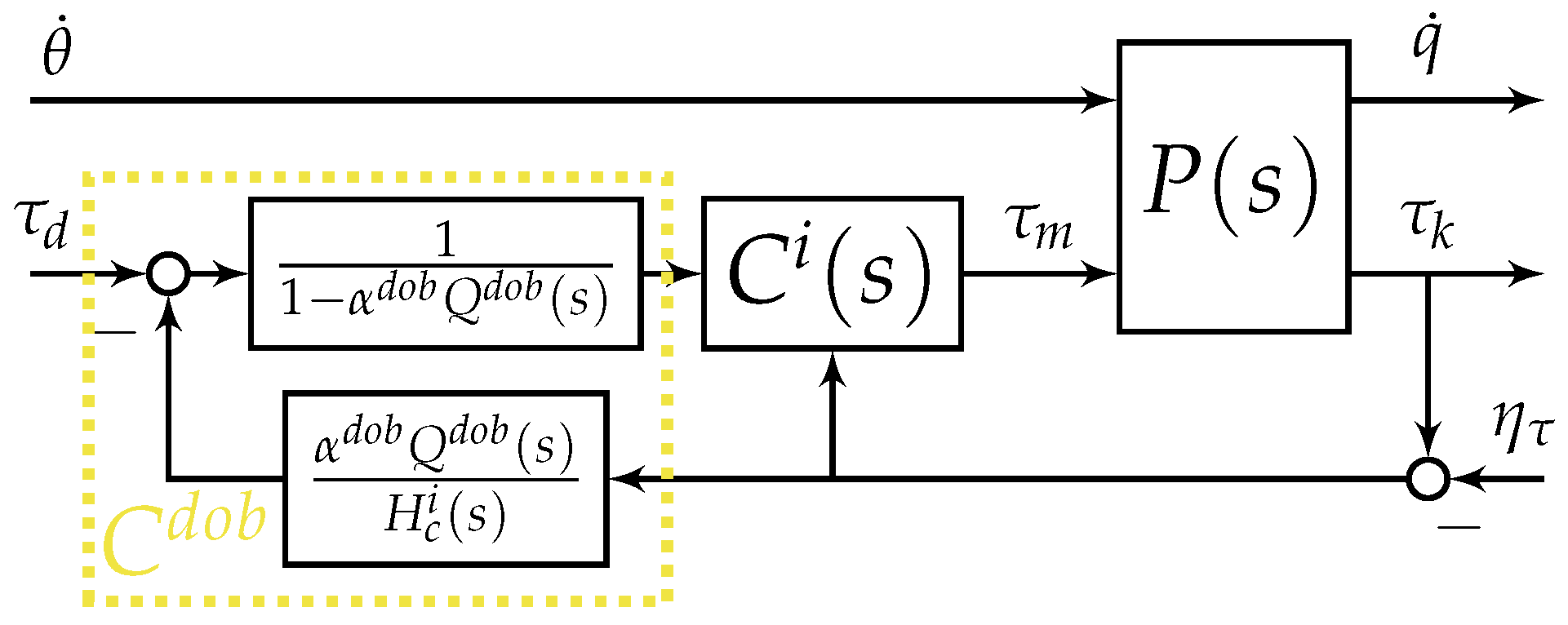
2.2.1. Disturbance Observer
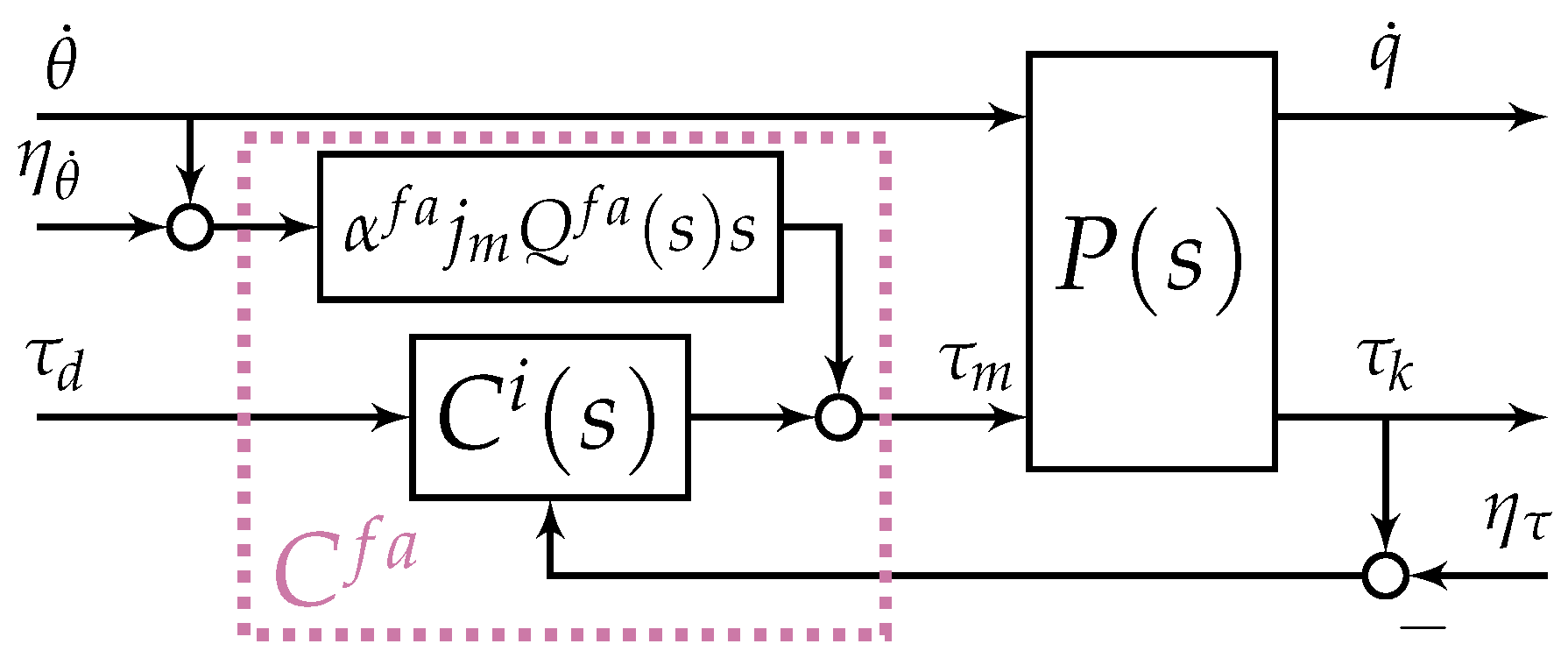
2.2.2. Acceleration Feedback
3. Nominal System Comparison
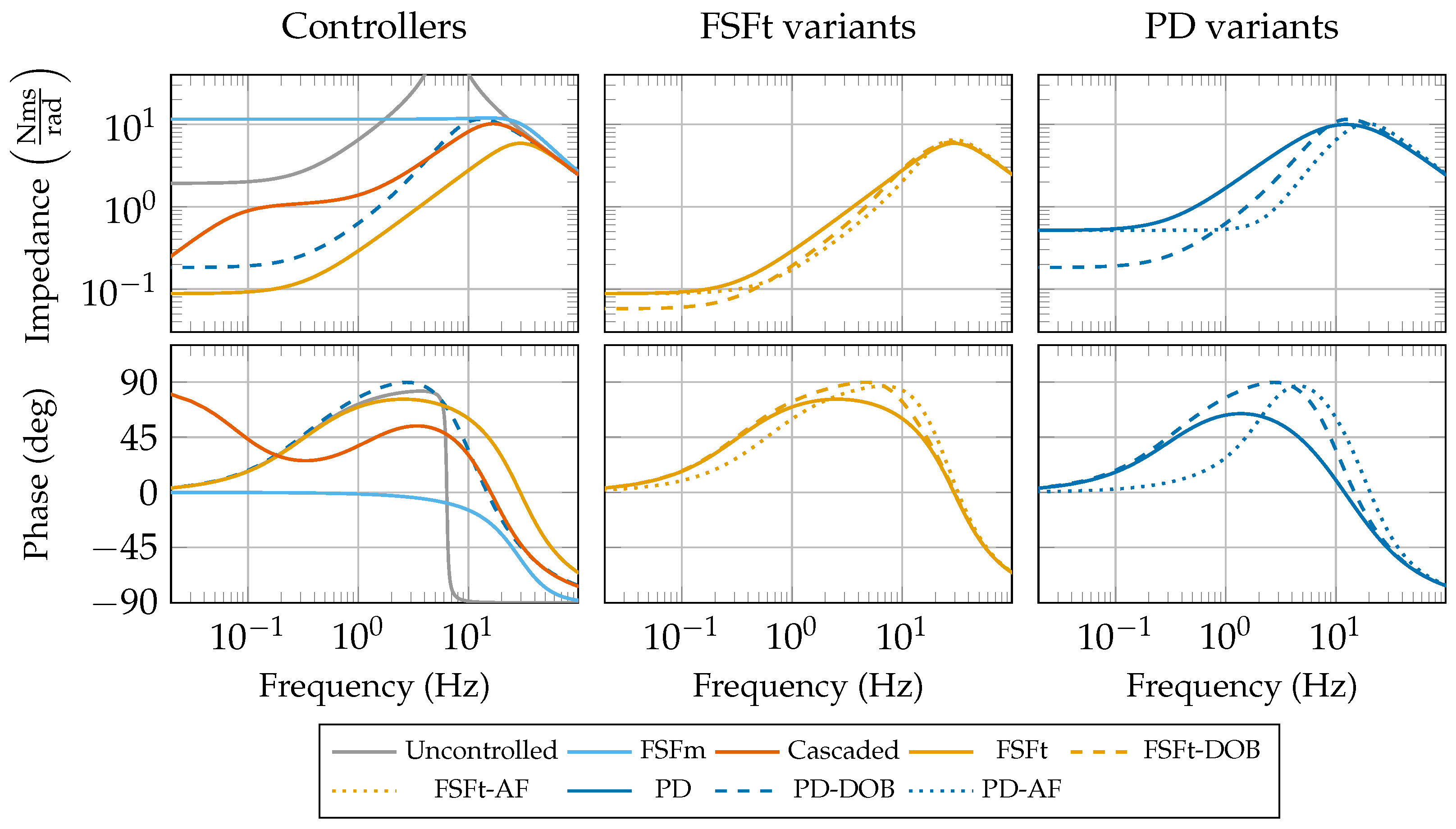
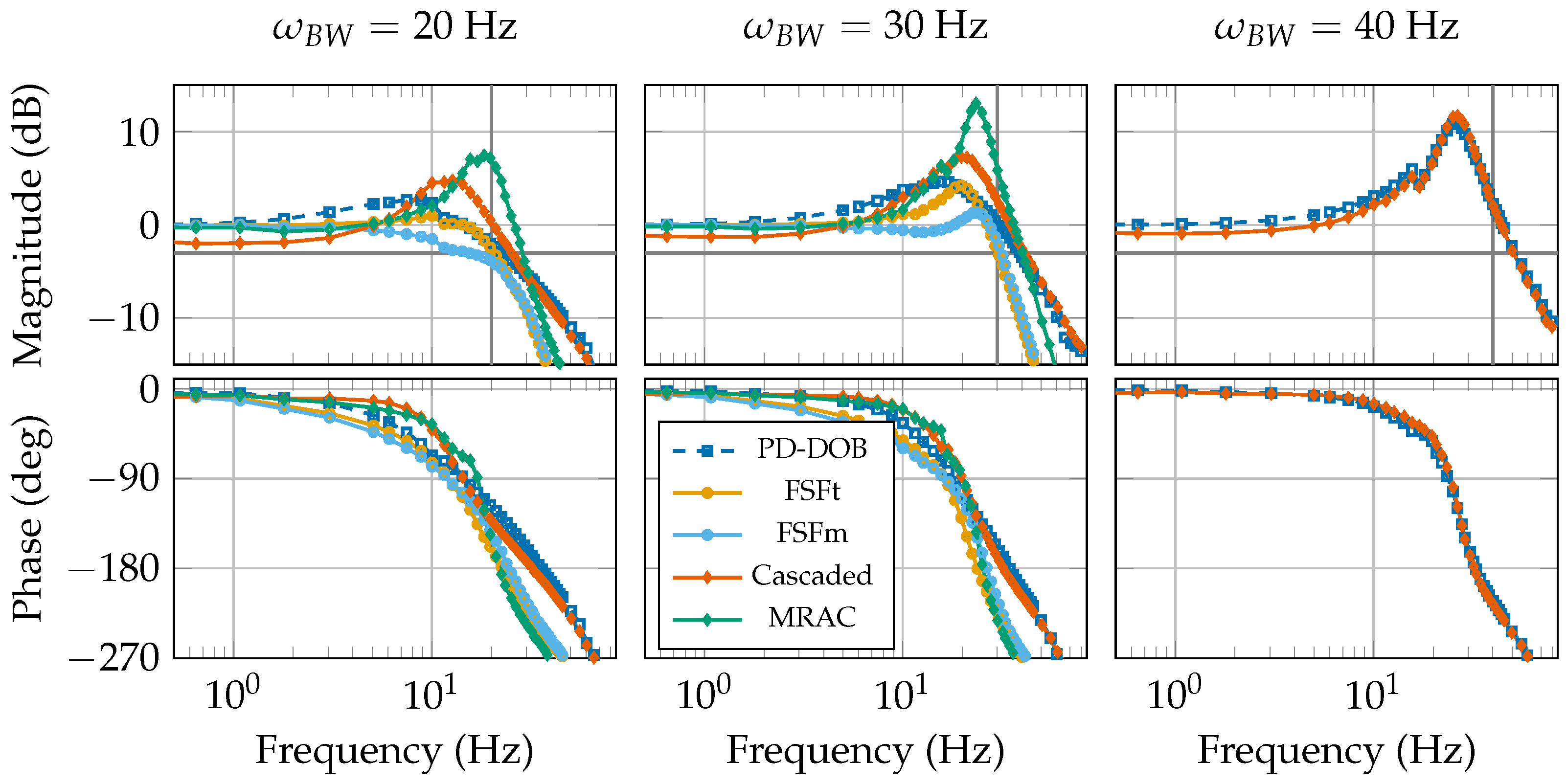
3.1. Torque Loop Shaping
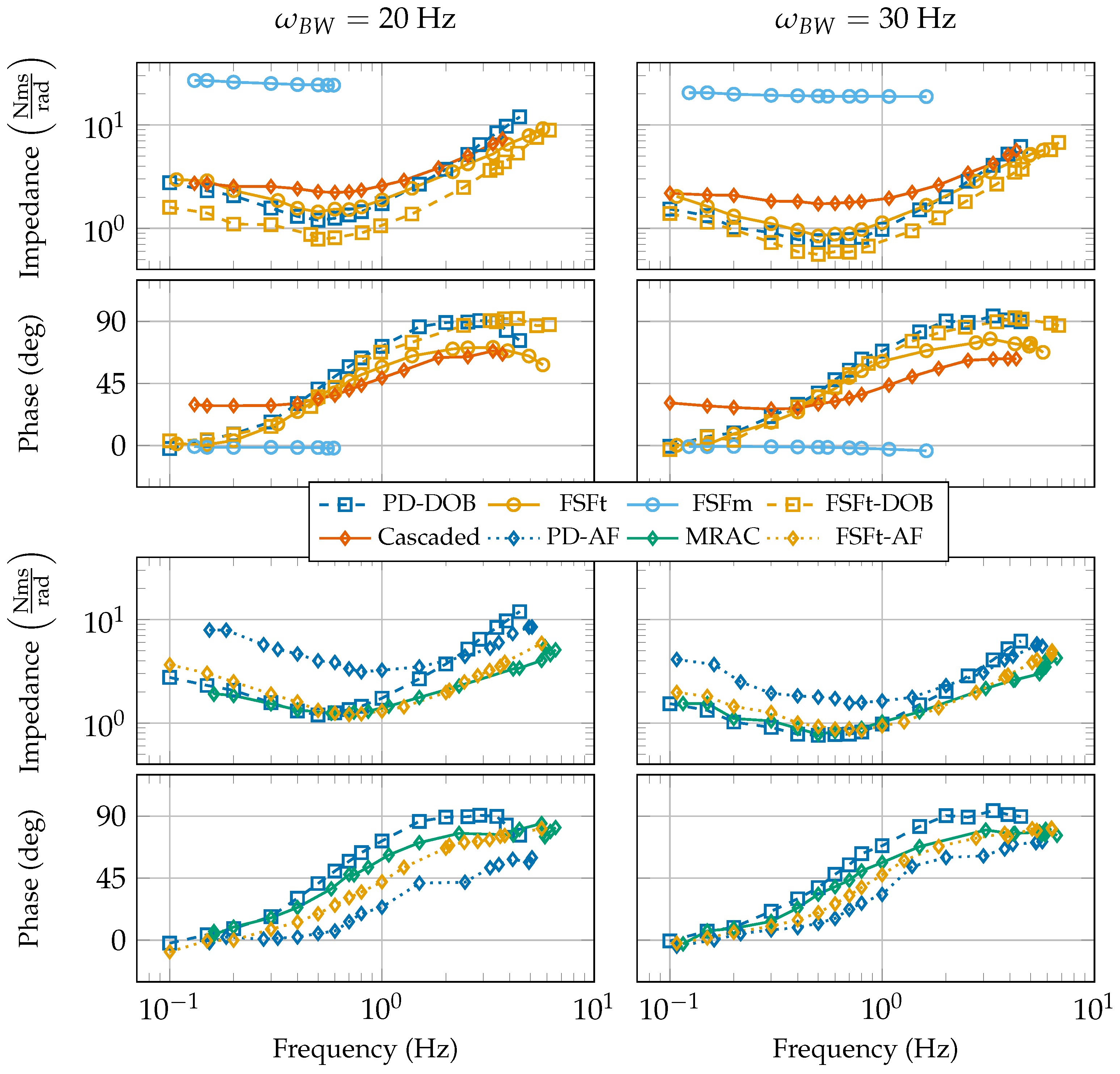
3.2. Apparent Impedance
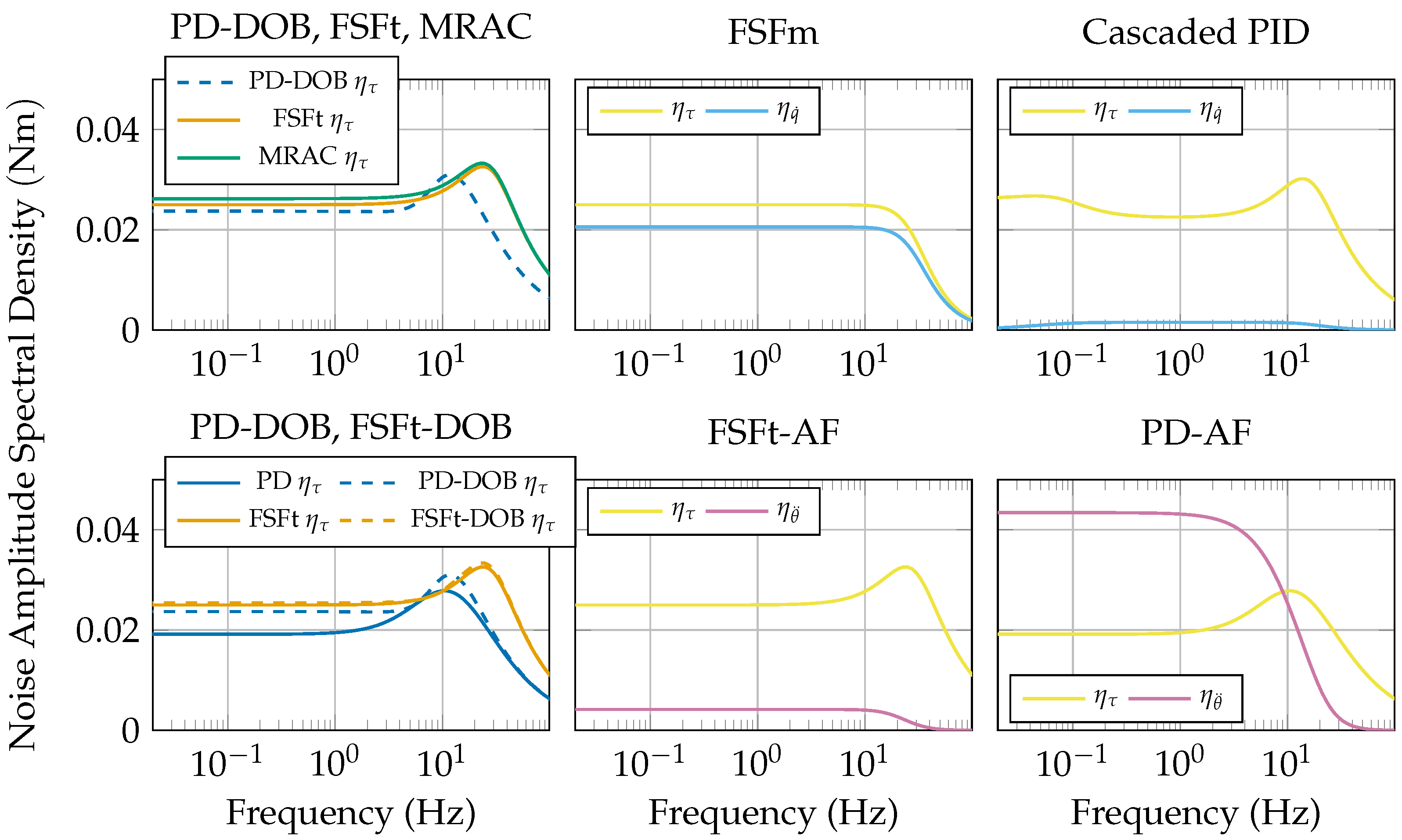
3.3. Noise Sensitivity
4. Experimental Methods
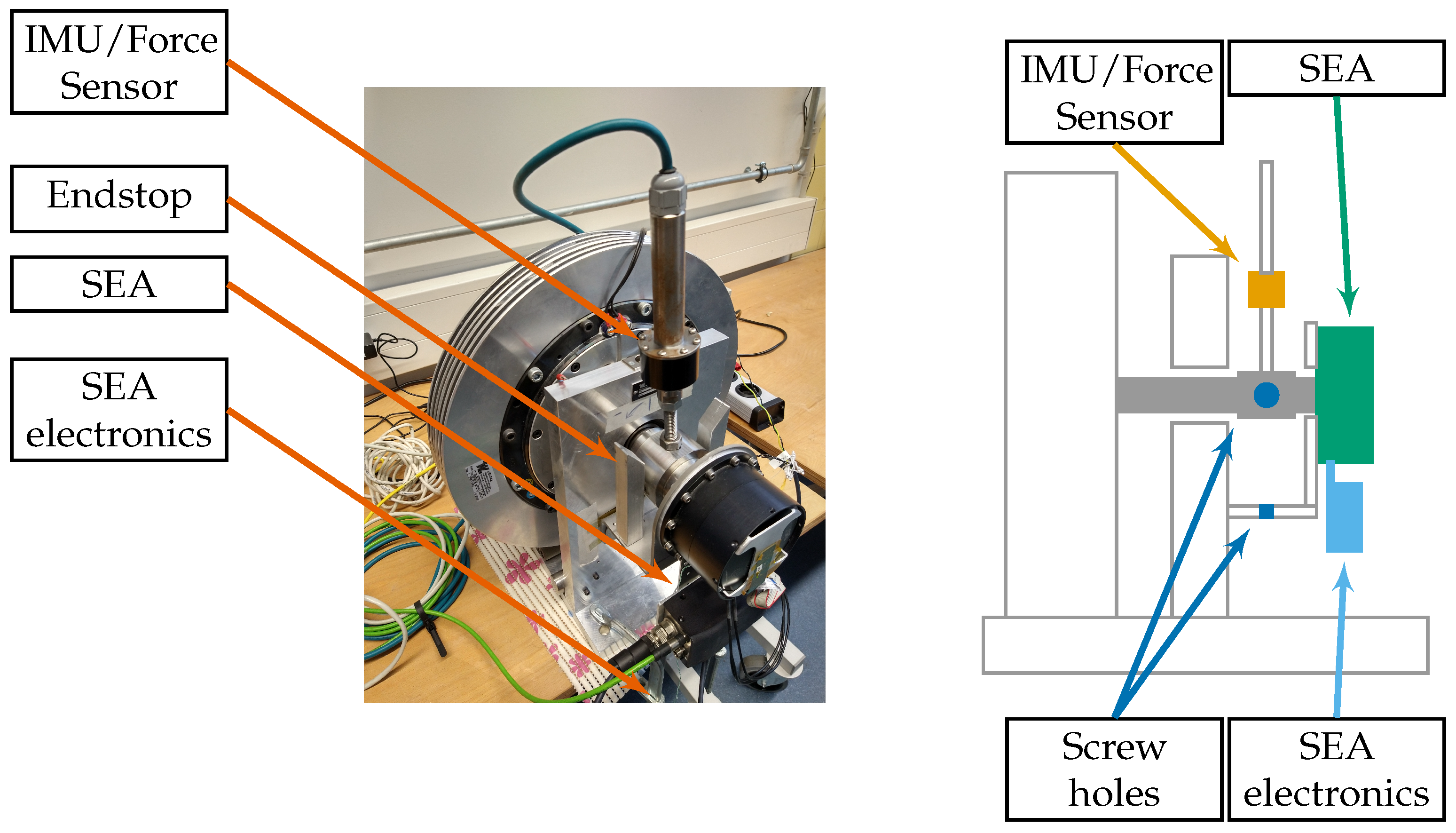
4.1. Setup
4.2. Controller Implementation
- Torque derivatives are filtered with a second order Butterworth filter with a cutoff frequency of 160 Hz.
- Motor velocity is unfiltered.
- Integrators are implemented as discrete leaky integrators with a linear leak rate of to avoid windup, and to allow identical integrator behavior across different controllers.
- Filters and reference models are discretized via the bilinear transform.
4.3. Identification Experiments
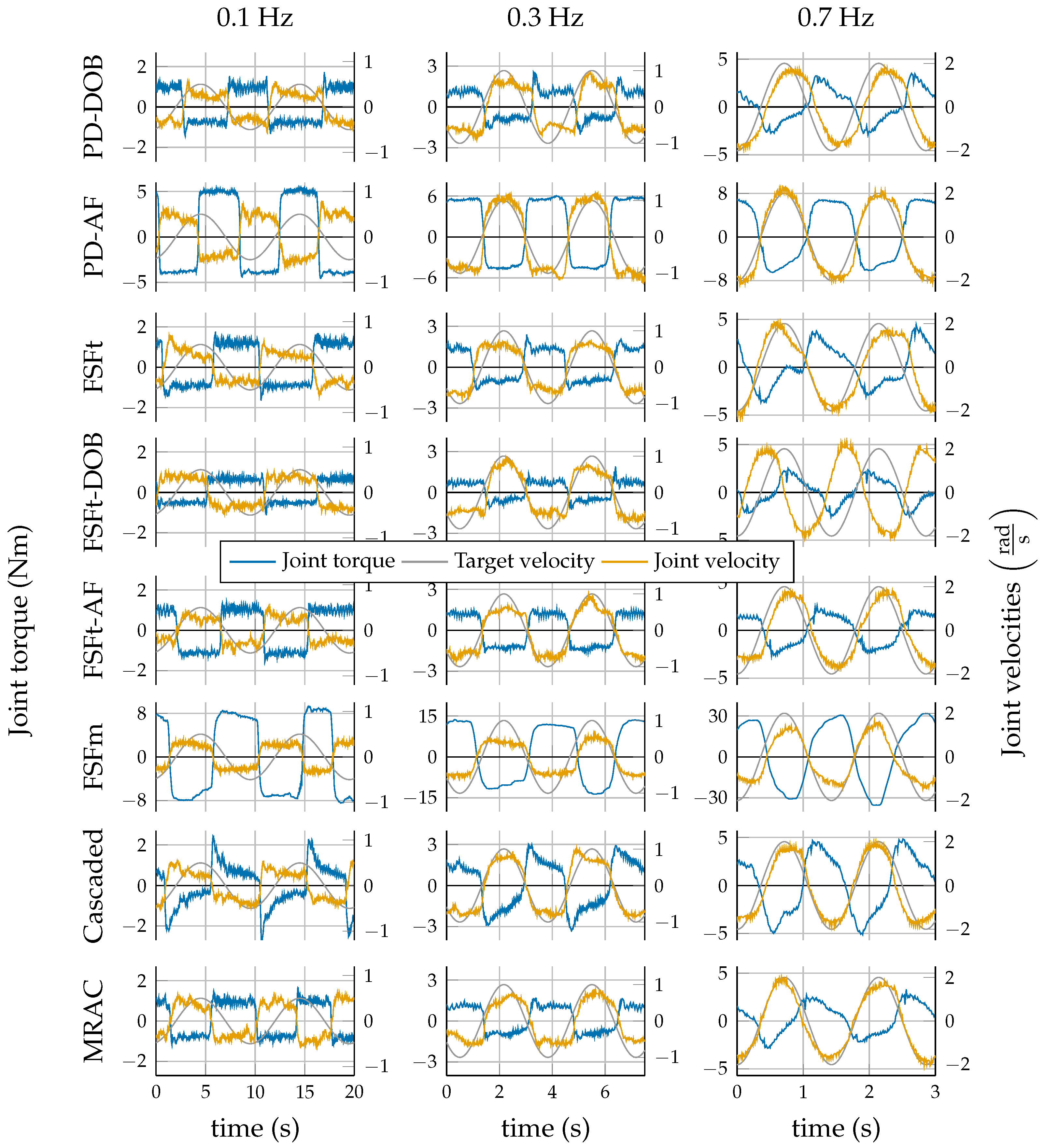
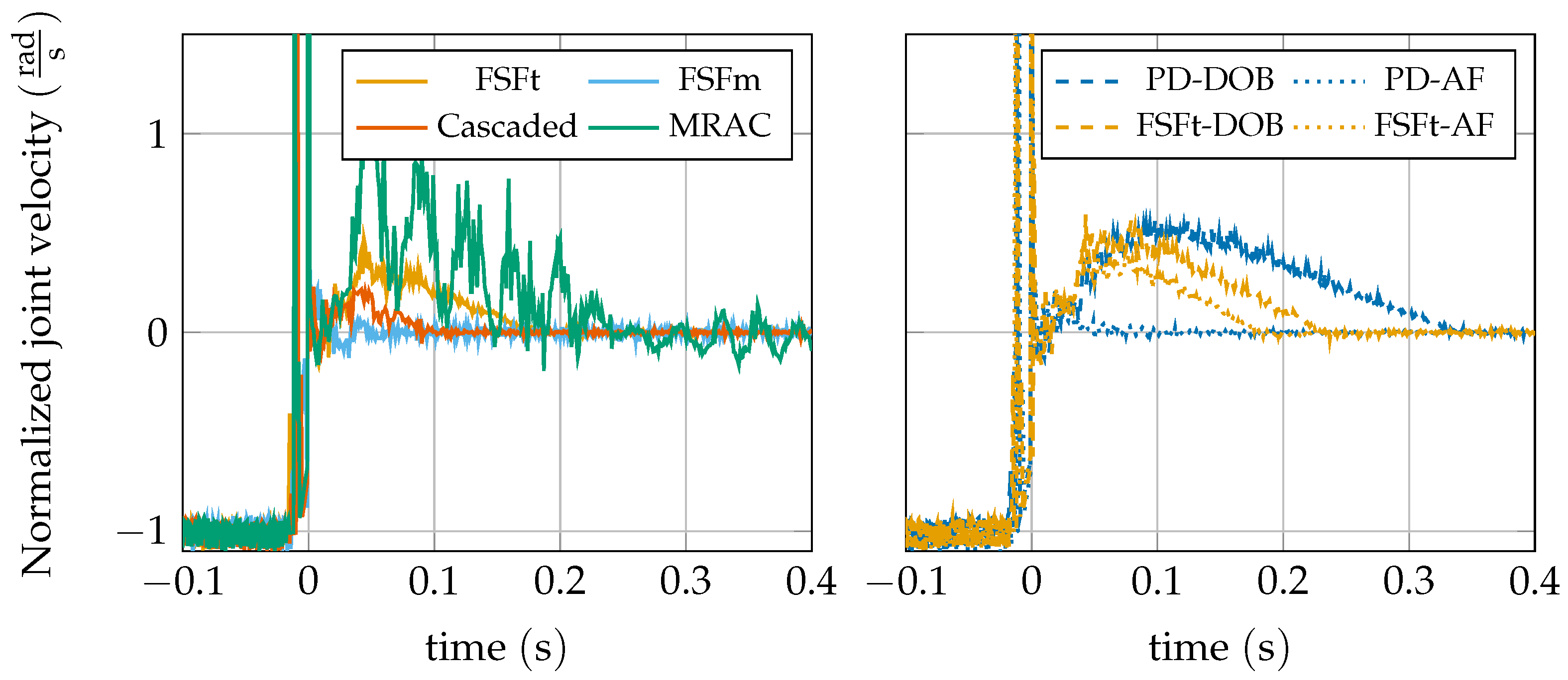
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Control Laws
Appendix A.1. FSFBm
Appendix A.2. MRAC
Appendix B. Derivations of Passivity Limits
Appendix B.1. Disturbance Observer
Appendix B.2. Acceleration Feedback
References
- Hopkins, M.A.; Ressler, S.A.; Lahr, D.F.; Leonessa, A.; Hong, D.W. Embedded joint-space control of a series elastic humanoid. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3358–3365. [Google Scholar]
- Radford, N.A.; Strawser, P.; Hambuchen, K.; Mehling, J.S.; Verdeyen, W.K.; Donnan, A.S.; Holley, J.; Sanchez, J.; Nguyen, V.; Bridgwater, L.; et al. Valkyrie: Nasa’s first bipedal humanoid robot. J. Field Robot. 2015, 32, 397–419. [Google Scholar] [CrossRef]
- Tsagarakis, N.G.; Morfey, S.; Cerda, G.M.; Zhibin, L.; Caldwell, D.G. Compliant humanoid coman: Optimal joint stiffness tuning for modal frequency control. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 673–678. [Google Scholar]
- Meijneke, C.; van Oort, G.; Sluiter, V.; van Asseldonk, E.; Tagliamonte, N.; Tamburella, F.; Pisotta, I.; Masciullo, M.; Arquilla, M.; Molinari, M.; et al. Symbitron Exoskeleton: Design, control, and evaluation of a modular exoskeleton for incomplete and complete spinal cord injured individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 330–339. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, L.; Meijneke, C.; Van Asseldonk, E.; Hoellinger, T.; Cheron, G.; Ivanenko, Y.; La Scaleia, V.; Sylos-Labini, F.; Molinari, M.; et al. Design and control of the MINDWALKER exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Witte, K.A.; Zhang, J.; Jackson, R.W.; Collins, S.H. Design of two lightweight, high-bandwidth torque-controlled ankle exoskeletons. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1223–1228. [Google Scholar]
- Pratt, G.A.; Williamson, M.M. Series elastic actuators. In Proceedings of the Proceedings 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 1, pp. 399–406. [Google Scholar]
- Robinson, D.W.; Pratt, J.E.; Paluska, D.J.; Pratt, G.A. Series elastic actuator development for a biomimetic walking robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No. 99TH8399), Atlanta, GA, USA, 19–23 September 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 561–568. [Google Scholar]
- Hutter, M.; Gehring, C.; Jud, D.; Lauber, A.; Bellicoso, C.D.; Tsounis, V.; Hwangbo, J.; Bodie, K.; Fankhauser, P.; Bloesch, M.; et al. Anymal-a highly mobile and dynamic quadrupedal robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 38–44. [Google Scholar]
- Carney, M.E.; Shu, T.; Stolyarov, R.; Duval, J.F.; Herr, H.M. Design and preliminary results of a reaction force series elastic actuator for bionic knee and ankle prostheses. IEEE Trans. Med. Robot. Bionics 2021, 3, 542–553. [Google Scholar] [CrossRef]
- Calanca, A.; Fiorini, P. A rationale for acceleration feedback in force control of series elastic actuators. IEEE Trans. Robot. 2018, 34, 48–61. [Google Scholar] [CrossRef]
- Lee, Y.S.; Chiao, K.W.; Lan, C.C. A hybrid impedance controller for series elastic actuators to render a wide range of stable stiffness in uncertain environments. IEEE Robot. Autom. Lett. 2021, 6, 739–746. [Google Scholar] [CrossRef]
- Chen, T.; Casas, R.; Lum, P.S. An elbow exoskeleton for upper limb rehabilitation with series elastic actuator and cable-driven differential. IEEE Trans. Robot. 2019, 35, 1464–1474. [Google Scholar] [CrossRef]
- Sensinger, J.W.; Weir, R.F.F. Improvements to series elastic actuators. In Proceedings of the 2006 2nd IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications, Beijing, China, 13–16 August 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–7. [Google Scholar]
- Vallery, H.; Ekkelenkamp, R.; Van Der Kooij, H.; Buss, M. Passive and accurate torque control of series elastic actuators. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 3534–3538. [Google Scholar]
- Wyeth, G. Demonstrating the safety and performance of a velocity sourced series elastic actuator. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3642–3647. [Google Scholar]
- Vallery, H.; Veneman, J.; Van Asseldonk, E.; Ekkelenkamp, R.; Buss, M.; Van Der Kooij, H. Compliant actuation of rehabilitation robots. IEEE Robot. Autom. Mag. 2008, 15, 60–69. [Google Scholar] [CrossRef]
- Tosun, F.E.; Patoglu, V. Necessary and sufficient conditions for the passivity of impedance rendering with velocity-sourced series elastic actuation. IEEE Trans. Robot. 2020, 36, 757–772. [Google Scholar] [CrossRef]
- Calanca, A.; Muradore, R.; Fiorini, P. Impedance control of series elastic actuators: Passivity and acceleration-based control. Mechatronics 2017, 47, 37–48. [Google Scholar] [CrossRef]
- Ott, C.; Albu-Schaffer, A.; Kugi, A.; Stamigioli, S.; Hirzinger, G. A passivity based cartesian impedance controller for flexible joint robots-part I: Torque feedback and gravity compensation. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings, New Orleans, LA, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2659–2665. [Google Scholar]
- Albu-Schäffer, A.; Ott, C.; Hirzinger, G. A unified passivity-based control framework for position, torque and impedance control of flexible joint robots. Int. J. Robot. Res. 2007, 26, 23–39. [Google Scholar] [CrossRef]
- Ragonesi, D.; Agrawal, S.; Sample, W.; Rahman, T. Series elastic actuator control of a powered exoskeleton. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3515–3518. [Google Scholar]
- Losey, D.P.; Erwin, A.; McDonald, C.G.; Sergi, F.; O’Malley, M.K. A time-domain approach to control of series elastic actuators: Adaptive torque and passivity-based impedance control. IEEE/ASME Trans. Mechatron. 2016, 21, 2085–2096. [Google Scholar] [CrossRef]
- Kong, K.; Bae, J.; Tomizuka, M. Control of rotary series elastic actuator for ideal force-mode actuation in human–robot interaction applications. IEEE/ASME Trans. Mechatron. 2009, 14, 105–118. [Google Scholar] [CrossRef]
- Paine, N.; Mehling, J.S.; Holley, J.; Radford, N.A.; Johnson, G.; Fok, C.L.; Sentis, L. Actuator control for the NASA-JSC valkyrie humanoid robot: A decoupled dynamics approach for torque control of series elastic robots. J. Field Robot. 2015, 32, 378–396. [Google Scholar] [CrossRef]
- Kim, M.J.; Werner, A.; Loeffl, F.C.; Ott, C. Enhancing joint torque control of series elastic actuators with physical damping. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1227–1234. [Google Scholar]
- Rampeltshammer, W.F.; Keemink, A.Q.; Van Der Kooij, H. An improved force controller with low and passive apparent impedance for series elastic actuators. IEEE/ASME Trans. Mechatron. 2020, 25, 1220–1230. [Google Scholar] [CrossRef]
- Kong, K.; Tomizuka, M. Nominal model manipulation for enhancement of stability robustness for disturbance observer-based control systems. Int. J. Control Autom. Syst. 2013, 11, 12–20. [Google Scholar] [CrossRef]
- Haninger, K.; Asignacion, A.; Oh, S. Safe high impedance control of a series-elastic actuator with a disturbance observer. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 921–927. [Google Scholar]
- Ahn, J.; Kim, D.; Bang, S.; Paine, N.; Sentis, L. Control of a high performance bipedal robot using viscoelastic liquid cooled actuators. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 146–153. [Google Scholar]
- Huo, W.; Alouane, M.A.; Amirat, Y.; Mohammed, S. Force control of SEA-based exoskeletons for multimode human–robot interactions. IEEE Trans. Robot. 2019, 36, 570–577. [Google Scholar] [CrossRef]
- Kong, K.; Bae, J.; Tomizuka, M. A compact rotary series elastic actuator for human assistive systems. IEEE/ASME Trans. Mechatron. 2011, 17, 288–297. [Google Scholar] [CrossRef]
- Oh, S.; Kong, K. High-precision robust force control of a series elastic actuator. IEEE/ASME Trans. Mechatron. 2016, 22, 71–80. [Google Scholar] [CrossRef]
- Lee, C.; Oh, S. Development, analysis, and control of series elastic actuator-driven robot leg. Front. Neurorobot. 2019, 13, 17. [Google Scholar] [CrossRef]
- Asignacion, A.; Haninger, K.; Oh, S.; Lee, H. High-stiffness Control of Series Elastic Actuators using a Noise Reduction Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 69, 8212–8219. [Google Scholar] [CrossRef]
- Shim, H.; Park, G.; Joo, Y.; Back, J.; Jo, N.H. Yet another tutorial of disturbance observer: Robust stabilization and recovery of nominal performance. Control Theory Technol. 2016, 14, 237–249. [Google Scholar] [CrossRef]
- Calanca, A.; Sartori, E.; Maris, B. Force control of lightweight series elastic systems using enhanced disturbance observers. Robot. Auton. Syst. 2023, 164, 104407. [Google Scholar] [CrossRef]
- Wan, H.; Chen, S.; Zhang, C.; Chen, C.Y.; Yang, G. Compliant Control of Flexible Joint by Dual-Disturbance Observer and Predictive Feedforward. IEEE/ASME Trans. Mechatron. 2023. [Google Scholar] [CrossRef]
- Calanca, A.; Fiorini, P. Understanding environment-adaptive force control of series elastic actuators. IEEE/ASME Trans. Mechatron. 2018, 23, 413–423. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, Z.; Yao, B. Decoupled torque control of series elastic actuator with adaptive robust compensation of time-varying load-side dynamics. IEEE Trans. Ind. Electron. 2019, 67, 5604–5614. [Google Scholar] [CrossRef]
- Zhang, J.; Cheah, C.C.; Collins, S.H. Experimental comparison of torque control methods on an ankle exoskeleton during human walking. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 5584–5589. [Google Scholar]
- Kenanoglu, C.U.; Patoglu, V. Passivity of series elastic actuation under model reference force control during null impedance rendering. IEEE Trans. Haptics 2022, 15, 51–56. [Google Scholar] [CrossRef]
- Ugurlu, B.; Sariyildiz, E.; Kansizoglu, A.T.; Ozcinar, E.C.; Coruk, S. Benchmarking torque control strategies for a torsion-based series elastic actuator. IEEE Robot. Autom. Mag. 2021, 29, 85–96. [Google Scholar] [CrossRef]
- Schrijver, E.; Van Dijk, J. Disturbance observers for rigid mechanical systems: Equivalence, stability, and design. J. Dyn. Syst. Meas. Control 2002, 124, 539–548. [Google Scholar] [CrossRef]
- Cerna, M.; Harvey, A.F. The Fundamentals of FFT-Based Signal Analysis and Measurement; Technical Report; Application Note 041; National Instruments: Austin, TX, USA, 2000. [Google Scholar]
- Lee, C.; Oh, S. Performance Analysis of Series Elastic Actuator Based on Maximum Torque Transmissibility. IEEE Trans. Control Syst. Technol. 2021, 30, 392–399. [Google Scholar] [CrossRef]




| Symbol | Definition |
|---|---|
| motor inertia and damping | |
| k | spring stiffness |
| motor and load position | |
| motor and interaction torque | |
| natural and target damping ratio | |
| natural and target frequency | |
| target bandwidth | |
| damping correction factor | |
| Feedback signal | |
| additive noise for signal n | |
| standard deviation of | |
| noisy signal n | |
| s | complex frequency |
| transfer functions | |
| Controller | |
| Gain | |
| controller gain x for controller i | |
| control law of controller i | |
| scaling gain for controller i | |
| closed loop torque transfer for controller n | |
| closed loop apparent impedance for controller n | |
| closed loop noise sensitivity for feedback signal n of controller i | |
| noise spectral density for feedback signal n of controller i | |
| Parameter | Value |
|---|---|
| Reflected motor inertia | |
| Reflected motor damping | |
| Spring stiffness k | |
| Target bandwidth | |
| Target damping ratio | |
| Target damping ratio | 1 |
| Torque sensor noise | |
| Motor velocity sensor noise | |
| Output acceleration noise | |
| Cascaded PID controller | |
| DOB variants | |
| Filter frequency | |
| Gain | |
| Gain | |
| Acceleration feedback variants | |
| Filter frequency | |
| Gain | |
| Gain | |
| Parameter | 20 Hz | 30 Hz | 40 Hz | Unit |
|---|---|---|---|---|
| 20 | 30 | 40 | Hz | |
| 1 | 1 | 1 | ||
| 15 | 19 | N/A | Hz | |
| 0.7 | 0.7 | N/A | ||
| 0.74 | 0.65 | N/A | ||
| 0.44 | 0.35 | N/A | ||
| 0.9 | 0.8 | N/A | ||
| 0.62 | 0.45 | N/A | ||
| Cascaded PID controller | ||||
| 1 | rad/Nms | |||
| rad/Nm | ||||
| 6 | 8 | Nms/rad | ||
| 3 | 4 | Nm/rad | ||
| MRAC | ||||
| 20 | 30 | 40 | Hz | |
| 0 | s | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rampeltshammer, W.; Keemink, A.; Sytsma, M.; van Asseldonk, E.; van der Kooij, H. Evaluation and Comparison of SEA Torque Controllers in a Unified Framework. Actuators 2023, 12, 303. https://doi.org/10.3390/act12080303
Rampeltshammer W, Keemink A, Sytsma M, van Asseldonk E, van der Kooij H. Evaluation and Comparison of SEA Torque Controllers in a Unified Framework. Actuators. 2023; 12(8):303. https://doi.org/10.3390/act12080303
Chicago/Turabian StyleRampeltshammer, Wolfgang, Arvid Keemink, Menno Sytsma, Edwin van Asseldonk, and Herman van der Kooij. 2023. "Evaluation and Comparison of SEA Torque Controllers in a Unified Framework" Actuators 12, no. 8: 303. https://doi.org/10.3390/act12080303
APA StyleRampeltshammer, W., Keemink, A., Sytsma, M., van Asseldonk, E., & van der Kooij, H. (2023). Evaluation and Comparison of SEA Torque Controllers in a Unified Framework. Actuators, 12(8), 303. https://doi.org/10.3390/act12080303






