Abstract
Currently, most control systems of the aero-engines possess a central controller. The core tasks for the control system, such as control law calculations, are executed in this central controller, and its performance and reliability greatly impact the entire control system. This paper introduces a control system design named Software Defined Control Systems (SDCS), which features a controller-decentralized architecture. In SDCS, a network composed of a set of nodes serves as the controller, so there is no central controller in the system, and computations are distributed throughout the entire network. Since the controller is decentralized, there is a need for decentralized control tasks. To address this, this paper introduces a method for designing decentralized control tasks using periodic linear iteration. Each node in the network periodically broadcasts its own state and updates its next-step state as a weighted sum of its current state and the received current states of other nodes in the network. Each node in the network acts as a linear dynamic controller and maintains an internal state through information exchange with other nodes. We modeled the decentralized controller and obtained the model of the entire control system, and the workload of each obtained decentralized control task is balanced. Then, we obtained a parameter tuning method for each decentralized controller node based on Linear Matrix Inequalities (LMI) to stabilize the closed-loop system. Finally, the effectiveness of the proposed method was verified through digital simulation.
1. Introduction
The traditional aero-engine control system uses a centralized control scheme, and the controller is connected to the analog sensors and actuator through cables and connectors. The controller executes most of the tasks of the control system, such as control law calculation, digital-to-analog conversion (D/A), analog-to-digital conversion (A/D), and so on, and the workload of the controller is large. Meanwhile, the centralized control scheme increases the difficulty and cost of upgrading and maintaining aero-engines throughout their entire life cycle. In addition, the presence of rotating components results in a large amount of cables within the system, which reduces the thrust-to-weight ratio of the aero-engines. To overcome the drawbacks of centralized control schemes, researchers have introduced the design concept of distributed control into the design of aero-engine control systems [1,2,3,4,5].
The Distributed Control System (DCS) first appeared in industrial process control [6,7], and it has been widely adopted in many fields [8,9,10]. The core design concept of the distributed control system for aero-engines is functional decentralization, which means that some functions of a centralized control system, such as signal conditioning and state monitoring, are executed by intelligent sensors and actuators, while the central controller focuses on the core tasks of the control system, such as control law calculation [11]. In a DCS, the controller, intelligent sensors, and intelligent actuators are connected through a common and standardized digital bus [12,13]. Compared to centralized control, DCS has the following advantages: (1) digital intelligent sensors and actuators reduce the control tasks of the central controller. (2) The digital bus reduces the weight of the aero-engine control system. (3) Modular design solutions lower the difficulty and cost of system upgrades and maintenance processes.
In addition to the above advantages, DCS also has some disadvantages:
- As the performance of aircraft and aero-engines gradually improve, the functionality and complexity of central control tasks also rapidly increase, which requires high-performance, multi-core microprocessors as controllers, and it places high demands on the thermal management system of the aviation engine.
- Due to the increasing functionality and complexity of core control tasks, the amount of software code in the control system rapidly increases, reducing the software reliability of the control system.
- Control tasks are centralized on the central controller. The central controller determines the performance of the aero-engine’s control system, and its damage or failure have a significant impact on the control system.
The analysis of the DCS for aero-engines mentioned above shows that the drawbacks in the system are caused by the central controller present in the system. The drawbacks of DCS suggest that a feasible scheme is to make the controllers in the control system decentralized. This involves using a network of decentralized nodes as the system controller, where multiple microprocessors work together to execute the control tasks of the central controller of DCS. As a result, the workload of each decentralized node is significantly reduced. With the decrease in workload, the software code volume for each node also decreases, thereby improving the software reliability of the control system. Additionally, several low-performance, but highly reliable microprocessors, can be used as decentralized controllers, which enhances the reliability of individual nodes.
The origin of the decentralized control design scheme dates back to the 1970s, and its concept was mainly proposed to solve the control problem of large-scale systems. Large-scale systems are characterized by extensive spatial distribution, numerous external signals, or dynamic changes in control structure. The core problem is that the control system is too large, and the control problem is too complex [14]. It is generally difficult to achieve control objectives by using more powerful microprocessors and larger storage space for large-scale systems. Due to the characteristics of large-scale systems, it is usually necessary to analyze and process the controlled plants, divide the system control problems into independent sub-problems, and handle signal delays caused by large spaces [15]. Distributed control in the industrial process control field adopts this design concept. This includes the later network control systems (NCS) and wireless networked control systems (WNCS). In WNCS, wireless communication is used to transmit data between system components. Compared with wired communication, wireless communication has its advantages and disadvantages. Its advantages include flexibility in installation, easy configuration, and strong adaptability; disadvantages include communication delays, data packet loss, etc. Ref. [16] conducted a study on the decentralized control system for the autonomous guided vehicles (AGVs) path planning problem, proposing two decentralized control methods to solve the AGV control problem: task allocation for AGVs through consensus method and path planning coordination through decentralized control strategy. In this design scheme, the microprocessors of several vehicles form the controller for the AGV problem, specifically targeting path optimization in a large spatial range. However, for each vehicle, there still exists a central controller in its control system. Ref. [17] researched the decentralized control of automation systems, such as smart factories and smart cities. In addition to data related to control tasks, there is also data interaction, such as images and voices, resulting in high communication requirements for the system. Inspired by concepts, such as software-defined networking (SDN), a decentralized data interaction control method was designed for large space and large data flow systems through extending Lyapunov drift-plus-penalty (LDP) control to a new queuing system to adjust the data flow within the system. Ref. [18] studied the decentralized control problem of two coupled power systems, including wind turbines and diesel generators. In this paper, the system was not decoupled and treated as a whole, and a decentralized controller was designed consisting of two PI-lead controllers. This scheme mainly focused on the research of PI controllers and parameter tuning, but the application of this scheme is limited for cases where the control effect of some PI controllers is poor. Ref. [19] proposed a decentralized control scheme for aero-engines, which replaced the central controller in traditional aero-engine control systems with multiple controllers to control different subsystems of the aero-engine. However, in this scheme, the controllers are fixedly mapped to the subsystems, and this means that there exists a central controller for each subsystem, and the control system structure is relatively inflexible. In the aforementioned studies, each decentralized controller can independently complete specific control tasks.
Ref. [20] proposed a controller decentralized design method, namely, the Software-Defined Control System (SDCS). In SDCS, the network composed of decentralized nodes serves as the controller to execute control tasks, such as control law execution. Therefore, the control tasks executed by the decentralized nodes are also decentralized, and each decentralized control task is a part of the core control tasks. The core control tasks are the sum of these decentralized control tasks in a specific way, no individual decentralized node can complete the system control task alone. The aero-engine is a safety-critical system that requires high reliability of the control system. When applying SDCS to the aero-engine control system, highly reliable but low-performance microprocessors should be used as decentralized nodes. This requires that the workload and software code volume of each decentralized control task are low, and complex control functions need to be executed.
The contributions of this paper are as follows. A linear iterative-based decentralized design scheme for control tasks was introduced. In this scheme, a network composed of several decentralized nodes act as the controller to undertake the system control task. Each decentralized node broadcasts its own state information to other decentralized nodes in each cycle period. Other nodes receive the broadcasted state information, and when all decentralized nodes have completed broadcasting their state information, all nodes update their own states as a weighted sum of their current state and the received states from other nodes. Therefore, each task node can act as a small dynamic controller. Through the linear iterative process, a model of the decentralized controller was constructed, which obtained the task executed on each decentralized node and the model of the entire control system. Due to the controller being located in the forward path and the linear iterative process introducing new internal state variables, conventional state feedback or output feedback design schemes cannot be used for decentralized controller node parameter tuning. Additionally, since the parameters with respect to the Lyapunov condition are nonlinear, conventional Lyapunov methods and LMI methods cannot be directly applied to parameter tuning of decentralized controller nodes. A parameter tuning method for decentralized controller nodes based on LMI was presented for the designed decentralized control task to ensure that the control system is Schur stable.
The remainder of this paper is organized as follows.
Section 2 describes a linear model for aero-engines. Section 3 presents the structure of the Software Defined Control System for aero-engines and a periodic linear iterative-based decentralized controller implementation scheme, along with control system modeling. Section 4 introduces a parameter tuning method for the controller based on LMI. Section 5 conducts simulation verification of the designed scheme. Section 6 is the final chapter of this paper, which summarizes and discusses the future outlook.
2. Aero-Engine Model
The mathematical model of aero-engines is crucial for the design of aero-engines control systems. As aero-engines are complex, time-varying, and strongly nonlinear systems, their mathematical models should be nonlinear [21,22,23,24]. The current controllers are designed based on linear systems for aero-engines [25,26]. The decentralized controller proposed later in this paper is designed based on a periodic linear iterative scheme and is linear, hence requiring a linear model of the aero-engines.
The modeling methods for aero-engines generally include two types: identification method and analytical method. The identification method requires corresponding experimental conditions, has high costs, and some of its algorithms have large computational consumption. Moreover, the resulting model may lose certain characteristics of the engine. The analytical method is based on the principles of aero-engines to build models. Firstly, the components of the aero-engines are modeled; then, a series of nonlinear equations that describe the working process of the aero-engines by following the aerodynamic and thermodynamic principles during their operation are utilized to obtain the mathematical model of the aero-engines [27,28].
In this section, we analyze the case of a turbofan engine using the method described in Refs. [27,28]. This section first introduces the nonlinear model of turbofan engines and then describes the linearization method for the nonlinear model of turbofan engines.
2.1. Nonlinear Model of Turbofan Engines
In this sub-section, the models of various components of turbofan engines are presented, including the inlet, fan, compressor, combustor, turbine, bypass duct, mixer, and exhaust nozzle.
- (1)
- Intake
When air enters the aero-engines, it first flows through the intake. The intake’s inlet parameters are:
When ,
When ,
where; and are the total temperature and the total pressure at the inlet of the intake, respectively.
- (2)
- Fan
The inlet parameters of aero-engines fan are:
where; and are the total temperature and the total pressure at the inlet of the fan, respectively, is Mach number, is the total pressure recovery coefficient of the intake, and is the air adiabatic index.
The outlet parameters of aero-engines fan are:
where; and are the total temperature and the total pressure at the outlet of the fan, respectively, is the air adiabatic index, is the fan pressure ratio, and is the efficiency of the fan.
- (3)
- Compressor
The inlet parameters of aero-engines compressor are:
where; and are the total temperature and the total pressure at the inlet of the compressor, respectively, is the total pressure recovery coefficient of the fan.
The outlet parameters of aero-engines compressor are:
where; and are the total temperature and the total pressure at the outlet of the compressor, respectively, is the pressure ratio of the compressor, is the efficiency of the compressor, and is the air adiabatic index.
- (4)
- Combustion chamber
According to the energy conservation law, the simplified energy balance equation for the combustion chamber is:
where; is the temperature at the outlet of the combustion chamber, is the fuel flow, is the calorific value of the fuel, is the combustion efficiency, is the air flow at the inlet of the combustion chamber, and is the specific heat capacity of air at constant pressure. The outlet pressure of the combustion chamber can be calculated using the above equation.
where; is the pressure at the outlet of the combustion chamber, and is the total pressure recovery coefficient of the combustion chamber.
- (5)
- High-pressure turbine
The outlet parameters of aero-engines high-pressure turbine are:
where; and are the total temperature and the total pressure at the outlet of the high-pressure turbine, respectively, is the gas flow of the high-pressure turbine, is the proportion coefficient of the high-pressure compressor bleed air used to cool the high-pressure turbine, is the total flow of added air, is the outlet air flow of the high-pressure turbine, is the high-pressure turbine pressure ratio, is the efficiency of the high-pressure turbine, and is the gas adiabatic index.
- (6)
- Low-pressure turbine
The outlet parameters of aero-engines low-pressure turbine are:
where; and are the total temperature and the total pressure at the outlet of the low-pressure turbine, respectively, is the gas flow converted by the high-pressure turbine, and is the inlet temperature of the low-pressure turbine, which is approximately equals to the outlet temperature of the high-pressure turbine . is the inlet pressure of the low-pressure turbine, which is approximately equals to the outlet pressure of the high-pressure turbine . is the proportion coefficient of the high-pressure compressor bleed air used to cool the low-pressure turbine, is the outlet air flow of the low-pressure turbine, is the low-pressure turbine pressure ratio, is the efficiency of the low-pressure turbine, and is the gas adiabatic index.
- (7)
- Bypass duct
The outlet parameters of aero-engines bypass duct are:
where; and are the total temperature and the total pressure at the outlet of the bypass duct, respectively, and is the total pressure recovery coefficient of the bypass duct.
- (8)
- Mixer
The gas flow at the outlet of the mixer is the sum of the air flow at the outlet of the bypass duct and the gas flow at the outlet of the low-pressure turbine, let denotes the total pressure recovery coefficient of the mixer, then the physical parameters at the outlet of the mixer are:
where: , , and are the specific enthalpy of the gas at the outlet of the low-pressure turbine, air at the outlet of the bypass duct, and gas at the outlet of the mixer, respectively. From , it is easy to obtain the temperature at the outlet of the mixer.
- (9)
- Nozzle
The outlet parameters of aero-engines nozzle are:
where; are the pressure at the outlet of nozzle, is the sectional area of the nozzle, is the state coefficient of the nozzle, refers to the function related to the characteristics of the bypass duct and the core duct, is the available pressure drop of the nozzle, and denotes the standard atmospheric pressure.
2.2. Common Working Equations
In this paper, the high-pressure turbine and high-pressure compressor form the high-pressure rotor in the turbofan engine. The high-pressure compressor is driven by the high-pressure turbine. The low-pressure turbine and fan form the low-pressure rotor. After passing through the inlet duct and fan, the gas flow is divided into two parts, with one entering the bypass duct and the other entering the core flow. Based on the flow rate, pressure and power balance between each engine component and the principle of constant rotational speed, the following common working equation can be obtained.
- (1)
- Power balance equation of the high-pressure rotor:
When the aero-engine is in stable state, , and ignore the power lost by transmission friction force , that Equation (14) is simplified into:
- (2)
- Power balance equation of the low-pressure rotor:
When the engine is in a stable state, . Ignoring the power loss caused by transmission friction, a simplified power balance equation for the low-pressure rotor can be obtained, similar to that of the high-pressure rotor.
where; is the power of low-pressure turbine, and is the power of low-pressure compressor.
- (3)
- Flow balance equation of the fan:
After passing through the fan, the gas is divided into two parts: one enters the bypass duct and the other enters the high-pressure compressor. Ignoring loss of gas flow, we have:
where; denotes the air flow from the fan, denotes the air flow into the high-pressure compressor, and denotes the air flow into bypass duct.
- (4)
- Flow balance equation of the high-pressure turbine:
The gas flow of the high-pressure turbine satisfies the following equation.
where; denotes the air flow into the high-pressure turbine, denotes the air flow from the high-pressure compressor, and denotes the fuel flow.
- (5)
- Flow balance equation of the low-pressure turbine:
The air flow at the inlet of the low-pressure turbine is equal to the air flow at the outlet of the high-pressure gas turbine , then:
where; is the proportion coefficient of the high-pressure compressor bleed air used to cool the high-pressure turbine, and is the total air flow into the high-pressure turbine.
- (6)
- Flow balance equation of the nozzle:
The gas flow of the nozzle satisfies the following equation.
where; is the gas flow at the low-pressure turbine outlet, and is the gas flow into the bypass duct.
2.3. Linearization of Nonlinear Models
The current design of control systems is mainly linear, so it is necessary to obtain a linear model of aero-engines. Aero-engines have strong non-linear characteristics. The common method is to select several operating points within the flight envelope and establish a linear model at these points, thus obtaining a segmented linear model of the aero-engine [29].
The partial derivative method is a common method for obtaining the linear model of aero-engines [30]. This method first perturbs a given state variable with a small disturbance, while keeping all other control variables and state variables constant. The partial derivatives of the state variables with the perturbation are then calculated to obtain the state matrix and output matrix of the state space model of the aero-engine. Then, a small perturbation is given to a given control variable, while keeping all other control variables and all state variables constant. The input matrix of the state space model is obtained by taking the partial derivatives of the control variable with the perturbation. This method only has theoretical significance because most state variables and control variables are coupled, and it is difficult to change only a single state variable or control variable without affecting other state variables or control variables. This leads to large modeling errors in this method.
This section briefly introduces the fitting method of linearization for aero-engines [31]. Firstly, a small perturbation state variable model of the aero-engine is obtained based on the selected state variables, control variables, and output variables. The linear dynamic response is calculated by giving a small step input to each control variable. Similarly, the nonlinear dynamic response is obtained by giving the same step input to the control variables of the nonlinear model of the aero-engine. Using the nonlinear dynamic response data as a reference, the matrices in the linear model are fitted to make the linear dynamic response data as close as possible to the nonlinear dynamic response data, thus obtaining the linear model of the aero-engine.
Here, taking the bivariate state-space model of aero-engines as an example, the state-space model is given below:
where; the state variables are selected as the low-pressure rotor speed and high-pressure rotor speed , the output variables are selected as the low-pressure rotor speed and the turbine pressure ratio , the control variables are selected as the fuel flow , and the area of the nozzle . That is, , , and .
Let,
From the selected output variables and state variables, , .
Giving a small step to the fuel flow while keeping the nozzle area constant, then:
where; and are the eigenvalues of the state matrix .
At the same steady-state point, by keeping the nozzle area and fuel flow constant, respectively, small steps are applied to the nozzle area and fuel flow to obtain the component-level nonlinear model’s small step response data for aero-engines.
Linear and nonlinear models are given the same amplitude of control variable step at the same steady-state point; the target is to make the linear and nonlinear dynamic responses as close as possible. By establishing and fitting the equation group, the state–space model of aero-engines at that steady-state point can be obtained.
3. Aero-Engines’ Linear Iterative Controller
3.1. Software Defined Control Systems of the Aero-Engines
Ref. [32] proposed the Software Defined Control Systems (SDCS) for aero-engines. The SDCS for aero-engines is based on the DCS for aero-engines, and it has been proposed alongside advancements in computer technology, communication technology, sensor technology, data storage technology, and other related support technologies. First, a brief introduction to the DCS for aero-engines will be provided. The DCS for aero-engines was developed based on a centralized control system. In the centralized control system for aero-engines, the controller is connected to the engine’s sensors, actuators, and other devices via cables. These devices do not have signal processing or control capabilities and interact with the controller through cables. The controller undertakes all control functions of the control system, including signal acquisition and processing, control law calculation, and control signal output. The structure of the DCS for aero-engines is shown in Figure 1 [33]. In the aero-engine DCS, signal conditioning, A/D, D/A, and other functions are delegated to the sensors and actuators, while the controller only performs core control tasks, such as control law calculations [34,35]. The sensors and actuators integrate microprocessors internally, making them intelligent sensors and intelligent actuators. Communication between the controller, intelligent sensors, and intelligent actuators is performed through a digital bus. Intelligent sensors convert measurement signals into digital signals and provide them to the controller. The functions performed by intelligent sensors include A/D, redundancy management, and interface with the digital bus. Intelligent actuators receive control commands from the controller and control the actuator. The functions performed by intelligent actuators include D/A, closed-loop feedback, redundancy management, and interface with the digital bus. The controller sends control commands to intelligent actuators at a fixed rate through the digital bus. The bus structure of the aero-engine DCS is generally divided into circle structure and linear structure. The circle bus connects each node through a circular structure and has a simple structure. The linear bus uses fewer cables but has a more complex structure. Commonly used buses in aero-engine DCS research include MIL-STD-1553, Field Bus, CAN, and others. Currently, the tasks of controllers are becoming increasingly complex and require new, high-performance microprocessors as controllers. Therefore, this has a certain impact on the reliability of the control system.
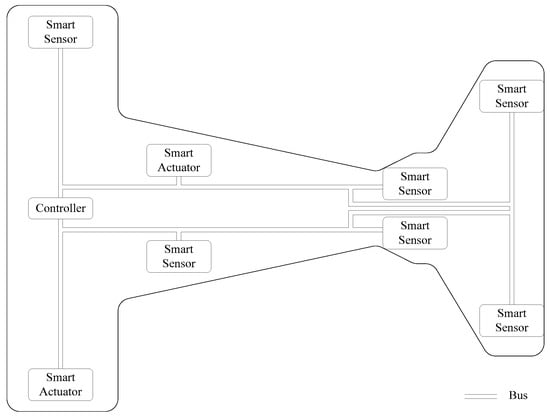
Figure 1.
Overview of a traditional aero-engine DCS.
The feature of SDCS is that the controllers are decentralized. In an SDCS, a decentralized network is formed by a set of low-cost, highly reliable, but low-performance, microprocessor nodes. As shown in Figure 2, each microprocessor node has computing, storage, and communication functions, and data can be transmitted between nodes. Aero-engines SDCS replaces the central controller in aero-engines’ DCS with this decentralized network, and the entire decentralized network acts as the controller of the aero-engine control system. Some microprocessors in the network possess bus communication capabilities, allowing the entire decentralized network to communicate directly with intelligent sensors and actuators in the aero-engine control system. In Figure 2, green circles represent conventional nodes, and blue circles represent nodes with bus communication capabilities.
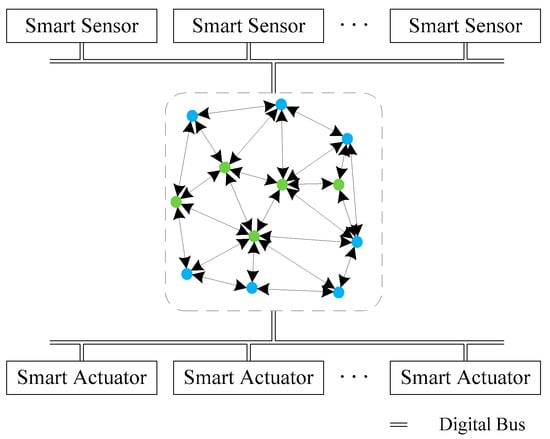
Figure 2.
Overview of an aero-engine SDCS.
With the structure of aero-engines, the SDCS requires decentralized control tasks to be performed on each decentralized node. The process of obtaining decentralized control tasks from core control tasks is named control task virtualization, and each decentralized task is called a virtual control task (VCT). It can be seen that the core control tasks of the control system are the sum of these VCTs, and each VCT is mapped to a decentralized node in the network. Since each VCT is a subtask of the core control tasks of the control system, the task load on each decentralized node is effectively reduced, which allows for the use of low-cost, high-reliability, and low-performance microprocessors as decentralized nodes of the control system. At the same time, the amount of software code on each node is effectively reduced, which can improve the software reliability of each decentralized node.
3.2. Linear Iterative Controller Design Scheme
For the structure of a SDCS, nodes in the network act as controllers to execute system control tasks. Sensors, actuators, and nodes in the network can exchange information with each other, and each node maintains its own internal state. Let denote the set of all nodes, denote the set of all error tracking nodes, denote the set of nodes that send data to the actuators, denote the set of nodes that execute VCTs, and represent the neighboring node set of node in .
The linear iterative working mechanism of the nodes in the network is that each VCT node in the network broadcasts its own state information to other nodes in the network at each cycle. Other task nodes receive the broadcasted state information. After all, the VCT nodes have completed their state broadcasting, and each VCT node updates its own state as a weighted sum of its previous cycle state and the received state information of other VCT nodes. Thus, each task node can act as a small dynamic controller.
Consider the example of the linear iterative network shown in Figure 3, where each node maintains a scalar state. Nodes broadcast their own states to other nodes in the network in a certain order (it is known from the analysis process below that the broadcast order has no effect on the iteration solution model). In each cycle, node broadcasts its state first, then node broadcasts its state, and so on, with node being the last node to broadcast its state in each cycle. Any node receives the states of other nodes in , and updates its own state as a weighted sum of its previous cycle state and the received states of all other nodes. Let denote the state of node in the cycle. Taking the example of placing a decentralized controller in the forward path to complete unity feedback control, where is the tracking error between the output and input, and is the output of the decentralized controller, based on the linear iterative process of the decentralized controller, we have:
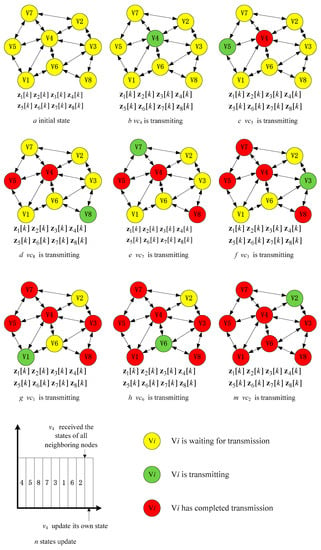
Figure 3.
Example of a linear iteration scheme.
The actuator input is obtained as a linear combination of the tracking error value and the node states in :
The vector , which is a concatenation of all node states in (where is the number of internal state variables maintained by the node in ), we obtain the iteration process of the entire network as:
Let,
Then,
This sub-section describes the working process of the linear iteration strategy for nodes in the network and obtains the system model of the linear iteration strategy. From the above analysis, it can be concluded that the broadcasting order of nodes in Figure 3 has no impact on modeling the linear iteration strategy of the network, and the tasks of each node are balanced. The key to designing the linear iteration strategy is to determine the link weights (i.e., , , and in Equation (26)). A simple method for obtaining link weight parameters will be introduced in the following sub-sections of this paper.
3.3. Control System Modeling
As shown in Figure 4, this is a schematic diagram of the control system structure for aero-engines, with the controller placed in the forward path. In Figure 4, represents the system input, represents the system output, represents the tracking error between the output and input, and represents the output of the controller. The control system adopts unity negative feedback design. The controller calculates the control signal using the difference between the system reference input and output and sends the control signal to the actuator to complete the system control task. The system control task is centralized at a specific controller node.
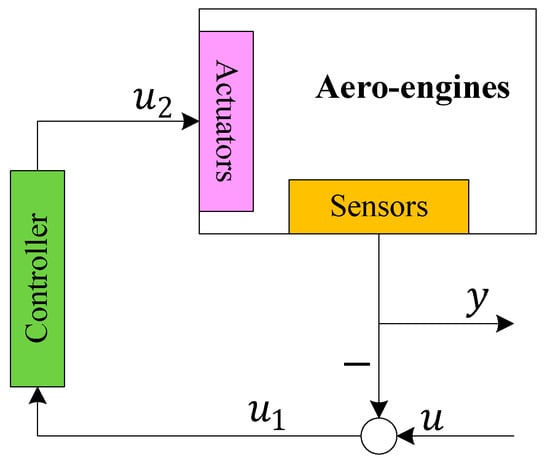
Figure 4.
Structure of a unit feedback control system.
For SDCS, the system feature is that the controller is decentralized, that is, a controller is composed of several decentralized nodes in the network with computing, storage, and communication capabilities. The corresponding SDCS control system structure diagram is shown in Figure 5. In the figure, is the system input, is the system output, is the tracking error between the output and input, is the output of the decentralized node based controller, the dashed box represents the decentralized nodes, the blue lines represent communication between nodes, and for simplicity, not all data transmission relationships between decentralized nodes are shown. Each decentralized node has computing, storage, and communication capabilities. The node used to calculate the tracking error between the output and input is called the error tracking node, which is isomorphic to other nodes in the network.
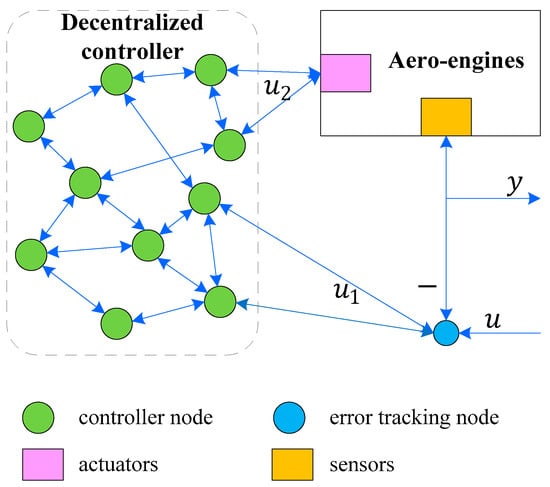
Figure 5.
Decentralized controller structure with unit negative feedback.
The general time-discrete linear time-invariant model of the aero-engine in Figure 5 is:
From the control system structure in Figure 5,
Based on the periodic linear iterative strategy derived from Equations (24) and (25), the state–space model of the control system can be represented as . In Figure 5, when the nodes in the network adopt the linear iterative strategy shown in Figure 3, the state equation of the closed-loop system is:
Let,
Then,
From the above analysis, it can be concluded that the control-related computing tasks performed by the decentralized controller nodes responsible for system control are described by Equation (22), which is a linear weighted sum process. The linear weighted sum of a single node is equivalent to a VCT. It can be seen that, for each VCT, only simple addition and multiplication operations are required, with minimal computational requirements and low utilization of node computing resources. Each VCT actually uses its own state and the state of other task nodes to perform linear iterations in order to maintain its own state.
Based on the running process and mathematical description of the linear iterative SDCS closed-loop control system presented in this section, the following advantages of this method can be identified:
- Low resource consumption
In the linear iteration scheme proposed in this section, the task of each VCT is a linear weighted sum of the node’s own state and the states of other task nodes. The computation is simple and requires minimal resources, resulting in low computational overhead for the nodes. As aero-engines are safety-critical systems that often use mature and stable but low-performance electronic devices, the SDCS control system design based on the linear iteration scheme is suitable for aero-engine control systems. It can use limited computing resources to perform simple periodic tasks and complete system control tasks.
- 2.
- Balanced resource consumption
As mentioned earlier, the task of each VCT is a linear weighted sum of multiple node states, resulting in equal task loads for each task node and balanced resource consumption across the nodes.
- 3.
- Good software performance
Since the tasks of each task node are the same, with only different link weights, there is no need to design the software system for each VCT separately. In addition, the simple weighted summation task of each VCT results in less code and simpler tasks, making it less likely to affect the control system due to software system failures during operation.
- 4.
- Easy to develop
This solution does not require homogeneous hardware nodes, as long as the nodes meet the basic requirements of computing, communication, and storage performance, they can be easily added to the control system for system expansion.
In this section, a SDCS model based on the linear iterative strategy was obtained, and a fully distributed decentralized controller was implemented, where VCT represents the linear weighted combination process executed on a single task node. Not every node needs to directly exchange data with sensors and actuators, as data exchange mainly occurs between decentralized nodes in the network. The tuning of link weights in the linear iteration process of this scheme will be described in detail in the next section.
4. Controller Parameter Tuning Method Based on LMI
To ensure the normal running of the control system, it is essential to ensure that the control system is stable. For the design scheme in this paper, since the linear iterative process of the decentralized controller is discrete, it is required that the system be Schur stable.
The most intuitive method is to use the Lyapunov method [36], which involves finding a matrix that satisfies the following equation.
However, since the linear iterative method of the decentralized controller in this paper does not impose any restrictions on the network topology of the nodes, and the parameters and in Equation (31) are nonlinear with respect to the Lyapunov condition, it is difficult to solve using general Linear Matrix Inequality (LMI) methods. Here, the following lemma is introduced,
Lemma 1.
System
is Schur stable if and only if there exist matrices
and
, such that the following equation holds:
Proof.
From Equation (31), according to the Schur complement theorem, we can conclude that,
Let, , then,
According to the Schur complement theorem, we can obtain that,
Additionally, and are positive definite matrices. □
From Refs. [37,38], we can obtain the following lemma.
Lemma 2.
For positive definite matrices and
, and are the optimal solutions to the following optimization problem, if and only if :
By Lemma 1 and Lemma 2, we can easily derive the following conclusion:
System is Schur stable, if and only if the following optimization problem has a solution.
In the above optimization condition, the four constraint conditions are linear, but the objective function is nonlinear. In order to facilitate solving the problem using LMI method, the objective function can be linearized at any and [38], that is:
In Equation (34), is a constant. Therefore, the optimization objective can take as the objective function. Since is linear, the LMI method can be used to solve the above optimization problem. Based on this conclusion, the following parameter tuning algorithm is given. First, the LMI problem is presented:
The flowchart for the parameter tuning algorithm is shown in Figure 6.
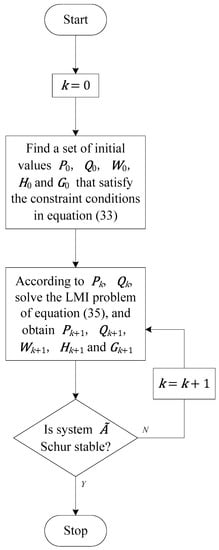
Figure 6.
The flowchart for the parameter tuning algorithm.
In the above algorithm, during each iteration, and are equivalent to and in Equation (34), and the matrix variables and to be solved are equivalent to and in Equation (34). Therefore, the optimization objective function in Equation (35), , is linear. The parameters , , and obtained from the above algorithm are the required parameters , , and for the decentralized controller. Under this control parameterization, the control system is Schur stable.
5. Simulation Analysis
The previous sections introduced a decentralized controller design based on linear iteration, provided the mathematical model of the control system, and presented a controller parameter tuning method based on LMI. The purpose of this simulation is to verify the feasibility of the proposed decentralized controller design of the aero-engines SDCS and parameter tuning algorithm in this paper.
By using the modeling method in Section 2, we obtain the discrete-time state space model of a turbofan engine under the conditions of 0 altitude and 0 Mach number, which is given by:
where,
and are the low-pressure and high-pressure rotor speeds of the turbofan engine, respectively, is the turbine pressure ratio, is the fuel flow, and is the area of the nozzle.
Using the LMI based algorithm designed in Section 4 and the MATLAB YALMIP toolbox, with “sdpt3” solver, the parameters , , and of the decentralized controller are calculated as follows:
It can be verified that is Schur stable. Therefore, it can be seen that only two nodes are required to form a decentralized controller of the aero-engine’s control system.
Figure 7 shows the schematic diagram of the low-pressure rotor speed response of an aero-engine under corresponding inputs. Figure 8 shows the schematic diagram of the turbine pressure ratio response of an aero-engine under corresponding inputs.
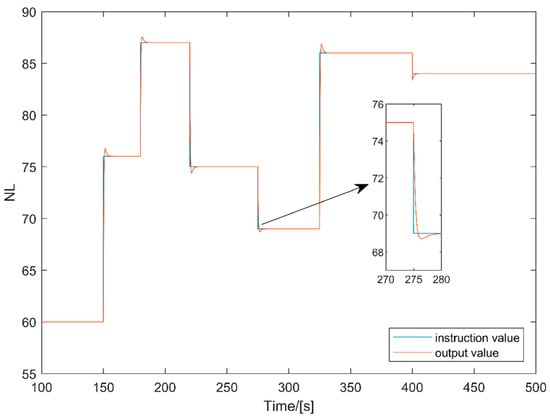
Figure 7.
Schematic diagram of the low-pressure rotor speed response.
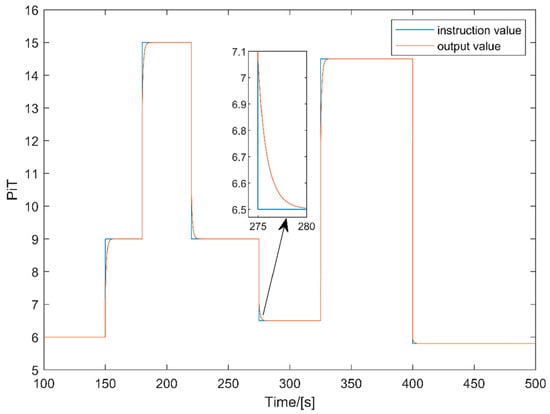
Figure 8.
Schematic diagram of the turbine pressure ratio response.
From the simulation results of Figure 7 and Figure 8, it can be seen that the response of the low-pressure rotor speed and turbine pressure ratio under the corresponding input is stable. In the design scheme proposed in this paper, a decentralized controller design scheme is first presented to obtain the VCT of the SDCS. The model of the control system is obtained through the model of the decentralized controller. A control parameter tuning scheme is given using LMI, which obtains the parameters of each VCT. For the parameter tuning scheme, the objective is to ensure the stability of the control system. By analyzing the result of the parameter tuning scheme, the system is Schur stable, meanwhile, the simulation results show that the system is stable, demonstrating the effectiveness of the proposed design.
In the design process of this paper, a decentralized controller can be composed using only a small number of nodes, making the design of the control system simple. Furthermore, because the internal nodes of the controller use periodic broadcasting for linear iteration, the communication resources consumed by the controller increase as the number of nodes executing the VCT increases. From the simulation results, it can be seen that using a decentralized node with the same number as the system order can complete the control task well.
The proposed design scheme makes the application of SDCS in aero-engine control systems simple. From the perspective of control system design, existing aero-engine models can be used to obtain the control tasks of decentralized controller nodes through the algorithm introduced in this paper, simplifying the system design. From the perspective of software design, the control tasks executed by each decentralized node in the controller are simply linearly weighted sums of the node’s own state and the states of other nodes. Different VCTs executed on different nodes only have different weights on the state, and the software structure is the same, making software code writing and development easy and short. From the perspective of hardware development, since the consumption of computing, storage, and communication resources between different VCTs is indistinguishable, and homogeneous nodes can be used for hardware system design, making hardware design easy without requiring specific designs for different VCTs, effectively reducing the difficulty and cycle of the hardware design process.
6. Conclusions
This paper briefly introduces the architecture of SDCS for aero-engines. The SDCS is composed of a network of low-cost, low-performance, and highly reliable nodes that serve as the controller for the aero-engine control system. The characteristic of SDCS is that the controller is decentralized, and there is no central controller node in the control system. In order to meet the decentralized characteristic of the SDCS controller, this paper introduces a virtualization scheme for control tasks based on node linear iteration, obtaining the virtual control tasks executed on each node. The linear iterative scheme for decentralized controllers is modeled, and the mathematical model of the aero-engine control system is obtained. In the proposed scheme, the control tasks executed on each node have balanced workloads, and the workloads of the decentralized nodes are small, making it easy to use low-cost, low-performance, and highly reliable microprocessors as decentralized controllers of the control system. To stabilize the control system with the designed controller, a controller parameter tuning scheme based on the LMI method is introduced. Finally, the feasibility of the proposed design scheme is verified through digital simulation.
Author Contributions
Conceptualization, X.J. and J.L.; data curation, J.R.; investigation, X.J. and J.R.; methodology, X.J., J.L. and Y.W.; software, X.J. and J.R.; supervision, J.L. and Y.W.; validation, X.J. and J.R.; writing—original draft, X.J.; writing—review and editing, X.J., J.L., J.R. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that they have no competing financial and non-financial interests.
References
- Wang, X.; Du, X.; Wang, X.; Sun, X.; Li, Y. Controller Design of Aero-engines under the Distributed Architecture with Time Delays. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar]
- De Giorgi, M.G.; Strafella, L.; Ficarella, A. Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model. Aerospace 2021, 8, 206. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, S.; Zhang, Y.; Ren, L.; Zhou, B.; Wang, H.; Peng, J.; Wang, L.; Li, Y. Aero-Engine DCS Fault-Tolerant Control with Markov Time Delay Based on Augmented Adaptive Sliding Mode Observer. Asian J. Control. 2020, 22, 788–802. [Google Scholar] [CrossRef]
- Lv, C.; Chang, J.; Bao, W.; Yu, D. Recent Research Progress on Airbreathing Aero-Engine Control Algorithm. Propuls. Power Res. 2022, 11, 1–57. [Google Scholar] [CrossRef]
- Culley, D.; Thomas, R.; Saus, J. Concepts for Distributed Engine Control. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Gianluca, A. Interconnected Dynamic Systems: An Overview on Distributed Control. IEEE Contr. Syst. Mag. 2013, 33, 76–88. [Google Scholar]
- Xu, S.; Bao, J. Distributed Control of Plantwide Chemical Processes. J. Process. Control. 2009, 19, 1671–1687. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. Distributed Tracking of Multiple Under-actuated Lagrangian Systems with Uncertain Parameters and Actuator Faults. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Chen, T.; Shan, J. Distributed Adaptive Attitude Control for Multiple Underactuated Flexible Spacecraft. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar]
- Chen, T.; Shan, J. Distributed Tracking of a Class of Underactuated Lagrangian Systems with Uncertain Parameters and Actuator Faults. IEEE Trans. Ind. Electron. 2020, 67, 4244–4253. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiu, H.; Song, H. Distributed Measurement and Control System of the Test-rig of Ram-compressed Rotor Aero-engine Based on PLC and PXI bus. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012. [Google Scholar]
- Li, G.; Wang, X.; Ren, X. Multi-package Transmission Aero-engine DCS Neural Network Sliding Mode Control Based on Multi-Kernel LS-SVM Packet Dropout Online Compensation. PLoS ONE 2020, 15, e0234356. [Google Scholar]
- Zhang, S.; Zhang, D.; Zhang, Z.; Zhang, Q.; Lu, B. Dynamic Control Allocation Fault-Tolerant Method for a Class of Distributed Control Systems. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar]
- Lubomir, B. Decentralized Control: An Overview. Annu. Rev. Control 2008, 32, 87–98. [Google Scholar]
- Lubomir, B. Decentralized Control: Status and Outlook. Annu. Rev. Control 2014, 38, 1367–5788. [Google Scholar]
- Maria, F.; Agostino, M.; Giovanni, P.; Walter, U. A Decentralized Control Strategy for the Coordination of AGV Systems. Control Eng. Pract. 2018, 70, 86–97. [Google Scholar]
- Yang, C.; Jaime, L.; Antonia, T.; Andreas, M. Decentralized Control of Distributed Cloud Networks with Generalized Network Flows. IEEE. Trans. Commun. 2023, 71, 256–268. [Google Scholar]
- Shojaee, M.; Azizi, M. Optimal Decentralized Control of a Wind Turbine and Diesel Generator System. Optim. Control Appl. Meth. 2023, 44, 677–698. [Google Scholar] [CrossRef]
- Pan, M.; Cao, L.; Zhou, W.; Huang, J.; Chen, Y. Robust Decentralized Control Design for Aircraft Engines: A Fractional Type. Chin. J. Aeronaut. 2019, 32, 347–360. [Google Scholar] [CrossRef]
- Ji, X.; Li, J.; Ren, J.; Wu, Y.; Wang, K. Fully Connected Clustering Based Software Defined Control System and Node Failure Analysis. J. Northwest. Polytech. Univ. 2019, 37, 1238–1247. [Google Scholar] [CrossRef]
- Stöhr, M.; Geigle, K.; Hadef, R.; Boxx, I.; Carter, C.; Grader, M.; Gerlinger, P. Time-Resolved Study of Transient Soot Formation in an Aero-engine Model Combustor at Elevated Pressure. Proc. Combust. Inst. 2019, 37, 5421–5428. [Google Scholar] [CrossRef]
- Zheng, Q.; Fang, J.; Hu, Z.; Zhang, H. Aero-Engine On-Board Model Based on Batch Normalize Deep Neural Network. IEEE Access 2019, 7, 54855–54862. [Google Scholar] [CrossRef]
- Pang, S.; Li, Q.; Feng, H. A Hybrid Onboard Adaptive Model for Aero-engine Parameter Prediction. Aerosp. Sci. Technol. 2020, 105, 105951. [Google Scholar] [CrossRef]
- Ren, L.; Ye, Z.; Zhao, Y. A Modeling Method for Aero-engine by Combining Stochastic Gradient Descent with Support Vector Regression. Aerosp. Sci. Technol. 2020, 99, 105775. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Fu, Y.; Shi, Y.; Chen, C. Rate Bumpless Transfer Control for Switched Linear Systems with Stability and Its Application to Aero-Engine Control Design. IEEE Trans. Ind. Electron. 2020, 67, 4900–4910. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, X. Bumpless Transfer Control for Switched Linear Systems and Its Application to Aero-Engines. IEEE Trans. Circuits I. 2021, 68, 2171–2182. [Google Scholar] [CrossRef]
- Morteza, M.; Ali, R.; Ali, J.; Milad, E. Design and Implementation of MPC for Turbofan Engine Control System. Aerosp. Sci. Technol. 2019, 92, 99–113. [Google Scholar]
- Morteza, M.; Ali, R. Analyzing Different Numerical Linearization Methods for the Dynamic Model of a Turbofan Engine. Mech. Ind. 2019, 20, 303. [Google Scholar]
- Gou, L.; Zeng, X.; Wang, Z.; Han, G.; Lin, C.; Cheng, X. A Linearization Model of Turbofan Engine for Intelligent Analysis Towards Industrial Internet of Things. IEEE Access. 2019, 7, 145313–145323. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, J.; Pan, M.; Lu, F. A Novel Real-Time Mechanism Modeling Approach for Turbofan Engine. Energies 2019, 12, 3791. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, W.; Zhu, P.; Zeng, J. Modeling of a Large Envelope System for Turbofan Engine. J. Nanjing Univ. Aeronaut. Astronaut. 2021, 53, 529–536. [Google Scholar]
- Ji, X.; Li, J.; Ren, J.; Wu, Y. A Decentralized LQR Output Feedback Control for Aero-Engines. Actuators 2023, 12, 164. [Google Scholar] [CrossRef]
- Belapurkar, R. Stability and Performance of Proplusion Control Systems with Distributed Control Architectures and Failure. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2012. [Google Scholar]
- Thompson, H.; Fleming, P. Distributed Aero-Engine Control Systems Architecture Selection Using Multi-Objective Optimisation. In Proceedings of the 5th IFAC Workshop on Algorithm & Architecture for Real Time Control (AARTC’ 98), Cancun, Mexico, 15–17 April 1998. [Google Scholar]
- Skira, C.; Agnello, M. Control Systems for the Next Century’s Fighter Engines. J. Eng. Gas Turbines Power. 1992, 114, 749–754. [Google Scholar] [CrossRef]
- Ricardo, C.; Pedro, L. LMI Conditions for Robust Stability Analysis Based on Polynomially Parameter-dependent Lyapunov Functions. Syst. Control Lett. 2006, 55, 52–61. [Google Scholar]
- Bruno, M.; Joao, Y.; Eduardo, S. LMI-based Consensus of Linear Multi-agent Systems by reduced-order Dynamic Output Feedback. ISA Trans. 2020, 129, 121–129. [Google Scholar]
- Ghaoui, L.; Oustry, F.; AitRami, M. A cone complementarity linearization algorithm for static output-feedback and related problems. IEEE Trans. Automat. Contr. 1997, 42, 1171–1176. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).