A Hierarchical Control Scheme for Adaptive Cruise Control System Based on Model Predictive Control
Abstract
1. Introduction
2. System Modeling
2.1. Adaptive Cruise Control System Modeling
2.2. Vehicle Longitudinal Dynamics Modeling
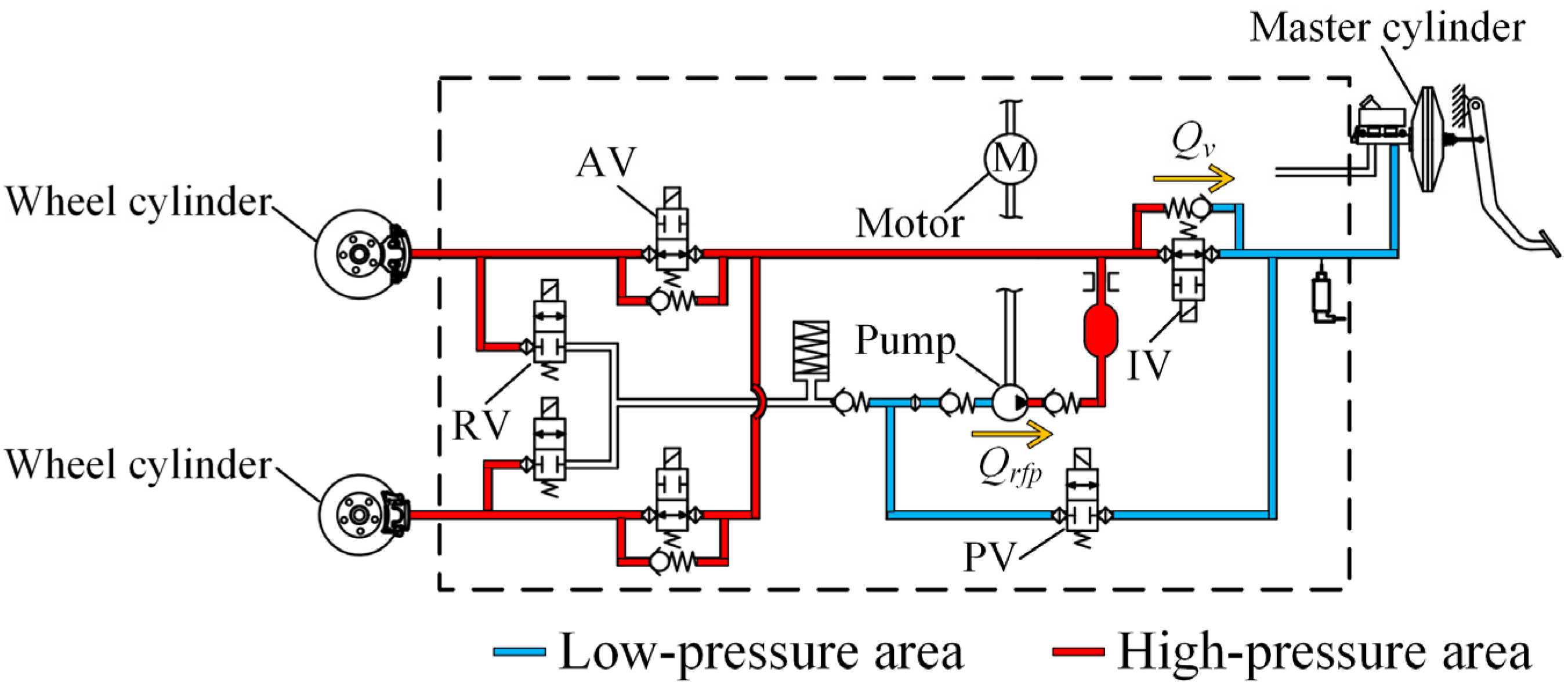
2.3. Hydraulic Control Unit Modeling
2.3.1. Wheel Cylinder and Braking Pipeline Model
2.3.2. Motor and Plunger Pump Model
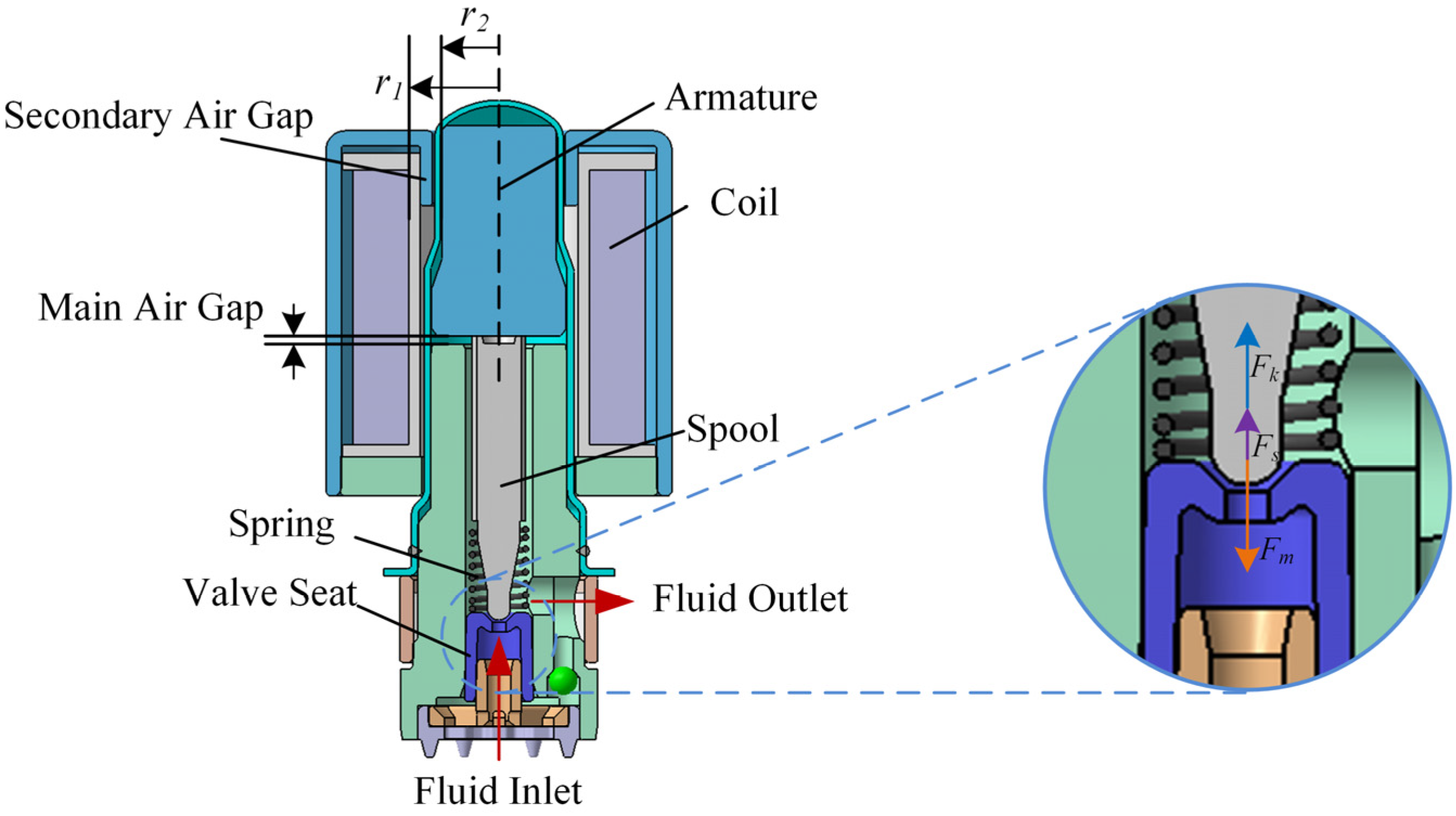
2.3.3. Solenoid Valve and Coil Model
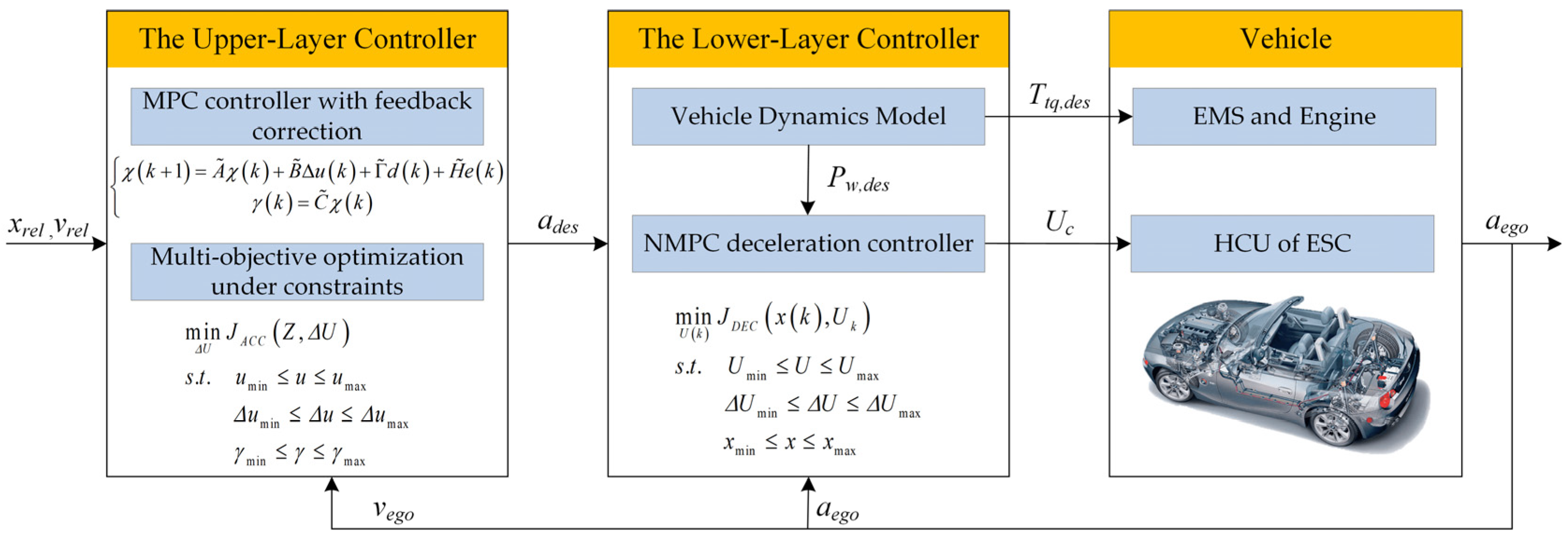
3. Controller Design
3.1. The Design of the Upper-Layer Controller
3.2. The Design of the Lower-Layer Controller
4. Simulation and Experiment
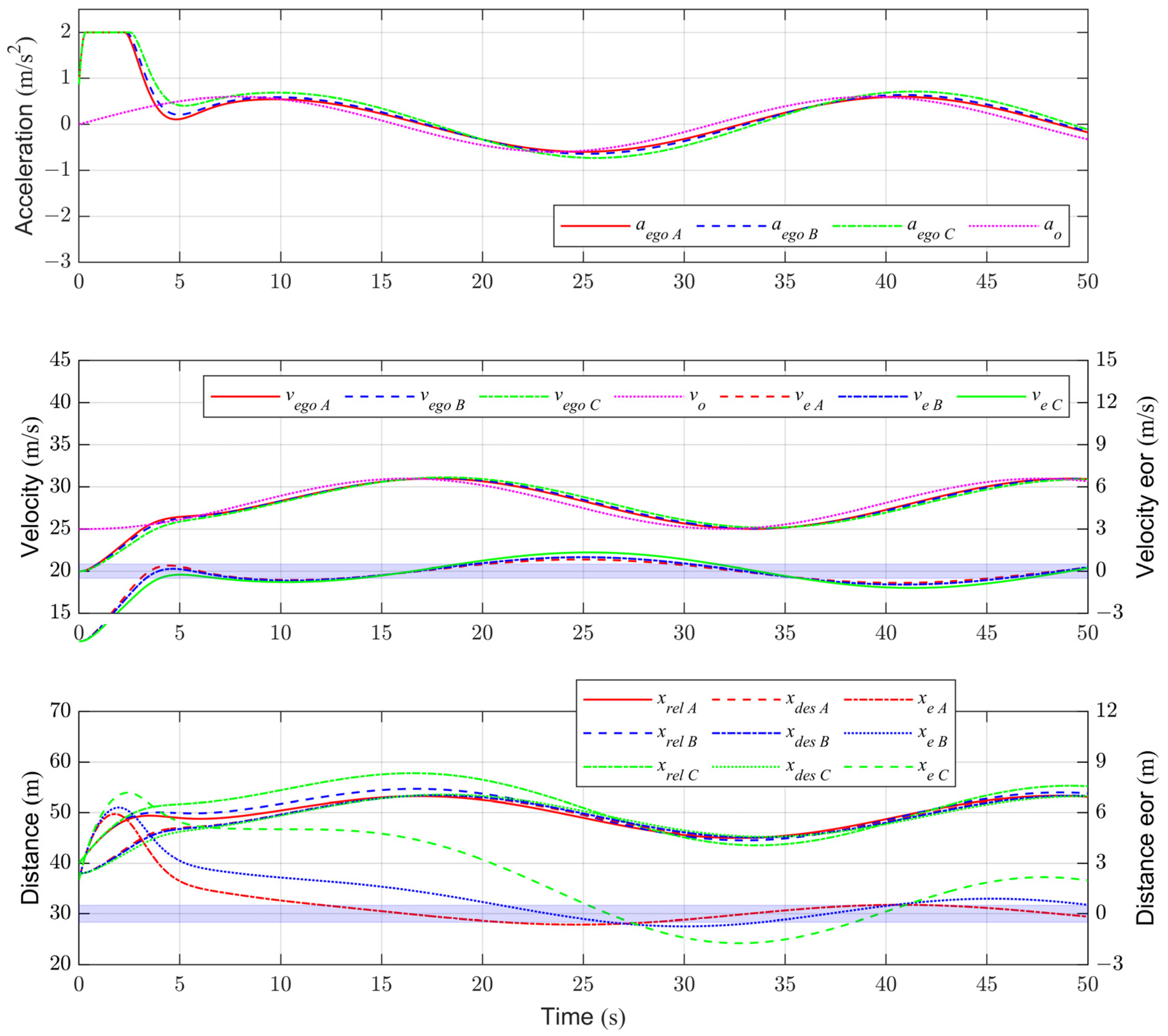
4.1. Simulation Results
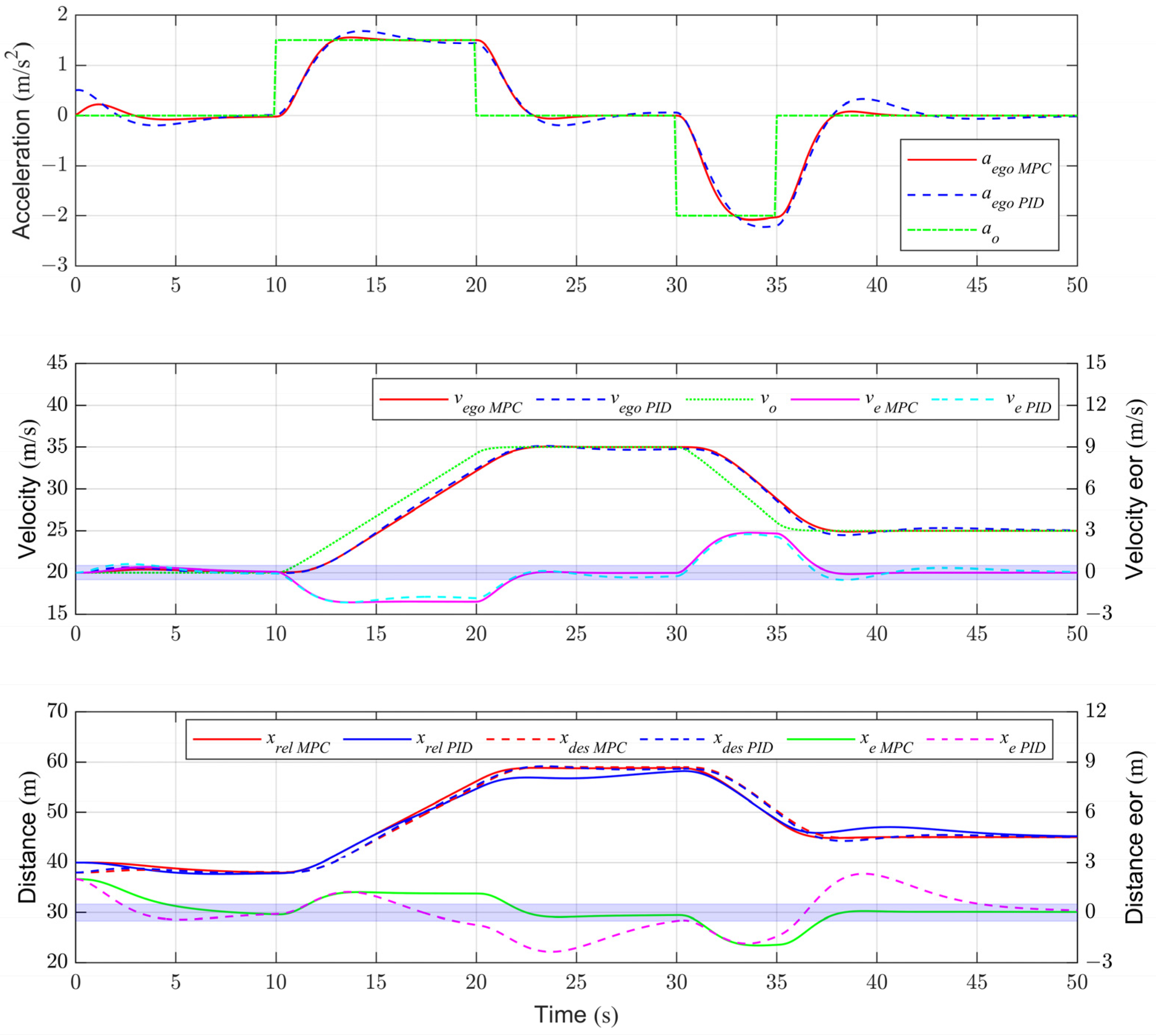
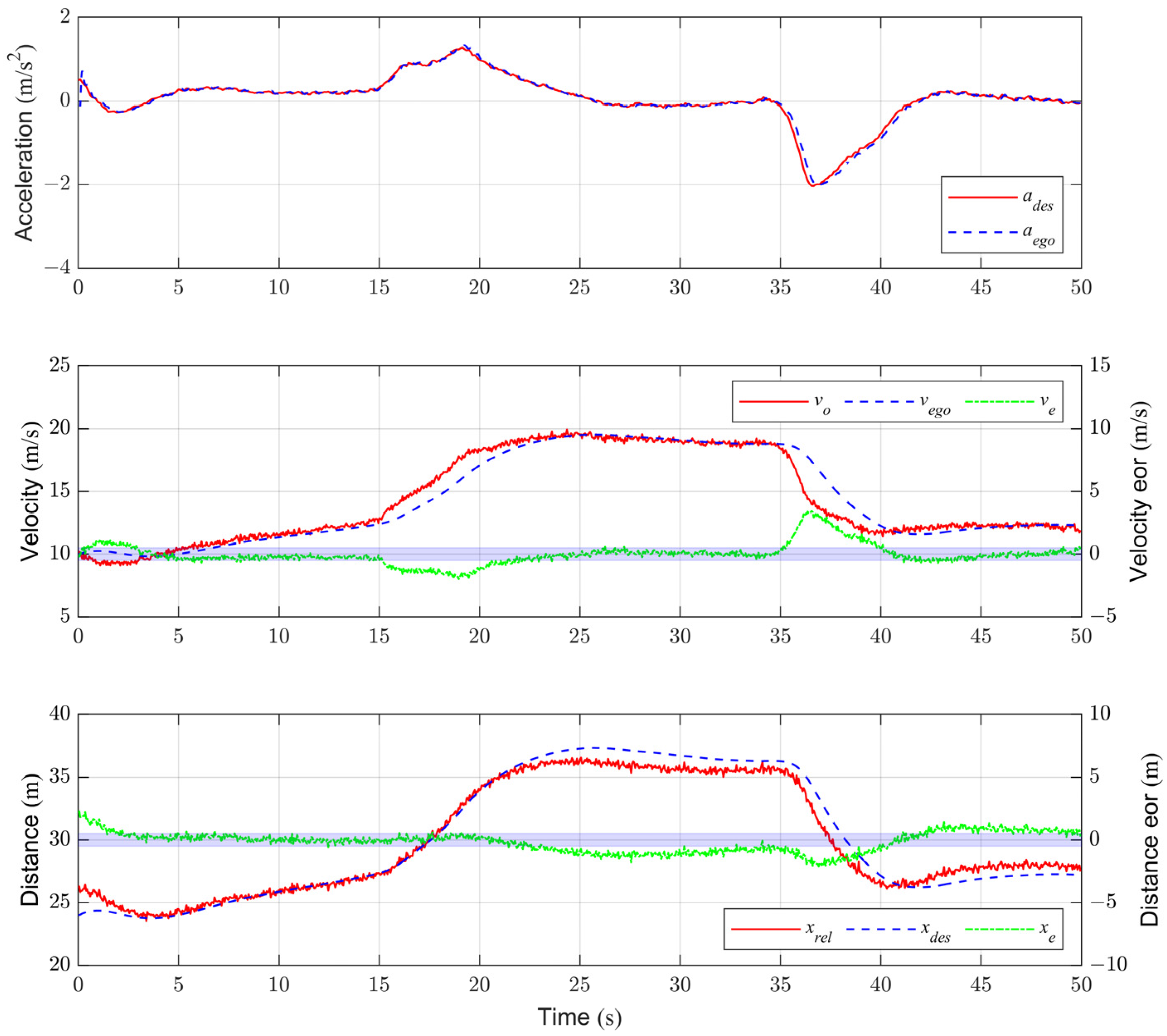
4.1.1. Testing Results of Scenario A
4.1.2. Testing Results of Scenario B
4.2. Experiments Results
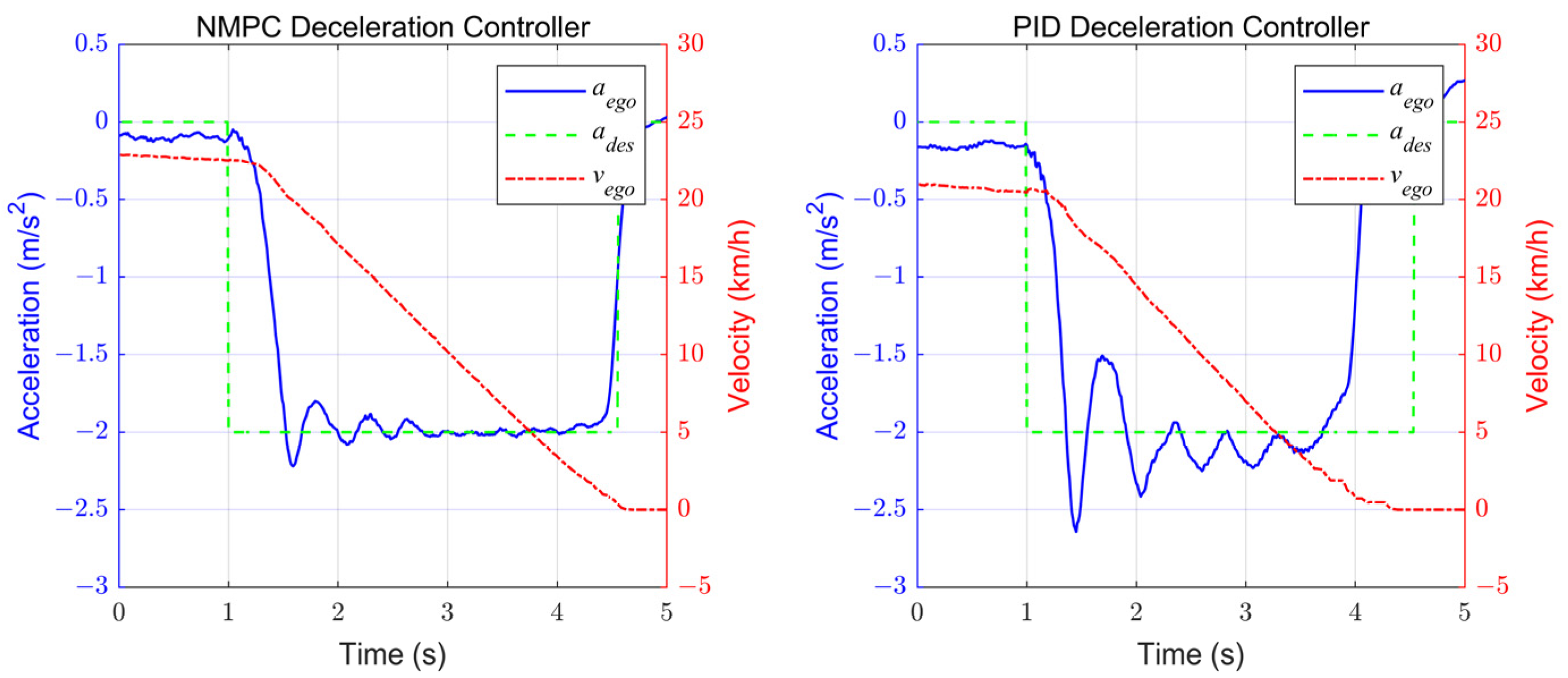
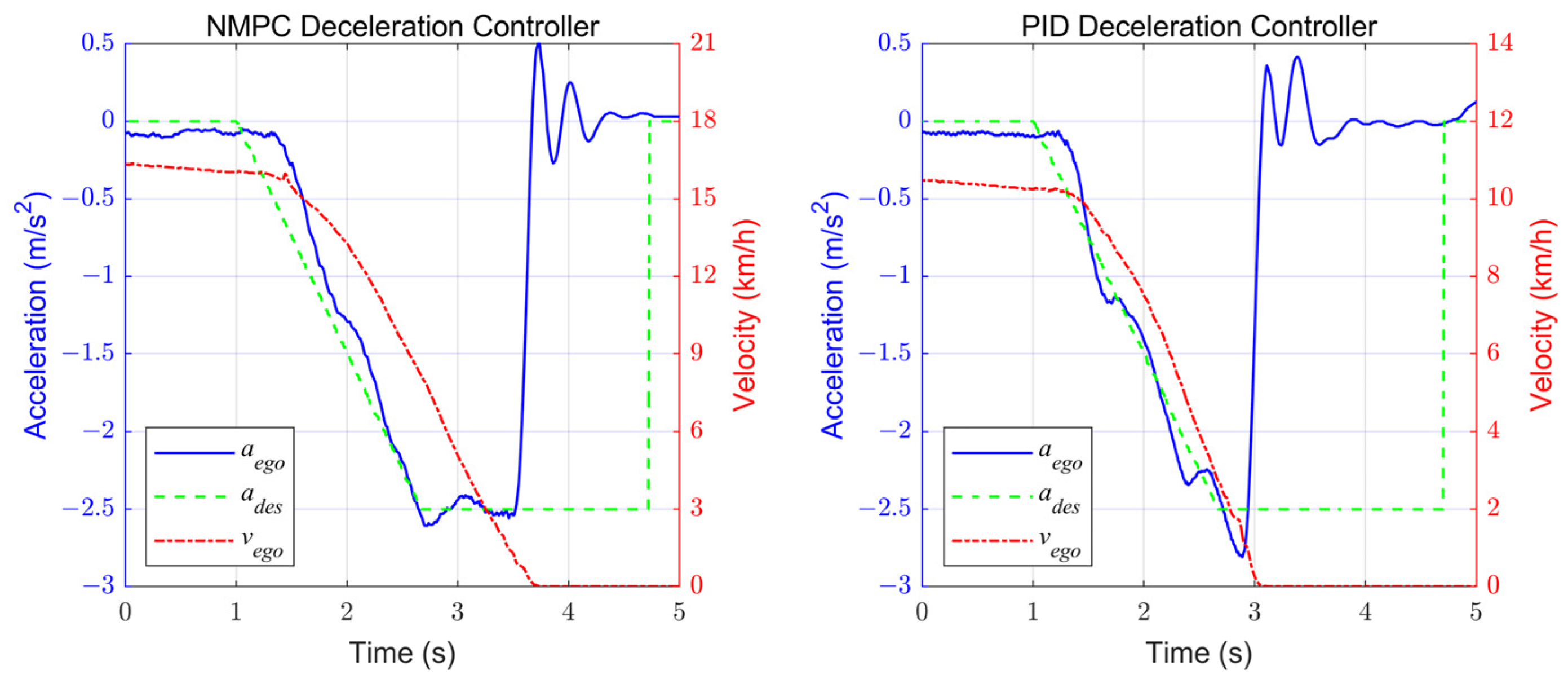
4.2.1. Experiments results of Deceleration Controller
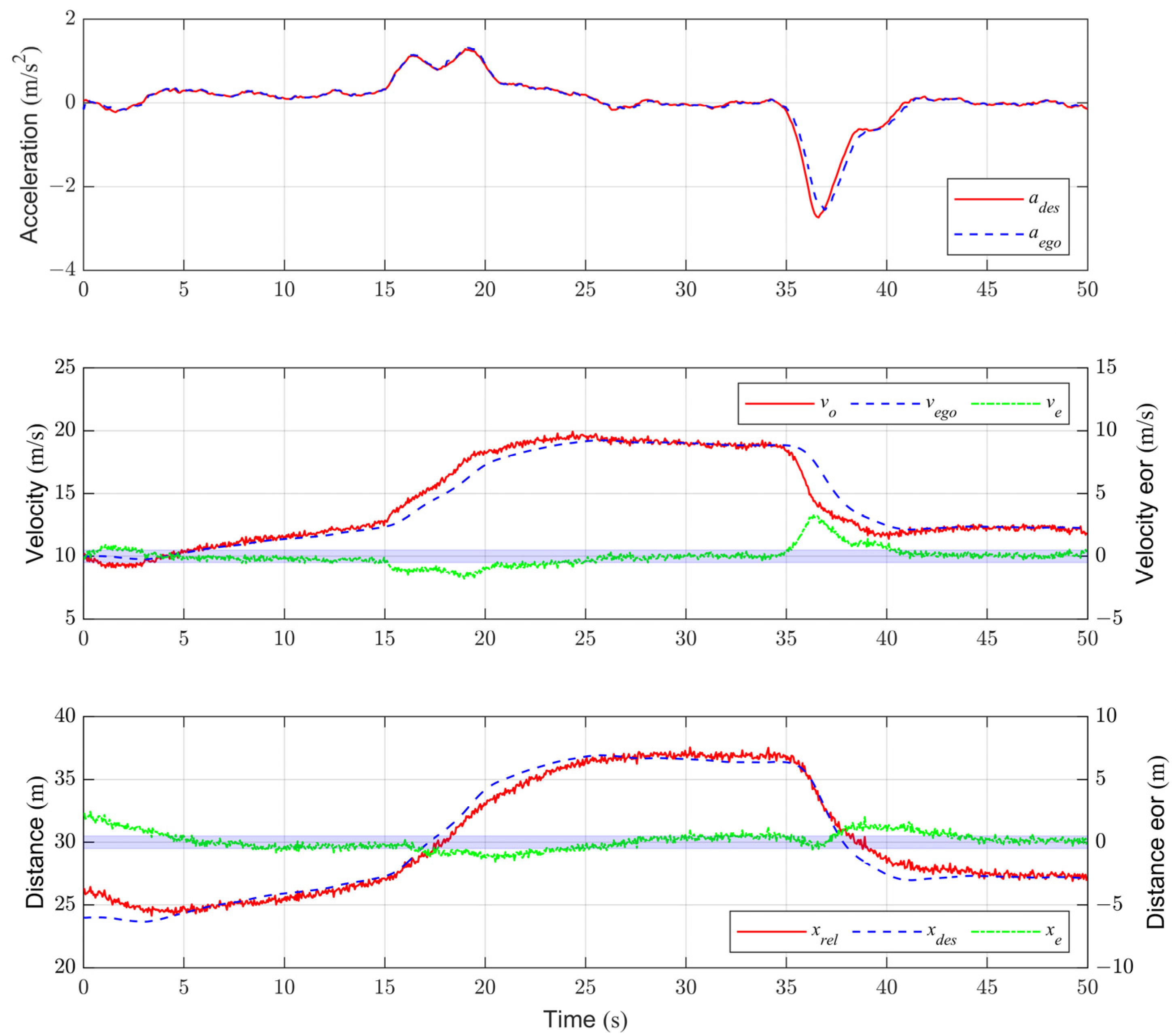
4.2.2. Experiments Results of ACC Strategies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shakouri, P.; Ordys, A.; Askari, M.R. Adaptive cruise control with stop&go function using the state-dependent nonlinear model predictive control approach. ISA Trans. 2012, 51, 622–631. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Wang, Z.; Yan, M. An Optimization Design of Adaptive Cruise Control System Based on MPC and ADRC. Actuators 2021, 10, 110. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Wang, Z.; Deng, J.; Dorrell, D.G. Chassis Coordinated Control for Full X-by-Wire Vehicles-A Review. Chin. J. Mech. Eng. 2021, 34, 42. [Google Scholar] [CrossRef]
- Souza, A.M.d.; Pedrosa, L.L.C.; Botega, L.C.; Villas, L. Itssafe: An Intelligent Transportation System for Improving Safety and Traffic Efficiency. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–7. [Google Scholar]
- Vahidi, A.; Eskandarian, A. Research advances in intelligent collision avoidance and adaptive cruise control. IEEE Trans. Intell. Transp. Syst. 2003, 4, 143–153. [Google Scholar] [CrossRef]
- Spiliopoulou, A.; Perraki, G.; Papageorgiou, M.; Roncoli, C. Exploitation of ACC systems towards improved traffic flow efficiency on motorways. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Naples, Italy, 26–28 June 2017; pp. 37–43. [Google Scholar]
- Yu, Q.; Lei, L.; Bao, Y.; Wang, L. Research on Safety and Traffic Efficiency of Mixed Traffic Flows in the Converging Section of a Super-Freeway Ramp. Sustainability 2022, 14, 13234. [Google Scholar] [CrossRef]
- Zhang, J.; Ioannou, P.A. Longitudinal control of heavy trucks in mixed traffic: Environmental and fuel economy considerations. IEEE Trans. Intell. Transp. Syst. 2006, 7, 92–104. [Google Scholar] [CrossRef]
- Pradhan, R.; Majhi, S.K.; Pradhan, J.K.; Pati, B.B. Antlion optimizer tuned PID controller based on Bode ideal transfer function for automobile cruise control system. J. Ind. Inf. Integr. 2018, 9, 45–52. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Kumar, N. Design and Implementation of an Optimized PID Controller for the Adaptive Cruise Control System. IETE J. Res. 2021, 1–8. [Google Scholar] [CrossRef]
- Sawant, J.; Chaskar, U.; Ginoya, D. Robust Control of Cooperative Adaptive Cruise Control in the Absence of Information About Preceding Vehicle Acceleration. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5589–5598. [Google Scholar] [CrossRef]
- Li, S.E.; Deng, K.; Li, K.; Ahn, C. Terminal sliding mode control of automated car-following system without reliance on longitudinal acceleration information. Mechatronics 2015, 30, 327–337. [Google Scholar] [CrossRef]
- Ma, H.; Chu, L.; Guo, J.; Wang, J.; Guo, C. Cooperative Adaptive Cruise Control Strategy Optimization for Electric Vehicles Based on SA-PSO With Model Predictive Control. IEEE Access 2020, 8, 225745–225756. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Adaptive Cruise Control for Eco-Driving Based on Model Predictive Control Algorithm. Appl. Sci. 2020, 10, 5271. [Google Scholar] [CrossRef]
- Xu, Y.; Chu, L.; Zhao, D.; Chang, C. A Novel Adaptive Cruise Control Strategy for Electric Vehicles Based on a Hierarchical Framework. Machines 2021, 9, 263. [Google Scholar] [CrossRef]
- Remfrey, J.; Gruber, S.; Ocvirk, N. Hydraulic brake systems for passenger vehicles. In Handbook of Driver Assistance Systems; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–23. [Google Scholar] [CrossRef]
- Liu, H.; He, R.; Wu, J.; Sun, W.; Zhu, B. Linear Electro-Magnetic Valve Characteristic Analysis and Precise Pressure Control of the Electro-Hydraulic Brake System. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016. [Google Scholar]
- Jin, L.; Song, C.; Li, J. Controll algorithm of combination with logic gate and PID control for vehicle electronic stability control. In Proceedings of the 2010 2nd International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010; pp. 345–349. [Google Scholar]
- Meng, A.; Wang, Z.; Song, J.; Pan, N. Critical Component Modeling and System Simulation of Hydraulic Control Unit of Automotive Electronic Stability Program. Trans. Chin. Soc. Agric. Mach. 2013, 44, 1–5. [Google Scholar] [CrossRef]
- Fang, J.; Wang, X.; Wu, J.; Yang, S.; Li, L.; Gao, X.; Tian, Y. Modeling and Control of a High Speed On/Off Valve Actuator. Int. J. Automot. Technol. 2019, 20, 1221–1236. [Google Scholar] [CrossRef]
- Han, W.; Xiong, L.; Yu, Z. Braking pressure control in electro-hydraulic brake system based on pressure estimation with nonlinearities and uncertainties. Mech. Syst. Signal Process. 2019, 131, 703–727. [Google Scholar] [CrossRef]
- Zhao, X.; Li, L.; Song, J.; Li, C.; Gao, X. Linear Control of Switching Valve in Vehicle Hydraulic Control Unit Based on Sensorless Solenoid Position Estimation. IEEE Trans. Ind. Electron. 2016, 63, 4073–4085. [Google Scholar] [CrossRef]
- Braun, T.; Reuter, J.; Rudolph, J. Observer Design for Self-Sensing of Solenoid Actuators with Application to Soft Landing. IEEE Trans. Control Syst. Technol. 2019, 27, 1720–1727. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y. Pressure control for pneumatic electric braking system of commercial vehicle based on model predictive control. IET Intell. Transp. Syst. 2021, 15, 1522–1532. [Google Scholar] [CrossRef]
- Kayacan, E. Multiobjective H∞ Control for String Stability of Cooperative Adaptive Cruise Control Systems. IEEE Trans. Intell. Veh. 2017, 2, 52–61. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Mei, M.M.; Nie, Y.L.; Zhao, L. Multiple-Objective Adaptive Cruise Control System Integrated With DYC. IEEE Trans. Veh. Technol. 2019, 68, 4550–4559. [Google Scholar] [CrossRef]
- Sun, X.; Cai, Y.; Wang, S.; Xu, X.; Chen, L. Optimal control of intelligent vehicle longitudinal dynamics via hybrid model predictive control. Robot. Auton. Syst. 2019, 112, 190–200. [Google Scholar] [CrossRef]
- Meng, A.; Garris, C.; Wei, L.; Liu, H. Visual System Analysis of High Speed On-Off Valve Based on Multi-Physics Simulation; SAE Technical Paper: Warrendale, PA, USA, 2022; ISSN 0148-7191. [Google Scholar]
- Gao, X.; Yang, Y.; Zhao, X.; Li, C. Non-linear dynamic modelling of a switching valve driven by pulse width modulation in the hydraulic braking system of a vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 1511–1529. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, S.; Ji, X.; Li, L.; Wei, L. A Hierarchical Anti-Disturbance Path Tracking Control Scheme for Autonomous Vehicles Under Complex Driving Conditions. IEEE Trans. Veh. Technol. 2021, 70, 11244–11254. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Data update frequency | 15–20 Hz |
| Relative distance accuracy | ±0.4 m |
| Relative velocity accuracy | ±0.1 km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, H.; Li, L.; Mei, M.; Zhao, Y. A Hierarchical Control Scheme for Adaptive Cruise Control System Based on Model Predictive Control. Actuators 2023, 12, 249. https://doi.org/10.3390/act12060249
Mu H, Li L, Mei M, Zhao Y. A Hierarchical Control Scheme for Adaptive Cruise Control System Based on Model Predictive Control. Actuators. 2023; 12(6):249. https://doi.org/10.3390/act12060249
Chicago/Turabian StyleMu, Hongyuan, Liang Li, Mingming Mei, and Yongtao Zhao. 2023. "A Hierarchical Control Scheme for Adaptive Cruise Control System Based on Model Predictive Control" Actuators 12, no. 6: 249. https://doi.org/10.3390/act12060249
APA StyleMu, H., Li, L., Mei, M., & Zhao, Y. (2023). A Hierarchical Control Scheme for Adaptive Cruise Control System Based on Model Predictive Control. Actuators, 12(6), 249. https://doi.org/10.3390/act12060249






