A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery
Abstract
1. Introduction
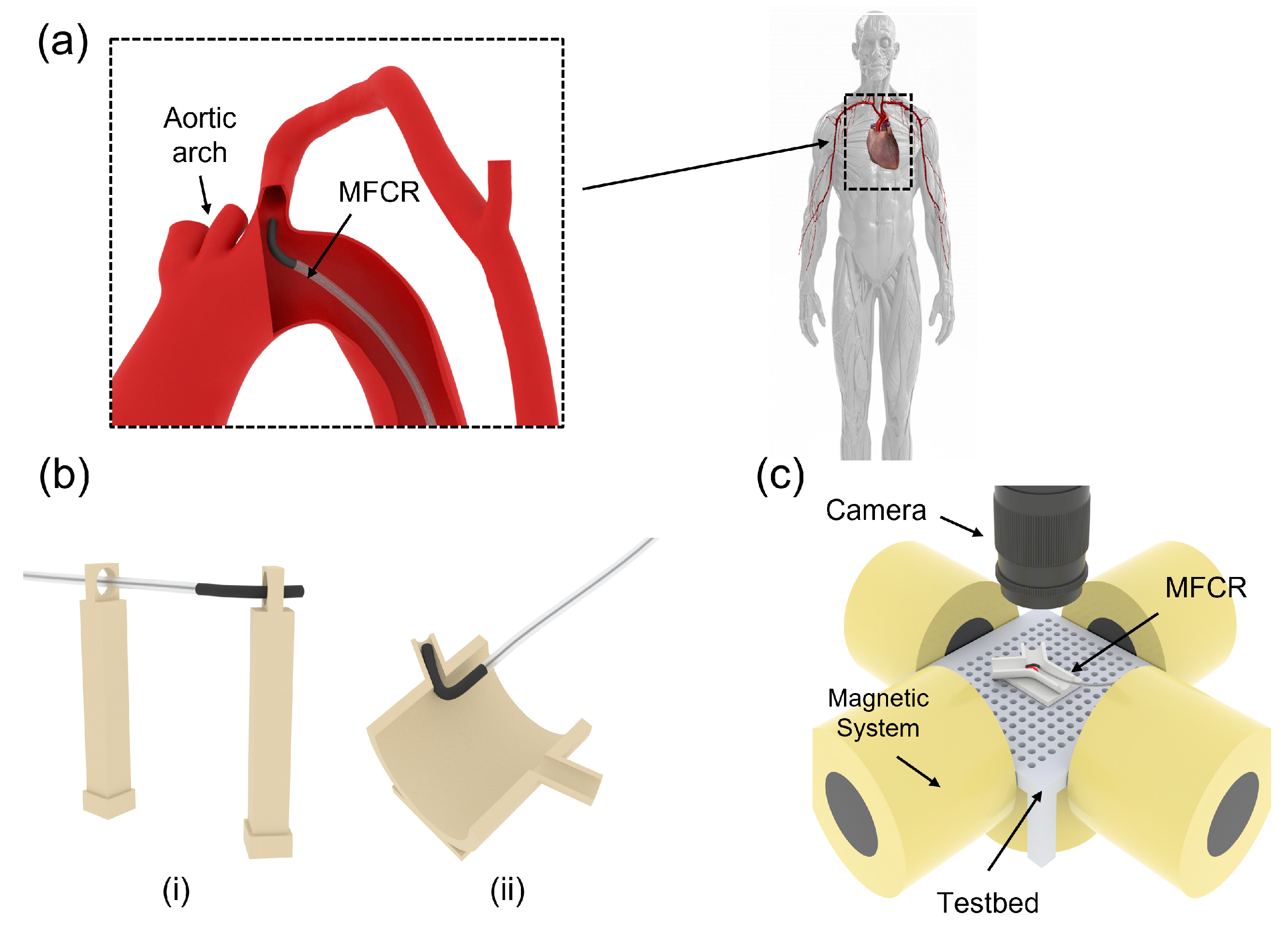
2. Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes
2.1. Deformation Principle of the Magnetic-Controlled Flexible Continuum Robot
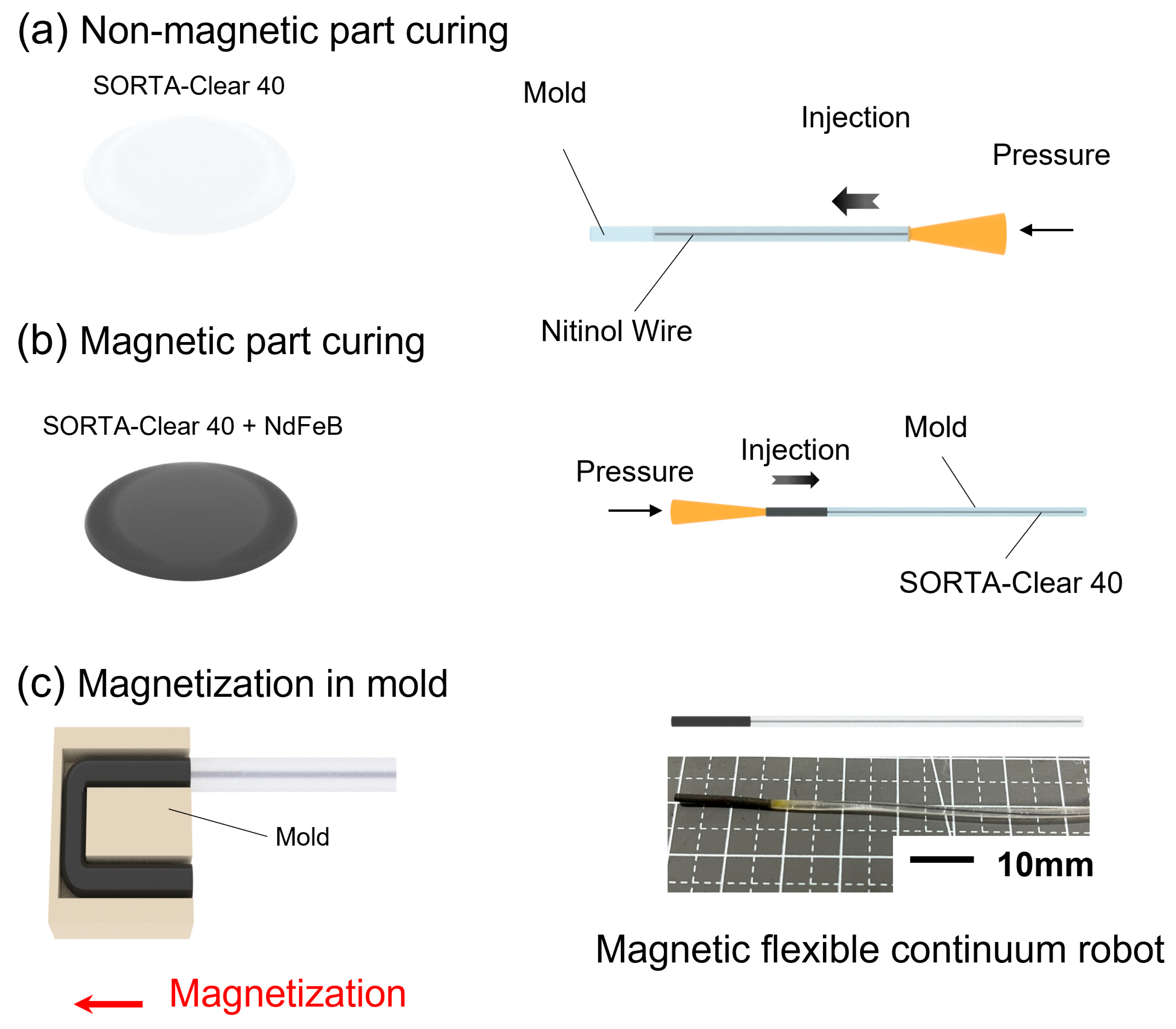
2.2. Manufacture of the Magnetic-Controlled Flexible Continuum Robot
3. Control of the Magnetic-Controlled Flexible Continuum Robot
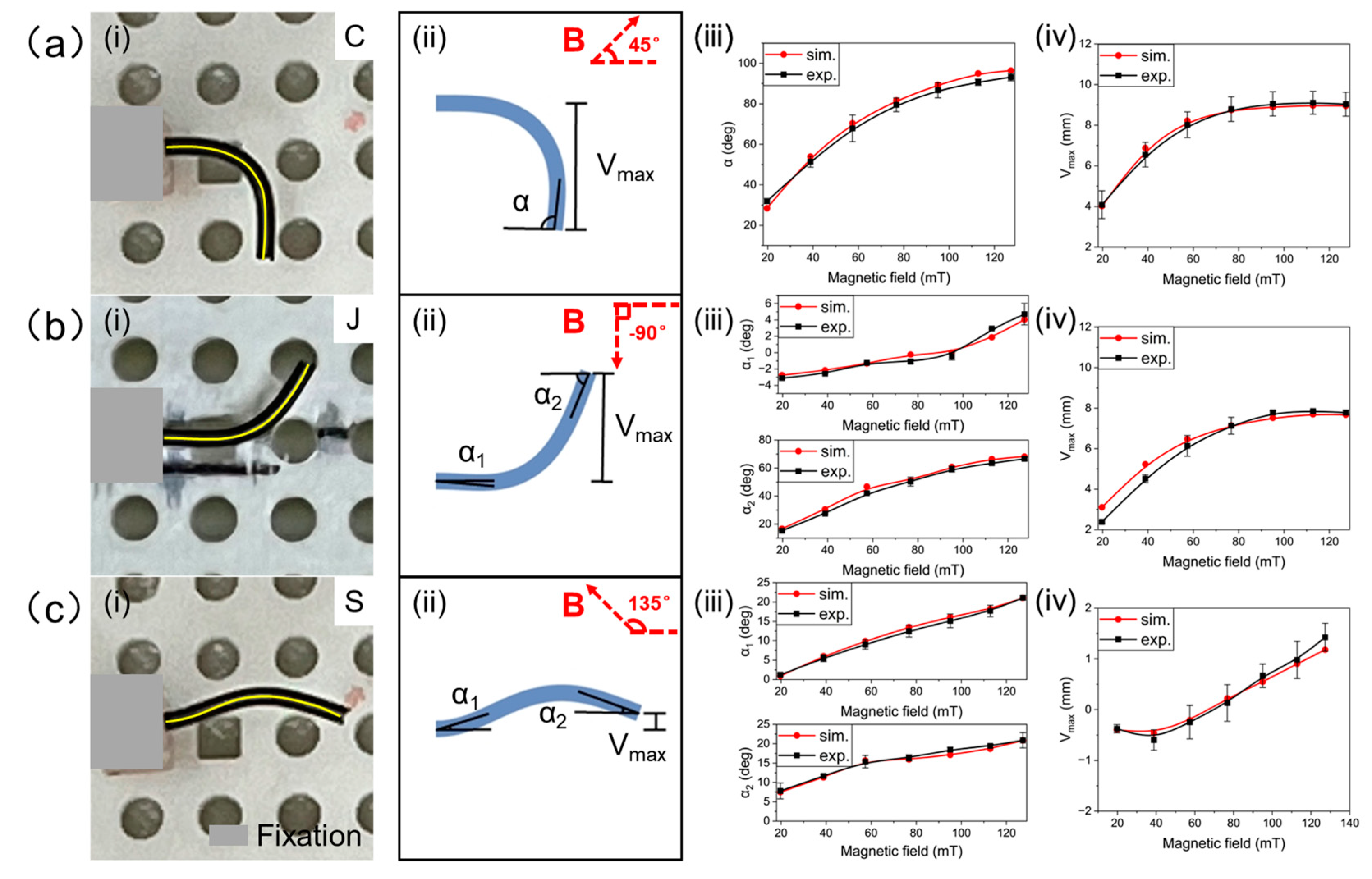
3.1. Deformation Simulation of the Magnetic-Controlled Flexible Continuum Robot
3.2. Deformation Ability of the Magnetic-Controlled Flexible Continuum Robot
3.3. Deformation in Different Situations of the Magnetic-Controlled Flexible Continuum Robot
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018, 558, 274–279. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, W.; Xi, N.; Wang, Y.; Liu, L. Development and future challenges of bio-syncretic robots. Engineering 2018, 4, 452–463. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, C.; Wang, X.; Wang, W.; Xi, N.; Liu, L. Development of micro-and nanorobotics: A review. Sci. China Technol. Sci. 2019, 62, 1–20. [Google Scholar] [CrossRef]
- Yang, G.-Z.; Fischer, P.; Nelson, B. New materials for next-generation robots. Sci. Robot. 2017, 2, eaap9294. [Google Scholar] [CrossRef]
- Yang, G.-Z.; Bellingham, J.; Dupont, P.E.; Fischer, P.; Floridi, L.; Full, R.; Jacobstein, N.; Kumar, V.; McNutt, M.; Merrifield, R. The grand challenges of Science Robotics. Sci. Robot. 2018, 3, eaar7650. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Ilami, M.; Ahmed, R.J.; Petras, A.; Beigzadeh, B.; Marvi, H. Magnetic needle steering in soft phantom tissue. Sci. Rep. 2020, 10, 2500. [Google Scholar] [CrossRef]
- Chautems, C.; Tonazzini, A.; Boehler, Q.; Jeong, S.H.; Floreano, D.; Nelson, B.J. Magnetic continuum device with variable stiffness for minimally invasive surgery. Adv. Intell. Syst. 2020, 2, 1900086. [Google Scholar] [CrossRef]
- Jager, E.W.H.; Inganäs, O.; Lundström, I. Microrobots for Micrometer-Size Objects in Aqueous Media: Potential Tools for Single-Cell Manipulation. Science 2000, 288, 2335–2338. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Kim, S.; Yoon, C.-H.; Park, H.-J.; Kim, J.-Y.; Choi, H. Fabrication and Characterization of a Magnetic Drilling Actuator for Navigation in a Three-dimensional Phantom Vascular Network. Sci. Rep. 2018, 8, 3691. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [PubMed]
- Sitti, M.; Ceylan, H.; Hu, W.; Giltinan, J.; Turan, M.; Yim, S.; Diller, E. Biomedical Applications of Untethered Mobile Milli/Microrobots. Proc. IEEE 2015, 103, 205–224. [Google Scholar] [CrossRef] [PubMed]
- Sitti, M. Voyage of the microrobots. Nature 2009, 458, 1121–1122. [Google Scholar] [CrossRef]
- Ivar Seldinger, S. Catheter replacement of the needle in percutaneous arteriography: A new technique. Acta Radiol. 2008, 49, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Louvard, Y.; Lefèvre, T.; Morice, M.-C. Percutaneous coronary intervention for bifurcation coronary disease. Heart 2004, 90, 713–722. [Google Scholar] [CrossRef] [PubMed]
- Khasawneh, F.A.; Smalligan, R.D. Guidewire-related complications during central venous catheter placement: A case report and review of the literature. Case Rep. Crit. Care 2011, 2011, 287261. [Google Scholar] [CrossRef]
- Roubin, G.S.; Yadav, S.; Iyer, S.S.; Vitek, J. Carotid stent-supported angioplasty: A neurovascular intervention to prevent stroke. Am. J. Cardiol. 1996, 78, 8–12. [Google Scholar] [CrossRef]
- Levin, D.C.; Rao, V.M.; Parker, L.; Bonn, J.; Maitino, A.J.; Sunshine, J.H. The changing roles of radiologists, cardiologists, and vascular surgeons in percutaneous peripheral arterial interventions during a recent five-year interval. J. Am. Coll. Radiol. 2005, 2, 39–42. [Google Scholar] [CrossRef]
- Jones, W.S.; Mi, X.; Qualls, L.G.; Vemulapalli, S.; Peterson, E.D.; Patel, M.R.; Curtis, L.H. Trends in settings for peripheral vascular intervention and the effect of changes in the outpatient prospective payment system. J. Am. Coll. Cardiol. 2015, 65, 920–927. [Google Scholar] [CrossRef]
- Dupont, P.E.; Simaan, N.; Choset, H.; Rucker, C. Continuum Robots for Medical Interventions. Proc. IEEE Inst. Electr. Electron. Eng. 2022, 110, 847–870. [Google Scholar] [CrossRef]
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum Robots: An Overview. Adv. Intell. Syst. 2023, 5, 2200367. [Google Scholar] [CrossRef]
- Ghoreishi, S.F.; Sochol, R.D.; Gandhi, D.; Krieger, A.; Fuge, M. Bayesian Optimization for Design of Multi-Actuator Soft Catheter Robots. IEEE Trans. Med. Robot. Bionics 2021, 3, 725–737. [Google Scholar] [CrossRef] [PubMed]
- Phelan Iii, M.F.; Tiryaki, M.E.; Lazovic, J.; Gilbert, H.; Sitti, M. Heat-Mitigated Design and Lorentz Force-Based Steering of an MRI-Driven Microcatheter toward Minimally Invasive Surgery. Adv. Sci. 2022. [Google Scholar] [CrossRef]
- Gunduz, S.; Albadawi, H.; Oklu, R. Robotic devices for minimally invasive endovascular interventions: A new dawn for interventional radiology. Adv. Intell. Syst. 2021, 3, 2000181. [Google Scholar] [CrossRef]
- Wang, T.; van Soest, G.; van der Steen, A.F.W. A micromotor catheter for intravascular optical coherence tomography. Engineering 2015, 1, 15–17. [Google Scholar] [CrossRef]
- Hou, S.; Li, Y.; Zou, C.; Li, Y.; Tang, H.; Liu, Z.; Chen, S.; Peng, J. A Novel Distal Micromotor-Based Side-Looking Intravascular Ultrasound Transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021, 69, 283–290. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yang, X.; Zheng, X.; Du, N.; Zhen, H.; Hou, Z. Design and Analysis for Minimally Invasive Vascular Interventional Surgical Robot System. Adv. Sci. Lett. 2012, 8, 31–36. [Google Scholar] [CrossRef]
- Wang, K.; Lu, Q.; Chen, B.; Shen, Y.; Li, H.; Liu, M.; Xu, Z. Endovascular intervention robot with multi-manipulators for surgical procedures: Dexterity, adaptability, and practicability. Robot. Comput. -Integr. Manuf. 2019, 56, 75–84. [Google Scholar] [CrossRef]
- Ai, X.; Gao, A.; Lin, Z.; He, C.; Chen, W. A Multi-Contact-Aided Continuum Manipulator with Anisotropic Shapes. IEEE Robot. Autom. Lett. 2021, 6, 4560–4567. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Lueth, T.C. Optimization of Stress Distribution in Tendon-Driven Continuum Robots Using Fish-Tail-Inspired Method. IEEE Robot. Autom. Lett. 2022, 7, 3380–3387. [Google Scholar] [CrossRef]
- Tutcu, C.; Baydere, B.A.; Talas, S.K.; Samur, E. Quasi-static modeling of a novel growing soft-continuum robot. Int. J. Robot. Res. 2021, 40, 86–98. [Google Scholar] [CrossRef]
- Couture, T.; Szewczyk, J. Design and experimental validation of an active catheter for endovascular navigation. J. Med. Devices 2018, 12, 011003. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M. Nonlinear geometrically exact dynamics of fluid-conveying cantilevered hard magnetic soft pipe with uniform and nonuniform magnetizations. Mech. Syst. Signal Process. 2023, 188, 110016. [Google Scholar] [CrossRef]
- Kim, Y.; Genevriere, E.; Harker, P.; Choe, J.; Balicki, M.; Regenhardt, R.W.; Vranic, J.E.; Dmytriw, A.A.; Patel, A.B.; Zhao, X. Telerobotic neurovascular interventions with magnetic manipulation. Sci. Robot. 2022, 7, eabg9907. [Google Scholar] [CrossRef] [PubMed]
- Zrínyi, M.; Barsi, L.; Büki, A. Deformation of ferrogels induced by nonuniform magnetic fields. J. Chem. Phys. 1996, 104, 8750–8756. [Google Scholar] [CrossRef]
- Kumar, N.; Wirekoh, J.; Saba, S.; Riviere, C.N.; Park, Y.-L. Soft miniaturized actuation and sensing units for dynamic force control of cardiac ablation catheters. Soft Robot. 2021, 8, 59–70. [Google Scholar] [CrossRef]
- Guo, Z.; Dong, Z.; Lee, K.-H.; Cheung, C.L.; Fu, H.-C.; Ho, J.D.L.; He, H.; Poon, W.-S.; Chan, D.T.-M.; Kwok, K.-W. Compact design of a hydraulic driving robot for intraoperative MRI-guided bilateral stereotactic neurosurgery. IEEE Robot. Autom. Lett. 2018, 3, 2515–2522. [Google Scholar] [CrossRef]
- Martin, J.W.; Scaglioni, B.; Norton, J.C.; Subramanian, V.; Arezzo, A.; Obstein, K.L.; Valdastri, P. Enabling the future of colonoscopy with intelligent and autonomous magnetic manipulation. Nat. Mach. Intell. 2020, 2, 595–606. [Google Scholar] [CrossRef]
- Leong, F.; Garbin, N.; Natali, C.D.; Mohammadi, A.; Thiruchelvam, D.; Oetomo, D.; Valdastri, P. Magnetic Surgical Instruments for Robotic Abdominal Surgery. IEEE Rev. Biomed. Eng. 2016, 9, 66–78. [Google Scholar] [CrossRef]
- Bacchetti, A.; Lloyd, P.; Taccola, S.; Fakhoury, E.; Cochran, S.; Harris, R.A.; Valdastri, P.; Chandler, J.H. Optimization and fabrication of programmable domains for soft magnetic robots: A review. Front. Robot. AI 2022, 9, 1040984. [Google Scholar] [CrossRef]
- Jeon, S.; Hoshiar, A.K.; Kim, S.; Lee, S.; Kim, E.; Lee, S.; Kim, K.; Lee, J.; Kim, J.-Y.; Choi, H. Improving guidewire-mediated steerability of a magnetically actuated flexible microrobot. Micro Nano Syst. Lett. 2018, 6, 15. [Google Scholar] [CrossRef]
- Lin, D.; Wang, J.; Jiao, N.; Wang, Z.; Liu, L. A Flexible Magnetically Controlled Continuum Robot Steering in the Enlarged Effective Workspace with Constraints for Retrograde Intrarenal Surgery. Adv. Intell. Syst. 2021, 3, 2000211. [Google Scholar] [CrossRef]
- Yang, X.; Shang, W.; Lu, H.; Liu, Y.; Yang, L.; Tan, R.; Wu, X.; Shen, Y. An agglutinate magnetic spray transforms inanimate objects into millirobots for biomedical applications. Sci. Robot. 2020, 5, eabc8191. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Huang, T.-Y.; Luo, Z.; Testa, P.; Gu, H.; Chen, X.-Z.; Nelson, B.J.; Heyderman, L.J. Nanomagnetic encoding of shape-morphing micromachines. Nature 2019, 575, 164–168. [Google Scholar] [CrossRef] [PubMed]
- Ze, Q.; Kuang, X.; Wu, S.; Wong, J.; Montgomery, S.M.; Zhang, R.; Kovitz, J.M.; Yang, F.; Qi, H.J.; Zhao, R. Magnetic shape memory polymers with integrated multifunctional shape manipulation. Adv. Mater. 2020, 32, 1906657. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Jiao, N.; Wang, Z.; Liu, L. A Magnetic Continuum Robot with Multi-Mode Control Using Opposite-Magnetized Magnets. IEEE Robot. Autom. Lett. 2021, 6, 2485–2492. [Google Scholar] [CrossRef]
- Jeon, S.; Hoshiar, A.K.; Kim, K.; Lee, S.; Kim, E.; Lee, S.; Kim, J.-Y.; Nelson, B.J.; Cha, H.-J.; Yi, B.-J. A magnetically controlled soft microrobot steering a guidewire in a three-dimensional phantom vascular network. Soft Robot. 2019, 6, 54–68. [Google Scholar] [CrossRef]
- Xu, W.; Liu, T.; Li, Y. Kinematics, dynamics, and control of a cable-driven hyper-redundant manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Ouyang, B.; Liu, Y.; Tam, H.Y.; Sun, D. Design of an Interactive Control System for a Multisection Continuum Robot. IEEE/ASME Trans. Mechatron. 2018, 23, 2379–2389. [Google Scholar] [CrossRef]
- Renda, F.; Giorelli, M.; Calisti, M.; Cianchetti, M.; Laschi, C. Dynamic model of a multibending soft robot arm driven by cables. IEEE Trans. Robot. 2014, 30, 1109–1122. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef]
- Li, Q.; Li, S.; Zhang, X.; Xu, W.; Han, X. Programmed magnetic manipulation of vesicles into spatially coded prototissue architectures arrays. Nat. Commun. 2020, 11, 232. [Google Scholar] [CrossRef] [PubMed]
- Lum, G.Z.; Ye, Z.; Dong, X.; Marvi, H.; Erin, O.; Hu, W.; Sitti, M. Shape-programmable magnetic soft matter. Proc. Natl. Acad. Sci. USA 2016, 113, E6007–E6015. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Wang, L.; Xia, N.; Yang, Z.; Zhang, C.; Pan, C.; Jin, D.; Zhang, J.; Majidi, C.; Zhang, L. Untethered small-scale magnetic soft robot with programmable magnetization and integrated multifunctional modules. Sci. Adv. 2022, 8, eabn8932. [Google Scholar] [CrossRef] [PubMed]
- Pittiglio, G.; Lloyd, P.; da Veiga, T.; Onaizah, O.; Pompili, C.; Chandler, J.H.; Valdastri, P. Patient-Specific Magnetic Catheters for Atraumatic Autonomous Endoscopy. Soft Robot. 2022, 9, 1120–1133. [Google Scholar] [CrossRef]
- Jiles, D. Introduction to Magnetism and Magnetic Materials; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Zhao, R.; Kim, Y.; Chester, S.A.; Sharma, P.; Zhao, X. Mechanics of hard-magnetic soft materials. J. Mech. Phys. Solids 2019, 124, 244–263. [Google Scholar] [CrossRef]
- Wang, L.; Kim, Y.; Guo, C.F.; Zhao, X. Hard-magnetic elastica. J. Mech. Phys. Solids 2020, 142, 104045. [Google Scholar] [CrossRef]

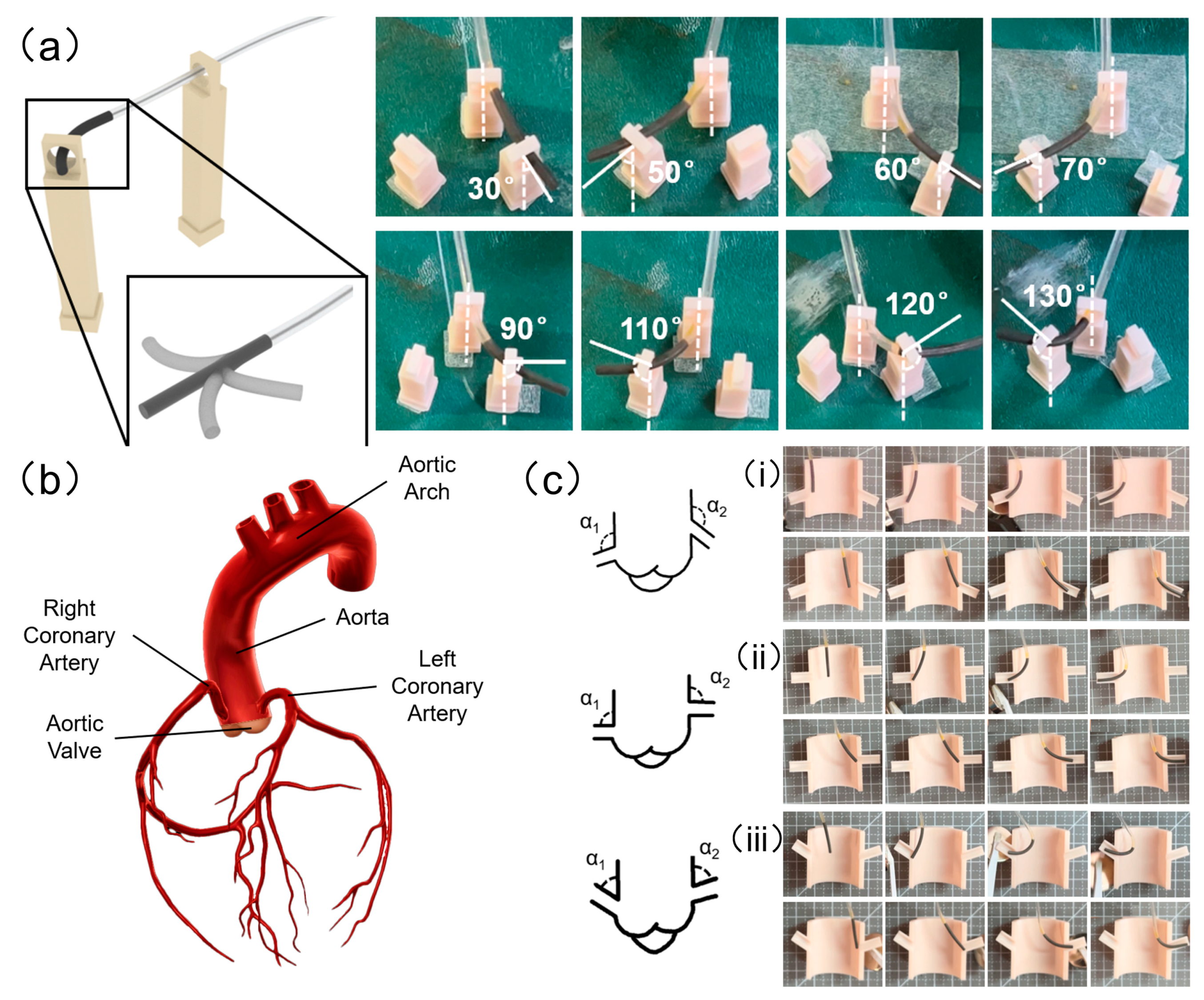

| Type | α1 | α2 |
|---|---|---|
| Acute Angle | 123.0° | 109.3° |
| Right Angle | 90.0° | 90.0° |
| Obtuse Angle | 72.0° | 65.0° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Weng, D.; Li, Z.; Chen, L.; Ma, Y.; Wang, J. A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery. Actuators 2023, 12, 247. https://doi.org/10.3390/act12060247
Wang Z, Weng D, Li Z, Chen L, Ma Y, Wang J. A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery. Actuators. 2023; 12(6):247. https://doi.org/10.3390/act12060247
Chicago/Turabian StyleWang, Zili, Ding Weng, Zhaoxin Li, Lei Chen, Yuan Ma, and Jiadao Wang. 2023. "A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery" Actuators 12, no. 6: 247. https://doi.org/10.3390/act12060247
APA StyleWang, Z., Weng, D., Li, Z., Chen, L., Ma, Y., & Wang, J. (2023). A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery. Actuators, 12(6), 247. https://doi.org/10.3390/act12060247







