Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension
Abstract
1. Introduction
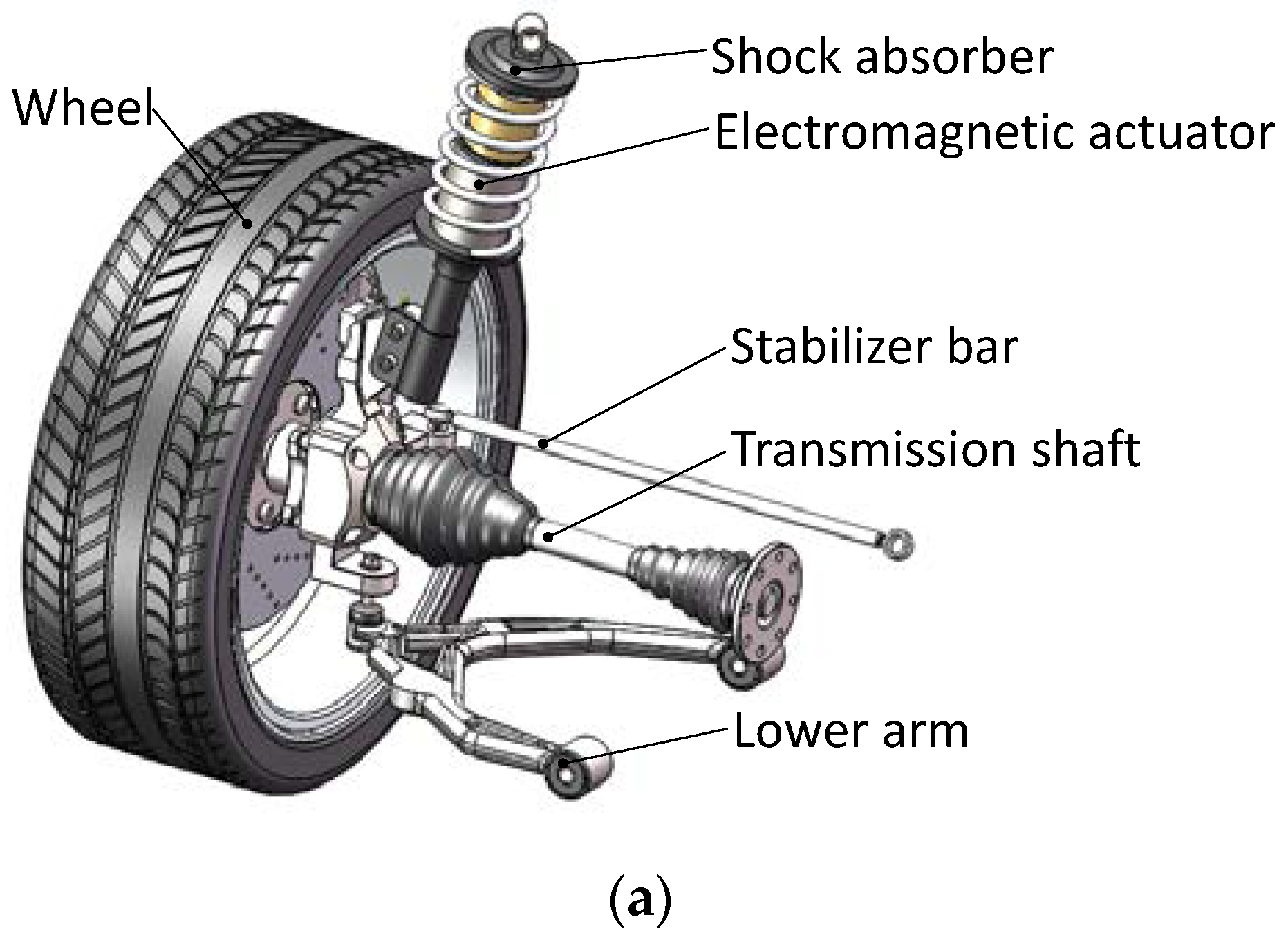
2. Structure and Principle
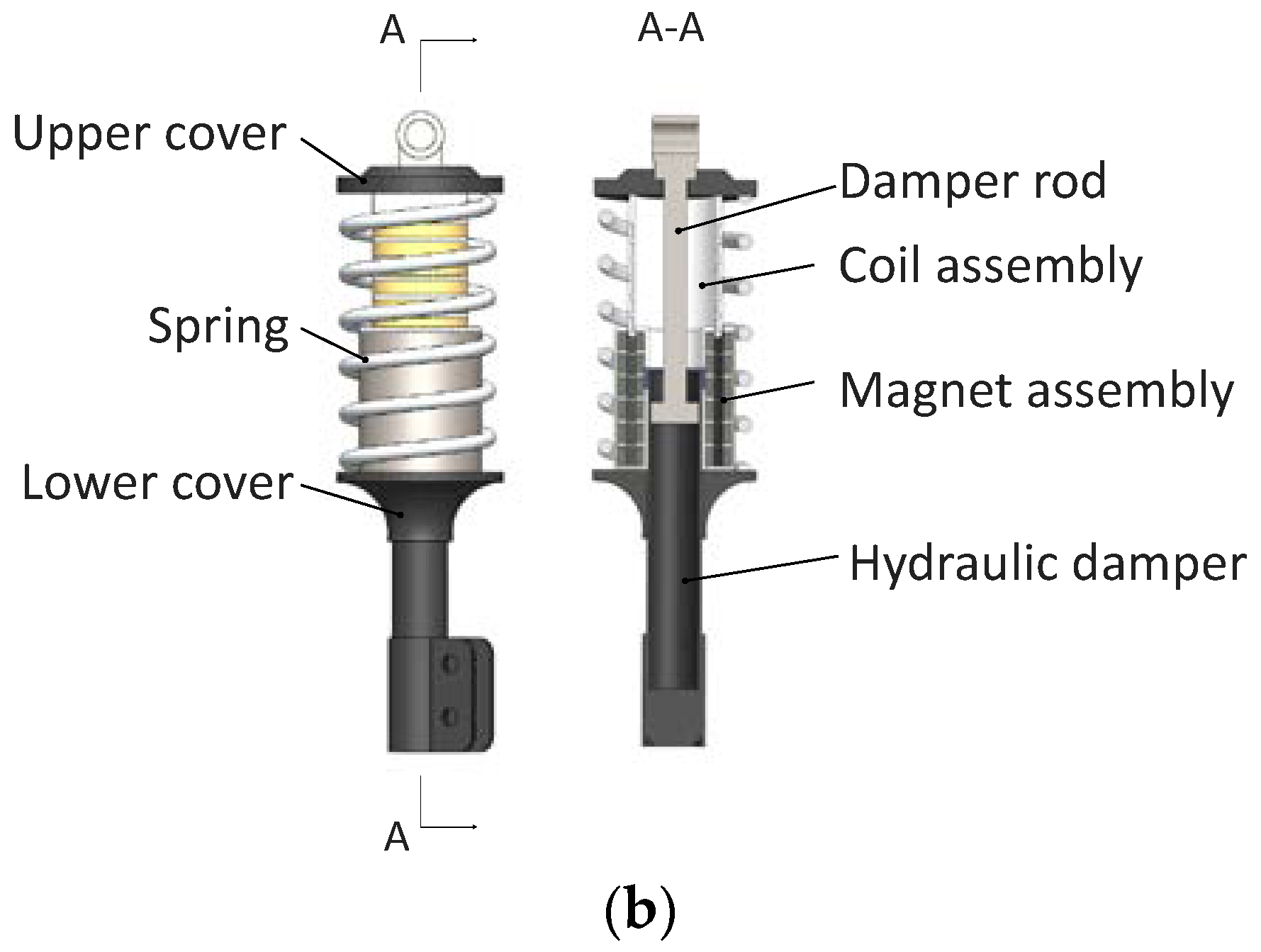
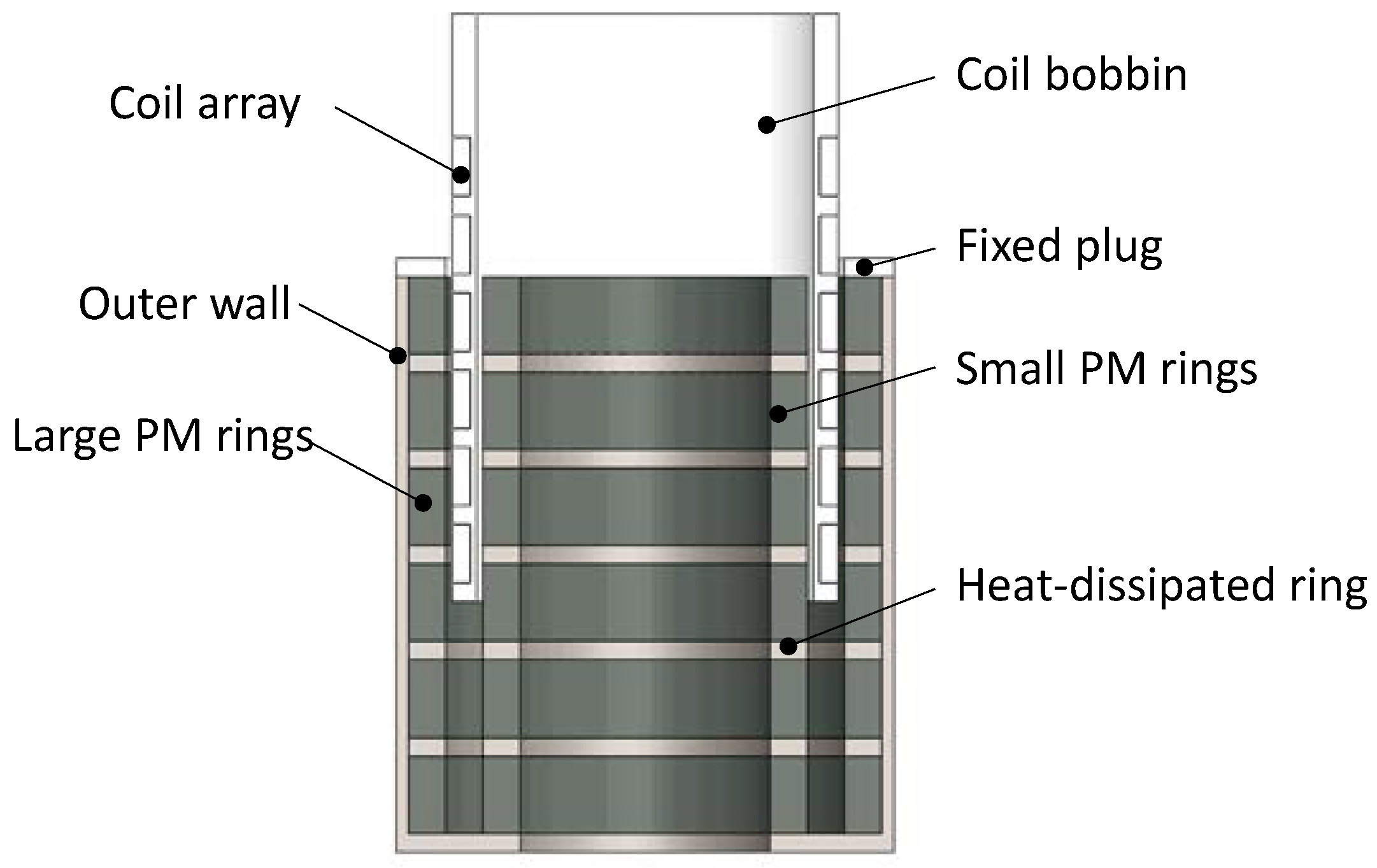
2.1. Design of the Electromagnetic Actuator
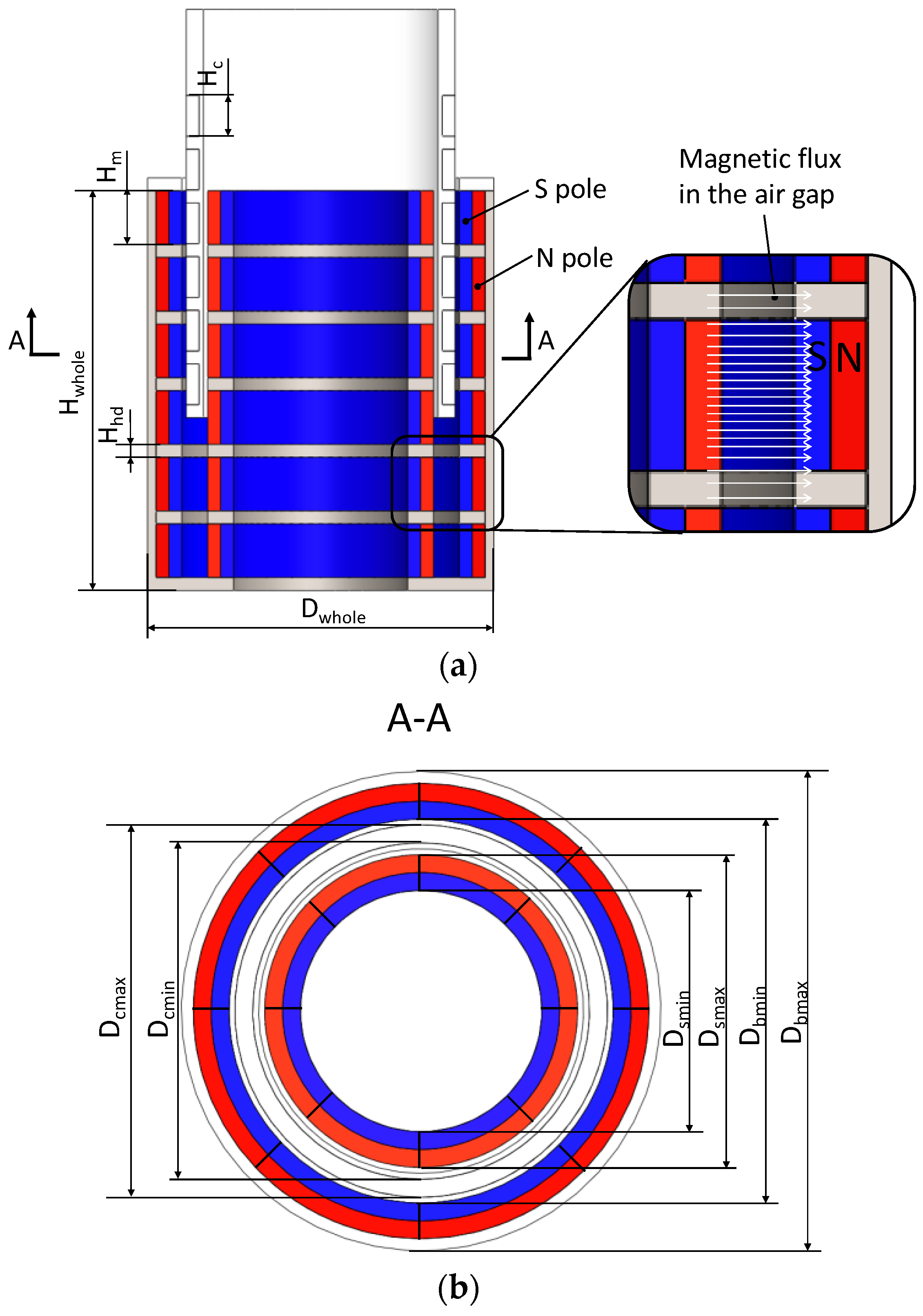
2.2. Sizes and Principles of the Electromagnetic Actuator
3. Model and Analysis of the Magnetic Field
3.1. Magnetic Flux Density Model of a Single PM Ring
3.2. Magnetic Flux Density Model of the Magnet Assembly
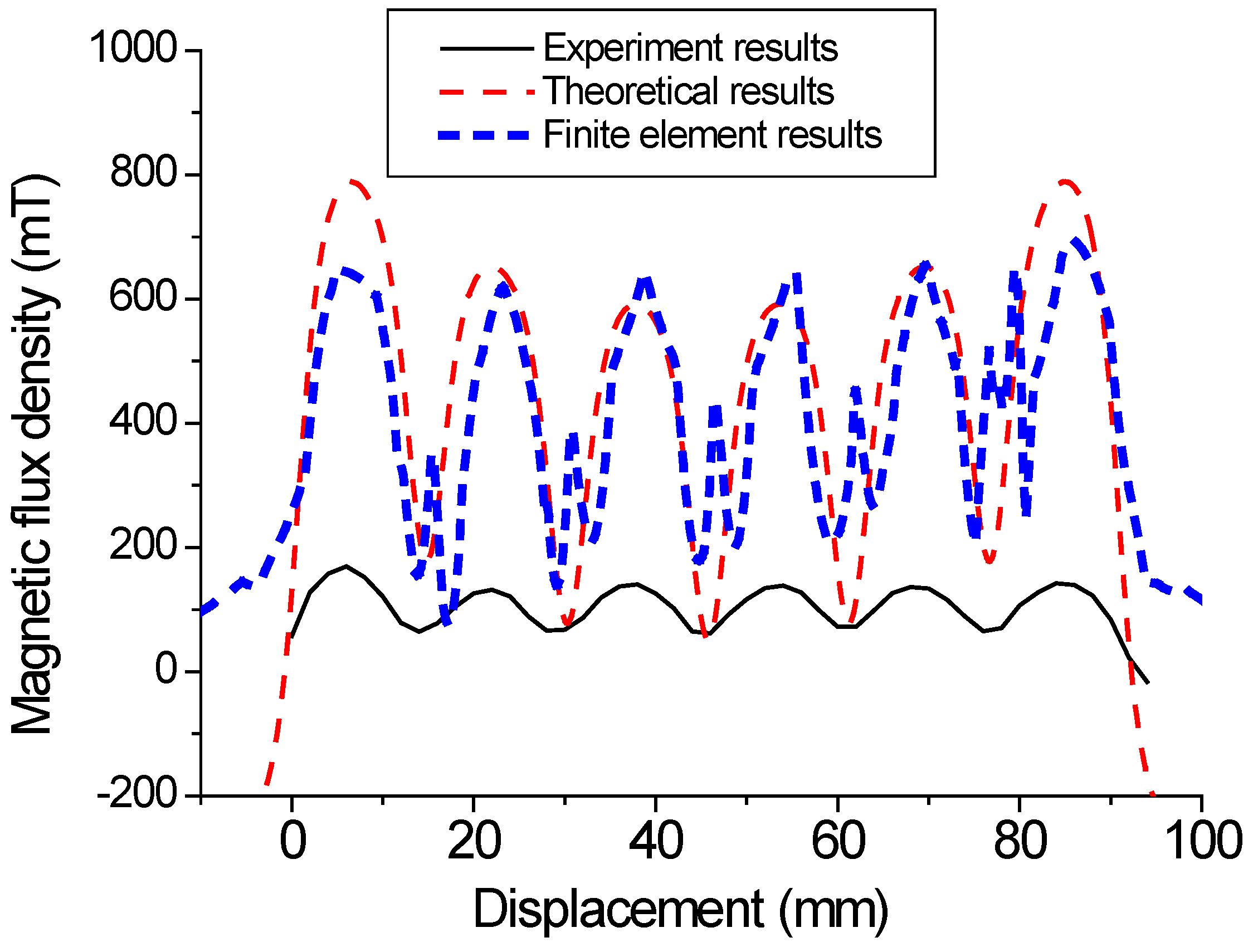
3.3. Theoretical Analysis of Magnetic Flux Density
4. FEM Analysis of the Magnetic Field
4.1. FEM Analysis Model
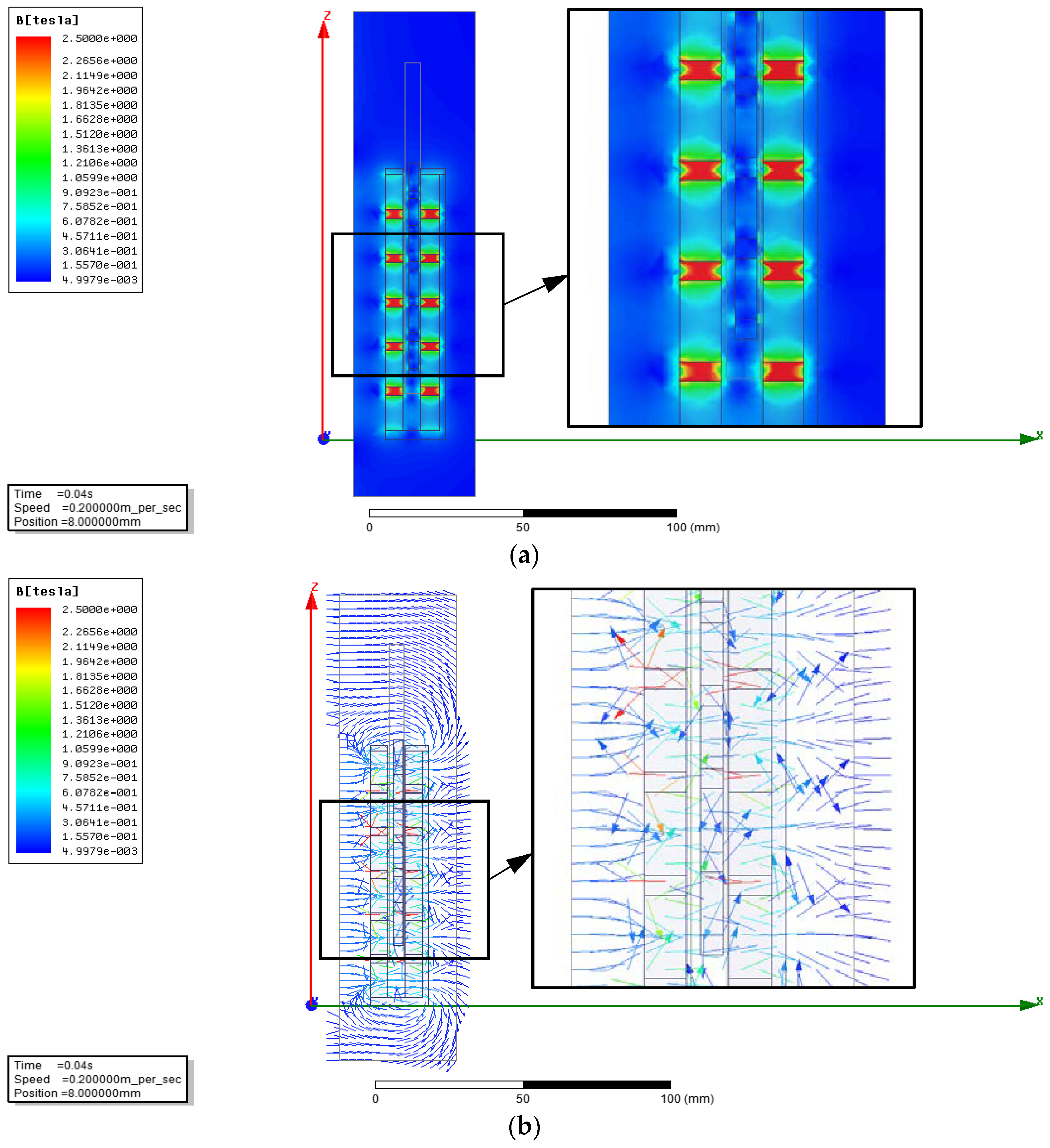
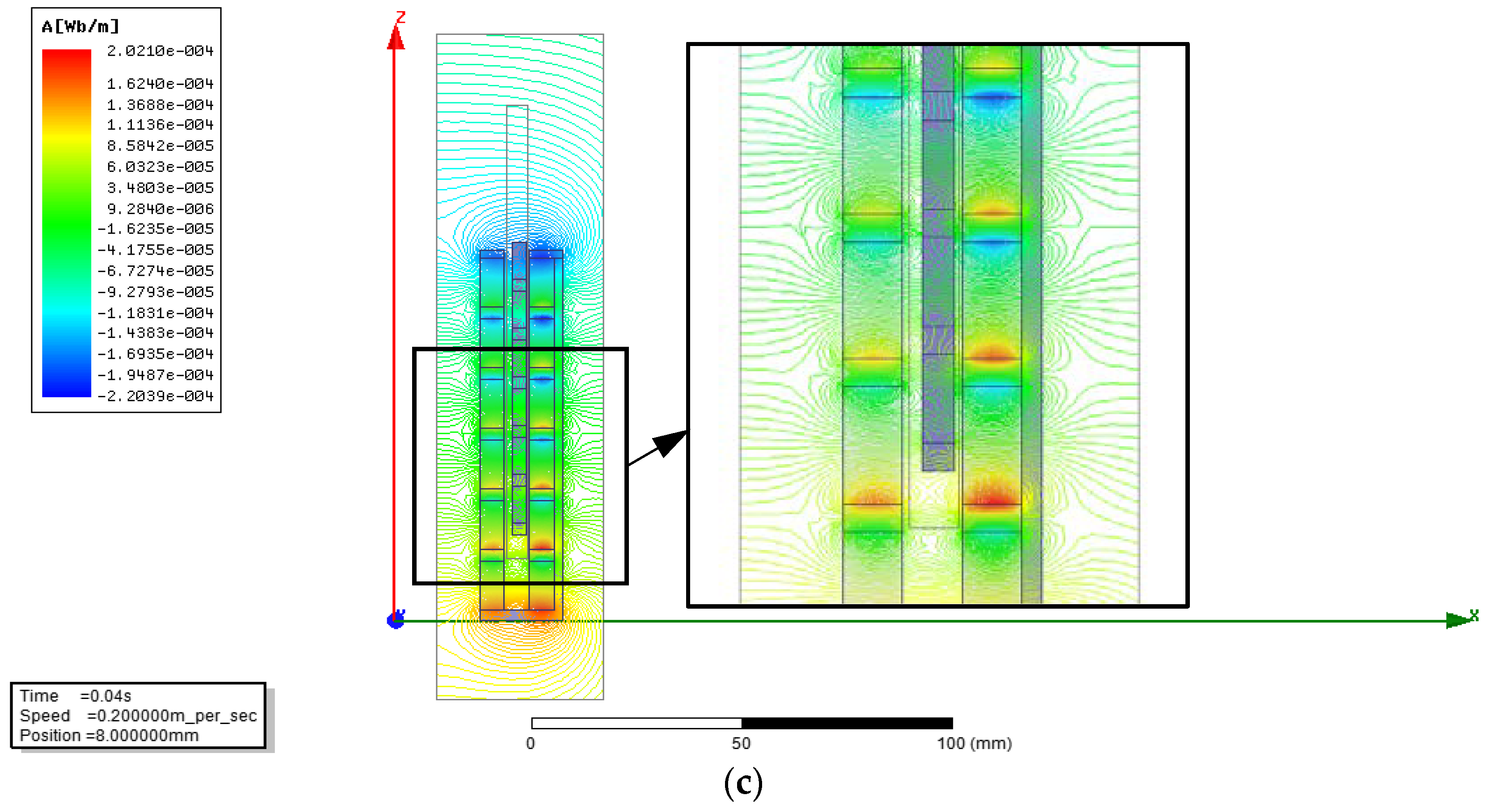
4.2. FEM Analysis on the Magnetic Field
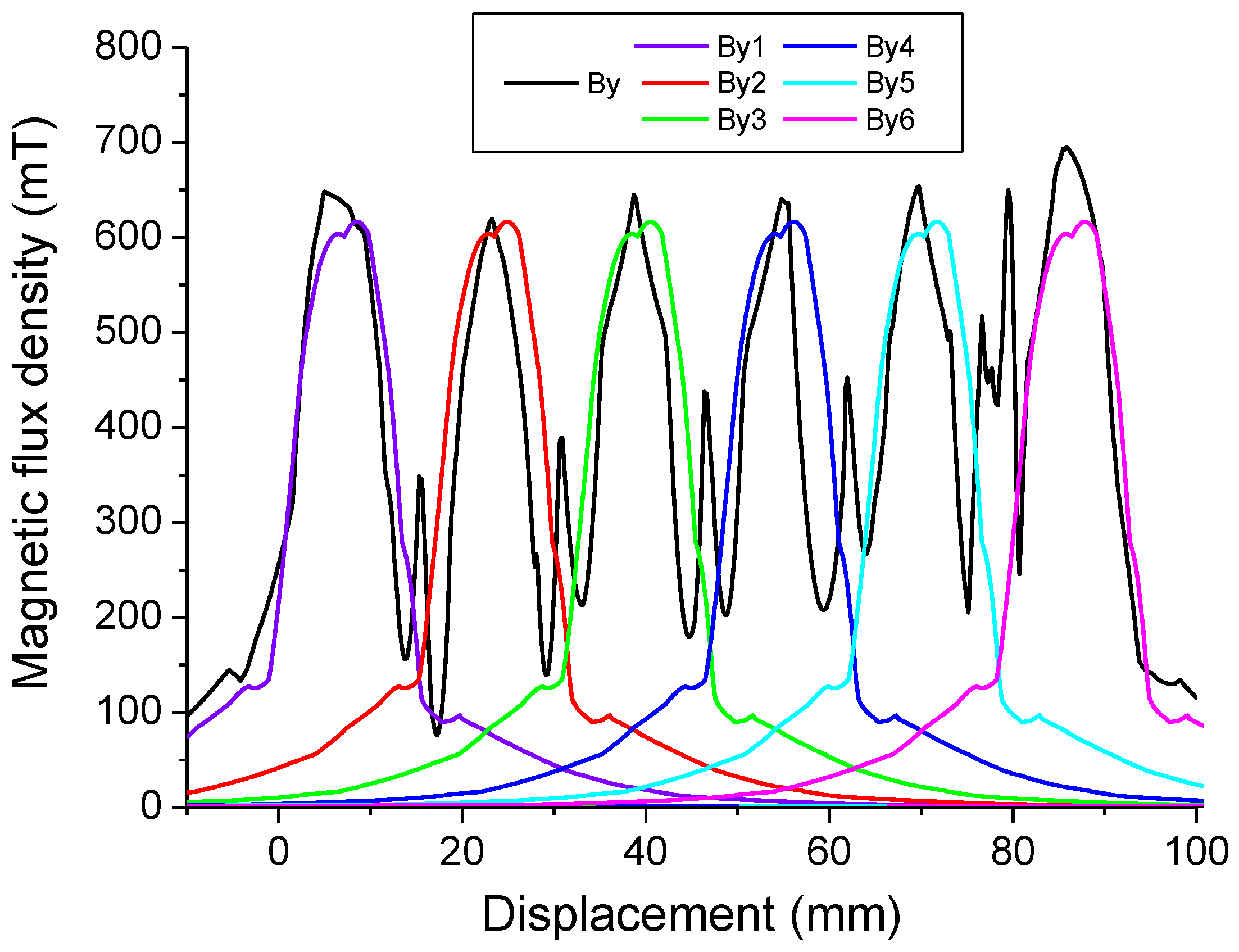
4.3. FEM Analysis of the Magnetic Flux Density
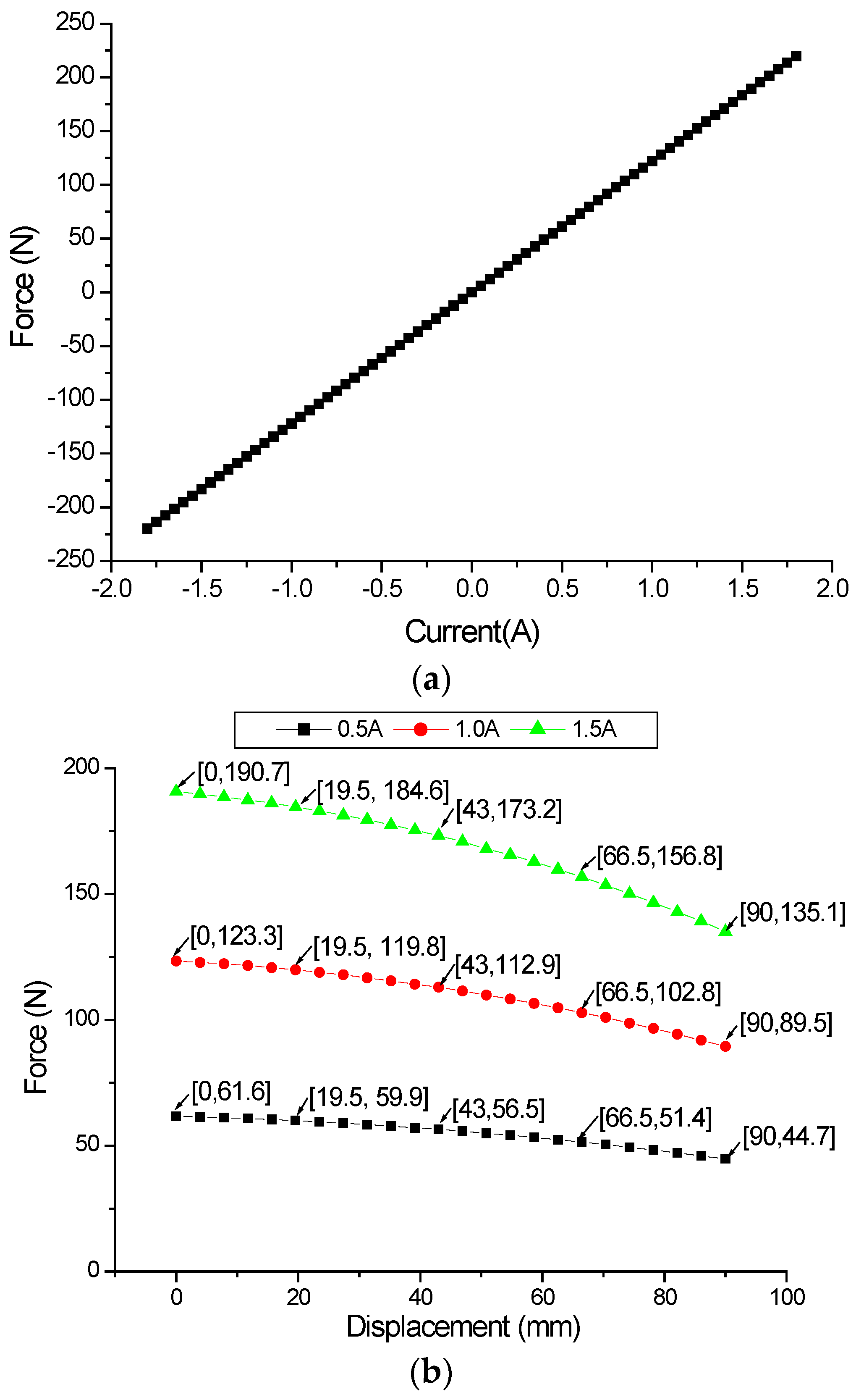
4.4. FEM Analysis on Magnetic Force
5. Vehicle Simulation Based on the Fuzzy PID Algorithm
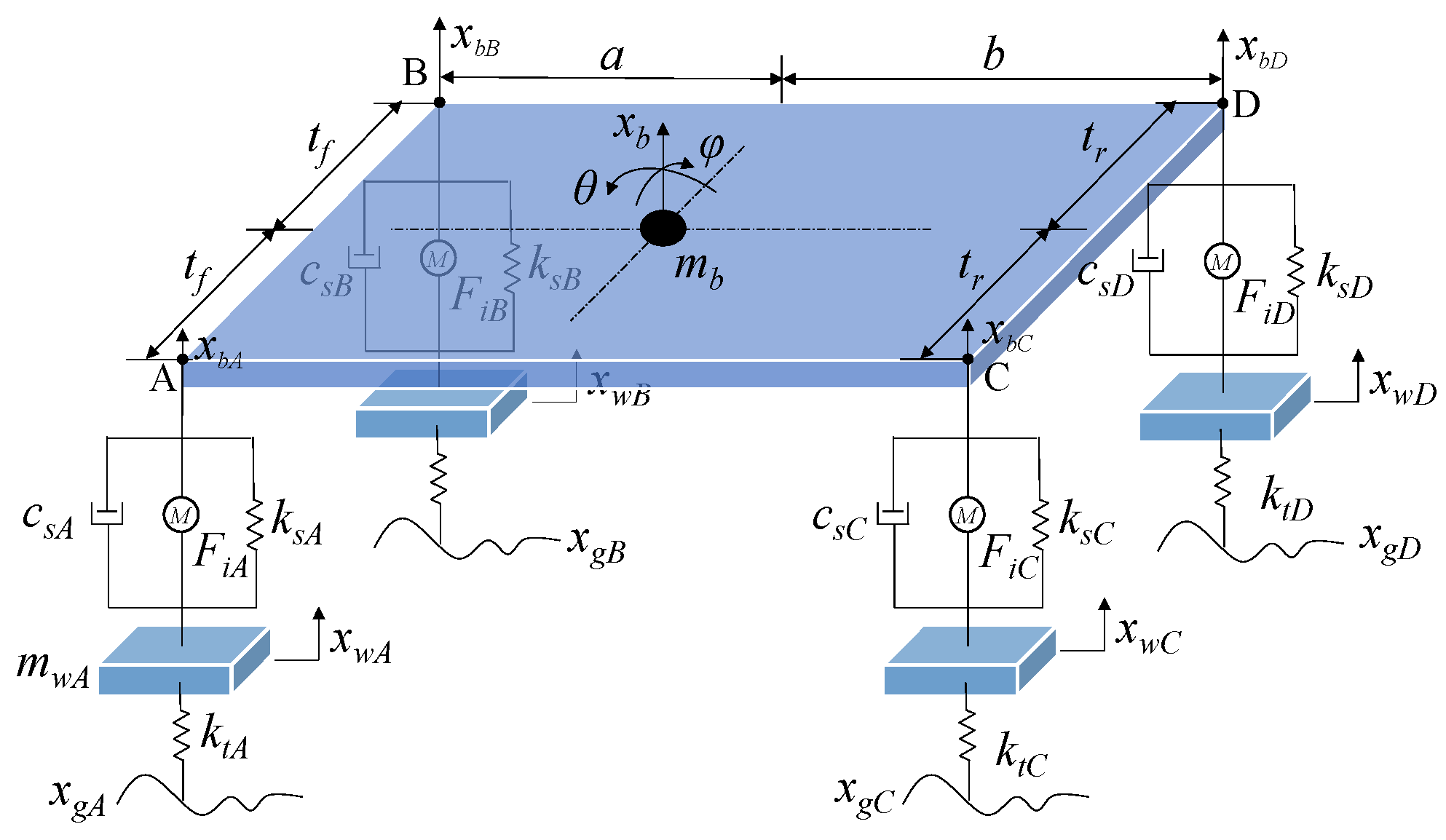
5.1. Vehicle Dynamics Model
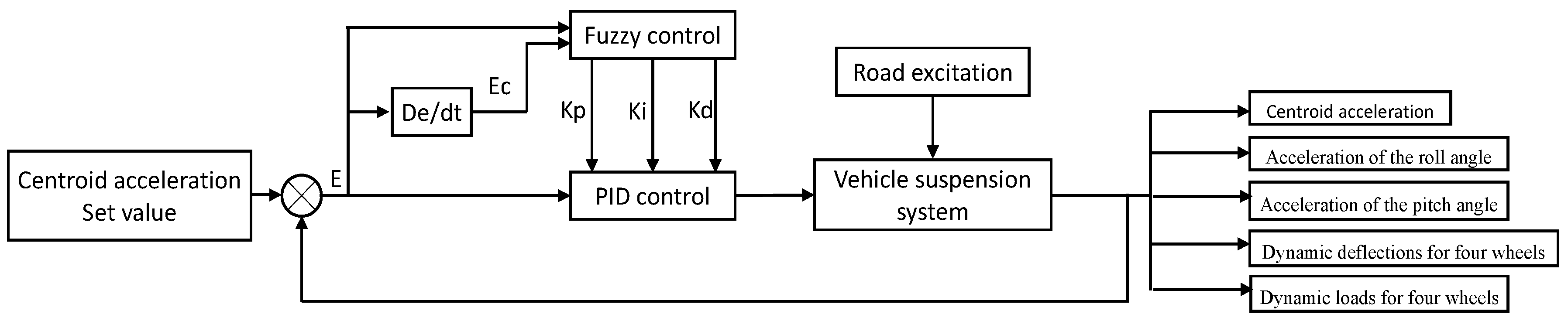
5.2. Fuzzy PID Control Algorithm
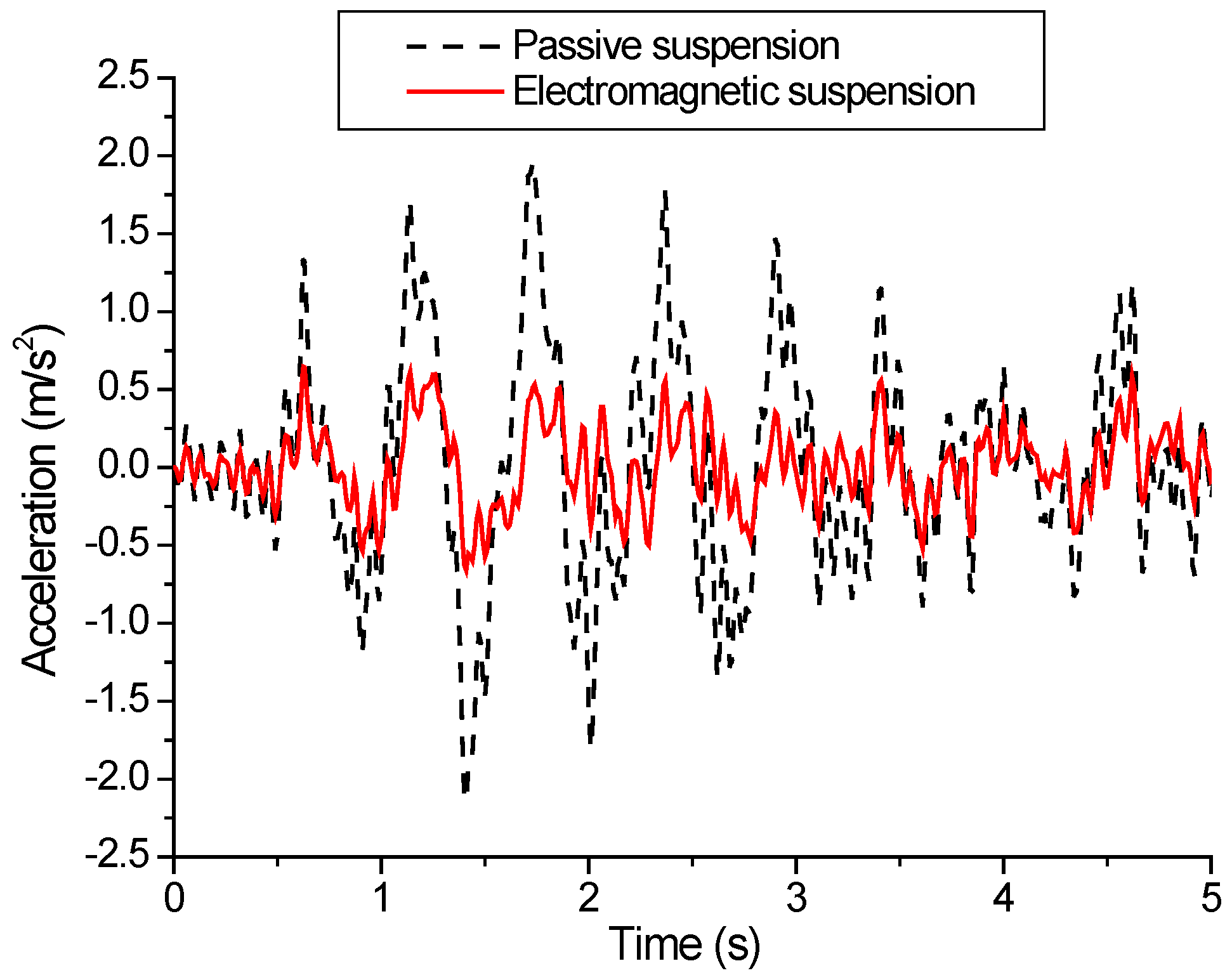
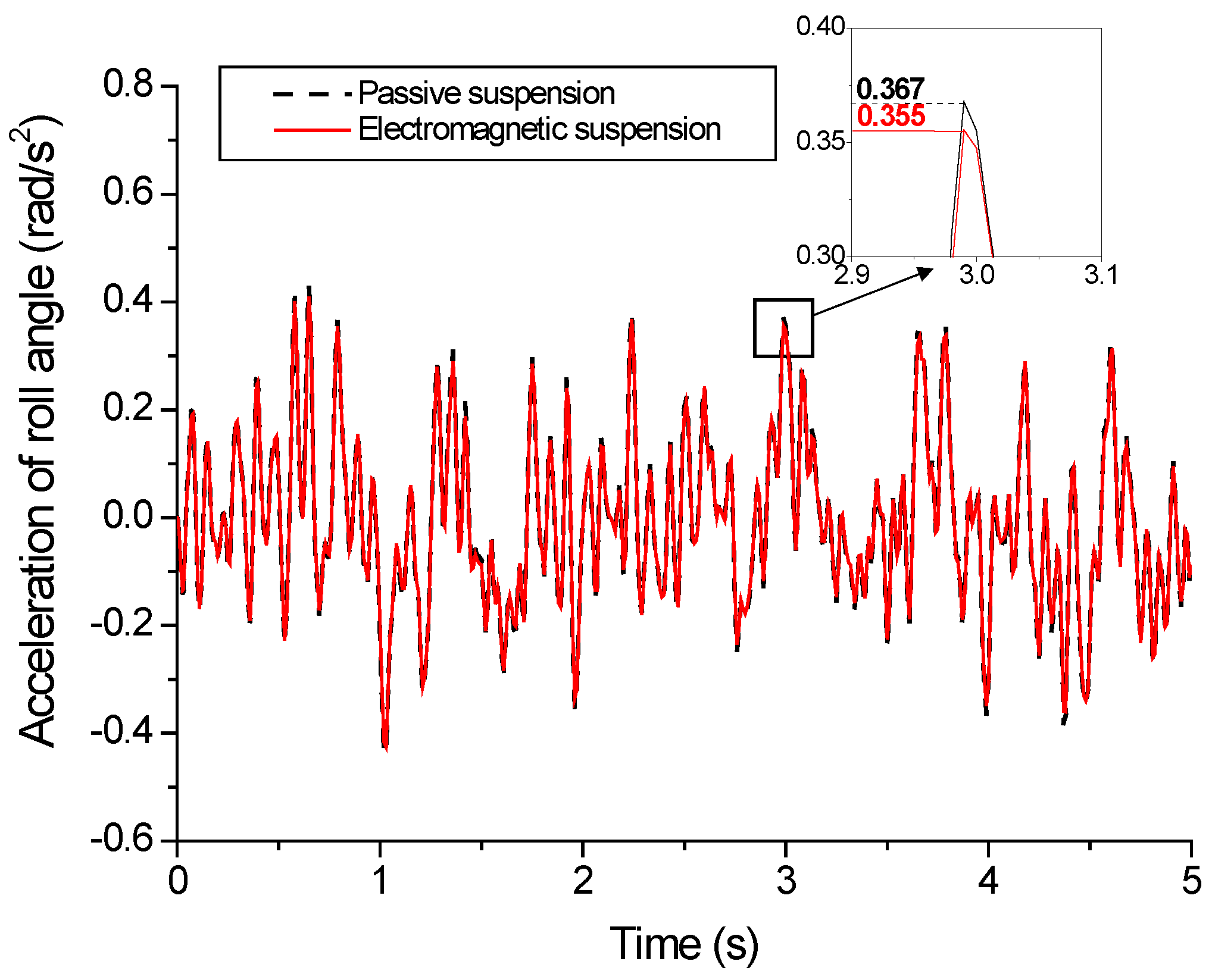
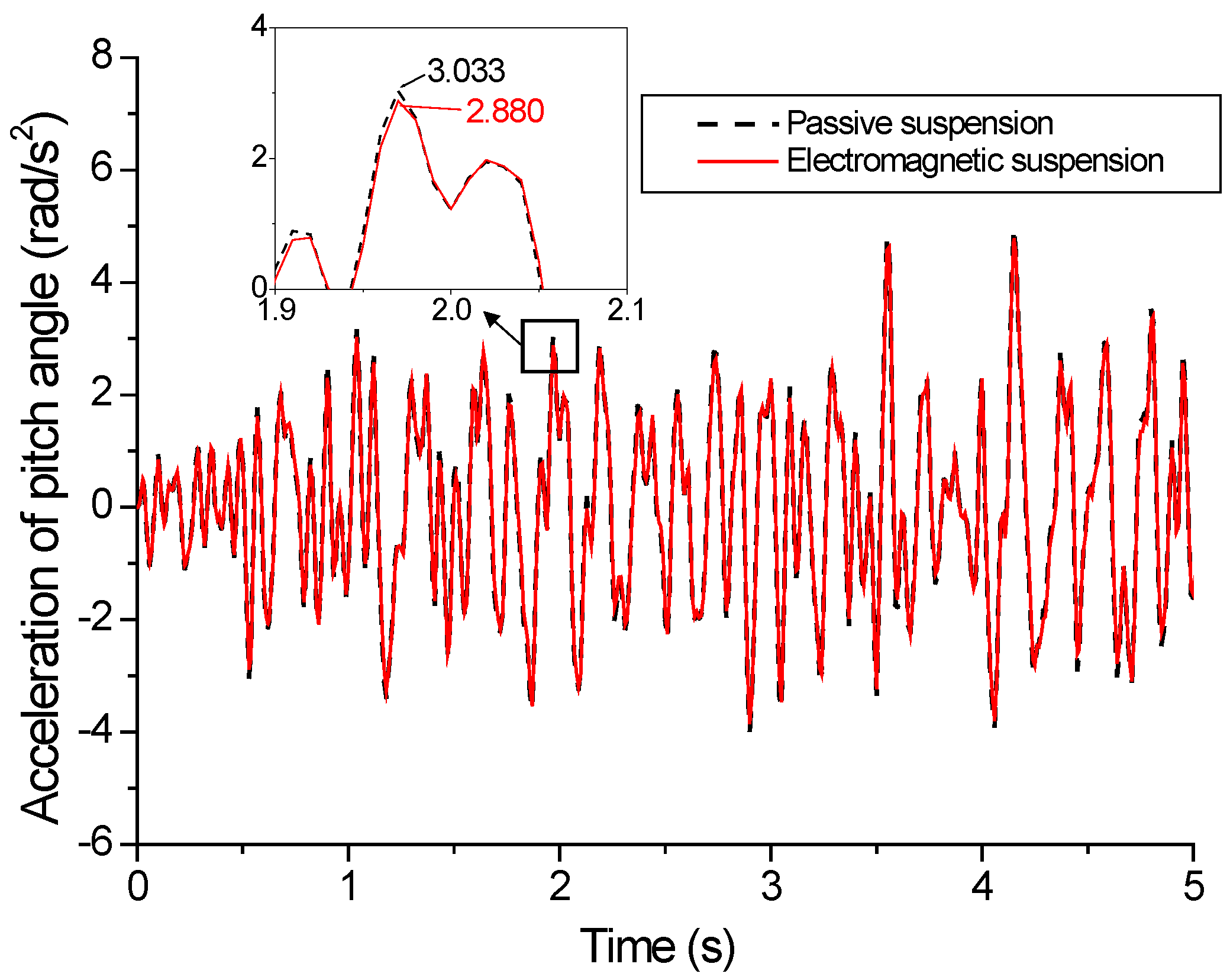
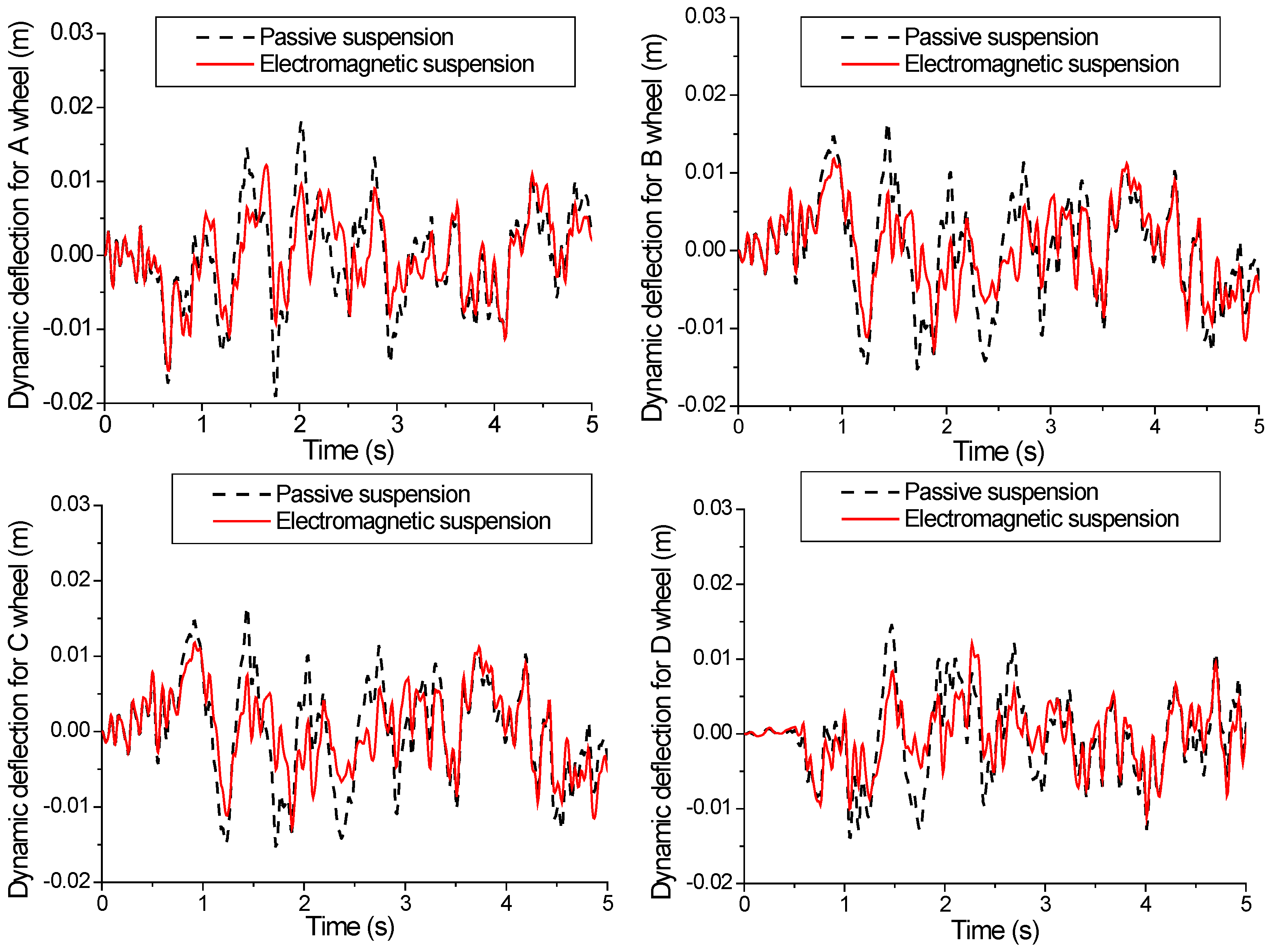
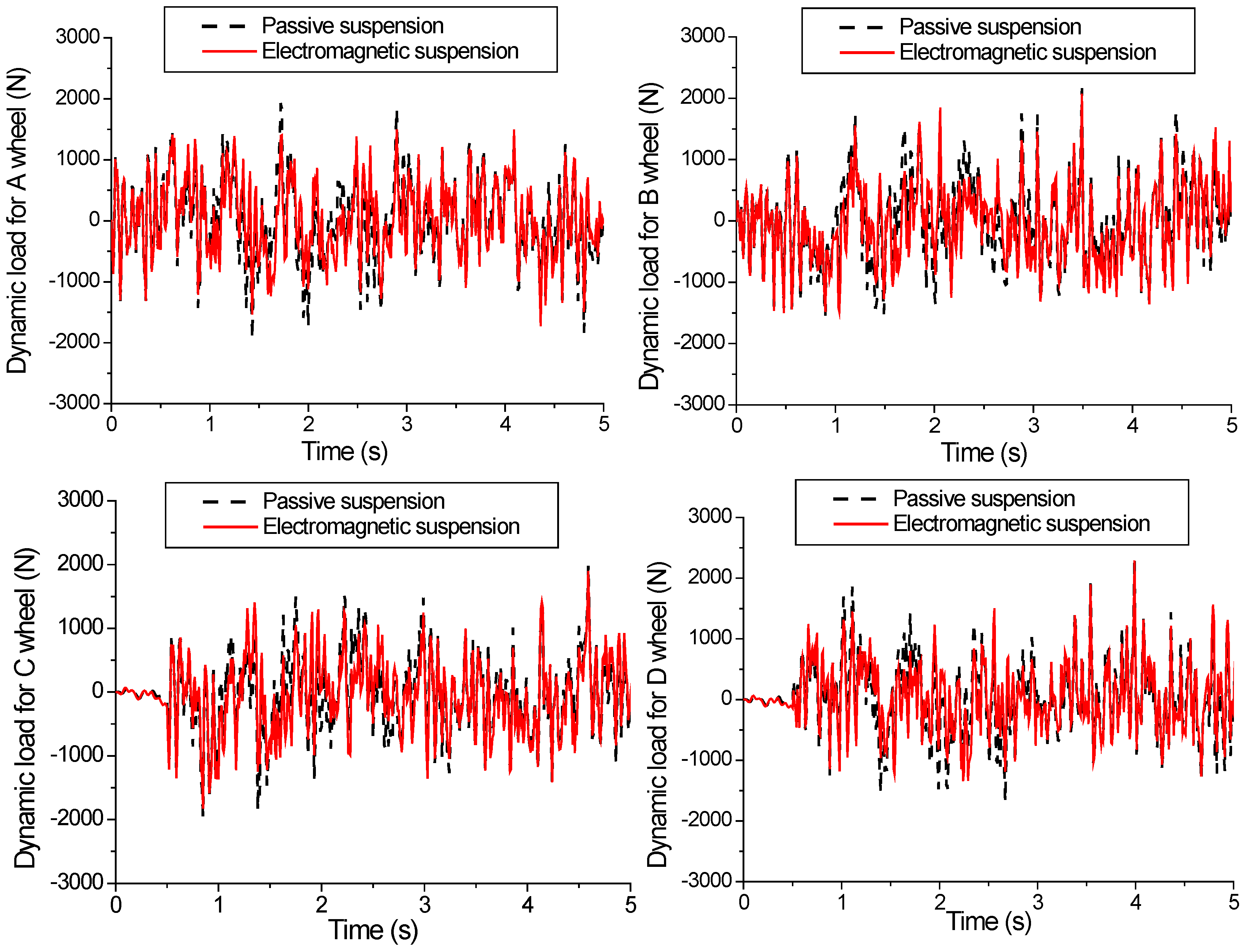
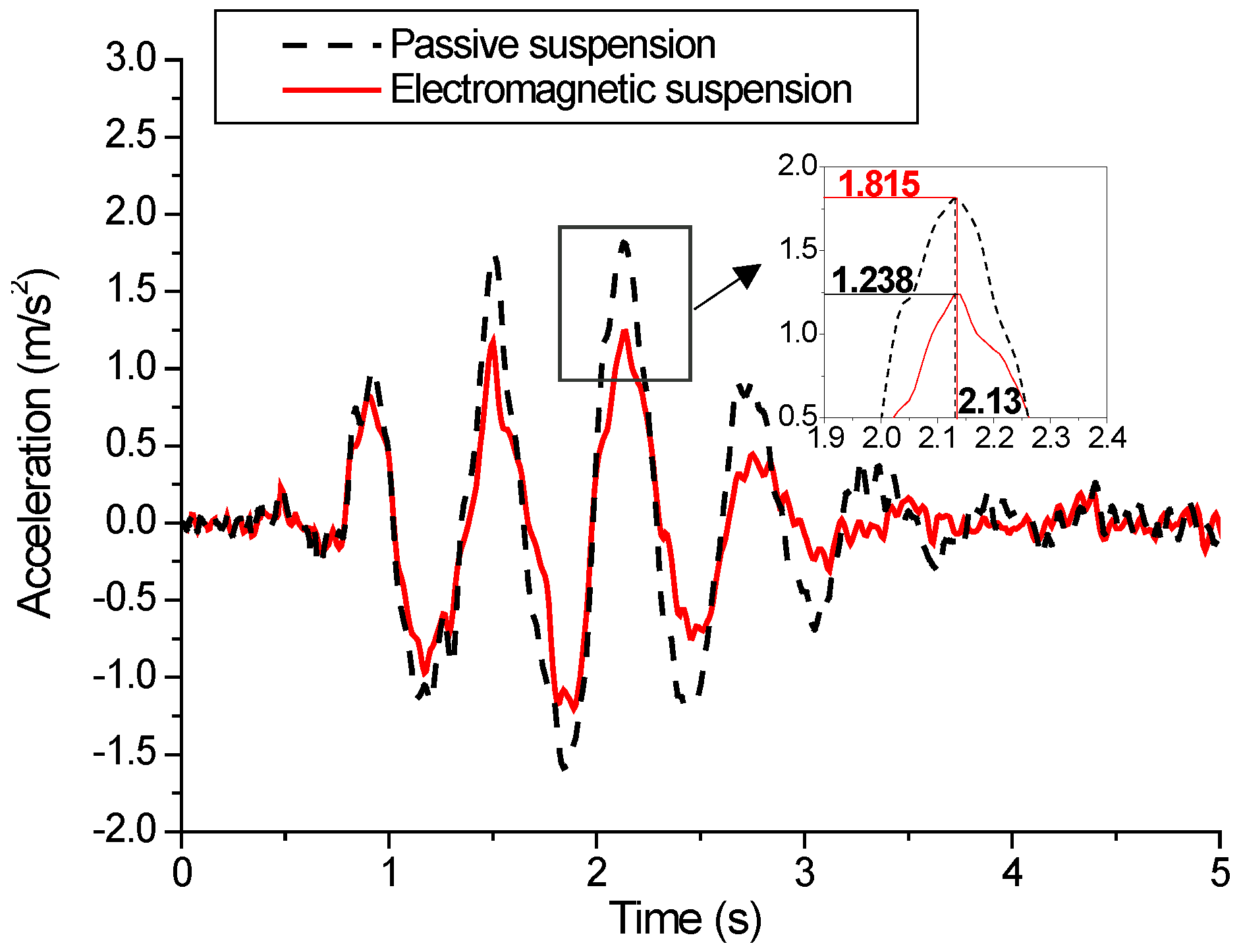
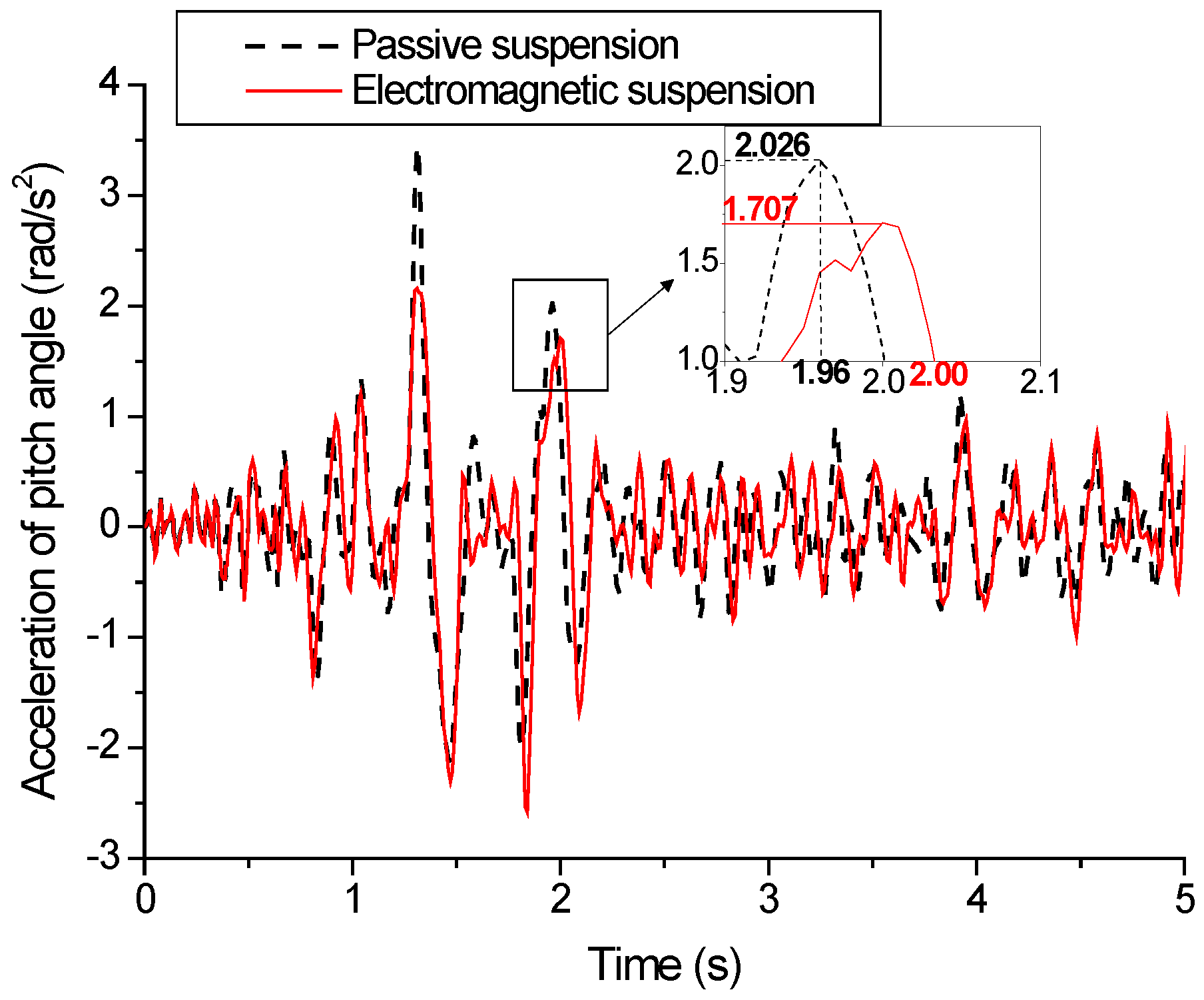
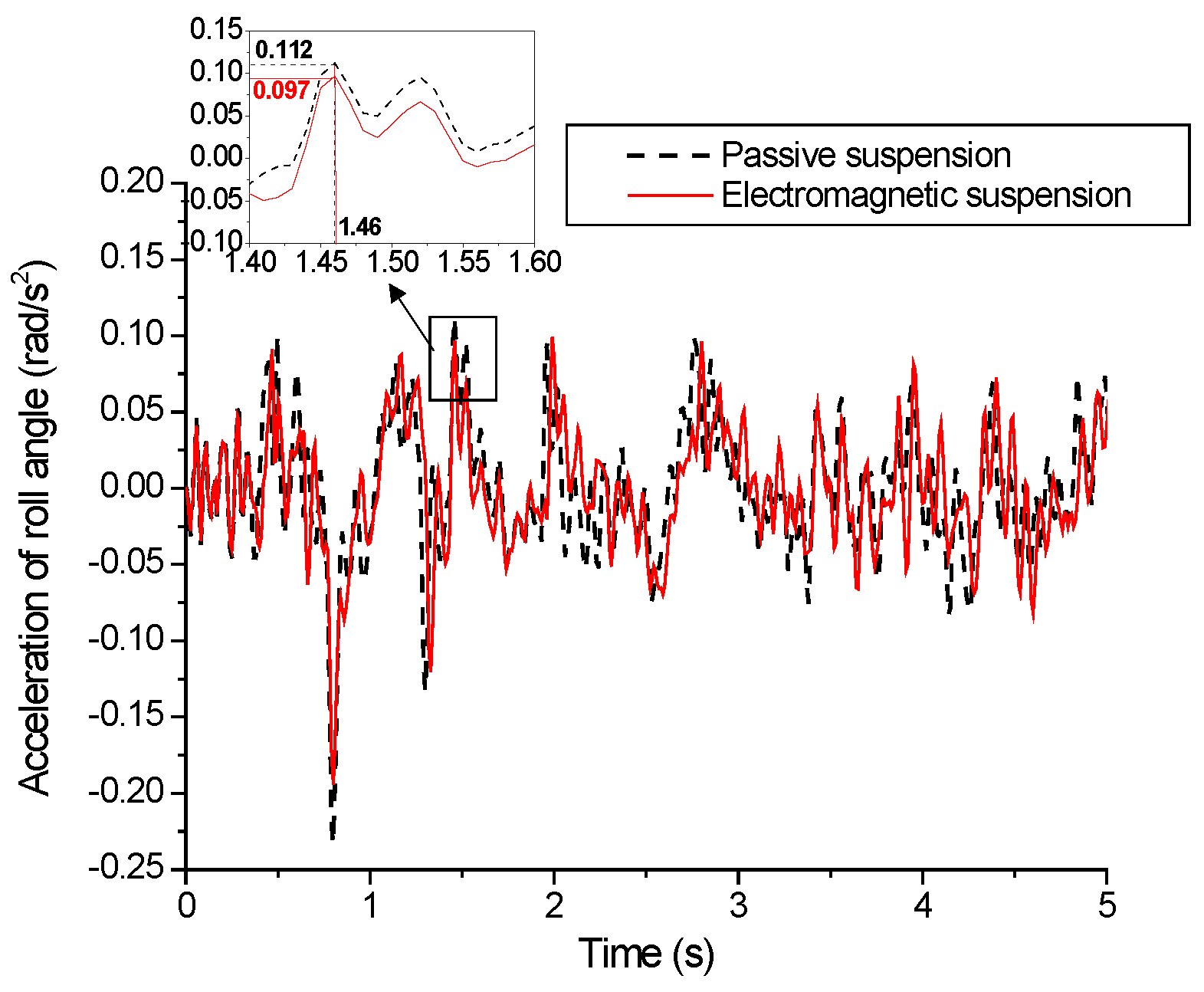
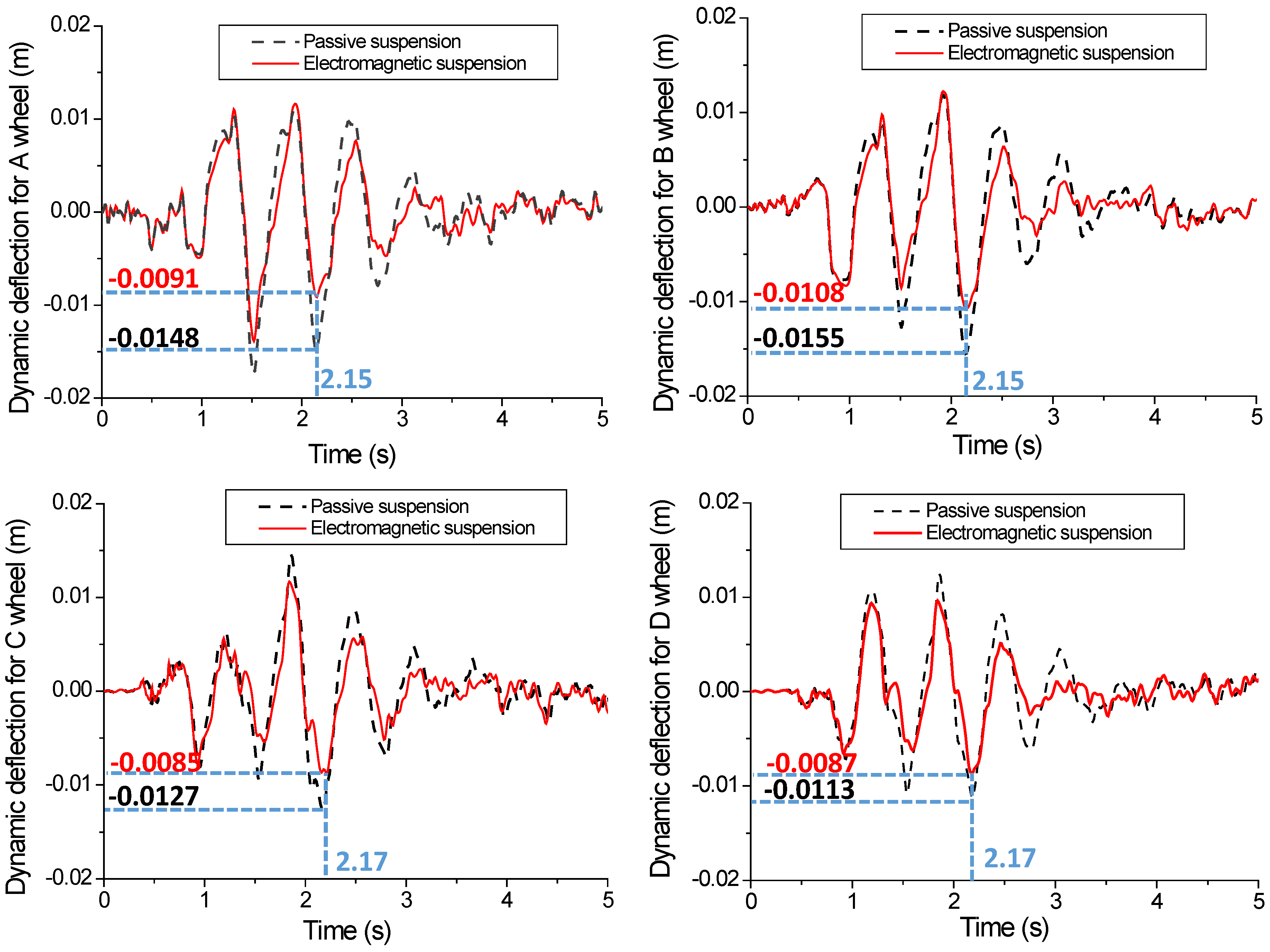
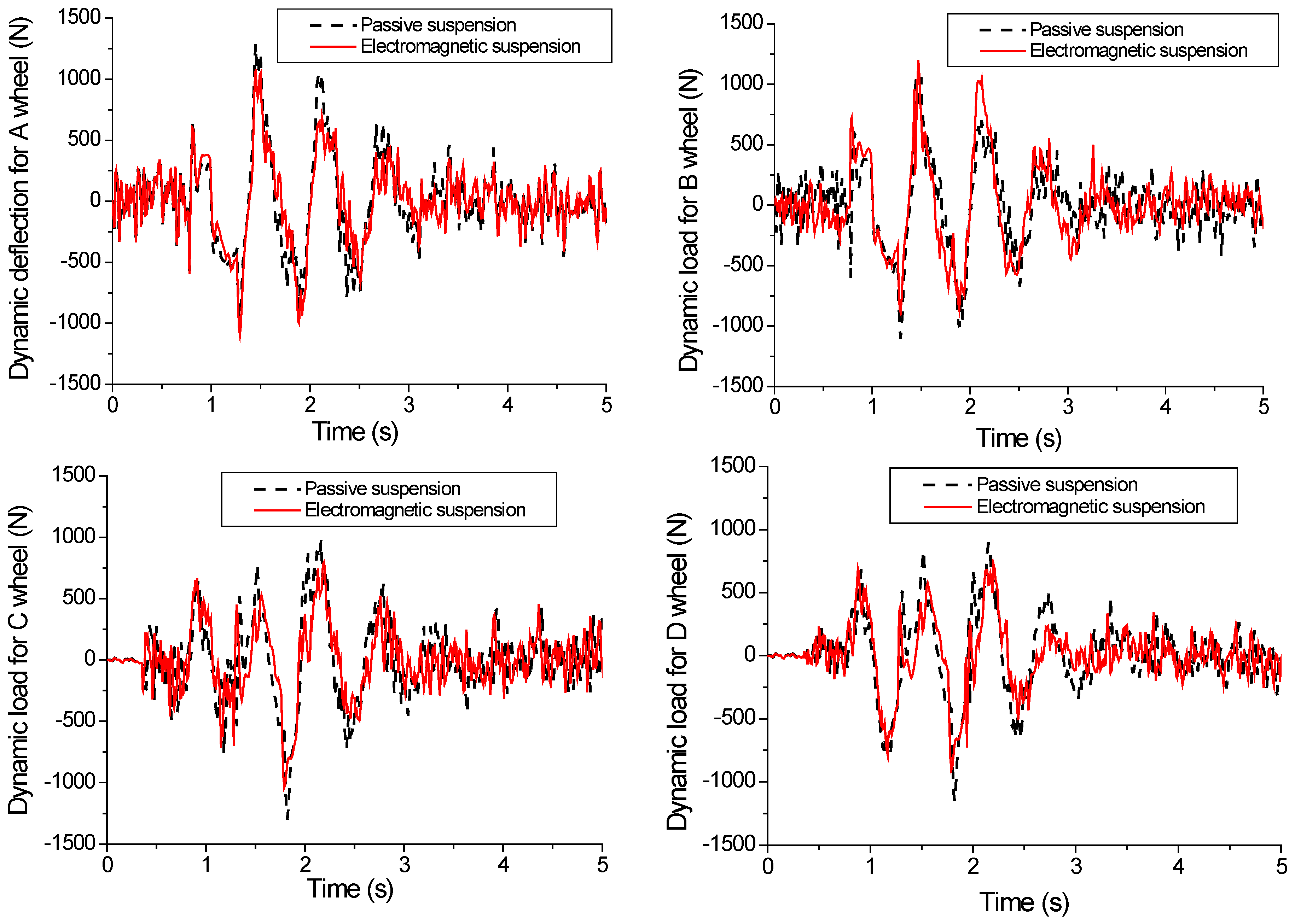
5.3. Vehicle Simulation Results Based on Fuzzy PID under C-Grade Surface
5.4. Vehicle Simulation Results Based on Fuzzy PID under a Deceleration Strip Surface
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Cao, D.; Song, X.; Ahmadian, M. Editors’ perspectives: Road vehicle suspension design, dynamics, and control. Veh. Syst. Dyn. 2011, 49, 3–28. [Google Scholar] [CrossRef]
- Kim, K.H.; Woo, D.K. Linear tubular permanent magnet motor for an electromagnetic active suspension system. IET Electr. Power Appl. 2021, 15, 1648–1665. [Google Scholar] [CrossRef]
- Zhou, H.; Zhen, L.; Zhao, W.; Liu, G.; Xu, L. Design and analysis of low-cost tubular fault-tolerant interior permanent-magnet motor. IEEE Trans. Magn. 2016, 52, 8104804. [Google Scholar] [CrossRef]
- Basaran, S.; Basaran, M. Vibration control of truck cabins with the adaptive vectorial backstepping design of electromagnetic active suspension system. IEEE Access 2020, 8, 173056–173067. [Google Scholar] [CrossRef]
- Harikrishnan, P.M.; Varun, P.G. Vehicle vibration signal processing for road surface monitoring. IEEE Sens. J. 2017, 17, 5192–5197. [Google Scholar] [CrossRef]
- Majdoub, K.E.; Giri, F.; Chaoui, F.Z. Adaptive backstepping control design for semi-active suspension of half-vehicle with magnetorheological damper. IEEE/CAA J. Autom. Sin. 2022, 8, 582–596. [Google Scholar] [CrossRef]
- Envelope, K.; Envelope, K.H. Vibration control of semi-active suspension by the neural network that learned the optimal preview control of MLD model. IFAC-Pap. 2022, 55, 515–520. [Google Scholar]
- Basargan, H.; Mihály, A.; Gáspár, P.; Sename, O. An LPV-based online reconfigurable adaptive semi-active suspension control with MR damper. Energies 2022, 15, 3648. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.; Ding, R.; Meng, X.; Yang, L. On-line estimation of road profile in semi-active suspension based on unsprung mass acceleration. Mech. Syst. Signal Process. 2020, 135, 106370. [Google Scholar] [CrossRef]
- Beno, J.H.; Weeks, D.A.; Bresie, D.A.; Guenin, A.M.; Wisecup, J.S.; Bylsma, W. Experimental comparison of losses for conventional passive and energy efficient active suspension systems. SAE Technical Paper Series. In Proceedings of the SAE International SAE 2002 World Congress & Exhibition, Detroit, MI, USA, 4 May 2002. SAE Technology Paper, 2002-01-0282. [Google Scholar]
- Weeks, D.A.; Beno, J.H.; Guenin, A.M.; Bresie, D.A. Electro mechanical active suspension demonstration for off-road vehicles. In Direct Injection SI Engine Technology, Proceedings of the SAE 2000 World Congress, Detroit, MI, USA, 6 March 2000; SAE International: Warrendale, PA, USA, 2000; SAE Technology Paper, 2000-01-0102. [Google Scholar]
- Bylsma, W.; Guenin, A.M.; Beno, J.H.; Weeks, D.A.; Bresie, D.A.; Raymond, M.E. Electromechanical suspension performance testing. SAE Technical Paper Series. In Proceedings of the 2001 SAE International SAE 2001 World Congress, Detroit, MI, USA, 5–8 March 2001. SAE Technology Paper, 2001-01-0492. [Google Scholar]
- Hayes, R.J.; Beno, J.H.; Weeks, D.A.; Guenin, A.M.; Mock, J.R.; Worthington, M.S.; Triche, E.J.; Chojecki, D.; Lippert, D. Design and testing of an active suspension system for a 2-1/2 ton military truck. SAE Technology Paper. In Proceedings of the SAE International SAE 2005 World Congress & Exhibition, Detroit, MI, USA, 11 April 2005. SAE Technology Paper, 2005-01-1715. [Google Scholar]
- Yu, F.; Cao, M.; Zheng, X.C. Research on the feasibility of vehicle active suspension with energy regeneration. Vib. Shock. 2005, 24, 27–30. [Google Scholar]
- Yu, F.; Fang, T.; Pattipati, K.R. A novel congruent organizational design methodology using group technology and a nested genetic algorithm. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2005, 36, 5–18. [Google Scholar]
- Zhang, Y.C.; Yu, F.; Gu, Y.H. Isolation and energy-regenerative performance experimental verification of automotive electrical suspension. J. Shanghai Jiaotong Univ. 2008, 42, 874–877. [Google Scholar]
- Huang, K.; Yu, F.; Zhang, Y.C. Model predictive controller design for electromagnetic active suspension. J. Shanghai Jiaotong Univ. 2010, 44, 1619–1624. [Google Scholar]
- Huang, S.J.; Chen, H.Y. Adaptive sliding controller with self-tuning fuzzy compensation for vehicle suspension control. Mechatronics 2006, 16, 607–622. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Suda, Y.; Inoue, H.; Kondo, T. Modeling of electromagnetic damper for automobile suspension. J. Syst. Des. Dyn. 2007, 1, 524–535. [Google Scholar] [CrossRef]
- Hayashi, R.; Suda, Y.; Nakano, K. Anti-rolling suspension for an automobile by coupled electromagnetic devices. J. Mech. Syst. Transp. Logist. 2008, 1, 43–55. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Suda, Y.; Inoue, H.; Kondo, T. Electro-mechanical suspension system considering energy consumption and vehicle manoeuvre. Veh. Syst. Dyn. 2008, 46, 1053–1063. [Google Scholar] [CrossRef]
- Asadi, E.; Ribeiro, R.; Khamesee, M.B.; Khajepour, A. Analysis, prototyping and experimental characterization of an adaptive hybrid-electromagnetic damper for automotive suspension systems. IEEE Trans. Veh. Technol. 2017, 66, 3703–3713. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Zuo, L. Design, modeling, lab, and field tests of a mechanical-motion-rectifier-based energy harvester using a ball-screw mechanism. IEEE/ASME Trans. Mechatron. 2017, 22, 1933–1943. [Google Scholar] [CrossRef]
- Eckert, P.R.; Flores Filho, A.F.; Perondi, E.A.; Dorrell, D.G. Dual quasi-halbach linear tubular actuator with coreless moving-coil for semiactive and active suspension. IEEE Trans. Ind. Electron. 2018, 65, 9873–9883. [Google Scholar] [CrossRef]
- Eckert, P.R.; Flores Filho, A.F.; Perondi, E.; Ferri, J.; Goltz, E. Design Methodology of a Dual-Halbach Array Linear Actuator with Thermal-Electromagnetic Coupling. Sensors 2016, 16, 360. [Google Scholar] [CrossRef] [PubMed]
- Beltran-Carbajal, F.; Valderrabano-Gonzalez, A.; Favela-Contreras, A. An active vehicle suspension control approach with electromagnetic and hydraulic actuators. Actuators 2019, 8, 35. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Zheng, M.; Li, W.; Zhang, N.; Jia, Z. An electromagnetic variable stiffness device for semiactive seat suspension vibration control. IEEE Trans. Ind. Electron. 2020, 67, 6773–6784. [Google Scholar] [CrossRef]
- Wang, J.J.; Cai, Y.F.; Chen, L.; Shi, D.; Wang, S.; Zhu, Z. Research on compound coordinated control for a power-split hybrid electric vehicle based on compensation of non-ideal communication network. IEEE Trans. Veh. Technol. 2020, 69, 14818–14833. [Google Scholar] [CrossRef]
- Wang, J.J.; Cai, Y.F.; Chen, L.; Shi, D.; Wang, R.; Zhu, Z. Review on multi-power sources dynamic coordinated control of hybrid electric vehicle during driving mode transition process. Int. J. Energy Res. 2020, 44, 6128–6148. [Google Scholar] [CrossRef]
- Wei, W.; Li, Q.; Xu, F.; Zhang, X.; Jin, J.; Jin, J.; Sun, F. Research on an electromagnetic actuator for vibration suppression and energy regeneration. Actuators 2020, 9, 42. [Google Scholar] [CrossRef]
- Wei, W.; Sun, F.; Jin, J.Q.; Zhao, Z.Y.; Miao, L.G.; Li, Q.; Zhang, X.Y. Proposal of energy-recycle type active suspension using magnetic force. Int. J. Appl. Electromagn. Mech. 2019, 59, 577–585. [Google Scholar] [CrossRef]
- Ye, X.M.; Long, H.Y.; Pei, W.C.; Li, Y.G.; Zhang, S.; Chu, J. Fuzzy control of automotive magnetorheological semi-active suspension. J. North China Univ. Sci. Technol. 2018, 40, 79–87. [Google Scholar]
- Bashir, A.O.; Rui, X.; Zhang, J. Ride comfort improvement of a semi-active vehicle suspension based on hybrid fuzzy and fuzzy-PID controller. Stud. Inform. Control. 2019, 28, 421–430. [Google Scholar] [CrossRef]
- El-Taweel, H.; Elhafiz, M.; Metered, H. Vibration Control of Active Vehicle Suspension System Using Optimized Fuzzy-PID. SAE Technical Paper Series. In Proceedings of the WCX World Congress Experience, Detroit, MI, USA, 3 April 2018. SAE International by Univ of California Berkeley, 2018-01-1402. [Google Scholar]
- Wang, X.; Yang, B.T.; Zhu, Y. Adaptive model-based feedforward to compensate Lorentz force variation of voice coil motor for the fine stage of lithographic equipment. Optik 2019, 135, 27–35. [Google Scholar] [CrossRef]
- Lian, J.Q.; Xie, S.Y.; Wang, J. Analysis of cogging torque of PM motor with radial magnetic field and parallel magnetic field. Appl. Mech. Mater. 2011, 105–107, 2289–2294. [Google Scholar] [CrossRef]
- Jing, L.B.; Zhang, Y.S.; Li, C.; Zhang, K. Magnetic field computa-tion and optimization design for a concentric magnetic gear with hal-bach permanent-magnet arrays. Proc. CSEE 2013, 33, 163–169. [Google Scholar]
- Wang, X.; Yang, B.T.; Zhu, Y. Modeling and analysis of a novel rectan-gular voice coil motor for the 6-DOF fine stage of lithographic equip-ment. Optik 2016, 127, 2246–2250. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Zhu, Y. Optimization of voice coil motor to enhance dynamic response based on an improved magnetic equivalent circuit model. IEEE Trans. Magn. 2011, 47, 2247–2251. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C. Improvement in the Analytical Calculation of the Magnetic Field Produced by Permanent Magnet Rings. Prog. Electromagn. Res. C 2016, 5, 71–82. [Google Scholar]
- Xia, Z.P.; Zhu, Z.Q.; Howe, D. Senior member. analytical magnetic Field analysis of halbach Magnetized permanent-magnet machines. IEEE Trans. Magn. 2004, 40, 1864–1872. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, K.L. Analytic calculation of the magnetic field created by Halbach permanent magnets array. J. Magn. Mater. Devices 2014, 45, 1–4. [Google Scholar]
- Wei, W.; Li, Q.; Sun, F.; Zhang, X.Y. Vibration control and energy regeneration of active suspension based on electromagnetic actuator—Development of electromagnetic actuator. In Proceedings of the International Conference on Precision Engineering (ICPE), Hakodate, Japan, 5–7 September 2018. C03-1. [Google Scholar]



| Level | Height of Large/Small PM Rings (mm) A | Radial Length of Large/Small PM Rings (mm) B | Height of Coils (mm) C |
|---|---|---|---|
| 1 | 10.5 | 10 | 5.5 |
| 2 | 11.5 | 11 | 9.5 |
| 3 | 12.5 | 12 | 12.5 |
| Number | Height of Large/Small PM Rings (mm) | Radial Length of Large/Small PM Rings (mm) | Height of Coils (mm) | Magnetic Force (N) |
|---|---|---|---|---|
| 1 | A1 | B1 | C1 | 156 |
| 2 | A1 | B2 | C2 | 171 |
| 3 | A1 | B3 | C3 | 156 |
| 4 | A2 | B1 | C2 | 135 |
| 5 | A2 | B2 | C3 | 159 |
| 6 | A2 | B3 | C1 | 171 |
| 7 | A3 | B1 | C3 | 165 |
| 8 | A3 | B2 | C1 | 150 |
| 9 | A3 | B3 | C2 | 180 |
| Value Name | Height of Coil2 (mm) | Thickness of Coil2 (mm) | Height of Soft Iron Ring1 (mm) |
|---|---|---|---|
| Kj1 | 543 | 516 | 537 |
| Kj2 | 525 | 540 | 546 |
| Kj3 | 555 | 567 | 540 |
| Kjp1 | 181 | 172 | 179 |
| Kjp2 | 175 | 180 | 182 |
| Kjp3 | 185 | 189 | 180 |
| Rj | 10 | 17 | 3 |
| Primary and secondary order | B > A > C | ||
| Optimal levels | A3 | B3 | C2 |
| Optimal combination | A3B3C2 | ||
| Size Parameter | Description | Value (Unit: mm) |
|---|---|---|
| Hc | Axial length of the coils | 9.5 |
| Hm | Axial length of the PM ring | 12.5 |
| Hhd | Axial length of the heat-dissipated ring | 3 |
| Hwhole | Axial length of the actuator | 96 |
| Dwhole | Outside diameter of the actuator | 80.6 |
| Dcmax | Outside diameter of the coils | 62.3 |
| Dcmin | Inside diameter of the coils | 56.6 |
| Dsmax | Outside diameter of the small PM rings | 52.6 |
| Dsmin | Inside diameter of the small PM rings | 40.6 |
| Dbmax | Outside diameter of the large PM rings | 76.6 |
| Dbmin | Inside diameter of the large PM rings | 64.6 |
| Variable | Description |
|---|---|
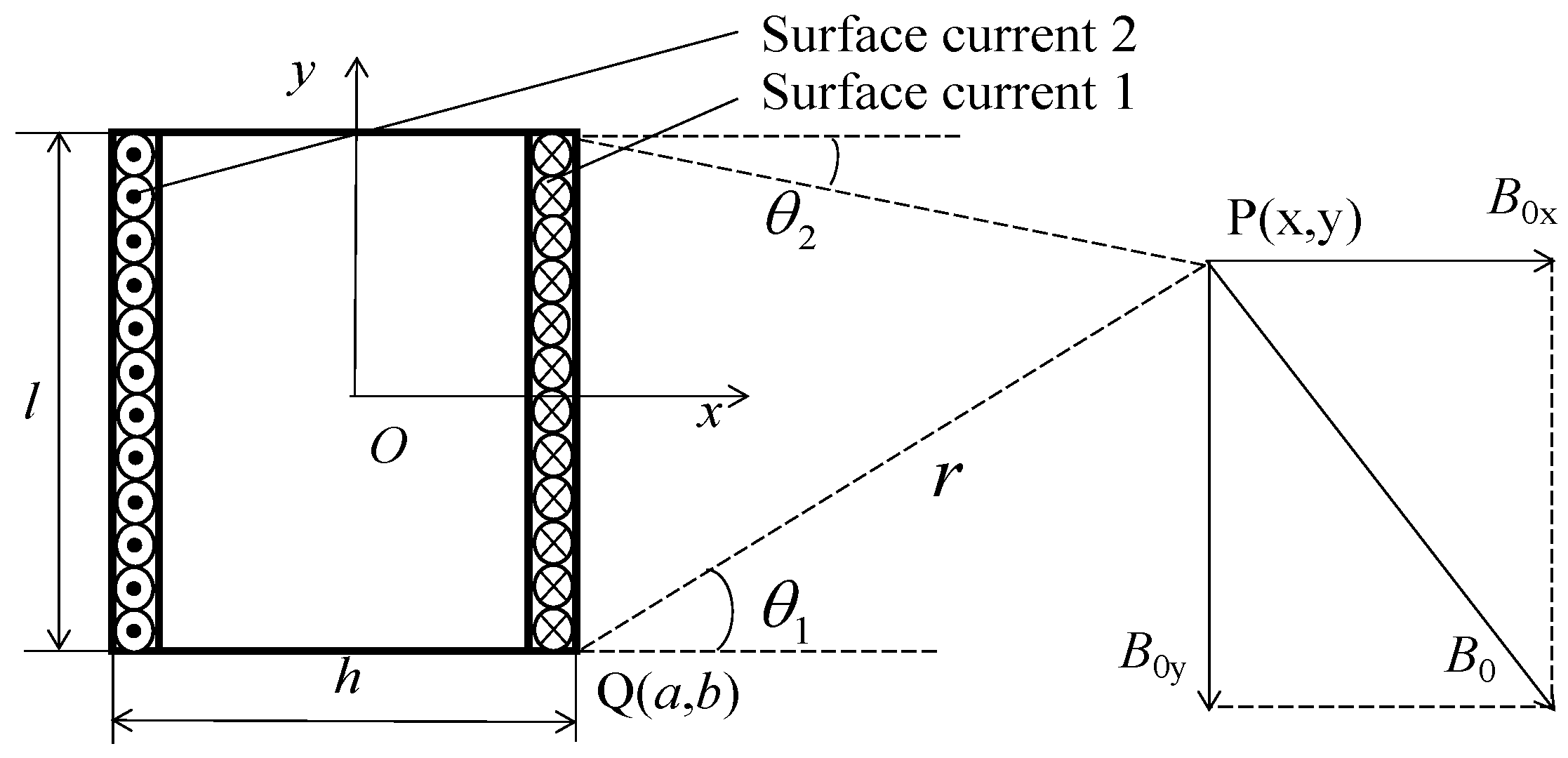
| Q(a, b) | Horizontal and vertical coordinates of any current source |
| P(x, y) | Horizontal and vertical coordinates of any point in a plane |
| j | Ring number from left to right, j = 1–6 |
| θ1, θ2 | Angle between the upper and lower points of surface current 1 |
| θ | Angle between the line of point Q and point P and the horizontal line |
| r | Distance between point Q and point P |
| Byj1 | Magnetic flux density of surface current 1 |
| Byj2 | Magnetic flux density of surface current 2 |
| By1 | Magnetic flux density of large PM rings |
| By2 | Magnetic flux density of small PM rings |
| By | Magnetic flux density of the PM ring array |
| Variable | Description |
|---|---|
| xb | Displacement of body centroid |
| mb | Mass of body centroid |
| θ | Pitch angle |
| φ | Roll angle |
| a | Distance from the center of mass to the front axle |
| b | Distance from the center of mass to the rear axle |
| tf | 1/2 front track |
| tr | 1/2 rear track |
| mwA | Mass of the left front wheel |
| mwB | Mass of the right front wheel |
| mwC | Mass of the left rear wheel |
| mwD | Mass of the right rear wheel |
| xwA | Displacement of the left front wheel |
| xwB | Displacement of the right front wheel |
| xwC | Displacement of the left rear wheel |
| xwD | Displacement of the right rear wheel |
| ktA | Stiffness of the left front wheel |
| ktB | Stiffness of the right front wheel |
| ktC | Stiffness of the left rear wheel |
| ktD | Stiffness of the right rear wheel |
| ksA | Stiffness of the left front wheel spring |
| ksB | Stiffness of the right front wheel spring |
| ksC | Stiffness of the left rear wheel |
| ksD | Stiffness of the right rear wheel |
| csA | Left front wheel damping coefficient |
| csB | Right front wheel damping coefficient |
| csC | Left rear wheel damping coefficient |
| csD | Right rear wheel damping coefficient |
| xgA | Left front wheel road displacement |
| xgB | Right front wheel road displacement |
| xgC | Left rear wheel road displacement |
| xgD | Right rear wheel road displacement |
| xbA | Left front wheel spring mass displacement |
| xbB | Right front wheel spring mass displacement |
| xbC | Left rear wheel sprung mass displacement |
| xbD | Right rear wheel sprung mass displacement |
| Parameters (Unit) | Value | Parameters (Unit) | Value |
|---|---|---|---|
| ms (kg) | 1836 | csA (N/(m/s)) | 1800 |
| mwA (kg) | 50 | csB (N/(m/s)) | 1800 |
| mwB (kg) | 50 | csC (N/(m/s)) | 2000 |
| mwC (kg) | 50 | csD (N/(m/s)) | 2000 |
| mwD (kg) | 50 | ktA (N/m) | 230,000 |
| Ip (kg·m2) | 3411 | ktB (N/m) | 230,000 |
| Ir (kg·m2) | 676 | ktC (N/m) | 230,000 |
| ksA (N/m) | 57,000 | ktD (N/m) | 230,000 |
| ksB (N/m) | 57,000 | a (m) | 1.455 |
| ksC (N/m) | 64,000 | b (m) | 1.514 |
| ksD (N/m) | 64,000 | tl (m)/tr (m) | 0.805 |
| U | Ec | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | ||
| E | NB | PB | PB | PM | PM | PS | Z | Z |
| NM | PB | PB | PM | PS | PS | Z | NS | |
| NS | PM | PM | PS | PS | Z | NS | NS | |
| Z | PM | PM | PS | Z | NS | NM | NM | |
| PS | PS | PS | Z | NS | NS | NM | NM | |
| PM | PS | Z | NS | NM | NM | NM | NB | |
| PB | Z | Z | NM | NM | NM | NB | NB | |
| U | Ec | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | ||
| E | NB | PB | PB | PM | PM | PS | Z | Z |
| NM | PB | PB | PM | PS | PS | Z | NS | |
| NS | PM | PM | PS | PS | Z | NS | NS | |
| Z | PM | PM | PS | Z | NS | NM | NM | |
| PS | PS | PS | Z | NS | NS | NM | NM | |
| PM | PS | Z | NS | NS | NM | NB | NB | |
| PB | Z | Z | NM | NM | NM | NB | NB | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, W.; Yu, S.; Li, B. Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension. Actuators 2023, 12, 203. https://doi.org/10.3390/act12050203
Wei W, Yu S, Li B. Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension. Actuators. 2023; 12(5):203. https://doi.org/10.3390/act12050203
Chicago/Turabian StyleWei, Wei, Songjian Yu, and Baozuo Li. 2023. "Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension" Actuators 12, no. 5: 203. https://doi.org/10.3390/act12050203
APA StyleWei, W., Yu, S., & Li, B. (2023). Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension. Actuators, 12(5), 203. https://doi.org/10.3390/act12050203





