A Multi-Scale Attention Mechanism Based Domain Adversarial Neural Network Strategy for Bearing Fault Diagnosis
Abstract
:1. Introduction
- (1)
- A feature extractor based on a multi-scale convolution structure and attention mechanism is designed. It is adopted to broaden the network width, fuse feature information of different scales, focus on the key features with identification ability to suppress irrelevant features, and improve the accuracy of fault identification.
- (2)
- A class domain adaptation based on the maximum mean difference is designed. MMD is introduced into the predictive label space for domain adaptation to measure the distribution difference between the target and source domains.
- (3)
- Experimental results on a public bearing dataset and data collected by the test bench confirm that the proposed methodology has higher recognition accuracy.
2. Theoretical Background
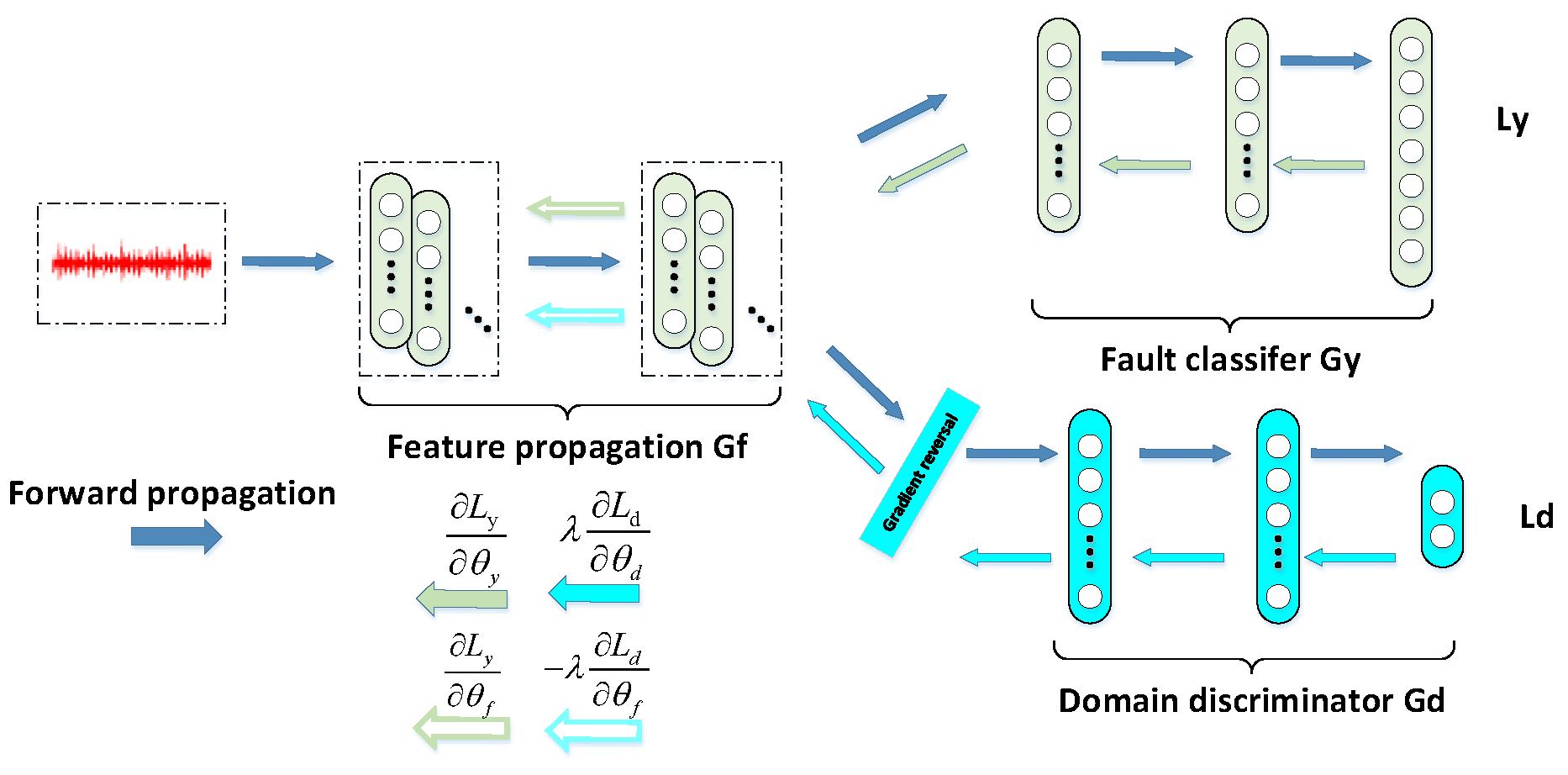
2.1. Domain Adversarial Neural Network
2.2. Maximum Mean Discrepancy
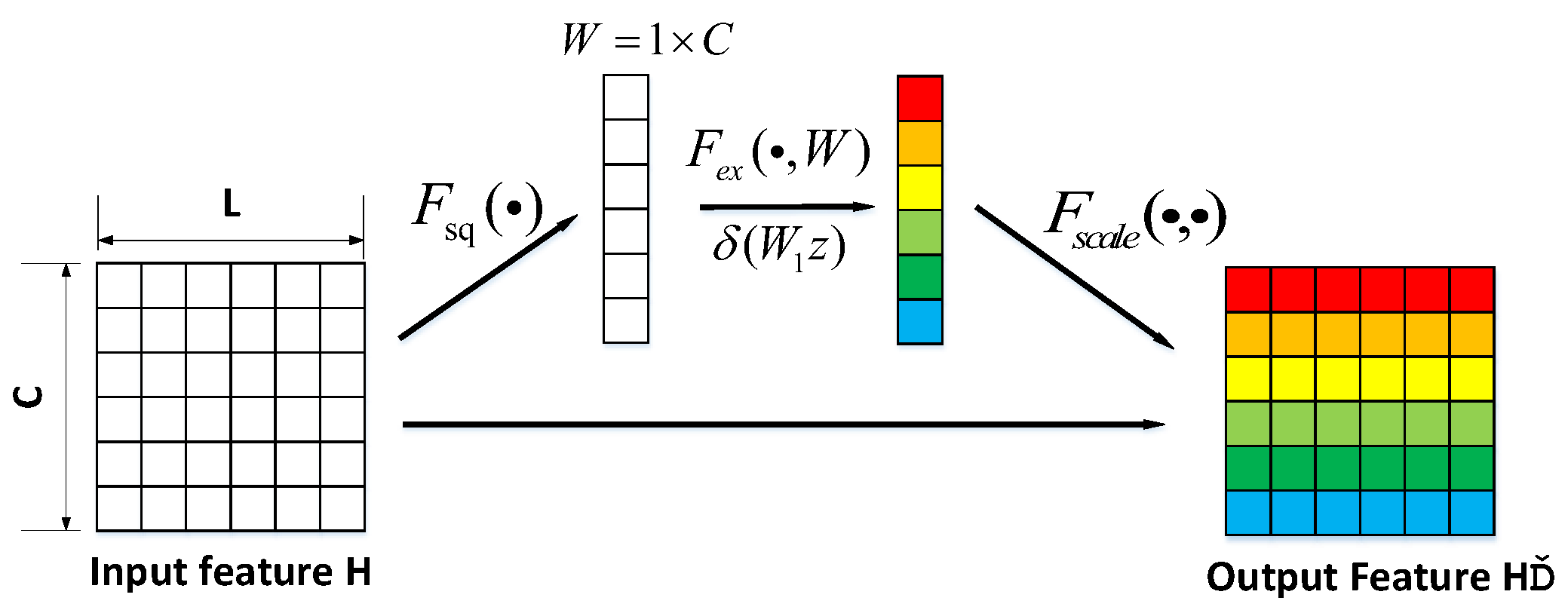
2.3. Attention Mechanism
3. A Multi-Scale Attention Mechanism Domain Adversarial Neural Network for Bearing Fault Diagnosis
3.1. Fault Diagnosis Method Framework
3.2. Feature Extraction Method Based on a Multi-Scale Module and an Attention Mechanism
3.3. Design of Feature Classifier
3.4. Design of Domain Discriminator
3.5. Class Domain Adaptation Design Based on the Maximum Mean Difference
3.6. Total Loss Function Design
3.7. Algorithm Flow
- (1)
- The bearing vibration data under different working conditions are collected and normalized, and then they are converted into frequency–domain signals using fast Fourier transform as input, which is divided into source domain data and target domain data . Finally, the source domain data is divided into two parts: the verification set and the training set, and the target domain data is divided into two parts: the test set and the training set.
- (2)
- The training sets of the source domain data and the target domain data are input into the shared multi-scale feature extractor, and the source domain multi-scale features and the target domain multi-scale features are extracted, respectively, via Equations (16)–(18). Additionally, use Formula (19) to fuse the multi-scale features of the source domain and the target domain to obtain . Through the attention mechanism, the source domain feature and the target domain feature , with more discriminative power, are extracted through Formulas (20)–(22), and the feature extracted from the source domain is input to the feature classifier for classification. The classification loss is calculated by Formulas (25) and (27), and then the features extracted from the source domain and the target domain are input to the category domain adapter to calculate the MMD loss by Formula (32), and the domain discriminator is used to calculate the domain discriminator loss by Formulas (29) and (30), and the three loss functions are constructed into a total loss function . Finally, the model is iteratively trained to minimize the classification loss and MMD loss and maximize the domain discriminator loss.
- (3)
- The model is tested, and the target domain test set is input into the feature extractor and classifier for actual fault diagnosis to test the effectiveness of diagnosis.
4. Application Results and Analysis
4.1. Case Western Reserve University Bearing Data Analysis
4.1.1. Data Preparation
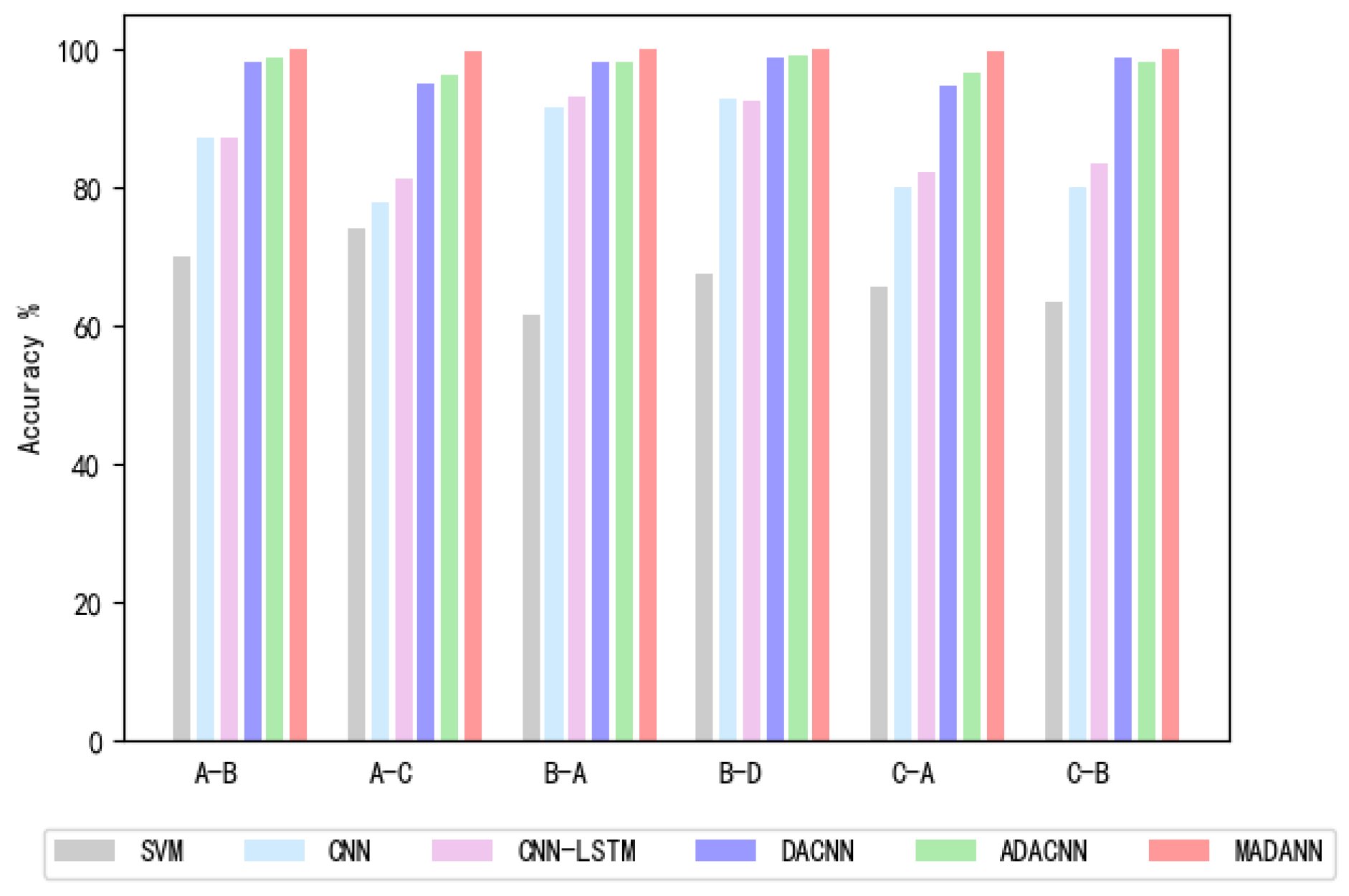
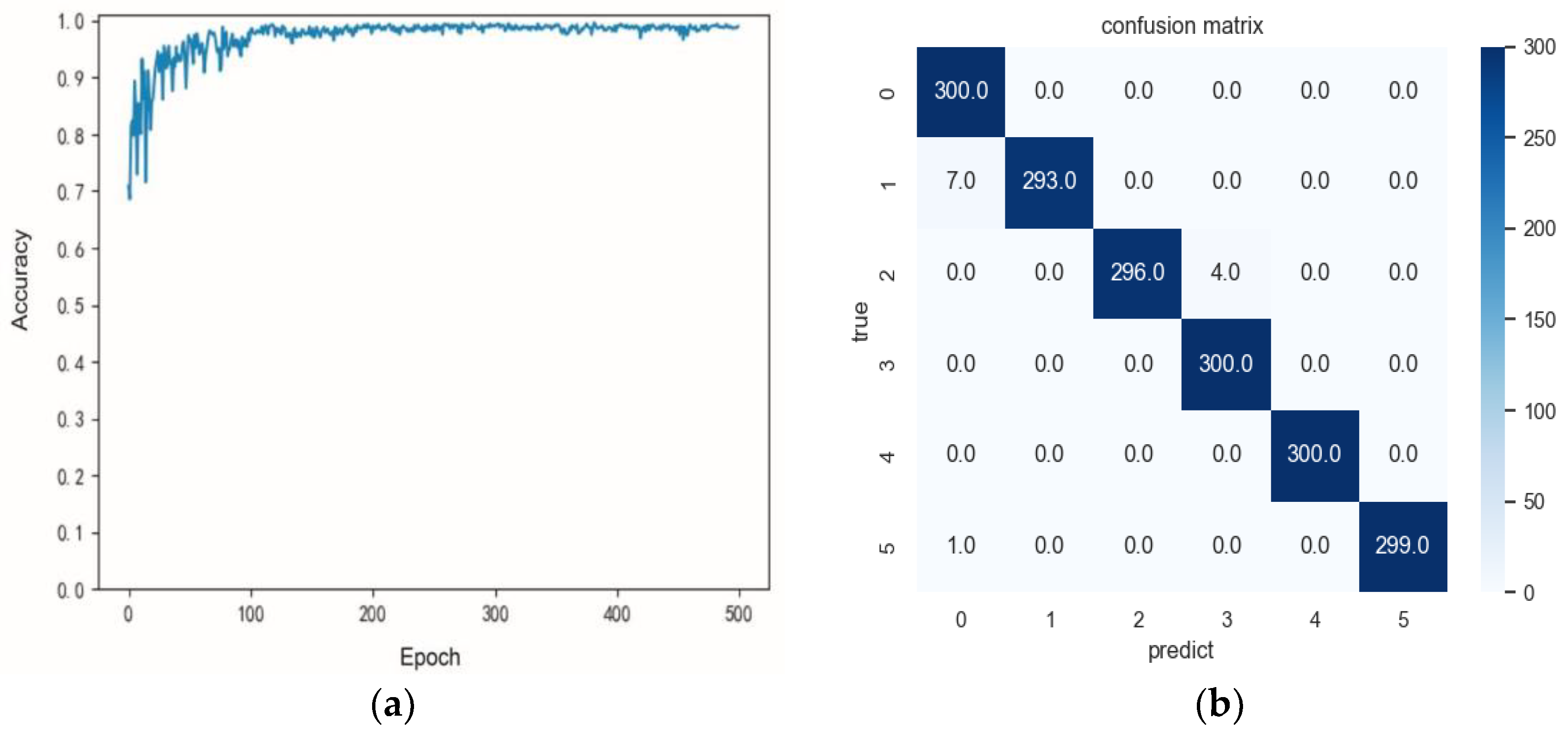
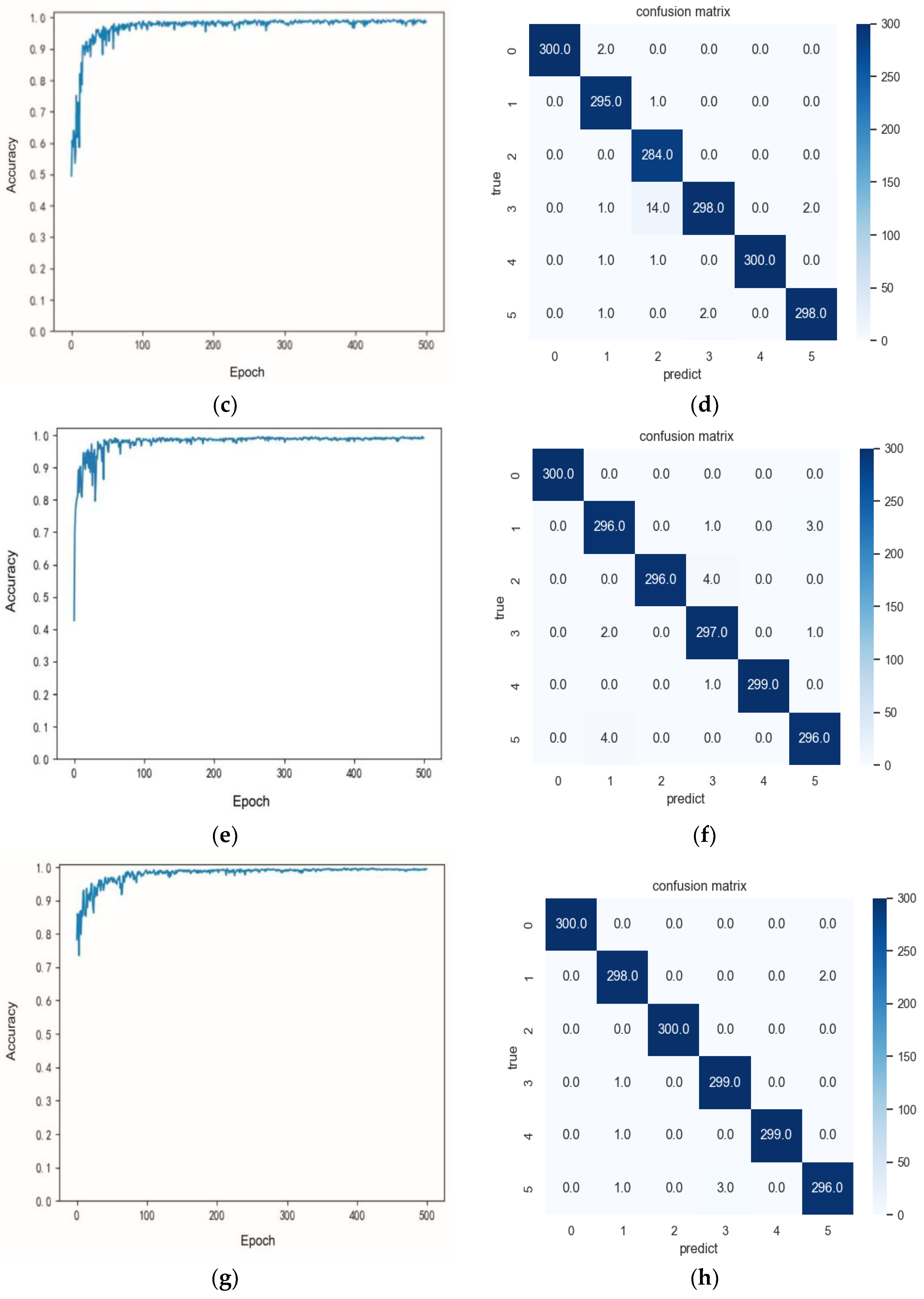
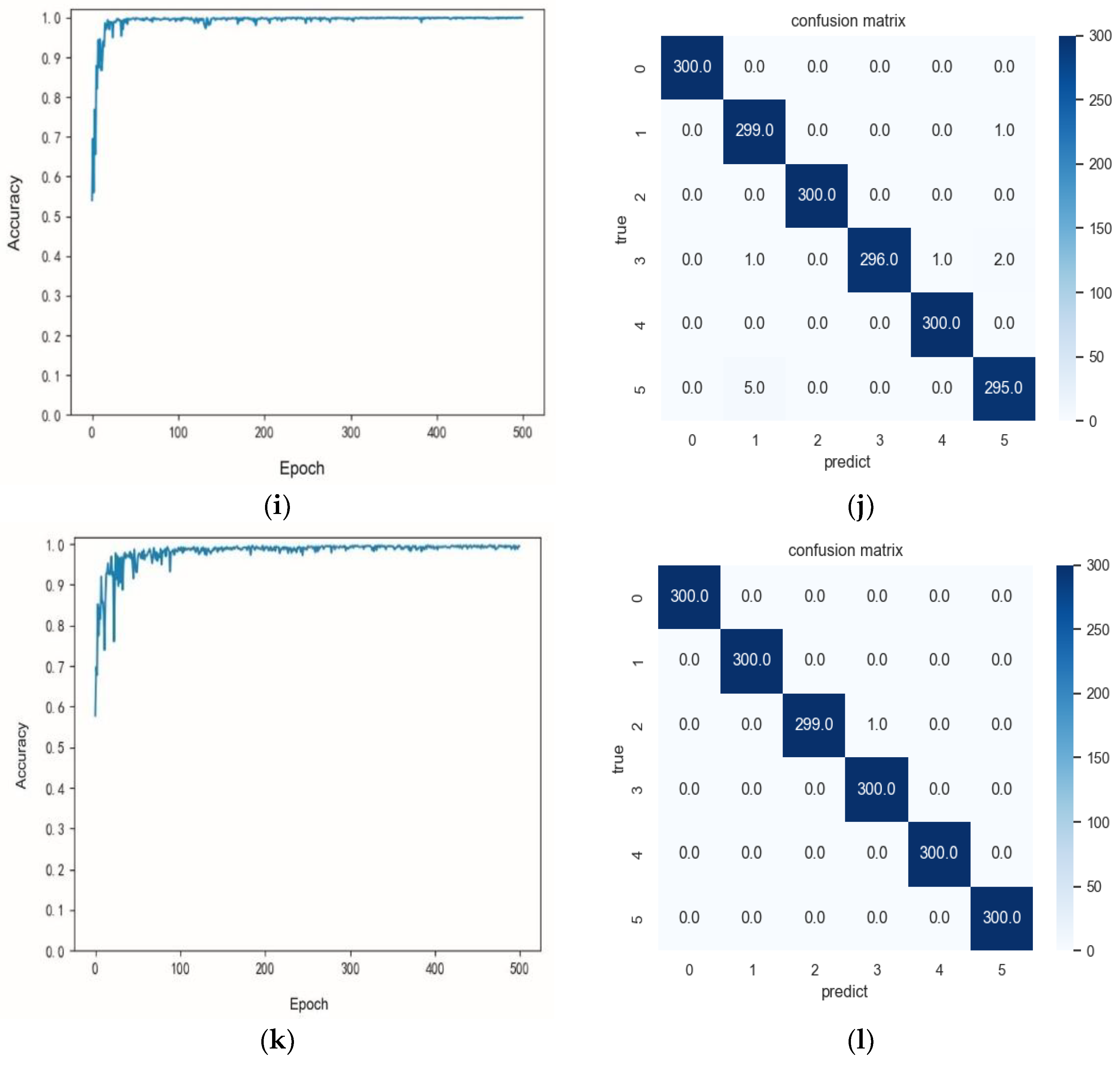
4.1.2. Performance Comparison and Analysis of Different Algorithms
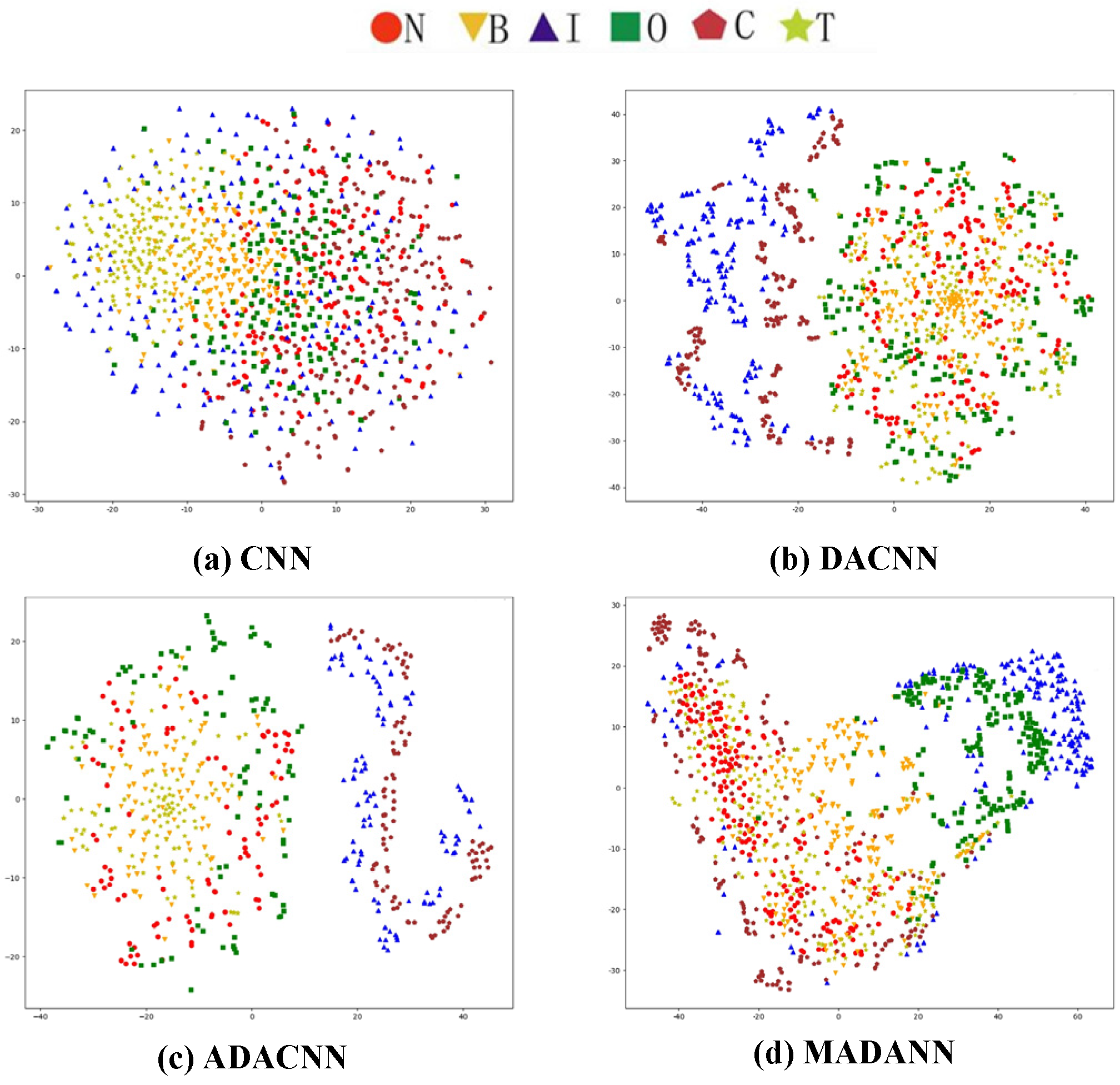
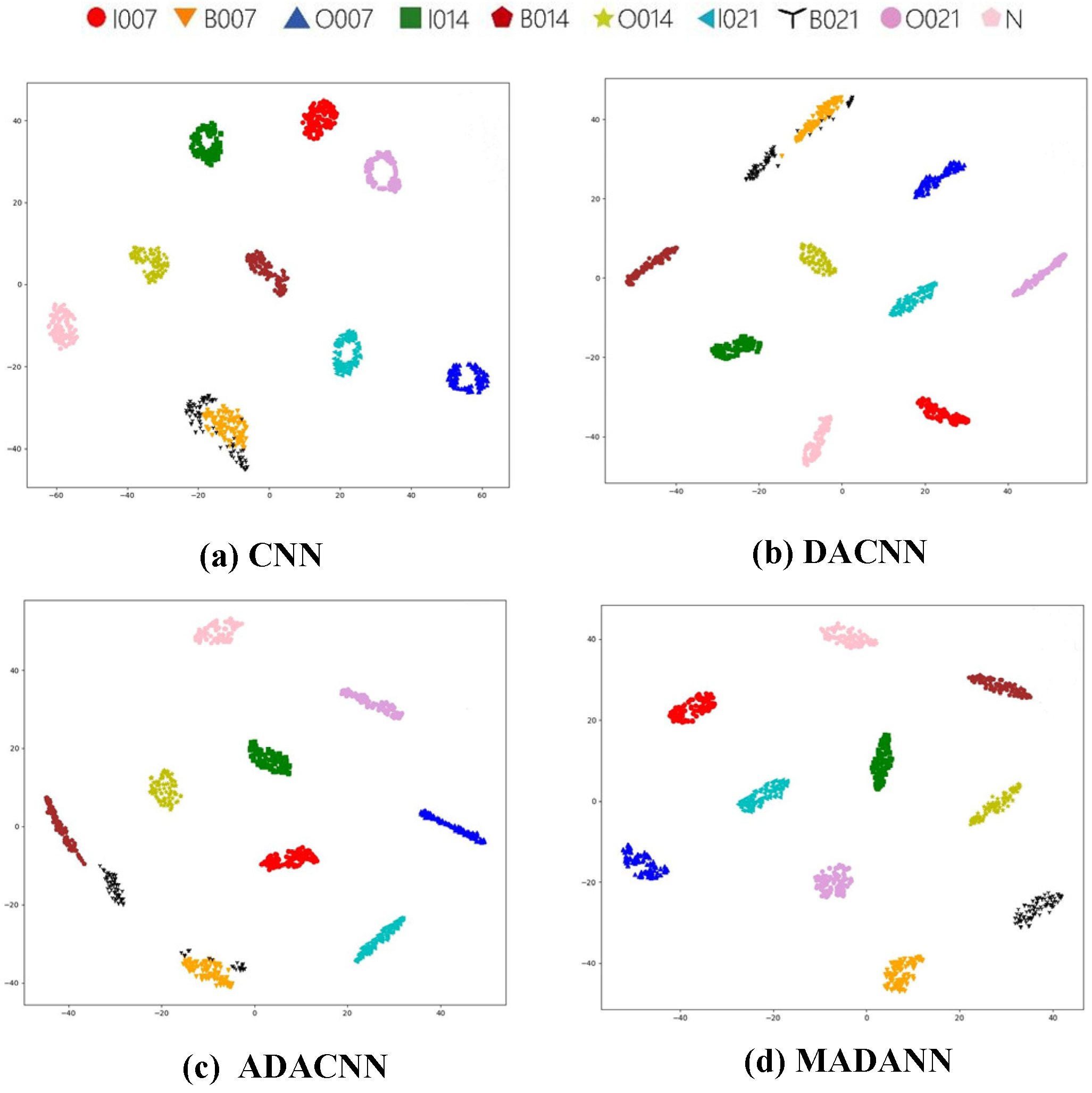
4.1.3. Feature Visualization and Analysis
4.2. Data Analysis of PT500mini Mechanical Bearing Fault Simulation Test Bed
4.2.1. Data Preparation
4.2.2. Experimental Results and Analysis
4.3. Computational Expense
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Dong, Y.; Zhou, H.; Tang, G. Deep dynamic adaptive transfer network for rolling bearing fault diagnosis with considering cross-machine instance. IEEE Trans. Instrum. Meas. 2021, 70, 3525211. [Google Scholar] [CrossRef]
- Chen, C.; Lu, N.; Jiang, B.; Xing, Y. A data-driven approach for assessing aero-engine health status. IFAC-Pap. Online 2022, 55, 737–742. [Google Scholar] [CrossRef]
- Wang, C.; Lu, N.; Cheng, Y.; Jiang, B. A data-driven aero-engine degradation prognostic strategy. IEEE Trans. Cybern. 2021, 51, 1531–1541. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Si, X.; Qin, A.; Lv, Y.; Liu, M. Balanced adaptation regularization based transfer learning for unsupervised cross-domain fault diagnosis. IEEE Sens. J. 2022, 22, 12139–12151. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, W.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106578. [Google Scholar] [CrossRef]
- Su, K.; Liu, J.; Xiong, H. A multi-level adaptation scheme for hierarchical bearing fault diagnosis under variable working conditions. J. Manuf. Syst. 2022, 64, 251–260. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics–a comprehensive review. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Paris, France, 27–30 August 2019. [Google Scholar]
- Xu, J.; Tong, S.; Cong, F.; Zhang, Y. The application of time–frequency reconstruction and correlation matching for rolling bearing fault diagnosis. ARCHIVE Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 33291–33295. [Google Scholar] [CrossRef]
- Zheng, J.; Cao, S.; Pan, H.; Ni, Q. Spectral envelope-based adaptive empirical Fourier decomposition method and its application to rolling bearing fault diagnosis. ISA Trans. 2022, 129, 476–492. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Xiong, J.; Xiao, M.; Sun, G.; He, J. Fault diagnosis of a rolling bearing using wavelet packet denoising and random forests. IEEE Sens. J. 2017, 17, 5581–5588. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]
- Liu, S.; Sun, Y.; Zhang, L. A novel fault diagnosis method based on noise-assisted MEMD and functional neural fuzzy network for rolling element bearings. IEEE Access 2018, 6, 27048–27068. [Google Scholar] [CrossRef]
- Goyal, D.; Dhami, S.; Pabla, B. Non-contact fault diagnosis of bearings in machine learning environment. IEEE Sens. J. 2020, 20, 4816–4823. [Google Scholar] [CrossRef]
- Zuo, L.; Xu, F.; Zhang, C.; Xiahou, T.; Liu, Y. A multi-layer spiking neural network-based approach to bearing fault diagnosis. Reliab. Eng. Syst. Saf. 2022, 225, 108561. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y. Rolling bearing fault diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- Tan, H.; Xie, S.; Liu, R.; Ma, W. Bearing fault identification based on stacking modified composite multiscale dispersion entropy and optimised support vector machine. Measurement 2021, 186, 110180. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Chen, G.; Ding, J. Modified multiscale weighted permutation entropy and optimized support vector machine method for rolling bearing fault diagnosis with complex signals. ISA Trans. 2021, 114, 470–484. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar] [CrossRef]
- Gao, S.; Pei, Z.; Zhang, Y.; Li, T. Bearing fault diagnosis based on adaptive convolutional neural network with Nesterov Momentum. IEEE Sens. J. 2021, 21, 9268–9276. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, X.; Zeng, Q.; Wang, L.; Shao, Y. Intelligent rolling bearing fault diagnosis via vision ConvNet. IEEE Sens. J. 2021, 21, 6600–6609. [Google Scholar] [CrossRef]
- Sun, J.; Wen, J.; Yuan, C.; Liu, Z.; Xiao, Q. Bearing fault diagnosis based on multiple transformation domain fusion and improved residual Dense Networks. IEEE Sens. J. 2022, 22, 1541–1551. [Google Scholar] [CrossRef]
- Sadoughi, M.; Hu, C. Physics-Based convolutional neural network for fault diagnosis of rolling element bearings. IEEE Sens. J. 2019, 19, 4181–4192. [Google Scholar] [CrossRef]
- Udmale, S.; Singh, S.; Singh, R.; Sangaiah, A.K. Multi-Fault bearing classification using sensors and ConvNet-Based transfer learning approach. IEEE Sens. J. 2020, 20, 1433–1444. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Cheng, W.; Zhao, D.; Wen, W. Rolling bearing fault severity recognition via data mining integrated with convolutional neural network. IEEE Sens. J. 2022, 22, 5768–5777. [Google Scholar] [CrossRef]
- Lu, S.; Qian, G.; He, Q.; Liu, F.; Liu, Y.; Wang, Q. In situ motor fault diagnosis using enhanced convolutional neural network in an embedded system. IEEE Sens. J. 2020, 20, 8287–8296. [Google Scholar] [CrossRef]
- Li, G.; Wu, J.; Deng, C.; Chen, Z. Parallel multi-fusion convolutional neural networks based fault diagnosis of rotating machinery under noisy environments. ISA Trans. 2021, 128, 545–555. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Qin, Y. Understanding and learning discriminant features based on multi-attention 1DCNN for wheelset bearing fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 5735–5745. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Magar, R.; Ghule, L.; Li, J.; Zhao, Y.; Farimani, A.B. FaultNet: A Deep Convolutional Neural Network for bearing fault classification. IEEE Access 2021, 9, 25189–25199. [Google Scholar] [CrossRef]
- Wang, Q.; MiChau, G.; Fink, O. Domain adaptive transfer learning for fault diagnosis. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019. [Google Scholar]
- Li, J.; Huang, R.; He, G.; Wang, S.; Li, G.; Li, W. A deep adversarial transfer learning network for machinery emerging fault detection. IEEE Sens. J. 2020, 20, 8413–8422. [Google Scholar] [CrossRef]
- Lu, N.; Xiao, H.; Sun, Y.; Han, M.; Wang, Y. A new method for intelligent fault diagnosis of machines based on unsupervised domain adaptation. Neurocomputing 2021, 427, 96–109. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, R.; Ma, H.; He, Q.; Du, S.; Wu, J. Adversarial domain adaptation convolutional neural network for intelligent recognition of bearing faults. Measurement 2022, 195, 111150. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, H.; Guo, J.; Ji, Y.; Pecht, M. Imbalanced bearing fault diagnosis under variant working conditions using cost-sensitive deep domain adaptation network. Expert Syst. Appl. 2022, 193, 116459. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, K.; Li, Z.; Ding, G.F.; Zou, Y.S. Transfer learning method for bearing fault diagnosis based on fully convolutional conditional Wasserstein adversarial Networks. Measurement 2021, 180, 109553. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, Y.; Deng, J.; Jiang, Y.; Zhang, W. A novel transfer learning method for bearing fault diagnosis under different working conditions. Measurement 2021, 171, 108767. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Liu, S.; Yang, C. A Gaussian-guided adversarial adaptation transfer network for rolling bearing fault diagnosis. Adv. Eng. Inform. 2022, 53, 101651. [Google Scholar] [CrossRef]




| Type | Length | Quantity | Label |
|---|---|---|---|
| Normal | 2048 | 300 | 9 |
| Inner ring fault (0.007 inch) | 2048 | 300 | 0 |
| Rolling element failure (0.007 inch) | 2048 | 300 | 1 |
| Outer ring fault (0.007 inch) | 2048 | 300 | 2 |
| Inner ring fault (0.014 inch) | 2048 | 300 | 3 |
| Rolling element failure (0.014 inch) | 2048 | 300 | 4 |
| Outer ring fault (0.014 inch) | 2048 | 300 | 5 |
| Inner ring fault (0.021 inch) | 2048 | 300 | 6 |
| Rolling element failure (0.021 inch) | 2048 | 300 | 7 |
| Outer ring fault (0.021 inch) | 2048 | 300 | 8 |
| Methods | A-B | A-C | B-A | B-C | C-A | C-B | Average |
|---|---|---|---|---|---|---|---|
| SVM | 70 | 74 | 61.6 | 67.6 | 65.7 | 63.3 | 67.0 |
| CNN | 87.3 | 77.8 | 91.5 | 92.7 | 80.0 | 79.9 | 84.9 |
| CNN-LSTM | 87.3 | 81.4 | 93.1 | 92.6 | 82.2 | 83.4 | 86.7 |
| DACNN | 98.1 | 95.1 | 98 | 98.8 | 94.6 | 98.7 | 97.2 |
| ADACNN | 98.6 | 96.2 | 98 | 99.2 | 96.6 | 98 | 97.7 |
| MADANN | 99.9 | 99.7 | 99.9 | 100 | 99.8 | 100 | 99.8 |
| Sample Type | Sample Length | Number of Samples | Category Tag |
|---|---|---|---|
| N | 2048 | 1000 | 0 |
| B | 2048 | 1000 | 1 |
| C | 2048 | 1000 | 2 |
| I | 2048 | 1000 | 3 |
| O | 2048 | 1000 | 4 |
| T | 2048 | 1000 | 5 |
| Domain Adaptation | Source Domain | Target Domain | Accuracy |
|---|---|---|---|
| A-B | 1000 r/min | 1500 r/min | 99.1 |
| A-C | 1000 r/min | 2000 r/min | 98.6 |
| B-A | 1500 r/min | 1000 r/min | 99.1 |
| B-C | 1500 r/min | 2000 r/min | 99.5 |
| C-A | 2000 r/min | 1000 r/min | 99.3 |
| C-B | 2000 r/min | 1500 r/min | 99.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Tang, N.; Fu, X.; Peng, H.; Bo, C.; Wang, C. A Multi-Scale Attention Mechanism Based Domain Adversarial Neural Network Strategy for Bearing Fault Diagnosis. Actuators 2023, 12, 188. https://doi.org/10.3390/act12050188
Zhang Q, Tang N, Fu X, Peng H, Bo C, Wang C. A Multi-Scale Attention Mechanism Based Domain Adversarial Neural Network Strategy for Bearing Fault Diagnosis. Actuators. 2023; 12(5):188. https://doi.org/10.3390/act12050188
Chicago/Turabian StyleZhang, Quanling, Ningze Tang, Xing Fu, Hao Peng, Cuimei Bo, and Cunsong Wang. 2023. "A Multi-Scale Attention Mechanism Based Domain Adversarial Neural Network Strategy for Bearing Fault Diagnosis" Actuators 12, no. 5: 188. https://doi.org/10.3390/act12050188
APA StyleZhang, Q., Tang, N., Fu, X., Peng, H., Bo, C., & Wang, C. (2023). A Multi-Scale Attention Mechanism Based Domain Adversarial Neural Network Strategy for Bearing Fault Diagnosis. Actuators, 12(5), 188. https://doi.org/10.3390/act12050188







