Research on Self-Recovery Control Algorithm of Quadruped Robot Fall Based on Reinforcement Learning

Abstract

When a quadruped robot is climbing stairs, due to unexpected factors, such as the size of the differing from the international standard or the stairs being wet and slippery, it may suddenly fall down. Therefore, solving the self-recovery problem of the quadruped robot after falling is of great significance in practical engineering. This is inspired by the self-recovery of crustaceans when they fall; the swinging of their legs will produce a resonance effect of a specific body shape, and then the shell will swing under the action of external force, and self-recovery will be achieved by moving the center of gravity. Based on the bionic mechanism, the kinematics model of a one-leg swing and the self-recovery motion model of a falling quadruped robot are established in this paper. According to the established mathematical model, the algorithm training environment is constructed, and a control strategy based on the reinforcement learning algorithm is proposed as a controller to be applied to the fall self-recovery of quadruped robots. The simulation results show that the quadruped robot only takes 2.25 s to achieve self-recovery through DDPG on flat terrain. In addition, we compare the proposed algorithm with PID and LQR algorithms, and the simulation experiments verify the superiority of the proposed algorithm.

1. Introduction

Since the advent of the quadruped robot, it has been widely used in disaster rescue, anti-terrorist explosive clearance, material transportation, military attack, field exploration, planet exploration, agricultural production, and other scenarios due to its advantages of easy control, design, and maintenance [1]. It not only has higher load capacity and higher stability than biped robots but also has larger leg movement space than multi-legged robots, reducing the redundancy and complexity of the mechanism [2]. However, when a robot carries out soil radioactive pollutant detection work under complex terrain conditions, it is easy for the robot to be overturned while walking due to the complex and changeable mountain environment and the combined effect of various factors, such as the unevenness of the ground, the offset of the center of gravity of the robot, and the instability of the control. In particular, the γ-rays emitted by radioactive pollutants may cause damage to the equipment [3], which will lead to performance attenuation, distortion of sending and receiving signals, and rollover of the robot. In addition, when the robot must climb stairs in the course of daily environmental work, if the size of the stair pedal is not suitable or the staircase surface is too smooth, etc., the robot may also fall. If the robot is in a completely inverted state due to a fall, it is difficult for it to perform reverse rotation of the body and continue to work normally [4]. Thus, a method is required to help the robot achieve self-recovery from a fall.

Falling self-recovery refers to the motion that can use the swinging motion of the robot’s legs or a series of continuous movements while avoiding self-collisions from falling to a typical operation state (standing or walking). As early as 1995, scholars such as M. Inaba et al. [5] implemented the fall recovery motion of the “Hanzou” bipedal robot by playing back a series of designed static joint angles. Subsequently, many small bipedal robots such as Sony SDR-3X [6], SDR-4X [7], and Darwin-OP [8] were able to recover from falls in real robot experiments. Mordatch et al. [9] proposed an optimal control method for a motion synthesis framework, including getting up from the ground, crawling, climbing, etc., but the method requires analysis of dynamic models and usually predefined contact sequences. Traditional fall self-recovery methods mainly adopted teleoperation. For example, in the literature [10], Semini et al. outlined the HyQ2Max robot design and demonstrated the robot’s automatic correction capability through rigid-body dynamics simulations. In the literature [11], Stückler et al. proposed a generalized control method for bipedal robots with sequential action from supine to sitting, then to standing. Inspired by the initial success of the empirically tuned controller, Saranli et al. [12] proposed a feedback controller based on the sagittal model of the robot, which could overcome the actuator torque limitation and achieve dynamic self-recovery of the hexapod robot RHex.

In recent years, methods of achieving self-recovery based on control algorithms have mainly been divided into model-based control, such as model predictive control [13,14], and model-free control, such as deep reinforcement learning [15]. The model predictive control method is to collect the current state information of the robot and establishes a regression model to predict the overturned state according to the collected state information, such as the robot’s acceleration. Then, based on the predicted state, the corresponding behavior is performed. For example, Y. Kakiuchi et al. [13] built a state transition diagram for falling, lying on its back, kneeling, etc., which could search for the behavior closest to the current sensed state when the robot fell to execute the “StateNet” strategy for recovery. This method requires a long execution time to re-plan foot trajectory, which may lead to the landing point failing to reach the specified position.

With the advancement of machine learning (ML) techniques, model-free reinforcement learning (RL) [16] has made it possible to autonomously design motion strategies for legged robots [15,17,18]. For example, L Joonho et al. [15] proposed a method of controlling the recovery actions of quadruped robots using hierarchical behavior-based controllers based on model-free deep reinforcement learning (RL). Xie et al. [17] used an RL algorithm to learn a robust movement strategy for Cassie. Sheng et al. [18] drew inspiration from the rhythmic movement behavior of animals and proposed a biomimetic control architecture composed of RG and PF networks to control the rhythmic movement of quadruped robots. Robot state recovery based on model-free reinforcement learning has high accuracy, but it requires extensive training in the early stage to achieve the ideal effect.

In addition, Shen et al. and Tan et al. [19,20] adopted the method of changing the body structure to realize the self-recovery of the robot from falls. This method uses modular, reconfigurable wheel, track, or body modules that can be reconfigured via self-reorganization to change the overall shape to achieve self-recovery from falls. The disadvantage of this method is that it must add structures, such as connecting rods and motors, which leads to an increase in the complexity of the control algorithm and cost. KNK Nguyen et al. [21] proposed a method that regards the angle trajectory of the robot joint as a multivariable function of time and the direction of the robot root link, and successfully realized the fall recovery function of the biped robot.

In the above-mentioned literature, the designed controller must cover a larger state space to better generate complex combinatorial actions to recover from a fall. However, most quadrupeds in nature, such as dogs, cats, cows, etc., have three ways to recover from falls. First, relying on bending their spine to get up and restore standing posture under the action of gravity. Second, relying on their arms/tails to support themselves with external forces to help them recover their standing posture. Third, rolling to the sides to change their body to a lying position, and returning to a standing position. However, for crustaceans [22], vertebrates’ fall self-recovery methods are obviously inappropriate, because their shells cannot bend, and their claws have limited degrees of freedom. Their claws bend inwards and can grab objects to turn over by force, while the angle of the outward bend is so small that it cannot stand on the ground and turn over. In order to adapt to their physical structure, they have a unique self-recovery method. When they are in a state of complete fall, the highest point of the curved shell is in contact with the ground. Then, under the action of gravity, the shell is easy to be swung by external forces, and the center of gravity will shift. Thus, their self-recovery method is to generate a resonance effect of a specific body shape through the special movement of their legs. With the increase in the amplitude of leg movement, the oscillation amplitude of the body will also increase. When the amplitude of leg movement reaches a certain value, it will make the shell creature inevitably flip. The method of self-recovery of crustaceans from a fall is shown in Figure 1.

To a certain extent, the flipping mode of crustaceans has the generalization ability. Therefore, this paper designs a fall self-recovery control algorithm for quadruped robots by drawing on the fall self-recovery mode of shell organisms in nature and combining the flip process of the inverted pendulum model [23,24,25,26,27,28,29,30,31]. The main contributions of this paper are as follows:

(1) The motion principle based on bionics is adopted to model the self-recovery motion of a quadruped robot after falling. Suppose the shell of the body touches the ground after the quadruped robot falls. As the robot’s legs swing from side to side, the center of gravity of the body will change. When the amplitude of the leg swing reaches a certain value, the robot will turn over and finally recover the standing position, as shown in Figure 2.

(2) According to the behavioral characteristics of animals, DDPG is used to study the behavioral evolution of the quadruped robot, so that it can acquire the ability to self-recover from falls in an unknown environment without prior knowledge.

The remainder of this paper is organized as follows: Section 2 introduces the mathematical model of self-recovery of quadruped robots. Section 3 reveals the control strategy DDPG used in reinforcement learning. Section 4 shows the simulation experiment results. The feasibility and effectiveness of the proposed control strategy are verified by comparing it with classical PID control and linear quadratic regulator (LQR). Section 5 summarizes this paper and discusses possible future steps.

2. Self-Recovery Motion Model of Quadruped Robot Fall

As a mobile platform, the movement of the quadruped robot is mainly achieved by the movement of its supporting legs. When the robot is in an inverted position, the swing of the legs changes the center of gravity of the body to restore the robot from an inverted position to a standing position. Considering the symmetry of the quadruped robot, the kinematic model of the single-leg swing is first analyzed, and then the self-recovery motion model of the quadruped robot is established.

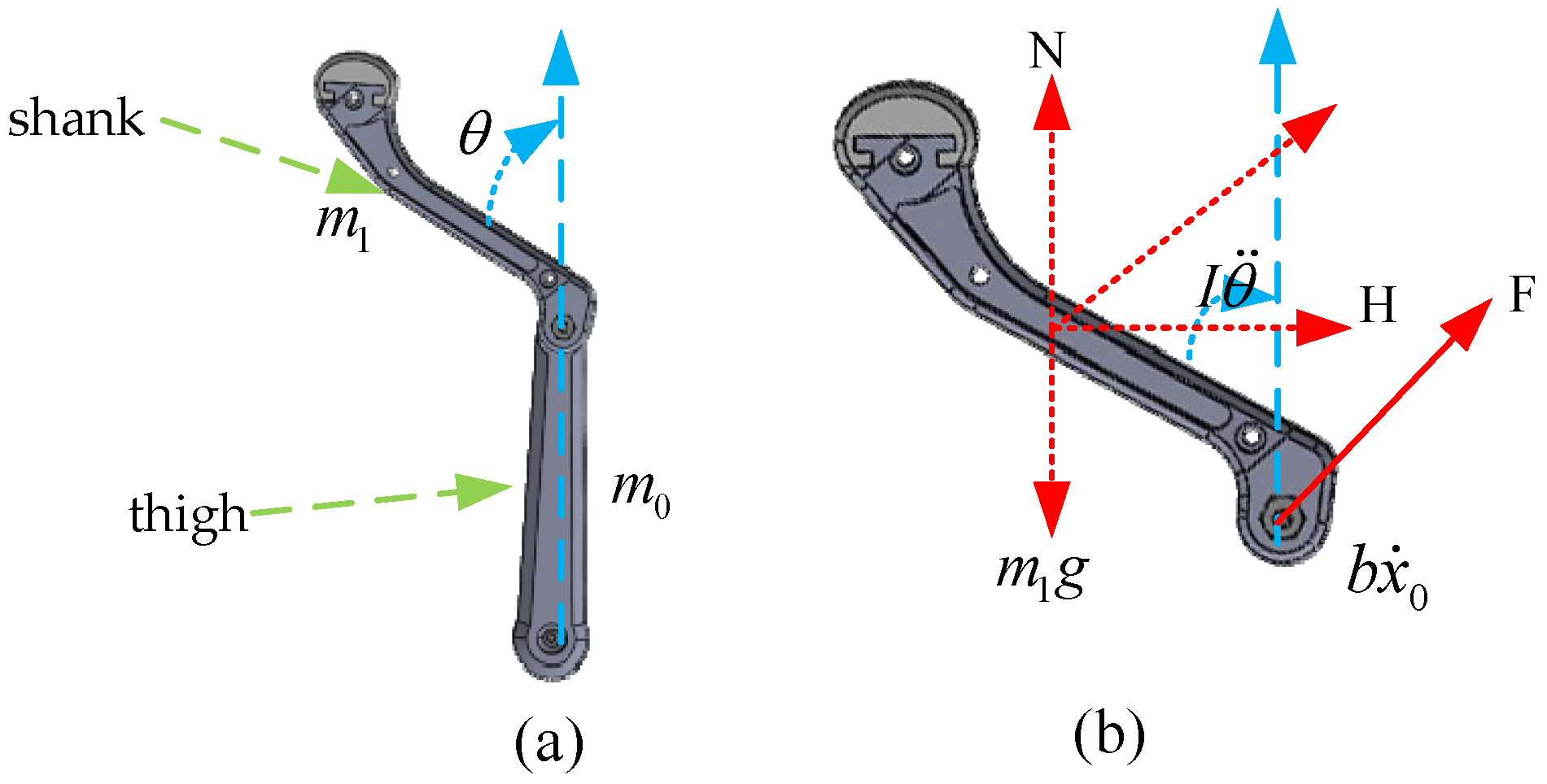
2.1. The Kinematic Model of Single-Leg Swing

Figure 3 shows the kinematic model of the single-leg swing of a quadruped robot. In Figure 3, $m_0$ represents the mass of the thigh; $m_1$ represents the mass of the shank; $\theta$ represents the angle of the shank swing; $F$ represents the driving force provided by the motor at the knee joint; $H$ represents the horizontal force on the shank; $N$ represents the vertical force on the shank; $I$ represents the moment of inertia; $l$ represents the length of the shank; $b$ represents the friction coefficient between the joints. According to Newton’s second theorem, the force equation in the horizontal direction at the knee joint of the quadruped robot can be deduced as

$$m_0\ddot{x}=F-b{\dot{x}}_0-H$$

(1)

Among them, $x_0$ is the horizontal position of the knee joint of the quadruped robot. The torque balance equation of the quadruped robot’s single-leg rotating around the center of mass can be obtained by

$$-Hlcos\theta -Nlsin\theta =I\ddot{\theta }$$

(2)

Assume that $\phi$ is much smaller than the unit radian; that is, $\phi \ll 1$, and set $\theta =\pi -\phi$. Subsequently, the following approximations can be made: ${\left(\frac{d\theta }{dt}\right)}^2=0,cos\theta =1,sin\theta =\phi$. According to Equations (1) and (2), and the force analysis of the quadruped robot in the vertical direction, the kinematic model of the single-leg swing of the quadruped robot can be obtained as

$$\left\{\begin{array}{c}-m_1{\ddot{x}}_{0}l-m_{1}gl\phi =\left(I+m_1{l}^2\right)\ddot{\theta }\\ F=b{\dot{x}}_0+\left(m_0+m_1\right){\ddot{x}}_0+m_{1}l\ddot{\theta }\end{array}\right.$$

(3)

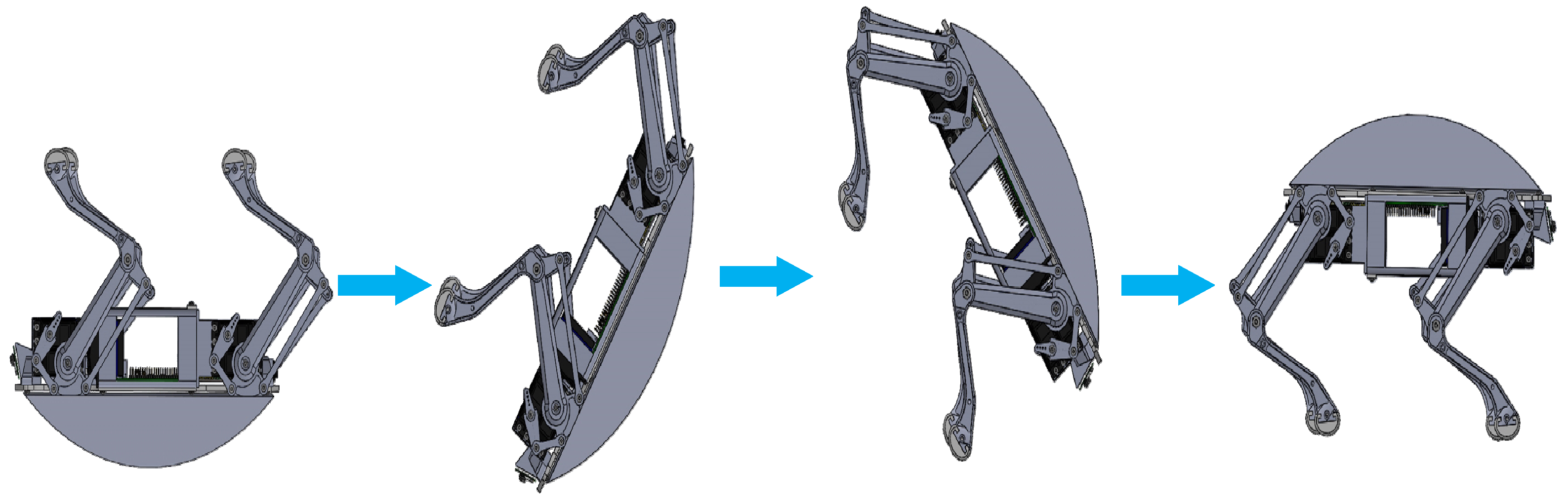
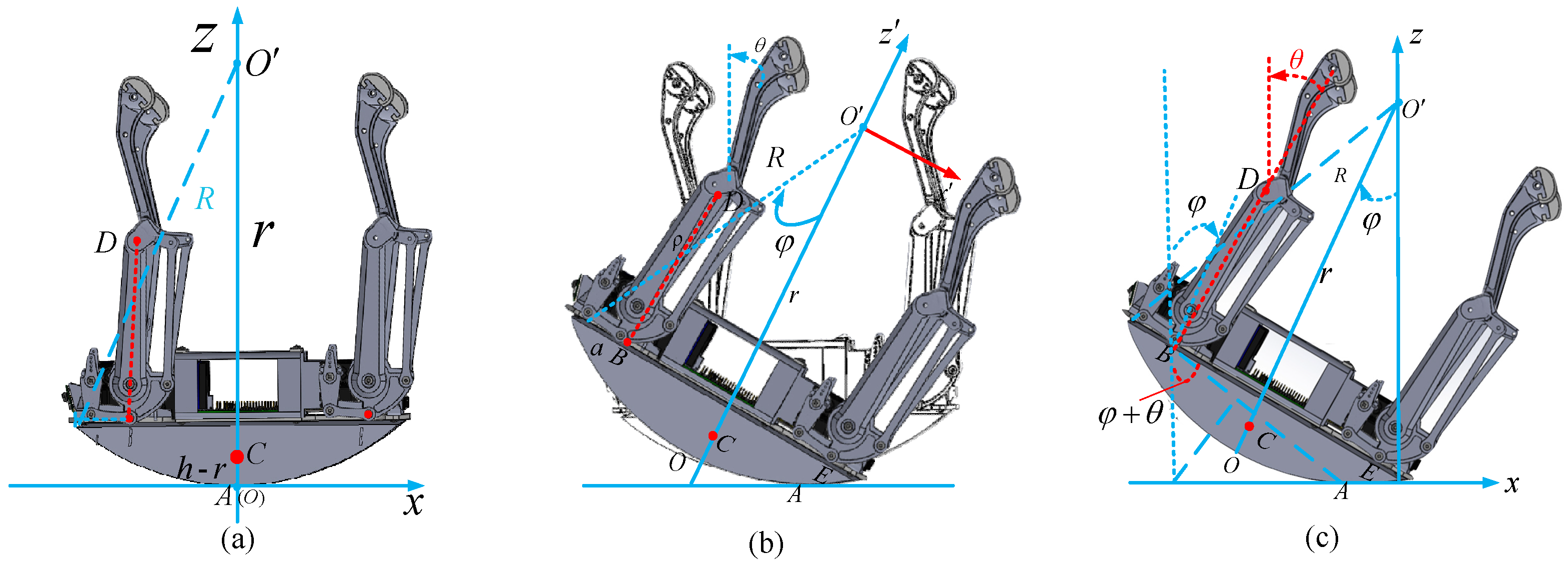
2.2. Self-Recovery Motion Model of Quadruped Robot after Falling

It is assumed that the cylinder-like body of the quadruped robot is of uniform mass, and the contact point between the robot and the ground after tipping over is point A, as shown in Figure 4a. The radius of the circular surface of the cylinder-like body is $R$, the center of the cylinder-like body is $O^{\prime }$, the distance from the cross-section is $h$, the center of mass of the cylinder-like body is point C, the mass is about $M$, the distance from the center of the circle is $r$, and the moment of inertia is $J$. Suppose the mass of the quadruped robot’s one leg is $m_0+m_1$, and a connecting rod with distance $a$ from the outer edge of the section is connected to point B through the motor. The leg can be rotated at an angle of $\theta$, the centroid of the leg is point D, the distance between point D and point B is $\rho$, and the rotational moment of inertia is $J_r$. The other leg of the quadruped robot is connected at point E in the same way, and the mass of the leg is $m_0+m_1$. The point of contact with the ground at the highest point of the shell is the origin O, and the absolute coordinate system is established with this point. In the coordinate system, the ground reference line is the $x$-axis (the right direction of the $x$-axis is the positive direction), and the axis perpendicular to the ground reference line is the $z$-axis (the upward direction of the $z$-axis is the positive direction).

In order to restore the robot to its normal state, the robot’s shell will be rotated around its circle center by an angle $\phi$, and the state of the robot after the rotation is shown in Figure 4b. Since the robot’s shell is an arc-shaped structure, point A is always the contact point between the robot shell and the ground. When the robot starts to rotate around the center of the circle $O^{\prime }$, the distance moved on the $x$-axis should be the length of the arc it bypasses (without movement on the $z$-axis), and the coordinates of point A is $\left(R\phi ,0\right)$. When taking point A as a base point, we can obtain the coordinates of points B, C, and E as follows:

$$B\left(R\phi -hsin\phi -\left(\sqrt{R^2-h^2}-a\right),R-hcos\phi +\left(\sqrt{R^2-h^2}-a\right)sin\phi \right),$$

$$C\left(R\phi -rsin\phi ,R-rcos\phi \right),D\left(x_B+\rho sin\left(\phi +\theta \right),z_B+\rho cos\left(\phi +\theta \right)\right),$$

$$E\left(R\phi -hsin\phi +\left(\sqrt{R^2-h^2}-a\right)cos\phi ,R-hcos\phi -\left(\sqrt{R^2-h^2}-a\right)sin\phi \right).$$

Among them, $\theta$ represents the rotation angle of the robot’s shank. Thereby, the displacements $l_{AB}$, $l_{AC}$, $l_{AD}$, $l_{AE}$ of each point can be calculated from the coordinates of each point.

To study the movement of the center of mass, we establish the relative coordinate system between each point on the shell and the center of the circle. The relative coordinate system takes the center of the shell $O^{\prime }$ as the origin, and the direction of BE as the positive direction to establish the $x^{\prime }$ axis. In addition, the $z^{\prime }$ axis is perpendicular to the $x^{\prime }$ axis, and the positive direction is upward, as shown in Figure 4b. Thus, the coordinates of points C, B, D, and E under the relative coordinate system are obtained as

$$({x^{\prime }}_C=0,{z^{\prime }}_C=-r), ({x^{\prime }}_B=-\sqrt{R^2-h^2}+a,{z^{\prime }}_B=-h),$$

$$({x^{\prime }}_D={x^{\prime }}_B+\rho sin\theta ,{z^{\prime }}_D={z^{\prime }}_B+\rho cos\theta ), ({x^{\prime }}_E=\sqrt{R^2-h^2}-a,{z^{\prime }}_E=-h).$$

Furthermore, the coordinate $\left({x^{\prime }}_{cm},{z^{\prime }}_{cm}\right)$ of the center of mass of the quadruped robot in the relative coordinate system can be calculated as ($\frac{\left(m_0+m_1\right)\rho sin\theta }{M+2\left(m_0+m_1\right)},\frac{\left(m_0+m_1\right)\left(-2h+\rho cos\theta \right)-Mr}{M+2\left(m_0+m_1\right)}$). The centroid relationship between the absolute coordinate system with $O$ as the origin and the relative coordinate system with $O^{\prime }$ as the origin can be expressed as

$$x_{cm}=R\phi +\frac{\left(m_0+m_1\right)\rho sin\left(\phi +\theta \right)-S_{1}sin\phi }{M+2\left(m_0+m_1\right)}=R\phi +{z^{\prime }}_{cm}sin\phi +{x^{\prime }}_{cm}cos\phi$$

(4)

$$z_{cm}=R+\frac{\left(m_0+m_1\right)\rho cos\left(\phi +\theta \right)-S_{1}cos\phi }{M+2\left(m_0+m_1\right)}=R+{z^{\prime }}_{cm}cos\phi -{x^{\prime }}_{cm}sin\phi$$

(5)

Among them, $S_1=Mr+2\left(m_0+m_1\right)h$. In Figure 4b, the force arm of the quadruped robot from the center of mass to point A is ${z^{\prime }}_{cm}sin\phi +{x^{\prime }}_{cm}cos\phi$, then the gravitational moment $M_A$ of the quadruped robot at point A is

$$M_A=\left(M+m_0+m_1\right)g\left({z^{\prime }}_{cm}sin\phi +{x^{\prime }}_{cm}cos\phi \right)$$

(6)

When $M_A=0$, the quadruped robot is in the equilibrium position and ${z^{\prime }}_{cm}sin\phi +{x^{\prime }}_{cm}cos\phi =0$. According to the relationship between displacement distance and velocity, the relative velocities of points B, C, D, and E can be obtained as

$$\begin{gathered} {\dot{x}}_B=\frac{d{x}_B}{dt}=R\dot{\phi }-hcos\phi \dot{\phi }+\left(\sqrt{R^2-h^2}-a\right)sin\phi \dot{\phi }=A{B}_z\dot{\phi } \\ {\dot{z}}_B=\frac{d{z}_B}{dt}=hsin\phi \dot{\phi }+\left(\sqrt{R^2-h^2}-a\right)cos\phi \dot{\phi }=-A{B}_x\dot{\phi } \end{gathered}$$

(7)

$$\begin{gathered} {\dot{x}}_C=\frac{d{x}_C}{dt}=R\dot{\phi }-rcos\phi \dot{\phi }=A{C}_z\dot{\phi } \\ {\dot{z}}_C=\frac{d{z}_C}{dt}=rsin\phi \dot{\phi }=-A{C}_x\dot{\phi } \end{gathered}$$

(8)

$$\begin{gathered} {\dot{x}}_D=\frac{d{x}_D}{dt}={\dot{x}}_B+\rho cos\left(\phi +\theta \right)(\dot{\phi }+\dot{\theta })=A{B}_z\dot{\phi }+\rho cos\left(\phi +\theta \right)(\dot{\phi }+\dot{\theta }) \\ {\dot{z}}_D=\frac{d{z}_D}{dt}=-A{B}_x\dot{\phi }-\rho sin\left(\phi +\theta \right)(\dot{\phi }+\dot{\theta }) \end{gathered}$$

(9)

$$\begin{gathered} {\dot{x}}_E=\frac{d{x}_E}{dt}=R\dot{\phi }-hcos\phi \dot{\phi }-\left(\sqrt{R^2-h^2}-a\right)sin\phi \dot{\phi }=A{E}_z\dot{\phi } \\ {\dot{z}}_E=\frac{d{z}_E}{dt}=hsin\phi \dot{\phi }-\left(\sqrt{R^2-h^2}-a\right)cos\phi \dot{\phi }=-A{E}_x\dot{\phi } \end{gathered}$$

(10)

It is analyzed that the entire quadruped robot system has a rotational angular velocity $\dot{\phi }$, while point D has a rotational angular velocity. Assuming that the moment of inertia of the rod equivalent to the center of mass of the quadruped robot’s leg is $J_r$, and the moment of inertia of the quadruped robot’s shell relative to the section BE is $J$, the corresponding moments of inertia of the two rotational angular velocities are

$$\begin{gathered} K_{\phi }=J_r+J+M{\left|AC\right|}^2+\left(m_0+m_1\right){\left(\rho +\left|AB\right|\right)}^2+\left(m_0+m_1\right){\left|AE\right|}^2 \\ {K}_{\theta }=J_r+\left(m_0+m_1\right)\left({\rho }^2+\rho \left|AB\right|\right) \end{gathered}$$

(11)

Among them, ${\left|AC\right|}^2={\left(A{C}_x\right)}^2+{\left(A{C}_z\right)}^2$, ${\left|AE\right|}^2={\left(A{E}_x\right)}^2+{\left(A{E}_z\right)}^2$, ${\left|AB\right|}^2={\left(A{B}_x\right)}^2+{\left(A{B}_z\right)}^2$. Further, the angular momentum $K_A$ at point A can be calculated as

$$K_A=K_{\phi }\dot{\phi }+K_{\theta }\dot{\theta }$$

(12)

According to Newton’s second law, the total external force on the mass is equal to the momentum transformation rate, and the derivative of the angular momentum relative to time is equal to the moment of the external force when the radius vector is constant. Therefore, the momentum change equation of point A can be calculated by

$$\frac{d{K}_A}{dt}=-R\dot{\phi }{Q}_z=M_{\sigma }g\left(x_{cm}-R\phi \right)$$

(13)

Among them, $Q_x=M_{\sigma }{z}_{cm}\dot{\phi }+\left(m_0+m_1\right)\rho cos\left(\phi +\theta \right)\dot{\theta }$, $Q_z=-M_{\sigma }\left(x_{cm}-R\phi \right)\dot{\phi }-\left(m_0+m_1\right)\rho sin\left(\phi +\theta \right)\dot{\theta }$, and $M_{\sigma }=M+2\left(m_0+m_1\right)$. It can be derived from Equations (12) and (13)

$${\dot{K}}_{\phi }\dot{\phi }+K_{\phi }\ddot{\phi }+{\dot{K}}_{\theta }\dot{\theta }+K_{\theta }\ddot{\theta }-R\dot{\phi }{Q}_z=M_{\sigma }g\left(x_{cm}-R\phi \right)$$

(14)

For simplicity, suppose that the motion of a quadrupedal robot occurs at the instant of $\dot{\theta }=\ddot{\theta }=0$ to achieve the body turning to the normal position. According to Equation (11), Equation (14) can be simplified as

$$\ddot{\phi }-\frac{R{M}_{\sigma }\left(x_{cm}-R\phi \right)}{K_{\phi }}{\dot{\phi }}^2=\frac{M_{\sigma }g\left(x_{cm}-R\phi \right)}{K_{\phi }}$$

(15)

Making $b_1\left(\phi \right)=-\frac{R{M}_{\sigma }\left(x_{cm}-R\phi \right)}{K_{\phi }}$ and $x\left(\phi \right)={\dot{\phi }}^2$, then $\frac{dx\left(\phi \right)}{d\phi }=2\ddot{\phi }$. Thus, Equation (15) can be expressed as

$$\frac{dx\left(\phi \right)}{d\phi }+2b_1\left(\phi \right)x\left(\phi \right)=-\frac{2g}{R}{b}_1\left(\phi \right)$$

(16)

It can be obtained by solving the differential Equation (16)

$${\dot{\phi }}^2=\left[\frac{g}{R}+{\dot{\phi }}_0^2\right]e^{-\tau }-\frac{g}{R}, \tau =2{{\displaystyle \int }}_{{\phi }_0}^{\phi }{b}_1\left(\phi \right)d\phi$$

(17)

Substitute $b_1\left(\phi \right)$, $K_{\phi },$ and $x_{cm}$ into $\tau$ to obtain

$$\tau =2{{\displaystyle \int }}_{{\phi }_0}^{\phi }-\frac{R{M}_{\sigma }\left(z_{cm}^{’}sin\phi +x_{cm}^{’}cos\phi \right)}{K_{\phi }}d\phi$$

(18)

When the value $\theta$ is constant, $\tau =In\frac{K_{\phi }}{K_{{\phi }_0}}$. Thus, Equation (17) can be rewritten as

$${\dot{\phi }}^2=\left[\frac{g}{R}+{\dot{\phi }}_0^2\right]\frac{K_{\phi }}{K_{{\phi }_0}}-\frac{g}{R}$$

(19)

Considering the body structure of the quadruped robot, the rotation angle of the knee joint is set to $45°\sim 315°$. When the rotation angle of the knee joint reaches its extreme value, the connection between the shank and the thigh becomes rigid. Thus, during the quadruped robot self-recovery, the swing angle $\phi ={\phi }_m$. When $\dot{\phi }=0$ and ${\phi }_m=0$, it is obtained that $\frac{K_{\phi }}{K_{{\phi }_0}}=1$. Further, according to Equations (4)–(11), it can be deduced that

$${z^{\prime }}_{cm}cos{\phi }_0-{x^{\prime }}_{cm}sin{\phi }_0={z^{\prime }}_{cm}cos{\phi }_m-{x^{\prime }}_{cm}sin{\phi }_m$$

(20)

If $cos\beta =\frac{{z^{\prime }}_{cm}}{\sqrt{{\left({z^{\prime }}_{cm}\right)}^2+{\left({x^{\prime }}_{cm}\right)}^2}}$ and $sin\beta =\frac{{x^{\prime }}_{cm}}{\sqrt{{\left({z^{\prime }}_{cm}\right)}^2+{\left({x^{\prime }}_{cm}\right)}^2}}$, Equation (20) can be replaced by

$$cos\left({\phi }_m+\beta \right)=cos\left({\phi }_0+\beta \right)$$

(21)

The solution of Equation (21) is ${\phi }_m={\phi }_0$ or ${\phi }_m=-\left({\phi }_0+2\beta \right)$. Suppose $\beta ={\beta }_1$, the robot moves from $\phi ={\phi }_0>0$ to $\phi ={\phi }_m$. Additionally, when $\beta ={\beta }_2$, it moves from $\phi ={\phi }_m$ to the opposite direction. At this time, the new initial value of angle ${\phi }_0^{\left(1\right)}$ is ${\phi }_0^{\left(1\right)}={\phi }_0+2\left({\beta }_1-{\beta }_2\right)$. If ${\beta }_1-{\beta }_2>0$, ${\phi }_0^{\left(1\right)}>{\phi }_0$, after n iterations, it can be obtained that ${\phi }_0^{\left(n\right)}={\phi }_0+2n\left({\beta }_1-{\beta }_2\right)$. The amplitude of the oscillation will increase with the increase in the number of iterations n, and the quadruped robot will inevitably flip through point E or B. Finally, it will achieve self-recovery.

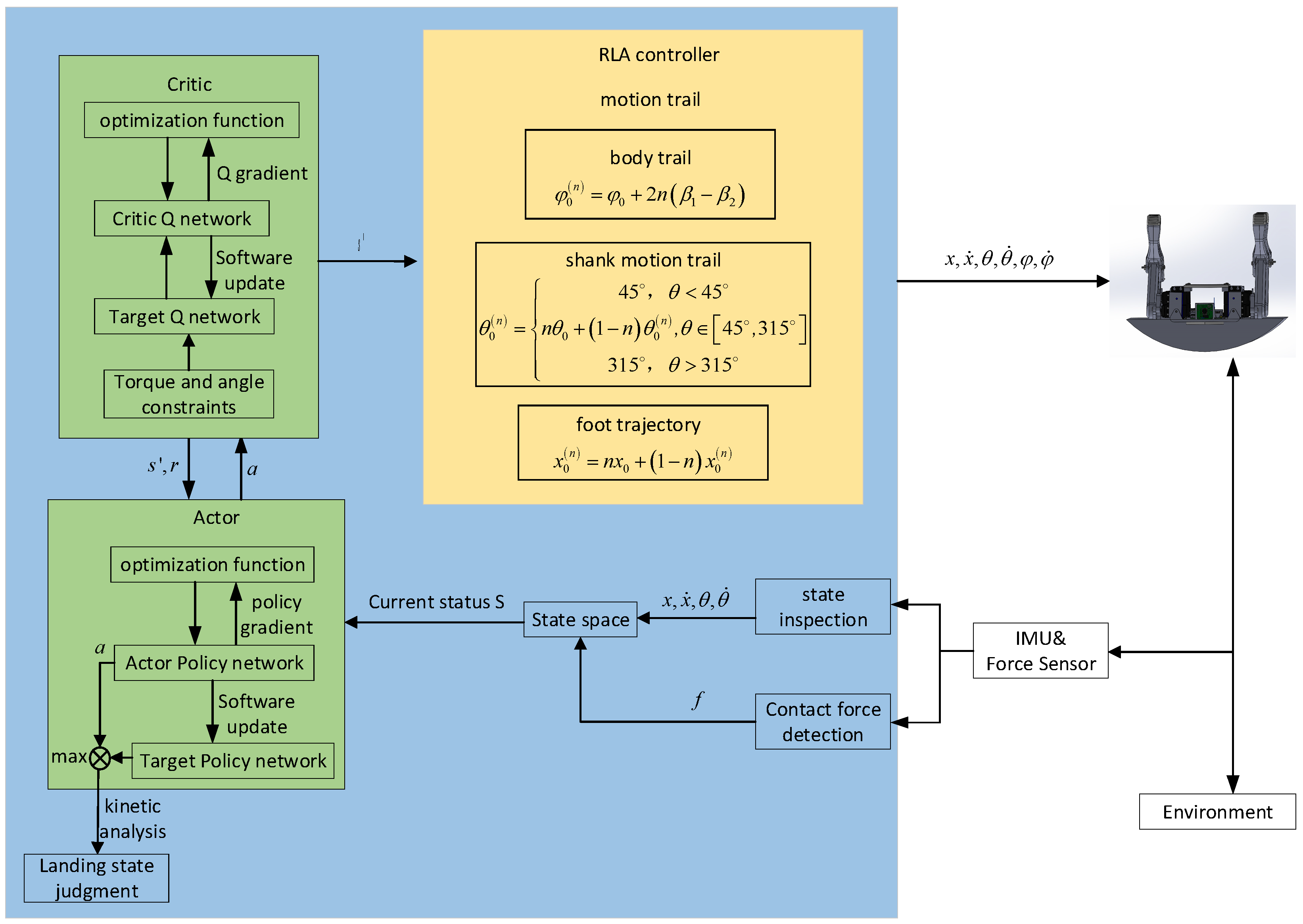
3. Control Strategy

Deep Deterministic Policy Gradient (DDPG), which is an actor–critic framework based on deterministic action strategies, was first proposed by Lillicrap et al. [32]. This paper applies DDPG as a control strategy to the self-recovery of quadruped robots. Considering that the motion of the robot has continuous characteristics, batch normalization is used to solve the problem that different inputs’ features have different units and data ranges. The implementation framework of DDPG is shown in Figure 5.

It can be seen from the environment model of the quadruped robot that the state space of the quadruped robot is $S=\left[x,\dot{x},\theta ,\dot{\theta },\phi ,\dot{\phi }\right]$. Among them, $x$ represents the position of the foot; $\dot{x}$ represents the motion speed of the foot; $\theta$ represents the rotation angle of the knee joint; $\dot{\theta }$ represents the angular velocity of the knee joint rotation; $\phi$ is the angle of thigh-driven body rotation; $\dot{\phi }$ represents the angular speed when the thigh drives the body to rotate. The action space, which is $A=\left[-1,1\right]$, is expanded to $\left[-40,40\right]$ according to the requirements of this paper; that is, the maximum driving force is 40 N, and the minimum is −40 N.

The actor uses the reward function to achieve the optimization of behavior decisions and maps states into actions. Its input is the state space variable $S$ and contact force $f$ of a quadruped robot, and its output is the action space $A$. The critic evaluative feedback signal, which is obtained from the environment, accumulates the weighting of the feedback signal at the next moment and generates a reward function to evaluate the quality of the current action. The inputs of the critic evaluative feedback signal are the state variable $S$, contact force $f$, and action space $A$. Its outputs are the evaluation function and the state of the feedback. When the next state and evaluation situation are input to the robot model, the model will adjust the corresponding attitude. Then, the adjustment situation is fed back to the actor by the new state quantity, which is measured through IMU and other sensors to realize closed-loop control. The learning network architecture designed according to the mathematical model of quadruped robot self-recovery is shown in Figure 6.

The control strategy is that the agent interacts with the environment to obtain the state $s=\left[S,f\right]$ of the quadruped robot. Then, the action $a$ acting on the foot is obtained by the sampling network, which acts as a label during the training process. Finally, the cumulative reward is obtained by accumulating and normalizing the cumulative reward after the action.

Actor–critic is a combination of two neural networks, consisting of an input layer, a fully connected layer, an activation function, and an output layer [33]. The fully connected layer connects each neuron in one layer to each neuron in the next layer, and often needs to introduce a nonlinear activation function. The activation function has the effect of preventing gradient diffusion, sparse activation, and efficient calculation, and can better train deeper networks [34,35]. In this paper, the ReLu activation function is used to increase the nonlinear factors of the neural network model. In particular, the last activation function of the actor and critic neural networks is different (one is ReLu, and the other is Tanh).

In addition to the activation function, other hyperparameters also need to be determined during model training, such as the optimizer category, step size, and training epoch [15]. The hyperparameter settings for the neural network in this paper are shown in

Table 1. The hyperparameter settings of the neural network.

Hyperparameter	Selection	Description
optimizer	Adam	Optimizer for the neural network
step size	25	The maximum time step that each episode lasts
epoch	2000	The number of training times for all samples in the training set

.

First, the training process requires initialization of the agent and the environment, including the definition of hyperparameters such as the learning rate of the two networks, the current state $S$, the state of the next moment $S^{\prime }$, and the corresponding reward $R$. The action $A$ obtained by the actor. Then, the constructed policy network selects the action according to the current state. After executing the action, the corresponding punishment and new states are obtained. Next, the environment stores the previous state, action, reward, and new state, and then feeds them back to the strategy network for training. The first term of the penalty function (in this paper, the penalty function can also be called a reward function) is the penalty for the angle difference between the current position of the leg and the target position of the leg. The second term of the penalty function is the penalty for angular velocity. Although the robot reaches the target position (returning to a standing position), if the speed of the robot is too fast, it may cause a fall again. The third term of the penalty function is the penalty for the robot’s foot position. Since the farther the position of the foot moves, the more torque the motor requires, which is bad for the robot. Thus, the position of the foot moves farther, the greater the penalty value given. The DDPG control Algorithm 1 is as follows:

Algorithm 1 The DDPG Control Algorithm
Input: state space $\mathit{s} \left(\mathit{s}\in \mathit{S}\right)$ and action space $\mathit{a} \left(\mathit{a}\in \mathit{A}\right)$;
Output: action;
1:	Initial agent and environment;
2:	while doTraining = true do
3:	if $episodes<maxepisode$ then
4:	Set episode $T_1=0$;
5:	Select action $a$ according to the current observed state $s$;
6:	Observe reward $r$ and observe new state $s^{\prime }$ after executing action $a$;
7:	Store transition $\left(s,a,r,s^{\prime }\right)$ in $R$
8:	Perform the action $T_{step}$;
9:	Store data and update state $T_1=T_1+T_{step}$;
10:	Identify and update the target neural network;
11:	Identify and train evaluation neural network;
12:	else
13:	End the training;
14:	end if
15:	end while

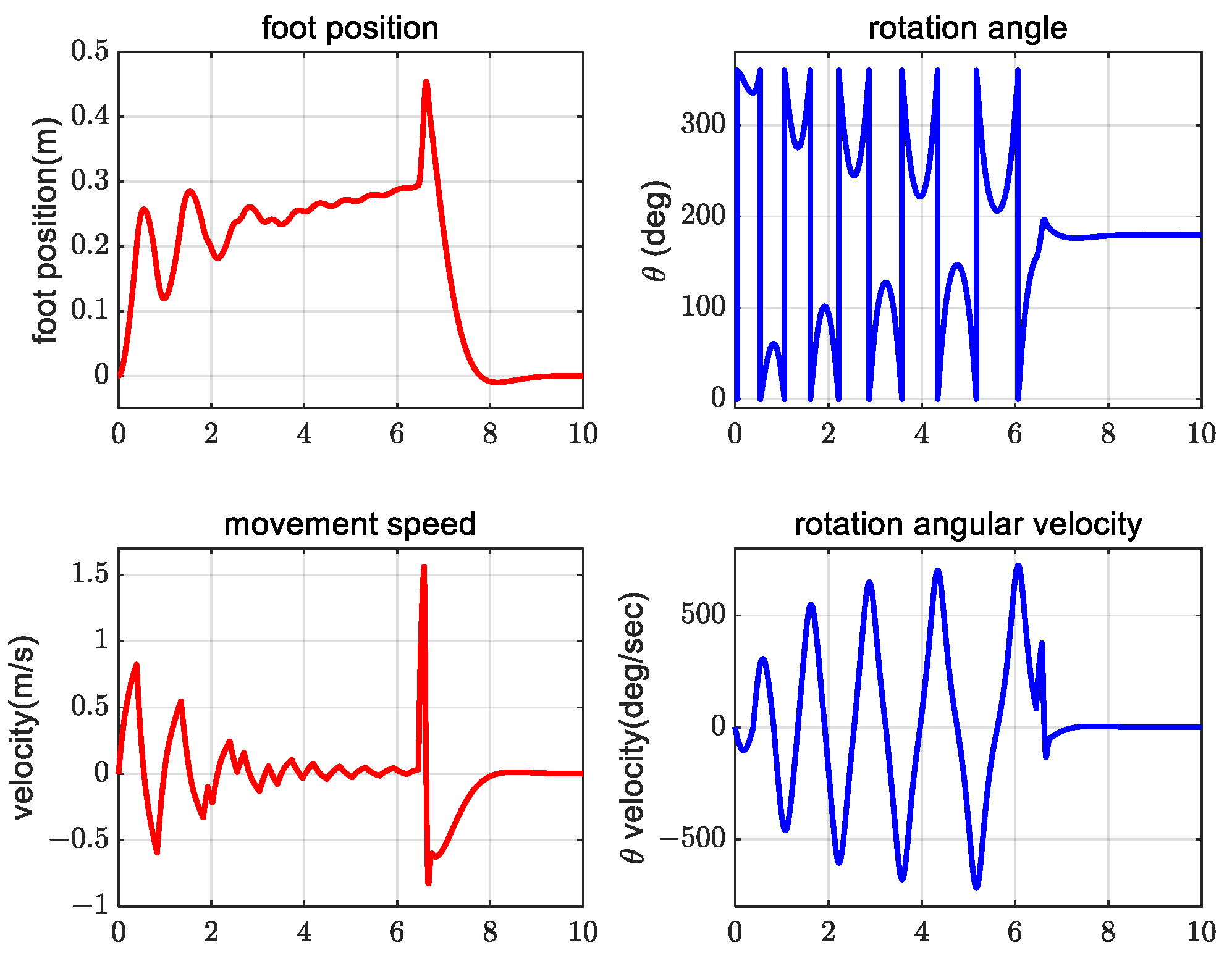
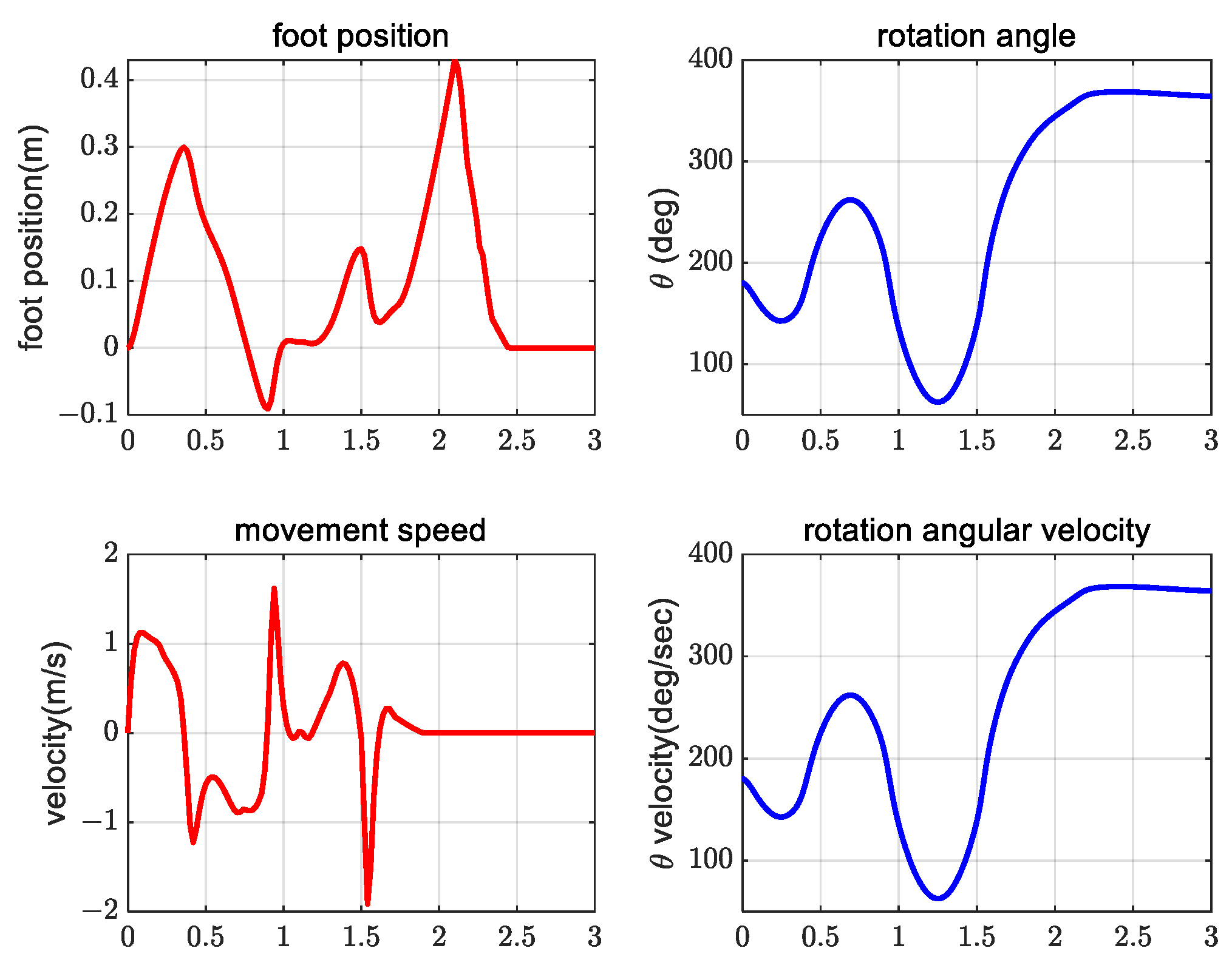
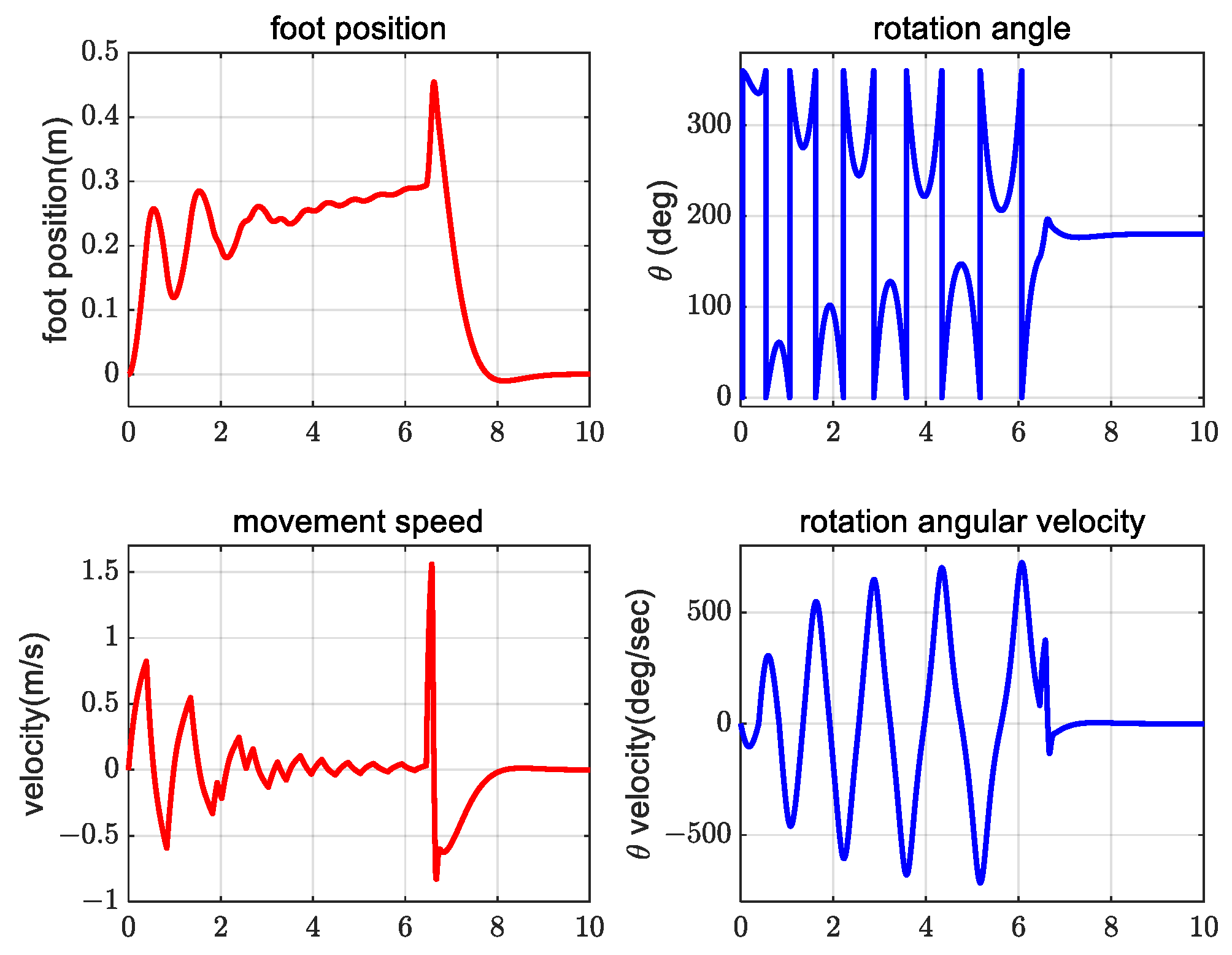
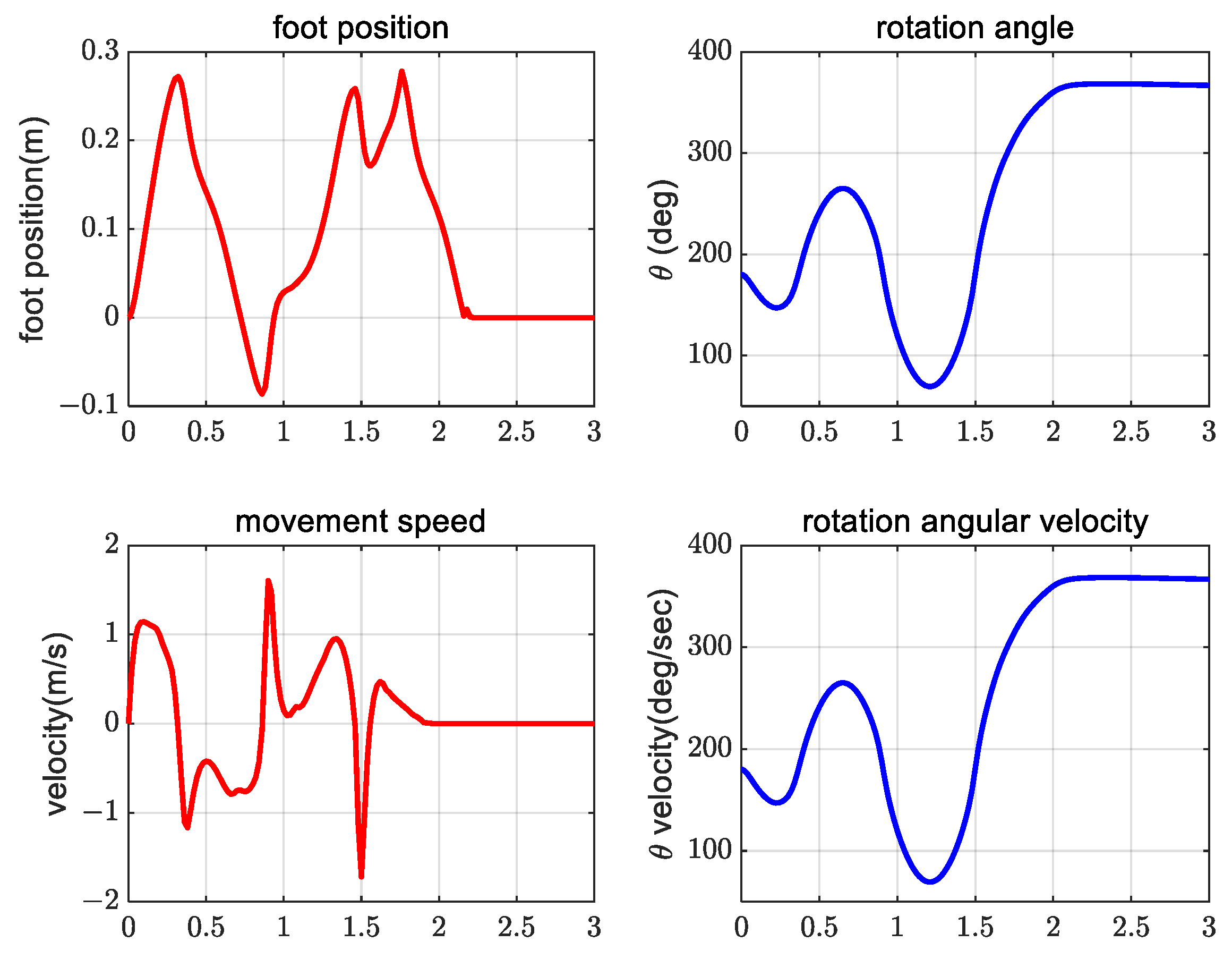
4. Simulation Verification Experiment

In this paper, the simulation experiments were carried out by using the Simulink toolbox of MATLAB (R2022b) [26]. Considering that the robot’s feet need to have anti-slip and wear-resistant characteristics, the material of the robot’s feet in this paper is rubber, the density of which is 1.3 $g/c{m}^3$. The overall height, length, and mass of the robot are 0.95 m, 1 m, and 5 kg, respectively. In the preliminary experiment, hundreds of random seeds were tried. The initial state directly affects the distribution of the entire state motion sequence of the agent. In order to ensure that the random numbers generated by each run were the same and to facilitate the reproduction of results, the random seed of the DDPG control strategy was set to 0. Multiple experiments found that when the cost function was less than −530 after more than 1500 rounds of training, the training situation reached the expected result.

Considering the leg structure of the robot, the angle at which the thigh can drive the body rotation is limited. So, we selected the foot position $x$, foot movement speed $\dot{x}$, knee joint rotation angle $\theta$ and knee joint rotation angular velocity $\dot{\theta }$ from the state space S of the robot for comparison to judge the quality of the controller. This paper compares the self-recovery effects of the three control algorithms DDPG, PID [36,37], and LQR [38,39,40] after the robot falls, and the control effects without interference are shown in Figure 7, Figure 8 and Figure 9, respectively.

It can be seen from Figure 7, Figure 8 and Figure 9 that the control mode of PID made the foot position of the robot move more. In addition, the displacement changed quickly in the early stage of the movement, and the landing was easily made unstable, causing the robot damage. At the same time, affected by the robot’s movement speed, the stability of the robot after returning to standing was poor.

LQR control mode was less movement than PID, and its movement speed was moderate. However, this control method in the swing to reach the resonance frequency needed to occur a sudden change in displacement so that the robot returned to a standing posture. The specific phenomenon was that the foot of the robot moved multiple times, driving the body to swing. When the swing frequency reached the resonance frequency, the robot’s body position and standing posture angle reached 45°. At this time, the robot moved quickly to the left or right to promote the recovery of the standing posture.

In contrast, the control method of DDPG was more accurate in controlling the angle of swing and force due to experience gained from extensive experiments in the early stage. The recovery of standing posture could be achieved with fewer swings, which reduced the possibility of repeated friction between the robot’s body and the ground. In addition, the moving speed of the robot did not change abruptly, reducing the pressure on the structure of the robot’s legs and the motors, causing no secondary damage to the robot.

From the control point of view, there are three main evaluation performance indicators: stability, accuracy, and rapidity. Among them, stability is an important judgment property of automatic control. Figure 10, Figure 11 and Figure 12, respectively, show the control results of three control modes in the case of interference.

From the comparison of Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, it can be seen that after the interference was introduced, the recovery process of the LQR-controlled robot was the same as that without interference, while PID and DDPG made use of the interference to speed up the recovery process. The key indicators of three algorithms in the self-recovery process are shown in

Table 2. The key indicators of three algorithms in the self-recovery process.

Performance Index	PID	LQR	DDPG
Adjustment time/s	10	7.2	2.25
Swing frequency/period	4	4	2
Interference with adjustment time/s	0.5	0	0.3
Immunity to interference/percentage	0.01	0.01	1

.

In Table 2, the adjustment time refers to the time required for the robot to recover from the fully inverted stable state to the standing stable state; the swing frequency refers to the swing cycle required by the robot to achieve self-recovery of the body; the interference adjustment time refers to the difference between the time required for the robot to recover from a fully inverted steady state to a standing steady state after the introduction of interference and the time required without interference; the anti-interference ability refers to the maximum interference force that all control methods can withstand, taking the maximum interference force that DDPG can withstand as a reference.

5. Conclusions and Future Work

5.1. Conclusions

Although the other two control methods have the anti-interference ability, the interference force they can withstand is only 1% of DDPG. When the limit of what can be withstood is exceeded, PID and LQR will directly lose control. However, the control method based on reinforcement learning can dynamically adjust the parameters, and each movement of the robot can be used as the input for the next learning. With the increase in the training times, the controller will become more and more stable, and the self-adaptation ability to the environment will become stronger, which ensures the stability, accuracy, and rapidity of the self-recovery. From the overall control situation, the control effect of the three control methods is that DDPG is better than LQR, and LQR is better than PID. In addition, the training model based on reinforcement learning shows the best effect. Through theoretical analysis and extensive simulation experiments, the feasibility and superiority of the DDPG control method for achieving self-recovery of the quadruped robot after falling are verified.

5.2. Future Work

In this paper, a training model based on reinforcement learning was used to control the quadruped robot in a way that mainly utilized the neural network composed of actor and critic. Although the control accuracy and the adaptability to the environment are improved by the self-learning ability of the neural network, there are also following limitations. First, it takes a long time to train the network. If training is not over, the network may fail to control the system. Second, reinforcement learning relies on early data training. However, the data collection process in the real environment is uncontrollable. Third, random exploration and poor interpretability do not have supervised learning basic correct rate, and the control effect only relies on the reward curve and actual control feedback. These limitations mentioned above can be optimized by adjusting the network architecture and modifying the discount function.

In addition, this paper only considers the self-recovery of the robot after falling on flat ground. In the future, a more complex environment, such as complex mountain terrain, will be considered to further improve the proposed self-recovery algorithm for quadruped robots.