Vibration Performance of Traction Gearbox of a High-Speed Train: Theoretical Analysis and Experiments
Abstract
1. Introduction
2. Dynamic Model of Traction Gear Transmission System
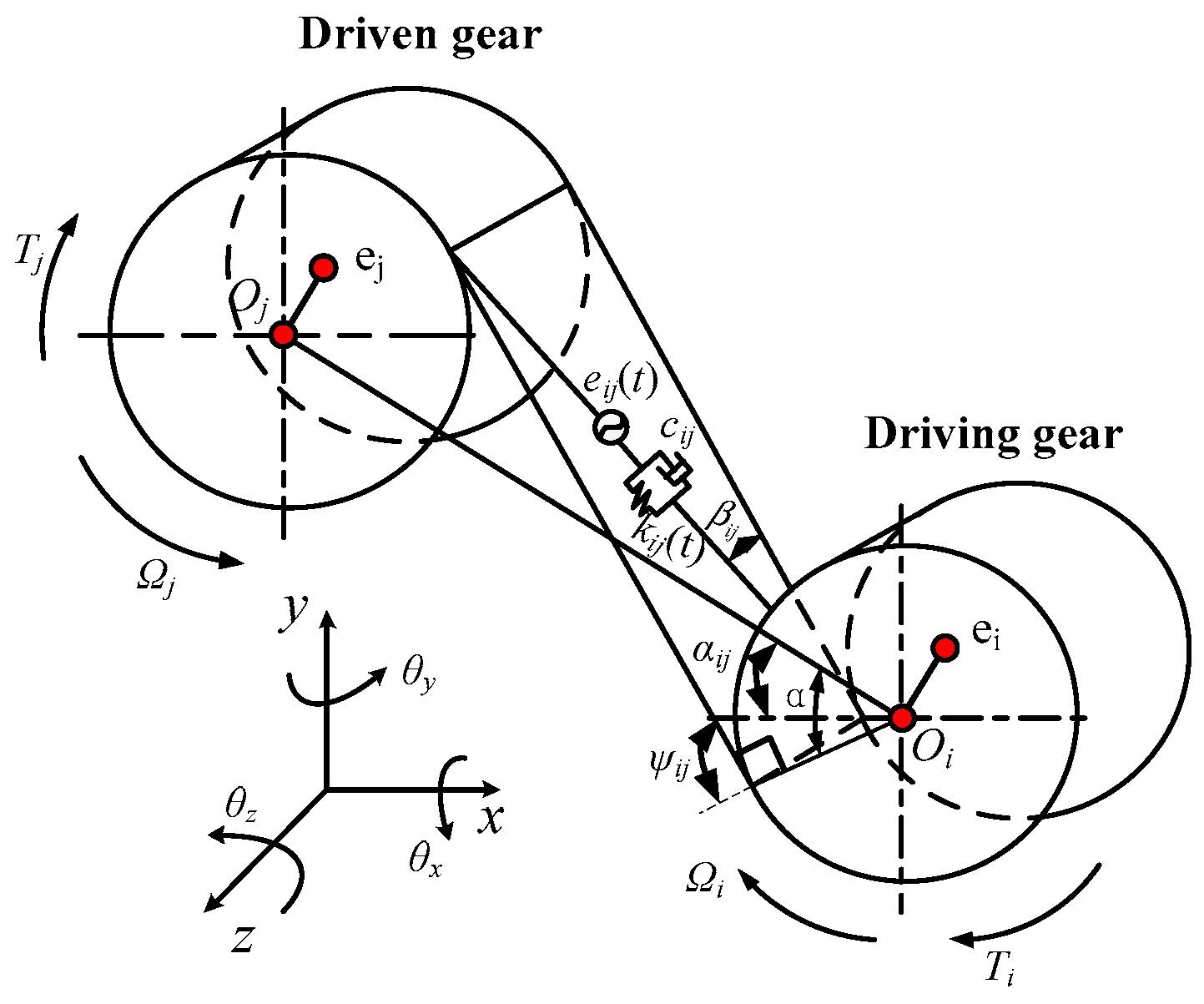
2.1. Gear Meshing Unit Model
2.1.1. Parameters of Gear Pair
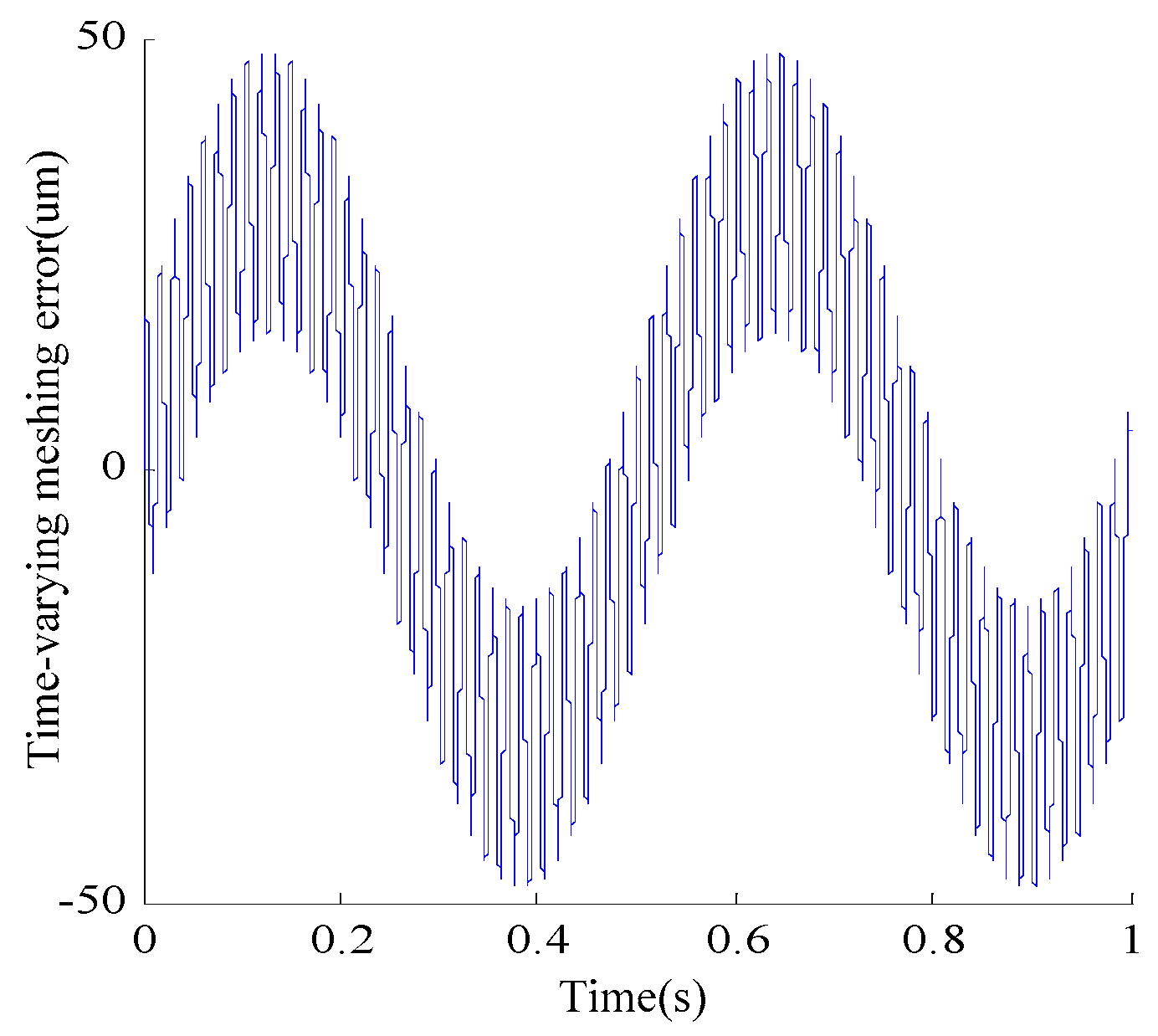
2.1.2. Time-Varying Meshing Stiffness and Time-Varying Meshing Error
2.1.3. Mathematical Model of Helical Gear Pair Meshing
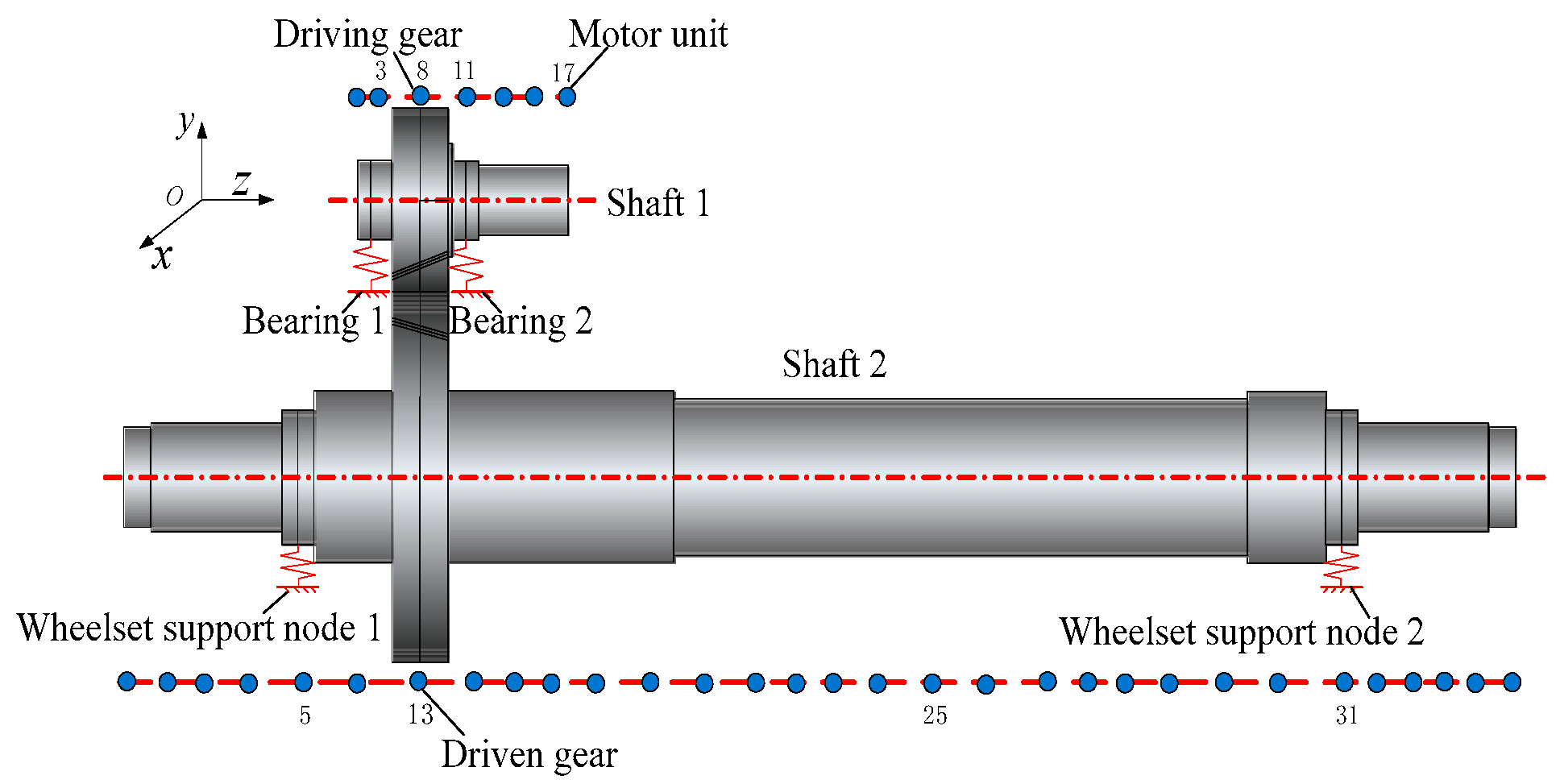
2.2. Transmission System Dynamics Model
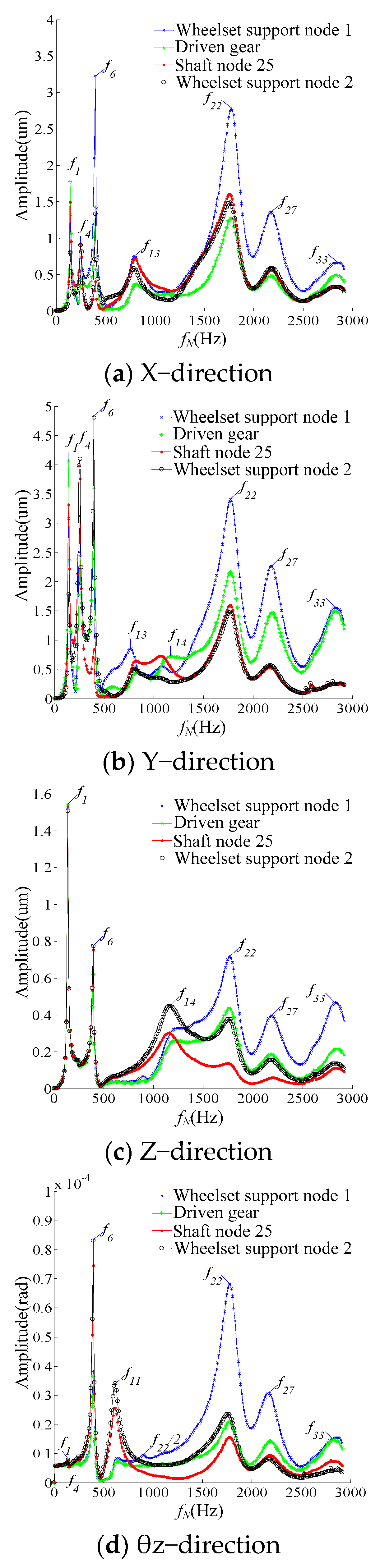
3. Dynamic Response of Traction Gear Transmission System
3.1. Gear Meshing Force
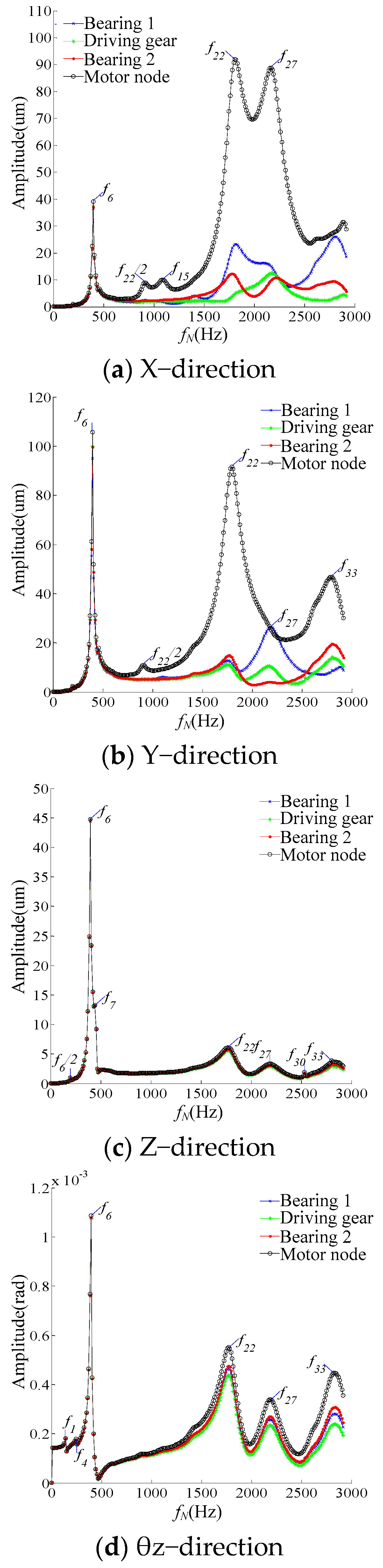
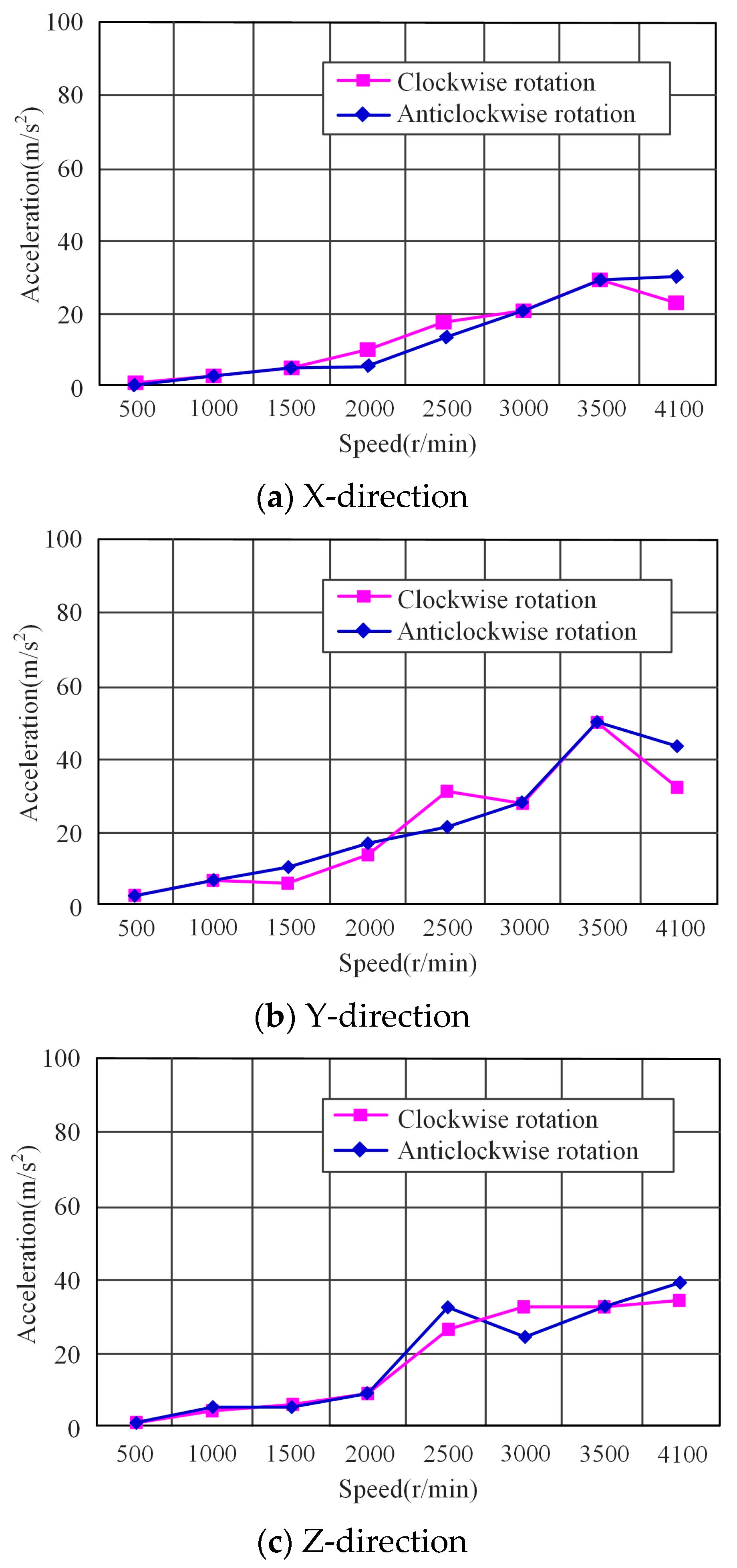
3.2. Vibration Response of the System Varying with the Rotational Speed
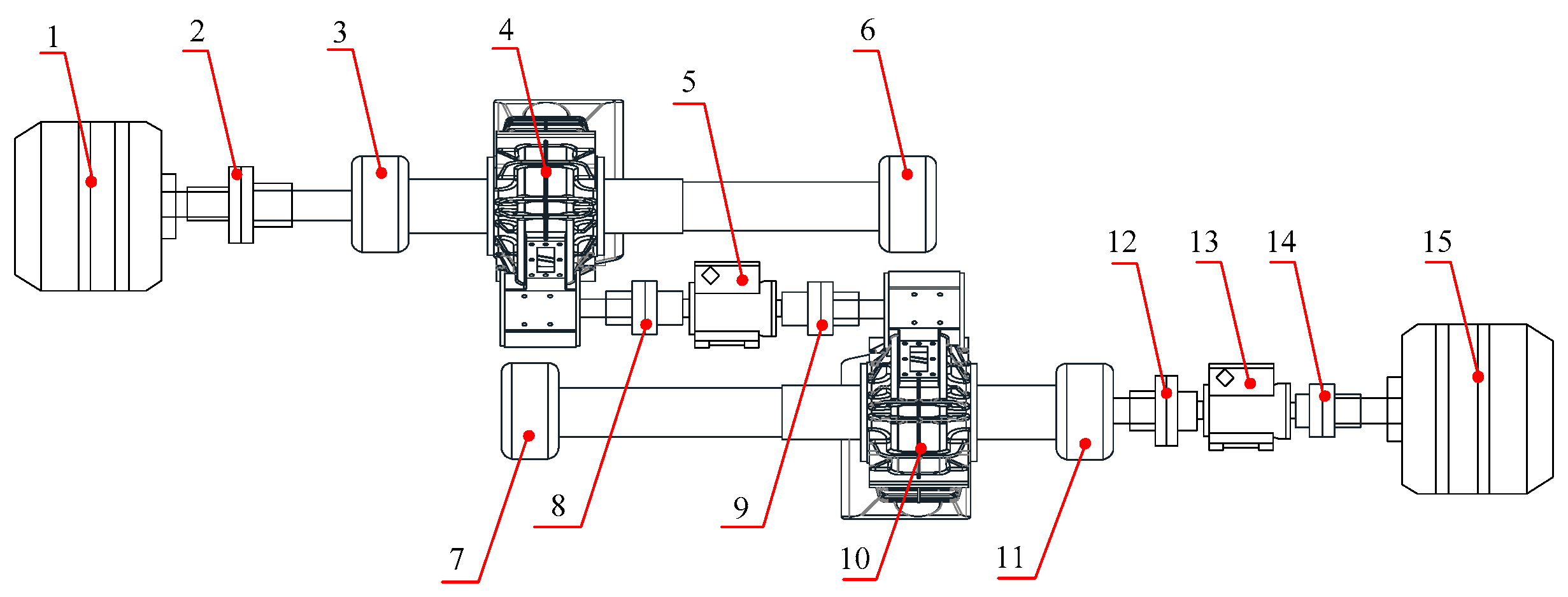
4. Test Methods for Vibration and Noise
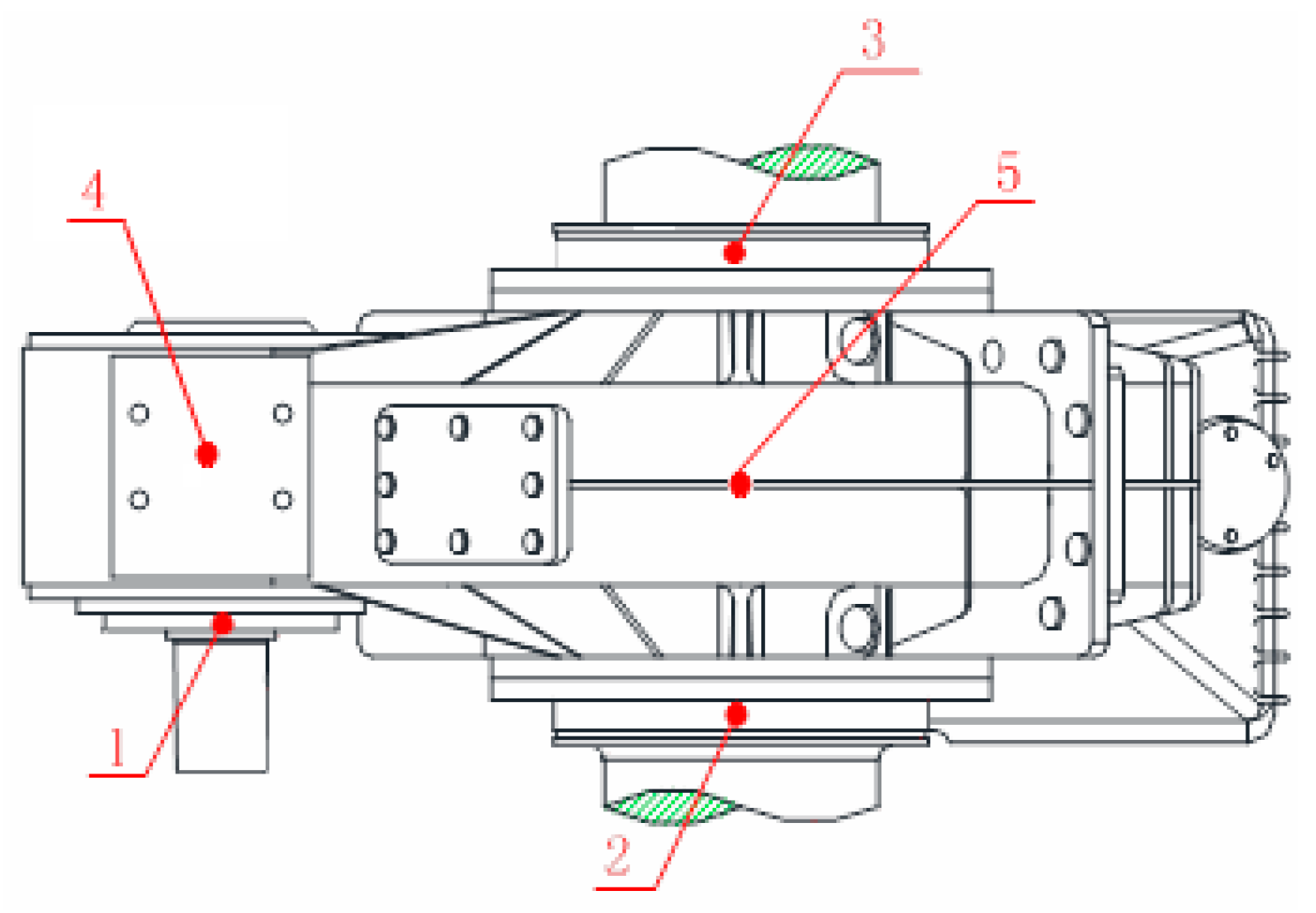
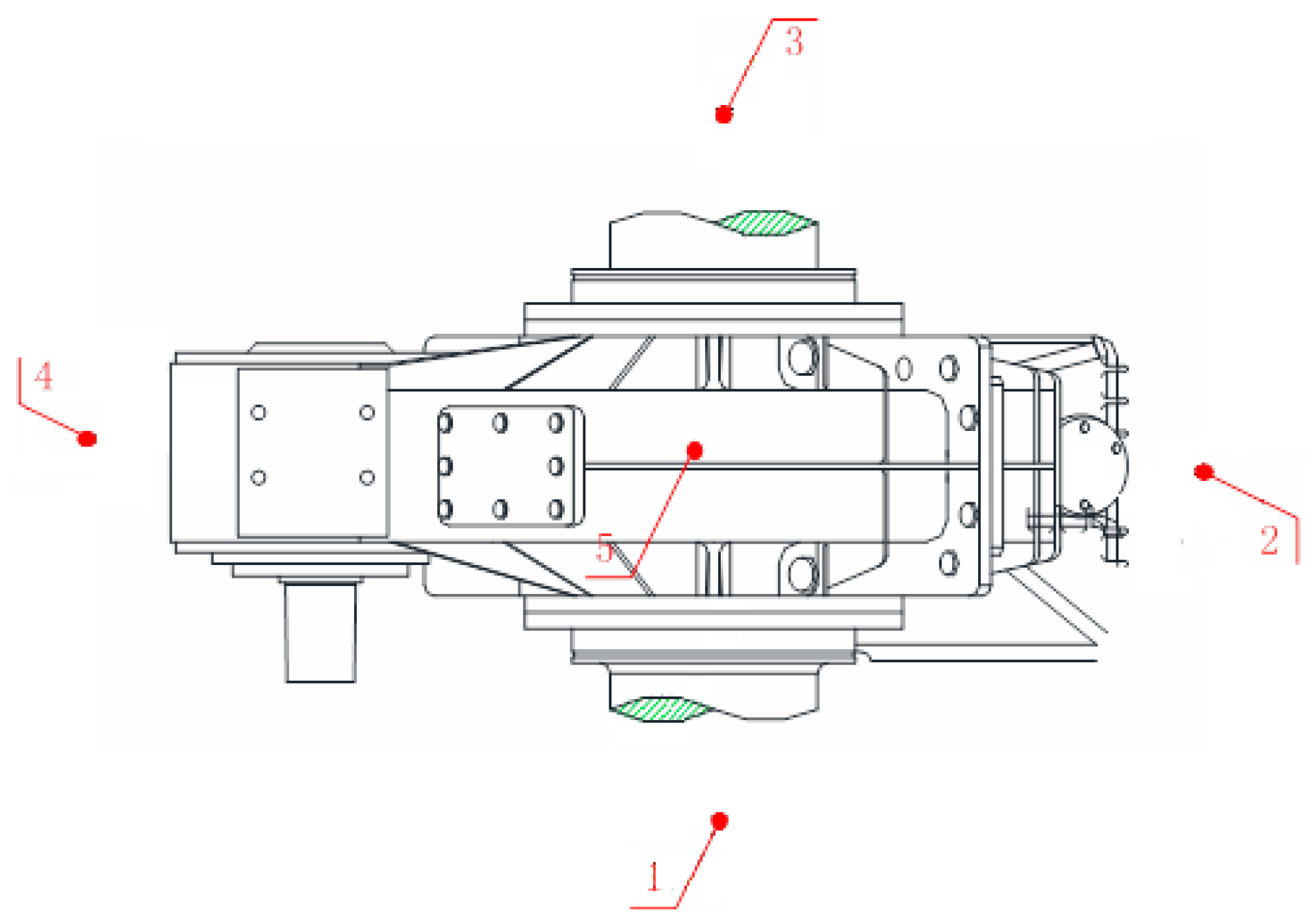
4.1. Test Equipment
4.2. Test Method
- (a).
- Vibration acceleration test method
- (b).
- Vibration intensity test method
- (c).
- Air noise test method
4.3. Test Conditions
5. Test Results and Discussion
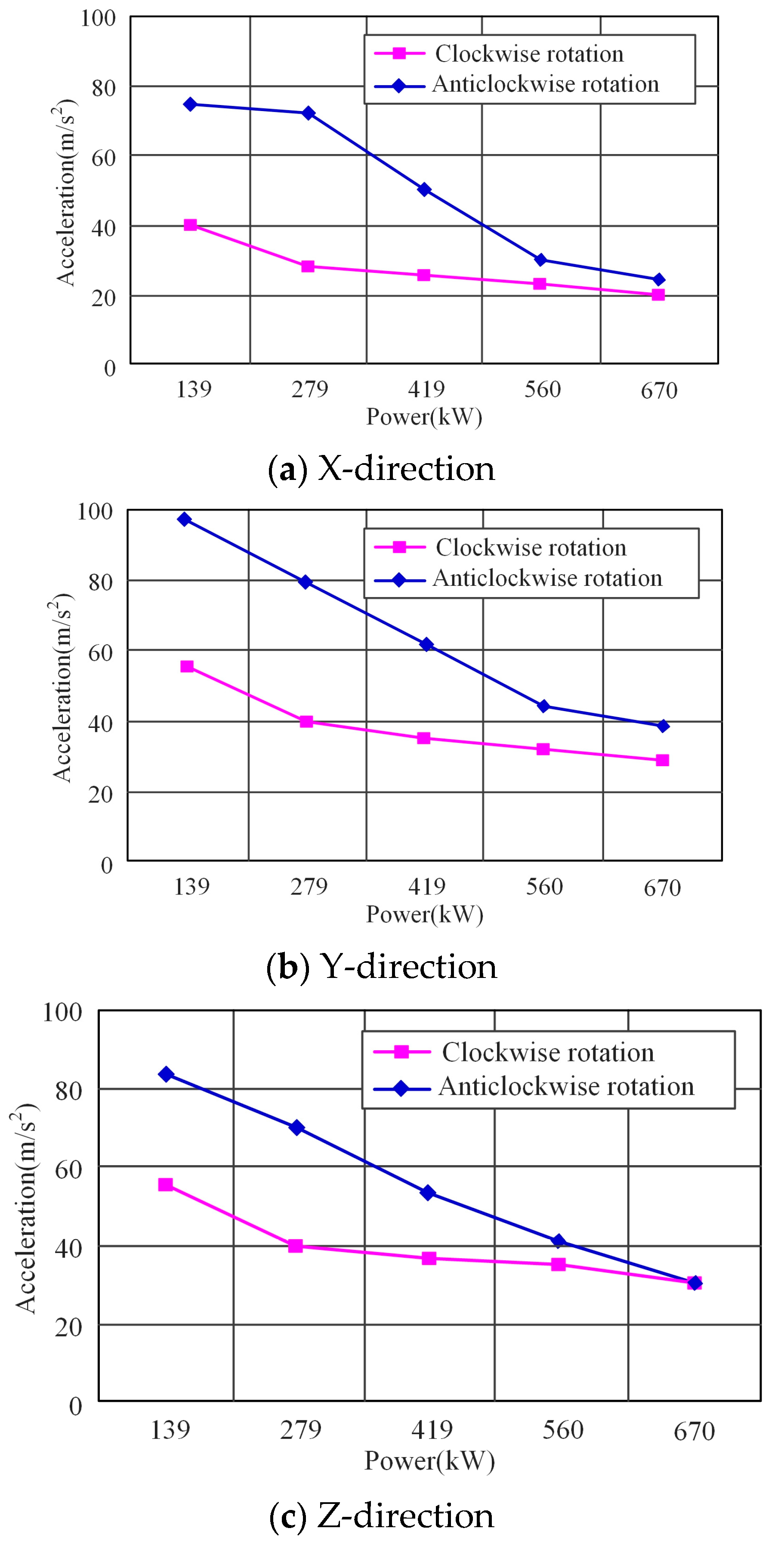
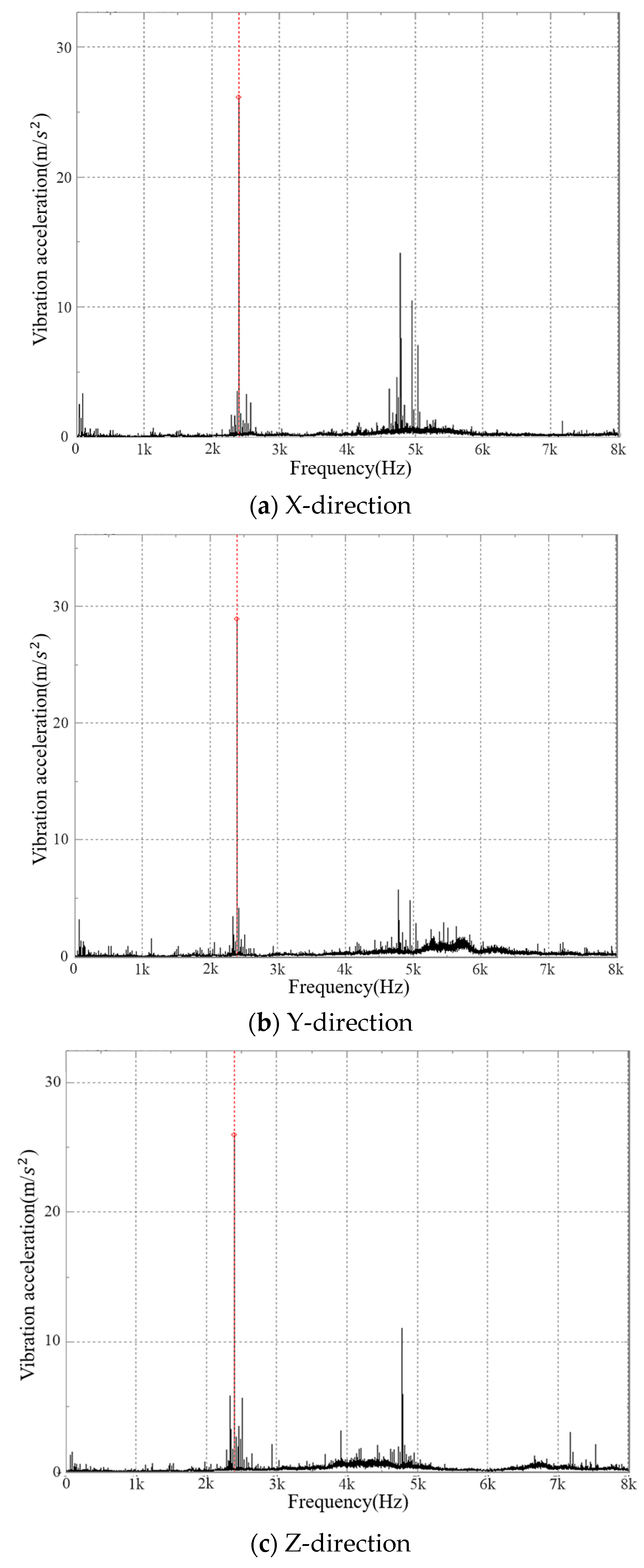
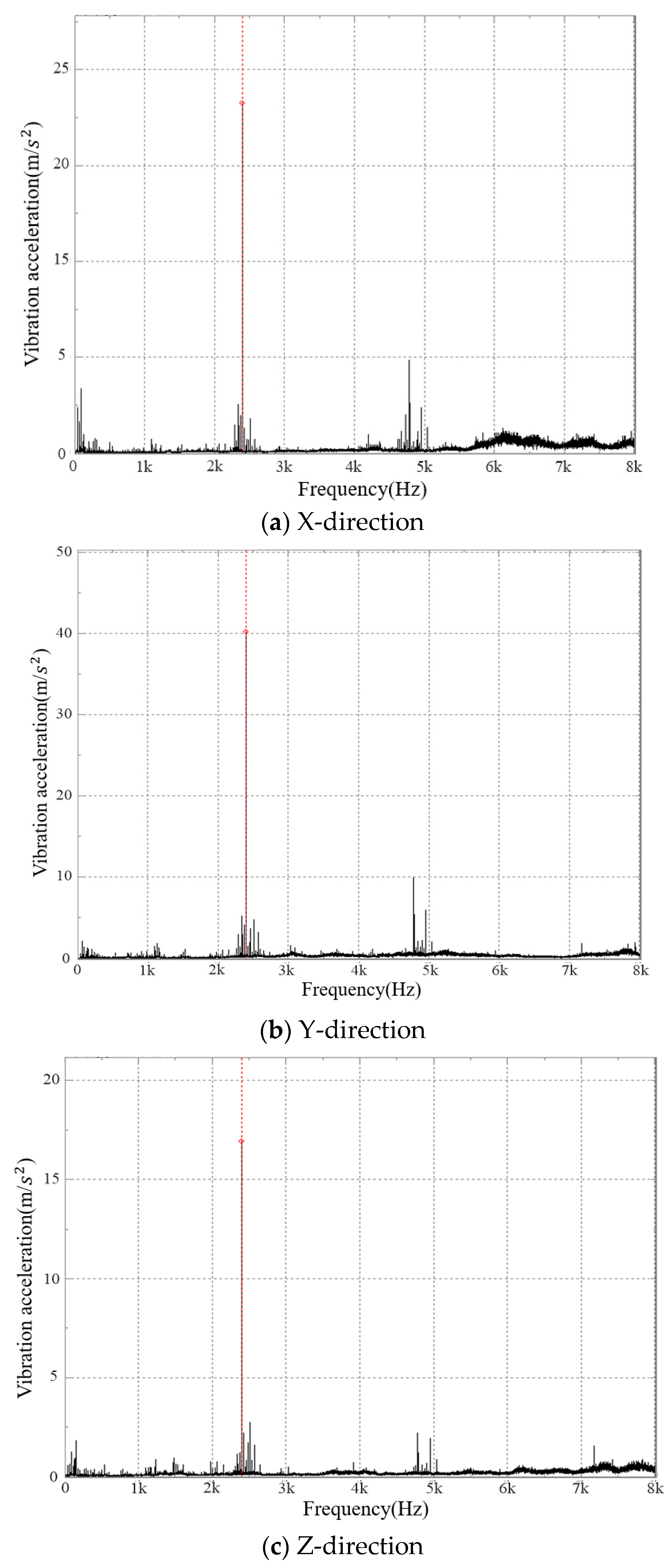
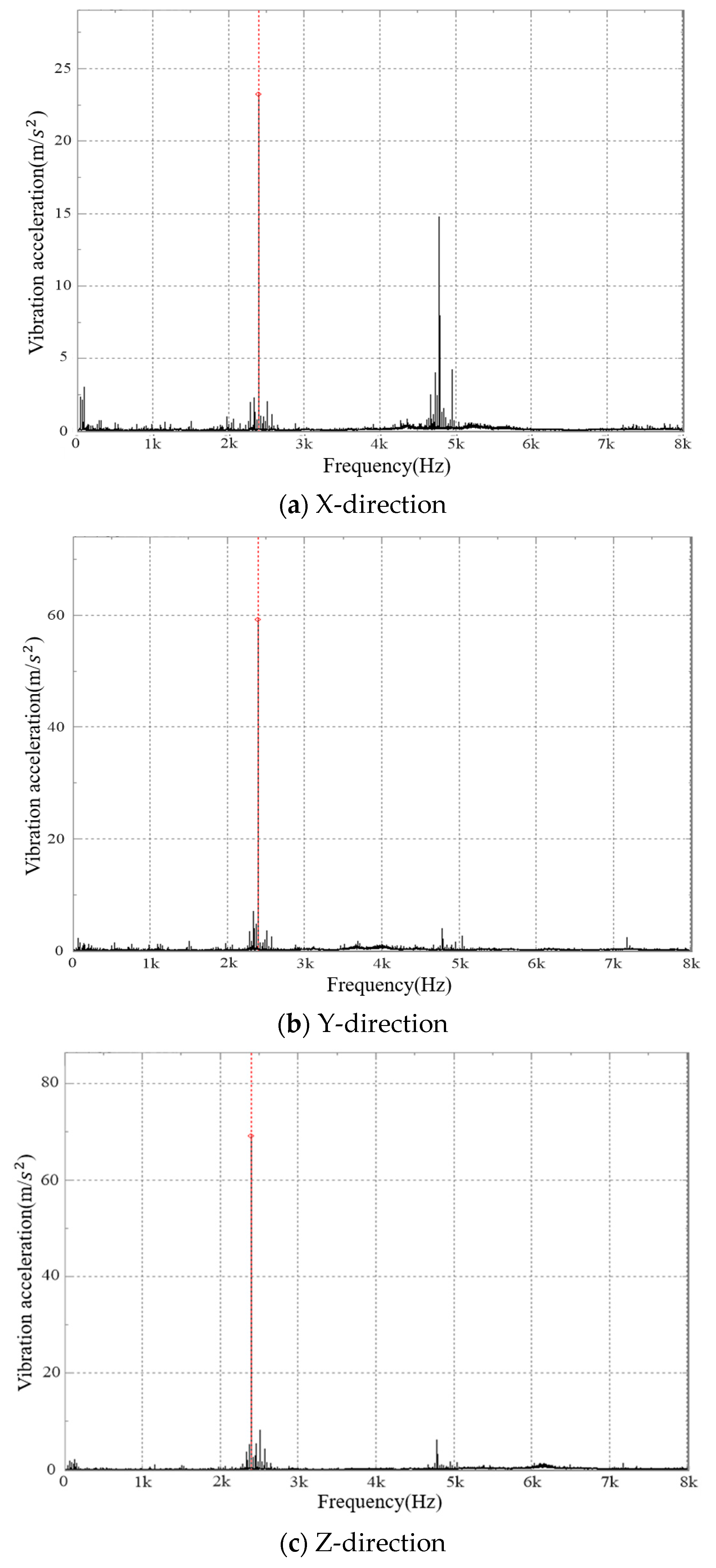
5.1. Vibration Acceleration Test Results and Analysis
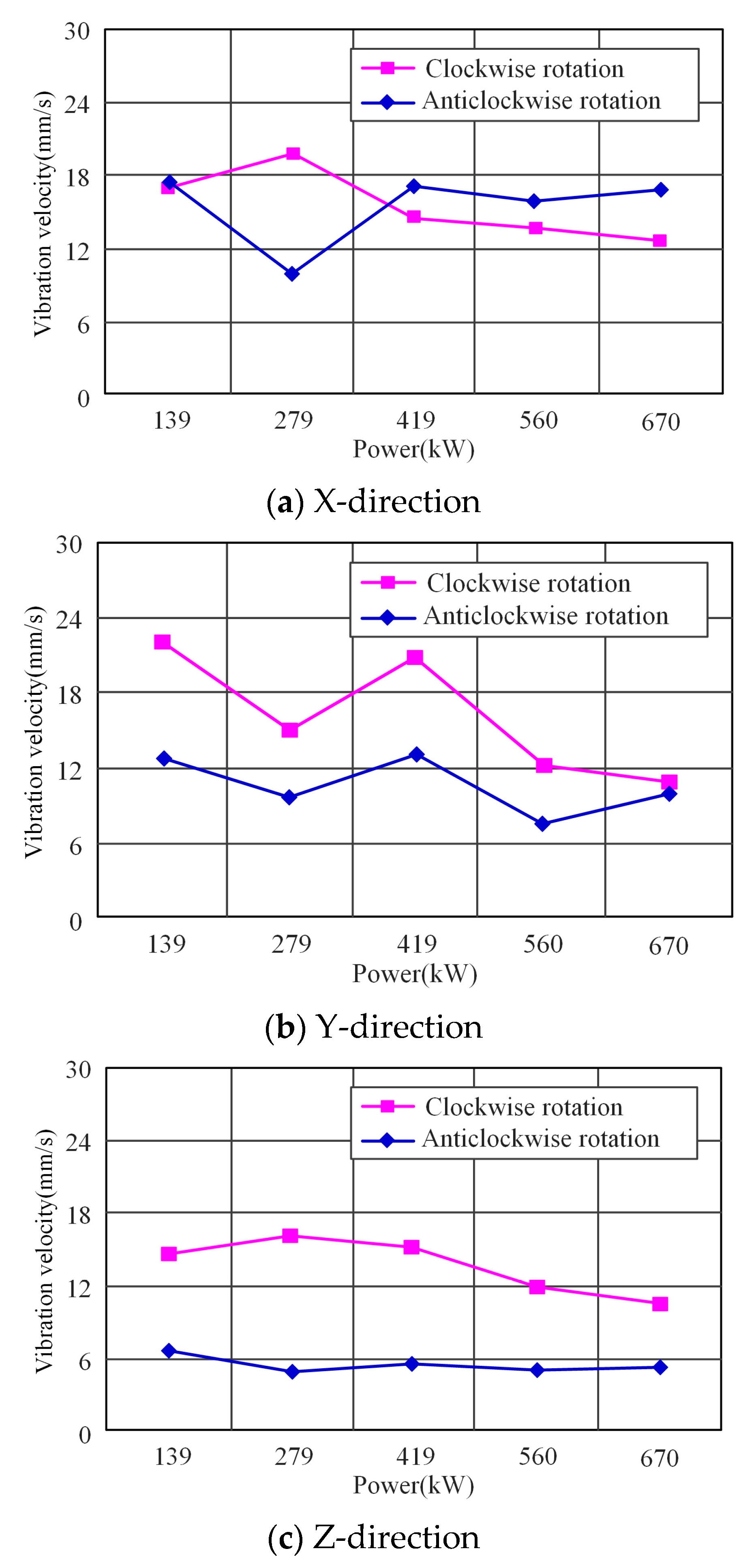
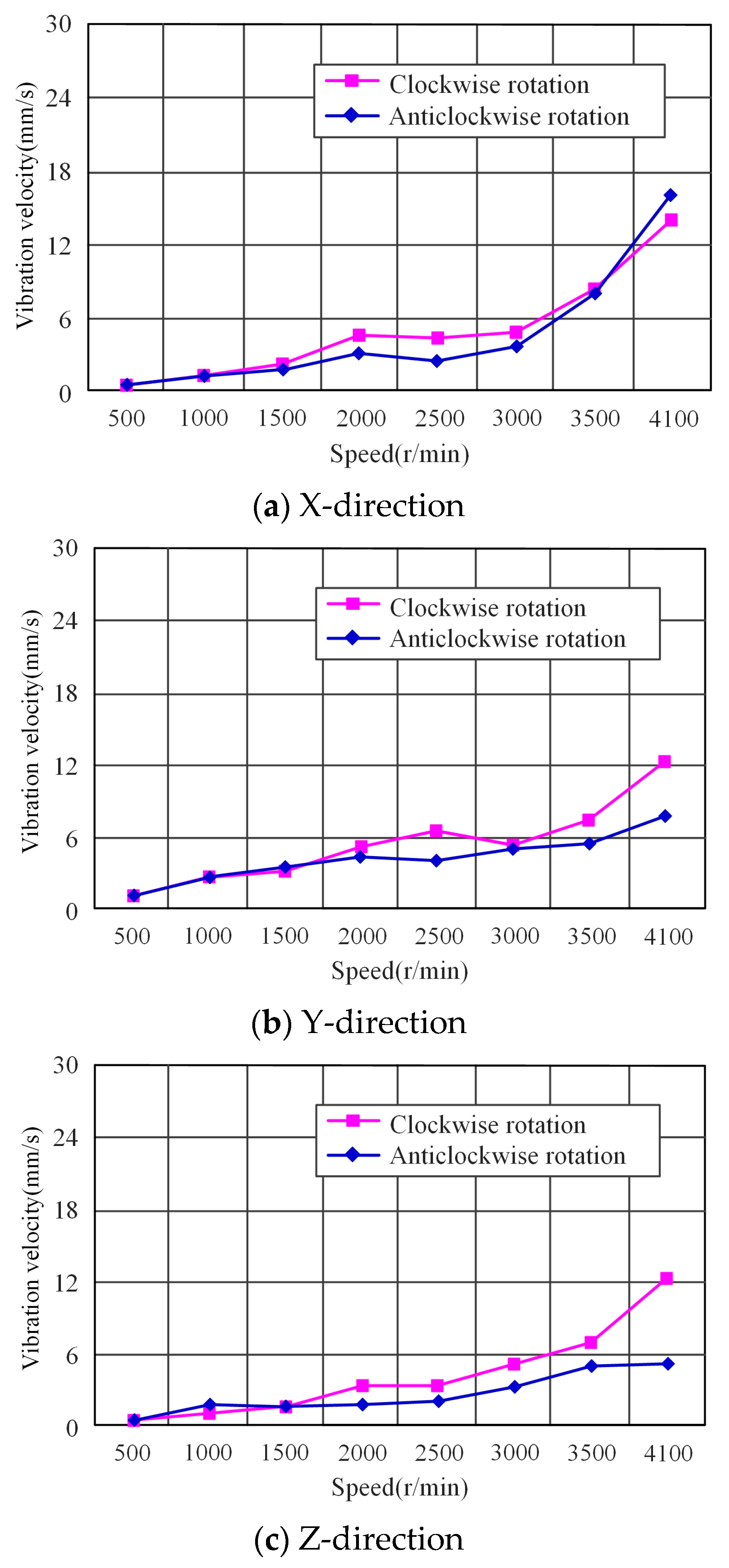
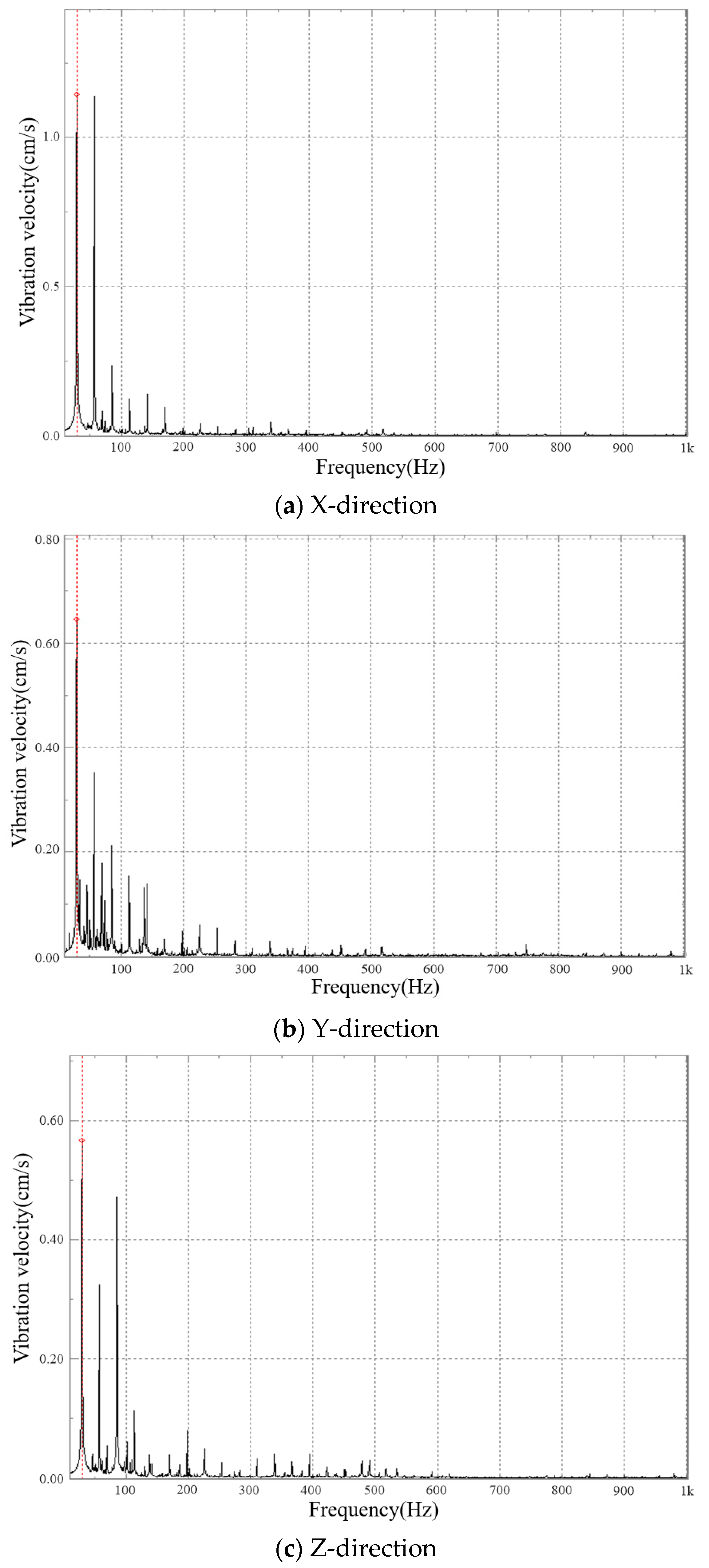
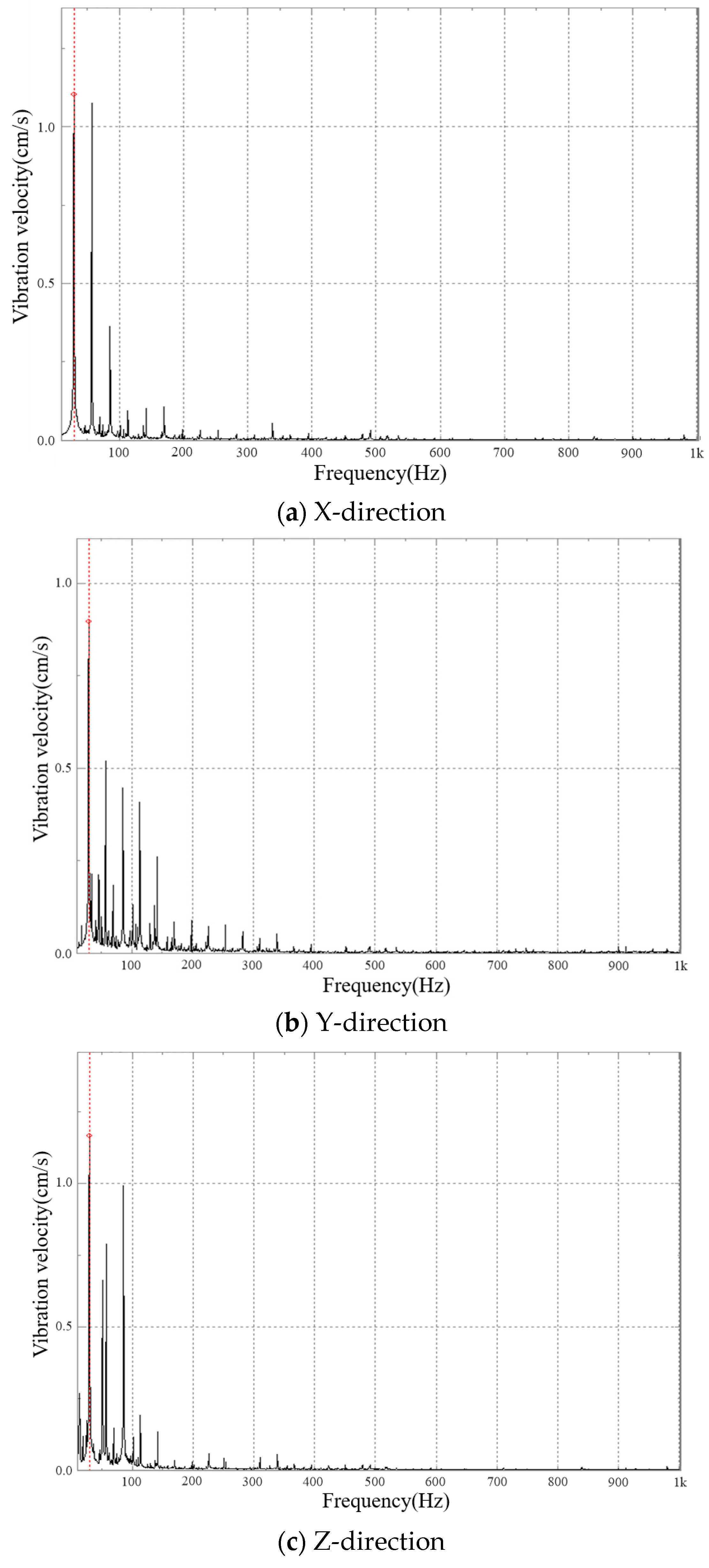
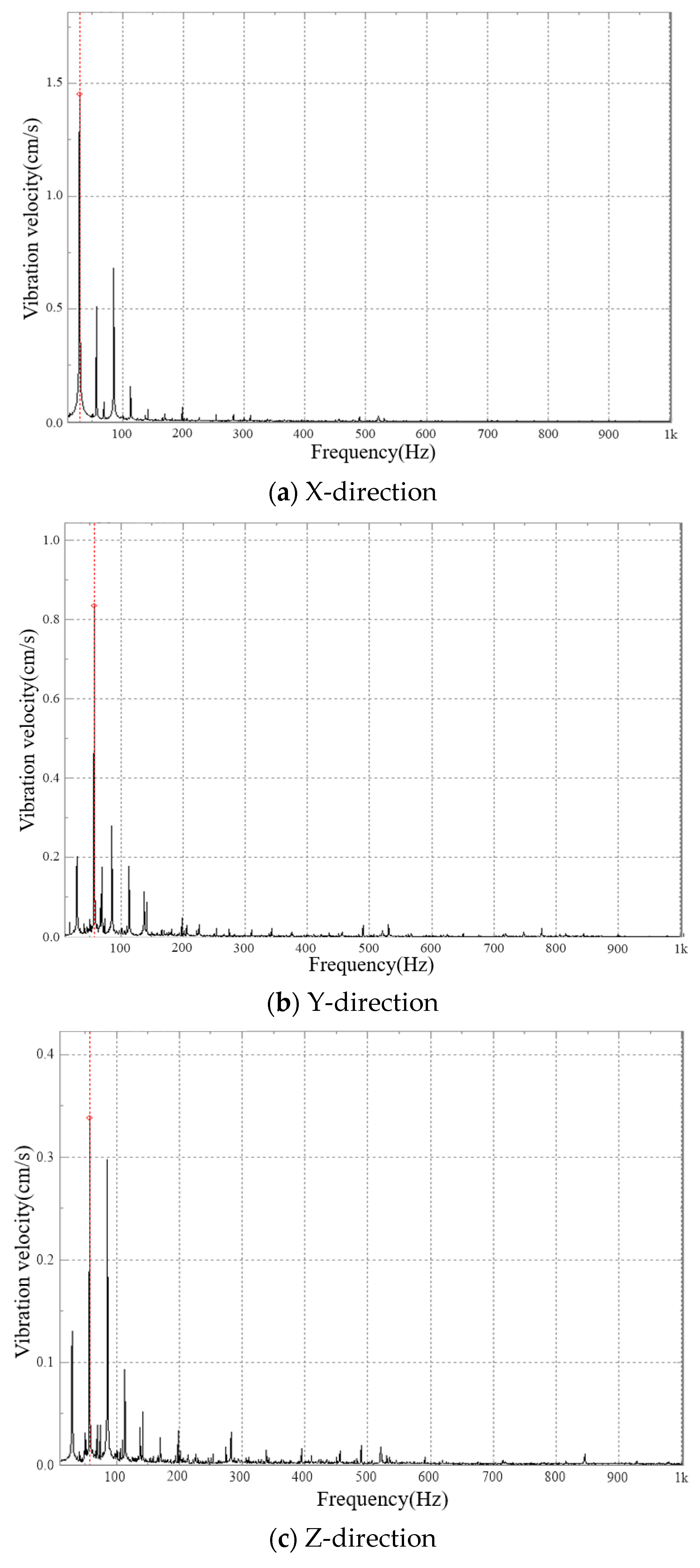
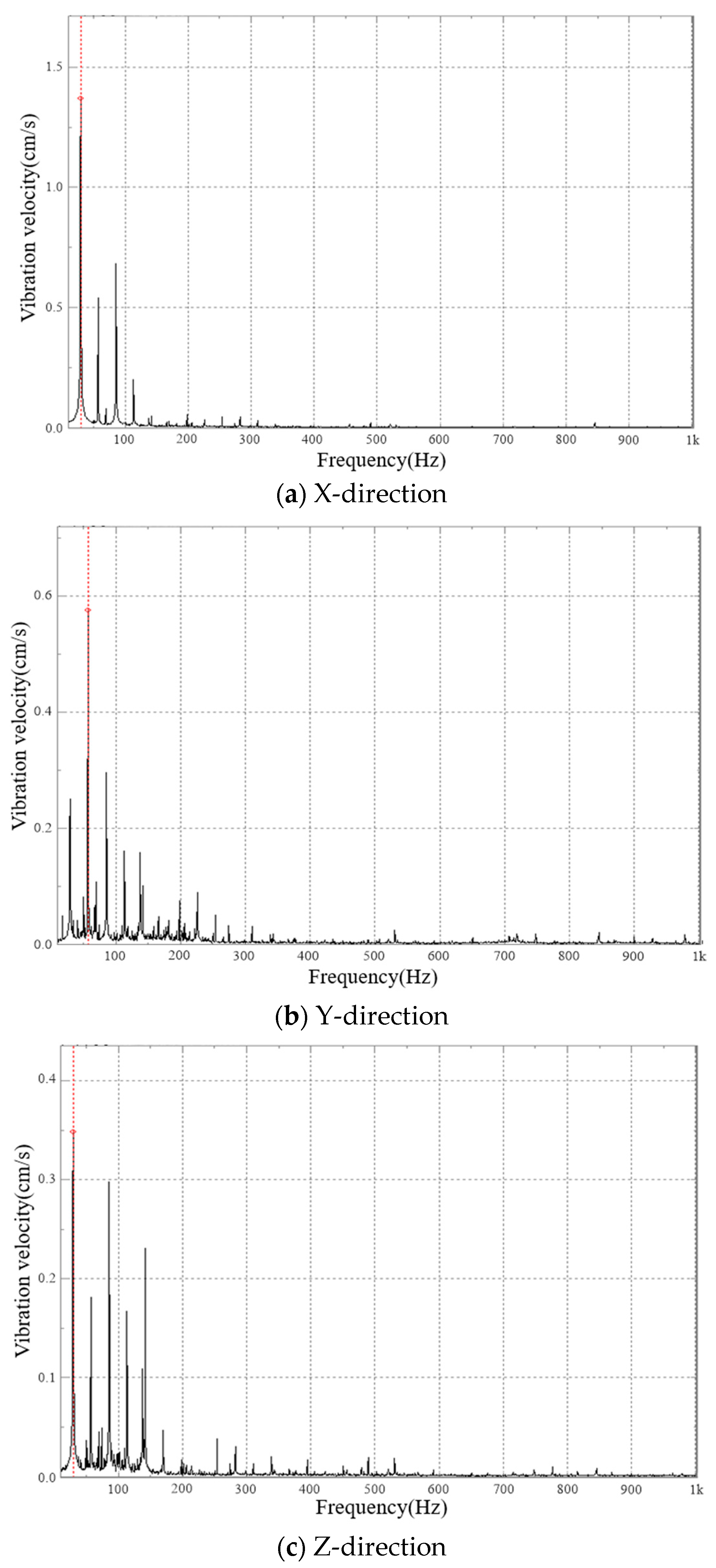
5.2. Vibration Velocity Test Results and Analysis
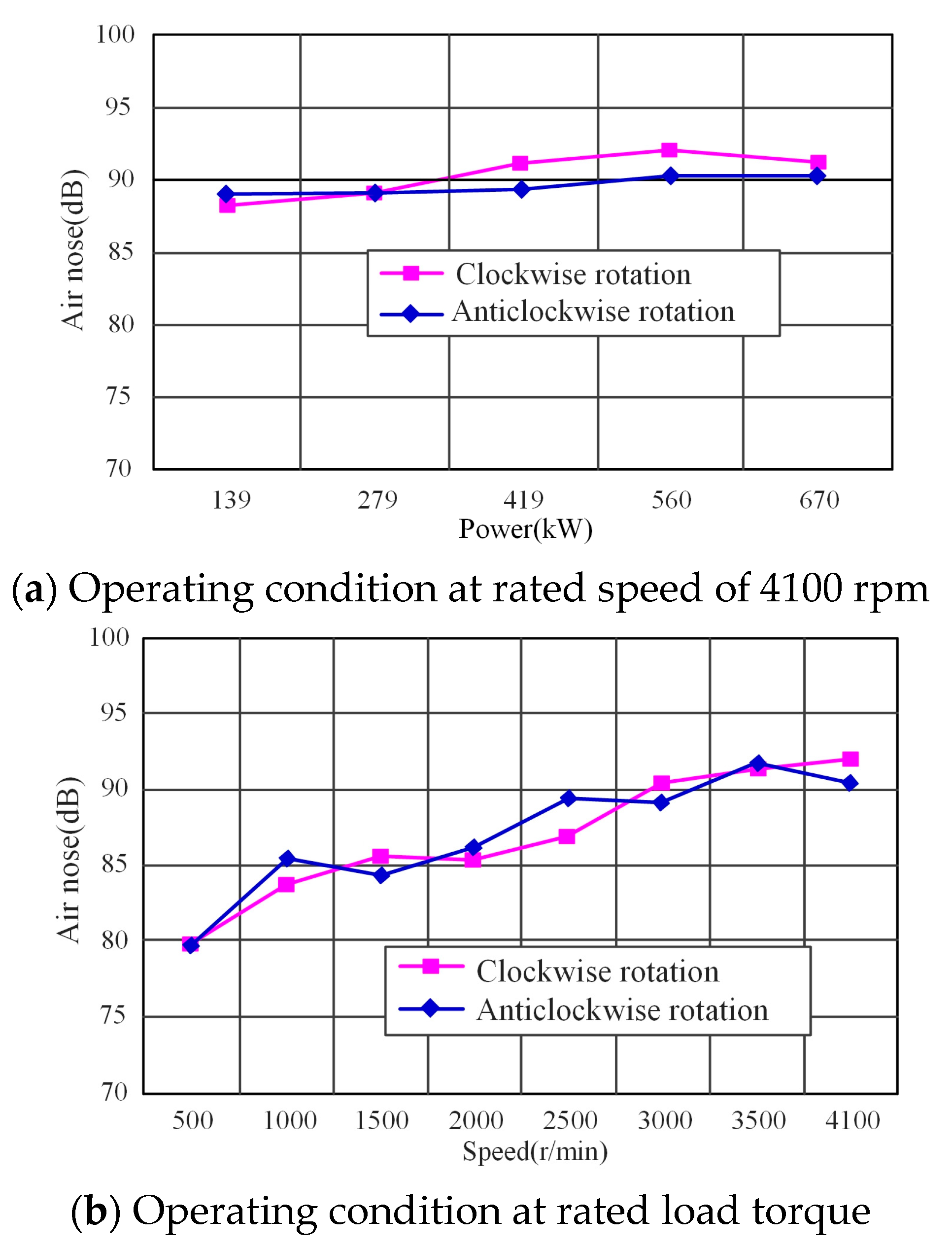
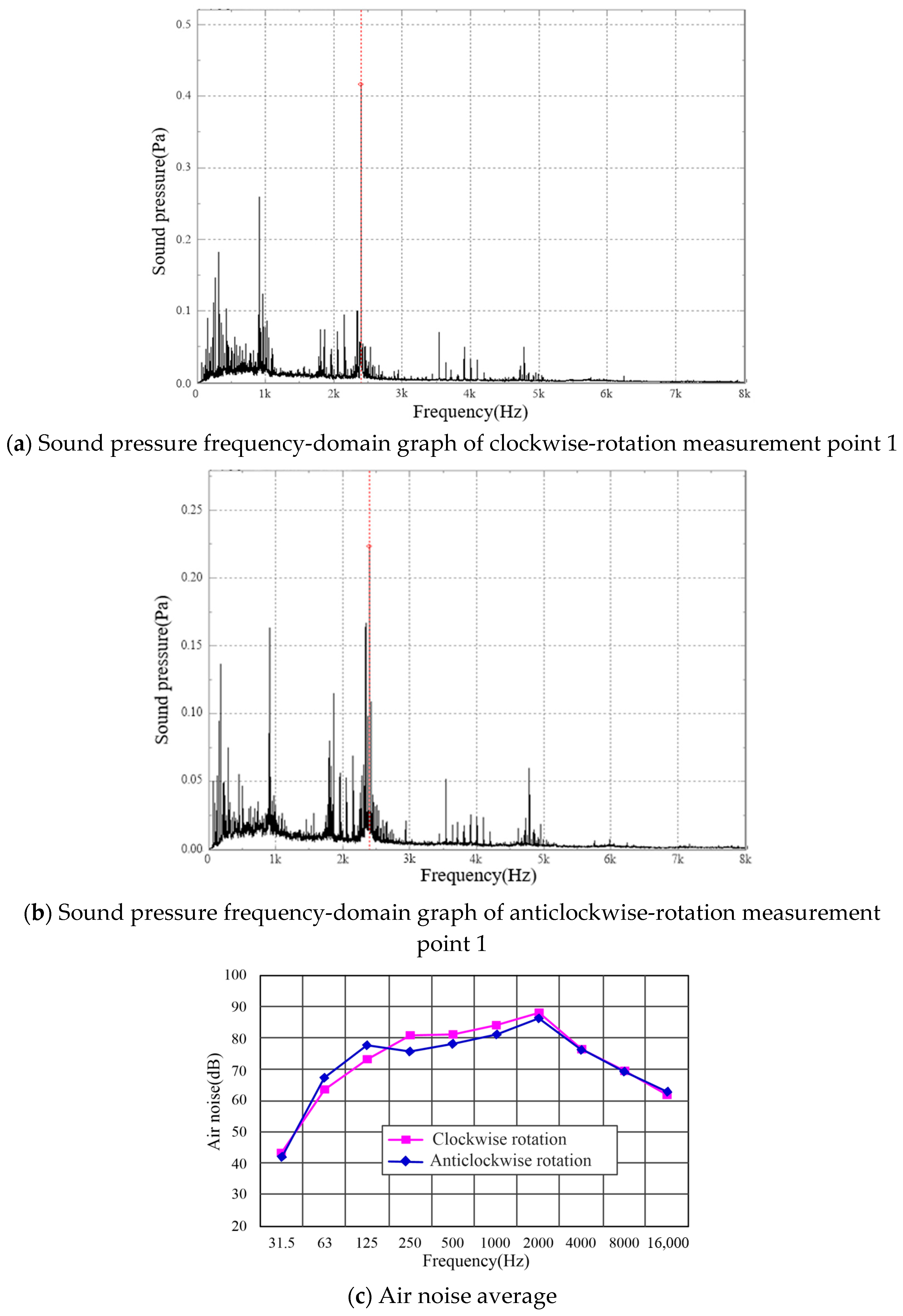
5.3. Air Noise Test Results and Analysis
6. Conclusions
- (1)
- Theoretical analysis results showed that when fN was equal to some order of the natural frequencies of the system, shaft 1 and shaft 2 would resonate. The vibration amplitude of shaft 1 was greater than that of shaft 2.
- (2)
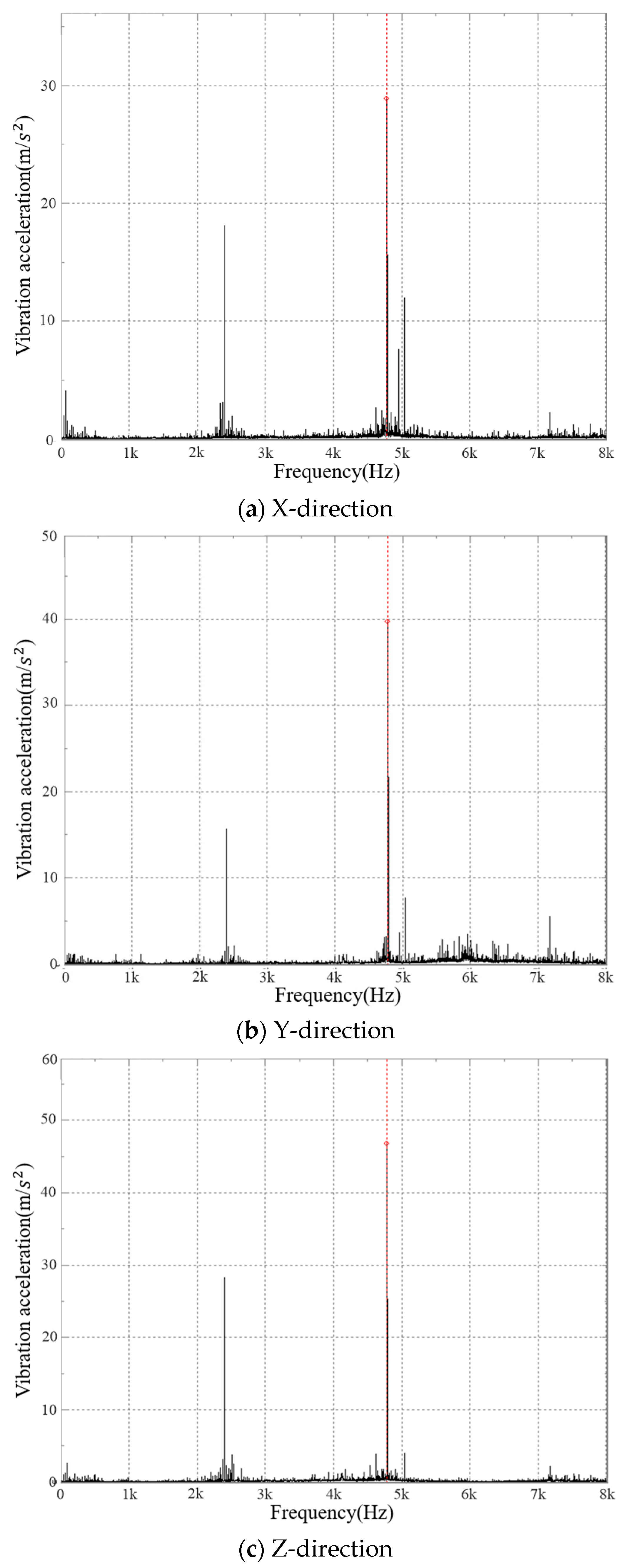
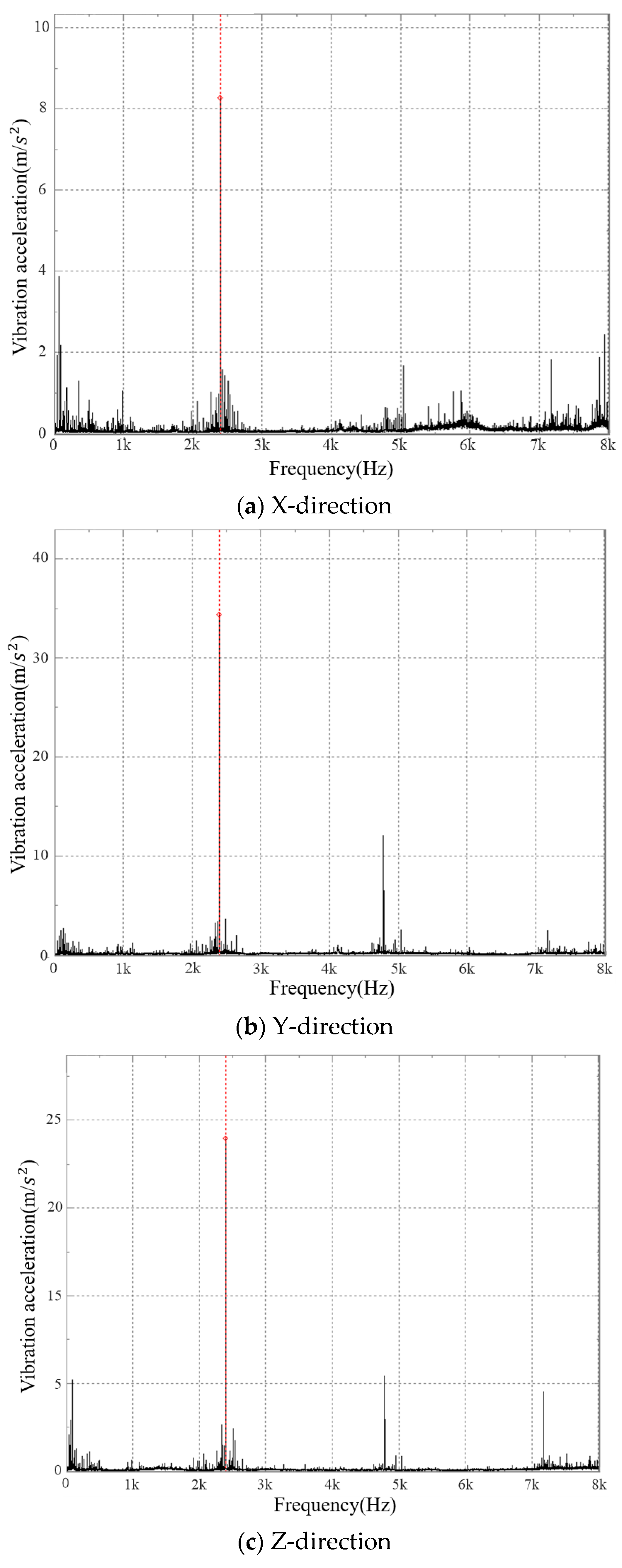
- The test results showed that the peak value of the vibration acceleration frequency-domain graph mainly appeared near fN and 2fN, and the maximum peak frequency was at fN. At the same time, the acceleration frequency domain graph peak value also appeared near fZ1 and fZ2 and their frequency doubling as well as 3fN, but their amplitudes were small. There were side bands next to fN and its frequency doubling. The side frequency interval was fZ1 and fZ2, but the amplitude was also very small.
- (3)
- The peak of the vibration speed frequency-domain graph of the traction gearbox mainly appeared near fZ2 and its frequency doubling, the larger main peak value mainly appeared at the first third-order frequency doubling, and the major peak value mainly appeared at fZ2, 2fZ2, and 3fZ2; the peak attenuation after 3fZ2 was drastic. The maximum peak frequency basically appeared at fZ2 when the input shaft rotated clockwise, and the maximum peak frequency basically appeared at 2fZ2 when the input shaft rotated anticlockwise.
- (4)
- At the rated load condition, when the input shaft rotated clockwise, the average air noise of the traction gear box after the correction was greater than that of the air noise when the input shaft rotated anticlockwise. Its maximum value was 91.99 dB (A), which was in a good range according to ISO 10816.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| kij | Time-varying meshing stiffness |
| βij | Spiral angle |
| eij(t) | Dynamic transmission error |
| αij | Orientation angle of the gear |
| ψij | Direction angle from the Y-axis positive direction to the meshing surface |
| Mean meshing stiffness | |
| Amplitude of meshing stiffness | |
| Gear meshing frequency | |
| Fi′ | Gear tangential comprehensive total tolerance |
| Fp | Tolerance of cumulative total deviation of tooth pitch |
| fi′ | One-tooth tangential comprehensive tolerance |
| mn | Normal modulus |
| D | Diameter of the dividing circle |
| εr | Total coincidence |
| E | Meshing error |
| ωf | Shaft frequency |
| ωm | Meshing frequency |
| φm | Corresponding initial phases |
| Corresponding initial phases | |
| Relative position of the gear meshing normal to the contact surface | |
| Mij | Mass matrix of the gear pair |
| F | External force vector of the gear pair |
| Kij | Gear meshing stiffness matrix |
| Cij | Meshing damping matrix of the gear |
| ξ | Meshing damping ratio |
| kij | Meshing stiffness of the gear |
| r(i,j) | Radius of the gear dividing circle |
| VX, VY, VZ | Vibration velocity effective values in three mutually perpendicular directions |
| NX, NY, NZ | Number of measuring points in three mutually perpendicular directions |
| Average surface sound pressure level of the test gearbox | |
| Average background noise sound pressure level of the measurement surface | |
| NF | Actual noise |
| NA | Average noise |
| NM | Measurement noise value |
References
- Zhu, H.; You, X.; Zhang, Y.; Wu, P.; Zeng, J. Research progress on vibration Characteristics of Gear Boxes for high-speed Trains. Mod. Manuf. Eng. 2018, 11, 149–154. [Google Scholar]
- Yang, Y.; Wei, J.; Lai, Y.; Zhang, A. Vibration response analysis of helical gear transmission with tooth tip trimming. J. Chongqing Univ. 2017, 40, 30–40. [Google Scholar]
- Wei, J.; Wang, G.; Qin, D.; Lai, Y.; Ru, X. Nonlinear excitation modeling and dynamic characteristics of helical gears with modification. J. Vib. Eng. 2018, 31, 561–572. [Google Scholar]
- Wei, J.; Zhang, A.; Wang, G.; Qin, D.; Lim, T.C.; Wang, Y.; Lin, T. A study of nonlinear excitation modeling of helical gears with modification: Theoretical analysis and experiments. Mech. Mach. Theory 2018, 128, 314–335. [Google Scholar] [CrossRef]
- Huang, G.; Wang, X.; Mei, G.; Zhang, W.; Shao, S. Dynamic response analysis of gearbox housing system subjected to internal and external excitation in high-speed train. J. Mech. Eng. 2015, 51, 95–100. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Qu, J.; Li, G.; Dai, X. Tell the research on dynamic stress response and fatigue reliability of train gearbox. China Railw. Sci. 2018, 39, 90–97. [Google Scholar]
- Wu, H. Dynamic Modeling of Traction Drive System of High Speed Train and Analysis of Vibration Characteristics of Gearbox. Ph.D. Thesis, Southwest Jiaotong University, Xian, China, 2020. [Google Scholar]
- Xia, Z. Performance Analysis and Fault Diagnosis of High-Speed Train Gearbox. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2021. [Google Scholar]
- Xun, Q.; Wei, J.; Wu, H.; Li, W. Study on the influence of curving parameters on the dynamic response of high-speed train traction gear transmission system. J. Vib. Shock. 2022, 41, 283–293. [Google Scholar]
- Ru, X.; Wang, G.; Lai, Y.; Zhu, W. Experimental study on traction gear box of high-speed railway based on test rig. Mech. Strength 2018, 3, 589–595. [Google Scholar]
- He, Z.; Sun, S.; Deng, Z. Analysis and experimental study on vibration characteristics of subway drive gearbox. Mech. Transm. 2016, 10, 110–113. [Google Scholar]
- Que, H.; Lin, X. Research on noise test of gear box of high-speed EMU. Train Veh. Technol. 2016, 1, 34–35. [Google Scholar]
- Hu, W.; Liu, Z.; Liu, D.; Hai, X. Fatigue failure analysis of high Speed train gearbox housings. Eng. Fail. Anal. 2017, 73, 57–71. [Google Scholar] [CrossRef]
- Huang, G.; Zhou, N.; Zhang, W. Effect of internal dynamic excitation of the traction system on the dynamic behavior of a high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1899–1907. [Google Scholar] [CrossRef]
- Li, G. Study on dynamic Characteristics and Fatigue Reliability of High-speed Train Gearbox. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Wang, Z.; Mei, G.; Xiong, Q.; Yin, Z.; Zhang, W. Motor car–track spatial coupled dynamics model of a high-speed train with traction transmission systems. Mech. Mach. Theory 2019, 137, 386–403. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, G.; Zhang, W.; Zou, H.; Huang, G.; Li, F. Effects of polygonal wear of wheels on the dynamic performance of the gearbox housing of a high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 232, 1852–1863. [Google Scholar] [CrossRef]
- Wu, H.; Wu, P.; Li, F.; Shi, H.; Xu, K. Fatigue analysis of the gearbox housing in high-speed trains under wheel polygonization using a multibody dynamics algorithm. Eng. Fail. Anal. 2019, 100, 351–364. [Google Scholar] [CrossRef]
- Yang, G.; Li, G.; Liu, Z.; Wang, W. Analysis and Research on vibration characteristics of gearbox box of high-speed train under wheel rail excitation. J. Railw. 2017, 39, 46–52. [Google Scholar]
- Zhai, W.; Liu, P.; Lin, J.; Wang, K. Experimental investigation on vibration behaviour of a CRH train at speed of 350 km/h. Int. J. Rail Transp. 2015, 3, 1–16. [Google Scholar] [CrossRef]
- Zhang, M. Research on Gear Tooth Modification and Transmission Efficiency of High-Speed Railway Gearbox. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2020. [Google Scholar]
- Zhang, Z. Research on Gear Fault Diagnosis Method of HXD2 Locomotive Based on Electromechanical Coupling Model. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2020. [Google Scholar]
- TB/T 3134-2013; Drive Gearbox for EMU. China Railway Publishing House: Beijing, China, 2013.
- ISO 8579-2:1993; Acceptance Code for Gears—Part 2: Determination of Mechanical Vibrations of Gear Units during Acceptance Testing. International Organization for Standardization: Geneva, Switzerland, 1993.
- ISO 2372:1974/AMD 1:1983; Mechanical Vibration of Machines with Operating Speeds from 10 to 200 rev/s—Basis for Specifying Evaluation Standards—Amendment 1. International Organization for Standardization: Geneva, Switzerland, 1983.
- ISO 10816-8:2014; Mechanical Vibration-Evaluation of Machine Vibration by Measurements on Non-Rotating Parts Part 8: Reciprocating Compressor Systems. International Organization for Standardization: Geneva, Switzerland, 2014.
- ISO 3744-2010; Acoustics—Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure—Engineering Methods for an Essentially Free Field over a Reflecting Plane. International Organization for Standardization: Geneva, Switzerland, 1993.
- ISO 20283-2:2008; Mechanical Vibration—Measurement of Vibration on Ships—Part 2: Measurement of Structural Vibration. International Organization for Standardization: Geneva, Switzerland, 2008.




| Parameter | Gear 1 | Gear 2 |
|---|---|---|
| Number of teeth/z | 35 | 85 |
| Normal modulus/mn (mm) | 6 | 6 |
| Helix angle/(°) | 18 | 18 |
| Tooth angle/(°) | 25 | 25 |
| Transmission ratio/i | 2.4286 | 2.4286 |
| Spiral direction | Left | Right |
| Equipment | Equipment Model | Manufacturer | Measurement Range | Measurement Accuracy |
|---|---|---|---|---|
| Acceleration sensor | BK4384 | BK, Herlev, Denmark | 0.1–12,600 Hz | ±2% |
| Charge voltage filter integral amplifier | DLF-8 | Beijing institute of Oriental vibration and noise technology, Beijing, China | / | / |
| Intelligent signal acquisition and processing analyzer | INV306U-5260 | Beijing institute of Oriental vibration and noise technology, Beijing, China | 0.625–10 V | ±0.01% |
| Sound level meter | NL-42 | Rion company, Tokyo, Japan | 25–138 dB | ±1% |
| Sound calibrator | NC-74 | Rion company, Tokyo, Japan | 94 dB | ±0.3 dB |
| Input Shaft Speed (rpm) | Output Shaft Speed (rpm) | Meshing Frequency (Hz) | Input Shaft Rotation Frequency (Hz) | Output Shaft Rotation Frequency (Hz) |
|---|---|---|---|---|
| 500 | 206 | 291.7 | 8.3 | 3.4 |
| 1000 | 412 | 583.3 | 16.7 | 6.9 |
| 1500 | 618 | 875.0 | 25.0 | 10.3 |
| 2000 | 823 | 1166.7 | 33.3 | 13.7 |
| 2500 | 1029 | 1458.3 | 41.7 | 17.2 |
| 3000 | 1235 | 1750.0 | 50.0 | 20.6 |
| 3500 | 1441 | 2041.7 | 58.3 | 24.0 |
| 4100 | 1688 | 2391.7 | 68.3 | 28.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Lin, H.; Sun, W.; Wei, J. Vibration Performance of Traction Gearbox of a High-Speed Train: Theoretical Analysis and Experiments. Actuators 2023, 12, 103. https://doi.org/10.3390/act12030103
Zhu W, Lin H, Sun W, Wei J. Vibration Performance of Traction Gearbox of a High-Speed Train: Theoretical Analysis and Experiments. Actuators. 2023; 12(3):103. https://doi.org/10.3390/act12030103
Chicago/Turabian StyleZhu, Wangang, Hao Lin, Wei Sun, and Jing Wei. 2023. "Vibration Performance of Traction Gearbox of a High-Speed Train: Theoretical Analysis and Experiments" Actuators 12, no. 3: 103. https://doi.org/10.3390/act12030103
APA StyleZhu, W., Lin, H., Sun, W., & Wei, J. (2023). Vibration Performance of Traction Gearbox of a High-Speed Train: Theoretical Analysis and Experiments. Actuators, 12(3), 103. https://doi.org/10.3390/act12030103






