Optimal Voltage Distribution on PZT Actuator Pairs for Vibration Damping in Beams with Different Boundary Conditions
Abstract
1. Introduction
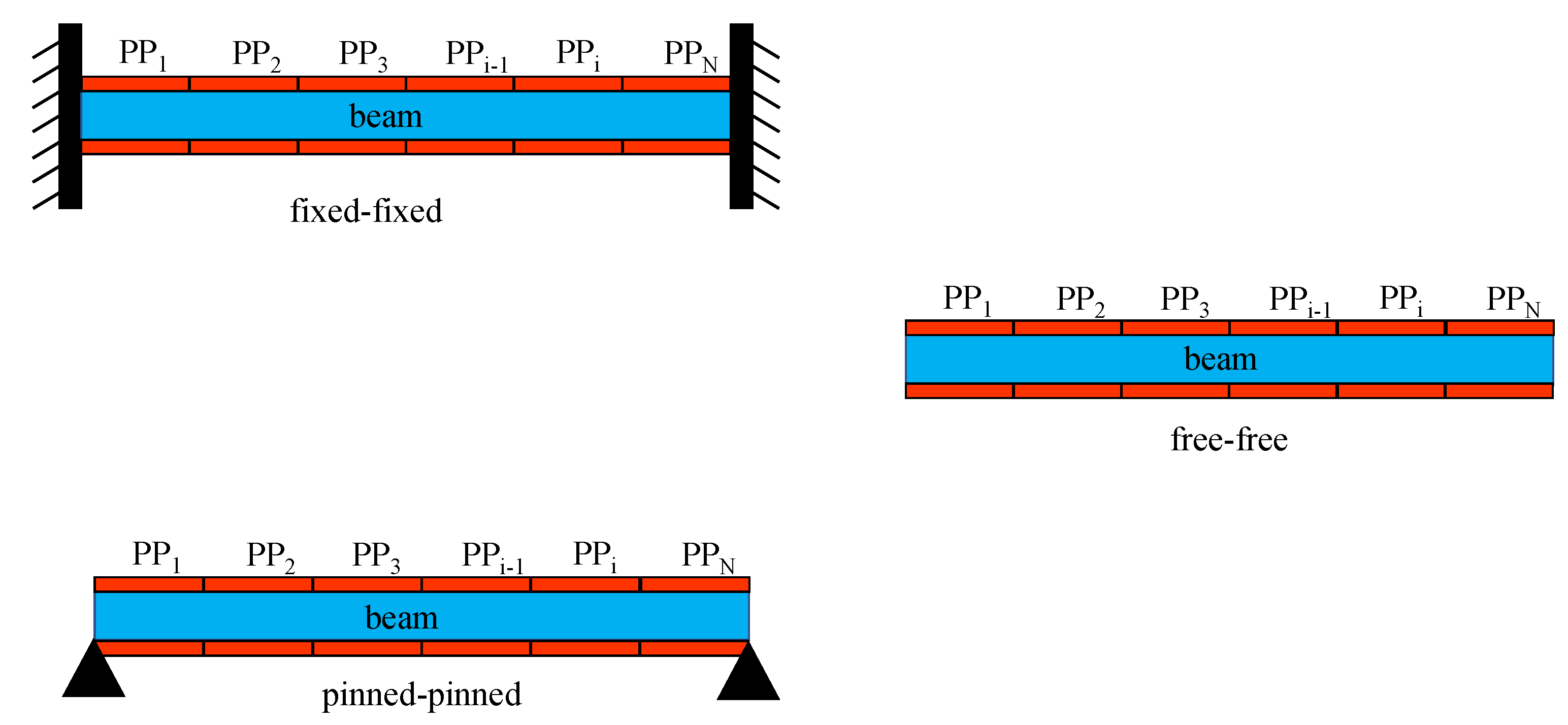
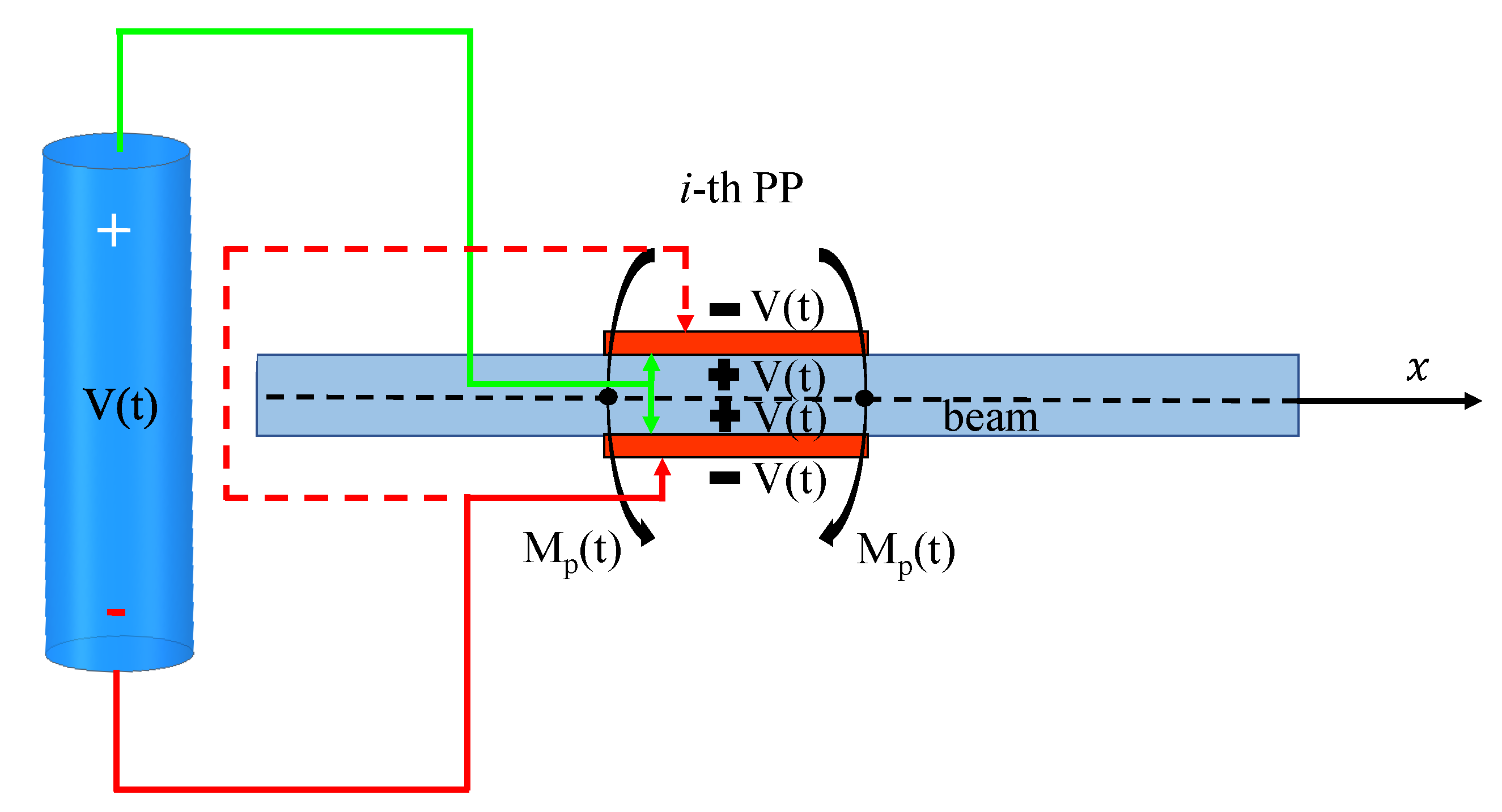
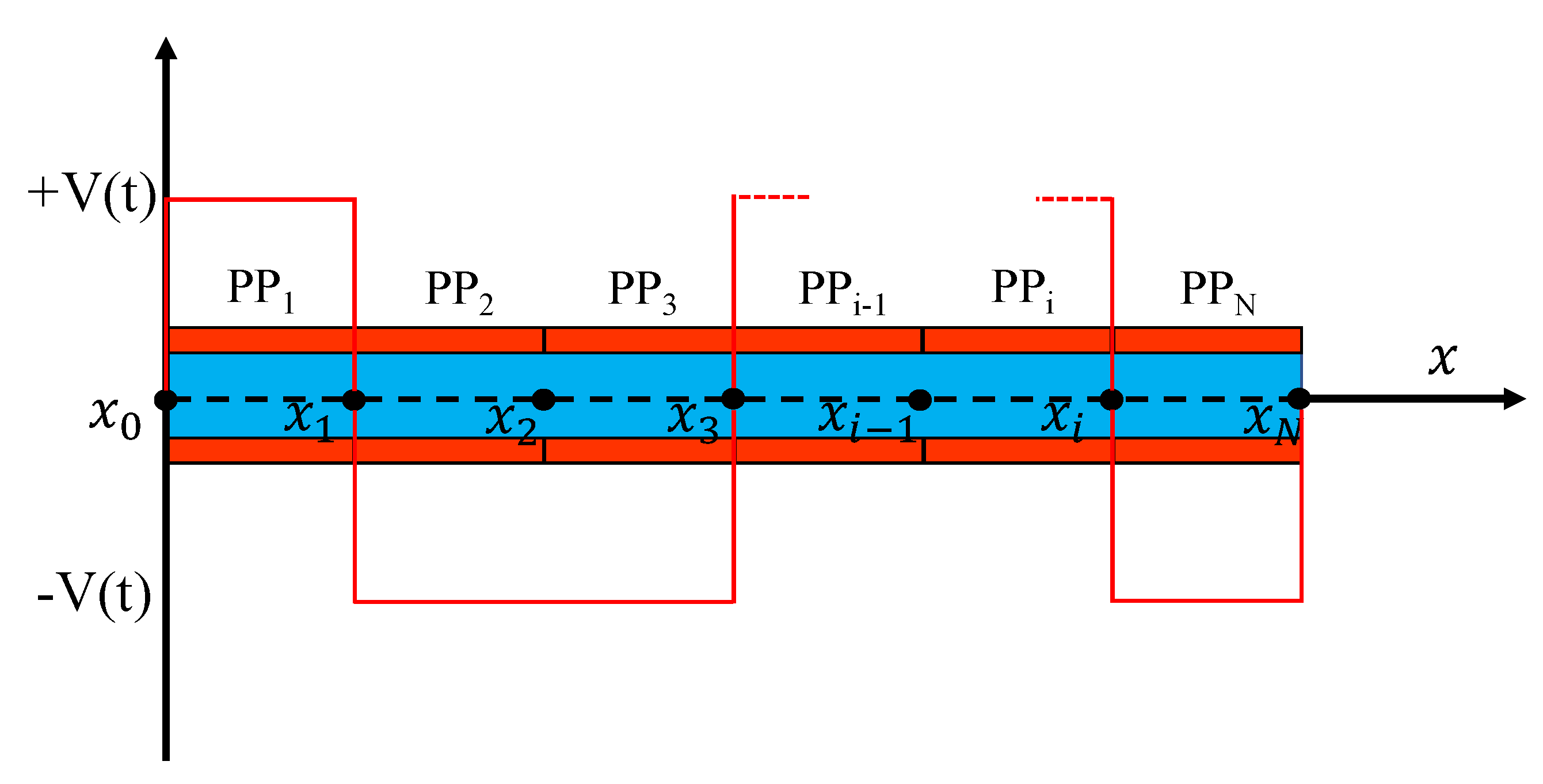
2. Optimal Voltage Distribution on Piezoelectric Actuators Coupled with Beams under Different Constraints
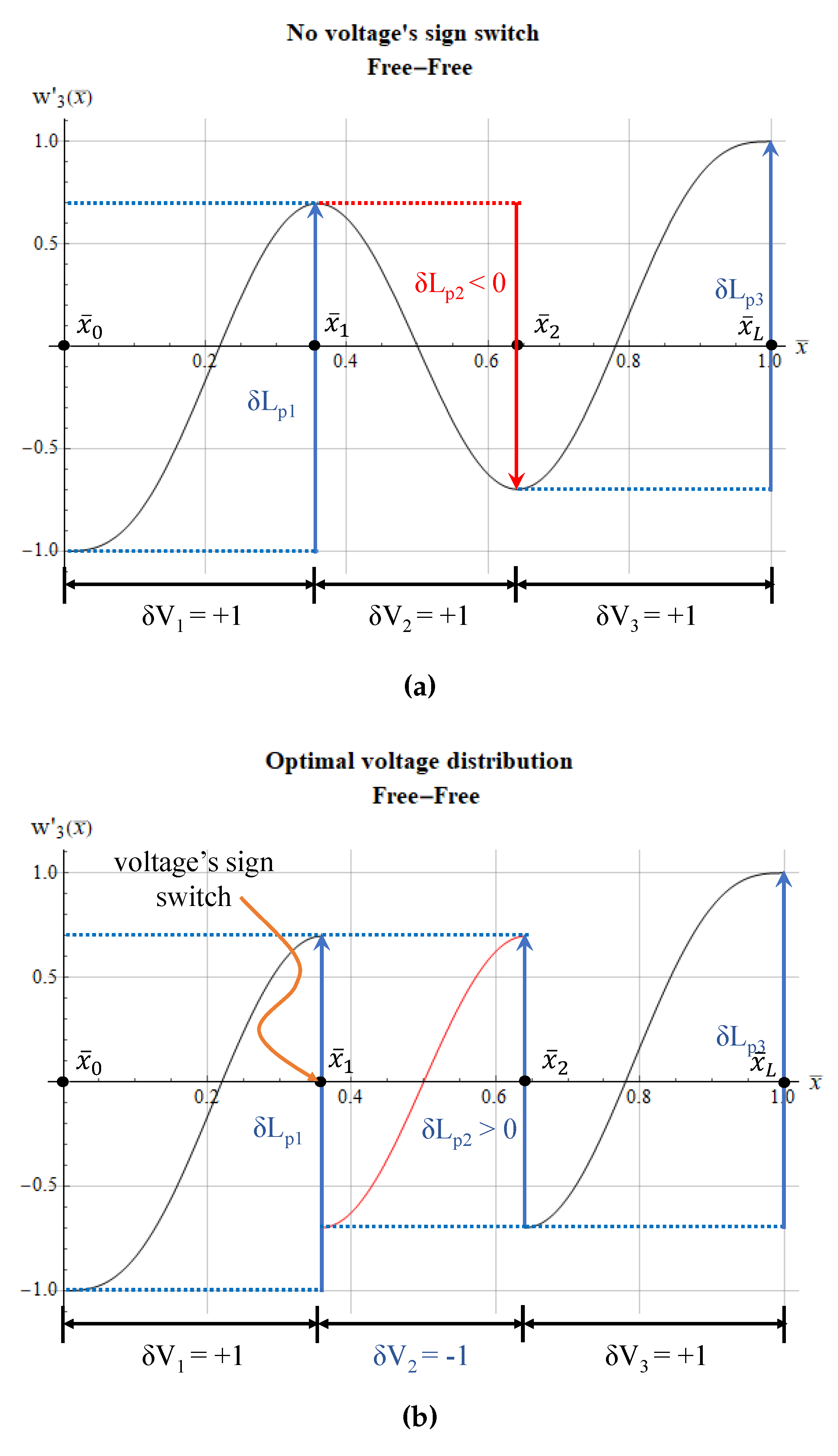
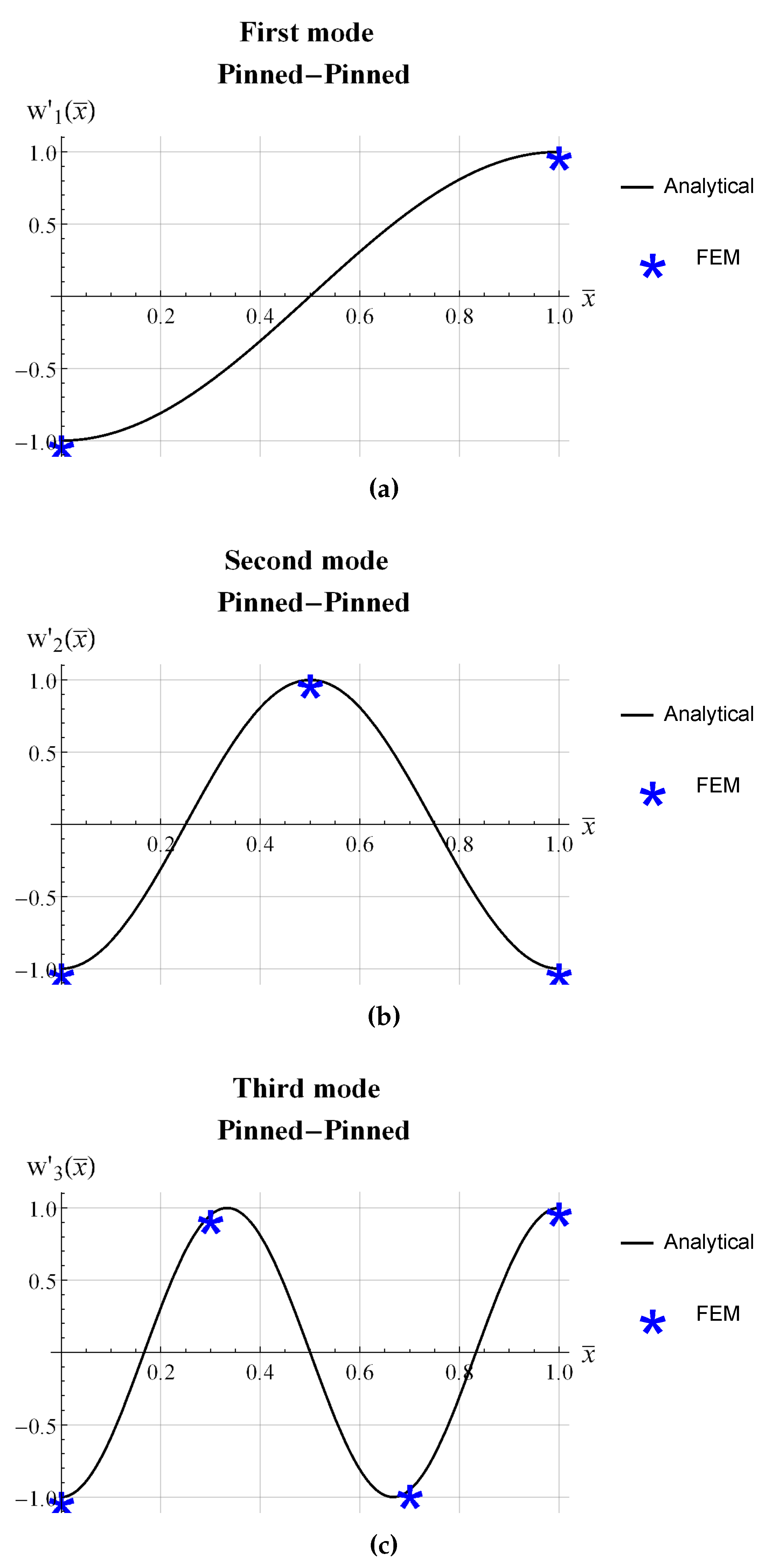
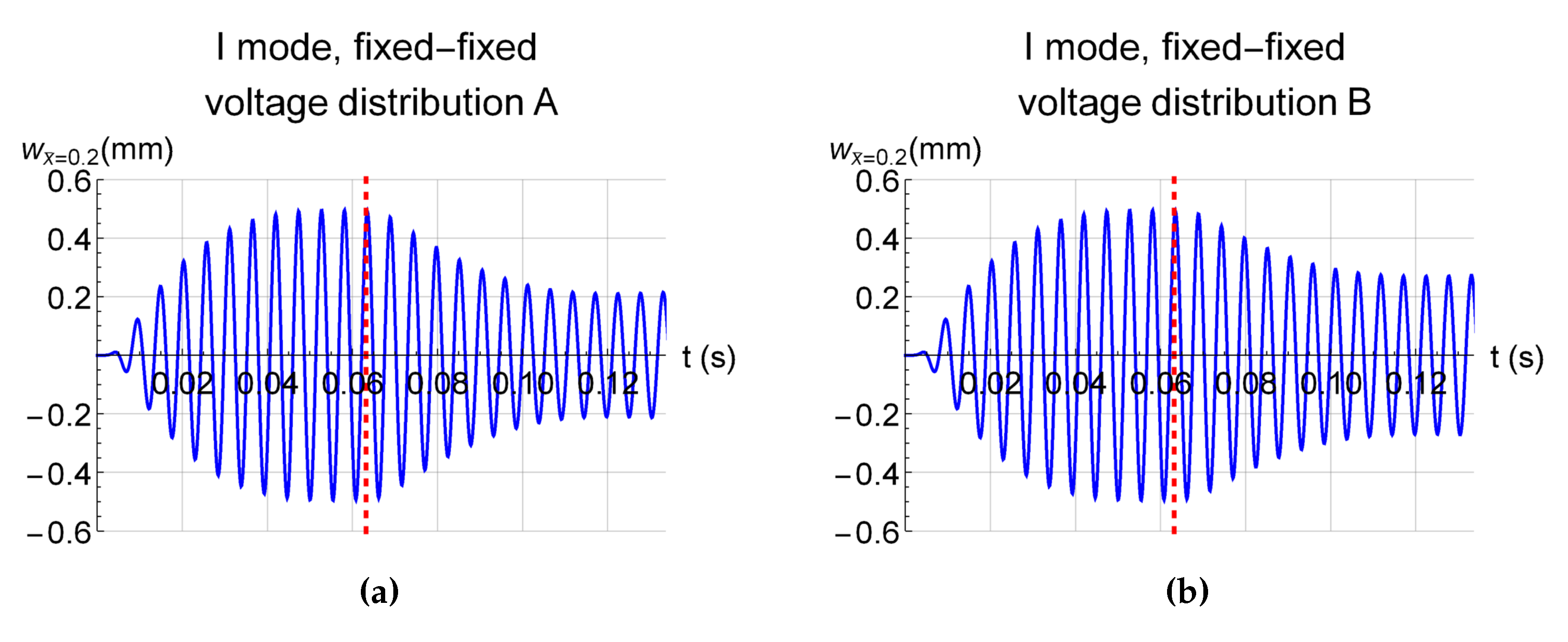
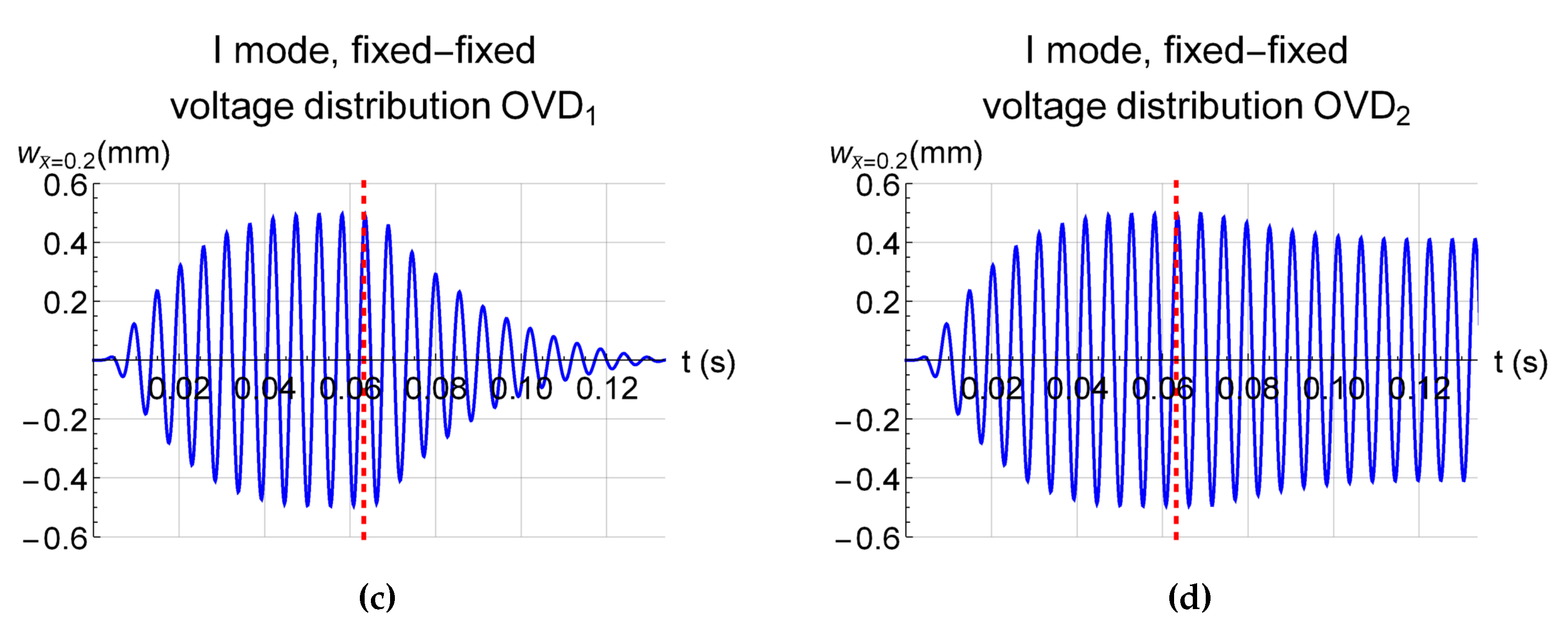
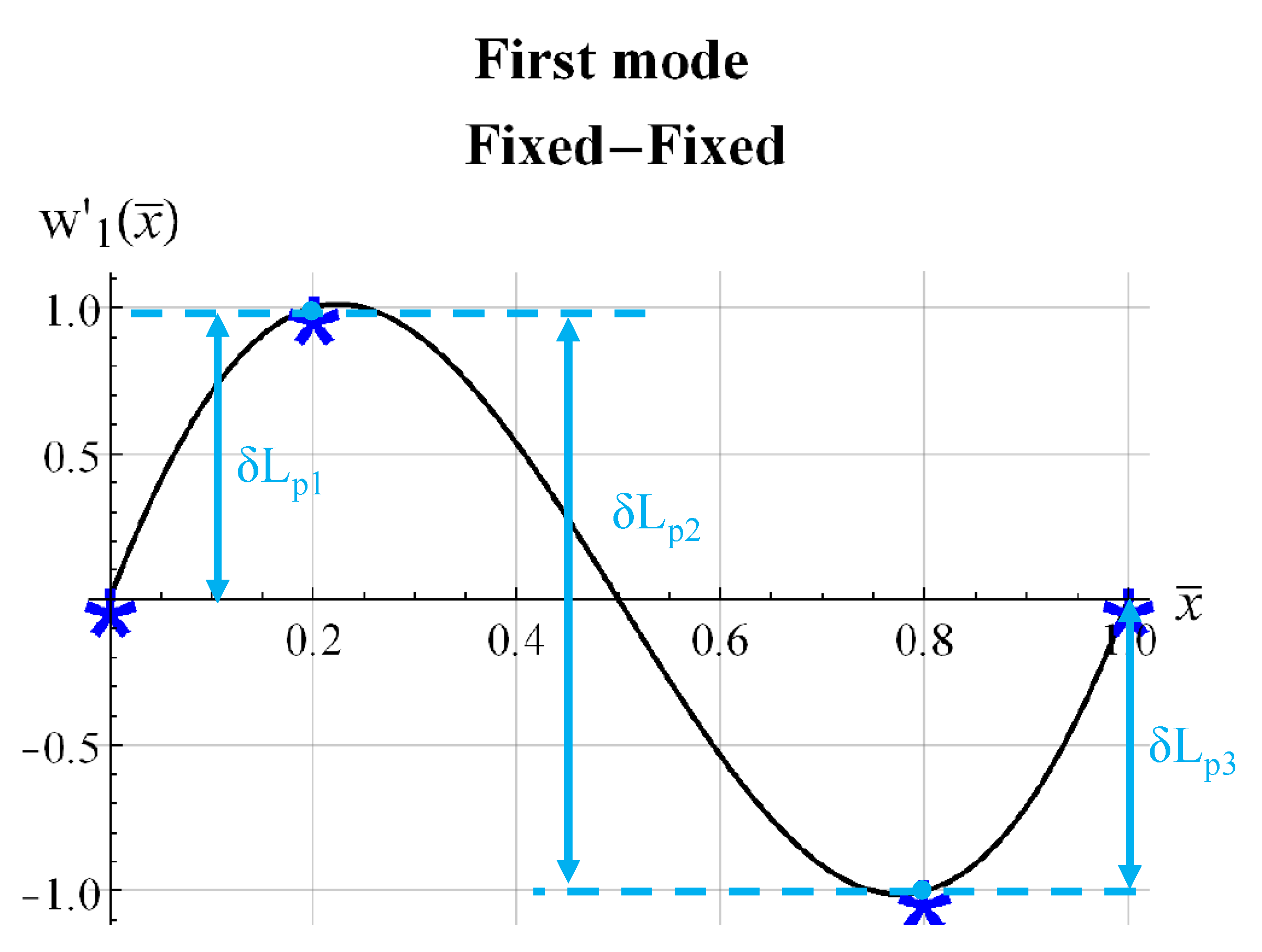
3. Numerical Model and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| L | beam’s length |
| piezoelectric coefficient | |
| beam’s density | |
| Young’s modulus of the piezoelectric actuator | |
| Young’s modulus of the beam | |
| piezoelectric bending moment | |
| piezoelectric actuator thickness | |
| beam’s thickness | |
| b | beam’s width |
| A | beam’s cross-section area |
| w | vertical displacement |
| virtual vertical displacement | |
| i-th flexural mode of the cantilever beam | |
| dimensionless length of the beam: | |
| points where the potential changes its sign | |
| dimensionless length | |
| derivative with respect to the axis |
References
- Tamer, O.; Walter, F.; Sinapius, M.; Böl, M. A Computational Geometric Parameter Optimization of the Thermomechanical Deicing Concept. Actuators 2022, 11, 223. [Google Scholar] [CrossRef]
- Shamim, M.B.; Hörsting, M.; Wulfinghoff, S. Variational Reduced-Order Modeling of Thermomechanical Shape Memory Alloy Based Cooperative Bistable Microactuators. Actuators 2023, 12, 36. [Google Scholar] [CrossRef]
- Nguyen, Q.A.; Jorgensen, S.; Ho, J.; Sentis, L. Characterization and Testing of an Electrorheological Fluid Valve for Control of ERF Actuators. Actuators 2015, 4, 135–155. [Google Scholar] [CrossRef]
- Oh, J.S.; Sohn, J.W.; Choi, S.B. Applications of Magnetorheological Fluid Actuator to Multi-DOF Systems: State-of-the-Art from 2015 to 2021. Actuators 2022, 11, 44. [Google Scholar] [CrossRef]
- Jeniš, F.; Kubík, M.; Michálek, T.; Strecker, Z.; Žáček, J.; Mazůrek, I. Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation. Actuators 2023, 12, 47. [Google Scholar] [CrossRef]
- Kang, M.G.; Jung, W.S.; Kang, C.Y.; Yoon, S.J. Recent Progress on PZT Based Piezoelectric Energy Harvesting Technologies. Actuators 2016, 5, 5. [Google Scholar] [CrossRef]
- Aabid, A.; Parveez, B.; Raheman, M.A.; Ibrahim, Y.E.; Anjum, A.; Hrairi, M.; Parveen, N.; Zayan, J.M. A Review of Piezoelectric Material-Based Structural Control and Health Monitoring Techniques for Engineering Structures: Challenges and Opportunities. Actuators 2021, 10, 101. [Google Scholar] [CrossRef]
- Harti, K.E.; Rahmoune, M.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator. Actuators 2019, 8, 19. [Google Scholar] [CrossRef]
- Barrett-Gonzalez, R.; Wolf, N. High Speed Microactuators for Low Aspect Ratio High Speed Micro Aircraft Surfaces. Actuators 2021, 10, 265. [Google Scholar] [CrossRef]
- Barrett-Gonzalez, R.; Wolf, N. High-Rate, High-Precision Wing Twist Actuation for Drone, Missile, and Munition Flight Control. Actuators 2022, 11, 239. [Google Scholar] [CrossRef]
- Botta, F.; Rossi, A.; Belfiore, N.P. A novel method to fully suppress single and bi-modal excitations due to the support vibration by means of piezoelectric actuators. J. Sound Vib. 2021, 510, 116260. [Google Scholar] [CrossRef]
- Botta, F.; Toccaceli, F. Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators 2018, 7, 23. [Google Scholar] [CrossRef]
- Botta, F.; Rossi, A. Introductory PZT actuators optimal working configuration experimental study in a turbofan engine fan rotor blade. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Online, 21–25 September 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84232, p. V011T30A035. [Google Scholar]
- Mokrani, B.; Bastaits, R.; Romanescu, I.; Horodinca, M.; Burda, I.; Preumont, A. Passive Damping of Rotationally Periodic Structures with Tuned Piezoelectric Inductive Shunt. Actuators 2018, 7, 41. [Google Scholar] [CrossRef]
- Rossi, A.; Botta, F.; Giovannelli, A.; Belfiore, N.P. High efficiency active damping on a fan rotor blade in case of resonant vibrations by means of piezoelectric actuators. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, GT 2021, Online, 7–11 June 2021; Volume 9A-2021. [Google Scholar] [CrossRef]
- Goltz, I.; Böhmer, H.; Nollau, R.; Belz, J.; Grüber, B.; Seume, J. Piezo-Electric Actuation of Rotor Blades in an Axial Compressor. In Proceedings of the ETC 2009—8th European Conference on Turbomachinery, Graz, Austria, 23–27 March 2009. [Google Scholar]
- Provenza, A.J.; Morrison, C.R. Control of Fan Blade Vibrations Using Piezoelectrics and Bi-Directional Telemetry. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2011; pp. 923–930. [Google Scholar]
- Choi, B.; Kauffman, J.; Duffy, K.; Provenza, A.; Morrison, C. Active vibration reduction of titanium alloy fan blades (FAN1) using piezoelectric materials. NASA/TM 2010, 2010, 216335. [Google Scholar]
- Rossi, A.; Botta, F.; Giovannelli, A.; Belfiore, N.P. A novel approach to reduce fan rotor blades stress in case of resonance due to inlet flow distortion by means of piezoelectric actuators. J. Sound Vib. 2023, 548, 117552. [Google Scholar] [CrossRef]
- Crawley, E.F.; De Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Ducarne, J.; Thomas, O.; Deü, J. Placement and dimension optimization of shunted piezoelectric patches for vibration reduction. J. Sound Vib. 2012, 331, 3286–3303. [Google Scholar] [CrossRef]
- Barboni, R.; Mannini, A.; Fantini, E.; Gaudenzi, P. Optimal placement of PZT actuators for the control of beam dynamics. Smart Mater. Struct. 2000, 9, 110. [Google Scholar] [CrossRef]
- Gupta, V.; Sharma, M.; Thakur, N. Optimization Criteria for Optimal Placement of Piezoelectric Sensors and Actuators on a Smart Structure: A Technical Review. J. Intell. Mater. Syst. Struct. 2010, 21, 1227–1243. [Google Scholar] [CrossRef]
- Botta, F.; Dini, D.; Schwingshackl, C.; di Mare, L.; Cerri, G. Optimal Placement of Piezoelectric Plates to Control Multimode Vibrations of a Beam. Adv. Acoust. Vib. 2013, 2013, 905160. [Google Scholar] [CrossRef]
- Botta, F.; Rossi, A.; Schinaia, L.; Scorza, A.; Orsini, F.; Sciuto, S.; Belfiore, N. Experimental validation on optimal placement of pzt plates for active beam multimode vibrations reduction. In Proceedings of the AIMETA 2017 Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno, Italy, 4–7 September 2017; Volume 3, pp. 2258–2269. [Google Scholar]
- Rossi, A.; Botta, F.; Maiozzi, R.; Scorza, A.; Sciuto, S.A. Experimental results for active control of multimodal vibrations by optimally placed piezoelectric actuators. MATEC Web Conf. 2018, 211, 20001. [Google Scholar] [CrossRef]
- Botta, F.; Scorza, A.; Rossi, A. Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Appl. Sci. 2018, 8, 551. [Google Scholar] [CrossRef]
- Cross, R. Factors affecting the vibration of tennis racquets. Sport. Eng. 2015, 18, 135–147. [Google Scholar] [CrossRef]
- Brody, H. Models of baseball bats. Am. J. Phys. 1990, 58, 756–758. [Google Scholar] [CrossRef]
- Vigneshwaran, K.; Behera, R.K. Vibration Analysis of a Simply Supported Beam with Multiple Breathing Cracks. Procedia Eng. 2014, 86, 835–842. [Google Scholar] [CrossRef]
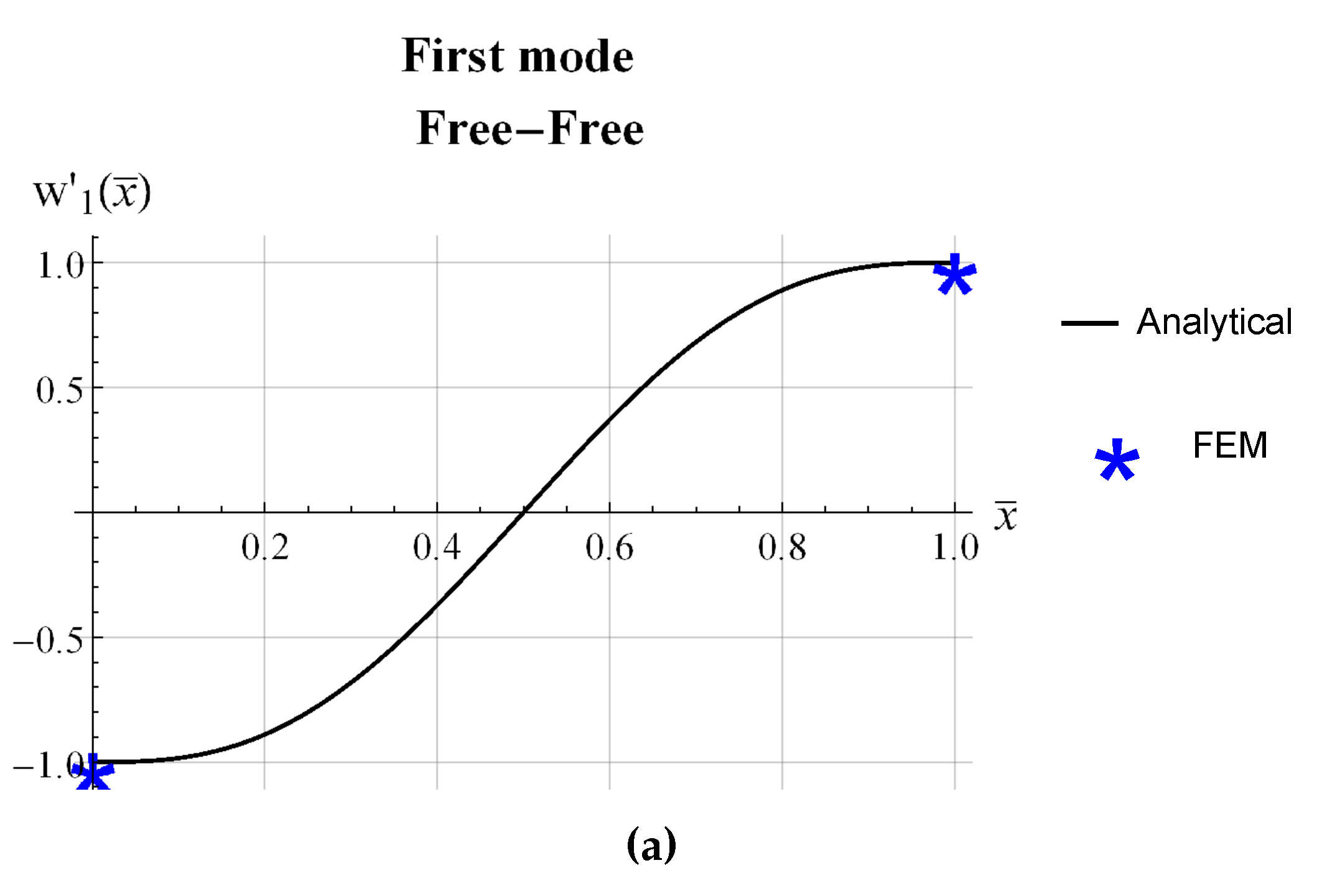
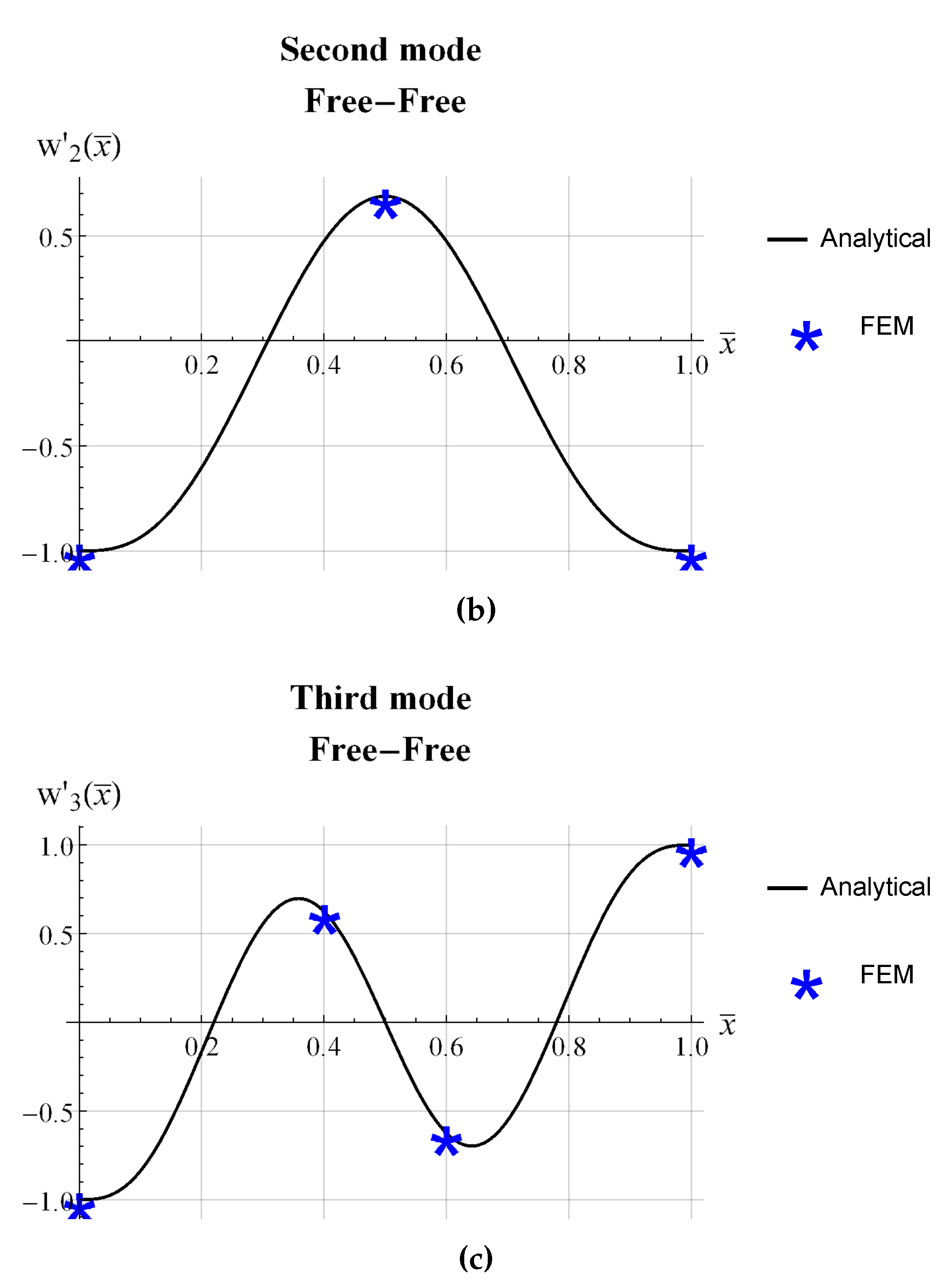
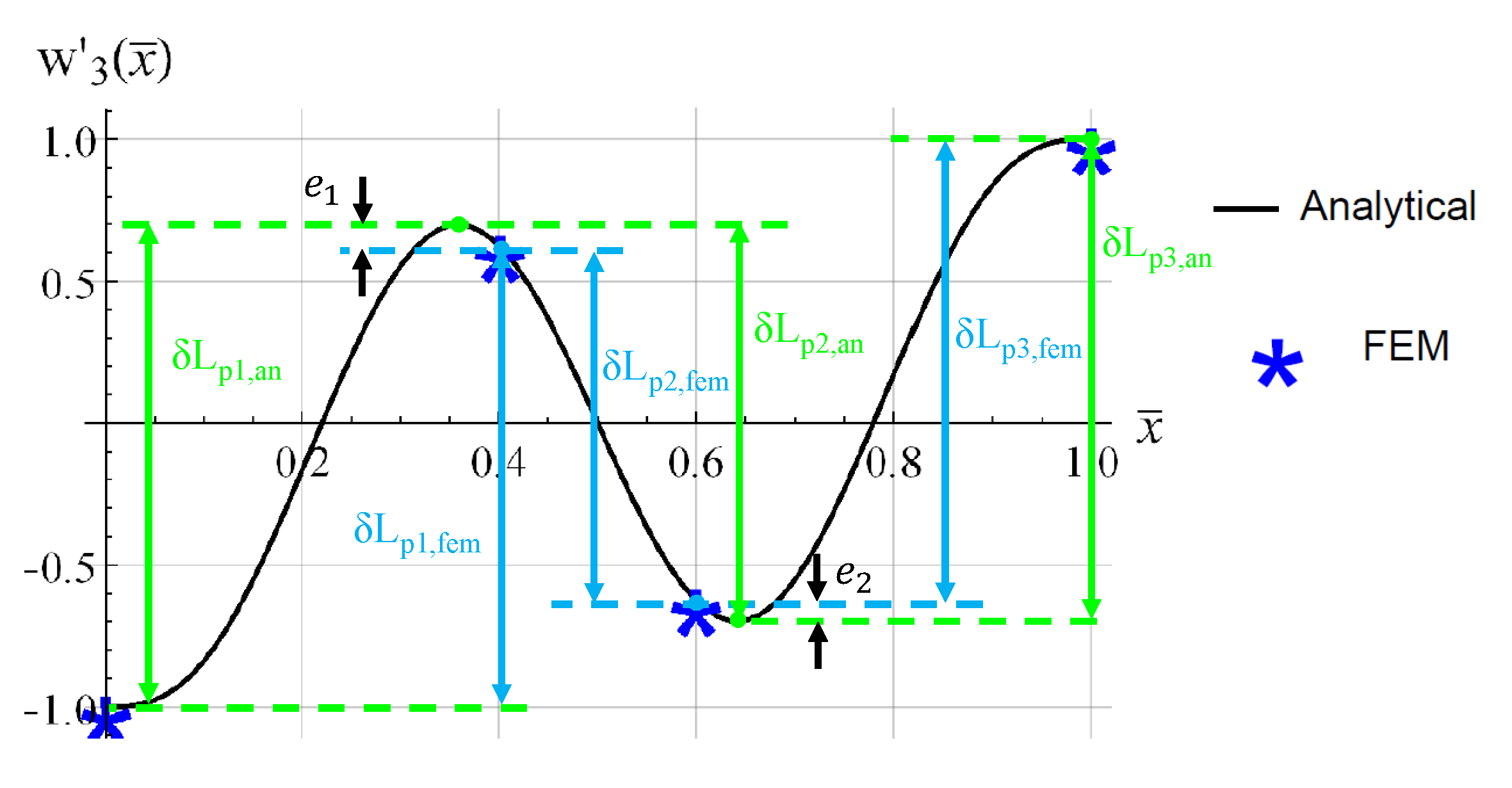
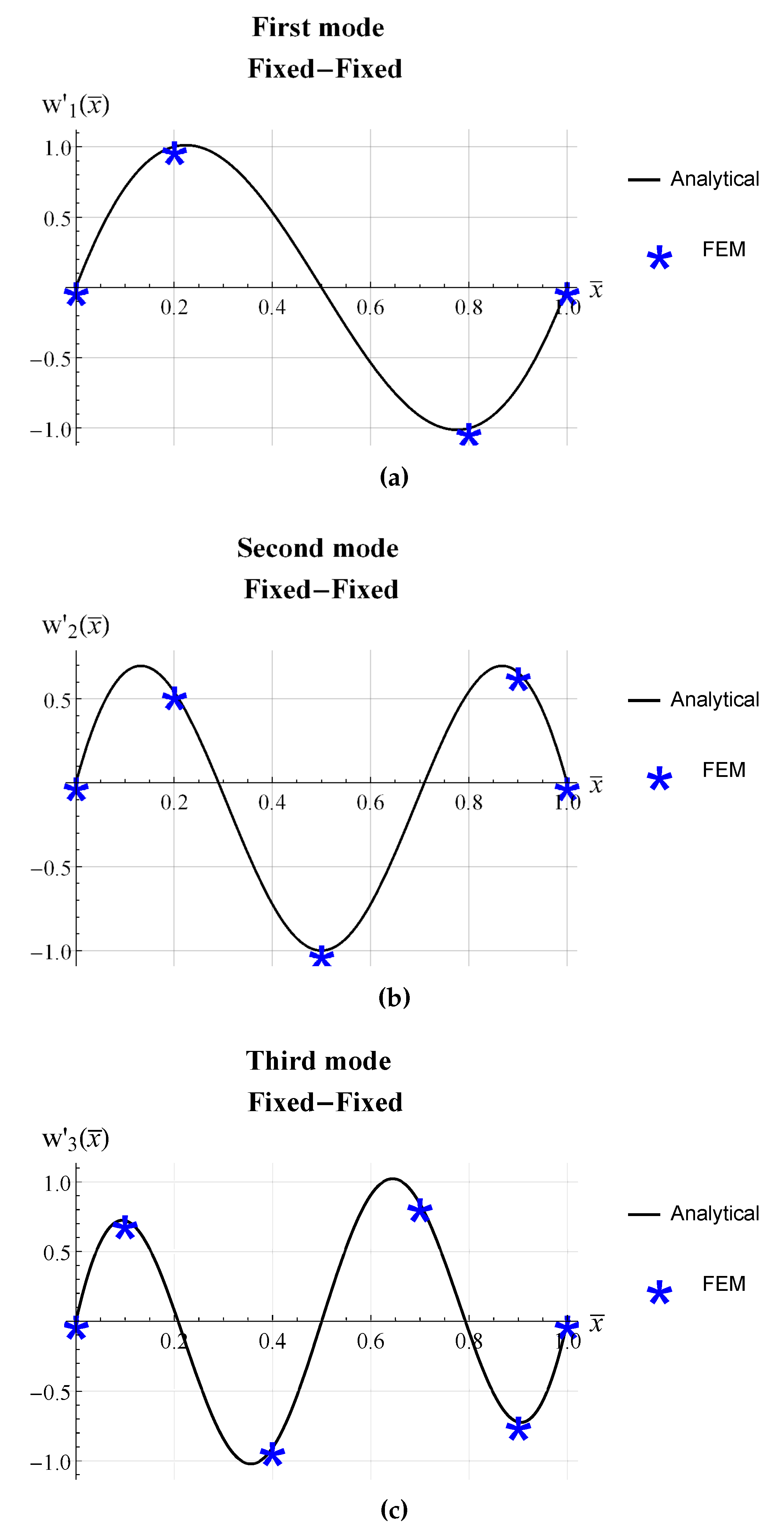
| beam | L (mm) | b (mm) | (mm) |
| 300 | 30 | 3 | |
| PZT | (mm) | (mm) | (mm) |
| 30 | 30 | 0.3 |
| Distribution\PP | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 2 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 |
| 3 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | - | +1 |
| 4 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 | +1 |
| 5 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 | +1 | +1 |
| … | … | … | … | … | … | … | … | … | … | … |
| k | +1 | −1 | +1 | −1 | −1 | +1 | −1 | +1 | +1 | −1 |
| … | … | … | … | … | … | … | … | … | … | … |
| −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
| Label | Material | Density (kg/m) | Young’s Modulus (GPa) | Poisson’s Ratio | |
|---|---|---|---|---|---|
| Beam | Aluminium | 2700 | 70 | 0.3 | – |
| Actuator | PZT-5A | 7750 | 39 | – | 374 |
| Distribution\PP | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | +1 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | +1 | +1 |
| B | +1 | +1 | −1 | −1 | −1 | +1 | +1 | −1 | −1 | +1 |
| OVD | +1 | +1 | −1 | −1 | −1 | −1 | −1 | −1 | +1 | +1 |
| OVD | +1 | +1 | −1 | −1 | −1 | +1 | +1 | +1 | +1 | −1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, A.; Botta, F. Optimal Voltage Distribution on PZT Actuator Pairs for Vibration Damping in Beams with Different Boundary Conditions. Actuators 2023, 12, 85. https://doi.org/10.3390/act12020085
Rossi A, Botta F. Optimal Voltage Distribution on PZT Actuator Pairs for Vibration Damping in Beams with Different Boundary Conditions. Actuators. 2023; 12(2):85. https://doi.org/10.3390/act12020085
Chicago/Turabian StyleRossi, Andrea, and Fabio Botta. 2023. "Optimal Voltage Distribution on PZT Actuator Pairs for Vibration Damping in Beams with Different Boundary Conditions" Actuators 12, no. 2: 85. https://doi.org/10.3390/act12020085
APA StyleRossi, A., & Botta, F. (2023). Optimal Voltage Distribution on PZT Actuator Pairs for Vibration Damping in Beams with Different Boundary Conditions. Actuators, 12(2), 85. https://doi.org/10.3390/act12020085






