Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation
Abstract
:1. Introduction
- The variable stiffness actuator is designed with two different mechanisms acting as the first and second stages of stiffness regulation. The first stage can store energy and absorb shocks of the input shaft. The second stage can be applied to bear heavy loads by an active motor.
- The required output torque can be adjusted to regulate the actuator stiffness.
- Two pairs of the rack-and-pinion systems of the first stage and the two pairs of the planetary gears of the second stage are arranged side by side, improving the stability and balance of the stiffness regulation process.
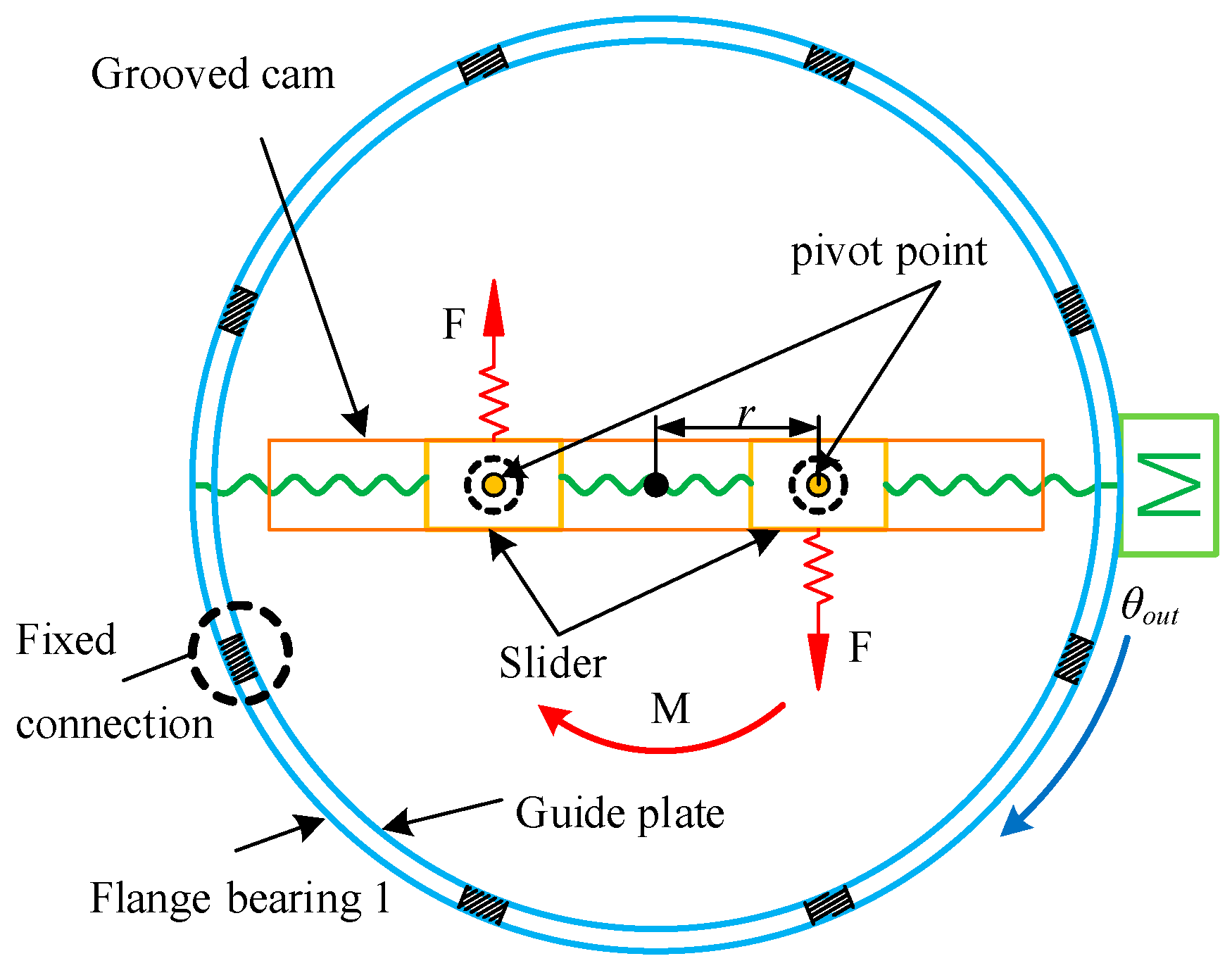
- The two cam-slider mechanisms are symmetrically arranged as the leverage pivot, guaranteeing the synchronous movements of the two rollers inside the cam.
2. Materials and Methods
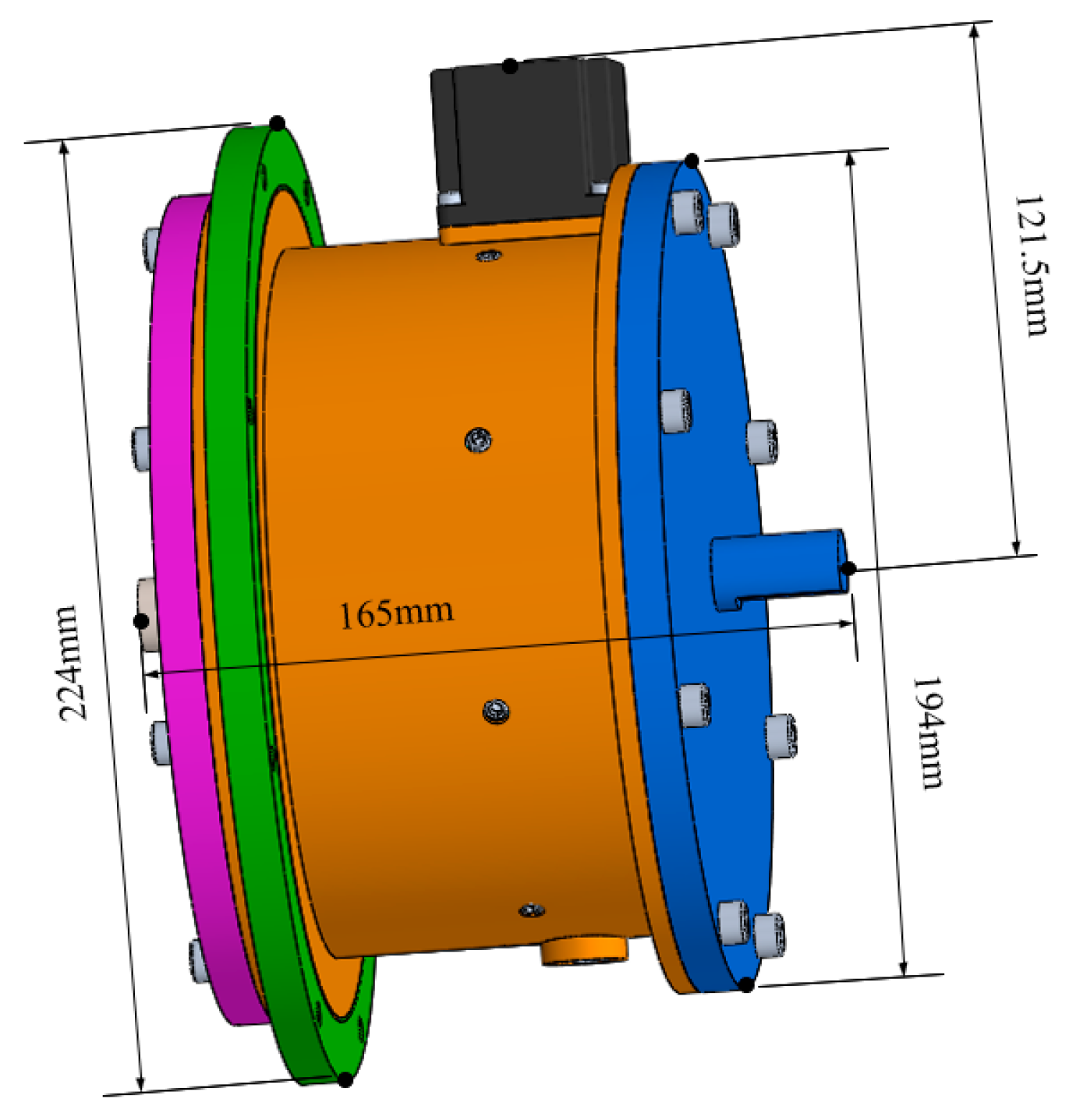
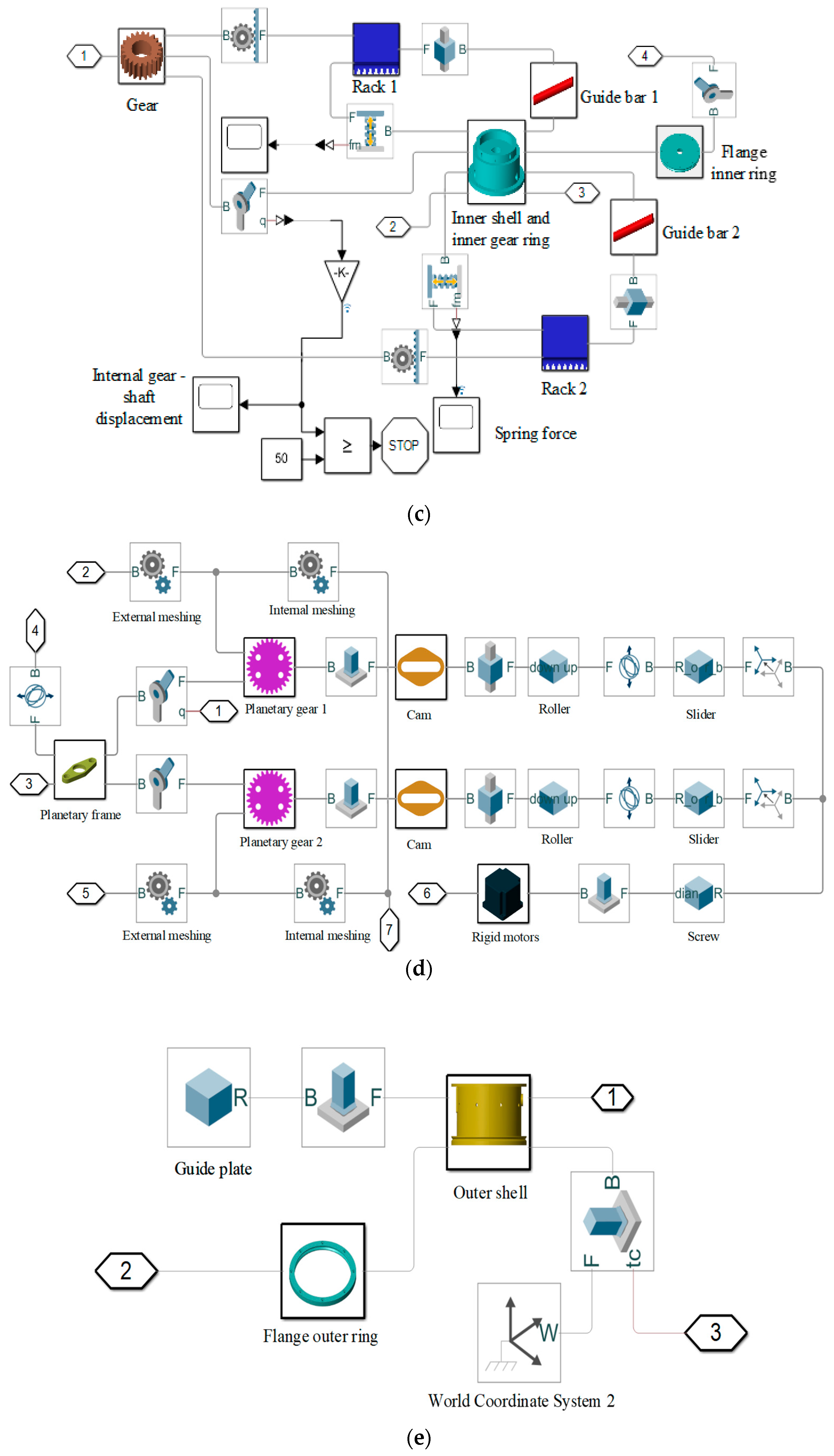
2.1. First Mechanism Design
2.2. Second Mechanism Design
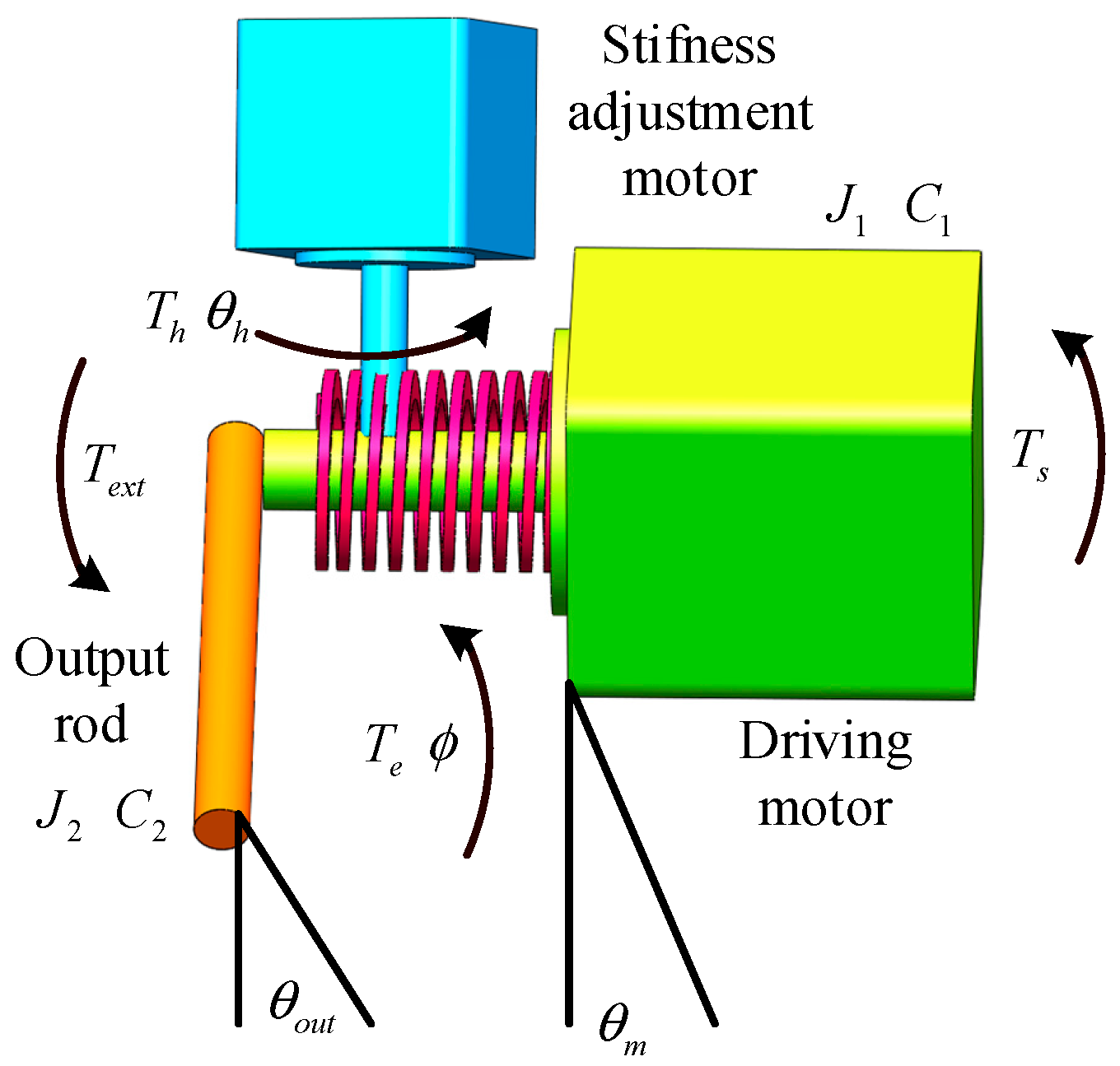
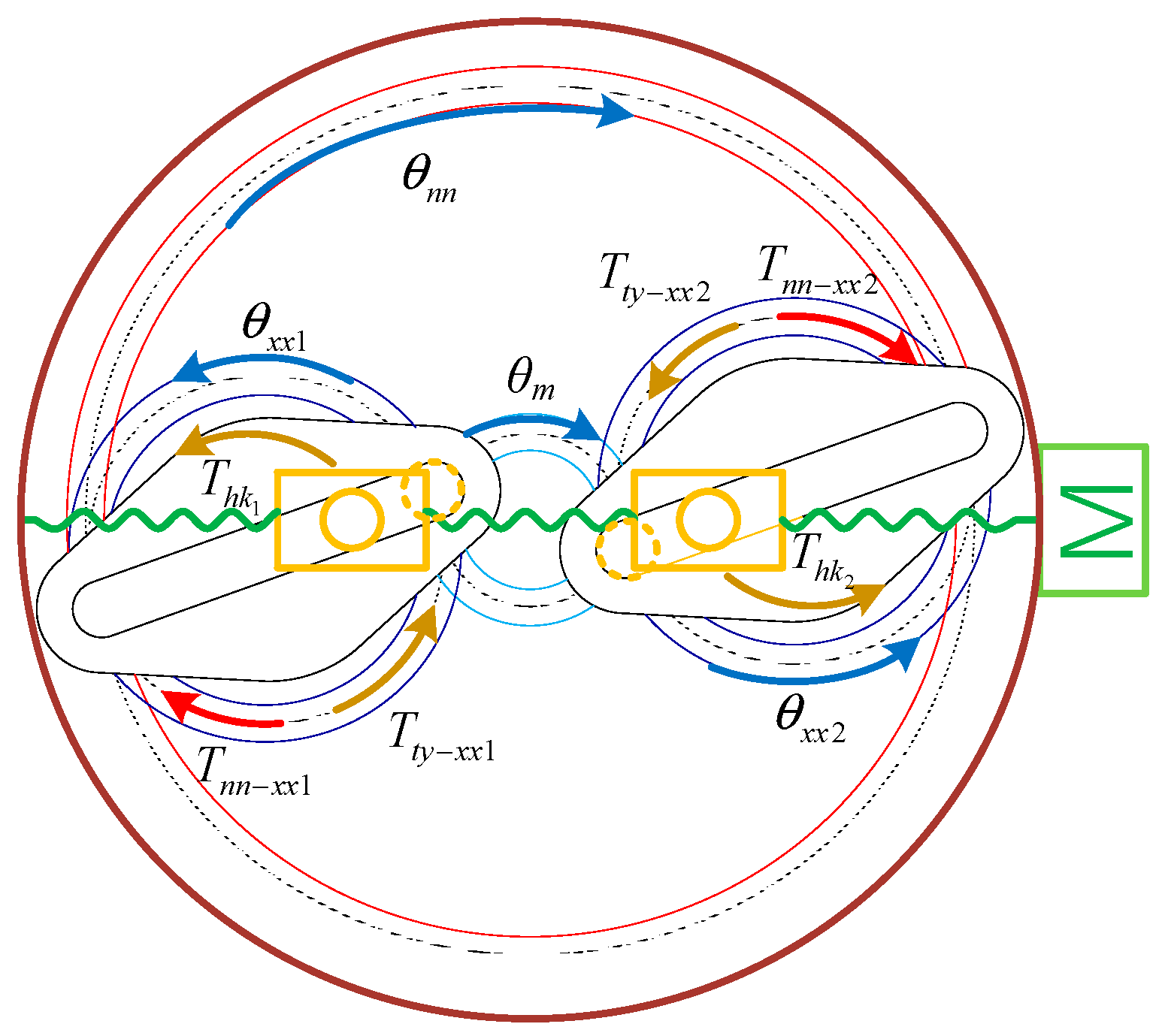
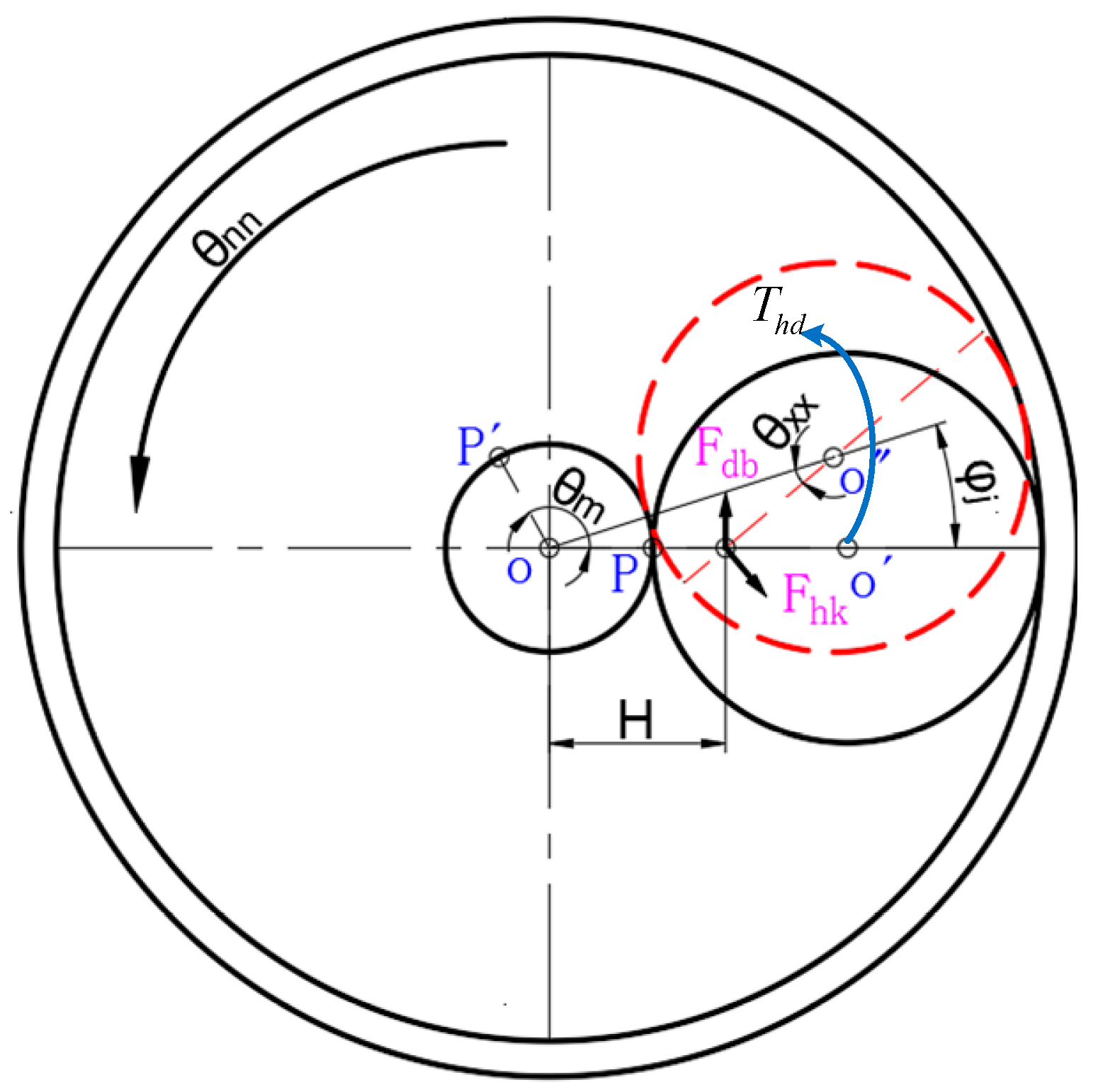
2.3. Mathematical Model for Describing the Dynamics of Developed Actuator
2.4. Stiffness Modelling
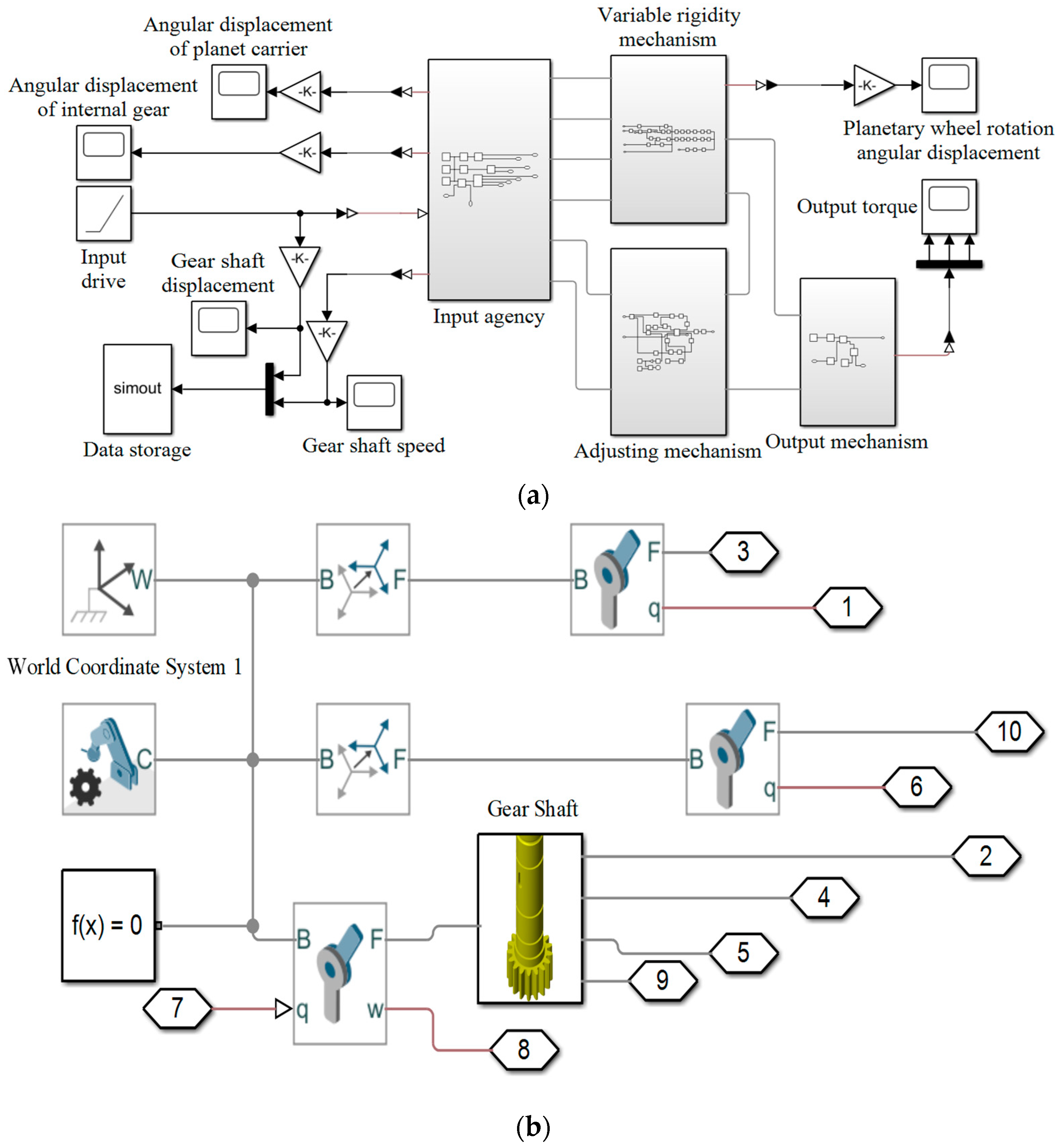
2.5. Simulation Setup
2.6. Experimental Setup
3. Results
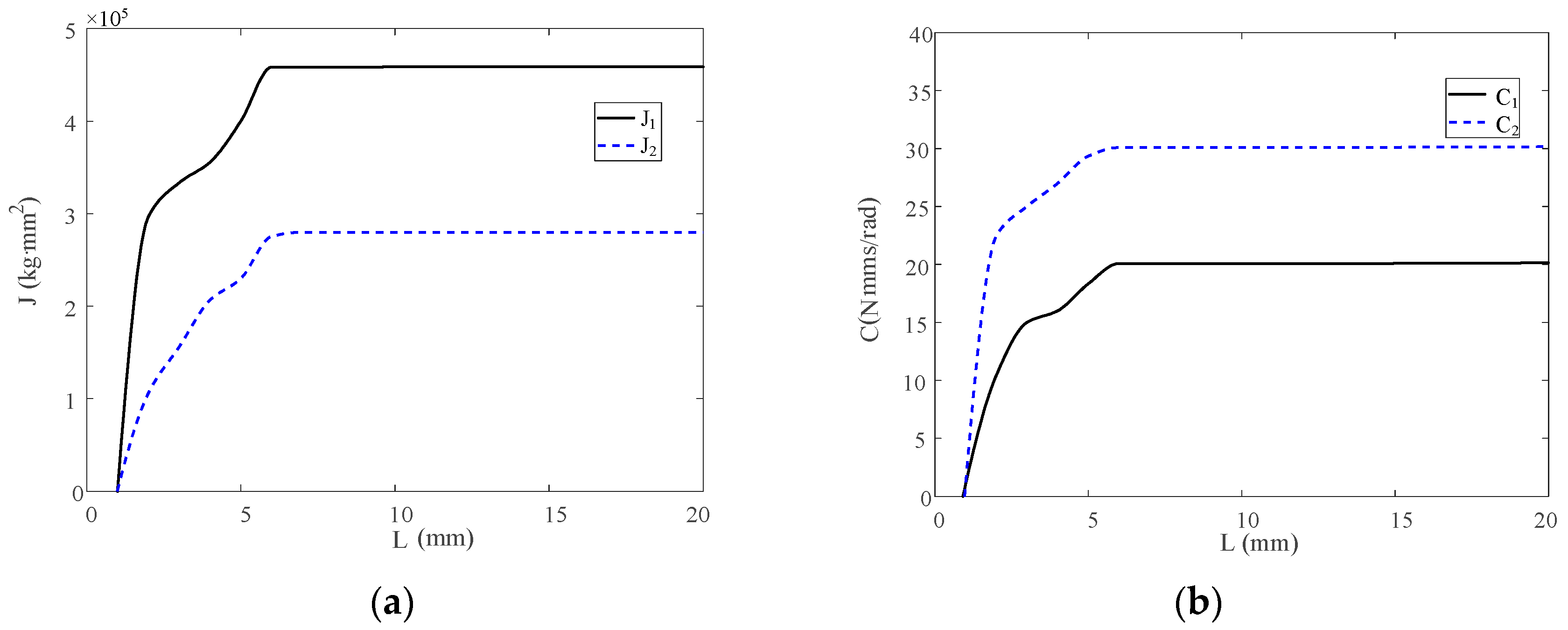
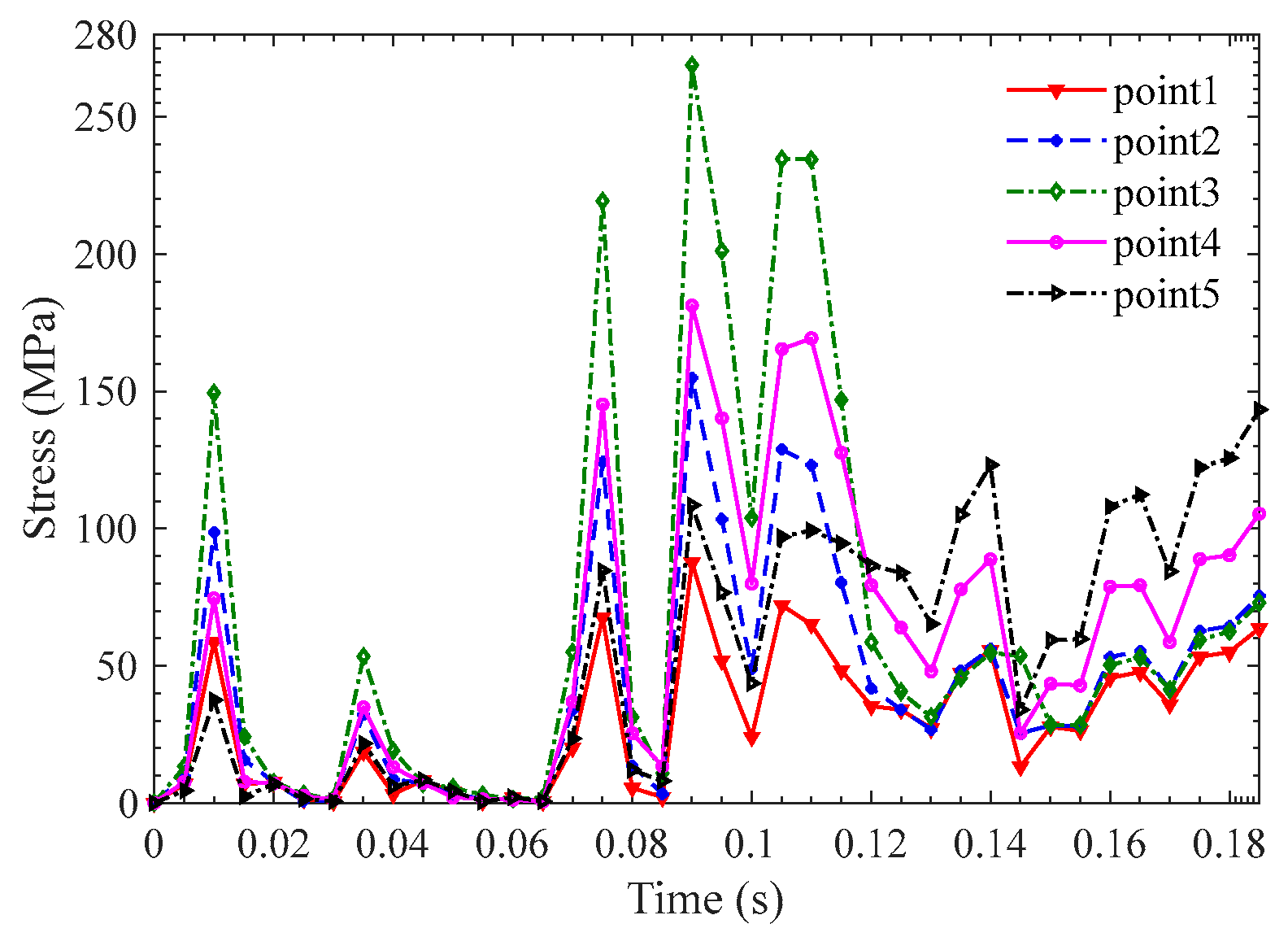
3.1. Strength Analysis
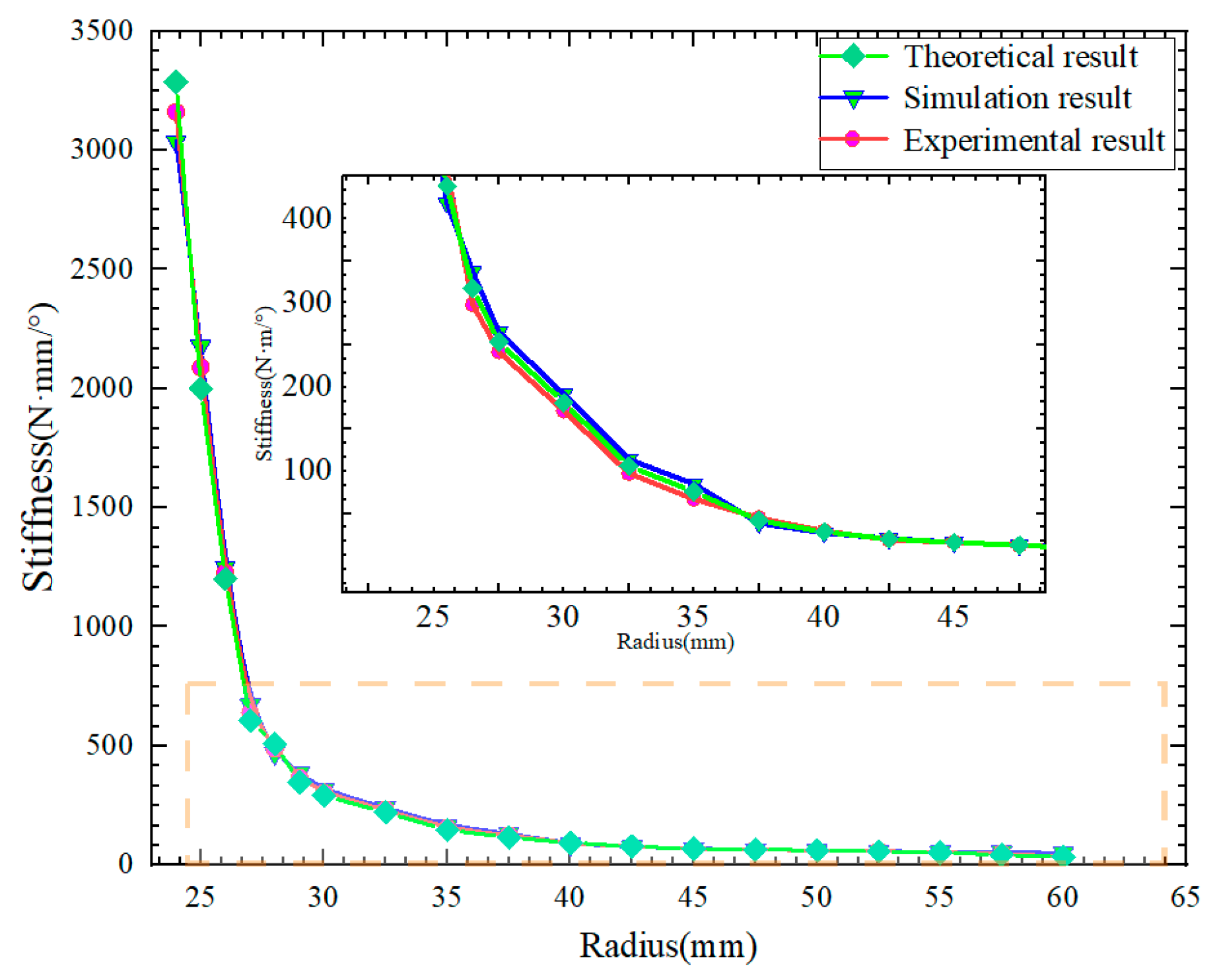
3.2. Stiffness Analysis of Simulation and Experimental Results
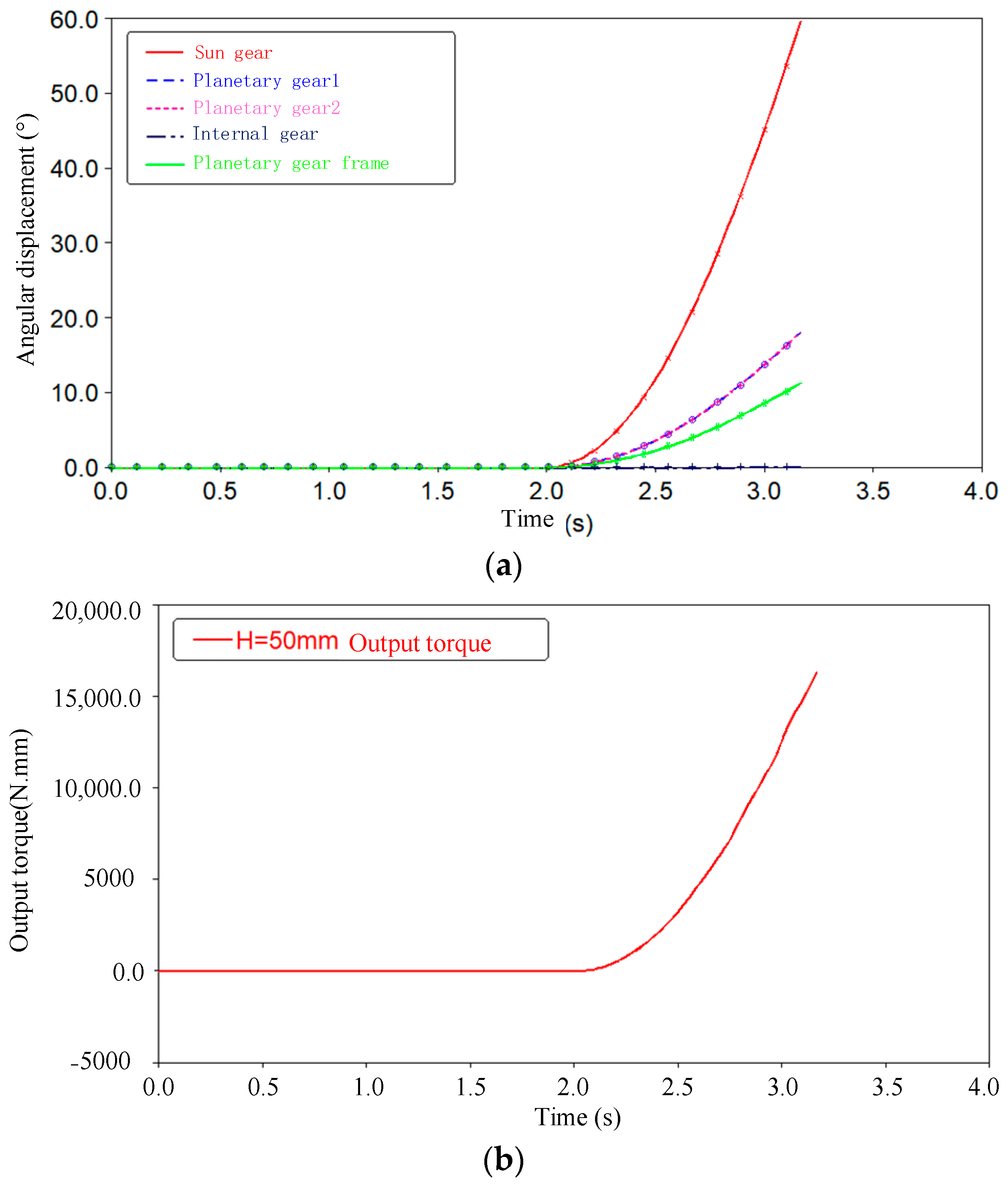
3.2.1. Stiffness Analysis of Simulation Results
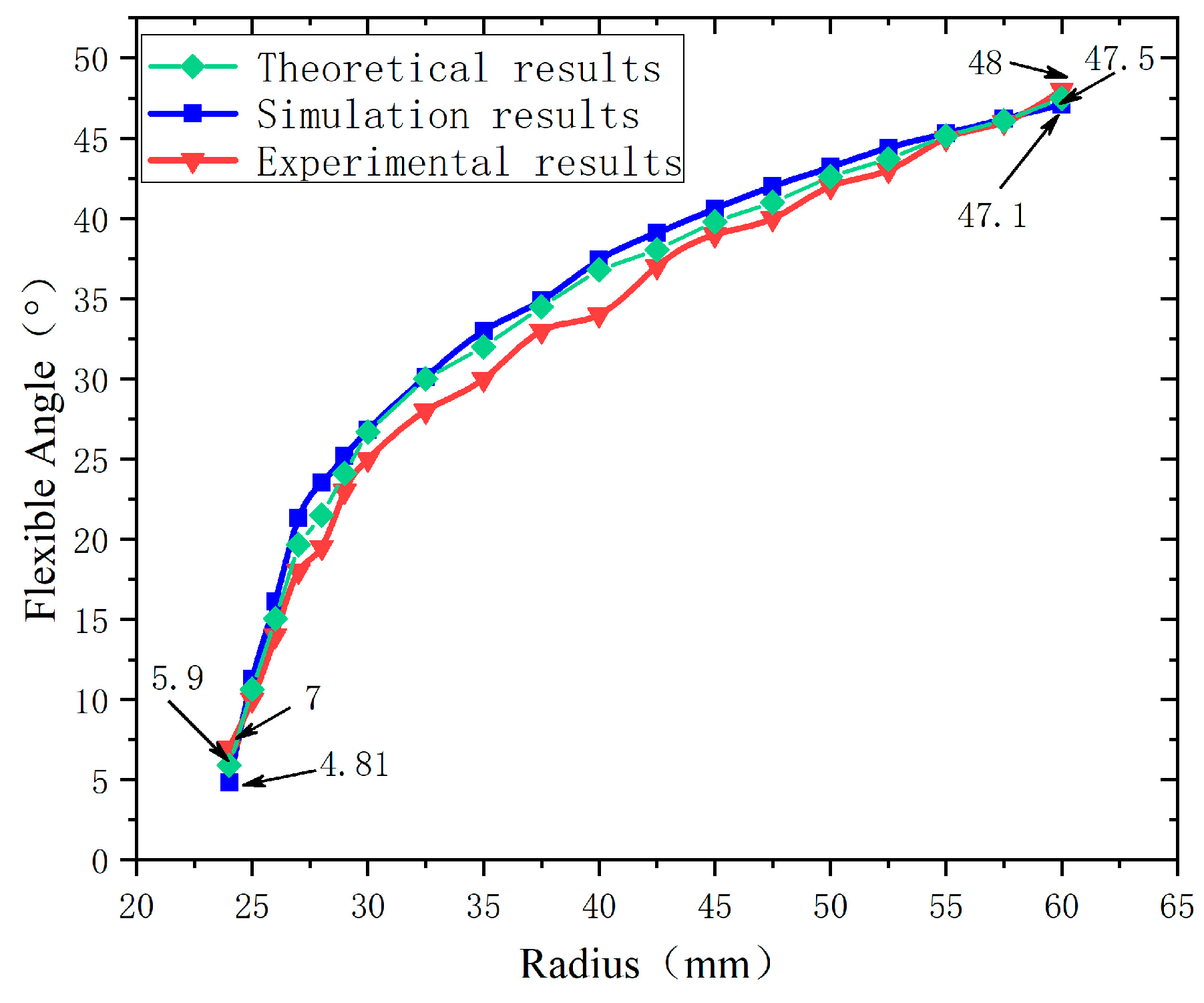
3.2.2. Stiffness Analysis of Experimental Results
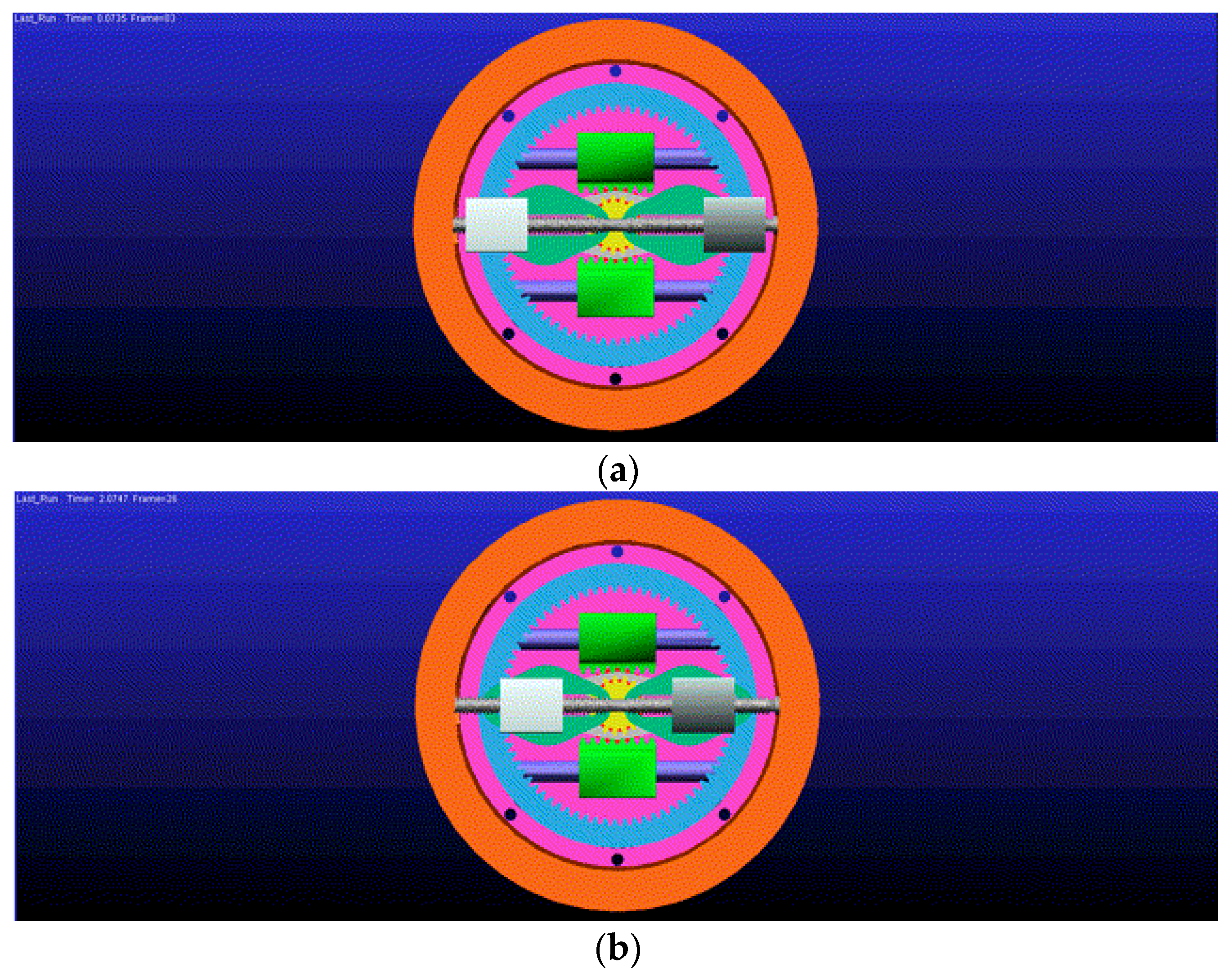
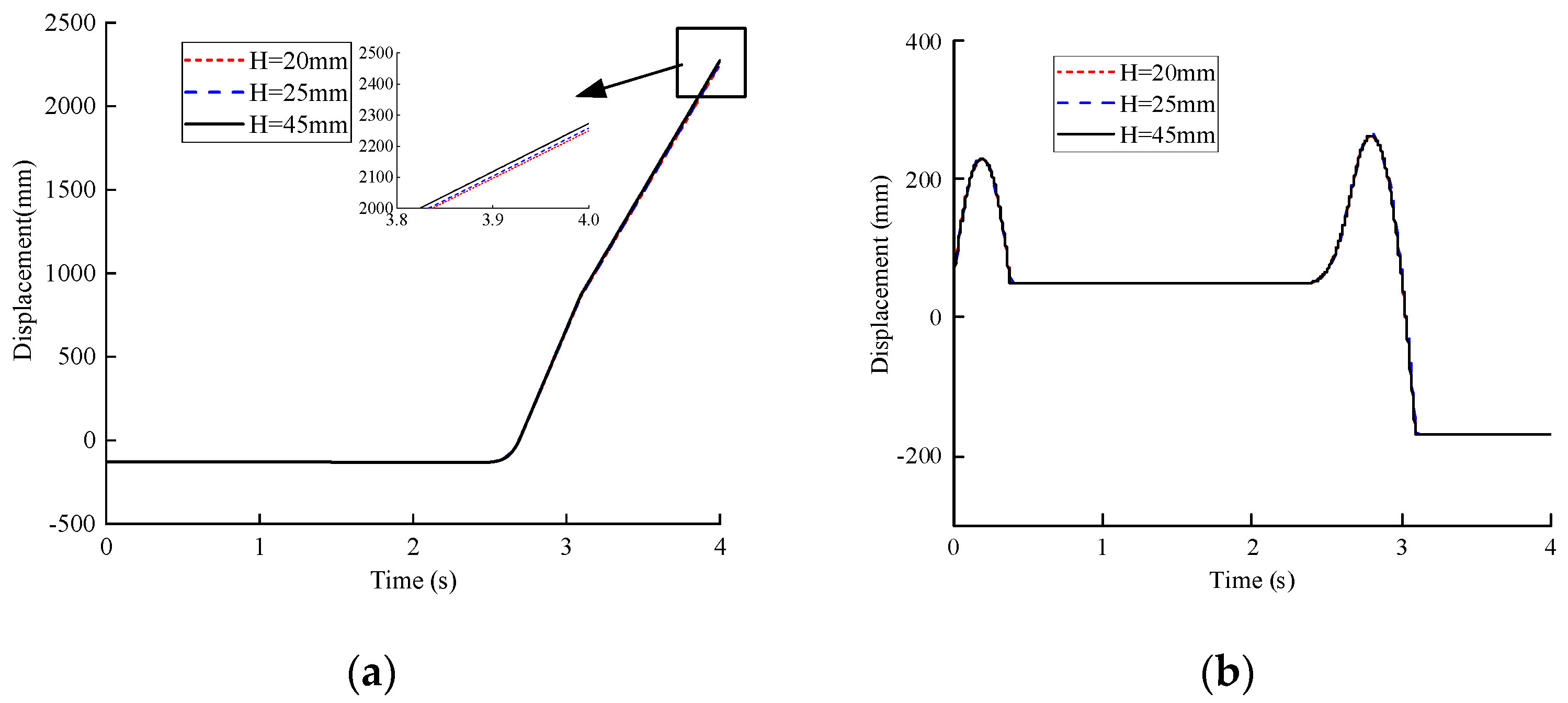
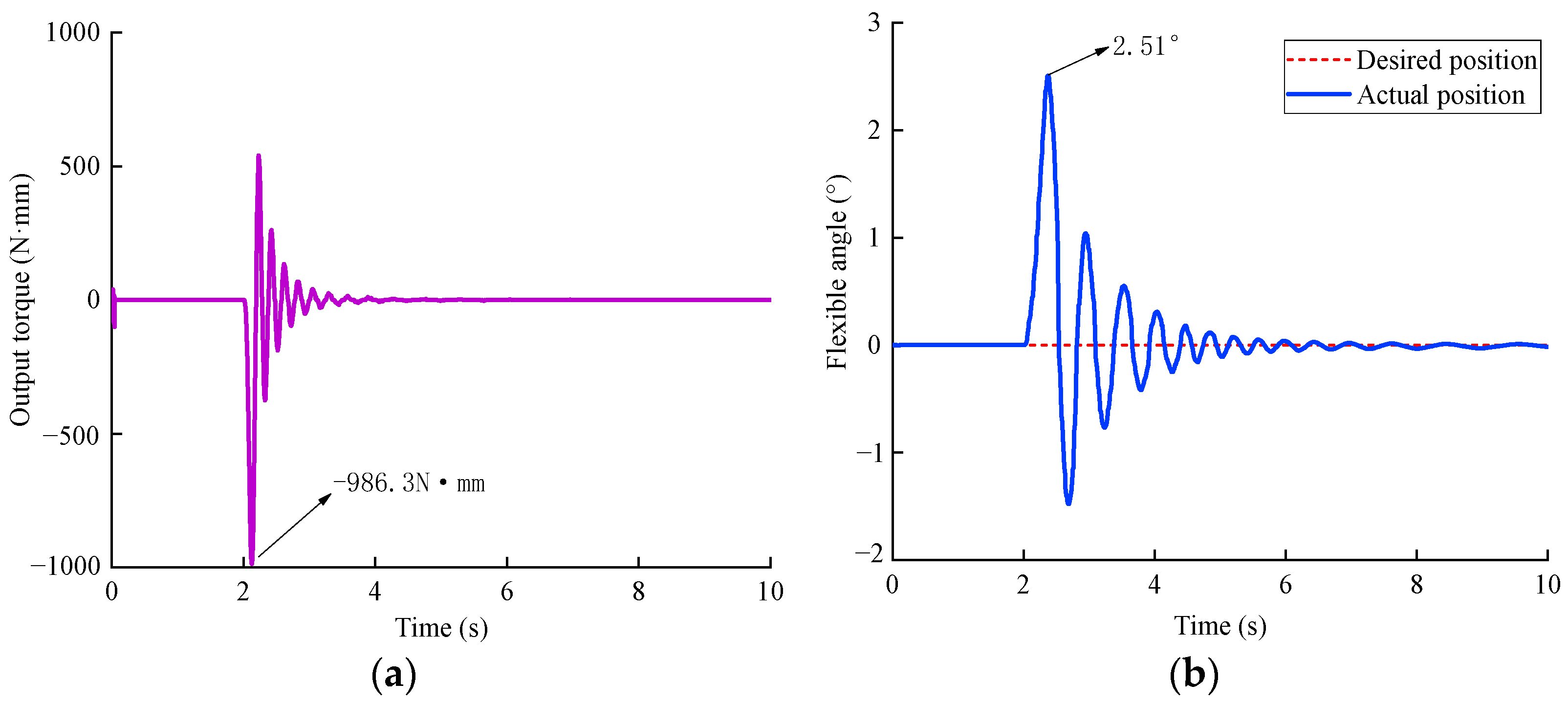
3.3. Simulation and Experiment of Dynamic Movements
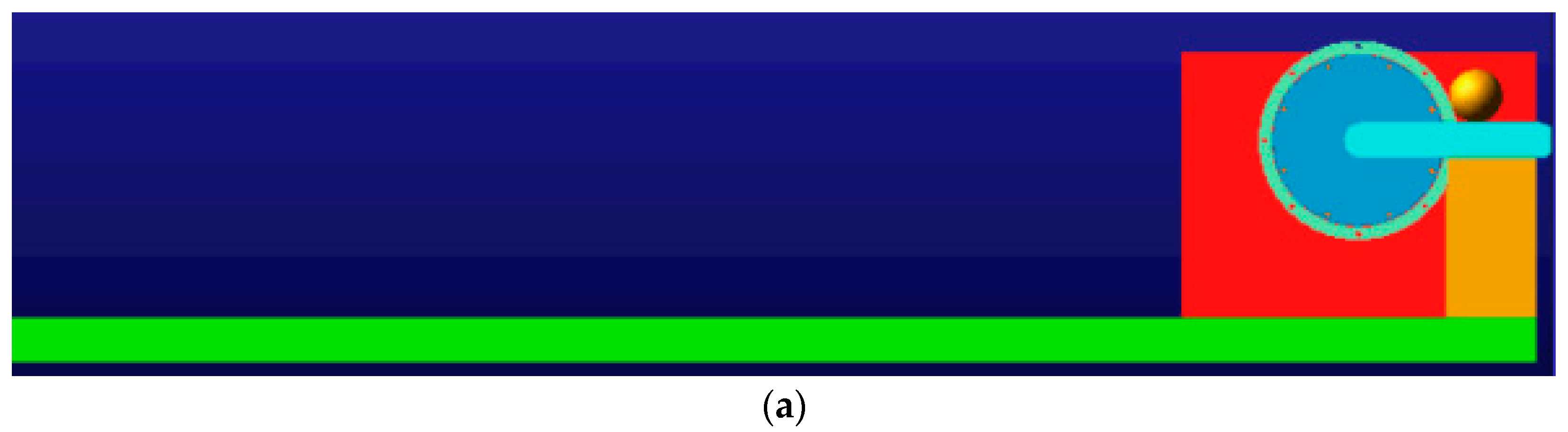
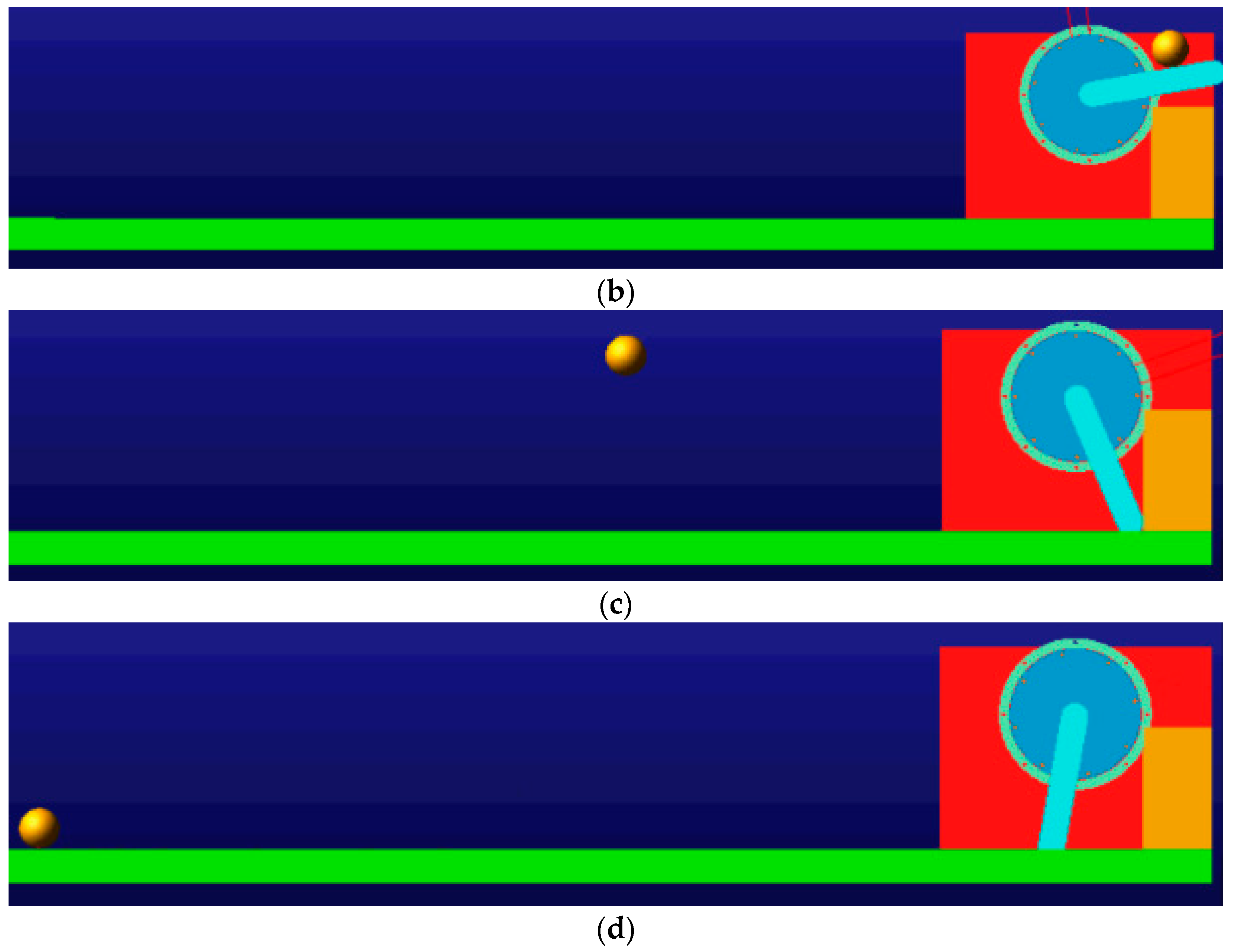
3.4. Ball Throwing Simulations
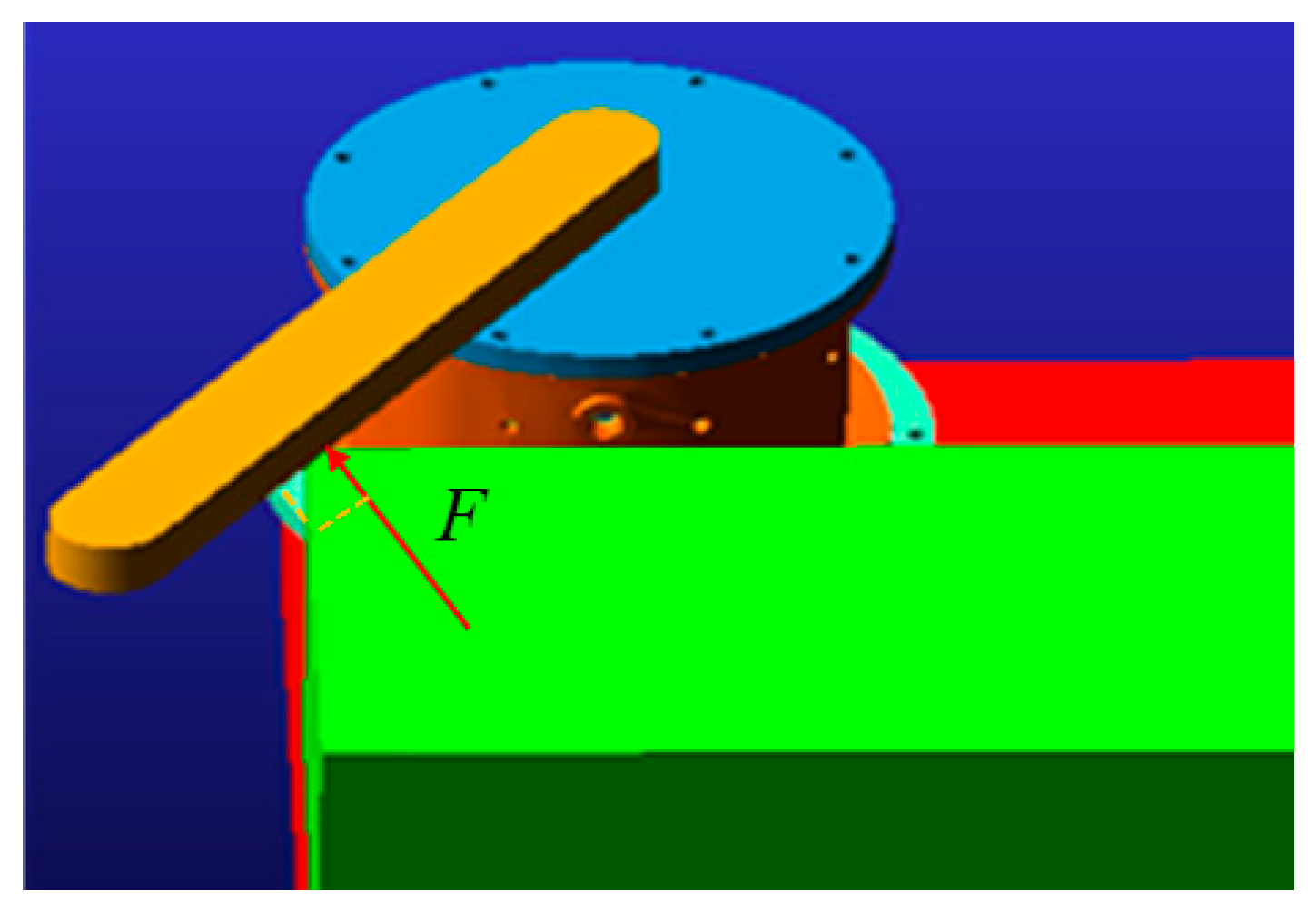
3.5. Static Analysis and Dynamic Analysis of Shock Resistance Performance
3.5.1. Static Analysis of Shock Resistance Performance
3.5.2. Dynamic Analysis of Shock Resistance Performance
4. Discussion
5. Conclusions
- The proposed actuator can adjust stiffness in the range of 35–3286 N·mm/deg, and the obtained range of the angle difference between the input shaft and output shaft is ±48°, which is wider than previously achieved ranges as in [21,22]. In addition, the performance of the designed actuator can be used to meet the needs of the collaborative robots according to [34,35];
- The passive mechanism is connected to the active mechanism to store energy and absorb shocks of the input shaft for achieving hybrid passive–active stiffness regulation;
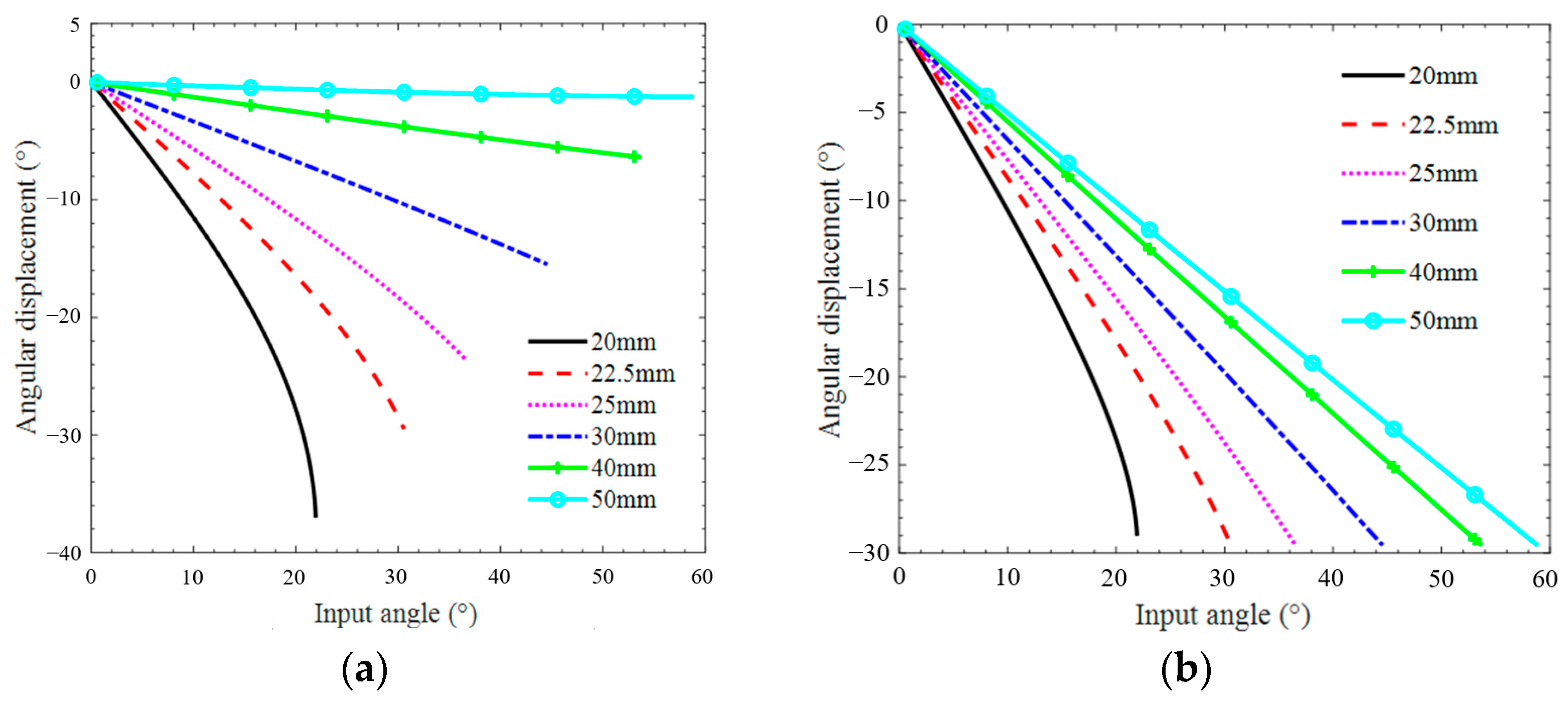
- It has been observed that the output angle of the internal gear behaves linearly with the input angle of the input shaft when the parameter r is in the range of 25–50 mm. This way, the stiffness can be precisely controlled by adjusting the input angle;
- The passive and active mechanisms are composites of simple structures and standard motors. This can be easily applied for adjusting rotational stiffness;
- On the basis of the achieved stiffness range, obtained angle difference, strength analysis, analysis of dynamic movement, and analysis of ball throwing simulations, the proposed actuator can be applied in the future with required performances.
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, X.; Dai, J. Theoretical Difficulties and Research Progresses of Mechanism Reconfiguration in Mechanisms-Evolution Connotation, Furcation Principle, Design Synthesis and Application of Metamorphic Mechanisms. Chin. J. Mech. Eng. Engl. 2020, 31, 57–71. [Google Scholar]
- Rodriguez, A.G.; Rodriguez, N.E.N.; Rodriguez, A.G.G. Design and Validation of a Novel Actuator with Adaptable Compliance for Application in Human-like Robotics. Ind. Robot 2009, 36, 84–90. [Google Scholar] [CrossRef]
- Bi, S.; Liu, C.; Zhou, X. Variable Stiffness Actuators: A Review of the Structural Research. Chin. J. Mech. Eng. Engl. 2018, 54, 34–46. [Google Scholar] [CrossRef]
- Yao, J.; Chen, X.; Chen, J. Design and Analysis of Soft Manipulator Teleoperation Systems. Chin. J. Mech. Eng. Engl. 2020, 31, 1968–1977. [Google Scholar]
- Dagalakis, N.G.; Yoo, J.M.; Oeste, T. Human-robot Collaboration Dynamic Impact Testing and Calibration Instrument for Disposable Robot Safety Artifacts. Ind. Robot. 2016, 43, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.; Eiberger, O.; Hirzinger, G. The DLR FSJ: Energy Based Design of a Variable Stiffness Joint. In Proceedings of the IEEE International Conference on Robotics and Automation(ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Liu, B.; Ge, W.; Zhao, D.; Zou, Z.; Li, B. Mechanical Design and Energy Storage Efficiency Research of a Variable Stiffness Elastic Actuator. Int. J. Adv. Robot. Syst. 2020, 17, 5–12. [Google Scholar] [CrossRef]
- Gao, C.; Huang, H.; Li, B. Design and Analysis of a Novel Deployable Robotic Grasper. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Dali, China, 6–8 December 2019. [Google Scholar]
- Li, X.; Pan, Y.; Chen, G.; Yu, H. Continuous Tracking Control for a Compliant Actuator with Two-Stage Stiffness. IEEE Trans. Autom. Sci. Eng. 2018, 15, 57–66. [Google Scholar] [CrossRef]
- Guo, J.; Tian, G. Conceptual Design and Analysis of Four Types of Variable Stiffness Actuators Based on Spring Pretension. Int. J. Adv. Robot. Syst. 2015, 12, 62–69. [Google Scholar] [CrossRef]
- Lavate, M.; Todkar, R.G. Variable Stiffness Actuators: A General Review. Int. J. Eng. Technol. 2015, V4, 201–205. [Google Scholar]
- Xu, Y.; Guo, K.; Sun, J.; Li, J. Design and Analysis of a Linear Digital Variable Stiffness Actuator. IEEE Access 2021, 9, 13992–14004. [Google Scholar] [CrossRef]
- Moore, R.; Schimmels, J.M.; Zhu, J.; Wang, Y.; Jiang, J. Unidirectional Variable Stiffness Hydraulic Actuator for Load-carrying Knee Exoskeleton. Int. J. Adv. Robot. Syst. 2017, 14, 1–12. [Google Scholar]
- Mengacci, R.; Garabini, M.; Grioli, G.; Catalano, M.G.; Bicchi, A. Overcoming the Torque/Stiffness Range Tradeoff in Antagonistic Variable Stiffness Actuators. IEEE/ASME Trans. Mechatron. 2021, 26, 3186–3197. [Google Scholar] [CrossRef]
- Xiong, J.; Sun, Y.; Zheng, J.; Dong, D.; Bai, L. Design and Experiment of a SMA-based Continuous-stiffness-adjustment Torsional Elastic Component for Variable Stiffness Actuators. Smart Mater. Struct. 2021, 30, 13–21. [Google Scholar] [CrossRef]
- Albu, S.A.; Wolf, S.; Eiberger, O.; Haddadin, S.; Petit, F.; Chalon, M. Dynamic Modelling and Control of Variable Stiffness Actuators. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–5 May 2010. [Google Scholar]
- Eiberger, O.; Haddadin, S.; Weis, M.; Albu-Schäffer, A.; Hirzinger, G. On Joint Design with Intrinsic Variable Compliance: Derivation of the DLR QA-joint. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–5 May 2010. [Google Scholar]
- Liu, L.; Leonhardt, S.; Bergmann, L.; Misgeld, B.J. Composite Performance of Variable Stiffness Actuator for Exoskeleton Administrated Via Impedance Control and Disturbance Observer. Mech. Mach. Theory 2023, 179, 96–105. [Google Scholar] [CrossRef]
- Wang, C.; Sheng, B.; Li, Z.; Sivan, M.; Zhang, Z.Q.; Li, G.Q. A Lightweight Series Elastic Actuator With Variable Stiffness: Design, Modeling, and Evaluation. IEEE/ASME Trans. Mechatron. 2023, 287, 1–10. [Google Scholar] [CrossRef]
- Shin, W.; Kim, J. Switchable Compliant Actuator with Fast Stiffness Modulation and Energy Efficient Power Transmission. Micromechatronics 2023, 90, 92–102. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Yuan, Z. Design and Analysis of Spring Parallel Variable Stiffness Actuator based on Antagonistic Principle. Mech. Mach. Theory 2019, 140, 44–58. [Google Scholar] [CrossRef]
- Ayoubi, Y.; Laribi, M.A.; Zeghloul, S. V2SOM: A Novel Safety Mechanism Dedicated to a Cobot’s Rotary Joints. Robotics 2019, 8, 18–26. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, X.; Zhang, M. Design and Analysi s of a Active-passive Variable Stiffness Flexible Joint. J. Mech. Eng. Engl. 2018, 54, 55–62. [Google Scholar] [CrossRef]
- Wang, W.; Fu, X.; Li, Y. Design and implementation of a variable stiffness actuator based on flexible gear rack mechanism. Robotica 2018, 36, 448–462. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, H.J.; Lee, K.H. A novel Variable Stiffness Scotch Yoke Series Elastic Actuator for Enhanced Functional Stiffness. Microsyst. Technol. 2020, 26, 3395–3402. [Google Scholar] [CrossRef]
- Karim, A.; Lindner, P.; Verl, A. Control-based Compensation of Friction and Backlash within Rack and Pinion Drives. Prod. Eng. 2018, 12, 589–596. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Z.; Sun, D. Design, modeling and control of a novel compact, energy-efficient, and rotational serial variable stiffness actuator (SVSA-II). Mech. Mach. Theory 2018, 130, 123–136. [Google Scholar] [CrossRef]
- Qiu, W.; Yang, F.; Wang, D. Design and Free Vibration Characteristics of Linkage Planetary Gear Trains. J. Braz. Soc. Mech. Sci. 2022, 19, 44–58. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Sardellitti, I. A New Actuator with Adjustable Stiffness Based on a Variable Ratio Lever Mechanism. IEEE/ASME Trans. Mechatron. 2014, 19, 55–63. [Google Scholar] [CrossRef]
- Groothuis, S.S.; Rusticelli, G.; Zucchelli, A. The Variable Stiffness Actuator VSA UT-II: Mechanical Design, Modeling, and Identification. IEEE/ASME Trans. Mechatron. 2014, 19, 589–597. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. A Novel Intrinsically Energy Efficient Actuator with Adjustable Stiffness (AWAS). IEEE/ASME Trans. Mechatron. 2013, 18, 355–365. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, S.; Liu, X. Nonlinear dynamics of a spur gear pair with time varying stiffness and backlash. Int. J. Mech. Sci. 2004, 23, 179–187. [Google Scholar]
- Zhu, P.; Li, Y.; Chen, B. Effects of Zero Time Holding Quenching Temperature on Tempering Microstructure and Mechanical Properties of 40cr steel. In Proceedings of the Chinese Materials Conference (CMC), Chengdu, China, 10–14 July 2019. [Google Scholar]
- Zeng, X.; Morrison, T.; Fu, Y. Variable stiffness mechanisms and their applications to collaborative robots. Int. Technol. 2022, 11, 36–47. [Google Scholar]
- Pang, G.; Yang, G.; Heng, W. CoboSkin: Soft robot skin with variable stiffness for safer human–robot collaboration. IEEE Trans. Ind. Electron. 2020, 68, 3303–3314. [Google Scholar] [CrossRef]
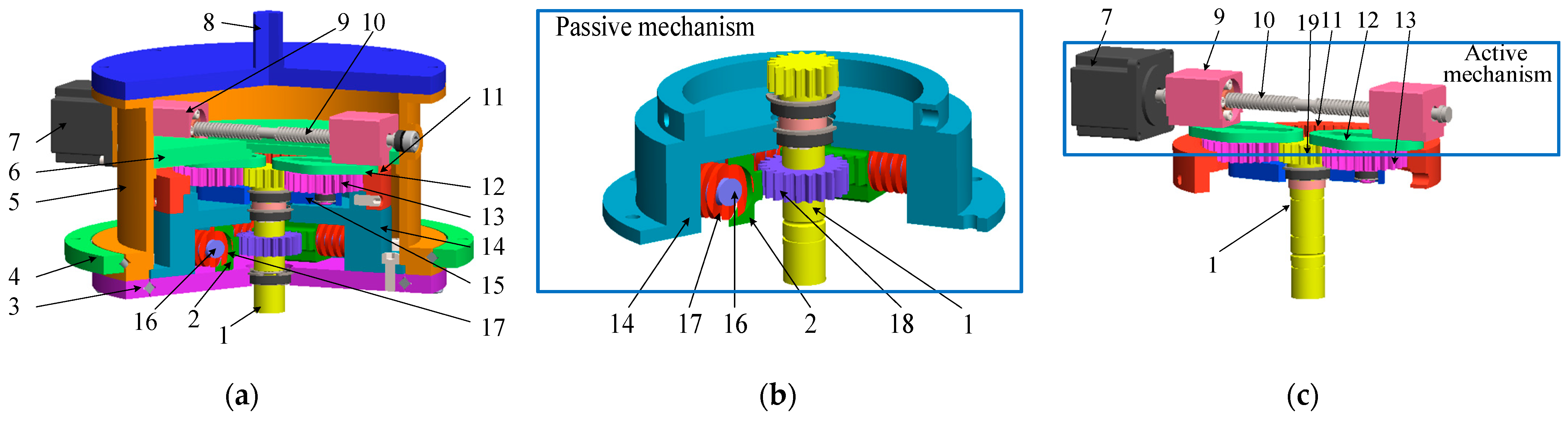
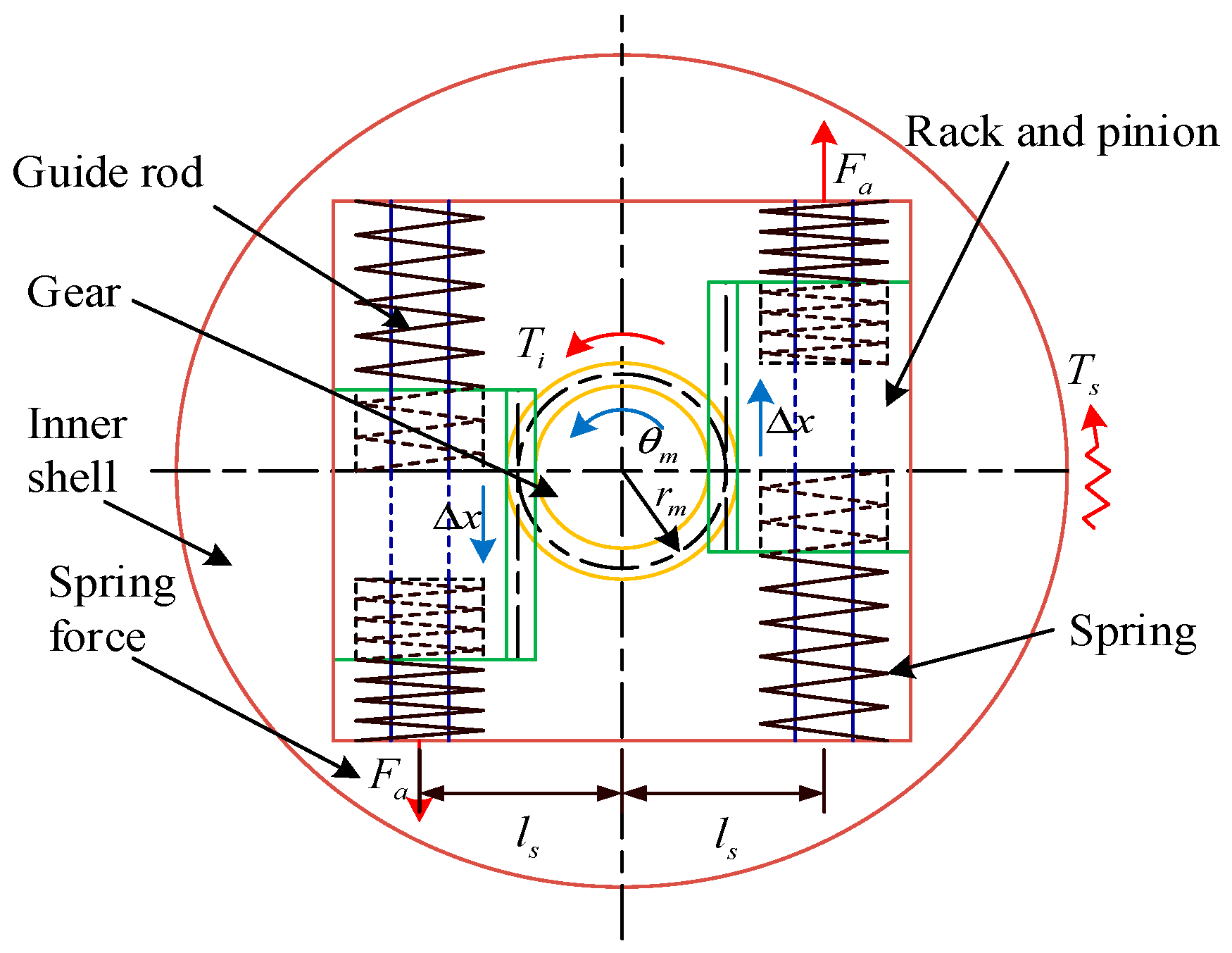
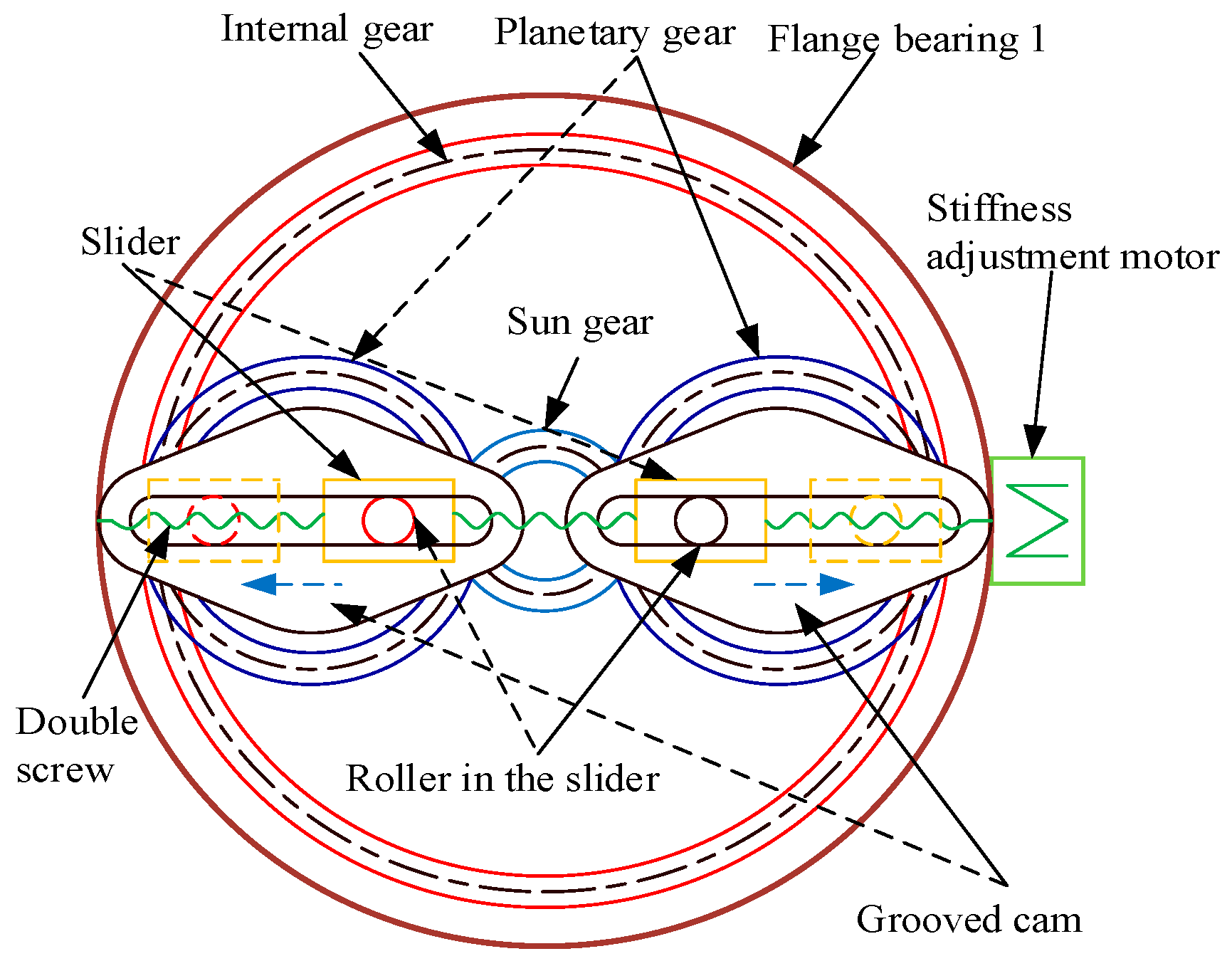
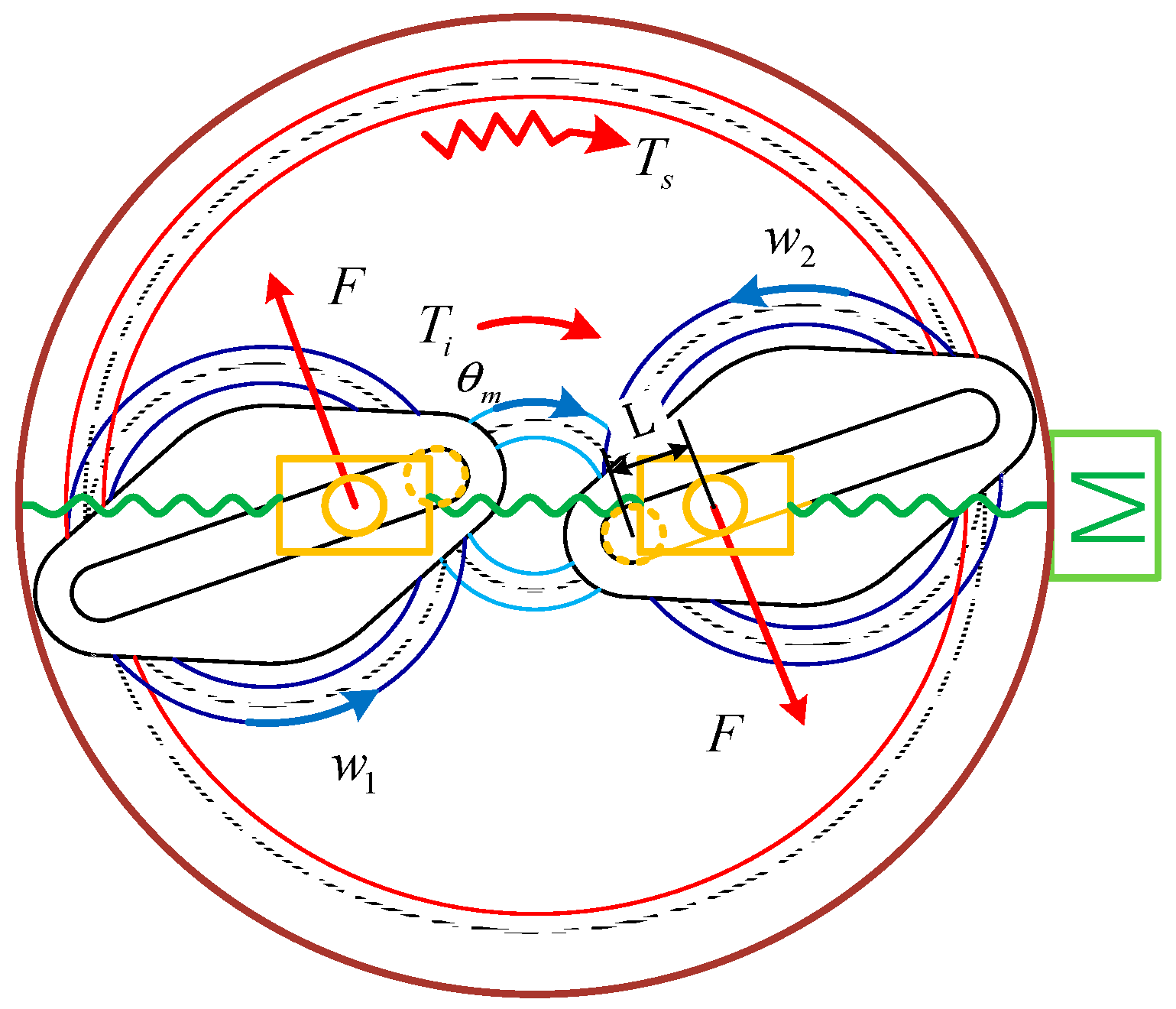

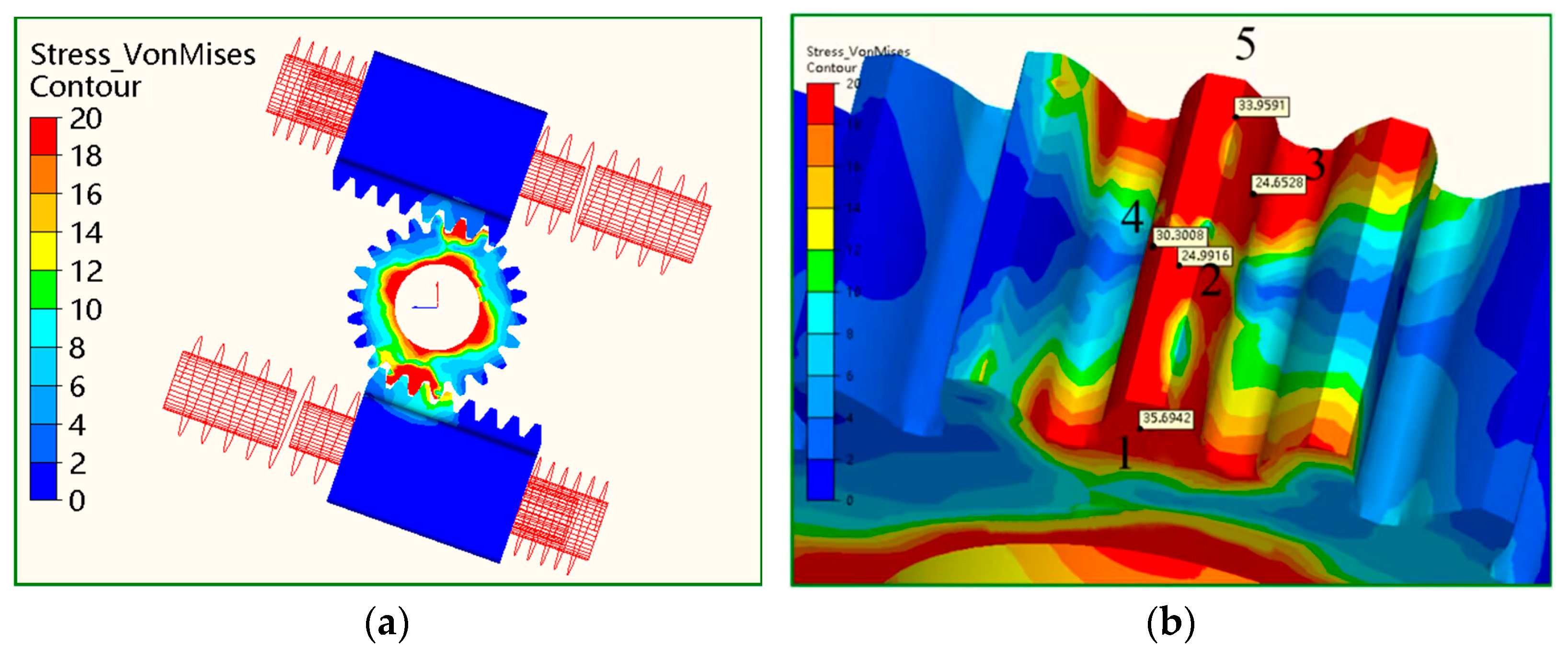
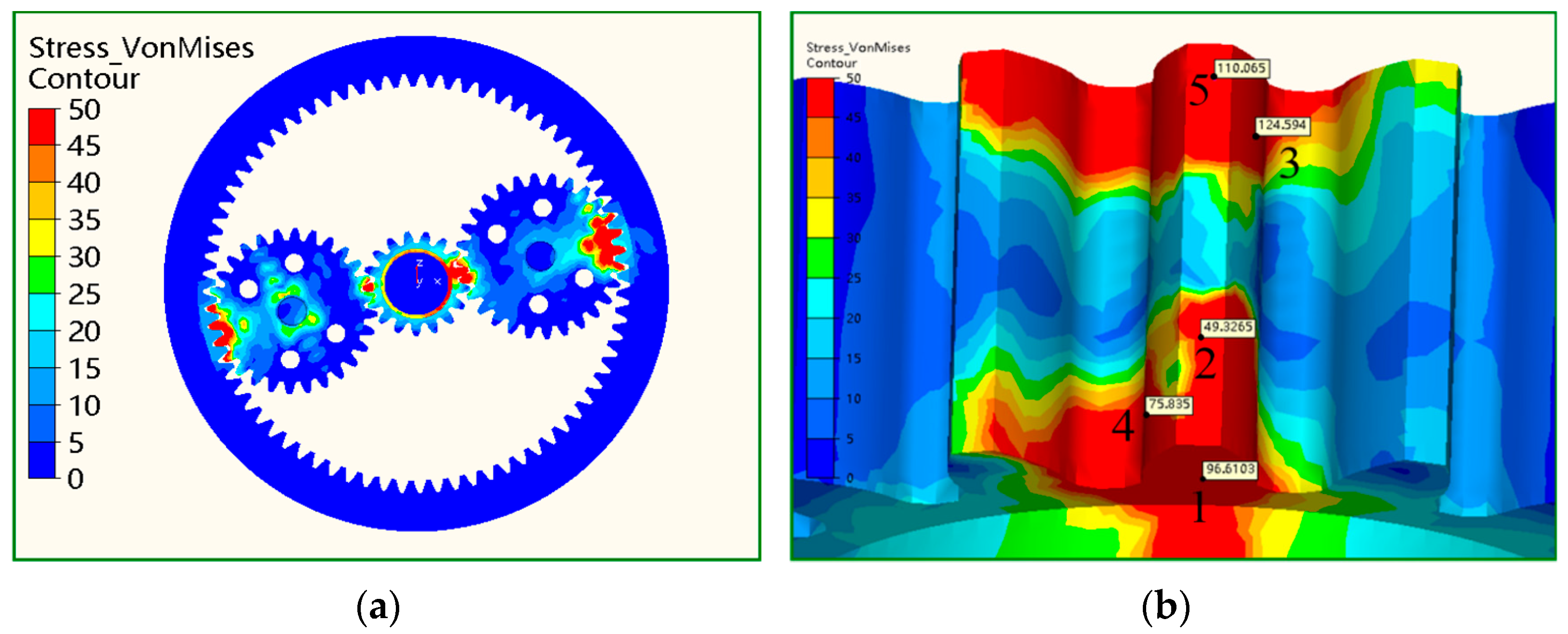
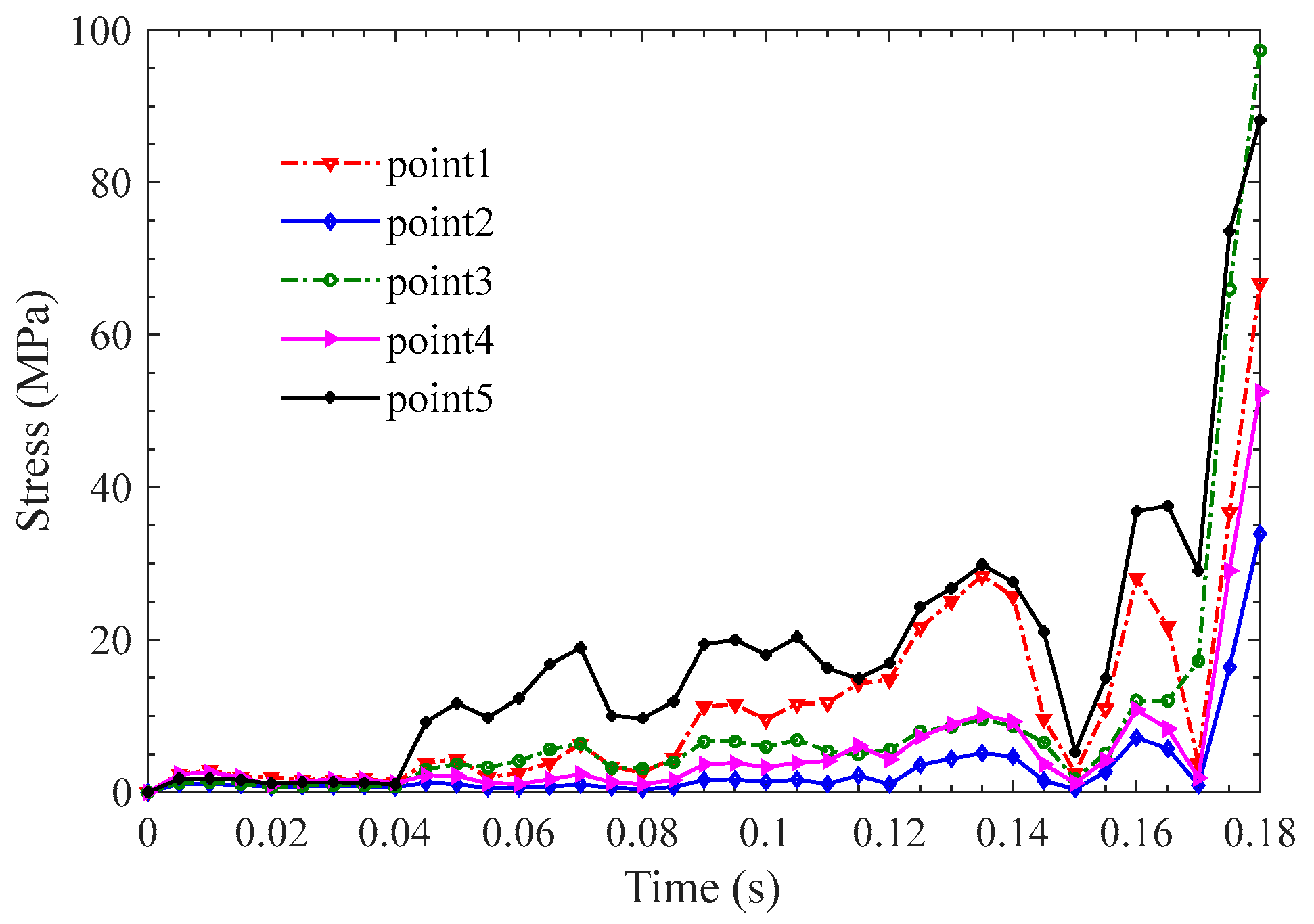
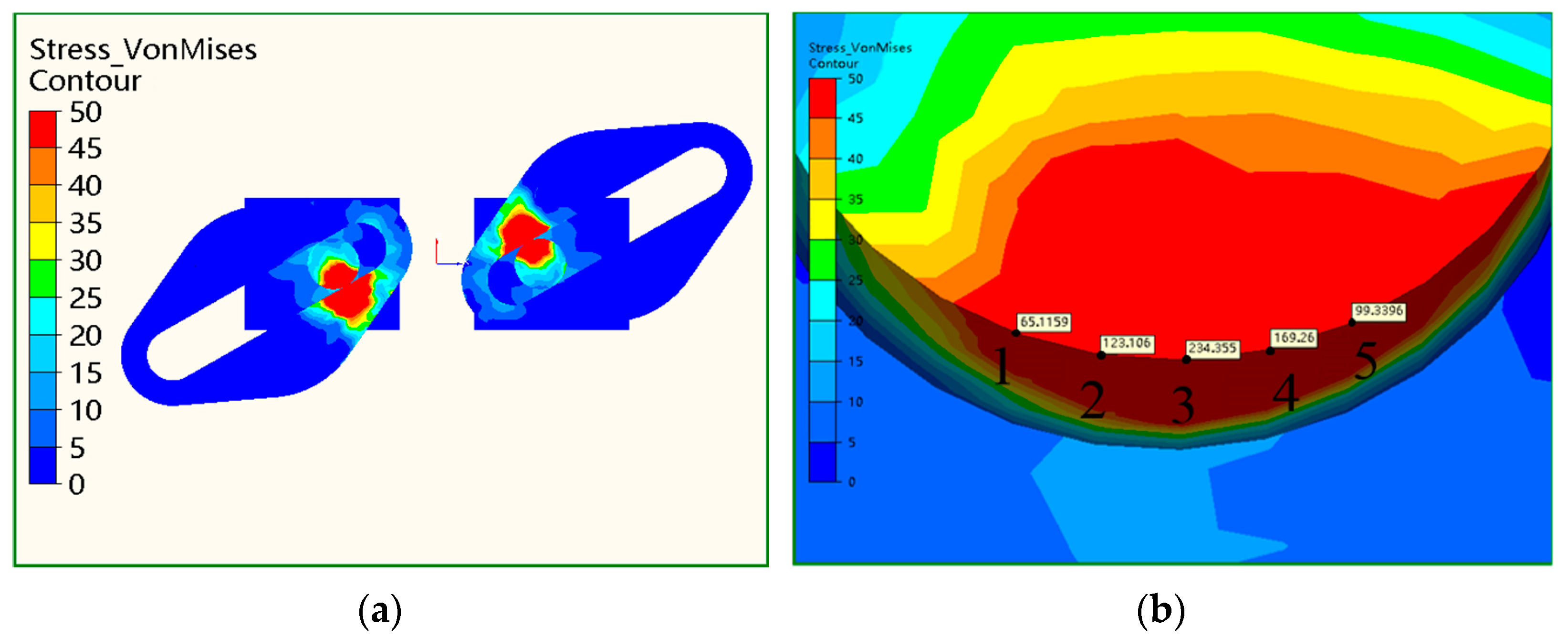




| Gears | Reference Circle Diameter (mm) | Number of Teeth | Module | Face Width (mm) |
|---|---|---|---|---|
| Gear 18 | 33.0 | 22 | 1.5 | 10 |
| Rack 2 | — | 8 | 1.5 | 10 |
| Sun gear 19 | 25.5 | 17 | 1.5 | 10 |
| Planetary gear 13 | 42.0 | 28 | 1.5 | 10 |
| Internal gear 11 | 109.5 | 73 | 1.5 | 10 |
| Serial Number | Parameter | Value |
|---|---|---|
| 1 | Outer diameter (mm) | 20.0 |
| 2 | Inner diameter (mm) | 10.0 |
| 3 | Assembly length (mm) | 45.0 |
| 4 | Stiffness (N/mm) | 3 |
| Stats | Numerical Value |
|---|---|
| Modulus of elasticity | 1.92 N/m2 |
| Poisson’s ratio | 0.27 |
| Mass density | 8000 kg/m3 |
| Tensile strength | 5.8 N/m2 |
| Yield strength | 1.72 N/m2 |
| Thermal expansion coefficient | 1.6 /K |
| Thermal conductivity | 16.3 W/(m·K) |
| Specific heat | 500 J/(kg·K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Gao, P.; Wang, X.; Wang, H.; Liu, X.; Zheng, H. Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation. Actuators 2023, 12, 450. https://doi.org/10.3390/act12120450
Wang C, Gao P, Wang X, Wang H, Liu X, Zheng H. Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation. Actuators. 2023; 12(12):450. https://doi.org/10.3390/act12120450
Chicago/Turabian StyleWang, Caidong, Pengfei Gao, Xinjie Wang, Hong Wang, Xiaoli Liu, and Huadong Zheng. 2023. "Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation" Actuators 12, no. 12: 450. https://doi.org/10.3390/act12120450
APA StyleWang, C., Gao, P., Wang, X., Wang, H., Liu, X., & Zheng, H. (2023). Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation. Actuators, 12(12), 450. https://doi.org/10.3390/act12120450





