Research on High Precision Magnetic Positioning Technology Based on Facility Transport Platform
Abstract
:1. Introduction
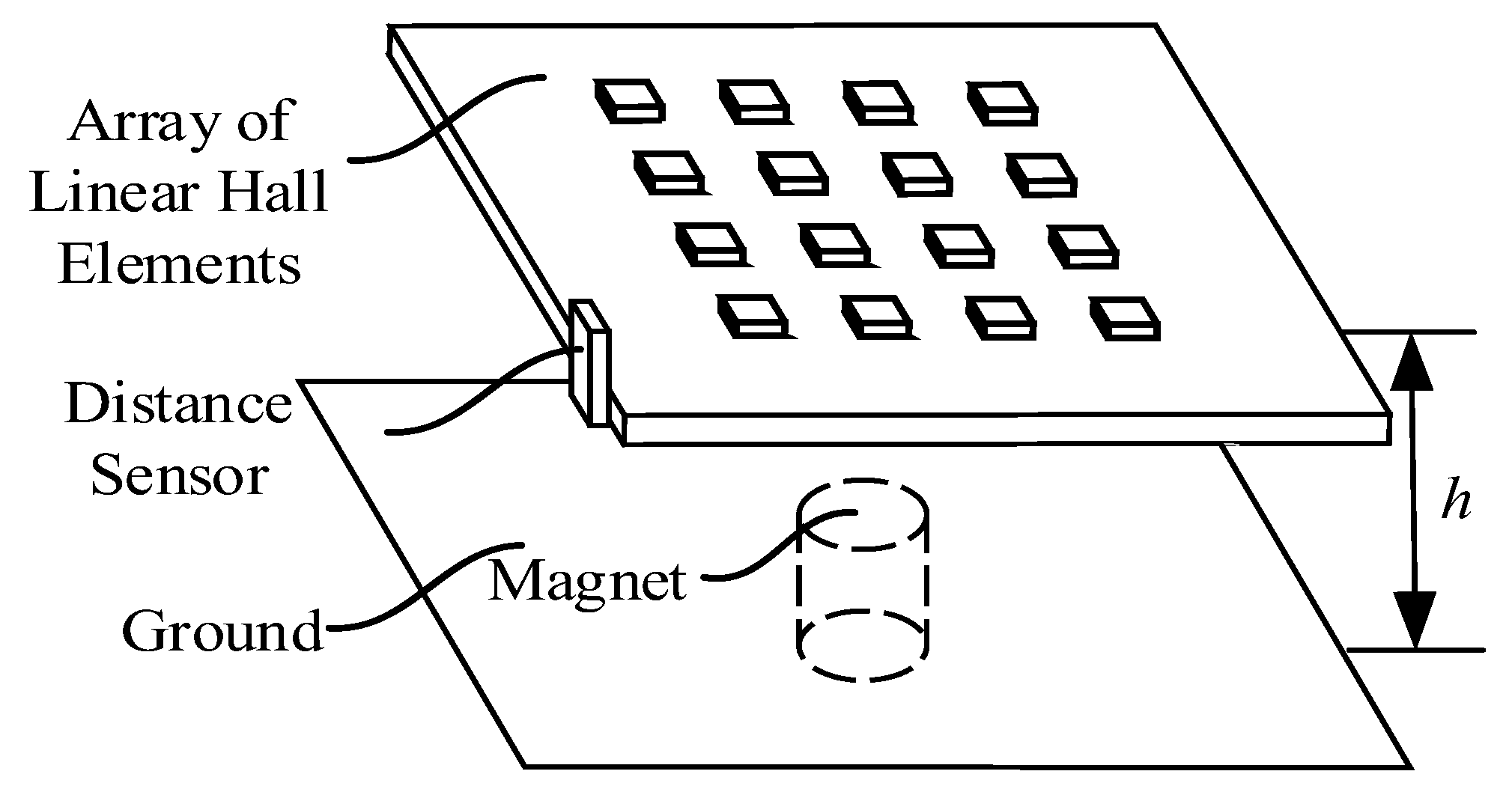
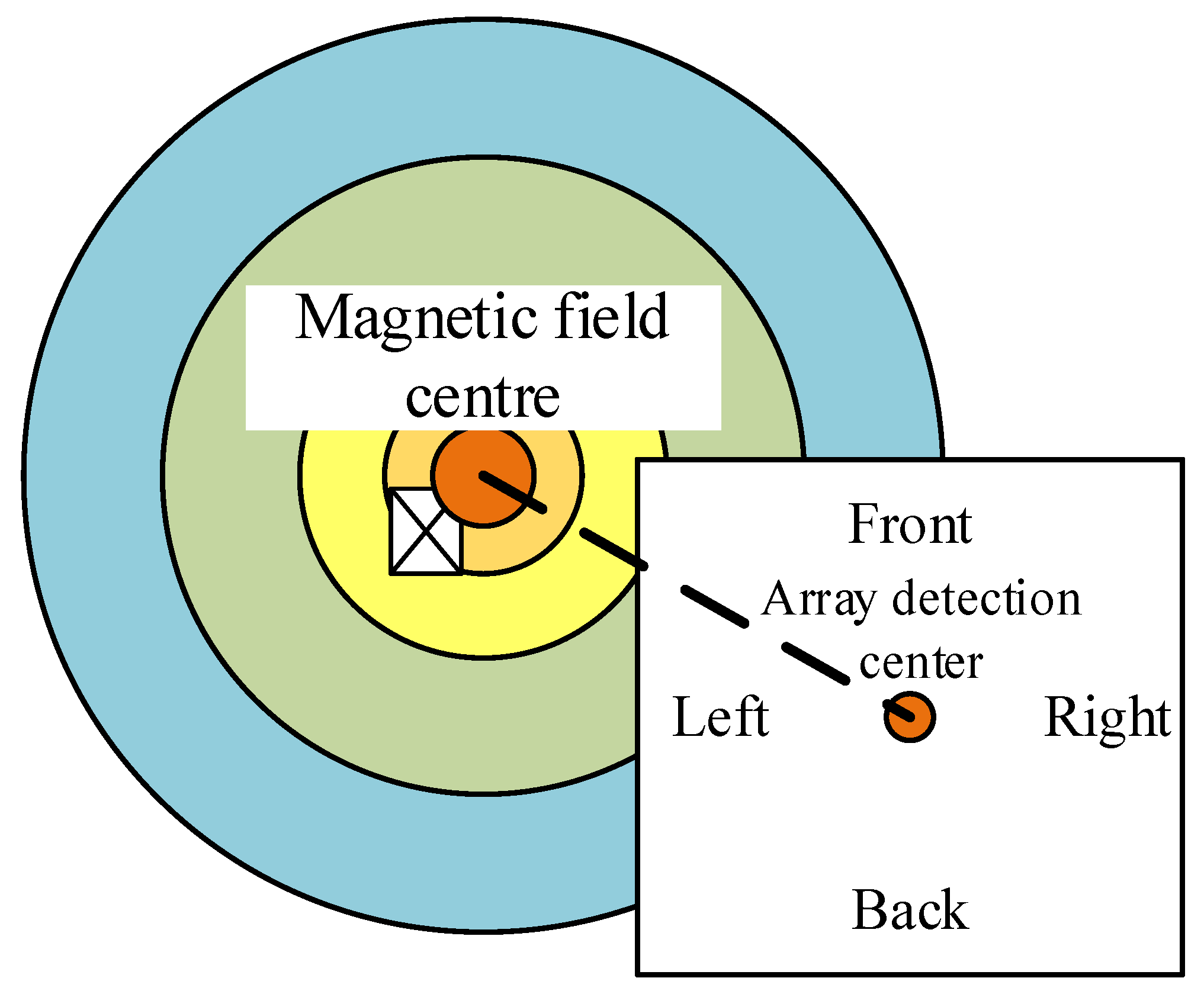
2. Magnetic Positioning Principle and Device Selection
2.1. Magnetic Positioning Principe and Device
2.2. The Selection of Sensor
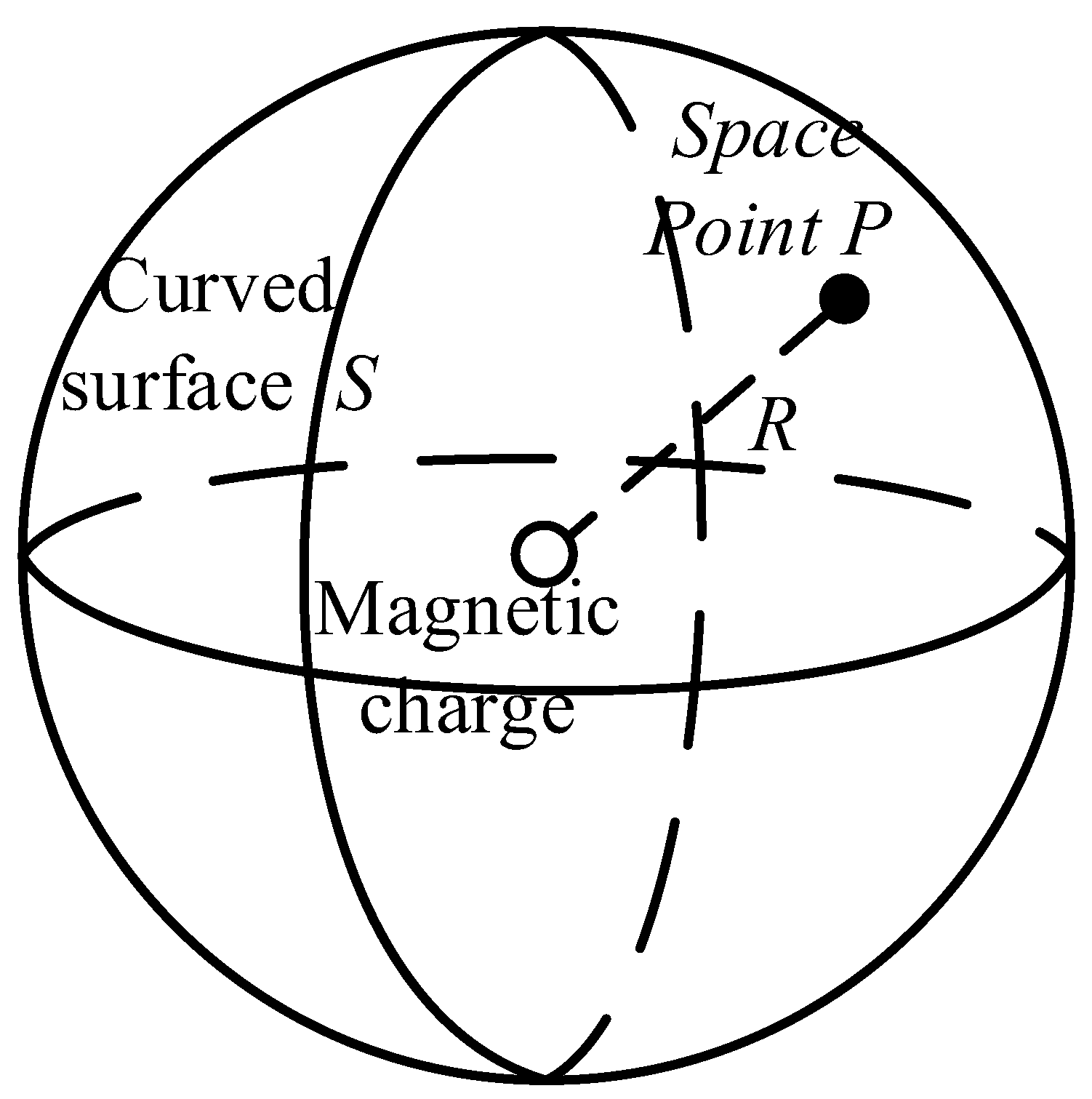
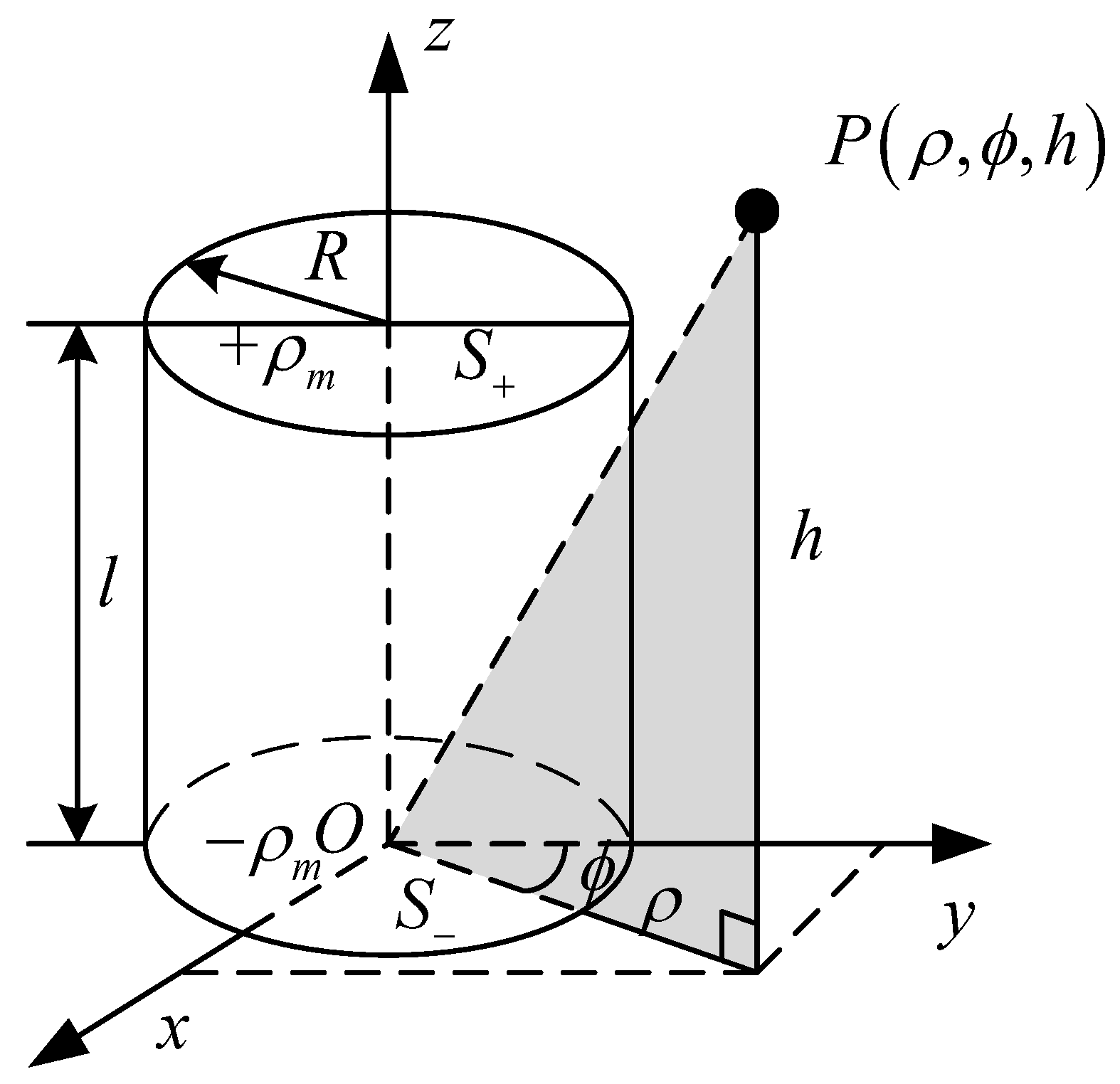
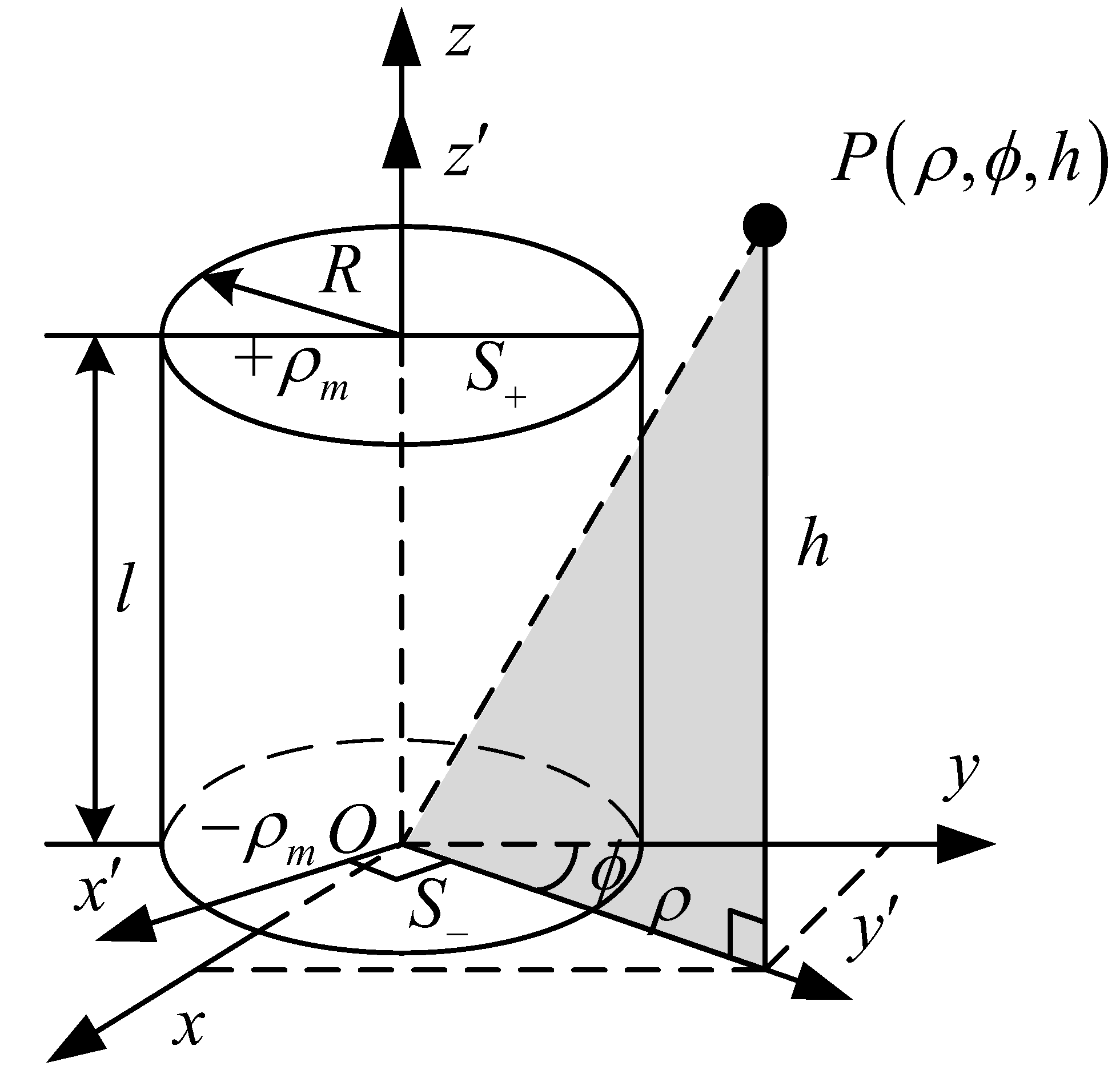
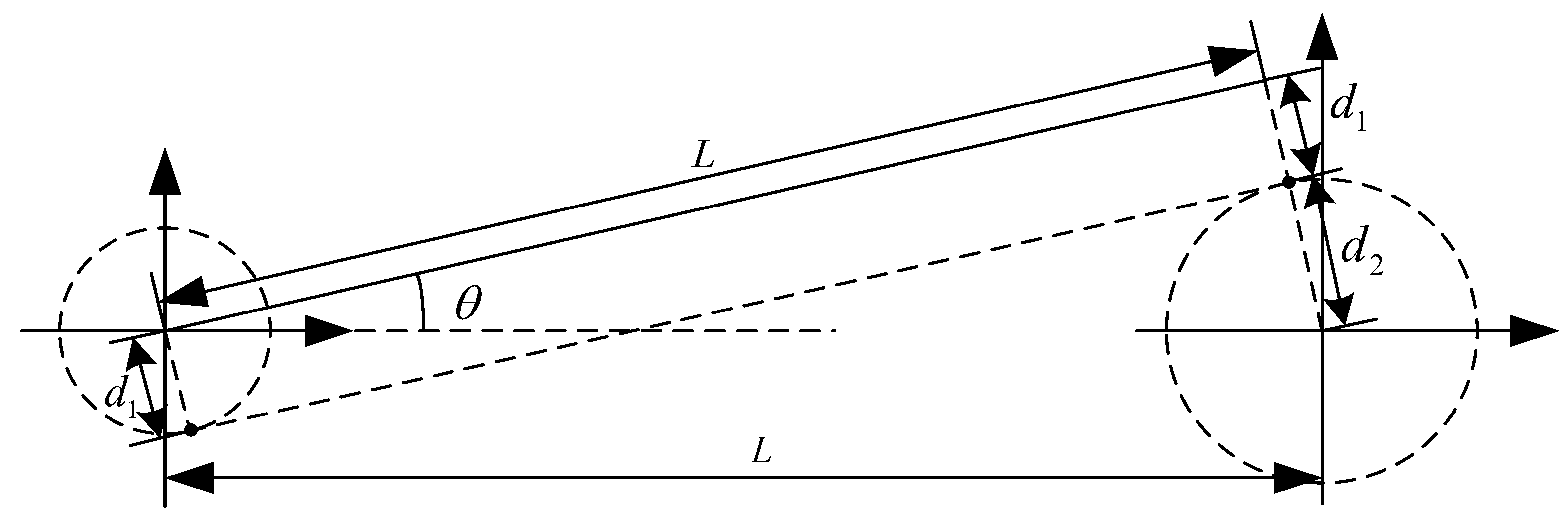
3. Analytical Solution Modeling of the Magnetic Field Strength of Permanent Magnets
4. Simulation of the Magnetic Field Strength of Permanent Magnets and the Magnetic Field Strength Formula Correction
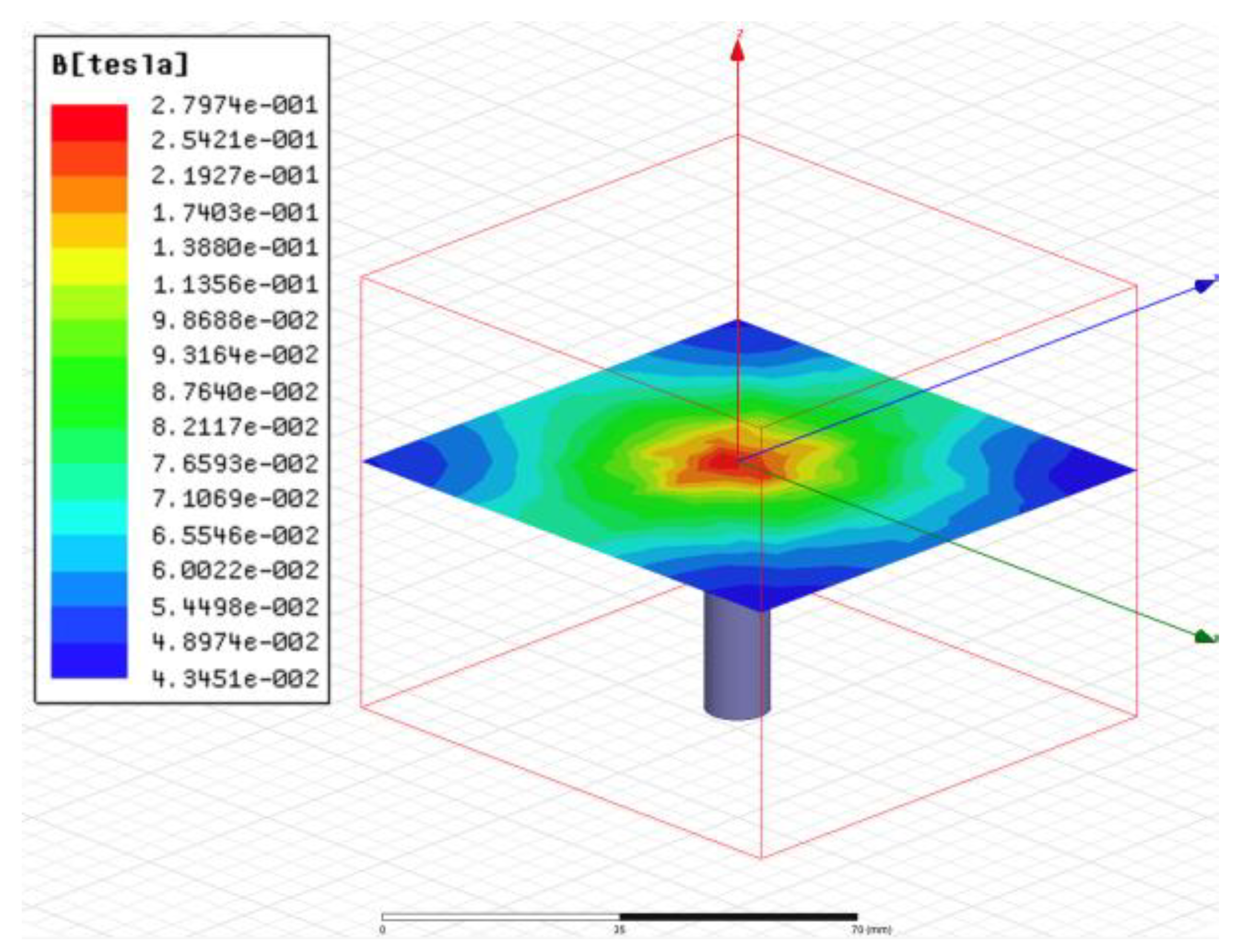
4.1. Simulation of Magnetic Field Strength of Permanent Magnets
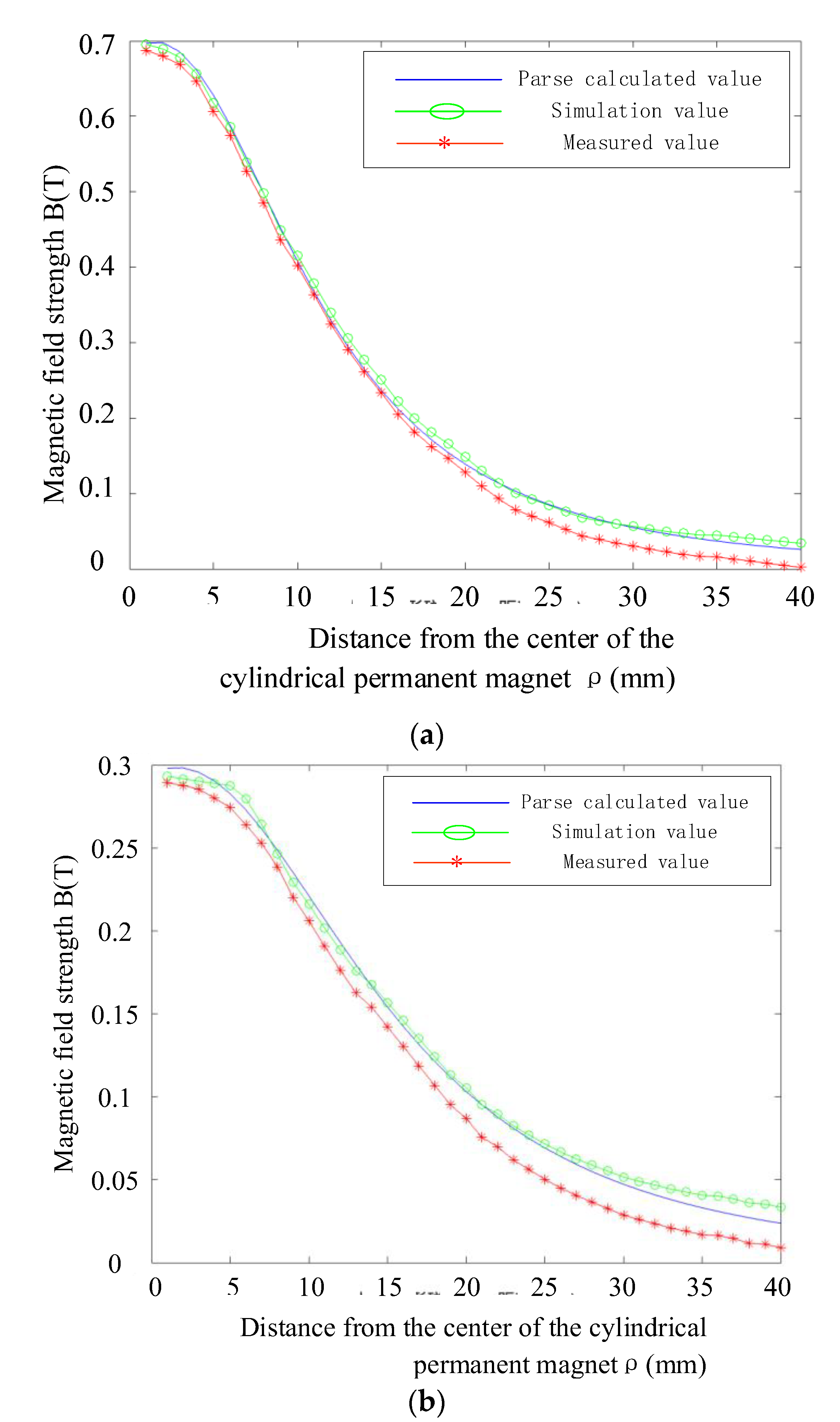
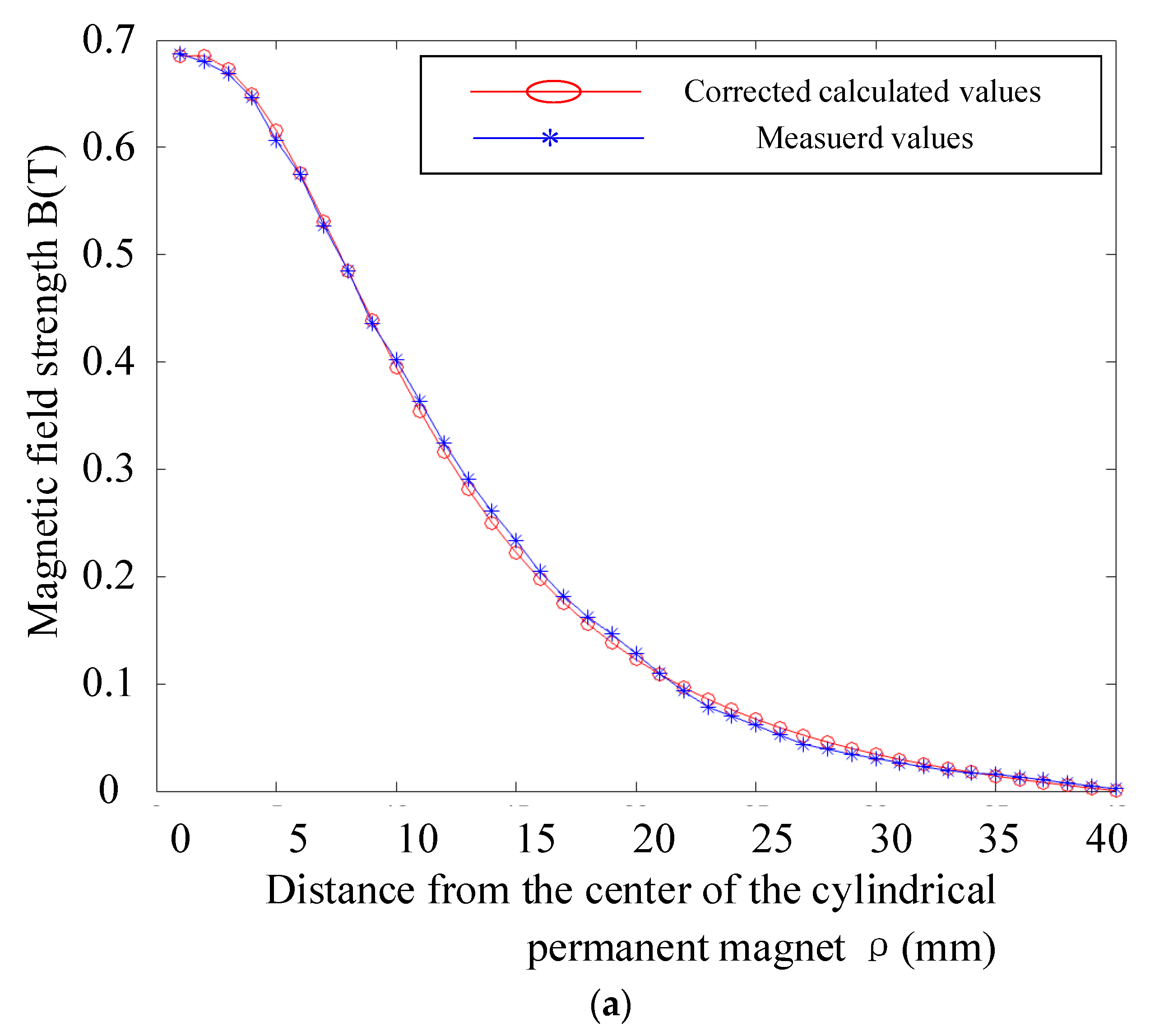
4.2. Magnetic Field Strength Formula Correction
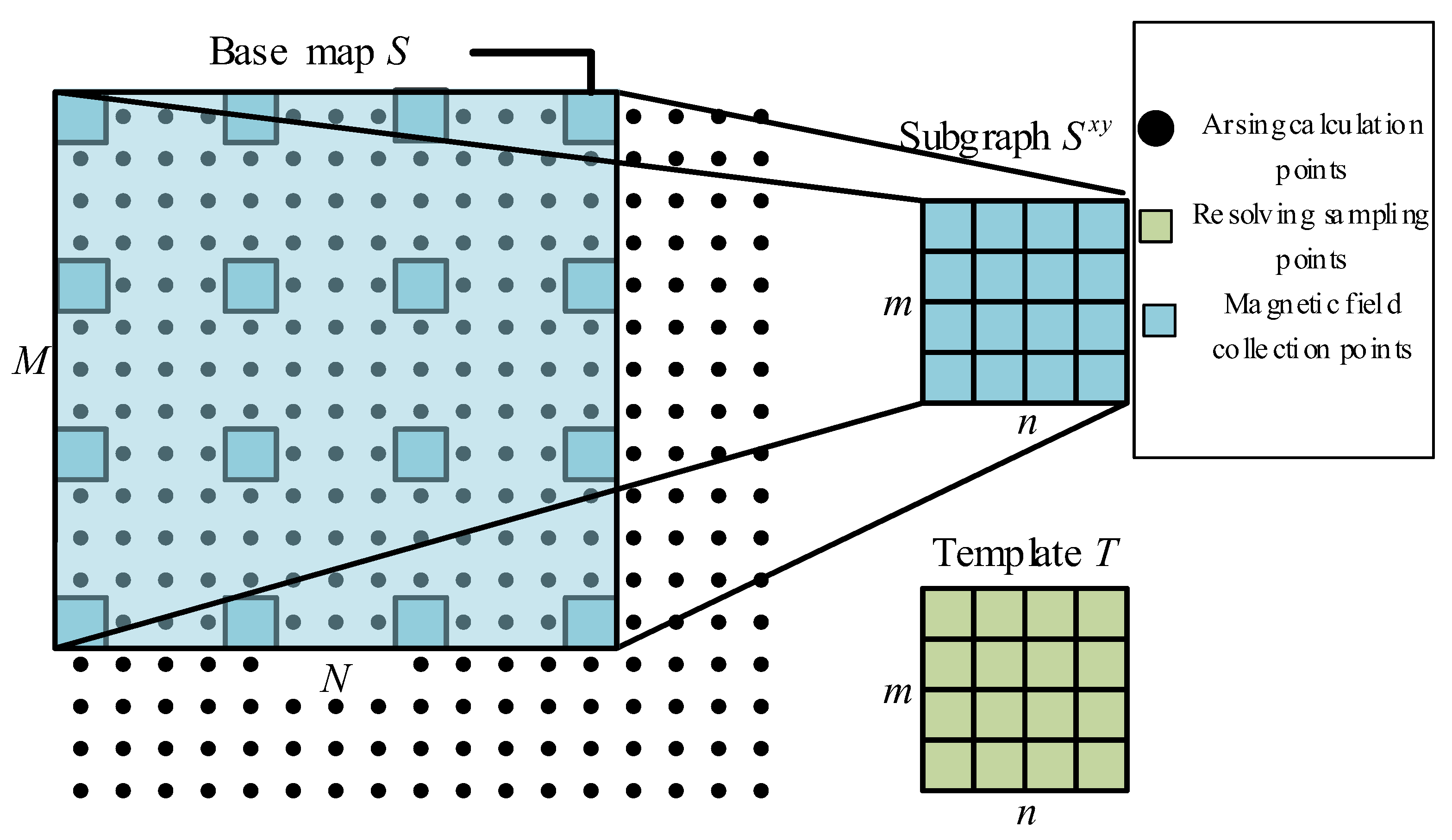
5. Matching Model based on Magnetic Field Analytical Solution
5.1. Magnetic Field Matching Model
5.2. Magnetic Field Matching Model Optimization
5.3. Accurate Positioning Model Based on Magnetic Field Matching
6. Accurate Positioning Result Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pei, F.Q.; Yang, K.W.; Wang, M.; Tong, Y.F. Analysis of application status of intelligent manufacturing in agricultural machinery. J. Intell. Agric. Mech. 2022, 3, 7–19. [Google Scholar]
- Liu, Q.; Zhu, Q.Y.; Feng, S. Review of indoor positioning technology. Computer Era. 2016, 8, 13–15. [Google Scholar] [CrossRef]
- Han, W.; Hao, L.; Cheng, H.L. Overview of indoor location technology. Smart Partn. 2018, 2, 133. [Google Scholar]
- Wang, X.X.; Cong, S. Review of indoor positioning research methods. Softw. Guide 2019, 18, 9–12. [Google Scholar] [CrossRef]
- Yao, W.Y.; Wei, L.X.; Zhang, H. Indoor Positioning design based on infrared beacon. J. Xuchang Univ. 2018, 37, 62–67. [Google Scholar]
- Li, J.K.; Feng, J.; Chen, J.Q. A Design of Ultrasonic Indoor Positioning System Based on Time Synchronized Wireless Network. Modern Radar. 2022, 44, 76–80. [Google Scholar] [CrossRef]
- Bu, X.Y.; Xiang, Y. Positioning Technology of intelligent mobile Robot. Sci. Technol. 2016, 26, 181. [Google Scholar] [CrossRef]
- Yang, H.J.; Hou, Y.Q.; Wang, L.X.; Cao, Y.L.; Jiao, H.T.; Yang, H. A ROS-based Bluetooth location-based courier delivery robot design. Technol. Innov. Appl. 2021, 11, 65–69, 72. [Google Scholar]
- Deng, K.D.; Qiang, S.; Ding, B.Y. Design of Concrete Unmanned Transportation Fleet Model System Based on Arduino and UWB Positioning Technology. Tech. Autom. Appl. 2020, 39, 143–145, 149. [Google Scholar]
- Zhao, S.W.; Ma, S.C.; Wu, S.M. Research on infrared and ultrasonic positioning technology. Value Eng. 2014, 33, 187–188. [Google Scholar] [CrossRef]
- Wei, L.X. Design and Research of Indoor Positioning System Based on Infrared Beacon Technology; North China Electric Power University: Beijing, China, 2018. [Google Scholar]
- Wang, P.; Wang, Y.; Wang, X.; Liu, Y.; Zhang, J. An Intelligent Actuator of an Indoor Logistics System Based on Multi-Sensor Fusion. Actuators 2021, 10, 120. [Google Scholar] [CrossRef]
- Song, Y.; Yu, W.J.; Cheng, C. Research on Indoor Geomagnetic Positioning Based on FCM Clustering and Location Area Switching. Mod. Electron. Technique. 2018, 41, 96–100. [Google Scholar]
- Liu, T.H. Indoor Positioning Using Magnetic Fingerprint Map Captured by Magnetic Sensor Array. Sensors 2021, 21, 5707. [Google Scholar]
- Jiang, S.C.; Liu, J.X. An Indoor Geomagnetic Positioning System Based on Smartphone. GNSS World of China. 2018, 43, 9–16. [Google Scholar]
- Zhang, C.C.; Wang, X.Y.; Dong, Y.N. Simultaneous Localization and Mapping Based on Indoor Magnetic Anomalies. Chin. J. Sci. Instrum. 2015, 36, 181–186. [Google Scholar]
- Sun, Z.S.; Wang, Q.; Luo, H.Y.; Tang, H.Y. Online Magnetic Fingerprints Based Personal Dead Reckoning Calibration Algorithm. Electron. Meas. Technol. 2017, 40, 147–152. [Google Scholar]
- Hou, X.L.; Xiu, B.G.; Zhou, Y.; Wang, D.S.; Lu, Y.J. Continuous Positioning Based on Multi-Sensor Fusion of GPS/INS/Magnetometer. Chin. J. Sens. Actuators 2020, 33, 1320–1326. [Google Scholar]
- Yu, Z.T.; Lv, J.W.; Zhang, B.T. A Method to Localize Magnetic Target Based on A Seabed Array of Magnetometer. J. Wuhan Univ. Technol. 2012, 34, 131–135. [Google Scholar]
- Hou, W.S.; Zheng, X.L.; Peng, C.L.; Wu, X.D. Study of Micro Medical Device Location System Inside Human Body Based on Permanent Magnet Field Detecting. Beijing Biomed. Eng. 2004, 2, 81–83, 87. [Google Scholar]
- Zhang, Y. Research on Magnetic Localization Technologies for Intelligent Vehicle. Shanghai Jiao Tong University, Shanghai. 2008. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CMFD&dbname=CMFD2008&filename=2008052847.nh&uniplatform=NZKPT&v=bjpuOFfCRbxtD5yBZ-e-NMnVOmuHPcCiGlStfitNzBaOgkP2iV22AhRZWsuEhear (accessed on 1 December 2022).
- Wang, Z.; Song, T.; Wang, J.G.; Wang, Z.; Yang, C.Y. Differential Magnetic Localization Algorithm in High Background Magnetic Field and Its Application. Chin. J. Sci. Instrum. 2009, 30, 2384–2389. [Google Scholar]
- Li, G.; Sui, Y.T.; Liu, L.M. Magnetic Dipole Single-point Tensor Positioning Based on the Difference Method. J. Detect. Control 2012, 34, 5. [Google Scholar]
- Yi, J.Z. Magnetic Field Calculation and Magnetic Circuit Design; Chengdu Telecommunication Institute Press: Chengdu, China, 1987. [Google Scholar]
- Parra, L.; Spence, C. On-line convolutive blind source separation of non-stationary signals. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2000, 26, 39–46. [Google Scholar] [CrossRef]
- Hashimoto, M.; Sumi, K.; Sakaue, Y. High-speed template matching algorithm using information of contour points. Syst. Comput. Jpn. 1992, 23, 78–87. [Google Scholar] [CrossRef]





| Magnetic Field Type | Magnetic Positioning Algorithm | Average Error | Sensing Equipment | |
|---|---|---|---|---|
| This article | artificial magnetic field | Improved search algorithm | 0.89 mm | Linear Hall element |
| Song [13]. | geomagnetic field | Fuzzy C-mean clustering algorithm | 1.46 m | Smartphone |
| Liu [14]. | geomagnetic field | recurrent probabilistic neural network | 0.78 m | Three magnetic sensors |
| Li [23]. | artificial magnetic field | magnetic dipole single point tensor positioning | 2.3 mm | Magnetometer |
| Zhang [21] | artificial magnetic field | Vehicle location algorithm | 0.1 m | Magneto resistive sensors |
| Parameter | Value |
|---|---|
| Voltage | 4.50 V~10.5 V |
| Current | 7.0 mA (Max 8.7 mA) |
| Temperature | −40~150 °C |
| Magnetic field detection range | ±760 mT |
| Idle voltage value | 2.50 ± 0.075 V |
| Sensitivity | 3.125 ± 0.094 mV/G |
| Idle shift | ±0.04%/°C |
| Sensitivity shift | −0.00% + 0.06% (<25 °C) |
| Parameter | Value |
|---|---|
| Magnetism | 1.0997 |
| (A/meter) | −890,000 |
| (Tesla) | 1.23 |
| x-axis component | 1.00 |
| y-axis component | 0 |
| z-axis component | 0 |
| Magnetization rate (siemens/m) | 625,000 |
| Material Properties | solid |
| Distance from Upper Face (mm) | Error Rate (%) |
|---|---|
| 10 | 6.74 |
| 11 | 5.23 |
| 12 | 7.21 |
| 13 | 6.19 |
| 14 | 6.73 |
| 15 | 7.55 |
| Average Error (%) | 6.61 |
| Advantage | Disadvantage | The feature in this research | |
|---|---|---|---|
| MAD | ① ethe sum of the absolute value of the difference between the gray value in the corresponding position of the subgraph, and then the average is found. ② The idea is easy to understand. The calculation process is simple, and the matching accuracy is high. | ① Large amount of computation. ② Very sensitive to noise. | The noise of the agricultural machinery operating environment is really heavy. |
| SSDA | Some pixels of the subgraph participate in the calculation, but not all pixels, which greatly improves the algorithm speed. | Part, instead of all, the precision is slightly reduced. | Strict precision is required. |
| Improved search algorithms | An improved model considering positioning error and calculation time is proposed | The use environment is high, especially the embedded flatness of the magnet. The excessive inclination will affect the judgment heavily. | In the cost, accuracy, and process time, the proposed method showed a strong advance |
| System Modules | System Configuration |
|---|---|
| operating system | Windows 10 |
| Development tools | PyCharm 2020 |
| Development language | Python3.6 |
| RAM | 16 G |
| CPU | Intel® Core™ i7-1260P 2.1 GHz |
| Method | Average Error (mm) | Average Time (ms) |
|---|---|---|
| MAD algorithm | 0.365 | 105.81 |
| SSDA algorithm | 2.671 | 16.56 |
| Improved search algorithms | 0.89 | 2.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, S.; Tong, Y.; Pei, F.; Song, Z.; Shao, Y. Research on High Precision Magnetic Positioning Technology Based on Facility Transport Platform. Actuators 2023, 12, 13. https://doi.org/10.3390/act12010013
Mei S, Tong Y, Pei F, Song Z, Shao Y. Research on High Precision Magnetic Positioning Technology Based on Facility Transport Platform. Actuators. 2023; 12(1):13. https://doi.org/10.3390/act12010013
Chicago/Turabian StyleMei, Song, Yifei Tong, Fengque Pei, Zhiyu Song, and Yifan Shao. 2023. "Research on High Precision Magnetic Positioning Technology Based on Facility Transport Platform" Actuators 12, no. 1: 13. https://doi.org/10.3390/act12010013
APA StyleMei, S., Tong, Y., Pei, F., Song, Z., & Shao, Y. (2023). Research on High Precision Magnetic Positioning Technology Based on Facility Transport Platform. Actuators, 12(1), 13. https://doi.org/10.3390/act12010013





