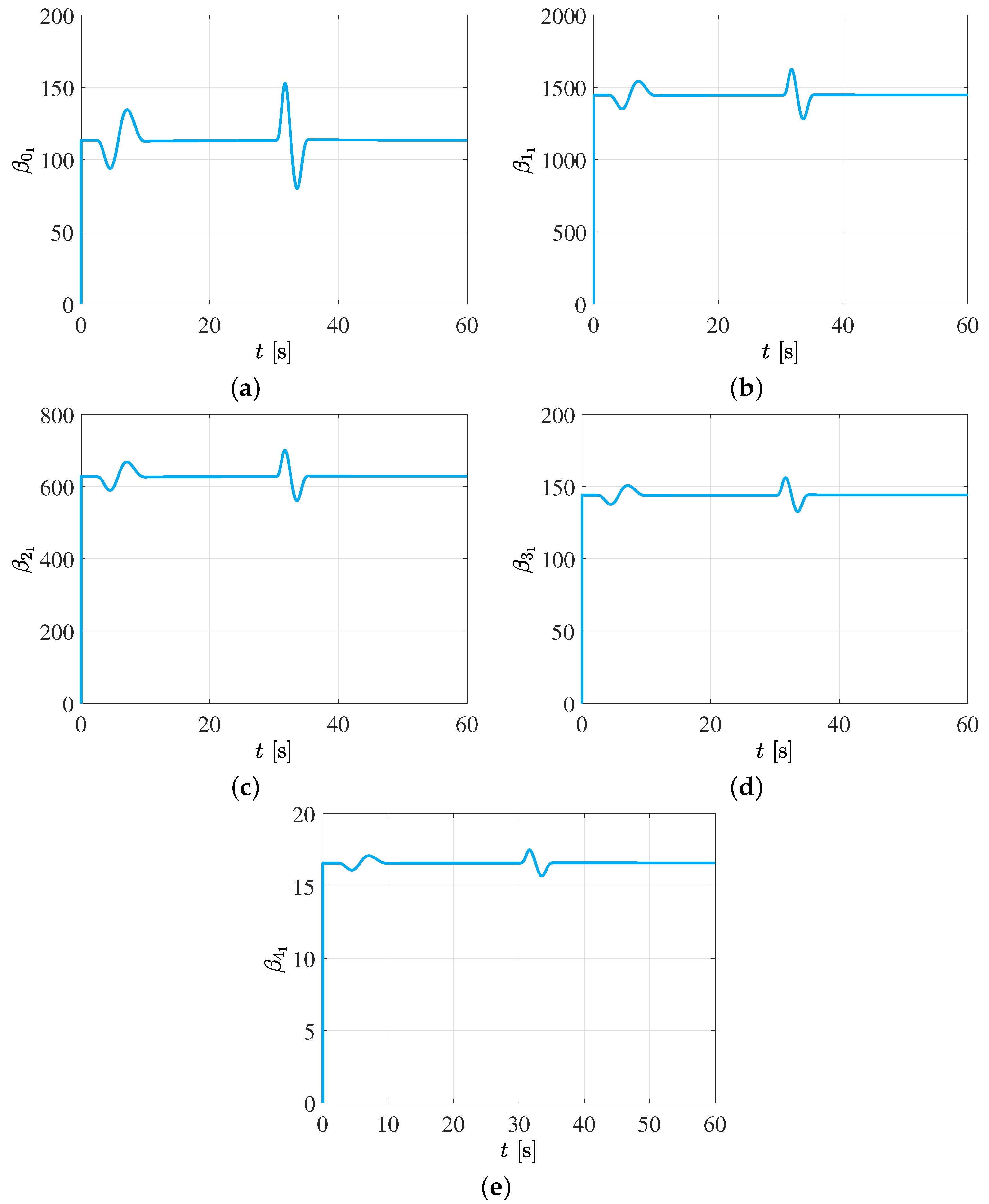Neural Adaptive Robust Motion-Tracking Control for Robotic Manipulator Systems

Abstract

This paper deals with the motion trajectory tracking control problem based on output feedback and artificial neural networks for anthropomorphic manipulator robots under disturbed operating scenarios. This class of manipulator robots constitutes nonlinear dynamic systems subjected to disturbance torques induced mainly by work payload. Parametric uncertainty and possible dynamic modeling errors stand for other kind of disturbances that can deteriorate the efficiency and robustness of the tracking of controlled nonlinear robotic system trajectories. In fact, the presence of unknown dynamic disturbances is unavoidable in industrial robotic engineering systems. Therefore, for high-precision applications, such as laser cutting, marking, or welding, effective control schemes should be designed to guarantee adequate motion profile tracking planned on this class of disturbed nonlinear robotic system. In this context, a new adaptive robust motion trajectory tracking control scheme based on output feedback and artificial neural networks of anthropomorphic manipulator robots is presented. Three-layer B-spline artificial neural networks and time-series modeling are properly exploited in the design of novel adaptive robust motion tracking controllers for robotic applications of laser manufacturing. In this way, dependency on detailed nonlinear mathematical modeling of robotic systems is considerably reduced, and real-time estimation of uncertain dynamic disturbances is not required. Furthermore, several cases studies to demonstrate the motion planning tracking control robustness for a class of MIMO nonlinear robotic systems are described. blue Insights for the extension of the introduced output-feedback adaptive neural control design approach for other architecture of nonlinear robotic systems are depicted.

1. Introduction

The study and application of intelligent control techniques, such as fuzzy logic and neural networks, have gained widespread recognition in recent years. The basis of these techniques consists of learning in a prescribed manner the input–output behavior of a system to subsequently be controlled [1]. The importance of these types of techniques is found in nonlinear systems, variants in time, and those that are subjected to different types of disturbances [2]. Manipulator robots have complex nonlinear dynamics that can make accurate and robust control difficult. In today’s manufacturing environments, velocity and accuracy requirements increase when compared to earlier generations of robots. However, the efficiency of fixed-gain PID controllers often is limited for providing adequate performance in real-time operations of robot motion [3].

Since there are no adaptive or learning capabilities, control accuracy is significantly affected when a variation due to unknown frictions and disturbing torques is presented during motion control in laser manufacturing applications, such as cutting, welding, marking, and additive 3D printing [4]. The main purpose of controlling a manipulator robot is to accomplish a specific task, such as payload transport [5], and motion profile tracking for material processing [6], among others. To perform the required tasks, the manipulator is commanded for reaching the desired position, velocity, acceleration, or force at a specific time [7]. The nonlinear nature of manipulator robots makes it difficult to obtain an adequate control law to perform different programmed tasks. There are computational methods that improve the control laws efficiency, such as the artificial neural networks [8] that are used to online update the control parameters value to improve the robotic system’s closed-loop response. The exhibited adaptive behavior learns from the nonlinear nature of the robot intelligently. So using neural networks for the tuning of the parameters of a controller applied to a nonlinear and strongly coupled system represents a great advantage. The recent renewed interest in neural networks can be attributed to different factors, one of them is that different learning techniques have been developed for sophisticated artificial neural network architectures, which are capable of eliminating the limitations of the past associated with simple neural networks [9]. Neural networks are parallel computer models that mimic a human’s learning process. The networks process information by adapting their connections and nodes, based on the information they are given [10]. One important feature is the intrinsic parallel architecture that allows fast computation of the solution. This is achieved when the networks are implemented on digital computers or in specialized hardware [11].

Artificial neural networks (ANN) have been used for the control of manipulator robots for different applications in recent years. In [12], a trajectory planning methodology of a manipulator robot is proposed through the design of an adaptive robust controller that uses a neural network activated with radial basis functions; this is done to solve nonlinearity and uncertainty problems and improve the performance during trajectory tracking. In [13], a fixed-time control algorithm for the trajectory tracking of manipulator robots with uncertainty and input saturation is designed, which combines the non-singular terminal sliding mode control with the reinforcement learning method. To compensate for the saturation of the actuators due to the effect of joint torque overflow, a nonlinear anti-windup compensator is designed. Authors in [14] introduce a multi-layer neural network with iterative learning for controller design to compensate for the dynamics of an articulated industrial manipulator robot for trajectory tracking tasks. The iterative learning control commands the robot motion, which corresponds to a set of desired joint trajectories. Additionally, the torques of the input/output trajectories are used for training the inner control loop through inverse dynamics. In this scheme, the trajectory is used as the input desired joint of the robot, and the output is related to the commanded robot motion. In [15], a modified artificial neural network algorithm is suggested to be applied as an adaptive adjustment algorithm. A mathematical modulation is introduced to promote the scanning form, and no initial parameters are set. The suggested algorithm is tested to select the gains, and an appropriate configuration is selected. This algorithm is applied for improving a PID-like joint motion controller for a manipulator robot. In [16], the output error constraints and input saturation of robot manipulators are considered and presented with a trajectory tracking controller to attend to these requirements simultaneously through an artificial neural network structure with radial basis functions that can approximate the pooled uncertainties. In [17], a deep convolutional neural network is designed to implement a fractional order sliding mode control strategy for trajectory tracking control in manipulator robots. The neural network compensates for system uncertainty without the need to know the upper bounds, thus the controller switching gain is greatly reduced. The main advantage of the controller used lies in the elimination of chattering, so continuous control signals can be obtained and applied in practical applications. In [18], a control scheme is proposed to handle the unknown dynamics and the external disturbances in a manipulator robot by combining a self-tuning PID structure with an artificial neural network using radial basis activation functions to handle the different uncertainties. In [19], to track the trajectory of a robot and supply constant force during contact working conditions, a PID fuzzy neural network controller is developed. For manufacturing applications, changing the contact force during machining operations will affect the quality, so it is crucial to maintain them constantly throughout the process. For the parameters of the PID controller to be adjusted quickly and effectively, a fuzzy algorithm is proposed that includes neural networks in such a way that the controller has two functions: path following and bounded shifting online whilst maintaining the contact force constant. In [20], an adaptive neural control scheme for manipulator robots that includes actuator dynamics under model uncertainty is proposed based on prescribed performance without measuring input current, acceleration, or velocity. A neural adaptive second-order PID controller is combined with an acceleration velocity observer. The proposed method demonstrates that semi-global bounds are found for tracking and state observation errors, and they eventually converge in a small circle about the origin.

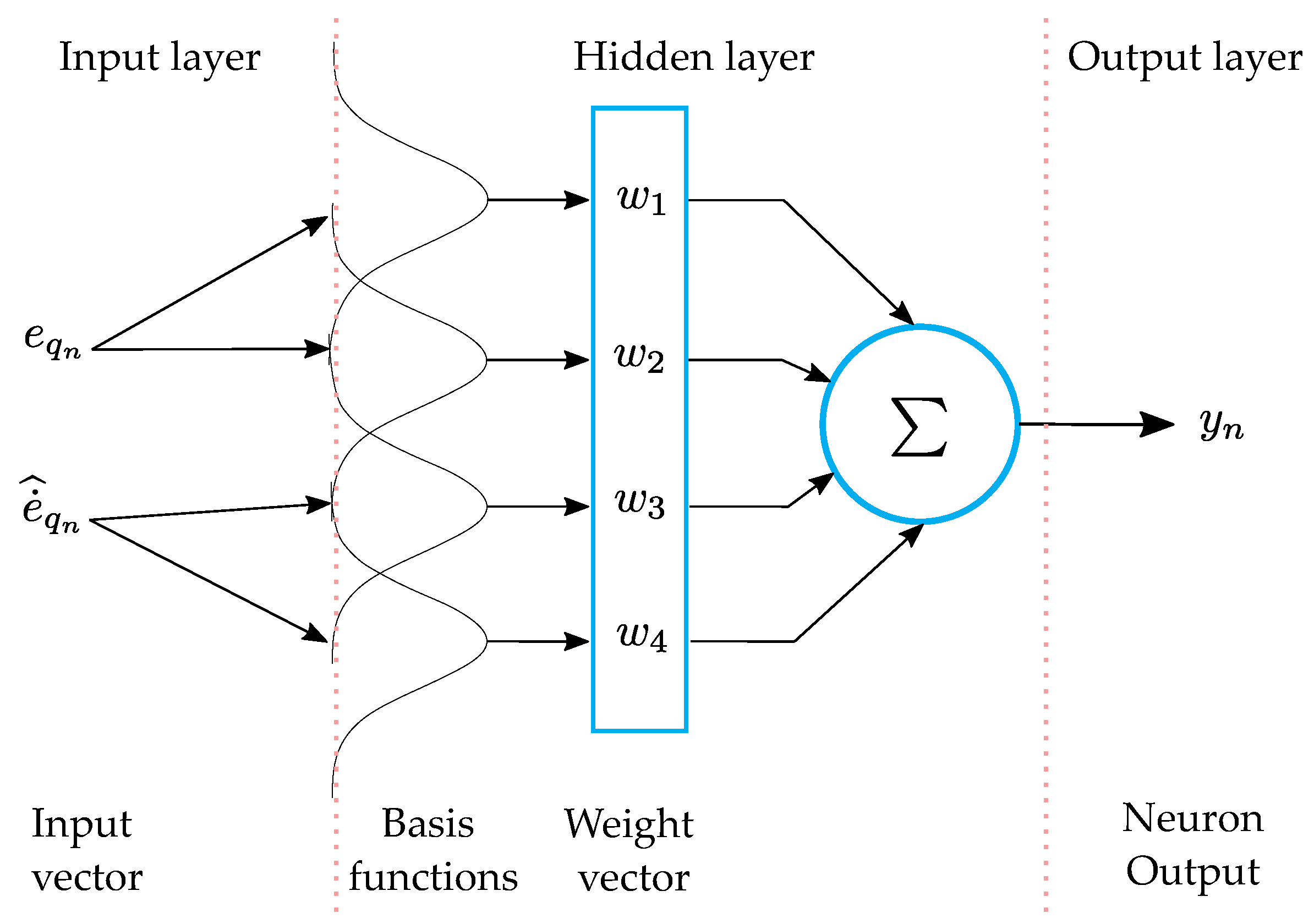
With the B-spline artificial neural networks (Bs-ANN), adaptive control and modeling of systems are possible both online and with nonlinearities taken into account [21]. In the literature, the estimation of harmonics and DC offset component of multi-frequency oscillating electric signals [22], control of electric power systems [23], different types of electric motors, such as DC shunt [24], induction [25] and permanent magnet synchronous [9] as well as unmanned aerial vehicles [26] are some examples of the successful implementation of B-spline neural networks. Nevertheless, there is no evidence of the previous implementation in anthropomorphic manipulator robots. The main advantage of the B-spline neural network is that it can limit the input to a set of values defined in the base function. This reduces computational effort and time because there are only a limited number of basis functions involved in the output; not all weights need to be calculated every time iterations are performed [26]. The proposal allows calculating and updating the values of the parameters of the proposed controller through the neural network for each operating condition of the robot. A proper design requires prior information: the maximum and minimum values for the input signal and defining the shape of the basis functions. This information allows for limiting the input space of the B-spline neural networks, which improves their convergence and stability in adaptation. Additionally, this information is used to determine the optimal weights for the neural network [27]. The B-spline neural networks used in this work are created by third-order uni-variable basis functions considering that the input signal is bounded.

The main contribution of this work is a new neural adaptive robust motion trajectory tracking control technique based on output feedback for a very important class of nonlinear robotic manipulator systems used in applications of laser manufacturing. In this context, advantages and differences with respect to other relevant contributions reported in the literature are as follows. Position measurements are only required. Time derivatives of measured output signals are not requested. Accurate real-time estimation of different types of disturbances is unnecessary. B-spline artificial neural networks are used correctly to prevent high-gain control actions to suppress unknown time-varying disturbances. The number of control parameters that need to be adaptively adjusted is lessened. Dependency on detailed nonlinear mathematical modeling of the manipulator robot system is reduced. Robustness against external disturbances, such as external vibrating torques, is also obtained. Moreover, the introduced output feedback adaptive neural control design approach can be extended for other architectures of complex nonlinear robotic systems.

A summary of the contents of the manuscript is as follows. The robotic system model is described in Section 2. The robot motion control approach is presented in Section 3. In Section 4, the artificial neural networks-based robot motion control is described. Subsequently, some numeric simulation experiments are presented in Section 5 to highlight the performance of the introduced methodology. Finally, some conclusions and remarks are mentioned in the conclusions section.

2. 3-DOF Robot Mathematical Modeling

2.1. System Description

The geometry of interest in this work is anthropomorphic as shown in Figure 1. The robotic system configuration is composed of three rotational joints. This configuration represents the most dexterous structure, which can be adapted to almost any type of task.

Figure 2 depicts projections of the anthropomorphic manipulator robot on XY and XZ planes for the derivation of a nonlinear dynamic model. Generalized coordinates of the configuration space are denoted by $q_i$, $i=1,\dots ,3$. Here, $q_1$ is the rotation angle of link 1 about the Z axis. $q_2$ and $q_3$ are the rotation angles of links 2 and 3 about the Y axis. $d_1$ is the distance between point O of the fixed inertial coordinate reference frame $XYZ$ and the rotation axis of $q_2$. $l_2$ corresponds to the distance between the rotation axis of $q_2$ and the rotation axis of $q_3$. $l_{c_2}$ is the distance from the rotation axis of $q_2$ to the center of mass of link 2. $l_3$ is the distance between the rotation axis of $q_3$ and the center of the end effector. $l_{c_3}$ is the distance from the rotation axis of $q_3$ to the center of mass of link 3. $m_1$ is the mass of link 1. $m_2$ corresponds to the mass of link 2. $m_3$ is the mass of link 3, which also includes the mass of the end effector.

2.2. Kinematic Modeling

The direct kinematic model of a 3-DOF anthropomorphic manipulator robot [28,29] is expressed as

$$\begin{array}{cc}\hfill x& =cos\left(q_{{}_1}\right)[l_{{}_2}cos\left(q_{{}_2}\right)+l_{{}_3}cos(q_{{}_2}+q_{{}_3})]\hfill \\ \hfill y& =sin\left(q_{{}_1}\right)[l_{{}_2}cos\left(q_{{}_2}\right)+l_{{}_3}cos(q_{{}_2}+q_{{}_3})]\hfill \\ \hfill z& =d_{{}_1}+l_{{}_2}sin\left(q_{{}_2}\right)+l_{{}_3}sin(q_{{}_2}+q_{{}_3})\hfill \end{array}$$

(1)

The inverse kinematic model of the 3-DOF anthropomorphic manipulator robot [28,29] is then described as

$$\begin{array}{cc}\hfill q_{{}_1}& ={tan}^{-1}\left({\displaystyle \frac{y}{x}}\right)\hfill \\ \hfill q_{{}_2}& ={tan}^{-1}\left({\displaystyle \frac{z-d_{{}_1}}{\sqrt{x^2+y^2}}}\right)-{tan}^{-1}\left[{\displaystyle \frac{l_{{}_3}\sqrt{1-{\left({\displaystyle \frac{x^2+y^2+{(z-d_{{}_1})}^2-l_{{}_2}^2-l_{{}_3}^2}{2l_{{}_2}{l}_{{}_3}}}\right)}^2}}{l_{{}_2}+l_{{}_3}\left({\displaystyle \frac{x^2+y^2+{(z-d_{{}_1})}^2-l_{{}_2}^2-l_{{}_3}^2}{2l_{{}_2}{l}_{{}_3}}}\right)}}\right]\hfill \\ \hfill q_{{}_3}& ={tan}^{-1}\left[{\displaystyle \frac{\pm \sqrt{1-{\left({\displaystyle \frac{x^2+y^2+{(z-d_{{}_1})}^2-l_{{}_2}^2-l_{{}_3}^2}{2l_{{}_2}{l}_{{}_3}}}\right)}^2}}{\left({\displaystyle \frac{x^2+y^2+{(z-d_{{}_1})}^2-l_{{}_2}^2-l_{{}_3}^2}{2l_{{}_2}{l}_{{}_3}}}\right)}}\right]\hfill \end{array}$$

(2)

2.3. Dynamic Modeling

The analysis of a manipulator robot requires the use of differential equations to understand the relationship between the elements that compose it. By modeling the dynamic behavior of a manipulator robot, all physical phenomena found in its mechanical structure are explained, including inertial effects, centripetal and Coriolis forces, gravitational torque, and friction, which are physical phenomena resulting from the robot’s dynamic nature [30]. The development of the dynamic model of an anthropomorphic manipulator robot through the Euler–Lagrange methodology was widely studied in [28,29,30].

The nonlinear behavior of a manipulator robot can be thus modeled by the Euler–Lagrange equations

$$\begin{array}{cc}\hfill \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}& =Q_{i}i=1,\dots ,n\hfill \end{array}$$

(3)

with

$$\begin{array}{c}\hfill L=K-V\end{array}$$

(4)

where L is the Lagrangian, K and V are the kinetic and potential energy. n denotes the number of degrees of freedom, $q=(q_1,q_2,\dots ,q_n)$ represents the generalized coordinates of the robotic system, and $Q_i$ stands for components of the generalized force.

The kinetic energy of the robotic system depicted in Figure 1 and Figure 2 is given by

$$\begin{array}{cc}\hfill K& =K_1+K_2+K_3\hfill \end{array}$$

(5)

with

$$\begin{array}{cc}\hfill K_1& =\frac{1}{2}{I}_{z_1}{\dot{q}}_1^2\hfill \\ \hfill K_2& =\frac{1}{2}{m}_2{l}_{c_2}^2[(1-sin{\left(q_2\right)}^2){\dot{q}}_1^2+{\dot{q}}_2^2]+\frac{1}{2}{I}_{z_2}{\dot{q}}_1^2+\frac{1}{2}{I}_{y_2}{\dot{q}}_2^2\hfill \\ \hfill K_3& =\frac{1}{2}{m}_3[(l_2^2+l_2^{2}cos\left(2q_2\right)+2l_2{l}_{c_3}cos(2q_2+q_3)+2l_2{l}_{c_3}cos\left(q_3\right)+l_{c_3}^{2}cos(2q_2+2q_3)\hfill \\ \hfill & +l_{c_3}^2)\frac{{\dot{q}}_1^2}{2}+(l_2^2+2l_2{l}_{c_3}cos\left(q_3\right)+l_{c_3}^2){\dot{q}}_2^2+(2l_2{l}_{c_3}cos\left(q_3\right)+2l_{c_3}^2){\dot{q}}_2{\dot{q}}_3+l_{c_3}^2{\dot{q}}_3^2]+\frac{1}{2}{I}_{z_3}{\dot{q}}_1^2\hfill \\ \hfill & +\frac{1}{2}{I}_{y_3}{({\dot{q}}_2+{\dot{q}}_3)}^2\hfill \end{array}$$

The potential energy is obtained as

$$\begin{array}{cc}\hfill V& =V_1+V_2+V_3\hfill \end{array}$$

(6)

with

$$\begin{array}{cc}\hfill V_1& =m_{1}g{d}_1\hfill \\ \hfill V_2& =m_{2}g[d_1+l_{c_2}sin\left(q_2\right)]\hfill \\ \hfill V_3& =m_{3}g[d_1+l_{2}sin\left(q_2\right)+l_{c_3}sin(q_2+q_3)]\hfill \end{array}$$

From Equations (3) and (4), nonlinear dynamics of the robotic system can be then described by the vector differentialequation

$$\begin{array}{cc}\hfill \mathbf{D}\left(\mathbf{q}\right)\ddot{\mathbf{q}}+\mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)\dot{\mathbf{q}}+\mathbf{G}\left(\mathbf{q}\right)& =\mathit{\tau }-{\mathit{\tau }}_d\hfill \end{array}$$

(7)

where $\mathbf{D}\left(\mathbf{q}\right)\in {\mathbb{R}}^{n\times n}$ stands for the inertia matrix, $\mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)\in {\mathbb{R}}^{n\times n}$ represents the Coriolis and centripetal matrix and $\mathbf{G}\left(\mathbf{q}\right)\in {\mathbb{R}}^n$ denotes the torque vector due to gravity [28]. Moreover, $\mathit{\tau }$ and ${\mathit{\tau }}_d$$\in {\mathbb{R}}^n$ are the joint driving torque and the external load torque, respectively.

From Equation (7) and without loss of generality, the dynamic model for a 3-DOF anthropomorphic manipulator robot is given by

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array}\right]\left[\begin{array}{c}{\ddot{q}}_1\\ {\ddot{q}}_2\\ {\ddot{q}}_3\end{array}\right]+\left[\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ c_{21}& c_{22}& c_{23}\\ c_{31}& c_{32}& c_{33}\end{array}\right]\left[\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\\ {\dot{q}}_3\end{array}\right]+\left[\begin{array}{c}{g}_{11}\\ g_{21}\\ g_{31}\end{array}\right]g=\left[\begin{array}{c}{\tau }_{{}_1}\\ {\tau }_{{}_2}\\ {\tau }_{{}_3}\end{array}\right]-\left[\begin{array}{c}{\tau }_{d_1}\\ {\tau }_{d_2}\\ {\tau }_{d_3}\end{array}\right]\\ \hfill \end{array}$$

(8)

Grouping terms according to the joint accelerations of the robot $\left({\ddot{q}}_1,{\ddot{q}}_2,{\ddot{q}}_3\right)$, the inertia matrix is expressed as

$$\begin{array}{c}\hfill \mathbf{D}\left(\mathbf{q}\right)=\left[\begin{array}{ccc}{d}_{11}& 0& 0\\ 0& d_{22}& d_{23}\\ 0_{31}& d_{32}& d_{33}\end{array}\right]\left[\begin{array}{c}{\ddot{q}}_1\\ {\ddot{q}}_2\\ {\ddot{q}}_3\end{array}\right]\end{array}$$

(9)

with

$$\begin{array}{cc}\hfill d_{11}& =I_{z_1}+I_{z_2}+I_{z_3}+\left(\frac{m_2}{2}\right)\left[l_{c_2}^2\left(1+cos\left(2q_{{}_2}\right)\right)\right]\hfill \\ \hfill & +\left(\frac{m_3}{2}\right)[2l_2{l}_{c_3}\left(cos\left(2q_{{}_2}+q_{{}_3}\right)+cos\left(q_{{}_3}\right)\right)+l_2^2\left(1+cos\left(2q_{{}_2}\right)\right)+l_{c_3}^2\left(1+cos\left(2q_{{}_2}+2q_{{}_3}\right)\right)]\hfill \\ \hfill d_{22}& =I_{y_2}+I_{y_3}+m_2{l}_{c_2}^2+2m_3{l}_2{l}_{c_3}cos\left(q_{{}_3}\right)+m_3\left(l_2^2+l_{c_3}^2\right)\hfill \\ \hfill d_{23}& =I_{y_3}+m_3{l}_2{l}_{c_3}cos\left(q_{{}_3}\right)+m_3{l}_{c_3}^2\hfill \\ \hfill d_{32}& =I_{y_3}+m_3{l}_2{l}_{c_3}cos\left(q_{{}_3}\right)+m_3{l}_{c_3}^2\hfill \\ \hfill d_{33}& =I_{y_3}+m_3{l}_{c_3}^2\hfill \\ \hfill \end{array}$$

Similarly, by grouping terms according to the joint velocities of the robot $\left({\dot{q}}_1,{\dot{q}}_2,{\dot{q}}_3\right)$, the matrix of centripetal and Coriolis forces is expressed as

$$\begin{array}{c}\hfill \mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)=\left[\begin{array}{ccc}0& c_{12}& c_{13}\\ c_{21}& c_{22}& c_{23}\\ c_{31}& c_{32}& 0\end{array}\right]\left[\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\\ {\dot{q}}_3\end{array}\right]\end{array}$$

(10)

with

$$\begin{array}{cc}\hfill c_{12}& =-\left(m_2{l}_{c_2}^{2}sin\left(2q_{{}_2}\right)+m_3\left(l_2^{2}sin\left(2q_{{}_2}\right)+2l_2{l}_{c_3}sin\left(2q_{{}_2}+q_{{}_3}\right)+l_{c_3}^{2}sin\left(2q_{{}_2}+2q_{{}_3}\right)\right)\right){\dot{q}}_1\hfill \\ \hfill c_{13}& =-\left(m_3{l}_{c_3}\left(l_2\left(sin\left(2q_{{}_2}+q_{{}_3}\right)+sin\left(q_{{}_3}\right)\right)+l_{c_3}sin\left(2q_{{}_2}+2q_{{}_3}\right)\right)\right){\dot{q}}_1\hfill \\ \hfill c_{21}& =\left(\left(\frac{m_2}{2}\right)l_{c_2}^{2}sin\left(2q_{{}_2}\right)+\left(\frac{m_3}{2}\right)\left(l_2^{2}sin\left(2q_{{}_2}\right)+2l_2{l}_{c_3}sin\left(2q_{{}_2}+q_{{}_3}\right)+l_{c_3}^{2}sin\left(2q_{{}_2}+2q_{{}_3}\right)\right)\right){\dot{q}}_1\hfill \\ \hfill c_{22}& =-2m_3{l}_2{l}_{c_3}sin\left(q_{{}_3}\right){\dot{q}}_3\hfill \\ \hfill c_{23}& =-m_3{l}_2{l}_{c_3}sin\left(q_{{}_3}\right){\dot{q}}_3\hfill \\ \hfill c_{31}& =\left(\frac{m_3}{2}\right)\left(l_{c_3}^{2}sin\left(2q_{{}_2}+2q_{{}_3}\right)+l_2{l}_{c_3}\left(sin\left(2q_{{}_2}+q_{{}_3}\right)+sin\left(q_{{}_3}\right)\right)\right){\dot{q}}_1\hfill \\ \hfill c_{32}& =m_3{l}_2{l}_{c_3}sin\left(q_{{}_3}\right){\dot{q}}_2\hfill \\ \hfill \end{array}$$

The gravitational torque vector of the manipulator robot is finally expressed as

$$\begin{array}{c}\hfill \mathbf{G}\left(\mathbf{q}\right)=\left[\begin{array}{c}0\\ \left(m_2{l}_{c_2}+m_3{l}_2\right)cos\left(q_{{}_2}\right)+m_3{l}_{c_3}cos\left(q_{{}_2}+q_{{}_3}\right)\\ m_3{l}_{c_3}cos\left(q_2+q_3\right)\end{array}\right]g\end{array}$$

(11)

3. Robot Motion Control Synthesis

The mathematical model (7) has been widely used to describe the controlled dynamics of several architectures of complex nonlinear robotic systems [28,29].From Equation (7), the tracking error dynamics on controlled nonlinear robotic system trajectories can be expressed as follows:

$$\begin{array}{cc}\hfill {\ddot{\mathbf{e}}}_{\mathbf{q}}& =\mathbf{v}+\mathit{\xi }\hfill \end{array}$$

(12)

with

$$\begin{array}{c}\hfill \mathit{\xi }=-{\ddot{\mathbf{q}}}^{★}-{\mathbf{D}}^{-1}\left(\mathbf{q}\right)\mathbf{G}\left(\mathbf{q}\right)-{\mathbf{D}}^{-1}\left(\mathbf{q}\right)\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}-{\mathbf{D}}^{-1}\left(\mathbf{q}\right){\mathit{\tau }}_d\end{array}$$

(13)

where $\mathbf{v}={\mathbf{D}}^{-1}\left(\mathbf{q}\right)\mathit{\tau }$ denotes an auxiliary (virtual) control input vector.

The trajectory tracking error vector is ${\mathbf{e}}_{\mathbf{q}}={\left[e_{q_1}{e}_{q_2}{e}_{q_3}\right]}^{\mathsf{T}}$ with $e_{q_{{}_i}}=q_{{}_i}-q_{{}_i}^{★}$ for $i=1,2,3$. Here, $q_i^{★}\left(t\right)$ stands for angular position reference trajectories planned for the operation of the robotic system.

In the present study, the integral reconstruction approach of velocity state variables is suitably exploited [31]. In this fashion measurements of velocity signals are unnecessary. Dependence on disturbed nonlinear dynamic system models is also reduced. Furthermore, differentiation of generalized coordinates with respect to time is not requested, avoiding the possible generation of undesirable corrupting noise during the measurement signal processing. Thus, from Equation (12), the integral reconstructor of the reference trajectory tracking error velocity vector is proposed as follows:

$$\begin{array}{cc}\hfill {\widehat{\dot{\mathbf{e}}}}_{\mathbf{q}}& ={\int }_{t_0}^t\mathbf{v}dt\hfill \end{array}$$

(14)

For robust control design purposes, $\mathit{\xi }={\left[{\xi }_1{\xi }_2{\xi }_3\right]}^{\mathsf{T}}$ is considered a completely unknown time-varying disturbance vector to be actively rejected, which can be approximated into a self-adjusting, very small window of time by the Taylor series polynomial expansion

$$\begin{array}{cc}\hfill \xi & ={\mathbf{p}}_0+{\mathbf{p}}_{1}t\hfill \end{array}$$

(15)

Moreover, parameter vectors of the disturbance signal model (15), ${\mathbf{p}}_0={\left[p_{0_1}{p}_{0_2}{p}_{0_3}\right]}^{\mathsf{T}}$ and ${\mathbf{p}}_1={\left[p_{1_1}{p}_{1_2}{p}_{1_3}\right]}^{\mathsf{T}}$, are assumed to be unknown as well. Small uncertainties in components of the matrix $\mathbf{D}\left(\mathbf{q}\right)$ and dynamic modeling errors could be also considered into the disturbance vector $\mathit{\xi }$. In contrast to other active disturbance rejection control approaches, the real-time estimation of disturbances and time derivatives of position output signals is not required in the present contribution.

Then, the real and reconstructed tracking error velocity vectors holds the following relationship:

$$\begin{array}{cc}\hfill {\dot{\mathbf{e}}}_{\mathbf{q}}& ={\widehat{\dot{\mathbf{e}}}}_{\mathbf{q}}+{\mathbf{a}}_{0}t+{\mathbf{a}}_1{t}^2\hfill \end{array}$$

(16)

where vector parameters ${\mathbf{a}}_0={\left[a_{0_1}{a}_{0_2}{a}_{0_3}\right]}^{\mathsf{T}}$ and ${\mathbf{a}}_1={\left[a_{1_1}{a}_{1_2}{a}_{1_3}\right]}^{\mathsf{T}}$ are also assumed to be unknown, which depend on initial conditions of the nonlinear robotic system and parameters of the polynomial signal model (15). The interested reader on integral reconstructors as an alternative to bypass time derivatives of measurement signals and design of asymptotic state observers is referred to the contribution [31].

The auxiliary control vector $\mathbf{v}$ is proposed as follows

$$\begin{array}{cc}\hfill \mathbf{v}& =-{\mathbf{B}}_{\mathbf{4}}{\widehat{\dot{\mathbf{e}}}}_{\mathbf{q}}-{\mathbf{B}}_{\mathbf{3}}{\mathbf{e}}_{\mathbf{q}}-{\mathbf{B}}_{\mathbf{2}}\int {\mathbf{e}}_{\mathbf{q}}-{\mathbf{B}}_{\mathbf{1}}{\int }_{}^{\left(2\right)}{\mathbf{e}}_{\mathbf{q}}-{\mathbf{B}}_{\mathbf{0}}{\int }_{}^{\left(3\right)}{\mathbf{e}}_{\mathbf{q}}\hfill \end{array}$$

(17)

where

$$\begin{array}{cc}\hfill {\mathbf{B}}_i=& \left[\begin{array}{ccc}{\beta }_{i_1}& 0& 0\\ 0& {\beta }_{i_2}& 0\\ 0& 0& {\beta }_{i_3}\end{array}\right]\hfill \end{array}$$

(18)

for $i=0,1,\dots ,3$, and ${\displaystyle {\int }_{}^{\left(n\right)}}$ stands for the $n\mathrm{th}$ integral respect to time. Here, integral error action is properly embedded into auxiliary control to actively compensate disturbances $\mathit{\xi }$ as well as differences between real and reconstructed velocity vectors as described by Equation (16).

By considering the torque controllers defined by

$$\begin{array}{c}\hfill \mathit{\tau }=\mathbf{D}\left(\mathbf{q}\right)\mathbf{v}\end{array}$$

(19)

the closed-loop tracking error dynamics results in

$$\begin{array}{c}\hfill {\mathbf{e}}_{\mathbf{q}}^{\left(5\right)}+{\mathbf{B}}_{\mathbf{4}}{\mathbf{e}}_{\mathbf{q}}^{\left(4\right)}+{\mathbf{B}}_{\mathbf{3}}{\mathbf{e}}_{\mathbf{q}}^{\left(3\right)}+{\mathbf{B}}_{\mathbf{2}}{\ddot{\mathbf{e}}}_{\mathbf{q}}+{\mathbf{B}}_{\mathbf{1}}{\dot{\mathbf{e}}}_{\mathbf{q}}+{\mathbf{B}}_{\mathbf{0}}{\mathbf{e}}_{\mathbf{q}}=0\end{array}$$

(20)

Then, the gain matrices are suitably selected as matching the following Hurwitz stable characteristic polynomials:

$$\begin{array}{c}\hfill {\mathbf{P}}_{\mathbf{H}}\left(s\right)=s^5{\mathbf{I}}_{3\times 3}+{\mathbf{B}}_{H_4}{s}^4+{\mathbf{B}}_{H_3}{s}^3+{\mathbf{B}}_{H_2}{s}^2+{\mathbf{B}}_{H_1}s+{\mathbf{B}}_{H_0}\end{array}$$

(21)

4. Artificial Neural Networks-Based Robot Motion Control

In the robust control approach introduced above, the control gains vector can be selected as a constant. However, this vector can be dynamically updated to improve the dynamic response of the system. Artificial neural networks are intelligent agents capable of learning from experiences. These artificial entities employ a massive interconnection of neurons, referred to in the literature as simple computing or processing cell units [1]. In this research, the role of the B-spline artificial neural networks is to provide adaptation capabilities to the introduced robot motion control strategy by updating online the controller gains, as shown in scheme of Figure 3. With the online training of the Bs-ANN, the control law is constantly updated based on the tracking error information. In contrast with other conventional multilayer networks, used in identification and control applications, B-spline networks are based on a defined three-layer structure which decreases its complexity, consequently making them a powerful alternative in real-time implementations.

Adaptive Outline for Control Purposes

Without high-gain feedback or high-frequency switching, adaptive control schemes have successfully handled parametric uncertainties and achieved asymptotic stability [32]. Using a linear combination of mono-variable and multi-variable basis functions, a B-spline function is a polynomial function defined by its extremes. In this work, an adaptive robust control scheme was dynamically tuned using B-spline artificial neural networks. Each Bs-ANN updates its synaptic weights based on different learning indexes and inputs. By continually learning the variables associated with the physical system, this type of network can cope with the system’s nonlinearities and uncertainties [27].

In Figure 3, an implementation of Bs-ANN is shown as a set of associative networks with synaptic weights that can be adjusted to reproduce a specific function. The author in [33] proposes the following output

$$\begin{array}{ccc}\hfill y_n& =& \mathbf{a}\mathbf{w},\mathbf{w}={\left[w_1{w}_2\dots w_j\right]}^T,\mathbf{a}=\left[a_1{a}_2\dots a_j\right]\hfill \end{array}$$

(22)

where $w_j$ and $a_j$ are the j-th weight and the j-th basis function input, respectively, and j is the number of synaptic weights. Here, the B-spline functions are used to calculate the gains of the controllers, with the input of each neural network defined as the tracking error and the error derivatives, and with the output $y_n\left(t\right)$ defined as the control parameters. To determine the initial weight values and input thresholds, it is common to perform offline training of the network by studying the system in different and relevant operational conditions, which can be easily done by using bio-inspired optimization algorithms [26]. The minimization error, i.e., the difference between the actual output vector and its desired value, is a key element of the learning process. For this development, the following instant learning rule was adopted [34]:

$$w_n\left(t\right)=w_n\left(t-1\right)+\frac{\ell e_n\left(t\right)}{\Vert \mathbf{a}\left(t\right){\Vert }_2^2}\mathbf{a}\left(t\right)$$

(23)

here, ${\Vert ·\Vert }_2$ is the vector 2-norm or Euclidean norm; ℓ is the learning rate, and $e_n\left(t\right)$ is the instantaneous output error. Through this method, training is performed online and continuously, with weight values updated in response to tracking error and derivative error feedback. With the boundaries properly set by choosing the correct knot vector and basis function form, this single-inner-layer structure becomes an extremely powerful mechanism. For the proposed adaptive control scheme, four third-order base functions are used: two related to the tracking error and two for the error derivative.

5. Numeric Simulation Results

The proposed motion control scheme was evaluated through several numeric simulations. During the first scenario, the proposal is implemented for motion control in joint-space mode. Secondly, the approach is used in motion control in the operative space, where the independence of a precise robot dynamical model is exhibited, and control gains are suitably updated online. Finally, the proposed control scheme is compared with a PID-like control scheme when the system is subjected to external disturbance torques. It is important to note that in the different laser manufacturing applications, the precise motion of the robot is required, even in the presence of disturbances, as addressed in the numeric experiments.

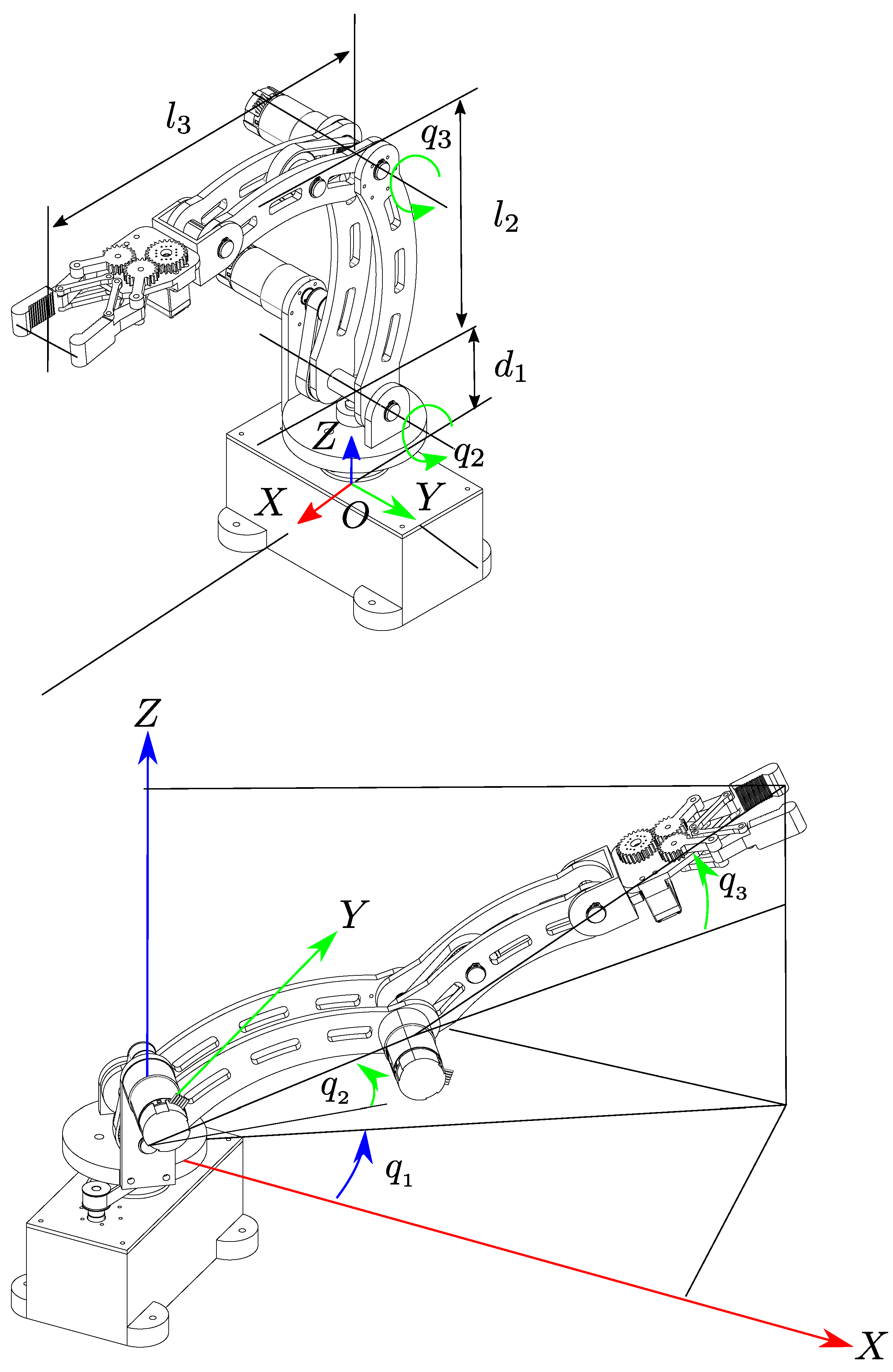
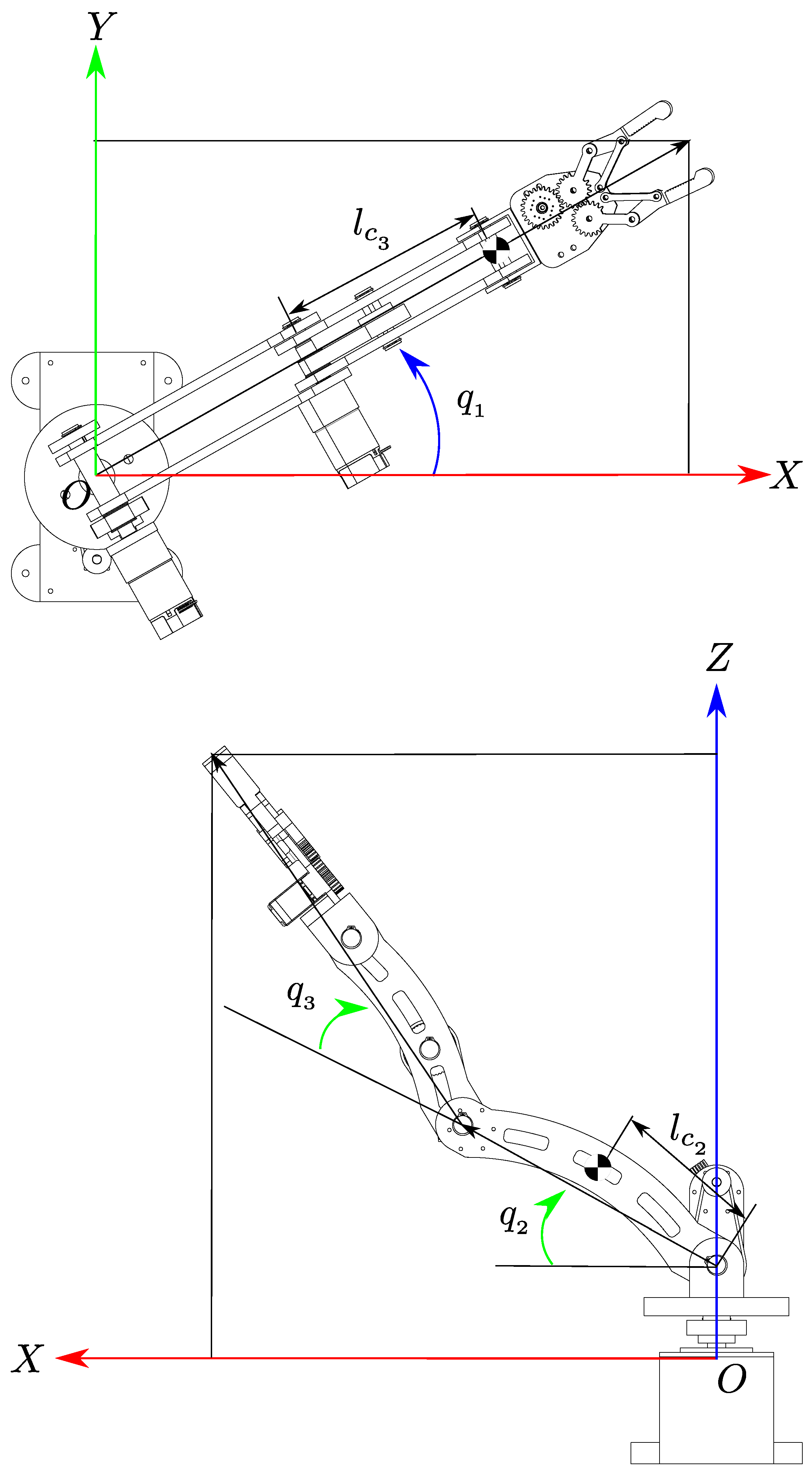
During the simulations, the anthropomorphic manipulator robot with three degrees of freedom previously described is considered, which is characterized by the set of parameters presented in

Table 1. System parameters used during simulation scenarios.

Parameter	Quantity	Units	Description
$m_1$	0.73	Kg	Link 1 mass
$m_2$	0.85	Kg	Link 2 mass
$m_3$	0.51	Kg	Link 3 mass
$d_1$	0.14	m	Link 1 length
$l_{c_2}$	0.10	m	Link 2 length to the center of mass
$l_2$	0.20	m	Link 2 length
$l_{c_3}$	0.20	m	Link 3 length to the center of mass
$l_3$	0.30	m	Link 3 length
$I_{z_1}$	0.0015	Kg m2	Inertia of link 1 in the Z axis
$I_{y_2}$	0.0054	Kg m2	Inertia of link 2 in the Y axis
$I_{z_2}$	0.0013	Kg m2	Inertia of link 2 in the Z axis
$I_{y_3}$	0.0031	Kg m2	Inertia of link 3 in the Y axis
$I_{z_3}$	0.0032	Kg m2	Inertia of link 3 in the Z axis
g	9.81	m/s 2	Gravitational acceleration constant

.

5.1. Scenario 1: Joint Space Control

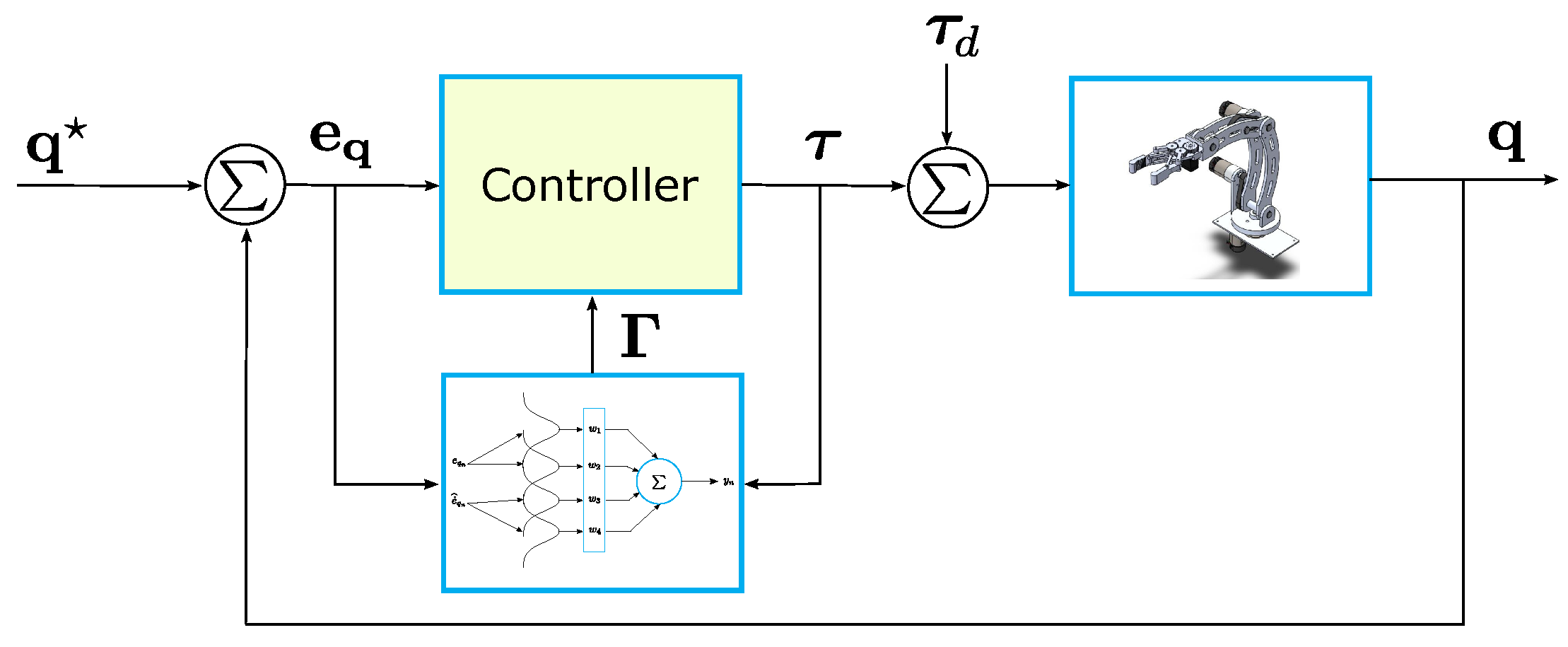
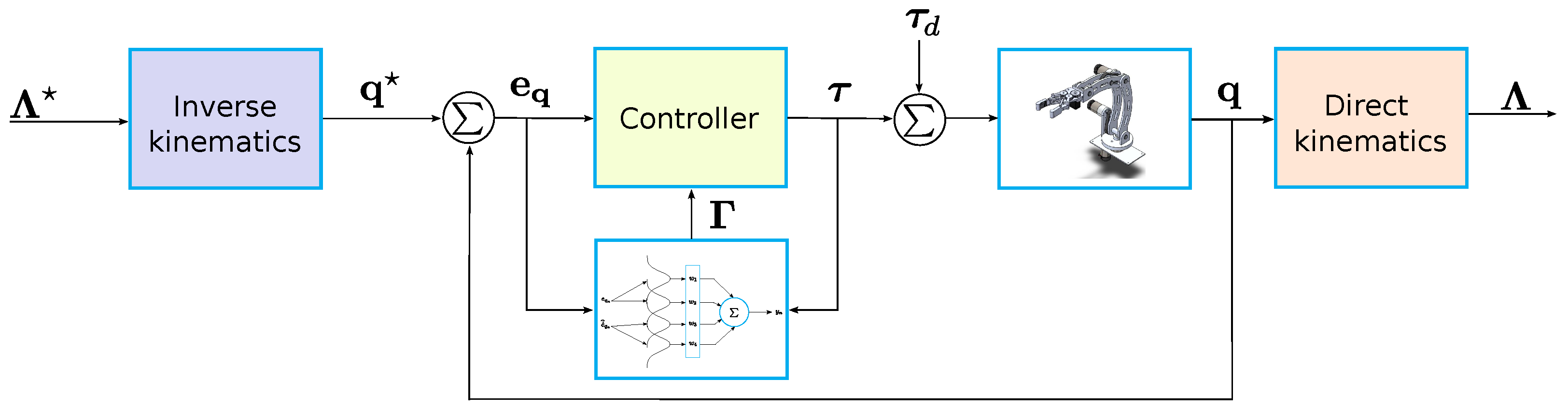
In Figure 4, it is presented the proposed control scheme for the first scenario. It is evident from this figure that only measurements of the angular positions are required for the adaptive robust controller.

On the other hand, it is relevant to mention that in order to tune a reduced number of control parameters, the following Hurwitz stable polynomial is considered for each degree of freedom:

$$P_d\left(s\right)={(s^2+2{\zeta }_c{\omega }_{c}s+{\omega }_c^2)}^2(s+P_c)$$

(24)

here ${\omega }_c,{\zeta }_c,P_c>0$, are the tuning parameters.

Therefore, to ensure closed-loop stability and proper tracking of the planned trajectory, control gains can be selected as follows:

$$\begin{array}{cc}\hfill {\beta }_{4_i}& =4{\zeta }_c{\omega }_c+P_c\hfill \\ \hfill {\beta }_{3_i}& =2{\omega }_c^2+4{\zeta }_c^2{\omega }_c^2+4P_c{\zeta }_c{\omega }_c\hfill \\ \hfill {\beta }_{2_i}& =4{\omega }_c^3{\zeta }_c+2P{\omega }_c^2+4P_c{\zeta }_c^2{\omega }_c^2\hfill \\ \hfill {\beta }_{1_i}& =4P_c{\omega }^3{\zeta }_c+{\omega }_c^4\hfill \\ \hfill {\beta }_{0_i}& =P_c{\omega }_c^4\hfill \end{array}$$

(25)

As a result, only three tuning parameters are required instead of six.

During the first simulation scenario, the robot performs motion regulation in the articular space. For smooth transitions between initial and final angular positions, let us introduce the position reference profile in (26), which is implemented in order to avoid abrupt motion:

$${\mathsf{\Pi }}^{★}=\left\{\begin{array}{cc}{\mathsf{\Pi }}_0& 0\le t<T_1\left[\mathrm{s}\right]\\ {\mathsf{\Pi }}_0+\left({\mathsf{\Pi }}_f-{\mathsf{\Pi }}_0\right){\mathcal{B}}_z(t,T_1,T_2)& T_1\le t\le T_2\left[\mathrm{s}\right]\\ {\mathsf{\Pi }}_f& t>T_2\left[\mathrm{s}\right]\end{array}\right.$$

(26)

where ${\mathsf{\Pi }}_0$ and ${\mathsf{\Pi }}_f$ stand for desired initial and final values of angular motion trajectories planned for the manipulator robot. Meantime, ${\mathcal{B}}_z$ is a Bézier polynomial defined as

$$\begin{array}{c}\hfill {\mathcal{B}}_z(t,T_1,T_2)=\sum _{k=0}^n{\delta }_k{\left(\frac{t-T_1}{T_2-T_1}\right)}^k\end{array}$$

(27)

with $n=6$, and ${\delta }_1=252,{\delta }_2=1050,{\delta }_3=1800,{\delta }_4=1575,{\delta }_5=700,{\delta }_6=126$ [35].

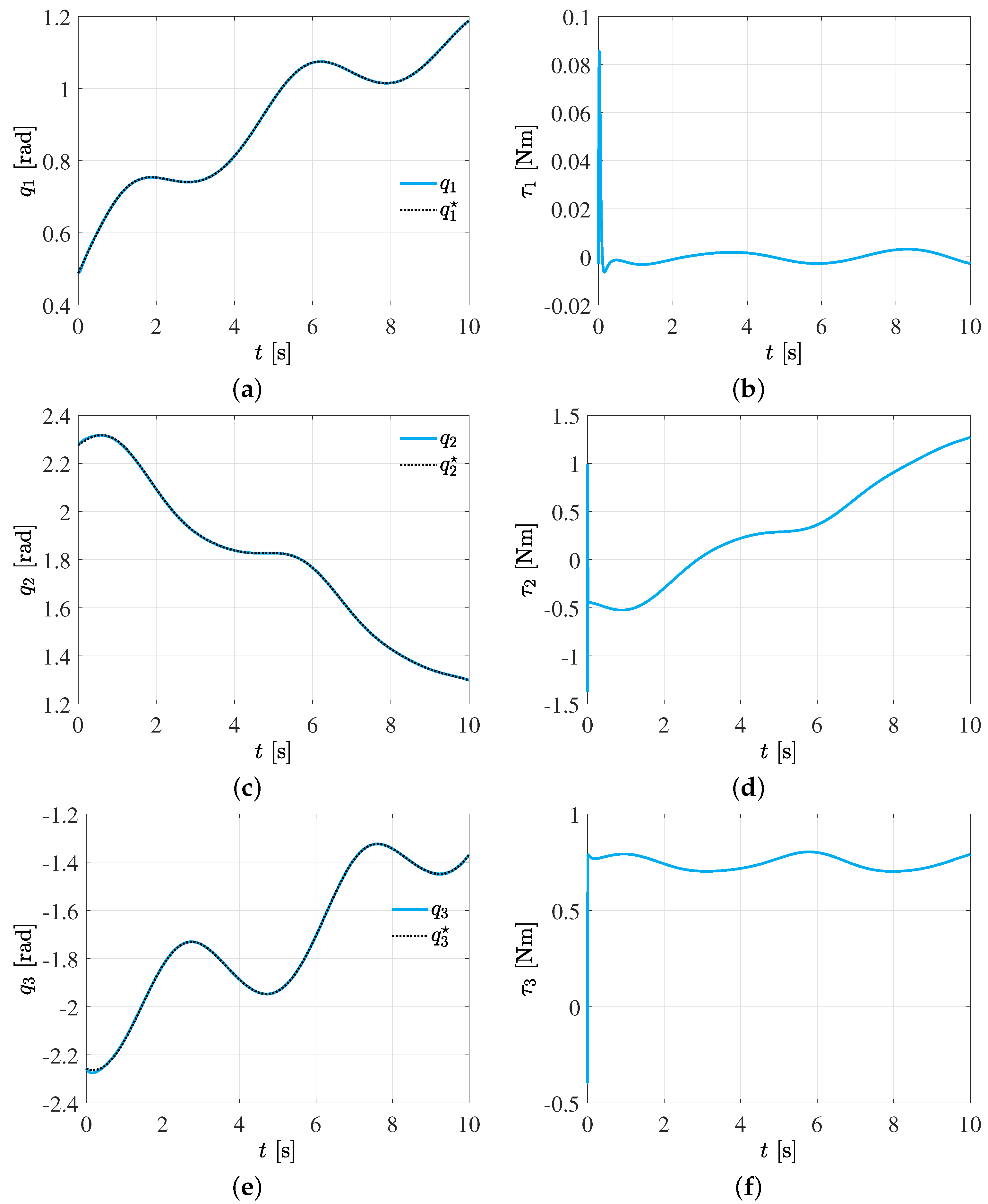
In Figure 5, it is portrayed the results for the first scenario, where several changes in the trajectory references are commanded for each joint by using the expression in (27). From the figure, it is evident a suitable tracking of the Bézier motion profiles. The computed driving torques for each joint are soft and reachable. A very common problem in the design of controllers is the saturation of the actuators due to the high magnitude of the required torque signals, something that in this case is solved satisfactorily.

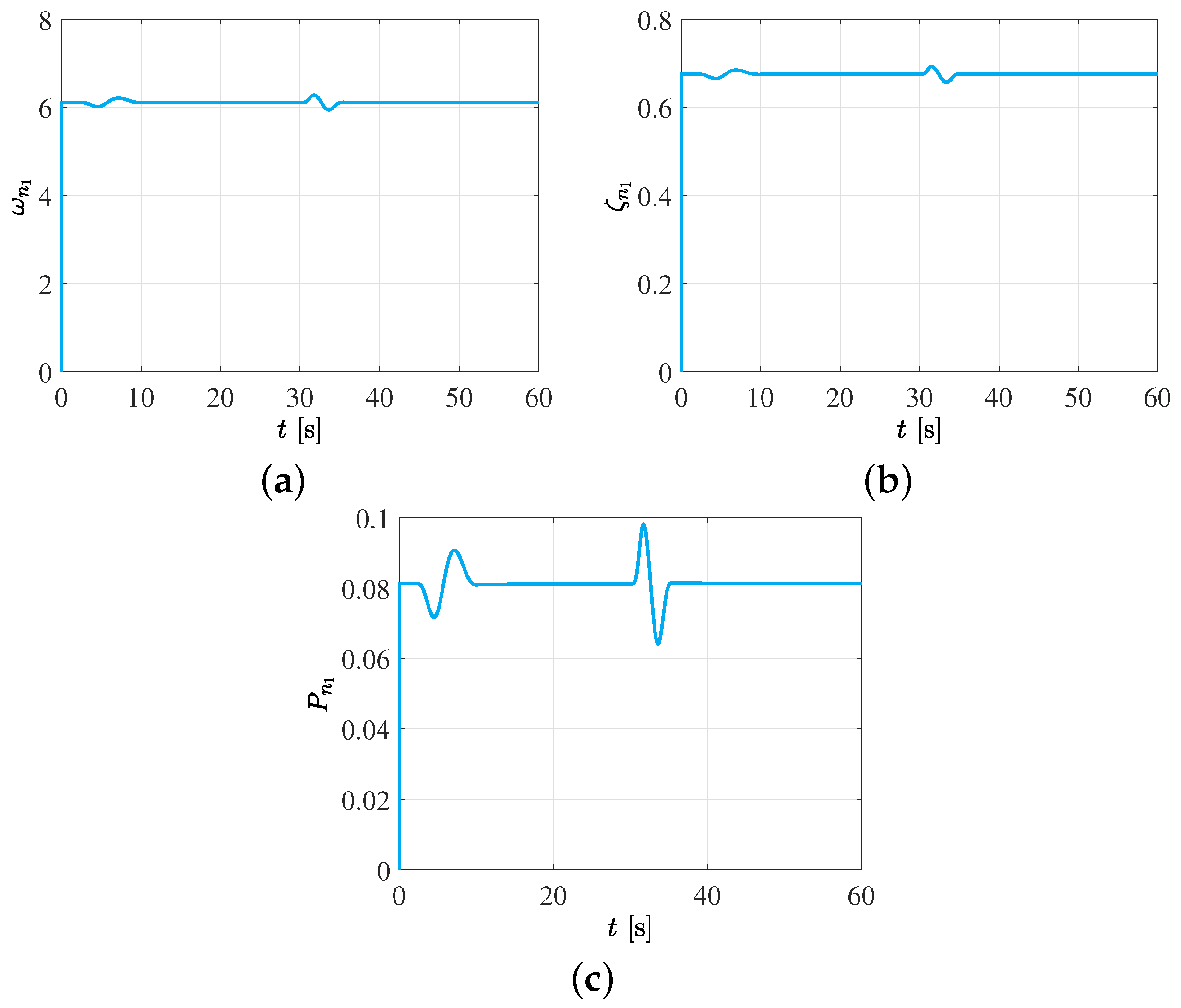
Notwithstanding, the gain values are based on the computation of the ${\omega }_c,{\zeta }_c,P_c$ parameters, as shown in Figure 6 and Figure 7. In this case of joint movement control, the evolution of the control parameters in the first joint is presented. This is because it is the joint that bears the full weight of the robot, so it would be expected to require a greater magnitude of torque to perform the required movements. However, due to the proposed control scheme, it should be noted that the demanded torque has a very small magnitude, and an excellent follow-up of the programmed joint trajectory is obtained.

Notice from figures that the control gains are dynamic, updated online by the adaptive scheme based on the information of the tracking error dynamics, as shown in Figure 3.

5.2. Scenario 2: Cartesian Space Control

In the second scenario, the Cartesian space control is considered. Here, the inverse kinematics of the robot is used for computing the joint tracking references. In this experiment, a Cartesian reference trajectory is selected that is typically used in laser applications. The Cartesian position references ${\mathsf{\Lambda }}^{★}$ are as follows:

$$\begin{array}{cc}{x}^{★}& =0.08+0.15\left(t_k/4\right)\left[\mathrm{m}\right]\hfill \\ \hfill y^{★}& =-0.15+0.05cos(\pi +t_k)sin(\pi +t_k)\left[\mathrm{m}\right]\hfill \\ \hfill z^{★}& =0.4-0.1cos(\pi +t_k)cos(\pi +t_k)\left[\mathrm{m}\right]\hfill \end{array}$$

(28)

where $t_k=(t_k+{\mathsf{\Delta }}_{tk})/10$ s, with initial values of $t_k$ and ${\mathsf{\Delta }}_{tk}$ are zero and updated each iteration as ${\mathsf{\Delta }}_{tk}={\mathsf{\Delta }}_{tk}+0.1\times {10}^{-3}$.

In the same way as in the previous case, it is only necessary to know the desired angular positions of the robot in order to carry out the trajectory tracking satisfactorily. Figure 8 presents the block diagram of the proposed control scheme in the Cartesian space.

Figure 9 presents the results of the robot motion control scheme in Cartesian space. It is highlighted that the proposed scheme presents excellent tracking results without the need to provide the speeds and accelerations of the reference to be followed.

Finally, Figure 10 presents the tracking of the system in the joint space. It can be noted that the system demands very small torque magnitudes to execute the movement of the system. This is a very important aspect to prevent the actuators from saturation due to very high magnitudes of torque.

In scenarios where non-modeled dynamics and/or disturbances occur, the proposed control scheme can present excellent results, so it would be an excellent alternative to be implemented in high-precision manufacturing systems, such as laser cutting and welding robots. This aspect can be better appreciated in the following scenario.

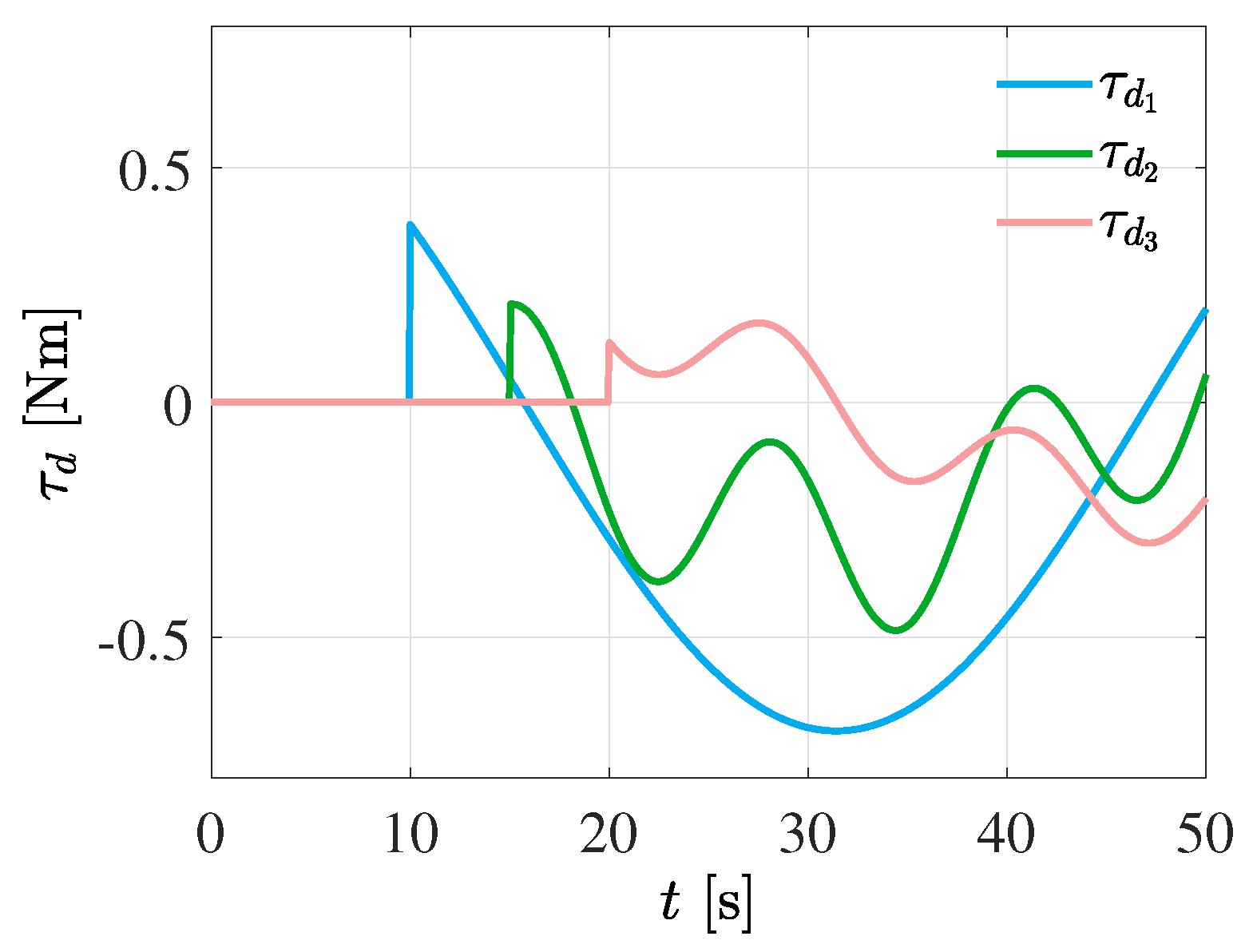
5.3. Scenario 3: Joint Space Robot Motion Subjected to External Vibrating Torques

To demonstrate the effectiveness of the proposed control strategy, the joint space motion control of the manipulator robot subjected to disturbance torques ${\mathit{\tau }}_d={\left[{\tau }_{d_1}{\tau }_{d_2}{\tau }_{d_3}\right]}^{\mathsf{T}}$ is presented. Here, the robotic system is intentionally suddenly perturbed with unknown and undesired vibrating torques, portrayed in Figure 11, which are given as follows:

$${\tau }_{d_1}=\left\{\begin{array}{cc}0\left[\mathrm{Nm}\right]& 0\le t<10\left[\mathrm{s}\right]\\ 0.7cos\left(0.1t\right)\left[\mathrm{Nm}\right]& t\ge 10\left[\mathrm{s}\right]\end{array}\right.$$

(29)

$${\tau }_{d_2}=\left\{\begin{array}{cc}0\left[\mathrm{Nm}\right]& 0\le t<15\left[\mathrm{s}\right]\\ 0.3cos\left(0.1t\right)+0.2sin\left(0.5t\right)\left[\mathrm{Nm}\right]& t\ge 15\left[\mathrm{s}\right]\end{array}\right.$$

(30)

$${\tau }_{d_3}=\left\{\begin{array}{cc}0\left[\mathrm{Nm}\right]& 0\le t<20\left[\mathrm{s}\right]\\ 0.2sin\left(0.1t\right)+0.1sin\left(0.5t\right)\left[\mathrm{Nm}\right]& t\ge 20\left[\mathrm{s}\right]\end{array}\right.$$

(31)

On the other hand, the model-based PID-like plus a dynamic inversion controller introduced in Equation (32) is presented for contrasting the capabilities of the introduced motion controller.

$$\begin{array}{cc}\hfill \mathit{\tau }& =\mathbf{D}\left(\mathbf{q}\right)\left[{\ddot{\mathbf{q}}}^{★}-\mathbf{u}\right]+\mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)\dot{\mathbf{q}}+\mathbf{G}\left(\mathbf{q}\right)\hfill \end{array}$$

(32)

where $\mathbf{u}$ is a PID-like controller vector given by

$$\begin{array}{c}\hfill \mathbf{u}={\mathbf{K}}_p{\mathbf{e}}_{\mathbf{q}}+{\mathbf{K}}_i{\int }_{t_0}^t{\mathbf{e}}_{\mathbf{q}}dt+{\mathbf{K}}_d{\dot{\mathbf{e}}}_{\mathbf{q}}\end{array}$$

(33)

and ${\mathbf{e}}_{\mathbf{q}}=\mathbf{q}-{\mathbf{q}}^{★}$. Notice from the equations that there exists a high dependence of the mathematical model, which is not desirable in manufacturing applications due to the parameter uncertainty of both the robot and the objects it must manipulate and the presence of the non-modeled dynamics and unknown perturbations, which is the case of frictions and vibrations that can occur during the operation of the system.

In Figure 12, the unperturbed responses are portrayed for both controllers. It is evident that an acceptable performance is achieved. Notwithstanding, in the presence of undesired and unknown vibration torques, the PID-like controller is unable to stabilize the system or to track the reference, as observed in Figure 13. Here, it is observed that the motion controller performance is significantly deteriorated when external disturbances are present. Notice that in the proposed motion control scheme, the suitable integration of the Bézier polynomials as the reference motion profiles allows to achieve a superior robot motion performance.

Figure 12 shows the comparison in the robot motion control between a PID-like controller dependent on the mathematical model of the system and the proposed robust adaptive controller without considering external disturbances. In the trajectory tracking with the PID-like controller, it is clearly observed that the system does not reach the desired reference with the requirements that are being demanded, but instead presents a delay, which is not desirable in high-precision manufacturing applications. In contrast, the proposed control strategy reaches the references with smooth and controlled movements, which allows to avoid collisions and damages in cases of application in real environments both for the robot and also for what it is going to manipulate. A system with a PID-like controller in most cases can only work under pre-established conditions.

It is also true that the tuning of the PID controller gains could be improved, but this does not make it less dependent on the model and due to the non-modeled dynamics existing in the robot environment, it would still not work properly if subjected to external disturbances. In addition, a greater number of control parameters than those calculated with the proposed controller would have to be considered.

Figure 13 shows that when the system with the PID controller is subjected to external disturbances, it has a very low performance, so the robot does not have the ability to perform the required trajectory tracking, unlike the proposed control scheme in which it can be seen that no deviation is generated from the paths that the robot is required to follow despite the disturbances that are being input.

Finally, it is considered a last experiment, where parametric uncertainty in matrix $\mathbf{D}\left(\mathbf{q}\right)$ is presented, which might affect considerably the system performance since the controllers introduced in Equations (19) and (32) depend on the matrix values. In this fashion, let us consider additional variations of $\pm 20\%$ in the matrix value used for control purposes under the previous scenario conditions. A quantitative comparison of the controllers performance is carried out by using the integral time absolute error (ITAE) and the integral squared control input (ISCI) indexes, which are associated with the tracking error and control input efforts for each joint as follows:

$$\begin{array}{c}\hfill \mathrm{ITAE}={\int }_0^{t}t\left|e\right|dt\end{array}$$

(34)

$$\begin{array}{c}\hfill \mathrm{ISCI}={\int }_0^t{u}^{2}dt\end{array}$$

(35)

where e and u stand for the tracking errors and control inputs for each degree of freedom. From

Table 2. $0\%$ variation from the real $\mathbf{D}\left(\mathbf{q}\right)$ matrix in the controller implementation.

	PID-Like		Proposal
Joint	ITAE	ISCI	ITAE	ISCI
$q_1$	37.08	8.75	0.05	8.02
$q_2$	13.50	323.68	$2.60\times {10}^{-3}$	322.76
$q_3$	36.54	41.11	$3.80\times {10}^{-4}$	39.51

, it is corroborated a better performance of the proposed control scheme for the robotic manipulator systems, even when less information is required from the physical system in contrast with the PID-like controller. Moreover, in

Table 3. $20\%$ variation from the real $\mathbf{D}\left(\mathbf{q}\right)$ matrix in the controller implementation.

	PID-Like		Proposal
Joint	ITAE	ISCI	ITAE	ISCI
$q_1$	45.85	8.64	0.04	8.02
$q_2$	16.10	324.08	$2.21\times {10}^{-3}$	322.67
$q_3$	45.06	41.33	$2.81\times {10}^{-4}$	39.77

and

Table 4. $-20\%$ variation from the real $\mathbf{D}\left(\mathbf{q}\right)$ matrix in the controller implementation.

	PID-Like		Proposal
Joint	ITAE	ISCI	ITAE	ISCI
$q_1$	31.22	8.84	3.01	35.53
$q_2$	11.78	324.10	0.08	324.4972
$q_3$	30.91	41.06	0.0014	39.77

, it is summarized the performance indexes when there exist variations in the matrix values used by the control schemes, which are $\pm 20$ of the nominal real matrix value. Furthermore, from Equations (19) and (32), it is evident that when uncertainty is also considered in the Coriolis and centripetal forces matrix $\mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)$, the performance of the PID-like controller is further deteriorated. On the other hand, the low system model information dependence of the proposed adaptive robust motion tracking controller allows the system to portray a better performance when the system is subjected to parametric uncertainty, non-modeled dynamics and unknown disturbing vibrating load torques. Overall, the presented results demonstrate that the proposal is a feasible and robust alternative to achieve an acceptable performance in motion tracking control for robotic manipulator systems.

6. Conclusions

In this paper, the anthropomorphic robot manipulation problem was addressed with an adaptive robust motion control scheme, where B-spline artificial neural networks and dynamic compensators are successfully integrated in motion controllers for regulation and output tracking tasks, where just the angular position information is demanded. In this contribution, it is neither required the use of a disturbance observer, angular velocity measurements nor the feed-forward of the tracking references information. The performance of the proposed controller is demonstrated in exhaustive simulation experiments where the system is subjected to both external undesired forced torques and non-modeled dynamics. Acceptable levels of the tracking error are corroborated when the proposed motion control scheme is implemented in a three degree of freedom virtual robot system in the articular and Cartesian space perspectives. It is worth mentioning that this novel proposal can be easily further extended to n-degrees of freedom robotic manipulator systems. Future research work will deal with the synthesis of high-efficiency adaptive output-feedback planned motion profile tracking control strategies based on artificial neural networks for MIMO nonlinear robotic systems under operational scenarios where uncertainty on dimensional specifications of mechanical design could be expected.