Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission
Abstract
:1. Introduction
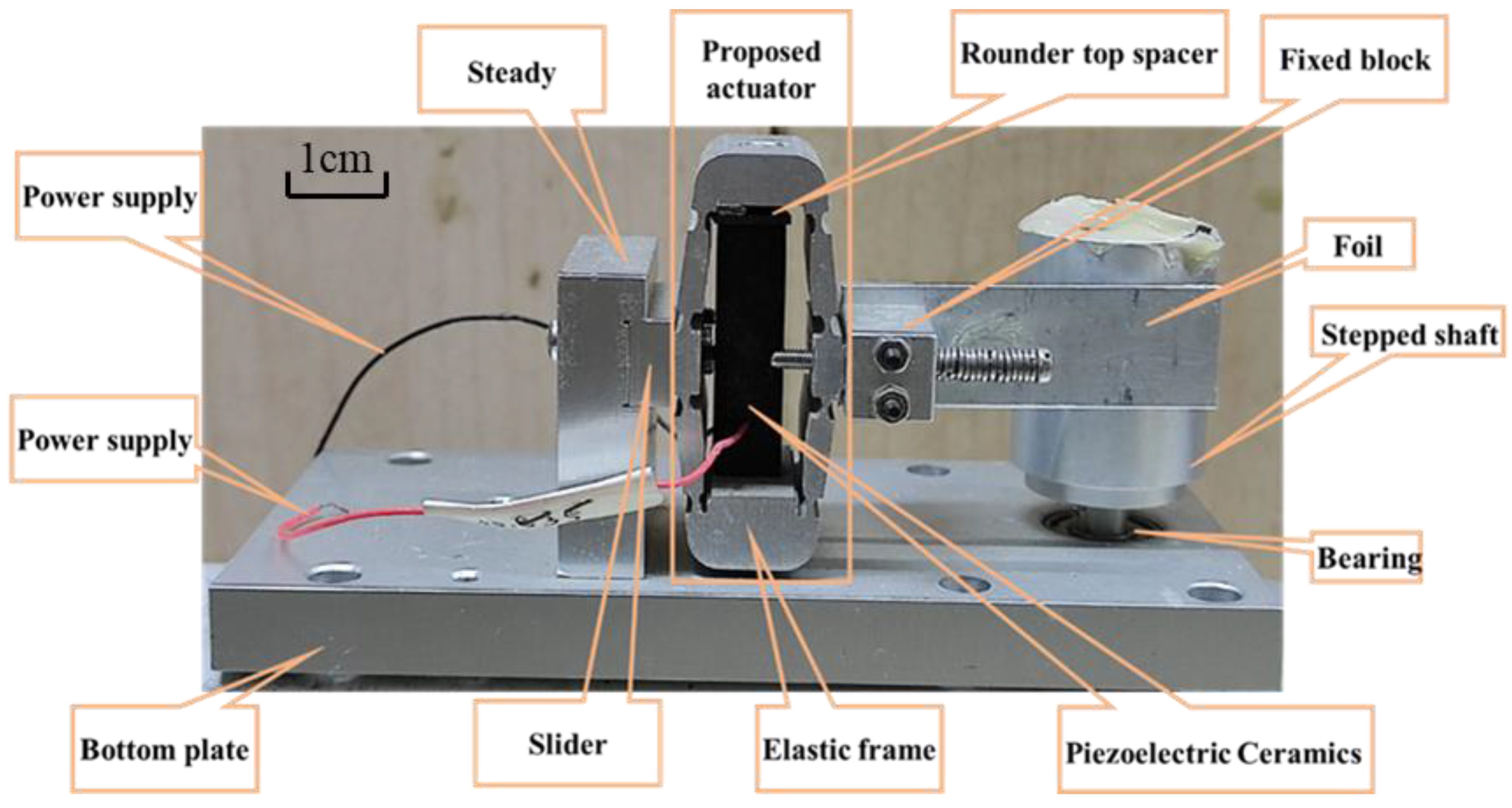
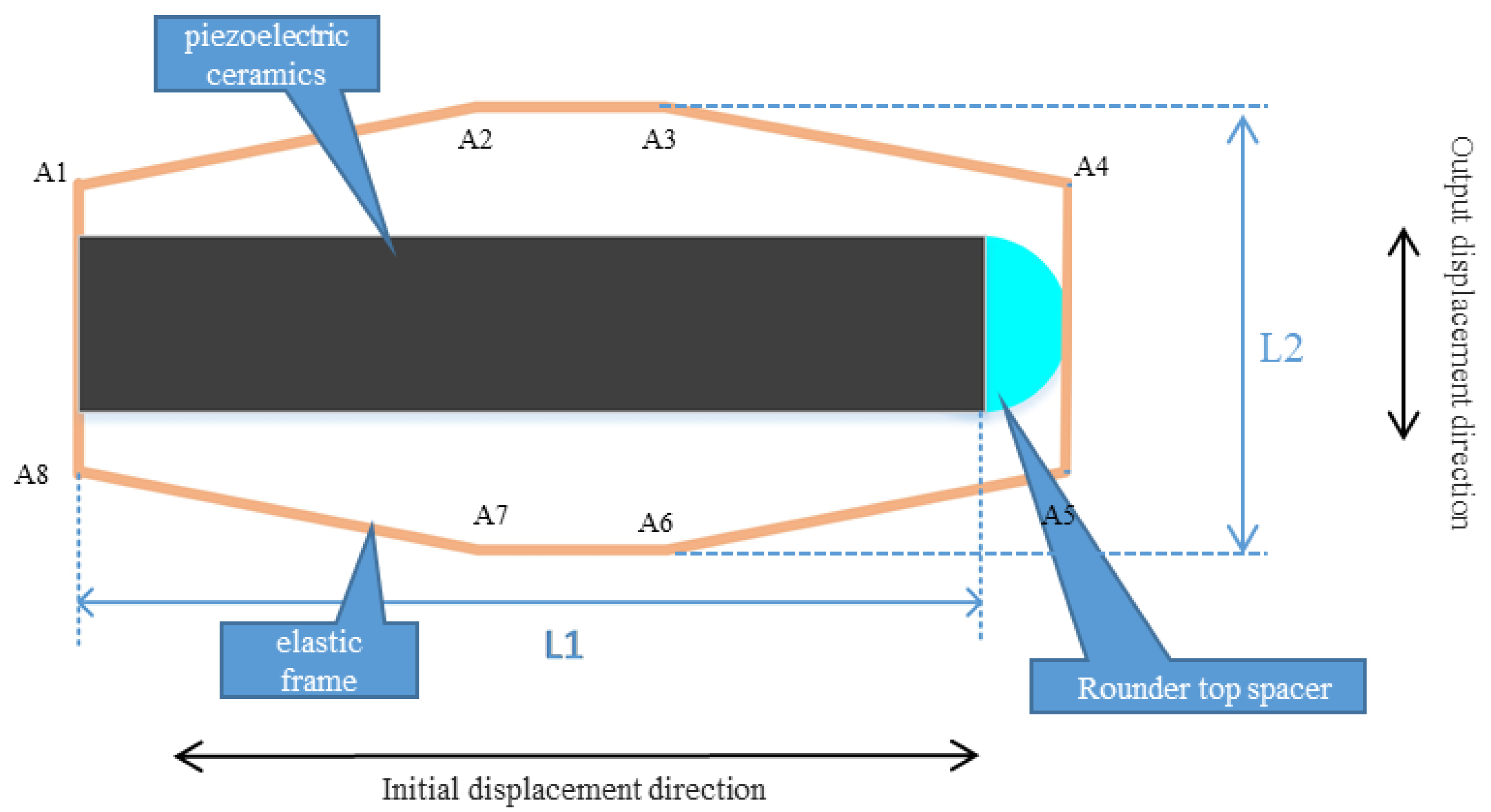
2. Overall Design of the Proposed Panoramic Scanning Device
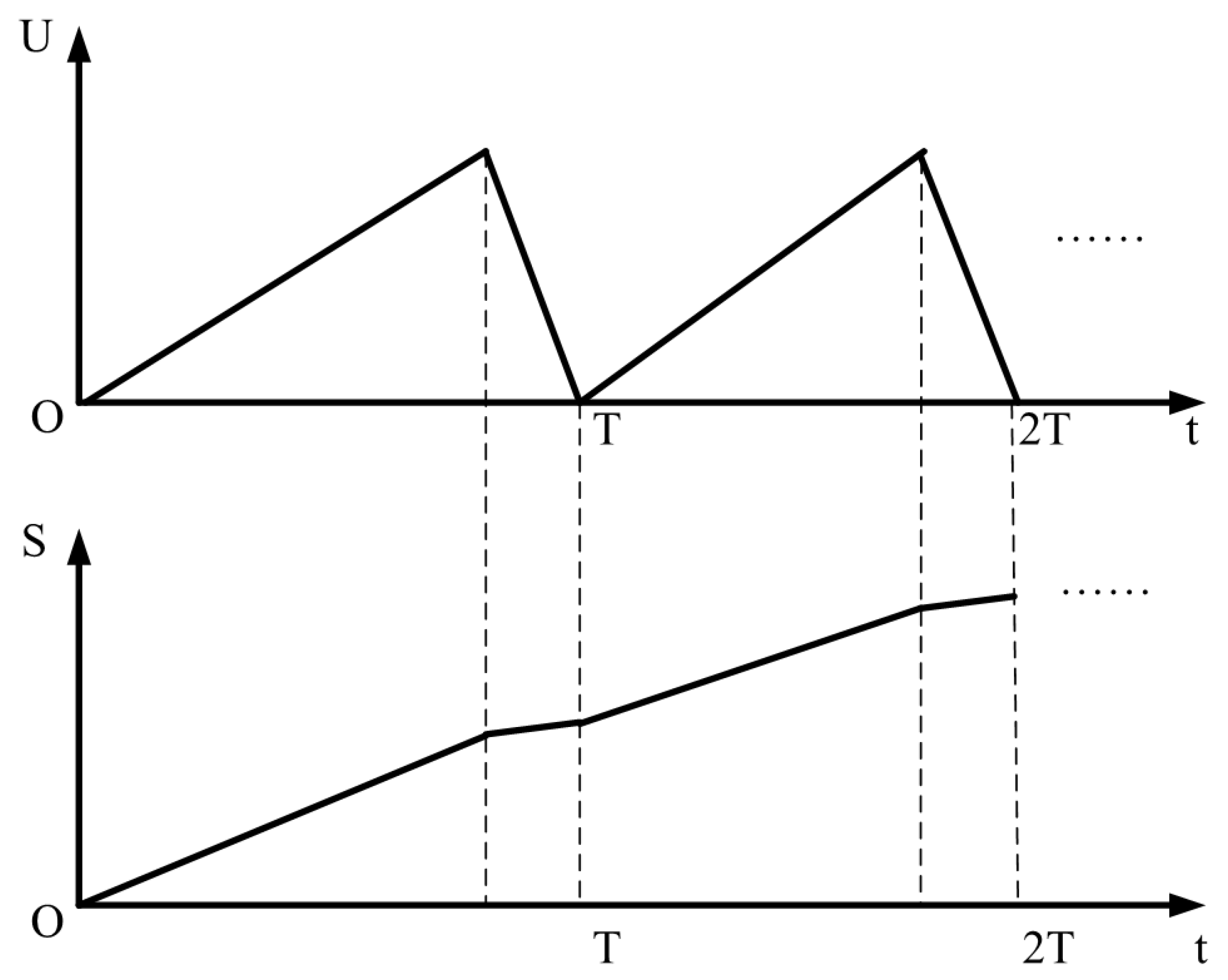
3. Mathematical Models
4. Simulation Analysis
4.1. Extension Simulation and Estimation
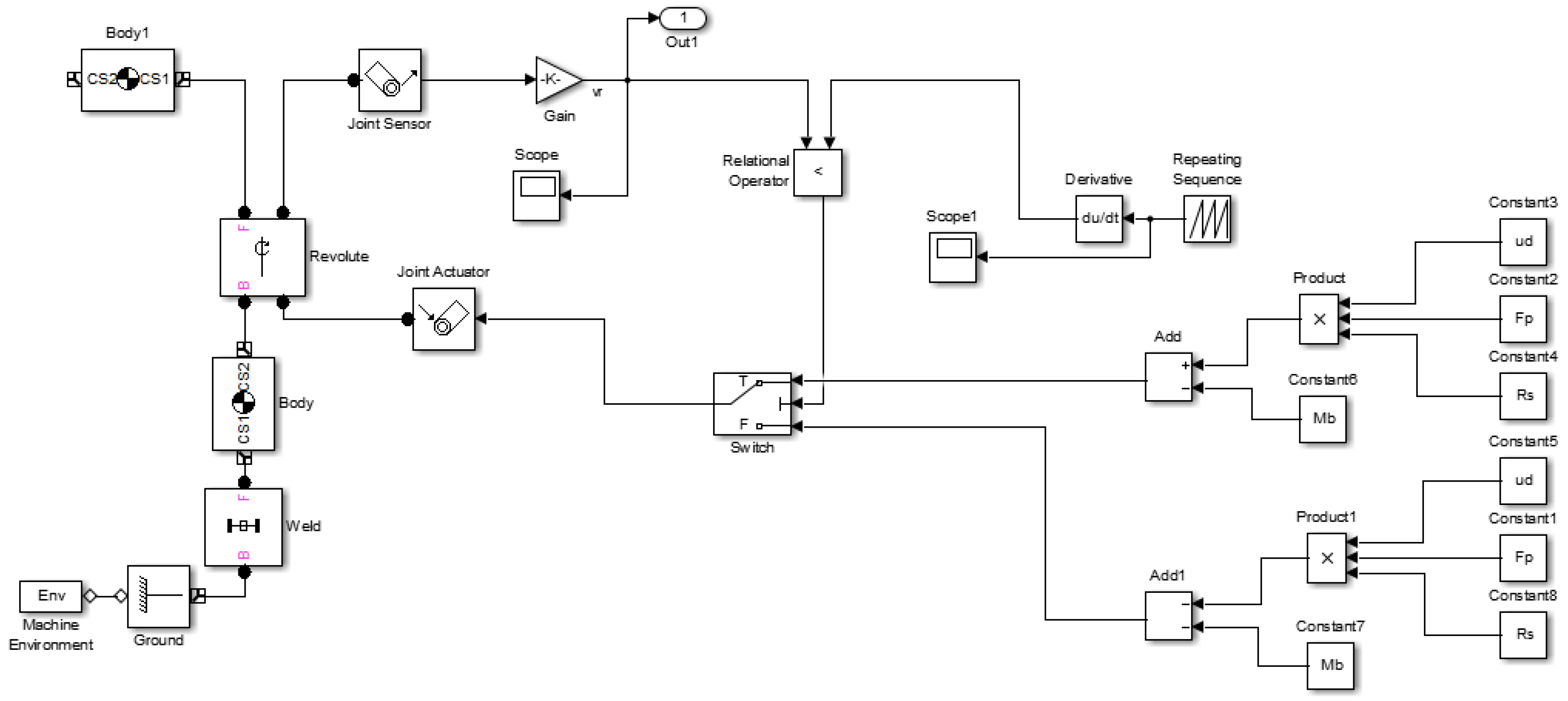
4.2. Dynamic Simulation
- (1)
- While ignoring the nonlinear characteristics of piezoelectric ceramics and elastic frame itself, the designed actuator is considered to be an ideal displacement actuator;
- (2)
- The dynamic and static friction coefficients between the foil and the shaft are equal;
- (3)
- The friction torque of the bearing is constant;
- (4)
- Each parameter is independent.
4.3. Modality Simulation
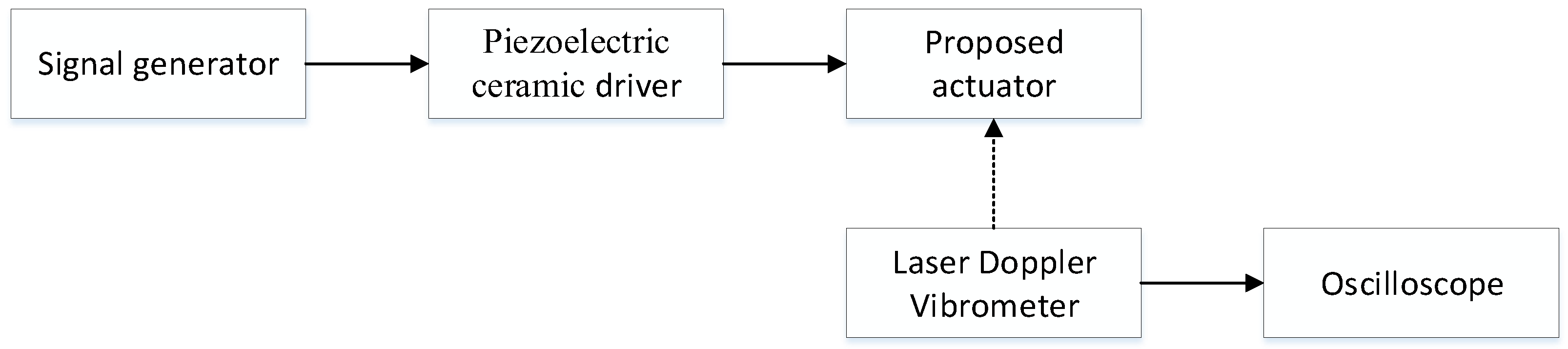
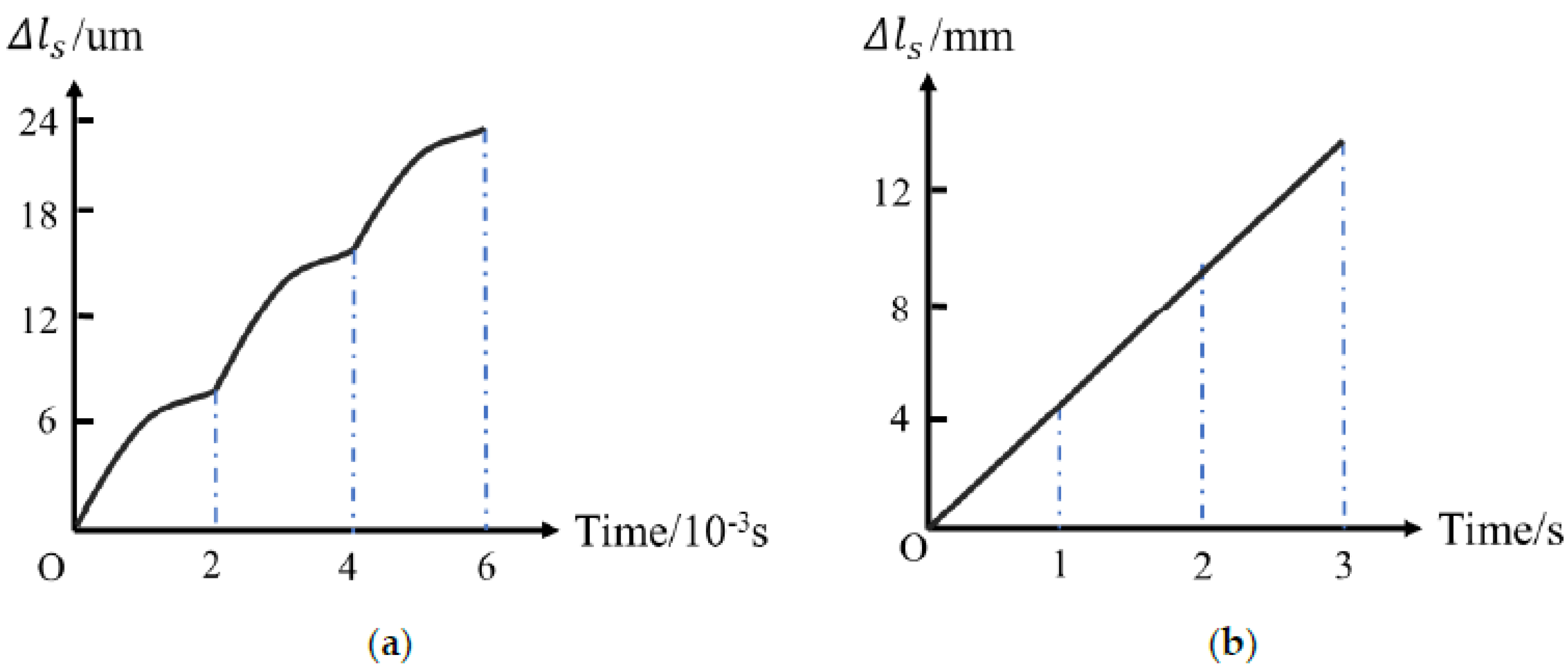
5. Experiment and Discussion
6. Conclusions
7. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duke, G.; Tian, G.Y.; Dave, T. Panoramic imaging—A review. Comput. Graph. 2003, 27, 435–445. [Google Scholar]
- Tian, D.; Wang, Y.; Wang, Z.; Wang, F.; Gao, H. Long Integral Time Continuous Panorama Scanning Imaging Based on Bilateral Control with Image Motion Compensation. Remote Sens. 2019, 11, 1924. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Jiang, W.; Luo, Z.; Yang, L. Application of a Vision-Based Single Target on Robot Positioning System. Sensors 2021, 21, 1829. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hu, Q. A Visualization Progress Management Approach of Bridge Construction Based on Mixed Panoramic and Oblique Photogrammetry. In Proceedings of the 2018 26th International Conference on Geoinformatics, Kunming, China, 28–30 June 2018; pp. 1–6. [Google Scholar]
- Skormin, V.A.; Busch, T.E.; Givens, M.A. Model reference control of a fast steering mirror of a pointing, acquisition and tracking system for laser communications. In Proceedings of the Aerospace & Electronics Conference, Dayton, OH, USA, 22–26 May 1995. [Google Scholar]
- Barth, M.; Barrows, C. A fast panoramic imaging system and intelligent imaging technique for mobile robots. In Proceedings of the International Conference on Intelligent Robots & Systems, Osaka, Japan, 4–8 November 1996. [Google Scholar]
- Karaca, A.C.; Erturk, A.; Gullu, M.K.; Erturk, S. A novel panoramic stereo hyperspectral imaging system. In Proceedings of the 2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014. [Google Scholar]
- Kerbyson, G.M. High-Resolution Full-Panoramic Imaging Surveillance System; SPIE—The International Society for Optical Engineering: Orlando, FL, USA, 2002; Volume 4708, pp. 173–183. [Google Scholar]
- Godber, S.X.; Petty, R.S.; Robinson, M. Panoramic Line-Scan Imaging System for Teleoperator Control; SPIE the International Society for Optical Engineering: San Jose, CA, USA, 1994. [Google Scholar]
- Li, W.; Li, Y.F. Single-camera panoramic stereo imaging system with a fisheye lens and a convex mirror. Opt. Express 2011, 19, 5855–5867. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Huang, X.; Bai, J.; Wang, K.W.; Hua, Y.X. Design of high resolution panoramic annular lens system. In Proceedings of the SPIE 11338, AOPC 2019: Optical Sensing and Imaging Technology, Beijing, China, 7–9 July 2019; Volume 113382. [Google Scholar]
- Zou, X.; Song, H. The fast formation of high-precision panoramic image for the processing of borehole camera video of deep rock mass structures. Bull. Eng. Geol. Environ. 2021, 80, 2199–2213. [Google Scholar] [CrossRef]
- Song, W.; Liu, X.; Lu, P.; Huang, Y.; Weng, D.; Zheng, Y.; Liu, Y.; Wang, Y. Design and assessment of a 360° panoramic and high-performance capture system with two tiled catadioptric imaging channels. Appl. Opt. 2018, 57, 3429–3437. [Google Scholar] [CrossRef] [PubMed]
- Hunstig, M. Piezoelectric Inertia Motors—A Critical Review of History, Concepts, Design, Applications, and Perspectives. Actuators 2017, 6, 7. [Google Scholar] [CrossRef] [Green Version]
- Higuchi, T.; Yamagata, Y.; Furutani, K.; Kudoh, K. Precise positioning mechanism utilizing rapid deformations of piezoelectric elements. In Proceedings of the Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines & Robots, Napa Valley, CA, USA, 11–14 February 1990. [Google Scholar]
- Yao, K.; Uchino, K.; Xu, Y.; Dong, S.; Lim, L.C. Compact Piezoelectric Stacked Actuators for High Power Applications; IEEE: Piscataway, NJ, USA, 2000; Volume 47, pp. 819–825. [Google Scholar]
- Kim, J.; Kim, H.-K.; Choi, S.-B. A hybrid inchworm linear motor. Mechatronics 2002, 12, 525–542. [Google Scholar] [CrossRef]
- Wischnewski, M.; Delibas, B.; Wischnewski, A. Piezoelectric motor operated both in resonance and DC modes. In Proceedings of the ACTUATOR International Conference and Exhibition on New Actuator Systems and Applications, Online, 17–19 February 2021; pp. 1–4. [Google Scholar]
- Dubois, F.; Belly, C.; Saulot, A.; Berthier, Y. Stick-slip in stepping piezoelectric Inertia Drive Motors—Mechanism impact on a rubbing contact. Tribol. Int. 2016, 100, 371–379. [Google Scholar] [CrossRef]
- Claeyssen, F.; Le Letty, R.; Barillot, F.; Sosnicki, O. Amplified Piezoelectric Actuators: Static & Dynamic Applications. Ferroelectrics 2007, 351, 3–14. [Google Scholar]
- Gang, Y.; Dai, H.; Shi, D. Single piezoelectric ceramic stack actuator based fast steering mirror with fixed rotation axis and large excursion angle. Sens. Actuators A Phys. 2015, 235, 292–299. [Google Scholar]
- Six, M.F.; LeLetty, R.; Coste, P.; Claeyssen, F. Rotating step by step piezomotor for nanopositioning and space applica-tions. In Proceedings of the Actuator 2006: 10th International Conference on New Actuators & 4th International Exhibition on Smart Actuators and Drive Systems, Bremen, Germany, 14–16 June 2006. [Google Scholar]
- Claeyssen, F.; Ducamp, A.; Barillot, F.; Le Letty, R.; Porchez, T.; Sosnicki, O.; Belly, C. Stepping piezoelectric actuators based on APAs. In Proceedings of the Actuator 2008: 11th International Conference on New Actuators & 5th International Exhibition on Smart Actuators and Drive Systems, Bremen, Germany, 9–11 June 2008. [Google Scholar]





| 170° | 172° | 174° | 176° | 178° | |
|---|---|---|---|---|---|
| (simulation) (μm) | 4 | 4.6 | 5.28 | 5.68 | 4.44 |
| (estimation) (μm) | 4.52 | 5.28 | 6.16 | 6.76 | 5.54 |
| Items (Unit) | Values |
|---|---|
| Material | Aluminum alloy |
| Length of the linkage A1A2 (mm) | 11.5 |
| θ (°) | 173 |
| The thickness of the foil (mm) | 0.5 |
| Stiffness of the elastic frame kl (N m/rad) | 5.7498 |
| Rotary inertia of the stepped shaft (kg m2) | 3.325 × 10−6 |
| Radius of the upper shaft (mm) | 12 |
| Items (Unit) | Values |
|---|---|
| Company | Suzhou PANT Piezoelectric Ceramics Co., Ltd., Suzhou, China |
| Model | PTJ1500707321 |
| Types of piezoelectric ceramics | Rectangular piezoelectric ceramic laminated actuator |
| Dimensions of piezoelectric ceramics (mm3) | 7 × 7 × 30 |
| Official website | http://www.pantpiezo.com/product/3.html (accessed on 1 June 2022). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, M.; Ding, H.; Huang, C.; Zhu, Y.; Wang, M. Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission. Actuators 2022, 11, 159. https://doi.org/10.3390/act11060159
Dai M, Ding H, Huang C, Zhu Y, Wang M. Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission. Actuators. 2022; 11(6):159. https://doi.org/10.3390/act11060159
Chicago/Turabian StyleDai, Minpeng, Hao Ding, Chenwei Huang, Yi Zhu, and Ming Wang. 2022. "Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission" Actuators 11, no. 6: 159. https://doi.org/10.3390/act11060159
APA StyleDai, M., Ding, H., Huang, C., Zhu, Y., & Wang, M. (2022). Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission. Actuators, 11(6), 159. https://doi.org/10.3390/act11060159





