Next Article in Journal
Transonic Buffet Active Control with Local Smart Skin
Previous Article in Journal
Design and Experiment Evaluation of Load Distribution on the Dual Motors in Cam-Based Variable Stiffness Actuator with Helping Mode
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Actuators
Volume 11
Issue 6
10.3390/act11060154
actuators-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review on Thomson Coil Actuators in Fast Mechanical Switching

by
Mohmmad Al-Dweikat
,
Jian Cui
,
Shuai Sun
,
Mingming Yang
,
Guogang Zhang
* and
Yingsan Geng
State Key Laboratory of Electrical Insulation and Power Equipment, Department of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China
*
Author to whom correspondence should be addressed.
Actuators 2022, 11(6), 154; https://doi.org/10.3390/act11060154
Submission received: 7 April 2022 / Revised: 2 June 2022 / Accepted: 6 June 2022 / Published: 10 June 2022
(This article belongs to the Section High Torque/Power Density Actuators)
Browse Figures
Versions Notes

Abstract

:
With the rapid development of DC power systems and the increasing demand for DC circuit breakers, electromagnetic repulsive drives-based Thomson coil actuators (TCA) are widely investigated to provide the high-speed actuating required for ultra-fast mechanical switches, especially those used in hybrid DC circuit breakers. The actuating mechanism is required to be fast, reliable, and economic. This article summarizes the development of Thomson coil actuators in circuit breakers in recent years, further illustrating the basic principles and the actuator topology. In addition, it discusses the various structural components of TCA and describes the utilized modeling and simulation methods. The main objective was to provide a comprehensive overview of the TCA field.

1. Introduction

In the wake of the fourth industrial revolution, the renaissance of direct current (DC) power has led to a significant development in both high- and medium-voltage DC systems. DC power transmission and distribution implementation provide higher efficiency, which enables a large-scale grid integration of renewable energy resources and a smart system operation and control. Still, reliable protection against faults is considered as one of the main drawbacks that prevents the propagation of DC power systems [1]. DC interruption is a challenging task mainly because of the absence of zero current crossings and the fault current fast rate of rise ( d i / d t ) in DC systems. Fast, rapid, and reliable DC circuit breakers (DCCBs) are considered as the key component to overcoming major constraints in the development of DC systems [2,3,4,5,6,7,8,9,10,11,12]. The existing DC circuit breakers are generally categorized into three main types: solid-state circuit breakers, mechanical circuit breakers, and hybrid circuit breakers. Generally, solid-state CBs (SSCBs) based on power electronic devices exhibit fast response speed and can interrupt DC currents in a few microseconds (μs). However, the technology suffers from high on-state losses, high capital cost, and individual device current and voltage limitations. Compared with a solid-state CB, a mechanical CB is reliable and cost effective and exhibits low operational losses due to its low resistance in normal conduction status. However, designed mostly for AC operations, such a CB cannot break a large DC, mainly due to the absence of a zero-crossing current and the relatively slow operation time for DC requirements. Combining the advantages of mechanical and solid-state CBs, a hybrid CB was introduced to solve the problems with operating speed and power losses [13,14,15]. A hybrid CB has been widely studied, and several designs of hybrid DCCBs have been introduced [16]. These devices generally share a common feature, having three main elements/branches in parallel, as shown, for example, in Figure 1. The normal operation branch contains a fast mechanical switch (FMS) or ultrafast disconnector (UFD). The main breaker path is formed by several power electronic switches (typically IGBT), and the energy dissipation branch consists of surge arresters. The hybrid CB operating time is mainly dependent on or even limited by the time used to separate the FMS contacts. Thus, it requires fast mechanical operation, which is usually achieved by implementing a high-speed actuation mechanism [17].
The currently existing actuating mechanisms deployed in are FMS are mainly dominated by electromagnetic actuators [8]. Compared to hydraulic, pneumatic, or spring-loaded actuation mechanisms that need at least several milliseconds of opening time, which is unsuitable for DC breaking, electromagnetic actuation systems may achieve sub-millisecond levels of opening time. Other actuation mechanisms based on smart materials, most notably, piezoelectric and magnetostrictive devices, also exist. However, despite its high controllability, life endurance, and low energy requirements, its small stroke is still considered a major drawback [18].
Electromagnetic repulsion-based actuation mechanisms have been the main research focus in recent publications [19,20]. There are several repulsion mechanisms, such as a moving coil actuator (voice coil), moving magnet actuator, and Thomson coil actuator (TCA) [21]. Other actuators based on electromagnetic repulsion, such as an induction switch, series coil switch, and railgun actuator, have also been reported [22,23,24]. However, the most commonly used is based on the Thomson coil actuator (TCA) principle. TCA, which is also referred to as a coil gun, repulsion actuator, linear pulse-induction electromechanical converter (LPIEC) or linear induction launcher [21], could provide longer stroke distances, faster actuation speeds, and larger driving forces, which fulfil the task of DC breaking in a hybrid CB, as demonstrated in the literature. Electromagnetic actuation systems utilizing a Thomson coil actuator may achieve sub-millisecond levels of opening time, widely considered fit for fast mechanical switching in a hybrid CB.
Numerous designs of Thomson coil actuators for hybrid circuit breakers have been published. Information about them is, however, scattered widely in the literature. A good overview of a TCA was given in [8,18,21]; still, the design, components, and structural detailed information have not been totally covered. This article was intended to provide a comprehensive review of TCA technology from the beginning through today. It aims to revive the technical discussion on this field by identifying the areas that are relevant to this key technology and the applications for which research and development are required. The basic principle and structural form of the electromagnetic repulsion mechanism-based TCA are introduced. The current research ideas and achievements are summarized. The main problems in the research were analyzed and combined with the current application status of a TCA in the field of mechanical switches. The key issues and research directions of the development of a TCA are given. The rest of this paper is organized as follows. Section 2 presents an overview of the TCA principle and the research background. Section 3 addresses the various structural components of a TCA. Section 4 describes the utilized modeling and simulation methods. Section 5 exemplifies the exploitation of a TCA. Section 6 summarizes the research state of the art while drawing some key conclusions and future trends.

2. Research Overview

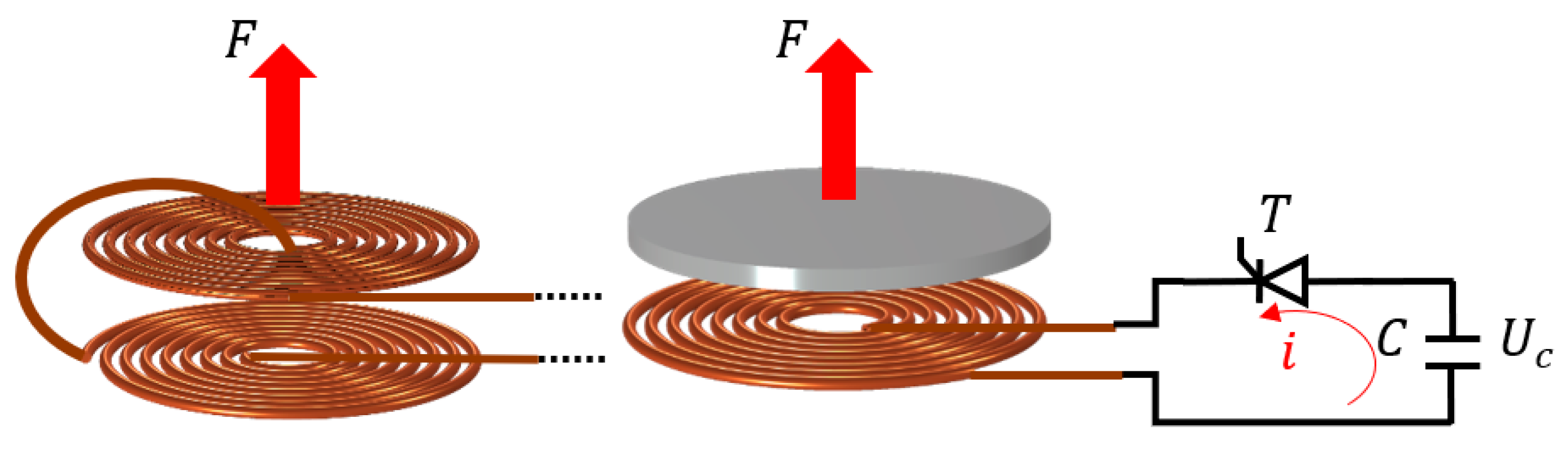
2.1. TCA Principle

Electromagnetic repulsion mechanisms-based TCAs could be categorized into two types according to the driving principle: a coil–disc repulsion mechanism (induction technique) and a coil–coil repulsion mechanism (series coils’ technique). The concept of a coil–disc repulsion mechanism is shown in Figure 2, where C is a storage capacitor, Uc is the charging voltage, T is the thyristor, and F is the electromagnetic repulsion force. Briefly, the coil is excited by a current pulse generated by discharging the pre-charged capacitor C. The pulse current generates an alternating magnetic field, which, in turn, generates a reverse induced eddy current on the metal disk. Due to the direction of the induced current and the ensuing magnetic field, a strong repulsive force between the coil and the disk armature is developed. The resulting electromagnetic force pushes the metal disk away from the coil. On the other hand, the coil–coil type repulsion mechanism is shown in Figure 2. In this arrangement, a movable coil is used to replace the metal disk. The movable coil and the fixed coil are wound in opposing directions. When a pulse current is applied to excite the coils, the induced magnetic fields result in an opposing force that drives the moving coil away. In summary, the Thomson effect uses the mutual inductance between the two electrical conductors to create a strong time-variant repelling (Lorentz) force between the conductors. Utilizing such a physical principle in switching is easily realized through connecting the armature (metal disk or moving coil) to the switch, moving the contact through a transmission rod. A comparison between the two concepts can be seen in [25,26,27,28].

2.2. Background

The electromagnetic repulsion mechanism TCA was first introduced in the late 1960s and early 1970s in [29,30,31,32,33]. Since then, it has been used in the field of switches. However, the research gained more momentum after the DC systems’ renaissance, and the need to achieve faster switching in hybrid DC circuit breakers became a trending topic [34]. In 1994, a 400 V/10 kA current-limiting CB utilizing a TCA was developed with an interrupting time of less than 1 ms [35]. In 1995, a 15 kV vacuum circuit breaker actuated by a TCA was produced, with a contact separation time of 1 ms, which can realize fault current interruption within 20 ms [36]. In 1998, a hybrid high-speed DC circuit breaker was developed using a TCA to realize a fault current interruption of 1250 V/275 A [37]. In [38], a high-speed switch that can open within 1 ms was developed and integrated into a hybrid drive.
Later in the 21st century, and as the hybrid circuit breaker technology became more feasible, more designs have been introduced [39,40,41,42,43]. In 2003, a 6 kV/400 A vacuum interrupter utilizing a TCA with an opening time of 0.8 ms and a closing time of 2.3 ms was developed [44]. Meanwhile, in [45], a repulsive drive capable of reaching speeds of up to 20 m/s was introduced. A drive that contained a conducting aluminum ring was used to bridge two current-carrying contacts, and a current pulse was injected in the driving coil, causing a repulsive force to operate this repulsion drive, achieving contact separation in as short a time as 100 µs. Later on, research on repulsive electromagnetic mechanical drives-based Thomson coils picked the norm, where a Thomson drive incorporating a closing coil, an opening coil, and a repulsion plate is used. Moreover, Thomson coil actuators are being used with vacuum interrupters to develop hybrid DC circuit breakers consisting of a mechanical switch, power IGCTs connected in parallel, diodes, and a metal-oxide varistor for energy dissipation. This can be seen in [46,47,48]. In 2007, a comparative experiment between an electromagnetic repulsion mechanism and a permanent magnet mechanism was conducted. The experimental results proved that the TCA has obvious advantages in starting time, initial acceleration, and overall velocity [49]. Other works were conducted, such as in [50], where a high-speed TCA was analyzed and compared with a permanent magnet actuator and the effect of two consecutive discharges through a Thomson drive were shown, respectively. To achieve higher velocities and more stable operational performance, a TCA was incorporated with a permanent magnetic spring in [51]. This design also incorporated two fixed coils and a movable coil in between. The current pulse is fed to the top and to movable coils for an opening operation and to the bottom and to movable coils for a closing operation. In summary, at this stage, a TCA was proven to deliver a significant force and achieve tremendous velocities. The electromagnetically generated force exerted by a TCA could easily reach tens of kilonewtons [52,53] and was able to drive contact loads of 2 kg at high accelerations up to 20,000 m/s2 with a 32 m/s speed [48]. The contact separation time (from actuation initiation to full detachment) was reported to be as low as 100 μs [46], and 7 mm of contact travel was completed within 600 μs [38]. Full contact opening travel of 27 mm required 2 ms in total [48]. However, the closing process will take a much longer time, such as 5.5 ms [38] or even 195 ms [48].
In the recent decade, research on TCAs has become more focused on feasible applications, design optimizations, efficient performance, reliable operation, and control. For example, the repulsive drive was used to investigate the interruption capability of DC by injecting a high-frequency counter current in [54]. In addition, a TCA was implemented in an arc eliminator in [55,56] and in DC hybrid current-limiting breakers in [57,58,59]; a 1.14 kV TCA prototype was developed in [60,61]. Other examples can be found in [62,63,64,65,66,67,68,69,70,71,72,73,74], in which prototypes of a TCA from 10 kV to 40.5 kV vacuum interrupters were introduced, with an average opening speed between 6 and 10 m/s. In addition, actuating in a vacuum with a TCA became a common approach [20], and vacuum multi-breaks were utilized to scale up voltage ratings [75,76]. The highest voltage rating reported is 500 kV [77], and the highest reported voltage rating achieved by fast vacuum insulation is 40.5 kV [71]. As research on TCAs grew, driven by the DC hybrid circuit breakers’ development, higher voltage ratings were required. Optimized designs were introduced with longer contact travel strokes and shorter separation times. Designs of a TCA were scaled for medium voltages [66,67] and high voltages [78,79]. Table 1 below shows the TCA performance progress in the recent two decades.
The proven feasibility of TCAs opened the door for commercial utilization [80] and further optimization research. Examples of structural optimization studies can be seen in [81,82,83,84], and an optimized lightweight TCA was introduced in [85]. Research has also focused on the structure and components of dynamic operation, thermomechanical behavior, and performance, which were also investigated in [86,87,88,89,90]. Moreover, the efficiency of Thomson coil actuators was also investigated. The highest theoretically calculated efficiency that could be achieved in a Thomson coil was of 54% [91].
Table
Table 1. Experimental performances of TCAs in the literature.
Table 1. Experimental performances of TCAs in the literature.
ReferenceDC Breaker RateActuation Characteristics
TimeSpeedForce/WeightDrive EnergyStroke
Polman et al., 2001 [39]600 V/6 kA1.2 ms 75 kN/0.8 kg6 kA6 mm
Steurer et al., 2003 [45]12 kV/2 kA100–250 μs **20 m/s0.05 kg-10 mm
Roodenburg, 2005 [48]3 kV/7 kA422 μs/2 ms *31.8 m/s100 kN/2 kg3.87 kJ
0.86 mF/3 kV		27 mm
Roodenburg, 2008 [52]8 kA450 μs/2 ms *18 m/s200 kN/2.7 kg1.4–2.75 kJ **28 mm
Li W. et al., 2010 [55,56]-20 ms6–8 m/s **2–3.5 kN **400 mF
250 V/1.6 kA		120 mm
Yang et al., 2011 [57]-2.5 ms8.4 m/s80 kN/4.1 kg5700 μF/980 V18 mm
Zheng et al., 2011 [60]1.14 kv500 µs/2 ms *-5 kN10,000 µF
200 V/3000 A		5 mm
Dong E. et al., 2011 [61]1.14 kV/600 A5.1 ms
4.75 ms
3.25 ms		--4700 µF/350 V
6800 µF/290 V
10,000 µF/210 V		6 mm
Bissal et al., 2012 [92]-0.6 ms12 m/s23 kN/3.6 kg7 mF/400 V7 mm
Wen et al., 2015 [71]40.5 kV/20 kA2.47 ms
2.3 ms		10 m/s50 kN/5 kg8.1 mF/780 V
2.5 mF/1.4 kV		26 mm
Peng C. et al., 2015 [88]30 kV/630 A300 µs/1 ms *1.3 m/s0.5 kg2 mF/300 V5 mm
Wu et al., 2015 [93]-5–8 ms2.2–3.2 m/s **110 kN/3.85 kg5 mF/1200 V30 mm
Yuan et al., 2016 [64]-2.7–4.5 ms **-250 kN2500 µF
1600 V/4000 A		5–22 mm
Hou C. et al., 2016 [70]-2.4 ms-19 kN/2.5 kg22,000 µF/400 V10 mm
Zhang et al., 2016 [94]12 kV/31.5 kA
20.6 kV/31.5 kA		500 μs
2 ms		5 m/s
1 m/s		90 kN/7.5 kg18 mF
13 kA		10–12 mm
Nanxun Z. et al., 2017 [28]10 kV3.5 ms
2.6 ms		3.8 m/s
6.8 m/s		20 kN/3.09 kg
30 kN/4.30 kg		5000 A
4300 A		10 mm
Ren et al., 2017 [72]40.5 kV2.5 ms5 m/s7.5 kg15 mF/650 V20 mm
Hedayati et al., 2017 [95]7 kV/100 A1.1–3.7 ms **-0.14 kg5 kA
90–170 V		3 mm
Rodriguez et al., 2017 [85]27 kV/200 A2 ms4 m/s0.5 kg122 J
1500 μF/425 V		6–12 mm
Stroehla et al., 2019 [24]5 A3 ms7 m/s2 kg-10 mm
Baudoin et al., 2019 [69]24 kV/8 kA2.8 ms3.8 m/s3.5 kg30/15 mF
260/325 V		6 mm
Hou Y. et al., 2019 [96]12 kV5 ms3.5–4.8 m/s **50 kN
2–5 kg **		250 µ F/3000 V
500 µ F/1250 V		10–13 mm
Zhou Y. et al., 2019 [97]110 kV1.4 ms
1.8 ms		20 m/s85 kN/6 kg6250 J/1 mF/2500 V
6252 J/2 mF/1768 V		50 mm
Guan C. et al., 2020 [98]72.5 kV 2–6 m/s **8 kN350–600 V28 mm
Zhu et al., 2020 [99]110 kV/3000 A3 ms-100 kN/7.4 kg2.5 mF/7 kA22 mm
* Contact separation time/full travel time. ** Values varied as test parameters varied.

3. Structural Composition

Recently, research on TCAs became more specific, as scholars settled on dividing the TCA system topology to the drive unit, buffer unit, holding unit (latching mechanism), and control circuit. Each part of these components had its share of research, as follows.

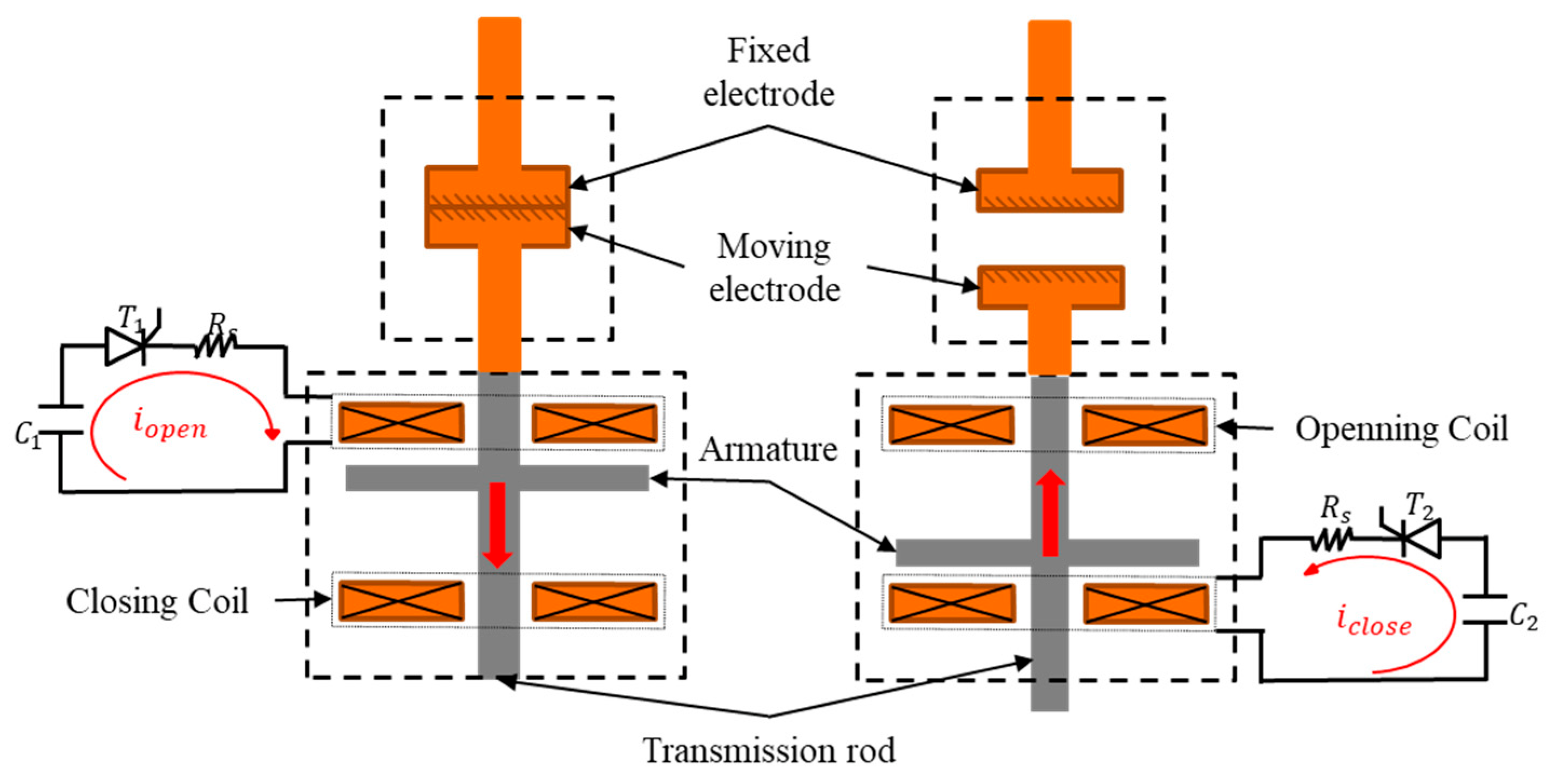
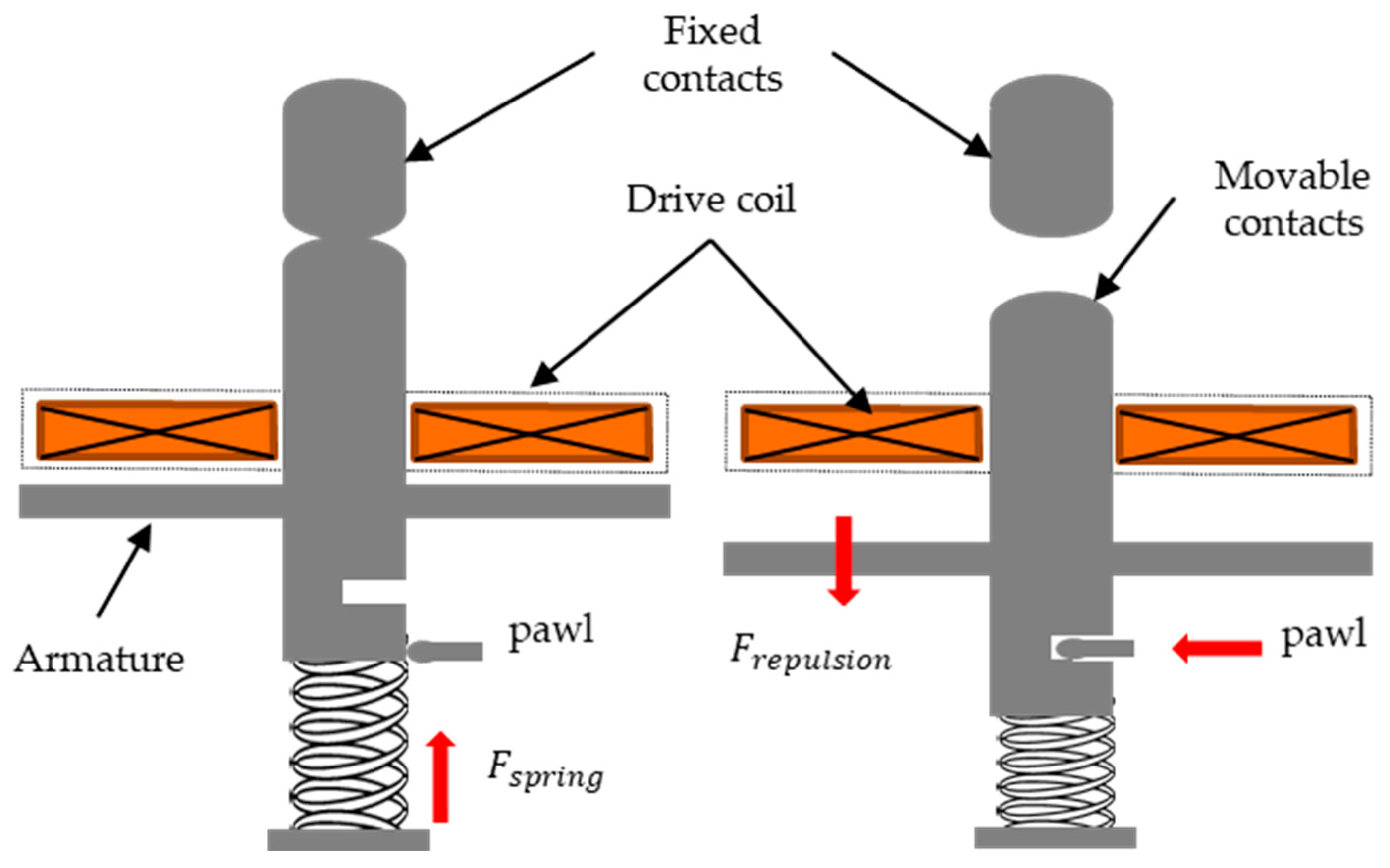
3.1. Drive Unit

According to the driving form of opening and closing, a TCA can be divided into a one-way mechanism and a two-way mechanism. The one-way repulsion mechanism has only one set of driving coils and a driving power supply. Generally, the TCA mechanism performs the opening operation that requires high speed, and the closing operation is performed by the relatively slow operating mechanism such as spring and hydraulic pressure. This was demonstrated in [89,100,101], as the repulsion mechanism was used as the driving unit of the grounding switch, utilizing the rapidity of the TCA to complete the rapid transfer of fault current, as shown in Figure 3. When there is a fault current in the line, the energy storage capacitor discharges to excite the drive coil. This drives the repulsion metal disc and the moving contact to move towards the static contact, thus transferring the fault current.
On the other hand, the two-way repulsion mechanism is also called a symmetrical repulsion mechanism. It consists of two sets of driving coils and a driving power supply, generally including two fixed coils and one movable metal disk (or coil in the case of a coil–coil mechanism). The general two-way repulsion mechanism is shown in Figure 4, where the opening and closing operation of the switch is carried out by the TCA mechanism. The two-way TCA repulsion mechanism design is more widely adopted than the one-way mechanism [38,71]. That is to ensure the rapidity of opening and closing; it is generally used in occasions where there is a high requirement for opening and closing speed.

3.2. Holding Unit

The holding device is used to maintain the actuator mechanism in the opening and closing position; it is an important component to keep the opening or closing state of the mechanical switch. Various holding units’ mechanisms were reported as utilizing helical spring mechanisms, a bi-stable spring mechanism, disc or buckling springs, and permanent magnet holding devices.

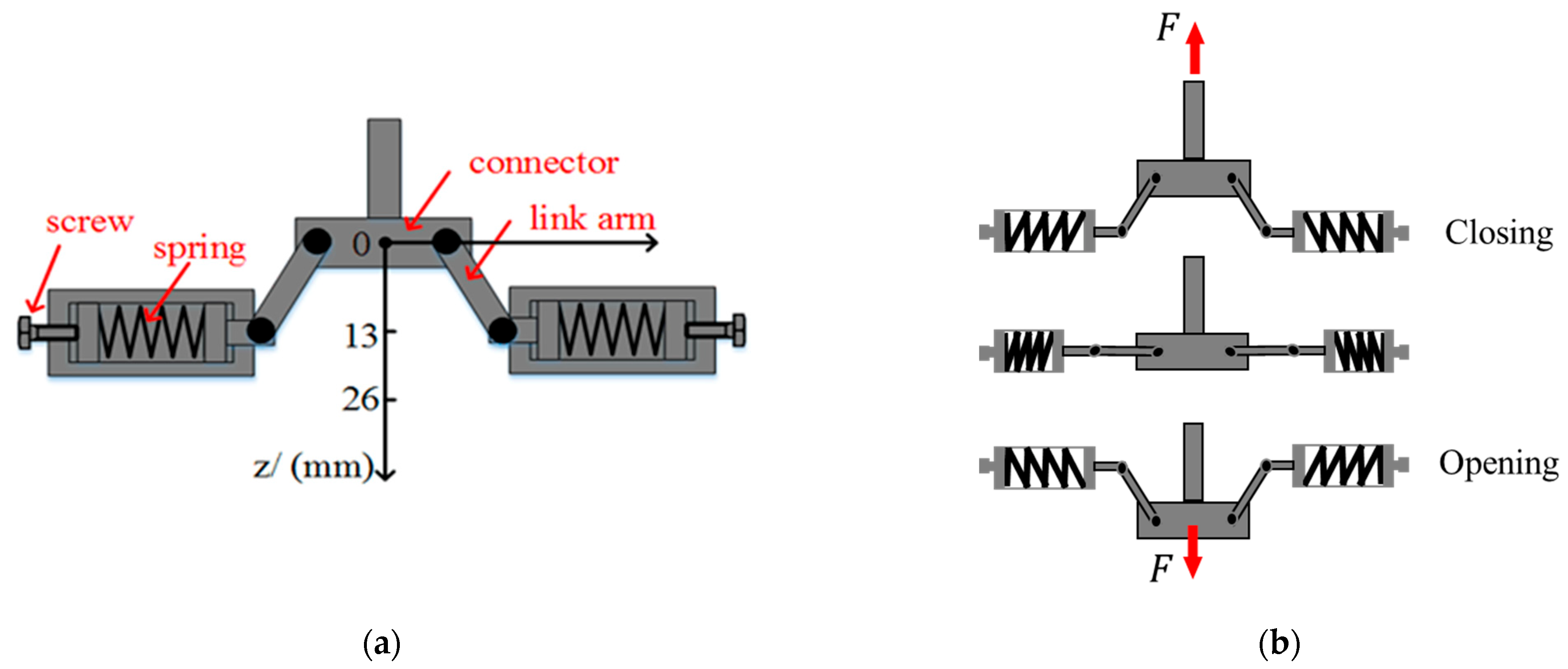
3.2.1. Helical Spring Mechanisms

The spring holding device uses the restoring force of a compressed spring to maintain the switch state; it is mostly used to keep the closed position. In conjunction, a lock structure is used with the spring mechanism to compress and store the spring when the switch is opened; the lock is used to maintain the open position. This was demonstrated by [48,52], as shown in Figure 5. This technique is relatively simple, and the volume and mass are small. However, during the opening process, the spring is always in a compressed state, which has a certain impact on the opening speed. It is not favorable to the rapid opening of the switch; it is suitable for applications where the required opening and closing speeds are relatively low.

3.2.2. Bi-Stable Spring Mechanism

The bi-stable spring mechanism used by [71,102], shown in Figure 6, has been widely adopted and is preferred [94,95,103]. It is easy to implement and adjust, while providing an adequate latching force. However, it requires an additional rod extension and components to mechanically link the armature and the holding system. This will increase the number of system components, moveable mass, and the required repulsion force and further complicate the mechanical design.
The spring unit has two stable states that keep the switch in the closed position or in the open position by providing a vertical upward force or vertical downward force, respectively. The working principle of the bi-stable spring unit in the opening operation is shown in Figure 6. At the closed stage, the springs are compressed, providing the contact pressure in the closed position. When the armature attached transmission rod moves down, pushed by the electromagnetic repulse force, the spring arrangement is compressed. Further pushing will release the springs down to provide the opening force.

3.2.3. Disc Spring Mechanism

A disc spring, also known as conical spring washer, is a conical shell spring type with a truncated conical section stamped from a steel plate, as shown in Figure 7. It was used as the holding mechanism of the repulsive mechanical switch to achieve a fast opening and reliable holding within 2-3 ms in [62,64]. Disc springs have a nonlinear load characteristic depending on the spring material type. They can be divided into one-way disc springs and two-way disc springs according to whether they can be turned over (Figure 7). The function of one-way disc springs is similar to that of ordinary helical coil springs. The characteristic is that when the deformation of the two-way disc spring exceeds a certain value, the truncated cone of the two-way disc spring will overturn and the force will also be reversed.
Similar approaches for a bi-stable mechanism, based on the buckling phenomenon, were developed and used in [38,66,67,85]. The spring is attached to the transmission rod or directly to the armature body, as shown in Figure 8. The latter allowed for abandoning the need for any rod extension, thus reducing the mass of the system compared to other designs. In general, the disc spring has the advantages of a short stroke, large load, compact axial space, and easy combination and use. At the same time, it also has the disadvantages of a large radial size and complicated installation when multiple pieces are used in combination.

3.2.4. Magnet Holding Mechanism

The typical permanent magnet (PM) holding mechanism is composed of a permanent magnet, a moving iron core, a static iron core, and a magnetic conducting ring, as shown in Figure 9. Different from the permanent magnet operating mechanism used for driving, the permanent magnet holding mechanism does not include an opening and closing coil for driving. The permanent magnet holding mechanism utilizes the magnetic force of the permanent magnet and the iron core to provide the holding force and is generally designed as a two-way holding mechanism to provide the holding of opening and closing. The permanent magnet holding mechanism was used in [50,51,60,61] due to its simple structure, its maximum holding force at the opening and closing positions, its small output force in the middle position, and its output characteristics, which meet the requirements of the rapidity of the TCA repulsion mechanism. However, the permanent magnet holding mechanism has problems such as a large moving mass and demagnetization of the permanent magnet, which limit its application in the TCA repulsion mechanism switch. Table 2 below shows a comparison of holding mechanisms in the literature.

3.3. Buffer Unit (Damping Mechanism)

A TCA could exert a significant amount of power. This tremendous generated force can easily reach tens of kilonewtons. For example, a TCA could generate a force as high as 35 kN [47], 50 kN [71], 100 kN [48], and 200 kN [52]. This force exposes the TCA structure to huge mechanical stress, reducing its mechanical life, and even jeopardizes the interruption process. The kinetic energy stored in the switch moving components must be dissipated in order to avoid excessive mechanical stresses, accelerated aging, dielectric breakdown, or destruction of the actuator. The buffer unit is a device used to absorb the kinetic energy of the moving parts, while reducing the speed and preventing the opening and closing bouncing during the actuation of the mechanical switch. Many buffering and damping techniques have been used in mechanical switches, which could mainly be divided to active damping or passive damping [104]. These techniques include spring buffer, hydraulic buffer, material buffer, cylinder buffer, and electromagnetic buffer.
The principles of spring, hydraulic, and material buffering are similar; the kinetic energy is transmitted through the collision of the moving parts and the buffering devices. In the spring buffer, the spring is compressed during the buffering process. The absorbed kinetic energy is stored and could be used for the closing stage. However, contacts bouncing will still be the problem at the closing operation [105].
Hydraulic and material buffers absorb the kinetic energy by using the energy difference between the compression and the recovery process of the buffer. The most prominent is oil dampers, which were used to absorb the kinetic energy of the moving parts, limiting the maximum travel of the fast actuator. This was demonstrated in [96,98,106,107]. Material buffering utilizing polymer materials such as polyurethane was also used and tested in [64,108]. The study verified the possibility of using polyurethane as buffer devices in a TCA. However, the output characteristics of the material and the reduction in the buffer capacity problems appeared as the number of rapid impacts increased.
Cylindrical buffering was used, as demonstrated by [52,109] and as shown in Figure 10. In this mechanism, the armature repulsion disc was used as the piston in the cylinder. When the repulsion disc drives the contacts to move downward, the air, or SF6 gas as in [93], at the lower part of the cylinder is compressed and a pressure difference is formed on the upper and lower surfaces of the repulsion disc such that the repulsion disc provides a cushioning effect against the counterforce that hinders the downward movement. The cylindrical buffer structure is simple and compact and could be utilized in both opening and closing directions. In addition, the reaction force increases rapidly with the actuation travel curve, which plays an effective buffering role. However, the cylinder buffer has the disadvantages of difficult design and calculation, high production accuracy requirements, difficult short-stroke buffering implementation, and great requirements for the strength of the original parts, which is why, at present, it is rarely used.
Electromagnetic buffering was introduced in [71] and, since then, it was widely adopted. It utilizes the same actuation principle, using the eddy current repulsion. In the opening process, and at a certain travel stage, the closing coil will be energized by a pulse current, which generates an induced eddy current in the repulsion disk, thereby exerting an opposite force to the movement direction of the armature disk to play a buffering role. This is also applicable in the closing process, as the opening coil will act as the buffering unit.
The mechanism of the electromagnetic buffering is well suited for the requirements of rapid operation for buffering reaction force characteristics. The buffering action time and reaction force can be controlled by controlling the energization time and current size of the buffer coil. It has good adjustability and can achieve a good buffering effect. However, this arrangement will double the power circuit size as it requires additional capacitors to provide buffer energy. This will increase the overall volume of the switch. Furthermore, the buffer current input time requires high precision and calibration, and the buffer effect is slightly different for each travel process. For this reason, independent buffering units based on the electromagnetic effect utilizing eddy current dampers were also introduced. Active dampers were investigated in [110,111,112], while passive damping utilizing a linear Halbach passive magnetic damper was demonstrated in [113,114]. A comparison between the two techniques is demonstrated in [104].

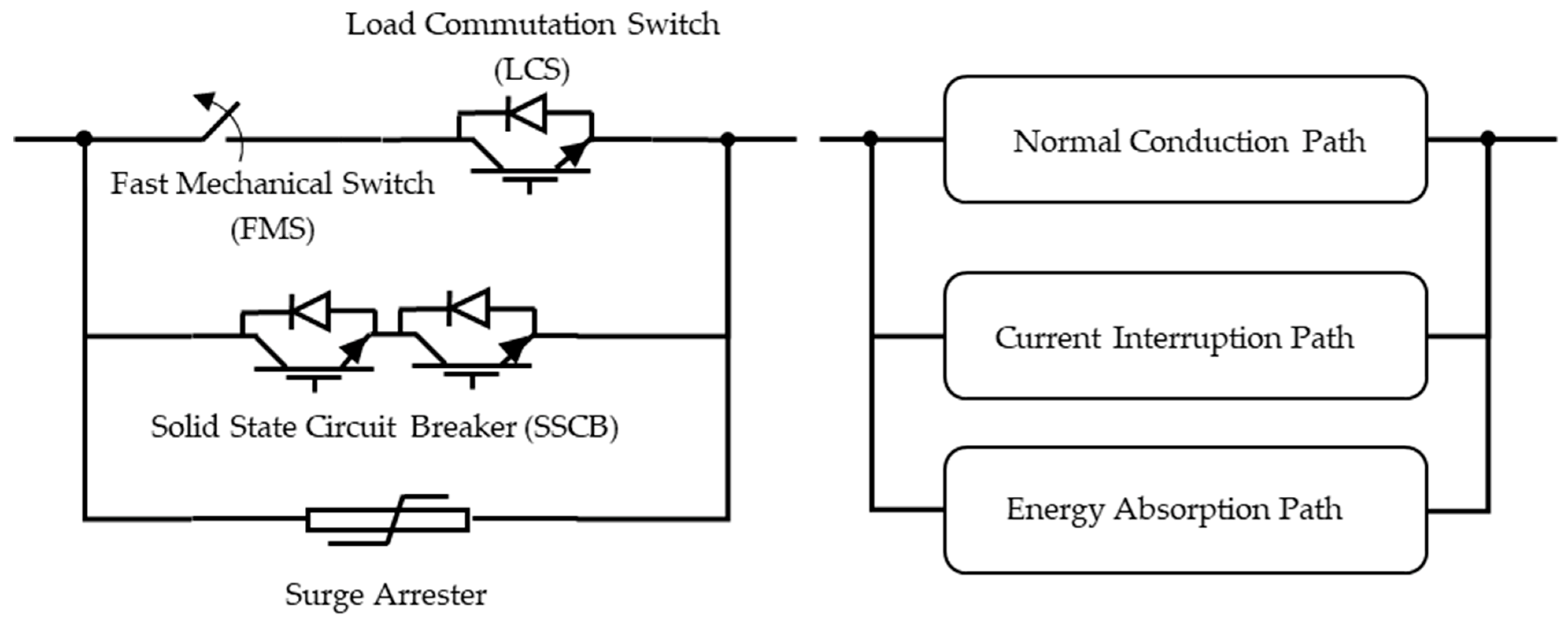
3.4. Control Circuit

The fast-opening speed, high interruption force, and long stroke distance are all supported by the impulse energy input from the pre-charged capacitors. Most Thomson coils need several kilojoules of energy from capacitors stored in millifarads of capacitance with kilovolts of pre-charged voltage. Such high-voltage, high-capacitance capacitors need extra attention to select, implement, and maintain because high-capacitance capacitors tend to slowly degrade over time and consequently fail after their service life. In addition to these challenges, a TCA is required to actuate the moving mass as fast as possible for a designated duration while insuring the effectiveness of the energy transfer from storage to motion. This fueled the research to design, improve, and optimize a TCA’s control circuits, as in [97,115,116,117].
In general, a TCA’s control circuit could be divided into a single pulse circuit and a multiple pulse circuit. The conventional single pulse circuit has a much simpler structure and its configuration varies, as shown in Figure 11a–c. The multiple pulse circuit for a TCA was first introduced in [118] and was called a “two-stage fast actuator power supply”, using only one control switch but two capacitors pre-charged to different voltage levels. The circuit configuration is shown in Figure 12a. Later, a pulse-forming network, as shown in Figure 12b, to generate multiple pulses into the coil was proposed in [62]. These circuits have more components and, thus, require more detailed optimization. This was carried extensively by [97,119], where research on control methodology was investigated during opening and closing operations and the dynamic response of a TCA was investigated. In summary, the single pulse circuit is the most convenient control method; thus, it is the most implemented in the literature for TCA control, as in [31,33,51,52,71]. Moreover, the use of a double- or multiple-stage pulse control circuits’ approach seems to add no significant advantages, as reported by [120].

4. Modeling and Simulation of TCA

As the research on TCAs gained momentum, the need to perform faster, more reliable, and accurate modeling, simulation, and optimization to investigate the operating mechanism performance was also growing. Numerous studies have presented simulation results of Thomson coil actuators designed for fast mechanical switching, with or without experimental validation. Modeling of a TCA is crucial to be able to design such complex drives for the new, emerging switching devices. The main purposes of simulation models were to determine the structural parameters of driving circuits [57,117], the actuator structure [89,121,122,123], and damping systems [52,93,112] in addition to evaluating and optimizing design variables [88] or to improving actuator performances and efficiency [91,124,125,126].
There are mainly two types of analysis to simulate the TCA: analytical, which is dominated by the equivalent-circuit method (ECM), and numerical, which generally uses the finite element method (FEM). Both methods were extensively used to predict the Thomson coil actuator performance, and the results were usually validated by experiments [122,126]. Reports on a TCA using ECM were usually arguing for FEM time and computational cost [71,82,83,100,101,102,127,128]. On the other hand, ECM lacks the simplicity and the physical varieties that FEM can provide [92,121]. Combining the two methods was introduced to achieve less computational time and more accuracy [129], while comparing the two methods was demonstrated in [46]. Other methods were also presented, such as in [130,131], where an electromagnetic forming system with a flat spiral coil as the actuator was solved using the Biot–Savart Law specifically with the use of MATLAB® software.

4.1. Analytical Analysis

In ECM, the simple circuit-based schemes were used to describe the system elements. The theoretical circuit coupled all the physical characteristics of the investigated system and sought to simplify calculation and aid analysis. In a TCA, the lumped equivalent inductance, which contributes the induced electromagnetic force (EMF), is used to reflect the coupling effect of the distributed electromagnetic field in the electric circuit. The gradient of the equivalent inductance contributes to the motional EMF, reflecting the coupling effect of mechanical motion on the electric circuit and the equivalent resistance that varies with temperature, reflecting the coupling effect of the temperature field on the electric circuit. The lumped inductance and its gradient could be extracted by an analytical computational formula or by FEM. Finally, combining the circuit equation, the mechanical motional equation, and the temperature variation equation, the system state equations are presumed, describing the dynamic operation of the TCA actuator. The system state equation is then solved by the fourth-order Runge–Kutta method (see Appendix A for detailed analysis).
Traditionally, ECM is usually preferred to minimize computational effort; the simulation method developed as the modeling tools advanced. For example, an equation-based modeling of a Thomson drive was implemented in [128], while an adaptive equivalent circuit modeling method is shown in [101]. Additionally, an analytical model is shown in [132,133], and a reduced modeling of an eddy current-driven electromechanical drive is explained in [127]. A general method for modeling fast-acting actuators using an interpolation function and electric equivalent networks to account for the eddy currents was introduced in [23]. Equivalent circuit methods were also used to improve the efficiency of the TCA, as in [134]. Moreover, ECM was used in TCA optimization, and an optimal design was introduced in [82,102]. In summary, ECM has the features of a short simulation time, low computational cost, simplified structure, and high accuracy. However, the method has accuracy limits on the relative position of the moving parts. Furthermore, accurate data on the values of each element are needed for the equivalent circuit to be valid. Elements’ non-linearities also need to be considered; adding the resistance temperature-dependent coupling will increase the system complexity, which most of studies had avoided [71,135,136].

4.2. Numerical Analysis

The finite element method (FEM) utilizing multi-physical simulations was used to merge all necessary physics in one simulation model environment that describes the behavior of a TCA. The dynamic electro-magnetic-mechanical formulation system is imposed on the TCA geometry approximation. The highly coupled multiphysics are then iterated for field solution. Examples of such coupling can be seen in detail in [92,121,137,138,139], where the field computations were coupled with circuits to model the TCA (see Appendix B for detailed analysis).
Many FEM studies have been reported as introducing magneto-thermal-mechanical coupled simulation models, and a unified, multi-physical, validated model that can accurately predict the behavior of a TCA was realized via FEM. For example, a comprehensive multi-physical simulation model of a TCA was introduced in [121], and a detailed FEM model was experimentally validated in [122,126]. Additionally, a comparison of coil–disk and coil–coil TCA concepts was introduced in [25,129]. In [87], the TCA load ability and scaling aspects were investigated, while the influence of the velocity term and thermal effects were investigated in [138]. Moreover, the efficiency of a TCA was investigated in [91,140], where FEM was used to improve the efficiency of the TCA.
The physical properties and mechanical parameters of the TCA components were also investigated and simulated in FEM, as in [141]. FEM was also crucial in defining the optimal materials for the TCA components. For example, oxygen-free highly conductive copper, aluminum 6082-T651, and Aluminum 7075-T651 were all simulated and tested for the armature [126]. In [142], the deformation of the armature under the repulsive force action and the drive efficiency was analyzed. In [143], the armature was assumed to be a flexible body, and the curve of repulsive force changing with time was obtained by FEM. In [99], the armature vibration characteristics were studied by coupling magnetic fields and solid mechanics in FEM. A similar study, conducted in [144], analyzed the structural strength of a TCA’s components utilizing two commercial FEM software packages. The stress–time curves results were then compared to a prototype. Furthermore, in [145], the TCA fatigue and life expectancy were investigated by FEM. The study identified the spring connector and the repulsion plate as the most vulnerable parts in a TCA, with a fatigue life of 3600 and 6990 times of operations, respectively.
In summary, FEM could provide a wider approach in investigating the operational performance of a TCA. Despite its time consuming and high computational cost, FEM still represents a powerful tool in the optimization and validation of TCA studies.

5. Exploitation of TCA

TCA applications, and thus circuit topologies, varied as research progressed. They were used in DC as well as in AC switching [146]. In the literature, TCA experimental set-ups could be divided into actuation tests and circuit breaking tests. The earlier only considered the TCA dynamic performance and reported various proof of concepts and design aspects. This was covered in previous sections. In circuit breaking tests, TCAs were deployed alongside different switching units in various circuit breakers’ topologies [147]. This could be further classified into two major categories, arc and arc-less switching, depending upon whether the TCA is driving an interruption switch or a disconnect switch, respectively. The major difference is their fault current interruption capability, and the utilized DC interruption method (Counter voltage, Divergent oscillation, or Current injection) [148].
In HCBs, disconnect switches, also known as ultra-fast disconnect switches, are used if a zero-crossing current is created in the normal conduction path (Figure 1). In the counter voltage method, the arc voltage facilitates the current commutation, and an interruption switch is typically needed. The current interruption capability greatly influences the TCA mechanism in terms of stroke, contact mass, and actuation speed. Higher arc voltage results in a more successful and faster current commutation [149]. Fault current interruption with a TCA-based fast switch was reported in [94,150]. Arc voltage measurement was reported in [151,152]. In [153], the actuator design was optimized to increase the arc voltage by increasing the maximum speed of TCA up to 80 m/s.
Regarding the interruption/disconnecting medium, a vacuum was the mostly frequently used [20]. However, other insulation media were also reported such as air [154], SF6 [155], N2 [156,157,158], and oil [159]. Fast vacuum switching technology, utilizing a high-speed TCA, can reduce the interruption time to a half-cycle of a fault current [146]. The application feasibility was demonstrated for voltage levels up to 500 kV [160,161,162,163], 363 kV [164,165,166], and 252 kV in [76]. Furthermore, as the technology became more mature, multiple applications of TCAs could be seen in the literature, from contactors through disconnectors and reclosers to CBs. For example, a TCA was used for fault current limiting in [167], over current relay (OCR) [168], and transfer switch [44] and was recently applied to the superconducting fault current limiter (SFCL) [169,170].

6. Summary and Conclusions

Hybrid DC circuit breakers have extremely high requirements for the speed, reliability, and the economy of fast mechanical switches. The advantages of a TCA in operating speed allows for considerable application prospects in DC circuit breakers. This article introduces the principle and characteristics and discusses the requirements and construction of the component subassemblies of the TCA mechanism. The underlying challenges and the leading candidate solutions were analyzed, aiming to provide a comprehensive overview of the field. In general, and through the accumulation of the large amount of work in simulation calculations and prototype tests on TCAs, the research concluded that the factors affecting the driving characteristics of the electromagnetic repulsion mechanism include:
  • The structure size and number of turns of the driving coil. Increasing the coil inductance can increase the induced magnetic field, thus increasing the eddy current of the armature. However, it will reduce the current rise rate, and a relatively optimal value is required. In addition, the magnetic circuit can be improved by increasing the magnetic material, the reasonable design of the coil frame material, optimizing the magnetic field coupling, and improving the driving efficiency.
  • The structure size and material of the repulsion disk. When the outer diameter of the armature and the driving coil are the same, the electromagnetic repulsive force is larger and the driving efficiency is higher. Furthermore, the higher the electrical conductivity of the armature material, the greater the induced eddy current, the greater the electromagnetic repulsion force, and the higher the driving efficiency. Considering the skin effect, the driving efficiency could be increased when the thickness of the repulsion plate is twice the corresponding skin depth at a certain discharge frequency of the coil. Considering the armature type, the driving efficiency of the coil–coil type repulsive force mechanism is about twice that of the coil–disk type, but the moving mass is larger. The coil–coil type repulsive force mechanism is suitable when the load mass is large.
  • The initial gap between the coil and the disk. A smaller initial coil–armature gap will result in a greater repulsive force and higher drive efficiency.
  • The capacitance of the energy storage capacitor. A TCA is highly sensitive to the chosen capacitance and charging voltage. For a particular geometry, load, and material, there exists an optimum capacitance and charging voltage. Studies indicate that a larger voltage and smaller capacitance result in a higher current peak and speed, which are better in terms of force and speed. When the capacitance value of the capacitor is large, the pulse width of the current and the repulsive force is large. However, the rising rate became smaller with a slower initial acceleration, and the other way around. Thus, a trade-off needs to be optimized.
Finally, based on the research status, the following key points could be drafted for the development of TCA performance.
  • Efficiency improvement.
    At present, the driving efficiency of the TCA is very low. The highest theoretically calculated efficiency that could be achieved in a Thomson coil was of 54%, which does not meet the economic requirements of the future DC grids. There is still much work that could be performed by promoting research on improving the driving characteristics, reducing the capacity of the energy storage power supply, and forming a driving efficiency optimization design method.
  • Buffering and holding mechanisms.
    A TCA has a short response time and a fast initial movement speed. The research could be focused on the development of the buffer and holding devices that better match the output characteristics of the repulsion mechanism. This is to enhance buffering and holding effects while ensuring the rapidity of the overall mechanism.
  • Mechanical transmission structure.
    A TCA has a very large repulsion peak during the driving process and a short duration, which brings a great mechanical load to the transmission structure and puts forward great requirements on the structural strength while reducing the motion quality and ensuring the rapidity of the action. It is of great significance to improve the reliability of a TCA and even the overall reliability of the DC circuit breaker by analyzing the impact stress in the operation process and designing an efficient and reliable transmission system. Analyzing the influence of the impact force on the transmission rod and optimizing the structure of the key weak components are the research focus of studying the impact stress of the transmission system and improving the mechanical life.
  • Stroke feasibility.
    A TCA basically relies on inertia in the later stage of the movement and is mostly used in short-stroke drives. Utilizing the rapidity of the repulsion mechanism for higher voltage levels’ and larger strokes’ requirements is of great significance to the application of a TCA to a wider switchgear application.

Author Contributions

Conceptualization, M.A.-D. and G.Z.; literature survey, M.A.-D., J.C., S.S. and M.Y.; writing—original draft preparation, M.A.-D.; writing—review and editing, M.A.-D. and G.Z.; visualization, M.A.-D.; supervision and project administration, G.Z. and Y.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the Science and Technology Project of State Grid Corporation of China, grant number 5500-202199527A-0-5-ZN.

Data Availability Statement

The data presented in this study are available on request from the corresponding authors.

Acknowledgments

The first author would like to take this opportunity to extend his thanks to Xi Bin from the School of International Education at Xi’an Jiaotong University for his continued support, especially during the pandemic.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A. Equivalent Circuit Model (ECM)

This section illustrates the opening process of a TCA simulation by ECM. The TCA is divided into three parts: the drive circuit, the buffer circuit, and the armature circuit. The drive circuit consists of a capacitor Cd, thyristors Td, and the drive coil Ld. Similarly, the buffer circuit includes a capacitor Cb, thyristor Tb, and the buffer coil Lb. The system is shown in Figure A1, and the equations for the opening drive circuit are as follows:
L d d i d d t − d M a d i a d t + R d i d = U C d
L a d i a d t − d M a d i d d t + R a i a = 0
The relationships between the drive current and the capacitor voltage in the drive coil circuit are stated as follows:
C d d U C d d t + i d = 0
Similarly, the equations for the buffer circuit are shown as follows:
L b d i b d t − d M a b i a d t + R b i b = U C b
L a d i a d t − d M a b i b d t + R a i a = 0
The relationship between the buffer current and the capacitor voltage in the buffer circuit is stated as follows:
C b d U C b d t + i b = 0
The electromagnetic forces between the drive/buffer coil and armature metal plate are shown as follows:
F d = d M a d d z i d i a
F b = d M a b d z i b i a
F = F d + F b
The motional equations of the metal plate are as follows:
d z d t = v
d v d t = F − f m l o a d
where Ld and Lb are the self-inductance of the drive and buffer coil, respectively. Rd and Rb are the equivalent resistance of the drive and buffer coil, respectively. La is the self-inductance of the armature metal plate. Ra is the equivalent resistance of the armature metal plate. UCd and UCb are the voltages of the capacitors Cd and Cb, respectively. Mad and Mab are the mutual inductances between the drive/buffer coils and the armature metal plate, respectively. The id and ib are the corresponding drive and buffer currents, respectively. The ia stands for the eddy current in the armature metal plate.
Actuators 11 00154 g0a1 550
Figure A1. ECM schematic of the TCA drive, buffer, and armature circuits.
Figure A1. ECM schematic of the TCA drive, buffer, and armature circuits.
Actuators 11 00154 g0a1
Since the system as a whole is considered axis-symmetric, and because the eddy current in the armature plate is unevenly distributed, the armature plate could be divided into a series of segments, relatively similar to FEM mesh; the current is assumed to be uniform in each segment []. Each segment represents a conducting ring that corresponds to resistance and inductance, as shown in Figure A2.
Actuators 11 00154 g0a2 550
Figure A2. Partition principle of the armature.
Figure A2. Partition principle of the armature.
Actuators 11 00154 g0a2
Based on this modeling technique, the armature plate circuit could be represented by a matrix of Laij, Raij, and iaij, with each corresponding to a mutual inductance matrix Madij and Mabij, where i and j represent the segment raw no. and column no., respectively. The armature equation system could be rewritten as:
L a = ∑ i , j n , m L a i j
R a = ∑ i , j n , m R a i j
i a = ∑ i , j n , m i a i j
M a b = ∑ i , j n , m M a b i j
M a d = ∑ i , j n , m M a d i j
where n and m are the segment raw and column total number, respectively. The coils’ self and mutual inductances could be calculated by either using the FEM magnetostatics solver [129] or by analytical methods such as in [171]. The latter is preferred to keep the continuity of the ECM calculation code.

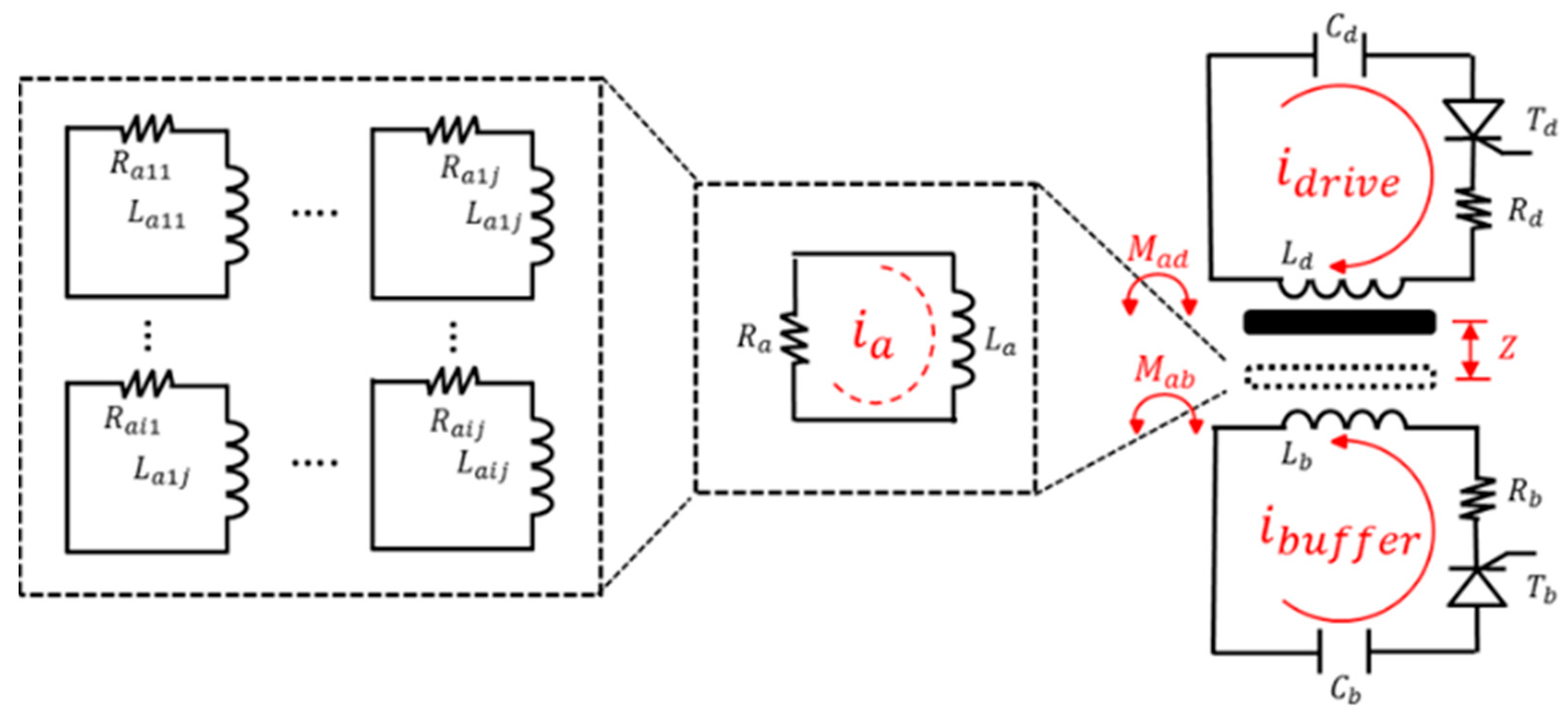
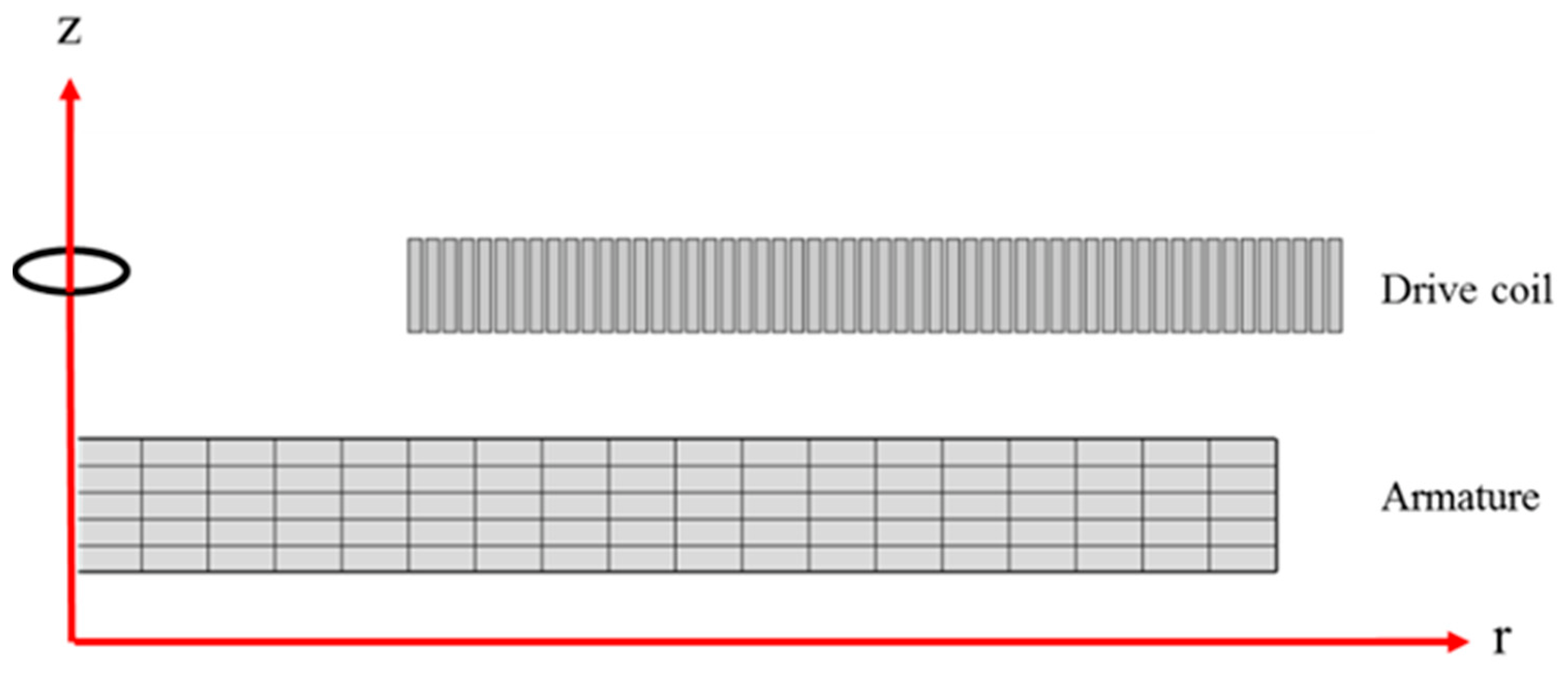
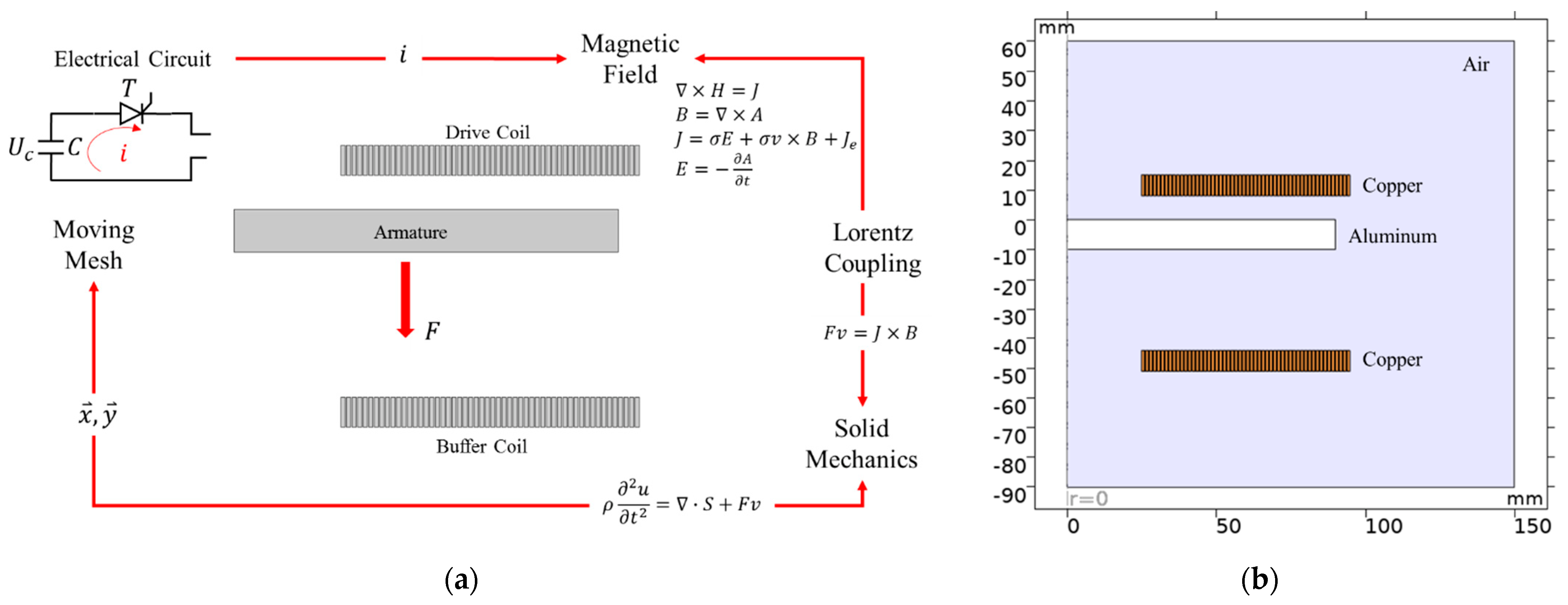
Appendix B. Finite Element Method (FEM)

The TCA mechanism includes electrical, magnetic, and mechanical physics. These operations are highly coupled and need to be studied simultaneously. FEM is used to model the drive/buffer circuit, the spiral coils, and the armature comprising the electromagnetic and mechanical equations. The electric control circuits could also be included in the FEM environment, utilizing the electric circuit interface (for example, as in COMSOL Multiphysics) or live-linked to FEM using other software (for example, SPICE or MATLAB).
The TCA system is axis-symmetric. Thus, the rotational symmetry approach is adapted. This modeling technique is used to reduce the model complexity, avoiding the need to use 3D simulations. The geometry of the actuator is simplified and drawn in a two-dimensional, axis-symmetric coordinate system to reduce computation time. The coil is modeled as a number of adjacent and insulated rectangles representing its turns. The width and depth of each rectangle correspond to the cross-section of the copper conductor used to wound the coil. The same principle applies to the armature. The model geometry is shown in Figure A3.
Actuators 11 00154 g0a3 550
Figure A3. FEM geometry showing the drive coil, armature, and buffer coil. (a) FEM coupling; (b) 2D, axial-symmetric geometry configuration and materials.
Figure A3. FEM geometry showing the drive coil, armature, and buffer coil. (a) FEM coupling; (b) 2D, axial-symmetric geometry configuration and materials.
Actuators 11 00154 g0a3
The electric circuit interface is used to model the control circuits, and the circuits were coupled to the coils. The magnetic field interface is used to model the coil–armature interaction. The interface solves for the induced current and the generated electromagnetic force. The mechanic’s interface sums up all the forces on the armature, including the electromagnetic force provided by the magnetic interface and the added load (moving contact mass). The mechanical module solves for the velocity and displacement of the armature. The new position of the armature is fed back to the magnetic field interface through the velocity Lorentz term coupling. A moving mesh based on the arbitrary Lagrange–Euler method (ALE) is used since the induced forces are highly dependent on the position of the armature. Subsequently, all the physics’ interfaces are coupled together and solved simultaneously.
The coupled differential equations describing the TCA physical system are shown from Equations (A17) to (A21). The electromagnetic field physics’ interface solves for the following equations:
∇ × H = J
B = ∇ × A
J = σ E + σ v × B + J e
E = − ∂ A ∂ t
where H is the magnetic field, J is the current density, B is the magnetic flux density, E is the electric field, σ is the electrical conductivity, v is the velocity, A is the magnetic vector potential, and t is the time. The mechanical interface solves for the following equation:
ρ ∂ 2 u ∂ t 2 = ∇ · S + F v
where ρ is the density, u is the displacement, S is the mechanical stress tensor, and F is the force.

References

  1. Saeedifard, M.; Graovac, M.; Dias, R.F.; Iravani, R. DC power systems: Challenges and opportunities. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25 July 2010; pp. 1–7. [Google Scholar]
  2. Li, G.; Balasubramaniam, S.; Tibin, J.; Ugalde-Loo, C.E.; Khadijat, F.J. Frontiers of DC circuit breakers in HVDC and MVDC systems. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
  3. Bayati, N.; Hajizadeh, A.; Soltani, M. Protection in DC microgrids: A comparative review. IET Smart Grid. 2018, 1, 66–75. [Google Scholar] [CrossRef]
  4. Mohammadi, F.; Rouzbehi, K.; Hajian, M.; Niayesh, K.; Gharehpetian, G.B.; Saad, H.; Ali, M.H.; Sood, V.K. HVDC Circuit Breakers: A Comprehensive Review. IEEE Trans. Power Electron. 2021, 36, 13726–13739. [Google Scholar] [CrossRef]
  5. Bini, R.; Backman, M.; Hassanpoor, A. Interruption technologies for HVDC transmission: State-of-art and outlook. In Proceedings of the 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017. [Google Scholar]
  6. Christian, M.F. HVDC Circuit Breakers: A Review Identifying Future Research Needs. IEEE Trans. Power Del. 2011, 26, 998–1007. [Google Scholar]
  7. Pei, X.; Cwikowski, O.; Vilchis-Rodriguez, D.S.; Barnes, M.; Smith, A.C.; Shuttleworth, R. A review of technologies for MVDC circuit breakers. In Proceedings of the IECON 2016 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
  8. Barnes, M.; Vilchis-Rodriguez, D.S.; Pei, X.; Shuttleworth, R.; Cwikowski, O.; Smith, A.C. HVDC circuit breakers–A review. IEEE Access. 2020, 8, 211829–211848. [Google Scholar] [CrossRef]
  9. Du, C.; Wang, C. Review of DC circuit breaker technology for HVDC application. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
  10. Mokhberdoran, A.; Carvalho, A.; Leite, H.; Silva, N. A review on HVDC circuit breakers. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014. [Google Scholar]
  11. Zheng, S.; Kheirollahi, R.; Pan, J.; Xue, L.; Wang, J.; Lu, F. DC Circuit Breakers: A Technology Development Status Survey. IEEE Trans. Smart Grid. 2021. [Google Scholar] [CrossRef]
  12. Thakur, H. HVDC circuit breaker: A review on challenges and innovations. Int. J. Electr. Eng. Technol. 2015, 6, 7–17. [Google Scholar]
  13. Häfner, J.; Jacobson, B. Proactive Hybrid HVDC Breakers—A Key Innovation for Reliable HVDC Grids; Paper 0264; Cigré: Bologna, Italy, 2011. [Google Scholar]
  14. Bösche, D.; Wilkening, E.D.; Köpf, H.; Kurrat, M. Hybrid DC circuit breaker feasibility study. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 7, 354–362. [Google Scholar] [CrossRef]
  15. Mitra, B.; Chowdhury, B. Comparative analysis of hybrid DC breaker and assembly HVDC breaker. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
  16. Shukla, A.; Demetriades, G.D. A survey on hybrid circuit-breaker topologies. IEEE Trans. Power Deliv. 2015, 30, 627–641. [Google Scholar] [CrossRef]
  17. Indragandhi, V.; Kumar, L.A.; Vishnumoorthy, K. Methods of operating mechanisms of high voltage circuit breakers—An overview. In Proceedings of the 2017 International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 2–5 October 2017. [Google Scholar]
  18. Xu, C.; Damle, T.; Graber, L. A survey on mechanical switches for hybrid circuit breakers. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
  19. Cheng, C.; Liu, Y.; Wei, J.; Yuan, H. Design and Research of Operating Repulsion Mechanism Suitable for 252kV High-Speed Breaking Circuit Breaker. J. Phys. Conf. Ser. 2022, 2166, 012018. [Google Scholar] [CrossRef]
  20. Yao, X.; Wang, J.; Ai, S.; Liu, Z.; Geng, Y.; Hao, Z. Vacuum Switching Technology for Future of Power Systems. Engineering, 2022; in press. [Google Scholar] [CrossRef]
  21. Stroehla, T.; Dahlmann, M.; Sattel, T. Electromagnetic Actuators. In Proceedings of the ACTUATOR, International Conference and Exhibition on New Actuator Systems and Applications 2021, Virtual Event, Online, 17–19 February 2021. [Google Scholar]
  22. Puumala, V.; Kettunen, L. Electromagnetic Design of Ultrafast Electromechanical Switches. IEEE Trans. Power Deliv. 2015, 30, 1104–1109. [Google Scholar] [CrossRef]
  23. Challita, A.; Uva, M. High Speed, Medium Voltage Direct Current Isolation Device. In Proceedings of the Electric Machines Technology Symposium, Villanova, PA, USA, 28–29 May 2014. [Google Scholar]
  24. Stroehla, T.; Dahlmann, M.; Kellerer, T.; Wagner, T.; Wagner, N.; Sattel, T. Ultra-fast moving coil actuator for power switches in medium-voltage grids. J. Eng. 2019, 2019, 4085–4089. [Google Scholar] [CrossRef]
  25. Bissal, A.; Magnusson, J.; Engdahl, G. Comparison of Two Ultra-Fast Actuator Concepts. IEEE Trans. Magn. 2012, 48, 3315–3318. [Google Scholar] [CrossRef]
  26. Zhao, Y.U.; Xinlin, Y.U.; Xiaoguang, W.E. Comprehensive optimization of coil-coil electromagnetic repulsive actuators. High Volt. Eng. 2015, 41, 4207–4212. [Google Scholar]
  27. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Barnes, M. Double-sided Thomson coil based actuator: Finite element design and performance analysis. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 19–21 April 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
  28. Nanxun, Z.; Chun, F.; Pan, G.; Wei, L.; Bi, Z.; Xiao, R. Comparison of two types of electromagnetic repulsive force actuators. In Proceedings of the 2017 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017. [Google Scholar]
  29. Henry, W.J.; Armstrong, S.H. High Speed Device for Interrupting and Completing High Voltage Power Circuits. U.S. Patent 3,268,687, 23 August 1966. [Google Scholar]
  30. Basu, S.; Srivastava, K.D. Electromagnetic Forces on a Metal Disk in an Alternating Magnetic Field. IEEE Trans. Power Appar. Syst. 1969, 88, 1281–1285. [Google Scholar] [CrossRef]
  31. Basu, S.; Srivastava, K.D. Analysis of a Fast Acting Circuit Breaker Mechanism Part I: Electrical Aspects. IEEE Trans. Power Appar. Syst. 1972, 91, 1197–1203. [Google Scholar] [CrossRef]
  32. Basu, S.; Srivastava, K.D. Analysis of a Fast Acting Circuit Breaker Mechanism, Part II: Thermal and Mechanical Aspects. IEEE Trans. Power Appar. Syst. 1972, 3, 1203–1211. [Google Scholar] [CrossRef]
  33. Rajotte, R.J.; Drouet, M.G. Experimental analysis of a fast acting circuit breaker mechanis Electrical aspects. IEEE Trans. Power Appar. Syst. 1975, 94, 89–96. [Google Scholar] [CrossRef]
  34. Pokryvailo, A.; Maron, V.; Melnik, D. Review of opening switches for long-charge fieldable inductive storage systems. In Proceedings of the Digest of Technical Papers 12th IEEE International Pulsed Power Conference (Cat. No. 99CH36358), Monterey, CA, USA, 27–30 June 1999. [Google Scholar]
  35. Genji, T.; Nakamura, O.; Isozaki, M.; Yamada, M.; Morita, T.; Kaneda, M. 400 V class high-speed current limiting circuit breaker for electric power system. IEEE Trans. Power Deliv. 1994, 9, 1428–1435. [Google Scholar] [CrossRef]
  36. Yamaji, Y.; Maruyama, T.; Kishida, Y.; Koyama, K. High speed switch applicated VI. In The Paper of Technical Meeting on Switching and Protection and High Voltage Engineering. IEE Japan, SP-95-40, HV-95-153. 1995. [Google Scholar]
  37. Jungblut, R.; Sittig, R. Hybrid high-speed DC circuit breaker using charge-storage diode. In Proceedings of the 1998 IEEE Industrial and Commercial Power Systems Technical Conference, Conference Record, Papers Presented at the 1998 Annual Meeting (Cat. No. 98CH36202), Edmonton, AB, Canada, 3–8 May 1998. [Google Scholar]
  38. Kishida, Y.; Koyama, K.; Sasao, H.; Maruyama, N.; Yamamoto, H. Development of the high speed switch and its application. In Proceedings of the 1998 IEEE Industry Applications Conference, Thirty-Third IAS Annual Meeting, St. Louis, MO, USA, 12–15 October 1998. [Google Scholar]
  39. Polman, J.; Ferreira, A.; Kaanders, M.; Evenblij, B.H.; van Gelder, P. Design of a bi-directional 600 V/6 kA ZVS hybrid DC switch using IGBTs. In Proceedings of the IEEE Industry Applications Conference 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001. [Google Scholar]
  40. Holaus, W. Design of elementary switches for high power with minimal moving mass. IASTED Conf. Power Energy Syst. 2001, 19, 22. [Google Scholar]
  41. Holaus, W.; Frohlich, K. Ultra-fast switches-a new element for medium voltage fault current limiting switchgear. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 02CH37309), New York, NY, USA, 27–31 January 2002. [Google Scholar]
  42. Koyama, K.; Takeuchi, T.; Kishida, Y.; Oshige, T.; Yoshizawa, T.; Sasao, H. Development of 24kV-rated High Speed Circuit Breaker. IEEJ Trans. Power Energy 2001, 121, 1187–1192. [Google Scholar] [CrossRef]
  43. Takeuchi, T.; Yoshizawa, T.; Kishida, Y.; Koyama, K.; Oshige, T.; Sasao, H. Electromagnetic field analysis coupling with motion for a high speed circuit breaker. IEEJ Trans. Power Energy 2001, 121, 1181–1186. [Google Scholar] [CrossRef] [Green Version]
  44. Li, Q.; Liu, W.; Xu, G.; Qian, J.-L. Research on High Voltage Fast Transfer Switch. High Volt. Appar. 2003, 39, 6–7. [Google Scholar]
  45. Steurer, M.; Frohlich, K.; Holaus, W.; Kaltenegger, K. A novel hybrid current-limiting circuit breaker for medium voltage: Principle and test results. IEEE Trans. Power Deliv. 2003, 18, 460–467. [Google Scholar] [CrossRef]
  46. Takeuchi, T.; Koyama, K.; Tsukima, M. Electromagnetic analysis coupled with motion for high speed circuit breakers of eddy current repulsion using the tableau approach. IEEJ Trans. Power Energy 2004, 124, 859–865. [Google Scholar] [CrossRef] [Green Version]
  47. Meyer, J.; Rufer, A. A DC hybrid circuit breaker with ultra-fast contact opening and integrated gate-commutated thyristors (IGCTs). IEEE Trans. Power Deliv. 2006, 21, 646–651. [Google Scholar] [CrossRef]
  48. Roodenburg, B.; Kaanders, M.; Huijser, T. First results from an electro-magnetic (EM) drive high acceleration of a circuit breaker contact for a hybrid switch. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005. [Google Scholar] [CrossRef]
  49. Dong, E.; Li, B.; Zou, J. Comparison analysis of experiment performance between high-speed repulsion mechanism and permanent magnetic mechanism. High Volt. Appar. 2007, 43, 125–126. [Google Scholar]
  50. Enyuan, D.; Yongxing, W.; Jiyuan, C.; Jiyan, Z. The analysis of high-speed repulsion actuator and performance comparisons with permanent magnetic actuator in vacuum circuit breaker. In Proceedings of the 2008 23rd International Symposium on Discharges and Electrical Insulation in Vacuum, Bucharest, Romania, 15–19 September 2008. [Google Scholar]
  51. Tsukima, M.; Takeuchi, T.; Koyama, K.; Yoshiyasu, H. Development of a high-speed electromagnetic repulsion mechanism for high-voltage vacuum circuit breakers. Electr. Eng. Japan 2008, 163, 34–40. [Google Scholar] [CrossRef]
  52. Roodenburg, B.; Evenblij, B.H. Design of a fast linear drive for (hybrid) circuit breakers–development and validation of a multi domain simulation environment. Mechatronics 2008, 18, 159–171. [Google Scholar] [CrossRef]
  53. Skarby, P.; Steiger, U. An ultra-fast disconnecting switch for a hybrid HVDC breaker—A technical breakthrough. In Proceedings of the CIGRE 265, Calgary, Alberta, 9–11 September 2013. [Google Scholar]
  54. Shi, Z.Q.; Jia, S.L.; Ma, M.; Song, X.C.; Yang, H.Y.; Liu, C.; Wang, L.J. Investigation on DC interruption based on artificial current zero of vacuum switch. In Proceedings of the 24th ISDEIV 2010, Braunschweig, Germany, 30 August–3 September 2010; pp. 158–161. [Google Scholar] [CrossRef]
  55. Li, W.; Jeong, Y.W.; Yoon, H.S.; Koh, C.S. Analysis of parameters influence on the characteristics of Thomson coil type actuator of arc eliminator using adaptive segmentation equivalent circuit method. J. Electr. Eng. Technol. 2010, 5, 282–289. [Google Scholar] [CrossRef] [Green Version]
  56. Li, W.; Koh, C.S. Design of the thomson-coil actuator of an arc eliminator using adaptive equivalent circuit method. In Proceedings of the 2010 International Conference on Electrical Machines and Systems 2010, Incheon, Korea, 10–13 October 2010. [Google Scholar]
  57. Yang, F.; He, H.; Rong, M.; Hu, Z.; Wu, Y. Operating property analysis of a new high-speed DC switch repulsion mechanism. In Proceedings of the 2011 1st International Conference on Electric Power Equipment-Switching Technology, Xi’an, China, 23–27 October 2011. [Google Scholar]
  58. Yang, F.; Zhang, X.F.; Zhuang, J.W.; Dai, C. Shipping distribution networks short circuit selective protection method base on fast recovery power breaker. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011. [Google Scholar]
  59. Wu, Y.; He, H.; Hu, Z.; Yang, F.; Rong, M.; Li, Y. Analysis of a new high-speed DC switch repulsion mechanism. IEICE Trans. Electron. 2011, 94, 1409–1415. [Google Scholar] [CrossRef]
  60. Zheng, Z.; Dong, E.; Zou, J.; Zhang, Z.; Tian, P.; Chen, X. A High Speed Actuator for 1.14 kV Rated Vacuum Switch. In Proceedings of the 2011 1st International Conference on Electric Power Equipment-Switching Technology, Xi’an, China, 23–27 October 2011. [Google Scholar]
  61. Dong, E.; Tian, P.; Wang, Y.; Liu, W. The design and experimental analysis of high-speed switch in 1.14 kV level based on novel repulsion actuator. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011. [Google Scholar]
  62. Wang, Z.; Junjia, H.E.; Xiaogen, Y.I.N.; Lu, J.; Hui, J. 10 kV high speed vacuum switch with electromagnetic repulsion mechanism. Trans. China Electrotech. Soc. 2009, 24, 68–75. [Google Scholar]
  63. Meng, H.; Li, M.K.; Xu, Z.C.; Kang, C.Q.; Sun, R.Z.; Tang, Z.F.; Jiang, H.T. Study on 10kV Quick Vacuum Circuit Breaker of Double Opening and Closing Coil. In Proceedings of the 4th International Conference on Artificial Intelligence & Computer Science 2016 (AICS 2016), Langkawi, Malaysia, 28–29 November 2016. [Google Scholar]
  64. Yuan, Z.; He, J.; Pan, Y.; Jing, X.; Zhong, C.; Zhang, N.; Wei, X.; Tang, G. Research on ultra-fast vacuum mechanical switch driven by repulsive force actuator. Rev. Sci. Instrum. 2016, 87, 125103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  65. Song, X.; Peng, C.; Huang, A.Q. A medium-voltage hybrid DC circuit breaker, Part I: Solid-state main breaker based on 15 kV SiC emitter turn-OFF thyristor. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 278–288. [Google Scholar] [CrossRef]
  66. Peng, C.; Song, X.; Huang, A.Q.; Husain, I. A Medium-Voltage Hybrid DC Circuit Breaker—Part II: Ultrafast Mechanical Switch. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 289–296. [Google Scholar] [CrossRef]
  67. Peng, C.; Husain, I.; Huang, A.Q.; Lequesne, B.; Briggs, R. A Fast Mechanical Switch for Medium-Voltage Hybrid DC and AC Circuit Breakers. IEEE Trans. Ind. Appl. 2016, 52, 2911–2918. [Google Scholar] [CrossRef]
  68. Xiaodong, X.; Zhibing, L.; Xianlgian, Y.; Beiyang, L.; Yang, T. Design and test of vacuum circuit breaker with hybrid fast operating mechanism. In Proceedings of the 2011 1st International Conference on Electric Power Equipment-Switching Technology, Xi’an, China, 23–27 October 2011. [Google Scholar]
  69. Baudoin, B.; Hátsági, M.; Álvarez, L.; Ängquist, S.; Nee, S.; Norrga, T. Modeer: Experimental results from a Thomson-coil actuator for a vacuum interrupter in an HVDC breaker. J. Eng. 2019, 2019, 3527–3531. [Google Scholar] [CrossRef]
  70. Chunguang, H.; Jinjin, W.; Ying, H.; Yundong, C.; Yuchen, C. Design and research of high stability repulsion mechanism of 12 kV vacuum circuit breaker. In Proceedings of the 27th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), Suzhou, China, 18–23 September 2016. [Google Scholar]
  71. Wen, W.; Huang, Y.; Al-Dweikat, M.; Cheng, T.; Gao, S.; Liu, W. Research on operating mechanism for ultra-fast 40.5-kV vacuum switches. IEEE Trans. Power Deliv. 2015, 30, 2553–2560. [Google Scholar] [CrossRef]
  72. Ren, L.; Huang, Y.; Song, Y.; Yao, X.; Zhang, B.; Hong, L.; Geng, Y.; Liu, Z.; Wang, J.; Bai, C.; et al. Development of an electromagnetic repulsion mechanism for a 40.5 kV fast vacuum circuit breaker. In Proceedings of the 2017 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017. [Google Scholar]
  73. Wang, K.; Zheng, X.; Zou, L.; Huang, Z.; Zou, J. A New Type Electromagnetic Repulsive Mechanism for 40.5 kV Vacuum Circuit Breaker. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  74. Jiang, J.; Wang, L.; Ma, J.; Jia, S.; Wu, S.; Pan, F.; Su, H.; Qiao, S. Research on the Coordination of 40.5 kV Fast Vacuum Switch Driven by Electromagnetic Repulsion Mechanism and Oil Damper. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  75. Liu, B.; Xie, P.; Yu, H.; Xiong, J.; Zhang, X. Experimental Study on Fast Isolating Switch With Vacuum Multi-breaks. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018. [Google Scholar]
  76. Ma, K.; Yao, X.; Ai, S.; Wang, S.; Liu, Z.; Wang, J.; Zhang, B. Development and Test of a 252 kV Multi-breaks Bus-tie Fast Vacuum Circuit Breaker. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  77. Zhang, X.; Yu, Z.; Zeng, R.; Huang, Y.; Zhao, B.; Chen, Z.; Yang, Y. A State-of-the-Art 500-kV Hybrid Circuit Breaker for a dc Grid: The World’s Largest Capacity High-Voltage dc Circuit Breaker. IEEE Ind. Electron. Mag. 2020, 14, 15–27. [Google Scholar] [CrossRef]
  78. Karlström, P.O.; Eriksson, T.R.; Salinas, E.; Bissal, A. High Voltage Current Interrupter and an Actuator System for a High Voltage Current Interrupter. US Patent 9,183,996, 10 November 2015. [Google Scholar]
  79. Kim, B.C.; Chung, Y.H.; Hwang, H.D.; Mok, H.S. Development of HVDC circuit breaker with fast interruption speed. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015. [Google Scholar]
  80. Ohlsson, D.; Korbel, J.; Lindholm, P.; Steiger, U.; Skarby, P.; Simonidis, C.; Kotilainen, S. Opening move: 30 times faster than the blink of an eye, simulating the extreme in HVDC switchgear. ABB Rev. 2013, 3, 27–33. [Google Scholar]
  81. Li, W.; Jeong, Y.W.; Koh, C.S. Shape Optimization of a Thomson coil Actuator of Arc Eliminator Using Topology Modification. KoreaScience 2009, 7, 774–775. [Google Scholar]
  82. Pham, M.T.; Ren, Z.Y.; Li, W.; Koh, C.S. Optimal Design of a Thomson-Coil Actuator Utilizing a Mixed-Integer-Discrete-Continuous Variables Global Optimization Algorithm. IEEE Trans. Magn. 2011, 47, 4163–4167. [Google Scholar] [CrossRef]
  83. Li, W.; Ren, Z.Y.; Jeong, Y.W.; Koh, C.S. Optimal Shape Design of a Thomson-Coil Actuator Utilizing Generalized Topology Optimization Based on Equivalent Circuit Method. IEEE Trans. Magn. 2011, 47, 1246–1249. [Google Scholar] [CrossRef]
  84. Dong, E.Y.; Liu, M.W.; Li, Z.B.; Yan, X.L.; Chen, Y.S. Structure Optimization on High-speed Electromagnetic Repulsion Mechanism. Appl. Mech. Mater. 2014, 532, 611–615. [Google Scholar] [CrossRef]
  85. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Smith, A.C.; Barnes, M. Design, Construction, and Test of a Lightweight Thomson Coil Actuator for Medium-Voltage Vacuum Switch Operation. IEEE Trans. Energy Convers. 2019, 34, 1542–1552. [Google Scholar] [CrossRef] [Green Version]
  86. Ota, T.; Mitsutake, Y.; Hasegawa, Y.; Hirata, K.; Tanaka, T. Dynamic analysis of electromagnetic impact drive mechanism using eddy current. IEEE Trans. Magn. 2007, 43, 1421–1424. [Google Scholar] [CrossRef]
  87. Bissal, A.; Magnusson, J.; Engdahl, G.; Salinas, E. Loadability and scaling aspects of Thomson based ultra-fast actuators. In Proceedings of the Actuator 2012, Bremen Convention Center, Bremen, Germany, 18–20 June 2012. [Google Scholar]
  88. Peng, C.; Husain, I.; Huang, A.Q. Evaluation of design variables in Thompson coil based operating mechanisms for ultra-fast opening in hybrid AC and DC circuit breakers. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
  89. Park, S.H.; Jang, H.J.; Chong, J.K.; Lee, W.Y. Dynamic analysis of Thomson coil actuator for fast switch of HVDC circuit breaker. In Proceedings of the 2015 3rd International Conference on Electric Power Equipment–Switching Technology (ICEPE-ST), Busan, Korea, 25–28 October 2015. [Google Scholar]
  90. Zhou, Y.; Qi, L.; Zhuang, J.; Yuan, Z.; Jiang, Z.; Fang, W. Analysis and experimentation of motion characteristics in electromagnetic repulsion mechanism considering the elastic deformation. CSEE 2016, 36, 206–212. [Google Scholar]
  91. Bissal, A.; Jesper, M.; Engdahl, G. Electric to mechanical energy conversion of linear ultrafast electromechanical actuators based on stroke requirements. IEEE Trans. Ind. Appl. 2015, 51, 3059–3067. [Google Scholar] [CrossRef]
  92. Bissal, A.; Salinas, E.; Engdahl, G.; Ohrstrom, M. Simulation and Verification of Thomson Actuator Systems; KTH Royal Institute of Technology: Stockholm, Sweden, 2010. [Google Scholar]
  93. Wu, Y.; Wu, Y.; Rong, M.; Yang, F.; Zhong, J.; Li, M.; Hu, Y. A new Thomson coil actuator: Principle and analysis. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 1644–1655. [Google Scholar]
  94. Zhang, B.; Tan, Y.; Ren, L.; Wang, J.; Geng, Y.; Liu, Z.; Yanabu, S. Interruption capability of a fast vacuum circuit breaker with a short arcing time. In Proceedings of the 2016 27th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), Suzhou, China, 18–23 September 2016. [Google Scholar]
  95. Hedayati, M.; Jovcic, D. Low Voltage Prototype Design, Fabrication and Testing of Ultra-Fast Disconnector (UFD) for Hybrid DC CB. In Proceedings of the CIGRE B4, Winnipeg, MB, Canada, 30 September–6 October 2017. [Google Scholar]
  96. Hou, Y.; Shi, Z.; Li, S.; Yao, Q.; Miao, Y.; Zhang, S.; Qiu, N. Research on fast opening process in electromagnetic repulsion mechanism. IEEE Trans. Magn. 2019, 55, 8000704. [Google Scholar] [CrossRef]
  97. Zhou, Y.; Huang, Y.; Wen, W.; Lu, J.; Cheng, T.; Gao, S. Research on a novel drive unit of fast mechanical switch with modular double capacitors. J. Eng. 2019, 2019, 4345–4348. [Google Scholar] [CrossRef]
  98. Guan, C.; Yao, X.; Zhang, L.; Zhao, Q.; Wang, J.; Liu, Z.; Geng, Y. Research and Verification of Opening Characteristics of a Modular 72.5 kV Fast Vacuum Circuit Breaker. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020. [Google Scholar]
  99. Zhu, Z.; Yuan, Z.; Chen, L.; He, J.; Zhu, Z. Vibration Characteristics of Thomson Coil Actuator Based on Simulation and Experiments. IEEE Trans. Energy Convers. 2020, 35, 1228–1237. [Google Scholar] [CrossRef]
  100. Lim, D.-K.; Woo, D.-K.; Kim, I.-W.; Shin, D.-K.; Ro, J.-S.; Chung, T.-K.; Jung, H.-K. Characteristic Analysis and Design of a Thomson Coil Actuator Using an Analytic Method and a Numerical Method. IEEE Trans. Magn. 2013, 49, 5749–5755. [Google Scholar] [CrossRef]
  101. Li, W.; Jeong, Y.W.; Koh, C.S. An Adaptive Equivalent Circuit Modeling Method for the Eddy Current-Driven Electromechanical System. IEEE Trans. Magn. 2010, 46, 1859–1862. [Google Scholar] [CrossRef]
  102. Lou, J.; Li, Q.; Sun, Q.; Liu, W.D.; Qian, J.L. Dynamic characteristics simulation and optimal design of the fast electromagnetic repulsion mechanism. Proc. CSEE 2005, 25, 23–29. [Google Scholar]
  103. Zhang, B.; Ai, S.; Du, W.; Yao, X.; Zhang, R.; Wang, J.; Liu, Z.; Geng, Y.; Yanabu, S. Design of a 126 kV double-break fast vacuum circuit breaker for controlled switching. In Proceedings of the 2017 4th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017. [Google Scholar]
  104. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Smith, A.C.; Barnes, M. Comparison of damping techniques for the soft-stop of ultra-fast linear actuators for HVDC breaker applications. J. Eng. 2019, 2019, 4466–4470. [Google Scholar] [CrossRef]
  105. Cao, P.; Nan, J.; Zhao, C. Research on damping method for electromagnetic repulsion mechanism. Mar. Electr. Electron. Technol. 2014, 34, 35–37. [Google Scholar]
  106. Guan, C.; Yao, X.; Zhang, J.; Zhang, L.; Liu, Z.; Wang, J.; Geng, Y. Research on the Contact Bounce During the Closing Process of a Repulsion Mechanism Applied in a Superconductivity Direct-Current Vacuum Circuit Breaker. IEEE Trans. Appl. Supercond. 2021, 31, 5000605. [Google Scholar] [CrossRef]
  107. Shi, W.; Zhang, B.; Guan, C.; Yao, X.; Liu, Z.; Wang, J.; Geng, Y. Influence of Opening Velocity on Arcing Time Windows of Fast Vacuum Circuit Breaker in Duties of Terminal Fault Test T100s. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  108. Fang, S.; Zhao, Y.; Wei, X.; Gao, C.; Zhang, S.; Zhang, N. Force characteristic of polyurethane material and design of polyurethane buffer. High Volt. Appar. 2015, 51, 91–96. [Google Scholar]
  109. Guan, C.; Peng, D.; Shi, W.; Chen, J.; Zhang, B.; Yan, J.; Yao, X.; Liu, Z.; Geng, Y.; Wang, J. Influence of Moveable Mass on the Opening Velocity and Buffering Characteristics of Fast Vacuum Circuit Breaker with a Gas Pressure Buffer. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  110. Chen, C.; Bissal, A.; Salinas, E. Numerical modelling and experimental testing of eddy-current dampers. In Proceedings of the ACTUATOR 2014, Bremen, Germany, 23–25 June 2014. [Google Scholar]
  111. Bissal, A.; Salinas, E.; Magnusson, J.; Engdahl, G. On the design of a linear composite magnetic damper. IEEE Trans. Magn. 2015, 51, 8003305. [Google Scholar] [CrossRef]
  112. Peng, C.; Mackey, L.; Husain, I.; Huang, A.Q.; Yu, W.; Lequesne, B.; Briggs, R. Active damping of ultrafast mechanical switches for hybrid AC and DC circuit breakers. IEEE Trans. Ind. Appl. 2017, 53, 5354–5364. [Google Scholar] [CrossRef]
  113. Parekh, M.; Bissal, A.; Magnusson, J.; Engdahl, G. Study of a linear Halbach passive magnetic damper. In Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG), Dublin, Ireland, 24–28 April 2017. [Google Scholar]
  114. Parekh, M.; Bissal, A.; Magnusson, J.; Engdahl, G. Design of a linear Halbach magnetic damper. Int. J. Appl. Electromagn. Mech. 2019, 59, 587–595. [Google Scholar] [CrossRef]
  115. Zhuangxian, J.I.; Zhuang, J.; Chen, W.A. Effect of the driving capacitor of electro-magnetic repulsion mechanism on the initial gap of contact. Mar. Electr. Electron. Eng. 2012, 32, 1–4. [Google Scholar]
  116. Bissal, A.; Magnusson, J.; Engdahl, G. Optimal Energizing Source Design for Ultra-Fast Actuators. In Proceedings of the Soft Magnetic Materials 21 Conference, Budapest, Hungary, 1–4 September 2013. [Google Scholar]
  117. Peng, C.; Huang, A.; Husain, I.; Lequesne, B.; Briggs, R. Drive circuits for ultra-fast and reliable actuation of Thomson coil actuators used in hybrid AC and DC circuit breakers. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 20–24 March 2016. [Google Scholar]
  118. Kimblin, C.W. Development of current limiter using vacuum arc current commutation. Phase 2: Maximizing the current rating of a single 72kV device using a minimum amount of parallel capacitance; NASA STI/Recon Technical Report N. OSTI 1979, 77, 33427. [Google Scholar]
  119. Zhou, Y.; Huang, Y.; Wen, W.; Sun, K.; Men, B.; Zhu, J. Closing performance of the Thomson-coil actuator for a 110 kV FMS. J. Eng. 2019, 2019, 2846–2850. [Google Scholar] [CrossRef]
  120. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Smith, A.C.; Barnes, M. Performance of high-power thomson coil actuator excited by a current pulse train. J. Eng. 2019, 2019, 3937–3941. [Google Scholar] [CrossRef]
  121. Bissal, A.; Magnusson, J.; Salinas, E.; Engdahl, G.; Eriksson, A. On the design of ultra-fast electromechanical actuators: A comprehensive multi-physical simulation model. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012. [Google Scholar]
  122. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Barnes, M. Experimental validation of a finite element 2D axial thomson coil model with inductance and resistance compensation. In Proceedings of the 13th IET International Conference on AC and DC Power Transmission (ACDC 2017), Manchester, UK, 14–16 February 2017. [Google Scholar]
  123. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Barnes, M. Modelling thomson coils with axis-symmetric problems: Practical accuracy considerations. IEEE Trans. Energy Convers. 2017, 32, 629–639. [Google Scholar] [CrossRef] [Green Version]
  124. Bissal, A.; Craciun, O.; Biagini, V.; Magnusson, J. Multidomain Design and Optimization based on Comsol Multiphysics: Applications for Mechatronic Devices. In Proceedings of the 2015 COMSOL Conference in Grenoble 2015, Grenoble, France, 14–16 October 2015. [Google Scholar]
  125. Bissal, A.; Eriksson, A.; Magnusson, J.; Engdahl, G. Hybrid Multi-Physics Modeling of an Ultra-Fast Electro-Mechanical Actuator. Actuators 2015, 4, 314–335. [Google Scholar] [CrossRef] [Green Version]
  126. Bissal, A.; Magnusson, J.; Salinas, E.; Engdahl, G. Multiphysics modeling and experimental verification of ultra-fast electro-mechanical actuators. Int. J. Appl. Electromagn. Mech. 2015, 49, 51–59. [Google Scholar] [CrossRef]
  127. Lee, S.M.; Lee, S.H.; Choi, H.S.; Park, I.H. Reduced modeling of eddy current driven electromechanical system using conductor segmentation and circuit parameters extracted by FEA. IEEE Trans. Magn. 2005, 41, 1448–1451. [Google Scholar]
  128. Lee, S.-H.; Kwak, I.-G.; Choi, H.-S.; Lee, S.-M.; Park, I.-H.; Moon, W.-K. Fast Solving Technique for Mechanical Dynamic Characteristic in Electromagnetic Motional System by Electro-Mechanical State Equation Including Extracted Circuit Parameter. IEEE Trans. Appl. Supercond. 2004, 14, 1926–1929. [Google Scholar] [CrossRef]
  129. Wang, Z.; Lei, B.; Xu, L.; Yu, Q.; Wen, W.; Li, B. Novel Simulation Model for Coil-Coil Type Electromagnetic Repulsion Actuator in Low Voltage DC Circuit Breaker. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019. [Google Scholar]
  130. Paese, E.; Geier, M.; Homrich, R.P.; Pacheco, J.L. Simplified Mathematical Modeling for an Electromagnetic Forming System with Flat Spiral Coil as Actuator. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 324–331. [Google Scholar] [CrossRef] [Green Version]
  131. Paese, E.; Geier, M.; Homrich, R.P.; Pacheco, J.L.; Homrich, R.P.; Ortiz, J.C.S. Mathematical modeling of an electromagnetic forming system with flat spiral coils as actuator. In Proceedings of the 4 th International Conference on High Speed Forming, Columbus, OH, USA, 9–10 March 2010. [Google Scholar]
  132. Li, Q.; Liu, W.; Qian, J. An analytical method for electromagnetic repulsion mechanism. Trans. China Electrotech. Soc. 2004, 19, 20–24. [Google Scholar]
  133. Markovic, M.; Jufer, M.; Perriard, Y. Analytical force determination in an electromagnetic actuator. IEEE Trans. Magn. 2008, 44, 2181–2185. [Google Scholar] [CrossRef]
  134. Li, W.; Lu, J.; Jeong, Y.W.; Koh, C.S. A Numerically Efficient Performance Analysis of Thomson Coil Actuator of Arc Eliminators Using Equivalent Circuit Method. In Proceedings of the KIEE Conference 2009; The Korean Institute of Electrical Engineers: Seoul, Korea, 2009. [Google Scholar]
  135. Li, Y.; Xia, K.; Liu, W.; Li, D. Design and simulation anylysis of electromagnetic repulsion mechanism. In Proceedings of the 2010 IEEE International Conference on Industrial Technology 2010, Via del Mar, Chile, 14–17 March 2010. [Google Scholar]
  136. Wu, J.; Zhuang, J.; Wang, C.; Jiang, Z. Simplification and solution of the mathematical model to electromagnetic repulsion mechanism. CSEE 2013, 33, 175–182. [Google Scholar]
  137. Bissal, A. On the Design of Ultra-Fast Electro-Mechanical Actuators. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
  138. Bissal, A. Modeling and Verification of Ultra-Fast Electro-Mechanical Actuators for HVDC Breakers. Master Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2015. [Google Scholar]
  139. Jian, Z.; Zhuang, J.; Wang, C.; Wu, J.; Liu, L. Simulation analysis and design of a high speed mechanical contact base on electro-magnetic repulsion mechanism. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar]
  140. Vilchis-Rodriguez, D.S.; Shuttleworth, R.; Barnes, M. Finite element analysis and efficiency improvement of the Thomson coil actuator. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 19–21 April 2016. [Google Scholar]
  141. Lequesne, B.; Holp, T.; Schmalz, S.; Slepian, M.; Wang, H. Frequency-Domain Analysis and Design of Thomson-Coil Actuators. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar]
  142. Zhu, Z.; Yuan, Z.; Chen, L.; Xu, M.; He, J.; He, J. Impact stress analysis and structural optimization design of thomson coil actuators. In Proceedings of the 2019 4th IEEE Workshop on the Electronic Grid (eGRID), Xiamen, China, 11–14 November 2019. [Google Scholar]
  143. Li, M.; Gong, P.; Wu, Y.; Wu, Y. Analysis of structure strength for direct current high-speed switch based on flexible body theory. Adv. Mech. Eng. 2020, 12, 1687814020912984. [Google Scholar] [CrossRef]
  144. Wu, J.; Guo, J.; Wu, Y.; Wu, Y.; Han, G.; Wang, D. Analysis of structure strength in medium voltage DC system high speed repulsing mechanism. In Proceedings of the ICEPE-ST, Xi’an, China, 22–25 October 2017; pp. 435–440. [Google Scholar]
  145. Guan, C.; Yao, X.; Ding, J.; Liu, Z.; Wang, J.; Geng, Y. Study On Dynamic Characteristics of a Repulsion Mechanism in Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2021, 31, 5603805. [Google Scholar] [CrossRef]
  146. Yao, X.; Guan, C.; Wang, J.; Liu, Z.; Ai, S.; Ma, K.; Ma, F. Technology of AC short-circuit current controlled fast vacuum breaking in a short arcing time. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020. [Google Scholar]
  147. Huo, Q.; Xiong, J.; Zhang, N.; Guo, X.; Wu, L.; Wei, T. Review of DC circuit breaker application. Electr. Power Syst. Res. 2022, 209, 107946. [Google Scholar] [CrossRef]
  148. Augustin, T.; Parekh, M.; Magnusson, J.; Becerra, M.; Nee, H.P. Thomson-Coil Actuator System for Enhanced Active Resonant DC Circuit Breakers. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 800–810. [Google Scholar] [CrossRef]
  149. Holaus, W. Ultra Fast Switches—Basic Elements for Future Medium Voltage Switchgear. Doctoral Dissertation, Swiss Federal Institute of Technology (ETH), Zurich, Switzerland, 2001. ETH No. 14375. [Google Scholar]
  150. Zhang, B.; Ren, L.; Wang, J.; Liu, Z.; Geng, Y.; Yanabu, S. A relationship between minimum arcing interrupting capability and opening velocity of vacuum interrupters in short-circuit current interruption. IEEE Trans. Power Deliv. 2018, 33, 2822–2828. [Google Scholar] [CrossRef]
  151. Benard, D.J.; Nolden, P.T.; Mallonen, E.A. Factors related to speed and voltage capability of a new high-speed circuit breaker. In Proceedings of the Electrical Contacts—1999, Forty-Fifth IEEE Holm Conference on Electrical Contacts (Cat. No.99CB36343), Pittsburgh, PA, USA, 4–6 October 1999. [Google Scholar]
  152. Kadivar, A.; Niayesh, K. Practical methods for electrical and mechanical measurement of high speed elongated arc parameters. Measurement 2014, 55, 14. [Google Scholar] [CrossRef]
  153. Kadivar, A. Electromagnetic Actuators for Ultra-fast Air Switches to Increase Arc Voltage by Increasing Contact Speed. In Proceedings of the 34th International Power System Conference (PSC-2019), Tehran, Iran, 9–11 December 2019. [Google Scholar] [CrossRef]
  154. Kadivar, A.; Niayesh, K. Effects of Fast Elongation on Switching Arcs Characteristics in Fast Air Switches. Energies 2020, 13, 4846. [Google Scholar] [CrossRef]
  155. Wen, W.; Huang, Y.; Sun, Y.; Wu, J.; Al-Dweikat, M.; Liu, W. Research on Current Commutation Measures for Hybrid DC Circuit Breakers. IEEE Trans. Power Deliv. 2016, 31, 1456–1463. [Google Scholar] [CrossRef]
  156. Junaid, M.; Xiang, B.; Wang, J.; Liu, Z.; Geng, Y. Experimental Test of Superconductor Fault-Current Switchgear Using Liquid Nitrogen as the Insulation and Arc-Quenching Medium. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
  157. Junaid, M.; Xiang, B.; Ge, H.; Yang, K.; Liu, Z.; Geng, Y.; Wang, J. Direct Current Arc Investigations in Liquid Nitrogen Using Asymmetrical Electrodes. IEEE Trans. Appl. Supercond. 2018, 29, 1–6. [Google Scholar] [CrossRef]
  158. Junaid, M.; Wang, J.; Li, H.; Xiang, B.; Liu, Z.; Geng, Y. Flashover characteristics of vacuum interrupters in liquid nitrogen and its comparison with air and transformer oil for the superconducting switchgear applications. Int. J. Electr. Power Energy Syst. 2020, 125, 106504. [Google Scholar] [CrossRef]
  159. Jugelt, S.; Leu, C. Interruption of Medium-Voltage Direct-Currents by Seperation of Contact Elements in Mineral Oil Using an Ultra Fast Electro-Magnetic Actuator. Plasma Phys. Technol. 2019, 6, 73–77. [Google Scholar] [CrossRef]
  160. Chen, W.; Zeng, R.; He, J.; Wu, Y.; Wei, X.; Fang, T.; Yu, Z.; Yuan, Z.; Wu, Y.; Zhou, W.; et al. Development and prospect of direct-current circuit breaker in China. High Volt. 2021, 6, 9000406. [Google Scholar] [CrossRef]
  161. Pan, Y.; Yuan, Z.; Chen, L.; Xu, M.; Liu, L. Research on the coupling mechanical high voltage DC circuit breaker. Proc. Chin. Soc. Elect. Eng. 2018, 24, 7113–7120. [Google Scholar]
  162. Huang, L.; Fang, C.; Li, W.; Tang, X.; Zhang, N.; Chen, J. Research on motion characteristics and stability of 500kV fast mechanical switch. J. Phys. Conf. Ser. 2020, 1633, 012094. [Google Scholar] [CrossRef]
  163. Feng, L.; Gou, R.; Zhuo, F.; Yang, X.; Zhang, F. Research on the breaking branch for a hybrid DC circuit breaker in±500 kV voltage-sourced converter high-voltage direct current grid. IET Power Electron. 2020, 13, 3560–3570. [Google Scholar] [CrossRef]
  164. Shaogui, A.; Xiao, Y.; Yongning, H.; Fan, Y.; Yiping, F.; Xing, L. Study on voltage distribution characteristic of a 363 kV fast multi-break vacuum circuit breaker. J. Eng. 2019, 2019, 2693–2697. [Google Scholar] [CrossRef]
  165. Yu, X.; Yang, F.; Li, X.; Ai, S.; Huang, Y.; Fan, Y.; Du, W. Static Voltage Sharing Design of a Sextuple-Break 363 kV Vacuum Circuit Breaker. Energies 2019, 12, 2512. [Google Scholar] [CrossRef] [Green Version]
  166. Yao, X.; Guan, C.; Wang, C.; Wang, J.; Ai, S.; Liu, Z.; Geng, Y. Design and Verification of an Ultra-high Voltage Multiple-break Fast Vacuum Circuit Breaker. IEEE Trans. Power Deliv. 2021, 1, 9002. [Google Scholar] [CrossRef]
  167. Kadivar, A.; Niayesh, K. Dielectric Recovery of Ultrafast-Commutating Switches used for HVDC and Fault Current Limiting Applications. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019. [Google Scholar]
  168. Jeong, Y.-W.; Lee, H.-W.; Lee, S.-W.; Kim, Y.-G. High-speed AC circuit breaker and high-speed OCR. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweeden, 10–13 June 2013. [Google Scholar]
  169. Sato, Y.; Arazoe, S.; Anji, H.; Okumo, H.; Takao, N.; Yanabu, S. Parallel and Series Operation of Vacuum Interrupters for Circuit Breakers and a Superconducting Fault Current Limiter. IEEE Trans. Plasma Sci. 2011, 39, 1358–1363. [Google Scholar] [CrossRef]
  170. Tan, Y.; Kun, Y.; Xiang, B.; Wang, J.; Liu, Z.; Geng, Y.; Yanabu, S. Repulsion Mechanism Applied in Resistive-Type Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2016, 26, 1–9. [Google Scholar] [CrossRef]
  171. Fawzi, T.H.; Burke, P.E. The Accurate Computation of Self and Mutual Inductances of Circular Coils. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 464–468. [Google Scholar] [CrossRef]
Actuators 11 00154 g001 550
Figure 1. Schematic of a modular hybrid IGBT DC breaker.
Figure 1. Schematic of a modular hybrid IGBT DC breaker.
Actuators 11 00154 g001
Actuators 11 00154 g002 550
Figure 2. Principle of coil–coil and coil–disk repulsion mechanism.
Figure 2. Principle of coil–coil and coil–disk repulsion mechanism.
Actuators 11 00154 g002
Actuators 11 00154 g003 550
Figure 3. Transfer switch based on TCA, redrawn as depicted in [100].
Figure 3. Transfer switch based on TCA, redrawn as depicted in [100].
Actuators 11 00154 g003
Actuators 11 00154 g004 550
Figure 4. Two-way TCA repulsion mechanism [71].
Figure 4. Two-way TCA repulsion mechanism [71].
Actuators 11 00154 g004
Actuators 11 00154 g005 550
Figure 5. TCA utilizing a spring holding mechanism, redrawn as depicted in [48].
Figure 5. TCA utilizing a spring holding mechanism, redrawn as depicted in [48].
Actuators 11 00154 g005
Actuators 11 00154 g006 550
Figure 6. Schematic of di-stable spring mechanism: (a) redrawn as depicted in [71]; (b) Bi-stable spring working principle.
Figure 6. Schematic of di-stable spring mechanism: (a) redrawn as depicted in [71]; (b) Bi-stable spring working principle.
Actuators 11 00154 g006
Actuators 11 00154 g007 550
Figure 7. One-way and two-way disc springs’ principles.
Figure 7. One-way and two-way disc springs’ principles.
Actuators 11 00154 g007
Actuators 11 00154 g008 550
Figure 8. Disc spring mechanism: (a) disc spring, redrawn as depicted in [66]; (b) buckling spring ribbons, redrawn as depicted in [85].
Figure 8. Disc spring mechanism: (a) disc spring, redrawn as depicted in [66]; (b) buckling spring ribbons, redrawn as depicted in [85].
Actuators 11 00154 g008
Actuators 11 00154 g009 550
Figure 9. TCA utilizing permanent magnet (PM) holding mechanism, redrawn as depicted in [60].
Figure 9. TCA utilizing permanent magnet (PM) holding mechanism, redrawn as depicted in [60].
Actuators 11 00154 g009
Actuators 11 00154 g010 550
Figure 10. TCA utilizing a gas pressure buffer, redrawn as depicted in [109].
Figure 10. TCA utilizing a gas pressure buffer, redrawn as depicted in [109].
Actuators 11 00154 g010
Actuators 11 00154 g011 550
Figure 11. Single pulse control circuits of TCA. (a) Single pulse drive circuit freewheeling the coil; (b) single pulse drive circuit freewheeling coil-thyristor; (c) di-directional drive circuit.
Figure 11. Single pulse control circuits of TCA. (a) Single pulse drive circuit freewheeling the coil; (b) single pulse drive circuit freewheeling coil-thyristor; (c) di-directional drive circuit.
Actuators 11 00154 g011
Actuators 11 00154 g012 550
Figure 12. Multiple pulse control circuits of TCA; (a) two-stage pulse circuit; (b) pulse-forming drive circuit.
Figure 12. Multiple pulse control circuits of TCA; (a) two-stage pulse circuit; (b) pulse-forming drive circuit.
Actuators 11 00154 g012
Table
Table 2. Different holding mechanisms’ performance in the literature.
Table 2. Different holding mechanisms’ performance in the literature.
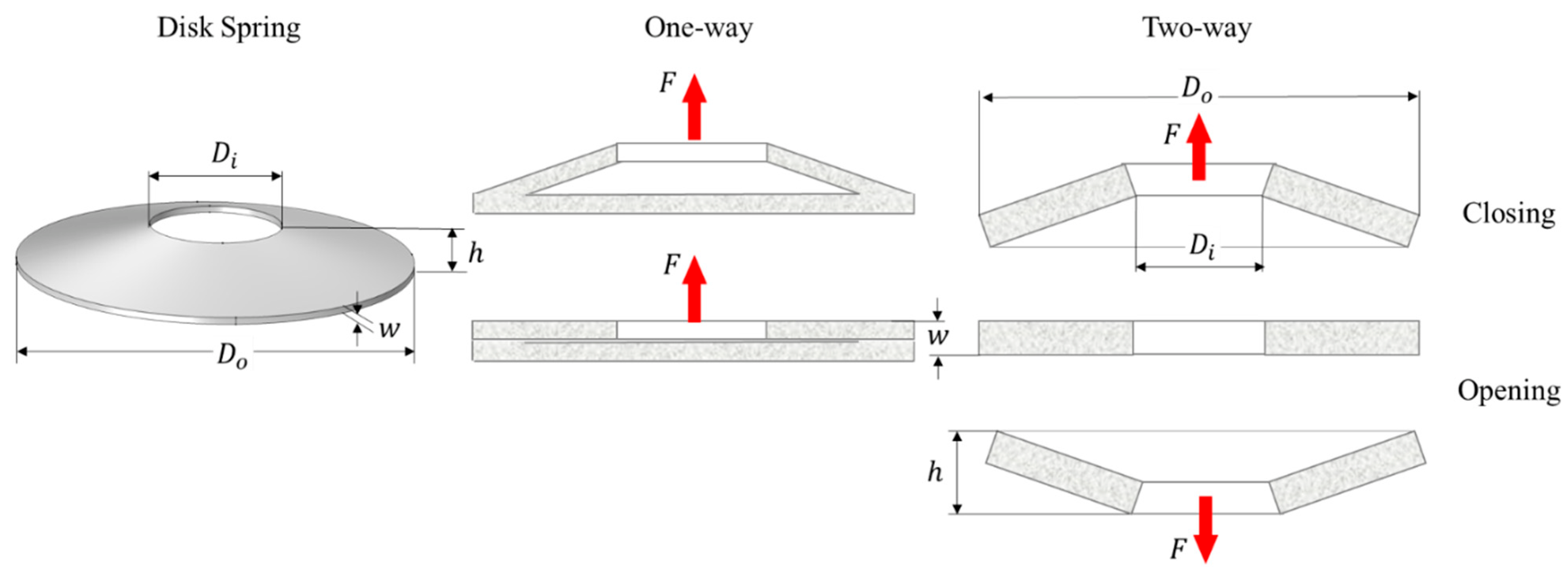
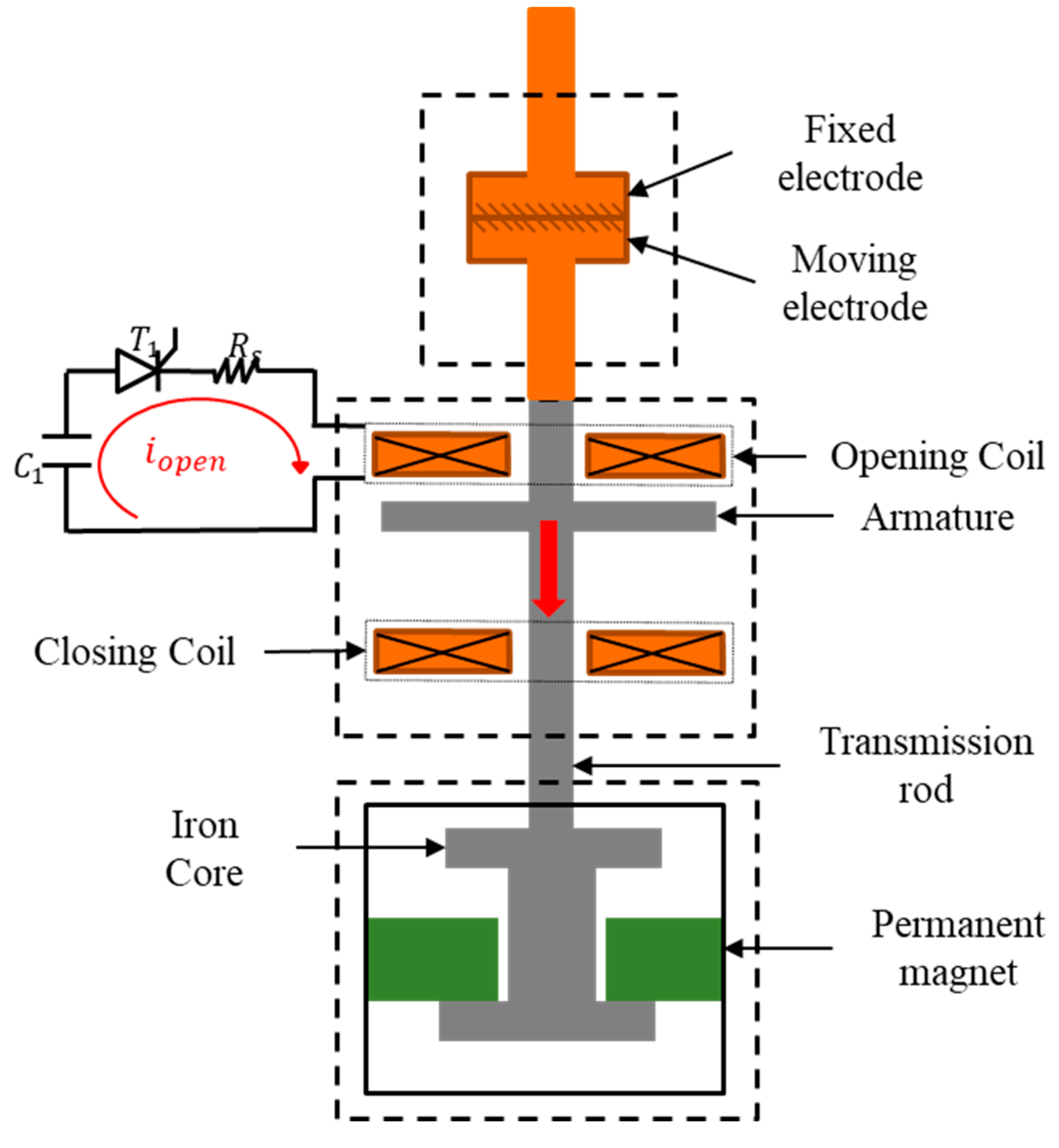
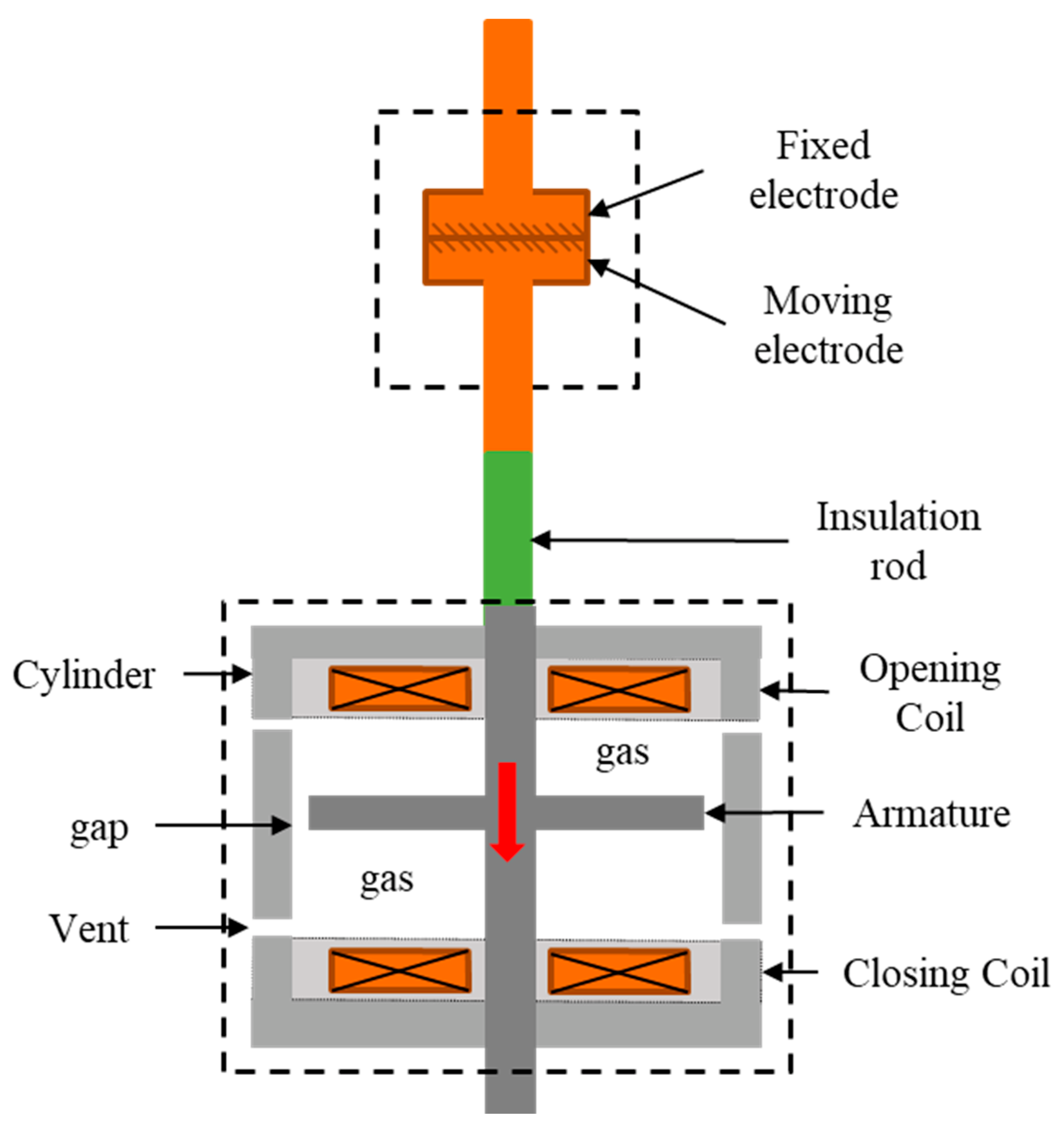
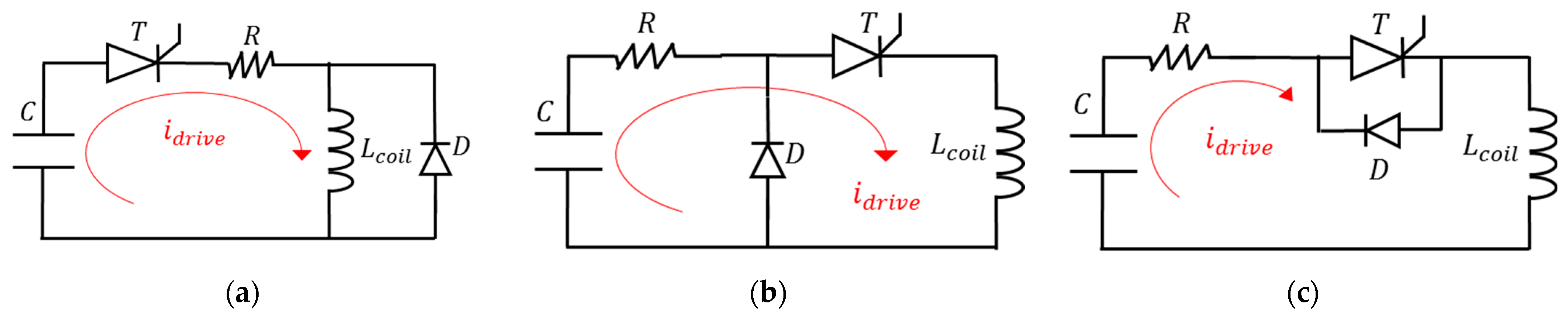
MechanismRef.Load/Contact ForceStrokeTimeDevice Stiffness/Weight
Helical Spring[48,52]2 kg/3.8 kN25 + 3 mm2 ms34.6 kN/m
Bi-Stable Spring[71]5 kg/1000 N26 mm2.3 ms63 N/mm
0.2 kg
Disc Spring[64]4 kN5–22 mm2.7–4.5 ms-
[85]0.5 kg/330 N11.68 mm2 ms1650 MPa
30 g
Magnet Holding[50,61]375–632 N *6 mm2.75 ms-
[60]1200 N5 mm4.9 ms-
* The opening holding force is 375 N and the closing is 632 N.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Al-Dweikat, M.; Cui, J.; Sun, S.; Yang, M.; Zhang, G.; Geng, Y. A Review on Thomson Coil Actuators in Fast Mechanical Switching. Actuators 2022, 11, 154. https://doi.org/10.3390/act11060154

AMA Style

Al-Dweikat M, Cui J, Sun S, Yang M, Zhang G, Geng Y. A Review on Thomson Coil Actuators in Fast Mechanical Switching. Actuators. 2022; 11(6):154. https://doi.org/10.3390/act11060154

Chicago/Turabian Style

Al-Dweikat, Mohmmad, Jian Cui, Shuai Sun, Mingming Yang, Guogang Zhang, and Yingsan Geng. 2022. "A Review on Thomson Coil Actuators in Fast Mechanical Switching" Actuators 11, no. 6: 154. https://doi.org/10.3390/act11060154

APA Style

Al-Dweikat, M., Cui, J., Sun, S., Yang, M., Zhang, G., & Geng, Y. (2022). A Review on Thomson Coil Actuators in Fast Mechanical Switching. Actuators, 11(6), 154. https://doi.org/10.3390/act11060154

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop