Flexible Control Strategy for Upper-Limb Rehabilitation Exoskeleton Based on Virtual Spring Damper Hypothesis

Abstract

The focus of this work is to design a control strategy with the dynamic characteristics of spring damping to realize the virtual flexibility and softness of a rigid-joint exoskeleton without installing real, physical elastic devices. The basic idea of a “virtual softening control strategy” for a single rigid joint is that a virtual spring damper (VSD) is installed between the motor and the output shaft. By designing the control signal of the motor, the torque output of the joint actuator is softened so that the output has the characteristics of elasticity and variable stiffness. The transfer velocity profile of human limbs reaching from one posture to another always presents as bell-shaped. According to this characteristic, we constructed a trajectory planning method for a point-to-point position-tracking controller based on a normal distribution function, and it was successfully applied to the control of 5-DoF upper-limb rehabilitation exoskeleton. A multi-joint cooperative flexible controller based on the virtual spring damper hypothesis (VSDH) was successfully applied to solve the constrained control problem of the exoskeletons and the self-motion problem caused by redundant degrees of freedom (DoFs). The stability of the closed-loop controlled system is theoretically proven by use of the scalar energy function gradient method and the Riemann metric convergence analysis method.

1. Introduction

In recent decades, multifarious upper-limb rehabilitation exoskeletons have been developed to provide rehabilitation therapy and movement assistance for patients recovering from neurological disorders (e.g., strokes and pathological tremors) [1,2]. Research into exoskeleton design and control techniques is rapidly evolving to meet ever-increasing demands for effectiveness, comfort, and safety [3,4,5,6,7,8,9,10,11,12].

Existing rehabilitation exoskeletons are mainly driven by rigid motors, which can achieve high control accuracy but low compliance [13]. In the case of excessive movement or sudden abnormal force, it is easy to cause secondary injury to the patient’s affected limb [14]. Current exoskeleton robots limit the movement comfort and flexibility of the wearer and have safety problems, due to high-rigidity actuators and low material impact resistance [15]. The movement of rigid exoskeletons presents a mechanical stereotype; the exercise process is uncomfortable, and the effect of the rehabilitation treatment is also affected.

Many practical engineers and academic researchers have shown great interest in studying the application of flexible joints in exoskeleton manipulators [16]. In recent years, research on flexible exoskeleton robots has accelerated, from the laboratory to real life. Flexible exoskeleton robots are characterized by high flexibility, high environmental adaptability, and high compatibility [17].

Flexible joints have been utilized in different kinds of robotic applications, including rehabilitation robots [18,19], walking robots, humanoids [20], and haptics. According to whether the joint involves stiffness regulation, a flexible joint can be divided into two categories: series elastic actuator (SEA) and variable stiffness actuator (VSA) [18]. Regardless of which kind of physical flexible actuator is applied to the upper-limb exoskeleton, it will bring about three problems: First, it will increase the volume, weight, structural complexity, and manufacturing cost of the device. Second, the control of position accuracy will become extremely complex and difficult. Third, it will bring unwanted oscillation.

The main objective of upper-limb rehabilitation exoskeletons is to assist the movement of the affected limb of stroke patients gently and flexibly, move the joints, exercise the muscles, and achieve the purpose of auxiliary rehabilitation treatment [21]. Therefore, the exoskeleton manipulator should not only have a certain degree of rigidity, but also have good flexibility. It should have a rigid skeleton, soft joints, and flexible movements like human limbs to ensure safety and comfort while wearing the exoskeleton [22,23].

To achieve soft joints and flexible movements without installing real physical SEA and VSA in devices, we proposed a flexible control strategy for an upper-limb rehabilitation exoskeleton based on the virtual spring damper hypothesis (VSDH). It mainly includes the VSDH flexible control strategy for single-rigid-joint actuators and the VSDH flexible cooperative control strategy for multi-joint exoskeletons with redundant degrees of freedom (DoF). The innovations and contributions of the proposed methods are fourfold:

(1)

We propose an innovative concept and method of “virtual softening control strategy” for the rigid joint. It is assumed that a virtual spring damper (VSD) module is installed after the joint motor. By designing the control signal of the motor, the torque output of the joint actuator is softened so that it has the typical characteristics of elasticity and variable stiffness.

(2)

In this paper, the torque virtual tracking control method based on hyperbolic tangent function (HTF) is applied to deal with the torque control signal so that the output of the motor presents the characteristic of flexibility, avoids mechanical damage to the motor and reducer, and enhances the comfort of human–robot interaction.

(3)

We propose a trajectory planning method for a point-to-point position-tracking controller based on a normal distribution function. It is successfully applied to the control of the upper-limb exoskeleton.

(4)

A flexible multi-joint cooperative controller based on VSDH is successfully applied to solve the constrained control problem of the exoskeletons and the self-motion problem caused by redundant DoFs.

The remainder of the paper is organized as follows. Section 2 introduces the flexible control strategy based on VSDH for a single-rigid-joint actuator. The multi-joint cooperative flexible control strategy based on VSDH is proposed, and the feasibility is theoretically proven, in Section 3. Section 4 presents the simulation experiment results. The conclusions are presented in Section 5.

2. Single-Joint Model Flexible Control

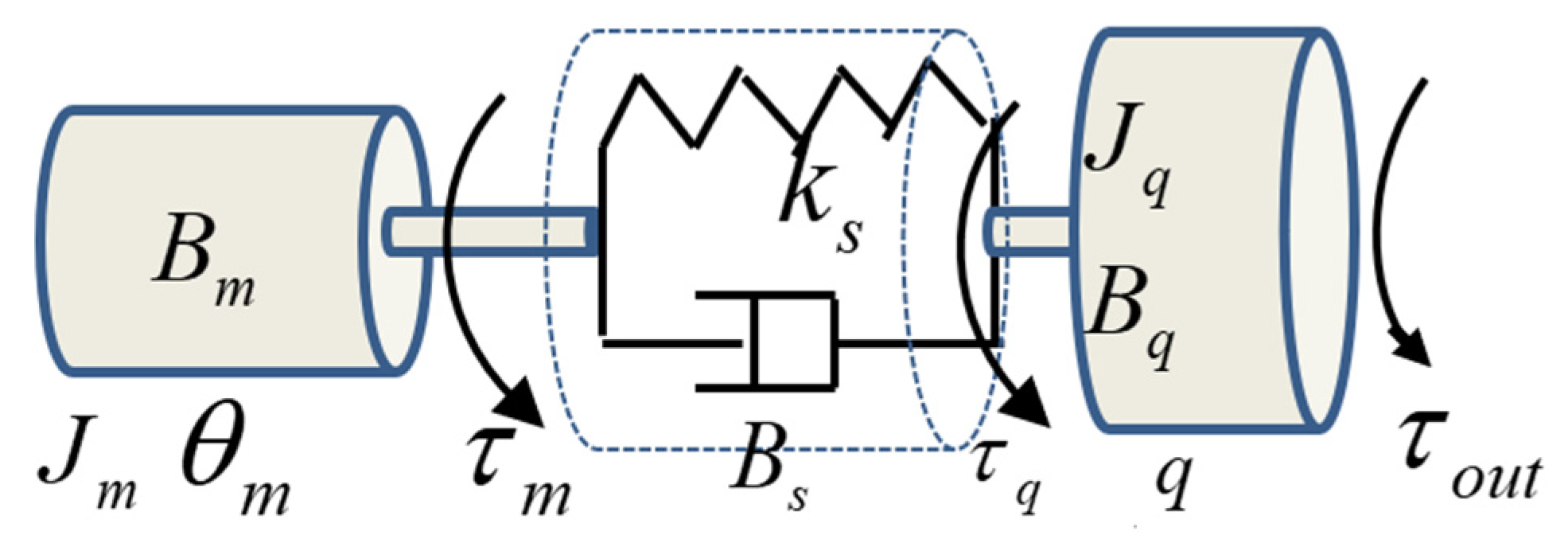
2.1. Single-Joint Flexible Based on VSDH

Between the rigid joint motor and the output shaft, it is assumed that a virtual spring damper (VSD) is installed in series to compose a flexible driving module. This module can be regarded as a virtualized flexible joint. The flexible effect is equivalently simulated by a linear spring and a damper in parallel, as shown in Figure 1, where ${\tau }_m$ is the output torque of the motor; ${\theta }_m$ is the angle of the motor; $J_m$ is the equivalent moment of inertia; $B_m$ is the total viscous damping coefficient; $k_s$ is the stiffness coefficient of virtual torsional spring; $B_s$ is the damping coefficient of the virtual damper; ${\tau }_q$ is torque at the output end of the flexible VSD module; $q$ is the angle of the output shaft; $J_q$ is the effective moment of inertia of the load shaft; $B_q$ is damping coefficient of the load shaft; and ${\tau }_{out}$ is external torque.

According to Hooke’s law and torque analysis, the output torque of the flexible module can be obtained as follows:

$${\tau }_q=k_s({\theta }_m-q)+B_s({\dot{\theta }}_m-\dot{q})$$

(1)

According to Newtonian dynamics, the dynamic equation of the flexible joint can be obtained as follows:

$$\left\{\begin{array}{c}{J}_m{\ddot{\theta }}_m+B_m{\dot{\theta }}_m+k_s({\theta }_m-q)+B_s({\dot{\theta }}_m-\dot{q})={\tau }_m\\ J_q\ddot{q}+B_q\dot{q}=k_s({\theta }_m-q)+B_s({\dot{\theta }}_m-\dot{q})-{\tau }_{out}\end{array}\right.$$

(2)

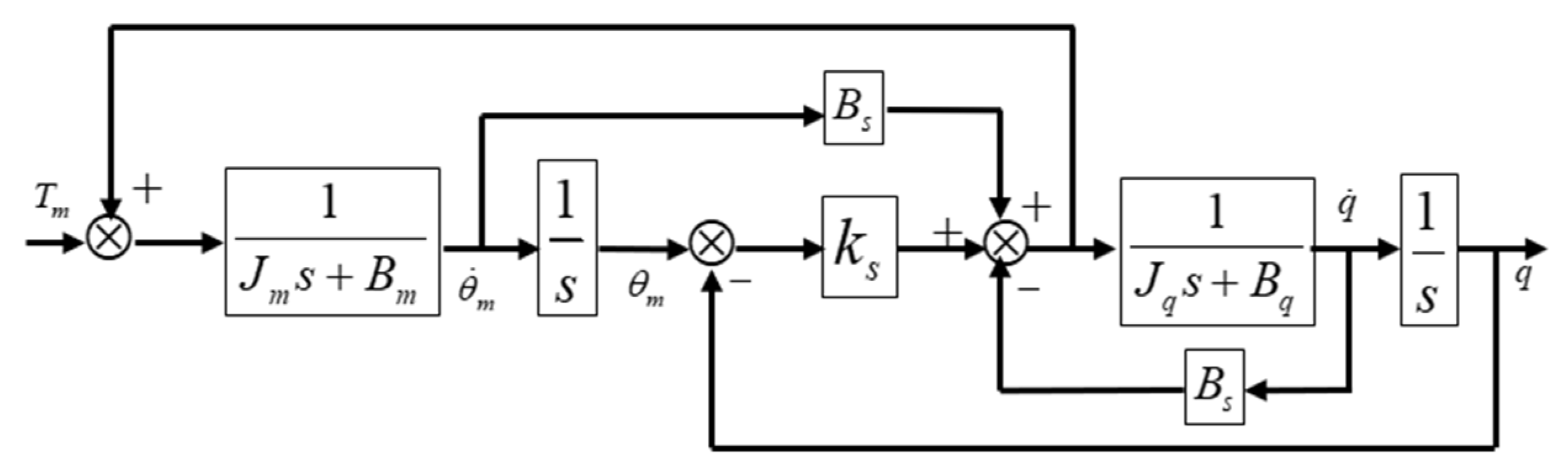
2.2. Velocity Tracking Control of VSD Flexible Joint

The Laplace transform is performed on both sides of Equation (2):

$$\left\{\begin{array}{c}[J_m{s}^2+(B_m+B_s)s+k_s]{\Theta }_m(s)=(B_{s}s+k_s)Q(s)+T_m(s)\hfill \\ [J_q{s}^2+(B_q+B_s)s+k_s]Q(s)=(B_{s}s+k_s){\Theta }_m(s)\hfill \end{array}\right.$$

(3)

where ${\Theta }_m\left(s\right)$, $Q\left(s\right)$, and $T_m\left(s\right)$ represent the Laplace transformation of ${\theta }_m$, $q$, and ${\tau }_m$, respectively. Thus, the transfer function can be obtained as follows:

$$\frac{Q(s)}{T_m(s)}=\frac{B_{s}s+k_s}{[J_m{s}^2+(B_m+B_s)s+k_s][J_q{s}^2+(B_q+B_s)s+k_s]-{(B_{s}s+k_s)}^2}$$

(4)

A structural block diagram of the control system of the virtual flexible joint is shown in Figure 2.

Assume that the joint motor is driven by a DC servo motor controlled by armature voltage. The dynamic equation of the motor driver is as follows:

$$\begin{array}{l}u(t)=L\frac{di(t)}{dt}+Ri(t)+k_b{\dot{\theta }}_m\\ {\tau }_m(t)=k_{m}i(t)\end{array}$$

(5)

where $u\left(t\right)$ is the control voltage; $i\left(t\right)$ is the actual current of motor armature coil; $L$ is the inductance of the armature coil; $R$ is the armature coil resistance; $k_b$ is the electromagnetic torque coefficient; ${\dot{\theta }}_m$ is the angular velocity of the motor shaft; and $k_m$ is the motor torque coefficient.

Combined with Equations (3) and (5), the system structure diagram of the servo-motor-driven virtual flexible joint speed-tracking control can be designed as shown in Figure 3. The $q^{\ast }$ in the figure represents the reference input.

A virtual spring-damper flexible module added in a joint actuator will not only produce time delay and reduce the response speed, but also increase the vibration of the joint, like adding a real spring. An angular-velocity-tracking controller with good performance can be designed by properly selecting the system parameters. In our case, the system parameters are assumed as $J_m$ = $J_q$ = 0.05; $B_m$ = 0.3; and $B_q$ = 0.3. The VSD parameters are set at $K_s$ = 10.0 and $B_s$ = 1.012, based on a large number of simulation experiments. If the input signal ${\tau }_m$ is a rectangular wave with an amplitude of 2, the responses of the four state variables ${\theta }_m,{\dot{\theta }}_m,q,\dot{q}$ are shown in Figure 4.

It can be seen from Figure 4 that the motor velocity ${\dot{\theta }}_m$(red) and the load speed $\dot{q}$ (black) can track the driving torque (${\tau }_m$ in the figure) very well. The delay time is relatively small, while the response is fast. Most importantly, it can be observed that there is no vibration during the tracking simulation. It not only makes the joint flexible, but also avoids undesired vibration.

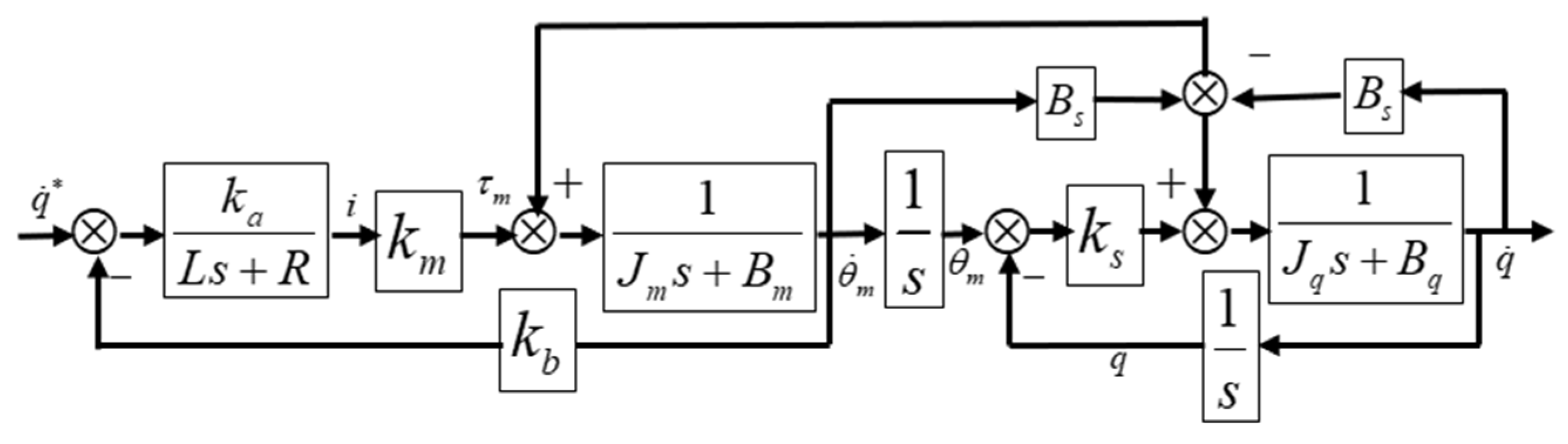
2.3. Torque Tracking Control Based on HTF

When the control torque suddenly increases or disappears, the hyperbolic tangent function (HTF)

$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(6)

is used to deal with the torque control signal to avoid mechanical damage to the motor and reducer and to enhance the flexibility of the exoskeleton and the comfort of human–robot interaction.

It is assumed that the output torque is ${\tau }_{m0}$ at the current moment k, and it needs to be suddenly increased to ${\tau }_{md}$ at the next moment (k + 1). The objective of the torque control signal process is to make the output elastic and flexible like a spring, rather than a sudden change without any delay. There are two signal processing methods:

Method 1. 

Interval mapping method.

The function $f\left({\tau }_m\right)$ is defined as the map from the torque boost interval [${\tau }_{m0}$,${\tau }_{md}$] to [−5, 5], which is the independent variable change interval of $\tan \mathrm{h}\left(\ast \right)$.

$$f({\tau }_m)=10\frac{{\tau }_m-{\tau }_{m0}}{{\tau }_{md}-{\tau }_{m0}}-5$$

(7)

Since the range interval of the function $\tan \mathrm{h}\left(\ast \right)$ is [−1, 1], the control torque can be designed as follows:

$$\begin{array}{l}{\tau }_q={\tau }_{m0}+0.5({\tau }_{md}-{\tau }_{m0})[1+\tanh (10\frac{{\tau }_m-{\tau }_{m0}}{{\tau }_{md}-{\tau }_{m0}}-5)]\\ ={\tau }_{m0}+0.5({\tau }_{md}-{\tau }_{m0})[1+\tanh (f({\tau }_m))]\end{array}$$

(8)

Method 2. 

Step-by-Step Approach.

It is assumed that the control torque ${\tau }_q$ of the virtual flexible driving module is step-by-step increased from ${\tau }_{m0}$ to ${\tau }_{md}$ in N steps, that is, in N signal-sampling period. The control torque can be designed as follows:

$$\begin{array}{c}{\tau }_q(k)={\tau }_{m0}+0.5({\tau }_{md}-{\tau }_{m0})[1+\tanh (\frac{5k}{\alpha }-5)]\\ \hspace{1em} ={\tau }_{m0}+0.5({\tau }_{md}-{\tau }_{m0})[1+\tanh (f(k,\alpha ))]\end{array}$$

(9)

where $k=0, 1, 2\dots \dots N$; $\alpha =N/2$; and $N$ can be set to 2, 4, 6, 8, or 10 as required. The value of the independent variable $f\left(k, \alpha \right)$ of HTF is shown in

Table 1. The corresponding value of the independent variable of HTF.

k	0	1	2	3	4	5	6	7	8	9	10
N = 2	−5	0	5	\	\	\	\	\	\	\	\
N = 4	−5	−2.5	0	2.5	5	\	\	\	\	\	\
N = 6	−5	−10/3	−5/3	0	5/3	10/3	5	\	\	\	\
N = 8	−5	−15/4	−10/4	−5/4	0	5/4	10/4	15/4	5	\	\
N = 10	−5	−4	−3	−2	−1	0	1	2	3	4	5

.

The driving signal ${\tau }_m$ is set as a rectangular wave signal [0→2→−2→2], and $N$ is chosen as 2, 4, 6, 8, and 10; the resulting tracking curve of ${\tau }_q$ tracking ${\tau }_m$ is shown in Figure 4. Tm denotes the rectangular wave driving signal ${\tau }_m$. Tq(α) denotes the virtual flexible driven torque ${\tau }_q\left(\mathsf{\alpha }\right)$ when α = 1, 2 $\dots \dots$5. When α = 5, the number of steps is $N=2\alpha =10$, that is, in 10 control command-sending periods, the output torque of the virtual flexible driving module is increased from ${\tau }_{m0}=0$ to ${\tau }_{md}=2$, or decreased from ${\tau }_{m0}=2$ to ${\tau }_{md}=-2$, or from ${\tau }_{m0}=-2$ to ${\tau }_{md}=2$. If α = 1, it is only equivalent to inserting an intermediate value in the interval [${\tau }_{m0}$, ${\tau }_{md}$], from one-step arrival to two-step arrival. In our case, α can be selected as 4 or 5.

It can be seen from the structure diagram (Figure 2) that the load module can be simplified to a first-order inertial system, and the transfer function can be simplified as follows:

$$\frac{Q(s)}{Tq(s)}=\frac{1}{J_{q}s+B_{q}s}\cdot \frac{1}{s}$$

(10)

where $Q\left(s\right)$ and $T_q\left(s\right)$ represent the Laplace transformation of $q$ and ${\tau }_q$, respectively. $J_q$ and $B_q$ are the total effective moment of inertia and the total viscous damping coefficient, respectively. For a joint motor, $J_q=5.468\ast {10}^{-4}$, $B_q=4.932\ast {10}^{-3}$, α = 5 is selected, ${\tau }_q$ is calculated by (5), the rectangular wave response of angular $q$ and angular velocity $\dot{q}$ is as shown in Figure 5, and ${\tau }_m$ and ${\tau }_q\left(5\right)$ in Figure 5 are the same as in Figure 4. $q_1$ and $D_{q1}$ represent the angular $q$ and angular velocity $\dot{q}$ driven by ${\tau }_m$, respectively. $q_2$ and $D_{q2}$ represent $q$ and $\dot{q}$ driven by ${\tau }_q\left(5\right)$, respectively. It can be observed from Figure 6 that the velocity-tracking curve $D_{q2}$ is smoother with less peak compared to $D_{q1}$. A similar situation applies to the angle-tracking curve $q_2$ compared to $q_1$.

According to the discussion and simulation results above, it can be concluded that the torque virtual tracking control method based on HTF (4) and (5) can smooth the peak of the response curve, which plays a role as soft buffering, protecting the motor and reducer. By properly selecting the control parameters, the response speed of the joint can be sacrificed as little as possible to ensure the fast tracking of torque, speed, and position. There is no undesired oscillation characteristic, which a real spring flexible joint would produce.

The proposed flexible control strategy for a single rigid joint can not only realize the flexible tracking of the joint, but can also avoid undesired vibration. The simulation results confirm the effectiveness and feasibility of the control method.

3. Multi-Joint Cooperative Flexible Control

3.1. Dynamic Equation and Control of Upper-Limb Exoskeleton

A prototype of a 5-DoF upper-limb exoskeleton manipulator was designed in our previous work [24], shown in Figure 7. It can realize movements including shoulder joint abduction/adduction, shoulder joint flexion/extension, shoulder joint internal/external rotation, elbow joint flexion/extension, forearm supination/pronation, and wrist joint flexion/extension. The exoskeleton was used as the control object.

The length of the upper arm of the exoskeleton manipulator is adjustable, ranging from 22 to 32 cm. The total weight of the upper arm including joint-3 and joint-4 is 4 kg. The length of the forearm can be adjusted from 25 cm to 35 cm. The total weight of the forearm, including joint-5 and wrist, is 3 kg. See

Table 2. Exoskeleton joint range of motion.

Joint	Action	Joint Code	Angle Range
Shoulder-1	abduction/adduction	Joint-1	0–100°/0–20°
Shoulder-2	flexion/extension	Joint-2	0–150°/0–20°
Shoulder-3	external/internal rotation	Joint-3	0–75°/0–45°
Elbow	flexion/extension	Joint-4	0–135°/0°
Wrist	external/internal rotation	Joint-5	0–90°/0–90°

for the rotation angle range of each joint.

Assumption 1. 

The mass (m1 = 4 kg) of the upper arm OA (the length l1 = 0.3 m) is concentrated at the center of the elbow joint-4, and the mass (m2 = 3 kg) of the forearm AB (the length l2 = 0.3 5m) is concentrated at the center of the wrist joint-5.

Assumption 2. 

Ignoring the influence of the wrist joint, only four joints (joint-1, -2, -3, -4) of two links were studied.

The inertial frame OXYZ is established as shown in Figure 8. The origin of coordinate O is on the center point of joint-1. The OX axis is perpendicular to the coronal plane of the human body and points to the front of the exoskeleton, the OZ axis is outward along the shoulder in the horizontal plane, and the OY axis is perpendicular to the ground and pointing upward. Points A and B represent the center point of the elbow joint and wrist joint, respectively. The link OA (represents the upper arm) rotates an angle $q_1$ around the axis OX, then rotates $q_2$ and $q_3$ around the new axis OZ₁ (not shown in the figure) and axis OA, respectively. The link AB (represents the forearm) rotates $q_4$ in the plane OAB with respect to the elbow joint-4.

The position coordinates of points A and B in Figure 8 are obtained by transform through spatial coordinates.

$$\left\{\begin{array}{c}{x}_A=l_1{s}_2\\ y_A=-l_1{c}_2{c}_1\\ z_A=-l_1{c}_2{s}_1\end{array}\right.$$

(11)

$$\left\{\begin{array}{l}{x}_B=(l_1+l_2{\mathrm{c}}_4){\mathrm{s}}_2+l_2{s}_4{c}_3{c}_2\\ y_B=-(l_1+l_2{\mathrm{c}}_4){\mathrm{c}}_2{c}_1+l_2{s}_4{c}_3{s}_2{c}_1-l_2{s}_4{s}_3{s}_1\\ z_B=-(l_1+l_2{\mathrm{c}}_4)c_2{s}_1+l_2{s}_4{c}_3{s}_2{s}_1+l_2{s}_4{s}_3{c}_1\end{array}\right.$$

(12)

where $s_i=\sin (q_i), c_i=\cos (q_i), i=1,2,3,4$ (the same as below).

The Jacobian matrix of the system is derived from Equation (12) and listed in Appendix B.

The Lagrangian dynamic equation of the 5-DoF upper-limb exoskeleton manipulator shown in Figure 7 can be described as follows:

$$M(q)\ddot{q}+S(q,\dot{q})\dot{q}+G(q)=\tau$$

(13)

where $q,\dot{q},\ddot{q}\in R^4$ represent the angular position, velocity, and acceleration. $\tau \in R^4$ is the joint torque. $S\left(q,\dot{q}\right)$ represents Coriolis/centripetal matrix. $G\left(q\right)\in R^4$ is the gravity vector. The generalized inertia matrix $M\left(q\right)\in R^{4\times 4}$ is symmetric and positive definite. Then, there exist two positive constants $h_m$ and $h_M$ such that (for any $q$):

$$h_{m}I\le M(q)\le h_{M}I$$

(14)

The calculation formula of $M\left(q\right)$, $S\left(q,\dot{q}\right)$, and $G\left(q\right)$ is given in Appendix A.

During the movement of the upper-limb exoskeleton manipulator from one position to another, shown in Figure 7, the cooperative rotation of four joints is constrained and limited. See Figure 9. OA and AB represent the upper arm and forearm, separately. B represents the starting position of the exoskeleton endpoint, and B’ represents the target position.

Constraint 1: If q₃ = 0, then the plane of triangle OAB is in the same plane as BOX, namely, the OX axis is in the plane of triangle OAB.

Constraint 2: The most convenient and comfortable movement path from B to B’ is straight line BB’, shown in Figure 9. The constraint condition is that the endpoint trajectory B(t) must move in the OBB’ plane. If there is a point Q on the arc $\stackrel{⌢}{B{B}^{\prime }}$ of the endpoint trajectory, the vertical point to OBB’ is P, and QP length is d, then the constraint condition on the control law is to make d = 0.

The initial position coordinates of the endpoints B (x_B0, y_B0, z_B0) and the target position B′ (x_B′, y_B′, z_B′), any point on the endpoint trajectory Q (x_B, y_B, z_B), and the normal vector of the OBB’ plane are as follows:

$$\begin{array}{l}\overrightarrow{n}=\left|\begin{array}{ccc}i& j& k\\ x_{B0}& y_{B0}& z_{B0}\\ x_{B^{\prime }}& y_{B^{\prime }}& z_{B^{\prime }}\end{array}\right|={\mathsf{\Psi }}_{i}i+{\mathsf{\Psi }}_{j}j+{\mathsf{\Psi }}_{k}k\\ =(y_{B0}{z}_{B^{\prime }}-y_{B^{\prime }}{z}_{B0})i+(z_{B0}{x}_{B^{\prime }}-z_{B^{\prime }}{x}_{B0})j+(x_{B0}{y}_{B^{\prime }}-x_{B^{\prime }}{y}_{B0})k\end{array}$$

(15)

where $i,j,k$ represent the unit vector, and ${\Psi }_{i,j,k}$ represents the corresponding coordinate values of three directions. Then, the distance from any point on the endpoint trajectory to the OBB’ plane can be obtained as follows:

$$d=\frac{{\Psi }_i{x}_B+{\Psi }_j{y}_B+{\Psi }_k{z}_B}{\sqrt{{\Psi }_i^2+{\Psi }_j^2+{\Psi }_k^2}}$$

(16)

The constraint condition is d = 0, that is, the numerator of the formula above is equal to zero. The constraint function is described as follows:

$$\begin{array}{l}\varphi (q)={\Psi }_i\left((l_1+l_2{\mathrm{c}}_4){\mathrm{s}}_2+l_2{s}_4{c}_3{c}_2\right)+{\Psi }_j\left(\begin{array}{l}-(l_1+l_2{\mathrm{c}}_4){\mathrm{c}}_2{c}_1\\ +l_2{s}_4{c}_3{s}_2{c}_1-l_2{s}_4{s}_3{s}_1\end{array}\right)\\ +{\Psi }_j\left(-(l_1+l_2{\mathrm{c}}_4)c_2{s}_1+l_2{s}_4{c}_3{s}_2{s}_1+l_2{s}_4{s}_3{c}_1\right)=0\end{array}$$

(17)

The partial derivative (gradient) of $\varphi \left(q\right)$ in $q$ is described as follows:

$$J_{\varphi }=\partial \varphi (q)/\partial q=\left[\begin{array}{cccc}{J}_{\varphi 1}& J_{\varphi 2}& J_{\varphi 3}& J_{\varphi 4}\end{array}\right]$$

(18)

The representation of $J_{\varphi i}$ (I = 1, 2, 3, 4) is shown in Appendix C.

The function of the joint driving torque controller is to drive each joint of the exoskeleton to rotate and to make the endpoint move from an initial position $B\left(x_0,y_0,z_0\right)$ to a given target position $B^{\prime }\left(x_d,y_d,z_d\right)$. Based on the virtual spring-damper hypothesis, the flexible multi-joint cooperative controller under constraint is designed as follows:

$$\tau =-C\dot{q}-J_x^{\mathrm{T}}(q)K\Delta x-\lambda J_{\varphi }^{\mathrm{T}}+\widehat{G}(q)$$

(19)

where $\tau$ denotes the control torque vector, $C$ is a positive definite diagonal matrix whose diagonal components express virtual damping coefficients, $J_x\left(q\right)=\partial x/\partial q$ is the 3 × 4 Jacobian matrix of x in q (presented in Appendix B), and $\mathsf{\Delta }x=x-x_d$ represents the difference between the real-time measured position $x$ of the end point and the target position $x_d$. K stands for a virtual stiffness parameter, and $\lambda$ denotes the constraint force coefficient. $J_{\varphi }$ is the constraint function gradient matrix (presented in Appendix C), and $\widehat{G}\left(q\right)$ represents the estimated value of the gravity term, which can be computed in real time based on measured angular data. Let us assume here $\widehat{G}\left(q\right)=G\left(q\right)$.

Substituting (19) into (14), the closed-loop control system equation of the whole upper-limb exoskeleton manipulator can be described in the following form:

$$M(q)\ddot{q}+[S(q,\dot{q})+C]\dot{q}+J_x^{\mathrm{T}}(q)K\Delta x+\lambda J_{\varphi }^{\mathrm{T}}=0$$

(20)

The controller (19) has the following characteristics:

(1)

It has the dynamic characteristics of “spring and damper”. Equation (19) contains four items. The first item represents the damping moment generated by the virtual damper in joint space, which plays a “braking” role in the system movement. The convergence speed of the system state is changed by designing the value of the damping coefficient matrix C. The second term represents the virtual spring torque. By selecting the stiffness coefficient K, the speed of the endpoint approaching the target position is adjusted.

(2)

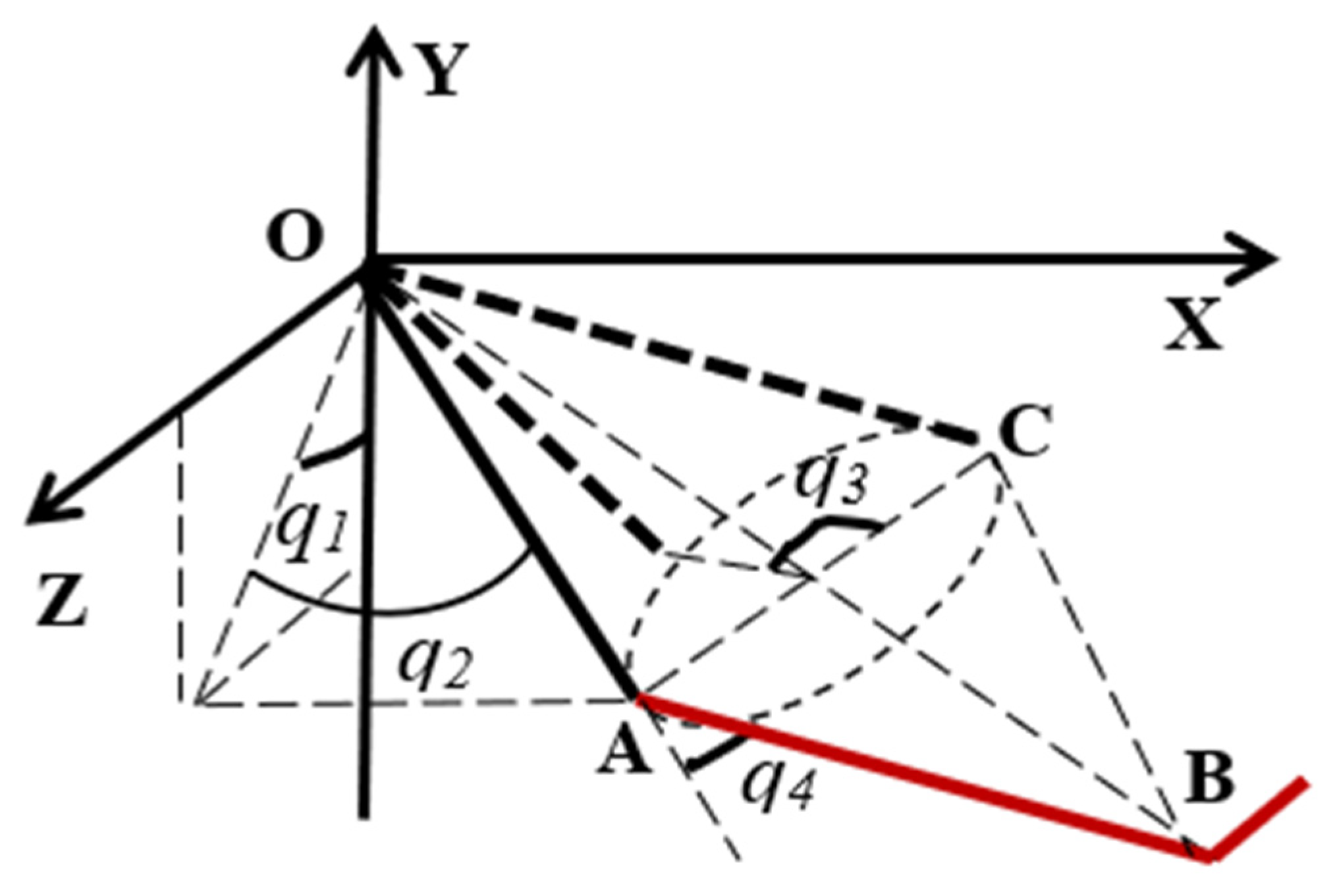
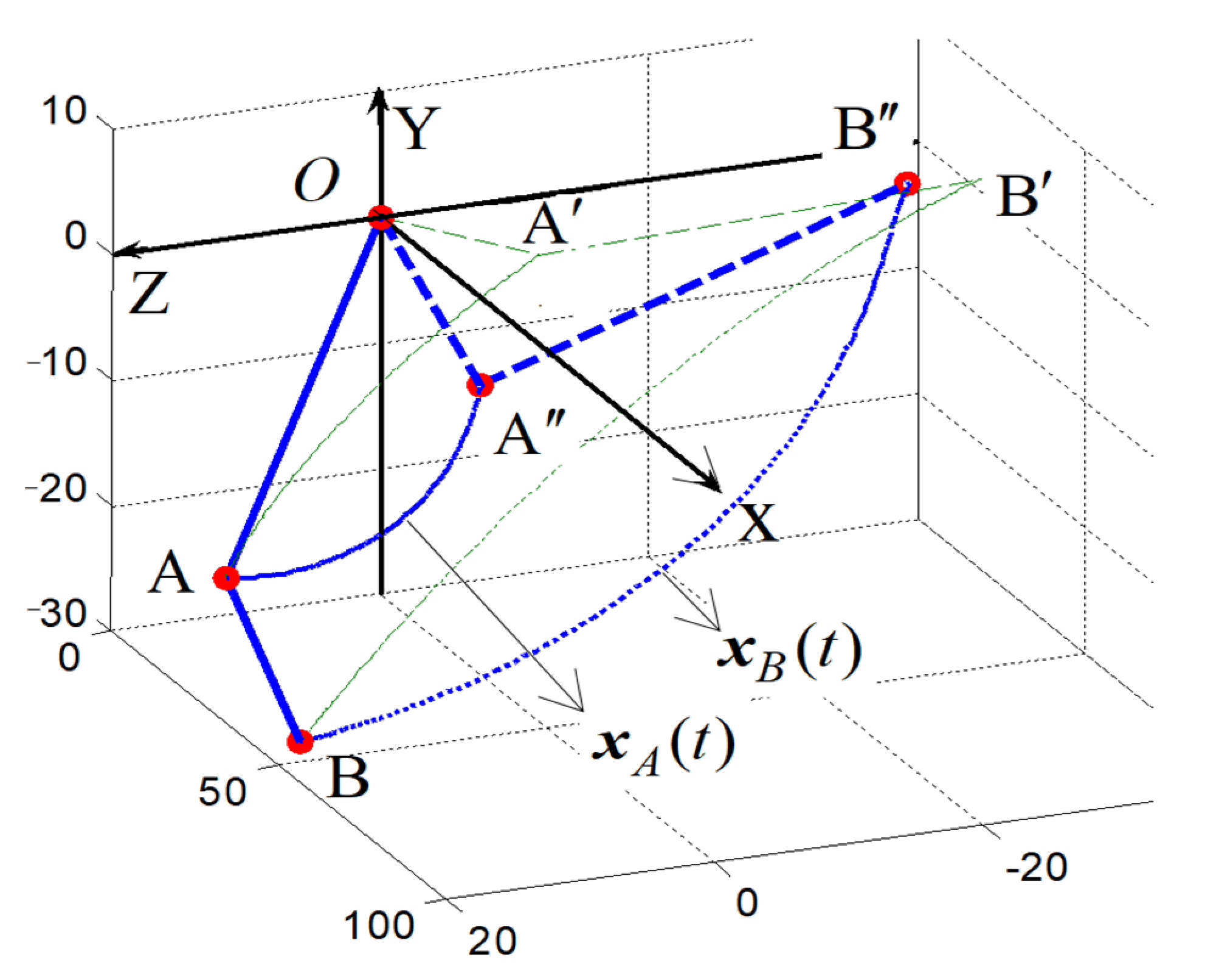
It has solved the “self-motion problem” [25] caused by redundant DoFs. The dynamic Equation (13) defaults that each joint is a cardan joint, resulting in redundant DoFs, and will produce the “self -motion” shown in Figure 8. Two links OA-AB will rotate freely around the OB axis. The third term is the constraint term. It is added to the controller and can limit the arbitrary self-motion of the exoskeleton.

(3)

To directly solve the control problem from task space to joint space, it is not necessary to solve the pseudo-inverse matrix and inverse kinematics. By selecting the appropriate controller parameters C and K, the state of the system can be driven to converge gradually. That is, when $t\to \infty$, not only $x\left(t\right)\to x_d$, but also $q\left(t\right)\to q^0, \dot{q}\left(t\right)\to 0$, where $q^0$ represents the most comfortable nominal position of the joint angle when the endpoint reaches the target position in the task space.

The next key problem is to prove that the closed-loop control system Equation (14) is stable, and to verify that the controller is available by use of simulation analysis.

3.2. Stability Analysis

The state variables of the closed-loop control system in Equation (13) include not only $q,\dot{q},\ddot{q}$ in the joint space, but also $\Delta x$ in the task space. Therefore, it is difficult to find the equilibrium points of the system, and it is more difficult to analyze the stability of the equilibrium point by Lyapunov method. Arimoto et al. [26] proposed some concepts related to the reference equilibrium state and its neighborhood, including a six-dimensional manifold in the neighborhood and its stability on the manifold, which solved the problem of stability analysis of the closed-loop control system in Equation (20) well.

The method and idea of stability analysis are as follows: to prove that as $t\to \infty$, $x\left(t\right)\to x_d$, then $q\left(t\right)\to q^0, \dot{q}\left(t\right)\to 0$, just prove that any solution of Equation (20) is stable on a manifold and asymptotically tends to a sub-manifold.

Since $\dot{x}=J\left(q\right)\dot{q}$, taking an inner product in Equation (20) with $\dot{q}$ leads to the following [26]:

$$\frac{d}{dt}E=-{\dot{q}}^{\mathrm{T}}C\dot{q}$$

(21)

where

$$E(q,\dot{q})=\frac{1}{2}\left\{{\dot{q}}^{\mathrm{T}}M(q)\dot{q}+k{‖\Delta x(q)‖}^2\right\}$$

(22)

E stands for the total energy of the system, including the quadratic function of $\dot{q}$ and $\mathsf{\Delta }x\left(q\right)=x\left(q\right)-x_d$. In fact, the scalar function $E\left(q,\dot{q}\right)$ is not positive definite with respect to the state vector $\left(q,\dot{q}\right)\in R^8$, because E includes only a quadratic term of three-dimensional vector $\mathsf{\Delta }x$ and a positive definite quadratic function of $\dot{q}$. Therefore, it cannot be used as a Lyapunov function to analyze the stability of the closed-loop control system in Equation (20).

We define the one-dimensional manifold as follows:

$$H_1=\left\{(q,\dot{q}=0):\varphi (q)=0,x(q)=x_d, y(q)=y_d, z(q)=z_d\right\}$$

(23)

The constrained 6-dimensional manifold is as follows:

$$H_6=\left\{(q,\dot{q}=0):\varphi (q)=0 \& \dot{\varphi }=J_{\varphi }\dot{q}=0\right\}$$

(24)

We consider a reference equilibrium state posture $\left(q^0,{\dot{q}}^0=0\right)\in R^8$ with still state (i.e., $\dot{q}=0$), whose endpoint is located at $x_d$, that is, $x\left(q^0\right)=x_d$, and hence $\left(q^0,0\right)\in H_1$. We define a neighborhood N₈(r) of the reference state $\left(q^0,0\right)$ with radius r in such a manner that:

$$N_8(r)=\left\{(q,\dot{q}):\frac{1}{2}{\dot{q}}^{\mathrm{T}}M\dot{q}+\frac{1}{2}\Delta q^{\mathrm{T}}M\Delta q\le r^2\right\}$$

(25)

where $\mathsf{\Delta }q=q-q^0$. We define a family of neighborhoods of the reference state $\left(q^0,0\right)$ on the constraint manifold H₆ in such a way that:

$$N_6(\epsilon )=\left\{(q,\dot{q}):\varphi (q)=0,J_{\varphi }\dot{q}=0, \& E(\Delta x(q),\dot{q})\le {\epsilon }^2\right\}$$

(26)

where $E$ is shown in Equation (23). Through careful analysis and understanding of these manifolds and regions, it can be obtained that any state lying on H₁ ∩ N₈(r₀) is included in N₆(ε) ∩ N₈(r₀) for any ε ≥ 0.

Now, let us consider that the reference equilibrium state $\left(q^0,0\right)$ is stable on the manifold $H_1\cap N^8\left(r_0\right)$. It is possible to choose a positive parameter r₀ > 0 for Equation (17) and construct a neighborhood N8(r0) such that for any $\left(q,\dot{q}\right)\in N_8\left(r_0\right)$, $J_x\left(q\right)={\left(\partial x_B/\partial q,\partial y_B/\partial q,\partial z_B/\partial q\right)}^T$ is nondegenerate. Then, there exist two positive constants ${\sigma }_0$ and ${\sigma }_1$ such that:

$${\delta }_1{I}_3\ge J_x(q)J_x^{\mathrm{T}}(q)\ge J_x(q)P_{\varphi }{J}_x^{\mathrm{T}}(q)\ge {\delta }_0{I}_3$$

(27)

where $I_3$ is the 3 × 3 unit matrix. $P_{\varphi }=I-J_{\varphi }^{+}{J}_{\varphi }$, $J_{\varphi }^{+}=J_{\varphi }^T{(J_{\varphi }{J}_{\varphi }^T)}^{-1}$ (see reference [27]), and $J_{\varphi }=\partial \varphi \left(q\right)/\partial q$ (see Appendix C). The scalar function E, defined in Equation (19), does not increase as $t\to \infty$, so it is possible to choose some positive parameter ${\delta }_1$ such that the following inequality holds:

$$E(t)\le E(0)=\frac{1}{2}\left\{{\dot{q}}^{\mathrm{T}}(0)M(q(0))\dot{q}(0)+\Delta {\mathit{x}}^{\mathrm{T}}(0)k\Delta \mathit{x}(0)\right\}\le {\delta }_1^2$$

(28)

Now, let us consider another extended scalar function [27]:

$$V=E+\gamma {\dot{q}}^{\mathrm{T}}M(q)P_{\varphi }{J}_x^{\mathrm{T}}k\Delta \mathit{x}$$

(29)

where γ > 0 is a constant that is determined later. The time-derivative of V is as follows:

$$\begin{array}{l}\dot{V}=\dot{E}-\gamma {\left\{\left(S(q,\dot{q})+C\right)\dot{q}+J_x^{\mathrm{T}}K\Delta \mathit{x}-J_{\varphi }^{\mathrm{T}}\Delta \lambda \right\}}^{\mathrm{T}}{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta x\\ +\gamma {\dot{q}}^{\mathrm{T}}\left\{(\dot{M}{P}_{\varphi }{J}_x^{\mathrm{T}}+M{\dot{P}}_{\varphi }{J}_x^{\mathrm{T}}+M{P}_{\varphi }{\dot{J}}_x^{\mathrm{T}})K\Delta \mathit{x}+M{P}_{\varphi }{J}_x^{\mathrm{T}}K\dot{x}\right\}\\ =\dot{E}-\gamma \Delta {\mathit{x}}^{\mathrm{T}}\left(K{J}_x^{}{P}_{\varphi }{J}_x^{\mathrm{T}}K\right)\Delta \mathit{x}-\gamma {\dot{q}}^{\mathrm{T}}C{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta \mathit{x}\\ +\gamma {\dot{q}}^{\mathrm{T}}\left\{\left(\frac{1}{2}\dot{M}{P}_{\varphi }{J}_x^{\mathrm{T}}+M{\dot{P}}_{\varphi }{J}_x^{\mathrm{T}}+M{P}_{\varphi }{\dot{J}}_x^{\mathrm{T}}+S{P}_{\varphi }{J}_x^{\mathrm{T}}\right)K\Delta x+M{P}_{\varphi }{J}_x^{\mathrm{T}}K\dot{x}\right\}\end{array}$$

(30)

The above formula looks very complex. In fact, the fourth term is the sum of the quadratic function of the angular velocity vector $\dot{q}$. All variable elements in $M,P_{\varphi },J_x,\mathsf{\Delta }x$ are composed of sine (cosine) functions of $q$. Their time derivatives $\dot{M},{\dot{P}}_{\varphi },{\dot{J}}_x,\dot{x}$ and $S\left(q,\dot{q}\right)$ are all homogeneous in $\dot{q}$, that is, they vanish when $\dot{q}=0$. Therefore, there exists a constant ${\alpha }_0$ such that the following formula holds:

$${\dot{q}}^T\left\{\begin{array}{l}\left(\frac{1}{2}\dot{M}{P}_{\varphi }{J}_x^T+M{\dot{P}}_{\varphi }{J}_x^T+M{P}_{\varphi }{\dot{J}}_x^T+S{P}_{\varphi }{J}_x^T\right)K\Delta x\\ +M{P}_{\varphi }{J}_x^{T}K\dot{x}\end{array}\right\}\le \frac{{\alpha }_0}{2}{\dot{q}}^{T}M\dot{q}$$

(31)

The third item in Equation (31) meets the following condition:

$$-{\dot{\mathit{q}}}^{\mathrm{T}}C{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta \mathit{x}\le \frac{1}{2}\left({\dot{\mathit{q}}}^{\mathrm{T}}C{P}_{\varphi }C\dot{\mathit{q}}+\Delta {\mathit{x}}^{\mathrm{T}}K{J}_x^{}{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta \mathit{x}\right)$$

The first three items in Equation (31) can be expressed as follows:

$$\begin{array}{l}\dot{E}-\gamma \Delta {\mathit{x}}^{\mathrm{T}}K{J}_x^{}{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta \mathit{x}-\gamma {\dot{\mathit{q}}}^{\mathrm{T}}C{P}_{\varphi }{J}_x^{\mathrm{T}}K\Delta \mathit{x}\\ \le -{\dot{\mathit{q}}}^{\mathrm{T}}\left(C-\frac{\gamma }{2}C{P}_{\varphi }C\right)\dot{\mathit{q}}-\frac{\gamma }{2}\Delta {\mathit{x}}^{\mathrm{T}}(K{J}_x^{}{P}_{\varphi }{J}_x^{\mathrm{T}}K)\Delta \mathit{x}\end{array}$$

(32)

Substituting Equations (31) and (32) into Equation (30), considering that $C{P}_{\varphi }C\le C^2$, selecting parameters $C=c{I}_4$, $K=k{I}_3$, and noting that ${\mathrm{h}}_M$ is the maximum eigenvalue of $M\left(q\right)$ over all $q$, Equation (30) can be reduced to the following:

$$\begin{array}{l}\dot{V}\le -\left(c-\frac{\gamma c^2}{2}-\frac{\gamma {\alpha }_0{h}_m}{2}\right){‖\dot{\mathit{q}}‖}^2-\frac{\gamma k^2}{2}\Delta {\mathit{x}}^{\mathrm{T}}{P}_{\varphi }\Delta \mathit{x}\\ \le -\left(\frac{2c}{h_m}-\frac{\gamma c^2}{h_m}-\gamma {\alpha }_0\right)\frac{h_m}{2}{‖\dot{\mathit{q}}‖}^2-(\gamma k{\delta }_0)\frac{k}{2}{‖\Delta \mathit{x}‖}^2\end{array}$$

(33)

Reasonably selecting parameters $0.004\le c\le 0.1$, $\gamma =k,$ and ${\delta }_0$,${\mathrm{h}}_M$, it is possible to reach the following:

$$\begin{array}{l}\frac{2c}{h_m}-\frac{k{c}^2}{h_m}-k{\alpha }_0>k^2{\delta }_0=\sigma \\ \dot{V}\le -\sigma \left(\frac{h_M}{2}{‖\dot{\mathit{q}}‖}^2+\frac{k}{2}{‖\Delta \mathit{x}‖}^2\right)\le -\sigma E\end{array}$$

(34)

We construct an inequality $\left|ab\right|\le \left(1/8\right)a^2+2b^2$ and use it to analyze the inequality of scalar function V from another perspective.

$$\begin{array}{l}V\le E+\gamma {\dot{q}}^{T}M(q)P_{\varphi }{J}_x^{T}K\Delta x\\ \le E+\gamma \left\{\frac{k^2}{8}{\dot{q}}^T{M}^2(q)\dot{q}+2\Delta x^T{J}_x^{}{P}_{\varphi }{J}_x^{}\Delta x\right\}\\ \le E+\left(\frac{\gamma h_M{k}^2}{4}\right)\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}+\left(\frac{4\gamma {\delta }_1}{k}\right)\cdot \frac{k}{2}{‖\Delta x‖}^2\end{array}$$

$$V\le E+\frac{1}{3}\left\{\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}+\frac{k}{2}{‖\Delta x‖}^2\right\}=\frac{4}{3}E$$

(35)

and similarly:

$$V\ge E-\frac{1}{3}\left\{\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}+\frac{k}{2}{‖\Delta x‖}^2\right\}=\frac{2}{3}E$$

(36)

It follows from Equations (35)–(37) that:

$$\dot{V}(t)\le -\frac{3}{4}\sigma V, E\le \frac{3}{2}V$$

(37)

which leads to:

$$E(t)\le \frac{3V(0)}{2}{e}^{-(3\sigma /4)t}\le 2E(0)e^{-(3\sigma /4)t}$$

(38)

The results of this inequality in Equation (38) are used to analyze the stability of the closed-loop control system. To prove that for any initial condition value $\left(q\left(0\right),\dot{q}\left(0\right)\right)\in N_6\left(\delta \left(\epsilon \right)\right)\cap N_8\left(r_1\right)$, the solution $\left(q\left(t\right),\dot{q}\left(t\right)\right)$ will remain in $N_6\left(\epsilon \right)\cap N_8\left(r_0\right)$, two metrics are defined as follows:

$$\begin{array}{l}{‖q(t)-q(0)‖}_{\overline{H}}={\left\{\frac{h_M}{2}{‖q(t)-q(0)‖}^2\right\}}^{1/2}\\ {‖q(t)-q(0)‖}_H={\left\{\frac{1}{2}{\left[q(t)-q(0)\right]}^{\mathrm{T}}H(q(t))\left[q(t)-q(0)\right]\right\}}^{1/2}\end{array}$$

(39)

Then, it follows that:

$$\begin{array}{l}\frac{d}{dt}{‖q(t)-q(0)‖}_{\overline{H}}=\frac{h_M{\dot{q}}^{\mathrm{T}}(t)\left[q(t)-q(0)\right]}{2{‖q(t)-q(0)‖}_{\overline{H}}}\\ \le \frac{\sqrt{h_m/h_M}}{{‖q(t)-q(0)‖}_{\overline{H}}}{\left\{\frac{1}{2}{q}^{\mathrm{T}}(t)H(q(t))\dot{q}(t)\right\}}^{1/2}{‖q(t)-q(0)‖}_{\overline{H}}\\ =\sqrt{h_m/h_M}{‖\dot{q}(t)‖}_H\end{array}$$

(40)

Hence, it follows from Equations (14), (30), and (31) that:

$$\begin{array}{l}{‖q(t)-q(0)‖}_H\le {‖q(t)-q(0)‖}_{\overline{H}}\le {\displaystyle {\int }_0^t\sqrt{h_M/h_m}}{‖\dot{q}(\varsigma )‖}_{H}d\varsigma \\ \le \sqrt{h_M/h_m}{\displaystyle {\int }_0^t{\left\{E(\varsigma )\right\}}^{1/2}d\varsigma =}\sqrt{h_M/h_m}{(2E(0))}^{1/2}\frac{8}{3\sigma }\end{array}$$

(41)

Now, for an arbitrarily given $\epsilon >0$, choose $r_1=r_0/3$ and $\delta \left(\epsilon \right)>0$ in the following way:

$$\delta (\epsilon )=\left\{\begin{array}{c}\frac{1}{\sqrt{2}}\overline{\epsilon }, \mathrm{if} \epsilon \ge \overline{\epsilon }\hfill \\ \frac{1}{\sqrt{2}}\epsilon , \mathrm{if} 0<\epsilon \ge \overline{\epsilon }\hfill \end{array}\right.\mathrm{where} \overline{\epsilon }=\min \left\{\frac{r_0}{3},{\delta }_1,\frac{\alpha r_0}{8}\sqrt{h_m/h_M}\right\}$$

(42)

Substituting the initial condition Equation (29) $E\left(0\right)\le {\delta }^2\left(\epsilon \right)$ into Equation (42), and $\delta \left(\epsilon \right)=\overline{\epsilon }/\sqrt{2}$, leads to the following:

$$\begin{array}{l}{‖q(t)-q(0)‖}_H\le \sqrt{h_M/h_m}{\left\{2{\left(\frac{\overline{\epsilon }}{\sqrt{2}}\right)}^2\right\}}^{1/2}\frac{8}{3\sigma }\\ =\sqrt{h_M/h_m}\frac{8\overline{\epsilon }}{3\sigma }\le \frac{r_0}{3}\end{array}$$

(43)

In the case that $0<\epsilon <\overline{\epsilon }, \delta \left(\epsilon \right)=\epsilon /\sqrt{2}<\overline{\epsilon }/\sqrt{2}$. According to Equation (44), it follows that:

$${‖q(t)-q(0)‖}_H\le \frac{r_0}{3}$$

(44)

If $\left(q\left(0\right),\dot{q}\left(0\right)\right)\in N_6\left(\delta \left(\epsilon \right)\right)\cap N^8\left(r_1\right),$ then, noting the definition of $N_8\left(r_1\right)$, it can be seen that:

$${‖q(0)-q^0‖}_H<r_1=\frac{r_0}{3}$$

(45)

From Equations (28) and (43)–(45), it can be seen that:

$$\begin{array}{l}{\left\{{‖q(t)-q^0‖}_H^2+{‖\dot{q}(t)‖}_H^2\right\}}^{1/2}\le {‖q(t)-q^0‖}_H^{}+{‖\dot{q}(t)‖}_H^{}\\ \le {‖q(t)-q(0)‖}_H^{}+{‖q(0)-q^0‖}_H^{}+{‖\dot{q}(t)‖}_H^{}\le \frac{r_0}{3}+\frac{r_0}{3}+\delta (\epsilon )\le \frac{2r_0}{3}+\frac{\overline{\epsilon }}{\sqrt{2}}\le r_0\end{array}$$

(46)

It is evident that $E\left(0\right)\le \delta {(\epsilon )}^2\le {\epsilon }^2$ implies that $E\left(t\right)\le {\epsilon }^2$ and $\left(q\left(t\right),\dot{q}\left(t\right)\right)\in N_6\left(\epsilon \right)$. Therefore, it is concluded that the solution $\left(q\left(t\right),\dot{q}\left(t\right)\right)$ remains in $N_6\left(\epsilon \right)\cap N_8\left(r_0\right)$. As $t\to \infty$, $x\left(t\right)\to x_d$, then $q\left(t\right)\to q^0, \dot{q}\left(t\right)\to 0$.

4. Simulation Results

4.1. Simulation Conditions

The upper-limb exoskeleton manipulator introduced in Section 3 and shown in Figure 7 is used as the simulation research object. The parameter matrix model of the closed-loop control system Equation (13) is shown in Appendix A. We note Assumption 1 and 2 and assume that $S\left(q,\dot{q}\right)=0$. In Cartesian space (see Figure 9), the initial location coordinates of the endpoint B are $x_0=\left(0.4473,-0.2968, 0.1713\right)$ and those of the target position B′ are $x_d=\left(0.4989, 0.0887,-0.3229\right)$. In the joint space, the corresponding initial posture at $x_0$ is $q\left(0\right)=\left(q_1, q_2, q_3, q_4\right)=\left(-30°, 20°, 0°, 60°\right)$, and a corresponding target posture at $x_d$ is $q\left(\infty \right)=\left(-60°, 100°,-20°, 45°\right)$.

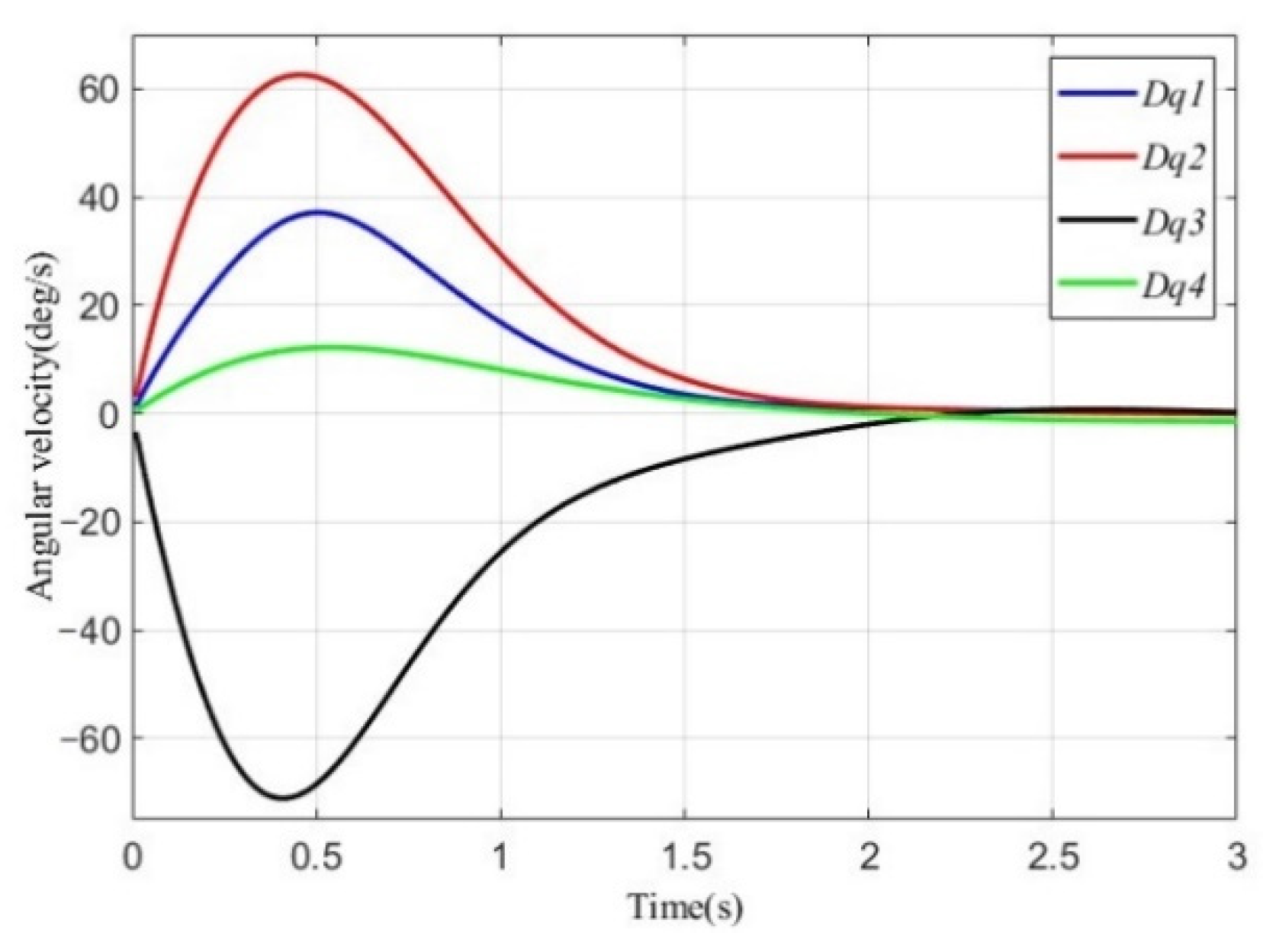
4.2. A Velocity Driving Control Method Base on SNDF

In order to compare the simulation results of different control strategies, we propose an innovative velocity drive control method based on standard normal distribution functions (SNDF). This idea comes from the research conclusion in [26], that is, human skilled multi-joint reaching is characterized as follows: (a) the profile of the endpoint trajectory in task space becomes closely rectilinear, (b) the velocity profile of it becomes symmetric and bell-shaped, and (c) the acceleration profile has double peaks. As we all know, the SNDF curve is a bell shape. Therefore, we construct the driving velocity control signal of the closed-loop control system Equation (14) by use of SNDF. The design steps are as follows:

Step 1:

Determine the initial posture $q\left(0\right)$ and target posture $q\left(\infty \right)$;

Step 2:

Map the interval [$q\left(0\right)$, q($\infty$)] to the independent variable interval [-4, +4] of SNDF, and construct the angular velocity $\dot{q}\left(t\right)$ as follows:

$$\dot{q}(t)=\frac{1}{\sqrt{2\pi }}\exp \left\{-\frac{1}{2}{\left[8\frac{q(t)-q(0)}{q{(\infty )}_1-q(0)}-4\right]}^2\right\}$$

(47)

Step 3:

The angular velocity Equation (47) is used as the driving angular velocity of the joint motor. According to the properties of the SNDF, the area enclosed by the function curve and the independent variable coordinate axis is equal to 1. Thus, we can get:

$${\displaystyle {\int }_{-\infty }^{+\infty }\dot{q}(\varsigma )}d\varsigma =1,{\displaystyle {\int }_{-4}^4\dot{q}(\varsigma )}d\varsigma \approx 1$$

(48)

Then, it can be found that:

$$\Delta q=q(\infty )-q(0)\approx [(q(\infty )-q(0)]{\displaystyle {\int }_{-4}^4\dot{q}(\varsigma )}d\varsigma$$

(49)

Function $\mathsf{\Omega }=\Delta q\dot{q}\left(t\right)$ can be used to construct the driving control torque of joints, as follows:

$$\tau =H(q)\frac{d\Omega }{dt}+S(q,\dot{q})\Omega +g(q)$$

(50)

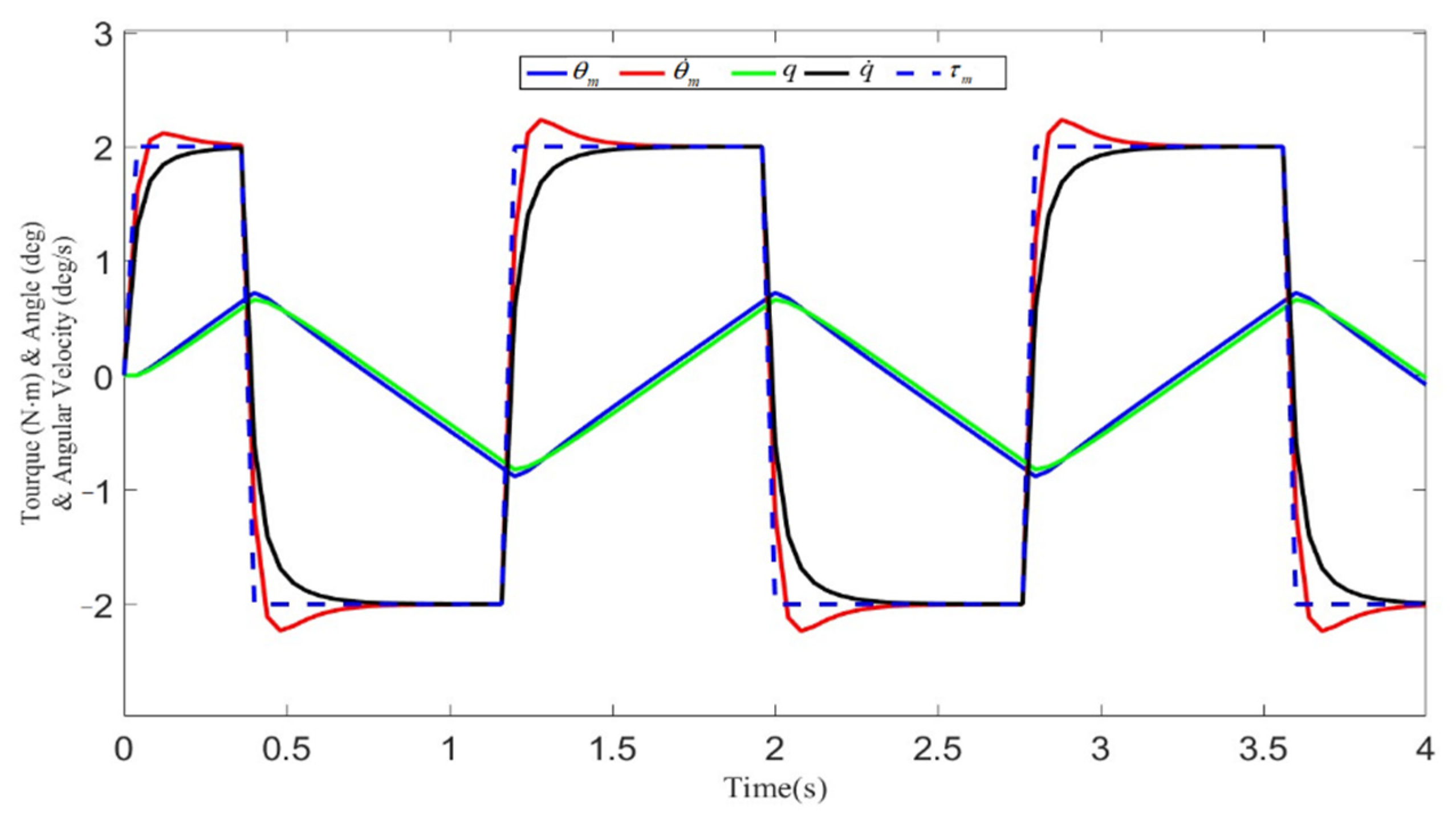
4.3. Simulation Results

Firstly, the simulation results under the action of Equation (50) are shown in Figure 10. Figure 10 shows the four constructed angular velocities ${\Omega }_i, i=1, 2, 3, 4$. Those four curves are obviously applied to standard normal distribution. Figure 11 shows the change of posture and the endpoint trajectories in Cartesian space. The initial positions of the upper arm and forearm are located at OA and AB, respectively, while the end positions are at OA’ and A’B’. $x_A\left(t\right)$ represents the trajectory of point A, while $x_B\left(t\right)$ represents the trajectory of endpoint B. From the simulation results, the target position is accurately reached, and the control task is fulfilled.

Secondly, let us simulate the control effect of Equation (19) without constraint item $\lambda J_{\varphi }^T$, and assuming that the gravity term is fully compensated, that is:

$$\tau =-C\dot{q}-J_x^T(q)K\Delta x$$

(51)

Selecting elements of diagonal matrix C and K, $\left(c_{11},c_{22},c_{33},c_{44}\right)=\left(1,2.5,0.3,0.5\right)$, $\left(k_{11},k_{22},k_{33},k_{44}\right)=\left(10,15,15,1\right)$, the simulation results are shown in Figure 12, Figure 13, Figure 14 and Figure 15. The angular velocities of the four joints under the action of controller in Equation (51) are shown in Figure 12, denoted by $Dq1$, $Dq2$, $Dq3$, and $Dq4$, respectively. Unlike the velocity distribution shown in Figure 10, the angular velocity increases rapidly at the beginning, reaching the maximum peak in 0.5 s. The posture and endpoint trajectories under the action of Equation (50) (green curve) and Equation (51) (blue curve) are shown in Figure 13. Obviously, despite starting from the same initial point, the two endpoint trajectories are completely different. Figure 14 shows the change process of the four joint angles with two different control methods: the curve $q$i-1 indicates (50), while the curve $q$i-2 indicates (51). As can be seen from Figure 14, the angles change processes of solid (50) and dotted lines (51) of the same color are completely different, despite starting from the same initial angle (−30° 20°, 0°, 60°). In particular, the change trend of angle q₁ is completely opposite: one positive $(q$_1-1) turn, and the other reverse $(q$_1-2). The redundant DoFs in the system lead to the rotation of the angle from another direction in the process of tracking the change of spatial position. Figure 15 shows the change process of the endpoint position coordinates $x_b\left(t\right), y_b\left(t\right),$ and $z_b\left(t\right)$. The solid line represents method in Equation (50), and the dashed line represents method in Equation (51). Under the action of the two control methods, the movement trends of the two endpoints are consistent, although one speed-up is earlier, and the other is later.

Thirdly, let us simulate the control effect of Equation (19). In the control method in Equation (19), the constraint term $J_{\varphi }^T{\lambda }_d={\left({\partial }_{\varphi }/{\partial }_q\right)}^T{\lambda }_d$ is added to the control law to ensure that the motion trajectory of the endpoint is kept within the plane formed by the initial position $x\left(0\right)$ and the target position $x\left(\infty \right)$ as much as possible. It could be found that the system performs better when the elements of diagonal matrix C and K are selected as $\left(c_{11},c_{22},c_{33},c_{44}\right)=\left(8,10,6,2\right)$, $\left(k_{11},k_{22},k_{33},k_{44}\right)=\left(25,35,30,20\right),$ and ${\lambda }_d=50$. The simulation results are shown in Figure 16 and Figure 17. The variation tendencies of the four joint angles for the control method in Equation (51) and Equation (19) are shown in Figure 16. The dashed curves $q_{i-2}$ are the same as in Figure 14 and represent the results of control method in Equation (51). The solid curves $q_{i-1}$ in the Figure 16 represent the results of control method in Equation (19). Figure 17 shows the joint posture changes and endpoint trajectories under three control methods. The curves $\stackrel{⌢}{B{B}^{\prime }}$ (by Equation (50)), $\stackrel{⌢}{B{B}^{″}}$ (by Equation (51)), and $\stackrel{⌢}{B{B}^{‴}}$ (by Equation (19)) represent the three trajectories of endpoints under three different control methods, respectively.

4.4. Comparative Analysis

By analyzing the above simulation results, the following conclusions can be drawn:

(1)

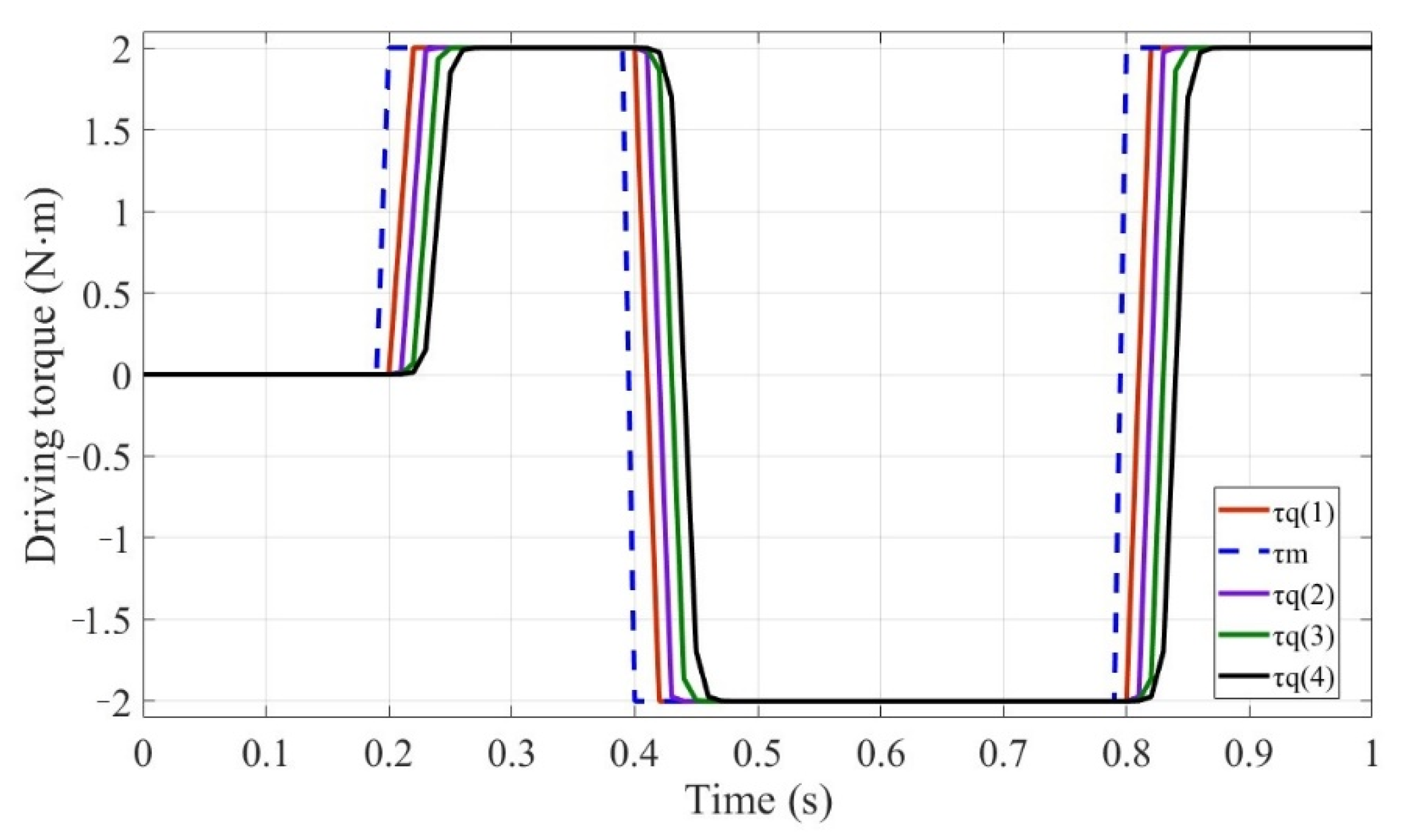
The system in Equation (20) is controllable. The control in Equation (51) can realize that as $t\to \infty$.$\Delta x_B=x_B\left(t\right)-x_B\left(\infty \right)\to 0$, and $q\left(t\right)\to q\left(\infty \right), \dot{q}\left(t\right)\to 0$. That is to say that $q\left(t\right)$ and $\dot{q}\left(t\right)$ can both be controlled by $\Delta x_B$.

(2)

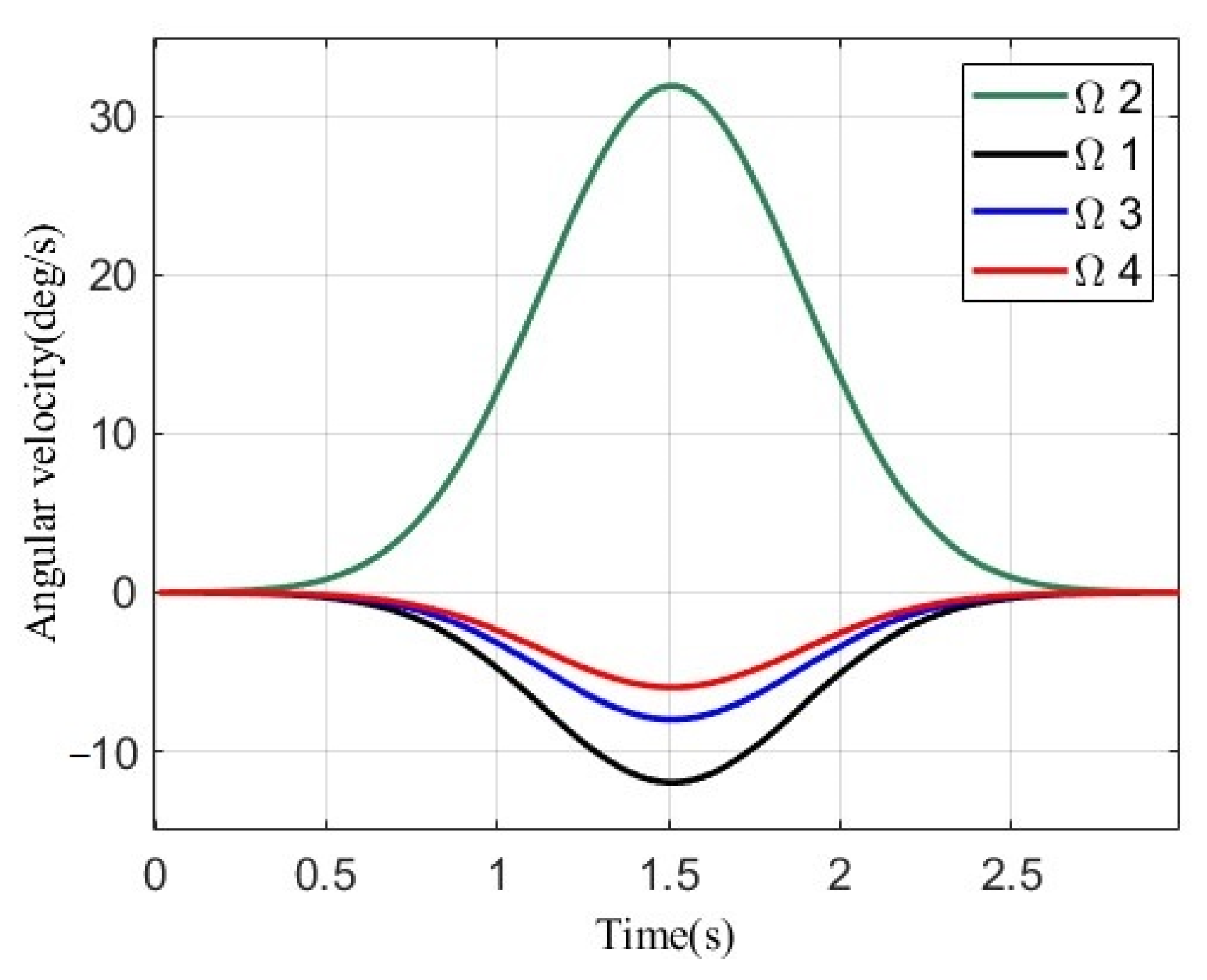
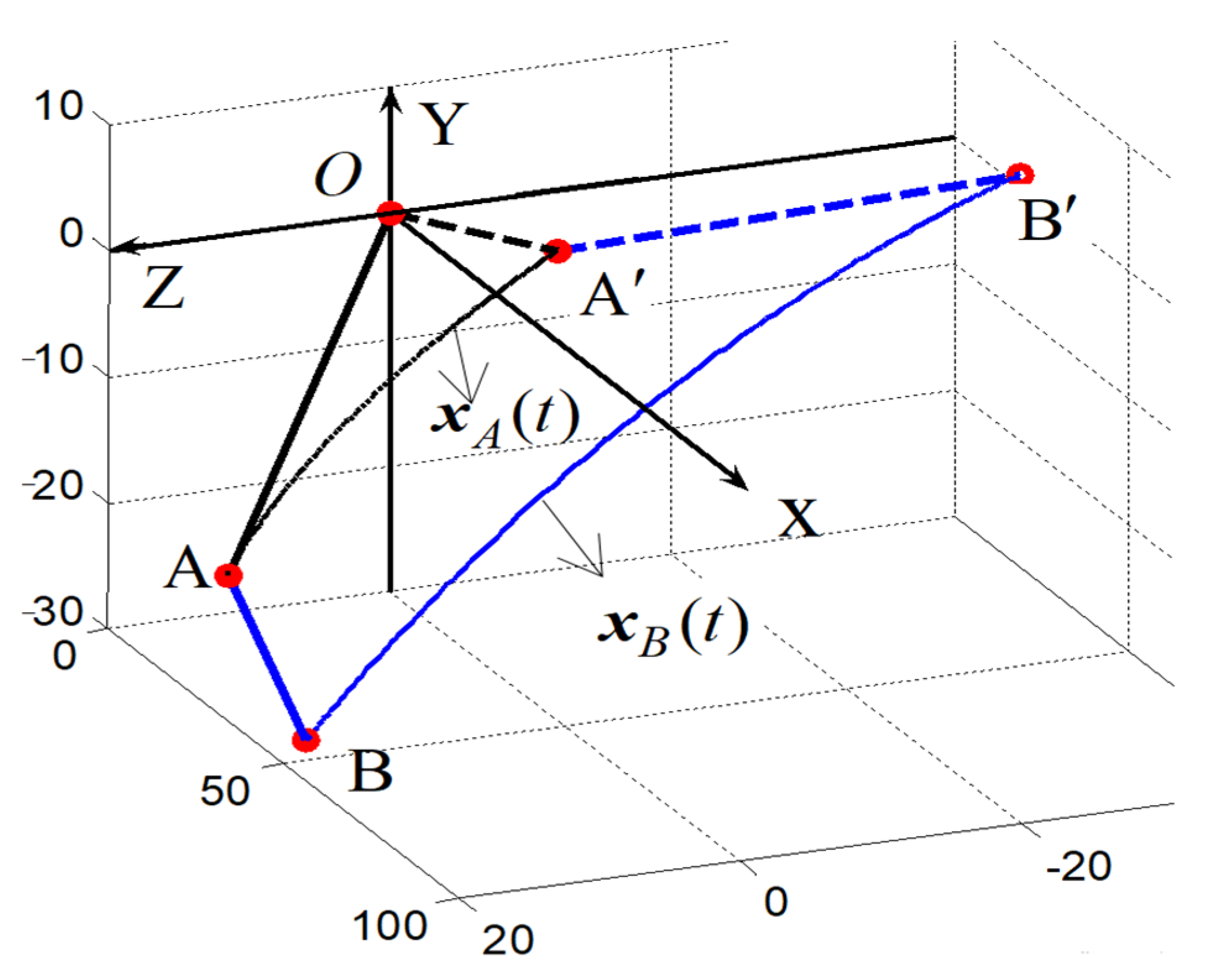
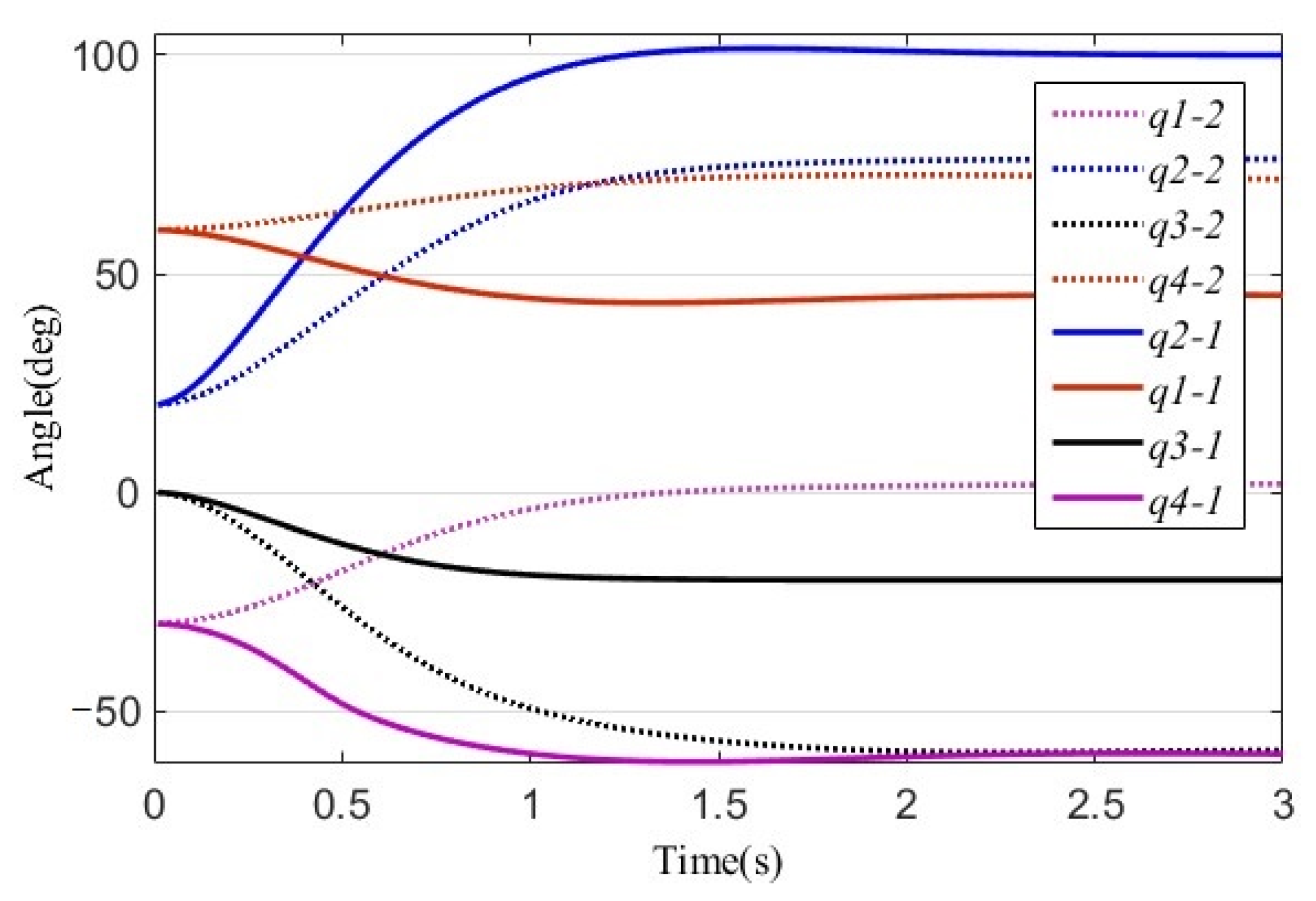
The “self-motion problem” caused by redundant DoFs will lead to the uncertainty of the posture paths. Two control methods in Equations (50) and (51), achieved completely different posture change paths and endpoint trajectories for the same control target $\Delta x_B\to 0$. It can be seen from Figure 14 that the trend of solid and dotted lines of the same color is completely different. The joint angle changes monotonically from $q\left(0\right)$ to $q\left(\infty \right)$ under the control of Equation (50). However, the joint angle under the control of Equation (51) varies according to an uncertain law and finally reaches an uncertain angle position, although the control objectives of $\Delta x_B\approx 0$ and $\dot{q}\left(t\right)\approx 0$ have been achieved already. Compared with the two trajectories $\widehat{BB\prime }$ and $\widehat{BB\prime }\prime$ of endpoint B in Figure 13, it can be seen that the trajectories are completely different.

(3)

The constraint term $J_{\varphi }^T{\lambda }_d$ added to the controller limits the arbitrary self-motion of the exoskeleton manipulator. It can be seen from Figure 16 that the posture paths of $q\left(t\right)$ controlled by Equation (19) are completely correct; this trend is the same as that of Equation (50) and completely different from that of Equation (51). Comparative analysis of the three endpoint trajectories is shown in Figure 17. The trajectory $\stackrel{⌢}{B{B}^{‴}}$ of $q\left(t\right)$ controlled by Equation (19) is closely rectilinear, and the accuracy is the highest.

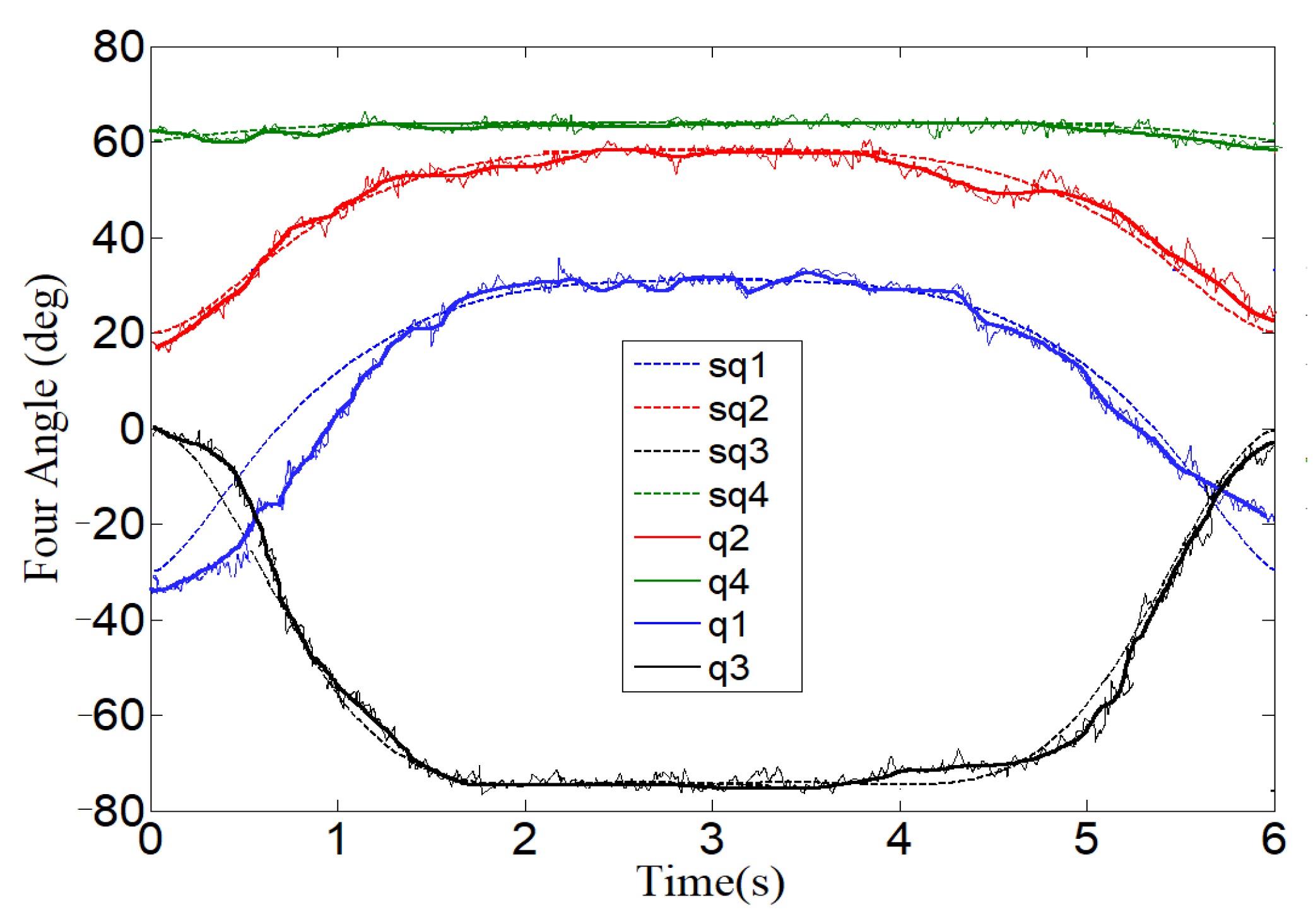
4.5. Experimental Verification

We use the prototype of an upper-limb rehabilitation exoskeleton designed by our team, as shown in Figure 7, to verify the feasibility and the reliability of the VSDH algorithm (19). A 24-year-old male volunteered to conduct the experiment. The initial posture of the exoskeleton is vertical down, as shown in Figure 18a, and the end position coordinates are (44, −30, 17) (cm). The target position is above the front of the body, shown in Figure 18b, and the end position coordinates are (50, 10, −30) (cm). In one experiment, an action of lifting and falling was performed. The initial parameters of the controller are set as (c11, c22, c33, c44) = (12.85, 16.6, 3, 8.7), (k11, k22, k33, k44) = (20, 30, 40, 30), and λ = 0.80. Collect the voltage signal data output by the encoder that comes with the servo motor (sampling period is 0.05 s) and convert it into joint angle data. A set of four joint angle data sets is plotted, as shown in Figure 19. The dotted lines $sq1$, $sq2$, $sq3$, and $sq4$ in Figure 19 represent the digital simulation data curves of the four joint angles, respectively, the tortuous solid lines q1, q2, q3, and q4 represent the measured data curves of the four joint angles, respectively, and the smoother solid lines represent the data curve after filtering. It can be seen from Figure 19 that the experimental data are highly close to the simulation results. The error between them is caused by the motion uncertainty of the human upper limb.

The overall feeling of the experimenter is that the exoskeleton runs smoothly, the acceleration and stop are gentle and natural, and there is no discomfort of sudden change. Repeated experiments verified that the VSDH algorithm in Equation (19) has good feasibility and reliability.

5. Conclusions

An upper-limb rehabilitation exoskeleton should have a rigid skeleton, soft joints, and flexible movements like human limbs so that it can meet ever-increasing demands for high flexibility, high environmental adaptability, and good comfort. Flexible joints have been successfully utilized in rehabilitation robots and shown some benefits. The flexible control strategy based on VSDH proposed in this paper was successfully applied to the controller design for an upper-limb rehabilitation exoskeleton to solve the virtual softening problem of a single-rigid-joint actuator and the constrained control problem of a multi-joint exoskeleton with redundant DoFs. Theoretical design and simulation results confirm that it is feasible to soften the torque output of the single-joint actuator by designing the control signal of the motor according to VSDH. The multi-joint cooperative flexible controller in Equation (19) presented the dynamic characteristics of spring damping and has solved the self-motion problem caused by redundant DoFs.

The control methods proposed in this paper are mainly suitable for passive rehabilitation training with an upper-limb exoskeleton. The initial pose and target position are set artificially. In future work, the focus of this project is to carry out active rehabilitation training according to the patient’s active exercise intention. Apart from this issue, the unmeasurable noise caused by system vibration would also influence the precision of the controller; thus, we will be focusing on solving that problem too.