Downsizing Effects on Micro and Nano Comb Drives
Abstract
1. Introduction
2. Design and Operating Principles
3. Numerical Approach
- preparation of the device model for the electromechanical simulations;
- applications of the voltage between the electrodes for a variety of values;
- determination of the voltage variability ranges due to the presence of critical voltage values; such ranges depend on the pull-in voltages [49] at which the fingers may induce short-circuits because of instability effects;
- analysis of the device response in terms of motion, as well as of mechanical stress;
- iteration of the procedure for different sets of and values;
- mapping of the results with the limits due to the fabrication process;
- arranging the design charts to offer a friendly display of the scaling effects on the device performances.
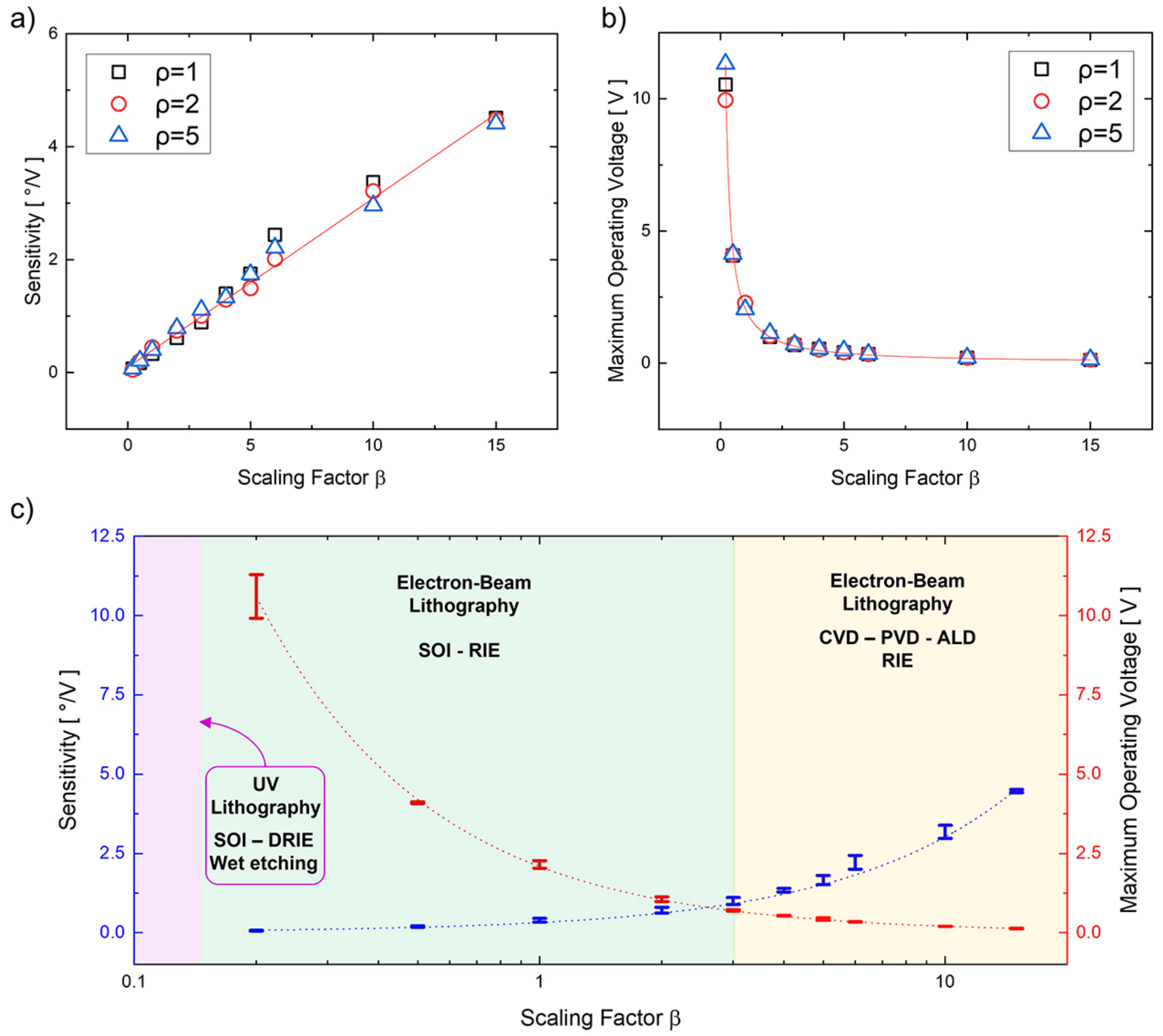
- the maximum operating voltage that the comb configuration is able to sustain with no pull-in occurrence;
- the device maximum sensitivity in terms of angular displacement per unit Volt (°/V).
4. Results and Discussion
4.1. Numerical Results
4.2. Technological Demonstration
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thompson, S.E.; Parthasarathy, S. Moore’s law: The future of Si microelectronics. Mater. Today 2006, 9, 20–25. [Google Scholar] [CrossRef]
- Thompson, S.E.; Chau, R.S.; Ghani, T.; Mistry, K.; Tyagi, S.; Bohr, M.T. In Search of “Forever,” Continued Transistor Scaling One New Material at a Time. IEEE Trans. Semicond. Manuf. 2005, 18, 26–36. [Google Scholar] [CrossRef]
- Frey, H. Handbook of Thin-Film Technology; Chapter Applications and Developments of Thin Film Technology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Swain, N.; Venkatesh, V.; Kumar, P.; Srinivas, G.; Ravishankar, S.; Barshilia, H.C. Review on the machining characteristics and research prospects of conventional microscale machining operations. Mater. Manuf. Process. 2017, 32, 34–42. [Google Scholar] [CrossRef]
- Wise, K.D.; Najafi, K. Microfabrication Techniques for Integrated Sensors and Microsystems. Science 1991, 254, 1335–1342. [Google Scholar] [CrossRef] [PubMed]
- Judy, J.W. Microelectromechanical systems (MEMS): Fabrication, design and applications. Smart Mater. Struct. 2001, 10, 1115–1134. [Google Scholar] [CrossRef]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Hashwan, S.S.B.; Junaid, M.M. A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices. Nanoscale Res. Lett. 2021, 16, 16. [Google Scholar] [CrossRef]
- Poenar, D.P. Microfluidic and Micromachined/MEMS Devices for Separation, Discrimination and Detection of Airborne Particles for Pollution Monitoring. Micromachines 2019, 10, 483. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Mechanical Structure. J. Mech. Des. Trans. ASME 2017, 139, 060801. [Google Scholar] [CrossRef]
- Vargas-Chable, P.; Garcia, J.M., Jr.; Rodriguez-Fuentes, S.F.; Valle-Morales, S.I.; Tecpoyotl-Torres, M. Microgripper Based on Simple Compliance Configurations, Improved by Using Parameterization. Actuators 2020, 9, 140. [Google Scholar] [CrossRef]
- Vargas-Chable, P.; Tecpoyotl-Torres, M.; Cabello-Ruiz, R.; Rodriguez-Ramirez, J.; Vargas-Bernal, R. A Modified U-Shaped Micro-Actuator with a Compliant Mechanism Applied to a Microgripper. Actuators 2019, 8, 28. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. The Effects of Structure Thickness, Air Gap Thickness and Silicon Type on the Performance of a Horizontal Electrothermal MEMS Microgripper. Actuators 2018, 7, 38. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Portelli, B.; Sammut, N. Essential design and fabrication considerations for the reliable performance of an electrothermal MEMS microgripper. Microsyst. Technol. 2019, 1–16. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. The effects of cold arm width and metal deposition on the performance of a U-beam electrothermal MEMS microgripper for biomedical applications. Micromachines 2019, 10, 167. [Google Scholar] [CrossRef] [PubMed]
- Pfusterschmied, G.; Kucera, M.; Wistrela, E.; Manzaneque, T.; Ruiz-Díez, V.; Sánchez-Rojas, J.; Bittner, A.; Schmid, U. Temperature dependent performance of piezoelectric MEMS resonators for viscosity and density determination of liquids. J. Micromech. Microeng. 2015, 25, 105014. [Google Scholar] [CrossRef]
- Ferrara-Bello, A.; Vargas-Chable, P.; Vera-Dimas, G.; Vargas-Bernal, R.; Tecpoyotl-Torres, M. XYZ Micropositioning System Based on Compliance Mechanisms Fabricated by Additive Manufacturing. Actuators 2021, 10, 68. [Google Scholar] [CrossRef]
- Qiao, Q.; Sun, H.; Liu, X.; Dong, B.; Xia, J.; Lee, C.; Zhou, G. Suspended silicon waveguide with sub-wavelength grating cladding for optical mems in mid-infrared. Micromachines 2021, 12, 1311. [Google Scholar] [CrossRef]
- Hahn, K.; Popp, J.; Wagener, A. Process management and design for MEMS and microelectronics technologies. In Microelectronics: Design, Technology, and Packaging; Abbott, D., Eshraghian, K., Musca, C.A., Pavlidis, D., Weste, N., Eds.; International Society for Optics and Photonics, SPIE: Perth, WA, Australia, 2004; Volume 5274, pp. 322–330. [Google Scholar] [CrossRef]
- Fedder, G.K.; Howe, R.T.; Liu, T.J.K.; Quevy, E.P. Technologies for Cofabricating MEMS and Electronics. Proc. IEEE 2008, 96, 306–322. [Google Scholar] [CrossRef]
- Ozaydin-Ince, G.; Coclite, A.M.; Gleason, K.K. CVD of polymeric thin films: Applications in sensors, biotechnology, microelectronics/organic electronics, microfluidics, MEMS, composites and membranes. Rep. Prog. Phys. 2011, 75, 016501. [Google Scholar] [CrossRef]
- Brand, O. Microsensor Integration Into Systems-on-Chip. Proc. IEEE 2006, 94, 1160–1176. [Google Scholar] [CrossRef]
- Varadan, V.; Varadan, V. Microsensors, microelectromechanical systems (MEMS), and electronics for smart structures and systems. Smart Mater. Struct. 2000, 9, 953–972. [Google Scholar] [CrossRef]
- Spearing, S. Materials issues in microelectromechanical systems (MEMS). Acta Mater. 2000, 48, 179–196. [Google Scholar] [CrossRef]
- Feynman, R.P. There’s plenty of room at the bottom. J. Microelectromech. Syst. 1992, 1, 60–66. [Google Scholar] [CrossRef]
- Roukes, M. Plenty of Room, Indeed. Sci. Am. 2001, 285, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Liu, X.; Shi, Q.; He, T.; Sun, Z.; Guo, X.; Liu, W.; Sulaiman, O.B.; Dong, B.; Lee, C. Development trends and perspectives of future sensors and MEMS/NEMS. Micromachines 2020, 11, 7. [Google Scholar] [CrossRef] [PubMed]
- Roukes, M.L. Nanoelectromechanical systems face the future. Phys. World 2001, 14, 25–32. [Google Scholar] [CrossRef]
- Jianrong, C.; Yuqing, M.; Nongyue, H.; Xiaohua, W.; Sijiao, L. Nanotechnology and biosensors. Biotechnol. Adv. 2004, 22, 505–518. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B. Nanotribology and nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS materials and devices. Microelectron. Eng. 2007, 84, 387–412. [Google Scholar] [CrossRef]
- Fraga, M.; Pessoa, R. Progresses in Synthesis and Application of SiC Films: From CVD to ALD and from MEMS to NEMS. Micromachines 2020, 11, 799. [Google Scholar] [CrossRef]
- Neuville, S. Selective Carbon Material Engineering for Improved MEMS and NEMS. Micromachines 2019, 10, 539. [Google Scholar] [CrossRef]
- Veroli, A.; Buzzin, A.; Crescenzi, R.; Frezza, F.; de Cesare, G.; D’Andrea, V.; Mura, F.; Verotti, M.; Dochshanov, A.; Belfiore, N.P. Development of a NEMS-technology based nano gripper. In Advances in Service and Industrial Robotics, Proceedings of the International Conference on Robotics in Alpe-Adria Danube Region, Torino, Italy, 21–23 June 2017; Springer: Cham, Switzerland, 2017; pp. 601–611. [Google Scholar] [CrossRef]
- Vurchio, F.; Ursi, P.; Buzzin, A.; Veroli, A.; Scorza, A.; Verotti, M.; Sciuto, S.A.; Belfiore, N.P. Grasping and releasing agarose micro beads in water drops. Micromachines 2019, 10, 436. [Google Scholar] [CrossRef]
- Luisetto, I.; Tuti, S.; Marconi, E.; Veroli, A.; Buzzin, A.; De Cesare, G.; Natali, S.; Verotti, M.; Giovine, E.; Belfiore, N.P. An Interdisciplinary Approach to the Nanomanipulation of SiO2 Nanoparticles: Design, Fabrication and Feasibility. Appl. Sci. 2018, 8, 2645. [Google Scholar] [CrossRef]
- Belfiore, N.P. Micromanipulation: A challenge for actuation. Actuators 2018, 7, 85. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Bagolini, A.; Rossi, A.; Bocchetta, G.; Vurchio, F.; Crescenzi, R.; Scorza, A.; Bellutti, P.; Sciuto, S.A. Design, fabrication, testing and simulation of a rotary double comb drives actuated microgripper. Micromachines 2021, 12, 1263. [Google Scholar] [CrossRef] [PubMed]
- Hou, M.T.K.; Huang, J.Y.; Jiang, S.S.; Yeh, J.L.A. In-plane rotary comb-drive actuator for a variable optical attenuator. J. Micro/Nanolithogr. MEMS MOEMS 2008, 7, 043015. [Google Scholar] [CrossRef]
- Verotti, M.; Crescenzi, R.; Balucani, M.; Belfiore, N.P. MEMS-based conjugate surfaces flexure hinge. J. Mech. Des. 2015, 137, 012301. [Google Scholar] [CrossRef]
- Veroli, A.; Buzzin, A.; Frezza, F.; De Cesare, G.; Hamidullah, M.; Giovine, E.; Verotti, M.; Belfiore, N.P. An approach to the extreme miniaturization of rotary comb drives. Actuators 2018, 7, 70. [Google Scholar] [CrossRef]
- Buzzin, A.; Cupo, S.; Giovine, E.; de Cesare, G.; Belfiore, N.P. Compliant Nano-Pliers as a Biomedical Tool at the Nanoscale: Design, Simulation and Fabrication. Micromachines 2020, 11, 1087. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Pan, Y.; Fedder, G.K. A CMOS-MEMS mirror with curled-hinge comb drives. J. Microelectromech. Syst. 2003, 12, 450–457. [Google Scholar] [CrossRef]
- Chang, C.M.; Wang, S.Y.; Chen, R.; Yeh, J.A.; Hou, M.T. A comb-drive actuator driven by capacitively-coupled-power. Sensors 2012, 12, 10881–10889. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. Compliance synthesis of CSFH MEMS-based microgrippers. J. Mech. Des. 2017, 139, 022301. [Google Scholar] [CrossRef]
- Crescenzi, R.; Balucani, M.; Belfiore, N.P. Operational characterization of CSFH MEMS technology based hinges. J. Micromech. Microeng. 2018, 28, 055012. [Google Scholar] [CrossRef]
- Zhuang, Y.; Menon, A. On the stiction of MEMS materials. Tribol. Lett. 2005, 19, 111–117. [Google Scholar] [CrossRef]
- Van Spengen, W.M. MEMS reliability from a failure mechanisms perspective. Microelectron. Reliab. 2003, 43, 1049–1060. [Google Scholar] [CrossRef]
- Buzzin, A.; Veroli, A.; de Cesare, G.; Giovine, E.; Verotti, M.; Belfiore, N.P. A new NEMS based linear-to-rotary displacement-capacity transducer. In Proceedings of the 2019 IEEE 8th International Workshop on Advances in Sensors and Interfaces (IWASI), Otranto, Italy, 13–14 June 2019; pp. 201–204. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N.P. A comprehensive survey on microgrippers design: Operational strategy. J. Mech. Des. 2017, 139, 070801. [Google Scholar] [CrossRef]
- Zhang, W.M.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuators A Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Sardan, O.; Alaca, B.E.; Yalcinkaya, A.D.; Bøggild, P.; Tang, P.T.; Hansen, O. Microgrippers: A case study for batch-compatible integration of MEMS with nanostructures. Nanotechnology 2007, 18, 375501. [Google Scholar] [CrossRef]
- Brede, M. The brittle-to-ductile transition in silicon. Acta Metall. Et Mater. 1993, 41, 211–228. [Google Scholar] [CrossRef]
- Dumon, P.; Bogaerts, W.; Wiaux, V.; Wouters, J.; Beckx, S.; Van Campenhout, J.; Taillaert, D.; Luyssaert, B.; Bienstman, P.; Van Thourhout, D.; et al. Low-loss SOI photonic wires and ring resonators fabricated with deep UV lithography. IEEE Photonics Technol. Lett. 2004, 16, 1328–1330. [Google Scholar] [CrossRef]
- Manfrinato, V.R.; Zhang, L.; Su, D.; Duan, H.; Hobbs, R.G.; Stach, E.A.; Berggren, K.K. Resolution limits of electron-beam lithography toward the atomic scale. Nano Lett. 2013, 13, 1555–1558. [Google Scholar] [CrossRef]
- Biswas, A.; Bayer, I.S.; Biris, A.S.; Wang, T.; Dervishi, E.; Faupel, F. Advances in top–down and bottom–up surface nanofabrication: Techniques, applications & future prospects. Adv. Colloid Interface Sci. 2012, 170, 2–27. [Google Scholar] [CrossRef]
- Rudenko, T.; Nazarov, A.; Lysenko, V. The advancement of silicon-on-insulator (SOI) devices and their basic properties. Semicond. Phys. Quantum Electron. Optoelectron. 2020, 23, 227–252. [Google Scholar] [CrossRef]
- Dao, D.V.; Nakamura, K.; Bui, T.T.; Sugiyama, S. Micro/nano-mechanical sensors and actuators based on SOI-MEMS technology. Adv. Nat. Sci. Nanosci. Nanotechnol. 2010, 1, 013001. [Google Scholar] [CrossRef]
- Zortman, W.A.; Trotter, D.C.; Watts, M.R. Silicon photonics manufacturing. Opt. Express 2010, 18, 23598–23607. [Google Scholar] [CrossRef]
- Wu, B.; Kumar, A.; Pamarthy, S. High aspect ratio silicon etch: A review. J. Appl. Phys. 2010, 108, 9. [Google Scholar] [CrossRef]
- Buzzin, A.; Veroli, A.; De Cesare, G.; Belfiore, N. NEMS-technology based nano gripper for mechanic manipulation in space exploration mission. Adv. Astro. Sci. 2018, 163, 61–67. [Google Scholar]
- Yoshikawa, K.; Kawasaki, H.; Yoshida, W.; Irie, T.; Konishi, K.; Nakano, K.; Uto, T.; Adachi, D.; Kanematsu, M.; Uzu, H.; et al. Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nat. Energy 2017, 2, 1–8. [Google Scholar] [CrossRef]
- Nomura, K.; Ohta, H.; Takagi, A.; Kamiya, T.; Hirano, M.; Hosono, H. Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors. Nature 2004, 432, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Winderbaum, S.; Reinhold, O.; Yun, F. Reactive ion etching (RIE) as a method for texturing polycrystalline silicon solar cells. Sol. Energy Mater. Sol. Cells 1997, 46, 239–248. [Google Scholar] [CrossRef]
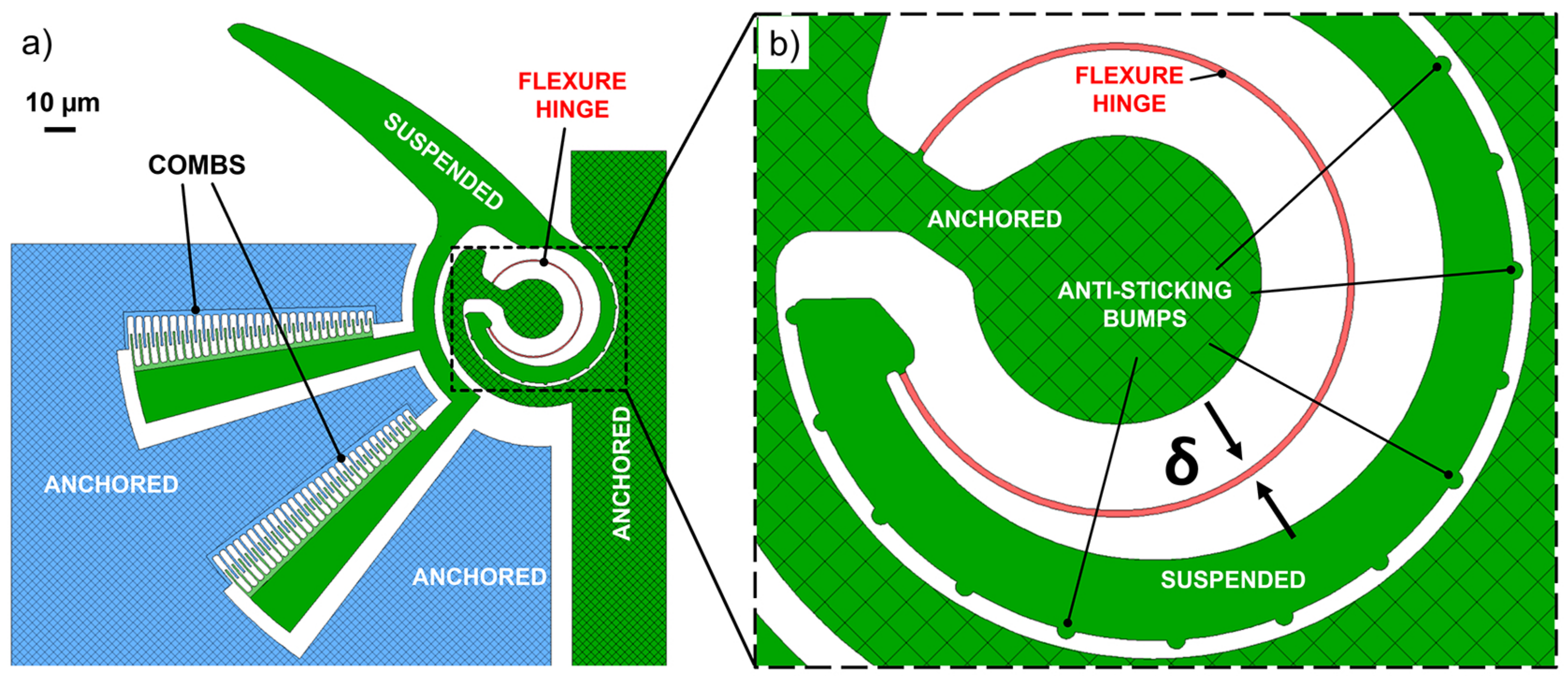
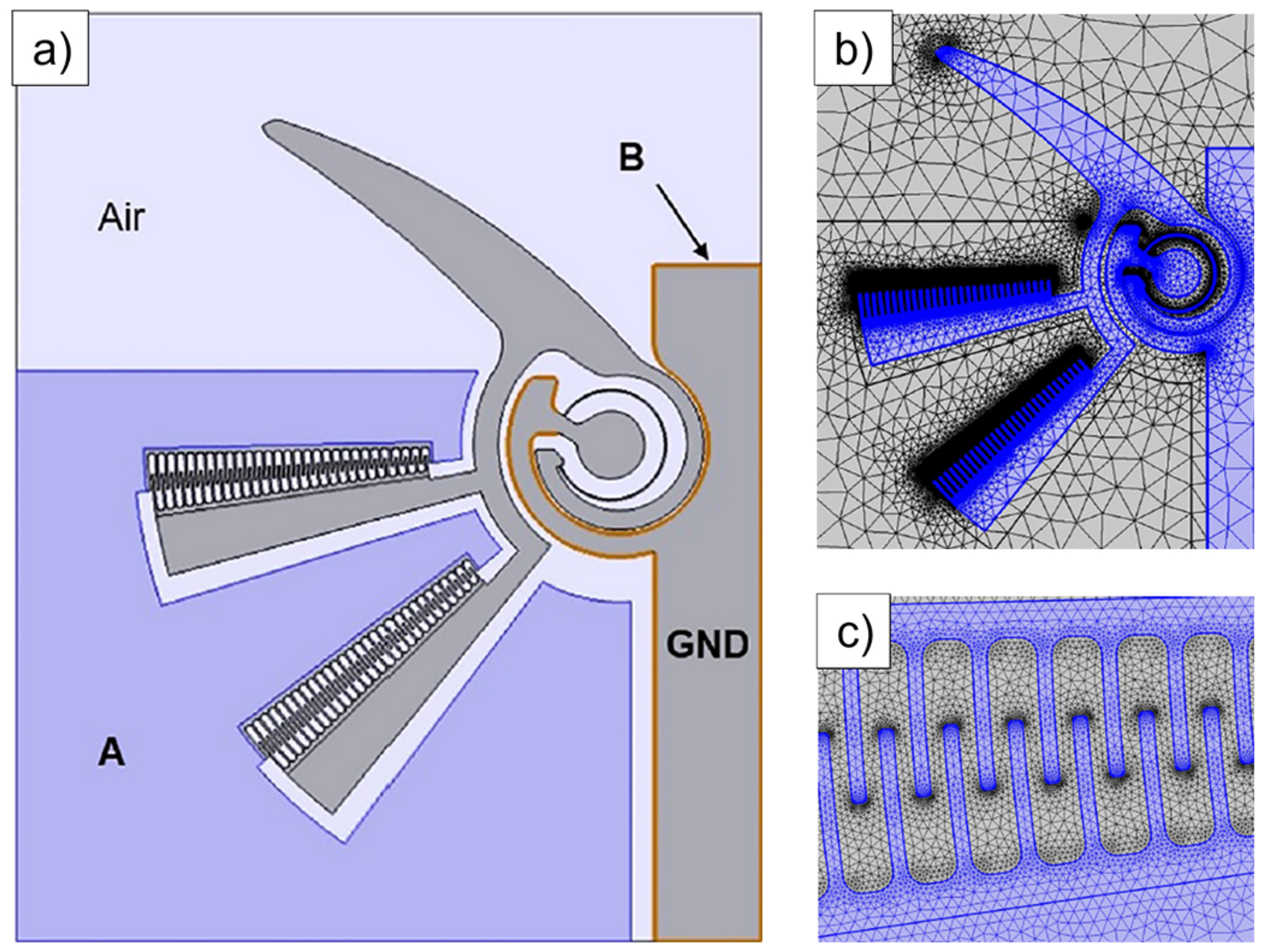
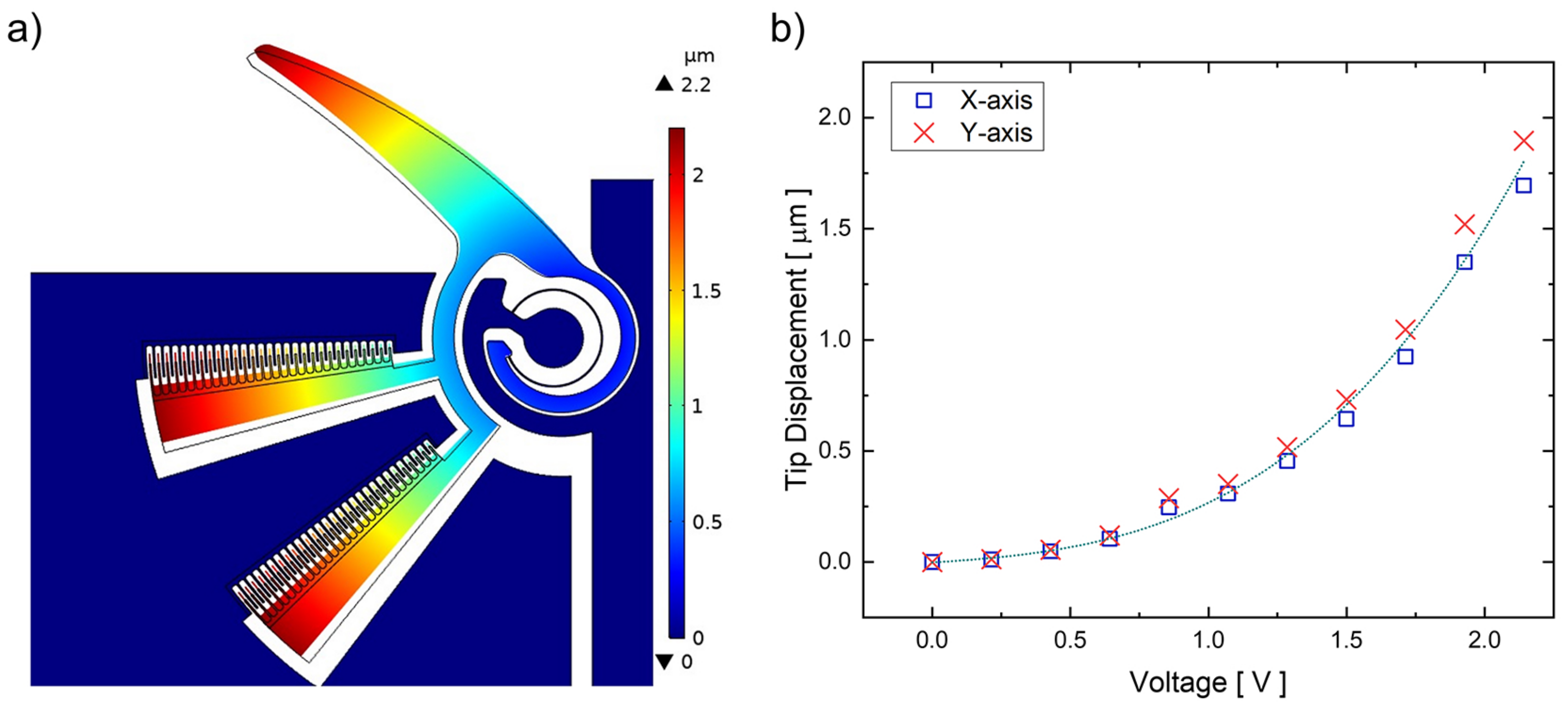
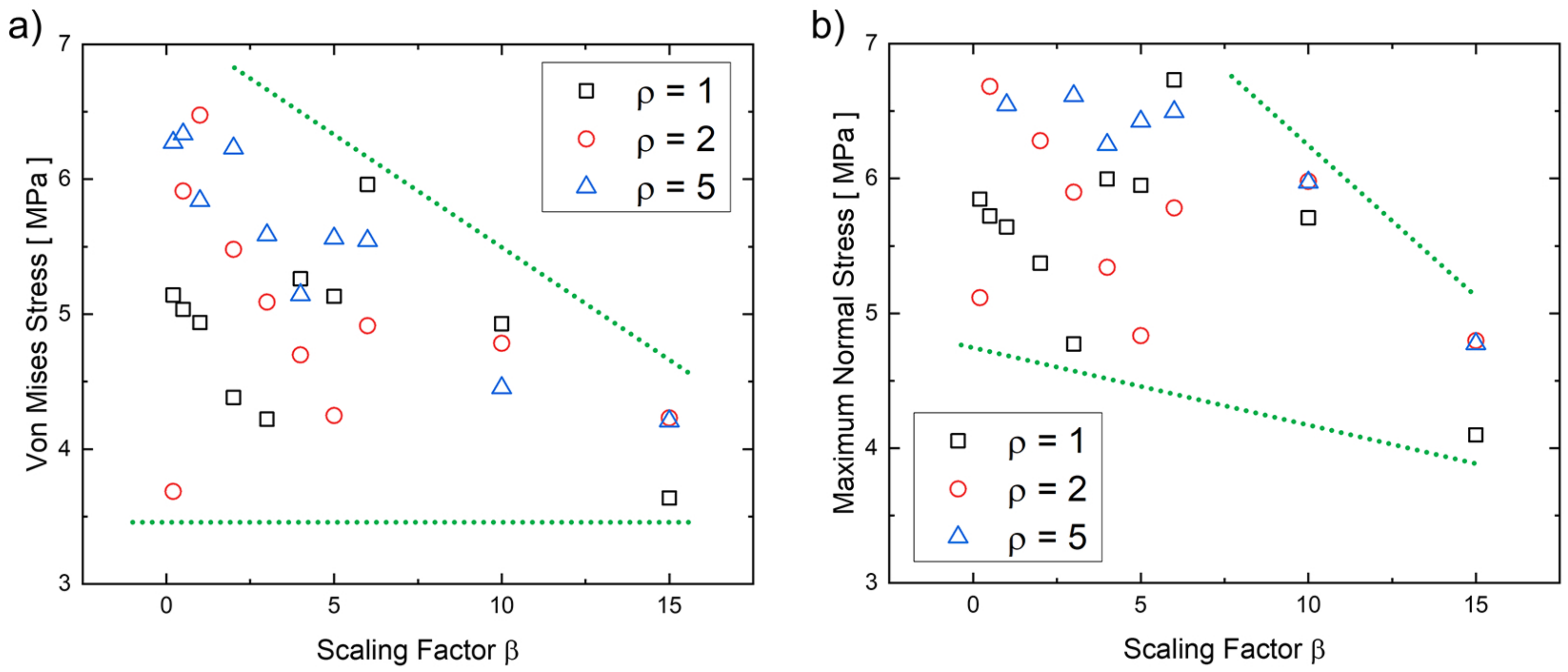

| Component | Feature | Value |
|---|---|---|
| Comb-drive | Number of fingers | 29 |
| Fingers width | 0.8 m | |
| Fingers minimum length | 5.5 m | |
| Fingers maximum length | 12.5 m | |
| Fingers radial spacing | 2.8 m | |
| Rotor-Stator fingers distance | 1 m | |
| Initial overlapping angle | 2 | |
| Maximum comb-drive angular displacement | 2.5 | |
| CSFH | Curved beam length | 106 m |
| Curved beam width | 0.6 m | |
| Curvature radius | 20 m |
| Si ⟨100⟩ | |||
|---|---|---|---|
| Property | Value | Unit | |
| 165.6 | GPa | ||
| Stiffness coefficients | 63.9 | GPa | |
| 79.5 | GPa | ||
| Tensile strength | 170 | MPa | |
| Relative permittivity | 11.9 | – | |
| Density | 2320 | ||
| Poisson’s ratio | 0.22 | – | |
| Specific heat | 680 | ||
| Operative temperature | 298.15 | K | |
| Air | |||
| Density | 1.225 | ||
| Specific heat | 1005 | ||
| Relative permittivity | 1 | – | |
| Scaling Factor (β) | Pull-in Voltage (V) | ||
|---|---|---|---|
| 0.2 | 11.71 | 11.06 | 12.58 |
| 0.5 | 4.53 | 4.56 | 4.59 |
| 1 | 2.38 | 2.53 | 2.27 |
| 2 | 1.11 | 1.15 | 1.27 |
| 3 | 0.76 | 0.81 | 0.78 |
| 4 | 0.60 | 0.58 | 0.61 |
| 5 | 0.45 | 0.45 | 0.53 |
| 6 | 0.38 | 0.38 | 0.39 |
| 10 | 0.23 | 0.23 | 0.23 |
| 15 | 0.13 | 0.15 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buzzin, A.; Rossi, A.; Giovine, E.; de Cesare, G.; Belfiore, N.P. Downsizing Effects on Micro and Nano Comb Drives. Actuators 2022, 11, 71. https://doi.org/10.3390/act11030071
Buzzin A, Rossi A, Giovine E, de Cesare G, Belfiore NP. Downsizing Effects on Micro and Nano Comb Drives. Actuators. 2022; 11(3):71. https://doi.org/10.3390/act11030071
Chicago/Turabian StyleBuzzin, Alessio, Andrea Rossi, Ennio Giovine, Giampiero de Cesare, and Nicola Pio Belfiore. 2022. "Downsizing Effects on Micro and Nano Comb Drives" Actuators 11, no. 3: 71. https://doi.org/10.3390/act11030071
APA StyleBuzzin, A., Rossi, A., Giovine, E., de Cesare, G., & Belfiore, N. P. (2022). Downsizing Effects on Micro and Nano Comb Drives. Actuators, 11(3), 71. https://doi.org/10.3390/act11030071









