Abstract
In this paper, the implementation of a robotic painting system using a sponge and the watercolor painting technique is presented. A collection of tools for calibration and sponge support operations was designed and built. A contour-filling algorithm was developed, which defines the sponge positions and orientations in order to color the contour of a generic image. Finally, the proposed robotic system was employed to realize a painting combining etching and watercolor techniques. To the best of our knowledge, this is the first example of robotic painting that uses the watercolor technique and a sponge as the painting media.
1. Introduction
At the present time, there is a growing interest in creating artworks using machines and robotic systems, and the introduction of machine creativity and intelligence in art fascinates both engineers and artists [1,2]. Robotic art is a niche sector of robotics, which includes different types of performance such as theater, music, and painting. Robotic art painting is a sector in which artists coexist with experts in robotics, computer vision, and image processing. Robotic art projects can be seen as a new art sector in which art and technology mix together and the exact representation of the world is not the main focus.
In recent years, technology has entered our lives more and more, and the use of robots in art projects can be seen as the natural progression of this continuous increase of the presence of technology in our daily lives. Robotic art should no longer be seen simply as an exercise to see how robots can be moved freely or a test of robots’ abilities, but also as a novel art sector with its syntax and artistic characteristics. Currently, several drawing machines and robotic systems capable of producing artworks can be found in the present literature. The majority of these systems adopt image-processing and non-photorealistic-rendering techniques to introduce elements of creativity into the artistic process [3,4]. Furthermore, most robotic machines capable of creating artworks are focused on drawing and brush painting as artistic media. eDavid is a robotic system based on non-photorealistic rendering techniques, which produces impressive artworks with dynamically generated strokes [5]. Paul the robot is an installation capable of producing sketches of people guided by visual feedback with impressive results [6]. Further examples of artistically skilled machines are given by the compliant robot able to draw dynamic graffiti strokes shown in [7] and by the robot capable of creating full-color images with artistic paints in a human-like manner described in [8]. In [9], non-photorealistic rendering algorithms were applied for the realization of artworks with the watercolor technique using a robotic brush painting system. In [10], the authors presented a Cartesian robot for painting artworks by interactive segmentation of the areas to be painted and the interactive design of the orientation of the brush strokes.
Furthermore, in [11], the authors adopted a machine learning approach for realizing brushstrokes as human artists, whereas in [12], a drawing robot, which can automatically transfer a facial picture to a vivid portrait and then draw it on paper within two minutes on average, was presented. More recently, in [13], a humanoid painting robot was shown, which draws facial features extracted robustly using deep learning techniques. In [14], a fast robotic pencil drawing system based on image evolution by means of a genetic algorithm was illustrated. Finally, in [15], a system based on a collaborative robot that draws stylized human face sketches interactively in front of human users by using generative-adversarial-network-style transfer was presented.
There are also examples of painting and drawing on 3D surfaces, such as in [16], where an impedance-controlled robot was used for drawing on arbitrary surfaces, and in [17], where a visual pre-scanning of the drawing surface using an RGB-D camera was proposed to improve the performance of the system. Moreover, in [18], a 3D drawing application using closed-loop planning and online picked pens was presented.
In addition to brush painting and drawing, other artistic media have been investigated in the context of robotic art. Interesting examples are the spray painting systems based on a serial manipulator [19] or on an aerial mobile robot [20], the robotic system based on a team of mobile robots equipped for painting [21], and the artistic robot capable of creating artworks using the palette-knife technique proposed in [22]. Other applications of robotic systems to art include light painting, performed with a robotic arm [23] or with an aerial robot [24], as well as the stylized water-based clay sculpting realized with a robot with six degrees of freedom in [25].
Elements of creativity in the creation process can be also acquired by means of the interaction between the painting machine and human artist. Examples are given by the human–machine co-creation of artistic paintings presented in [26] and by the Skywork-daVinci, a painting support system based on a human-in-the-loop mechanism [27]. Furthermore, in [28], a flexible force-vision-based interface was employed to draw with a robotic arm in telemanipulation, whereas the authors in [29] presented a system for drawing portraits with a remote manipulator via the 5G network. Further examples of human–machine interfaces for robotic drawing are given by the use of the eye-tracking technology, which is applied to allow a user paint using the eye gaze only, as in [30,31].
In this paper, we present a robotic sponge and watercolor painting system based on image-processing and contour-filling algorithms. To the best of our knowledge, this is the first example of robotic painting that uses the watercolor technique and a sponge as the painting media. In this work, we focused on filling continuous, irregular areas of a processed digital image with uniform color through the use of a sponge. More in detail, an input image was pre-processed before the execution of a custom-developed contour-filling algorithm, with the main focus being to find the best position of the sponge imprint inside the contour of a figure in order to color it.
In summary, the main contributions of this paper are the following: (a) the implementation of a robotic sponge and watercolor painting system; (b) the development of an algorithm for the image processing and the contour filling of an image to be painted using a brush with a pre-defined shape; (c) the experimental validation of the proposed method with the realization of two artworks also using a robotic etching technique.
This work fits into the context of figurative art, which, in contrast to abstract art, refers to artworks (paintings and sculptures) that are derived from real object sources. Within this expressive set, there are situations in which, in order to represent the subject, the activity of reproducing the contours is separated from the activity of filling in the backgrounds with colors or grey-scale tints. For example, it is well known that, in the case of comic books, the artist who is in charge of making the images of the panels (penciller) is different from the artist who is later in charge of coloring the backgrounds (inker or colorist). Another example is given by the engravings by Henry Fletcher (1710–1750). The artist realized the contours of the subject by means of etching; in a second step, he colored the flower petals [32].
In this work, we present two artistic subjects as test cases: the “Palazzo della Civiltà Italiana” and “Wings”. The former is a benchmark example to test the performance of the contour-filling algorithm. The latter was realized with a combination of etching and the watercolor technique. The etching was an intaglio printmaking process in which lines or areas are incised using acid into a metal plate in order to hold the ink [33]. In this case, the proposed algorithm was adopted to color an image for which the contours were first obtained with the etching technique.
The paper is organized as follows: Section 2 describes the image-processing and contour-filling algorithm. In Section 3, the watercolor technique, the experimental setup, and the software implementation are illustrated, followed by a description of the calibration process. The experimental results are shown in Section 4. Finally, the conclusions of the paper are given in Section 5.
2. Theoretical Framework
As explained in the Introduction, the purpose of the research was to identify an appropriate strategy to evenly fill an area of the canvas using a sponge as the painting tool. The problem involved a complex solution since the layout of the sponge, unlike that of a brush, can have a non-circular shape; in fact, often, the sponge has a rectangular design. We call the algorithm that fulfills this task the contour-filling algorithm. The input of the algorithm was an RGB image. The contour-filling algorithm was composed of four steps:
- Image preparation: The image was analyzed, and a color reduction was performed. After that, the contours of the uniformly colored areas were carried out;
- Area division: This passage can be skipped according to the artist that uses the software tool; if selected, it performs a Voronoi partition of the area to be painted. This possibility was introduced for two reasons: (1) in order to break up the excessive regularity of a large background, which is usually not aesthetically pleasing; (2) to stop the painting process in case the partial results are not as expected;
- Image erosion: The obtained contours were eroded in such a way to prevent the sponge from painting beyond the area bounded by the edges;
- Contour-filling algorithm: This is the heart of the algorithm, where sponge positions and orientations (poses) are defined.
2.1. Image Preparation
In this first step, the image to be reproduced was selected and saved in a proper format: a matrix with dimensions . In this work, RGB images were considered, as the one of Figure 1a. The number of colors of the image was reduced according to the user-defined parameter , since the number of colors that the robot can manage was limited. Furthermore, the mixing of multiple colors to obtain particular shades has not yet been implemented. The resulting image was an RGB image, with pixel values in the range , as in Figure 1b.

Figure 1.
Original image (a); image after reducing its number of colors (b).
During the whole process, only one color at a time was analyzed. The considered color image was converted to a black and white image (addressed as L in the following), and the obtained areas were labeled and converted into MATLAB polyshape objects for computational reasons. The area of possible internal holes was considered negligible with respect to the larger one, and for this reason, it was removed using a simple filter.
2.2. Area Division
The image can now be divided into smaller areas. This division was implemented to break the whole robotic task into several sub-processes in order to carry out eventual on-the-fly adjustments during the painting process. There are several ways to subdivide an area. We discarded the simplest ones, which consisted of dividing the area into regular subareas (such as squares), because graphic regularity, when perceived by the observer’s eye, is seen as aesthetically poor.
The image was therefore divided by applying a Voronoi diagram to the considered shape to paint. In the present work, the Euclidean distance and a 2D space were considered. In usual terms, the Voronoi diagram resulted in a series of regions in which every point inside was closer to , the center of the considered region k, than to the generic . The points that define the Voronoi cells were random ones that fell inside the area to paint.
The area division was performed by superimposing the Voronoi cells lines on the original image. In this way, the original image area was divided into smaller subareas. Formally, V is the image matrix that represents the lines that define the Voronoi cells ( at the pixel belonging to the lines; elsewhere). L is the image matrix to be divided ( at pixels of the area to paint; elsewhere). The final image F is defined by the logical operator: . An example of Voronoi area division is shown in Figure 2, where, for the sake of clarity, each separated area is represented with a different color.

Figure 2.
Voronoi area division of the bigger contour of the image of Figure 1b.
2.2.1. Image Erosion
As described below, the algorithm for filling an area aimed at generating a sequence of positions and orientations of the sponge (poses) in such a way that the envelope of all sponge imprints covered the entire area to be painted without exiting excessively from the area edges. To do this, some points were selected on the image where the center of the sponge would be sequentially positioned during the painting process. To facilitate the point selection, the area to be painted was divided into subsets of pixels through an erosion process applied to the initial area, as shown in Figure 3. An example of a typical binary erosion can be found in [34].
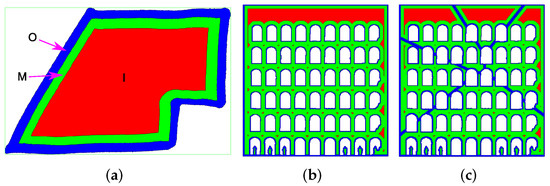
Figure 3.
Example of image erosion. (a) Example of the eroded contour of a region and the definition of the obtained areas. (b) Eroded image obtained without dividing the area. (c) Eroded image obtained by dividing the area.
The original contours (referred to as ) of the colored areas inside the image F were considered. The divided areas were eroded, and three regions were created:
A lower point density was set in the innermost area than in the median area. Indeed, in the innermost area, all points were valid positions for the sponge, since its imprint always fell inside the contour , whatever the sponge orientation was. On the other side, in the median area, a higher density of points was necessary to better follow the small details of the contour by properly defining the sponge orientation. Finally, in the outermost area, no points were placed because the sponge imprint in this area would surely fall out of the contour to paint. The acceptable distance of going beyond the contour was a user-defined percentage of the sponge area (e.g., 5%). This parameter also influenced the amount of erosion computed by the algorithm.
2.2.2. Contour-Filling Algorithm
The contour-filling algorithm was the core of the proposed strategy for robotic sponge and watercolor painting. In the following, it is established how the sponge positions were selected and how they were considered valid or not.
There are two possible approaches the user can choose to define the center sponge points : random or based on a grid. For each generated point , the algorithm evaluates if it falls inside the contour to paint. Let us define as the angular orientation of the sponge with respect to the horizontal axis (see Figure 4a). Inside the innermost area I, for every value of , the sponge imprint completely belongs to the area to be painted (, where B is the sponge imprint); therefore, a random value was assigned to the points belonging to I.
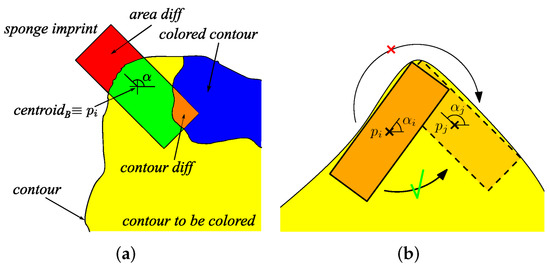
Figure 4.
Variables introduced in the algorithm (a); sponge rotation in the dragging technique (b).
No points were placed in the outermost area O since . However, there could be a rare situation in which the sponge imprint corresponding to a particular point would fall within the area to be painted, for a particular value of . This could happen because image erosion is a coarse way to define the positions of the points. However, this strategy has the merit of speeding up the algorithm.
In the median region M, the sponge is rotated by an angle to define the best orientation that makes the sponge imprint fall as much as possible inside the contour to paint. This can be seen in Figure 4a, where the area to be minimized is the red one (). To better follow the contour, a series of points were also placed on the line C that divides the outermost and the median regions. These points were chosen among the ones that define the contour vertices: if two consecutive vertices and are too far apart, a series of intermediate points are automatically added.
To find the best angular rotation of the sponge (or the brush) in every defined point, the algorithm flowchart shown in Figure 5 is provided. The variables and parameters used in the flowchart are illustrated in Figure 4a. Their definitions are the following:
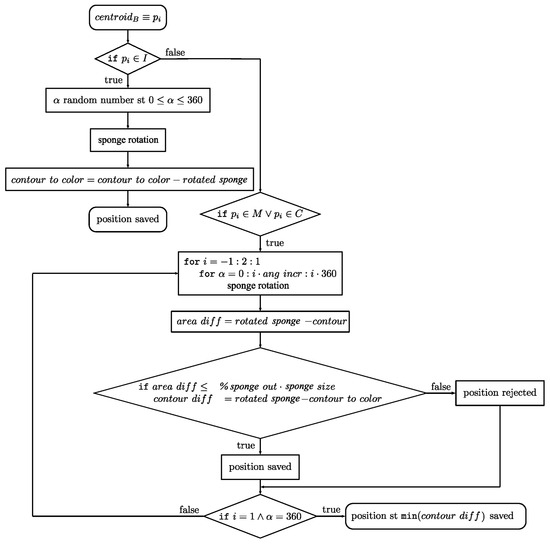
Figure 5.
Flowchart of the algorithm for the definition of sponge angular rotation.
- : coordinates of the sponge centroid;
- : point in which the sponge is placed. There are 3 possibilities:
- –
- ;
- –
- ;
- –
- ;
- : angle of rotation of the sponge around its centroid;
- contour to color: contour yet to be colored;
- ang incr: angular increment used in the for cycle;
- contour: external contour to color;
- area diff: area of the sponge imprint that falls outside the contour to color; this is the variable to minimize;
- % sponge out: maximum user-defined percentage of the sponge size accepted to be outside of the contour to color;
- contour diff: area where the already painted contour and the rotated sponge overlap.
As can be seen in Figure 5, if , the sponge is at first rotated clockwise and then counterclockwise. It was also evaluated if it fell sufficiently inside the image contour. If there was a valid position, the one that paints most of the yet-to-be-colored area was saved. In Figure 6, an example of a sequence of sponge positions resulting from the processing of Figure 2 with the proposed algorithm is provided.
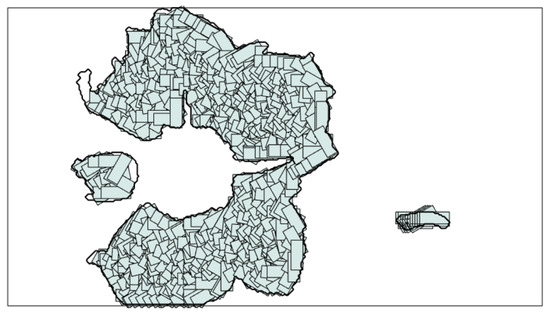
Figure 6.
Sequence of sponge positions for the image of Figure 2.
Once the sequence of sponge positions is defined, two different painting technique can be selected:
- Dabbing technique: The sponge is moved between positions on the canvas by raising the sponge in the passage between points. This technique does not require particular care since the sponge positions are already defined;
- Dragging technique: The sponge is moved between positions on the canvas without being raised. This technique is more complex to simulate. Considering two defined points, and , if , with a user-defined maximum distance, a series of n intermediate points that connect and are created. In these intermediate points , the sponge imprint has to be verified; if it falls outside the area to paint, the sponge is raised. Furthermore, during the movement through the intermediate points , the sponge is smoothly rotated between the rotation configuration of and (the sequence of consecutive poses is interpolated). If the starting angular position is and the ending one is , the intermediate points’ angular positions are . It was also evaluated if the rotation was convenient to be clockwise or counterclockwise, with the goal of maximizing the coloring contribution to the area yet to be painted (Figure 4b). This process substantially corresponds to the addition of several poses to the original ones.
3. Materials and Methods
In this section, we first briefly recall the watercolor painting technique. Then, the robotic system used in the experimental tests and the calibration operations needed for sponge painting are described.
3.1. Watercolor Painting
In the watercolor painting technique, ground pigments are suspended in a solution of water, binder, and surfactant [35]. This technique exhibits textures and patterns that show the movements of the water on the canvas during the painting process. The main uses have been on detailed pen-and-ink or pencil illustrations. Great artists of the past such as J. M. W. Turner (1775–1851), John Constable (1776–1837), and David Cox (1783–1859) began to investigate this technique and the unpredictable interactions of colors with the canvas, which produce effects such as dry-brush, edge darkening, back runs, and glazing. In more recent years, authors, such as Curtis et al. [36], Lum et al. [37], and Van Laerhoven et al. [38], have investigated the properties of watercolor to create digital images by simulating the interactions between pigment and water.
Great importance in this technique is given to the specific paper and pigment used: the canvas should be made of linen or cotton rags pounded into small fibers, and the pigment should be formed by small separate particles ground in a milling process. In the tests performed in the present work, the Fabriano Rosaspina paper was adopted. This is an engraving paper made of cotton fibers and characterized by a high density per square meter. Color pigments in tube format specifically made for watercolor were used as well.
This complex and unpredictable painting technique combined with the use of a sponge as the painting media is challenging. In fact, a trial and error process to fine-tune the system was necessary to find the perfect ratio between color and water and the best compression of the sponge during the releasing of color on the canvas.
3.2. Robotic Painting System
The painting system was built on a KUKA LBR iiwa 14 R820 robotic platform, shown in Figure 7a. This 7-axis robot arm offers a payload of 14 kg and a reach of 820 mm. The repeatability of the KUKA LBR iiwa 14 R820 robot is ±0.1 mm [39]. The manipulator was equipped with a Media flange Touch electrical, a universal interface that enables the user to connect electrical components to the robot flange (Figure 7b). The flange position is described by its tool center point, which is user defined and can be personalized depending on the tool attached to the robot flange.

Figure 7.
KUKA LBR iiwa 14 R820 manipulator (a); Media flange Touch electrical (b).
In order to equip the robot for sponge painting, three components were designed (Figure 8): a connector, a calibration tip, and a sponge support. These components were fabricated using an Ultimaker 2+ Extended 3D printer. The connector was fixed to the robot flange with four screws. The calibration tip and the sponge support can be easily interfaced with the connector thanks to a pair of magnets with a 4 mm diameter, which were inserted into the printed material. The sponge used for painting was a make-up sponge (20 × 4 cm) with a piece of fabric glued on its top (Figure 8e). The size of the sponge was chosen empirically. However, the algorithm works with any size and section of sponge, but the larger the sponge, the less details can be painted and the less time it takes for the robot to paint. The piece of fabric on the tool was used to improve the dosage of water: the sponge works as an absorber, and the piece of fabric reduces the quantity of water that is deposited on the canvas. The main problems are related to the great variability given by the sponge behavior, by the color that can be less or more diluted, but also by the canvas paper that, after some time, becomes soaked by the water contained in the pigment solution.

Figure 8.
The 3D-printed parts for robotic sponge painting: connector (a); calibration tip (b); sponge support (c–e).
The KUKA LBR iiwa was programmed in the Java environment, and the Sunrise Workbench application by KUKA was used to develop the applications needed to control the robot and set the software parameters. The image-processing and contour-filling algorithms (described in Section 2) were developed in MATLAB. To facilitate the software interface, a user-friendly MATLAB app was developed, which allows the user to set the parameters for the non-photorealistic rendering techniques, as well as to calibrate the painting setup and send commands to the manipulator (Figure 9).
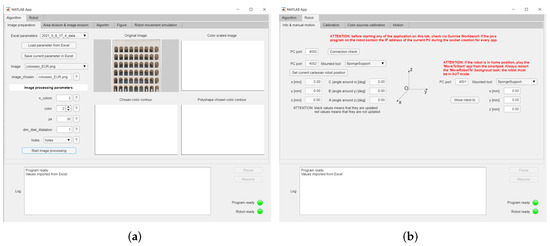
Figure 9.
MATLAB app: image-processing section (a); robot-control section (b).
A client–server socket communication based on the TCP protocol was implemented to establish the communication between the MATLAB app and the Java program loaded on the robot, which interprets the MATLAB commands sent by the user. In this manner, the coordinates of the points resulting from the image processing can be fed to the robot controller and executed by the manipulator. The motion of the robot was planned using a trapezoidal speed profile for each couple of subsequent points. The painting operation was performed by limiting the joint speed of the manipulator to 30% of its maximum value, since abrupt movements of the sponge could damage the paper, especially during dragging.
3.3. Calibration
The robotic sponge painting required a calibration of the painting surface, as well as a calibration of the height of the sponge during color discharge. The canvas surface was calibrated using a procedure similar to the one implemented in [9,22]. More in detail, the robot equipped with the calibration tip was manually moved in contact with the canvas surface in five calibration points, as shown in Figure 10. The z position of the robot tool on each of these points was acquired using the MATLAB app. Actually, only three points could be sufficient, but a higher number was considered to improve accuracy. The interpolating plane was then generated starting from the five calibration coordinates and used to define the corresponding z coordinate for each planar position generated by the image-processing algorithm.
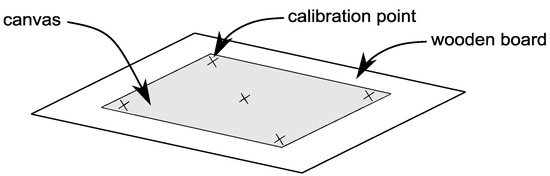
Figure 10.
Calibration points on the painting canvas.
A calibration of the sponge height during color discharge was also needed to adjust the sponge compression during painting and, therefore, the quantity of color released. This operation was performed with a trial-and-error approach, since in this work, force control was not implemented on the robot. Figure 11 shows a scheme of the sponge discharge and some examples of sponge imprints for different heights. As can be seen from the figure, a compromise between a complete sponge imprint and a good amount of released water was needed. Indeed, if too much water were released on the canvas, the wet paper would produce ripples and undulations that would affect the quality of the results.
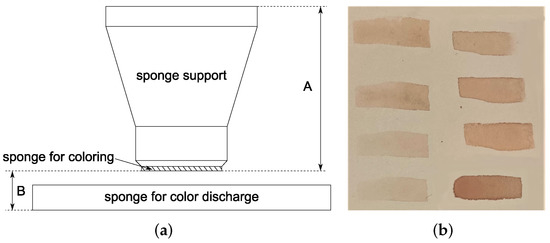
Figure 11.
Sponge discharge scheme (a); examples of sponge imprints for different heights (b).
4. Experimental Results and Discussion
In order to provide a validation of the algorithm presented in Section 2, we set up an experimental campaign using two artistic subjects as test cases. The first was the “Palazzo della Civiltà Italiana”, a monument by architects Guerrini, La Padula, and Romano and located in Rome (1938). It was chosen for its regular geometric shape and high contrast. The second artwork was “Wings”, which was exposed at the Arte Fiera public exhibition in Padova, Italy, in 2021. In the following, we report the results of the pre-processing and painting of the two subjects together with a brief discussion of the results.
4.1. The “Palazzo Della Civiltà Italiana”
The original image used for the processing of this subject is shown in Figure 12. To paint it, we used the dabbing technique and the tool shown in Figure 8e. The results obtained with this subject are shown in Figure 13, where the figures on the left show the simulated painting and those on the right show the real painting. The overlapping between the windows and the wall area was due to the tolerance set on the sponge area, which can exit the contour to color (see Figure 13a), as previously explained.

Figure 12.
Palazzo della Civiltà Italiana in Eur District in Rome, Italy. Source: [40]. (a) Original image. (b) Image used in the proposed algorithm: the original one was cropped, and the top inscription was removed.

Figure 13.
Processing of the “Palazzo della Civiltà Italiana”: in (a) the planned poses of the sponge on the canvas; in (b), a detailed view of some poses on the real painting; in (c), the simulated painting; in (d), the experimental result (dimensions: 35 × 35 cm.)
There were still some creases caused by the water content in the pigment solution, which tended to accumulate inside them, but this problem can hardly be mitigated because water naturally soaks the canvas. The texture of the wall was still visible in some areas, but with a reduced entity. Some areas, for example the one between some windows, were not painted, since the points generated by the algorithm did not satisfy the constraints on the percentage of brush area exceeding the contour. This is visible in Figure 13a,b.
The variation of the intensity in the experimental results (as in Figure 13b,d) was due to the excess of water on the canvas and to the wet paper wrinkles. To eliminate the unwanted color variations, the amount of water adsorbed by the sponge and the dipping height should be reduced, and the robot should be moved more slowly during dipping and color releasing.
4.2. “Wings”
This work was obtained using two different technique: etching and sponge-based watercolor. The first technique was used to obtain the contours of the image (shown in Figure 14) and the second one to color it. The original image was initially processed by an algorithm that created a series of strokes representing the image contours and some internal traits with the intent to give the final work a more artistic look. These strokes were reproduced using the etching technique, in which lines are incised using acid on a metal plate. The engraved lines would then keep the ink inside them for printing.

Figure 14.
Original image for “Wings”. Source: [41].
The full process is shown in Figure 15. The metal plate was not directly incised: its surface was covered with an acid-protecting substance, in this case wax, which was effectively incised by an UR10 robot equipped with a burin. The metal plate was then immersed in an acid solution, i.e., copper sulfate, that corroded only the areas not protected by the wax. Then, the wax was removed, and after covering the incised metal plate with a specific ink that penetrates only at the incised strokes, the plate was pressed on a sheet of paper. Consequently, the ink, which was present mainly in the incisions, was transposed on the canvas. However, it is possible to obtain a sufficiently clean background in the final painting depending on how much ink is removed from the metal plate. This process can be repeated a limited number of times, since the incisions deteriorate over time.

Figure 15.
Phases of the etching for “Wings”. (a) Result obtained after the incision of the wax. (b) Ink cover of the metal plate. (c) Pressing of the metal plate onto a canvas. (d) Result of the etching technique (dimensions: 24 × 30 cm).
After the contours of the image were obtained with the etching technique, the image was colored with the previously described sponge-based dabbing technique. The original image was initially split into three images by setting three threshold values. This process converted the original image into black and white format and set the pixels with an intensity lower than the considered threshold to black and those with a higher intensity to white. In order to selectively filter out the details, the image contours were then blurred using lens and Gaussian blur filters. The three obtained images are reported in Figure 16, arranged in order to match the orientation of the canvas with respect to the robot base. By using these filters, there were some areas on different threshold images that overlapped; this would result in an overlapping of the final colors; however, we considered this an artistic effect.

Figure 16.
Threshold images used in the algorithm for “Wings“. (a) First threshold image. (b) Second threshold image. (c) Third threshold image.
In this work, tea was used as the pigment; in order to have a more intense color, a concentrated infusion was prepared. The goal of this work was to color the internal contour of the previously produced artwork; a monochromatic coloring was selected in order to avoid defining precise color regions, but rather to produce some shades that enrich the original painting. In this case, a sponge was used with a 10 × 4 mm imprint, half of the previous ones; this was necessary because the details of this image are smaller than the previous. By using the original sponge, large regions of the image contour would have failed to be colored.
The simulations of the coloring of the three different threshold images are reported in Figure 17. From the figure, it is possible to note that the threshold images overlapped due to the filtering applied during the algorithm execution.
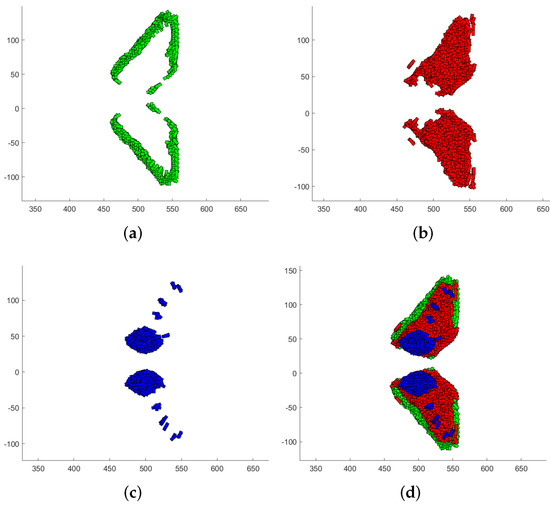
Figure 17.
Simulated results for “Wings”. (a) First threshold image simulation. (b) Second threshold image simulation. (c) Third threshold image simulation. (d) Final image simulation.
The final result is presented in Figure 18a. The color was reapplied to the sponge every 25 points passed on the canvas. However, the number of dots that can be painted well with one dip of the sponge is defined by the user and depends on many variables, such as the viscosity of the color, the size of the sponge, the dipping height, and the level of liquid in the container. From the results, it appears that the performance of the algorithm was quite good, since the color was always within the contours obtained with the etching technique. This was also granted by the calibration process. In fact, during the pre-incision calibration, only three calibration points were used: the darker crosses visible in the three corners of the final painting. In the algorithm used for this work piece, we used five calibration points; for this reason, two calibration points (the lighter crosses in the lower left corner and in the center) were added to the three initial ones. By having the same calibration points as a reference, the canvas was correctly positioned with respect to the robot base (the canvas was fixed at the same height of the robot base and at a distance of 60 cm from the robot base reference frame).

Figure 18.
Final results for “Wings”. (a) First artwork. (b) Second artwork, with more diluted colors than in the first one.
The different color intensities were obtained by adding multiple passes over the same area; the first threshold image contours were colored with two color passes; the second one was obtained with one color pass and the third with two color passes. The overlap of the different areas was visible because of the stronger color intensities in these overlapping areas; the edge darkening effects were clearly visible as well.
A second test with the same settings was carried out and is shown in Figure 18b; this time, the pigment solution was slightly more diluted. The first and third threshold layers were obtained with three color passes and the second with two; the result was more uniform, and the edge darkening effects were mitigated.
5. Conclusions
In this paper, the implementation of a robotic system using a sponge tool and the watercolor painting technique was presented. A collection of tools for calibration operations and sponge support were designed and realized. A contour-filling algorithm was developed, which defines the sponge positions and orientations in order to color the contours of a generic image. The system was also employed to realize artworks combining etching and watercolor techniques.
The results of this work highlighted the challenges that arise in the robotic sponge and watercolor painting. First of all, defining a sequence of positions and rotations of the sponge to paint the contours of an image requires the definition of an appropriate strategy that has to consider the shape of the available sponge, as well as the desired detail level. Furthermore, a proper calibration is needed for both the painting surface and the sponge height during color discharge. The quantity of water adsorbed by the sponge and released on paper is indeed fundamental to avoid ripples and undulations of the wet paper, which produced a variation of intensity in the experimental results. Care should be also taken when adopting the dragging technique, since abrupt movements of the sponge could damage the paper. On the other hand, the dabbing technique does not require particular care, since the sponge is raised by the robot in the passage between each couple of points. However, this approach is more time consuming and does not take advantage of the previous position of the sponge on the canvas.
Future works will include the improvement of the contour-filling algorithm and the optimization of the sponge placements to prevent repeated application of paint at the same location and to ensure a better coverage of the area to be painted without putting too much water on the paper. The sponge shape will be also optimized with respect to the size of the details to be painted, and alternative strategies for the coverage of an area will be performed in future developments of this work.
In future developments of this work, we will also consider objective criteria and quantitative metrics to evaluate the results of the study according to subjective data. Objective criteria could be, for example, the painting rate of the picture, the amount of painted area outside the borders of the picture, the number of points applied by the sponge, and the amount of overlapped sponge imprints. However, it has to be noted that these criteria are useful from a scientific point of view, but not from an artistic point of view, since the appreciation of an artwork is subjective and personal.
Furthermore, visual feedback will be implemented to allow the robot to identify uncolored areas or defects of the painting operation. Finally, force control will be introduced to ensure a better uniformity of the color deposition, and a suction table will be adopted to keep the paper flat, avoiding ripples and undulations produced by the wet paper.
Author Contributions
Conceptualization, P.G.; methodology, software, validation, G.C. and P.G.; formal analysis, investigation, resources, data curation, and writing—original draft preparation, L.S., G.C., S.S. and P.G.; writing—review and editing, L.S., G.C., S.S., A.G. and P.G.; visualization and supervision, A.G. and P.G.; project administration, P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Laboratory for Advanced Mechatronics—LAMA FVG, an international research center for product and process innovation of the three Universities of Friuli Venezia Giulia Region (Italy).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gomez Cubero, C.; Pekarik, M.; Rizzo, V.; Jochum, E. The Robot is Present: Creative Approaches for Artistic Expression with Robots. Front. Robot. 2021, 8, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Leymarie, F.F. Art. Machines. Intelligence. Enjeux Numer. 2021, 13, 82–102. [Google Scholar]
- Scalera, L.; Seriani, S.; Gasparetto, A.; Gallina, P. Non-photorealistic rendering techniques for artistic robotic painting. Robotics 2019, 8, 10. [Google Scholar] [CrossRef] [Green Version]
- Karimov, A.; Kopets, E.; Kolev, G.; Leonov, S.; Scalera, L.; Butusov, D. Image Preprocessing for Artistic Robotic Painting. Inventions 2021, 6, 19. [Google Scholar] [CrossRef]
- Deussen, O.; Lindemeier, T.; Pirk, S.; Tautzenberger, M. Feedback-guided stroke placement for a painting machine. In Proceedings of the Eighth Annual Symposium on Computational Aesthetics in Graphics, Visualization, and Imaging; Eurographics Association: Geneve, Switzerland, 2012; pp. 25–33. [Google Scholar]
- Tresset, P.; Leymarie, F.F. Portrait drawing by Paul the robot. Comput. Graph. 2013, 37, 348–363. [Google Scholar] [CrossRef]
- Berio, D.; Calinon, S.; Leymarie, F.F. Learning dynamic graffiti strokes with a compliant robot. In Proceedings of the Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference, Daejeon, Korea, 9–14 October 2016; pp. 3981–3986. [Google Scholar]
- Karimov, A.I.; Kopets, E.E.; Rybin, V.G.; Leonov, S.V.; Voroshilova, A.I.; Butusov, D.N. Advanced tone rendition technique for a painting robot. Robot. Auton. Syst. 2019, 115, 17–27. [Google Scholar] [CrossRef]
- Scalera, L.; Seriani, S.; Gasparetto, A.; Gallina, P. Watercolor robotic painting: A novel automatic system for artistic rendering. J. Intell. Robot. Syst. 2019, 95, 871–886. [Google Scholar] [CrossRef]
- Igno-Rosario, O.; Hernandez-Aguilar, C.; Cruz-Orea, A.; Dominguez-Pacheco, A. Interactive system for painting artworks by regions using a robot. Robot. Auton. Syst. 2019, 121, 103263. [Google Scholar] [CrossRef]
- Bidgoli, A.; De Guevara, M.L.; Hsiung, C.; Oh, J.; Kang, E. Artistic Style in Robotic Painting; a Machine Learning Approach to Learning Brushstroke from Human Artists. In Proceedings of the 2020 29th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), Naples, Italy, 31 August–4 September 2020; pp. 412–418. [Google Scholar]
- Gao, F.; Zhu, J.; Yu, Z.; Li, P.; Wang, T. Making robots draw a vivid portrait in two minutes. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 9585–9591. [Google Scholar]
- Chen, G.; Sheng, W.; Li, Y.; Ou, Y.; Gu, Y. Humanoid Robot Portrait Drawing Based on Deep Learning Techniques and Efficient Path Planning. Arab. J. Sci. Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Adamik, M.; Goga, J.; Pavlovicova, J.; Babinec, A.; Sekaj, I. Fast robotic pencil drawing based on image evolution by means of genetic algorithm. Robot. Auton. Syst. 2022, 148, 103912. [Google Scholar] [CrossRef]
- Wang, T.; Toh, W.Q.; Zhang, H.; Sui, X.; Li, S.; Liu, Y.; Jing, W. RoboCoDraw: Robotic Avatar Drawing with GAN-based Style Transfer and Time-efficient Path Optimization. Proc. AAAI Conf. Artif. Intell. 2020, 34, 10402–10409. [Google Scholar] [CrossRef]
- Song, D.; Lee, T.; Kim, Y.J.; Sohn, S.; Kim, Y.J. Artistic Pen Drawing on an Arbitrary Surface using an Impedance-controlled Robot. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Song, D.; Kim, Y.J. Distortion-free robotic surface-drawing using conformal mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 627–633. [Google Scholar]
- Liu, R.; Wan, W.; Koyama, K.; Harada, K. Robust Robotic 3-D Drawing Using Closed-Loop Planning and Online Picked Pens. IEEE Trans. Robot. 2021. [Google Scholar] [CrossRef]
- Scalera, L.; Mazzon, E.; Gallina, P.; Gasparetto, A. Airbrush Robotic Painting System: Experimental Validation of a Colour Spray Model. In International Conference on Robotics in Alpe-Adria Danube Region; Springer: Berlin/Heidelberg, Germany, 2017; pp. 549–556. [Google Scholar]
- Vempati, A.S.; Siegwart, R.; Nieto, J. A Data-driven Planning Framework for Robotic Texture Painting on 3D Surfaces. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9528–9534. [Google Scholar]
- Santos, M.; Notomista, G.; Mayya, S.; Egerstedt, M. Interactive Multi-Robot Painting Through Colored Motion Trails. Front. Robot. 2020, 7, 143. [Google Scholar] [CrossRef] [PubMed]
- Beltramello, A.; Scalera, L.; Seriani, S.; Gallina, P. Artistic Robotic Painting Using the Palette Knife Technique. Robotics 2020, 9, 15. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Tsang, S.C.; Wong, H.T.T.; Lam, M.L. Computational light painting and kinetic photography. In Proceedings of the Joint Symposium on Computational Aesthetics and Sketch-Based Interfaces and Modeling and Non-Photorealistic Animation and Rendering, Victoria, BC, Canada, 17–19 August 2018; pp. 1–9. [Google Scholar]
- Ren, K.; Kry, P.G. Single stroke aerial robot light painting. In Proceedings of the 8th ACM/Eurographics Expressive Symposium on Computational Aesthetics and Sketch Based Interfaces and Modeling and Non-Photorealistic Animation and Rendering, Genoa, Italy, 5–6 May 2019; pp. 61–67. [Google Scholar]
- Ma, Z.; Duenser, S.; Schumacher, C.; Rust, R.; Baecher, M.; Gramazio, F.; Kohler, M.; Coros, S. Stylized Robotic Clay Sculpting. Comput. Graph. 2021, 98, 150–1664. [Google Scholar] [CrossRef]
- Zhuo, F. Human-machine Co-creation on Artistic Paintings. In Proceedings of the 2021 IEEE 1st International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 15 July–15 August 2021; pp. 316–319. [Google Scholar]
- Guo, C.; Bai, T.; Lu, Y.; Lin, Y.; Xiong, G.; Wang, X.; Wang, F.Y. Skywork-daVinci: A novel CPSS-based painting support system. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 673–678. [Google Scholar]
- Quintero, C.P.; Dehghan, M.; Ramirez, O.; Ang, M.H.; Jagersand, M. Flexible virtual fixture interface for path specification in tele-manipulation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5363–5368. [Google Scholar]
- Chen, L.; Swikir, A.; Haddadin, S. Drawing Elon Musk: A Robot Avatar for Remote Manipulation. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4244–4251. [Google Scholar]
- Dziemian, S.; Abbott, W.W.; Faisal, A.A. Gaze-based teleprosthetic enables intuitive continuous control of complex robot arm use: Writing & drawing. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 1277–1282. [Google Scholar]
- Scalera, L.; Maset, E.; Seriani, S.; Gasparetto, A.; Gallina, P. Performance evaluation of a robotic architecture for drawing with eyes. Int. J. Mech. Control. 2021, 22, 53–60. [Google Scholar]
- Art Institute Chicago. Henry Fletcher. Available online: https://www.artic.edu/artists/34495/henry-fletcher (accessed on 24 December 2021).
- The Metropolitan Museum of Art. Etching. Available online: https://www.metmuseum.org/about-the-met/collection-areas/drawings-and-prints/materials-and-techniques/printmaking/etching (accessed on 24 December 2021).
- Van den Boomgaard, R.; Van Balen, R. Methods for fast morphological image transforms using bitmapped binary images. Cvgip Graph. Model. Image Process. 1992, 54, 252–258. [Google Scholar] [CrossRef]
- Mayer, R. The Artist’s Handbook of Materials and Techniques; Viking: New York, NY, USA, 1991. [Google Scholar]
- Curtis, C.J.; Anderson, S.E.; Seims, J.E.; Fleischer, K.W.; Salesin, D.H. Computer-generated watercolor. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 3–8 August 1997; pp. 421–430. [Google Scholar]
- Lum, E.B.; Ma, K.L. Non-photorealistic rendering using watercolor inspired textures and illumination. In Proceedings of the Ninth Pacific Conference on Computer Graphics and Applications. Pacific Graphics, Tokyo, Japan, 16–18 October 2001; pp. 322–330. [Google Scholar]
- Van Laerhoven, T.; Liesenborgs, J.; Van Reeth, F. Real-time watercolor painting on a distributed paper model. In Proceedings of the Computer Graphics International, Crete, Greece, 16–19 June 2004; pp. 640–643. [Google Scholar]
- KUKA. LBR Iiwa. Available online: https://www.kuka.com/en-us/products/robotics-systems/industrial-robots/lbr-iiwa (accessed on 24 December 2021).
- Uozzart. Colosseo Quadrato, il Capolavoro dell’Eur e il Riferimento al Duce. Available online: https://uozzart.com/2020/06/14/palazzo-della-civilta-italiana-colosseo-quadrato-eur/ (accessed on 24 December 2021).
- Pixabay. Blue Wings. Available online: https://pixabay.com/photos/blue-wings-at-liberty-blue-bird-2471094/ (accessed on 24 December 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).