Design, Computational Modelling and Experimental Characterization of Bistable Hybrid Soft Actuators for a Controllable-Compliance Joint of an Exoskeleton Rehabilitation Robot

Abstract

This paper presents the mechatronic design of a biorobotic joint with controllable compliance, for innovative applications of “assist-as-needed” robotic rehabilitation mediated by a wearable and soft exoskeleton. The soft actuation of robotic exoskeletons can provide some relevant advantages in terms of controllable compliance, adaptivity and intrinsic safety of the control performance of the robot during the interaction with the patient. Pneumatic Artificial Muscles (PAMs), which belong to the class of soft actuators, can be arranged in antagonistic configuration in order to exploit the variability of their mechanical compliance for the optimal adaptation of the robot performance during therapy. The coupling of an antagonistic configuration of PAMs with a regulation mechanism can achieve, under a customized control strategy, the optimal tuning of the mechanical compliance of the exoskeleton joint over full ranges of actuation pressure and joint rotation. This work presents a novel mechanism, for the optimal regulation of the compliance of the biorobotic joint, which is characterized by a soft and hybrid actuation exploiting the storage/release of the elastic energy by bistable Von Mises elastic trusses. The contribution from elastic Von Mises structure can improve both the mechanical response of the soft pneumatic bellows actuating the regulation mechanism and the intrinsic safety of the whole mechanism. A comprehensive set of design steps is presented here, including the optimization of the geometry of the pneumatic bellows, the fabrication process through 3D printing of the mechanism and some experimental tests devoted to the characterization of the hybrid soft actuation. The experimental tests replicated the main operating conditions of the regulation mechanism; the advantages arising from the bistable hybrid soft actuation were evaluated in terms of static and dynamic performance, e.g., pressure and force transition thresholds of the bistable mechanism, linearity and hysteresis of the actuator response.

1. Introduction

The field of soft robotics has attracted considerable interest from researchers since intrinsically safe interaction with humans and the environment, adaptability of the control performance and new robot capabilities can be gained through use of soft and compliant materials [1]. The hyperelastic properties of the mechanical hardware of soft robots allow one to outperform conventional rigid robots, e.g., in manipulation of delicate objects [2], surgical navigation in endoluminal space [3], actuation of biologically inspired locomotion [4], and in impact absorption, e.g., see [5,6].

Compressed air is used as primary source of energy in many soft actuators, ranging from bellows actuators to Pneumatic Artificial Muscles (PAMs). A relevant example of soft actuators is that of the pneumatic fiber-reinforced actuators [7], which are made by a fiber shell in a double-helix pattern enclosing a silicone rubber chamber. The soft actuator called PneuNet [8] is another well-known example of pneumatic bellows used as a bending actuator.

The fabrication of PneuNet exploits the combined use of stiff material for the bottom portion of the actuator and an elastomer for pneumatic chambers. The use of elastomeric and hyperelastic materials can provide the highlighted advantages, but at the same time, it results in a degradation of the control performance. Therefore, the low stiffness of the hyperelastic material of the robot body needs to be compensated through rigid structures or inextensible fibers embodied in the actuator structure. This is a common design principle for many soft pneumatic actuators. Among these, PAMs consist of a rubber shell enveloped by fiber threads; the combined use of rubber and reinforced fibers confers to PAMs the elasticity required to obtain the required intrinsic safety and adaptability.

In response to the air inflation, the actuator bladder contracts while its longitudinal length decreases, and this results in a pulling force on the load. A couple of PAMs is required for bidirectional actuation of a robot joint, since a single PAM can provide active actuation only during inflation. PAMs can be classified as variable stiffness actuators; the inherent variability of their mechanical stiffness can be exploited to control the compliance of the joints of robotic exoskeletons.

The implementation of some control strategies promoting the cooperation between the patient and the rehabilitation, as well as the adaptation of the robot assistance on the basis of the patient’s feature and performance during rehabilitation sessions, is one of the most relevant result from the side of rehabilitation robotics.

In the direction of the efficient adaptation of the level of assistance by the robot during rehabilitation sessions, PAMs allow the efficient control of the compliance of the actuated joints of lightweight, soft and wearable exoskeletons, as many design examples show in the development of robotic gait trainers [9], exoskeletons for upper arm training/rehabilitation [10] and wearable elbow exoskeletons [11]. The control of robots actuated by PAMs is quite challenging since the characteristics force vs. contraction length of a PAM is highly nonlinear, and therefore, nonlinear model-based compensation techniques are required [12].

The design principles underlying our bistable hybrid soft actuation are in line with the general applications of soft robotics. Indeed, the proposed solution exploits some inherently compliant and soft actuators. In comparison with conventional actuators, such as electric motors and rigid pneumatic actuators, soft actuators allow a safer interaction between robots and human beings by reducing the risk of injury in the case of collisions or unexpected interactions. The intrinsic safety guaranteed by soft actuators is of the utmost importance in wearable and medical robots.

Soft pneumatic actuation can be advantageously implemented in an antagonistic arrangement. The antagonistic set-up allows the efficient tuning of the joint stiffness which can be considered a must in robotic applications of rehabilitation as well as of assistance, e.g., for knee assistance based on PAMs [13] or hand-grasping assistance using soft bending actuators [14].

The antagonistic arrangements of soft pneumatic actuators are also implemented in a series of modular robot joints having a soft-rigid hybrid structure inspired by the biomechanics of the articular joints of the lobster [15]. The antagonistic set-up of soft bellows is assembled into a rigid shell; this solution achieves a bidirectional actuation enabling safe interaction, higher torque/force output and controllable stiffness. A position control algorithm with stiffness tuning is developed on the basis of a model for friction compensation originally proposed in [16].

Our previous work [17] provides an extension to the state-of-the-art control strategies for the regulation of the compliance of a biorobotic joint actuated by an antagonistic pair of PAMs, in order to optimize the performance of adaptive impedance control strategies for applications of wearable and rehabilitation robotics.

The proposed solution derives from the development of a novel control strategy which, in comparison to other methods, can extend the controllability of the mechanical compliance of the biorobotic joint over the full ranges of pressure and motion allowed by the antagonistic pairs of PAMs. The implementation of this control law implies the combination of the antagonistic pair with a third PAM and a parallelogram mechanism in order to achieve the full-range controllability of the compliance.

In this paper, a novel implementation of the actuation solution in [17] for the regulation of the joint compliance is proposed and experimentally tested. The additional PAM and the parallelogram mechanism are replaced here by a novel bistable hybrid soft actuator obtained from the integration of soft pneumatic bellows actuators and bistable Von Mises trusses (see [18,19]).

In the context of “assist-as-needed” control, our biorobotic joint, which is characterized by a cable-driven and soft actuation, can provide a lightweight and efficient solution for regulating, during some sessions of physical rehabilitation, the mechanical compliance of the robotic exoskeleton worn by the user.

A trajectory tracking control of the exoskeleton allows the execution of periodic trajectories for the flexion-extension of the patient’s arm. Within the specific application, the joint compliance is tuned in order to increase the stiffness of the biorobotic joint if a limited error from the tracked trajectory can be tolerated and/or a reduced participation to the motion is expected from the patient, whereas a lower joint stiffness can be regulated in order to promote the active contribution by the patient while reducing the robotic support for the trajectory tracking. Therefore, the joint compliance is regulated by controlling the tension of the cables connecting to the biorobotic joint the antagonistic couple of soft pneumatic actuators, i.e., PAMs.

The adoption of a bistable mechanism, based on Von Mises elastic trusses, allows one to maintain a preset cable tension without external power supply and/or active action by the controller. Through a controllable storage/release of elastic energy, the bistable mechanism can guarantee both an energy-saving and optimal control performance, other than achieving the intrinsic safety during the interaction between the patient and the robot. Concerning this latter point, the bistable and elastic behavior provided by the Von Mises trusses can mitigate the potentially harmful effects on the patient in the case of undesired interactions, e.g., due to muscle spams or voluntary reactions on the patient’s limb. In such circumstances, the bistable mechanism can promptly switch from an excessive value of tension of the joint cables, which could be associated with a dangerous interaction, to a lower and safe level of tension.

The local stability properties or multistability associated with a finite number of equilibrium points of a mechanical systems can be managed in order to improve the actuation and control performance of soft robots; see [20] for a comprehensive overview of applications.

Here, we present a hybrid soft actuation module leveraging bistability in order to exploit, as shown through experimental tests, an energetic advantage deriving from the capability by the module to rapidly store and release elastic energy during the actuation of the regulation mechanism of the compliance of the biorobotic joint. In addition to the intrinsic safety, this energetic advantage guarantees a reduced range of pressure required to drive the soft actuator, improved efficiency and dynamic performance with reduced friction effects on the actuator response, which potentially result in an extension of the controllability range of the joint compliance upon soft pneumatic actuation. Moreover, the reduced pressure of the pneumatic actuator, without side effects on the force output of the actuator itself, can provide further enhancement of the safety of human–robot interaction. As pointed out in [15], the operational pressure of hand-held and portable powered tools should be less than 203 kPa, on the basis of Occupational Safety and Health Administration Standard 1910.242.

In the general context of bistable hybrid soft actuation, which is conceived in extension to conventional set-ups of pneumatic soft actuators, the antagonistic arrangement of soft actuators can be augmented by some bistable mechanisms for rapid energy storage/release (see, e.g., [21]). The bistable hybrid soft actuation module proposed in [21] adopts a snap-through bistable mechanism which can switch between two stable states upon soft pneumatic bending actuation. The hybrid structure combines spring-based bistable linkages and soft pneumatic bending actuators.

Leveraging both elastic instabilities during the steps of mechanical design and the 3D printing parameters involved in automatic fabrication of our prototype allows one to tune the response of the hybrid actuator not only on the basis of standard constraints on force/deformation output but also taking into account some specifications on the maximum operating pressure, energy-saving performance and intrinsic safety. Moreover, the combination of bistable elastic structure with soft pneumatic actuators can compensate for the low stiffness of inflatable (and hyperelastic) chambers of the actuators which limits the maximum load capacity and the control performance.

The design of hybrid soft actuators involves the assembly of hyperelastic chambers with not-soft structures in order to improve the control performance which can be obtained through the soft actuation. For instance, bistable hybrid actuation enables one to efficiently adapt the force required for manipulating heavy and fragile loads. The stiffness modulation required for actuating grasping tasks can be regulated by exploiting tunable snap-through instabilities [20]. Other examples of robotic compliant manipulation and grasping are inspired by bistable biological mechanisms, e.g., the flytrap-inspired gripping mechanism [22]. The steps of structural design and fabrication by additive manufacturing enable one to optimize the actuator response, according to the mechanical properties required to manipulate heavy and fragile object through soft robotic grippers [21].

The paper is structured as follows. Section 2 presents the design principles of the bistable hybrid soft actuator and the steps followed in CAD modelling and 3D printing of the prototype. Section 3 provides the simulation results obtained for the synthesis of the response of the pneumatic actuator on the basis of the material properties and key design parameters (wall thickness and length-to-diameter ratio). Section 4 reports the experimental setups and results demonstrating the advantages of the bistable hybrid actuation in improving the full-range controllability of the compliance of the biorobotic joint through the optimized regulation mechanism. Finally, some concluding remarks are given in Section 5.

2. Design and 3D Printing of the Bistable Hybrid Soft Actuator

2.1. Mechanism of Regulation of the Joint Stiffness Exploiting Bistability of Von Mises Trusses

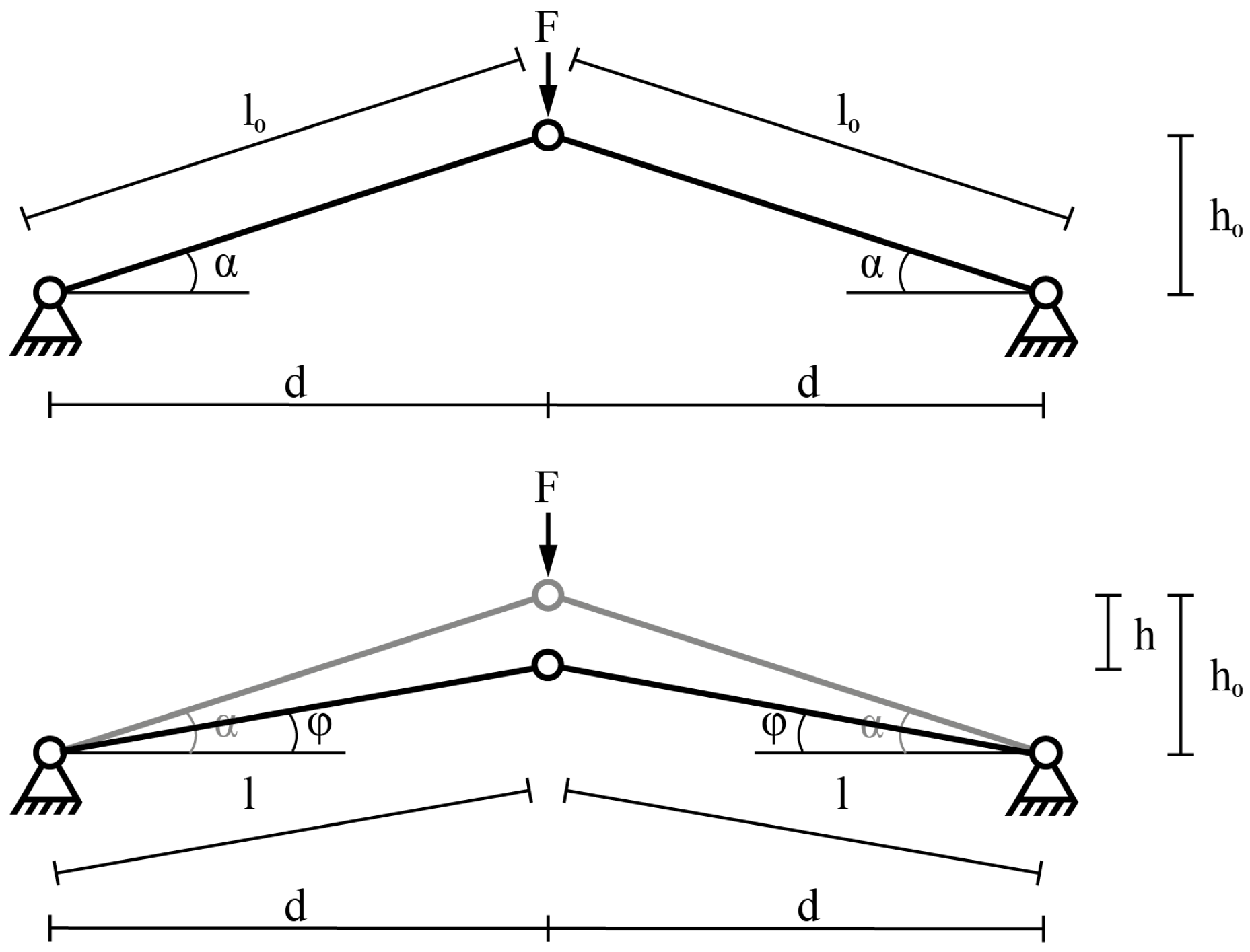
In the mechanism which takes its name by Austrian scientist Richard Von Mises, some elastic trusses allow one to switch between two stable states. The main advantage of this bistable system is that power is only required to switch between one stable state and the other one, while no power is required to keep these positions once they have been achieved instead. This bistable mechanical system is composed by two elastic links and three hinge joints, two of which are fixed while the other one, on the apex, has no costraints (Figure 1). When a normal force is applied to the free joint, the system undergoes a deformation depending on the Young module E and cross-section area A of the links [23]. In the following subsection, with reference to the variables and schemes reported in Figure 1, we take into account only the variation in the length of the links (and not their bending) in order to derive analytically the force required for the transition from one stable state to the other one. Therefore,

$$\begin{array}{c}\hfill \Delta l=l_0-l\end{array}$$

where l can be geometrically derived as

$$\begin{array}{c}\hfill l=\frac{d}{cos\varphi }\end{array}$$

and d can be replaced by

$$\begin{array}{c}\hfill d=l_{0}cos\alpha .\end{array}$$

In this way, the variation of the length of each link can be written as

$$\begin{array}{c}\hfill \Delta l=l_0-\frac{l_{0}cos\alpha }{cos\varphi }=l_0(1-\frac{cos\alpha }{cos\varphi })\end{array}$$

and the variation of the height of the apex joint reads

$$\begin{array}{c}\hfill \Delta h=h_0-lsin\varphi =l_{0}sin\alpha -\frac{l_{0}cos\alpha sin\varphi }{cos\varphi }=l_0(sin\alpha -cos\alpha tan\varphi )\end{array}$$

The total potential energy of the Von Mises mechanism can thus be calculated as

$$\begin{array}{c}\hfill \mathrm{\Pi }\left(\varphi \right)=\frac{EA}{l_0}\Delta l^2-F\Delta h=l_0[EA{(1-\frac{cos\alpha }{cos\varphi })}^2-F(sin\alpha -cos\alpha tan\varphi )]\end{array}$$

where the former term is the strain energy potential of the system for both links and the latter term is the mechanical work performed by the force F. From the principle of minimum potential energy, the system reaches the equilibrium when the first derivative of $\Pi \left(\varphi \right)$ is equal to zero

$$\begin{array}{c}\hfill \frac{d\Pi }{d\varphi }=0\end{array}$$

Thus

$$\begin{array}{c}\hfill l_0\frac{cos\alpha }{co{s}^2\varphi }[F-2EA(sin\varphi -tan\varphi cos\alpha )]=0\end{array}$$

from which the critical load for snap-through can be calculated as a function of $\varphi$

$$\begin{array}{c}\hfill F\left(\varphi \right)=2EA(sin\varphi -tan\varphi cos\alpha )\end{array}$$

where the values of the critical angles to switch between the two states are [24]

$$\begin{array}{c}\hfill \varphi =\pm arccos\sqrt[3]{cos\alpha }\end{array}$$

The integration of Von Mises bistable trusses with soft pneumatic actuators, which is originally conceived as a hybrid actuation solution, is adopted for the realization of a mechanism of regulation of the compliance of the joint of a rehabilitation exoskeleton actuated by PAMs (see Figure 2).

Some tests on the robot prototype and its PAMs-based actuation (including evaluations on ergonomics, user comfort and wearability of the rehabilitation exoskeletons) were carried out. The antagonistic arrangement of the PAMs pair, through some Bowden cables connecting the actuators and a pulley on the rotational joint, allows the bidirectional and smooth assistance of the rotation (flexion/extension) of the patient’s elbow (see Figure 3).

The flexion/extension motion is antagonistically actuated through the modulation of the PAMs pressure as

$$\begin{array}{cc}\hfill p_1=& p_{cc}+\Delta p\le p_{max}\mathrm{PAM}1\hfill \\ \hfill p_2=& p_{cc}-\Delta p\le p_{max}\mathrm{PAM}2\hfill \end{array}$$

where $p_{cc}$ represents the common value of pressure of both actuators (also called co-contraction pressure) which can be exploited to tune joint compliance independently from the joint rotation; $\Delta p$, i.e., the pressure variation from $p_0$, is used as control variable for actuating the joint rotation. The modulation of $p_{cc}$ over a range of pressure requires one to complement the standard antagonistic scheme by a mechanism of the regulation of the cables tension since the contraction of the PAMs, which depends on the preset value of $p_{cc}$, needs to be compensated through the variation of the length/tension of the cables connecting the PAMs extremities and the joint pulley.

The feedforward controller proposed in [17] implements a control law on $p_{cc}$ enabling the controllability of the joint compliance over the full range of pressure of the PAMs pair; the implementation of this control law on a prototype of the biorobotic joint combines a parallelogram mechanism which is actuated by a third PAM for compensating the variations of the cables tension. From [17] and Figure 3 and Figure 4 therein, it is clear that the previous prototype of the biorobotic joint with tunable compliance implements a regulation mechanism of the cables tension in which the force generated by a custom-made PAM is transmitted through a tie rod to a four-bar linkage acting on the joint cables.

The parallelogram mechanism and the additional PAMs required for regulating the compliance in [17] are replaced here by a more efficient and intrinsically safe solution exploiting the advantages of a bistable mechanism coupled to soft pneumatic actuators. Moreover, the novel solution also improves the mechanical performance of the parallelogram-based regulation under PAM actuation. Indeed, the regulation mechanism in [17] is affected by friction effect, hysteresis and stick-slip phenomena arising both from a mechanical transmission, based on tie-rods multijoint linkages, and from a custom-made PAM.

The bistability of the elastic Von Mises trusses can be exploited to maintain a predefined stable configuration and, therefore, a preset cable tension. The elastic energy storage allows both to improve dynamic response of the overall regulation mechanism and to amplify force output. Moreover, Von Mises trusses provide the amplified stroke of the regulation mechanism in comparison to a pneumatic actuator alone, as discussed in Section 4.

The operation of the bistable system may exhibit slight similarities with slip-clutches adopted in other actuators where a dissipative effect, which is modulated through the mechanical friction depending on the rotation velocity, is exploited for tuning the slipping torque.

Our bistable mechanism provides the best option in comparison with other solutions, e.g., based on slip-clutches. Indeed, as explained above in the context of a general description of the specific application of robotic rehabilitation, the snap-through mechanism needs to be activated on the basis of a threshold value of the cables tension, also in quasistatic conditions. Taking into account that the response of a slip-clutch mainly depends on the rotation velocity, the velocity-dependent friction effects could not be effectively exploited to trigger the transition between tension levels, since the rotation is actuated over a range of velocity of the exoskeleton joint, which is generally low.

The bistable mechanism provides some additional advantages over other solutions, e.g., based on slip-clutches, since the dissipative effects are replaced by the storage and release of elastic energy which can be efficiently used to optimize static and dynamic performance of the overall hybrid actuator, as shown through experimental tests. Moreover, the inherent nonlinearity and hysteresis, involved in the generation of the slipping torque through mechanical friction, could add uncertainties and complexity to the control system since nonlinear compensation strategies should be used for controlling the mechanical compliance of the robotic joint. Conversely, all the phases of design and implementation of our bistable hybrid soft actuator were developed in order to reduce all the sources of nonlinearity and uncertainty which can negatively impact the control of the mechanical compliance of the biorobotic joint. This is the same reason which has motivated the adoption of a custom-made air bellows actuator in place of a standard soft pneumatic actuator and, more precisely, a PAM.

Although PAMs could be used in conjunction with bistable trusses for actuating the mechanism of regulation of the cables of the biorobotic joint without violating the principle of the hybrid-soft actuation underlying the realization of the prototype, our custom-made air bellows provides, as one of the main advantages over PAMs, a linear mechanical response which can be profitably exploited for control. Indeed, although PAMs give undoubted advantages in terms of a high power/weight ratio, the control of PAMs requires some elaborate control strategies for compensating the inherently nonlinear mechanical response of PAMs. Moreover, from the point of view of the realization of the mechanism of regulation of the tension of the joint cables, we demonstrated, in our prior work, that the modulation of the cable tension, through a PAM which actively generates its actuation force only in contraction, increases the complexity of the regulation mechanism by requiring additional components, e.g., the parallelogram linkage and return springs involved in our previous design solution in [17]. Eventually, in comparison with the PAM-based actuation, the integration between bistable trusses and air bellows enables the optimal design of the regulation mechanism in order to reduce the impact of nonlinearities, backslash, stick-slip and other undesirable friction phenomena affecting the previous version of the mechanism.

During robotic therapy, some undesirable interactions are possible if the robot control cannot accommodate resistant torque on the robot joint, e.g., the patient’s elbow does not follow the trajectory imparted by the robot. The bistability properties can guarantee highly desirable intrinsic safety since, in the presence of an unsafe value of the resistant force acting on the mechanism, without intervention by the controller and thanks to the bistable behavior of the elastic trusses, the transition from a stable equilibrium (associated with high tension of the joint cable) to the other one (low tension of the joint cable) can be passively actuated. The value of force required for the equilibrium transition can be associated with a threshold which is commensurated to the detent force generated by the Von Mises trusses. Against the external disturbance, this detent force holds the mechanism in one of the positions corresponding to the stable equilibrium points.

The value of the transition threshold can be chosen on the basis of physical considerations on the robotic therapy, and its implementation on the robotic hardware can be obtained through the tuning of the stiffness of the elastic trusses. The parameters of infill, number of perimeters, number of top and bottom layers of the 3D printed models of the compliant structures of the exoskeleton are considered eligible for the stiffness tuning in the subsequent phases of mechatronic design and 3D printing. Moreover, the soft pneumatic actuator can be controlled, other than for driving the transition between stable states, also for the continuous regulation of the cables tension; in both cases, the passive contribution to the mechanism actuation by the elastic bistability can improve the energy efficiency of the regulation mechanism. Moreover, the positions associated with stable equilibrium points can be maintained without energy input or control intervention. Any position within the state transition from one stable state to the other one can be maintained only in continuous control mode, through the action by the soft pneumatic actuator.

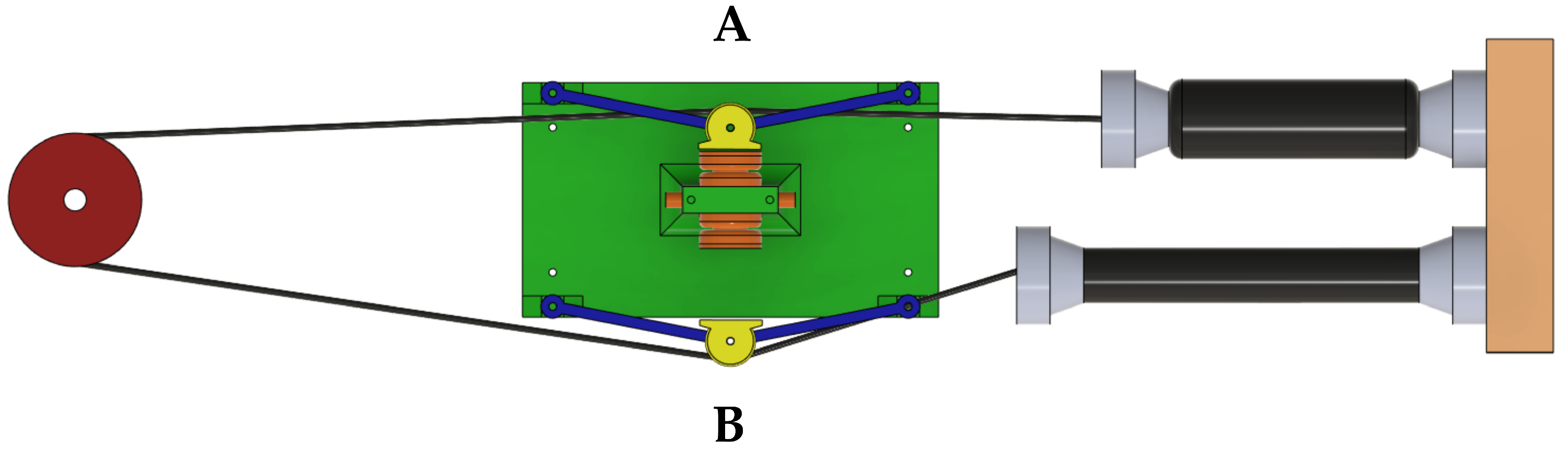
In the actual version of the regulation mechanism, the variability on $p_{cc}$ of the initial contraction lengths of the PAMs pair is compensated by regulating the cables tension through the displacement of the points denoted as A and B in Figure 4, where two complementary configurations required for regulating the cable tension are represented. Two soft pneumatic bellows (highlighted in orange) are adopted for independent regulation of the cables of the PAMs pairs. Each extremity (A or B) has two stable equilibrium positions associated with the open arrangement (position of the extremity B in the subsequent Figure 4) and the closed configuration (position of A in Figure 4); the transition between the equilibrium points is obtained in response to an external force input (pneumatically actuated or due to the patient’s interaction) overcoming the transition threshold.

A 3D view of the prototype of the regulation mechanism based on bistable hybrid soft actuation is given in Figure 5.

2.2. CAD-3D Modelling and 3D Printing

The 3D models of the soft actuators were designed through the 3D-CAD software AutoDesk Fusion 360; multiple versions of the 3D models were progressively refined in accordance with the results of Finite Element Analysis (FEA) which are presented in the subsequent section.

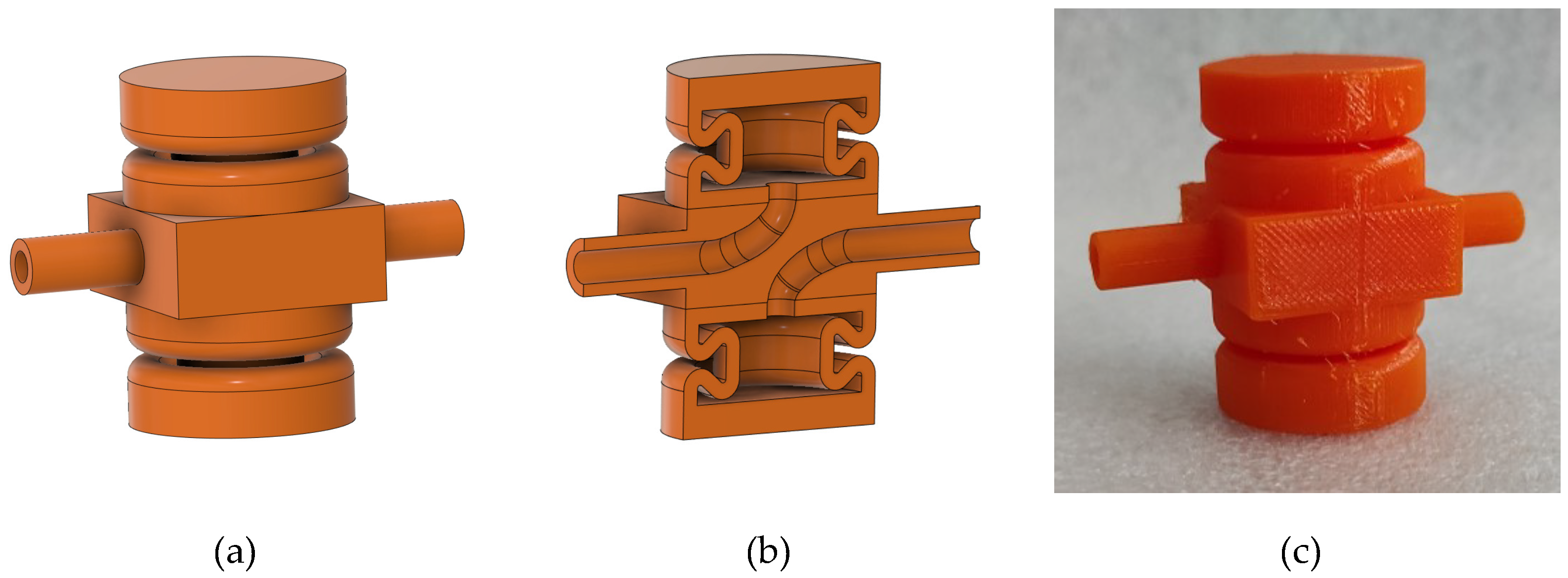
Completely different geometries of the bellows coils were evaluated in order to find the best one in terms of deformation in response to the input of inlet air pressure. One of the major problems to overcome has been the “printability” of the designed geometries, since the adoption of FDM (Fused Deposition Modelling) process implies some physical limitations during the printing of undercuts in 3D models. Accordingly with the achievements obtained by Arleo et al. [25], amongst all the tested geometries, a bellows-like chamber of the soft actuator, which is characterized by internal microchambers, has resulted to be the more efficient for our purpose, since the deformation of the walls, in response to the inlet pressure, is well distributed along the chamber of the soft actuator and the optimal distribution of the elastic strain over the chamber wall implies—as experimentally shown—a linear relationship between the inlet pressure and the displacement of the soft actuator along the actuator axis. Moreover, the final design of the motifs of the actuator coils possesses good features to be 3D printed. Once obtained, the desired behavior in FEA simulations, the corresponding actuator has been 3D printed using the settings listed in the next

Table 1. Main 3D printing parameters for the TPU actuators.

Main 3D Printing Parameters
Material	TPU Ninjaflex (Ninjatek ®)
3D Printer	Raise 3D Pro 2
Layer height	0.15 mm
Nozzle diameter	0.4 mm
Infill density	100%
Support	Only touching buildplate
Extrusion temperature	220 °C
Print speed	15 mm/s

. In accordance with [26], the wall thickness of the actuators is set to five perimeters corresponding to 2 mm, a value which guarantees the structural robustness of the pneumatic chamber and the resulting air tightness.

The in-line configuration of two soft actuators is obtained through an assembly-free 3D printing (see Figure 6); the position of the 3D printing model of the actuators is optimized during the fabrication process in order to avoid the presence of the printing support. One inlet air pipe for each actuator is hollowed within the common wall between the two actuators; these pipes provide the compressed air source needed for the independent control of the actuators pair (see Figure 6b).

The final setting of the printing parameters (the infill, number of perimeters, and number of top and bottom layers) is the result of some iterative cycles of design (from the 3D modelling to 3D printing) in order to achieve the bistability of the Von Mises mechanism through some values of the compliance which are compatible with the range of pressure and force of the actuated joint, as discussed in further development. The 3D printing settings are listed in

Table 2. Main 3D printing parameters for Von Mises mechanism.

Main 3D Printing Parameters for Von Mises Mechanism
Material	PLA (Raise 3D Premium)
3D Printer	Raise 3D Pro 2
Layer height	0.3 mm
Nozzle diameter	0.4 mm
Infill density	20%-Grid type
Support	Everywhere
Extrusion temperature	205 °C
Print speed	50 mm/s

.

In the phases of design of the Von Mises trusses, particular attention was devoted to the design of some housings for the ball bearings which are installed, in correspondence of the apex joint, in order to avoid friction problems during the transmission of forces between the bistable mechanism and the tendon cables of the joint.

All the 3D models are designed trying to reduce the dimensions of the overall mechanism as much as possible. In this perspective, the final dimensions, which result in a compact and light mechanism, are 186 mm × 84 mm × 43 mm, with a overall weight of 142.3 g (of which 28 g are from the soft actuators only). The 3D models were prepared for 3D printing through the slicer software IdeaMaker by RAISE 3D.

3. Computational Modelling and Structural Optimization

The FEA of the mechanical response of the soft actuators, mainly in terms of deformation of the pneumatic chamber in response to the inlet pressure, other than the structural optimization of the same actuators, were conducted through the Mechanics tools of the FEA software Ansys ®Academic. Due to its features, Ninjaflex (Ninjatek®), a thermoplastic polyurethane (TPU), was chosen to print the soft actuators. The modelling of the hyperelastic response of this material is described below.

3.1. FEA Modelling

Due to the hyperelastic properties of the TPU used for fabricating the soft pneumatic actuators, it is necessary to take into account that since, generally speaking, the deflection amplitude is bigger than the thickness of realized structures, linear models are no more accurate and, therefore, according to [27,28], hyperelastic models are needed. A measurement of the deformation on an hyperelastic material can be conducted by means of the stretch ratio

$$\begin{array}{c}\hfill \lambda =\frac{l}{l_0}\end{array}$$

There are three principal stretch ratios (${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$, one for every dimension), and for uniaxial tension, they can be assumed as [29]

$$\begin{array}{c}\hfill {\lambda }_1=\lambda =\frac{l}{l_0};{\lambda }_2={\lambda }_3=\frac{1}{\sqrt{\lambda }}\end{array}$$

From the stretch ratios, the strain invariants can be derived as

$$i_1={\lambda }_{12}+{\lambda }_{22}+{\lambda }_{32}$$

$$i_2={\lambda }_{12}{\lambda }_{22}+{\lambda }_{22}{\lambda }_{32}+{\lambda }_{32}{\lambda }_{12}$$

$$i_3={\lambda }_{12}{\lambda }_{22}{\lambda }_{32}$$

and the volume ratio (ratio of strained to unstrained volume of the material) can be obtained by

$$\begin{array}{c}\hfill J={\lambda }_1{\lambda }_2{\lambda }_3=\frac{V}{V_0}\end{array}$$

On the basis on these relationships, the strain energy potential can be derived as a function of strain invariants according to different hyperelastic models, by choosing the one that best fits the strain/stretch curve which can be identified experimentally for a chosen material. Accordingly with the result by Tawk et al. in [30], the model which fits better the strain/stretch curve of Ninjaflex is the Five Parameters Mooney–Rivlin model which can be defined as

$$\begin{array}{c}\hfill W=c_{10}(i_1-3)+c_{01}(i_2-3)+c_{20}{(i_1-3)}^2+c_{11}(i_1-3)(i_2-3)+c_{02}{(i_2-3)}^2+\frac{1}{p_c}{(J-1)}^2,\end{array}$$

where W is the strain energy potential, $p_c$ is a parameter of compressibility of the material and $c_{ij}$ are parameters that represent the shear behavior [31].

In [30], Tawk et al. assumes the same values of the coefficient of Five Parameters Mooney-Rivlin model for Ninjaflex as listed in

Table 3. Mooney–Rivlin Five Parameters model for used TPU.

Mooney–Rivlin Five Parameters Model for Used TPU
Parameter	Value [MPa]
$C_{10}$	$-0.233$
$C_{01}$	$2.562$
$C_{20}$	$0.116$
$C_{11}$	$-0.561$
$C_{02}$	$0.900$

, where $p_c$ is not listed because it is considered null in order to represent a fully incompressible material.

The Shore hardness of the Ninjaflex TPU is 85 A, and the density value used for the simulations is 1190 kg/m³, as described by the Ninjatek ® datasheets. The behavior of the designed actuators was analyzed through Ansys simulations. Once the hyperelastic model was declared, a fixed costraint was imposed to the boundary linked to the air pipe. Then, a boundary load was imposed to all the internal boundaries of the air chamber of every actuator, in order to simulate the air inlet. In the set of time-dependent simulations, which were carried out in order to optimize the response of the soft actuator, the boundary load pressure was modulated through a ramp signal saturated at discrete values of steady-state pressure taken in the interval [0–400] kPa; the chosen values of the steady-state pressures are achieved at time 1 s.

3.2. Optimization of the Geometry of the Pneumatic Actuators

As mentioned in Section 2.2, the FEA results were exploited for testing different geometries in order to choose, for the peculiar application, the best one amongst the solutions we originally designed or are already available in the literature.

Through FEA simulations, the key parameters of the mechanical response of the actuator, i.e., wall thickness, ratio length/cross-sectional area of the actuator and number and shape of the coils of the actuator bellows, were tuned in combination in order to find the optimal design solution in terms both of sensitivity of the actuator response to the pressure input and of enhancement of the structural properties, including those required to avoid the buckling behavior.

After the optimization of the parameters of the mechanical response of the actuator, we validated the best option also in terms of printability. Therefore, the final printing settings, which are described in Table 1, are adjusted in order to find the best matching between the FEA simulations and the real behavior of the actuator.

In accordance with the FEA simulations, the bellows-like soft actuator activates the snap-through Von Mises mechanism when the inlet pressure is 300 kPa, by reaching an elongation of 8.8 mm. The behavior of the actuator was characterized in a range of inlet pressure ranging from 0 to 400 kPa. Figure 7 shows the comparison between the real and the FEA-predicted behavior.

4. Experimental Tests and Results

4.1. Identification of the Key Parameters of the Bistable Response of the Actuators

The values of some key parameters can be extracted from the mechanical response of the hybrid soft pneumatic actuator through a set of experimental tests. The magnitudes of threshold force and actuation pressure required for the state transitions can be measured by replicating the operating conditions at different values of the co-contraction pressure of the PAMs. An experimental test-rig was designed and built for this purpose. Therefore, to measure the external force required to change the arrangement of the regulation mechanism, e.g., from open (expanded) to contracted (closed) configuration, the points A or B in Figure 4 are held in contact with the linear stage of the test-rig actuating a controlled displacement along its horizontal axis. The resistant force exerted by the Von Mises mechanism is measured through a load cell (SEN-13329, SparkFun) with a measurement range of 0–10 kg. The linear stage is actuated by a stepper motor coupled to a ball screw drive (see Figure 8). One end of the load cell is in contact with the apex joint of the Von Mises mechanism; the other one is fixed to the frame of the linear stage which, in a series of isobaric tests, can be actuated at the constant rate of 2.24 mm/s. The overall structure of the linear stage allows the motion along the horizontal axis while any rotation or linear displacement along other axes is constrained. The position of the linear stage is measured through the angular steps of the stepper motor. The frame of the test-rig is 3D printed in ABS P430XL subjected to the annealing process which improves the mechanical features of the filament.

The measurement of the actuation pressure is obtained through the analogic gauge pressure installed on the pressure regulator MS4-LR-1/4-D7-AS, FESTO. This latter is used to provide to the pneumatic soft actuator an increasing pressure input, which is modulated through a discrete ramp obtained through a series of steps at increments of 20 kPa/step. In a first set of experiments, this ramp signal is used as a pressure input on the bellows actuator in order to estimate the minimum value of pressure guaranteeing state transition; its value is read from the pressure gauge. Moreover, the measurement of the force needed to the state transition, which associated with the threshold of pressure defined above, was carried out; the estimated value of the threshold force is 14.71 N ± $\sigma$, with $\sigma$ = 0.26 (see Figure 9). Both force and pressure readings were digitally acquired through an Arduino-based embedded microcontroller. The experiments were triplicated for each test.

4.2. Isometric Tests

First, the characterization of the mechanical response of the hybrid actuator is obtained through an isometric setup. From the experiments, the characteristics force vs. actuation pressure is obtained; the isometric setup replicates the operating conditions occurring during the force control in which the air pressure of the actuator chamber is modulated in order to regulate the force transmitted between the actuator and the load. Moreover, from the experimentally identified characteristics force vs. pressure, it is possible to quantify the maximum load carrying capacity at the full scale of the actuation pressure, i.e., the maximum load which the hybrid soft actuator (or the soft pneumatic bellows alone) can move at a maximum pressure of 400 KPa.

To obtain the isometric characterization, the extremity A of the mechanism (Figure 4) is constrained in an intermediate position between the transition point and the stable equilibrium corresponding to the closed configuration of the mechanism. The hybrid soft actuation is inflated while the extremity A is held in position by the linear stage. The force is measured through the load cell on the linear stage; the pressure input is modulated though an incremental variation of minimum 20 kPa and maximum 50 kPa per step in order to reach the maximum pressure of 400 kPa in 18 steps.

To quantify the improvement in the force output of the hybrid actuator, which is obtained from the combination of soft bellows and Von Mises trusses, the isometric tests are repeated by disassembling the Von Mises trusses from the overall mechanism. The tests were repeated three times in order to obtain the mean value of force for each sampling pressure (see Figure 10) with a $\sigma$ = 0.48 for the soft actuator only and $\sigma$ = 0.98 for the hybrid actuator. The upper branch of the loop is associated to the rising sequence of applied pressure.

The results in Figure 10 show that the elastic storage by the Von Mises trusses amplifies, to some extent, the force output achievable by the soft actuator alone. The maximum carrying load capacity of the hybrid actuator is 84.14 N at 400 kPA; this value of force is 5.85% greater than the maximum load capacity supported by the soft pneumatic actuator alone. Arising from the elastic storage, further advantages are in terms of the holding force which can resist, against external perturbations on the cables tension, without external power supply in correspondence of the equilibrium points of the Von Mises mechanism.

In the hybrid actuator, a more marked hysteresis occurs (1% for soft actuator alone and 9.5% for the hybrid Von Mises solution) although, in this latter, the hysteresis is comparable with that exhibited by commercial PAMs. On the other hand, the main improvements motivated by the careful design of the hybrid soft solution are the linearity in the characteristics force vs. pressure. Through the Curve Fitting Toolbox of MATLAB, these characteristics can be estimated through a linear function $f\left(p\right)=mp+q$, with m = 0.195 and q = 1.466 for the soft actuator alone and m = 0.212 and q = −0.577 for the hybrid actuator; the goodness-of-fit is estimated through the values of $r^2=0.996$ for the soft actuator and $r^2=0.987$ for the hybrid actuator, respectively. Since the stress relaxation is a potential limitation arising from the structural properties of TPU, which can affect the actuator response in terms of drift, each isometric test was repeated ten times. The experimental loops do not exhibit any drift effect related to the stress relaxation of the hyperelastic material.

4.3. Isobaric Tests

For further characterization of the hybrid soft pneumatic actuator, an isobaric setup was employed. In this case, a constant value of pressure is maintained in the pneumatic chamber through the proportional pressure regulator. A set of three experimental curves was obtained at pressure 50, 100 and 200 kPa. Therefore, by keeping a constant pressure, the actuator and joined Von Mises trusses undergo a controlled compression which, after a maximum displacement of 5 mm, is reversed in order to trace a loop. The force output was measured through the load cell, whereas the pressure reference was kept constant through the pressure regulator. All the experimental profiles were acquired through a DAQ board based on 8-bit AVR RISC-based microcontroller ATmega 328. For each value of pressure (at 50, 100 and 200 kPa, respectively), the tests were repeated three times in order to obtain the mean value of force, with $\sigma =0.36,0.17,0.16$ for the soft actuator alone and $\sigma =0.30,0.52,0.22$ for the hybrid actuator, respectively.

Figure 11 shows the force vs. length curves obtained from the isobaric setup. In comparison with commercial PAMs, the hysteresis on the experimental responses of the hybrid soft pneumatic solution is quite limited. This result can be interpreted as a byproduct of the hybrid solution which limits the occurrence of stick-slip and other phenomena related to the mechanical friction. Therefore, the adoption of Von Mises trusses in combination with pneumatic bellows potentially improve the control performance for the regulation of the mechanical compliance of biorobotic joints. Looking at Figure 11, a singular phenomenon is evident near the inversion points of the curves; this can be explained both through the nonlinear elastic behavior of the soft actuator and through the contact between its spires which changes in accordance with the inlet pressure and the compression exerted on the soft actuator by the linear stage of the test-rig. Both soft and hybrid actuator show a linear behavior in a range of displacement having an upper value of 4 mm; therefore, this value can be chosen as the allowed stroke for both actuators. In

Table 4. Percentage hysteresis $h\%$ calculated for isobaric tests at 50, 100 and 200 kPa.

Pressure [kPa]	$\mathit{h}\%$ for Soft Actuator		$\mathit{h}\%$ for Hybrid Actuator
	5 mms Stroke	4 mms Stroke	5 mms Stroke	4 mms Stroke
50	10.80	2.27	7.80	5.19
100	7.60	2.46	7.30	5.38
200	3.90	3.51	8.90	9.68

, the percentage hysteresis is compared for full-scale and linear range cases. The percentage hysteresis $h\%$ is calculated by dividing the maximum hysteresis amplitude by the output span of the force response and multiplied by 100.

5. Conclusions

In Rehabilitation and Assistive Robotics, through the regulation of the mechanical compliance of the robot joints, it is possible to synthesize some strategies of adaptive control which can take into account the patient’s features, e.g., its neurological conditions and physical ability during the robotic therapy or the human–robot interaction. Antagonistic mechanisms characterized by PAMs-based soft actuation demonstrated all their effectiveness in several applications of rehabilitation robotics. However, the advantages in terms of flexibility, adaptability and intrinsic safety can be obtained through soft actuators at the cost of low mechanical performance and reduced actuator efficiency.

In our hybrid design solution, some 3D-printed and soft pneumatic actuators are complemented by a set of Von Mises trusses which can recover the advantage of storing/releasing the elastic energy under an external trigger of force, thus overcoming the limitations of some pre-existing mechanisms of regulation of the mechanical compliance of a biorobotic joint actuated by PAMs in antagonistic configurations. The multiple steps of design, fabrication and testing of the novel prototype were presented and discussed in this work. The fabrication process has taken the advantages of the additive manufacturing which has enabled both the rapid prototyping of the mechanism and the structural optimization of the mechanical assembly—this as the final result of some iterative cycles of the process of mechanism design.

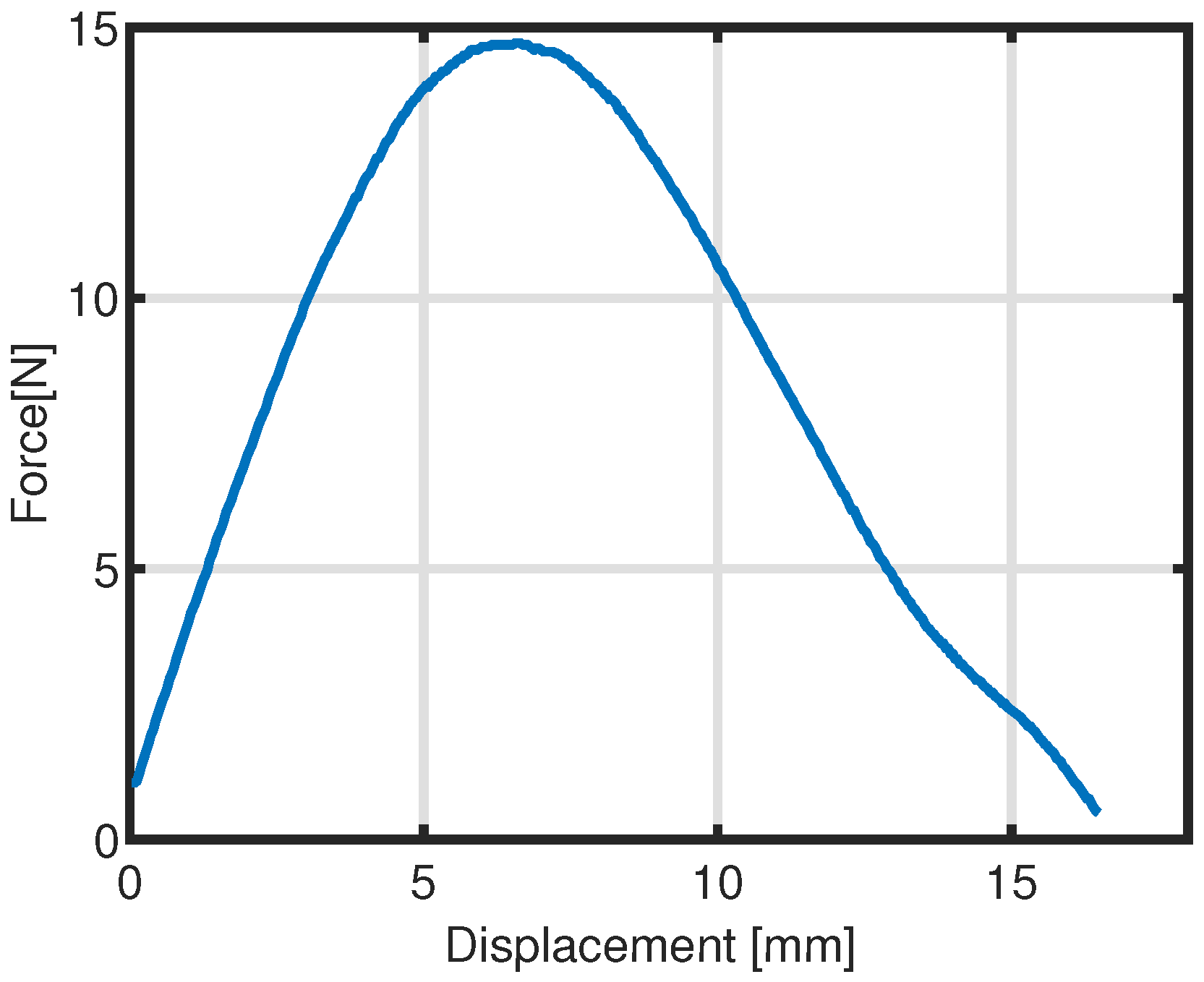
FEA modeling and simulations were conducted in order to optimize the geometry and material properties of the soft actuation modules, other than for improving the control performance and the efficiency of the overall regulation mechanism required for adaptive, biomimetic and safe robot performance. The experimental tests, which replicate the load conditions involved in the regulation of the mechanical compliance, show that the mechanical response of the bistable hybrid soft actuation is characterized by increased efficiency since the pneumatic actuator can be driven at low-pressure range while the force output can be amplified through the elastic deformation of the Von Mises trusses, together with energetic advantages.

The elastic and bistable behavior of the hybrid soft actuation based on Von Mises trusses enables the robust and safe control performance required, during human–robot interaction, for the regulation of the compliance of a biorobotic joint through the modulation of the tension of the cables of a PAMs-actuated joint. The performance expected from the mechanism of regulation of the compliance, through the integration of Von Mises trusses with pneumatic bellows, is validated by the experimental results.

Some isometric tests were carried out to replicate the load conditions in force control which are implemented for regulating the tension of the cables of the antagonistic joint. Moreover, the experimental response of the hybrid soft actuator was obtained at constant values of pressure. Both isobaric and isometric tests show the linearity in the actuator characteristics force output vs. displacement and force output vs. pressure, respectively.

From the analysis of the behavior of the novel bistable hybrid soft actuator, the linearity in the response of the actuator is one of the main improvements which imply the enhanced controllability of the regulation mechanism, whereas in the previous version of mechanism, the adoption of a PAM generates a nonlinear response. In the pre-existing prototype, the PAM actuating the regulation mechanism is placed in a series to a closed chain of a set of links which are interposed between the PAM and the joint cables in order to transmit the actuation forces. The actual version of the mechanism is implemented through Von Mises trusses and soft pneumatic bellows which are interconnected in a parallel (and more compact) configuration. As a byproduct of the novel solution, the negative impacts on the actuator response, which arise from further nonlinearities, backslash, stick-slip and other effects related to the friction in the previous regulation mechanism, can be strongly reduced.

For future developments of this work, we plan the implementation of “assist-as-needed” control strategies through the modulation of the compliance of the robot joint during some repetitive exercises of physical rehabilitation mediated by our biorobotic exoskeleton which, therefore, can adaptively support the patient in the tracking of the reference trajectory. After the planned steps of design and experimental testing of assist-as-needed control strategies on our biorobotic exoskeleton, another point worthy of further investigation is the evaluation of the control performance of the robot in terms of the muscular activation measured through sEMG signals on a group of patients.