Multi-Disturbance Observers-Based Nonlinear Control Scheme for Wire Rope Tension Control of Hoisting Systems with Backstepping
Abstract
1. Introduction
- (1)
- A differentiable tension model suited for nonlinear control is developed by taking the force model errors into account. By considering coupled disturbances in two hydraulic actuators, a differentiable speed model representing the transmission properties of coupled disturbances is established. Finally, a novel model for the ACS is derived by considering the noncoupled and coupled disturbances.
- (2)
- To mitigate the detrimental impact of noncoupled and coupled disturbances, a TDO and a CDO are proposed to estimate the nonlinear mapping element of the model and compensate for nonlinear uncertainty, resulting in a smaller tension difference.
- (3)
- To combine the TDO and the CDO with the backstepping controller, the tension derivative is chosen as the ACS’s state variable to release the displacement term. To demonstrate the stability of the proposed control method, proper Lyapunov functions are developed.
- (4)
- To verify the proposed control methodology, a series of experimental studies are conducted on the experimental test rig. Comparative experimental results show that the proposed controller exhibits a better performance than a CDO based BC, a TDO based BC, a BC, or a conventional PI controller.
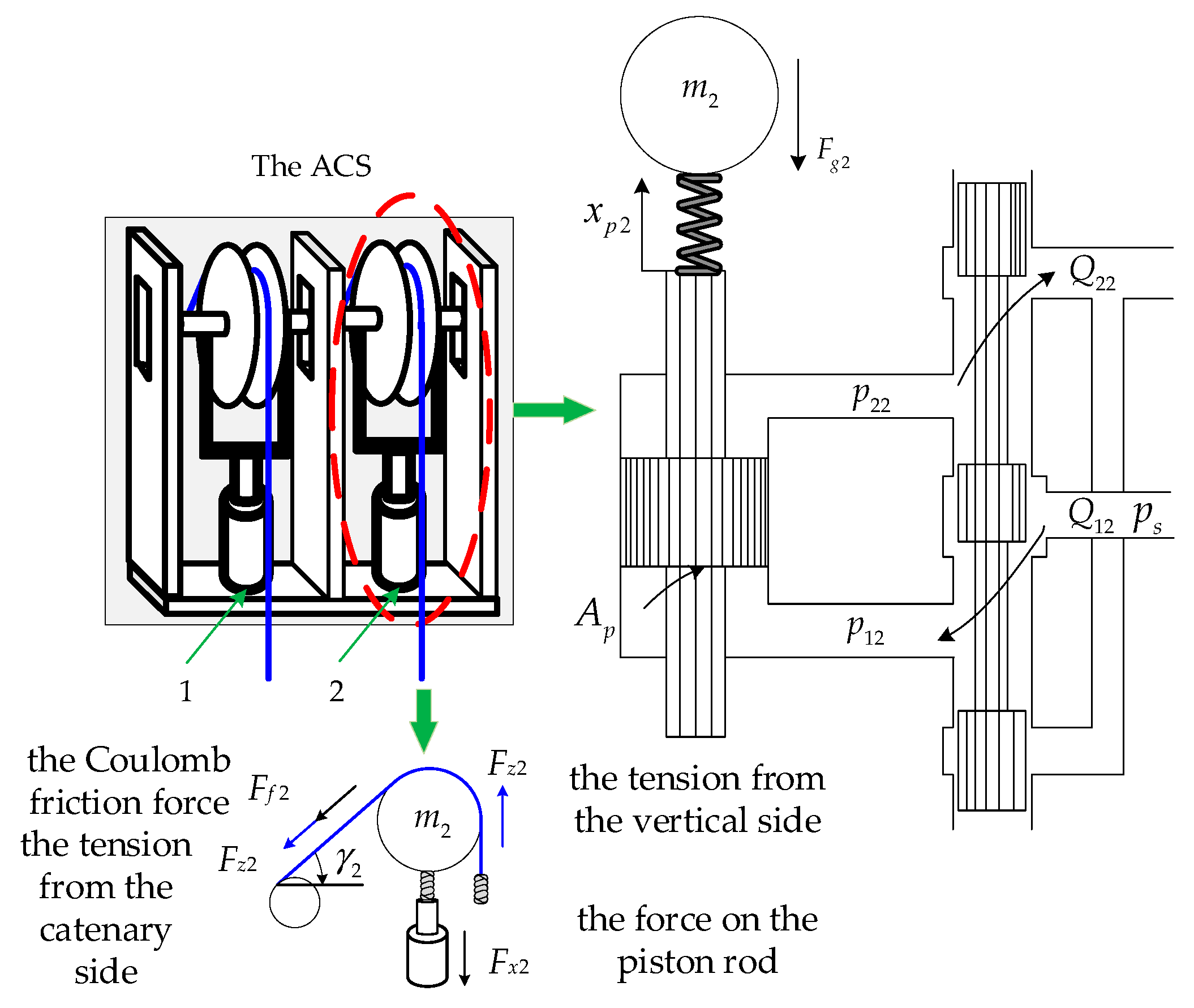
2. Problem Formulation and Preliminaries
3. Controller Design
3.1. Development of the TDO
3.2. Development of the CDO
3.3. Development of the MDOBC
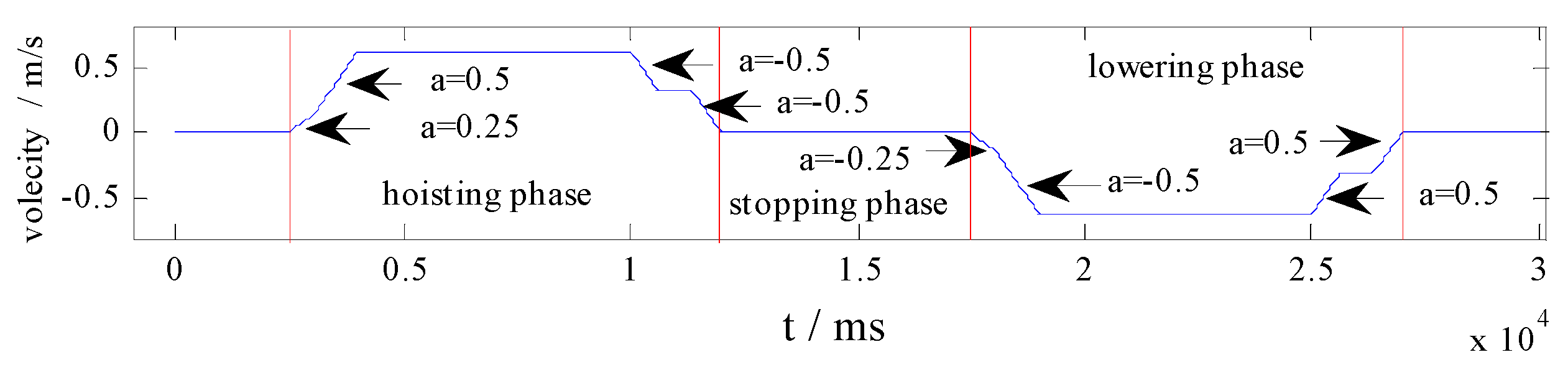
4. Comparative Experimental Study
4.1. The Experimental Test Rig
4.2. Comparative Experimental Results
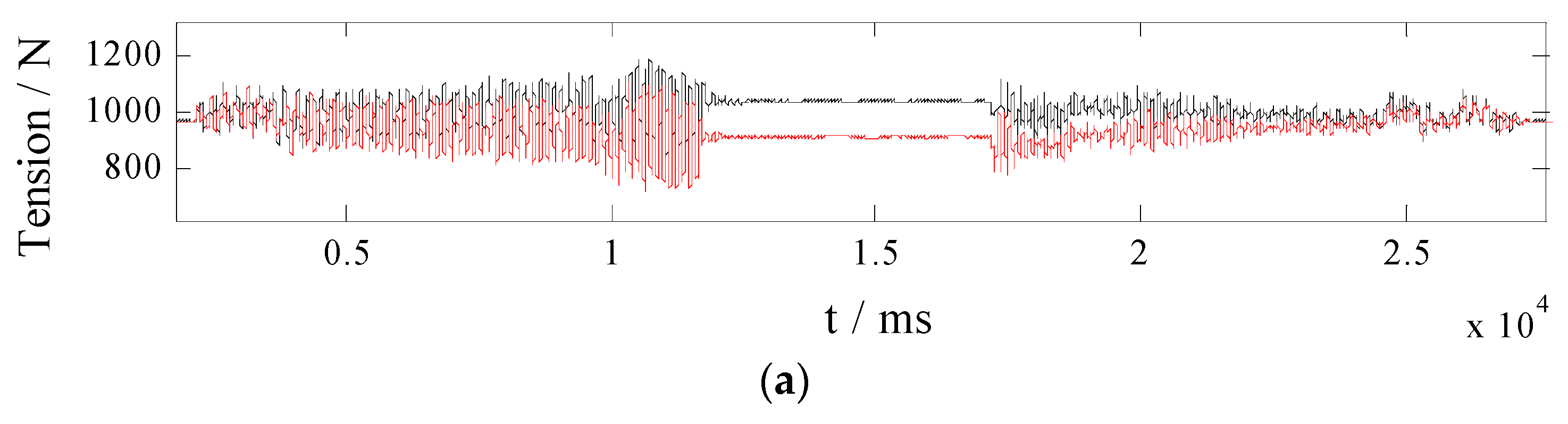
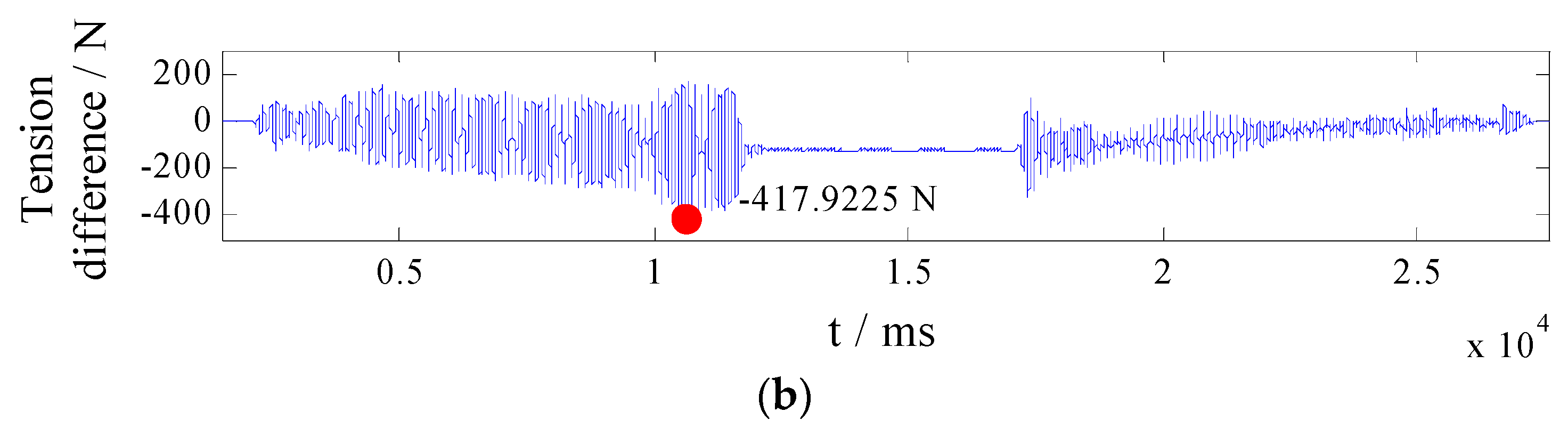
- No controller: Without any A controller, wire rope tensions are presented in Figure 5.
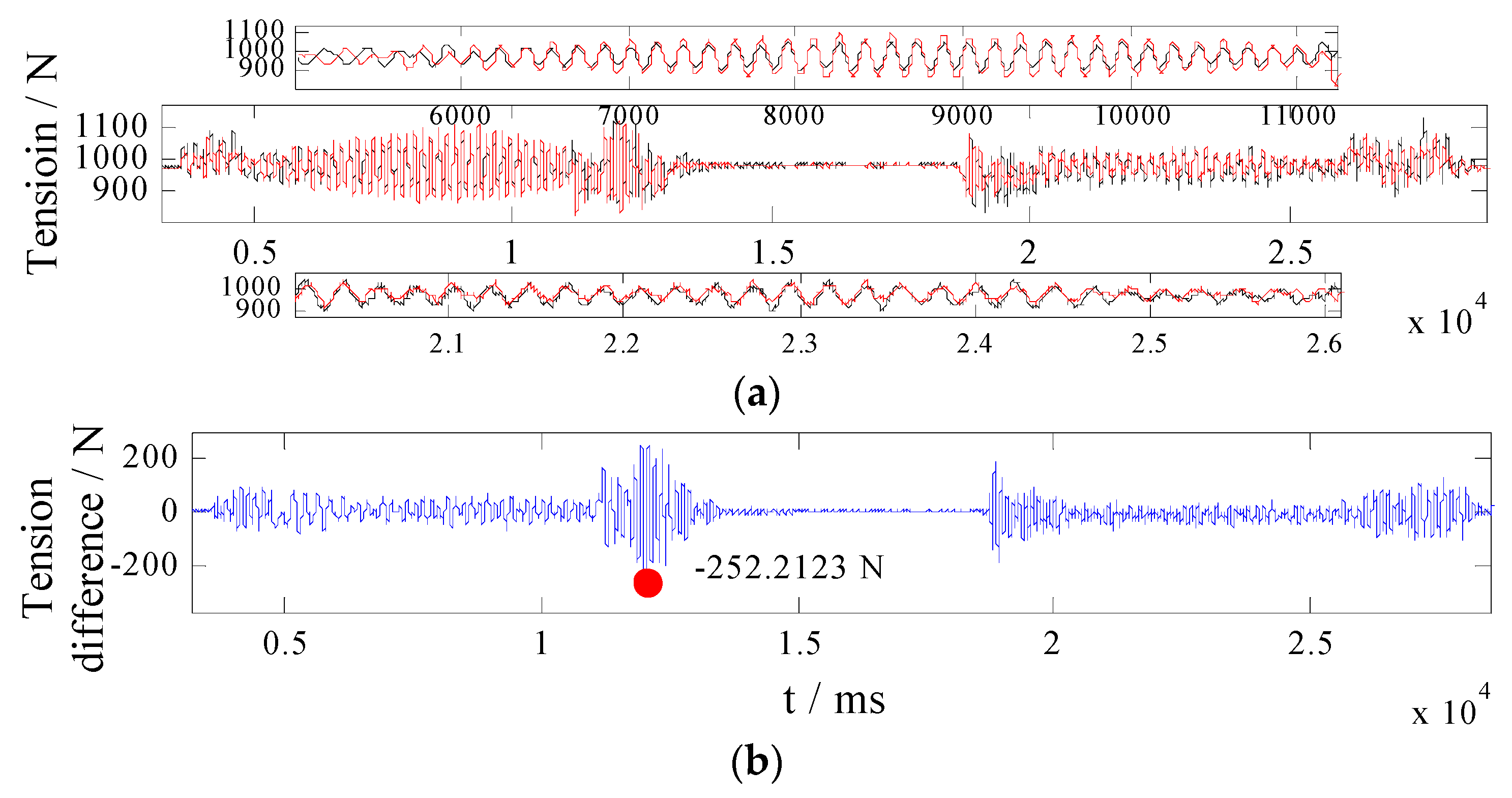
- The PI controller: The PI controller can be expressed as uLi = Kpi × e + KIiΣe. e denotes the tension tracking error. Control gains are selected as Kpi = 0.012 and KIi = 0.05. The experimental results are presented in Figure 6;
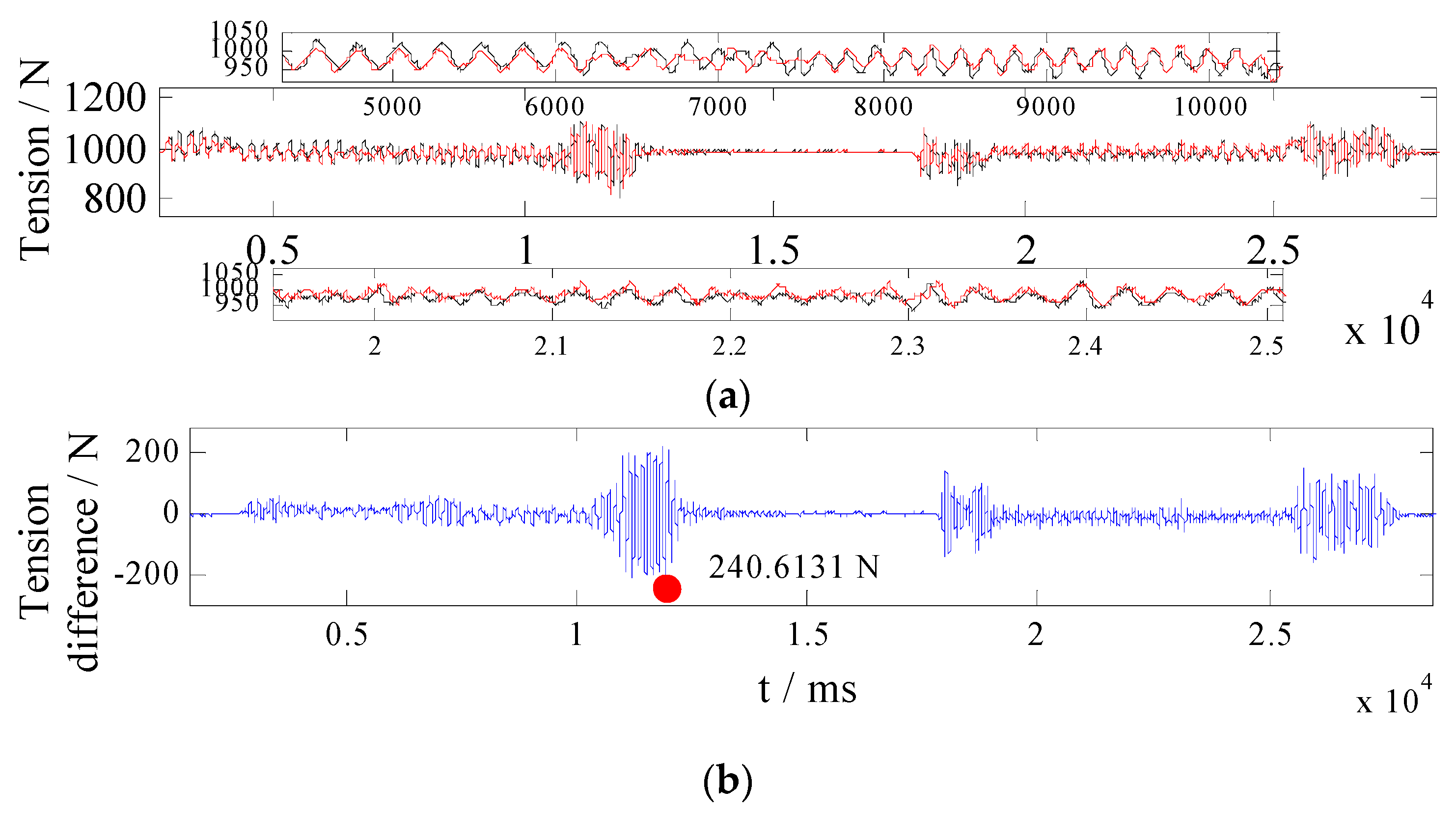
- The BC: With estimation values from the TDO and the CDO being defined as zero, the BC controller is conducted on the ACS. Control gains are selected as ki1 = 3000, ki2 = 1000, ki3 = 1200. The experimental results are presented in Figure 7;
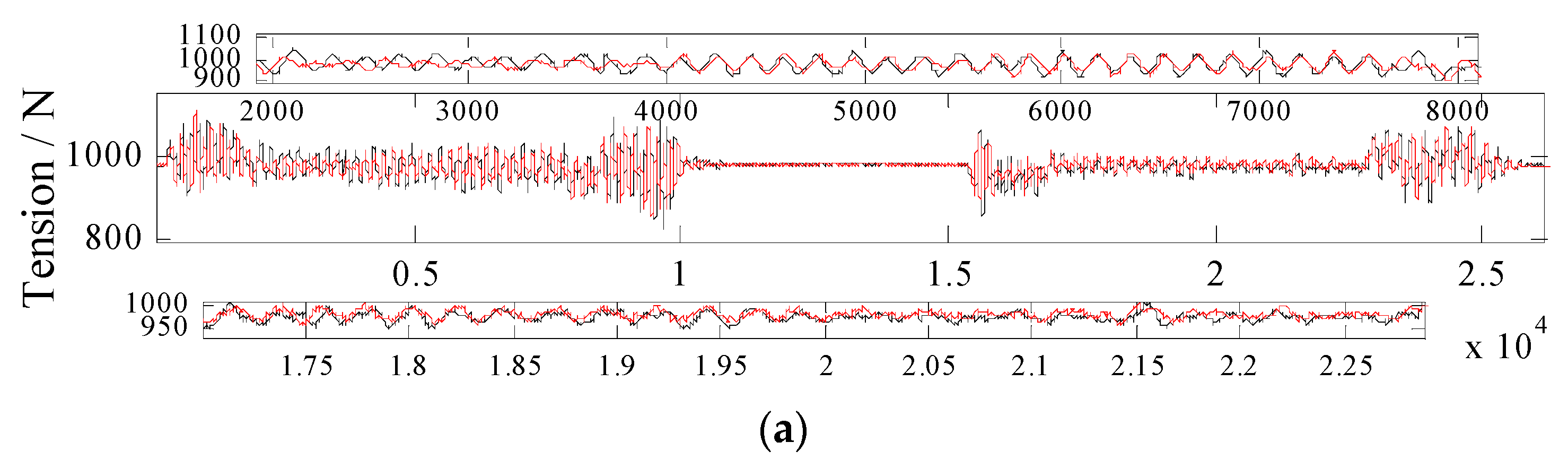
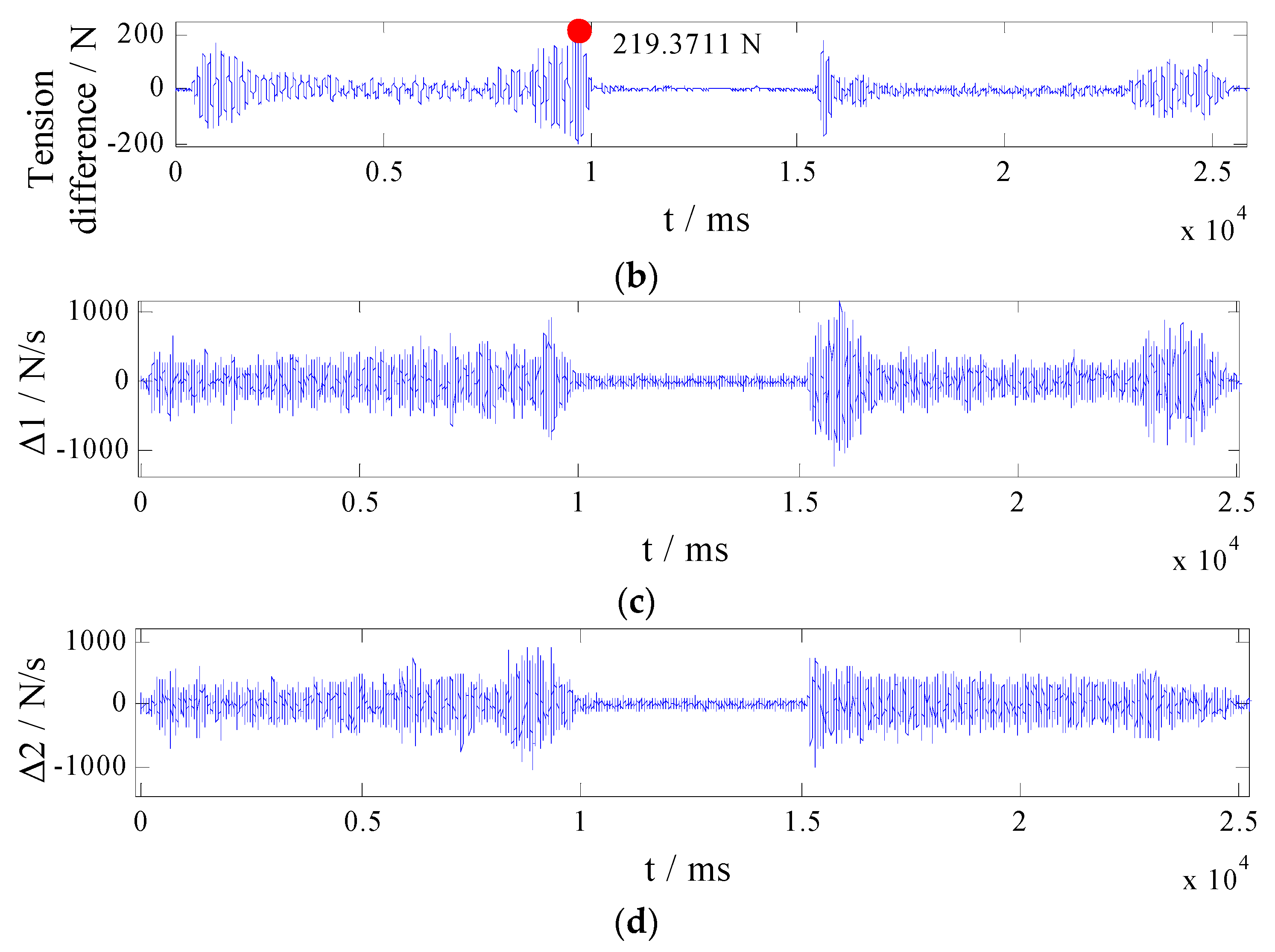
- The TDO based BC: With estimation values from the CDO are defined as zeros, the TDO based BC is conducted on the ACS. Control gains are selected as λi = 0.1, ki1 = 3000, ki2 = 1000, ki3 = 1200. Figure 8 presents the experimental results;
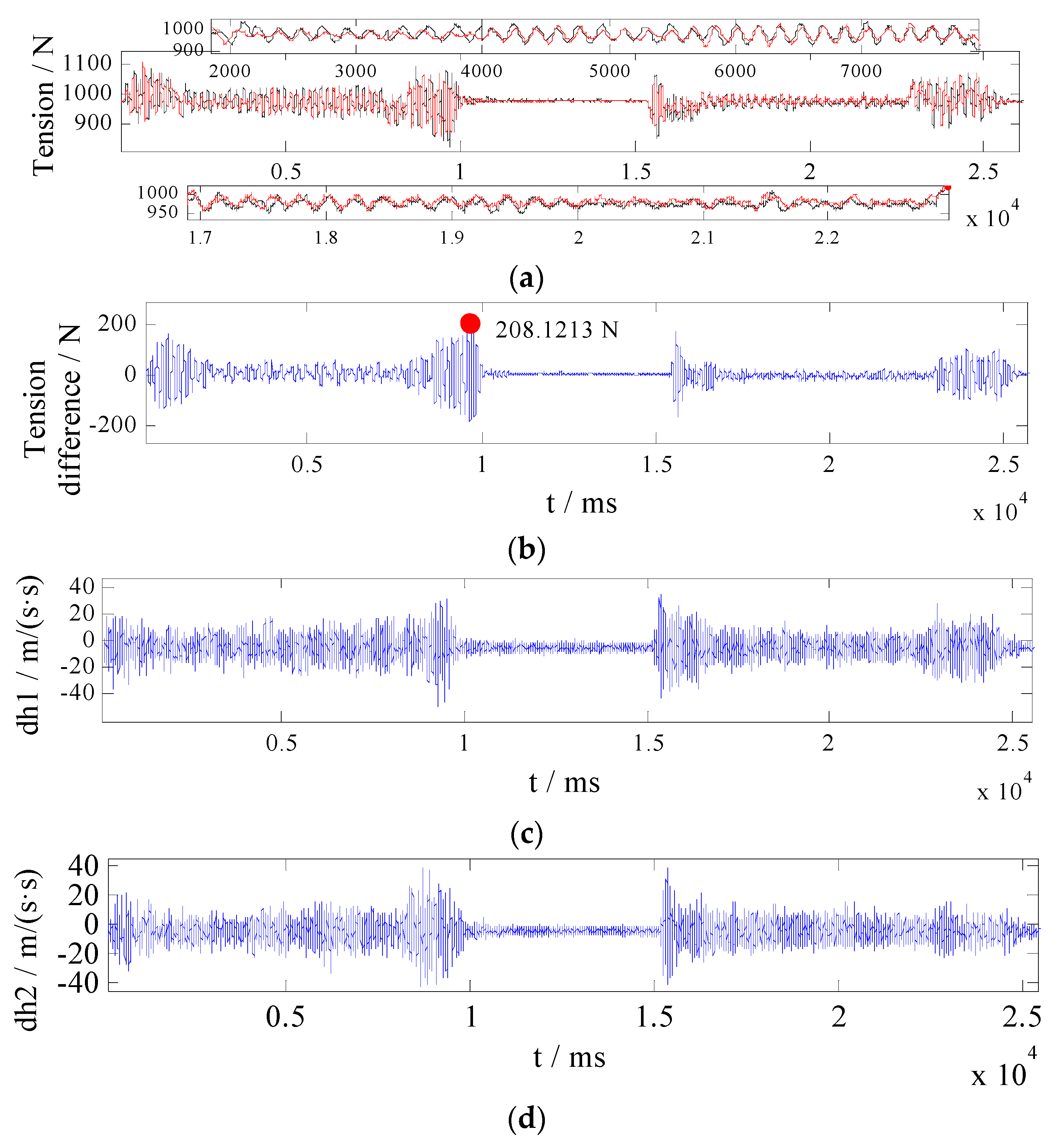
- The CDO based BC: With estimation values from the TDO are defined as zeros, the CDO based BC is conducted on the ACS. Control gains are selected as kd11 = 20, kd12 = 0.1, kd21 = 0.1, kd22 = 20, ki1 = 3000, ki2 = 1000, ki3 = 1200. The experimental results are presented in Figure 9;
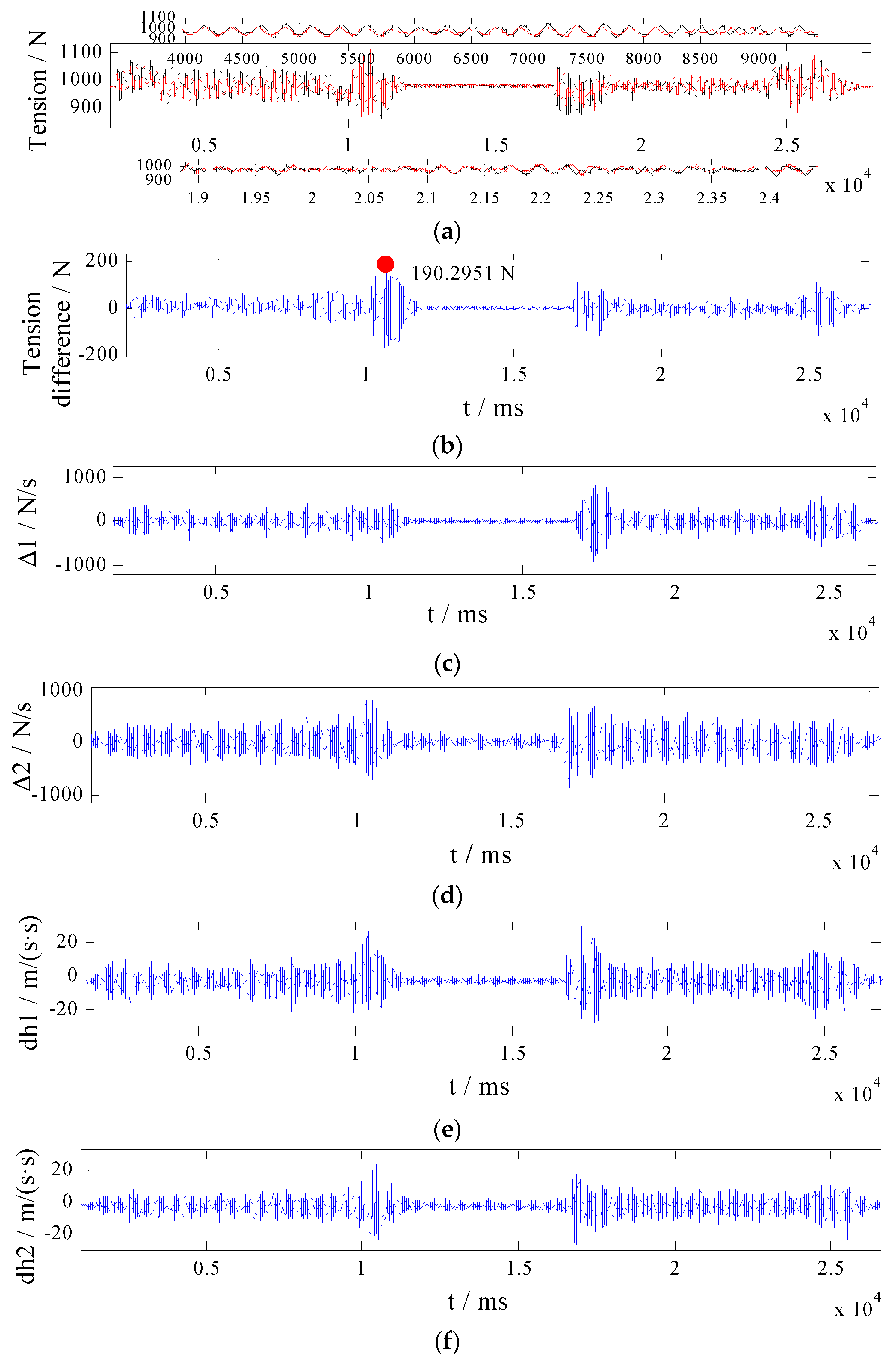
- The MDOBC: With the state representation, the MDOBC is designed and conducted on the ACS. Control gains are selected as λi = 0.1, kd11 = 20, kd12 = 0.1, kd21 = 0.1, kd22 = 20, ki1 = 3000, ki2 = 1000, ki3 = 1200. The corresponding experimental results are presented in Figure 10.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| γi, i = 1, 2. | the angle between the catenary wire rope and the upper plane |
| Fxi, i = 1, 2. | the force of the No. i hydraulic cylinder |
| Fzi, i = 1, 2. | the No. i wire rope tension |
| kf | the stiff of the force detector |
| xpi, i = 1, 2. | the displacement of the No. i hydraulic cylinder |
| xpfi, i = 1, 2. | the displacement of the No. i movable head sheave |
| , i = 1, 2. | the disturbance in the force dynamics |
| Ap | the effective area of chamber |
| PLi, i = 1, 2. | the load pressure |
| mi, i = 1, 2. | the load mass |
| Bpi, i = 1, 2. | the damping coefficient |
| dhi, i = 1, 2. | the total disturbance in the speed dynamics |
| d12, d21 | the coupled disturbances |
| QLi, i = 1, 2. | the load flow from the valve to the actuator chambers |
| Ctli, i = 1, 2. | the total leakage coefficient |
| Vti, i = 1, 2. | the total volume |
| xvi, i = 1, 2. | the spool displacement of servo valves |
| Cd | the discharge coefficient of servo valves |
| w | the throttle area gradient of servo valves |
| ρo | the density of the supply oil |
| ps | the supply pressure |
| uLi | the control voltage of servo valves |
| Qr | the rated flow under the rated load pressure Δpr |
| umax | the maximum control voltage |
| , i = 1, 2. | the state variables |
| θi, i = 1, 2. | kf/(1 + sinγi) |
| θi1, i = 1, 2. | Ap/mi |
| θi2, i = 1, 2. | Bpi/mi |
| θi3, i = 1, 2. | 1/mi |
| θi4, i = 1, 2. | 4Apβe/Vti |
| θi5, i = 1, 2. | 4Ctliβe/Vti |
| θi6, i = 1, 2. | 4βe/Vti |
| , i = 1, 2. | the maximum bounded value of |
| , i = 1, 2. | the maximum bounded value of |
| , i = 1, 2. | the maximum bounded value of |
| , i = 1, 2. | the maximum bounded value of |
| , i = 1, 2. | the estimation of |
| , i = 1, 2. | the estimation error |
| , i = 1, 2. | an auxiliary variable |
| p(xi1, xi2), i = 1, 2. | a function that needs to be designed |
| λi, i = 1, 2. | the control gain of the TDO |
| , i = 1, 2. | the estimation error dynamics |
| , i = 1, 2. | the estimation value dynamics |
| , i = 1, 2. | the estimation value of dhi |
| , i = 1, 2. | the estimation value of xi2 |
| A = [kd11, kd12; kd21, kd22] | the control gain matrix of the CDO |
| , i = 1, 2. | the dynamics of the estimation value of the CDO |
| , i = 1, 2. | the estimation error dynamics of the CDO |
| e = [ei1, ei2, ei3], i = 1, 2. | the system tracking error matrix |
| ei1, i = 1, 2. | two wire rope tension tracking errors |
| ei2, i = 1, 2. | two displacement velocity tracking errors |
| ei3, i = 1, 2. | two load pressure tracking errors |
| αi1, αi2, i = 1, 2. | the virtual control laws |
| Hr | a bounded hypersphere ball |
| , i = 1, 2; j = 1, 2, 3. | the Lyapunov functions |
| , i = 1, 2; j = 1, 2, 3. | the time derivative of the Lyapunov functions |
| Kpi, i = 1, 2. | the control gains of the PI controller |
| KIi, i = 1, 2. | the control gains of the PI controller |
Appendix A
References
- Tanaka, K.; Nishimura, M.; Wang, H.O. Multi-objective fuzzy control of high rise/high speed elevators using LMIs. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 26 June 1998; pp. 3450–3454. [Google Scholar]
- Zhu, Z.; Li, X.; Shen, G.; Zhu, W. Wire rope tension control of hoisting systems using a robust nonlinear adaptive backstepping control scheme. ISA Trans. 2018, 72, 256–272. [Google Scholar] [CrossRef] [PubMed]
- Zang, W.; Shen, G.; Rui, G.; Li, X.; Li, G.; Tang, Y. A flatness-based nonlinear control scheme for wire tension control of hoisting systems. IEEE Access 2019, 7, 146428–146442. [Google Scholar] [CrossRef]
- Ma, H.; Tang, G.Y.; Hu, W. Feedforward and feedback optimal control with memory for offshore platforms under irregular wave forces. J. Sound Vib. 2009, 328, 369–381. [Google Scholar] [CrossRef]
- Lee, S.G. Modeling and advanced sliding mode controls of crawler cranes considering wire rope elasticity and complicated operations. Mech. Syst. Signal Process. 2018, 103, 250–263. [Google Scholar]
- Zhang, D.; Wu, Q.; Yao, X.; Jiao, L. Active disturbance rejection control for looper tension of stainless steel strip processing line. J. Control Eng. Appl. Inform. 2018, 20, 60–68. [Google Scholar]
- Lu, J.S.; Cheng, M.Y.; Su, K.H.; Tsai, M.C. Wire tension control of an automatic motor winding machine-an iterative learning sliding mode control approach. Robot. Comput. Integr. Manuf. 2018, 50, 50–62. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Shen, G. A switching-type controller for wire rope tension coordination of electro-hydraulic-controlled double-rope winding hoisting systems. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 1126–1144. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Z.; Shen, G.; Li, W. Tension coordination control of double-rope winding hoisting system using hybrid learning control scheme. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 1265–1281. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Z.; Li, W.; Shen, G. Fault-tolerant control of double-rope winding hoists combining neural-based adaptive technique and iterative learning method. IEEE Access 2019, 7, 50476–50491. [Google Scholar] [CrossRef]
- Zhao, J.; Na, J.; Gao, G. Adaptive dynamic programming based robust control of nonlinear systems with unmatched uncertainties. Neurocomputing 2020, 35, 56–65. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Ohnishi, K. An adaptive reaction force observer design. IEEE/ASME Trans. Mechatron. 2014, 20, 750–760. [Google Scholar] [CrossRef]
- He, H.; Na, J.; Huang, Y.; Liu, T. Integrated Modeling and Adaptive Parameter Estimation for Hammerstein systems with Asymmetric Dead-Zone. IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Na, J.; Zhao, J.; Gao, G.; Li, Z. Output-feedback robust control of uncertain systems via online data-driven learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2650–2662. [Google Scholar] [CrossRef] [PubMed]
- Sariyildiz, E.; Ohnishi, K. On the explicit robust force control via disturbance observer. IEEE Trans. Ind. Electron. 2014, 62, 1581–1589. [Google Scholar] [CrossRef]
- Na, J.; Li, Y.; Huang, Y.; Gao, G.; Chen, Q. Output feedback control of uncertain hydraulic servo systems. IEEE Trans. Ind. Electron. 2019, 67, 490–500. [Google Scholar] [CrossRef]
- Na, J.; He, H.; Huang, Y.; Dong, R. Adaptive estimation of asymmetric dead-zone parameters for sandwich systems. IEEE Trans. Control Syst. Technol. 2021, 30, 1336–1344. [Google Scholar] [CrossRef]
- Xiao, L.; Lu, B.; Yu, B.; Ye, Z. Cascaded sliding mode force control for a single-rod electrohydraulic actuator. Neurocomputing 2015, 156, 117–120. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, P.; He, B.; Deng, G.; Zhang, C.; Huang, X. An adaptive neural sliding mode control with ESO for uncertain nonlinear systems. Int. J. Control Autom. Syst. 2020, 19, 687–697. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-gain disturbance observer-based backstepping control with output tracking error constraint for electro-hydraulic systems. IEEE Trans. Control Syst. Technol. 2014, 23, 787–795. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- He, W.; Sun, C.; Ge, S.S. Top tension control of a flexible marine riser by using integral-barrier Lyapunov function. IEEE/ASME Trans. Mechatron. 2014, 20, 497–505. [Google Scholar] [CrossRef]
- Zang, W.; Zhang, Q.; Shen, G.; Fu, Y. Extended sliding mode observer based robust adaptive backstepping controller for electro-hydraulic servo system: Theory and experiment. Mechatronics 2022, 85, 102841. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Trans. Ind. Electron. 2019, 67, 2042–2053. [Google Scholar] [CrossRef]
- Wei, X.J.; Wu, Z.J.; Karimi, H.R. Disturbance observer-based disturbance attenuation control for a class of stochastic systems. Automatica 2016, 63, 21–25. [Google Scholar] [CrossRef]
- Kai, G.; Wei, J.; Fang, J.; Feng, R.; Wang, X. Position tracking control of electro-hydraulic single-rod actuator based on an extended disturbance observer. Mechatronics 2015, 27, 47–56. [Google Scholar]
- Besnard, L.; Shtessel, Y.B.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Lu, Y.S. Sliding-mode disturbance observer with switching-gain adaptation and its application to optical disk drives. IEEE Trans. Ind. Electron. 2009, 56, 3743–3750. [Google Scholar]
- Zhang, J.; Liu, X.; Xia, Y.; Zuo, Z.; Wang, Y. Disturbance observer-based integral sliding-mode control for systems with mismatched disturbances. IEEE Trans. Ind. Electron. 2016, 63, 7040–7048. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Robust constrained control for MIMO nonlinear systems based on disturbance observer. IEEE Trans. Autom. Control 2015, 60, 3281–3286. [Google Scholar] [CrossRef]
- Zheng, M.; Lyu, X.; Liang, X.; Zhang, F. A generalized design method for learning-based disturbance observer. IEEE/ASME Trans. Mechatron. 2021, 26, 45–54. [Google Scholar] [CrossRef]
- Rashad, R.; El-Badawy, A.; Aboudonia, A. Sliding mode disturbance observer-based control of a twin rotor MIMO system. ISA Trans. 2017, 69, 166–174. [Google Scholar] [CrossRef] [PubMed]
- Ginoya, D.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 98–107. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chen, Z.; Wei, C. Sliding mode disturbance observer-based backstepping control for a transport aircraft. Sci. China Inf. Sci. 2013, 57, 1–16. [Google Scholar] [CrossRef][Green Version]
- Guo, Q.; Yin, J.M.; Yu, T.; Jiang, D. Coupled-disturbance-observer-based position tracking control for a cascade electro-hydraulic system. ISA Trans. 2017, 68, 367–380. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.O. Hooke’s law. Science 1926, 64, 298–299. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Hoisting height | 4.5 m | Width | 3.4 m |
| Whole height | 7 m | Length | 4.4 m |
| Diameter of head sheave | 0.5 m | Dimensions of the conveyance | 0.375 × 0.375 × 0.125 m |
| Hoisting weight | 200 Kg | Diameter of two winding drum | 0.4 m |
| Parameters | Values/Unit | Parameters | Values/Unit |
|---|---|---|---|
| Ap | 1.88 × 10−3/m2 | Vti | 0.38 × 10−3 m3 |
| mi | 110/Kg | umax | 10 V |
| ΔPr | 21 MPa | Ps | 15 × 106 Pa |
| Bpi | 25,000 N/(m/s) | Qr | 30 L/min |
| Ctli | 6.9 × 10−13 m3/s/Pa | βe | 6.9 × 108 Pa |
| Controllers | Peak Error/N | RMSE/N |
|---|---|---|
| Without any A controller | 417.9225 | 106.5372 |
| The PI controller | 252.2123 | 38.1489 |
| The BC | 240.6131 | 37.5700 |
| The TDO based BC | 219.3711 | 32.7556 |
| The CDO based BC | 208.1213 | 30.7174 |
| The proposed controller | 190.2951 | 28.2601 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, W.; Chen, X.; Zhao, J. Multi-Disturbance Observers-Based Nonlinear Control Scheme for Wire Rope Tension Control of Hoisting Systems with Backstepping. Actuators 2022, 11, 321. https://doi.org/10.3390/act11110321
Zang W, Chen X, Zhao J. Multi-Disturbance Observers-Based Nonlinear Control Scheme for Wire Rope Tension Control of Hoisting Systems with Backstepping. Actuators. 2022; 11(11):321. https://doi.org/10.3390/act11110321
Chicago/Turabian StyleZang, Wanshun, Xiao Chen, and Jun Zhao. 2022. "Multi-Disturbance Observers-Based Nonlinear Control Scheme for Wire Rope Tension Control of Hoisting Systems with Backstepping" Actuators 11, no. 11: 321. https://doi.org/10.3390/act11110321
APA StyleZang, W., Chen, X., & Zhao, J. (2022). Multi-Disturbance Observers-Based Nonlinear Control Scheme for Wire Rope Tension Control of Hoisting Systems with Backstepping. Actuators, 11(11), 321. https://doi.org/10.3390/act11110321






