Intermediate-Variable-Based Distributed Fusion Estimation for Wind Turbine Systems

Abstract

In wind turbine systems, the state of the generator is always disturbed by various unknown perturbances, which leads to system instability and inaccurate state estimation. In this paper, an intermediate-variable-based distributed fusion estimation method is proposed for the state estimation problem in wind turbine systems. By constructing an augmented state error system and using the idea of bounded recursive optimization, the local estimators and distributed fusion criterion are designed, which can be used to estimate the disturbance signals and system states. Then, the local estimator gains and the distributed weighting fusion matrices are obtained by solving the established convex optimization problems. Furthermore, a compensation strategy is designed by using the estimated disturbance signals, which can potentially reduce the influence of the disturbance signals on the system state. Finally, a numerical simulation is provided to show that the proposed method can effectively improve the accuracy of the estimation of the wind turbine state and disturbance, and the superiority of the proposed method is illustrated as a comparison to the Kalman fusion method.

1. Introduction

As a new, eco-friendly, low-cost power generation technology, wind power generation not only fills up the energy demand gap, but also reduces the use of fossil energy. Recently, wind power technology has been widely applied worldwide [1]. To utilize the abundant and flexible wind energy resources, wind turbines are often installed in mountainous or offshore areas, where wind resources are rich [2]. It is important to note that the working environment for the turbines is relatively harsher. Therefore, wind turbines are frequently disturbed by random variables, such as changes in wind speed, wind profile variations and so on. Meanwhile, these disturbances will affect the operation of the generator through the transmission system and can cause an unstable status of the generator, resulting in fluctuations of the output current, voltage and power of the generator, and subsequently affecting the stability of the entire power generation system. As a result of the remote location of the wind farm and the harsh working environment, the control centers are ordinarily away from the wind farms, and thus various sensors are installed inside the generator to detect its status. In this sense, this paper will focus on the multi-sensor fusion estimation problem for the wind turbine state and disturbance signals.

In previous works, various estimation algorithms and models have been proposed to estimate the state of wind turbines [3,4,5,6,7,8]. For the unknown nonlinear input signal in the wind generator model, a dynamic state estimation method based on Kalman filtering was proposed in [3], which could accurately estimate the state of the generator under the condition of uncertain wind speed. Moreover, for the local phasor measurement units (PMUs) of a doubly fed induction generator (DFIG) connected to a multi-area power system, an unscented particle filter was developed in [4]. The unscented particle filter could more accurately track the state of the power system when it was disturbed, and solved the particle degradation problem. Particularly, combined with the Newton–Raphson method and the Kalman filter, an new estimation algorithm was proposed in [5] to estimate the aerodynamic torque acting on the rotor of the turbine. For doubly fed induction generators connected to complex power systems, where electric faults occur in the power system, an unscented Kalman filter with a bad data detection scheme was proposed in [6] to estimate the state of the DFIG. Furthermore, a data-driven method based on multivariate state estimation technology (MSET) that could recognize fault warnings of the wind turbines was used to monitor their state in [7]. Based on the historical data of the normal wind turbine gearbox, nonlinear state estimation technology was proposed in [8] to model the gearbox, and then, combined with time series filtering and Welch’s t-test in the fault detection algorithm, the abnormal condition of the wind turbine could be detected. However, the disturbance estimation was not considered in the above work. In reality, the wind turbine is usually interfered with by the disturbance signals during operation. When the disturbance is too large, the system state estimation will be impacted, causing damages to the generator.

In response to the problems of the disturbance signal during the operation of the wind turbine system, assorted approaches were proposed in the literature. A disturbance observer for an aerodynamic moment estimation, as well as subsequent compensation, was proposed in [9] to eliminate unstable factors, such as the instability of the small-signal model under high wind speeds in the wind turbine system. The Kalman filter was used to estimate the harmonic signal of the turbine side angular velocity, in addition, a new empirical mode decomposition method was introduced to separate the harmonics caused by the interference [10]. The unknown input observer was combined with the linear parameter varying approach in [11], which was used to estimate the disturbance in the input aerodynamic torque caused by the wind shear and tower shadow. In addition, based on the linear variable parameter model, an unknown input observer was designed to estimate the actuator and sensor fault signals of the wind power system by constructing an augmented system [12]. Particularly, the disturbance estimation problem based on the wind turbine transmission system was investigated in [13], where the estimation accuracy of the extended Kalman filter and the unknown input observer were presented, respectively. Though many state estimation algorithms have been developed and applied in various fields [14,15,16], the robustness, reliability and fault tolerance are not displayed well in the single sensor estimation. Thus, multi-sensor information fusion technology [17,18] was presented, which could overcome the limitations of single sensor estimation in order to integrate redundant information of multiple sensors and then to obtain a better estimation performance. It is worth noting that the distributed multi-sensor fusion estimation problems of the wind power systems were not widely studied in the past research works. At present, the well-known fusion estimation method is Kalman fusion filtering, and extended research has been carried out regarding this method [17,19]. The major limitation of this method is that it requires the statistical characteristics of the system noises in advance. However, the noises and disturbances in the actual system are always random but bounded, and the statistical information cannot be accurately obtained. Therefore, the bounded recursion idea, which does not require the statistical information of the disturbances or noises, will be used to design a fusion estimation method based on intermediate variables in this paper.

Although certain achievements have been made in the wind turbine state estimation and disturbance estimation, respectively, the area of the fusion estimation of the wind turbine system state with disturbance has not been well studied. Motivated by the above analysis, a real-time fusion estimation algorithm is proposed to jointly estimate the system state and disturbance signals for wind turbine systems. Firstly, the relationship between state and disturbance is established by constructing an intermediate variable. Then, both the local gain of the observer and the distributed fusion weighting matrices are determined by solving two convex optimization problems based on the idea of bounded recursive optimizations. Particularly, a compensation control strategy based on the estimated signal of the intermediate observer in order to reduce the impact of disturbance that occurs during operation is proposed in this paper. Finally, the effectiveness and the advantages of the proposed method are verified by a numerical simulation.

2. Model Building

Generally, wind power plants are situated in remote areas that are far away from towns, such as mountains or coastlines, where the control centers are often not nearby. Therefore, to determine the status of operating wind turbines, various sensors are equipped in the turbines to accurately detect the running conditions and to then transmit the collected data to the control center through the communication network. Recently, the most widely used wind power generation system is the doubly fed induction generator, its structure is shown in Figure 1 [20]. The wind power generation system consists of wind wheel, gearbox, induction generator and back-to-back converter. The stator of DFIG is directly connected to the grid, whereas the rotor is connected to the grid by two AC/DC IGBT-based voltage source converters, and two converters are connected by a DC-link. The converter provides a variable frequency power supply for the rotor, and when the mechanical speed of the rotor or the load of the motor changes, the frequency and phase of the rotor current can be adjusted by the converter to keep the voltage and frequency output stable, thus realizing the variable speed operation of the wind turbine.

Based on the characteristics of the induction generator model, which are non-linearity, high-order and strong coupling, the following hypotheses are made before modelling: 1. Ignoring the spatial harmonics, the magnetomotive force is distributed sinusoidally along the circumference of the air gap; 2. Ignoring the saturation of the magnetic circuit, the self-inductance and mutual inductance of each winding are linear; 3. Ignoring the influence of the frequency, temperature changes on the winding resistance are not considered. Based on the above assumptions, the voltage equation of the generator in the two-phase coordinate system [20] is listed as

$$\left\{\begin{array}{c}{v}_{ds}=-R_s{i}_{ds}-{\omega }_s{\psi }_{qs}+{\dot{\psi }}_{ds}/{\omega }_b\hfill \\ v_{qs}=-R_s{i}_{qs}+{\omega }_s{\psi }_{ds}+{\dot{\psi }}_{qs}/{\omega }_b\hfill \\ v_{dr}=R_r{i}_{dr}-s{\omega }_s{\psi }_{qr}+{\dot{\psi }}_{dr}/{\omega }_b\hfill \\ v_{qr}=R_r{i}_{qr}+s{\omega }_s{\psi }_{dr}+{\dot{\psi }}_{qr}/{\omega }_b\hfill \end{array}\right.$$

(1)

and the flux linkage equation is

$$\left\{\begin{array}{c}{\psi }_{ds}=-L_s{i}_{ds}+L_m{i}_{dr}\hfill \\ {\psi }_{qs}=-L_s{i}_{qs}+L_m{i}_{qr}\hfill \\ {\psi }_{dr}=L_r{i}_{dr}-L_m{i}_{ds}\hfill \\ {\psi }_{qr}=L_r{i}_{qr}-L_m{i}_{qs}\hfill \end{array}\right.$$

(2)

where $i_{ds}$ and $i_{dr}$ are the component of the stator current and the rotor current on the d axis; $i_{qs}$ and $i_{qr}$ are the component of the stator current and the rotor current on the q axis; $v_{ds}$ and $v_{qs}$ are the stator voltages in the d and q axes, respectively; $v_{dr}$ and $v_{qr}$ are the rotor voltages in the d and q axes, respectively; ${\phi }_{ds}$ and ${\phi }_{qs}$ are the stator flux linkage in the d and q axes, respectively; ${\phi }_{dr}$ and ${\phi }_{qr}$ are the rotor flux linkage in the d and q axes, respectively; $R_s$ and $R_r$ are the stator and rotor resistances, respectively; $L_s$, $L_r$, $L_m$ are the stator, rotor and magnetizing reactances, respectively; ${\omega }_b$, ${\omega }_s$, ${\omega }_r$ are the base, stator and rotor angular velocity, respectively, $s=({\omega }_s-{\omega }_r)/{\omega }_s$.

Selecting the generator current $x={\left[\begin{array}{cccc}{i}_{ds}& i_{qs}& i_{dr}& i_{qr}\end{array}\right]}^T$ as the state variable and voltage $u={\left[\begin{array}{cccc}{v}_{ds}& v_{qs}& v_{dr}& v_{qr}\end{array}\right]}^T$ as the input variable, and then combining the voltage in Equation (1) and the flux in Equation (2), the state space model can be expressed by [21]

$$\dot{x}\left(t\right)=A_{c}x\left(t\right)+B_{c}u\left(t\right)+E_{c}w\left(t\right)$$

(3)

where $w\left(t\right)$ is a disturbance signal, $E_c$ is a constant matrix and $A_c$ and $B_c$ are the system transfer matrix and control matrix, respectively,

$$A_c=\gamma \left[\begin{array}{cccc}-L_r{R}_s& \alpha {\omega }_s& -L_m{R}_r& -L_m{L}_r{\omega }_r\\ -\alpha {\omega }_s& -L_r{R}_s& L_m{L}_r{\omega }_r& -L_m{R}_r\\ -L_m{R}_s& L_m{L}_s{\omega }_r& -L_s{R}_r& -\beta {\omega }_s\\ -L_m{L}_s{\omega }_r& -L_m{R}_s& \beta {\omega }_s& -L_s{R}_r\end{array}\right]$$

$$B_c=\gamma \left[\begin{array}{cccc}-L_r& 0& L_m& 0\\ 0& -L_r& 0& L_m\\ -L_m& 0& L_s& 0\\ 0& -L_m& 0& L_s\end{array}\right]$$

where $\alpha =L_s{L}_r-s{L}_m^2$, $\beta =L_m^2-s{L}_s{L}_r$, $\gamma ={\omega }_b/(L_r{L}_s-L_m^2)$.

By discretizing the continuous system (3), one has

$$x(k+1)=Ax\left(k\right)+Bu\left(k\right)+Ew\left(k\right)$$

(4)

where $A=e^{A_{c}T}$, $B={\int }_0^T{e}^{A\tau }{B}_{c}d\tau$, $E={\int }_0^T{e}^{A\tau }{E}_{c}d\tau$, and T is the sampling period.

For the purposes of monitoring and maintenance, a variety of sensors are embedded in the wind turbine to measure different information of the generator, such as the motor speed, current, voltage, etc. Let $y_i\left(k\right)$ be the measurement output of the ith sensor, and define the observation equation as

$$y_i\left(k\right)=C_{i}x\left(k\right)+D_i{v}_i\left(k\right)(i=1,2,...,L)$$

(5)

where $C_i$ is the measurement matrix of the ith sensor, $v_i\left(k\right)$ is the measurement noise and $D_i$ is the constant matrix of the measurement noise of the ith sensor. Generally, the measurement data of each sensor are sent to the control center through the communication network. Thus, the engineer can remotely monitor the running status of the generator. A distributed fusion estimation algorithm based on the measurement information will be developed in the next section to jointly estimate the states and disturbance signals of the wind turbine.

3. Distributed Fusion Estimation Based on Intermediate Variable

In this section, an intermediate observer is developed to estimate the wind turbine state and disturbance simultaneously [22]. Firstly, an intermediate variable is introduced as follows:

$$\tau \left(k\right)=w(k-1)-\mu E^{T}x\left(k\right)$$

(6)

where $\mu >0$ is a predefined parameter that can affect the estimation performance of the intermediate observer. Combining (4) and (6), we have

$$\begin{array}{cc}\hfill \tau (k+1)=& (I-\mu E^{T}E)\Delta w\left(k\right)+(I-\mu E^{T}E)\tau \left(k\right)\hfill \\ \hfill & +(\mu E^T-{\mu }^2{E}^{T}E{E}^T-\mu E^{T}A)x\left(k\right)-\mu E^{T}Bu\left(k\right)\hfill \end{array}$$

(7)

where $\Delta w\left(k\right)=w\left(k\right)-w(k-1)$.

Define $z\left(k\right)\stackrel{\Delta }{=}{\left[\begin{array}{cc}{x}^T\left(k\right)& {\tau }^T\left(k\right)\end{array}\right]}^T$. Then, from (4)–(7), an augmented system can be written as

$$\left\{\begin{array}{c}z(k+1)=\overline{A}z\left(k\right)+\overline{B}u\left(k\right)+\overline{E}\Delta w\left(k\right)\hfill \\ y_i\left(k\right)={\overline{C}}_{i}z\left(k\right)+D_i{v}_i\left(k\right)\hfill \end{array}\right.$$

(8)

where $\overline{A}=\left[\begin{array}{cc}A+\mu E{E}^T& E\\ \mu E^T-{\mu }^2{E}^{T}E{E}^T-\mu E^{T}A& I-\mu E^{T}E\end{array}\right]$, $\overline{B}=\left[\begin{array}{c}B\\ -\mu E^{T}B\end{array}\right]$, $\overline{E}=\left[\begin{array}{c}E\\ I-\mu E^{T}E\end{array}\right]$, ${\overline{C}}_i=\left[\begin{array}{cc}{C}_i& 0\end{array}\right]$.

In this case, an intermediate observer for System (8) is proposed to be

$$\left\{\begin{array}{c}{\widehat{y}}_i(k+1)={\overline{C}}_i\overline{A}{\widehat{z}}_i\left(k\right)+{\overline{C}}_i\overline{B}u\left(k\right)\hfill \\ {\widehat{z}}_i(k+1)=\overline{A}{\widehat{z}}_i\left(k\right)+\overline{B}u\left(k\right)+L_i\left(k\right)(y_i(k+1)-{\widehat{y}}_i(k+1))\hfill \\ {\widehat{w}}_i\left(k\right)=M{\widehat{z}}_i(k+1)\hfill \end{array}\right.$$

(9)

where $M=\left[\begin{array}{cc}\mu E_{}^T& I\end{array}\right]$. ${\widehat{y}}_i(k+1)$, ${\widehat{z}}_i(k+1)$, ${\widehat{w}}_i\left(k\right)$ are the local estimates of $y_i(k+1)$, $z_i(k+1)$ and $w\left(k\right)$, respectively. $L_i\left(k\right)$ is the intermediate observer gain of the ith sensor.

Then, based on local state estimates (LSEs) ${\widehat{z}}_i(k+1)$, the distributed fusion estimate (DFE) of $z(k+1)$ is given by

$${\widehat{z}}_F(k+1)=\sum _{i=1}^L{\Omega }_i(k+1){\widehat{z}}_i(k+1)$$

(10)

where ${\sum }_{i=1}^L{\Omega }_i\left(k\right)=I$, ${\Omega }_i\left(k\right)$ is the distributed weighting fusion matrix, and the DFE of the disturbance is given by

$${\widehat{w}}_F\left(k\right)=M{\widehat{z}}_F(k+1)$$

(11)

Consequently, the goal of this section is to design the local intermediate observer gain and the distributed weighting matrix, such that the upper bound of the local estimation error and the fusion estimation error is minimal at each moment.

Theorem 1.

Each local intermediate observer gain $L_i\left(k\right)$ can be obtained by solving the following optimization problem:

$$\begin{array}{c}\underset{{\mathsf{\Theta }}_i\left(k\right)>0,{\alpha }_i\left(k\right),{\beta }_i\left(k\right),{\gamma }_i\left(k\right)>0}{min}\mathrm{Tr}\left\{{\beta }_i\left(k\right)\right\}+\mathrm{Tr}\left\{{\gamma }_i\left(k\right)\right\}\\ \mathrm{s}.\mathrm{t}.:\left\{\begin{array}{c}\left[\begin{array}{cccc}-I& A_{Li}\left(k\right)& E_{Li}\left(k\right)& F_{Li}\left(k\right)\\ \ast & -{\alpha }_i\left(k\right)& -{\nu }_i\left(k\right)& -{\xi }_i\left(k\right)\\ \ast & \ast & -{\beta }_i\left(k\right)& -o_i\left(k\right)\\ \ast & \ast & \ast & -{\gamma }_i\left(k\right)\end{array}\right]<0\hfill \\ {\alpha }_i\left(k\right)-{\mathsf{\Theta }}_i\left(k\right)I<0\hfill \\ {\mathsf{\Theta }}_i\left(k\right)<1\hfill \end{array}\right.\end{array}$$

(12)

where

$$\left\{\begin{array}{c}{A}_{Li}\left(k\right)\stackrel{\Delta }{=}\overline{A}-L_i\left(k\right){\overline{C}}_i\overline{A}\hfill \\ E_{Li}\left(k\right)\stackrel{\Delta }{=}\overline{E}-L_i\left(k\right)C_i\overline{E}\hfill \\ F_{Li}\left(k\right)\stackrel{\Delta }{=}-L_i\left(k\right)D_i\hfill \end{array}\right.$$

(13)

Moreover, the weighting fusion matrix $\Omega \left(k\right)$ can be obtained by solving the following optimization problem:

$$\begin{array}{c}\underset{\epsilon \left(k\right),\zeta \left(k\right),\eta \left(k\right)>0}{min}Tr\left\{\epsilon \left(k\right)\right\}+Tr\left\{\zeta \left(k\right)\right\}+Tr\left\{\eta \left(k\right)\right\}\\ \mathrm{s}.\mathrm{t}.:\left[\begin{array}{cccc}-I& \Omega \left(k\right)A_z\left(k\right)& \Omega \left(k\right)E_z\left(k\right)& \Omega \left(k\right)F_z\left(k\right)\\ \ast & -\epsilon \left(k\right)& -\theta \left(k\right)& -\iota \left(k\right)\\ \ast & \ast & -\zeta \left(k\right)& -\kappa \left(k\right)\\ \ast & \ast & \ast & -\eta \left(k\right)\end{array}\right]<0\end{array}$$

(14)

where

$$\left\{\begin{array}{c}{A}_z\left(k\right)\stackrel{\Delta }{=}\mathrm{diag}\{\overline{A}-L_1\left(k\right)C_1\overline{A},...,\overline{A}-L_L\left(k\right)C_L\overline{A}\}\hfill \\ E_z\left(k\right)\stackrel{\Delta }{=}\mathrm{col}\{\overline{E}-L_1\left(k\right)C_1\overline{E},\dots ,\overline{E}-L_L\left(k\right)C_L\overline{E}\}\hfill \\ F_z\left(k\right)\stackrel{\Delta }{=}\mathrm{diag}\{-L_1\left(k\right)D_1,...,-L_L\left(k\right)D_L)\}\hfill \\ \Omega \left(k\right)\stackrel{\Delta }{=}[{\Omega }_1^{}\left(k\right),...,{\Omega }_{L-1}^{}\left(k\right),I-{\sum }_{i=1}^{L-1}{\Omega }_i^{}\left(k\right)]\hfill \end{array}\right.$$

(15)

Proof of Theorem 1.

Define $e_{zi}\left(k\right)\stackrel{\Delta }{=}z\left(k\right)-{\widehat{z}}_i\left(k\right)$. Then, the local estimation error can be written as

$$e_{zi}(k+1)=A_{Li}\left(k\right)e_{zi}\left(k\right)+E_{Li}\left(k\right)\Delta w\left(k\right)+F_{Li}\left(k\right)v_i(k+1)$$

(16)

where $A_{Li}\left(k\right)$, $E_{Li}\left(k\right)$ and $F_{Li}\left(k\right)$ are defined in (13). Then, a performance index is introduced [23]

$$\begin{array}{cc}\hfill J_i(k+1)\stackrel{\Delta }{=}& e_{zi}^T(k+1)e_{zi}^{}(k+1)-e_{zi}^T\left(k\right){\alpha }_i\left(k\right)e_{zi}\left(k\right)-2e_{zi}^T\left(k\right){\nu }_i\left(k\right)\Delta w\left(k\right)\hfill \\ & -2e_{zi}^T\left(k\right){\xi }_i\left(k\right)v_i(k+1)-\Delta w^T\left(k\right){\beta }_i\left(k\right)\Delta w\left(k\right)-2\Delta w^T\left(k\right)o_i\left(k\right)v_i(k+1)\hfill \\ & -v_i^T(k+1){\gamma }_i\left(k\right)v_i(k+1)\hfill \end{array}$$

(17)

According to (17), the inequality can be expressed by

$$J_i(k+1)={\left[\begin{array}{c}{e}_{zi}^{}\left(k\right)\\ \Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]}^T\underset{\Xi \left(k\right)}{\underbrace{\left[\begin{array}{ccc}{\Xi }_1\left(k\right)& {\Xi }_2\left(k\right)& {\Xi }_3\left(k\right)\\ \ast & {\Xi }_4\left(k\right)& {\Xi }_5\left(k\right)\\ \ast & \ast & {\Xi }_6\left(k\right)\end{array}\right]}}\left[\begin{array}{c}{e}_{zi}^{}\left(k\right)\\ \Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]$$

(18)

where ${\Xi }_1\left(k\right)=A_{Li}^T\left(k\right)A_z^{}\left(k\right)-{\alpha }_i\left(k\right)$, ${\Xi }_2\left(k\right)=A_{Li}^T\left(k\right)E_{Li}\left(k\right)-{\nu }_i\left(k\right)$, ${\Xi }_3\left(k\right)=A_{Li}^T\left(k\right)F_{Li}\left(k\right)-{\xi }_i\left(k\right)$, ${\Xi }_4\left(k\right)=E_{Li}^T\left(k\right)E_{Li}\left(k\right)-{\beta }_i\left(k\right)$, ${\Xi }_5\left(k\right)=E_{Li}^T\left(k\right)F_{Li}\left(k\right)-o_i\left(k\right)$ and ${\Xi }_6\left(k\right)=F_{Li}^T\left(k\right)F_{Li}\left(k\right)-{\gamma }_i\left(k\right)$. It can be seen from the Schur complement lemma [24] that $\Xi \left(k\right)<0$ is equivalent to the first inequality in (12). Therefore, one has

$$\begin{array}{cc}\hfill e_{z_i}^T(k+1)e_{z_i}(k+1)<& e_{z_i}^T\left(k\right){\alpha }_i\left(k\right)e_{z_i}\left(k\right)\hfill \\ & +{\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]}_{}^T\left[\begin{array}{cc}{\beta }_i\left(k\right)& o_i\left(k\right)\\ \ast & {\gamma }_i\left(k\right)\end{array}\right]\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]\hfill \end{array}$$

(19)

In addition, the second inequality ${\alpha }_i\left(k\right)-{\mathsf{\Theta }}_i\left(k\right)I<0$ in (12) holds, and one has ${\lambda }_{max}\left({\alpha }_i\left(k\right)\right)<{\mathsf{\Theta }}_i\left(k\right)$. Then, (19) can be written as

$$\begin{array}{cc}\hfill e_{z_i}^T(k+1)e_{z_i}(k+1)<& {\mathsf{\Theta }}_i\left(k\right)e_{z_i}^T\left(k\right)e_{z_i}\left(k\right)\hfill \\ & +{\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]}_{}^T\left[\begin{array}{cc}{\beta }_i\left(k\right)& o_i\left(k\right)\\ \ast & {\gamma }_i\left(k\right)\end{array}\right]\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]\hfill \end{array}$$

(20)

Hence, it is derived from (20) that [23]

$$\begin{array}{cc}\hfill e_{z_i}^T(k+1)& e_{z_i}(k+1)<\left(\prod _{\vartheta =0}^k{\mathsf{\Theta }}_i(k-\vartheta )\right)e_{z_i}^T\left(0\right)e_{z_i}\left(0\right)+\sum _{\vartheta =0}^k\left\{\left(\prod _{\rho =0}^{\vartheta }{\mathsf{\Theta }}_i(k-\rho )\right)\right.\hfill \\ & \times \left.{\left[\begin{array}{c}\Delta w(k-\vartheta )\\ v_i(k+1-\vartheta )\end{array}\right]}_{}^T\left[\begin{array}{cc}{\beta }_i(k-\vartheta )& o_i(k-\vartheta )\\ \ast & {\gamma }_i(k-\vartheta )\end{array}\right]\left[\begin{array}{c}\Delta w(k-\vartheta )\\ v_i(k+1-\vartheta )\end{array}\right]\right\}\hfill \end{array}$$

(21)

Since the third inequality ${\mathsf{\Theta }}_i\left(k\right)<1$ in (12) holds, it is easy to see that

$$\underset{k\to \infty }{\overset{}{lim}}\prod _{\vartheta =0}^k{\mathsf{\Theta }}_i(k-\vartheta )=0$$

(22)

$$\underset{\vartheta \to \infty }{\overset{}{lim}}\prod _{\rho =0}^{\vartheta }{\mathsf{\Theta }}_i(k-\rho )=0$$

(23)

Then, it can be concluded from (21)–(23) that $\underset{k\to \infty }{\overset{}{lim}}{e}_{z_i}^T(k+1)e_{z_i}(k+1)$ is bounded. Meanwhile, it can easily be verified that ${\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]}_{}^T\left[\begin{array}{cc}{\beta }_i\left(k\right)& o_i\left(k\right)\\ \ast & {\gamma }_i\left(k\right)\end{array}\right]\left[\begin{array}{c}\Delta w\left(k\right)\\ v_i(k+1)\end{array}\right]<{\lambda }_{max}(\left[\begin{array}{c}\Delta w\left(k\right)\\ v(k+1)\end{array}\right]{\left[\begin{array}{c}\Delta w\left(k\right)\\ v(k+1)\end{array}\right]}_{}^T)\left(\mathrm{Tr}\left\{{\beta }_i\left(k\right)\right\}+\mathrm{Tr}\left\{{\gamma }_i\left(k\right)\right\}\right)$. Hence, the following inequality holds

$$\begin{array}{cc}\hfill e_{z_i}^T(k+1)e_{z_i}(k+1)<& {\alpha }_i\left(k\right)e_{z_i}^T\left(k\right)e_{z_i}\left(k\right)+{\lambda }_{max}(\left[\begin{array}{c}\Delta w\left(k\right)\\ v(k+1)\end{array}\right]{\left[\begin{array}{c}\Delta w\left(k\right)\\ v(k+1)\end{array}\right]}_{}^T)\hfill \\ & \times \left(\mathrm{Tr}\left\{{\beta }_i\left(k\right)\right\}+\mathrm{Tr}\left\{{\gamma }_i\left(k\right)\right\}\right)\hfill \end{array}$$

(24)

Under this case, the right term of inequality (24) can be viewed as an upper bound of $e_{zi}^T(k+1)e_{zi}^{}(k+1)$, and “min $\mathrm{Tr}\{{\beta }_i\left(k\right)\}+\mathrm{Tr}\{{\gamma }_i\left(k\right)\}$” can be treated as the optimization objective to solve the local intermediate observer gain $L_i\left(k\right)$.

Now, the distributed weighting matrix $\Omega \left(k\right)$ is determined by solving the convex optimization problem (14). Define $e_F\left(k\right)\stackrel{\Delta }{=}z\left(k\right)-\widehat{z}\left(k\right)$. The fusion estimation error is written as

$$e_F\left(k\right)=\sum _{i=1}^L{\Omega }_i^{}\left(k\right)e_{zi}\left(k\right)$$

(25)

To calculate the optimal weighting matrices, substituting (16) into fusion estimation error (25), the fusion estimation error system can be written as

$$\left\{\begin{array}{c}{e}_Z(k+1)=A_z\left(k\right)e_Z\left(k\right)+E_z\left(k\right)\Delta w\left(k\right)+F_z\left(k\right)V(k+1)\hfill \\ e_F(k+1)=\Omega \left(k\right)e_Z(k+1)\hfill \end{array}\right.$$

(26)

where $e_Z\left(k\right)=\mathrm{col}\{e_{z1}\left(k\right),...,e_{zL}\left(k\right)\}$, $V\left(k\right)=\mathrm{col}\{v_1\left(k\right),...,v_L\left(k\right)\}$, while $A_z\left(k\right)$, $E_z\left(k\right)$ and $F_z\left(k\right)$ are defined in (15). Then, introduce the matrices $\epsilon \left(k\right)>0,\zeta \left(k\right)>0,\eta \left(k\right)>0$ such that

$$e_F^T(k+1)e_F(k+1)<{\left[\begin{array}{c}{e}_Z^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]}^T\left[\begin{array}{ccc}\epsilon \left(k\right)& \theta \left(k\right)& \iota \left(k\right)\\ & \zeta \left(k\right)& \kappa \left(k\right)\\ & \ast & \eta \left(k\right)\end{array}\right]\left[\begin{array}{c}{e}_Z^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]$$

(27)

In this case, the right term of inequality (27) can be regarded as the upper bound of $e_F^T\left(k\right)e_F\left(k\right)$, and the following inequality should be satisfied

$${\left[\begin{array}{c}{e}_F^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]}^T\underset{\mathrm{O}\left(k\right)}{\underbrace{\left[\begin{array}{ccc}{\mathrm{O}}_1\left(k\right)& {\mathrm{O}}_2\left(k\right)& {\mathrm{O}}_3\left(k\right)\\ \ast & {\mathrm{O}}_4\left(k\right)& {\mathrm{O}}_5\left(k\right)\\ \ast & \ast & {\mathrm{O}}_6\left(k\right)\end{array}\right]}}\left[\begin{array}{c}{e}_F^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]<0$$

(28)

where ${\mathrm{O}}_1\left(k\right)=A_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)A_z^{}\left(k\right)-\epsilon \left(k\right)$, ${\mathrm{O}}_2\left(k\right)=A_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)E_z\left(k\right)-\theta \left(k\right)$, ${\mathrm{O}}_3\left(k\right)=A_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)F_z\left(k\right)-\iota \left(k\right)$, ${\mathrm{O}}_4\left(k\right)=E_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)E_z\left(k\right)-\zeta \left(k\right)$, ${\mathrm{O}}_5\left(k\right)=E_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)F_z\left(k\right)-\kappa \left(k\right)$ and ${\mathrm{O}}_6\left(k\right)=F_z^T\left(k\right){\Omega }_{}^T\left(k\right)\Omega \left(k\right)F_z\left(k\right)-\eta \left(k\right)$.

According to the Schur complement lemma [24], $\mathrm{O}\left(k\right)<0$ is equivalent to the inequality in (13). Moreover, $\mathrm{Tr}\{\left[\begin{array}{ccc}\epsilon \left(k\right)& \theta \left(k\right)& \iota \left(k\right)\\ \ast & \zeta \left(k\right)& \kappa \left(k\right)\\ \ast & \ast & \eta \left(k\right)\end{array}\right]\}$ is equivalent to $\mathrm{Tr}\{\epsilon \left(k\right)\}+\mathrm{Tr}\{\zeta (k\left)\right\}+\mathrm{Tr}\{\eta \left(k\right)\}$. Thus,

$$\begin{array}{cc}\hfill e_F^T(k+1)e_F(k+1)<& {\lambda }_{max}(\left[\begin{array}{c}{e}_Z^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]{\left[\begin{array}{c}{e}_Z^{}\left(k\right)\\ \Delta w\left(k\right)\\ V(k+1)\end{array}\right]}^T)(\mathrm{Tr}\left\{\epsilon \left(k\right)\right\}\hfill \\ & +\mathrm{Tr}\left\{\zeta \right(k\left)\right\}+\mathrm{Tr}\left\{\eta \right(k\left)\right\})\hfill \end{array}$$

(29)

Therefore, “min $\mathrm{Tr}\{\epsilon \left(k\right)\}+\mathrm{Tr}\{\zeta (k\left)\right\}+\mathrm{Tr}\{\eta \left(k\right)\}$” can be regarded as the optimization objective for determining the weighting fusion matrices of the state. The proof is completed. □

Remark 1.

The convex optimization problems in (12) and (14) are constructed by linear matrix inequalities (LMIs), which can be solved by the “mincx” function in the MATLAB LMI Toolbox. On the other hand, the disturbance signal may lead to system performance degradation, and even system instability. However, the intermediate variable fusion algorithm proposed in this paper can be used to reconstruct the disturbance signals, and then the compensation controller can be designed as follows:

$$u_1\left(k\right)=-B^{†}AE{\widehat{w}}_F(k-1)$$

(30)

where $B^{†}$ is the generalized inverse matrix of B. Then, the state space model of the System (4) after compensation can be described as follows:

$$x(k+1)=Ax\left(k\right)+B(u\left(k\right)+u_1\left(k\right))+Ew\left(k\right)$$

(31)

Since the intermediate observer can estimate disturbance signals in real time, the controller is designed by using the estimated disturbance signal to compensate for the system deviation caused by the disturbance. Meanwhile, it reduces the influence of the disturbance signals during the operation of the wind turbine. In particular, when the disturbance signal continues to affect the operation of the generator, it will increase the fatigue of the generator, and can even cause irreversible damage to the internal components. Thus, the compensation strategy introduced in this paper has great significance for the safe operation of the wind turbine.

To summarize, the implementation steps of the fusion estimation algorithm and compensation strategy are given in Algorithm 1.

Algorithm 1. Intermediate-variable-based distributed fusion estimation.

1: Given $\mu$, initialize state vector $x_0$ for each time step: $k=1,2...,end$; 2: Solve the convex optimization problem through the LMI toolbox to obtain the local intermediate observer gain matrix $L_i\left(k\right)$ $\begin{array}{c}\underset{{\mathsf{\Theta }}_i\left(k\right),{\alpha }_i\left(k\right),{\beta }_i\left(k\right),{\gamma }_i\left(k\right)>0}{min}\mathrm{Tr}\left\{{\beta }_i\left(k\right)\right\}+\mathrm{Tr}\left\{{\gamma }_i\left(k\right)\right\}\\ \mathrm{s}.\mathrm{t}.:\left\{\begin{array}{c}\left[\begin{array}{cccc}-I& A_{Li}\left(k\right)& E_{Li}\left(k\right)& F_{Li}\left(k\right)\\ \ast & -{\alpha }_i\left(k\right)& -{\nu }_i\left(k\right)& -{\xi }_i\left(k\right)\\ \ast & \ast & -{\beta }_i\left(k\right)& -o_i\left(k\right)\\ \ast & \ast & \ast & -{\gamma }_i\left(k\right)\end{array}\right]<0\hfill \\ {\alpha }_i\left(k\right)-{\mathsf{\Theta }}_i\left(k\right)I<0\hfill \\ {\mathsf{\Theta }}_i\left(k\right)<1\hfill \end{array}\right.\end{array}$ 3: Calculate the local state and disturbance estimate ${\widehat{z}}_i(k+1)=\overline{A}{\widehat{z}}_i\left(k\right)+\overline{B}u\left(k\right)+L_i\left(k\right)(y_i(k+1)-{\widehat{y}}_i(k+1))$ ${\widehat{w}}_i\left(k\right)=M{\widehat{z}}_i(k+1)$ 4: Obtain the distributed weighted fusion matrix ${\Omega }_i(k+1)$ by solving convex optimization problem $\begin{array}{c}\underset{\epsilon (k+1),\zeta (k+1),\eta (k+1)>0}{min}Tr\left\{\epsilon (k+1)\right\}+Tr\left\{\zeta (k+1)\right\}+Tr\left\{\eta (k+1)\right\}\\ \mathrm{s}.\mathrm{t}.:\left[\begin{array}{cccc}-I& \Omega (k+1)A_z(k+1)& \Omega (k+1)E_z(k+1)& \Omega (k+1)F_z(k+1)\\ & -\epsilon (k+1)& -\theta (k+1)& -\iota (k+1)\\ & \ast & -\zeta (k+1)& -\kappa (k+1)\\ & \ast & \ast & -\eta (k+1)\end{array}\right]<0\end{array}$ 5: Calculate the distribute fusion estimate of state and disturbance ${\widehat{z}}_F(k+1)=\sum _{i=1}^L{\Omega }_i(k+1){\widehat{z}}_i(k+1)$ ${\widehat{w}}_F\left(k\right)=M{\widehat{z}}_F(k+1)$ 6: Calculate the compensation control input $u_1(k+1)=-B^{†}AE{\widehat{w}}_F\left(k\right)$

4. Simulation Examples

In this section, the estimation performance of the proposed method was verified by a numerical simulation of a wind turbine. The parameters of the generator [21] are shown in Table

Table 1. The parameters of wind generator.

Parameter	Value (p.u.)
Rotor frequency	1.29
Stator resistance	0.00488
Rotor resistance	0.00549
Stator reactance	0.09241
Rotor reactance	0.09955
Excitation reactance	3.9527

. Three sensors are used to measure the state of the generator, and the measurement matrices are $C_1=[0,0,0,1;0,0,1,0;1,0,0,1]$, $C_2=[0,0,0,1;0,0,1,0;1,0,1,0]$, $C_3=[1,0,0,0;0,0,1,0;0,0,0,1]$, respectively. The constant matrix is $E=[0,0,1,1]$, $D_1=[0,1;1,0;0,1]$, $D_2=[0,1;1,0;1,1]$, $D_3=[1,0;0,1;1,1]$. The disturbance signal and measurement noises are given by

$$\left\{\begin{array}{c}w\left(k\right)=0.2{\sigma }_1\left(k\right)-0.2{\sigma }_2\left(k\right)\hfill \\ v_1\left(k\right)=[0.12{\sigma }_3\left(k\right)-0.1{\sigma }_4\left(k\right);0.11{\sigma }_5\left(k\right)-0.12{\sigma }_6\left(k\right)]\hfill \\ v_2\left(k\right)=[0.18{\sigma }_7\left(k\right)-0.2{\sigma }_8\left(k\right);0.19{\sigma }_9\left(k\right)-0.17{\sigma }_{10}\left(k\right)]\hfill \\ v_3\left(k\right)=[0.16{\sigma }_{11}\left(k\right)-0.14{\sigma }_{12}\left(k\right);0.15{\sigma }_{13}\left(k\right)-0.16{\sigma }_{14}\left(k\right)]\hfill \end{array}\right.$$

(32)

where ${\sigma }_l\left(k\right)\in [0,1](l=1,2,3,4,5,6,7,8,9,10,11,12,13,14)$ are random variables that can be generated by the function “rand” of MATLAB. The parameter $\mu$ of the intermediate observer is 1.

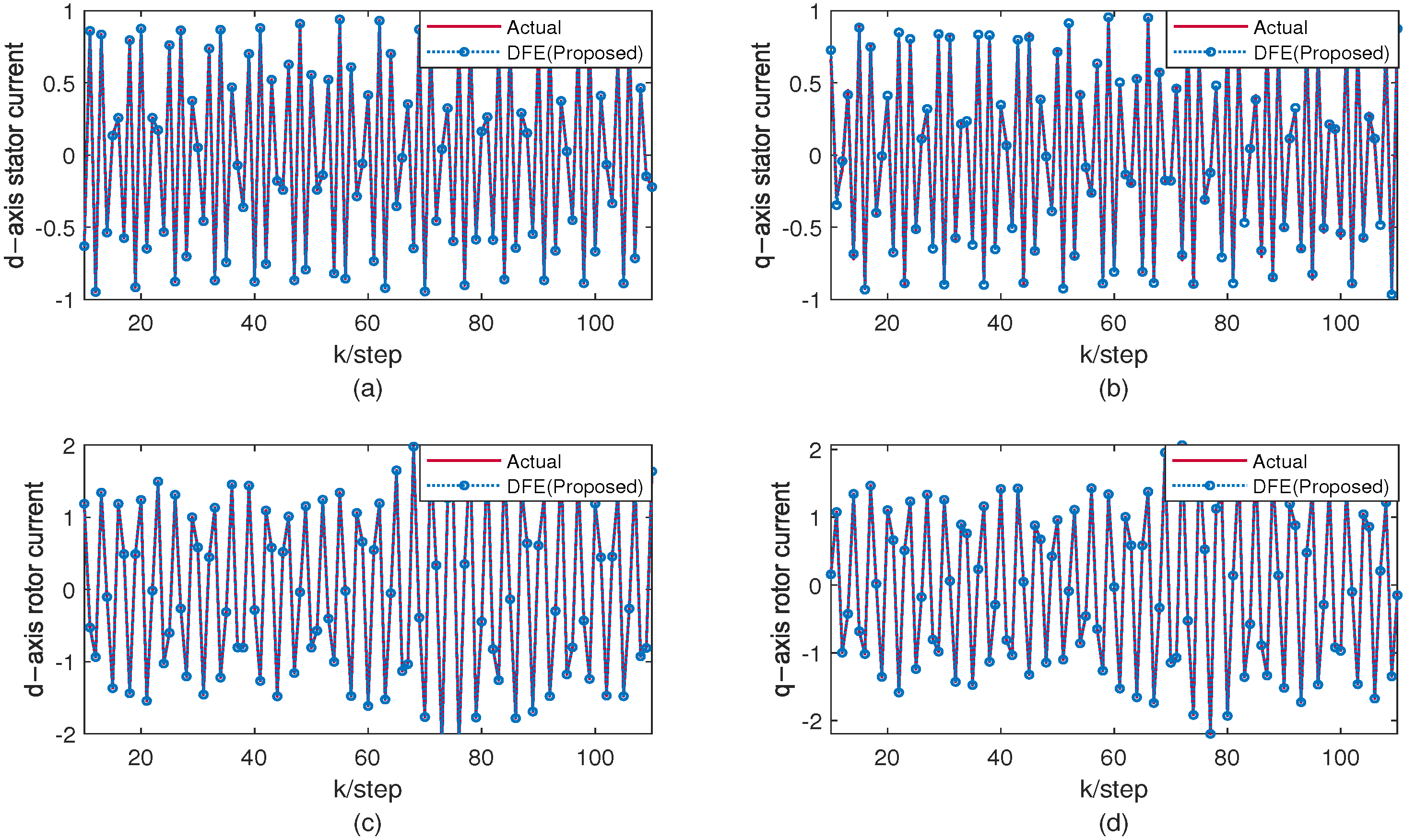
By using Algorithm 1, the distributed fusion estimation trajectory and the system actual state trajectory are plotted in Figure 2. It can be seen from these figures that the fusion estimators could follow the trajectory of the system state in each dimension. Notice that the matrix $E=[0,0,1,1]$ represents the fact that the rotor current is interfered by the disturbance signals, and the current $i_{dr}\left(k\right)$ and $i_{qr}\left(k\right)$ will exceed the per unit (P.U.), as shown in Figure 2c,d, which cause the generator to be in a dangerous working state. Since the disturbance signal have a great impact on the stable operation of the system, the accurate estimation of the disturbance signal can provide effective information for the further control of the generator. In particular, the fusion estimator designed in this paper can jointly estimate the system state and disturbance signal, and the disturbance fusion estimation also has a higher accuracy, as shown in Figure 3.

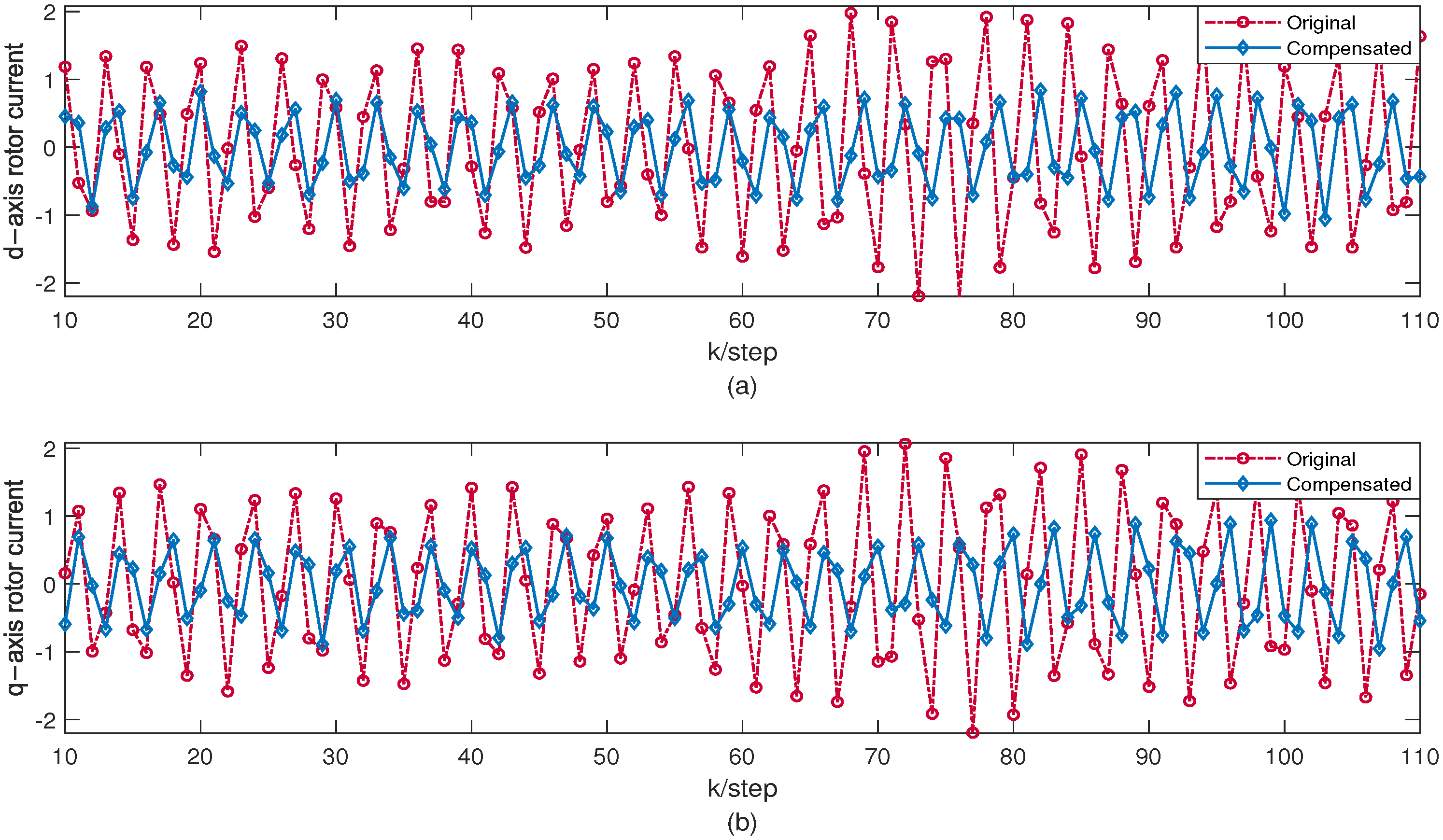
In general, the larger working current of the generator will cause the coil to heat up, while the high temperature will damage the insulation layer of the coil, and eventually burn the generator. From Figure 2c,d, the disturbance signals cause the current to increase, which will cause serious harm to the generator operation. However, the proposed intermediate-variable-based fusion estimation method can effectively estimate the disturbance signal of the system. Based on the fusion estimation of the disturbance, a compensation control strategy is designed to compensate the system performance wastage caused by the disturbance, and the compensated state trajectory is shown in Figure 4. Obviously, the compensated current is smaller than the original, and it is stable in the safe operation range. This result indicates that the designed compensation controller can effectively ensure the safe operation of the generator under disturbance.

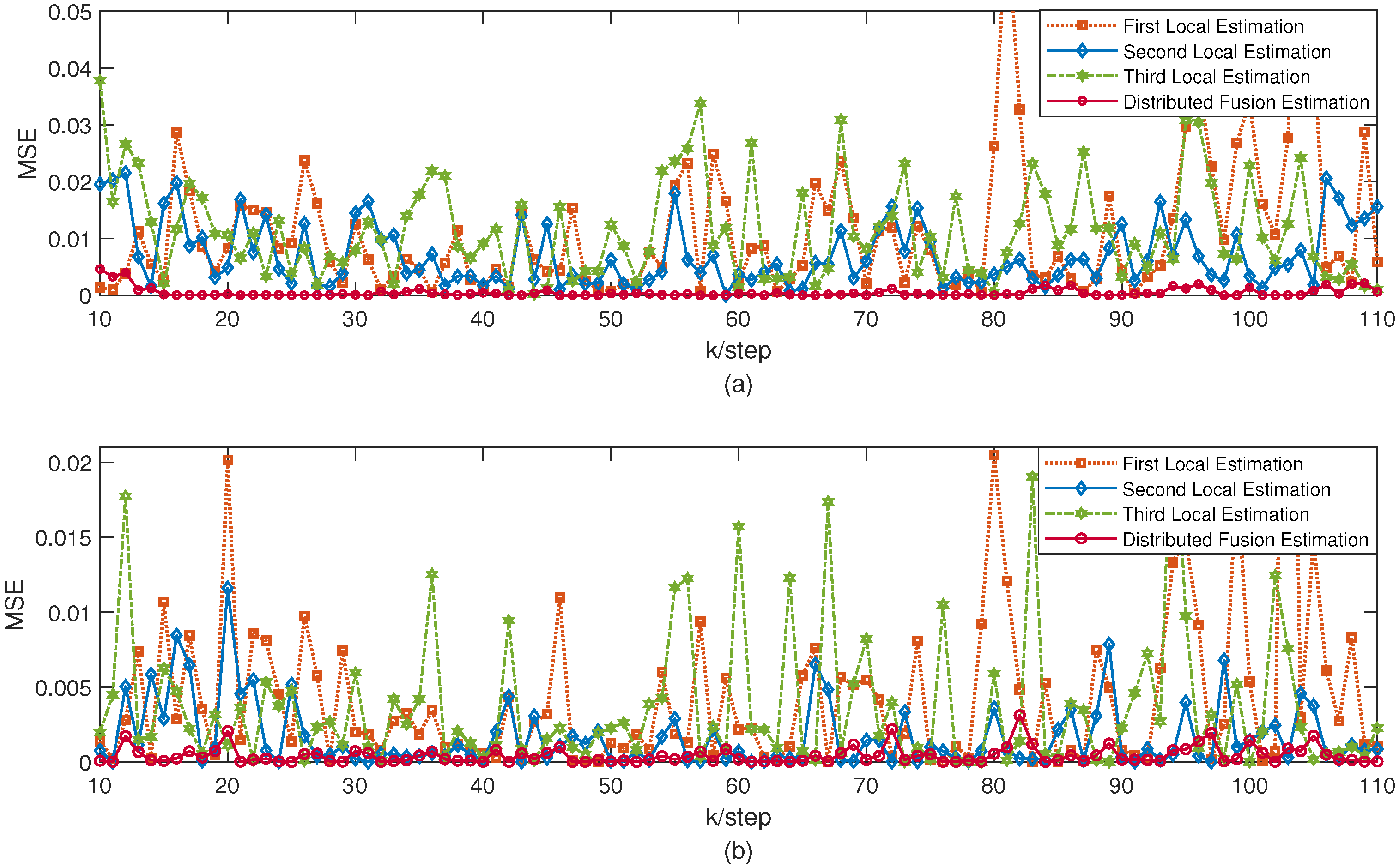
In order to prove the ascendancy of the proposed fusion estimation method, the mean square error (MSE) of the local state estimates (LSEs) and distributed fusion estimate (DFE) calculated by the Monte Carlo method, with an average of 100 runs, is shown in Figure 5. It can be seen that the error trajectory of each local estimator is different. However, the sensor fusion algorithm can use the redundant information and complementary information between multiple sensors to optimize the combination, and then obtain the state and disturbance fusion estimation of the system. Moreover, the fusion estimation accuracy of the state and disturbance is better than the local estimator, verifying that the intermediate-variable-based distributed fusion estimation method is better than the estimation method based on a single sensor. Therefore, this algorithm can more accurately monitor the current state and disturbance of the wind turbine.

Furthermore, to further demonstrate the superiority of the proposed algorithm, the method is compared with the classic Kalman fusion estimation method [19]. The state estimation performance of the two fusion estimation methods is shown in Figure 6. The estimation accuracy of the fusion estimator designed in this paper was found to be better than the Kalman fusion estimator. This is mainly because the Kalman filter is mostly used to process Gaussian white noise with known covariance. However, the process noises and the measurement noises are usually bounded in practice [18], and the statistical characteristics of the noise are difficult to accurately obtain. The fusion estimation method based on the intermediate variable proposed in this paper is independent of the noise statistical characteristics, which is more suitable for actual wind power systems.

5. Discussion

The proposed work mainly investigated the application of distributed fusion estimation methods based on intermediate variables in wind turbine systems. The results shown are from simulations carried out in a MATLAB environment with a mathematical model of the DFIG system. When the system is influenced by disturbance signals during operation, and when the measurements of the sensors are affected by the noises, the fusion estimator designed in this paper can still reconstruct the state information and disturbance signals of the system.

In order to verify the performance of the designed fusion estimator, comparative experiments were given in the simulation section. The performance comparison between the local estimators and the distributed fusion estimator was shown in Figure 5; it can be seen that the MSE of the fusion estimation is smaller than that of the local estimators. Compared with Kalman fusion filtering—the estimation performances are given in Figure 6—a superiority of the proposed method was shown. Generally, the Kalman filter [25] is a highly efficient recursive filter that can generate an estimate of the system state based on the joint distribution of measurement information at each time. However, the Kalman filter needs the known noise covariance information to calculate the gain of the local estimator [3,15], and the fusion weighting matrix also needs to calculate the cross covariance between every pair of sensors [16,19], whereas the relevant statistical information about the disturbance signals or noises of the actual wind turbine system cannot be easily obtained because of the various internal or external reasons. Therefore, when the disturbance signal or noise covariance information of the system is inaccurate, the estimation performance of the Kalamn filter is not ideal [23]. The estimator designed in this paper is based on the idea of bounded recursion optimization, which does not require knowing the statistical information of the disturbance signals and noises. Then, the gains and weighting matrix of the estimator were solved by constructing convex optimization problems, and the state and disturbance can be estimated at the same time through intermediate variables.

In addition, many complex wind turbine systems are modeled by nonlinear dynamics. However, the proposed algorithm in this paper is limited to linear dynamics, and applications in nonlinear systems need to be further explored. It is of great practical significance to study the cooperative design of the disturbance signal estimator and the real-time compensation strategy in a nonlinear wind energy system to reduce the system performance loss caused by disturbance signals. Moreover, since the wide application of the internet of things technology in logistics, industry, home furnishing and other fields, it has received widespread attention. Soon, wind turbines will be connected to the internet of things, and engineers will be able to monitor and control the operation of the wind turbines anytime and anywhere through their smart phone. However, the introduction of the communication network will cause new security risks to the system. For example, hackers invade the system through the communication network and launch network attacks. Therefore, investigating how to design detection algorithms for false data injection attack signals and corresponding defense strategies is one of the important directions of future research.

6. Conclusions

In this paper, a distributed fusion estimation method based on the intermediate variable was designed to estimate the state and unknown disturbance signals of the doubly fed induction generator system. By constructing the connection between the state and the disturbance signals through the intermediate variable, the intermediate variable was treated as a part of the state variable of the augmented system, and then the local estimators and a distributed fusion criterion based on the intermediate observer were developed. The proposed estimated method can obtain the estimator gains and distributed weighted fusion matrices by solving the convex optimization problem based on linear matrix inequality. Meanwhile, the estimated disturbance signal was used to design a compensation controller that can reduce the influence of disturbance and keep the generator operation stable. Finally, a wind turbine system was used to verify the proposed approach, and the simulation results demonstrated the effectiveness of the proposed fusion estimation algorithm. By comparing with the traditional Kalman fusion estimator, the superiority of the proposed method was also shown.