Numerical and Experimental Study of a Flexible Trailing Edge Driving by Pneumatic Muscle Actuators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flexible Trailing Edge
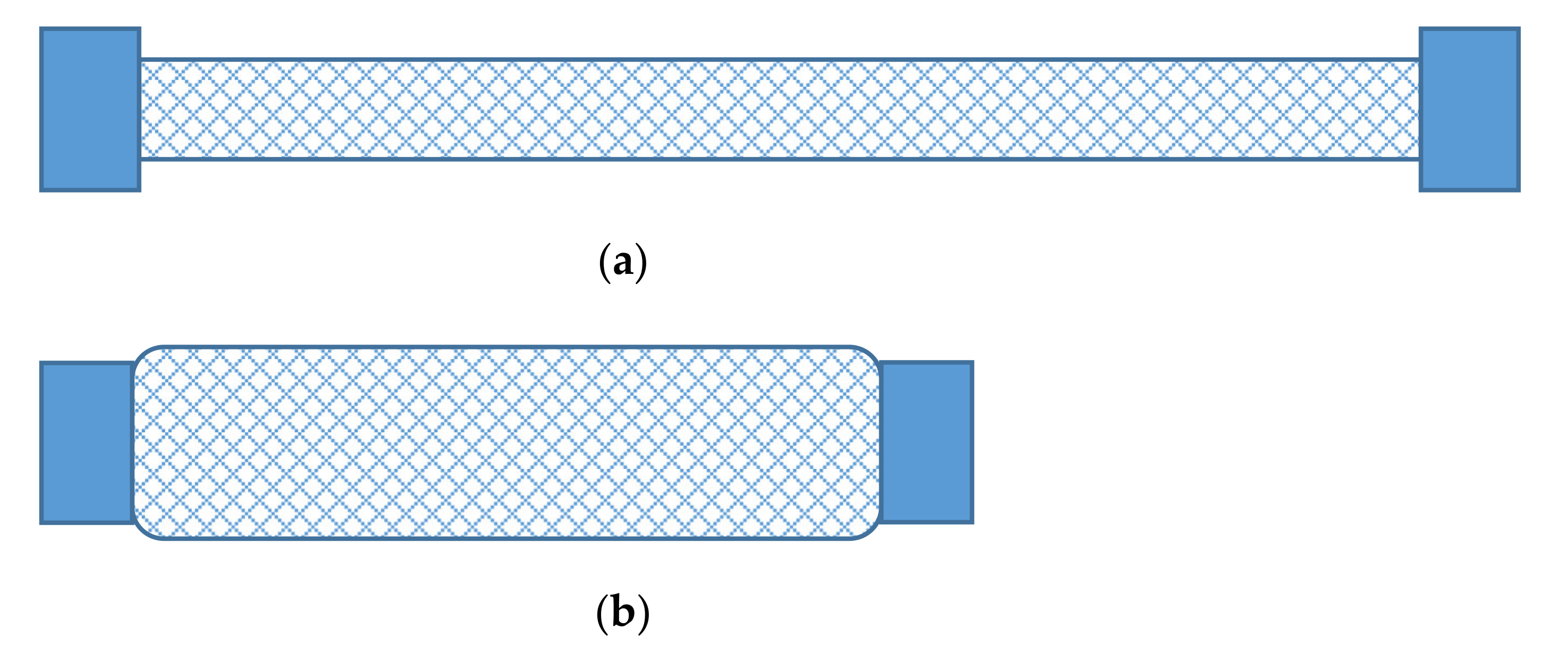
2.1.1. Actuator Model
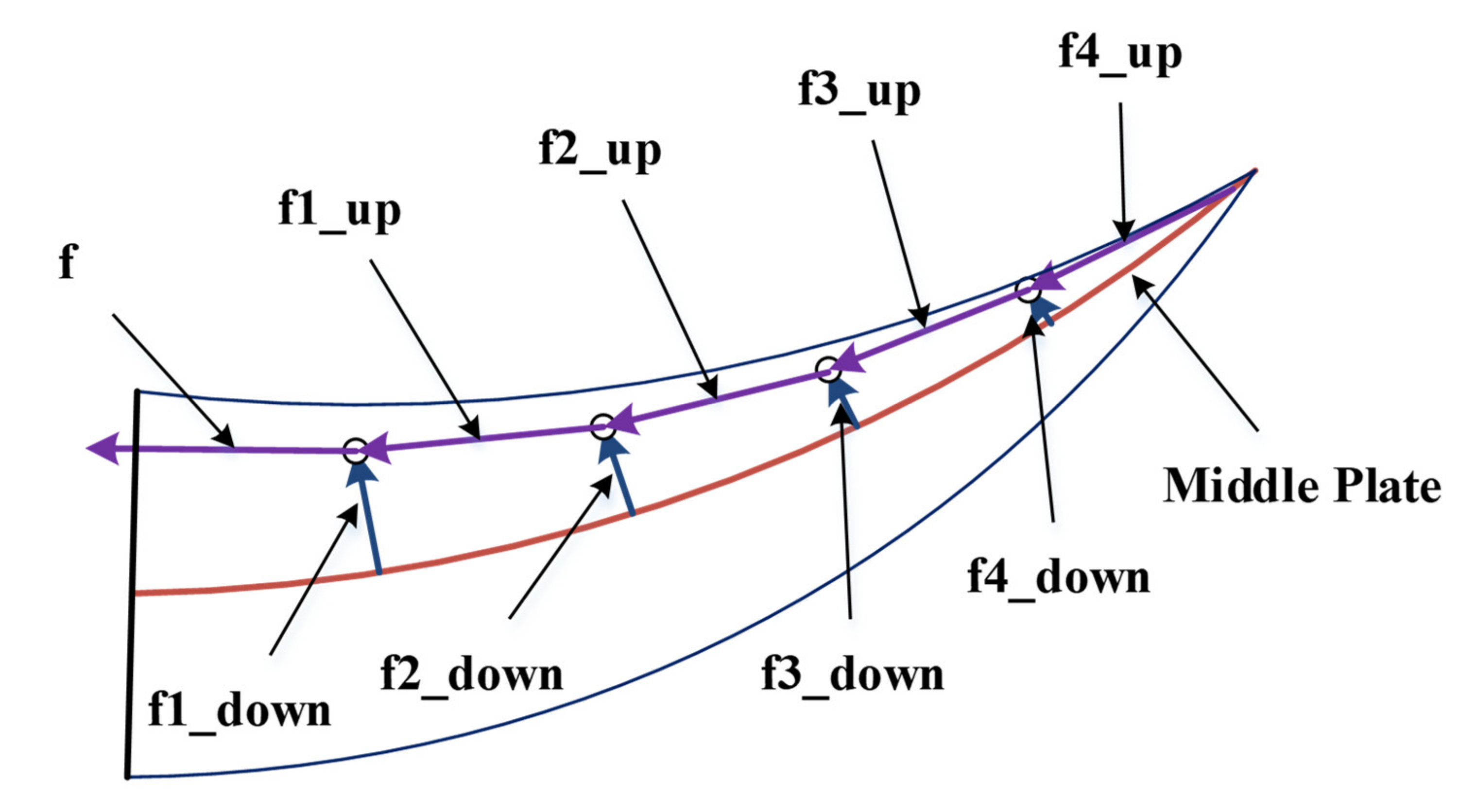
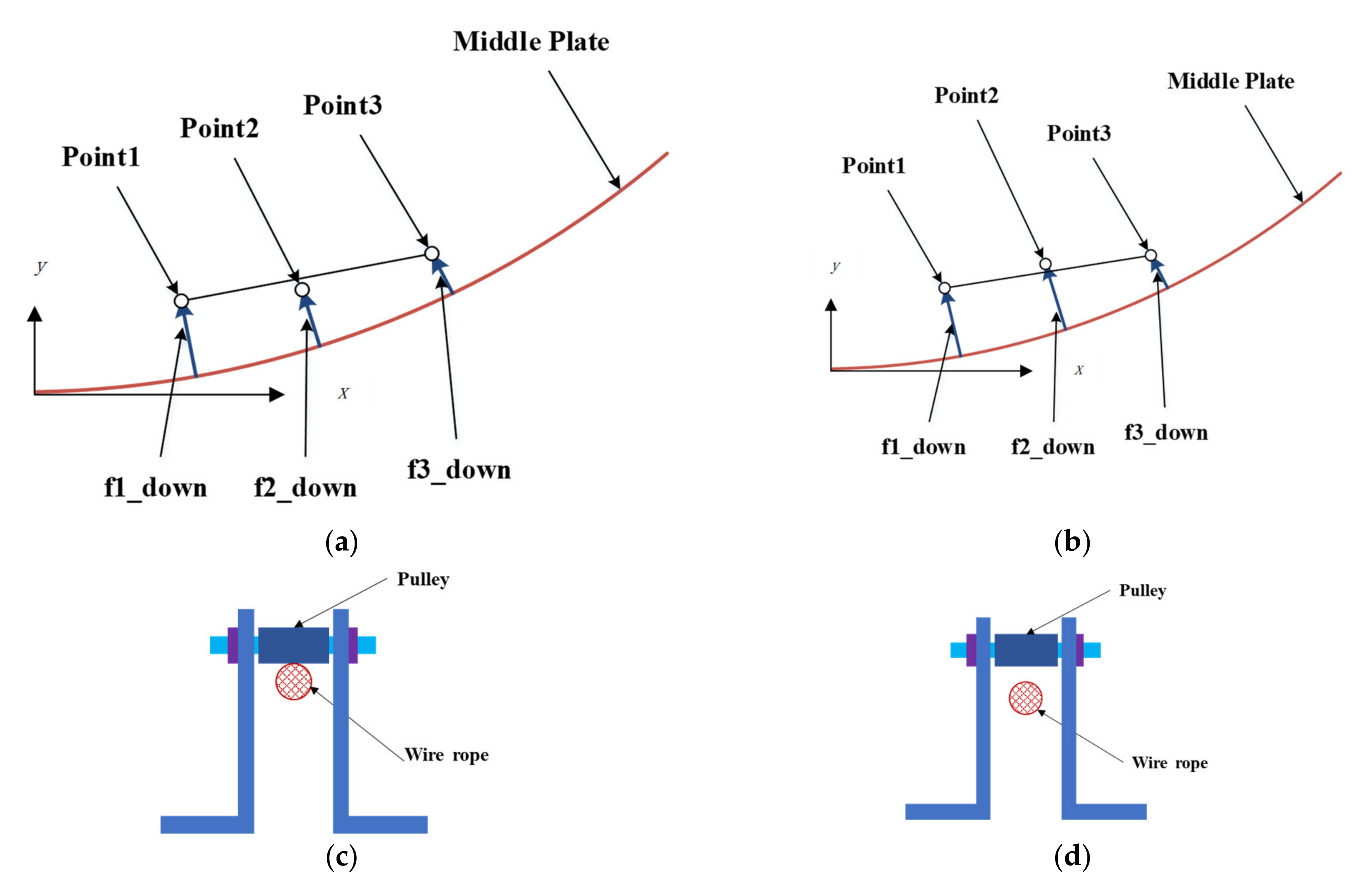
2.1.2. Wire-Pulley Transmission Model
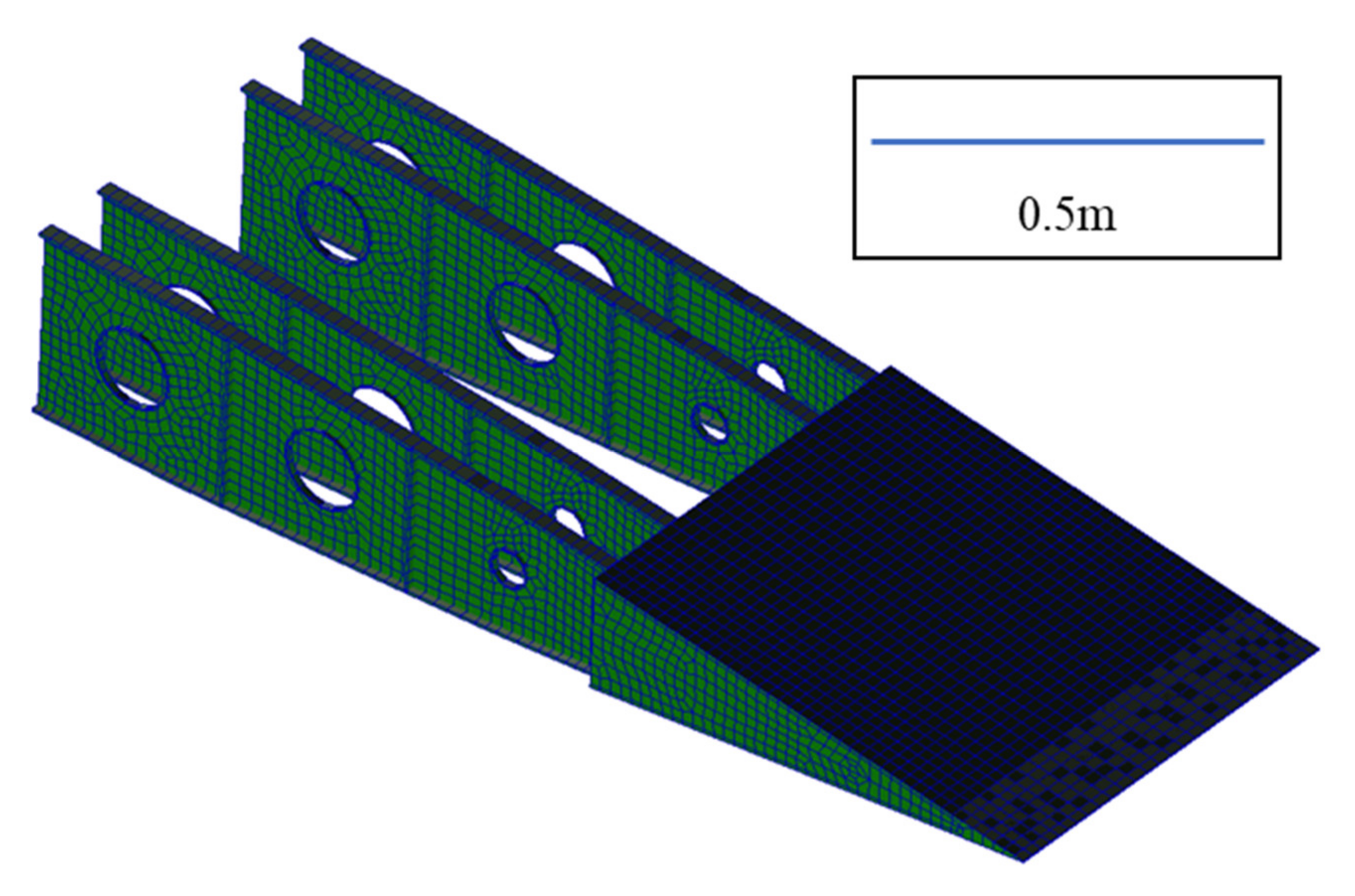
2.1.3. Flexible Trailing Edge Model
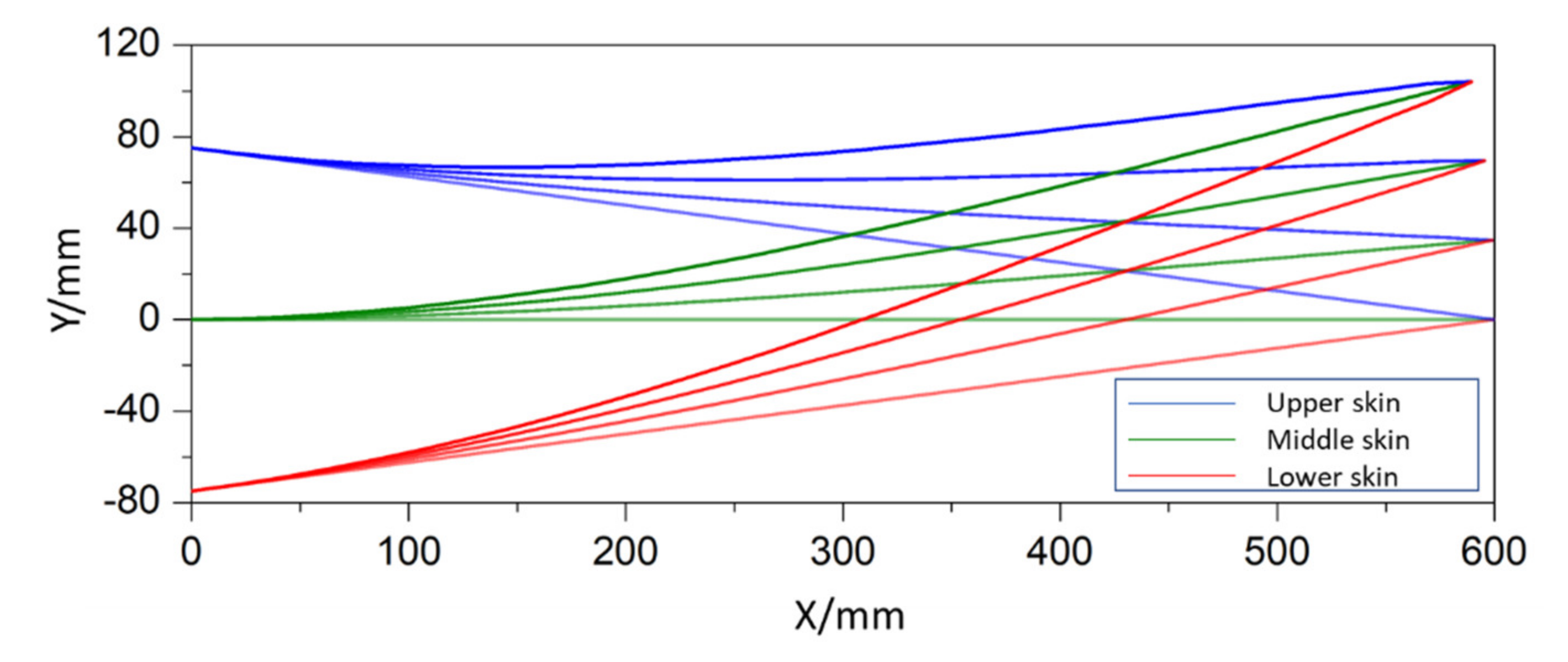
2.1.4. Physical Flexible Trailing Edge
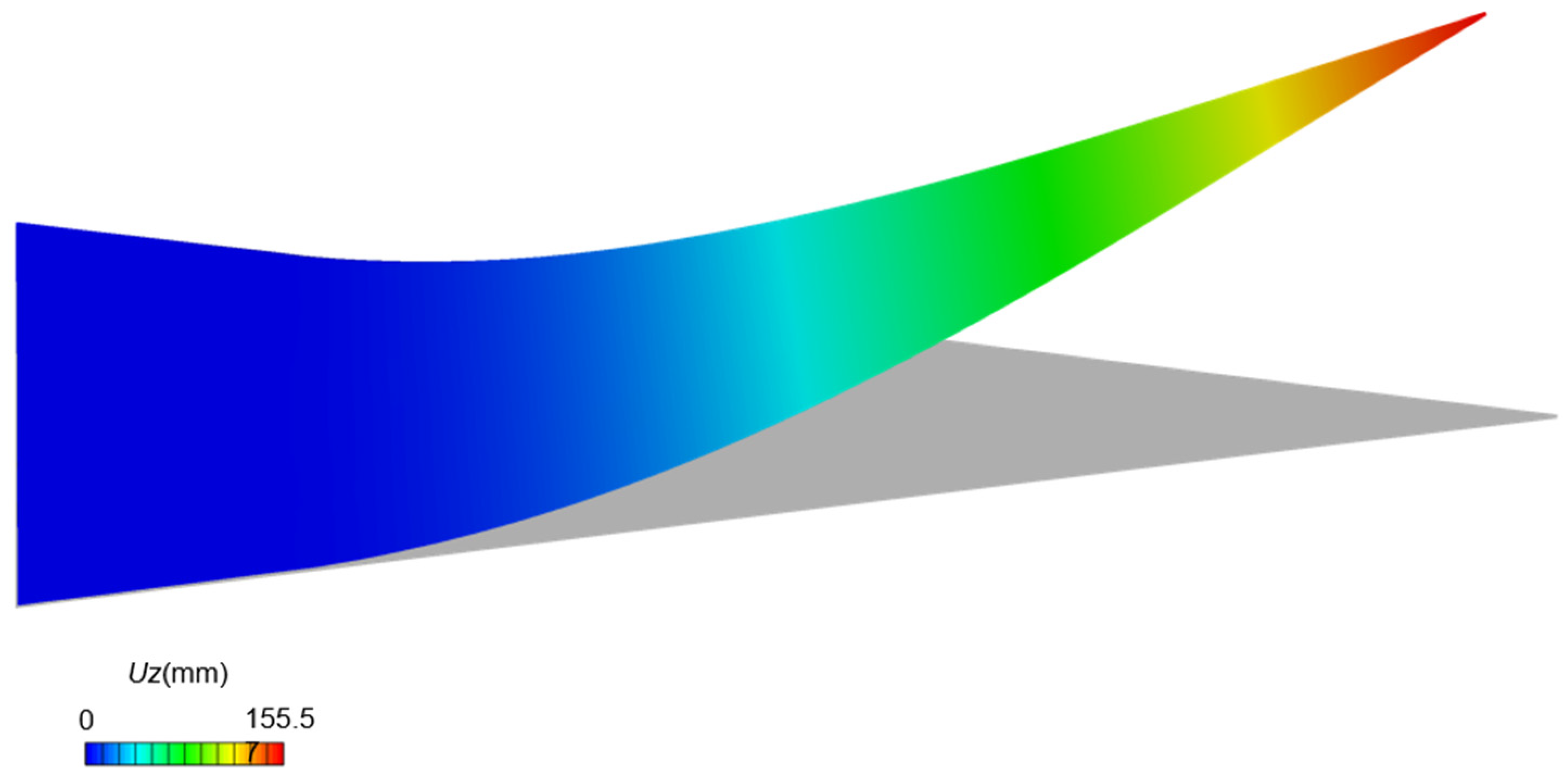
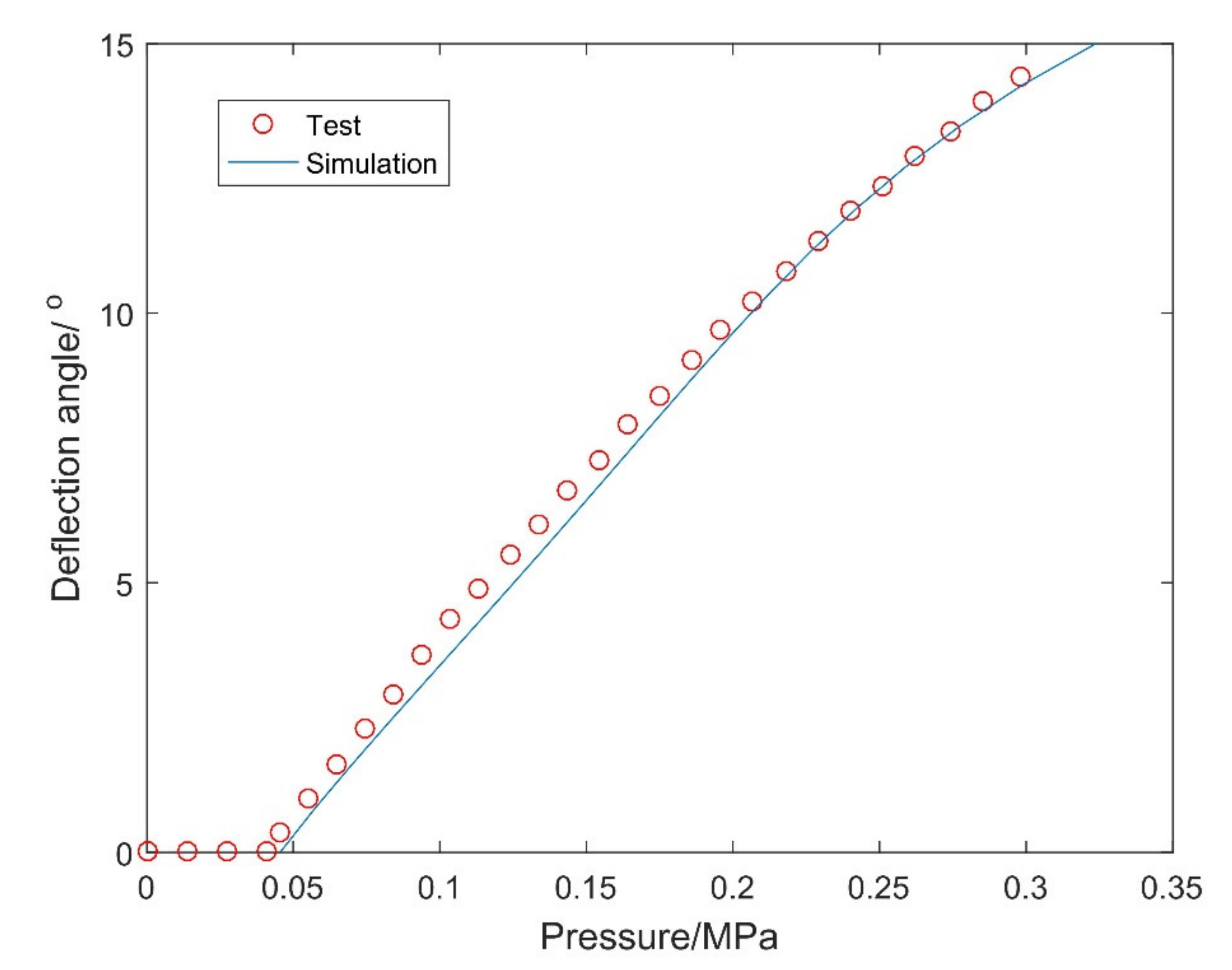
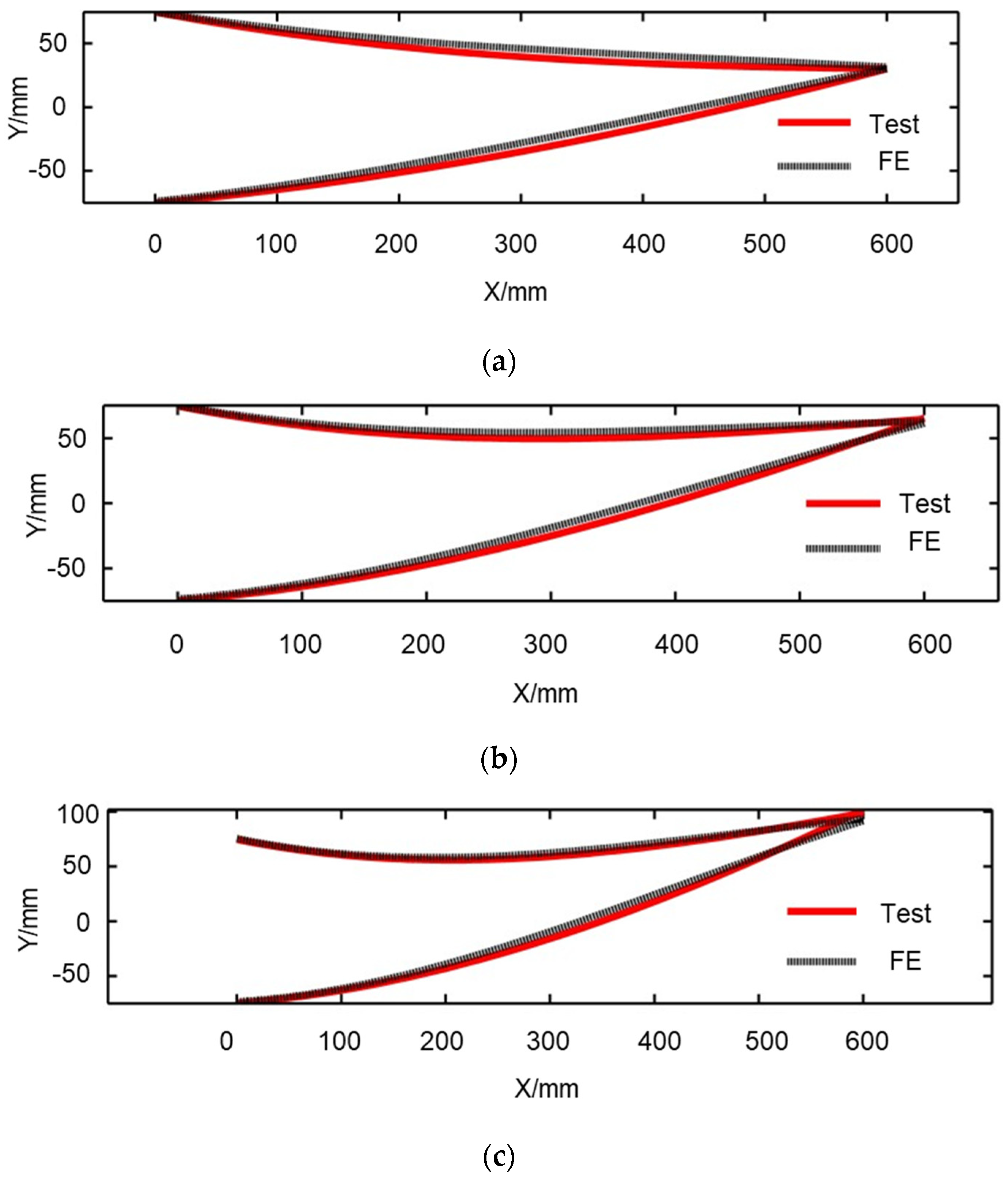
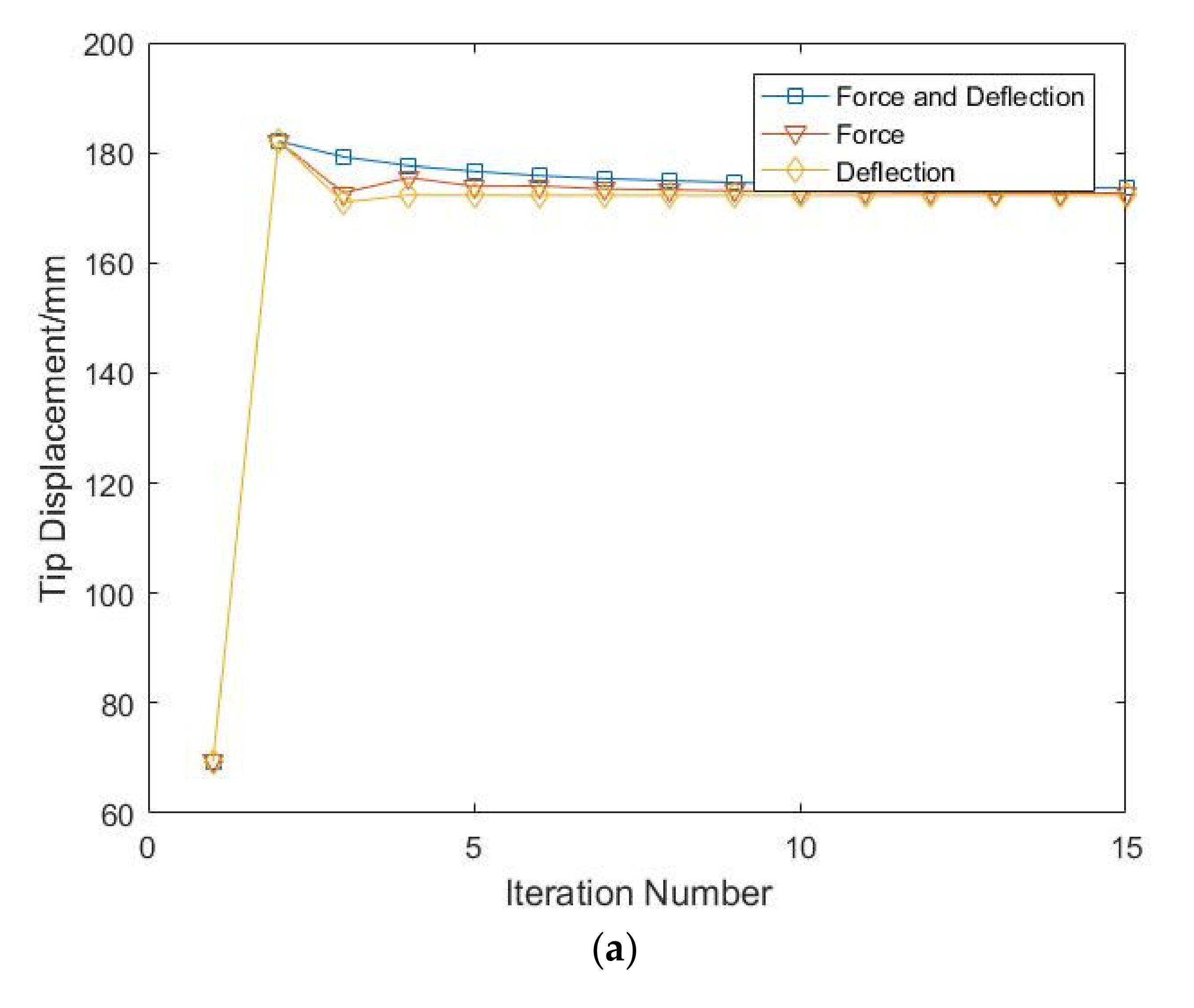
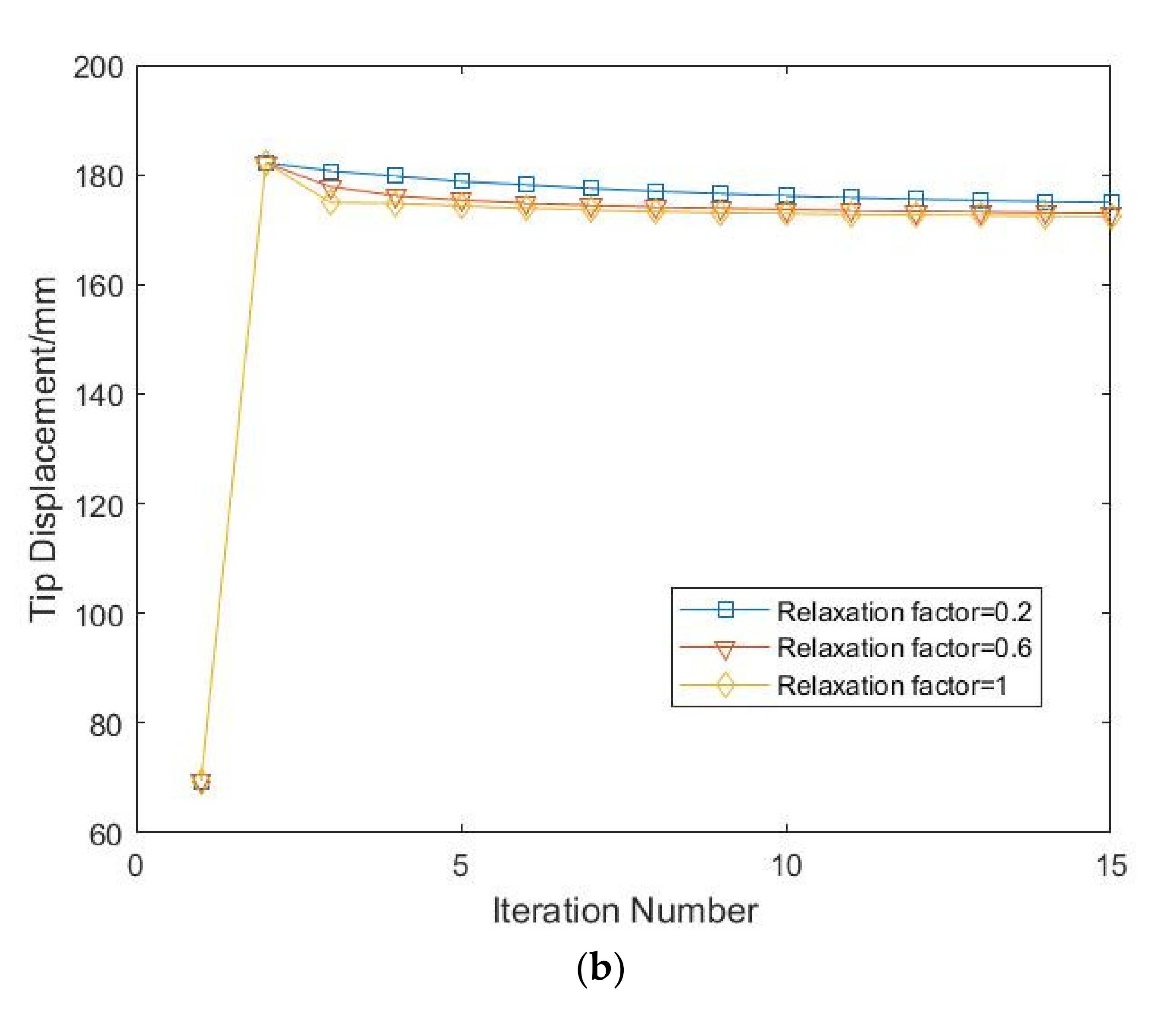
2.1.5. Validation of the Structure Model
2.2. Static Aeroelastic Analysis
2.2.1. Aerodynamic Model
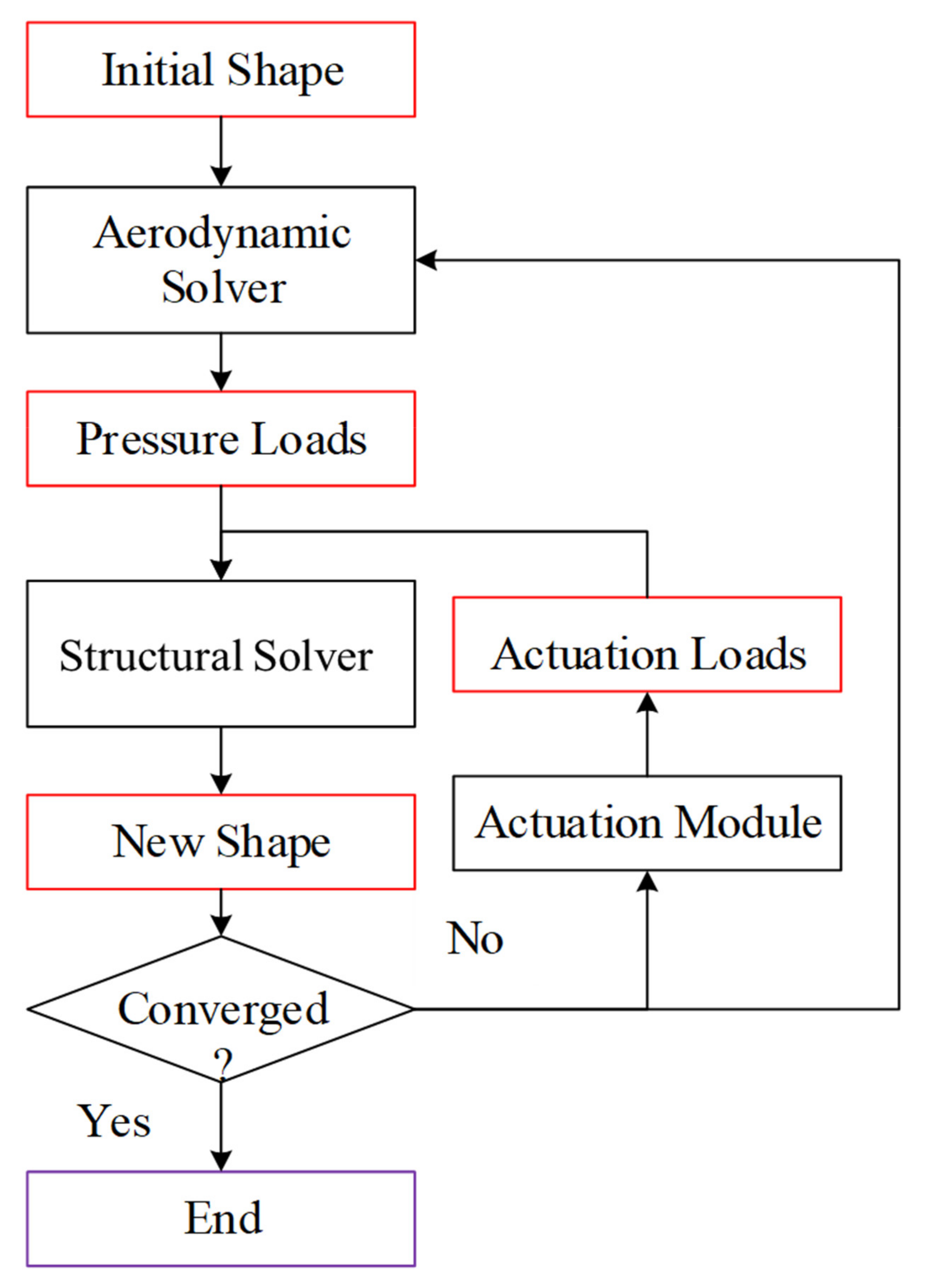
2.2.2. Static Aeroelastic Analysis
2.2.3. Aerodynamic Load Transformation
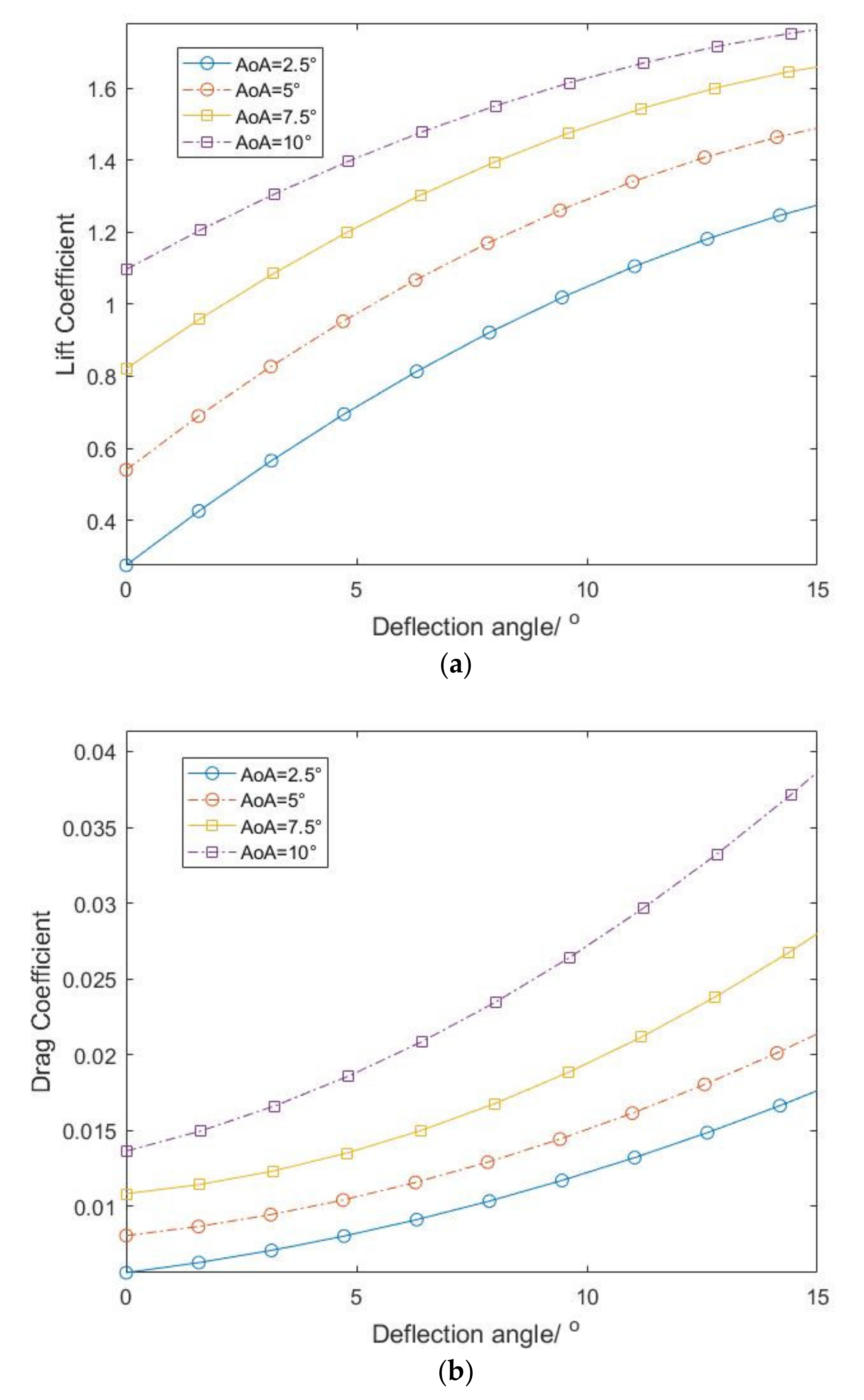
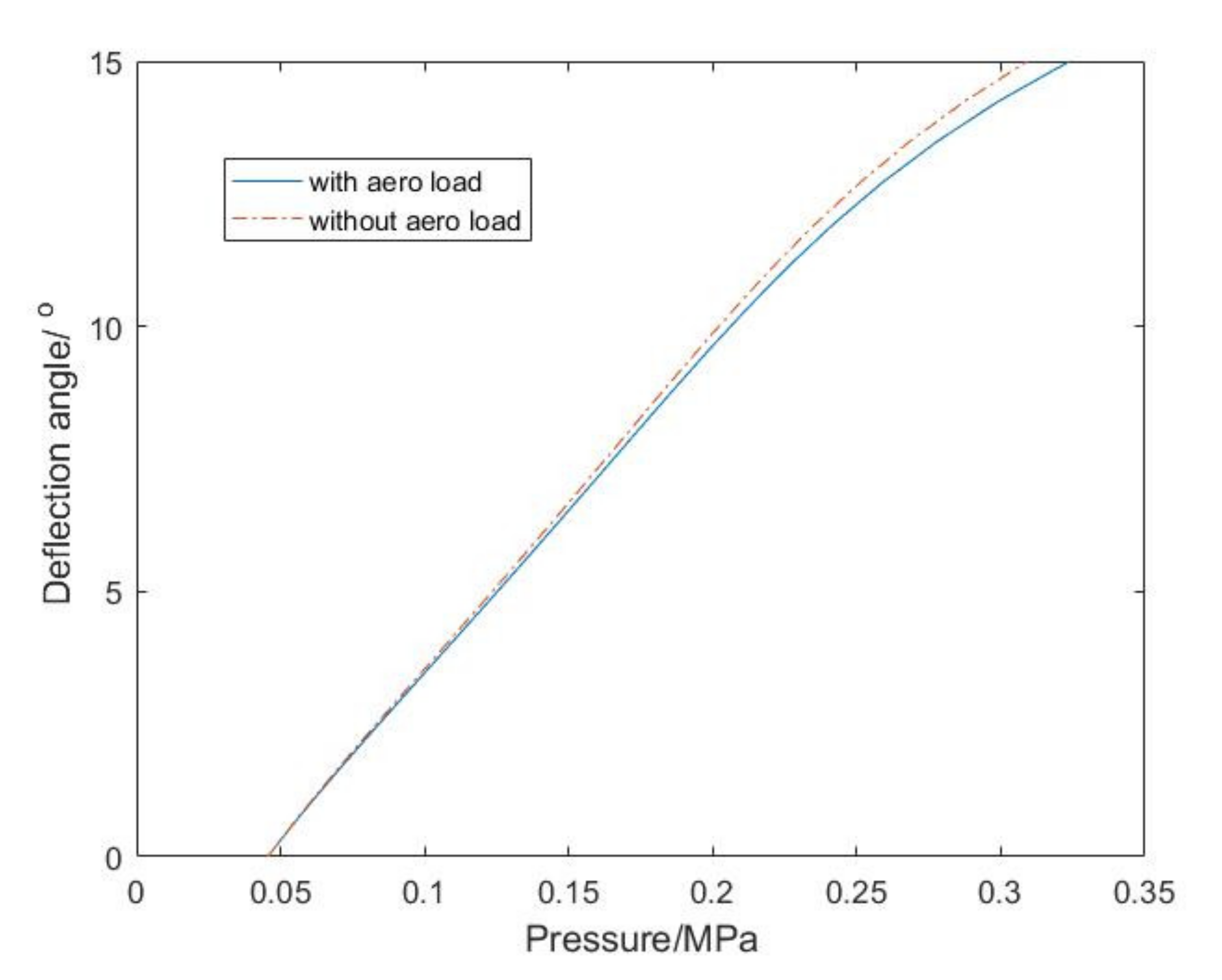
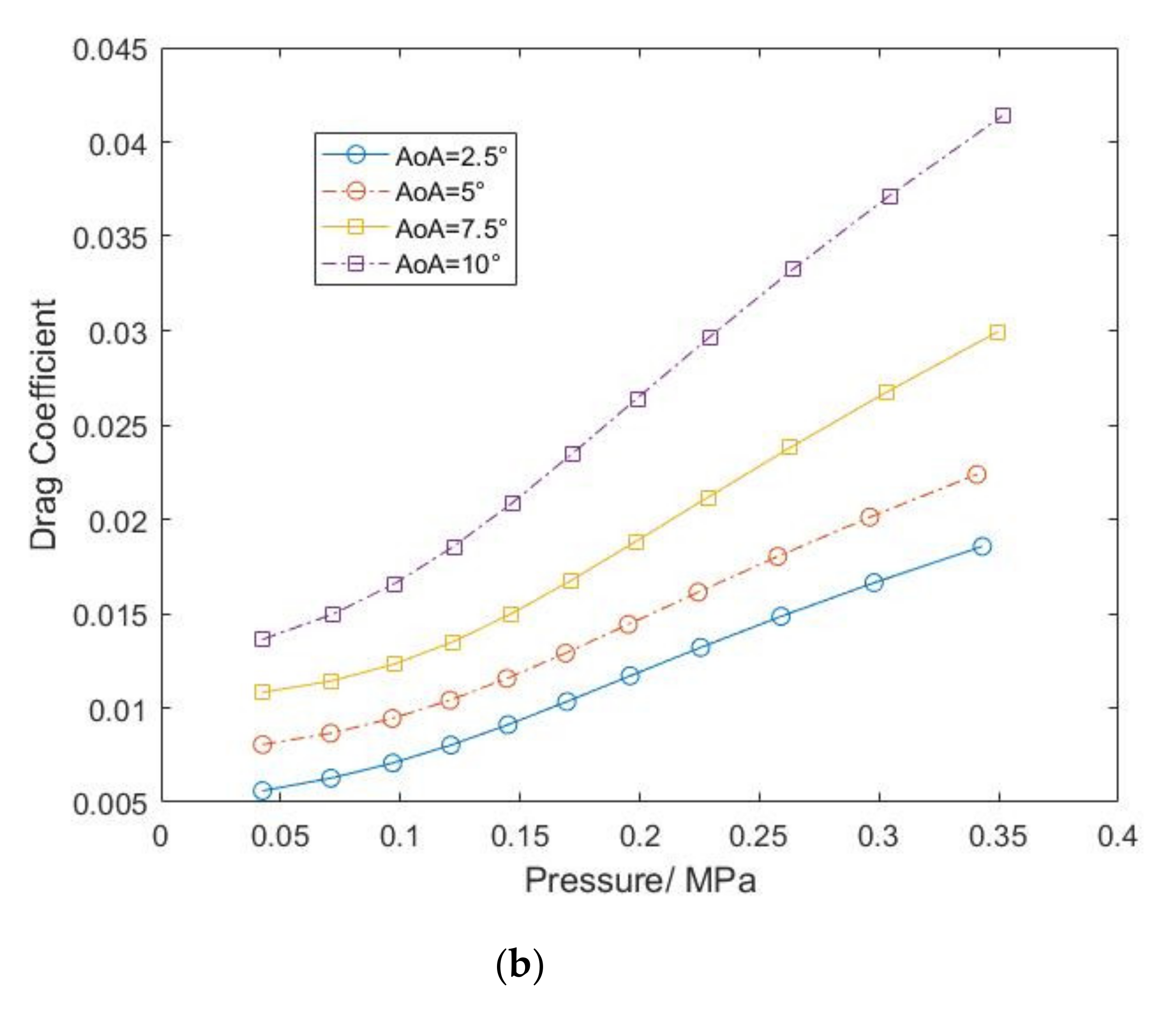
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef] [Green Version]
- Ismail, N.; Zulkifli, A.; Abdullah, M.; Basri, M.H.; Abdullah, N.S. Optimization of aerodynamic efficiency for twist morphing MAV wing. Chin. J. Aeronaut. 2014, 27, 475–487. [Google Scholar] [CrossRef] [Green Version]
- Huang, R.; Qiu, Z. Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process. Chin. J. Aeronaut. 2013, 26, 1430–1438. [Google Scholar] [CrossRef] [Green Version]
- Koreanschi, A.; Gabor, O.S.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Manou, Y.; Mebarki, Y. Optimization and design of an aircraft’s morphing wing-tip demonstrator for drag reduction at low speed, Part I—Aerodynamic optimization using genetic, bee colony and gra-dient descent algorithms. Chin. J. Aeronaut. 2017, 30, 149–163. [Google Scholar] [CrossRef]
- Koreanschi, A.; Gabor, O.S.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M. Optimization and design of an aircraft’s morphing wing-tip demonstrator for drag reduction at low speeds, Part II-Experimental validation using Infra-Red transition measure-ment from Wind Tunnel tests. Chin. J. Aeronaut. 2017, 30, 164–174. [Google Scholar] [CrossRef]
- Li, D.; Liu, Q.; Wu, Y.; Xiang, J. Design and analysis of a morphing drag rudder on the aerodynamics, structural deformation, and the required actuating moment. J. Intell. Mater. Syst. Struct. 2018, 29, 1038–1049. [Google Scholar] [CrossRef]
- Kan, Z.; Li, D.; Xiang, J. Delaying stall of morphing wing by periodic trailing-edge deflection. Chin. J. Aeronaut. 2020, 33, 493–500. [Google Scholar] [CrossRef]
- Xiang, J.; Liu, K.; Li, D.; Cheng, C.; Sha, E. Unsteady aerodynamic characteristics of a morphing wing. Aircr. Eng. Aerosp. Technol. 2018, 91, 1–9. [Google Scholar] [CrossRef]
- Li, D.; Guo, S.; Aburass, T.O.; Yang, D.; Xiang, J. Active control design for an unmanned air vehicle with a morphing wing. Aircr. Eng. Aerosp. Technol. 2016, 88, 168–177. [Google Scholar] [CrossRef]
- Li, D.; Guo, S.; Xiang, J. Modeling and nonlinear aeroelastic analysis of a wing with morphing trailing edge. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 227, 619–631. [Google Scholar] [CrossRef]
- Li, D.; Guo, S.; He, Y.; Xiang, J. Nonlinear aeroelastic analysis of a morphing flap. Int. J. Bifurc. Chaos 2012, 22, 1250099. [Google Scholar] [CrossRef]
- Woods, B.K.; Bilgen, O.; Friswell, M.I. Wind Tunnel Testing of the Fishbone Active Camber Morphing Concept. J. Int. Mat. Syst. Str. 2014, 5, 772–785. [Google Scholar] [CrossRef]
- Chen, Q.; Bai, P.; Yin, W.; Leng, J.; Zhan, H.; Liu, Z. Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge. Acta Phys. 2010, 28, 46–53. [Google Scholar]
- Woods, B.K.S.; Dayyani, I.; Friswell, M. Fluid/Structure-Interaction Analysis of the Fish-Bone-Active-Camber Morphing Concept. J. Aircr. 2015, 52, 307–319. [Google Scholar] [CrossRef] [Green Version]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development of Variable Camber Morphing Airfoil Using Corrugated Structure. J. Aircr. 2014, 51, 1023–1029. [Google Scholar] [CrossRef] [Green Version]
- Airoldi, A.; Crespi, M.; Quaranti, G.; Sala, G. Design of a Morphing Airfoil with Composite Chiral Structure. J. Aircr. 2012, 49, 1008–1019. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, L.; Cheng, W.; Qiu, T. Conceptual Design and Experimental Demonstration of a Distributedly Actuated Morphing Wing. J. Aircr. 2015, 52, 452–461. [Google Scholar] [CrossRef]
- Xie, D.; Ma, Z.; Liu, J.; Zuo, S. Pneumatic Artificial Muscle Based on Novel Winding Method. Actuators 2021, 10, 100. [Google Scholar] [CrossRef]
- Cao, Y.; Fu, Z.; Zhang, M.; Huang, J. Extended-State-Observer-Based Super Twisting Control for Pneumatic Muscle Actuators. Actuators 2021, 10, 35. [Google Scholar] [CrossRef]
- Zhao, W.; Song, A. Active Motion Control of a Knee Exoskeleton Driven by Antagonistic Pneumatic Muscle Actuators. Actuators 2020, 9, 134. [Google Scholar] [CrossRef]
- Yin, W.; Liu, L.; Chen, Y.; Leng, J. Variable camber wing based on pneumatic artificial muscles. In Proceedings of the Second International Conference on Smart Materials and Nanotechnology in Engineering, Weihai, China, 8–11 July 2009. [Google Scholar]
- Barbarino, S.; Pecora, R.; Lecce, L.; Concilio, A.; Ameduri, S.; Calvi, E. A Novel SMA-based Concept for Airfoil Structural Morphing. J. Mater. Eng. Perform. 2009, 18, 696–705. [Google Scholar] [CrossRef]
- Bae, J.S.; Kyong, N.H.; Seigler, T.M. Aeroelastic Considerations on Shape Control of an Adaptive Wing. J. Int. Mat. Syst. Str. 2005, 16, 1051–1056. [Google Scholar] [CrossRef]
- Campanile, L.F.; Anders, S. Aerodynamic and aeroelastic amplification in adaptive belt-rib airfoils. Aerosp. Sci. Technol. 2005, 9, 55–63. [Google Scholar] [CrossRef]
- Bilgen, O.; Flores, E.I.S.; Friswell, M.I. Optimization of Surface-Actuated Piezocomposite Variable-Camber Morphing Wings. In Smart Materials, Adaptive Structures and Intelligent Systems, Proceedings of the ASME 2011 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Scottsdale, AZ, USA, 18–21 September 2011; Adaptive Structures and Intelligent Systems American Society of Mechanical Engineers: New York, NY, USA, 2011; pp. 315–322. [Google Scholar]
- Daynes, S.; Weaver, P.M. Morphing Blade Fluid-Structure Interaction. In Proceedings of the 53rd AIAA Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; pp. 1–15. [Google Scholar]
- Botez, R.M.; Koreanschi, A.; Gabor, O.S. Numerical and experimental transition results evaluation for a morphing wing and aileron system. Aeronaut. J. 2018, 122, 747–784. [Google Scholar] [CrossRef]
- Communier, D.; Botez, R.; Wong, T. Experimental validation of a new morphing trailing edge system using Price—Païdoussis wind tunnel tests. Chin. J. Aeronaut. 2019, 32, 1353–1366. [Google Scholar] [CrossRef]
- Yerkes, N.; Wereley, N. Pneumatic Artificial Muscle Activation for Trailing Edge Flaps. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008; pp. 1–10. [Google Scholar]
- Woods, B.K.S. Pneumatic Artificial Muscle Driven Trailing Edge Flaps for Active Rotors[M]; University of Maryland: College Park, MD, USA, 2012. [Google Scholar]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision in C++ with the OpenCV Library; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013. [Google Scholar]
- Drela, M. XFOIL: An Analysis and Design System of Low Reynolds Number Aerofoils. Low Reynolds Number Aerodyn. 1989, 54, 1–12. [Google Scholar]
- Cody, L.; Kelly, C.; Shaaban, A. Use of XFOIL in design of camber-controlled morphing UAVs. Comput. Appl. Eng. Educ. 2012, 20, 673–680. [Google Scholar]
- Woods, B.; Fincham, J.H.S.; Friswell, M.I. Aerodynamic modelling of the fish bone active camber morphing concept. In Proceedings of the RAeS Applied Aerodynamics Conference 2014, Bristol, UK, 22–24 July 2014. [Google Scholar]
- Fincham, J.H.S.; Friswell, M.I. Aerodynamic optimisation of a camber morphing aerofoil. Aerosp. Sci. Technol. 2015, 43, 245–255. [Google Scholar] [CrossRef] [Green Version]



| Parameters | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|
| Value | 0.094 | 0.181 | 0.58 | 1.88e3 | 228.46 | 270.66 |
| Item | By Binocular Vision/mm | Known/mm | Relative Error/% |
|---|---|---|---|
| Transverse | 100.087 | 100 | 0.087 |
| Longitudinal | 50.096 | 50 | 0.192 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Li, D.; Zhou, J.; Sha, E. Numerical and Experimental Study of a Flexible Trailing Edge Driving by Pneumatic Muscle Actuators. Actuators 2021, 10, 142. https://doi.org/10.3390/act10070142
Zhao S, Li D, Zhou J, Sha E. Numerical and Experimental Study of a Flexible Trailing Edge Driving by Pneumatic Muscle Actuators. Actuators. 2021; 10(7):142. https://doi.org/10.3390/act10070142
Chicago/Turabian StyleZhao, Shiwei, Daochun Li, Jin Zhou, and Enlai Sha. 2021. "Numerical and Experimental Study of a Flexible Trailing Edge Driving by Pneumatic Muscle Actuators" Actuators 10, no. 7: 142. https://doi.org/10.3390/act10070142
APA StyleZhao, S., Li, D., Zhou, J., & Sha, E. (2021). Numerical and Experimental Study of a Flexible Trailing Edge Driving by Pneumatic Muscle Actuators. Actuators, 10(7), 142. https://doi.org/10.3390/act10070142







