Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators
Abstract
1. Introduction
2. Robotic Device
2.1. Rehabilitation-Arm Design
2.2. Kinematics and Dynamics Analysis
3. System Modeling
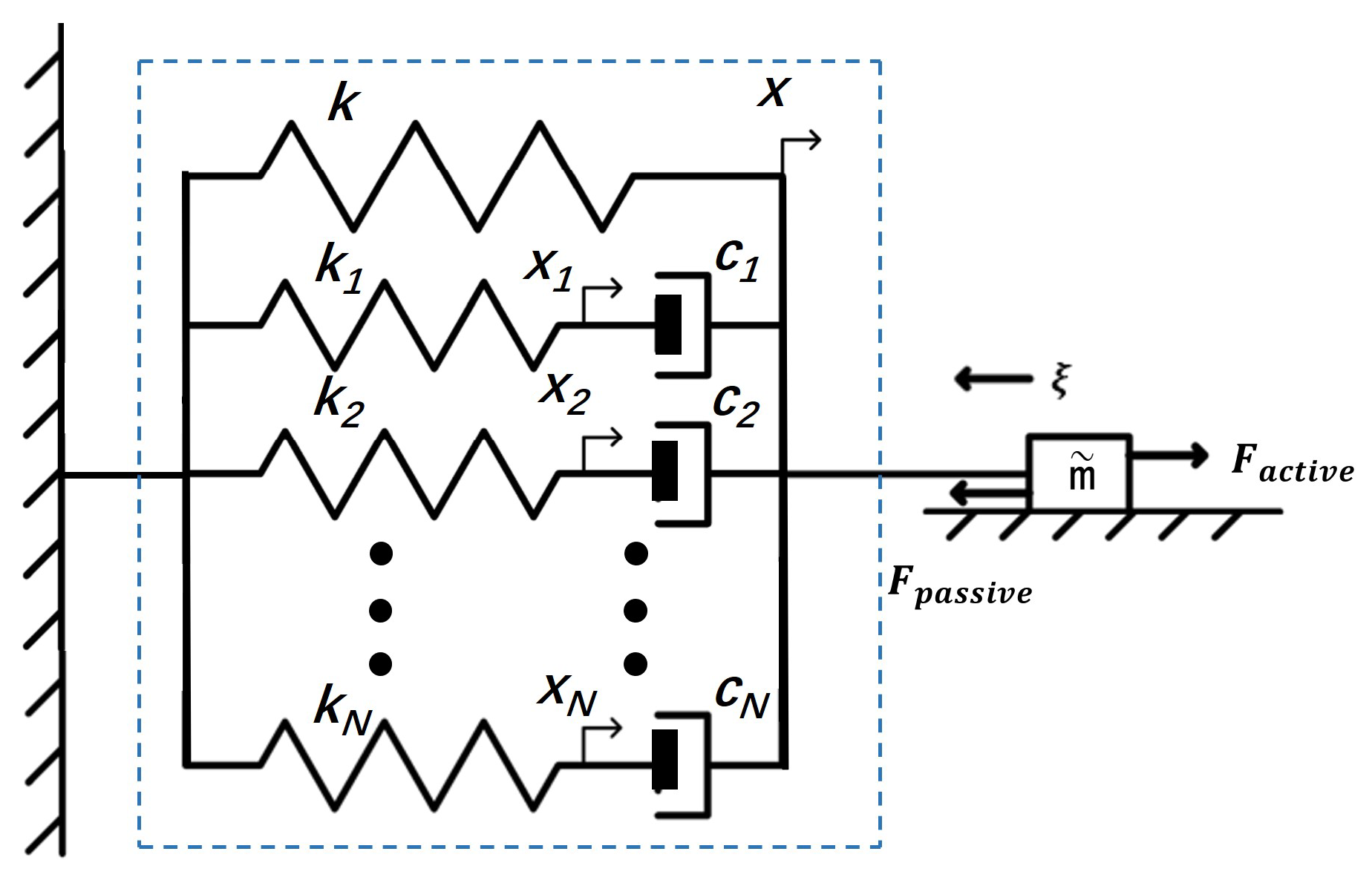
3.1. Modularization Design
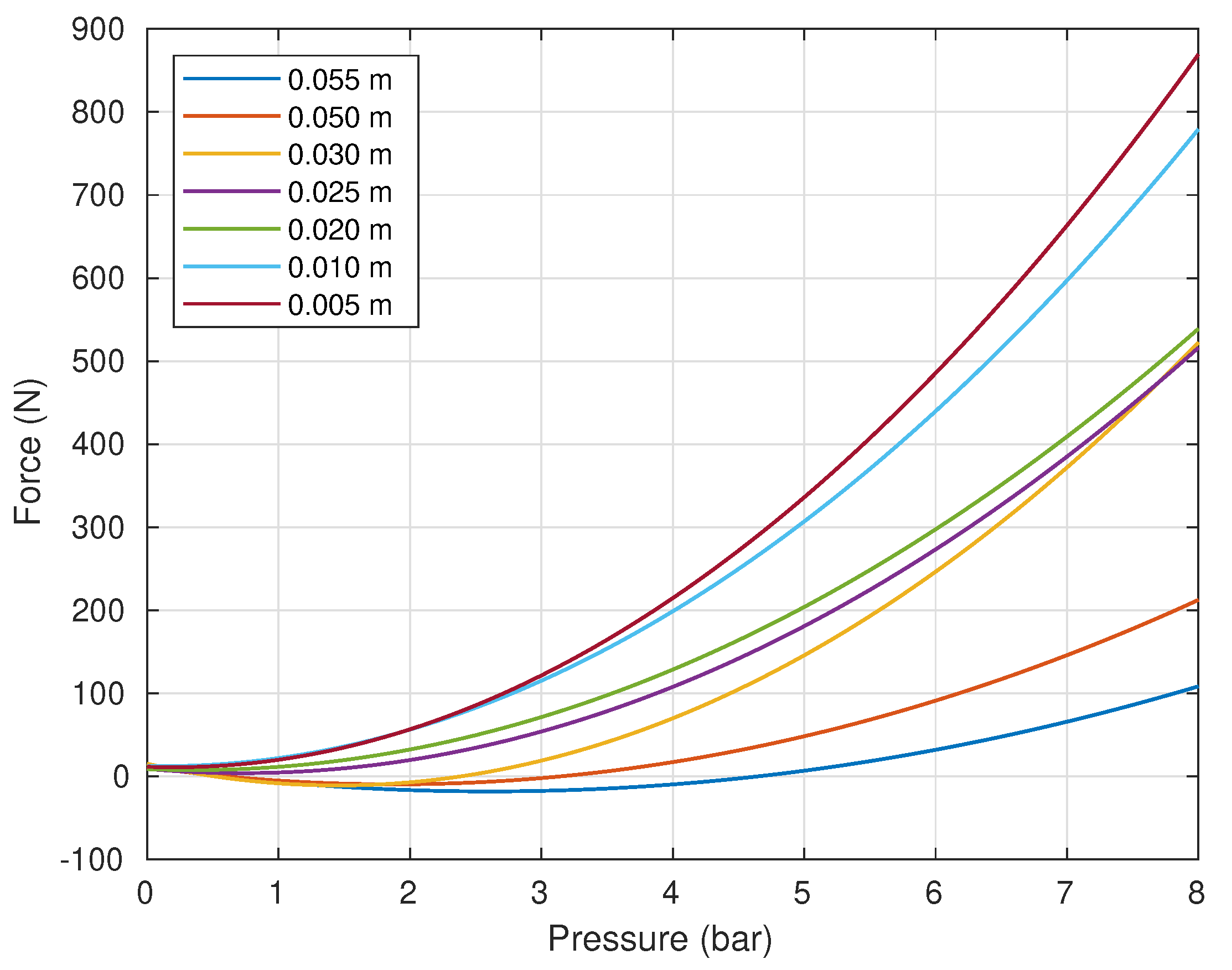
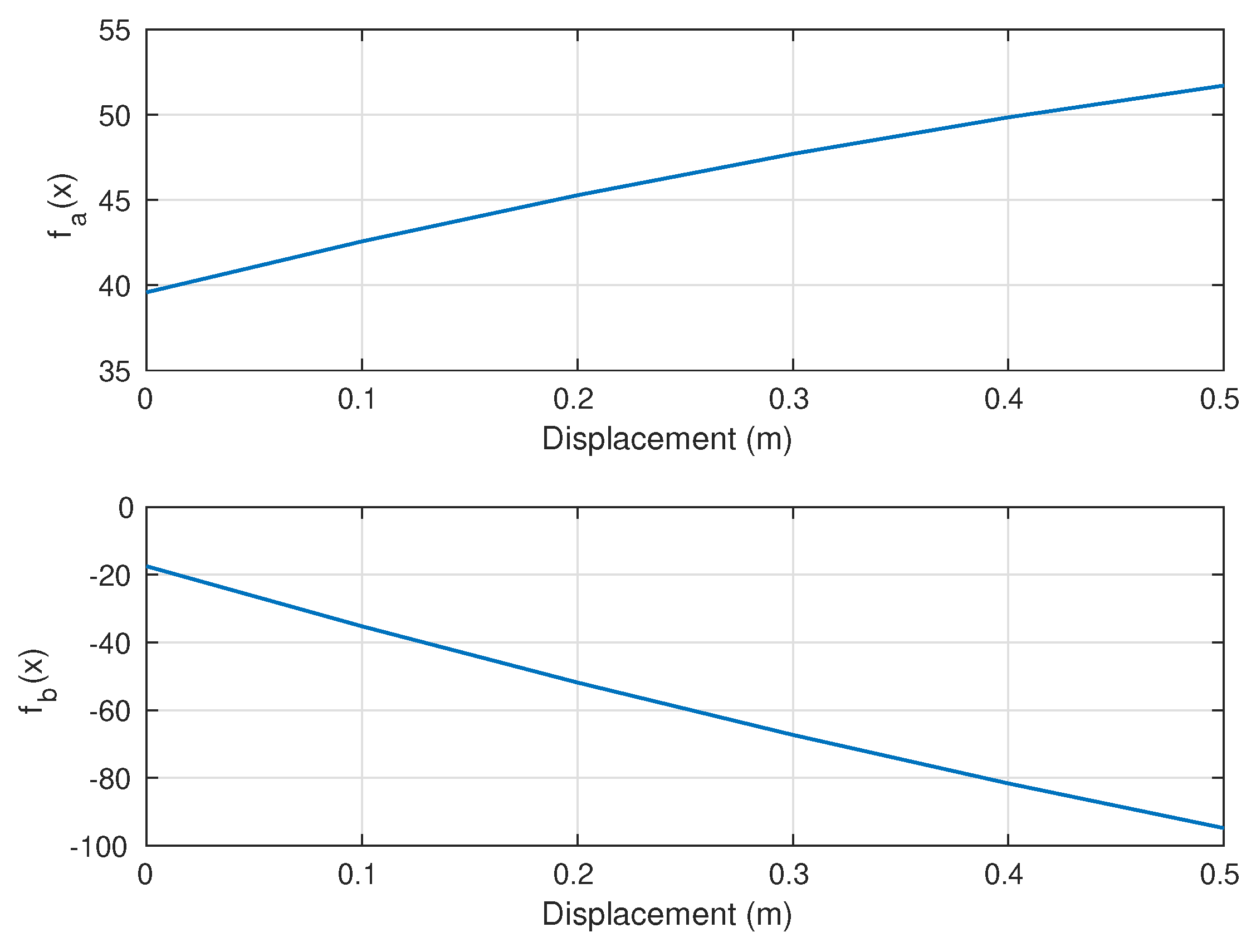
3.2. Knowledge-Guided Modeling
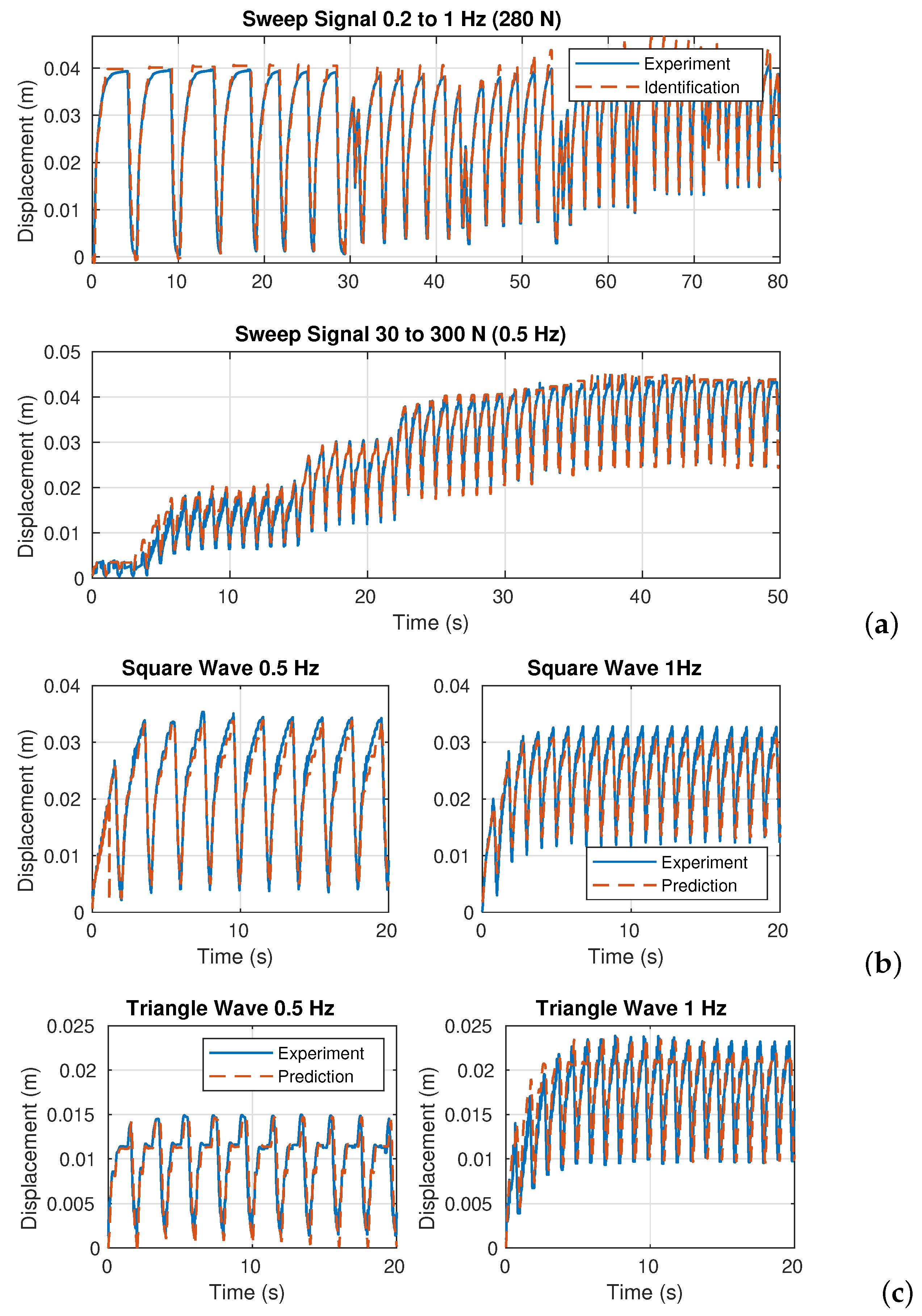
3.3. System Identification
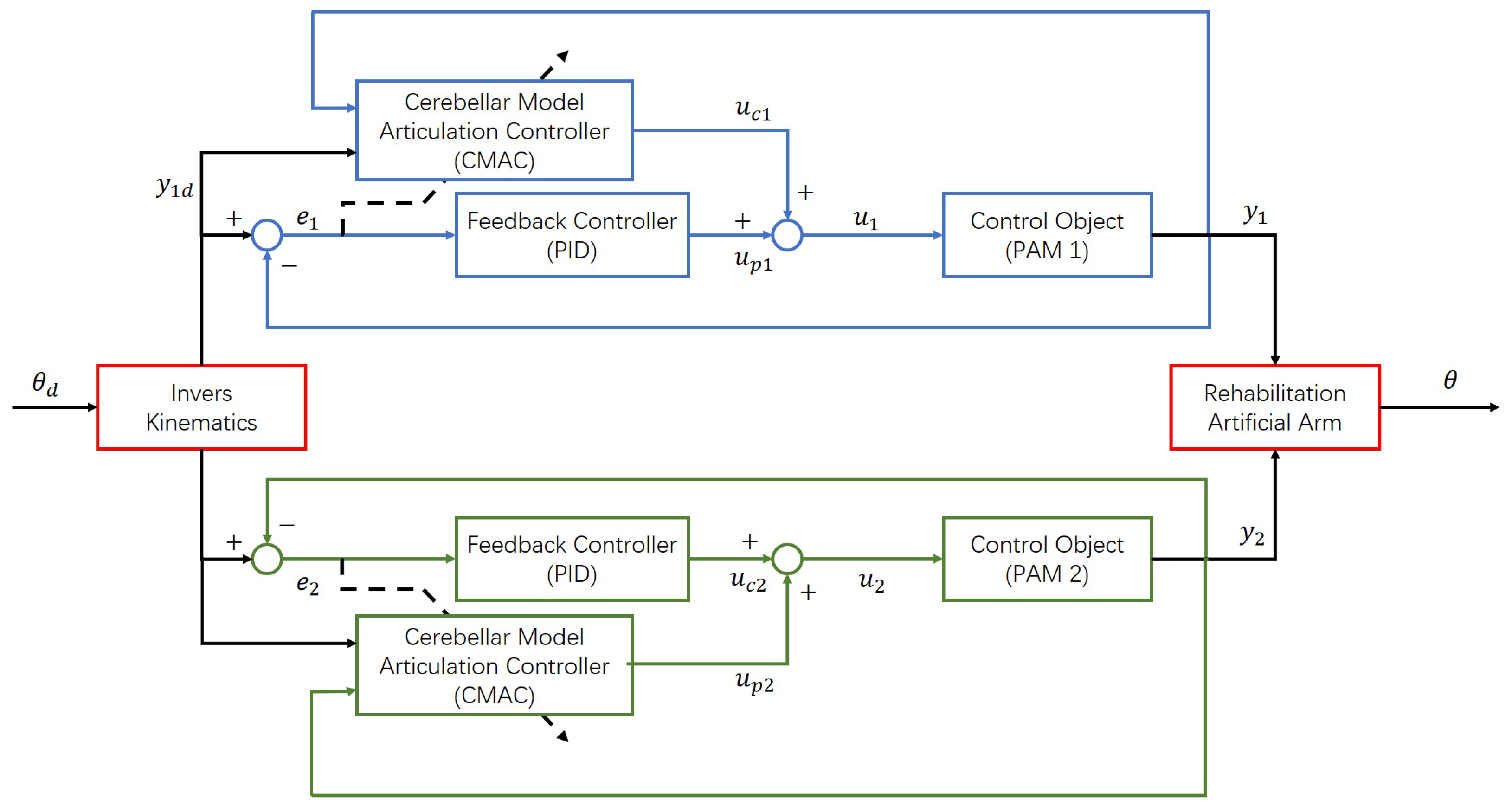
4. Control Scheme
4.1. Feedforward–Feedback Control Scheme
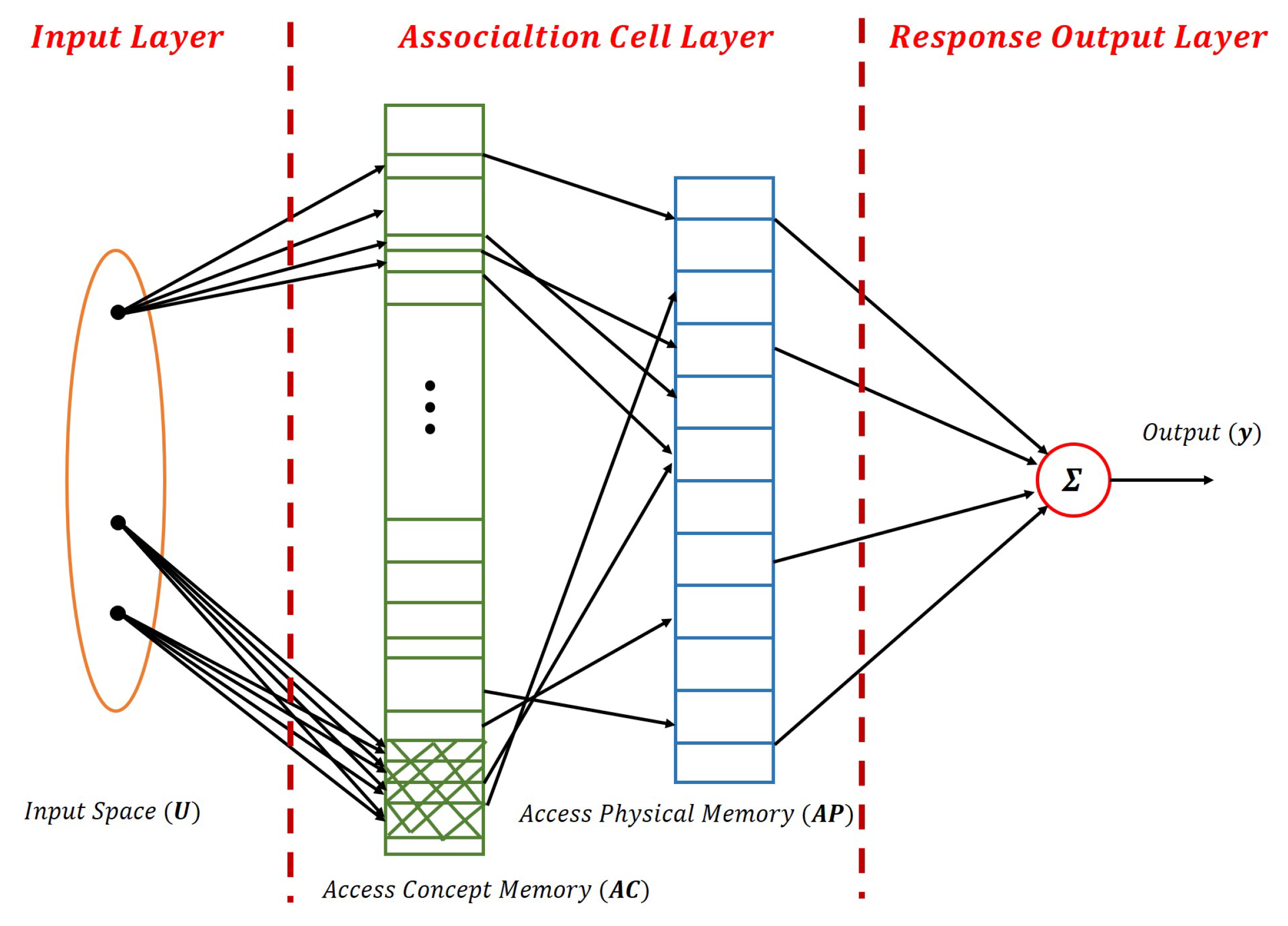
4.2. Cerebellar Model Articulation Controller
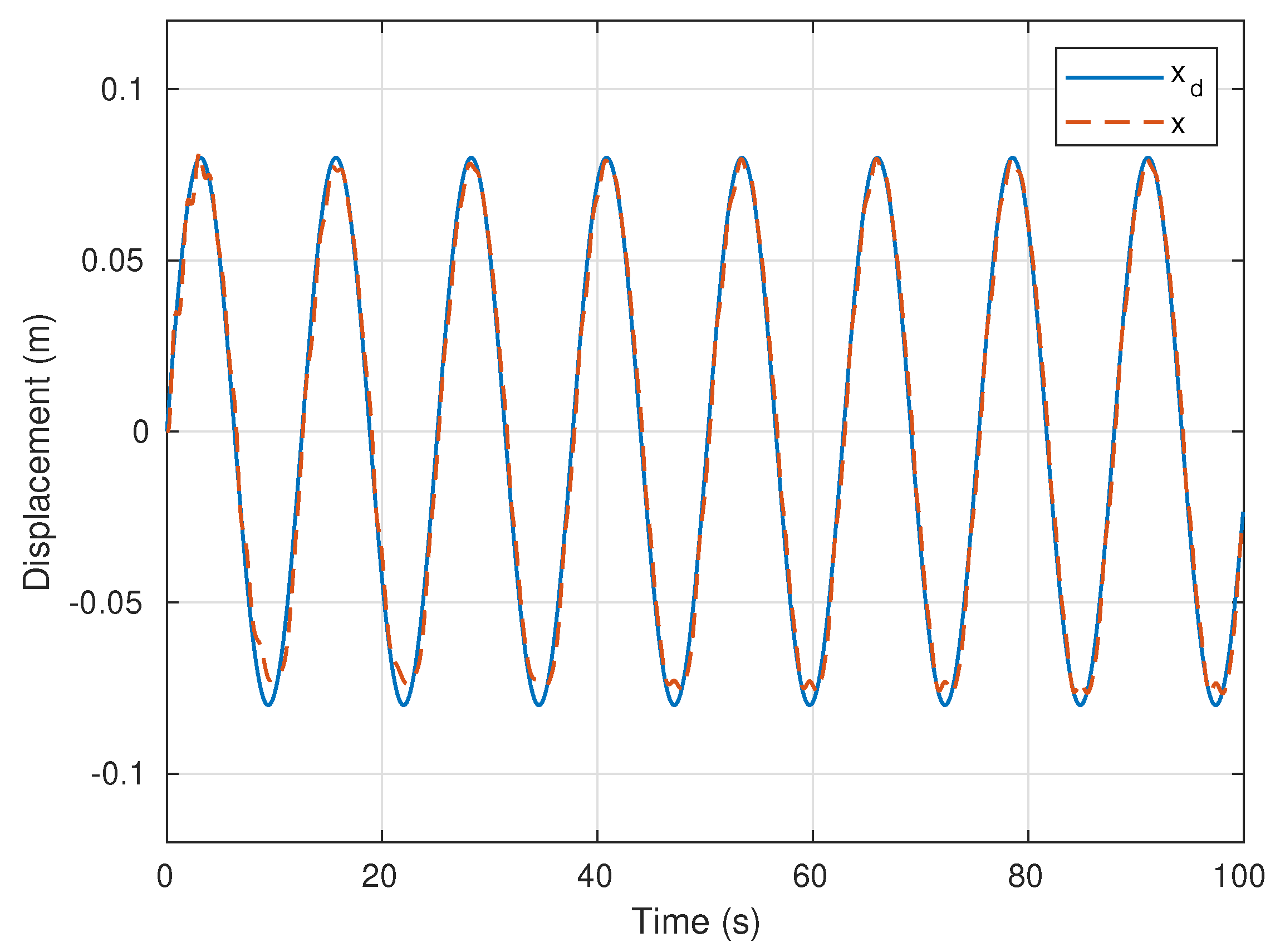
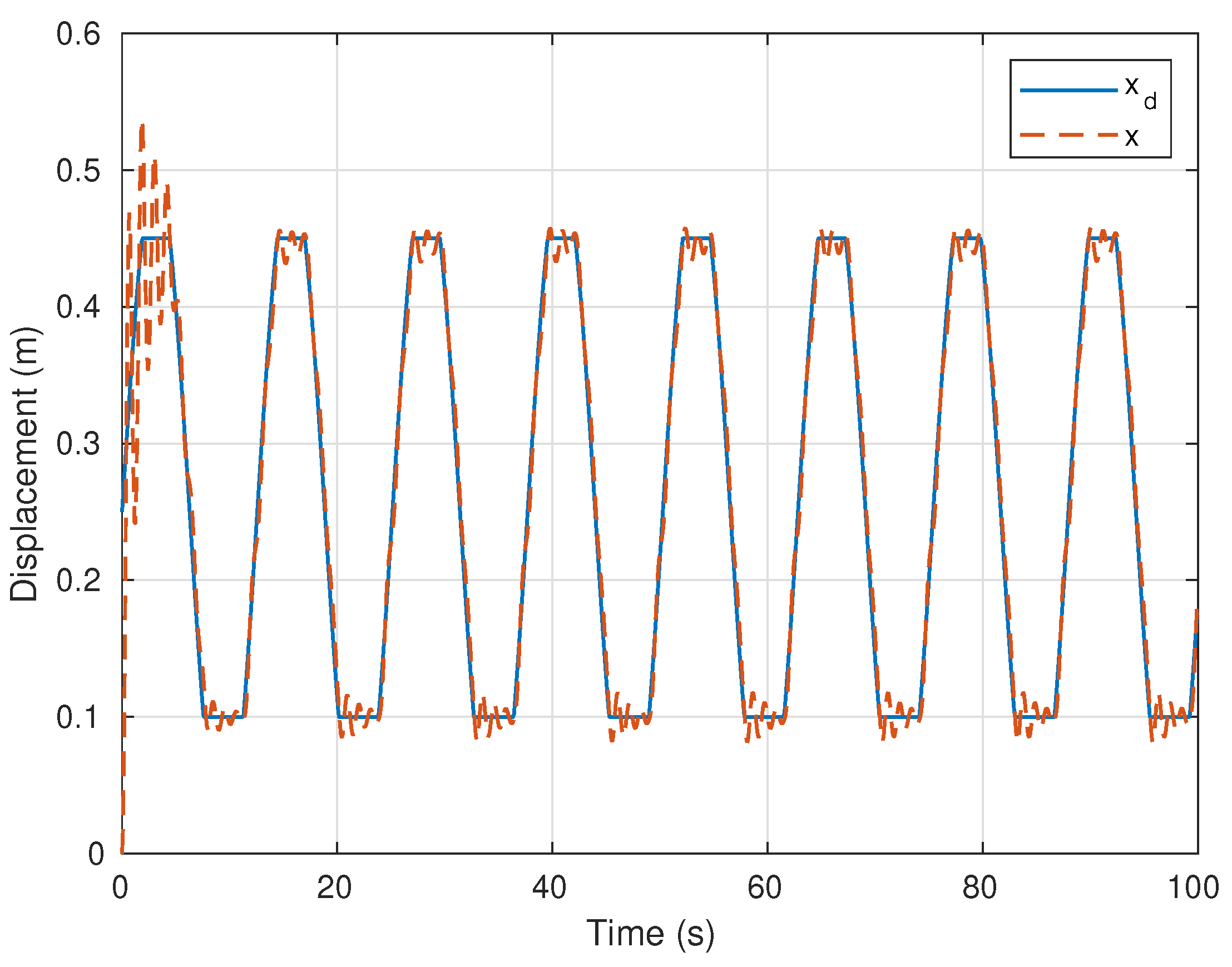
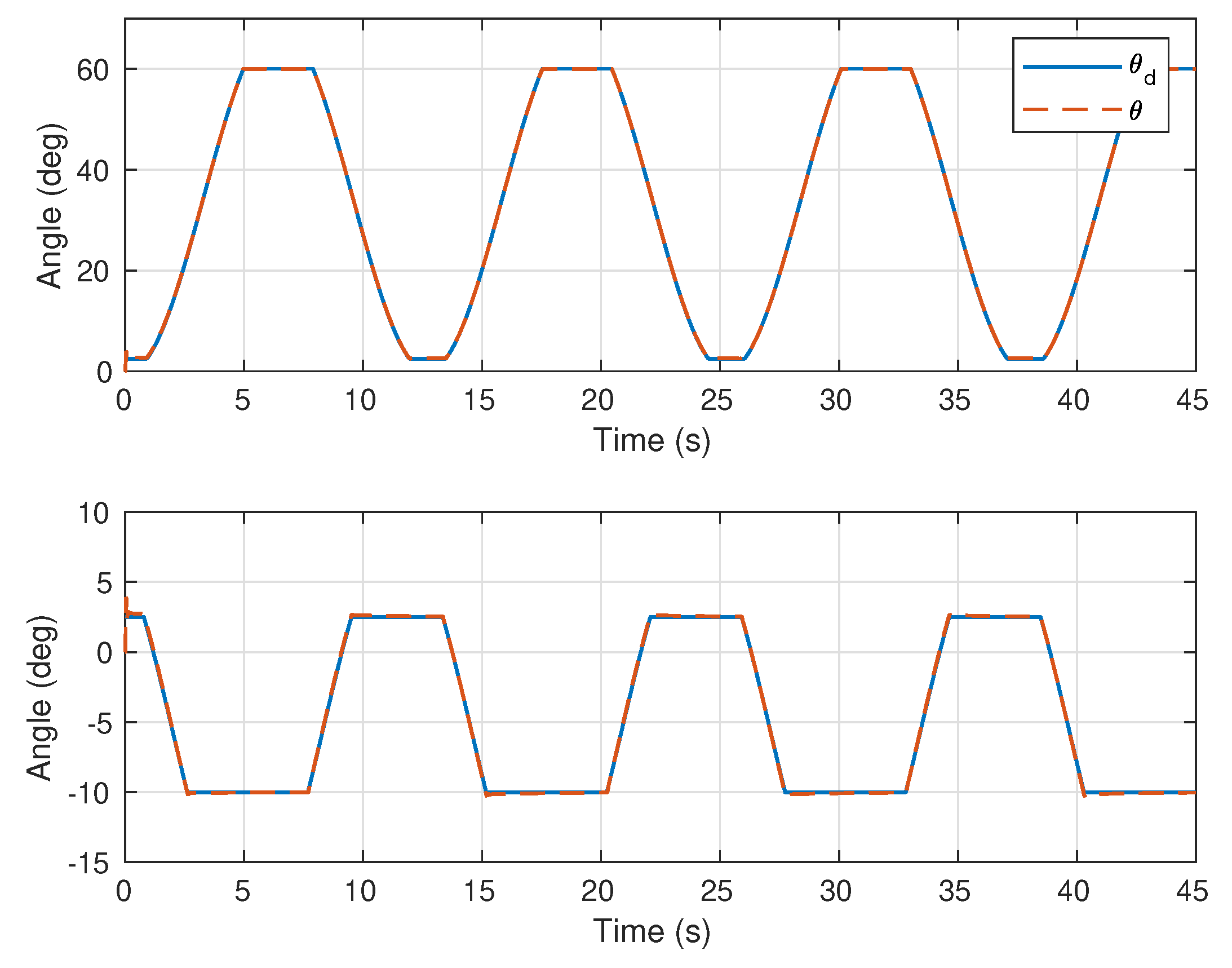
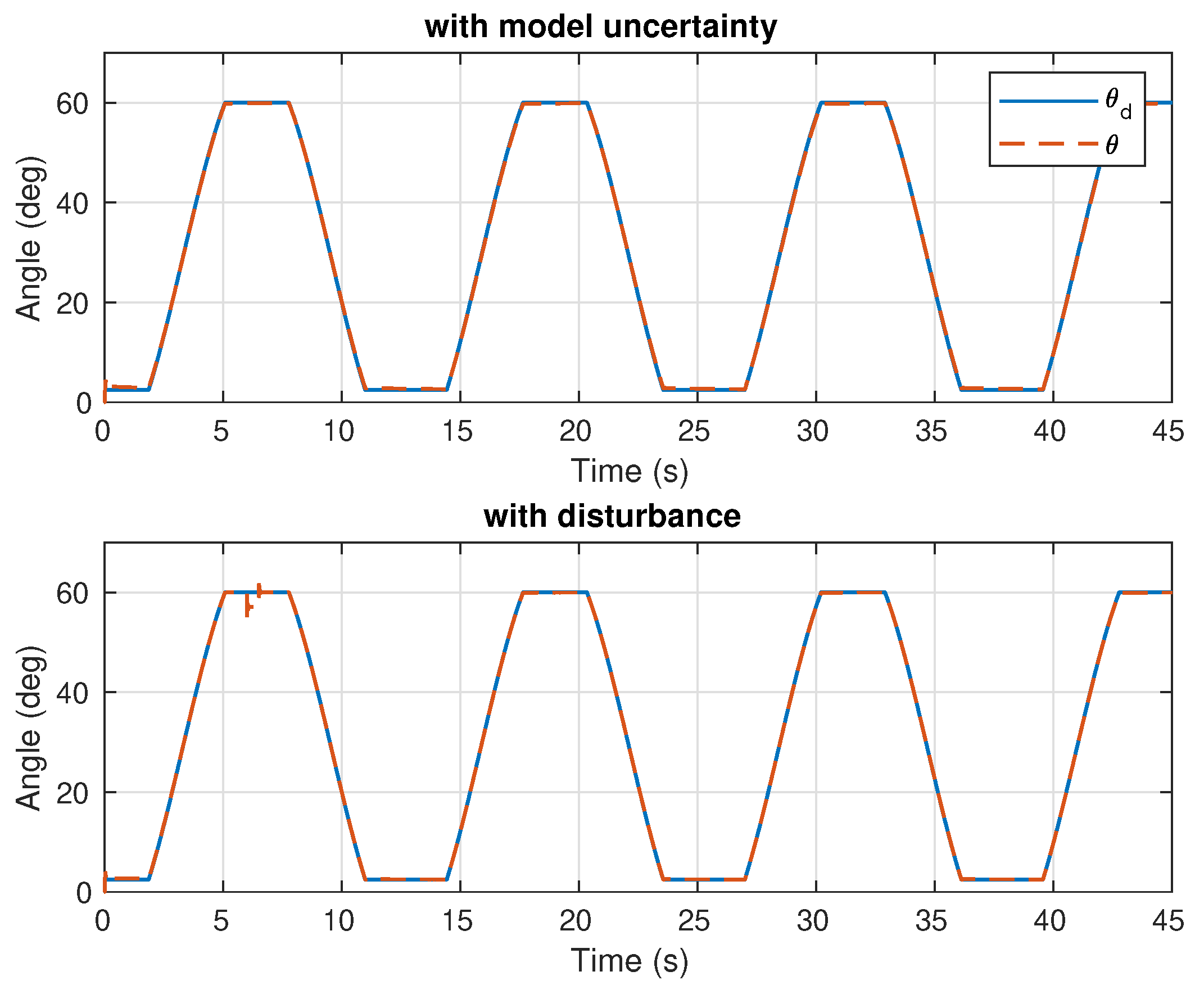
5. Simulation and Experimental Results
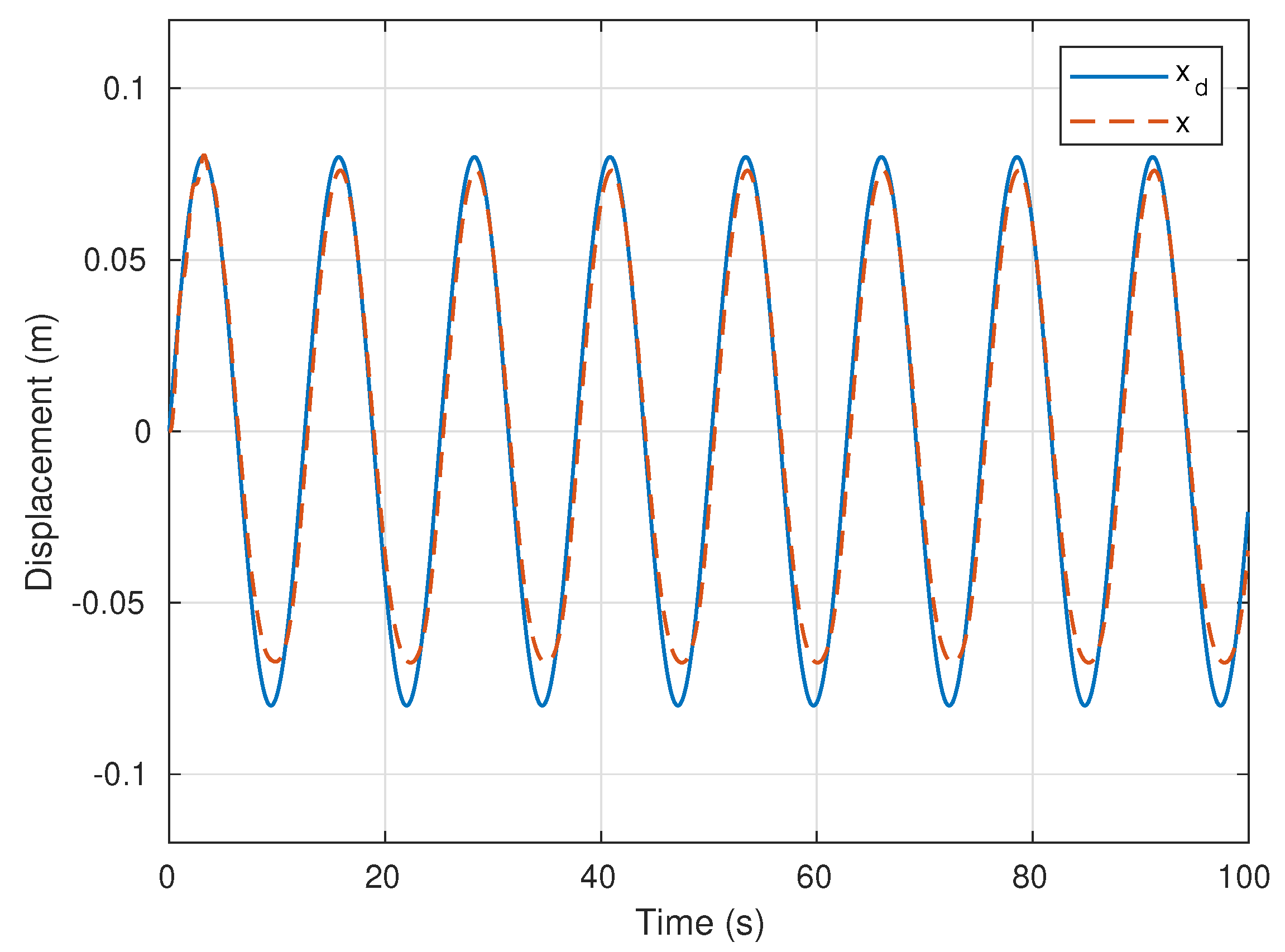
5.1. Simulation
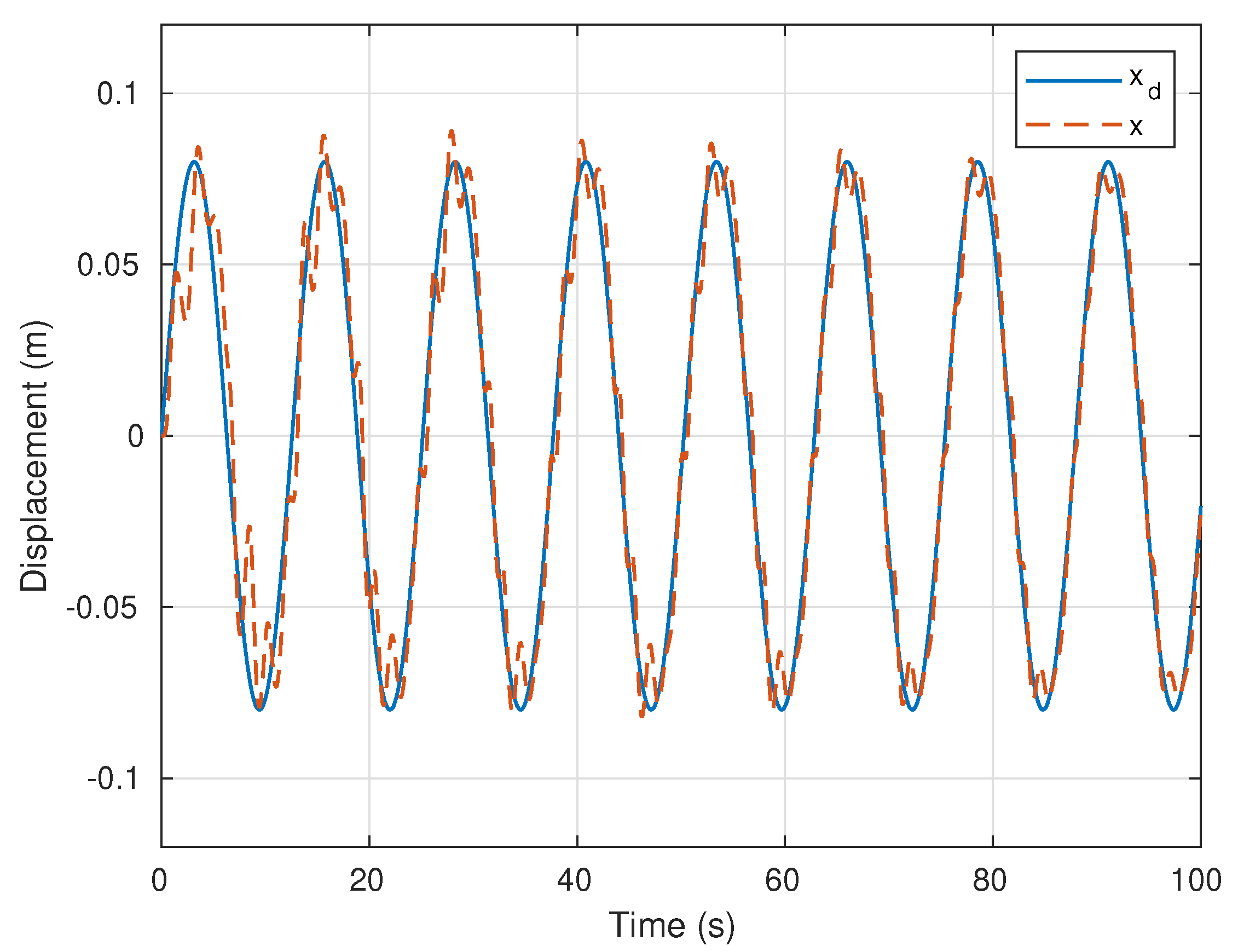
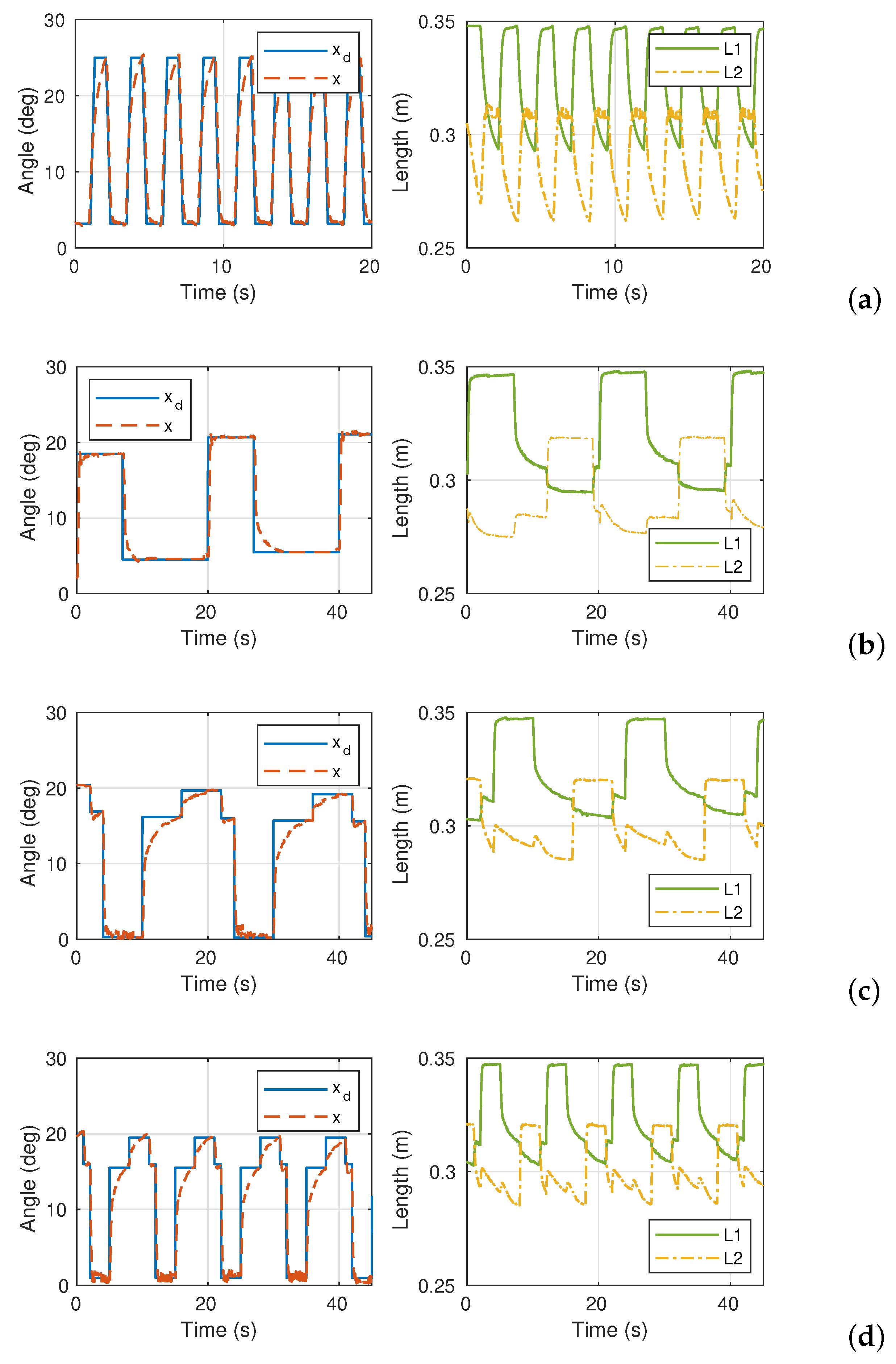
5.2. Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- World Health Organization. Neurological Disorders: Public Health Challenges; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Johnson, C.O.; Nguyen, M.; Roth, G.A.; Nichols, E.; Alam, T.; Abate, D.; Abd-Allah, F.; Abdelalim, A.; Abraha, H.N.; Abu-Rmeileh, N.M.; et al. Global, regional, and national burden of stroke, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 2019, 18, 439–458. [Google Scholar] [CrossRef]
- Nakayama, H.; Jrgensen, H.S.; Raaschou, H.O.; Olsen, T.S. Recovery of upper extremity function in stroke patients: The Copenhagen Stroke Study. Arch. Phys. Med. Rehabil. 1994, 75, 394–398. [Google Scholar] [CrossRef]
- Van Peppen, R.P.; Kwakkel, G.; Wood-Dauphinee, S.; Hendriks, H.J.; Van der Wees, P.J.; Dekker, J. The impact of physical therapy on functional outcomes after stroke: What’s the evidence? Clin. Rehabil. 2004, 18, 833–862. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.; Li, Z.; Su, C.Y.; Xue, A. Development and Learning Control of a Human Limb With a Rehabilitation Exoskeleton. Ind. Electron. IEEE Trans. 2014, 61, 3776–3785. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. A survey on applications of Pneumatic Artificial Muscles. In Proceedings of the 2011 19th Mediterranean Conference on Control and Automation, MED 2011, Corfu, Greece, 20–23 June 2011; pp. 1439–1446. [Google Scholar]
- Ranzani, T.; Cianchetti, M.; Gerboni, G.; Falco, I.D.; Menciassi, A. A soft modular manipulator for minimally invasive surgery: Design and characterization of a single module. IEEE Trans. Robot. 2016, 32, 187–200. [Google Scholar] [CrossRef]
- Deng, Z.; Stommel, M.; Xu, W. Mechatronics design, modeling, and characterization of a soft robotic table for object manipulation on surface. IEEE/ASME Trans. Mechatron. 2018, 23, 2715–2725. [Google Scholar] [CrossRef]
- Wang, W.; Ahn, S.H. Shape memory alloy-based soft gripper with variable stiffness for compliant and effective grasping. Soft Robot. 2017, 4, 379–389. [Google Scholar] [CrossRef]
- Motzki, P.; Khelfa, F.; Zimmer, L.; Schmidt, M.; Seelecke, S. Design and Validation of a reconfigurable Robotic End-Effector Based on Shape Memory Alloys. IEEE/ASME Trans. Mechatron. 2019, 24, 293–303. [Google Scholar] [CrossRef]
- Cao, J.; Liang, W.; Ren, Q.; Gupta, U.; Chen, F.; Zhu, J. Modelling and control of a novel soft crawling robot based on a dielectric elastomer actuator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4188–4193. [Google Scholar]
- Gu, G.Y.; Gupta, U.; Zhu, J.; Zhu, L.M.; Zhu, X. Modeling of viscoelastic electromechanical behavior in a soft dielectric elastomer actuator. IEEE Trans. Robot. 2017, 33, 1263–1271. [Google Scholar] [CrossRef]
- Onal, C.D.; Rus, D. Autonomous undulatory serpentine locomotion utilizing body dynamics of a fluidic soft robot. Bioinspir. Biomim. 2013, 8, 026003. [Google Scholar] [CrossRef]
- Fras, J.; Noh, Y.; Macias, M.; Wurdemann, H.; Althoefer, K. Bio-inspired octopus robot based on novel soft fluidic actuator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1583–1588. [Google Scholar]
- Gong, Z.; Cheng, J.; Chen, X.; Sun, W.; Fang, X.; Hu, K.; Xie, Z.; Wang, T.; Wen, L. A bio-inspired soft robotic arm: Kinematic modeling and hydrodynamic experiments. J. Bionic Eng. 2018, 15, 204–219. [Google Scholar] [CrossRef]
- Tsagarakis, N.G.; Caldwell, D.G. Development and Control of a ’Soft-Actuated’ Exoskeleton for Use in Physiotherapy and Training. Auton. Robot. 2003, 15, 21–33. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 10–21. [Google Scholar]
- Sugar, T.G.; He, J.; Koeneman, E.J.; Koeneman, J.B.; Herman, R.; Huang, H.; Schultz, R.S.; Herring, D.E.; Wanberg, J.; Balasubramanian, S.; et al. Design and control of RUPERT: A device for robotic upper extremity repetitive therapy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 336–346. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.; Wei, R.; Perez, M.; Shepard, B.; Koeneman, E.; Koeneman, J.; He, J. RUPERT: An exoskeleton robot for assisting rehabilitation of arm functions. In Proceedings of the 2008 Virtual Rehabilitation, Vancouver, BC, Canada, 25–27 August 2008; 2008; pp. 163–167. [Google Scholar]
- Huang, J.; Tu, X.; He, J. Design and evaluation of the RUPERT wearable upper extremity exoskeleton robot for clinical and in-home therapies. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 926–935. [Google Scholar] [CrossRef]
- Nef, T.; Mihelj, M.; Colombo, G.; Riener, R. ARMin—Robot for rehabilitation of the upper extremities. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 3152–3157. [Google Scholar]
- Nef, T.; Guidali, M.; Riener, R. ARMin III—Arm Therapy Exoskeleton with an Ergonomic Shoulder Actuation. Appl. Bionics Biomech. 2009, 6, 127–142. [Google Scholar] [CrossRef]
- Just, F.; Ozen, O.; Tortora, S.; Riener, R.; Rauter, G. Feedforward model based arm weight compensation with the rehabilitation robot ARMin. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 72–77. [Google Scholar]
- Mao, Y.; Agrawal, S.K. A cable driven upper arm exoskeleton for upper extremity rehabilitation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4163–4168. [Google Scholar]
- Rahman, M.H.; Saad, M.; Kenné, J.P.; Archambault, P.S. Control of an exoskeleton robot arm with sliding mode exponential reaching law. Int. J. Control Autom. Syst. 2013, 11, 92–104. [Google Scholar] [CrossRef]
- Nuchkrua, T.; Leephakpreeda, T.; Chen, S.L. Experimental validation for fuzzy control of servo pneumatic artificial muscle driven by metal hydride. Int. J. Fuzzy Syst. 2016, 18, 1–15. [Google Scholar] [CrossRef]
- Ahn, K.K.; Anh, H.P.H. Design and implementation of an adaptive recurrent neural networks (ARNN) controller of the pneumatic artificial muscle (PAM) manipulator. Mechatronics 2009, 19, 816–828. [Google Scholar] [CrossRef]
- Kovacs, G.; Lochmatter, P.; Wissler, M. An arm wrestling robot driven by dielectric elastomer actuators. Smart Mater. Struct. 2007, 16, 306. [Google Scholar] [CrossRef]
- Peng, Y.F.; Lin, C.M. Intelligent hybrid control for uncertain nonlinear systems using a recurrent cerebellar model articulation controller. IEE Proc. Control Theory Appl. 2004, 151, 589–600. [Google Scholar] [CrossRef]
- Chen, X.; Liang, W.; Zhao, H.; Al Mamun, A. Adaptive robust controller using intelligent uncertainty observer for mechanical systems under non-holonomic reference trajectories. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Chi, H.; Li, X.; Liang, W.; Wu, Y.; Ren, Q. Motion control of a soft circular crawling robot via iterative learning control. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 6524–6529. [Google Scholar]
- Chen, Z.; Wang, S.; Wang, J.; Xu, K.; Lei, T.; Zhang, H.; Wang, X.; Liu, D.; Si, J. Control strategy of stable walking for a hexapod wheel-legged robot. ISA Trans. 2021, 108, 367–380. [Google Scholar] [CrossRef]
- Krebs, H.I.; Hogan, N.; Volpe, B.; Aisen, M.; Edelstein, L.; Diels, C. Overview of clinical trials with MIT-MANUS: A robot-aided neuro-rehabilitation facility. Technol. Health Care 1999, 7, 419–423. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Liang, W.; Zhu, J.; Ren, Q. Control of a muscle-like soft actuator via a bioinspired approach. Bioinspir. Biomim. 2018, 13, 066005. [Google Scholar] [CrossRef] [PubMed]
- Chi, H.; Li, X.; Liang, W.; Cao, J.; Ren, Q. Iterative learning control for motion trajectory tracking of a circular soft crawling robot. Front. Robot. AI 2019, 6, 113. [Google Scholar] [CrossRef] [PubMed]
- Pardalos, P.M.; Yatsenko, V.A. Optimization and Control of Bilinear Systems: Theory, Algorithms, and Applications; Springer: New York, NY, USA, 2010; Volume 11. [Google Scholar]
- Kiong Tan, K.; Liang, W.; Huang, S.; Pham, L.P.; Chen, S.; Wee Gan, C.; Yee Lim, H. Precision control of piezoelectric ultrasonic motor for myringotomy with tube insertion. J. Dyn. Syst. Meas. Control 2015, 137, 064504. [Google Scholar] [CrossRef]
- Albus, J.S. A new approach to manipulator control: The cerebellar model articulation controller (CMAC). J. Dyn. Syst. Meas. Control 1975, 97, 220–227. [Google Scholar] [CrossRef]
- Ouyang, W.; Liang, W.; Li, C.; Zheng, H.; Ren, Q.; Li, P. Steering motion control of a snake robot via a biomimetic approach. Front. Inf. Technol. Electron. Eng. 2019, 20, 32–44. [Google Scholar] [CrossRef]
- DE, R.; Mcclelland, J. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]




| 0.0893 | |||
| 0.1768 | |||
| 1.49 | 0.06 | ||
| 0.328 | 0.09 | ||
| 0.447 | |||
| 0.857 | |||
| Curve Type | MSE | MAPE | RMSE | R-Squared | |
|---|---|---|---|---|---|
| Identification | Sweep (0.2 to 1 Hz) | 0.1103 | 0.0024 | 0.9553 | |
| Sweep (30 to 300 N) | 0.1102 | 0.0028 | 0.9565 | ||
| Validation | Square (0.5 Hz) | 0.1183 | 0.0024 | 0.9312 | |
| Square (1 Hz) | 0.1068 | 0.0025 | 0.8591 | ||
| Triangle (0.5 Hz) | 0.1163 | 0.0018 | 0.8701 | ||
| Triangle (1 Hz) | 0.1035 | 0.0023 | 0.8534 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, H.; Su, H.; Liang, W.; Ren, Q. Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators. Actuators 2021, 10, 123. https://doi.org/10.3390/act10060123
Chi H, Su H, Liang W, Ren Q. Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators. Actuators. 2021; 10(6):123. https://doi.org/10.3390/act10060123
Chicago/Turabian StyleChi, Haozhen, Hairong Su, Wenyu Liang, and Qinyuan Ren. 2021. "Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators" Actuators 10, no. 6: 123. https://doi.org/10.3390/act10060123
APA StyleChi, H., Su, H., Liang, W., & Ren, Q. (2021). Control of a Rehabilitation Robotic Device Driven by Antagonistic Soft Actuators. Actuators, 10(6), 123. https://doi.org/10.3390/act10060123






