A Robust Noise-Free Linear Control Design for Robot Manipulator with Uncertain System Parameters
Abstract
1. Introduction
2. Problem Description
3. Preliminary
4. Stability Analysis
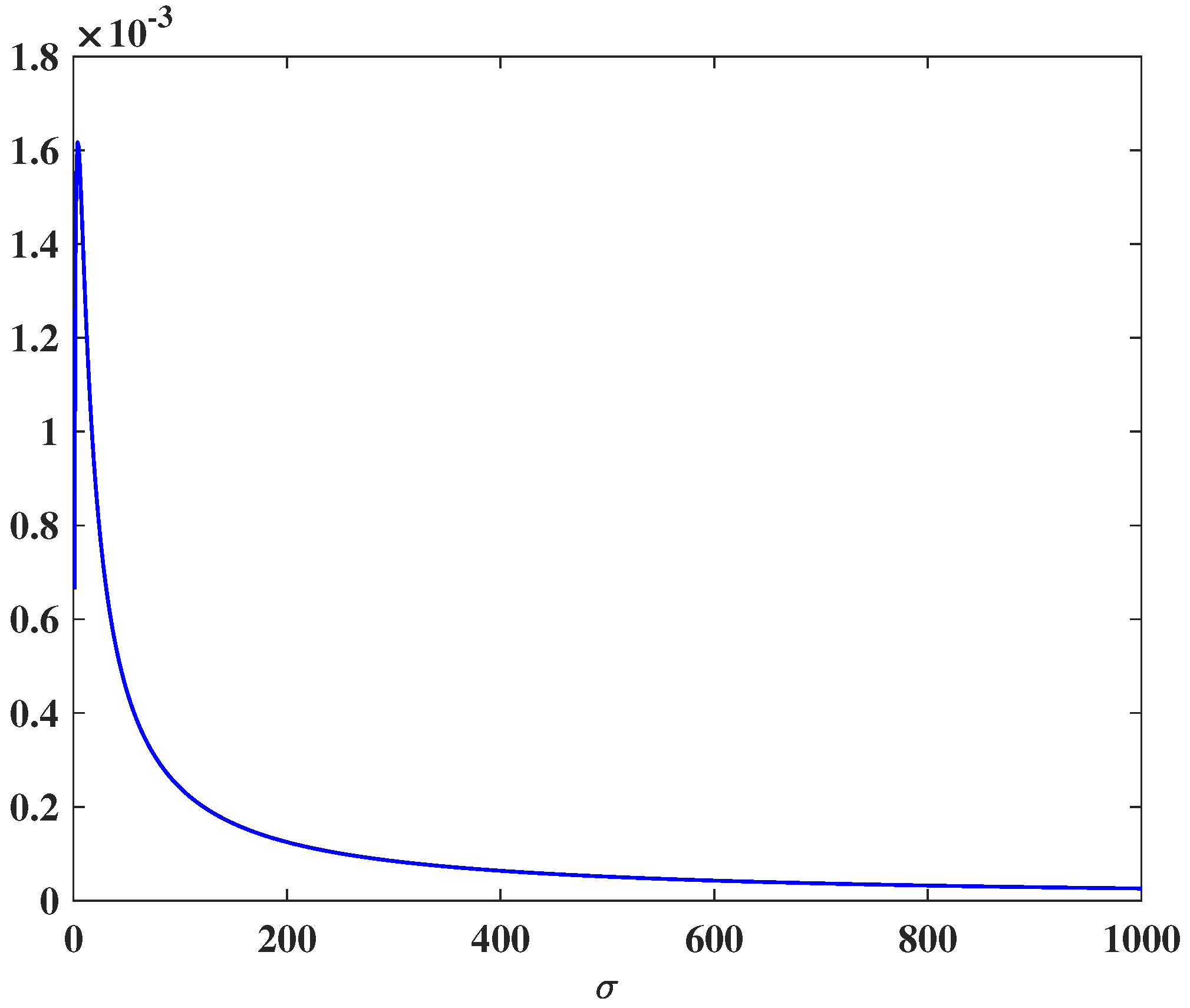
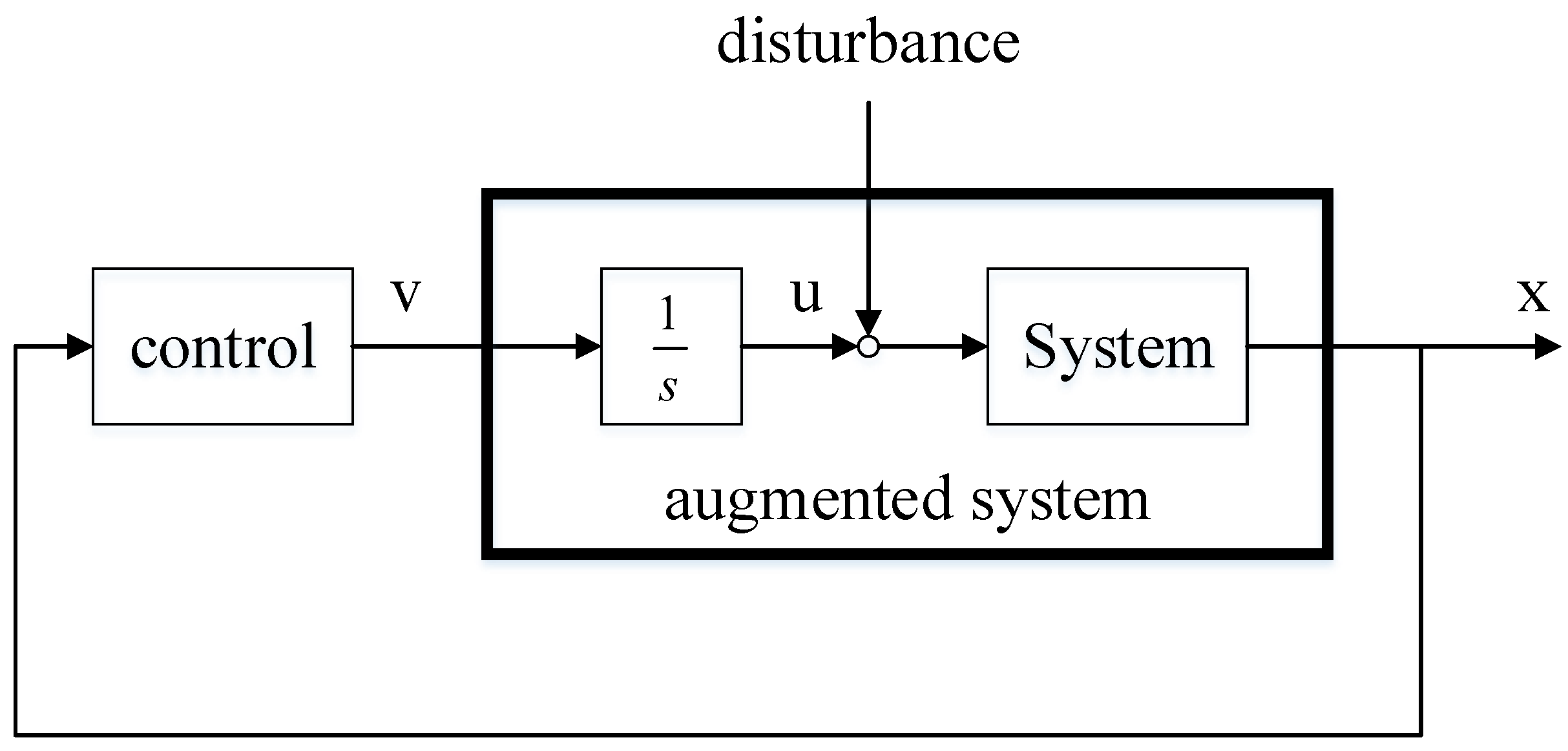
5. Noise-Free Control Design
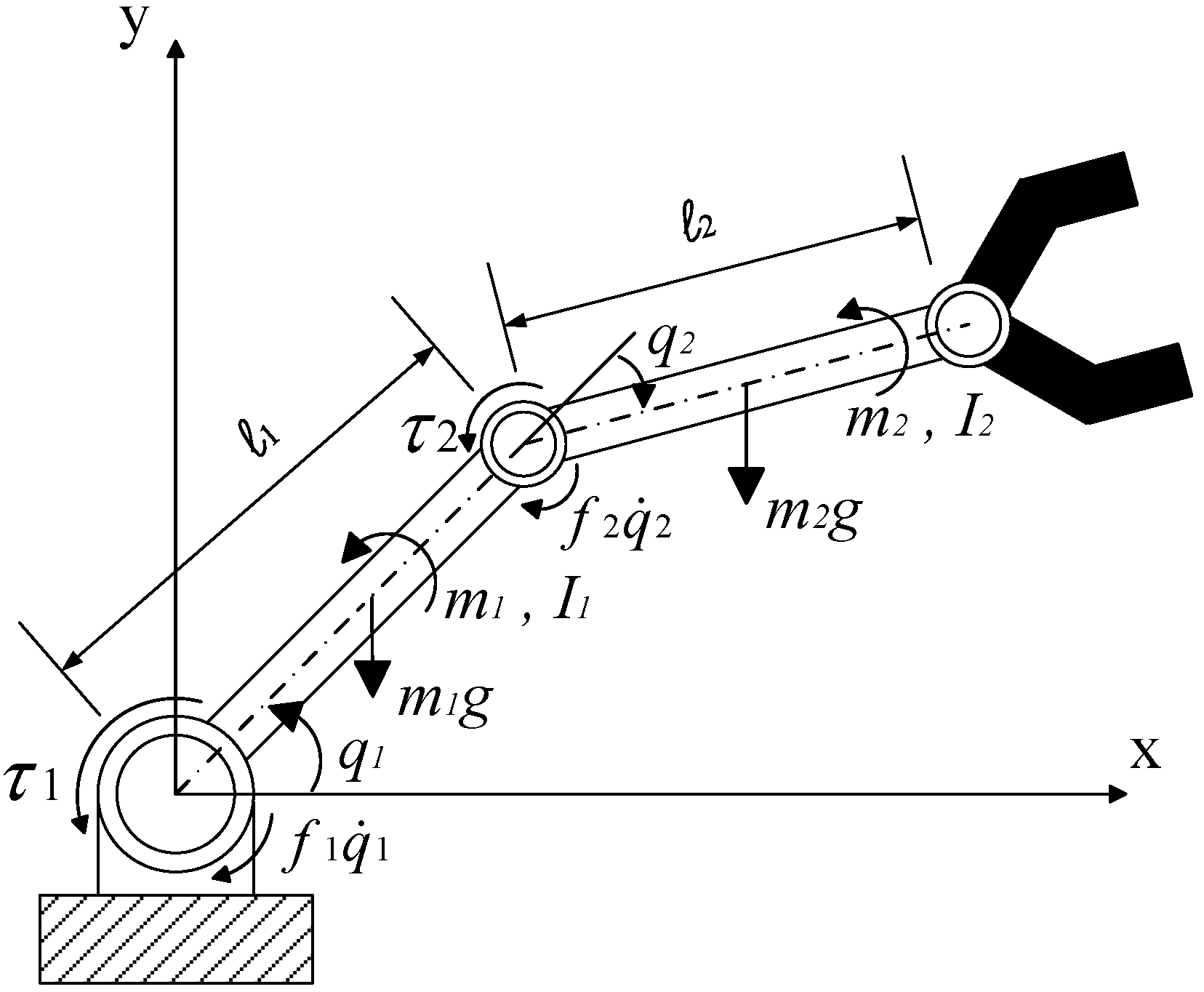
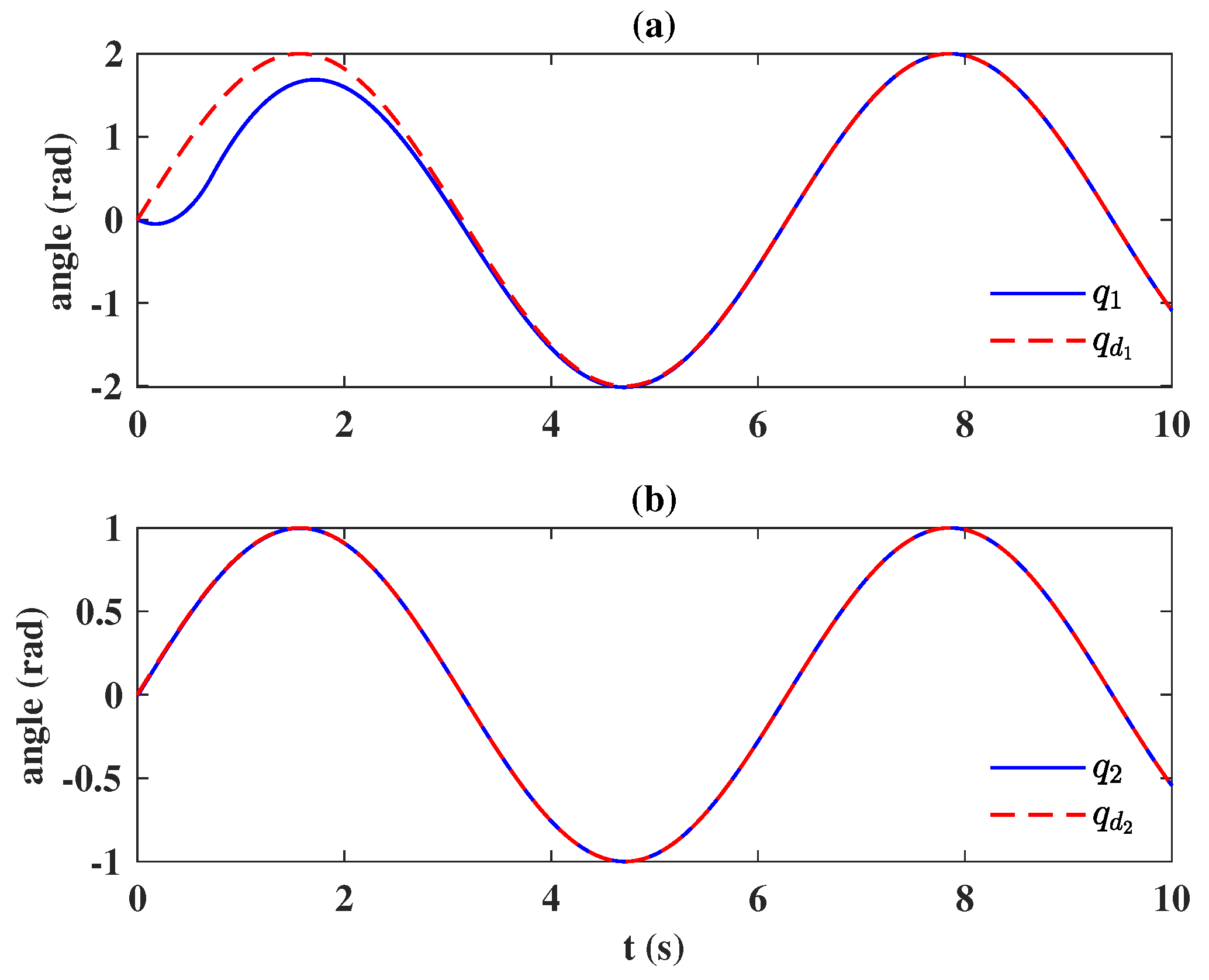
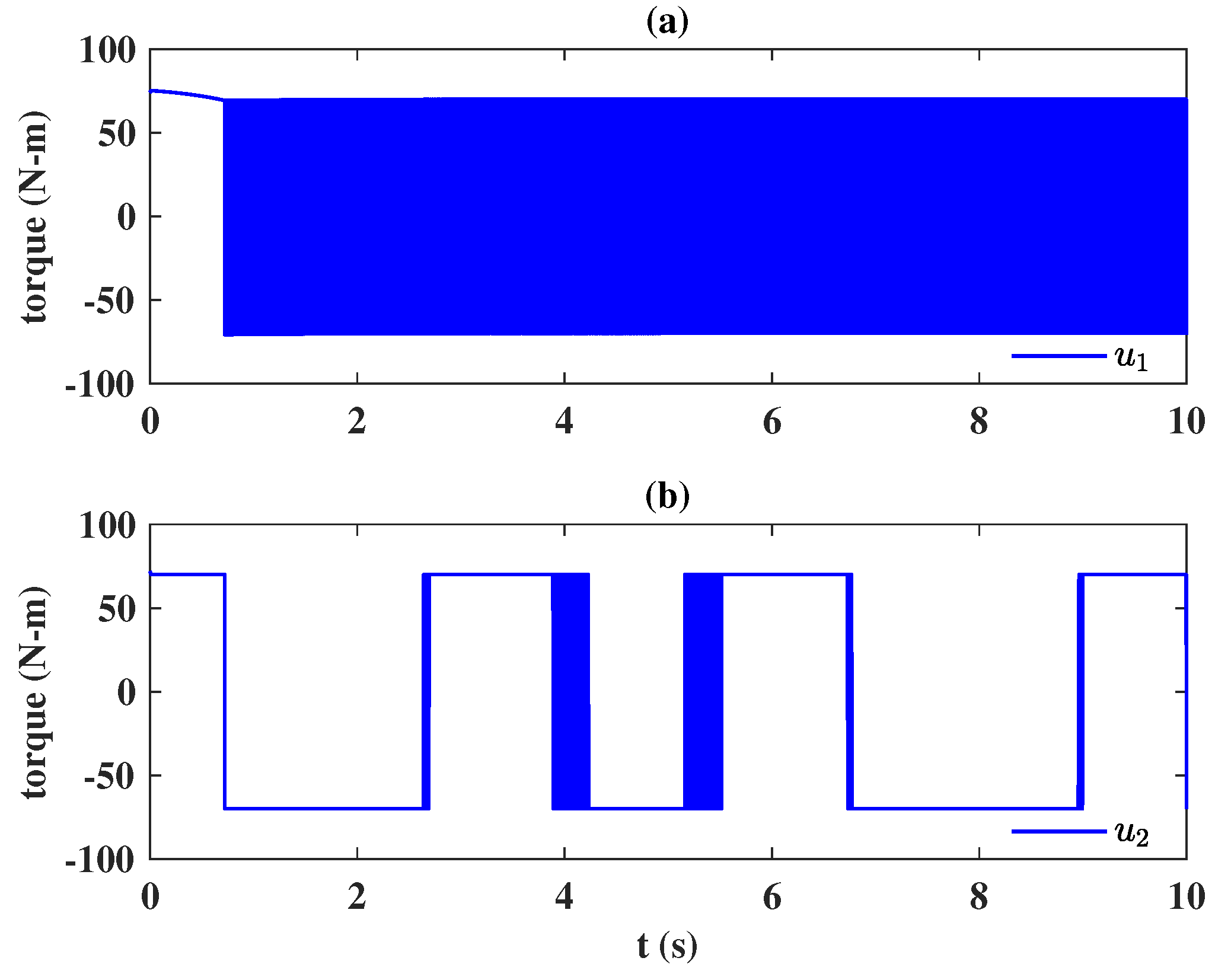
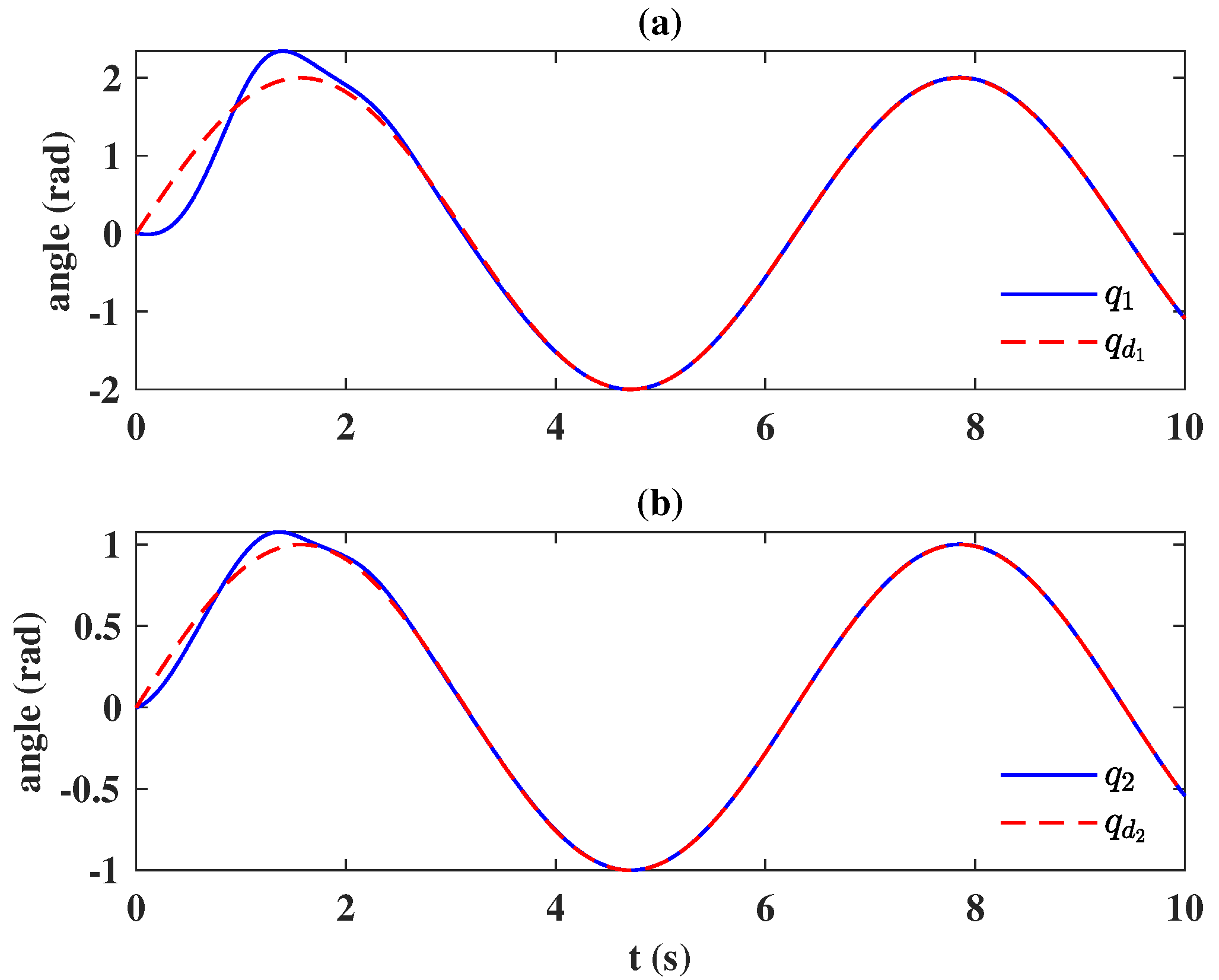
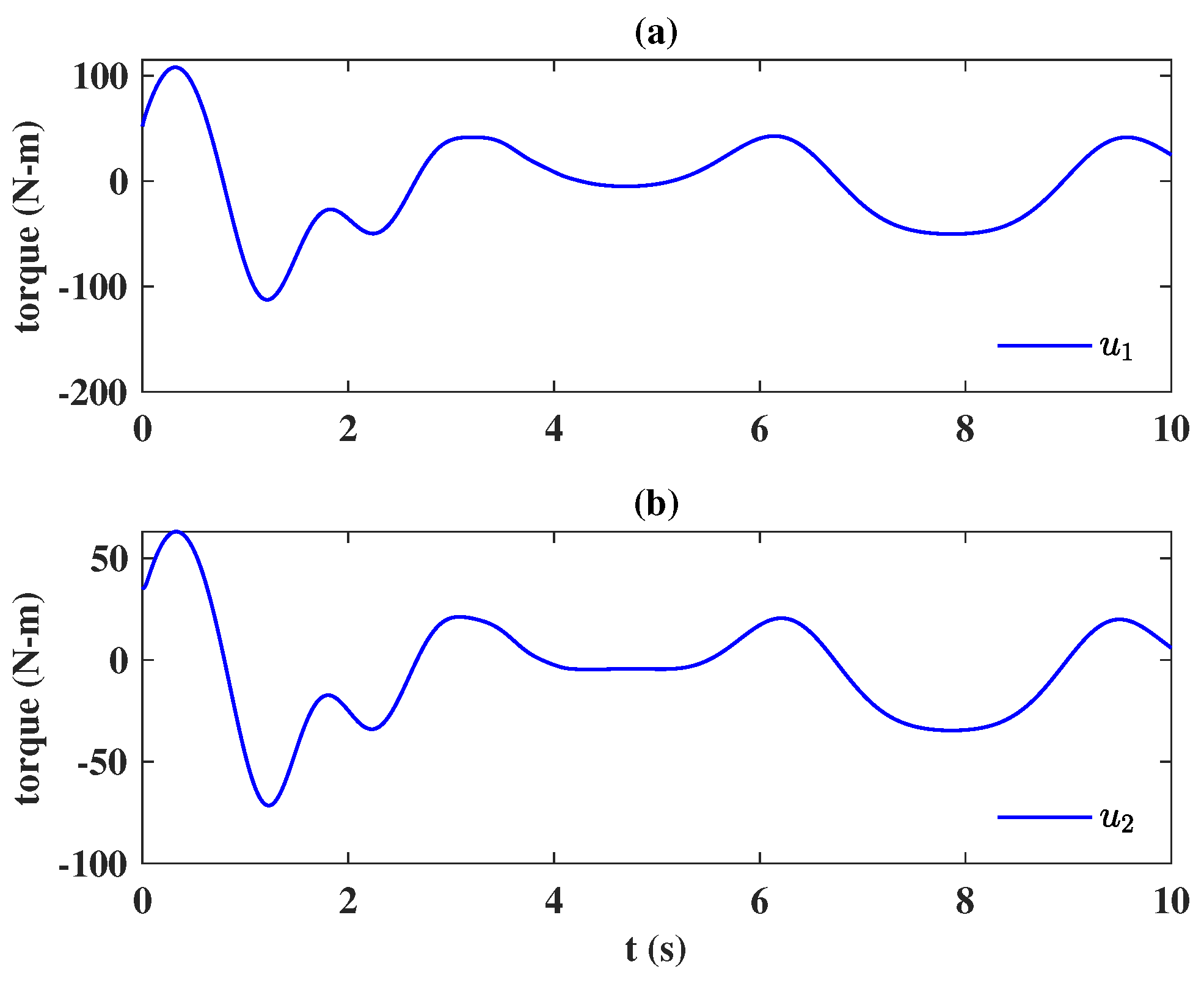
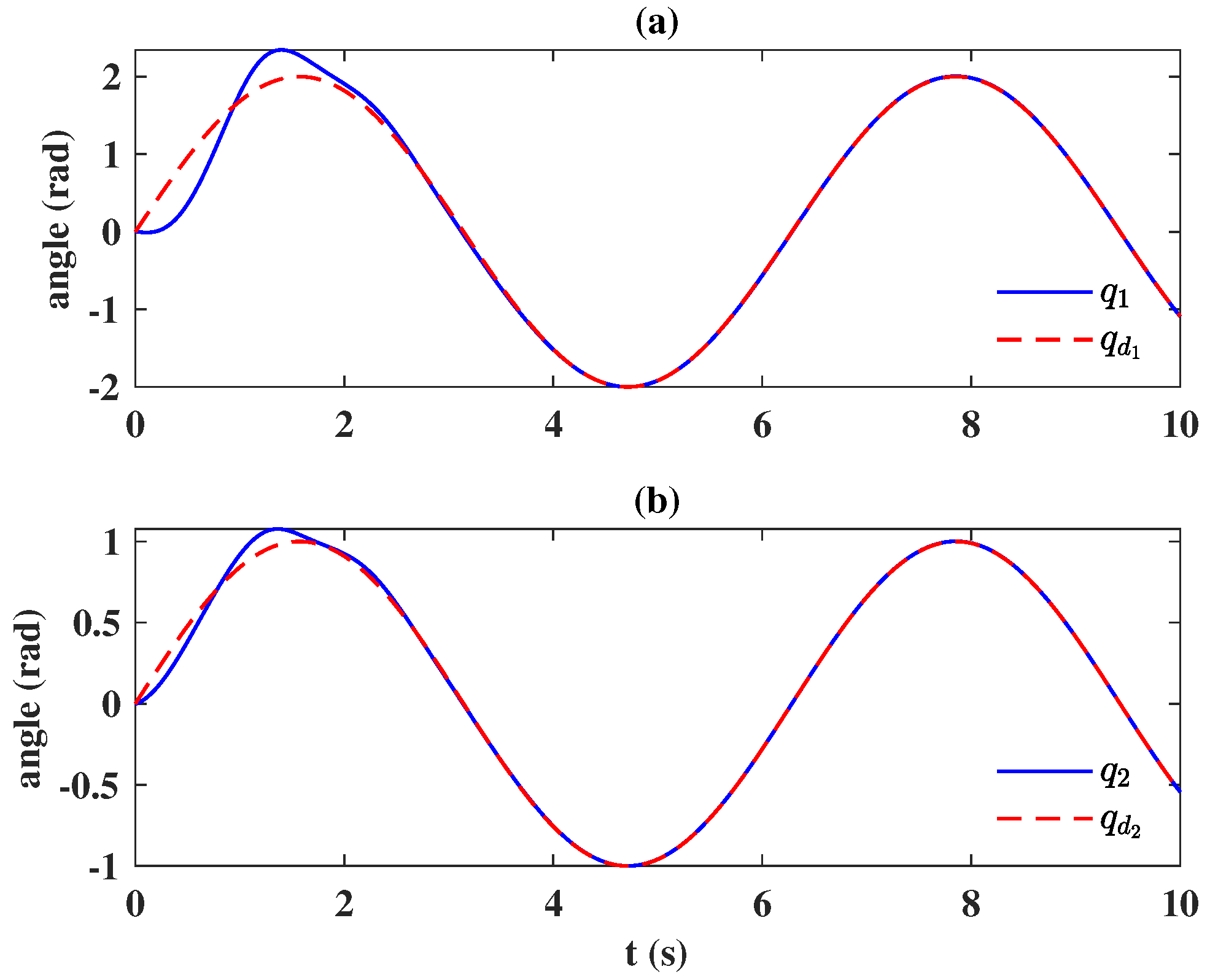
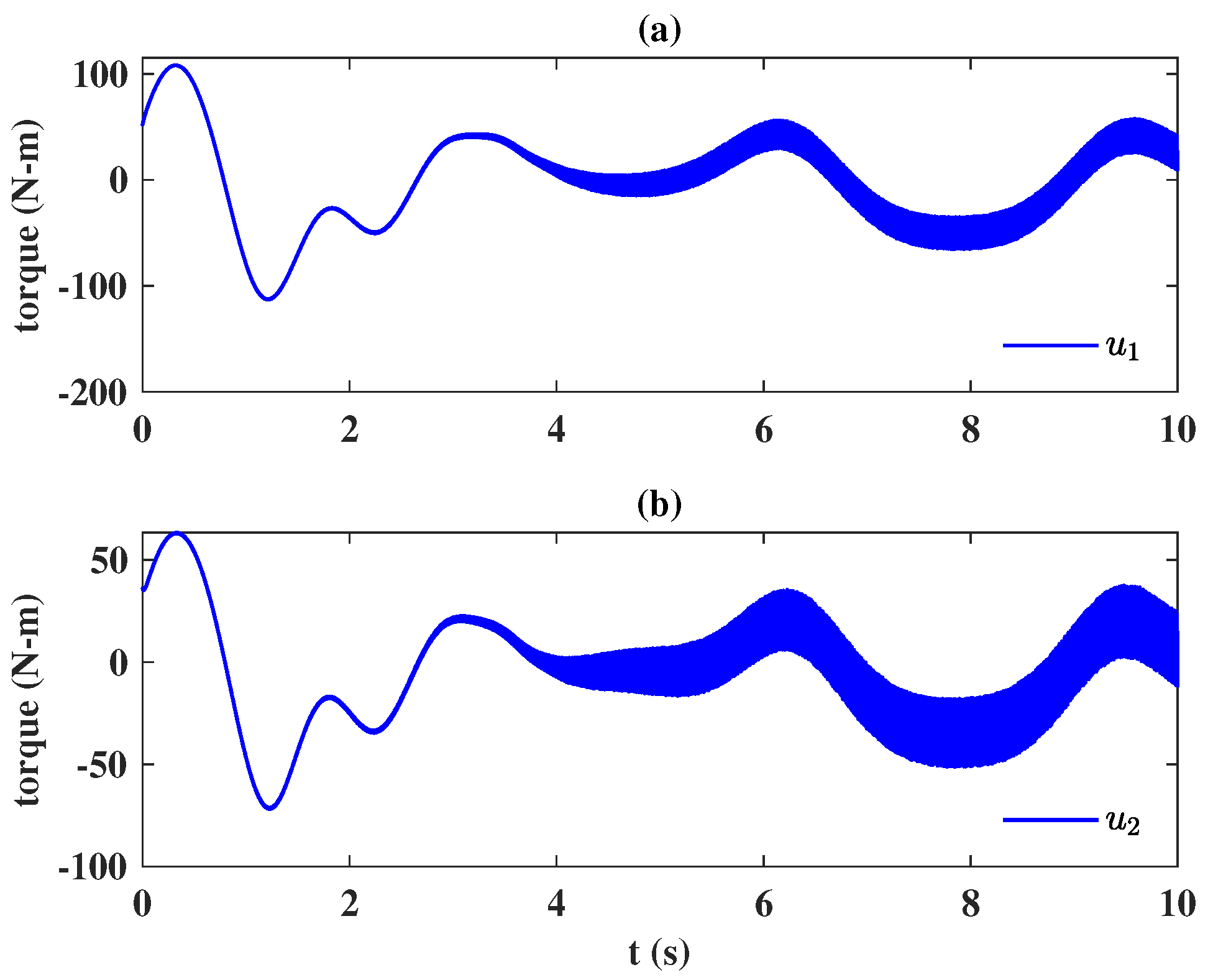
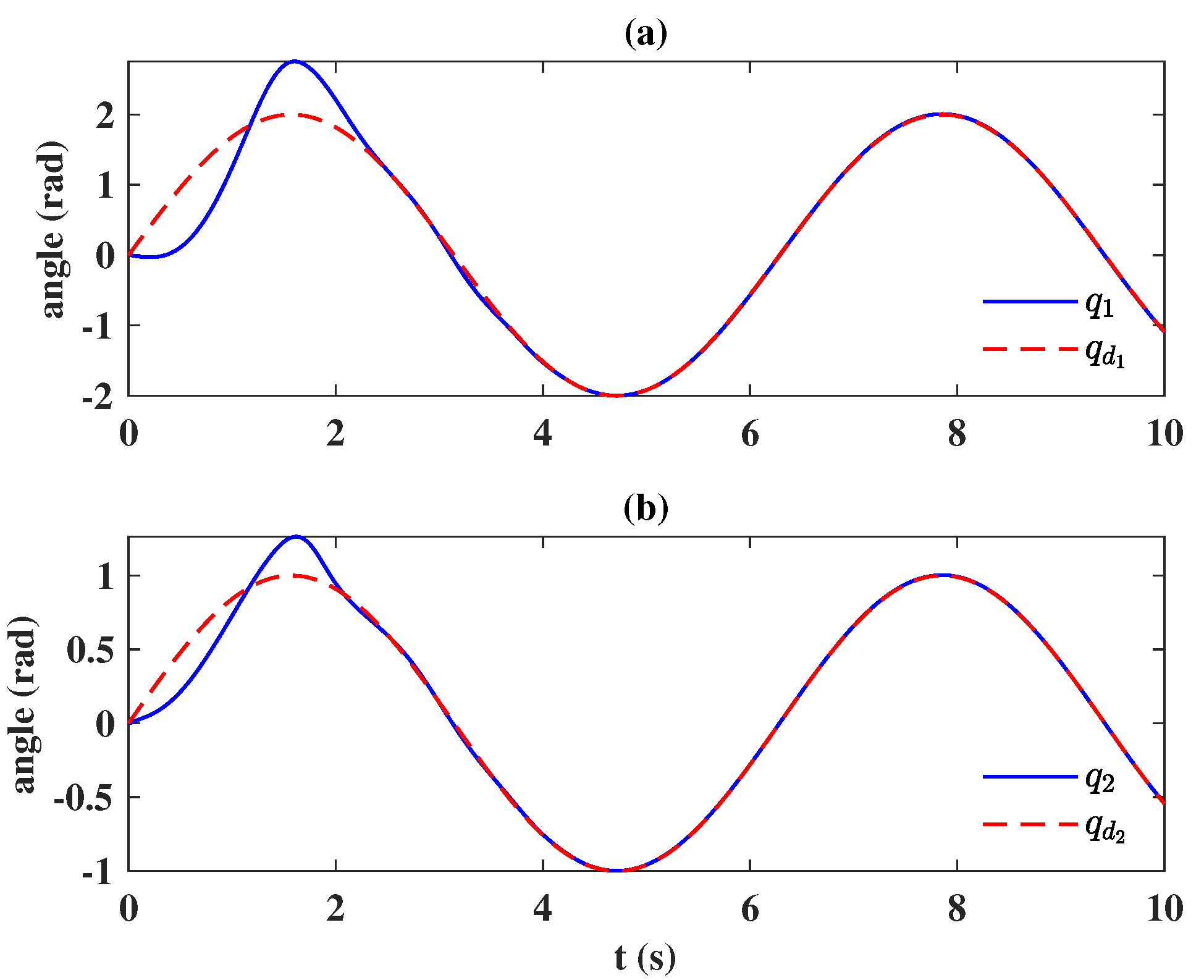
6. Application to a Two DOF Robot Manipulator
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lewis, F.L.; Dawson, D.M.; Abdallah, C.T. Robot Manipulator Control: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Callier, F.M.; Desoer, C.A. Linear System Theory; Springer Science & Business Media: Boston, NY, USA, 2012; Chapter 7.2. [Google Scholar]
- Slotine, J.J.E.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. Adaptive Control for Robotic Manipulators; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Jin, M.; Lee, J.; Tsagarakis, N.G. Model-free robust adaptive control of humanoid robots with flexible joints. IEEE Trans. Ind. Electron. 2016, 64, 1706–1715. [Google Scholar] [CrossRef]
- Slotine, J.J.; Sastry, S.S. Tracking control of non-linear systems using sliding surfaces, with application to robot manipulators. Int. J. Control 1983, 38, 465–492. [Google Scholar] [CrossRef]
- Doulgeri, Z. Sliding regime of a nonlinear robust controller for robot manipulators. IEE Proc. Control Theory Appl. 1999, 146, 493–498. [Google Scholar] [CrossRef]
- Fu, L.C.; Liao, T.L. Systems Using Variable Structure Control and with an Application to a Robotic. IEEE Trans. Autom. Control 1990, 35, 1345–1350. [Google Scholar] [CrossRef]
- Lin, C.J. Variable structure model following control of robot manipulators with high-gain observer. JSME Int. J. Ser. Mech. Syst. Mach. Elem. Manuf. 2004, 47, 591–601. [Google Scholar] [CrossRef]
- Islam, S.; Liu, X.P. Robust sliding mode control for robot manipulators. IEEE Trans. Ind. Electron. 2010, 58, 2444–2453. [Google Scholar] [CrossRef]
- Navvabi, H.; Markazi, A.H. New AFSMC method for nonlinear system with state-dependent uncertainty: Application to hexapod robot position control. J. Intell. Robot. Syst. 2019, 95, 61–75. [Google Scholar] [CrossRef]
- He, W.; Dong, Y.; Sun, C. Adaptive neural impedance control of a robotic manipulator with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 334–344. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Yu, J.; He, J. Robot manipulator control using neural networks: A survey. Neurocomputing 2018, 285, 23–34. [Google Scholar] [CrossRef]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. An improved neural network algorithm to efficiently track various trajectories of robot manipulator arms. IEEE Access 2021, 9, 11911–11920. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gao, W.; Hung, J.C. Variable structure control: A survey. IEEE Trans. Ind. Electron. 1993, 40, 2–22. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; Chapter 14. [Google Scholar]
- Fridman, L.M. An averaging approach to chattering. IEEE Trans. Autom. Control 2001, 46, 1260–1265. [Google Scholar] [CrossRef]
- Boiko, I. Discontinuous Control Systems: Frequency-Domain Analysis and Design; Springer Science & Business Media: Boston, NY, USA, 2008. [Google Scholar]
- Burton, J.; Zinober, A.S. Continuous approximation of variable structure control. Int. J. Syst. Sci. 1986, 17, 875–885. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation, and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Tayebi-Haghighi, S.; Piltan, F.; Kim, J.M. Robust composite high-order super-twisting sliding mode control of robot manipulators. Robotics 2018, 7, 13. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Tian, Y. Adaptive high-order terminal sliding mode control based on time delay estimation for the robotic manipulators with backlash hysteresis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1128–1137. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Tian, Y. Adaptive Fractional High-order Terminal Sliding Mode Control for Nonlinear Robotic Manipulator under Alternating Loads. Asian J. Control 2020. [Google Scholar] [CrossRef]
- Brahmi, B.; Driscoll, M.; Laraki, M.H.; Brahmi, A. Adaptive high-order sliding mode control based on quasi-time delay estimation for uncertain robot manipulator. Control Theory Technol. 2020, 18, 279–292. [Google Scholar] [CrossRef]
- Yeh, Y.L.; Chen, M.S. Frequency domain analysis of noise-induced control chattering in sliding mode controls. Int. J. Robust Nonlinear Control 2011, 21, 1975–1980. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Estrada, A.; Fridman, L.M. Global and exact HOSM differentiator with dynamic gains for output-feedback sliding mode control. Automatica 2017, 81, 156–163. [Google Scholar] [CrossRef]
- Chen, B.S.; Wong, C.C. Robust linear controller design: Time domain approach. IEEE Trans. Autom. Control 1987, 32, 161–164. [Google Scholar] [CrossRef]
- Sobel, K.M.; Bandaj, S.S.; Yeh, H.H. Robust control for linear systems with structured state space uncertainty. Int. J. Control 1989, 50, 1991–2004. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer Science & Business Media: Boston, NY, USA, 2010; Chapter 9.3. [Google Scholar]
- Draženović, B. The invariance conditions in variable structure systems. Automatica 1969, 5, 287–295. [Google Scholar] [CrossRef]
- Bronson, R.; Saccoman, J.T.; Costa, G.B. Linear Algebra: Algorithms, Applications, and Techniques; Academic Press: Cambridge, MA, USA, 2013; Chapter 4.3. [Google Scholar]
- Chen, C.T. Linear System Theory and Design; Holt, Rinehart and Winston: New York, NY, USA, 1984; Chapter 4.4. [Google Scholar]
- Chen, M.S.; Chen, C.H.; Yang, F.Y. An LTR-observer-based dynamic sliding mode control for chattering reduction. Automatica 2007, 43, 1111–1116. [Google Scholar] [CrossRef]
- Vidyasagar, M. Nonlinear Systems Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993; Chapter 5.4. [Google Scholar]

| Parameters | Value |
|---|---|
| 1 m | |
| 2 m | |
| 1 kg | |
| 1 kg | |
| 1 m | |
| 2 m | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, Y.-L. A Robust Noise-Free Linear Control Design for Robot Manipulator with Uncertain System Parameters. Actuators 2021, 10, 121. https://doi.org/10.3390/act10060121
Yeh Y-L. A Robust Noise-Free Linear Control Design for Robot Manipulator with Uncertain System Parameters. Actuators. 2021; 10(6):121. https://doi.org/10.3390/act10060121
Chicago/Turabian StyleYeh, Yi-Liang. 2021. "A Robust Noise-Free Linear Control Design for Robot Manipulator with Uncertain System Parameters" Actuators 10, no. 6: 121. https://doi.org/10.3390/act10060121
APA StyleYeh, Y.-L. (2021). A Robust Noise-Free Linear Control Design for Robot Manipulator with Uncertain System Parameters. Actuators, 10(6), 121. https://doi.org/10.3390/act10060121






