Dynamic Performance Analysis of a Compact Annular-Radial-Orifice Flow Magnetorheological Valve and Its Application in the Valve Controlled Cylinder System
Abstract
1. Introduction
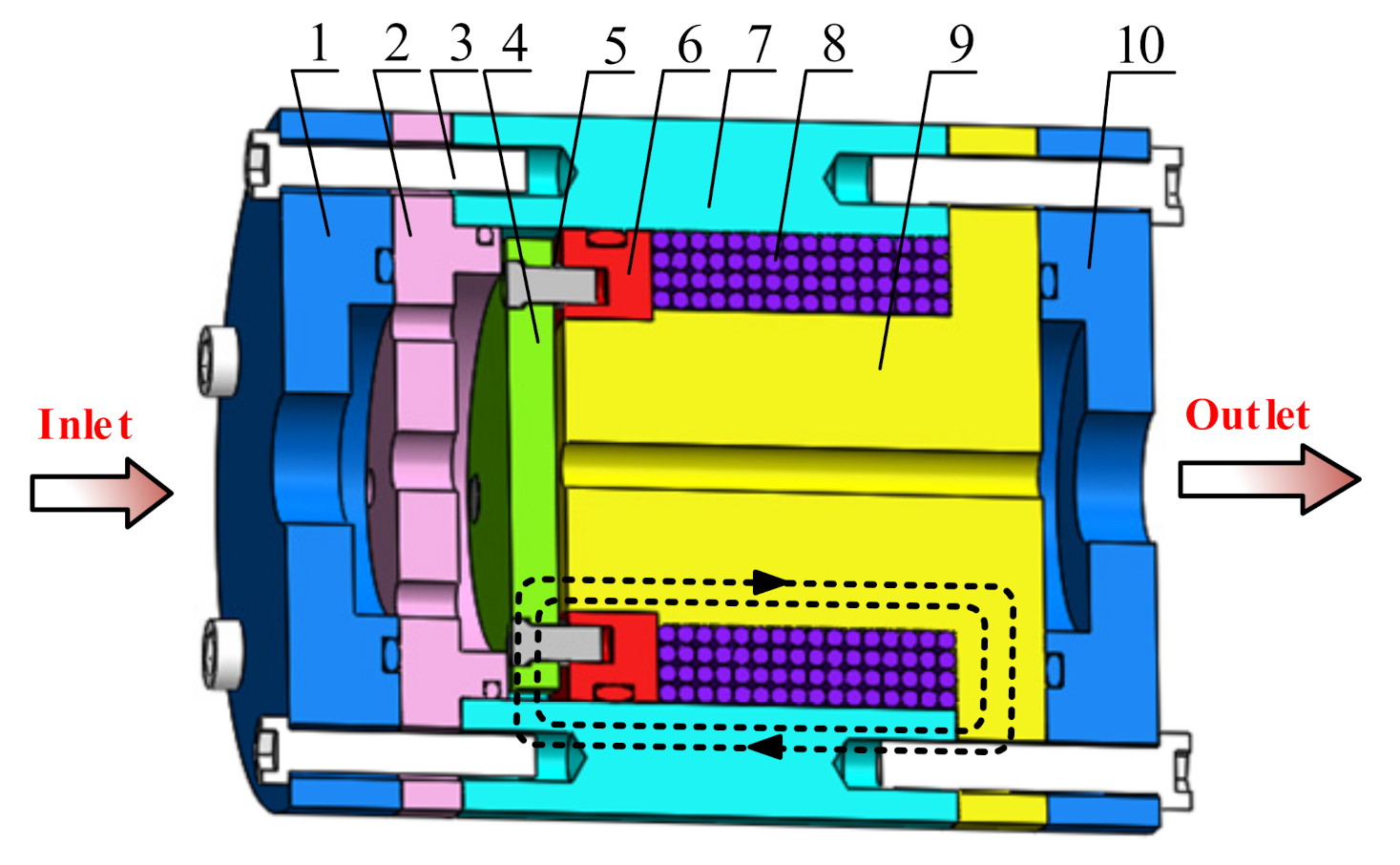
2. Design and Development of a Compact Annular-Radial-Orifice Flow MR Valve
2.1. Principle and Structure Analysis
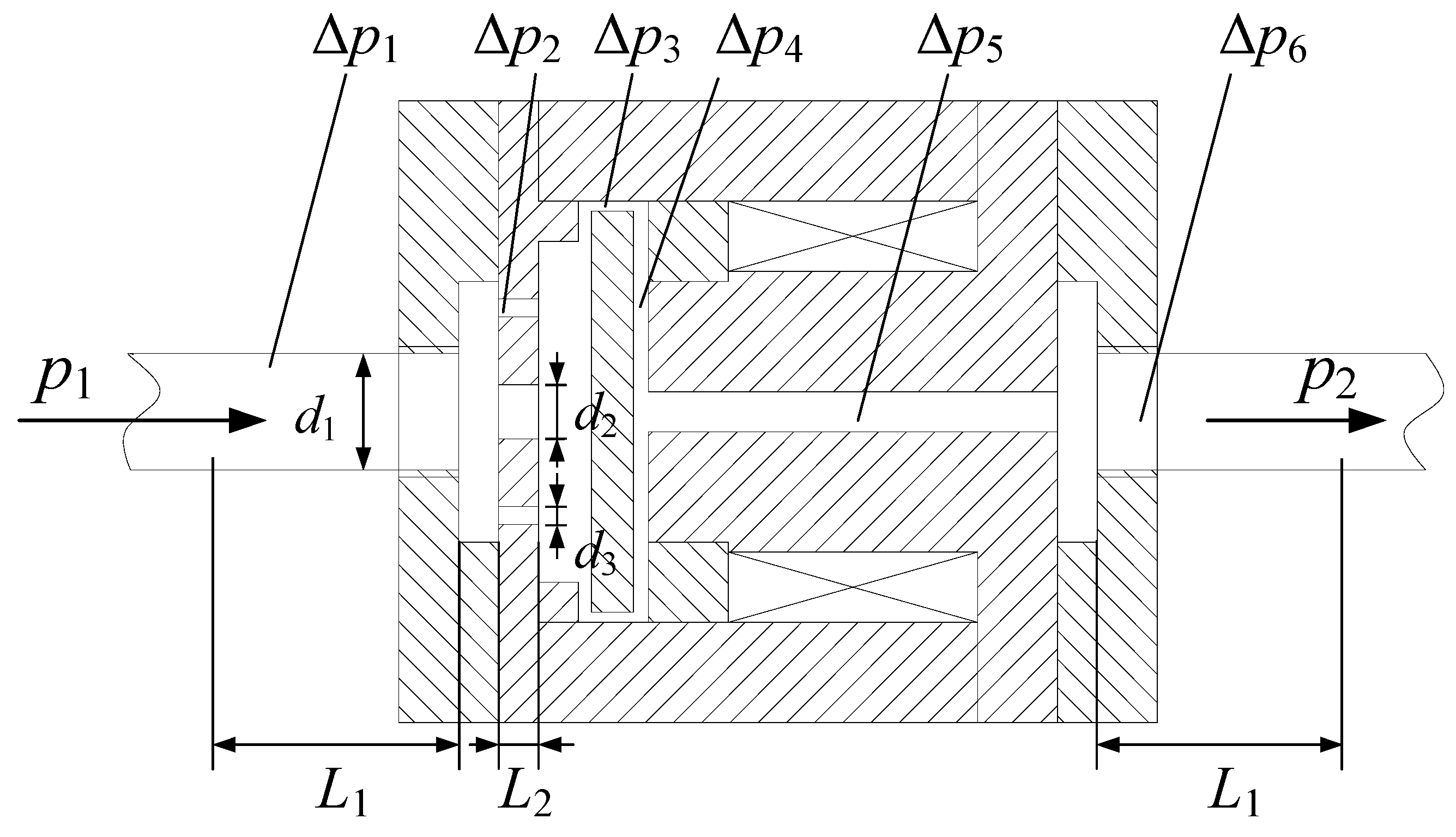
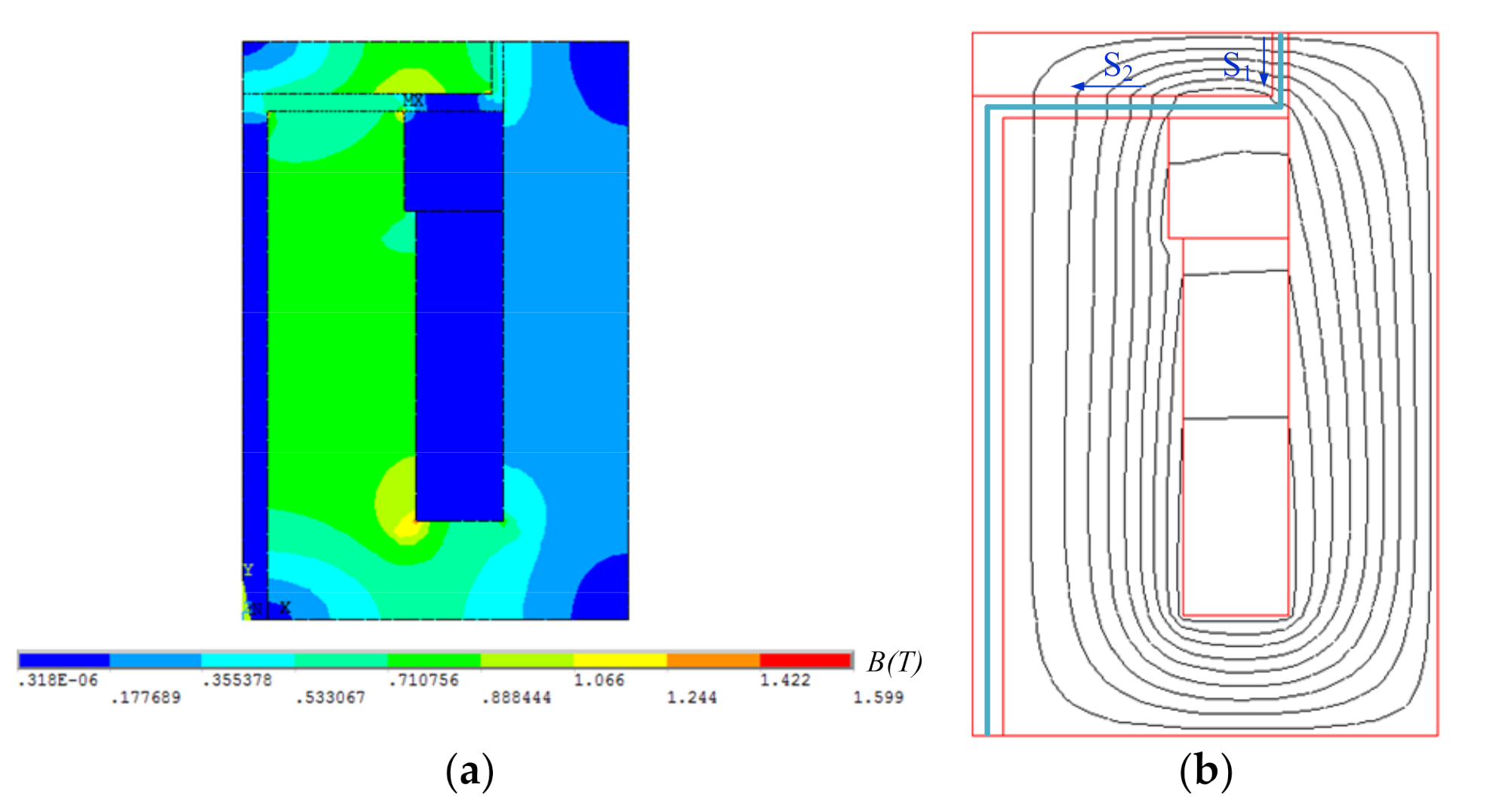
2.2. Magnetic Circuit Analysis
2.3. Mathematic Modeling of Pressure Drop
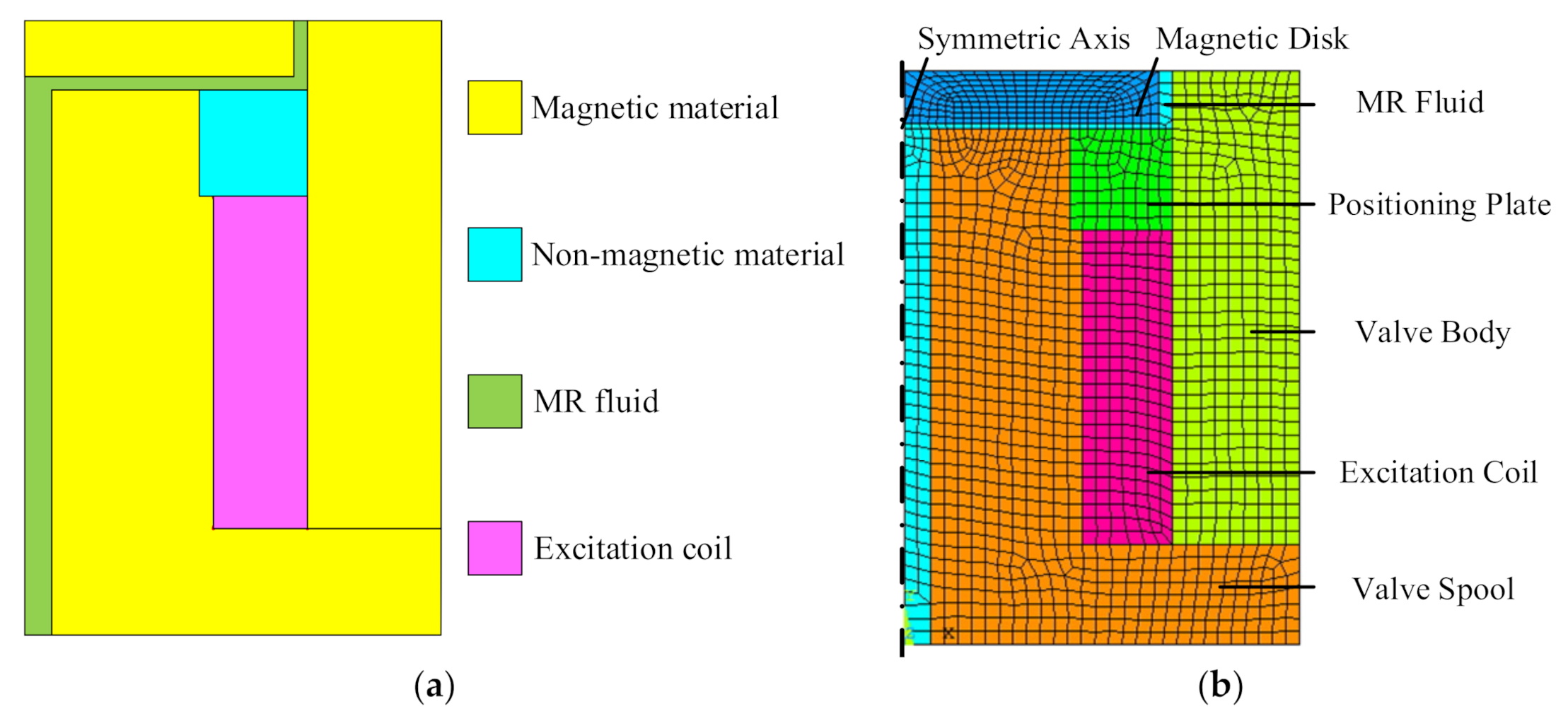
3. Magnetic Field Simulation of the Compact Annular-Radial-Orifice Flow MR Valve
3.1. Properties of the MR Fluid
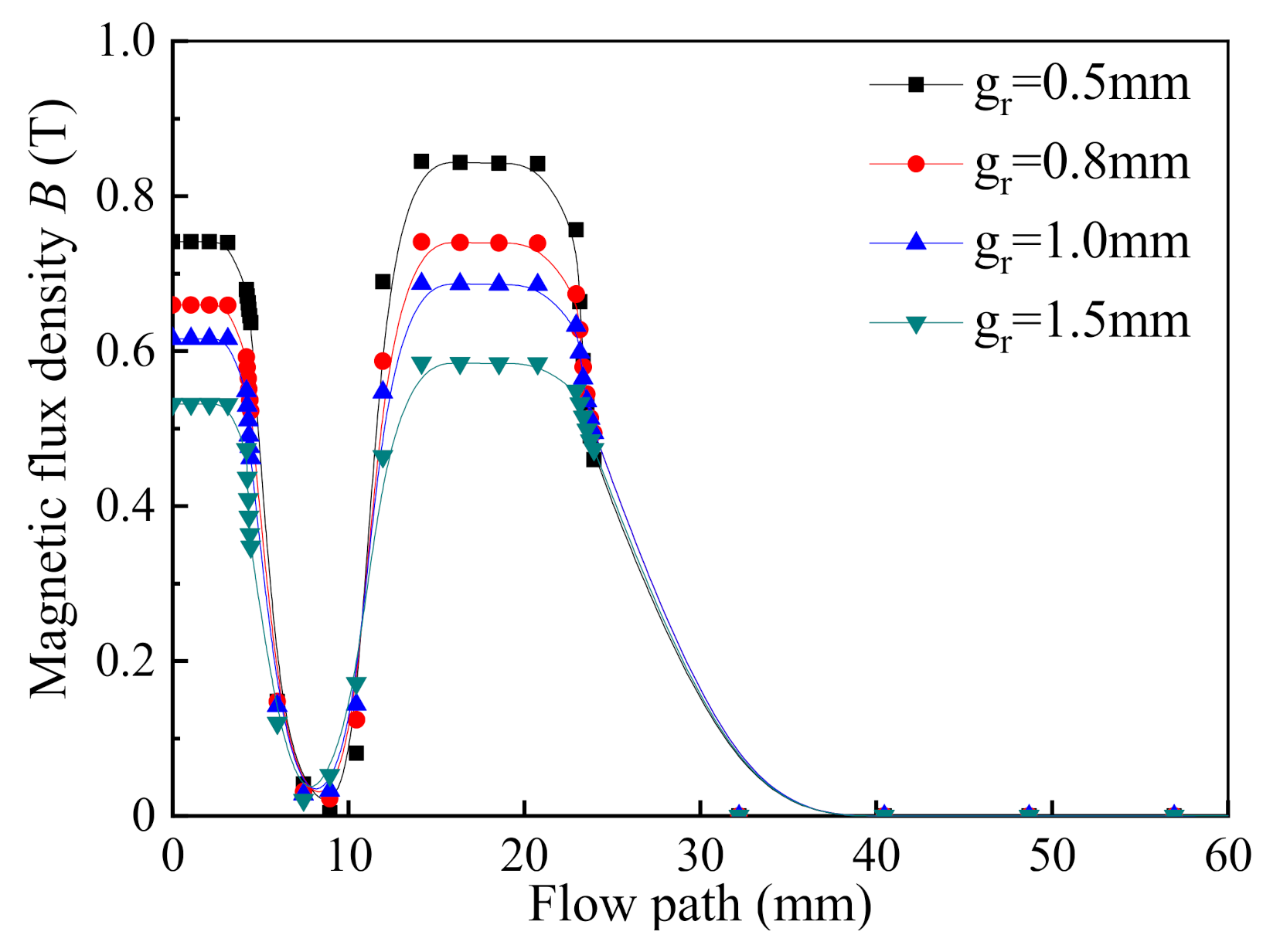
3.2. Finite Element Analysis of the Proposed MR Valve
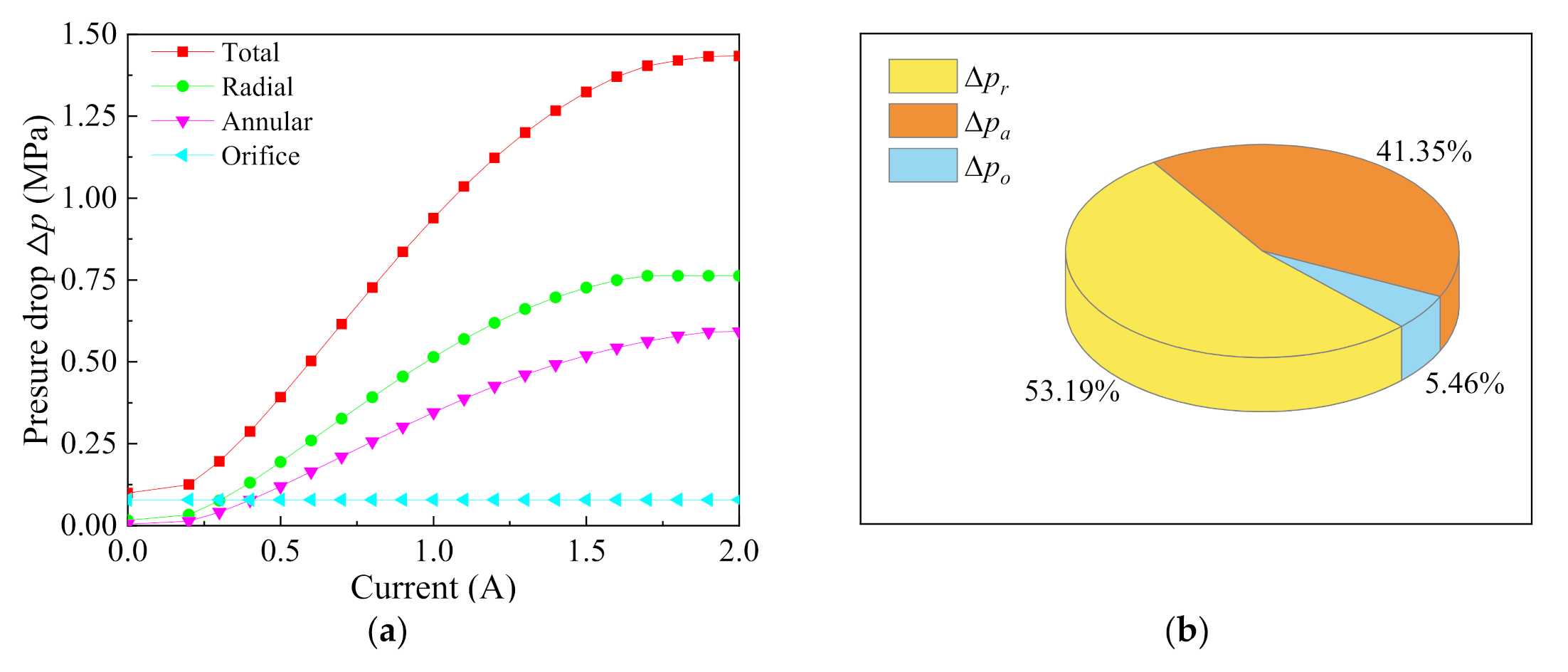
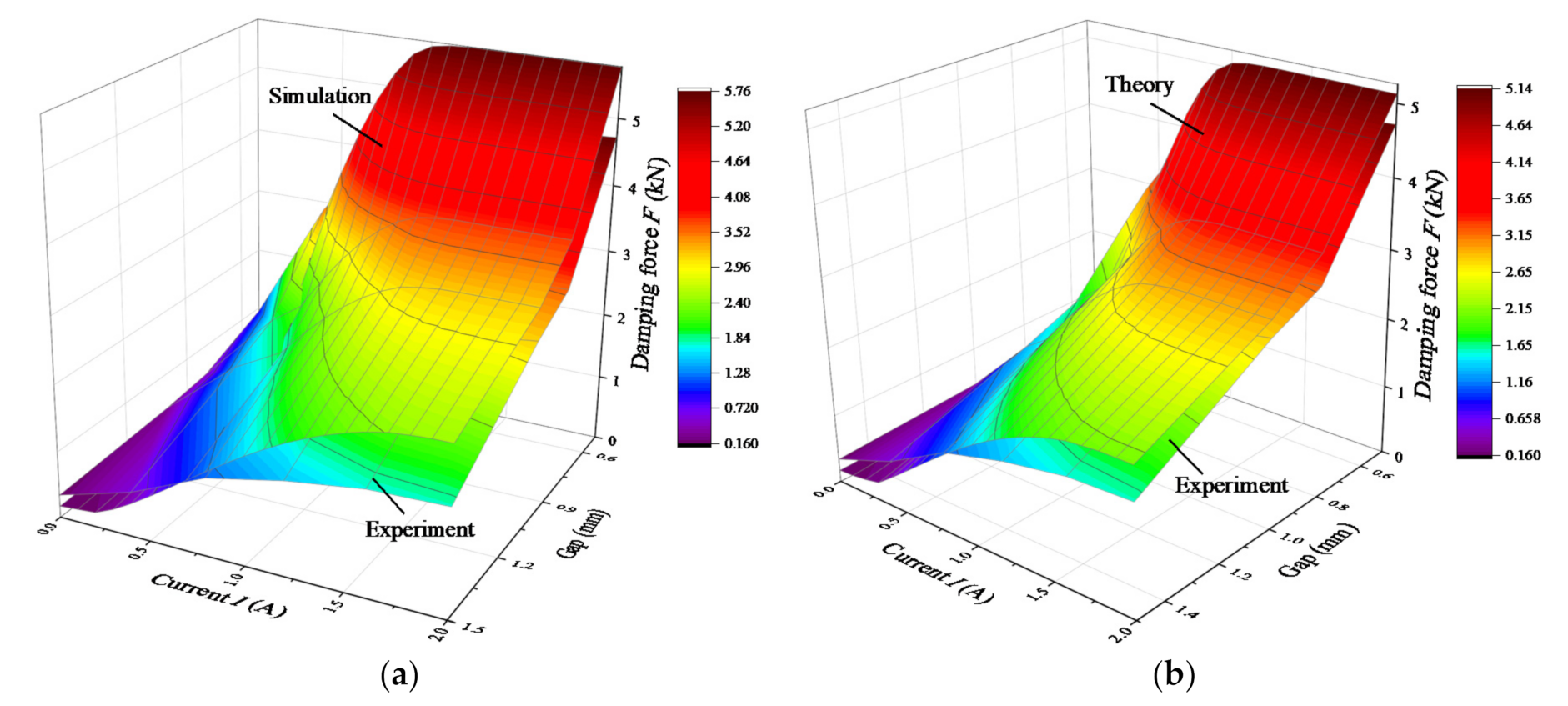
3.3. Simulation Analysis of Pressure Drop
4. Experimental Analysis of the Compact Annular-Radial-Orifice Flow MR Valve
4.1. Prototyping of the Proposed MR Valve
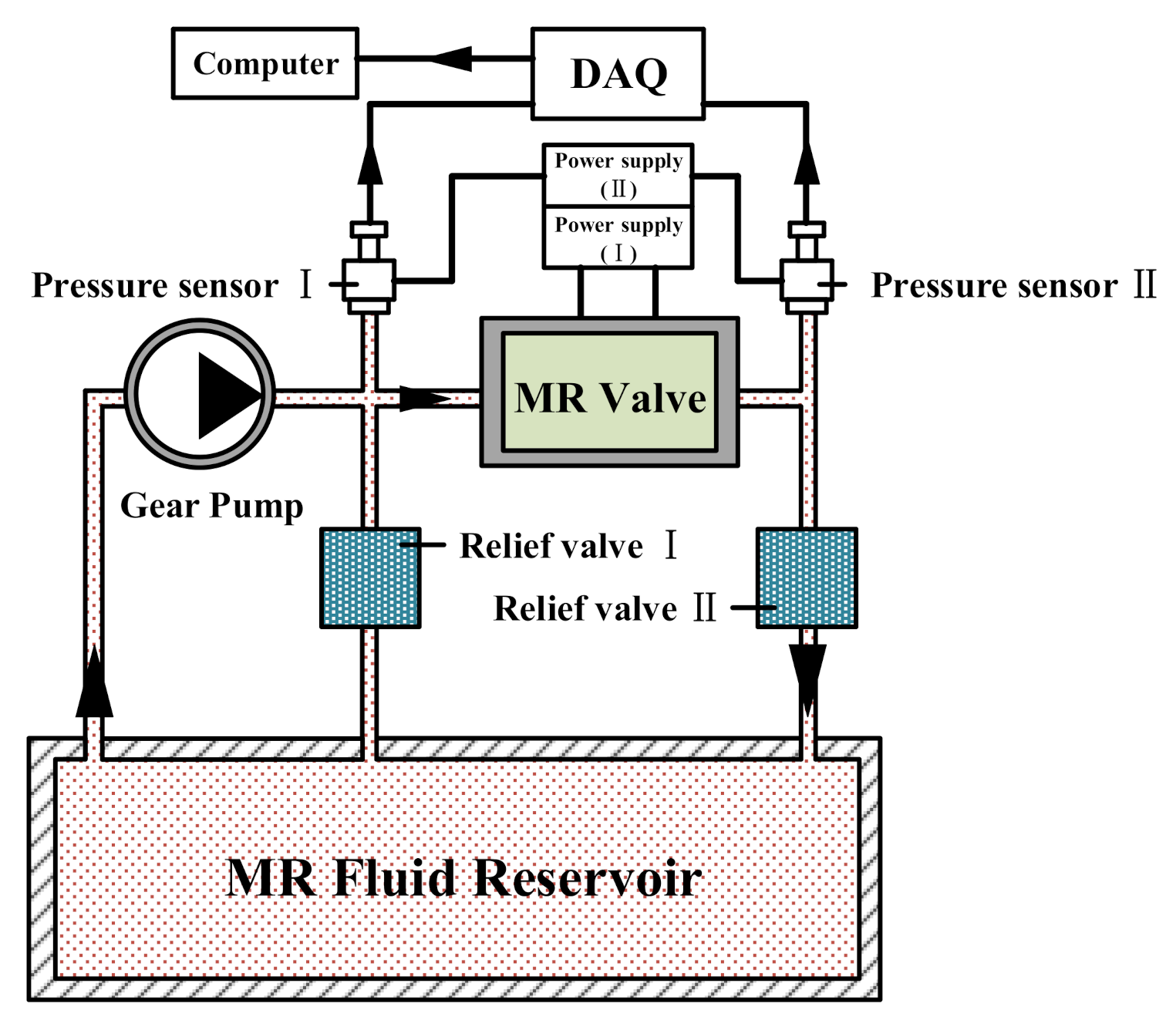
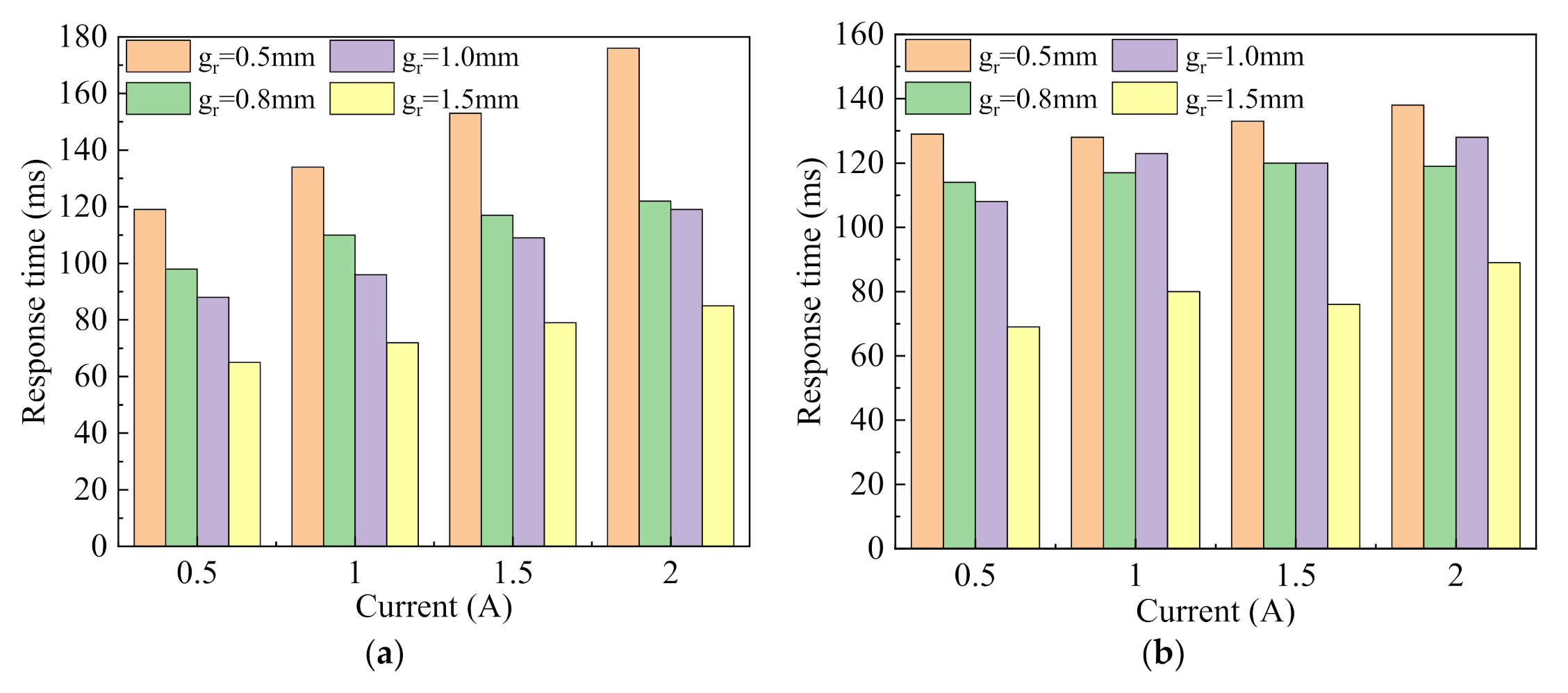
4.2. Experimental Analysis of Pressure Drop Performance and Response Characteristic
5. Experimental Analysis of the Valve Controlled Cylinder System
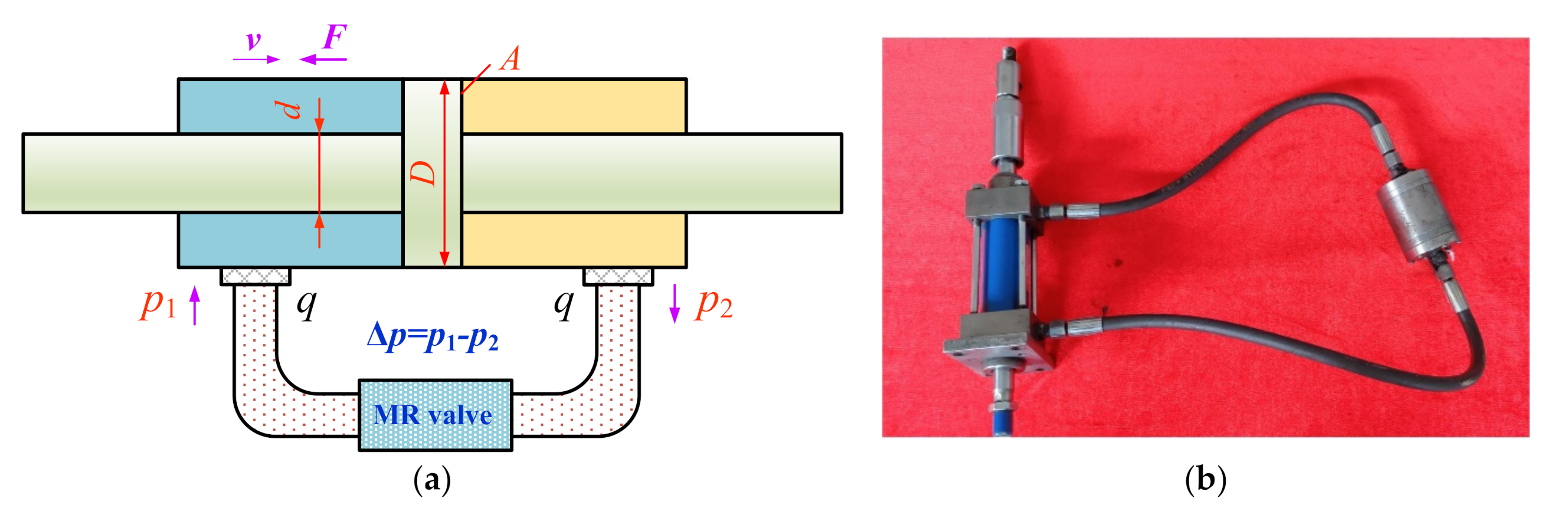
5.1. Test System of the Proposed MR Valve Controlled Cylinder System
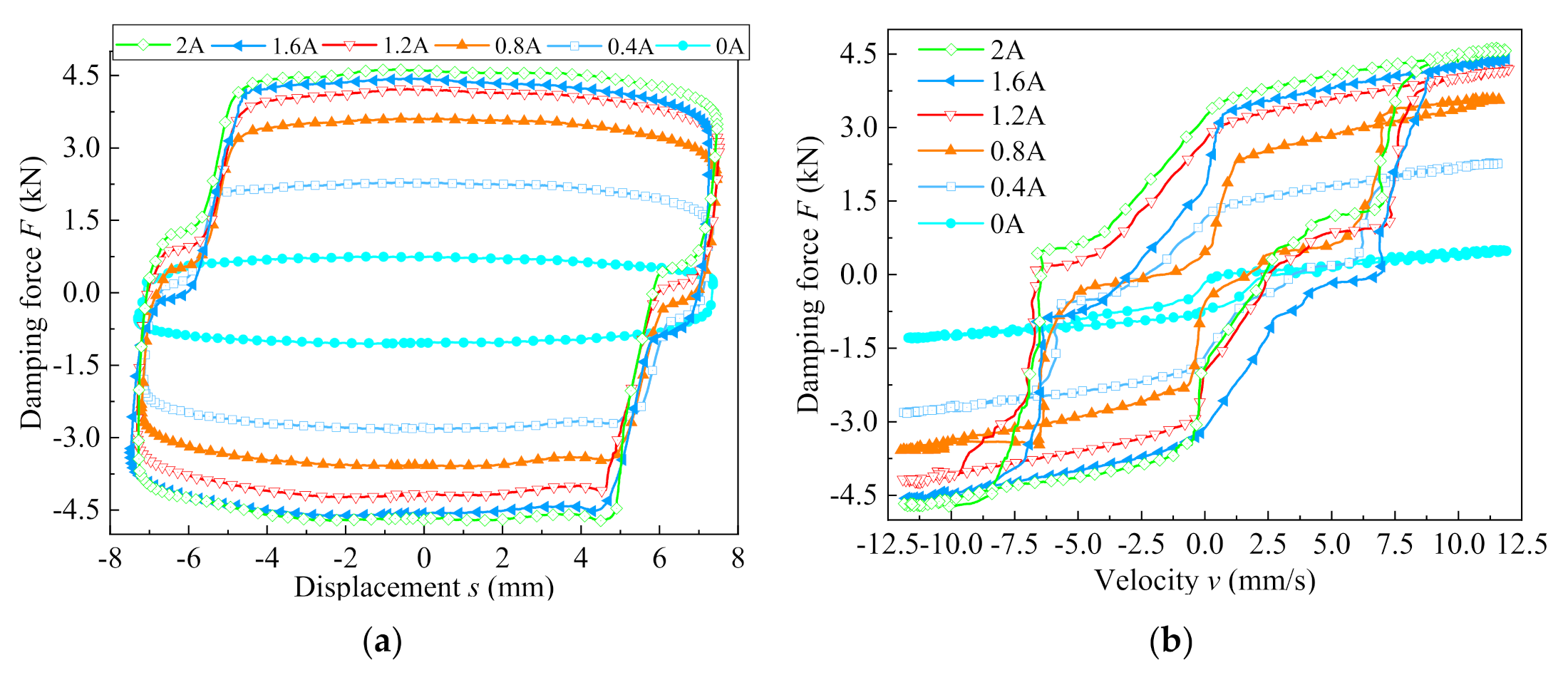
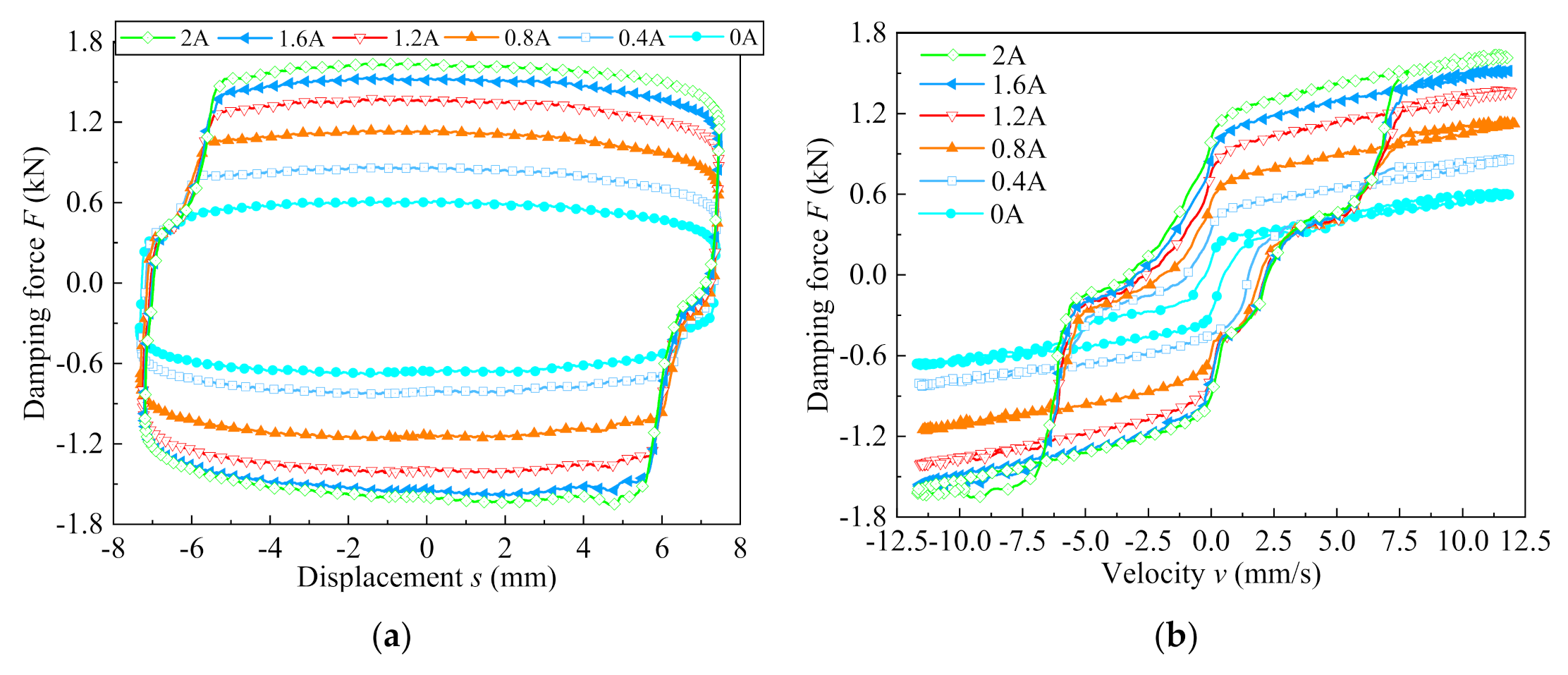
5.2. Dynamic Performance of the Valve Controlled Cylinder System at the Radial Gap of 0.5 mm
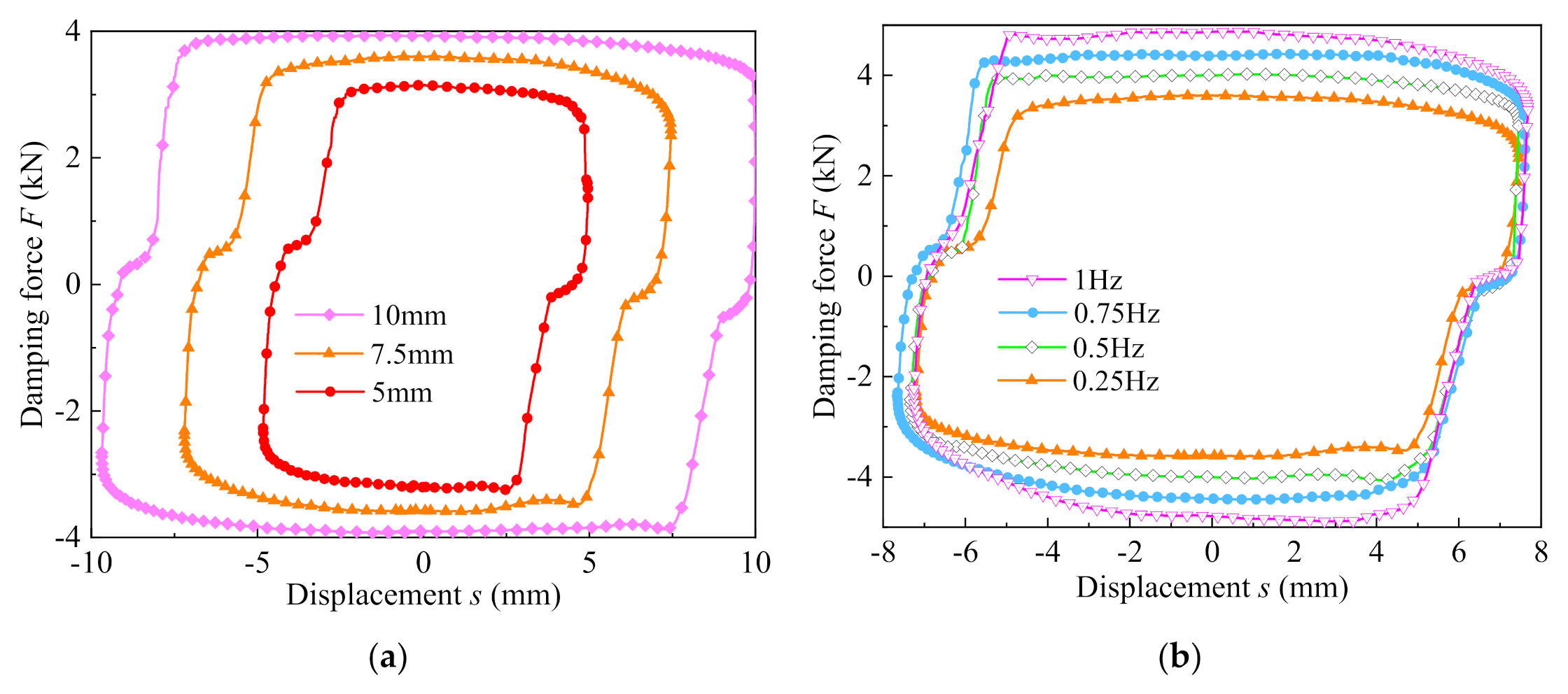
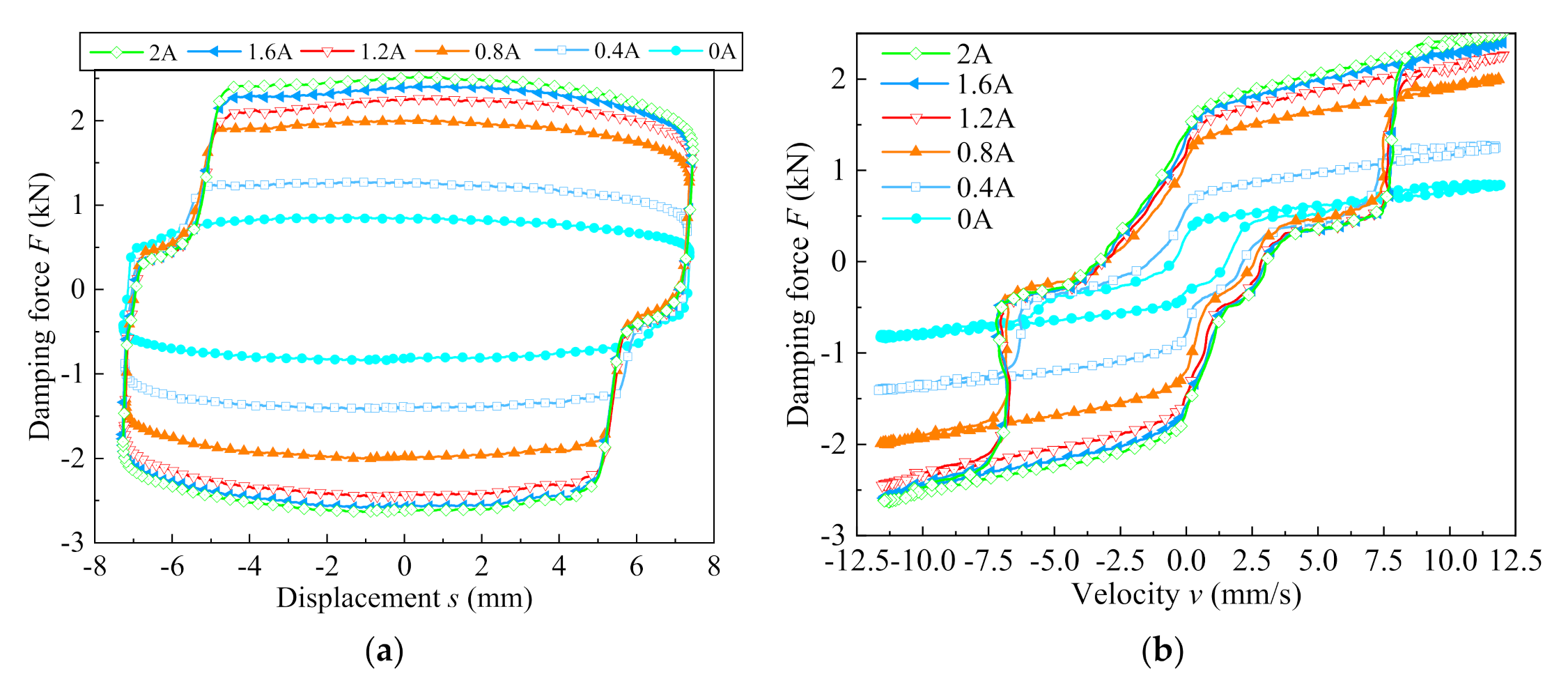
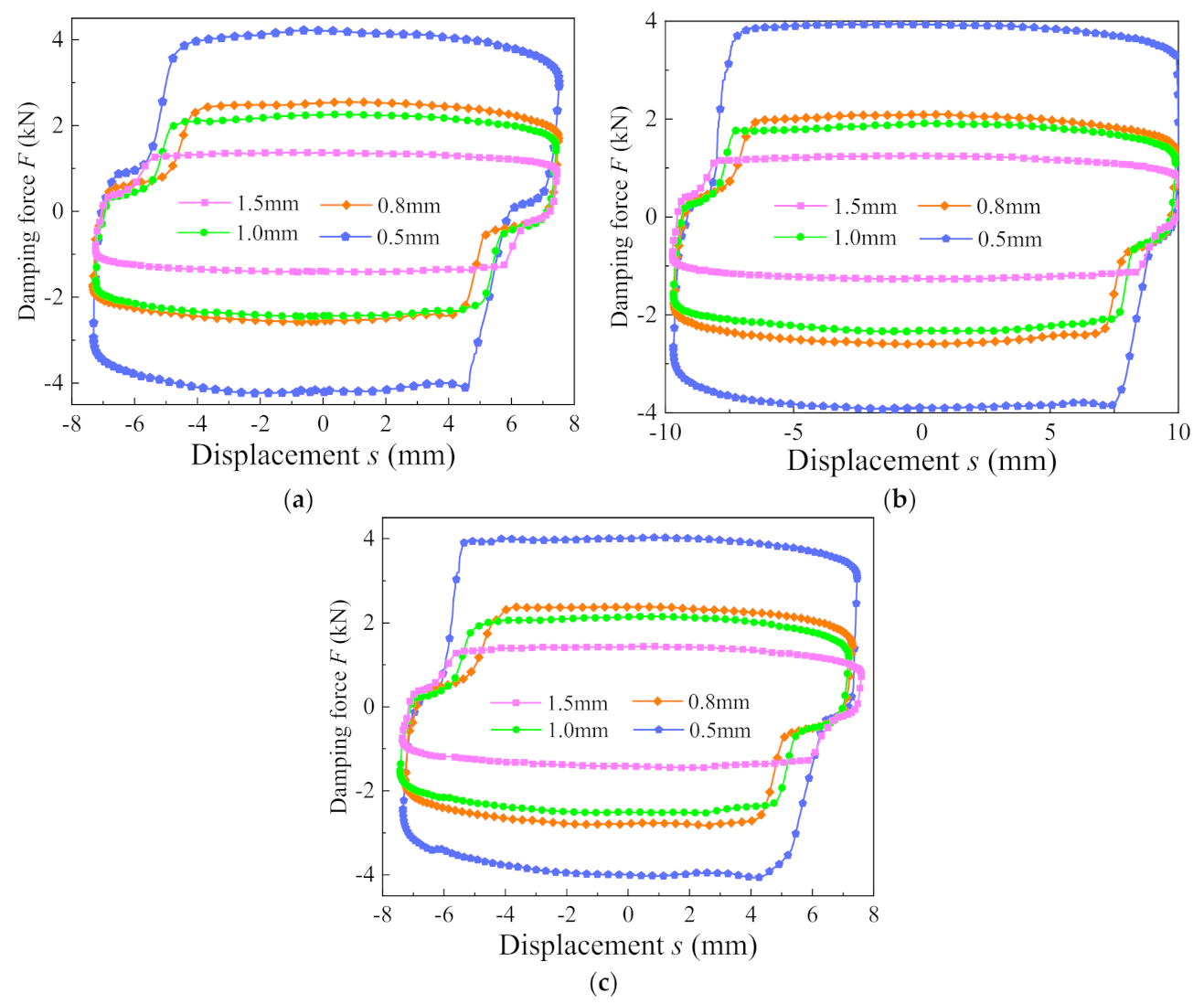
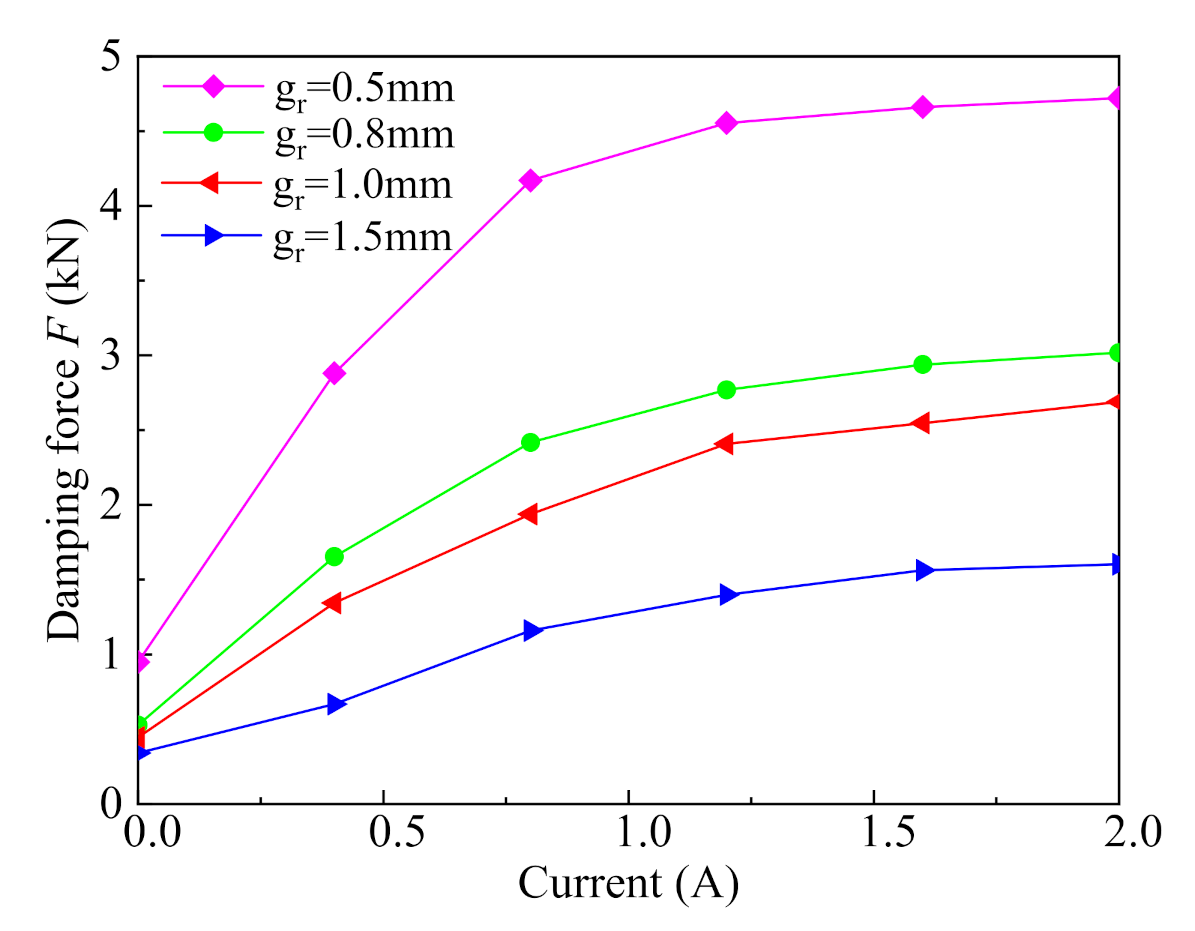
5.3. Dynamic Performance with Variable Radial Damping Gap
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A review of challenges and solutions in the preparation and use of magnetorheological fluids. Int. J. Mech. Mater. 2019, 14, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Cui, H.; Yang, J. A new modified model for the rheological properties of magnetorheological fluids based on different magnetic field. J. Magn. Magn. Mater. 2020, 500, 166377. [Google Scholar] [CrossRef]
- Ai, H.X.; Wang, D.H.; Liao, W.H. Design and modeling of a magnetorheological valve with both annular and radial flow paths. J. Intell. Mater. Syst. Struct. 2006, 17, 328–334. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhong, F.; Zhang, H.Y.; Ding, R.Q. Structure optimization and performance analysis of a multiple radial magnetorheological valve. J. Beijing Inst. Technol. 2017, 26, 458–467. [Google Scholar]
- Idris, M.H.; Imaduddin, F.; Mazlan, S.A.; Choi, S.B. A concentric design of a bypass magnetorheological fluid damper with a serpentine flux valve. Actuators 2020, 9, 16. [Google Scholar] [CrossRef]
- Hu, G.L.; Li, L.S.; Liu, H.; Liu, F.S. Effects of winding cylinder materials on dynamic performances of a new mr damper. IEEE Access 2020, 8, 87829–87841. [Google Scholar] [CrossRef]
- Bai, X.X.; Cai, F.; Chen, P. Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal Process. 2019, 117, 157–169. [Google Scholar] [CrossRef]
- Hu, G.L.; Wu, L.F.; Li, L.S.; Yu, L.F. Performance analysis of rotary magnetorheological brake with multiple fluid flow channels. IEEE Access 2020, 8, 173323–173335. [Google Scholar] [CrossRef]
- Sun, S.S.; Ning, D.H.; Yang, J. Development of an MR seat suspension with self-powered generation capability. J. Smart Mater. Struct. 2017, 26, 085025. [Google Scholar] [CrossRef]
- Bai, X.; Hu, W.; Wereley, N.M. Magnetorheological damper utilizing an inner bypass for ground vehicle suspensions. IEEE Trans. Magn. 2013, 4, 3422–3425. [Google Scholar] [CrossRef]
- Lee, T.H.; Shin, S.U.; Cha, S.W.; Choi, S.B. Fine position control of a vehicle maintenance lift system using a hydraulic unit activated by magnetorheological valves. J. Intell. Mater. Syst. Struct. 2019, 30, 896–907. [Google Scholar] [CrossRef]
- Ntella, S.L.; Duong, M.T.; Civet, Y.; Pataky, Z.; Perriard, Y. Design optimization of miniature magnetorheological valves with self-sensing capabilities used for a wearable medical application. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Boston, MA, USA, 6–9 July 2020; pp. 409–414. [Google Scholar]
- Grunwald, A.; Olabi, A.G. Design of magneto-rheological (MR) valve. Sens. Actuators A Phys. 2008, 148, 211–223. [Google Scholar] [CrossRef]
- Hu, G.L.; Long, M.; Huang, M.; Li, W.H. Design, Analysis, prototyping, and experimental evaluation of an efficient double coil magnetorheological valve. Adv. Mech. Eng. 2014, 6, 403410. [Google Scholar] [CrossRef]
- Sahin, H. Theoretical and Experimental Studies of Magnetorheological (MR) Fluids and MR Greases/Gels from Rheology to System Application; University of Nevada: Reno, NV, USA, 2008. [Google Scholar]
- Imaduddin, F.; Mazlan, S.A.; Zamzuri, H.; Yazid, I.I.M. Design and performance analysis of a compact magnetorheological valve with multiple annular and radial gaps. J. Intell. Mater. Syst. Struct. 2015, 26, 1038–1049. [Google Scholar] [CrossRef]
- Hu, G.L.; Long, M.; Yu, L.F.; Li, W.H. Design and performance evaluation of a novel magnetorheological valve with a tunable resistance gap. Smart Mater. Struct. 2014, 23, 127001. [Google Scholar] [CrossRef]
- Shou, M.j.; Liao, C.R.; Zhang, H.H.; Xie, L. A design methodology based on full dynamic model for magnetorheological energy absorber equipped with disc springs. Smart Mater. Struct. 2019, 28, 065020. [Google Scholar] [CrossRef]
- Armin, H.; Ramin, S.; Ebrahim, E. Design optimization of magnetorheological fluid valves using response surface method. J. Intell. Mater. Syst. Struct. 2013, 25, 1352–1371. [Google Scholar]
- Zhang, X.J.; Yang, Y.; Guo, K.H.; Sun, S.L.; He, G.J.; Li, Z.H. Methodology on a novel magnetorheological valve controlled damper synthesis design. Smart Mater. Struct. 2020, 29, 045006. [Google Scholar] [CrossRef]
- Manjeet, K.; Bhagyarajan, A.; Sujatha, C. Regression models for magnetic flux density using DoE techniques and geometric optimization of MR valve. Smart Mater. Struct. 2019, 28, 075008. [Google Scholar]
- Hu, G.L.; Liao, M.K.; Li, W.H. Analysis of a compact annular-radial-orifice flow magnetorheological valve and evaluation of its performance. J. Intell. Mater. Syst. Struct. 2017, 28, 1322–1333. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhang, J.W.; Liao, M.K.; Ding, R.Q. The effect of radial resistance gap on the pressure drop of a compact annular-radial-orifice flow magnetorheological valve. J. Beijing Inst. Technol. 2018, 27, 535–546. [Google Scholar]
- Hu, G.L.; Zhang, J.W.; Zhong, F.; Yu, L.F. Performance evaluation of an improved radial magnetorheological valve and its application in the valve controlled cylinder system. Smart Mater. Struct. 2019, 28, 047003. [Google Scholar] [CrossRef]
- Sahin, H.; Gordaninejad, F.; Wang, X.; Liu, Y.M. Response time of magnetorheological fluids and magnetorheological valves under various flow conditions. J. Intell. Mater. Syst. Struct. 2012, 23, 949–957. [Google Scholar] [CrossRef]
- Yoon, D.S.; Park, Y.J.; Choi, S.B. An eddy current effect on the response time of a magnetorheological damper: Analysis and experimental validation. Mech. Syst. Signal Process. 2019, 127, 136–158. [Google Scholar] [CrossRef]
| 1 | Thickness of positioning plate td |
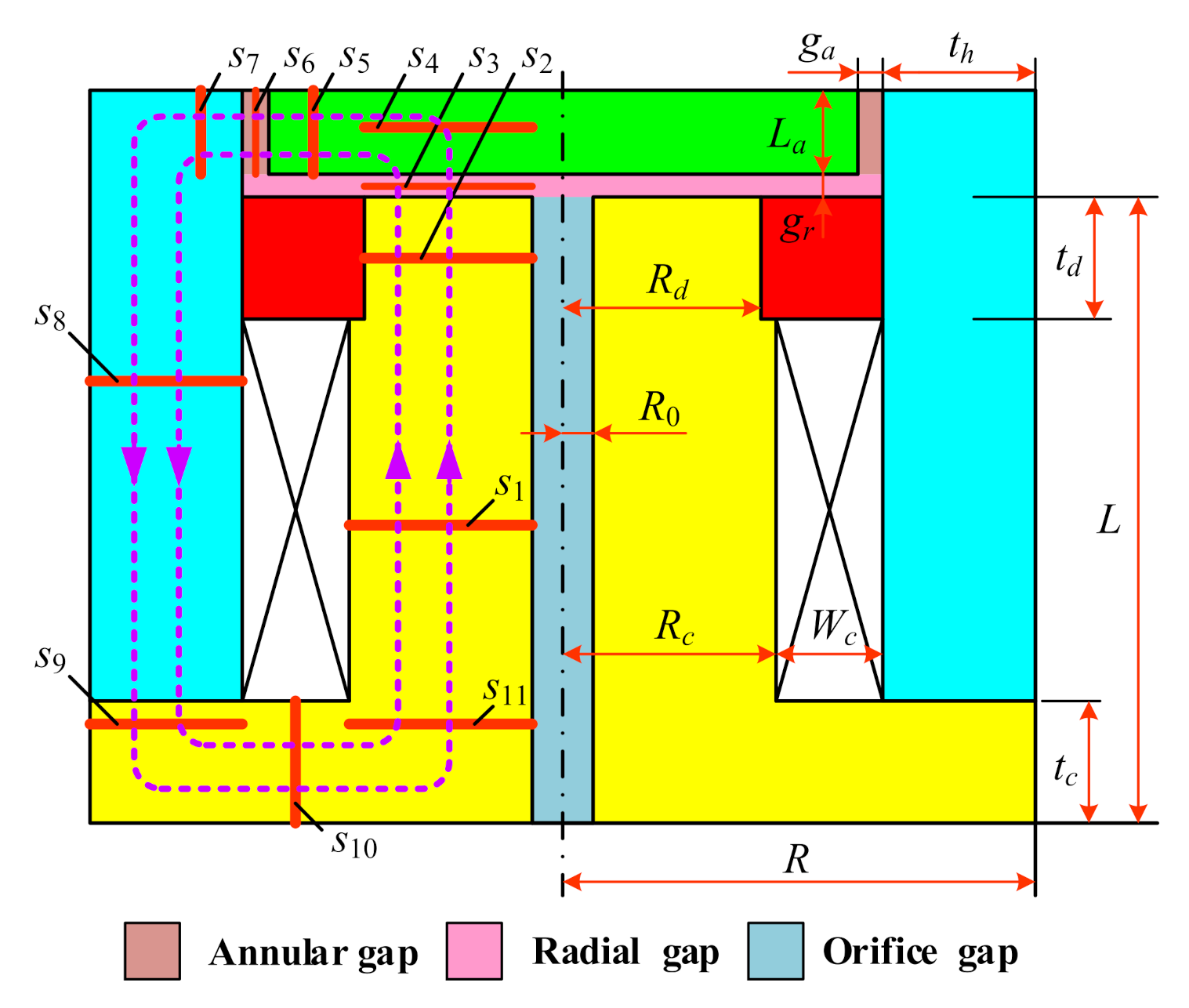


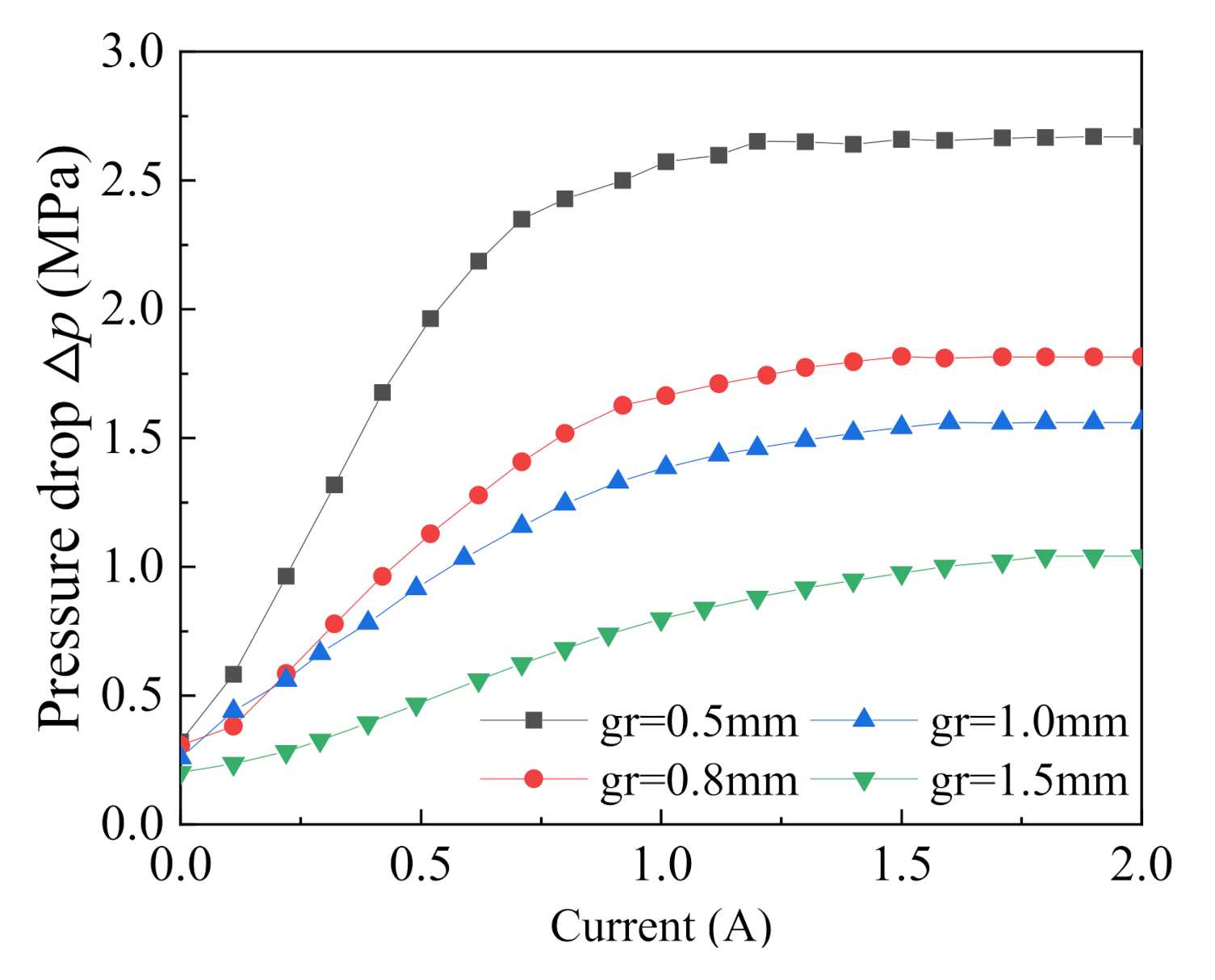
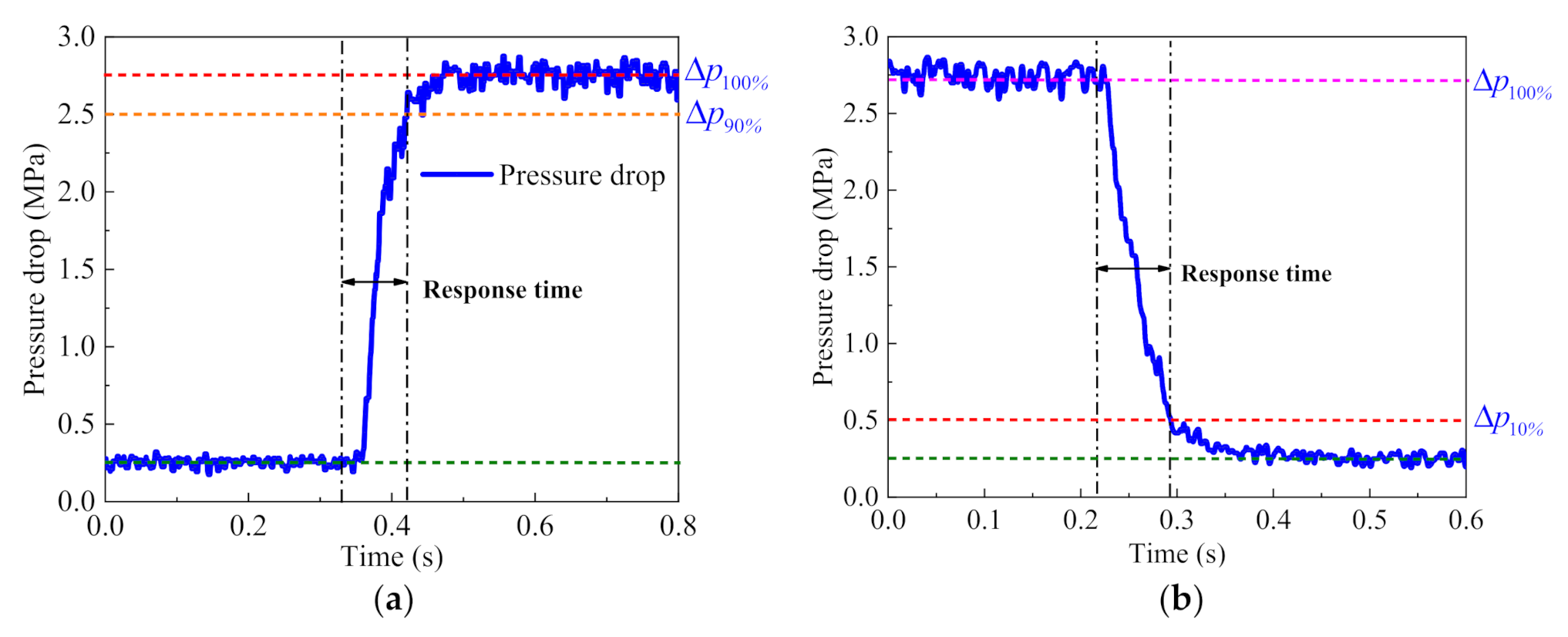

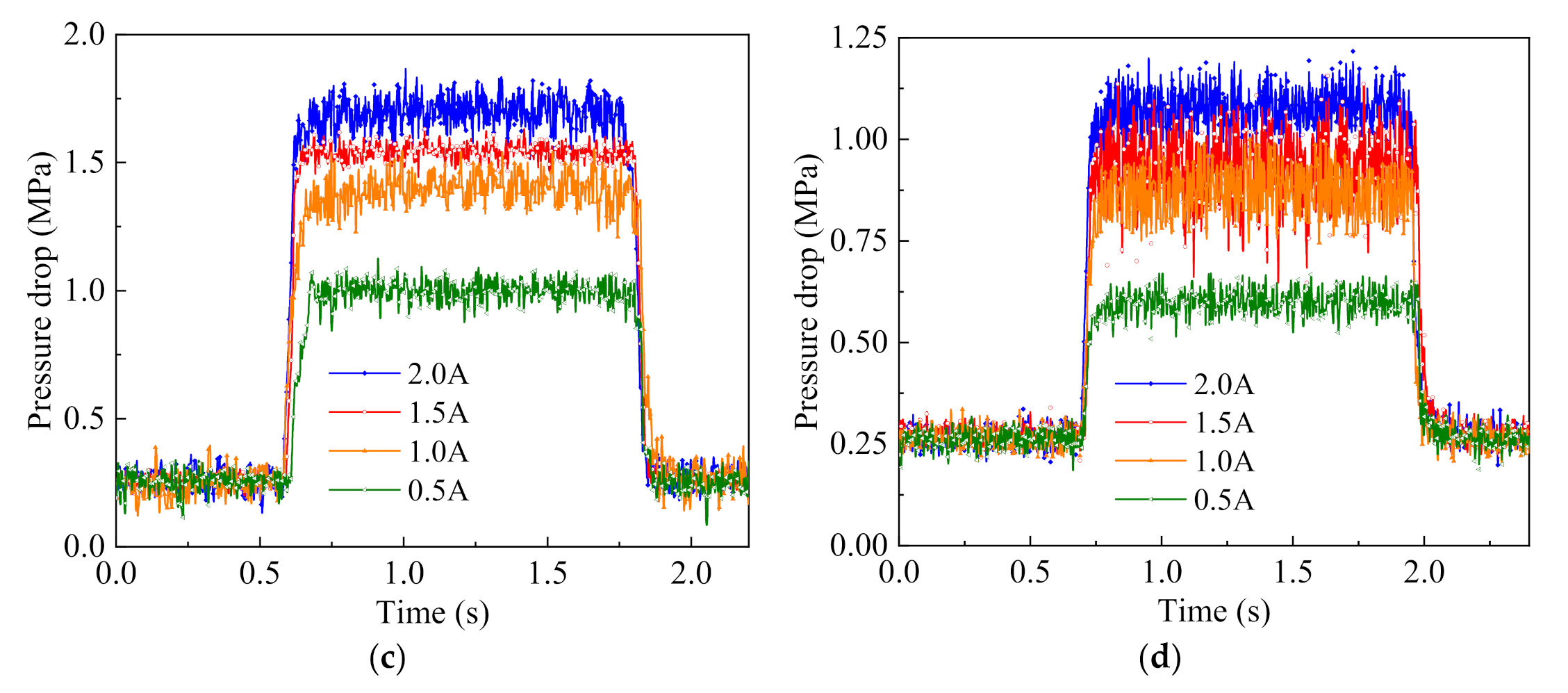

| Parameters | Values (mm) |
|---|---|
| Thickness of annular gap ga | 1 |
| Thickness of radial gap gr | 0.5~1.5 |
| Valve body thickness th | 10 |
| MR valve radius R | 31 |
| Valve spool length L | 41 |
| Thickness of winding groove Wc | 7 |
| Orifice radius R0 | 2 |
| Radius of left valve spool with screw thread Rd | 13 |
| Radius of left valve spool without screw thread Rc | 14 |
| Thickness of the right of valve spool tc | 8 |
| Annular gap length La | 4.2 |
| Radial gap length Lr | 11 |
| Thickness of positioning plate td | 8 |
| Current(A) | 0.5 mm | 0.8 mm | 1.0 mm | 1.5 mm | ||||
|---|---|---|---|---|---|---|---|---|
| trise | tfall | trise | tfall | trise | tfall | trise | tfall | |
| 0.5 | 119 ms | 129 ms | 98 ms | 114 ms | 88 ms | 108 ms | 65 ms | 69 ms |
| 1.0 | 134 ms | 128 ms | 110 ms | 117 ms | 96 ms | 123 ms | 72 ms | 80 ms |
| 1.5 | 153 ms | 133 ms | 117 ms | 120 ms | 109 ms | 120 ms | 79 ms | 76 ms |
| 2.0 | 176 ms | 138 ms | 122 ms | 119 ms | 119 ms | 128 ms | 85 ms | 89 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zhou, F.; Liao, M.; Yu, L. Dynamic Performance Analysis of a Compact Annular-Radial-Orifice Flow Magnetorheological Valve and Its Application in the Valve Controlled Cylinder System. Actuators 2021, 10, 104. https://doi.org/10.3390/act10050104
Hu G, Zhou F, Liao M, Yu L. Dynamic Performance Analysis of a Compact Annular-Radial-Orifice Flow Magnetorheological Valve and Its Application in the Valve Controlled Cylinder System. Actuators. 2021; 10(5):104. https://doi.org/10.3390/act10050104
Chicago/Turabian StyleHu, Guoliang, Feng Zhou, Mingke Liao, and Lifan Yu. 2021. "Dynamic Performance Analysis of a Compact Annular-Radial-Orifice Flow Magnetorheological Valve and Its Application in the Valve Controlled Cylinder System" Actuators 10, no. 5: 104. https://doi.org/10.3390/act10050104
APA StyleHu, G., Zhou, F., Liao, M., & Yu, L. (2021). Dynamic Performance Analysis of a Compact Annular-Radial-Orifice Flow Magnetorheological Valve and Its Application in the Valve Controlled Cylinder System. Actuators, 10(5), 104. https://doi.org/10.3390/act10050104






